A&A 431, 279-288 (2005)
DOI: 10.1051/0004-6361:20041917
Full computation of massive AGB evolution
I. The large impact of convection on nucleosynthesis
P. Ventura
-
F. D'Antona
Osservatorio Astronomico di Roma,
via Frascati 33, 00040 MontePorzio Catone, Italy
Received 27 August 2004 / Accepted 3 October 2004
Abstract
It is well appreciated that the description of overadiabatic convection
affects the structure of the envelopes of luminous asymptotic giant
branch (AGB) stars in the
phase of "hot bottom burning'' (HBB). We stress that this important
uncertainty in the modeling plays a role which is much more dramatic
than the role which can be ascribed, e.g., to the uncertainty in the
nuclear cross-sections. Due to the role tentatively attributed today to
the HBB nucleosynthesis as the site of self-enrichment of Globular
Clusters stars, it is necessary to explore the difference in
nucleosynthesis obtained by different prescriptions for convection.
We present results of detailed evolutionary calculations
of the evolution of stars of intermediate mass during the
AGB phase for the metallicity typical of the
Globular Clusters that show the largest spread in CNO abundances
(
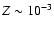 ). We follow carefully the nucleosynthesis at
the base of the external convective region,
showing that very different results can be obtained according to
the presciption adopted to find out the temperature gradient within
the instability regions. We discuss the uncertainties in
the yields of the various chemical species and the role which these
sources can play as polluters of the interstellar medium.
). We follow carefully the nucleosynthesis at
the base of the external convective region,
showing that very different results can be obtained according to
the presciption adopted to find out the temperature gradient within
the instability regions. We discuss the uncertainties in
the yields of the various chemical species and the role which these
sources can play as polluters of the interstellar medium.
Key words: stars: evolution -
stars: interiors -
stars: AGB and post-AGB -
stars: abundances
The intermediate mass stars (i.e. stars with initial masses
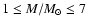 ,
hereinafter IMS) experience
a phase of thermal pulses (TPs) shortly after the exhaustion
of central helium (Schwarzschild & Harm 1965, 1967;
Iben 1975, 1976).
A CNO-burning shell supplies the global nuclear energy
for
,
hereinafter IMS) experience
a phase of thermal pulses (TPs) shortly after the exhaustion
of central helium (Schwarzschild & Harm 1965, 1967;
Iben 1975, 1976).
A CNO-burning shell supplies the global nuclear energy
for  90% of the time;
periodically, a thermal instability (associated with the
narrow dimensions of the helium-rich layer above the CO
degenerate core and with the steep dependence of the
cross-section of
90% of the time;
periodically, a thermal instability (associated with the
narrow dimensions of the helium-rich layer above the CO
degenerate core and with the steep dependence of the
cross-section of 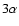 reactions on the temperature)
triggers a runaway-like ignition of helium burning, which
temporarily extinguishes the H-burning shell. As the mass
of the CO core increases, the CNO-burning shell becomes hotter
and hotter, so that the luminosity of the star increases: on
the HR diagram the evolutionary tracks climb the so called
"Asymptotic Giant Branch'' (hence the term "AGB evolution'',
commonly adopted). During their evolution these structures
suffer strong mass losses, which eventually stop their
AGB evolution, leaving just a central remnant which later
evolves into a CO white dwarf.
reactions on the temperature)
triggers a runaway-like ignition of helium burning, which
temporarily extinguishes the H-burning shell. As the mass
of the CO core increases, the CNO-burning shell becomes hotter
and hotter, so that the luminosity of the star increases: on
the HR diagram the evolutionary tracks climb the so called
"Asymptotic Giant Branch'' (hence the term "AGB evolution'',
commonly adopted). During their evolution these structures
suffer strong mass losses, which eventually stop their
AGB evolution, leaving just a central remnant which later
evolves into a CO white dwarf.
In the last decades the interest in the detailed
evolution of these stars
has grown, also because they have been suggested as
pollutors of the medium during the early phases
of evolution of globular clusters
(GCs), and responsible for the chemical anomalies
(in terms, e.g., of oxygen-sodium and
magnesium-aluminium anticorrelations) which are
observed in giants and turn-off stars of GCs.
At least in the latter because of the low temperatures
involved the chemical anomalies cannot be due
to "in-situ'' processes. The idea
behind this hypothesis (to which we usually
refer as "self-enrichment'') is that
the base of the external envelope of the
most massive IMS
during the AGB evolution may become so hot
(
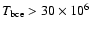 K) that it triggers strong
nucleosynthesis; the consequent changes in the originary
chemical abundances might easily reach the surface of the
star because of the rapidity of the convective motions, so that
the ejecta of these stars are contaminated by such
an advanced nucleosynthesis. The velocity of the ejected
material should be sufficiently low to survive ejection
from the cluster (D'Antona et al. 1983; Ventura et al.
2001, 2002).
K) that it triggers strong
nucleosynthesis; the consequent changes in the originary
chemical abundances might easily reach the surface of the
star because of the rapidity of the convective motions, so that
the ejecta of these stars are contaminated by such
an advanced nucleosynthesis. The velocity of the ejected
material should be sufficiently low to survive ejection
from the cluster (D'Antona et al. 1983; Ventura et al.
2001, 2002).
The self-pollution scenario is not without its shortcomings,
as pointed out by Denissenkov & Herwig (2003): the
temperatures needed to deplete oxygen would also
lead to sodium destruction, and to magnesium isotopic
ratios
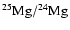 and
and
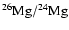 much larger than observed.
much larger than observed.
Unfortunately, the theoretical models for the
AGB evolution are characterized by several uncertainties
associated with the input physics which is commonly
adopted in the stellar evolutionary codes:
in the last decade the attention of modelists has
been mainly focused on: a) the amount of extra-mixing
from the base of the external region (Herwig 2000, 2004),
which favours a
larger efficiency of the so called third dredge-up
phenomenon (i.e. the external convective region which
reaches stellar layers previously touched by efficient
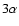 burning after a thermal pulse); b) the rate
of mass loss suffered by these stars; c) the nuclear
network adopted, particularly concerning the
nucleosynthesis of neon, sodium and magnesium isotopes.
burning after a thermal pulse); b) the rate
of mass loss suffered by these stars; c) the nuclear
network adopted, particularly concerning the
nucleosynthesis of neon, sodium and magnesium isotopes.
The present work does not discuss
the plausibility of the self-enrichment scenario, but
is aimed at pointing out quantitatively that,
before going into the details of the chemical composition
of the ejecta of AGBs, it is mandatory to understand
to which extent the results obtained depend on the
assumptions made in calculating the models.
We focus our attention on one of the most
relevant uncertainties connected with stellar evolution,
i.e. the treatment of convection, whose influence upon
AGB evolution in the context of HBB is well documented
in the literature, starting with the classic Renzini & Voli
(1981) paper, and with the discussion by Sackmann &
Boothroyd (1991) and Blöcker & Schönberner (1991).
Finally, D'Antona & Mazzitelli
(1996) discussed that the "Full Spectrum of Turbulence''
(FST, Canuto & Mazzitelli 1991) model for convection leads
to a much more efficient HBB than the Mixing Length Theory
(MLT). Neverthless, in these last years, no mention
has been made in many recent detailed computations
of the description adopted for convection, and,
more importantly, of the resulting uncertainty
in the nucleosynthesis.
We will compare the results obtained
with the two local models currently available, i.e.
MLT and the FST convective model; within the MLT
framework, we discuss the role played by the free
parameter 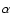 .
.
We show that the main physical properties of the models
depend strongly on the efficiency of convection, and
discuss the implications for the self-enrichment
scenario.
The stellar evolution models discussed
in this paper were calculated by
the code ATON, a full description of which can be found in
Ventura et al. (1998) (ATON2.0 version).
In this paper the interested reader may find
a detailed description of the numerical
structure of the code, and of the macro-
and micro-physics used to simulate the stellar
evolutions.
The code has now been updated concerning the nuclear
network, which has been widened in order to include more
chemical elements and nuclear reactions, according to
the detailed description given below. The current version is
therefore ATON2.1.
Here we briefly recall the most important input
data adopted.
The code allows us to calculate the temperature gradient
within instability regions either by adopting the
traditional MLT (Vitense 1953; Böhm-Vitense 1958),
or the FST model (Canuto & Mazzitelli 1991;
Canuto et al. 1996). The interested reader may
find a detailed
description of the physical differences between
the two models in Canuto & Mazzitelli (1991).
Briefly, we recall that within the MLT scheme both the
dimensions of the convective eddies and the mixing length
are assumed to be directly proportional to the local
value of 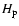 ,
the pressure scale height
(
,
the pressure scale height
(
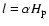 ); the free parameter
); the free parameter 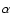 is calculated in order to reproduce the evolution of the
Sun. The most recent estimates give
is calculated in order to reproduce the evolution of the
Sun. The most recent estimates give
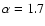 .
In the
FST model the mean dimension of the convective eddies
is found by integrating over the whole spectrum of the
dimensions, and the mixing length is simply assumed
to be l=z, the distance from the closest convective
boundary.
.
In the
FST model the mean dimension of the convective eddies
is found by integrating over the whole spectrum of the
dimensions, and the mixing length is simply assumed
to be l=z, the distance from the closest convective
boundary.
The differences between the results provided by the two
models can be summarized as follows:
-
within high-efficiency convective regions (i.e.
stellar regions where most of the energy is carried by
convection) the level of overadiabaticity
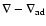 ,
(where
,
(where
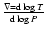 )
required by the FST models is lower;
)
required by the FST models is lower;
- within low-efficiency instability regions (e.g.
low density convective zones) the FST model exhibits
a superadiabaticity peak which is not found within
the MLT framework.
With respect to Ventura et al. (1998) the nuclear network has been
widened and now includes 30 chemicals: H, D,
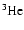 ,
,
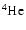 ,
,
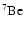 ,
,
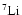 ,
,
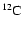 ,
,
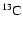 ,
,
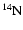 ,
,
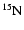 ,
,
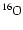 ,
,
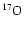 ,
,
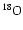 ,
,
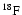 ,
,
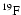 ,
,
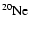 ,
,
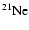 ,
,
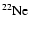 ,
,
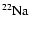 ,
,
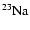 ,
,
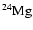 ,
,
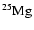 ,
,
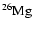 ,
,
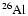 ,
,
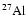 ,
,
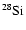 ,
,
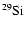 ,
,
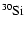 ,
,
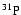 ,
,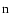 .
The nuclear reactions considered are 64. They include
all the main reactions of the p-p, CNO, Ne-Na and Mg-Al chains,
and the
.
The nuclear reactions considered are 64. They include
all the main reactions of the p-p, CNO, Ne-Na and Mg-Al chains,
and the 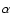 captures of all nuclei up to
captures of all nuclei up to
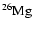 .
The relevant cross-sections can be taken
either from Caughlan & Fowler (1988) or from Angulo
et al. (1999).
.
The relevant cross-sections can be taken
either from Caughlan & Fowler (1988) or from Angulo
et al. (1999).
Since we expect a non-negligible fraction of the global
nuclear release to be generated within the convectively
unstable external regions, we decided to adopt for all the
evolution models presented here a diffusive algorithm
to deal with nuclear burning within convective regions,
in which nuclear burning and mixing of chemicals are
coupled self-consistently.
We therefore solve for each element the diffusion equation
(Cloutman & Eoll 1976):
![\begin{displaymath}\left( {{\rm d}X_i\over {\rm d}t} \right)=\left( {\partial X_...
... (4\pi r^2 \rho)^2 D {\partial X_i
\over \partial m_r}\right]
\end{displaymath}](/articles/aa/full/2005/07/aa1917/img46.gif) |
(1) |
stating mass conservation of element i. The diffusion coefficient D is
taken as
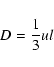 |
(2) |
where u is the convective velocity and l is the convective scale
length.
Within this diffusive framework it is necessary to specify the way
with which convective velocities decay outside the convective
boundaries (Deng at al. 1996a,b; Herwig et al. 1997;
Ventura et al. 1998).
In agreement with Xiong (1985) and Grossman (1996) and supported
by the numerical simulations by Freytag et al. (1996),
we assume that convective velocities decay exponentially
outside the formal convective boundary as:
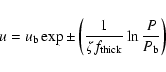 |
(3) |
where 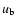 and
and 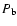 are, respectively, turbulent velocity and
pressure at the convective boundary, P is the local pressure,
are, respectively, turbulent velocity and
pressure at the convective boundary, P is the local pressure, 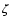 a free parameter connected with the e-folding distance of the decay,
and
a free parameter connected with the e-folding distance of the decay,
and
 is the thickness of the convective regions in
fractions of
is the thickness of the convective regions in
fractions of 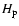 .
.
We computed three evolutions starting with
initial masses
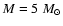 .
With the exception of the convective model, all the physical and
chemical input data adopted are the same, i.e.:
.
With the exception of the convective model, all the physical and
chemical input data adopted are the same, i.e.:
-
Since our purpose is to test how the uncertainties connected
with convection may reflect on the plausibility of the
"self-enrichment'' scenario, we adopt a chemistry which is
typical of those GCs which show most of self-enrichment like M 13,
NGC 6752 (Gratton et al. 2001; Sneden et al. 2004),
i.e. Z=0.001 and Y=0.24. For all chemicals
other than helium we adopted solar-scaled abundances.
- We assumed extra mixing from the external border of
any convective region as given by a parameter
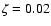 for the exponential decay of velocities starting from the formal
convective border; this is in agreement with the
calibration given in Ventura et al. (1998).
Since our purpose is to discuss the
uncertainties connected with the treatment of convection,
no inwards overshooting from the base of the
external convective region was adopted.
for the exponential decay of velocities starting from the formal
convective border; this is in agreement with the
calibration given in Ventura et al. (1998).
Since our purpose is to discuss the
uncertainties connected with the treatment of convection,
no inwards overshooting from the base of the
external convective region was adopted.
- For mass loss, Blöcker's (1995) prescription was used
in all cases: the free parameter
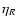 entering
Blöcker's formula was set to
entering
Blöcker's formula was set to
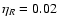 ,
in agreement with
the calibration for mass loss during the AGB evolution
given in Ventura et al. (2000).
,
in agreement with
the calibration for mass loss during the AGB evolution
given in Ventura et al. (2000).
- The Angulo et al. (1999) cross-sections were used.
-
Two models were calculated with an MLT treatment of convection
with parameters
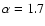 (MLT17 model) and
(MLT17 model) and
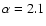 (MLT21 model). We also calculated an evolution model
with the FST convective prescription (FST model).
(MLT21 model). We also calculated an evolution model
with the FST convective prescription (FST model).
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{1917fig1.eps} %
\end{figure}](/articles/aa/full/2005/07/aa1917/Timg58.gif) |
Figure 1:
The tracks in the HR diagram of three models
with initial mass
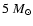 calculated with three
different tretaments of convection. Full: FST models;
dotted: MLT model with
calculated with three
different tretaments of convection. Full: FST models;
dotted: MLT model with
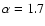 ;
dashed: MLT
model with ;
dashed: MLT
model with
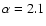 . . |
| Open with DEXTER |
Figure 1 shows the tracks in the HR diagram corresponding to
the three evolution models discussed above.
We note that the tracks are
very similar during the two major phases of nuclear burning within
the central regions, because convection within burning cores is
so efficient that the gradient is practically adiabatic,
independently
of the convective model. The only differences can be noticed
in the colors of the red giant branch (RGB) and the early AGB
evolution. These are the regions of the HR diagram where the
stars develop a very extended convective envelope,
in which a great part of the energy is carried by
radiation because of the low convective
efficiency: in these cases the temperature gradient
from the CNO-burning shell to the surface
(hence the effective temperature of the star) depends
sensibly on the convective model adopted.
A full discussion of the dependency on the
convective model of the effective temperature of IMS
during various evolutionary phases can
be found in Ventura & Castellani (2005).
What is most interesting here is that the main physical
properties and the duration of the various evolutionary
phases are approximately the same for the three models,
because in any case the nuclear sources
are either well within regions of radiative stability,
or inside central cores where the convective efficiency
is extremely high, making the gradient almost adiabatic.
The phase of H-burning lasts 90 Myr; during it the star develops a
central convective core of 
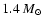 ,
which progressively
shrinks in mass until H-burning is extinguished in the central
regions.
Soon after hydrogen exhaustion the star expands, and surface
convection reaches inner layers which were previously at least
partly touched by nuclear burning (first dredge-up). The
lowest point (in mass) reached by the base of the
external envelope is for all the three models
,
which progressively
shrinks in mass until H-burning is extinguished in the central
regions.
Soon after hydrogen exhaustion the star expands, and surface
convection reaches inner layers which were previously at least
partly touched by nuclear burning (first dredge-up). The
lowest point (in mass) reached by the base of the
external envelope is for all the three models

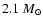 away from the centre; the whole duration
of this phase is
away from the centre; the whole duration
of this phase is  70 000 yr.
70 000 yr.
Shortly afterwards the central core becomes hot enough
to ignite 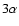 reactions. During helium burning the
star develops a central convective core of
reactions. During helium burning the
star develops a central convective core of

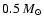 ;
the total duration of this phase
for the three models discussed is
;
the total duration of this phase
for the three models discussed is  12 Myr.
12 Myr.
After the central helium exhaustion, 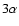 reactions
operate in an intermediate layer above the core of carbon
and oxygen. All the stellar layers above this He-burning
shell expand, and the CNO-burning shell is temporarily
extinguished. Convection penetrates inwards, reaching a
layer which is
reactions
operate in an intermediate layer above the core of carbon
and oxygen. All the stellar layers above this He-burning
shell expand, and the CNO-burning shell is temporarily
extinguished. Convection penetrates inwards, reaching a
layer which is
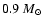 away from the centre (second
dredge-up).
The total duration of this phase of inner penetration
of surface convection is 0.55 Myr, after which
the CNO-burning shell is activated again, and the star
begins the AGB evolution.
away from the centre (second
dredge-up).
The total duration of this phase of inner penetration
of surface convection is 0.55 Myr, after which
the CNO-burning shell is activated again, and the star
begins the AGB evolution.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1917fig2.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg63.gif) |
Figure 2:
The variation with time of
the temperature at the base of the convective envelope
( top), luminosity due to helium burning ( middle), and core mass ( bottom)
of a
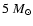 FST model during the AGB evolution.
Time was counted from the beginning of the AGB evolution.
FST model during the AGB evolution.
Time was counted from the beginning of the AGB evolution. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1917fig3.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg64.gif) |
Figure 3:
The variation with time of luminosity ( top),
mass loss rate ( middle) and total mass ( bottom)
of the model presented in Fig. 2. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1917fig4.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg65.gif) |
Figure 4:
Evolution with time of surface
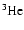 ( top),
lithium ( middle) and fraction of nuclear energy due to
proton-proton reactions ( bottom) of the FST
model presented in Fig. 2.
( top),
lithium ( middle) and fraction of nuclear energy due to
proton-proton reactions ( bottom) of the FST
model presented in Fig. 2. |
| Open with DEXTER |
Shortly after the second dredge-up the external layers
of the star contract and heat, thus favouring the re-ignition
of the CNO-burning shell. Hereinafter, the CNO cycle will
be the only nuclear source supporting the star, with
the only exception of the contribution of a 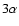 burning shell which once every
burning shell which once every  3000 yr is
ignited in a thermally unstable way, leading to a
thermal pulse (TP).
3000 yr is
ignited in a thermally unstable way, leading to a
thermal pulse (TP).
Figures 2-4 show the temporal evolution of
some physical quantities related to the evolution
of the FST model with initial mass
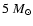 .
We note a rapid increase of the stellar luminosity
(Fig. 3, top panel), which is
associated with the fast increase of
.
We note a rapid increase of the stellar luminosity
(Fig. 3, top panel), which is
associated with the fast increase of
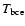 (Fig. 2, top panel), which is
almost doubled after three TPs. We will see that
the rapidity of this rise is strongly dependent on the
convective model adopted.
(Fig. 2, top panel), which is
almost doubled after three TPs. We will see that
the rapidity of this rise is strongly dependent on the
convective model adopted.
The periodic strong drop of the global luminosity and of
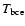 marks the ignition of TPs, which trigger an
expansion of the layers above the helium burning shell
with the consequent stop of CNO burning and shrinking
of the surface convective envelope.
marks the ignition of TPs, which trigger an
expansion of the layers above the helium burning shell
with the consequent stop of CNO burning and shrinking
of the surface convective envelope.
The CNO luminosity is generated in a shell which is
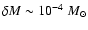 wide, and which
progressively moves outwards, burning at higher
and higher gravities and temperatures: this determines
the increase of luminosity shown in the upper panel
of Fig. 3, which is eventually
halted by the strong mass loss, which reduces the
mass of the envelope, as can be seen in the bottom
panel of Fig. 3. In the same figure we
see the rapid increase of the mass loss with
luminosity (middle panel):
within Blöcker (1995) prescription,
and with the adopted value of the free parameter
wide, and which
progressively moves outwards, burning at higher
and higher gravities and temperatures: this determines
the increase of luminosity shown in the upper panel
of Fig. 3, which is eventually
halted by the strong mass loss, which reduces the
mass of the envelope, as can be seen in the bottom
panel of Fig. 3. In the same figure we
see the rapid increase of the mass loss with
luminosity (middle panel):
within Blöcker (1995) prescription,
and with the adopted value of the free parameter 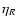 ,
we see that a maximum value of
,
we see that a maximum value of

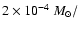 yr is attained,
almost in conjunction with the maximum luminosity
of the star.
Therefore, the rapidity with which the
luminosity increases plays a fundamental role
in determining the total duration of the whole
AGB evolution, triggering a fast reduction
of the mass of the envelope. For the model discussed here,
we see that the AGB phase lasts
yr is attained,
almost in conjunction with the maximum luminosity
of the star.
Therefore, the rapidity with which the
luminosity increases plays a fundamental role
in determining the total duration of the whole
AGB evolution, triggering a fast reduction
of the mass of the envelope. For the model discussed here,
we see that the AGB phase lasts  70 000 yr.
70 000 yr.
For a few TPs we note from the bottom panel of
Fig. 4 that a non-negligible
fraction of the nuclear energy release
is due to the proton-proton (p-p) chain:
during the 4th interpulse phase this latter
channel provides  10% of the luminosity
of the star. This is due essentially
to
10% of the luminosity
of the star. This is due essentially
to
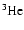 burning at the base of the external
envelope (see the top panel of Fig. 4),
which becomes efficient as soon as the
temperature reaches
burning at the base of the external
envelope (see the top panel of Fig. 4),
which becomes efficient as soon as the
temperature reaches 
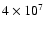 K.
The p-p contribution becomes negligible
as soon as the surface
K.
The p-p contribution becomes negligible
as soon as the surface
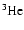 is all burnt (bottom panel).
We also note that this is associated with the lithium
production via the Cameron & Fowler (1971) mechanism,
as can be seen by the large increase of the
surface lithium abundance shown in the middle
panel of the same figure. The end of
is all burnt (bottom panel).
We also note that this is associated with the lithium
production via the Cameron & Fowler (1971) mechanism,
as can be seen by the large increase of the
surface lithium abundance shown in the middle
panel of the same figure. The end of
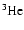 burning at the base of the convective envelope
is associated with the temporary plateau in the global
luminosity rising which can be detected in the
top panel of Fig. 3, after
burning at the base of the convective envelope
is associated with the temporary plateau in the global
luminosity rising which can be detected in the
top panel of Fig. 3, after
 12 000 yr.
12 000 yr.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1917fig5.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg70.gif) |
Figure 5:
Evolution with time of the surface chemical
abundances of the CNO elements ( top) and of some
neon, sodium and magnesium isotopes ( bottom) of
the FST model presented in Fig. 2. |
| Open with DEXTER |
We end this general description of AGB evolution
with a glance at the nucleosynthesis at the base
of the convective envelope: we recall that convection
is generally extremely fast in homogenizing the whole
external region; therefore the ejecta of these stars
are practically determined by the changes of the
chemical abundances at the base of the external zone.
We note from the top panel of Fig. 5 that
for the first  15 000 yr the oxygen abundance
is unchanged, while
15 000 yr the oxygen abundance
is unchanged, while
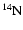 is produced at the
expenses of
is produced at the
expenses of
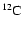 :
this is the signature of a
CN cycle, which is operating at temperatures not
exceeding
:
this is the signature of a
CN cycle, which is operating at temperatures not
exceeding 
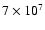 K. Later on,
when
K. Later on,
when
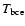 exceeds
exceeds 
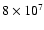 K, oxygen is depleted
at the base of the envelope, with the consequent
increase of the
K, oxygen is depleted
at the base of the envelope, with the consequent
increase of the
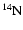 and
and
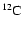 abundances.
After
abundances.
After  15 TPs, we can cleary see the signature
of the Third Dredge-Up (TDU) in the strong increase of the
surface
15 TPs, we can cleary see the signature
of the Third Dredge-Up (TDU) in the strong increase of the
surface
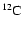 abundance following each TP.
More precisely, we find the first TDU episode
after 13 TPs; the efficiency parameter
abundance following each TP.
More precisely, we find the first TDU episode
after 13 TPs; the efficiency parameter 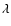 (defined as the ratio between the mass which is
dredged up following each TP and the mass gained
by the H-exhausted region since the precedent TP)
reaches an asymptotic value of
(defined as the ratio between the mass which is
dredged up following each TP and the mass gained
by the H-exhausted region since the precedent TP)
reaches an asymptotic value of
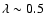 after 19 TPs.
after 19 TPs.
These results confirm, at least
within the FST framework,
the possibility of attaining deep oxygen burning
at the base of the external convective zone of these
stars: the final
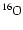 abundance is >10 times
lower, while the ejecta would have an
average oxygen content a factor of
abundance is >10 times
lower, while the ejecta would have an
average oxygen content a factor of  3 lower
than the initial abundance.
3 lower
than the initial abundance.
From the bottom panel of Fig. 5 we see an
early phase of
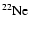 destruction, which favours
a temporary production of sodium, increased by another
factor of
destruction, which favours
a temporary production of sodium, increased by another
factor of  2 (in the comparison of the current
sodium abundance with the initial value, we must
recall that the second dredge-up had already favoured
a sodium increase of a factor
2 (in the comparison of the current
sodium abundance with the initial value, we must
recall that the second dredge-up had already favoured
a sodium increase of a factor  3). Shortly
after the beginning of oxygen depletion, the
surface sodium abundance starts decreasing due to
the NeNa chain.
3). Shortly
after the beginning of oxygen depletion, the
surface sodium abundance starts decreasing due to
the NeNa chain.
Later on, when TDU becomes operative, a considerable
amount of
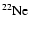 is carried outwards to the surface
following each TP: this favours sodium production
again, as we see in the bottom panel of Fig. 5.
The overall sodium abundance of the ejecta would be
sligtly lower than the initial value.
is carried outwards to the surface
following each TP: this favours sodium production
again, as we see in the bottom panel of Fig. 5.
The overall sodium abundance of the ejecta would be
sligtly lower than the initial value.
Finally, we note that
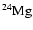 is also depleted at
the base of the external convective zone: the final
abundance is lower with respect to the initial
value by a factor of
is also depleted at
the base of the external convective zone: the final
abundance is lower with respect to the initial
value by a factor of  20.
20.
We stressed in Sect. 3 that prior to the TPs phase
the three evolutions are very similar.
Here we focus our attention
on the AGB phase, keeping in mind that at the
beginning of this phase the structures of the three
models are practically identical.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1917fig6.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg75.gif) |
Figure 6:
The comparison of the temporal variation of
the luminosity of three
models with initial mass
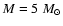 calculated with
three different prescriptions for the treatment of the
regions unstable to convection.
calculated with
three different prescriptions for the treatment of the
regions unstable to convection. |
| Open with DEXTER |
In Fig. 6 we show the variation with time
of the luminosity for the three models discussed.
We see a large difference starting already at the first
TPs; the more efficient the convective model is, the more
rapid is the increase of luminosity as the evolution proceeds.
We see that the FST model achieves a maximum luminosity
which is  70% larger than the corresponding value of
the MLT17 model.
70% larger than the corresponding value of
the MLT17 model.
This behaviour can be seen as an extreme case of the
break-down of the core mass vs. luminosity
relation which occurs when the hydrogen burning
region is not detached from the convective region
(Tuchman et al. 1983; Blöcker & Schönberner
1991).
Such a large difference in the evolution of luminosity
is inevitably reflected in the mass loss rate:
we see from Fig. 7 a much faster
consumption for the FST model, which loses
the whole envelope within  70 000 yr, to be
compared to the
70 000 yr, to be
compared to the  130 000 yr associated to the
MLT21 model, and
130 000 yr associated to the
MLT21 model, and  200 000 yr of the MLT17
model. We therefore can see that the
duration of the whole AGB phase may
differ by a factor of
200 000 yr of the MLT17
model. We therefore can see that the
duration of the whole AGB phase may
differ by a factor of  3 according to the
convective model adopted.
3 according to the
convective model adopted.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{1917fig7.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg76.gif) |
Figure 7:
The variation with time of the total mass
of the models shown in Fig. 6. |
| Open with DEXTER |
Before entering into the details of the consequences
which these differences may have for the chemistry
of the ejecta, hence for the way in which these sources
pollute the interstellar medium, we examine the
reasons for such large differences.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1917fig8.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg77.gif) |
Figure 8:
The variation with time of the total
luminosity ( top) and of the maximum CNO nuclear
energy release ( bottom) for the three models
discussed in Fig. 6. Only the early
evolution along the AGB is shown. |
| Open with DEXTER |
We show in Fig. 8 the comparison
between the evolution of the three models,
limited to the first 10 000 yr of AGB, or,
equivalently, the first 3-4 TPs.
The upper panel shows the total luminosity of the star,
in the bottom panel we report the maximum
value of the CNO-burning coefficient for nuclear energy
release. While the latter quantity is
very similar for each of the three models, the luminosities
diverge. We may therefore conclude that while the
internal structure of the models in terms of
thermal stratification and chemical profile
is similar up to the CNO-burning shell, some
difference must arise in the immediate proximity
of the latter, close to the inner boundary of the
convective envelope.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1917fig9.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg78.gif) |
Figure 9:
The internal nuclear structure of the
models presented in Fig. 6 at the
maximum luminosity between the 3rd and 4th
TPs. The abscissa gives the distance
(in solar masses) from the centre of
the star, and the ordinate
shows the coefficient for nuclear energy release.
The thin vertical lines indicate the location of
the inner border of the convective envelope. |
| Open with DEXTER |
To better clarify this point, we show in
Fig. 9 the interior stratifications
of the coefficient for the nuclear energy release;
for all the three models the figure refers to
the point of maximum luminosity during the
fourth interpulse phase,  9000 yr
after the beginning of the AGB evolution.
The mass coordinate of the MLT17 and MLT21
models has been artificially shifted
in order to have the peak value of
9000 yr
after the beginning of the AGB evolution.
The mass coordinate of the MLT17 and MLT21
models has been artificially shifted
in order to have the peak value of
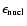 at the same abscissa. This
shift is much less than
at the same abscissa. This
shift is much less than
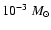 .
The thin
vertical lines indicate the
location of the bottom of the convective envelope
for each model.
.
The thin
vertical lines indicate the
location of the bottom of the convective envelope
for each model.
![\begin{figure}
{
\includegraphics[width=7cm,clip]{1917fig10.eps}\hspace*{4mm}
\includegraphics[width=7cm,clip]{1917fig11.eps} }
\par\end{figure}](/articles/aa/full/2005/07/aa1917/Timg81.gif) |
Figure 10:
Internal distribution of radiative gradient
( left), and temperature ( right) for the same
models shown in Fig. 9. |
| Open with DEXTER |
For each of the three models we see a very similar
behaviour. In the proximity of the
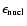 peak
there is a secondary maximum
at the border of the surface convection, which carries
peak
there is a secondary maximum
at the border of the surface convection, which carries
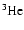 -rich material into the CNO-burning shell;
during these first TPs, as already discussed in
Sect.4, the p-p contribution is non-negligible
(see the bottom panel of Fig. 4).
Also, we see a secondary maximum
-rich material into the CNO-burning shell;
during these first TPs, as already discussed in
Sect.4, the p-p contribution is non-negligible
(see the bottom panel of Fig. 4).
Also, we see a secondary maximum 
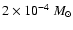 away, which is entirely due to
lithium burning; the contribution of the latter
to the overall energy release, however, is
negligible.
away, which is entirely due to
lithium burning; the contribution of the latter
to the overall energy release, however, is
negligible.
If we compare the three models, we note a
strong similarity up to the peak of the shell
and just beyond, with the only
difference that the location of the inner
border of the convective external zone is
closer to the CNO peak within the FST model,
while it is a few
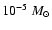 further
away in the MLT17 case; the MLT21 model is
intermediate. The proximity of
the convective border to the CNO peak
carries more
further
away in the MLT17 case; the MLT21 model is
intermediate. The proximity of
the convective border to the CNO peak
carries more
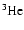 within a region whose
temperature is typical of CNO-burning regions
(
within a region whose
temperature is typical of CNO-burning regions
(
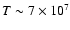 K), thus triggering a
considerable extra luminosity.
This extra contribution is smaller the more
distant the CNO peak and the base of the
envelope are, and it is practically negligible
within the MLT17 model.
K), thus triggering a
considerable extra luminosity.
This extra contribution is smaller the more
distant the CNO peak and the base of the
envelope are, and it is practically negligible
within the MLT17 model.
From the above discussion it becomes evident
that in understanding the different
luminosities of the models, despite
the similarity characterizing their structures
up to the CNO-burning shell, a key role is
played by the exact location of the inner border
of the convective envelope, or, equivalently, its
distance from the peak of the CNO shell.
Within the framework of the Schwartzschild's
criterion, which is used to fix the neutrality
point according to the condition
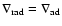 ,
the location of the border is
furhter inward the steeper the
,
the location of the border is
furhter inward the steeper the
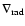 profile towards the external layers.
profile towards the external layers.
The comparison of the variations
of the
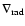 within the three models
presented in Fig. 9 is reported
in the left panel of Fig. 10.
We see in all cases that
within the three models
presented in Fig. 9 is reported
in the left panel of Fig. 10.
We see in all cases that
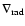 increases from the peak of the shell,
because of the rapid decrease of temperature
and pressure and the increase of the opacity;
near the convective region the
FST
increases from the peak of the shell,
because of the rapid decrease of temperature
and pressure and the increase of the opacity;
near the convective region the
FST
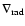 profile keeps the same slope,
while the MLT models, particularly MLT17,
become progressively flatter, thus moving
the neutral point, where
profile keeps the same slope,
while the MLT models, particularly MLT17,
become progressively flatter, thus moving
the neutral point, where
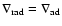 ,
outwards.
,
outwards.
The reason for this behaviour can be found in the
difference in the efficiency of the three convective
models, and the relative effect on the temperature
profile. It is well known that the FST model is more
efficient in high-efficiency convective regions, thus
requiring a lower degree of overadiabaticity to carry
the same amount of energy flux by convection: in
the layers next to the inner border of surface
convection shown in Fig. 9 the FST
overadiabaticity is  0.8 dex smaller.
In a small region very close to the border the
trend is reversed, because the MLT models attain an
extremely low level of overadiabaticy: this is due
to a physical inconsistency of the MLT assumption
that the mixing length is proportional to
0.8 dex smaller.
In a small region very close to the border the
trend is reversed, because the MLT models attain an
extremely low level of overadiabaticy: this is due
to a physical inconsistency of the MLT assumption
that the mixing length is proportional to 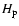 ,
which is meaningless near the border,
where the same quantity is expected to vanish, as
is consistently described in the FST
,
which is meaningless near the border,
where the same quantity is expected to vanish, as
is consistently described in the FST![[*]](/icons/foot_motif.gif) .
.
Within the instability regions, the fraction of
energy which is carried by radiation decreases
more rapidly in the FST than in
the MLT models; the necessity of keeping the
radiative flux
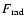 higher requires a lower and
flatter profile of
higher requires a lower and
flatter profile of
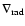 (we recall that
(we recall that
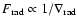 );
it is the necessity of matching this profile within
the convective region which forces the MLT radiative
gradient profile to bend near the border, thus
shifting the location of the neutrality point outwards.
);
it is the necessity of matching this profile within
the convective region which forces the MLT radiative
gradient profile to bend near the border, thus
shifting the location of the neutrality point outwards.
![\begin{figure}
{
\includegraphics[width=7cm,clip]{1917fig12.eps}\hspace*{4mm}
\includegraphics[width=7cm,clip]{1917fig13.eps} }
\end{figure}](/articles/aa/full/2005/07/aa1917/Timg89.gif) |
Figure 11:
The variation of the abundances of some
chemicals at the surface of the star as a function
of the total mass (decreasing due to mass loss).
Left: CNO abundances; Right: neon, sodium and
magnesium abundances. |
| Open with DEXTER |
The higher efficiency of the FST model thus has two
important consequences:
- The FST
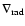 profile is steeper,
favouring a more internal location of the formal border;
this in turn favours a larger luminosity, because
we have an efficient extra contribution of the
p-p chain.
profile is steeper,
favouring a more internal location of the formal border;
this in turn favours a larger luminosity, because
we have an efficient extra contribution of the
p-p chain.
- The lower value of the overadiabaticity required
in the FST model (and, partially, in the MLT21
model) leads to a smaller temperature gradient
within the instability region
(see the right panel of Fig. 10),
which, in turn, acts in favour of a larger
contribution of the extra luminosity supplied by
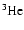 burning within these stellar layers.
burning within these stellar layers.
From a chemical point of view the differences among
the three models are also relevant.
Figure 11 shows the variation of the abundances
of some key elements included in our nuclear
network; in the left panel we report the evolution
of the CNO surface abundances, in the right
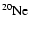 ,
,
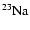 and
and
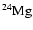 are shown.
In this case, to have an idea of the mean chemical
composition of the ejecta of the star, we use the
mass as abscissa instead of time
(Ventura et al. 2001); the
difference is relevant, because most of the mass
is lost in correspondence of the maximum luminosity,
in a time interval which is very short.
are shown.
In this case, to have an idea of the mean chemical
composition of the ejecta of the star, we use the
mass as abscissa instead of time
(Ventura et al. 2001); the
difference is relevant, because most of the mass
is lost in correspondence of the maximum luminosity,
in a time interval which is very short.
We note in the left panel of Fig. 11
that all three models achieve oxygen depletion,
though in MLT17 the final depletion is
just by a factor of  2. The MLT17 model,
which yields a longer lifetime,
experiences more TDUs, thus
it produces more
2. The MLT17 model,
which yields a longer lifetime,
experiences more TDUs, thus
it produces more
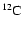 and
and
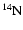 .
As in the FST case, we find that the
parameter connected to the efficiency of the
TDU approaches an asymptotic value of
.
As in the FST case, we find that the
parameter connected to the efficiency of the
TDU approaches an asymptotic value of
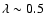 after
after  20 TPs.
20 TPs.
In the right
panel we note the different behaviour of sodium.
In all three cases we have an early phase of
production (which is due to the combined effects of
the second dredge-up and to the destruction of
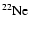 at the beginning of the AGB evolution),
and a later phase of depletion; in the MLT models,
however, the effect of several TDUs make the
surface content of sodium rise again, and
reach extraordinarily large values, particularly
within the MLT17 model. We also note a different
degree of
at the beginning of the AGB evolution),
and a later phase of depletion; in the MLT models,
however, the effect of several TDUs make the
surface content of sodium rise again, and
reach extraordinarily large values, particularly
within the MLT17 model. We also note a different
degree of
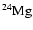 depletion in the three cases,
depletion in the three cases,
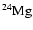 reduction being larger the larger the
efficiency of the convective model.
reduction being larger the larger the
efficiency of the convective model.
Table 1 summarises the chemical
composition of the ejecta
for each of the three models discussed. As we may see
there are just two robust conclusions which we can
draw, independently of the convective model adopted:
- The fraction (in mass) of helium in the
expelled material is
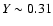 in all cases: this
can be understood on the basis of the fact that it
occurs essentially during the second dredge-up,
while the following production during AGB is negligible.
in all cases: this
can be understood on the basis of the fact that it
occurs essentially during the second dredge-up,
while the following production during AGB is negligible.
- The lithium content of the ejecta is
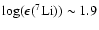 ,
slightly less
than the population II average abundance. This is because
the phases of lithium production and destruction
happen at the very beginning of the AGB evolution,
when the differences among the three models are
small.
,
slightly less
than the population II average abundance. This is because
the phases of lithium production and destruction
happen at the very beginning of the AGB evolution,
when the differences among the three models are
small.
Table 1:
Chemistry of the ejecta.
For all the other elements, the pollution of the
interstellar medium is extremely dependent on the
convective model:
In summary, we have seen that the stellar yields
depend dramatically on the convection model. There
are many other uncertainties in the results,
but those are less critical.
We take as an example the sodium content of the ejecta:
we saw that the results change significantly according
to the efficiency of convection at the base of the outer
convective zone. Figure 12 shows the variation with mass
of the surface sodium abundance within the three models
discussed so far (full, dotted, and dashed lines), plus a
further FST model (dashed-dotted line) calculated
by assuming the lower limit given in Angulo et al. (1999)
for the reactions destroying sodium
(
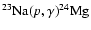 and
and
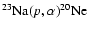 )
and the upper limit for reactions creating sodium
(
)
and the upper limit for reactions creating sodium
(
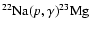 and
and
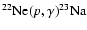 ).
We see that the influence of changing all the cross-sections
involving sodium is far less than the role played by
convection.
).
We see that the influence of changing all the cross-sections
involving sodium is far less than the role played by
convection.
The problems of reaction rates and mass loss will
be discussed in a forthcoming paper.
Deep spectroscopic observations of giant and TO stars
within globular clusters have shown star-to-star
variations in surface chemical composition.
Particularly, the observations
of NGC 6752 by Gratton et al. (2001) showed the presence of
an O-Na anticorrelation in all stars observed, independently
of their evolutionary stage, including those near the TO. Within
the same cluster, strong hints of a Mg-Al anticorrelation
were also found. Similar results were obtained for
other clusters (NGC 6397, M 30 and M 55: Carretta 2003;
M 71: Ramirez & Cohen 2002; M 5: Ramirez & Cohen 2003).
These results have also been recently confirmed
by a deep analysis of the surface abundances of giant
stars belonging to M 3 and M 13 by Sneden et al. (2004), where
a clear C-O anticorrelation was found.
The aforementioned results indicate that the surface matter
of these stars has been subject to nuclear processing
though CNO, Na-Ne and Mg-Al chains. Since these
anomalies were observed also in TO stars, where the internal
temperatures are too low to allow such nuclear
reactions, it was suggested (Ventura et al. 2001; Ventura
et al. 2002) that the stars
displaying such surface chemical anomalies must
have been contaminated by the ejecta
expelled during the AGB evolution of an early generation of
intermediate mass stars (Cottrell & Da Costa 1981;
D'Antona et al. 1983), or must have been formed
by these ejecta (D'Antona et al. 2002).
Recently, this scenario has been questioned by Denissenkov
& Weiss (2001). Denissenkov & Herwig (2003),
based on the computations of a
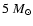 model with metallicity Z=0.0001, showed that a simultaneous
depletion of oxygen and enhancement of sodium (as indicated
by the anticorrelation observed) is made very difficult
by sodium burning at high temperatures, those necessary
to deplete oxygen; their analysis is independent of
the amount of extra mixing assumed at the base of
the convective envelope.
model with metallicity Z=0.0001, showed that a simultaneous
depletion of oxygen and enhancement of sodium (as indicated
by the anticorrelation observed) is made very difficult
by sodium burning at high temperatures, those necessary
to deplete oxygen; their analysis is independent of
the amount of extra mixing assumed at the base of
the convective envelope.
We postpone to a forthcoming paper
the discussion of the role which IMS may
play in the pollution of the interstellar medium within GCs,
because a more complete analysis, covering the whole range
of masses involved, and the most appropriate metallicities,
rather than a single model, is required.
In any case, the present work clearly suggests that
among all the uncertainties included
in the input physics adopted to calculate the evolutionary
sequences the treatment of convection has the greatest impact.
AGB evolution is one of the few cases in stellar
astrophysics where the results obtained are
globally dependent on the convective model
adopted, in terms of time scale, luminosity, temperature and
nucleosynthesis.
Let us summarize again what we can say about
some of the important elements for the self-enrichment
scenario.
- 1.
- Lithium:
the constant lithium content of the ejecta, independent of
the convective model, is in good agreement with the
observed lithium abundances of NGC 6397 TO stars (Bonifacio
et al. 2002), which all show approximately the same
population II standard value.
- 2.
- Helium:
D'Antona et al. (2002) and D'Antona & Caloi (2004)
have shown that the high helium content of the ejecta,
confirmed by the present calculations,
plays a role in the morphology of the horizontal branches
of GCs.
- 3.
- Sodium and Magnesium:
from Fig. 12 we see that the MLT models can achieve
sodium production quite efficiently, because of the TDU carrying
fresh
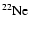 (later converted into sodium) to the surface;
on the other hand, the FST model, living shorter because of
a larger mass loss during the whole AGB evolution,
ejects almost all the envelope mass well before the stage
when TDU can operate significantly.
(later converted into sodium) to the surface;
on the other hand, the FST model, living shorter because of
a larger mass loss during the whole AGB evolution,
ejects almost all the envelope mass well before the stage
when TDU can operate significantly.
In terms of sodium-oxygen anticorrelation, if
the adopted mass loss rate holds, only the MLT21 model
seems to pollute the interstellar medium in the "right''
direction, because apart from producing sodium
efficiently it also depletes oxygen (see Table 1 and
Fig. 11), though other problems arise, because
in this case the polluted material would have
magnetisium isotope ratios
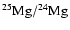 and
and
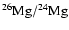 around
around  3, which disagrees with
the measured magnesium isotopic ratios by Yong et al.
(2003) for giant stars in NGC 6752. This problem
is shared by the FST model.
3, which disagrees with
the measured magnesium isotopic ratios by Yong et al.
(2003) for giant stars in NGC 6752. This problem
is shared by the FST model.
- 4.
- CNO: the C+N+O content of the ejecta is almost
unchanged with respect to the initial value
in the FST models, which would be in
agreement with the almost constant C+N+O value
found for various GCs stars observed (M 92: Pilachowski
et al. (1988); NGC 288 and NGC 362: Dickens et al. (1991);
M 3 and M 13: Smith et al. (1996); M 4: Ivans et al. (1999)).
The MLT models lead to a strong increase of the C+N+O
abundance, due to the effects of several TDUs.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{1917fig14.eps} %
\end{figure}](/articles/aa/full/2005/07/aa1917/Timg97.gif) |
Figure 12:
The variation of the surface sodium abundance
with mass within the three models precedently discussed, and
a further FST model where sodium production is favoured
chosing an appropriate nuclear network. |
| Open with DEXTER |
The self-enrichment hypothesis must be evaluated
on the basis of a much deeper analysis, but it is clear
that the uncertainties connected to convection can no
longer be neglected in the computation of the ejecta of
the various models.
We examine the effects of changing the treatment of
convection on the overall evolution of intermediate
mass stars. We compare the stellar evolution models of
initial mass
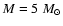 calculated with the MLT
treatment of the instability regions with those
calculated with the FST model for turbulent
convection. We show that while the evolutionary
phases preceding TPs are scarcely
affected (with the exception of RGB and early AGB
effective temperatures), the AGB evolution is heavily influenced
by the convective model adopted.
calculated with the MLT
treatment of the instability regions with those
calculated with the FST model for turbulent
convection. We show that while the evolutionary
phases preceding TPs are scarcely
affected (with the exception of RGB and early AGB
effective temperatures), the AGB evolution is heavily influenced
by the convective model adopted.
A higher convection efficiency at the bottom of the
outer convective zone of AGBs leads to a shorter distance
between the edge of the CNO-burning shell and the base
of external convection; this, in turn, leads to an extra-
luminosity (which, in the first TPs, is entirely due to
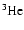 burning) which triggers a faster growth of the
luminosity itself, hence of mass loss.
burning) which triggers a faster growth of the
luminosity itself, hence of mass loss.
From the physical point of view, the overall duration of the
AGB evolution might be shorter by a factor of  3
if the MLT treatment of convection is replaced by the FST
model. Noticeable changes can be seen even if, still in
the MLT framework, the free parameter
3
if the MLT treatment of convection is replaced by the FST
model. Noticeable changes can be seen even if, still in
the MLT framework, the free parameter 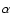 is changed.
The maximum luminosity achieved by the FST is
is changed.
The maximum luminosity achieved by the FST is  70%
larger, and the number of TPs (hence, of third dredge-up
episodes) experienced by the FST model is considerably
lower.
70%
larger, and the number of TPs (hence, of third dredge-up
episodes) experienced by the FST model is considerably
lower.
As for the chemical content of the ejecta, the only robust
conclusion which can be drawn is that these stars
pollute the interstellar medium with material which
is extremely Helium-rich (
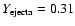 in all cases)
and with a lithium content which is only a factor
of two lower than the standard population II value.
in all cases)
and with a lithium content which is only a factor
of two lower than the standard population II value.
The extent of oxygen depletion, of sodium enrichment and of
the total C+N+O abundance of the ejecta are strongly
dependent on the convective model adopted.
Convection is one of the most important
parameters in the AGB evolution. Any evaluation
of the validity of the self-enrichment scenario
for GCs must deal with the uncertainties connected
to convection before deriving conclusions.
- Angulo, C., et al.
1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] (In the text)
- Blöcker, T.
1995, A&A, 297, 727 [NASA ADS] (In the text)
- Blöcker, T.,
& Schönberner, D. 1991, A&A, 244, L43 [NASA ADS] (In the text)
- Böhm-Vitense, E.
1958, Z. Astroph., 46, 108 [NASA ADS] (In the text)
- Bonifacio,
P., Pasquini, L., Spite, F., et al. 2002, A&A, 390, 91 [EDP Sciences] [NASA ADS] (In the text)
- Cameron, A. G.
V., & Fowler, W. A. 1971, ApJ, 164, 111 [NASA ADS] [CrossRef] (In the text)
- Canuto, V. M.,
Goldman, I., & Mazzitelli, I. 1996, ApJ, 473, 570 [NASA ADS] (In the text)
- Canuto, V. M.,
& Mazzitelli, I. 1991, ApJ, 370, 295 [NASA ADS] [CrossRef] (In the text)
- Carretta, E.
2003, Mem. S.A.It. Suppl., 3, 90 (In the text)
- Caughlan, G.
R., & Fowler, W. A. 1988, Atomic Data Nucl. Tab., 40, 283 [NASA ADS] (In the text)
- Cloutman, L.,
& Eoll, J. G. 1976, ApJ, 206, 548 [NASA ADS] [CrossRef] (In the text)
- Cloutman, L.,
& Whitaker, R. W. 1980, ApJ, 237, 900 [NASA ADS] [CrossRef]
- Cottrell, P.
L., & Da Costa, G. S. 1981, ApJ, 245, 79 [NASA ADS] [CrossRef] (In the text)
- D'Antona, F., &
Caloi, V. 2004, ApJ, 611, 871 [NASA ADS] [CrossRef] (In the text)
- D'Antona, F.,
Caloi, V., Montalban, J., Ventura, P., & Gratton, R. 2002,
A&A, 395, 69 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- D'Antona, F.,
Gratton, R., & Chieffi, A. 1983, Mem. S.A.It., 54, 173 [NASA ADS] (In the text)
- D'Antona, F., &
Mazzitelli, I. 1996, ApJ, 470, 1093 [NASA ADS] [CrossRef] (In the text)
- Deng, L., Bressan,
A., & Chiosi, C. 1996a, A&A, 313, 145 [NASA ADS] (In the text)
- Deng, L., Bressan,
A., & Chiosi, C. 1996b, A&A, 313, 159 [NASA ADS]
-
Denissenkov, P., & Herwig, F. 2003, ApJ, 590, L99 [NASA ADS] [CrossRef] (In the text)
-
Denissenkov, P., & Weiss, A. 2001, ApJ, 559, L115 [NASA ADS] [CrossRef] (In the text)
- Dickens, R. J.,
Croke, B. F. W., Cannon, R. D., & Bell, R. A. 1991, Nature,
351, 212 [NASA ADS] [CrossRef] (In the text)
- Fenner, Y.,
Campbell, S., Karakas, A. I., Lattanzio, J. C., & Gibson, B. K.
2004, MNRAS, 353, 789 [NASA ADS] [CrossRef] (In the text)
- Freytag, B.,
Ludwig, H. G., & Steffen, M. 1996, A&A, 313, 497 [NASA ADS] (In the text)
- Gratton, R.,
Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [EDP Sciences] [NASA ADS] (In the text)
- Grossman, S. A.
1996, MNRAS, 279, 305 [NASA ADS] (In the text)
- Grossman, S.
A., & Narayan, R. 1993, ApJS, 89, 361 [NASA ADS] [CrossRef]
- Hherwig, F. 2000,
A&A, 360, 952 [NASA ADS] (In the text)
- Herwig, F. 2004,
A&A, 605, 425 [NASA ADS] (In the text)
- Herwig, F.,
Blöcker, T., & Schönberner, D. 1997, A&A, 324,
L81 [NASA ADS] (In the text)
- Iben, I. J. 1975, ApJ,
196, 525 [NASA ADS] [CrossRef] (In the text)
- Iben, I. J. 1976, ApJ,
208, 165 [NASA ADS] [CrossRef] (In the text)
- Ivans, I. I., Sneden,
C., Kraft, R. P., et al. 1999, AJ, 118, 1273 [NASA ADS] [CrossRef] (In the text)
- Mazzitelli,
I., D'Antona, F., & Ventura, P. 1999, A&A, 348, 846 [NASA ADS]
-
Pilachowski, C. A. 1988, ApJ, 326, L57 [NASA ADS] [CrossRef] (In the text)
- Ramirez, S.,
& Cohen, J. G. 2002, AJ, 123, 3277 [NASA ADS] [CrossRef] (In the text)
- Ramirez, S.,
& Cohen, J. G. 2003, AJ, 125, 224 [NASA ADS] [CrossRef] (In the text)
- Renzini, A.,
& Voli, M. 1981, A&A, 94, 175 [NASA ADS] (In the text)
- Sackmann, J.,
& Boothroyd, A. I. 1991, ApJ, 366, 529 [NASA ADS] [CrossRef] (In the text)
-
Schwarzschild, M., & Harm, R. 1965, ApJ, 142, 855 [NASA ADS] [CrossRef] (In the text)
-
Schwarzschild, M., & Harm, R. 1967, A&A, 145, 486 (In the text)
- Smith, G. H.,
Shetrone, M. D., Bell, R. A., Churchill, C. W., & Briley, M. M.
1996, AJ, 112, 1511 [NASA ADS] [CrossRef] (In the text)
- Sneden, C., Kraft,
R. P., Guhathakurta, P., Peterson, R. C., & Fulbright, J. P.
2004, AJ, 127, 2162 [NASA ADS] [CrossRef] (In the text)
- Tuchman, Y.,
Glasner, A., & Barkat, Z. 1983, ApJ, 268, 356 [NASA ADS] [CrossRef] (In the text)
- Ventura, P.,
& Castellani, M. 2005, A&A, 430, 1035 [EDP Sciences] [CrossRef] (In the text)
- Ventura, P.,
D'Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550,
L65 [NASA ADS] [CrossRef] (In the text)
- Ventura, P.,
D'Antona, F., & Mazzitelli, I. 2002, A&A, 393, 215 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Ventura, P.,
D'Antona, F., & Mazzitelli, I. 2000, A&A, 363, 605 [NASA ADS] (In the text)
- Ventura, P.,
Zeppieri, A., D'Antona, F., & Mazzitelli, I. 1998, A&A,
334, 953 [NASA ADS] (In the text)
- Vitense, E. 1953,
Zs. Ap., 32, 135 [NASA ADS] (In the text)
- Xiong, D. R. 1980,
ChA, 4, 234 [NASA ADS]
- Xiong, D. R. 1985,
A&A, 150, 133 [NASA ADS] (In the text)
- Xiong, D. R., Cheng,
Q. L., & Deng, L. 1997, ApJS, 108, 529 [NASA ADS] [CrossRef]
- Yong, D., Grundahl, F.,
Nissen, P. E., & Shetrone, M. D. 2003, A&A, 402, 985 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2005
![\begin{displaymath}\left( {{\rm d}X_i\over {\rm d}t} \right)=\left( {\partial X_...
... (4\pi r^2 \rho)^2 D {\partial X_i
\over \partial m_r}\right]
\end{displaymath}](/articles/aa/full/2005/07/aa1917/img46.gif)
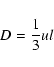
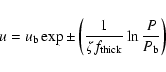
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{1917fig1.eps} %
\end{figure}](/articles/aa/full/2005/07/aa1917/Timg58.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1917fig2.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg63.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1917fig3.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg64.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1917fig4.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg65.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1917fig5.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg70.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1917fig6.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg75.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{1917fig7.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1917fig8.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg77.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1917fig9.eps}\end{figure}](/articles/aa/full/2005/07/aa1917/Timg78.gif)
![\begin{figure}
{
\includegraphics[width=7cm,clip]{1917fig10.eps}\hspace*{4mm}
\includegraphics[width=7cm,clip]{1917fig11.eps} }
\par\end{figure}](/articles/aa/full/2005/07/aa1917/Timg81.gif)
![\begin{figure}
{
\includegraphics[width=7cm,clip]{1917fig12.eps}\hspace*{4mm}
\includegraphics[width=7cm,clip]{1917fig13.eps} }
\end{figure}](/articles/aa/full/2005/07/aa1917/Timg89.gif)
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{1917fig14.eps} %
\end{figure}](/articles/aa/full/2005/07/aa1917/Timg97.gif)