A&A 431, 143-148 (2005)
DOI: 10.1051/0004-6361:20041830

The stellar content of the Hamburg/ESO survey^,

III. Field horizontal-branch stars in the Galaxy

N. Christlieb¹ - T. C. Beers² - C. Thom³ - R. Wilhelm⁴ - S. Rossi⁵ - C. Flynn⁶ - L. Wisotzki⁷ - D. Reimers¹

1 - Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
2 - Department of Physics & Astronomy and JINA: Joint Institute for Nuclear Astrophysics, Michigan State University, East Lansing, MI 48824, USA
3 - Centre for Astrophysics and Supercomputing, Swinburne University of Technology, Hawthorn, VIC 3122, Australia
4 - Department of Physics, Texas Tech University, Lubbock, TX 79409, USA
5 - Departamento de Astronomia Instituto de Astronomia, Geofísica e Ciências Atmosféricas, Universidade de São Paulo, 05508-900 São Paulo SP, Brazil
6 - Tuorla Observatory, University of Turku, Väisäläntie 20, 21500 Piikkiö, Finland
7 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany

Received 11 August 2004 / Accepted 20 October 2004

Abstract
We present a sample of 8321 candidate Field Horizontal-Branch (FHB) stars selected by automatic spectral classification in the digital data base of the Hamburg/ESO objective-prism survey. The stars are distributed over 8225 square degrees of the southern sky, at $\vert b\vert \gtrsim 30~\deg$. The average distance of the sample, assuming that they are all FHB stars, is 9.8 kpc, and distances of up to $\sim$30 kpc are reached. Moderate-resolution spectroscopic follow-up observations and UBV photometry of 125 test sample stars demonstrate that the contamination of the full candidate sample with main-sequence A-type stars is <16%, while it would be up to 50% in a flux-limited sample at high galactic latitudes. Hence more than $\sim$6800 of our FHB candidates are expected to be genuine FHB stars. The candidates are being used as distance probes for high-velocity clouds and for studies of the structure and kinematics of the Galactic halo.

Key words: stars: horizontal-branch - Galaxy: halo - Galaxy: kinematics and dynamics - surveys - methods: statistical

1 Introduction

Over the past few decades, as knowledge of the structure and nature of the stellar components of the Milky Way has increased, the level of complexity that has been revealed has also risen. Not only must astronomers attempt to describe and quantify the global properties of our Galaxy, but they also must contend with the presence (likely only partially recognized at present) of real structures - coherent streams arising from shredded dwarf galaxies, such as Sagittarius (e.g., Majewski et al. 2003; Ibata et al. 1994), and the still poorly-constrained Monoceros stream (Frinchaboy et al. 2004; Ibata et al. 2003; Newberg et al. 2002; Martin et al. 2004; Yanny et al. 2003), as well as the tidal tails of individual globular clusters (Dehnen et al. 2004, and references therein). Even within recognized stellar components, such as the thick disk, evidence exists for the presence of multiple populations, e.g., the so-called "metal-weak thick disk'' (see Beers et al. 2002, and references therein) perhaps arising from stars donated to the original thick disk by ravaged dwarf satellites. The overall shape of the inner and outer halo of the Galaxy are still not well known, though most recent evidence suggests that the outer halo is at least somewhat flattened (e.g., Chiba & Beers 2000; Helmi et al. 2003).

It is clear that, for progress to be made, further detailed examination of the positions, motions, and chemical compositions of the stars of the Milky Way is required. Although not ideal for examination of elemental abundances (due to their higher temperatures, and hence weaker metallic lines), Field Horizontal-Branch (hereafter, FHB) stars can provide valuable tracers of the structure, kinematics, and dynamics of the halo and thick disk of the Galaxy. They are numerous throughout the Galaxy, and sufficiently luminous to be identified up to large distances from the Sun.

One immediate application of a large sample of tracers located throughout the halo of the Galaxy is the opportunity to obtain dynamical estimates of its total mass. Wilkinson & Evans (1999) used the full set of 27 known satellite galaxies and globular clusters located at distances greater than 20 kpc to explore this question. For six of these objects proper motions are known. This data was later supplemented by Sakamoto et al. (2003), who added some 400 FHB stars (at distances less than 10 kpc) with available radial velocities, at least 50% of which also had available proper motions, in order to refine the mass estimate of the Galaxy. This sample was further expanded to include FHB stars from the early data release of the Sloan Digital Sky Survey (SDSS; York et al. 2000), adding stars up to 75 kpc away (Beers et al. 2003). Most recently, Clewley et al. (2004) have identified a new sample of 60 FHB stars located in six high Galactic latitude fields up to 50 kpc away, which will be combined with additional distant samples to obtain an improved estimate of the mass of the Galaxy.

In addition, FHB stars are of great importance as probes of the distances to High Velocity Clouds (HVCs). HVCs are clouds of neutral hydrogen at velocities incompatible with Galactic differential rotation (see Wakker 2004, for a recent review). With HVCs, we might observe a continuous infall of metal-poor ($\sim$1/10 solar) gas into the Galaxy, which dilutes the interstellar medium (ISM) (Wakker et al. 1999). A clearer understanding of the nature of HVCs would therefore be important for modeling the chemical evolution of the Galaxy.

Distances to HVCs can be determined by using stars of known distance in the line of sight to the clouds (Wakker & van Woerden 1997). Provided that the HVC under consideration has a detectable metal content, one can observe absorption lines of these metals at the velocity of the cloud in the spectra of stars located behind the cloud, but these same lines would not be seen in the spectra of stars located in front of the cloud. Therefore, one can constrain the HVC distance by using a sample of stars with different distances along the line of sight to the cloud. FHB stars are particularly well-suited for this purpose, because they are numerous, distant, and their spectra have only very weak intrinsic absorption lines of metals.

Previously, the largest catalogues of candidate FHB stars have come from objects selected on the basis of their distinctive appearance on objective-prism plates (e.g., the HK survey of Beers and collaborators; Beers et al. 1996). The HK survey possesses a magnitude limit, defined here as the B magnitude of the faintest objects present in the survey, of $B\simeq 15.5$, with a corresponding distance limit for FHB stars on the order of 10 kpc from the Sun. In the Hamburg/ESO survey (HES; Wisotzki et al. 2000,1996), the fainter limiting magnitude of $B\simeq 18.0$enables detection of FHB stars at distances of up to $\sim$30 kpc.

Colorimetric surveys, such as the SDSS, are now able to identify FHB candidates up $\simeq$100 kpc away (Yanny et al. 2000; Sirko et al. 2004). The 2MASS all-sky survey also provides a valuable resource for the colorimetric identification of FHB candidates. Brown et al. (2004), for example, show that 2MASS JHKphotometry can be used to efficiently select FHB candidates out to 10 kpc from the Sun. These authors provide a catalogue of some 100 000 FHB candidates located above Galactic latitude $\vert b\vert = 15\deg$ (note, however, the contamination issues described below). Many more are identifiable at lower latitudes; however, the patchiness and increased overall level of interstellar reddening presents additional difficulties. The 2MASS catalogues of FHB candidates provide a valuable complement to the SDSS approach, since the bright limit of SDSS ( $B \simeq 14.5$) is similar to the faint limit of the 2MASS FHB candidates. In due course, the all-sky survey presently underway in the far-UV and near-UV with the GALEX mission will provide another valuable source of FHB candidates.

It must be kept in mind that catalogues of FHB candidates can be easily confounded with high surface gravity A-type stars. A number of authors have pointed out that roughly 50% of all stars with colors that fall in the same range as FHB stars are in fact of this lower luminosity variety, many of which are likely to be halo blue stragglers (see, e.g., Wilhelm et al. 1999b; Preston et al. 1991; Norris & Hawkins 1991; Preston et al. 1994). The majority of the so-called "blue metal poor'' stars of Preston et al. (1994) are also likely to be blue stragglers (Preston & Sneden 2000). High-gravity A-type stars can be distinguished from lower gravity FHB stars through the use of broadband UBV photometry combined with medium-resolution spectroscopy (Wilhelm et al. 1999a), due to the large effect of surface gravity on the broadband U flux, and on the wings of the Balmer lines. Clewley et al. (2002) describe procedures that attempt to make this separation based on medium-resolution spectroscopy alone.

In the HES we have attempted to select a clean sample of FHB candidates; that is, we wanted to keep the "contamination'' with main-sequence stars as low as possible. If we can demonstrate by representative follow-up observations that the contamination is low, such a selection would allow us to isolate a large, statistical sample of FHBs, useful for many purposes, directly from the HES data base, without the need of any follow-up observations.

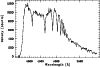	Figure 1: Sample HES prism spectrum of a candidate FHB star. Note that wavelength increases from right to left. The sharp drop at about 5400 Å is due to the sensitivity cutoff of the IIIa-J emulsion.
Open with DEXTER

In Sect. 2 we describe our procedure for selecting FHB candidates. In Sect. 3, the results of the application of the selection algorithm to a major fraction of the HES data base (i.e., spectra from 329 out of a total of 380 HES fields) are presented. We also demonstrate that a low contamination with high-gravity A-stars can indeed be achieved with this selection. We present our conclusions in Sect. 4.

  
2 Selection of FHB candidates

A-type stars are readily detectable in the HES due to their strong Balmer lines (for an example see Fig. 1). FHB candidates are selected in the HES in two steps. First, we apply B-V and U-B cutoffs, and then we employ automatic spectral classification to seperate main-sequence from horizontal-branch stars. The classification is based on the Strömgren c₁ colour index and the sum of the equivalent widths of the Balmer lines H$\beta$, H$\gamma$ and H$\delta$. All of this information is derived directly from the HES spectra. The calibrations of B-V, U-B and c₁ are accurate to 0.1, 0.09 and 0.15 mag, respectively (Christlieb et al. 2001b). The Balmer line strengths are measured with an iterative algorithm in which a Gaussian profile is fitted to the lines (Christlieb et al. 2001b). We note that using a Gaussian profile may lead to systematic underestimation of the strengths of the broad lines of hot stars. However, for our FHB candidate selection, the internal consistency of the measured values rather than their absolute scale is important. We estimate the internal accuracy of the equivalent width sum $\mbox{H}\beta+\mbox{H}\gamma+\mbox{H}\delta$, as measured from the HES spectra, to be on the order of a few Ångströms.

In the first step of the procedure, we select all stars that lie in the colour range

 

-0.2 < B-V < 0.3 (1)

and

 

-0.3 < U-B < 0.5. (2)

The B-V criterion selects all stars with effective temperatures in the range $7000~\mbox{K} \lesssim T_{\mbox{\scriptsize eff}}\lesssim 10~000~\mbox{K}$, while allowing for an error margin of 0.1 mag in B-V. The U-B criterion was chosen to include most FHB stars, while a potential contamination with DA white dwarfs is kept at a minimum (see Fig. 13 of Christlieb et al. 2001b).

In order to develop a method for the separation of main-sequence from horizontal-branch stars, we investigated a set of 259 HES spectra of stars that were analysed with the methods of Wilhelm et al. (1999a). This sample includes 214 stars from Wilhelm et al. (1999b) present on the HES plates. The remaining 45 stars resulted from our own follow-up spectroscopy and photometry of candidates selected with a preliminary selection algorithm. From this set of stars, 31 were classified either as "Am'' (i.e., metallic-line A-type stars), "Ap'' (i.e., peculiar A-type stars), or "FHB/A'' (i.e., no definitive conclusion could be reached as to whether these stars are on the horizontal-branch or are main-sequence stars). These were discarded, leaving 90 high-gravity A-type stars and 138 FHB stars.

Figure 2: Automatic classification of A-type stars in the two-dimensional feature space c1 versus sum of Balmer line equivalent widths $\mbox{H}\beta+\mbox{H}\gamma+\mbox{H}\delta$. In the left panel we show the learning sample of 228 stars before the classification is applied; in the right panel, crosses and dots denote the main-sequence and FHB stars that have been classified as main-sequence stars, respectively, and empty and full circles are the objects that have been classified as FHB stars.

Open with DEXTER

Inspection of the distribution of these stars in a c₁ versus $\mbox{H}\beta+\mbox{H}\gamma+\mbox{H}\delta$ diagram reveals that these two classes of objects are reasonably well separated in this feature space (see Fig. 2). We hence implemented an automatic spectral classification algorithm that makes use of these two features. The classification forms the second step of our FHB candidate selection, i.e., it is applied only to the subset of the objects in the HES data base that meet criteria (1) and (2).

A detailed description of the classification algorithm can be found in Christlieb et al. (2001a). The above described sample of 90 confirmed high-gravity A-type stars and 138 FHB stars is used as a training set. Based on this sample, the probability distributions for objects being member of one of the two classes, given their c₁ and Balmer line equivalent width sums, are estimated. These so-called class-conditional probability distributions are modeled by two-dimensional Gaussian distributions. This results in iso-probability lines in the two-dimensional feature space which have the shapes of ellipses, with their center being located at the point with the coordinates of the class means of c₁ and $\mbox{H}\beta+\mbox{H}\gamma+\mbox{H}\delta$. For example, the mean of c₁for the main-sequence stars in the left panel of Fig. 2 is 0.7 mag, and for the Balmer line sum it is 19 Å.

Our statistical classification requires an estimation of the prior probabilities of the two classes considered here, i.e., main-sequence or FHB star. Wilhelm et al. (1999b) analysed a sample of 1121 A-type stars selected from HK survey plates. We consider it to be a representative flux-limited sample at high galactic latitude, and use it to estimate the prior probabilities of "FHB'' and "A'' stars in the HES. Wilhelm et al. (1999b) find 416 "FHB'' and 444 "A'' stars in their sample. Therefore, we estimate the prior probabilities for these stars to be 0.396 and 0.371 in the HES, respectively.

Any given object with measured values for c₁ and $\mbox{H}\beta+\mbox{H}\gamma+\mbox{H}\delta$ can then be assigned to one of the two classes with various decision rule. If the so-called Bayes' rule is used, an object is assigned to the class with the highest posterior probability, given its values of the two features. This decision rule results in "dividing lines'' in the two-dimensional feature space that have the shape of a polynomial of second order (hence this classification method is called "quadratic discriminant analysis''). From looking at the right panel of Fig. 2, one can have a presentiment of the parabola-shaped selection boundary for our classification problem.

Classification with Bayes' rule minimizes the total number of misclassifications, if the true distributions of the class-conditional probabilities are used. However, in our case our classification aim is to compile a clean sample of FHB stars, which is different from minimizing the total number of misclassifications, because different classification errors will have different weight. For example, a misclassification of a high-gravity A-type star as an FHB star is worse for the compilation of a clean sample than a misclassification in the other direction.

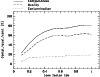	Figure 3: Adjusting the cost factor t2o by evaluating the classifcation results. For further explanation see text.
Open with DEXTER

In order to to reach our aims, we have employed a so-called minimum cost rule classification, which minimizes the total cost. Here, every misclassified object causes a cost, while a correctly classified object is cost-neutral. The choice of cost factors determines the relative weight of misclassifications from one class to another. As described in Christlieb et al. (2001a), the cost factor t2o determines the cost for misclassifications of an object of the target class ("t'') to ("2'') one of the other classes ("o''). With the cost factor o2t, the cost for the contamination of the target class is adjusted, and o2o is the cost factor for misclassifications between other classes. Since we are here only dealing with two classes - that is, the target class of FHB stars, and high-gravity A-type stars - the cost factor o2o does not have any meaning. Therefore, effectively only one cost factor has to be chosen. As explained in Christlieb et al. (2001a), only the relative cost factor values need to be adjusted. Therefore, we set o2t to a fixed value of 1.0 and investigated the classification results as a function of t2o, with $0.0 \leq \mbox{\texttt{t2o}} \leq 1.0$. The result is shown in Fig. 3.

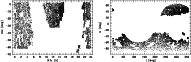	Figure 4: Distribution of the 8321 HES FHB candidates on the sky.
Open with DEXTER

We define the quality q of the classification as the completeness rate minus the contamination rate. This gives q = 100% for the perfect classification with respect to our classification aim, i.e., 100% completeness (all FHB stars classified correctly) and 0% contamination (no high-gravity A-type star erroneously classified as an FHB star). The highest value of q which is reachable is a measure of how well the objects of the target class can be seperated from objects of the other class(es).

In our case, the highest quality is achieved at $\mbox{\texttt{t2o}}\sim 0.9$. However, we decided to adopt $\mbox{\texttt{t2o}}=0.5$ for our classification, in order to keep the high-gravity A-type star contamination below 15%. Estimates of the expected error rates with the leaving-one-out method (for a description see Christlieb et al. 2001b) for the adopted value of t2o yield an expected completeness of the FHB sample of 73%.

  
3 Results

3.1 Application to 329 HES fields

Application of our selection algorithm to the 329 HES fields that are currently used for the exploitation of the stellar content of the HES yielded 8321 FHB candidates. As we argue in Sect. 3.2 below, statistically more than $\sim$6800 of these are expected to be genuine FHB stars. The distribution of these objects on the sky is shown in Fig. 4. In Table A.1 we list, for the entire sample, photometry (UBV, c₁), and Balmer line equivalent width sums, as derived directly from HES spectra, as well as coordinates of the stars.

We determined the distance distribution of the sample by assuming that all candidates are indeed FHB stars. Strictly speaking, this assumption is not valid, because our candidate sample will contain some non-FHB stars. However, this would change the distance distribution noticably only if the apparent magnitude distribution of the non-FHB contaminants were significantly different from that of the FHB stars (for which we do not have any indication from our sample of non-FHB stars in our training set), and if the fraction of contaminants were high (we will demonstrate the opposite below). The reddening of the stars was deduced from the maps of Schlegel et al. (1998), using the empirical formula of Beers et al. (2002) to correct for the suspected overestimate of the reddening by Schlegel et al. in the cases were E(B-V) > 0.1. This correction had to be applied to only 6% of our stars; the average reddening of our sample is only E(B-V) = 0.046. Therefore, the extinction corrections are negligible (i.e., the distances would change on average by $\sim$2%) compared to other sources of error in our rough distance estimates.

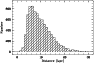	Figure 5: Distance distribution of the FHB candidate sample of 8321 stars, assuming that they are all indeed FHB stars.
Open with DEXTER

Estimates of the absolute visual magnitudes, M_V, of our FHB candidates are obtained following the procedures of Preston et al. (1991). These authors assembled a mean M_V versus B-V relation for blue horizontal branch stars in 15 Galactic globular clusters, normalized relative to an assumed absolute magnitude of RR Lyrae stars in each cluster. The metallicity dependence is accounted for using the corrections of Clementini et al. (1999) for RR Lyrae stars. Since [Fe/H] is not available for the full sample of HES FHB candidates, we assume that they all have the average value of Wilhelm et al. (1999b), i.e., $\mbox{[Fe/H]}=-1.9$. The correction is 0.36 mag with respect to assuming solar metallicity (that is, the absolute V magnitudes of the metal-poor FHB stars are brighter by this amount), resulting in distances increased by 18%. We then use the de-reddened HES B-V colours and V magnitudes to compute distance moduli, taking into account extinction.

The average distance of our sample, assuming that all of the candidates are FHB stars, is 9.8 kpc, while distances of up to 30 kpc are reached (see Fig. 5).

  
3.2 Contamination with high-gravity A-type stars

For 125 stars of our sample that are not part of the learning sample we have taken moderate-resolution ($\sim$2 Å) spectra with the CTIO 4 m/RCS in December 1999, and the ESO 3.6 m/EFOSC2 in November 2000. The spectra have signal-to-noise ratios of S/N > 20 per pixel at Ca II K. After the standard CCD reductions, the algorithm of Horne (1986) was employed to extract the spectra in order to maximize their S/N. UBV photometry was obtained at the ESO-Danish 1.54 m with DFOSC in observing runs in November 1998 and November 2000. The results of the photometry runs will be reported in Beers et al. (in preparation).

The spectra and photometry was analysed with the method of Wilhelm et al. (1999a), in which the observed Balmer line profiles, equivalent widths of Ca II K, and UBV photometry are compared to the respective properties of synthetic spectra. This technique allows the estimations of effective temperature $T_{\mbox{\scriptsize eff}}$, surface gravity $\log g$, and metallicity [Fe/H] with accuracies of $\sigma\left(T_{\mbox{\scriptsize eff}}\right)=\pm 250$ K, $\sigma\left(\log g\right)=\pm 0.14$ dex, and $\sigma\left(\mbox{[Fe/H]}\right)=\pm 0.12$ dex, which permits one to reliably seperate main-sequence A-type stars from FHB stars.

The result is shown in Table 1. A total of 103 stars (or 82%) were confirmed to be FHB stars, and a further 5 stars were classified as "FHB/A'' stars. Since the "FHB/A'' stars could be either "FHB'' or "A'' stars, the total fraction of FHB stars lies in the range 82-86%. A total of 15 stars (or 12%) were classified "A'' by the method of Wilhelm et al. (1999a), yielding a total contamination of 12-16%, which agrees very well with the contamination of $\sim$15% expected from the training of the classifier applied to the HES data base.

  
4 Conclusions

This large sample of HES FHB candidates, homogeneously distributed over the high-Galactic latitude sky, is of great value for studies of the structure and kinematics of the Galactic halo. The stars are also being used as distance probes for HVCs. In a forthcoming paper we will report on a cross-correlation of the sample with HVC moment maps generated from data of the H I Parkes All-Sky Survey (Thom et al., in preparation).

This sample of HES FHB candidates is expected to contain a contamination with main-sequence A-type stars of less than 16%, so that for many studies the stars can be used directly, without the need for extensive follow-up observations to further refine the classifications.

Table 1: Evaluation of the test sample of 125 FHB candidates.

Acknowledgements

We thank A. Frebel for technical help and careful proof-reading. T.C.B. acknowledges partial support from grants AST 00-98508 and AST 00-98548, and PHY 02-16783, Physics Frontier Centers/JINA: Joint Institute for Nuclear Astrophysics, awarded by the US National Science Foundation. C.T. acknowledges the financial support of the Australian Research Council through its Linkage International program. S.R. thanks the Brazilian Institutions FAPESP and CNPq for partial financial support. C.F. thanks the Academy of Finland for its support through the Antares program for space research.

Appendix A: The HES FHB candidates

In Table A.1 we list details of the sample of 8321 HES FHB candidates stars described in this paper. The table is available only electronically at the CDS. It contains the following columns:

hename	HE designation
ra2000	R.A. at equinox 2000.0, derived from DSS I
dec2000	Declination at equinox 2000.0, derived from DSS I
field	ESO-SERC field number
B	B magnitude
B-V	B-V magnitude, measured from HES spectra
U-B	U-B magnitude, measured from HES spectra
c1	Strömgren c1 index, measured from HES spectra
balmsum	Sum of equivalent widths of $\mbox{H}\beta$, $\mbox{H}\gamma$, and $\mbox{H}\delta$

References

• Beers, T. C., Chiba, M., Sakamoto, T., et al. 2003, in Dark Matter in Galaxies, IAU Symp., 220, (In the text)
• Beers, T. C., Drilling, J., Rossi, S., et al. 2002, AJ, 124, 931 [NASA ADS] [CrossRef] (In the text)
• Beers, T. C., Wilhelm, R., Doinidis, S. P., & Mattson, C. J. 1996, ApJS, 103, 433 [NASA ADS] [CrossRef] (In the text)
• Brown, W. R., Geller, M. J., Kenyon, S. J., et al. 2004, AJ, 127, 1555 [NASA ADS] [CrossRef] (In the text)
• Chiba, M., & Beers, T. C. 2000, AJ, 119, 2843 [NASA ADS] [CrossRef]
• Christlieb, N., Green, P., Wisotzki, L., & Reimers, D. 2001a, A&A, 375, 366 [EDP Sciences] [NASA ADS] (In the text)
• Christlieb, N., Wisotzki, L., Reimers, D., et al. 2001b, A&A, 366, 898 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Clementini, G., Gratton, R. G., Carretta, E., & Sneden, C. 1999, MNRAS, 302, 22 [NASA ADS] [CrossRef] (In the text)
• Clewley, L., Warren, S. J., Hewett, P. C., Norris, J. E., & Evans, N. W. 2004, MNRAS, 352, 285 [NASA ADS] [CrossRef] (In the text)
• Clewley, L., Warren, S. J., Hewett, P. C., et al. 2002, MNRAS, 337, 87 [NASA ADS] [CrossRef] (In the text)
• Dehnen, W., Odenkirchen, M., Grebel, E. K., & Rix, H.-W. 2004, AJ, 127, 2753 [NASA ADS] [CrossRef] (In the text)
• Frinchaboy, P. M., Majewski, S. R., Crane, J. D., et al. 2004, ApJ, 602, L21 [NASA ADS] [CrossRef]
• Helmi, A., White, S. D. M., & Springel, V. 2003, MNRAS, 339, 834 [NASA ADS] [CrossRef]
• Horne, K. 1986, PASP, 98, 609 [NASA ADS] [CrossRef] (In the text)
• Ibata, R. A., Irwin, M. J., Lewis, G. F., Ferguson, A. M. N., & Tanvir, N. 2003, MNRAS, 340, L21 [NASA ADS] [CrossRef]
• Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [NASA ADS] [CrossRef]
• Majewski, S. R., Skrutskie, M. F., Weinberg, M. D., & Ostheimer, J. C. 2003, ApJ, 599, 1082 [NASA ADS] [CrossRef]
• Martin, N. F., Ibata, R. A., Bellazzini, M., et al. 2004, MNRAS, 348, 12 [NASA ADS] [CrossRef]
• Newberg, H. J., Yanny, B., Rockosi, C., et al. 2002, ApJ, 569, 245 [NASA ADS] [CrossRef]
• Norris, J., & Hawkins, M. 1991, ApJ, 380, 104 [NASA ADS] [CrossRef]
• Preston, G. W., Beers, T. C., & Shectman, S. 1994, AJ, 108, 538 [NASA ADS] [CrossRef]
• Preston, G. W., Shectman, S., & Beers, T. C. 1991, ApJ, 375, 121 [NASA ADS] [CrossRef]
• Preston, G. W., & Sneden, C. 2000, AJ, 120, 1014 [NASA ADS] [CrossRef] (In the text)
• Sakamoto, T., Chiba, M., & Beers, T. C. 2003, A&A, 397, 899 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] (In the text)
• Sirko, E., Goodman, J., Knapp, G. R., et al. 2004, AJ, 127, 914 [NASA ADS] [CrossRef]
• Wakker, B. P. 2004, Ap&SS, 289, 381 [NASA ADS] (In the text)
• Wakker, B. P., Howk, J. C., Savage, B. D., et al. 1999, Nature, 402, 388 [NASA ADS] [CrossRef] (In the text)
• Wakker, B. P., & van Woerden, H. 1997, ARA&A, 35, 217 [NASA ADS] (In the text)
• Wilhelm, R., Beers, T. C., & Gray, R. 1999a, AJ, 117, 2308 [NASA ADS] [CrossRef] (In the text)
• Wilhelm, R., Beers, T. C., Sommer-Larsen, J., et al. 1999b, AJ, 117, 2329 [NASA ADS] [CrossRef]
• Wilkinson, M. I., & Evans, N. W. 1999, MNRAS, 310, 645 [NASA ADS] [CrossRef] (In the text)
• Wisotzki, L., Christlieb, N., Bade, N., et al. 2000, A&A, 358, 77 [NASA ADS]
• Wisotzki, L., Köhler, T., Groote, D., & Reimers, D. 1996, A&AS, 115, 227 [NASA ADS]
• Yanny, B., Newberg, H. J., Grebel, E. K., et al. 2003, ApJ, 588, 824 [NASA ADS] [CrossRef]
• Yanny, B., Newberg, H. J., Kent, S., et al. 2000, ApJ, 540, 825 [NASA ADS] [CrossRef]
• York, D. G., Adelman, J., Anderson, J. E., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef] (In the text)