M. Bejger1 - D. Gondek-Rosinska1,2 -
E. Gourgoulhon2 - P. Haensel1,2 -
K. Taniguchi3,![]() - J. L. Zdunik1
- J. L. Zdunik1
1 - N. Copernicus Astronomical Center, Polish Academy of
Sciences, Bartycka 18, 00-716 Warszawa, Poland
2 -
Laboratoire de l'Univers et de ses Théories, UMR 8102 du CNRS, Observatoire de Paris,
Université Paris 7, 92195 Meudon Cedex, France
3 -
Department of Earth Science and Astronomy, Graduate School of Arts and Sciences,
University of Tokyo, Komaba, Meguro, Tokyo 153-8902, Japan
Received 9 June 2004 / Accepted 13 October 2004
Abstract
We present calculations of quasi-equilibrium sequences
of irrotational binary neutron stars based on realistic equations of state (EOS) for the whole neutron star interior. Three realistic nuclear EOSs of various softness and
based on different microscopic models have been joined with a recent
realistic EOS of the crust, giving in this way three different
EOSs of a neutron-star interior. Computations of quasi-equilibrium
sequences are performed within the Isenberg-Wilson-Mathews
approximation to general relativity. For all evolutionary sequences,
the innermost stable circular orbit (ISCO) is found to be given
by mass-shedding limit (Roche lobe overflow).
The EOS dependence on the last orbits is found to be quite important:
for two
![]() neutron stars, the gravitational wave frequency at the ISCO (which
marks the end of the inspiral phase) ranges from 800 Hz to
1200 Hz, depending upon the EOS. Detailed comparisons with 3rd order
post-Newtonian results for point-mass binaries reveals a very good agreement until hydrodynamical effects (dominated by high-order functions of frequency) become important,
which occurs at a frequency ranging from 500 Hz to 1050 Hz,
depending upon the EOS.
neutron stars, the gravitational wave frequency at the ISCO (which
marks the end of the inspiral phase) ranges from 800 Hz to
1200 Hz, depending upon the EOS. Detailed comparisons with 3rd order
post-Newtonian results for point-mass binaries reveals a very good agreement until hydrodynamical effects (dominated by high-order functions of frequency) become important,
which occurs at a frequency ranging from 500 Hz to 1050 Hz,
depending upon the EOS.
Key words: dense matter - equation of state - binaries: close - stars: neutron - gravitational waves
Detection of gravitational waves (GW) with the use of ground-based laser interferometers, such as VIRGO (Acernese et al. 2004), LIGO (Abbot et al. 2004), GEO600 (Hewitson et al. 2003), or TAMA300 (Ando et al. 2001) will provide crucial information about various astrophysical objects. Among them, coalescing binary neutron stars (NS) are particularly interesting for the use of GWs to probe their interiors. Matched filtering techniques involving high-order post-Newtonian effects will provide the individual masses and spins of the NSs. The last few orbits before the final merger are dominated by the strong tidal forces acting between the components. The tidal deformation of NSs shape and of the matter distribution in the stellar interior are expected to depend rather strongly on the poorly known equation of state (EOS) of dense matter. The GW signal carries therefore some imprint of the EOS. In particular, the final frequency of the last stable circular orbit is strongly correlated with the compactness parameter M/R (Faber et al. 2002; Taniguchi & Gourgoulhon 2003), and thus can provide direct constraints on the theory of dense hadronic matter above the nuclear saturation density. A related event potentially rich in information about the dense matter EOS is the merger of a neutron star and a black hole (Prakash & Lattimer 2004; Prakash et al. 2004). In addition to locating the transition from inspiral to the merger phase, computations of the last stable orbits of binary NSs are also required for providing initial data to compute the dynamical merger phase (Shibata et al. 2003, and references therein).
The last orbits of inspiraling binary neutron stars have been studied by a number of authors in the quasi-equilibrium approximation, and in the framework of Isenberg-Wilson-Mathews (IWM) approximation of general relativity (see Baumgarte & Shapiro 2003, for a review). The quasi-equilibrium assumption approximates the evolution of the system by a sequence of exactly circular orbits (as the time evolution of the orbit is much larger than the orbital period). The IWM approximation amounts to using a conformally flat spatial metric (the full spacetime metric remaining non-conformally flat), which reduces the problem to solving only five of the ten Einstein equations. Within these two approximations, the most realistic studies have considered irrotational binaries, as opposed to synchronized ones, as the viscosity of neutron star matter is far too low to ensure synchronization during the late stage of the inspiral (Bildsten & Cutler 1992; Kochaneck 1992).
The quasi-totality of the existing quasi-equilibrium IWM studies
(Bonazzola et al. 1999; Taniguchi & Gourgoulhon 2002b; Marronetti et al. 1999; Gourgoulhon et al. 2001; Uryu et al. 2000; Taniguchi & Gourgoulhon 2003; Uryu & Eriguchi 2000)
employ a polytropic EOS to model the neutron star interior. The only
exception is the recent work of Oechslin et al. (2004) who have used
two EOSs: (i) a pure nuclear matter EOS, based on a relativistic
mean field model; and (ii) a "hybrid'' EOS with a phase transition
to quark matter at high density. At 2 ![]()
![]() (i.e. in the vicinity of nuclear density),
these two EOSs are matched with a polytropic one with
adiabatic index
(i.e. in the vicinity of nuclear density),
these two EOSs are matched with a polytropic one with
adiabatic index
![]() .
This last assumption of
Oechslin et al. is somewhat ad hoc, because the EOS of the neutron star crust is very
different from a polytrope, and its local adiabatic index is much
smaller. Indeed, the crust polytropic index within the inner
crust (which contains some 99.9% of the total crust mass) varies
from
.
This last assumption of
Oechslin et al. is somewhat ad hoc, because the EOS of the neutron star crust is very
different from a polytrope, and its local adiabatic index is much
smaller. Indeed, the crust polytropic index within the inner
crust (which contains some 99.9% of the total crust mass) varies
from
![]() near the neutron drip point to
near the neutron drip point to
![]() in the bottom layers near
the crust-core interface (Douchin & Haensel 2001). The crustal EOS plays a crucial role in defining the mass-shedding limit which marks the end point of quasi-equilibrium binary configurations.
in the bottom layers near
the crust-core interface (Douchin & Haensel 2001). The crustal EOS plays a crucial role in defining the mass-shedding limit which marks the end point of quasi-equilibrium binary configurations.
In the present article, we study the last orbits of irrotational binary neutron star systems by using a set of three dense matter EOSs which are representative of the contemporary many-body theory of dense matter. Contrary to Oechslin et al. (2004), we describe the neutron star crust by means of a realistic EOS obtained in the many-body calculations. As in the works mentioned above, we use the quasi-equilibrium and IWM approximations.
The paper is arranged in the following way: in Sect. 2 the differences between EOSs used in the computation are briefly described. Section 3 is devoted to a description of the numerical methods used to obtain the quasi-equilibrium orbital sequences. In Sect. 4 the results are presented, Sect. 5 contains discussion and final remarks.
The outer layer of a neutron star contains neutron-rich nuclei,
which due to Coulomb repulsion form a crystal lattice if the matter
temperature is below the corresponding melting temperature. This
layer is called the neutron star crust, and extends up to the density
at the crust-core interface,
![]() .
The precise value of
.
The precise value of
![]() is model dependent, and
varies within
(0.6-1.4)
is model dependent, and
varies within
(0.6-1.4) ![]()
![]() .
The EOS of the
crust is rather well established (for a review, see, e.g.,
Haensel 2003). In the present paper the EOS of the crust is
composed of three segments. For densities smaller than
.
The EOS of the
crust is rather well established (for a review, see, e.g.,
Haensel 2003). In the present paper the EOS of the crust is
composed of three segments. For densities smaller than
![]() we used the EOS of Baym et al. (1971). For
we used the EOS of Baym et al. (1971). For
![]() we applied the EOS of Haensel & Pichon (1994), which
makes maximal use of the experimental masses of neutron-rich
nuclei. Finally, for densities
we applied the EOS of Haensel & Pichon (1994), which
makes maximal use of the experimental masses of neutron-rich
nuclei. Finally, for densities
![]() we used the EOS of Douchin & Haensel (2001). For neutron stars of
we used the EOS of Douchin & Haensel (2001). For neutron stars of
![]() ,
the crust contains less than 2% of the stellar mass. However, it is the region most easily deformed under the action
of the tidal forces resulting from the gravitational field
produced by the companion star. Below the melting temperature, elastic
shear terms in the stress tensor are nonzero, but they are two
orders of magnitude smaller than the main diagonal pressure term
(Haensel 2001). Dissipative and thermal effects accompanying
matter flow inside neutron stars will be briefly discussed in
Sect. 5; they are expected to be small at the
quasi-equilibrium evolution stage. Therefore, to a very good
approximation, the crust layer behaves in the tidal force field
as an ideal degenerate fluid, described by a zero temperature EOS.
,
the crust contains less than 2% of the stellar mass. However, it is the region most easily deformed under the action
of the tidal forces resulting from the gravitational field
produced by the companion star. Below the melting temperature, elastic
shear terms in the stress tensor are nonzero, but they are two
orders of magnitude smaller than the main diagonal pressure term
(Haensel 2001). Dissipative and thermal effects accompanying
matter flow inside neutron stars will be briefly discussed in
Sect. 5; they are expected to be small at the
quasi-equilibrium evolution stage. Therefore, to a very good
approximation, the crust layer behaves in the tidal force field
as an ideal degenerate fluid, described by a zero temperature EOS.
An important quantity which actually determines the response of
the crust layer to the compression or decompression of matter is
the adiabatic index
![]() ,
where p is
the local pressure and n the corresponding baryon number
density. In the outer crust, the pressure is determined by the
ultra-relativistic electron gas, so that
,
where p is
the local pressure and n the corresponding baryon number
density. In the outer crust, the pressure is determined by the
ultra-relativistic electron gas, so that
![]() .
However, the
outer crust contains only 10-5 of the NS mass. Some thousand
times more, i.e., about
.
However, the
outer crust contains only 10-5 of the NS mass. Some thousand
times more, i.e., about
![]() ,
is contained in the inner crust, composed of a lattice of heavy neutron-rich nuclei
immersed in a neutron gas and an electron gas. Its adiabatic
index depends strongly on the density, varying from
,
is contained in the inner crust, composed of a lattice of heavy neutron-rich nuclei
immersed in a neutron gas and an electron gas. Its adiabatic
index depends strongly on the density, varying from
![]() near the neutron drip point (extreme softening of the EOS),
up to
near the neutron drip point (extreme softening of the EOS),
up to
![]() close to
close to
![]() (Douchin & Haensel 2001).
(Douchin & Haensel 2001).
The neutron star core contains matter of a density significantly larger
than the normal nuclear density, equal to the saturation density
of infinite symmetric nuclear matter,
![]()
![]()
![]() ,
and corresponding to the baryon number density
,
and corresponding to the baryon number density
![]() .
For
.
For
![]() the EOS of the core
is poorly known, and this uncertainty grows rapidly with
increasing density. The theoretical EOSs, derived using different
theories of dense matter and different methods of solution of the
many-body problem, differ significantly at
the EOS of the core
is poorly known, and this uncertainty grows rapidly with
increasing density. The theoretical EOSs, derived using different
theories of dense matter and different methods of solution of the
many-body problem, differ significantly at
![]() ,
characteristic of the central cores of neutron stars under study.
In the present paper, we will limit ourselves
to neutron star cores consisting of nucleons and hyperons, i.e.,
baryons whose properties are known from terrestrial experiments.
The speculative case of exotic phases of dense matter (kaon and
pion condensation, quark deconfinement), whose existence is - as
of this publication - not substantiated either by experiments or
by astronomical observations, will be considered in future
publications. The most extreme case of hypothetical strange stars
built of self-bound strange quark matter will also be studied
separately.
,
characteristic of the central cores of neutron stars under study.
In the present paper, we will limit ourselves
to neutron star cores consisting of nucleons and hyperons, i.e.,
baryons whose properties are known from terrestrial experiments.
The speculative case of exotic phases of dense matter (kaon and
pion condensation, quark deconfinement), whose existence is - as
of this publication - not substantiated either by experiments or
by astronomical observations, will be considered in future
publications. The most extreme case of hypothetical strange stars
built of self-bound strange quark matter will also be studied
separately.
Three EOSs of the core were considered. Two of them may be
considered as soft and stiff extremes of the EOSs of matter
composed of nucleons, electrons and muons. The first,
BPAL12, is of phenomenological type and can be considered as a
soft extreme of the nucleonic EOS of NS matter (Prakash et al. 1997; Bombaci 1995).
The second, APR, is based on precise variational calculations
and includes realistic two-body (Argonne A18) and three-body
(Urbana UIX) nucleon interactions (Akmal et al. 1998)![]() .
We considered also one EOS in which hyperons are present at
.
We considered also one EOS in which hyperons are present at
![]() ,
where
the threshold for the hyperon appearance
,
where
the threshold for the hyperon appearance
![]() (model 3 of Glendenning 1985); it will be referred to as the GNH3 EOS. This
EOS was obtained using the Relativistic Mean Field model of
baryonic matter. For
(model 3 of Glendenning 1985); it will be referred to as the GNH3 EOS. This
EOS was obtained using the Relativistic Mean Field model of
baryonic matter. For
![]() (nucleons only) this EOS
is very stiff but causal (
(nucleons only) this EOS
is very stiff but causal (
![]() ). The appearance of
hyperons strongly softens the EOS as compared to the pure nucleon
case. The hyperons soften the EOS because they are more massive
than nucleons, and when they start to fill their Fermi sea they
are slow and replace the highest energy nucleons.
). The appearance of
hyperons strongly softens the EOS as compared to the pure nucleon
case. The hyperons soften the EOS because they are more massive
than nucleons, and when they start to fill their Fermi sea they
are slow and replace the highest energy nucleons.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{1441f1.eps}\end{figure}](/articles/aa/full/2005/07/aa1441/Timg44.gif) |
Figure 1:
The pressure p against the energy density |
| Open with DEXTER | |
All three EOSs are displayed in Fig. 1. As we mentioned they are very different because they assume very different strong interaction models at supra-nuclear densities.
The differences between the three EOSs are reflected in the M(R) curves of statically stable models shown in Fig. 2 (M being the gravitational mass and R the area radius).
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{1441f2.eps}\end{figure}](/articles/aa/full/2005/07/aa1441/Timg45.gif) |
Figure 2: Gravitational mass of static isolated stars against area radius for the APR (dashed line), GNH3 (dotted line) and BPAL12 (solid line) EOSs. |
| Open with DEXTER | |
The BPAL12 EOS is overall quite soft, and therefore produces NSs
with R decreasing rapidly with increasing M. The BPAL12 EOS yields the smallest R(M) for
![]() .
The maximum allowable mass for this EOS is marginally consistent with
observations,
.
The maximum allowable mass for this EOS is marginally consistent with
observations,
![]() .
The APR EOS is stiff, with its radius staying nearly constant at
.
The APR EOS is stiff, with its radius staying nearly constant at
![]() km for
km for
![]() ,
and yields high
,
and yields high
![]() .
The BPAL12 and APR EOSs are soft and stiff extremes within our set of the EOSs as far as the values of
.
The BPAL12 and APR EOSs are soft and stiff extremes within our set of the EOSs as far as the values of
![]() are concerned. However, their M(R) intersect at
are concerned. However, their M(R) intersect at
![]() .
Therefore, these EOSs produce NSs with similar
values of the compaction parameter M/R for
.
Therefore, these EOSs produce NSs with similar
values of the compaction parameter M/R for
![]() .
.
The GNH3 EOS is different to the two previous ones, because its M(R) curve is composed of two different segments. The lower-mass segment (
![]() )
consists of stars with no or with
only small hyperon cores. The radius stays nearly constant at
)
consists of stars with no or with
only small hyperon cores. The radius stays nearly constant at
![]() km for
km for
![]() .
This segment is connected via a "knee'' with a high-mass segment consisting of neutron stars with increasingly larger soft hyperon cores. Along
this high-mass (hyperon-softened) segment, R decreases rapidly
with increasing M, reaching a very flat maximum at
.
This segment is connected via a "knee'' with a high-mass segment consisting of neutron stars with increasingly larger soft hyperon cores. Along
this high-mass (hyperon-softened) segment, R decreases rapidly
with increasing M, reaching a very flat maximum at
![]() .
.
Table 1:
Properties of isolated static neutron stars of gravitational mass
![]() for the three EOSs used in our computations.
for the three EOSs used in our computations.
![]() is the compaction parameter,
R is the areal radius,
is the compaction parameter,
R is the areal radius, ![]() is the baryon mass and
is the baryon mass and
![]() is the central energy density, respectively.
is the central energy density, respectively.
Different aspects of the EOSs show up if we consider the
![]() static stars. Their parameters, calculated
using three EOSs, are given in Table 1. A
NS configuration is a functional of the EOS at the
densities
static stars. Their parameters, calculated
using three EOSs, are given in Table 1. A
NS configuration is a functional of the EOS at the
densities ![]() smaller than the central density
smaller than the central density
![]() .
We see that for the GNH3 EOS the central density is barely higher than
the hyperon threshold
.
We see that for the GNH3 EOS the central density is barely higher than
the hyperon threshold
![]() ,
and therefore the EOS inside the NS is very stiff, actually the stiffest of all three.
The highest stiffness of the GNH3 EOS in the interior of a
,
and therefore the EOS inside the NS is very stiff, actually the stiffest of all three.
The highest stiffness of the GNH3 EOS in the interior of a
![]() NS can be clearly recognized by looking at Figs. 1 and 3. Looking at Fig. 1, we see that
this EOS has the highest P at any
NS can be clearly recognized by looking at Figs. 1 and 3. Looking at Fig. 1, we see that
this EOS has the highest P at any
![]() .
Additional information is contained in
Fig. 3: this EOS has particularly large
.
Additional information is contained in
Fig. 3: this EOS has particularly large ![]() for
for
![]() ,
i.e., in the outer layers of the NS core, which are therefore
quite "inflated'' in comparison with those in the other two
NS models. These features are responsible for the particularly large R for the GNH3 EOS.
The GNH3 configuration has the largest R and therefore the
smallest compaction parameter M/R. The BPAL12 EOS is clearly the
softest, with R smaller by 27% than for the GNH3 EOS.
The APR EOS, which is moderately stiff in this mass range,
yields R which is only 8% larger than for the BPAL12 model.
,
i.e., in the outer layers of the NS core, which are therefore
quite "inflated'' in comparison with those in the other two
NS models. These features are responsible for the particularly large R for the GNH3 EOS.
The GNH3 configuration has the largest R and therefore the
smallest compaction parameter M/R. The BPAL12 EOS is clearly the
softest, with R smaller by 27% than for the GNH3 EOS.
The APR EOS, which is moderately stiff in this mass range,
yields R which is only 8% larger than for the BPAL12 model.
The differences in stiffness reflect the characteristics of the
nuclear model underlying each of the EOSs of the NS core. Using
the density-dependent adiabatic index ![]() it is particularly
easy to visualize these differences, see Fig. 3. The
strong drop in
it is particularly
easy to visualize these differences, see Fig. 3. The
strong drop in ![]() above
above
![]() reflects the hyperon
softening in the GNH3 EOS. The values of
reflects the hyperon
softening in the GNH3 EOS. The values of ![]() increasing up to
the maximum at
increasing up to
the maximum at
![]() tell us about the stiffening of
the APR EOS at
tell us about the stiffening of
the APR EOS at
![]() ,
in contrast to the behavior of
the GNH3 EOS which softens close to this density. Finally, the
BPAL12 EOS remains close to a polytrope with
,
in contrast to the behavior of
the GNH3 EOS which softens close to this density. Finally, the
BPAL12 EOS remains close to a polytrope with
![]() ,
except for a small region around
,
except for a small region around ![]() .
.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{1441f3.eps}\end{figure}](/articles/aa/full/2005/07/aa1441/Timg68.gif) |
Figure 3:
The adiabatic index |
| Open with DEXTER | |
The present computations of close binary neutron star systems rely on the assumption of a quasi-equilibrium state (helical Killing vector approximation), with irrotational flow of the fluid, and a conformally flat spatial 3-m (Isenberg-Wilson-Mathews approximation). We construct the quasi-equilibrium sequences of binary neutron stars described by the realistic EOSs using a numerical code which solves the five coupled, nonlinear, elliptic equations for the gravitational field, supplemented by an elliptic equation for the velocity potential of irrotational flows. The code has been used successfully for calculating the final phase of the inspiral of binary neutron stars described by the polytropic equation of state (Taniguchi & Gourgoulhon 2002b,a,2003; Taniguchi et al. 2001). This code is built upon the C++ library L ORENE (http://www.lorene.obspm.fr) and can be downloaded freely from the L ORENE CVS repository, as Lorene/Codes/Bin_star/coal.C. The complete description of the resulting general relativistic equations, the whole algorithm, as well numerous tests of the code can be found in Gourgoulhon et al. (2001). Additional tests have been presented in Sect. 3 of Taniguchi & Gourgoulhon (2003).
The numerical technique relies on a multi-domain spectral method
with surface-fitted coordinates. We have used one domain for each star and 3 (resp. 4) domains for the space around them for a large (resp. small) separation. In each domain,
the number of collocation points of the spectral method is chosen
to be Nr ![]()
![]()
![]()
![]() = 25
= 25 ![]() 17
17 ![]() 16, where Nr,
16, where Nr,
![]() ,
and
,
and
![]() denote the number of points in the radial, polar and azimuthal directions respectively. The accuracy of the computed relativistic models
was estimated using a relativistic generalization of the the
Virial Theorem (Friedman et al. 2002; see also Sect. 3.A of Taniguchi & Gourgoulhon 2003). The virial relative error was a few times 10-5.
denote the number of points in the radial, polar and azimuthal directions respectively. The accuracy of the computed relativistic models
was estimated using a relativistic generalization of the the
Virial Theorem (Friedman et al. 2002; see also Sect. 3.A of Taniguchi & Gourgoulhon 2003). The virial relative error was a few times 10-5.
Let us briefly discuss a technical difference between the computations of the realistic EOS irrotational binary NS and the polytropic case considered by Bonazzola et al. (1999), Marronetti et al. (1999), Uryu & Eriguchi (2000), Uryu et al. (2000), Gourgoulhon et al. (2001) and Taniguchi & Gourgoulhon (2002b,2003).
The difference stems from the fact that the realistic EOS presented in Sect. 2 are
given in tabulated form, and a certain thermodynamic coefficient ![]() ,
(required in the computation of the velocity potential of the irrotational fluid flow, cf. Sect. 2 of Gourgoulhon et al. 2001) is not given explicitly by the tabulated EOS.
,
(required in the computation of the velocity potential of the irrotational fluid flow, cf. Sect. 2 of Gourgoulhon et al. 2001) is not given explicitly by the tabulated EOS.
As already discussed in Sect. 2, we adopt the approximation of
the perfect fluid for the form of the stress-energy tensor, and we
represent the NS matter by a zero-temperature EOS. In view of
this, we can use the Gibbs-Duhem identity:
Following Gourgoulhon et al. (2001), we write the equation for the
coefficient ![]() as
as
In practice, we used two methods to get the adiabatic index
![]() .
In the first method we used an
analytical formula for the adiabatic index being an approximation of
tabulated values of
.
In the first method we used an
analytical formula for the adiabatic index being an approximation of
tabulated values of ![]() .
In the second method the adiabatic
index was obtained directly from a tabulated EOS by taking the
derivative of the second order polynomial which goes through three
consecutive (p, n) EOS points. The value of the
.
In the second method the adiabatic
index was obtained directly from a tabulated EOS by taking the
derivative of the second order polynomial which goes through three
consecutive (p, n) EOS points. The value of the
![]() multiplied by the n/p ratio is evaluated at the middle point, and
the resulting discrete values of
multiplied by the n/p ratio is evaluated at the middle point, and
the resulting discrete values of ![]() are ready to be
interpolated, similar to the other quantities from the tabulated EOS.
are ready to be
interpolated, similar to the other quantities from the tabulated EOS.
The second method proved to be very robust, and acts as a consistency check; it was tested with EOS for which the precise values of the adiabatic index were obtained from the microscopic considerations, namely for the SLy EOS (Douchin & Haensel 2000).
In this section we present the numerical results for evolutionary
sequences of close neutron star binaries described by the three
realistic EOS introduced in Sect. 2. By evolutionary sequence, we mean a sequence of quasi-equilibrium
configurations of decreasing separation d and with constant
baryon mass ![]() .
Such a sequence is expected to
approximate the true evolution of binary neutron
stars, which is entirely driven by the reaction to gravitational
radiation and hence occur at fixed baryon number and fluid
circulation (zero in the irrotational case considered here). We
calculated evolutionary sequences of binary systems composed of two
identical neutron stars (equal mass system), with the baryon mass
.
Such a sequence is expected to
approximate the true evolution of binary neutron
stars, which is entirely driven by the reaction to gravitational
radiation and hence occur at fixed baryon number and fluid
circulation (zero in the irrotational case considered here). We
calculated evolutionary sequences of binary systems composed of two
identical neutron stars (equal mass system), with the baryon mass ![]() corresponding to the gravitational mass
corresponding to the gravitational mass
![]() for a static isolated star (see Table 1 for the values of
for a static isolated star (see Table 1 for the values of ![]() ).
We have selected the gravitational mass
).
We have selected the gravitational mass
![]() for two reasons:
(i) it agrees with the "average NS mass'' obtained from
observations of radio pulsars in binary system; and (ii) it allows
us to compare our results with calculations made by other authors
for polytropic models (Faber et al. 2002).
for two reasons:
(i) it agrees with the "average NS mass'' obtained from
observations of radio pulsars in binary system; and (ii) it allows
us to compare our results with calculations made by other authors
for polytropic models (Faber et al. 2002).
For the present discussion, let us recall the definition of the ADM mass
of the system, which measures the total energy content of a slice
![]() of spacetime (hypersurface
of spacetime (hypersurface ![]() ):
):
![\begin{figure}
\par\includegraphics[angle=-90,width=8.15cm,clip]{1441f4a.eps}\hs...
...ace*{2mm}
\includegraphics[angle=-90,width=8.15cm,clip]{1441f4f.eps}\end{figure}](/articles/aa/full/2005/07/aa1441/Timg89.gif) |
Figure 4: Baryon number density isocontours in the coordinate plane y=0 (containing the rotation axis) ( left panels) and in the coordinate plane z=0 (orbital plane) ( right panels), for configurations close to the mass-shedding limit. The upper (resp. middle, lower) panels correspond to the GNH3 (resp. APR, BPAL12) EOS. The thick solid lines denote stellar surfaces. |
| Open with DEXTER | |
At infinite separation, the ADM mass of the system, Eqs. (3) and (4), tends toward the sum of the gravitational masses of isolated static stars,
and will be denoted by ![]() :
:
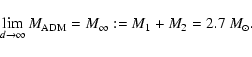 |
(5) |
| (6) |
Each evolutionary sequence terminates by a mass-shedding point, which marks the end of existence of quasi-equilibrium configurations. The shape of the stars close to this limit is presented in Fig. 4. The mass-shedding is revealed by the formation of a cusp at the stellar surface in the direction of the companion (Roche lobe overflow). This cusp is marginally visible in Fig. 4.
A turning point of
![]() along an evolutionary sequence
would indicate an orbital instability (Friedman et al. 2002).
This instability originates both from relativistic effects (the well-known
r=6M last stable orbit of Schwarzschild metric) and hydrodynamical
effects (for instance, such an instability exists for sufficiently
stiff EOS in the Newtonian regime, see e.g. Taniguchi et al. 2001 and
references therein). It is secular for synchronized systems and dynamical for irrotational ones, such as those considered here. Thus the quasi-equilibrium inspiral of binary neutron stars
can terminate by either the orbital instability (turning point
of
along an evolutionary sequence
would indicate an orbital instability (Friedman et al. 2002).
This instability originates both from relativistic effects (the well-known
r=6M last stable orbit of Schwarzschild metric) and hydrodynamical
effects (for instance, such an instability exists for sufficiently
stiff EOS in the Newtonian regime, see e.g. Taniguchi et al. 2001 and
references therein). It is secular for synchronized systems and dynamical for irrotational ones, such as those considered here. Thus the quasi-equilibrium inspiral of binary neutron stars
can terminate by either the orbital instability (turning point
of
![]() )
or the mass-shedding limit. In the latter case, there might exist
equilibrium configurations beyond the mass-shedding limit,
i.e. dumb-bell like configurations (see e.g. Eriguchi & Hachisu 1985).
However dynamical calculations for the
)
or the mass-shedding limit. In the latter case, there might exist
equilibrium configurations beyond the mass-shedding limit,
i.e. dumb-bell like configurations (see e.g. Eriguchi & Hachisu 1985).
However dynamical calculations for the
![]() polytrope
have shown that the time to coalescence was shorter than one
orbital period for configurations at the mass-shedding limit
(Marronetti et al. 2004; Shibata & Uryu 2001). Therefore we may safely
define the end of quasi-equilibrium inspiral by the mass-shedding
limit in the case where no turning point of
polytrope
have shown that the time to coalescence was shorter than one
orbital period for configurations at the mass-shedding limit
(Marronetti et al. 2004; Shibata & Uryu 2001). Therefore we may safely
define the end of quasi-equilibrium inspiral by the mass-shedding
limit in the case where no turning point of
![]() is found along the sequences
(which is actually the present case, as we shall discuss below).
is found along the sequences
(which is actually the present case, as we shall discuss below).
The variation of the orbital binding energy along evolutionary
sequences is presented in Fig. 5, where the points
correspond to the equilibrium configurations of binary system
calculated using a numerical method (see Sect. 3) and the
lines present our best fit described in detail in
Sect. 4.3. In the scale of Fig. 5 there is
no visible difference between our numerical results and the fit,
i.e. fitting curves pass through the points. We plotted also the
binding energy obtained in the framework of Newtonian theory and
the 3PN post-Newtonian approximation for point masses
(Blanchet 2002). Figure 5 shows clearly that no
turning point of
![]() occurs along the evolutionary sequences.
Hence there is no orbital instability prior to the mass-shedding
limit. We conclude that the innermost stable circular orbit (ISCO) of the computed
configurations are given by the mass-shedding limit.
occurs along the evolutionary sequences.
Hence there is no orbital instability prior to the mass-shedding
limit. We conclude that the innermost stable circular orbit (ISCO) of the computed
configurations are given by the mass-shedding limit.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.65cm,clip]{1441f5.eps}\end{figure}](/articles/aa/full/2005/07/aa1441/Timg95.gif) |
Figure 5:
Orbital binding energy
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.45cm,clip]{1441f6.eps}\end{figure}](/articles/aa/full/2005/07/aa1441/Timg96.gif) |
Figure 6:
Orbital binding energy of the binary system minus the (point mass)
Newtonian term
|
| Open with DEXTER | |
To compare different approaches to the relativistic description of binary
systems we present in Fig. 6 the orbital binding
energy after subtraction of the Newtonian term ![]()
![]() .
This figure shows the effects of general relativity and of
finite sizes (hydrodynamics). One can see that binary neutron star systems are quite far from
Newtonian and 1PN systems. On the contrary, 2PN and 3PN results
by Blanchet (2002) and 3PN results by Damour et al. (2000)
are very close to our results for a wide range of frequencies.
Note that the difference between 2PN and 3PN approximations are much larger
in the Damour et al. (2000) treatment (Effective One Body method)
than in that of Blanchet (2002) (standard post-Newtonian expansion).
.
This figure shows the effects of general relativity and of
finite sizes (hydrodynamics). One can see that binary neutron star systems are quite far from
Newtonian and 1PN systems. On the contrary, 2PN and 3PN results
by Blanchet (2002) and 3PN results by Damour et al. (2000)
are very close to our results for a wide range of frequencies.
Note that the difference between 2PN and 3PN approximations are much larger
in the Damour et al. (2000) treatment (Effective One Body method)
than in that of Blanchet (2002) (standard post-Newtonian expansion).
Following Faber et al. (2002), we have performed some polynomial fits to
each of the computed sequences. This is a very important step in order to obtain the first
derivative of the functions required for the energy spectrum of
gravitational waves (see below). We used two different approaches
to approximate our numerical results. The first one, similar to
that presented by Faber et al. (2002), is based on quadratic
approximation of numerical results. We decided to
make a fit only to the difference between exact results obtained
for the ADM mass
![]() (cf. Eq. (3)) and
the prediction of the Newtonian theory - i.e. we made a fit to the
function
(cf. Eq. (3)) and
the prediction of the Newtonian theory - i.e. we made a fit to the
function
![]() ,
where the second
term corresponds to the Newtonian point-like mass behaviour with
,
where the second
term corresponds to the Newtonian point-like mass behaviour with
![]()
![]()
![]() .
We found it sufficient to fit the numerical results
by a second order polynomial without any linear term:
.
We found it sufficient to fit the numerical results
by a second order polynomial without any linear term:
However it is possible to find a much better approximation of the
numerical results if one takes into account a high order
post-Newtonian approximation for the binding energy of point-mass
systems. The 3PN formula as obtained by Blanchet (2002) from the
standard![]() post-Newtonian
expansion reads
post-Newtonian
expansion reads
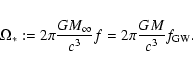
Table 2: Parameters of polynomial fits (7) and (9).
![\begin{figure}
\par\includegraphics[angle=-90,width=7.7cm,clip]{1441f7.eps}\end{figure}](/articles/aa/full/2005/07/aa1441/Timg117.gif) |
Figure 7:
Difference
|
| Open with DEXTER | |
In Fig. 7 we present the difference between our
numerical results and the 3PN approximation given by Eq. (8). Formula (8) approximates very well the behavior of a binary system of realistic neutron stars for a very
large range of binary periods (notice the scale of the y-axis of Fig. 7!). From Fig. 7, we can define the frequencies
![]() as those frequencies at which the
deviation from point-mass behavior becomes important. The values
of these frequencies for each of the three considered EOSs are
given in Table 3. Of course, they are not precise
numbers and should be treated as having a
as those frequencies at which the
deviation from point-mass behavior becomes important. The values
of these frequencies for each of the three considered EOSs are
given in Table 3. Of course, they are not precise
numbers and should be treated as having a ![]()
![]() uncertainty. We can approximate the results presented in Fig. 7 by the power-law dependence on frequency
uncertainty. We can approximate the results presented in Fig. 7 by the power-law dependence on frequency
![]() :
:
One can draw an important conclusion from the presented results and
their comparison with relativistic approximations for point masses
in a binary system. We can expect that taking into account the next
orders in a post-Newtonian approximation does not change the energy
by an amount larger than the difference between 2PN and 3PN models. As a consequence the large deviation of our numerical results from the 3PN approximation is caused by the effect of a
finite size of the star (e.g. tidal forces). The very high power n in relation (9) indicates that, even for small departures from a point mass approximation,
high-order tidal effects are very important, and dominate the relation
![]() .
Indeed the lowest order tidal term is known to be n=4 (Lai et al. 1994)
and the values obtained here are well above this.
.
Indeed the lowest order tidal term is known to be n=4 (Lai et al. 1994)
and the values obtained here are well above this.
We computed the energy spectrum of gravitational waves obtained as the first derivatives of the
fitted functions (Eq. (9)). The relation between
![]() and the GW frequency
and the GW frequency
![]() is presented in Fig. 8. In this figure we draw
straight lines corresponding to the Newtonian case
is presented in Fig. 8. In this figure we draw
straight lines corresponding to the Newtonian case ![]()
![]() to find the break frequencies at which the energy spectrum has dropped by 20%, 25%, 40%. These values are
important from the point of view of future detections: they show the difference between the amplitude of the real signal and the Newtonian template which allows to calculate the real wave form
amplitude from the detector noise. We also compare our results to the 25% case from Faber et al. (2002). There is no visible difference between our models for different EOSs at the break frequency level of 10% (the case considered by Faber et al. 2002) and the situation is then
very precisely described by the 3PN formula.
to find the break frequencies at which the energy spectrum has dropped by 20%, 25%, 40%. These values are
important from the point of view of future detections: they show the difference between the amplitude of the real signal and the Newtonian template which allows to calculate the real wave form
amplitude from the detector noise. We also compare our results to the 25% case from Faber et al. (2002). There is no visible difference between our models for different EOSs at the break frequency level of 10% (the case considered by Faber et al. 2002) and the situation is then
very precisely described by the 3PN formula.
Table 3:
Gravitational wave frequencies (in Hz) computed from the calculated data for GNH3, APR and BPAL12 EOSs: the
![]() denotes the frequency at which the non-point-mass effects start to be important,
denotes the frequency at which the non-point-mass effects start to be important,
![]() and
and
![]() are the so-called break-frequencies (see text), whereas
are the so-called break-frequencies (see text), whereas
![]() is the GW frequency on the final orbit.
is the GW frequency on the final orbit.
Up to now, all calculations (except those of Oechslin et al. 2004) of the hydrodynamical inspiral and merger phases have been done for the simplified equation of state of
dense matter, for the polytropic EOS, where the dependence between
pressure and baryon density is given by
![]() .
It has been shown that the results obtained
for these polytropic EOSs depend mainly on the compaction
parameter M/R. It is therefore interesting to check if the
properties of inspiraling neutron stars described by a realistic EOS
can be predicted, in a good approximation, by studying binaries
with assumed polytropic EOSs. In order to make such a comparison
we construct sequences of binary NSs described by polytropic EOS
parametrized by the compaction parameter M/R given in Table 1
for each of the three realistic equations of state. For a given
.
It has been shown that the results obtained
for these polytropic EOSs depend mainly on the compaction
parameter M/R. It is therefore interesting to check if the
properties of inspiraling neutron stars described by a realistic EOS
can be predicted, in a good approximation, by studying binaries
with assumed polytropic EOSs. In order to make such a comparison
we construct sequences of binary NSs described by polytropic EOS
parametrized by the compaction parameter M/R given in Table 1
for each of the three realistic equations of state. For a given
![]() ,
we calculate the value of the
,
we calculate the value of the ![]() coefficient which yields the same R at
coefficient which yields the same R at
![]() as that predicted by a selected realistic EOS used in the present paper.
The values of
as that predicted by a selected realistic EOS used in the present paper.
The values of ![]() ,
the pressure coefficient
,
the pressure coefficient ![]() ,
and the baryon masses of polytropic static isolated NSs of
,
and the baryon masses of polytropic static isolated NSs of
![]() are presented in Table 4.
are presented in Table 4.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.05cm,clip]{1441f8.eps}\end{figure}](/articles/aa/full/2005/07/aa1441/Timg128.gif) |
Figure 8: Energy spectrum of GW waves emitted by the binary neutron star system versus frequency of gravitational waves (twice the orbital frequency) along three irrotational quasi-equilibrium sequences. The straight lines correspond to the Newtonian dependence of energy multiplied by 1, 0.8, 0.75 and 0.6. |
| Open with DEXTER | |
Table 4:
Pressure coefficient ![]() ,
adiabatic index
,
adiabatic index ![]() and baryon mass
and baryon mass ![]() for polytropic NSs having the same compactness parameter and mass (
for polytropic NSs having the same compactness parameter and mass (
![]() )
than NSs described by realistic EOSs (Table 1) (
)
than NSs described by realistic EOSs (Table 1) (
![]()
![]()
![]() and
and
![]() ).
).
![\begin{figure}
\par\includegraphics[angle=-90,width=7.6cm,clip]{1441f9.eps}\end{figure}](/articles/aa/full/2005/07/aa1441/Timg133.gif) |
Figure 9:
Gravitational mass versus stellar radius for sequences of static neutron stars described by the Akmal et al. (1998) EOS (solid line) and polytropic EOS with |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.65cm,clip]{1441f10.eps}\end{figure}](/articles/aa/full/2005/07/aa1441/Timg134.gif) |
Figure 10:
Binding energy of a binary neutron star system as a function of gravitational wave frequency for the APR EOS (thick solid line) and two corresponding polytropic EOS with
|
| Open with DEXTER | |
In Fig. 9 we show the dependence of gravitational mass
versus radius for isolated non-rotating stars based on the APR EOS,
and two different polytropes having M/R = 0.176 and
![]() at infinite separation. Finally in Fig. 10 we present
the binding energy versus the frequency of gravitational waves at the
last orbits of the inspiral for the APR EOS and the two corresponding
polytropes. The differences between quasi-equilibrium sequences
described by realistic and polytropic sequences are small. For the three
different EOSs (APR and two polytropes) the frequency of gravitational
waves at the last calculated orbit (
at infinite separation. Finally in Fig. 10 we present
the binding energy versus the frequency of gravitational waves at the
last orbits of the inspiral for the APR EOS and the two corresponding
polytropes. The differences between quasi-equilibrium sequences
described by realistic and polytropic sequences are small. For the three
different EOSs (APR and two polytropes) the frequency of gravitational
waves at the last calculated orbit (
![]() )
is
)
is ![]()
![]() .
Also the binding energy of the system at the mass-shedding point is
close to each other, between -0.0372 and
.
Also the binding energy of the system at the mass-shedding point is
close to each other, between -0.0372 and
![]() .
However one can see the differences in the frequencies
.
However one can see the differences in the frequencies
![]() at which
non-point-mass effects start to be important. The
at which
non-point-mass effects start to be important. The
![]() has the
smallest value for the polytrope with
has the
smallest value for the polytrope with
![]() and the highest for
and the highest for
![]() .
Although the matter in the stellar interior is stiffer for
the APR EOS (
.
Although the matter in the stellar interior is stiffer for
the APR EOS (
![]() ,
see Fig. 3), which is also
clear from Fig. 9, the APR curve lies between the
,
see Fig. 3), which is also
clear from Fig. 9, the APR curve lies between the
![]() and
and
![]() polytropes in Fig. 10.
This is due to the relatively soft equation of state for the crust for realistic NS models, which makes the response of the crust to tidal forces different from that of a polytrope
with
polytropes in Fig. 10.
This is due to the relatively soft equation of state for the crust for realistic NS models, which makes the response of the crust to tidal forces different from that of a polytrope
with
![]() or
or ![]() .
.
We obtained similar results by comparing two other sequences of realistic EOS - BPAL12 and GNH3 with corresponding polytropic cases. The irrotational flow is weakly affected by the changes in the EOS of the core, but it is expected that the differences should be seen in the merger phase. The outer layers of the star (those with sub-nuclear densities, i.e., the crust), which are properly treated in the present paper have an influence on the properties of the binary system at the last stages of inspiral. However the crucial parameter which determines the energy-frequency spectrum (energy per frequency) of emitted gravitational energy is M/R.
We have presented a set of evolutionary sequences of binary neutron stars based on three selected realistic EOSs. These EOSs are based on modern many-body calculations. Three baryonic EOSs of a neutron-star core have been joined with a recent EOS of a neutron-star crust, and in this way we obtained three different models of the neutron star interior, from the surface to the stellar center. We restricted our analysis to models of neutron star cores without exotic phases (meson condensates, quark matter). In this way, the differences between the core EOSs reflect the uncertainties in the existing theories of the interactions in nuclear matter.
In the present paper we considered only those constituents of dense matter, that have been studied in the laboratory. We did not consider phase transitions to hypothetical exotic phases of dense matter, which were proposed by many authors, but which still remain speculative. Results obtained for the NS-NS binaries with exotic-phase neutron-star cores and realistic envelopes will be considered in future publications. Similarly, the case of a binary involving strange quark stars built of self-bound strange quark matter will also be presented in a separate paper.
We have computed quasi-equilibrium sequences of an irrotational NS-NS binary by keeping the baryon mass constant to a value that corresponds to individual gravitational masses of
![]() at infinite separation. For a long time of evolution of the binary system its binding energy
is very accurately given by the 3PN post-Newtonian formula for a point-mass
system. However the departure from this 3PN model at low binary periods has a quite abrupt character, presumably due to high order tidal effects. The sequences end at the onset of the mass transfer between the stars (i.e. when a cusp forms at the surface of the stars).
This point defines the ISCO since no turning point of the binding energy
has been found along the sequences, which would have revealed some
orbital instability. The gravitational wave frequency at the ISCO is
800 Hz, 1130 Hz and 1230 Hz, for the GNH3, APR and BPAL12 EOSs respectively.
at infinite separation. For a long time of evolution of the binary system its binding energy
is very accurately given by the 3PN post-Newtonian formula for a point-mass
system. However the departure from this 3PN model at low binary periods has a quite abrupt character, presumably due to high order tidal effects. The sequences end at the onset of the mass transfer between the stars (i.e. when a cusp forms at the surface of the stars).
This point defines the ISCO since no turning point of the binding energy
has been found along the sequences, which would have revealed some
orbital instability. The gravitational wave frequency at the ISCO is
800 Hz, 1130 Hz and 1230 Hz, for the GNH3, APR and BPAL12 EOSs respectively.
In a recent work based on the numerical integration of the full set of time-dependent Einstein
equations, Marronetti et al. (2004) have located the dynamical ISCO by comparing the time evolution of
quasi-equilibrium initial data at various separations
(see also Fig. 14 of Shibata & Uryu 2001). This defines the true ISCO, as opposed to the "quasi-equilibrium'' ISCO obtained here. For a polytropic EOS with ![]() and a compactness
parameter M/R=0.14, they obtain the ISCO at an orbital frequency which is 15% lower than the mass-shedding frequency of the quasi-equilibrium sequence of Taniguchi & Gourgoulhon (2002b).
This makes us confident that the values of the gravitational wave frequencies
given above are quite close to those of the end of the true inspiral.
and a compactness
parameter M/R=0.14, they obtain the ISCO at an orbital frequency which is 15% lower than the mass-shedding frequency of the quasi-equilibrium sequence of Taniguchi & Gourgoulhon (2002b).
This makes us confident that the values of the gravitational wave frequencies
given above are quite close to those of the end of the true inspiral.
When comparing our results with those of the recent work of Oechslin et al. (2004), one should stress the basic difference in the EOS of matter at sub-nuclear densities. Oechslin et al. represented
the EOS of the crust by a polytrope with the adiabatic index
![]() .
In this way, they made their EOS quasi-continuous at the crust-core interface, because their nuclear core EOS is very stiff. However, such an EOS for the crust is very unrealistic, because the real
.
In this way, they made their EOS quasi-continuous at the crust-core interface, because their nuclear core EOS is very stiff. However, such an EOS for the crust is very unrealistic, because the real ![]() can be as low as 0.5 near the neutron drip point. As the crust EOS is crucial for the last stable orbits
of the NS binary, this implies differences between their and our results,
even if for a
can be as low as 0.5 near the neutron drip point. As the crust EOS is crucial for the last stable orbits
of the NS binary, this implies differences between their and our results,
even if for a
![]() model, the compactness M/R resulting from the GNH3 EOS and their EOS are very close. In particular, Oechslin et al. (2004) have found a turning point in the binding
energy along their sequences, resulting in a quasi-equilibrium ISCO. This difference is certainly due to the stiffness of the polytropic EOS used by them in the outer layers of the star.
For polytropic irrotational binaries a turning point ISCO exists only if
model, the compactness M/R resulting from the GNH3 EOS and their EOS are very close. In particular, Oechslin et al. (2004) have found a turning point in the binding
energy along their sequences, resulting in a quasi-equilibrium ISCO. This difference is certainly due to the stiffness of the polytropic EOS used by them in the outer layers of the star.
For polytropic irrotational binaries a turning point ISCO exists only if
![]() (Uryu et al. 2000; Taniguchi & Gourgoulhon 2003).
(Uryu et al. 2000; Taniguchi & Gourgoulhon 2003).
In our calculations we treated the neutron-star matter as an ideal fluid. In other words, we neglected the elastic shear (in the crust - if not molten) and viscous (in the crust and in the core) terms in the matter stress tensor. There, the terms are believed to be small, but they lead to specific physical phenomena. In particular, the matter flow in NS interior will break the beta equilibrium between baryons and leptons, and this will imply a neutrino burst at the last stage of inspiral (see Haensel 1992). Moreover, dissipative processes will heat the matter. Both effects will be studied in future publications.
All numerical results presented here, including the full binary configurations, are available for downloading from the LORENE main server http://www.lorene.obspm.fr/data/
Acknowledgements
We are grateful to Luc Blanchet for providing us with the formulae for the binding energy at various post-Newtonian orders. We also warmly thank Koji Uryu for useful discussions and careful reading of the manuscript. This work has been funded by the KBN grants 5P03D.017.21, 2P03D.019.24, 1P03D.008.27 and PBZ-KBN-054/P03/2001 and has been partially supported by the Associated European Laboratory Astro-PF (Astrophysics Poland-France) and by the "Bourses de recherche 2004 de la Ville de Paris''. K.T. also acknowledges a Grant-in-Aid for Scientific Research (No. 14-6898) of the Japanese Ministry of Education, Culture, Sports, Science and Technology.