We describe a new explicit three-dimensional magnetohydrodymanic code, which solves the standard zero-
A&A 430, 1067-1087 (2005)
DOI: 10.1051/0004-6361:20041519
G. Aulanier1 - P. Démoulin1 - R. Grappin2
1 - Observatoire de Paris, LESIA, 92195 Meudon Cedex, France
2 - Observatoire de Paris, LUTH, 92195 Meudon Cedex, France
Received 23 June 2004 / Accepted 19 September 2004
Abstract
We describe a new explicit three-dimensional magnetohydrodymanic
code, which solves the standard zero-![]() MHD equations in
Cartesian geometry, with line-tied conditions at the lower boundary
and open conditions at the other ones. Using this code in the frame
of solar active regions, we simulate the evolution of an initially
potential and concentrated bipolar magnetic field, subject to
various sub-Alfvénic photospheric twisting motions which preserve
the initial photospheric vertical magnetic field. Both continuously
driven and relaxation runs are performed. Within the numerical
domain, a steep equilibrium curve is found for the altitude of
the apex of the field line rooted in the vortex centers as a
function of the twist. Its steepness strongly depends on the degree
of twist in outer field lines rooted in weak field regions. This
curve fits the analytical expression for the asymptotic behaviour
of force-free fields of spherical axisymmetric dipoles subject to
azimuthal shearing motions, as well as the curve derived for other
line-tied twisted flux tubes reported in previous works. This
suggests that it is a generic property of line-tied sheared/twisted
arcades. However, contrary to other studies we never find a
transition toward a non-equilibrium within the numerical domain,
even for twists corresponding to steep regions of the equilibrium
curve. The calculated configurations are analyzed in the frame of
solar observations. We discuss which specific conditions are
required for the steepness of the generic equilibrium curve to
result in dynamics which are typical of both fast and slow CMEs
observed below 3
MHD equations in
Cartesian geometry, with line-tied conditions at the lower boundary
and open conditions at the other ones. Using this code in the frame
of solar active regions, we simulate the evolution of an initially
potential and concentrated bipolar magnetic field, subject to
various sub-Alfvénic photospheric twisting motions which preserve
the initial photospheric vertical magnetic field. Both continuously
driven and relaxation runs are performed. Within the numerical
domain, a steep equilibrium curve is found for the altitude of
the apex of the field line rooted in the vortex centers as a
function of the twist. Its steepness strongly depends on the degree
of twist in outer field lines rooted in weak field regions. This
curve fits the analytical expression for the asymptotic behaviour
of force-free fields of spherical axisymmetric dipoles subject to
azimuthal shearing motions, as well as the curve derived for other
line-tied twisted flux tubes reported in previous works. This
suggests that it is a generic property of line-tied sheared/twisted
arcades. However, contrary to other studies we never find a
transition toward a non-equilibrium within the numerical domain,
even for twists corresponding to steep regions of the equilibrium
curve. The calculated configurations are analyzed in the frame of
solar observations. We discuss which specific conditions are
required for the steepness of the generic equilibrium curve to
result in dynamics which are typical of both fast and slow CMEs
observed below 3 ![]() .
We provide natural interpretations
for the existence of asymmetric and multiple concentrations of
electric currents in homogeneoulsy twisted sunspots, due to the
twisting of both short and long field lines. X-ray sigmoïds
are reproduced by integrating the Joule heating term along the
line-of-sight. These sigmoïds have inverse-S shapes
associated with negative force-free parameters
.
We provide natural interpretations
for the existence of asymmetric and multiple concentrations of
electric currents in homogeneoulsy twisted sunspots, due to the
twisting of both short and long field lines. X-ray sigmoïds
are reproduced by integrating the Joule heating term along the
line-of-sight. These sigmoïds have inverse-S shapes
associated with negative force-free parameters ![]() ,
which
is consistent with observed rules in the northern solar
hemisphere. We show that our sigmoïds are not formed
in the main twisted flux tube, but rather in an ensemble of
low-lying sheared and weakly twisted field lines, which
individually never trace the whole sigmoïd, and which
barely show their distorded shapes when viewed in projection.
We find that, for a given bipolar configuration and a given
twist, neither the
,
which
is consistent with observed rules in the northern solar
hemisphere. We show that our sigmoïds are not formed
in the main twisted flux tube, but rather in an ensemble of
low-lying sheared and weakly twisted field lines, which
individually never trace the whole sigmoïd, and which
barely show their distorded shapes when viewed in projection.
We find that, for a given bipolar configuration and a given
twist, neither the ![]() nor the altitude of the lines whose
envelope is a sigmoïd depends on the vortex size.
nor the altitude of the lines whose
envelope is a sigmoïd depends on the vortex size.
Key words: magnetohydrodynamics (MHD) - methods: numerical - Sun: magnetic fields - Sun: photosphere - Sun: corona
Several astrophysical objects are composed of an extended diluted
medium filled by highly ionized plasma, which is coupled to a much
denser region by magnetic fields which pass from one medium to
the other. Some stellar atmospheres, and the environment
of hot accretion disks, fall into this class. The case of the Sun
is particularly interesting in the study of such couplings, since
its proximity provides detailed observations which put strong
constraints on the theory. Below helmet streamers the low solar
corona is composed of a collisional plasma. Its ![]() parameter
is well below unity, so that it is dominated by magnetic fields.
Its pressure scale-height is of the order of the largest observable
structures, and its Lundquist number is larger than one by orders
of magnitude. The coronal magnetic fields are not "independent'',
since they penetrate the dense solar interior through the photospheric
interface in sunspot and network regions, where
parameter
is well below unity, so that it is dominated by magnetic fields.
Its pressure scale-height is of the order of the largest observable
structures, and its Lundquist number is larger than one by orders
of magnitude. The coronal magnetic fields are not "independent'',
since they penetrate the dense solar interior through the photospheric
interface in sunspot and network regions, where ![]() and the
pressure scale height increase rapidly with depth as
the photosphere becomes opaque. The density gradients then imply
that magnetosonic waves emitted in the corona are almost fully
reflected by the photosphere. So the photospheric dynamics (whose
time-scales are typically much larger than the Alfvén ones) are
barely influenced by the coronal evolution. However, the
long-term evolution of the corona is dominated by the
photospheric forcing. In this context, the evolution
of coronal magnetic fields forced by slow photospheric motions can
be studied in the frame of magnetohydrodynamics (MHD).
and the
pressure scale height increase rapidly with depth as
the photosphere becomes opaque. The density gradients then imply
that magnetosonic waves emitted in the corona are almost fully
reflected by the photosphere. So the photospheric dynamics (whose
time-scales are typically much larger than the Alfvén ones) are
barely influenced by the coronal evolution. However, the
long-term evolution of the corona is dominated by the
photospheric forcing. In this context, the evolution
of coronal magnetic fields forced by slow photospheric motions can
be studied in the frame of magnetohydrodynamics (MHD).
The very different physical regimes in the two media are very
difficult to treat numerically altogether, so that two major
simplications can be made. Firstly,
the photosphere can be treated as a so-called "line-tied'' boundary.
This extreme assumption implies that this boundary is infinitely
conductive, inertial and reflective. Secondly, the low corona can
be treated as a pressureless medium (![]() )
in which gravity
plays no role, so that only the Lorentz force can accelerate the
plasma. Even though this last assumption is not always made, it
becomes mandatory so as to treat large systems having magnetic
field contrasts of several orders of magnitude, so as to limit
the Alfvén speed variations.
In this paper we perform a limited parametric study of line-tied
bipolar flux tubes twisted by two simple photospheric vortices, and
we compare our results with those previously published on the same topic.
The aim is to derive generic properties of such systems.
)
in which gravity
plays no role, so that only the Lorentz force can accelerate the
plasma. Even though this last assumption is not always made, it
becomes mandatory so as to treat large systems having magnetic
field contrasts of several orders of magnitude, so as to limit
the Alfvén speed variations.
In this paper we perform a limited parametric study of line-tied
bipolar flux tubes twisted by two simple photospheric vortices, and
we compare our results with those previously published on the same topic.
The aim is to derive generic properties of such systems.
Since magnetic extrapolations (e.g. Schmieder et al. 1996) and vector magnetograms (e.g. Leka & Skumanich 1999) have shown that the magnetic fields are often non-potential (i.e. that distributed electric currents exist) in the solar atmosphere, three-dimensional sheared and twisted line-tied flux tubes have already been modeled, either starting from uniform or from potential fields. Note that even though some rotating sunspots have been reported in observations (e.g. Brown et al. 2003) and references therein), the shearing/twisting motions in MHD simulations, including ours, have always been ad-hoc and almost never pretended to simulate true photospheric velocity fields. They are considered either on a purely theoretical basis, or so as to simulate approximately the apparent photospheric displacement of field line footpoints induced by the emergence through the photosphere of flux tubes which have previously been twisted in the solar interior, as observed e.g. by Leka et al. (1996).
All theoretical studies have shown that for moderate footpoint
displacements, the system can always find an equilibrium (being
force-free in the zero-![]() case). However, the behaviour of
the system appears to be qualitiatively different depending on
the geometry. In a cylindrical geometry invariant by rotation with
two line-tied end-plates, flux tubes subject to different classes of
twisting motions always become unstable to the
kink mode, typically when the increasing toroidal component of
the magnetic field becomes comparable to the axial field
(see e.g. Mikic et al. 1990; Baty 2001; Hood 1992; Baty 2000, for a review).
This instability subsequently results in the formation of thin
current sheets, in which magnetic reconnexion occurs
(see e.g. Baty 2001). In an axisymmetric spherical geometry,
sheared flux
surfaces exhibit a highly increasing expansion rate as a function
of shear, but always following a sequence of equilibrium states in
ideal MHD (Mikic & Linker 1994; Roumeliotis et al. 1994). Note that
Sturrock et al. (1995) derived an analytical
expression for the asymptotic behaviour of these equilibria as
a function of footpoint displacement (see our Eq. (42)). In this geometry,
the only known mechanisms to achieve a loss of equilibrium are
resistive effects, either within highly sheared arcades
(Mikic & Linker 1994) or within surrounding separatrices formed in
quadrupolar topologies (Antiochos et al. 1999).
In Cartesian geometry, very few calculations of simple twisting of
initial potential fields have been performed without introducing
special boundary effects so as to create flux ropes and ejections.
Using very concentrated vortices embedded in strong fields, and
reaching an end-to-end twist of about 1.4 turns, van Hoven et al. (1995)
always found an equilibrium. Considering a similar system,
Amari & Luciani (1999) on the contrary found a kink-like instability
which resulted in a resistive disruption of the system
associated with magnetic reconnection between twisted and
overlaying potential fields. In the same context, but using a
fixed uniform density (which leads to a sharp decrease of
Alfvén speed with altitude), Tokman & Bellan (2002) calculated
that highly twisted configurations exhibit some dynamic behaviour
after magnetic reconnection occurs at several locations within
the twisted flux tube. Neither calculations from Amari & Luciani (1999)
nor from Tokman & Bellan (2002) resulted in a strong
vertical expansion of the system during their respective
dynamic phases. Using more extended vortices and a non-uniform
density distribution, Amari et al. (1996) first revealed
the "very fast opening'' of a continuously twisted system after
some critical twist was reached. Klimchuk et al. (2000) calculated
non-linear force-free field models of a similar configuration up
to one turn, noting that numerical relaxations became increasingly
long at the twist increased.
Very recently, Török & Kliem (2003)
calculated several systems comparable to the one studied in
Amari et al. (1996). They showed that their equilibrium curves
were very steep, and that they surprisingly followed the
Sturrock et al. (1995) expression. Performing a more detailed analysis of
one of their systems, they found a loss of equilibrium for
twists larger than 1.38-1.48 turns, characterized by a fast vertical
expansion of the mostly twisted flux. By analogy with calculations
in cylindrical geometry, they attributed this behaviour to a
kink-like instability. This might also be responsible for the "very
fast opening'' in Amari et al. (1996), as proposed in Baty (2000).
In spite of all these studies, no firm generic explanation has yet been
firmly advanced for the change of behaviour of twisted flux tubes
for twists larger than
case). However, the behaviour of
the system appears to be qualitiatively different depending on
the geometry. In a cylindrical geometry invariant by rotation with
two line-tied end-plates, flux tubes subject to different classes of
twisting motions always become unstable to the
kink mode, typically when the increasing toroidal component of
the magnetic field becomes comparable to the axial field
(see e.g. Mikic et al. 1990; Baty 2001; Hood 1992; Baty 2000, for a review).
This instability subsequently results in the formation of thin
current sheets, in which magnetic reconnexion occurs
(see e.g. Baty 2001). In an axisymmetric spherical geometry,
sheared flux
surfaces exhibit a highly increasing expansion rate as a function
of shear, but always following a sequence of equilibrium states in
ideal MHD (Mikic & Linker 1994; Roumeliotis et al. 1994). Note that
Sturrock et al. (1995) derived an analytical
expression for the asymptotic behaviour of these equilibria as
a function of footpoint displacement (see our Eq. (42)). In this geometry,
the only known mechanisms to achieve a loss of equilibrium are
resistive effects, either within highly sheared arcades
(Mikic & Linker 1994) or within surrounding separatrices formed in
quadrupolar topologies (Antiochos et al. 1999).
In Cartesian geometry, very few calculations of simple twisting of
initial potential fields have been performed without introducing
special boundary effects so as to create flux ropes and ejections.
Using very concentrated vortices embedded in strong fields, and
reaching an end-to-end twist of about 1.4 turns, van Hoven et al. (1995)
always found an equilibrium. Considering a similar system,
Amari & Luciani (1999) on the contrary found a kink-like instability
which resulted in a resistive disruption of the system
associated with magnetic reconnection between twisted and
overlaying potential fields. In the same context, but using a
fixed uniform density (which leads to a sharp decrease of
Alfvén speed with altitude), Tokman & Bellan (2002) calculated
that highly twisted configurations exhibit some dynamic behaviour
after magnetic reconnection occurs at several locations within
the twisted flux tube. Neither calculations from Amari & Luciani (1999)
nor from Tokman & Bellan (2002) resulted in a strong
vertical expansion of the system during their respective
dynamic phases. Using more extended vortices and a non-uniform
density distribution, Amari et al. (1996) first revealed
the "very fast opening'' of a continuously twisted system after
some critical twist was reached. Klimchuk et al. (2000) calculated
non-linear force-free field models of a similar configuration up
to one turn, noting that numerical relaxations became increasingly
long at the twist increased.
Very recently, Török & Kliem (2003)
calculated several systems comparable to the one studied in
Amari et al. (1996). They showed that their equilibrium curves
were very steep, and that they surprisingly followed the
Sturrock et al. (1995) expression. Performing a more detailed analysis of
one of their systems, they found a loss of equilibrium for
twists larger than 1.38-1.48 turns, characterized by a fast vertical
expansion of the mostly twisted flux. By analogy with calculations
in cylindrical geometry, they attributed this behaviour to a
kink-like instability. This might also be responsible for the "very
fast opening'' in Amari et al. (1996), as proposed in Baty (2000).
In spite of all these studies, no firm generic explanation has yet been
firmly advanced for the change of behaviour of twisted flux tubes
for twists larger than
![]() turns in Cartesian geometry: Is it
really due to a kink instability as in the cylindrical case, or is
it due to an increasing expansion rate of equilibrium states as in
the axisymmetric case? Answering this question requires a parametric
study using fully time-dependant MHD equations. It is the
first objective of the present paper.
turns in Cartesian geometry: Is it
really due to a kink instability as in the cylindrical case, or is
it due to an increasing expansion rate of equilibrium states as in
the axisymmetric case? Answering this question requires a parametric
study using fully time-dependant MHD equations. It is the
first objective of the present paper.
Apart from theoretical considerations, it would be insteresting to compare typical properties of line-tied twisted flux tubes with typical solar observations. This would not only permit to test the applicability of such calculations to the real Sun, but perhaps help to understand complex observations with simple (and controllable) physical effects. Unfortunately, apart from the brief mention of S-shape field lines and/or electric currents by Amari et al. (1996) and Török & Kliem (2003), no detailed analysis was ever published according to the author's knowledge. In this paper we address three fundamental issues which result from typical observations of the solar photosphere and corona.
Firstly, what is the origin of the typical fragmentation (often accompanied by changes in sign) of electric currents calculated from vector magnetograms observed in sunspots (see e.g. Pevtsov et al. 1995; Leka & Skumanich 1999; Régnier et al. 2002)? Secondly, can current-carrying magnetic field lines fully trace sigmoïdal structures often observed in X-rays in the corona projected onto the solar disc (Gibson et al. 2002; Sterling & Hudson 1997; Hudson et al. 1998; Manoharan et al. 1996; Pevtsov & Canfield 1999; Rust & Kumar 1996), as they typically do for other X-ray and EUV loops (see e.g. Burnette et al. 2004; Schmieder et al. 1996; Démoulin et al. 2002)? In other words, are sigmoïds a quantitative tracer of magnetic twist? Also, why are sigmoïds barely observed at the limb, and what is their typical altitude? Thirdly, can the dynamics of simple bipolar twisted flux tubes result in the typical height-time plots observed in coronal mass ejections (CMEs) at low altitude below helmet streamers (Srivastava et al. 2000,1999; Wang et al. 2003; Zhang et al. 2004)? Also, can a simple explanation be found for the existence of two classes of CMEs (MacQueen & Fisher 1983; Delannée et al. 2000; Andrews & Howard 2001; Gosling et al. 1976), i.e. the fast/flare-related ones and the slow/prominence-related others?
The plan of the paper is the following: in Sect. 2 we describe the main features of the code. The initial settings of the calculations are given in Sect. 3. In Sect. 4 we analyze the evolution of the magnetic configuration while it is continuously driven at the line-tied boundary. In Sect. 5 we report on the equilibrium analysis of the system for various parameters, and we numerically construct equilibrium curves for which we provide analytical expressions. In Sect. 6 we analyze the calculations in the frame of solar observations of photospheric electric currents and of X-ray sigmoïds. We also discuss the possible applications as well as the limitations of these calculations for coronal mass ejections. The results are summarized in Sect. 7.
Since this paper reports on the first application of our new code, this section explains in detail the numerical method.
The standard zero-![]() (pressureless) time-dependant MHD equations
for a fully ionised and collisional plasma can be written as:
(pressureless) time-dependant MHD equations
for a fully ionised and collisional plasma can be written as:
Our code solves these equations in three dimensions in Cartesian
geometry (x;y;z), in their fully developed form. Using Einstein's
notation for spatial derivatives (where subscripts i;j can be x;y;z),
these equations are written in our code as:
In the following, we define
![]() (resp.
(resp.
![]() )
as the
distance between the
)
as the
distance between the
![]() and
and
![]() gridpoints, and
gridpoints, and
![]() (resp.
(resp.
![]() )
as the minimal distance between the
)
as the minimal distance between the
![]() gridpoint and its two neighbors, along the x (resp. y;z) axis:
gridpoint and its two neighbors, along the x (resp. y;z) axis:
It is important to note that no special method is applied to ensure
that Eq. (5) is satisfied throughout any MHD evolution. It follows
that numerical errors naturally result in non-zero
![]() in more or less extended regions during the runs. However,
these errors do not result in numerical instabilities, probably because
the MHD equations are written in their fully developed form in our
code, so that no non-physical explicit term due to
in more or less extended regions during the runs. However,
these errors do not result in numerical instabilities, probably because
the MHD equations are written in their fully developed form in our
code, so that no non-physical explicit term due to
![]() exists. The measurement of the divergence of
magnetic field relative to the other magnetic field gradients
provides a measurement of the error in the evaluation of gradients.
The analysis of this error is reported in Sect. 4.7.
exists. The measurement of the divergence of
magnetic field relative to the other magnetic field gradients
provides a measurement of the error in the evaluation of gradients.
The analysis of this error is reported in Sect. 4.7.
Using the true viscous stress tensor or more simply a classical Laplacian for the velocity diffusion would be a priori desireable. However, such terms are not appropriate for non-uniform meshes for the following two reasons. Firstly, they can over-diffuse at small scales where the cells are small, greatly reducing the advantage of using a non-uniform mesh. Secondly, they can under-diffuse at large scales where the cells are large, so that sharp gradients (e.g. shocks, shear layers) invariably lead to numerical instabilities.
So we chose rather to use only a pseudo-Laplacian diffusion term
which is locally adapted to the mesh:
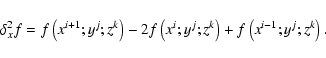 |
(19) |
For numerical stability, the inclusion of a diffusive term for
the magnetic field is necessary. However, the pseudo-Laplacian defined
above cannot be used for arbitrary magnetic fields for the following
reason. Consider for example a potential field which is by definition
in equilibrium and which satisfies
![]() .
This field
does not satisfy
.
This field
does not satisfy
![]() = 0, so that the use of
= 0, so that the use of
![]() will diffuse the field and generate artificial Lorentz forces. So our
magnetic field diffusion term is the standard collisional
(Laplacian) resistive term:
will diffuse the field and generate artificial Lorentz forces. So our
magnetic field diffusion term is the standard collisional
(Laplacian) resistive term:
| (20) | |||
| (21) |
In the applications studied in this paper, no additional explicit diffusive term for the density needed to be used.
Our code calculates third-order, five-point centered spatial derivations in
non-uniform meshes. For each variable f =
![]() ,
the expressions for the derivatives (e.g. along the x axis) are
directly calculated in the code as follows:
,
the expressions for the derivatives (e.g. along the x axis) are
directly calculated in the code as follows:
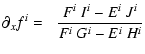 |
(22) | ||
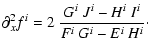 |
(23) |
| Ai = dxi + dxi+1 | |||
| Bi = dxi | |||
| Ci = dxi-1 | |||
| Di = dxi-1 +dxi-2 | |||
| Ei = Ai 2Bi 3 - Ai 3Bi 2 | |||
| Fi = Ci 3Di 2 - Ci 2Di 3 | |||
| Gi = ABi 3 - Ai 3B | |||
| Hi = CDi 3 - Ci 3D | |||
| (24) |
Such a high order scheme gives precise derivatives, but is not appropriate
for dealing with sharp discontinuities on the scale of the mesh. Therefore
we have to adjust the diffusion coefficients (
![]() )
defined
in Sect. 2.2 so as to ensure that every gradient is resolved over
at least four grid points.
)
defined
in Sect. 2.2 so as to ensure that every gradient is resolved over
at least four grid points.
Equations (24) show that some values "outside of the domain'' need to be specified for calculating derivatives at the boundary and at the first point above it. This is achieved by the inclusion of two layers of ghost cells at each boundary, whose distances to the boundary are equal to their mirrors inside the domain, and whose values are specified accordingly with the type of boundary (see Sects. 2.5 and 2.6). The total number of gridpoints which needs to be specified is thus ( nx+4;ny+4;nz+4).
Our time integration scheme is of the so-called "predictor-corrector''
family. It is calculated by linear combinations of Taylor expansions
of time derivatives at several time steps. At each step n corresponding
to a physical time tn, the calculation of the right-hand side
of Eqs. (6)-(12) for every quantity
![]() first results in their time
derivatives:
first results in their time
derivatives:
![]() .
.
Then the timestep
![]() to reach the time
to reach the time
![]() is dynamically adjusted according to the standard
Courant-Friedrich-Levy condition:
is dynamically adjusted according to the standard
Courant-Friedrich-Levy condition:
| (26) |
| |
= | 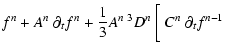 |
|
![$\displaystyle - B^{n}~ \partial_t f^{n-2} + \left(B^{n} - C^{n}\right)~ \partial_t f^n ~
\bigg{]}$](/articles/aa/full/2005/06/aa1519/img97.gif) |
|||
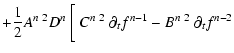 |
|||
![$\displaystyle + \left(B^{n~ 2} - C^{n~ 2}\right)~ \partial_t f^n ~ \bigg{]}.$](/articles/aa/full/2005/06/aa1519/img99.gif) |
(27) |
Using
![]() ,
Eqs. (6)-(12) are calculated
again, resulting in
,
Eqs. (6)-(12) are calculated
again, resulting in
![]() .
These are now used in
a second step, where the values
.
These are now used in
a second step, where the values
![]() are "corrected'' to their
final value fn+1:
are "corrected'' to their
final value fn+1:
| fn+1 | = | 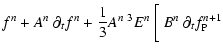 |
|
![$\displaystyle + A^{n}~ \partial_t f^{n-1} - (A^{n} + B^{n})~ \partial_t f^n ~
\bigg{]}$](/articles/aa/full/2005/06/aa1519/img102.gif) |
|||
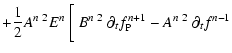 |
|||
![$\displaystyle + \left(A^{n~ 2} - B^{n~ 2}\right)~ \partial_t f^n ~ \bigg{]}.$](/articles/aa/full/2005/06/aa1519/img104.gif) |
(28) |
This method yields more precise and stable results than a simple Adams-Bashforth method, although it is time-consuming because the MHD equations have to be solved twice for each given time-step.
In the solar application studied in this paper, some of our boundaries need to be transparent, so as to allow information to go out of the numerical domain, since the corona is a physically open system, apart from its bottom. Using standard hard-wall with or without free-slip boundaries would naturally lead to wave and bulk-flow reflexions from these boundaries back into the domain, which would lead in particular to an artificial confinement of the system.
Open boundary conditions are often treated as follows when the characteristics are not used. Each variable is simply copied from the boundary value into the external ghost cells. However, Eqs. (7)-(9) show that this method is not sufficient in general. Consider a magnetic field which is in equilibrium analytically, but whose gradients are not zero near the boundaries (e.g. as it is the case for a dipole field). The ghost cells defined as above will inevitably result in spurious Lorentz forces which will accelerate the plasma from the boundaries. We tested this and found that, for the initial setting described in Sect. 3, the plasma quickly reached inflowing (followed by outflowing) velocities of the order of the Alfvén speed. These velocities then propagated into the domain and thus strongly influenced the system. In order to get rid of this effect, we only integrate Eqs. (7)-(9) where all the quantities required to calculate derivatives are specified within the domain, and not in the ghost cells.
In our code, "open'' boundaries are achieved by copying all variables
![]() from their value at the boundary onto the two
external ghost cells, while the values of
(ux;uy;uz) at two
gridpoints within the domain away from the boundary are copied
not only onto the ghost cells, but also onto the boundary itself
and onto the first point within the domain. This results in an
artifical decrease of gradients close and perpendicularly to
the boundary.
from their value at the boundary onto the two
external ghost cells, while the values of
(ux;uy;uz) at two
gridpoints within the domain away from the boundary are copied
not only onto the ghost cells, but also onto the boundary itself
and onto the first point within the domain. This results in an
artifical decrease of gradients close and perpendicularly to
the boundary.
This method allows a structure to leave the box without numerical instability as long as the physical width of this structure is larger than several grid points. However, it leads to some noise on the scale of the mesh near the boundary, whose amplitude depends on the length-scale of the exiting structure. It must be noted that this method also allows inflows, which when they occur bring into the domain zero-gradient quantities, as specified in the ghost cells. In our present applications, all the noise which developed at the open boundaries remained - at most - ten times lower than the signal, and was efficiently damped by the diffusion terms. Also, the existing inflows did not seem to play a significant role in the evolution of the system.
We use so-called "line-tied reflective boundary conditons'' which ensure that the footpoint of a magnetic field line can only move horizontally onto the boundary, and only if this motion is prescribed kinematically. Physically, this corresponds to an infinitely conducting and inertial plane, which cannot be forced by what happens in the domain. Such a boundary can be used to simulate the interface between an accretion disk or the interior of a star, with its surrounding diffuse corona. In the frame of solar applications it is taken to be the photosphere (see Sect. 1).
In a general case for which the magnetic field is neither purely tangential nor purely normal to the boundary, the standard Dirichlet-Neumann boundary (or parity) conditions cannot be used for every variable at a line-tied plane.
In our code, this boundary is placed in the plane (
xi;yj;zk=1),
and is specified as follows. At k=1, Eqs. (7)-(9) are not solved and the velocities are given by:
| uz1 = 0 | (29) | ||
| (30) | |||
| (31) |
| (32) | |||
| uz1-m = - uz1+m. | (33) |
In spite of their complexity and of the sharp transition which
exists between the boundary and the domain (in which Eqs. (7)-(9) are solved, with non-zero diffusion terms),
these settings provide a numerically stable boundary which satisfies
the line-tied and reflective conditions with no directly noticeable
boundary layer effect, as long as the scale-length
of any variable is larger than a few gridpoints. However, note
that these settings result in the formation of non-zero
![]() near the boundary (see Sect. 4.7).
near the boundary (see Sect. 4.7).
In this section, we describe the initial parameters which are chosen to perform our calculations, and the procedures which were applied to perform both continuously driven and relaxation runs.
We construct our initial conditions in two steps. First we define an
analytical vertical magnetic field bz at the line-tied (photospheric)
boundary z=0 as two circular gaussians of opposite flux:
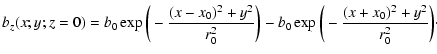 |
(35) |
![\begin{figure}
\par\includegraphics[width=8.15cm,clip]{1519f01.ps}\end{figure}](/articles/aa/full/2005/06/aa1519/Timg111.gif) |
Figure 1: Magnitude of the initial potential magnetic field versus altitude at the center of the domain at (x;y) = (0;0). |
| Open with DEXTER | |
This synthetic magnetogram is used to set boundary conditions for a
potential field extrapolation (
![]() )
using the Fourier code developed by Démoulin et al. (1997) which
is periodic in (x;y). The extrapolation is done with Nx
)
using the Fourier code developed by Démoulin et al. (1997) which
is periodic in (x;y). The extrapolation is done with Nx ![]() Ny = 10242 points uniformly distributed on the (x;y) plane with
Ny = 10242 points uniformly distributed on the (x;y) plane with
![]() Mm
Mm![]() Mm]. The extrapolation results in a magnetic field decrease with z which is plotted in Fig. 1.
Mm]. The extrapolation results in a magnetic field decrease with z which is plotted in Fig. 1.
In order to calculate an open rather than a periodic system in our
MHD runs, a domain
![]() is extracted from the periodic
domain used in the extrapolation. In the following, we consider
is extracted from the periodic
domain used in the extrapolation. In the following, we consider
![]() in
in
![]() Mm
Mm![]() Mm] and
Mm] and
![]() Mm
Mm![]() Mm]. Using linear interpolations between
the gridpoints of the Fourier extrapolation, the magnetic field values
are saved on a non-uniform mesh with nx
Mm]. Using linear interpolations between
the gridpoints of the Fourier extrapolation, the magnetic field values
are saved on a non-uniform mesh with nx ![]() ny
ny ![]() nz = 2013 points. The smallest cells are concentrated around x=y=z=0,
on top of the inversion line of bz(z=0) where (bx;by) are the
strongest at t=0. The mesh intervals vary in the range
nz = 2013 points. The smallest cells are concentrated around x=y=z=0,
on top of the inversion line of bz(z=0) where (bx;by) are the
strongest at t=0. The mesh intervals vary in the range
![]() Mm
Mm![]() Mm], expanding from x=y=z=0 following
dxi+1/dxi=dyj+1/dyj=1.027 and
dzk+1/dzk=1.013.
The resulting potential field is shown in Fig. 2.
Mm], expanding from x=y=z=0 following
dxi+1/dxi=dyj+1/dyj=1.027 and
dzk+1/dzk=1.013.
The resulting potential field is shown in Fig. 2.
As a result of the extrapolation, the ratio of the maximal to
the minimal value of b in
![]() is about 5
is about 5 ![]() 103.
In order to mimic (1) the filling of plasma in coronal loops
rooted in strong field regions, (2) the coronal density decrease
with altitude and (3) the fact that the Alfvén speeds
103.
In order to mimic (1) the filling of plasma in coronal loops
rooted in strong field regions, (2) the coronal density decrease
with altitude and (3) the fact that the Alfvén speeds ![]() always
remain much larger in the corona than the photospheric driving velocities,
we prescribe the ad-hoc initial density in
always
remain much larger in the corona than the photospheric driving velocities,
we prescribe the ad-hoc initial density in
![]() :
:
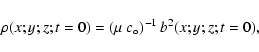 |
(36) |
![\begin{figure}
\par\includegraphics[width=6.75cm,clip]{1519f02a.ps}\hspace*{5mm}
\includegraphics[width=6.75cm,clip]{1519f02b.ps}\end{figure}](/articles/aa/full/2005/06/aa1519/Timg127.gif) |
Figure 2:
Top and projection views of the initial potential magnetic field within
the whole domain. The grey scale at the z=0 plane is white/black
for
|
| Open with DEXTER | |
 |
Figure 3:
( First row): Profiles of bz and uy along the (x; y=0,z=0) axis.
( Second row): Contours of
|
| Open with DEXTER | |
We apply a horizontal divergence-free boundary driving of the
field line footpoints at z=0 so as to kinematically twist the
initial potential configuration. We choose a velocity field which
preserves the initial distribution of bz(z=0), so that the
minimum magnetic energy remains the same during all runs, i.e.
the energy of the potential field at t=0. In this context,
Eq. (12) at z=0 turns into:
| (38) |
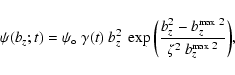 |
(39) |
![\begin{displaymath}%
\gamma(t) = \frac{1}{2}~ \tanh\bigg{[}\frac{2(t-t_\alpha)}{t_\omega}\bigg{]}
+ \frac{1}{2}\cdot
\end{displaymath}](/articles/aa/full/2005/06/aa1519/img137.gif) |
(40) |
In order to study the dependence of the system on the size of vortices,
we performed three sets of runs, with ![]() = 10; 0.9;0.5.
The first case results in extended vortices which twist most of
the flux and which shear the inversion line, the third case results
in concentrated vortices which twist only the strongest fields, and
the second case is intermediate. The associated velocity fields
are shown in Fig. 3.
= 10; 0.9;0.5.
The first case results in extended vortices which twist most of
the flux and which shear the inversion line, the third case results
in concentrated vortices which twist only the strongest fields, and
the second case is intermediate. The associated velocity fields
are shown in Fig. 3.
Even though the applied boundary driving is very slow (![]() of
the Alfvén speed), the continuously twisted runs always end up after
some time in velocities of the order of
of
the Alfvén speed), the continuously twisted runs always end up after
some time in velocities of the order of ![]() (see Sect. 4). This indicates that the system is far from equilibrium.
(see Sect. 4). This indicates that the system is far from equilibrium.
In order to find an equilibrium (or to reveal its absence) for
a given amount of twist reached at a time ![]() ,
we perform relaxations runs as follows. Time is reset to zero,
the magnetic field and mass density are set to
,
we perform relaxations runs as follows. Time is reset to zero,
the magnetic field and mass density are set to
![]() ,
the boundary driving is suppressed
(
,
the boundary driving is suppressed
(
![]() )
and the velocities are reset to
)
and the velocities are reset to
![]() .
So the further evolution of the system is only driven
by the residual Lorentz forces which exist at
.
So the further evolution of the system is only driven
by the residual Lorentz forces which exist at ![]() during
the continuously driven run.
during
the continuously driven run.
This method is more demanding numerically than applying a gradual
deceleration of the driving at z=0 while keeping its velocities
in
![]() .
However, it is more convenient because the amount
of twist is fixed during the relaxation (if
.
However, it is more convenient because the amount
of twist is fixed during the relaxation (if ![]() is small
enough), and essentially because velocities resulting from the
accumulation of momentum during the driven phase do not play a
role in the evolution of the system. This issue becomes important
when the velocities are of the order of the Alfvén speed.
is small
enough), and essentially because velocities resulting from the
accumulation of momentum during the driven phase do not play a
role in the evolution of the system. This issue becomes important
when the velocities are of the order of the Alfvén speed.
In order to avoid the formation of unresolved strong shear layers
at high altitudes z, which naturally appear due to prescribed
motions at the footpoints of strongly expanding flux tubes,
we apply a strong diffusion term for ![]() :
:
![]() .
However,
to ensure a high magnetic Reynolds number in the corona,
we set a much smaller diffusion term for
.
However,
to ensure a high magnetic Reynolds number in the corona,
we set a much smaller diffusion term for ![]() :
:
![]() .
.
Estimating (i) the typical length-scale as 30 Mm, which
is roughly equal to the initial length of the magnetic field
line rooted in
![]() as
well as the average transverse extension of the twisted flux
tube which forms in our runs; and (ii) typical velocities
as 0.1 c0, the characteristic dimensionless numbers are
(Re;Rm;Lu)=
(102;103;104). The value of the Reynolds number here is
only an upper limit, since the viscous term is defined at the scale
of the mesh in our code (see Eq. (17)).
as
well as the average transverse extension of the twisted flux
tube which forms in our runs; and (ii) typical velocities
as 0.1 c0, the characteristic dimensionless numbers are
(Re;Rm;Lu)=
(102;103;104). The value of the Reynolds number here is
only an upper limit, since the viscous term is defined at the scale
of the mesh in our code (see Eq. (17)).
The diffusion velocities (
![]() )
are kept
constant in space and time, and are the same for every run
(continuously driven, relaxation and varying
)
are kept
constant in space and time, and are the same for every run
(continuously driven, relaxation and varying ![]() ).
).
During the continuous photospheric driving, field lines
rooted in the prescribed vortices start to twist
around the "axial field line'' which is rooted in
![]() at the vortex centers. Figure 4
shows that both the magnetic and kinetic energies increase
monotonically for the three vortex sizes considered (
at the vortex centers. Figure 4
shows that both the magnetic and kinetic energies increase
monotonically for the three vortex sizes considered (
![]() )
as long as the boundary driving is maintained.
The kinetic energy for the small vortices naturally remains
smaller than the one for large vortices, since the coronal volume
at z>0 which is affected by the vortices depends on the vortex
size.
)
as long as the boundary driving is maintained.
The kinetic energy for the small vortices naturally remains
smaller than the one for large vortices, since the coronal volume
at z>0 which is affected by the vortices depends on the vortex
size.
 |
Figure 4:
Continuously twisted runs. All quantities are plotted
as a function of the central twist
|
| Open with DEXTER | |
Since the three vortices have different sizes, but with the
same maximum velocity and initial acceleration ramp, they
have different rotation rates around the axial field
line. So in the following, we study the variation of all
quantities as a function of twist ![]() rather than time,
so as to have a common time-scale.
rather than time,
so as to have a common time-scale. ![]() is
calculated analytically, and also checked numerically at various
timesteps by integrating many magnetic field lines along the
x axis for (
x<0;y=0;z=0) and by measuring the rotation
rate of their footpoints at (x>0;z=0). We find that the
prescribed motions result in a nearly rigid rotation inside a
small radius
is
calculated analytically, and also checked numerically at various
timesteps by integrating many magnetic field lines along the
x axis for (
x<0;y=0;z=0) and by measuring the rotation
rate of their footpoints at (x>0;z=0). We find that the
prescribed motions result in a nearly rigid rotation inside a
small radius
![]() Mm around the vortex centers, which gradually decreases away from
them. The twist unit
Mm around the vortex centers, which gradually decreases away from
them. The twist unit ![]() which we consider in the rest of
the paper is the rotation angle of the field line footpoints
in the small area which is subject to a quasi-rigid rotation.
We define the number of turns in the associated magnetic flux
tube by
which we consider in the rest of
the paper is the rotation angle of the field line footpoints
in the small area which is subject to a quasi-rigid rotation.
We define the number of turns in the associated magnetic flux
tube by
![]() .
.
For the three vortex sizes considered, the results of the
calculations are only shown up to twists equal to
![]() turns for
turns for
![]() for the following
reasons.
The physical meaning of the runs is indeed bounded by two limitations.
Firstly, the most relevant field lines (those anchored in strong field regions) can
reach (and then cross) the top boundary of the domain, which prevents communication
via Alfvén waves between their footpoints at z=0.
This limitation comes up
for
for the following
reasons.
The physical meaning of the runs is indeed bounded by two limitations.
Firstly, the most relevant field lines (those anchored in strong field regions) can
reach (and then cross) the top boundary of the domain, which prevents communication
via Alfvén waves between their footpoints at z=0.
This limitation comes up
for ![]() when
when
![]() ,
during continuously driven runs,
and for
,
during continuously driven runs,
and for ![]() when
when
![]() during relaxation runs (see next subsections).
Secondly, a current shell develops in all runs
for
during relaxation runs (see next subsections).
Secondly, a current shell develops in all runs
for ![]() at the interface
between the strongly and weakly twisted field lines : this shell must remain numerically
resolved.
For
at the interface
between the strongly and weakly twisted field lines : this shell must remain numerically
resolved.
For ![]() the shell becomes unresolved for
the shell becomes unresolved for
![]() ,
simply because the vortices are more concentrated than in the other runs.
This
leads to numerical instabilities which start to develop around
(x;y;z) = (
,
simply because the vortices are more concentrated than in the other runs.
This
leads to numerical instabilities which start to develop around
(x;y;z) = (
![]() )
Mm, where the cell intervals
(defined by Eq. (13)) are (
)
Mm, where the cell intervals
(defined by Eq. (13)) are (
![]() )
) ![]() (
0.3;0.6;0.6) Mm. Increasing the resistivity makes it possible
to bypass this problem. However, we did not go on in this direction,
because comparison with other runs would have been difficult.
(
0.3;0.6;0.6) Mm. Increasing the resistivity makes it possible
to bypass this problem. However, we did not go on in this direction,
because comparison with other runs would have been difficult.
During a first long quasi-static period, in the strongest and closed field regions, the slow velocities of the photospheric driving allow the low frequency Alfvén waves which are generated at z=0 by the vortices to travel several times along a given field line by rebouncing on the line-tied plane at z=0. This leads to a smooth distribution of the generated electric currents along each magnetic field line. This allows the magnetic configuration to remain close to a non-linear force-free state. This was checked by integrating both electric current and magnetic field lines, which become undistinguishable from one another after a short transition phase after the start of the runs. In the outer "open'' field lines rooted in weak field regions (which emerge out of the numerical domain) the waves are transmitted through the open boundaries with very little reflexion, thanks to the dissipative operator for the velocity applied on the non-uniform mesh. However, since these field lines are also continuously twisted, they do not come back to a potential state.
The whole magnetic configuration slowly expands in all directions, but mostly along z. This can be explained in the context of the van Tend & Kuperus (1978) model by the generation of surface currents at the infinitely conducting and inertial plane at z=0, which tend to expell the generated coronal currents away from them, and by the self-repulsion of the coronal currents for z>0. This can also be explained by the fact that since bz(z=0) remains constant, the currents at z>0 generated by the twisting motions at z=0 result in a global increase of magnetic energy, hence in local enhancement of magnetic pressure within the twisted flux tube, so in local expansion where the magnetic tension does not increase as fast as the magnetic pressure. During this quasi-static phase, the twisting flux tube expands with a vertical velocity uz which is smaller than the boundary driving maximal velocity. This first phase lasts until the accumulated vertical velocities become of the order of 5% of the Alfvén speed, i.e. uz=50 km s-1, which is nearly equal to the sum of the two vortex velocities, which is about the maximum amplitude of the torsional Alfvén wave propagating along the loop.
A second phase of dynamic nature then begins. The rates of
increase for uz, for the kinetic energy and for the apex altitude
of the axial field line gradually rise to much stronger values than
during the quasi-static phase. This smooth transition does not occur
for the same twist for all vortex sizes. Figure 4 shows
that the change occurs for central twists of
![]() turns respectively for
turns respectively for
![]() .
As the twist increases, the kinetic energy gains one order of
magnitude, and the vertical velocity of the axial field line reaches a
non-negligible fraction of the Alfvén speed. For a given twist
the vertical velocity of large overlaying field lines
is even higher (but always sub-Alfvénic in our
runs): these large field lines are pushed upward
and sideward together, both due to their own internal currents
and to the pushing from below by the more twisted flux tube.
Analyzis of the height-time curves for the axial field line
reveals an expansion rate which is slightly faster than
exponential. During this second phase the magnetic field
configuration becomes less and less force-free, as indicated not only
by the very fast expansion velocities, but also by an increasing
angle between the electric current and the magnetic field lines.
.
As the twist increases, the kinetic energy gains one order of
magnitude, and the vertical velocity of the axial field line reaches a
non-negligible fraction of the Alfvén speed. For a given twist
the vertical velocity of large overlaying field lines
is even higher (but always sub-Alfvénic in our
runs): these large field lines are pushed upward
and sideward together, both due to their own internal currents
and to the pushing from below by the more twisted flux tube.
Analyzis of the height-time curves for the axial field line
reveals an expansion rate which is slightly faster than
exponential. During this second phase the magnetic field
configuration becomes less and less force-free, as indicated not only
by the very fast expansion velocities, but also by an increasing
angle between the electric current and the magnetic field lines.
Regardless of the existence or not of a non-equilibrium, the observed departure from the force-free state is expected. Indeed, the vertical expansion results in longer and longer field lines. The rate of increase of field line length becomes such that the low frequency Alfvén waves emitted from the photospheric boundary at z=0 no longer have time to rebounce several times along a given field line, so that the currents cannot be quasi-statically distributed all along the field line. This results in a system which is always trying to reach an equilibrium (if any) that is located at larger and larger heights in z as the twist increases.
As the twist increases, the core twisted flux tube emerges out
the numerical domain at a rate which is faster than exponential,
with velocities of the order of the Alfvén speed. Meanwhile, the
surrounding twisted and potential loops lean sidewards. This whole
behaviour described above is qualitatively the same for all three
vortex sizes considered in this paper. It is also fully consistent
with what was reported for other classes of bipolar twisted fields
calculated by Amari et al. (1996) and Török & Kliem (2003) with
different zero-![]() MHD codes. Consequently, we conclude that
the "very fast opening'' initially reported by Amari et al. (1996)
is a generic property of continuously twisted bipolar
line-tied flux tubes.
MHD codes. Consequently, we conclude that
the "very fast opening'' initially reported by Amari et al. (1996)
is a generic property of continuously twisted bipolar
line-tied flux tubes.
 |
Figure 5:
Magnetic configurations for
|
| Open with DEXTER | |
The comparison of the height-time plots for the three vortex cases during both quasi-static and dynamic phases shows that the vertical expansion rate of the axial field line is much larger for large than for small vortices. The dependence on vortex size is much larger than linear. Since the outer field lines are twisted more by the large vortices, we interpret the above result as indicating that the degree of twist in the outer field lines has a large influence on the expansion rate of the strong fields.
This can be qualitatively explained by the expansion of
the outer field lines under the action of their own
internal currents, which adds up to pushing from
below due the twisted flux tube expansion. Quantitatively,
the high sensitivity to the vortex size may be associated
with the behaviour of large field lines in constant-![]() linear force-free field models, whose distortion and expansion
rates are typically much larger than those of low-lying field
lines for small increments of
linear force-free field models, whose distortion and expansion
rates are typically much larger than those of low-lying field
lines for small increments of ![]() ,
as explained below.
,
as explained below.
In (x;y) periodic linear force-free field models, the magnetic
field amplitude varies with z as
![]() where
where ![]() is the wavenumber
of the considered Fourier mode (see e.g. Aulanier & Démoulin 1998).
This readily shows that
low-wavenumber modes (i.e. large field lines) are much
more affected by
is the wavenumber
of the considered Fourier mode (see e.g. Aulanier & Démoulin 1998).
This readily shows that
low-wavenumber modes (i.e. large field lines) are much
more affected by ![]() variations (i.e. by injection
of electric currents) than high-wavenumber modes.
variations (i.e. by injection
of electric currents) than high-wavenumber modes.
Even though this explanation cannot be directly transposed
to the present MHD calculations since they result in
non-constant ![]() distributions and in departures from
the force-free state, we believe that it is at the origin
of the strong dependence of the system on the twisting
(or not) of large outer field lines.
distributions and in departures from
the force-free state, we believe that it is at the origin
of the strong dependence of the system on the twisting
(or not) of large outer field lines.
Figure 5 shows the structure of the magnetic configuration for the three vortices at the same twist during the dynamic phase. These figures show the sideward inclination of the field lines which surround the twisted core (drawn with pink field lines) and which are rooted in weak field regions on the edge of the photospheric bipole. This behaviour is similar to what Amari et al. (1996) reported.
A re-orientation of the core twisted flux tube is also
evident,
as found in the calculations of Török & Kliem (2003). We
find that this flux tube makes an angle with its initial orientation
along the x axis, which scales like the vortex size. However,
this re-orientation is neither associated to the dynamic
phase nor to some kink-like instability, since it is already
noticeable at
![]() during
the quasi-static phase. This phenomenon is in fact simply
caused by the swirling of initially low-lying field lines
having strong transverse fields which cross the
inversion line. This swirling results in the increase
of magnetic pressure along the y axis at low altitude on
one side of a given vortex. This pressure term is not present
on the other side of the vortex since the corresponding
larger field lines are relatively less deformed by the vortex.
The pressure imbalance pushes the lower parts of the flux tube
sideward from the x axis, and this deformation
propagates to larger heights along each field line thanks
to Alfvén waves, which results finally in the deformation of the
whole twisted flux tube.
during
the quasi-static phase. This phenomenon is in fact simply
caused by the swirling of initially low-lying field lines
having strong transverse fields which cross the
inversion line. This swirling results in the increase
of magnetic pressure along the y axis at low altitude on
one side of a given vortex. This pressure term is not present
on the other side of the vortex since the corresponding
larger field lines are relatively less deformed by the vortex.
The pressure imbalance pushes the lower parts of the flux tube
sideward from the x axis, and this deformation
propagates to larger heights along each field line thanks
to Alfvén waves, which results finally in the deformation of the
whole twisted flux tube.
When the core twisted flux tube, which is associated with
the strongest volumic currents, gets close to the top boundary,
it keeps accelerating even though the acceleration diminishes
(see Fig. 4 for the run with ![]() ). The apex
of flux tube eventually always passes through the top boundary,
just like some surrounding field lines rooted in weak field regions
do at smaller times. The decrease of acceleration when the axial
field lines passes
). The apex
of flux tube eventually always passes through the top boundary,
just like some surrounding field lines rooted in weak field regions
do at smaller times. The decrease of acceleration when the axial
field lines passes
![]() Mm is probably not physical,
this altitude being only at 9 mesh points from the boundary.
Mm is probably not physical,
this altitude being only at 9 mesh points from the boundary.
It is plausible that this effect is a direct consequence of
the condition which implies a zero-gradient condition for ![]() at the open boundary (see Sect. 2.5). However, since
all waves are strongly damped near the boundary because of
the larger mesh size, this artificial reflexion should not
significantly influence the system at lower heights, where the
magnetic field is larger.
at the open boundary (see Sect. 2.5). However, since
all waves are strongly damped near the boundary because of
the larger mesh size, this artificial reflexion should not
significantly influence the system at lower heights, where the
magnetic field is larger.
After the twisted flux tube exit, the vertical velocities in the domain start to fall, but always remain positive, thanks both to inertia and to the continuous photospheric driving which keeps injecting currents both in "open'' field lines and in lower sheared/twisted arcades.
As noted in Sects. 2.1 and 2.6, the solenoidal
condition for the magnetic field is not fully ensured in our calculations.
Even though this error is not noticeable in direct plots of various
quantities, it can be estimated by calculating the ratio of
![]() to the local derivatives of the magnetic field:
to the local derivatives of the magnetic field:
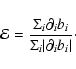 |
(41) |
We find that, if the regions near all boundaries are excluded,
the error calculated in several horizontal planes (at fixed z) globally
remains constant at all times, with
![]() and
and
![]() .
The maxima are always located in
a few gridpoints only for a given altitude, as suggested by the lower
rms values. These same errors are in fact already present at t=0, due
to the linear interpolations which were used to save the results of
the potential field extrapolation in a non-uniform mesh (see Sect. 3.1).
Including the regions near the open boundaries results in local enhancement
of the errors typically by one order of magnitude. The amplitudes of
these errors are also stable in time. A selection of the regions where the magnetic fields are the highest in the domain, i.e. for
.
The maxima are always located in
a few gridpoints only for a given altitude, as suggested by the lower
rms values. These same errors are in fact already present at t=0, due
to the linear interpolations which were used to save the results of
the potential field extrapolation in a non-uniform mesh (see Sect. 3.1).
Including the regions near the open boundaries results in local enhancement
of the errors typically by one order of magnitude. The amplitudes of
these errors are also stable in time. A selection of the regions where the magnetic fields are the highest in the domain, i.e. for
![]() Mm
Mm![]() Mm], but excluding
the lower and the top boundaries in z, result in errors which are
typically twice as low as for the whole box excluding the boundaries.
Mm], but excluding
the lower and the top boundaries in z, result in errors which are
typically twice as low as for the whole box excluding the boundaries.
The most important errors are located near the lower line-tied boundary
at z=0. They are already present at t=0 on two grid layers along z,
due to the magnetic field extrapolation in the ghost cells (see Eq. (34)). They increase with time at z=0 by a factor 2, while they slowly propagate inside the domain as the twist increases. This propagation of the errors occurs at typical speeds of 5-10 km s-1
which are much smaller than the velocities of Alfvén waves and of the
expanding flux tube, and which are also slower than the photospheric
driving velocities. For the twists considered in this paper, the errors
always remains confined to z<10 Mm. In this layer,
![]() (
(
![]() respectively) decrease exponentially with z from 1 (respectively 0.3)
to their values inside the domain given above.
respectively) decrease exponentially with z from 1 (respectively 0.3)
to their values inside the domain given above.
These numbers show that, even though the numerical scheme does
not ensure
![]() ,
the errors generated
within the volume and the open boundaries are acceptable since
they typically do not increase from their weak values at t=0.
However, even though the line-tied boundary apparently does not
result in a boundary layer when various fields are considered,
it still generates non-negligible errors in
,
the errors generated
within the volume and the open boundaries are acceptable since
they typically do not increase from their weak values at t=0.
However, even though the line-tied boundary apparently does not
result in a boundary layer when various fields are considered,
it still generates non-negligible errors in
![]() ,
which tend to propagate away from the boundary.
Unfortunately, at that stage it is difficult to estimate the
importance of these errors in the results of the calculations.
,
which tend to propagate away from the boundary.
Unfortunately, at that stage it is difficult to estimate the
importance of these errors in the results of the calculations.
 |
Figure 6:
Five examples of relaxation runs.
Pluses correspond to (
|
| Open with DEXTER | |
As pointed out in Sect. 4.3, the development of the dynamic phase in the continuously driven runs does not necessarily indicate the absence of equilibrium for a given twist. However, it does not show either that the system would always find an equilibrium if the driving velocities were smaller, since the expansion velocities become more than one order of magnitude larger than the driving velocities.
The motivations for analyzing the equilibrium properties
of our twisted flux tubes are the following. Firstly, relaxations runs
calculated from the continuously driven run shown in Amari et al. (1996)
appear to be longer and more difficult to achieve as the flux tube
enters the dynamic phase (Amari 2004, private communication).
The same difficulty arises in magneto-frictional calculations
of force-free twisted flux tubes, as shown by Klimchuk et al. (2000).
Secondly, Török & Kliem (2003) found a loss of equilibrium in one
of their models (the one defined by their parameter y0=1) for
![]() turns. This loss of equilibrium, which they
attributed to a kink-like instability, appeared as the fast
expansion of their core twisted flux tube in the absence of
photospheric driving. Thirdly, the comparison between our runs
(which have three different vortex sizes) and
those of Török & Kliem (2003)
(which have different initial bipolar potential fields)
will consist in a parametric study which can lead to the finding
of generic (non?) equilibrium properties of line-tied twisted
flux tubes in general.
turns. This loss of equilibrium, which they
attributed to a kink-like instability, appeared as the fast
expansion of their core twisted flux tube in the absence of
photospheric driving. Thirdly, the comparison between our runs
(which have three different vortex sizes) and
those of Török & Kliem (2003)
(which have different initial bipolar potential fields)
will consist in a parametric study which can lead to the finding
of generic (non?) equilibrium properties of line-tied twisted
flux tubes in general.
In order to search for the existence of equilibria from our
continuously driven runs, we perform relaxation calculations
following the method described in Sect. 3.3.
Figure 6 shows the typical behaviour of a few
relaxations of twisted flux tubes for various (
![]() ).
For all runs, during the relaxation phase, the magnetic energy
monotonically decreases by a few percent.
A part of the lost magnetic
energy is converted into kinetic energy. The latter is
due to the velocities which are generated by the Lorentz
forces present in the system at the start of the relaxations.
).
For all runs, during the relaxation phase, the magnetic energy
monotonically decreases by a few percent.
A part of the lost magnetic
energy is converted into kinetic energy. The latter is
due to the velocities which are generated by the Lorentz
forces present in the system at the start of the relaxations.
For some relaxation runs the vertical expansion velocities reached a few hundred km s-1, which is not negligible compared to the Alfvén speed. In spite of this, we always find that the velocities decrease after a time of 50-300 s, and that they eventually become negative shortly after (see Fig. 6). So the flux tube starts to shrink back to lower altitudes in z after its initial expansion. This behaviour is found for every relaxation run performed in this study, regardless of the initial altitude of the axial field line, i.e. of its distance to the top boundary. We checked that the vertical deceleration was always associated with a change in sign from positive to negative of the vertical component of the Lorentz forces, which eliminates a pure diffusive origin. Also, performing relaxations with increased resistivity by a factor 3 has not led to qualititative changes.
So we conclude that the system always enters an oscillatory
behaviour along a potential well around an equilibrium position.
These oscillations result from the initial position of the
flux tube away from the equilibrium point at the start of the
relaxation, so that inertia allows the system to
pass beyond this point, which is followed by the action of
restoring forces which pull back the system toward the equilibrium.
The existence of these oscillations obviously shows that
the system is not over-diffusive, in spite of the strong
value of
![]() which we chose in Sect. 3.4.
which we chose in Sect. 3.4.
Comparing various relaxation runs, we find that the initial vertical
acceleration, the peak vertical velocities and the amplitude in z of
the oscillations for a given vortex size are all larger as the
relaxation is performed for higher and higher twists
![]() .
This indicates that the system proceeds further and further away
from its equilibrium position as
.
This indicates that the system proceeds further and further away
from its equilibrium position as
![]() increases during
the dynamic phase of the continuously driven runs. However, our
calculations suggest that the system can always find an equilibrium.
increases during
the dynamic phase of the continuously driven runs. However, our
calculations suggest that the system can always find an equilibrium.
The rapid increase of expansion rate of the equilibria as function
of footpoint displacement that we find is consistent with other
numerical calculations of twisted bipoles in Cartesian geometry
by Amari et al. (1996), Klimchuk et al. (2000) and Török & Kliem (2003),
as well as with the behaviour of axisymmetric
sheared dipoles in a spherical geometry (Roumeliotis et al. 1994).
Our relaxation behaviour is consistent with Amari's qualitative
statements and with the results of Klimchuk et al. (2000), about the
increasing difficulty in relaxing the system for increasing
twists. However, contrary to Török & Kliem (2003), we find no evidence
for a loss of equilibrium in any of our systems, even though their
bipolar field resized to our scale results in a loss of equilibrium
when the altitude their axial field line is less than ![]() 40 Mm,
which is much smaller than the vertical extension of our domain.
40 Mm,
which is much smaller than the vertical extension of our domain.
This quantitative difference may be due to different numerical
prescriptions between codes. Firstly, Török & Kliem (2003) apparently
use a much stronger diffusion term for momentum (and for density)
than we do, since their "successful relaxation'' runs apparently do
not show oscillatory behaviour. Secondly, they use a non-uniform grid
which is typically 3.3 times more stretched in z than ours for
similar altitudes, if their spatial units are rescaled to ours
to have the same bipole size at z=0 (Törok 2004, private
communication). Thirdly, they use a different spatial scheme
than we do. Fourthly, the development and consequences of
non-zero
![]() in their runs must be different
than in ours. Indeed, they use the standard conservative form of
the MHD equations. Finally, their boundary conditions at z=0
on
in their runs must be different
than in ours. Indeed, they use the standard conservative form of
the MHD equations. Finally, their boundary conditions at z=0
on ![]() are not the same as ours, even though their bz(z=0)
varies only slowly with time. All these issues may result
in differences in the calculation of spatial derivatives, hence
of Lorentz forces.
are not the same as ours, even though their bz(z=0)
varies only slowly with time. All these issues may result
in differences in the calculation of spatial derivatives, hence
of Lorentz forces.
The analysis in our relaxation runs of each term that contributes
to the vertical acceleration in Eq. (9) shows that, around
the time at which we find a deceleration, and around (and above)
the altitude of the axial field line, the vertical derivative term
![]() is well resolved, and is at most 10 times
larger than the total vertical component of the Lorentz force.
A small difference in the calculation of this term, which may be
amplified in time, may result in a different sign for the
vertical Lorentz force. This issue will have to be addressed by
new calculations in the future, if possible with different codes.
is well resolved, and is at most 10 times
larger than the total vertical component of the Lorentz force.
A small difference in the calculation of this term, which may be
amplified in time, may result in a different sign for the
vertical Lorentz force. This issue will have to be addressed by
new calculations in the future, if possible with different codes.
 |
Figure 7:
Equilibrium curves derived from relaxation runs.
( Left): Same as Fig. 4, bottom left, overlaid
with [ triangles; diamonds; squares]
which correspond to "equilibrium'' positions found from
relaxation runs with
|
| Open with DEXTER | |
In order to derive the precise numerical equilibrium curves for our
three vortex sizes, we need in principle to perform prohibitively long
relaxation runs so as to follow the damping of the vertical oscillations
of the magnetic field. We rather choose a simplified method. We measure
the altitude in z of the axial field line at the time for which
the vertical acceleration first becomes negative during the
relaxations (see Fig. 6). Since this time is well matched
in our runs by the change in sign of the vertical component of the
Lorentz force, we then assume that this altitude corresponds to the
asymptotic equilibrium of the system. The measured positions for
various values of (
![]() )
are marked in Fig. 7, left on top of the height time plots from
the continuously twisted runs. The equilibrium positions for
a given twist are always located above those found when the
system is continuously twisted. As conjectured in Sect. 4.3, this can be explained by the fact that the currents
continuously generated by the vortices at z=0 do not have time
to distribute all along the expanding field lines by Alfvén waves, especially during the dynamic phase during which the expansion rate is comparable to the Alfvén speed.
)
are marked in Fig. 7, left on top of the height time plots from
the continuously twisted runs. The equilibrium positions for
a given twist are always located above those found when the
system is continuously twisted. As conjectured in Sect. 4.3, this can be explained by the fact that the currents
continuously generated by the vortices at z=0 do not have time
to distribute all along the expanding field lines by Alfvén waves, especially during the dynamic phase during which the expansion rate is comparable to the Alfvén speed.
We find that these positions are well aligned in Fig. 7, right, in accordance with the "successful relaxation'' plots of Török & Kliem (2003) which were calculated
for different physical conditions with a different code (recall
in particular our approximate relaxation method and our problems
with the
![]() constraint). For comparison,
the three curves which link the marks calculated for all three
constraint). For comparison,
the three curves which link the marks calculated for all three ![]() values are overplotted onto Fig. 7, left. So we find that all our equilibrium curves follow the analytical
expression:
values are overplotted onto Fig. 7, left. So we find that all our equilibrium curves follow the analytical
expression:
Our numerical reconstructions of these curves show that for
![]() ,
,
![]() .
By
comparison, Török & Kliem (2003) find
.
By
comparison, Török & Kliem (2003) find
![]() before their flux tube loses its equilibrium. This value
lies within the range of
before their flux tube loses its equilibrium. This value
lies within the range of
![]() which we found. Also it is now
clear that our magnetic configuration always enters an oscillatory stage
during its relaxation, even when the equilibrium curve is steeper
than the one of Török & Kliem (2003). Both these issues suggest a
posteriori that their loss of equilibrium is not be physical, and
that simple bipolar twisted flux tubes can always evolve quasistatically
if the photospheric driving velocities are infinitesimal.
which we found. Also it is now
clear that our magnetic configuration always enters an oscillatory stage
during its relaxation, even when the equilibrium curve is steeper
than the one of Török & Kliem (2003). Both these issues suggest a
posteriori that their loss of equilibrium is not be physical, and
that simple bipolar twisted flux tubes can always evolve quasistatically
if the photospheric driving velocities are infinitesimal.
As noted by Török & Kliem (2003), the analytical equilibrium curve given in Eq. (42) also applies to other geometries, specifically to spherical axisymmetric (2.5D) dipoles subject to azimuthal shearing motions (Sturrock et al. 1995; Roumeliotis et al. 1994). The derivation of this curve by both analytical and numerical means, by several authors and in various geometrical conditions, implies that it is a generic property of line-tied force-free fields, both sheared and twisted.
In the following we address the question of the applicability
of the continuously twisting bipolar flux tube model to the
coronal mass ejection (CME) phenomenon. We assume that the
analytical expression of the equilibrium curve (Eq. (42))
remains valid with altitude until the apex
of the axial field line reaches the top of helmet streamers, where
the solar wind becomes dominant (i.e.
![]() ). We also assume
a photospheric twisting rate
). We also assume
a photospheric twisting rate
![]() ), where
), where
![]() is the twisting velocity
and
is the twisting velocity
and
![]() is the radius of
the small region which defines the twist within each vortex
(
is the radius of
the small region which defines the twist within each vortex
(
![]() Mm for
Mm for
![]() Mm, see Sect. 4.1). Equation (42) then leads to:
Mm, see Sect. 4.1). Equation (42) then leads to:
![$\displaystyle h(t) = h_\circ \exp\bigg{[}\mathcal{A}~ \bigg{(}\frac{u_{\mbox{\rm {\tiny {phot}}}}~ t}{2 \pi R_{\mbox{\rm {\tiny {phot}}}}}\bigg{)}^2\bigg{]},$](/articles/aa/full/2005/06/aa1519/img209.gif) |
(43) | ||
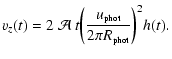 |
(44) |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{1519f08a.ps}\vspac...
...*{4mm}
\par\includegraphics[angle=-90,width=8.3cm,clip]{1519f08c.ps}\end{figure}](/articles/aa/full/2005/06/aa1519/Timg216.gif) |
Figure 8:
Simulated height-velocity-time plots of the axial field line of
continuously driven flux tubes twisted with
|
| Open with DEXTER | |
Regardless of the velocity magnitudes, Fig. 8
illustrates one typical property of Eq. (42): the
scale dependence. It is clear that the system size (i.e. prominence as opposed to active region) scales inversely with the acceleration and to the velocities. In particular,
the velocity (resp. acceleration) at
![]() roughly
scales like f-1 (resp. f-2).
All these properties are consistent with the two classes
of observed CMEs (MacQueen & Fisher 1983; Delannée et al. 2000; Andrews & Howard 2001; Gosling et al. 1976):
the fastest (resp. slowest) ones mostly originate from active
regions (resp. quiescent prominences), and once they reach the
inner edge of the SoHO/LASCO coronographs, they typically
have radial velocities of the order of 500-1500 km s-1
(resp. 50-300 km s-1). As in the flux rope model of
Chen & Krall (2003) which considers end-to-end twists of
about 4 turns (Chen 2004, private communication) the
present explanation for both classes of CMEs is based
on the size difference between prominences and active
regions. However, contrary to Chen & Krall (2003),
our model does not involve the evolution of the
flux tube curvature during a free expansion, but rather
a direct scaling effect of the equilibrium curve during
a driven expansion.
roughly
scales like f-1 (resp. f-2).
All these properties are consistent with the two classes
of observed CMEs (MacQueen & Fisher 1983; Delannée et al. 2000; Andrews & Howard 2001; Gosling et al. 1976):
the fastest (resp. slowest) ones mostly originate from active
regions (resp. quiescent prominences), and once they reach the
inner edge of the SoHO/LASCO coronographs, they typically
have radial velocities of the order of 500-1500 km s-1
(resp. 50-300 km s-1). As in the flux rope model of
Chen & Krall (2003) which considers end-to-end twists of
about 4 turns (Chen 2004, private communication) the
present explanation for both classes of CMEs is based
on the size difference between prominences and active
regions. However, contrary to Chen & Krall (2003),
our model does not involve the evolution of the
flux tube curvature during a free expansion, but rather
a direct scaling effect of the equilibrium curve during
a driven expansion.
The velocity magnitudes in Fig. 8 have been
calculated for a photospheric velocity of 1 km s-1
so as to obtain typical CME velocities at ![]() .
Even though the observed dynamics of CMEs have typically
been studied at greater heights, a few height-velocity-time
plots have been measured at lower altitudes
(Srivastava et al. 2000,1999; Wang et al. 2003; Zhang et al. 2004). Even
though these observed plots appear to be in qualitative agreement
with Fig. 8, two strong differences must be
emphasized. Firstly, the prescribed
.
Even though the observed dynamics of CMEs have typically
been studied at greater heights, a few height-velocity-time
plots have been measured at lower altitudes
(Srivastava et al. 2000,1999; Wang et al. 2003; Zhang et al. 2004). Even
though these observed plots appear to be in qualitative agreement
with Fig. 8, two strong differences must be
emphasized. Firstly, the prescribed
![]() is at least ten times larger than photospheric
velocities typically observable in rotating sunspots
(Brown et al. 2003, and references therein). Secondly, the
initial "quiet phase'' before the "very fast opening'' is not
longer than a few hours (resp. a day) for the active region
(resp. prominence) case. This is much too small compared
to observed time-scales which are of the order of days to
weeks.
is at least ten times larger than photospheric
velocities typically observable in rotating sunspots
(Brown et al. 2003, and references therein). Secondly, the
initial "quiet phase'' before the "very fast opening'' is not
longer than a few hours (resp. a day) for the active region
(resp. prominence) case. This is much too small compared
to observed time-scales which are of the order of days to
weeks.
The only way to bypass the first difficulty (too fast photospheric flows) would be to have twist either injected by reconnection rather than by flows, or by fast undetectable flows within sunspots due e.g. to twisted flux emergence through the photosphere. The second issue (too short quiet phase) would imply that twist is not injected continuously, but rather in episodic bursts well related with the launch of CMEs, with time scales of the order of a few hours to one or two days. Direct application of this model to the CME phenomenon thus requires the same artificially fast twisting as in the analytical driven model of Chen (1996).
However, as emphasized by Forbes (2001), "this point of view
is difficult to reconcile with the extremely tranquil conditions
that exist in the photosphere during flares and CMEs''.
In our opinion, since the dynamic evolution of the
weak fields surrounding the core twisted flux tubes plays
a very important role in the dynamics of the system
for twist values
![]() turn (see Sect. 4.4), their global reconfiguration
associated with e.g. distant flux emergence (Lin et al. 2001)
and/or magnetic reconnection (Antiochos et al. 1999) is most
likely to lead to a CME. In the frame
of our model, such reconfigurations may be associated
with dynamic changes of the value of the parameter
turn (see Sect. 4.4), their global reconfiguration
associated with e.g. distant flux emergence (Lin et al. 2001)
and/or magnetic reconnection (Antiochos et al. 1999) is most
likely to lead to a CME. In the frame
of our model, such reconfigurations may be associated
with dynamic changes of the value of the parameter
![]() in Eq. (42), which may solve the problem of the speed of the twist injection encountered
by the present model and in Chen (1996).
in Eq. (42), which may solve the problem of the speed of the twist injection encountered
by the present model and in Chen (1996).
 |
Figure 9:
( First row): Contours of
|
| Open with DEXTER | |
We calculate the vertical electric current densities from
the photospheric transverse fields,
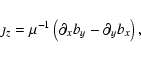 |
(45) |
Within each magnetic polarity, both direct and surrounding return
currents co-exist. The extended weak return currents
naturally form by shearing/twisting an initial line-tied potential
field, so as to maintain the outer untwisted fields potential.
The direct currents are more concentrated and intense. Their maximal
values are about
![]() mA m-2 for the largest
and the smallest vortex sizes respectively. If the magnetic field
amplitudes of the bipole were scaled to those of typical sunspots
(
mA m-2 for the largest
and the smallest vortex sizes respectively. If the magnetic field
amplitudes of the bipole were scaled to those of typical sunspots
(
![]() G instead of 480 G),
these currents would be
G instead of 480 G),
these currents would be
![]() mA m-2,
in accordance with typical vector field measurements within
sunspots (see e.g. Pevtsov et al. 1995; Leka & Skumanich 1999; Régnier et al. 2002).
mA m-2,
in accordance with typical vector field measurements within
sunspots (see e.g. Pevtsov et al. 1995; Leka & Skumanich 1999; Régnier et al. 2002).
These currents correspond to a negative value of the force-free
parameter ![]() which is defined as
which is defined as
![]() .
This sign is consistent with the prescribed boundary
motions, which result in a left-handed magnetic twist, so
a global negative magnetic helicity. For all three cases the
maximum values are nearly the same:
.
This sign is consistent with the prescribed boundary
motions, which result in a left-handed magnetic twist, so
a global negative magnetic helicity. For all three cases the
maximum values are nearly the same:
![]() Mm-1. This is so because the more concentrated the vortex,
the higher
Mm-1. This is so because the more concentrated the vortex,
the higher ![]() and the higher bz at the location of these
strong currents (see Fig. 9). So the typical
scale-length
and the higher bz at the location of these
strong currents (see Fig. 9). So the typical
scale-length
![]()
![]() 25 Mm of the strongest
current-carying field lines is the same for all three cases.
25 Mm of the strongest
current-carying field lines is the same for all three cases.
This ![]() value is typically 15-30 times larger than what
is found in linear force-free field models of large-scale loops
in sheared active regions (Démoulin et al. 2002; Schmieder et al. 1996).
It is also 5-10 times larger than in models of
intermediate and plage prominences (Aulanier & Démoulin 2003)
and X-ray sigmoïds (Gibson et al. 2002; van Driel-Gesztelyi et al. 2000).
Note that in these past works,
value is typically 15-30 times larger than what
is found in linear force-free field models of large-scale loops
in sheared active regions (Démoulin et al. 2002; Schmieder et al. 1996).
It is also 5-10 times larger than in models of
intermediate and plage prominences (Aulanier & Démoulin 2003)
and X-ray sigmoïds (Gibson et al. 2002; van Driel-Gesztelyi et al. 2000).
Note that in these past works, ![]() was
calculated for typically 2-8 times larger configurations than
those studied here. So the present rescaled
was
calculated for typically 2-8 times larger configurations than
those studied here. So the present rescaled ![]() values fall
in the range of those estimated for prominences and sigmoïds.
values fall
in the range of those estimated for prominences and sigmoïds.
Another generic property is a strong azimuthal asymmetry of the
distribution of the transverse fields and of ![]() with
respect to the vortex centers (compare Figs. 3 and 9). Consider one magnetic polarity, e.g. for x<0.
Firstly, the apparent vortex centers as deduced from the
transverse fields are always shifted from the real vortex centers
located at
with
respect to the vortex centers (compare Figs. 3 and 9). Consider one magnetic polarity, e.g. for x<0.
Firstly, the apparent vortex centers as deduced from the
transverse fields are always shifted from the real vortex centers
located at
![]() .
Secondly, the transverse fields originate radially from the
vortex centers
in a quadrant (
.
Secondly, the transverse fields originate radially from the
vortex centers
in a quadrant (
![]() ), where
(
), where
(
![]() )
are the coordinates of the left vortex.
On the contrary, the transverse fields tend
to follow the contours of bz
for another quadrant (
)
are the coordinates of the left vortex.
On the contrary, the transverse fields tend
to follow the contours of bz
for another quadrant (
![]() ). Thirdly,
). Thirdly, ![]() shows a swirling pattern around (
shows a swirling pattern around (
![]() ). Several
spiral arms of opposite signs for
). Several
spiral arms of opposite signs for ![]() and of various
widths appear for
and of various
widths appear for
![]() turn, and develop more
and more with time as the twist increases.
turn, and develop more
and more with time as the twist increases.
This azimuthal asymmetry is not present in cylindrical MHD
calculations in which both extremities of the cylinder
are line-tied. It is a geometrial property caused by
the curvature of the field lines which are line-tied onto
the same plane. This asymmetry comes from the fact that, even
though the same amount of twist ![]() is
injected for both short field lines (rooted on each side
of the inversion line around x=0) and large ones (located on
the edges of the bipole), stronger currents are generated
in the smaller field lines. This can be explained by considering
a simple cylindrical flux tube model in (
is
injected for both short field lines (rooted on each side
of the inversion line around x=0) and large ones (located on
the edges of the bipole), stronger currents are generated
in the smaller field lines. This can be explained by considering
a simple cylindrical flux tube model in (![]() ), where
l is the length of the flux tube along z. The electric current
and field line equations in cylindrical coordinates result
in:
), where
l is the length of the flux tube along z. The electric current
and field line equations in cylindrical coordinates result
in:
Interestingly, the complex asymmetric structure of ![]() in the photosphere is formed within a very simple magnetic
configuration which is initially smooth, bipolar and symmetric,
and which is twisted by vortex motions that are also very simple.
Also, this structure qualitatively remains very similar for extended
as well as concentrated vortices. So it is probably a generic
property of line-tied twisted flux tubes rooted in the photosphere.
It follows that twisted sunspots should naturally have - at least -
two more-or-less contrasted concentrations of strong direct
electric currents within a given magnetic polarity, and possibly
- at least - one patch of weak return current of opposite sign.
This is in very good agreement with the observations
(Pevtsov et al. 1995; Leka & Skumanich 1999; Régnier et al. 2002). In the frame of our model,
the observed fragmentation of the force-free parameter
in the photosphere is formed within a very simple magnetic
configuration which is initially smooth, bipolar and symmetric,
and which is twisted by vortex motions that are also very simple.
Also, this structure qualitatively remains very similar for extended
as well as concentrated vortices. So it is probably a generic
property of line-tied twisted flux tubes rooted in the photosphere.
It follows that twisted sunspots should naturally have - at least -
two more-or-less contrasted concentrations of strong direct
electric currents within a given magnetic polarity, and possibly
- at least - one patch of weak return current of opposite sign.
This is in very good agreement with the observations
(Pevtsov et al. 1995; Leka & Skumanich 1999; Régnier et al. 2002). In the frame of our model,
the observed fragmentation of the force-free parameter ![]() within sunspots is then not necessarily due to some hidden complexity
in the distribution of the photospheric flux or of the footpoint
twist.
within sunspots is then not necessarily due to some hidden complexity
in the distribution of the photospheric flux or of the footpoint
twist.
 |
Figure 10:
( First row): X-ray sigmoïds calculated from the vertical
integration of the Joule heating term. The minimal
(black) and maximal (white) intensities are scaled
to the same values for all three cases.
( Second row): Sigmoïd with field lines overplotted.
[Pink; green; red; blue] lines are rooted respectively
around [the vortex centers; the sigmoïd
ends; their brightest parts; their edges].
( Third row): Projection view of the same field lines with
greyscale for bz at z=0.
The [first; second; third] columns correspond to vortices defined by
|
| Open with DEXTER | |
A common assumption for the materialization of observed solar
structures is that they are directly traced by magnetic field
lines. However, it has already been shown for the case of filaments
and prominences that this assumption is not fully valid, and that
only portions of field lines trace the visible features, both
in H![]() and in EUV wavelengths (e.g. Aulanier & Schmieder 2002).
In the following we address the validity of this assumption
for sigmoïdal structures observed in X-rays. Our main
hypothesis is that since X-rays make it possible to visualize the hottest
parts of the corona, the observed intensity
and in EUV wavelengths (e.g. Aulanier & Schmieder 2002).
In the following we address the validity of this assumption
for sigmoïdal structures observed in X-rays. Our main
hypothesis is that since X-rays make it possible to visualize the hottest
parts of the corona, the observed intensity
![]() is nearly proportional to the Joule heating term
integrated along the line of sight. If we consider the bipole
to be at the disc center for simplicity, we simulate X-ray
observations by calculating:
is nearly proportional to the Joule heating term
integrated along the line of sight. If we consider the bipole
to be at the disc center for simplicity, we simulate X-ray
observations by calculating:
Figure 10, top shows that sigmoïdal structures
of various shapes naturally appear for all three cases, with an
inverse-S shape. Their orientation is compatible with the sign
of the force-free parameter ![]() found above and with the
hemispheric rule for observed sigmoïds and magnetic helicity,
i.e.
found above and with the
hemispheric rule for observed sigmoïds and magnetic helicity,
i.e. ![]() and inverse-S shapes in the northern hemisphere
(Pevtsov et al. 1995; Burnette et al. 2004; Seehafer 1990; Rust & Kumar 1996).
The sigmoïd formed by large vortices is the brightest of
all three, and its brightest region is right above the inversion
line. On the contrary, the sigmoïd formed by small vortices
has its brighests regions located at its extremities, on top of
the center of each vortex. The sigmoïd formed by medium vortices
is an intermediate case, where the brightest regions are located
at the elbows of the S-shape.
and inverse-S shapes in the northern hemisphere
(Pevtsov et al. 1995; Burnette et al. 2004; Seehafer 1990; Rust & Kumar 1996).
The sigmoïd formed by large vortices is the brightest of
all three, and its brightest region is right above the inversion
line. On the contrary, the sigmoïd formed by small vortices
has its brighests regions located at its extremities, on top of
the center of each vortex. The sigmoïd formed by medium vortices
is an intermediate case, where the brightest regions are located
at the elbows of the S-shape.
A global idea for the altitude of current formation
responsible for the sigmoïds and for their different
shapes as a function of vortex size can be obtained as follows:
on one hand some portions of the sigmoïds are well
matched by the distribution of
![]() (compare
Figs. 9 and 10). This shows
that they correspond to low altitude features. For a
given twist, these regions are brighter for smaller
vortices because the core twisted flux tube is more
confined at low altitude than for extended vortices (as
shown by the equilibrium curves, see Fig. 7),
which results in stronger electric currents (see Eqs. (46) and (47)). On the other hand some other portions of the sigmoïds cross the inversion
line at x=0. These originate from an emitting volume
located substantially above the photosphere. These
regions are brighter for larger vortices because their
extension results in a stronger shearing of the field lines
located near the inversion line at x=0 (as shown e.g. by
transverse fields in Fig. 9).
(compare
Figs. 9 and 10). This shows
that they correspond to low altitude features. For a
given twist, these regions are brighter for smaller
vortices because the core twisted flux tube is more
confined at low altitude than for extended vortices (as
shown by the equilibrium curves, see Fig. 7),
which results in stronger electric currents (see Eqs. (46) and (47)). On the other hand some other portions of the sigmoïds cross the inversion
line at x=0. These originate from an emitting volume
located substantially above the photosphere. These
regions are brighter for larger vortices because their
extension results in a stronger shearing of the field lines
located near the inversion line at x=0 (as shown e.g. by
transverse fields in Fig. 9).
The three-dimensional nature of the sigmoïds is revealed by the integration of field lines whose photospheric footpoints (at z=0) are located all along the projected bright sigmoïds. Generic results are found for all three cases (see Fig. 10, second & third rows).
First, it is evident that the sigmoïds are not traced by the core twisted flux tube which is rooted around the vortex centers (shown as pink field lines): the deformation of this flux tube by the antisymmetric generation of currents forms in fact a direct-S shape, opposite to the orientation of the sigmoïd. Also, one can see that the sigmoïd is always present, regardless of the vertical expansion of the flux tube. Indeed its apex almost reaches the top of the numerical box for the large vortex case at the time of the figure.
Actually, we find that the sigmoïds are traced by an ensemble of sheared (or weakly twisted) field lines located at low altitudes beneath the twisted flux tube, whose deformation from their initial potential configuration is directly related to the direction of the photospheric vortices.
But, when one attempts to match a sigmoïd by a unique field line from this ensemble, one sees that it is impossible. In reality, no single field line can trace the whole of the sigmoïds, even though a few ones which are nearly symmetric with respect to the inversion line can trace the central parts of the sigmoïds. This is mostly noticeable for the sigmoïd ends (especially for the large vortex case), where the field lines projected onto the z=0 plane rarely trace the shape of the simulated sigmoïds. This result, if true in general, implies that trying to match observed sigmoïdal structures directly with calculated field lines is impossible.
Projection views (Fig. 10, third
rows) show that the apex of the field lines which are rooted
on top of the brightest parts of the projected sigmoïds
(shown in red) and at their ends (shown in green) nearly
has the same altitude for all three vortex sizes for
![]() turns. This may look surprising at first sight for
two reasons. First, this behaviour is very different from that of the
core twisted flux tube, whose vertical expansion very strongly
depends on the vortex size. Second, the field lines which form
the sigmoïds are rooted in different regions for different
vortex sizes. However, this property is related to the
fact that both
turns. This may look surprising at first sight for
two reasons. First, this behaviour is very different from that of the
core twisted flux tube, whose vertical expansion very strongly
depends on the vortex size. Second, the field lines which form
the sigmoïds are rooted in different regions for different
vortex sizes. However, this property is related to the
fact that both ![]() (so the length-scale of the currents
(so the length-scale of the currents
![]()
![]() 25 Mm) and the distances between the
footpoints of these field lines are nearly the same for all cases.
This leads to the prediction that the altitude of current-carrying
field lines which form the sigmoïds for a given
photospheric magnetic field does not depend on the
width of the current-generating vortex, but only on
the degree of twist of the strongest fields.
25 Mm) and the distances between the
footpoints of these field lines are nearly the same for all cases.
This leads to the prediction that the altitude of current-carrying
field lines which form the sigmoïds for a given
photospheric magnetic field does not depend on the
width of the current-generating vortex, but only on
the degree of twist of the strongest fields.
The same analysis has been performed for lower and higher degrees of twist (always before the flux tube reaches the top boundary) for all three vortex classes. Apart from qualitative morphological differences, the same properties were found in every case. This leads to the conclusion that, under the hypothesis which we used to simulate X-ray observations, our findings are generic.
It is worth noting that the properties that we find
(i.e. sigmoïds being formed by Joule heating in an
ensemble of sheared field lines located beneath a twisted
flux tube and all rooted in the photosphere within the direct
currents) are contradictory with the results of the non-linear
force-free field model of Régnier et al. (2002). They associated
an observed sigmoïd both with
a strongly twisted flux tube and with a less twisted one,
each having a different sign for ![]() .
This contradiction
may either be attributed to the unreliability of our proxy
(see Eq. (48)) for simulating X-ray observations,
or to the fact that the X-ray loops analyzed by Régnier et al. (2002)
show a rather weak S-shape, so that they might
not be a real sigmoïd. This point will have to be addressed
again in the future.
.
This contradiction
may either be attributed to the unreliability of our proxy
(see Eq. (48)) for simulating X-ray observations,
or to the fact that the X-ray loops analyzed by Régnier et al. (2002)
show a rather weak S-shape, so that they might
not be a real sigmoïd. This point will have to be addressed
again in the future.
In this paper we calculated the structure and evolution of
slowly twisted flux tubes in the solar photosphere and in its corona,
using a new zero-![]() MHD code with line-tied boundary conditions
at the photosphere and open boundary conditions at the other faces.
We considered three
different vortex sizes which preserve bz at the photospheric
boundary. Our domain was
MHD code with line-tied boundary conditions
at the photosphere and open boundary conditions at the other faces.
We considered three
different vortex sizes which preserve bz at the photospheric
boundary. Our domain was ![]() 20 times higher than the initial
altitude of the field line which is rooted in the strongest field
regions. We compared our results with previously published
calculations of similar configurations. Our parametric study
resulted in the finding of generic properties in such systems.
20 times higher than the initial
altitude of the field line which is rooted in the strongest field
regions. We compared our results with previously published
calculations of similar configurations. Our parametric study
resulted in the finding of generic properties in such systems.
We have shown that continuously twisted and relaxing flux tubes all have the following generic properties:
Acknowledgements
G.A. thanks S. K. Antiochos and C. R. DeVore for very fruitful discussions about numerical methods, as well as T. Amari, B. Kliem and T. Törok for discussions about their work. The calculations in this paper were all done on the Digital-UNIX ES40 computer of the Service Informatique de l'Observatoire de Paris (SIO).