All Tables
- Table 1:
Weighted oscillator strength gf(AS),
17 configurations. Comparison with
gf(AS4), including n=4 correlation configurations; gf(AS5),
including n=5 correlation
configurations. The gf's were
calculated using AUTOSTRUCTURE.
- Table 2:
Fe+22 level energies in rydberg units relative to the
ground state. Theoretical results from the Breit-Pauli R-matrix
program. Observed results
from Corliss & Sugar (1982) assuming
1 Ry = 109737.32
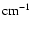 .
% diff is the
percentage difference between the theoretical and observed energies.
.
% diff is the
percentage difference between the theoretical and observed energies.
- Table 3:
Past and present label of energy levels and indexing.
- Table 4:
Fe+22: comparing the present wavelengths
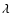 (R) and
weighted oscillator strengths gf(R) from AUTOSTRUCTURE with those of
Bathia & Mason (1981,
1986),
(R) and
weighted oscillator strengths gf(R) from AUTOSTRUCTURE with those of
Bathia & Mason (1981,
1986),
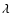 (BM) and gf(BM);
Bhatia et al. (1986),
(BM) and gf(BM);
Bhatia et al. (1986), 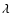 (BFS);
Fawcett (1984),
(BFS);
Fawcett (1984), 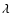 (F) and gf(F);
Sampson et al. (1984); gf(SGC);
Murakami & Kato (1996),
(F) and gf(F);
Sampson et al. (1984); gf(SGC);
Murakami & Kato (1996), 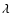 (MK);
Guo-Xin & Ong (1998a),
(MK);
Guo-Xin & Ong (1998a), 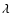 (GO) and gf(GO);
Fawcett's laboratory measurements (Fawcett et al. 1979),
(GO) and gf(GO);
Fawcett's laboratory measurements (Fawcett et al. 1979),
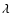 (Exp).
Wavelengths are in Å.
(Exp).
Wavelengths are in Å.
- Table 5:
High energy Born limits for forbidden transitions
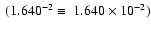 .
.
- Table 6:
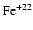 effective collision strengths
effective collision strengths
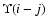 to n=2,3 levels for
to n=2,3 levels for
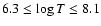 .
.
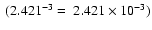 .
.
- Table 7:
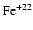 effective collision strengths
effective collision strengths
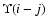 to n=4 levels for
to n=4 levels for
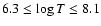 .
.
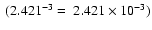 .
.
- Table 8:
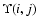 for
T = 107.1
for
T = 107.1 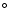 K.
CDMB, present results;
BM, Bhatia & Mason (1981, 1986);
GO, Guo-Xin & Ong (1998b);
B
K.
CDMB, present results;
BM, Bhatia & Mason (1981, 1986);
GO, Guo-Xin & Ong (1998b);
B ,
Bhatia;
SGC, Sampson et al. (1984).
,
Bhatia;
SGC, Sampson et al. (1984).
- Table 9:
Fractional level population Nj
for the n=2,3 levels, calculated at 109, 1014 (cm-3)
electron densities and the temperature T= 13 MK.
(R): computed with all the resonances and all the levels up to n=4;
(NR): computed with all the levels up to n=4, but neglecting the
contribution from the resonances;
(BM): computed with the DW collision strengths of Bhatia & Mason (1986), which
included only the n=2,3 levels.