A&A 430, 331-341 (2005)
DOI: 10.1051/0004-6361:20041358

Atomic data from the IRON Project

LVI. Electron excitation of Be-like Fe XXIII for the n = 2, 3, 4 configurations

M. C. Chidichimo^1, - G. Del Zanna¹ - H. E. Mason¹ - N. R. Badnell² - J. A. Tully³ - K. A. Berrington⁴

1 - Department of Applied Mathematics and Theoretical Physics, The Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 OWA, Cambridge, UK
2 - Department of Physics, University of Strathclyde, Glasgow G4 0NG, UK
3 - Département Cassiopée, Observatoire de la Côte d'Azur, BP 4229, 06304 Nice Cedex 4, France
4 - School of Science and Mathematics, Sheffield Hallam University, Sheffield S1 1WB, UK

Received 26 May 2004 / Accepted 10 August 2004

Abstract
Collision strengths for electron induced transitions in the beryllium-like ion Fe⁺²² are calculated using the intermediate coupling frame transformation (ICFT) version of the R-matrix programs. Our target has 98 fine structure states ${\rm 1s^2}~nl~n'l'~SLJ$ corresponding to n = 2 and n' = 2, 3, 4. The present calculation is for electron impact energies in the range 3.15 to 380 Ry. When T exceeds about ten million degrees one needs to take account of contributions to the thermally averaged collision strength $\sl\Upsilon$ coming from electrons with energies in excess of 380 Ry. We discuss a way of allowing for these contributions. Values of $\sl\Upsilon$ for all the transitions between the ground state and the excited states ${\rm 1s^2}~2l~n~l~n'l'~S'L'J'$, with n'=2,3,4 are tabulated as a function of ${\rm log}~T$. The temperature range $6.3 \le \log~ T \le 8.1$ is centred on ${\rm log}~T = 7.1$ which is approximately where Fe⁺²² has maximum abundance in ionization equilibrium. To the best of our knowledge these are the first R-matrix calculations for Fe⁺²² for excitations to the n = 3,4 levels. Good agreement with previous distored-wave calculations is found. However, the resonance contributions have an important effect on the effective collision strengths and in turn on the level populations.

Key words: atomic data - Sun: corona

1 Introduction

The present calculation has been carried out as part of the international IRON Project (Hummer et al. 1993), whose aim is to obtain reliable rate coefficients for collisional excitation of fine-structure transitions in positive ions induced by electron impact. In a previous calculation, Chidichimo et al. (1999) obtained level energies, oscillator strengths and effective collisions strengths for the n=2 complex of Fe⁺²². They also included a thorough discussion of collision calculations devoted to this ion up to the time of their own investigation. We will refer to this paper as Paper I. Previous published calculations for transitions to the n=3 complex of Fe⁺²² were carried out in the non-relativistic and relativistic distorted wave (DW) approximation.

Unpublished non-relativistic DW results are available for transitions up to n=4 (Bhatia, priv. comm.).

In the present paper we present new atomic data for transitions up to the n=2,3,4 complex in Fe⁺²². The data for the n=2 complex represent a revision of the data published in Paper I. These are the first R-matrix calculations for this ion for excitations to the n = 3 levels, and the first published calculations to n = 4. A complete list of IRON Project published papers and those in press is available on-line.

This work has been carried out as part of the UK RmaX network, which focuses on new atomic data for X ray spectra in astrophysics. Earlier work by the RmaX network includes ICFT calculations up to n=4 for C-like (Badnell & Griffin 2001) and B-like (Badnell et al. 2001) Fe ions.

Fe⁺²² $n=2 \to n\hbox{$^\prime$ }=3$ and $n=2 \to n\hbox{$^\prime$ }=4$ spectral lines have been observed in solar flares (see, e.g., Neupert et al. 1967; Neupert et al. 1973; Doschek et al. 1973; McKenzie et al. 1985; Fawcett et al. 1987), and are observed with the current X-ray missions such as Chandra and XMM in spectra from a variety of different sources. Fe⁺²² line ratios have a temperature sensitivity (as shown by Bhatia & Mason 1981), and are therefore a powerful diagnostic tool for a variety astrophysical applications. This paper focuses on the atomic calculations, while a follow-up paper (Del Zanna et al. 2004) will deal with line identifications and astrophysical applications.

2 Method of calculation and target

In what follows, we outline the steps taken in the present work which justify our belief that the results given here are the most reliable Fe⁺²² rate coefficients currently available. First of all we were careful to obtain a good target model.

As regards the collision calculation, we have made use of the R-matrix method (Hummer et al. 1993; Berrington et al. 1995) in conjunction with the intermediate frame coupling transformation (ICFT) (see Badnell & Griffin 2001; Badnell et al. 2001).

These R-matrix programs, which are based on approximations that take into account much of the collision physics responsible for resonance scattering and relativistic effects, are widely considered as the most elaborate and accurate ones in existence for this type of calculation.

2.1 Atomic orbitals for Fe⁺²²

In the present calculation, we used the same radial orbitals as those given in Paper I (see Table 2, where the numerical parameters needed to generate the orbitals are listed). We have used the 1s, 2s radial orbitals of Clementi & Roetti (1974) while 2p, 3s, 3p, 3d, 4s, 4p, 4d, 4f were obtained by means of the CIV3 code (Hibbert 1975; Hibbert et al. 1991). CIV3 uses analytic radial orbitals P_nl(r) which are expressed as sums of Slater typer orbitals as follows:

$$\begin{eqnarray*}P_{nl}= \sum_{j=1}^{k}c_{jnl}\frac{(2\zeta_{jnl})^{I_{jnl+1/2}}} {[(2 I_{jnl})!]^{1/2}} r^{~I_{jnl}} \exp(-\zeta_{jnl}r). \end{eqnarray*}$$

2.2 Target energy levels

For the collisional calculation, we used all the terms originating from the 17 configurations included in Table 2 (98 levels up to n=4). All 17 configurations in our calculation were treated as spectroscopic, i.e. there were no extra configurations treated as correlation. These correlation configurations are not found to contribute significantly for the highly charged ion Fe⁺²².

In order to assess how good our target is, we ran various atomic structure calculations by adding extra configurations, up to n=5, to our basic set of configurations. Configurations involving double promotion from the n=3,4,5 complex were treated as correlations. These calculations were performed with the AUTOSTRUCTURE code (Badnell 1997) and the results are presented in Table 1.

First, for consistency, we checked that the energies calculated with AUTOSTRUCTURE were basically (to within 10^-4 Ry) the same as those shown in Table 2, which were calculated with the R-matrix codes. Then, for each AUTOSTRUCTURE run, we compared the level energies and the oscillator strengths (or the high-energy limit for the forbidden lines) for all the transitions with the values obtained from the basic set of 17 configurations. We found variations of the order of 10%, i.e. of the order of the accuracy of the calculations themselves, thus giving us confidence on the accuracy of the target wavefunctions.

Table 1: Weighted oscillator strength gf(AS), 17 configurations. Comparison with gf(AS4), including n=4 correlation configurations; gf(AS5), including n=5 correlation configurations. The gf's were calculated using AUTOSTRUCTURE.

The theoretical target energies of Fe⁺²² produced by the Breit-Pauli branch of the R-matrix code are shown in Table 2 along with the configuration identification provided by AUTOSTRUCTURE and the observed energies for some of the levels taken from Corliss & Sugar (1982) and from the National Institute of Standards and Technology (NIST) database. The good agreement between the theoretical and observed energy levels gives us confidence in the target description.

There are minor differences between the level energies of Paper I (see Table 3) and the present calculations. This is expected since we chose to treat all configurations as spectroscopic ones and avoid the inclusion of extra configurations which were treated as correlation in Paper I. This approach also leads to a few changes in the level energy order compared to Paper I (see Table 3).

Table 2: Fe⁺²² level energies in rydberg units relative to the ground state. Theoretical results from the Breit-Pauli R-matrix program. Observed results from Corliss & Sugar (1982) assuming 1 Ry = 109737.32 $\rm cm^{-1}$. % diff is the percentage difference between the theoretical and observed energies.

2.3 The quality of the target

One way of testing the target is to calculate the corresponding oscillator strengths and see how these compare with those of other investigators and spectroscopic observations of laser-produced plasmas (Fawcett et al. 1979). Fawcett (1984, 1985) tabulates weighted oscillator strengths (i.e. gf values) and wavelengths for transitions $n=2 \to n\hbox{$^\prime$ }=3$ in many beryllium-like ions, including Fe⁺²². He made use of Robert D. Cowan's code, together with the Slater parameter optimisation procedure, which is widely thought to provide reliable benchmark data. Cowan's code only provides the length gauge oscillator strength, which in general is more reliable than the velocity gauge one.

The full set of wavelengths $\lambda$(Å) and transition probabilities A_ji(s^-1) for all the transitions occurring amongst the 98 levels as calculated with AUTOSTRUCTURE is provided in electronic form. Observed energies, applying adjustments to the LS energies, and refined A-values will be discussed in a forthcoming paper by Del Zanna et al. (2004). In Table 4 we compare our gf and wavelength values with those of Bhatia & Mason (1981), Bhatia & Mason (1986), Guo-Xin & Ong (1998a), Bhatia et al. (1986), Murakami & Kato (1996), together with the observed wavelengths from Fawcett et al. (1979). Guo-Xin & Ong (1998a) used the GRASP code (Parpia et al. 1996) with a 133-level multiconfiguration Dirack-Fock expansion, which should provide the most accurate results. From Table 4 we note that their inclusion of correlation and higher-order relativistic effects do not seem to play a prominent role in the 1-13 and 1-15 wavelengths, our calculations and theirs agree within 0.2% with the observed wavelengths. We also have good agreement, within 10% for the strongest transitions, between our gf results and theirs. This gives us confidence in our target.

Table 3: Past and present label of energy levels and indexing.

Table 4: Fe⁺²²: comparing the present wavelengths $\lambda$(R) and weighted oscillator strengths gf(R) from AUTOSTRUCTURE with those of Bathia & Mason (1981, 1986), $\lambda$(BM) and gf(BM); Bhatia et al. (1986), $\lambda$(BFS); Fawcett (1984), $\lambda$(F) and gf(F); Sampson et al. (1984); gf(SGC); Murakami & Kato (1996), $\lambda$(MK); Guo-Xin & Ong (1998a), $\lambda$(GO) and gf(GO); Fawcett's laboratory measurements (Fawcett et al. 1979), $\lambda$(Exp). Wavelengths are in Å.

2.4 The collision and effective collision strengths

Our ultimate aim is to tabulate the temperature-dependent effective collision strength $\Upsilon(i-j)$, defined by :

$$\Upsilon(i-j) = \int_0^\infty \Omega(i-j)~ {\rm exp}(-E_j/kT)~ {\rm d}(E_j/kT)$$

where E_j is the energy of the colliding electron after excitation has occurred and k is the Boltzmann constant. We performed the numerical integration by linearly interpolating the $\Omega(i,j)~{\rm exp}(-E_j/kT)$ data points as suggested by Burgess & Tully (1992). In order to try and delineate the resonance structure in the collision strengths we calculated each $\Omega(i-j)$ at 116 847 energy points, i.e. with an extremely fine mesh.

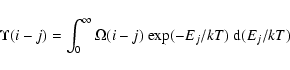
For electrons incident with kinetic energies relative to the ground state of the target less than or equal to 380 Ry we used the R-matrix method based on the close coupling approximation. This allows us to take account of channel coupling up to the n=4 levels. In order to delineate the multitude of resonance peaks we ran the code at 116 746 values of the collision energy starting at 3.1521 Ry (relative to the ground state), and up to 116  Ry. In this resonance region we used an energy step-length of $2 \times 10^{-6} z^2 = 9.68 \times 10^{-4}$ Ry. In the interval 116 < E_i < 382 Ry, in which there are no resonances, we calculated collision strengths at 101 energy points, with a step-length of $5.5 \times 10^{-3} z^2 = 2.662$ Ry.

In Paper I, the Breit-Pauli code was run at 7704 values of the collision energy starting at 3.1521 Ry, relative to the ground state and going up to 103.05816 Ry. The interval between 103.05816 and 116 Ry was covered by making a linear extrapolation backwards using the values of the collision strength at 116 and 127.5 Ry. Also by an unfortunate and regretful oversight, at low energies the higher partial wave contribution to the collision strength for dipole transitions was not included.

The R-matrix code also attends to the crucial issue of a top-up procedure in order to account for the higher partial waves in the collision strengths. With increasing energy, more and more partial waves need to be calculated. Details of how this top-up was done for C-like (Badnell & Griffin 2001) and B-like (Badnell et al. 2001) Fe ions are given in those publications.

In the present calculations, in order to ensure convergence of the expansion, we let the partial wave quantum number J extend up to J = 41.5 and then carried out a top-up procedure by estimating the contributions from higher partial waves.

In order to calculate reliable effective collision strengths at temperatures which are more than about $2 \times 10^7~{\rm K}$, we need to calculate, or estimate, the value of the collision strengths $\Omega(i,j)$ for energies even higher than 380 Ry, up to several thousand Rydbergs. We extended our R-matrix collision strengths beyond 382 Ry by using the method of scaling and extrapolating the collision strengths to the appropriate high-energy limits as described in Burgess & Tully (1992). For optically allowed transitions, the high-energy limits are directly obtained from the oscillator strengths. We used the gf values calculated with AUTOSTRUCTURE (see Table 4). For optically forbidden transitions between levels with the same parity and spin we calculated the high-energy Born limits in the manner described by Burgess et al. (1997). For optically forbidden intersystem transitions we used a comparable method developed by one of us (MCC) (see Appendix, Chidichimo et al. 2003). NRB has included this method in his AUTOSTRUCTURE code. The high-energy limits for the optically forbidden lines used for the extrapolation procedure are given in Table 5.

We developed an IDL graphical interactive program (a modified form (GDZ) of the codes used by the CHIANTI team) to inspect visually all the data. It is based on the program OmeUps of Burgess & Tully (1992), whereby spline fits are performed on the 101 $\Omega(i-j)$ data points and the high-energy limit (see Fig. 2). We then perform an interpolation to obtain $\Omega(i,j)$ values at energies ranging from 382 Ry to 10⁶ Ry, which we deem sufficient for the purpose of thermal averaging. The effective collision strength $\Upsilon(i-j)$ are then calculated. This procedure gives added reliability at high temperatures.

Table 5: High energy Born limits for forbidden transitions $~(1.640^{-2} \equiv ~ 1.640 \times 10^{-2})$.

Table 6: $\rm Fe^{+22}$ effective collision strengths ${\sl\Upsilon }(i-j)$ to n=2,3 levels for $6.3 \le \log T \le 8.1$. $~(2.421^{-3} = ~ 2.421 \times 10^{-3})$.

3 New collisional data

Collision strengths $\Omega(i-j)$ between all 4753 transitions among the 98 levels were calculated.

Thermal averaging of the collision strengths was done using the linear interpolation method described by Burgess & Tully (1992). The effective collision strengths $\sl\Upsilon$ were calculated for the temperature range $6.3 \leq {\rm log}~T \leq 8.1$, centred on the temperature where Fe⁺²² is abundant under conditions of coronal ionization equilibrium (see, e.g., Arnaud & Raymond 1992). For temperatures below five million degrees the abundance of Fe⁺²² will be negligible in equilibrium conditions. Astrophysical situations may exist where Fe⁺²² is abundant at temperatures lower than this; in these cases one would need to extend the temperature range below 10^6.3 K.

Tables 6 and 7 present the effective collision strengths $\sl\Upsilon$ for excitations from the ground state only, which are the dominant contributors for astrophysical plasmas (see below). A more comprehensive dataset, that includes an adf04 file (see ref. for definition) and collision strengths for excitations from all the n=2 states is provided on-line for completeness. Also the data with the target energies and the A values are available on-line in ascii form. Other data mentioned in this paper (e.g. collision strengths) are available upon request from one of the authors (GDZ).

Table 7: $\rm Fe^{+22}$ effective collision strengths ${\sl\Upsilon }(i-j)$ to n=4 levels for $6.3 \le \log T \le 8.1$. $~(2.421^{-3} = ~ 2.421 \times 10^{-3})$.

Table 8: $\Upsilon ({i,j})$ for T = 10^7.1 $^\circ$K. CDMB, present results; BM, Bhatia & Mason (1981, 1986); GO, Guo-Xin & Ong (1998b); B$^{\rm a}$, Bhatia; SGC, Sampson et al. (1984).

3.1 Comparisons with previous calculations

For the $n=2 \to n\hbox{$^\prime$ }=2$ transitions, the present effective collision strengths only differ from the values published in Paper I by about 10%, with the exception of the 1-6 (2s^{2 1}S $_{0}^{\rm e}$-2p^{2 3}P $_{0}^{\rm e}$) and 1-7 (2s^{2 1}S $_{0}^{\rm e}$-2p^{2 3}P $_{1}^{\rm e}$) where differences are larger (up to 60%).

Since these are the first calculations for the $n=2 \to n\hbox{$^\prime$ }=3$ and $n=2 \to n\hbox{$^\prime$ }=4$ transitions that take into account the resonance effects, it is interesting to compare both the $\Omega(i,j)$ and $\Upsilon ({i,j})$ values with the previous relativistic and non-relativistic DW results, to assess the importance of the resonances.

3.1.1 Allowed and forbidden ${n}={2 \to {n}\hbox {$^\prime $ }=3,4}$ transitions in comparison with DW

We give illustrations of the different types of collision strength encountered in the present investigation by plotting ${\sl\Omega}(i-j)$ versus $E_{\sl j}$, the final electron energy in rydbergs. We included comparisons with the published collision strengths for the $n=2 \to n\hbox{$^\prime$ }=3$ transitions, from the papers by Bhatia & Mason (1981, 1986; hereafter BM). This study provided collision strengths for the $n=2 \to n\hbox{$^\prime$ }=3$ transitions, and used distorted wave approximations which do not take account of resonance effects.

Figure 1 shows $\Omega(1 {-} 12)$, $\Omega(1 {-} 13)$, $\Omega (1{-}15)$, $\Omega(1 {-} 19)$, $\Omega(1 {-} 20)$, $\Omega(1 {-} 50)$ and $\Omega(1 {-} 52)$. The collision strengths $\Omega (1{-}15)$ and $\Omega(1 {-} 52)$ correspond to optically allowed transitions which increase logarithmically with energy as $E_j \to \infty$. The collision strengths $\Omega(1 {-} 13)$ and $\Omega(1 {-} 50)$ correspond to intersystem transitions that behave as though they were optically allowed owing to the breakdown of LS coupling. For this to happen the initial and final levels must have different parities and $\Delta J = 0, \pm 1$, subject to the condition that $J = 0 \not\to J' = 0$. $\Omega(1 {-} 12)$ and $\Omega(1 {-} 20)$ are forbidden transitions in which neither the parity nor the spin change. The collision strength for this type of transition tends to a finite limiting value as $E_j \to \infty$. $\Omega(1 {-} 19)$ is a forbidden intersystem transition for which the collision strength normally falls off like E_j^-2 in the high energy limit.

	Figure 1: $\log \Omega(i-j)$ as function of the final energy Ej in rydbergs. Circles indicate the DW values of Bhatia & Mason (1986).
Open with DEXTER

	Figure 2: Top figure shows $\Omega (1{-}15)$ as function of the incident energy in rydbergs. Bottom figure shows the collision strength high energy points in the scaled form and the fit to the infinity energy point.
Open with DEXTER

The graphs show that there is excellent agreement between our background collision strengths and the distorted wave results. Only for the forbidden transitions 1-20 (electric quadrupole) is the difference more noticeable. Figure 1 shows that the BM distorted wave collision strength $\Omega(1 {-} 20)$ is lower than ours. Our calculations show that the contribution, from partial waves $13 \le L \le 40$ at E_i = 282 Ry, to the total collision strength $\Omega(1 {-} 20)$ is 17%. For L>40 the contribution is negligible. Therefore, it is likely that insufficient high partial wave contribution was taken into account, for this type of transition, in BM's calculations. Note the prominent resonance structure at low energies which has been neglected in all previous calculations.

3.1.2 Comparison of $\Upsilon ({i,j})$ for the ${n}={2 \to {n}\hbox {$^\prime $ }=3,4}$

Sampson et al. (1984; hereafter SGC), and Guo-Xin & Ong (1998b, hereafter GO) used a relativistic DW method to calculate the collision strengths. BM and GO give collision strengths for transitions between the lowest 20 levels, at the energies E_i = 85.0, 127.5, 170.0, 250.0, 350 Ry. We used the Burgess & Tully (1992) method (with a linear extrapolation to estimate the value of $\Omega(i,j)$ at E_j = 0) to calculate the thermally-averaged $\Upsilon ({i,j})$ for these two datasets.

The $\Upsilon ({i,j})$ of SGC were obtained from the CHIANTI atomic database version 4 (Young et al. 2003). For the $n=2 \to n\hbox{$^\prime$ }=4$ transitions, we have added to the comparison the distorted-wave unpublished results kindly provided by A. Bhatia, included in the CHIANTI database (hereafter B).

Table 8 presents a comparison of the $\Upsilon ({i,j})$ calculated at $T = {\rm 1.2 \times 10^7}$ $^\circ$K with the present study (CDMB) with those of BM, B and SGC. From Table 8 we see that for optically allowed transitions between states with the same spin multiplicity the agreement is almost perfect in the case of (1, 52) where CDMB/B = 1.01 but otherwise varies from between CDMB/SGC = 0.93 for (1, 15) up to CDMB/SGC = 0.70 for (1, 25). For optically allowed transitions between singlet and triplet states the agreement varies from between CDMB/SGC = 1.11 for (1, 13) up to CDMB/SGC = 1.37 for (1, 42) and CDMB/B = 1.23 for (1, 50).

Table 9: Fractional level population N_j for the n=2,3 levels, calculated at 10⁹, 10¹⁴ (cm^-3) electron densities and the temperature T= 13 MK. (R): computed with all the resonances and all the levels up to n=4; (NR): computed with all the levels up to n=4, but neglecting the contribution from the resonances; (BM): computed with the DW collision strengths of Bhatia & Mason (1986), which included only the n=2,3 levels.

For the transitions $n=2 \to n\hbox{$^\prime$ }=3$ (1, 20), (1, 32), (1, 35), (1, 36), (1, 37) the differences between the present and other calculations are not larger than $35 \%$; for the transition (1, 12) we notice that CDMB/SGC = 0.19. For most of the remaining $n=2 \to n\hbox{$^\prime$ }=3$ transitions $\Upsilon$(CDMB) exceeds $\Upsilon$(SGC) and $\Upsilon$(BM) by up to a factor 3. The reason for this is undoubtedly the neglect by SGC and BM of resonances, which in our calculation occur in great profusion and have a profound effect on the collision strengths of optically forbidden transitions.

For the optically forbidden transitions up to n=4 the agreement between CDMB and B is strikingly good, which seems to indicate that the effect of resonances is negligible for these transitions.

3.2 Level populations

Transition probabilities were calculated with AUTOSTRUCTURE and the theoretical energies of Table 2, and used together with the $\Upsilon$ values to calculate the fractional level population N_j. Magnetic quadrupole transition probabilities were calculated with SUPERSTRUCTURE (see Eissner et al. 1974; Nussbaumer & Storey 1978). The level population equations were solved including the excitation and radiative decay between all levels. We obtain $N_j (N_{\rm e}, T_{\rm e})$, the population of level j relative to the total number density of the ion, as a function of the electron temperature and density.

The values corresponding to the n=2,3 levels calculated at the temperature of maximum ion fraction (T= 13 MK) and at two densities are shown in Table 9. At electron densities of 10¹⁴ cm^-3 most of the ion population is still in the $\rm ^1S_0$ ground state, with only a small fraction in the first $\rm ^3P$ excited states. This is a very high electron density for astrophysical plasmas. Therefore, for astrophysical plasmas, almost all of the excitations to the higher states will come from the ground state, even if collision strengths from excited states are much larger than the values from the ground.

In order to estimate the effects that resonances have on the level populations (hence on line intensities), we have also calculated the effective collision strengths using the spline fits to the 101 $\Omega(i-j)$ data points, i.e. by neglecting the contribution from the resonances. These values (NR) are also shown in Table 9. It is quite clear that the resonances have a dramatic effect on the populations of the n=2 levels, while the effect is much reduced for the n=3 levels.

For comparison, we have also calculated the level populations using the same set of transition probabilities and the effective collision strengths which we obtained from the DW data published in Bhatia & Mason (1986). Good agreement is found between these DW results (BM, Table 9) and the present ones that neglect the resonances (NR). Note that the original level populations published by Bhatia & Mason (1981) differ from the present result. This is due to two causes. First, the collision strengths were revised in Bhatia & Mason (1986). Second, Bhatia & Mason (1981) used a different set of transition probabilities.

4 Summary and conclusions

The background values of the collision strengths shown in Fig. 1 confirm the reliability of previous DW calculations (Bhatia & Mason 1981; Bhatia & Mason 1986). However, the resonance contributions have an important effect on the effective collision strengths and in turn on the level populations. For the $n=2 \to 2$ transitions, the contribution of the resonances is large. The resonance contributions of optically forbidden transitions are significant for the $n=2 \to 3$ complex, particularly at low temperatures, but not so important for the $n=2 \to 4$ transitions.

It is very important in these calculations to take account of the infinity energy limit to obtain effective collision strengths. This is now facilitated within the AUTOSTRUCTURE code for use with the ICFT version of the R-matrix programs.

The accurate calculations for Fe⁺²² presented in this paper provide an opportunity for reliably analysing the X-ray spectra from astrophysical plasmas.

Acknowledgements

This work was supported by PPARC (HEM, GDZ, NRB) and by the NSERC (M.C.C.) (Natural Sciences and Engineering Research Council of Canada). One of us (M.C.C.) wish to acknowledge the welcoming environment during her sabbatical visit to DAMTP, The Centre for Mathematical Sciences, Cambridge, funded via a PPARC fellowship. M.C.C. is also sincerely grateful to the Master and Fellows of St Edmund's College for the award of a Visiting Fellowship, and their wonderful hospitality.

References

• Arnaud, M., & Raymond, J. 1992, ApJ, 398, 394 [NASA ADS] [CrossRef] (In the text)
• Badnell, N. R. 1997, J. Phys. B: Atom. Mol. Phys., 30, 1 [NASA ADS] (In the text)
• Badnell, N. R., & Griffin, D. C. 2001, J. Phys. B: Atom. Mol. Phys., 34, 681 [NASA ADS] (In the text)
• Badnell, N. R., Griffin, D. C., & Mitnik, D. M. 2001, J. Phys. B: Atom. Mol. Phys., 34, 5071 [NASA ADS] (In the text)
• Berrington, K. A., Eissner, W. B., & Norrington, P. H. 1995, Comp. Phys. Commun., 92, 290 [NASA ADS] (In the text)
• Bhatia, A. K., Feldman, U., & Seely, J. F. 1986, Atom. Data and Nucl. Data Tables, 35, 449 [NASA ADS] (In the text)
• Bhatia, A. K., & Mason, H. E. 1981, A&A, 103, 324 [NASA ADS] (In the text)
• Bhatia, A. K., & Mason, H. E. 1986, A&A, 155, 413 [NASA ADS] (In the text)
• Burgess, A., Chidichimo, M. C., & Tully, J. A. 1997, J. Phys. B: Atom. Mol. Phys., 30, 33 [NASA ADS] (In the text)
• Burgess, A., & Tully, J. A. 1992, A&A, 254, 436 [NASA ADS] (In the text)
• Chidichimo, M. C., Badnell, N. R., & Tully, J. A. 2003, A&A, 401, 1177 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Chidichimo, M. C., Zeman, V., Tully, J. A., & Berrington, K. A. 1999, A&AS, 137, 175 [NASA ADS] (In the text)
• Clementi, E., & Roetti, C. 1974, Atom. Data and Nucl. Data Tables, 14, 177 [NASA ADS] (In the text)
• Corliss, C., & Sugar, J. 1982, J. Phys. Chemi. Ref. Data, 11, 135 [NASA ADS] (In the text)
• Del Zanna, G., Chidichimo, M. C., & Mason, H. E. 2004, A&A, submitted (In the text)
• Doschek, G. A., Meekins, J. F., & Cowan, R. D. 1973, Sol. Phys., 29, 125 [NASA ADS] [CrossRef] (In the text)
• Eissner, W., Jones, M., & Nussbaumer, H. 1974, Comp. Phys. Commun., 8, 270 [NASA ADS] (In the text)
• Fawcett, B. C. 1984, Atom. Data and Nucl. Data Tables, 30, 1 [NASA ADS] (In the text)
• Fawcett, B. C. 1985, Atom. Data and Nucl. Data Tables, 33, 479 (In the text)
• Fawcett, B. C., Jordan, C., Lemen, J. R., & Phillips, K. J. H. 1987, MNRAS, 225, 1013 [NASA ADS] (In the text)
• Fawcett, B. C., Ridgeley, A., & Hughes, T. P. 1979, MNRAS, 188, 365 [NASA ADS] (In the text)
• Guo-Xin, C., & Ong, P. P. 1998a, Phys. Rev. A, 58, 1070 [NASA ADS] [CrossRef] (In the text)
• Guo-Xin, C., & Ong, P. P. 1998b, Phys. Rev. A, 58, 1183 [NASA ADS] [CrossRef] (In the text)
• Hibbert, A. 1975, Comp. Phys. Commun., 9, 141 [NASA ADS] (In the text)
• Hibbert, A., Glass, R., & Froese Fischer, C. 1991, Comp. Phys. Commun., 64, 455 [NASA ADS] (In the text)
• Hummer, D. G., Berrington, K. A., Eissner, W., et al. 1993, A&A, 279, 298 [NASA ADS] (In the text)
• McKenzie, D. L., Landecker, P. B., Feldman, U., & Doschek, G. A. 1985, ApJ, 289, 849 [NASA ADS] [CrossRef] (In the text)
• Murakami, I., & Kato, T. 1996, Phys. Scr, 54, 463 [NASA ADS] (In the text)
• Neupert, W. M., Gates, W., Swartz, M., & Young, R. 1967, ApJ, 149, L79 [NASA ADS] [CrossRef] (In the text)
• Neupert, W. M., Swartz, M., & Kastner, S. O. 1973, Sol. Phys., 31, 171 [NASA ADS] (In the text)
• Nussbaumer, H., & Storey, P. J. 1978, A&A, 64, 139 [NASA ADS] (In the text)
• Parpia, F. A., Froese Fischer, C., & Grant, I. P. 1996, Comp. Phys. Commun., 94, 249 [NASA ADS] (In the text)
• Sampson, D. H., Goett, S. J., & Clark, R. E. H. 1984, Atom. Data and Nucl. Data Tables, 30, 125 [NASA ADS] (In the text)
• Young, P. R., Del Zanna, G., Landi, E., et al. 2003, ApJS, 144, 135 [NASA ADS] [CrossRef] (In the text)