E. Cappellaro1 - M. Riello2,3,4 - G. Altavilla5 - M. T. Botticella1,6 - S. Benetti3 - A. Clocchiatti7 - J. I. Danziger8 - P. Mazzali8 - A. Pastorello9 - F. Patat2 - M. Salvo10 - M. Turatto3 - S. Valenti1,11
1 - INAF - Osservatorio Astronomico di Capodimonte,
Salita Moiariello 16, 80131 Napoli, Italy
2 -
European Southern Observatory, K. Schwarzschild Str. 2,
85748 Garching, Germany
3 -
INAF - Osservatorio Astronomico di Padova, Vicolo
dell'Osservatorio 5, 35122 Padova, Italy
4 -
Dipartimento di Astronomia - Universitá di Padova, Vicolo
dell'Osservatorio 2, 35122 Padova, Italy
5 -
Departament d'Astronomia i Meteorologia, Universitat de Barcelona, Martí i
Franqués 1, 08028 Barcelona, Spain
6 -
Osservatorio Astronomico di Collurania, via M. Maggini, 64100 Teramo, Italy
Dipartimento di Scienze della Comunicazione, Universitá di Teramo,
viale Crucioli 122, 64100 Teramo, Italy
7 -
Departamento de Astronomía y Astrofísica, Pontificia Universidad
Católica, Chile
8 -
INAF - Osservatorio Astronomico di Trieste,
via Tiepolo 11, 34131 Trieste, Italy
9 -
INAF - Osservatorio Astronomico di Arcetri, Largo E. Fermi 5, 50125
Firenze, Italy
10 -
Australian National University, Mount Stromlo Observatory,
Cotter Road, Weston ACT 2611, Australia
11 -
Dipartimento di Fisica - Universitá di Ferrara, via del Paradiso 12,
44100 Ferrara, Italy
Received 7 May 2004 / Accepted 8 September 2004
Abstract
We report the first result of a supernova search program
designed to measure the evolution of the supernova rate with
redshift. To make the comparison with local rates more significant we
copied, as much as possible, the same computation recipes as
for the measurements of local rates. Moreover, we exploited the
multicolor images and the photometric redshift technique to
characterize the galaxy sample and accurately estimate the detection
efficiency.
Combining our data with the recently published measurements of the SN Ia rate at different redshifts, we derived the first, direct
measurement of the core collapse supernova rate at z = 0.26 as
![]() SNu [h=H0/75]. This is a
factor of three (
SNu [h=H0/75]. This is a
factor of three (![]() 50%) larger than the local estimate. The increase for a look
back time of 2.8 Gyr is more rapid than predicted by most of
the published models of SN rate evolution. Core-collapse SN rates
measure the death rate of massive stars and, because of the short time
scale of evolution, can be translated into a measurement of the ongoing
SFR. Assuming a Salpeter IMF and the standard scenario for
core-collapse progenitors we derived an estimate of the star
formation rate at redshift
50%) larger than the local estimate. The increase for a look
back time of 2.8 Gyr is more rapid than predicted by most of
the published models of SN rate evolution. Core-collapse SN rates
measure the death rate of massive stars and, because of the short time
scale of evolution, can be translated into a measurement of the ongoing
SFR. Assuming a Salpeter IMF and the standard scenario for
core-collapse progenitors we derived an estimate of the star
formation rate at redshift
![]() which compares very
well with a recent estimate based on the measurement of the H
which compares very
well with a recent estimate based on the measurement of the H![]() luminosity density at the same redshift.
luminosity density at the same redshift.
Key words: supernovae: general - star: formation - galaxy: evolution - galaxy: stellar content
Supernova rates represent a link between the evolution of individual stars and that of stellar systems. In particular, the rate of type II + Ib/c SNe measures the death rate for core-collapse (CC) of young, massive stars and, because of the short time-scale of the progenitor evolution (Heger et al. 2003), directly reflects the on-going star formation rate (SFR) in a given environment. On the contrary, the rate of type Ia SNe, which result from long-lived, low mass binary systems (Branch et al. 1995), reflects the long-term star formation history. Owing to the very high intrinsic luminosity, SNe can be seen at very large distances and hence measurements of SN rate evolution with redshift can be used to trace the history of the SFR with cosmic age.
Studies of the evolution of SN rates with resdhift are now strongly unbalanced towards theory. In recent years, many authors have published predictions of the SN rate as a function of redshift based on the SN progenitor scenarios and the modeling of the cosmic star formation history (Madau et al. 1998; Sadat et al. 1998; Calura & Matteucci 2003; Sullivan et al. 2000; Dahlén & Fransson 1999; Yungelson & Livio 2000; Kobayashi et al. 2000). Despite the strong interest, observational estimates of the SN rate at high redshift are still very scanty. The few published measurements are based on SN searches aimed at using type Ia SNe as cosmological probes (Tonry et al. 2003; Pain et al. 2002,1996) and, as a consequence, they are strongly biased towards type Ia. To date, there is no direct measurement of the evolution of core-collapse SN rates.
With the goal to fill this gap, we initiated a long term project
to measure the rate evolution with redshift for all SN types. In this paper we report the first results of this effort
namely an estimate of the core-collapse SN rate at redshift ![]() .
.
To reduce the systematics in the comparison with the local rate, our strategy followed as closely as possible the same approach used in that context (Cappellaro et al. 1999,1997). The process consists of four steps: i) SN candidate detection and, when possible, spectroscopic classification (Sect. 2); ii) characterization of the galaxy sample through galaxy photometric redshifts; estimation of distances and calibration of the absolute luminosities for each galaxy (Sect. 3); iii) evaluation of the SN detection efficiency and thus of the effective surveillance time for each galaxy of the sample (Sect. 4), iv) estimation of the SN rate per unit luminosity. We also discuss the main sources of uncertainty (Sect. 6) and the implication of our results (Sect. 7).
The basis of a SN search is the detection of variable sources by the comparison of images of selected sky fields obtained at different epochs. In general, the temporal sampling of the observations is tuned to the specific goal one wants to achieve. For the use of type Ia as cosmological distance indicators it is crucial to catch SNe as early as possible and hence, accounting for the typical rise time, the observations have to be spaced by 2-3 weeks. Instead, to maximize the event statistics, the time elapsed between exposures should be equal (or longer) than the time a typical event remains brighter than the search detection limit. The latter, of course, depends on the target distance (or redshift) and the SN type. Independently of the temporal sampling, to ensure that all SNe are detected, the time elapsed between the first and the last observation of a given field have to be longer than the time for a significant luminosity evolution for all SN types. This can be as long as 3-4 months for SN IIP and even longer for type IIn.
For our search we selected 21 fields, evenly distributed in right ascension, which have been monitored for about 2 years with an average sampling of one observation every three months. However, the results reported in this paper are based on observations of 5 fields only, i.e. those with the best temporal and filter coverage. The full sample will be presented in a future paper (Riello et al. in preparation). The observing log is shown in Table 1. For each field we give the center coordinates and, for the epochs when observations are available, we list the seeing.
Table 1: Observing log of the SN search fields. For each field, when observations in a given band are available, we report the measure of the seeing in arcsec ( FWHM on the stellar objects on the combined image).
A typical observing run was split into two parts: the search and the follow-up observation of candidates.
For the search, two consecutive nights were devoted at the ESO/MPI
2.2 m telescope at ESO, La Silla (Chile). The telescope was equipped
with the Wide Field Imager (WFI) and a mosaic of
![]() CCD detectors of
CCD detectors of
![]() pixels which image a
sky area of
pixels which image a
sky area of ![]() 0.25 deg2 with an excellent spatial resolution
of 0.238 arcsec/pix.
0.25 deg2 with an excellent spatial resolution
of 0.238 arcsec/pix.
When possible, the first observing night was dedicated to obtaining deep V band exposures for candidate detection while in the second night the same fields were observed through a different filter, B or R, to collect color information both for the candidates and the galaxies. Unfortunately, due to a number of technical, meteorological and scheduling constraints, in many cases we could not maintain this observing strategy, as can be seen from Table 1. This implies that only in a few cases could we derive the candidate color. For homogeneity, in the following statistical computation we considered only the candidates detected in the V band exposures.
In order to remove detector cosmetic defects, cosmic rays, satellite tracks and fast moving objects, for each field we obtained three 900 s exposures dithered by 5-10 arcsec.
Follow-up observations were scheduled about one week after the search
at the VLT+FORS1/2 at ESO Paranal for the
spectroscopic classification of some of the candidates. The VLT was
needed as most of our SN candidates are in the magnitude range
![]() mag. For a proper subtraction of the night sky
emission we selected grisms of moderate resolution, namely grism 300Vand/or 300I (resolution
mag. For a proper subtraction of the night sky
emission we selected grisms of moderate resolution, namely grism 300Vand/or 300I (resolution ![]() Å FWHM), which allowed us to cover a
quite wide wavelength range (
Å FWHM), which allowed us to cover a
quite wide wavelength range (
![]() Å). Depending on the
candidate magnitude, exposure times ranged from 900 s to 3 h.
Details of the reduction of the spectroscopic observations and of the
spectral analysis will be given elsewhere. Here we make use only of
the spectral classification and redshift.
Å). Depending on the
candidate magnitude, exposure times ranged from 900 s to 3 h.
Details of the reduction of the spectroscopic observations and of the
spectral analysis will be given elsewhere. Here we make use only of
the spectral classification and redshift.
The analysis of the search images began with the removal of the
instrument signature and calibration for which we used
IRAF![]() and MSCRED, a package specifically
designed to handle mosaic images (Valdes 1998). Indeed, after bias
subtraction and flat fielding, the individual dithered exposures were
astrometrically calibrated and stacked in a single image. For
photometric nights, observations of standard fields were used for
absolute calibration (Landolt 1992). Otherwise, the photometric zero
point was established by comparison with a calibrated image of the
same field.
and MSCRED, a package specifically
designed to handle mosaic images (Valdes 1998). Indeed, after bias
subtraction and flat fielding, the individual dithered exposures were
astrometrically calibrated and stacked in a single image. For
photometric nights, observations of standard fields were used for
absolute calibration (Landolt 1992). Otherwise, the photometric zero
point was established by comparison with a calibrated image of the
same field.
For each field we computed the difference between the image to be searched (target image) and a suitable archive frame (template image). Indeed, after accurate astrometric and photometric registrations, the most crucial step in this process is the matching of the point spread function (PSF) of the two images. This was done using the ISIS2.1 package (Alard 2000) that, from the comparison of the same sources in the two images, computes a space-varying convolution kernel to degrade the image with the best seeing to match the other one. Taking into account that the best subtraction is obtained when the two images have similar PSFs, and that we want to preserve as much as possible the resolution of the target image, we had to maintain an archive with template images with different seeing. Populating the archive required a significant investment of telescope time and this was the reason why the search became really efficient only some time after the first observations.
Table 2: SN candidates of the fields of Table 1.
Variable sources leave residuals in the difference image which have been detected and logged into a catalogue using the SExtractor program (Bertin & Arnouts 1996) which has also the capability to separate stars from galaxies. Due to residuals of poorly removed bright stars or cosmic rays, the variable source catalogue contains many false detections, most of which are quickly eliminated by means of a custom-made ranking program. This makes use of information from the difference image as well as from the target and template images and it has been tuned through extensive artificial star experiments. The surviving candidates, typically a few tens per field, are all checked visually by a human expert. Among these, a few obviously are still false detections which could not be properly flagged by our software but are quickly eliminated by visual inspection. Among these are residuals of moving objects which are not completely masked by our dithering strategy. After that, we are left with true variable sources from which we remove variable stars, i.e. objects with stellar profiles present both in the target and template image, but with different magnitudes. At the end of this process, one is left with SN candidates, typically from none to a handful per field.
Ideally, one would need spectroscopic confirmation for all the
candidates. Unfortunately, because of the limited VLT time available,
we could obtain spectroscopic observations for ![]()
![]() of the
detected SN candidates only. This is the main weakness of the work
presented here. On the other hand, we could verify the reliability of
our SN candidate selection criteria: out of the 29 candidates for
which we have obtained VLT spectra during the entire search project,
22 turned out to be SNe (45% type Ia and the other type II and Ib/c)
and 7 variable AGNs. We stress that our approach to candidate
selection was designed to avoid as much as possible any selection bias
and in particular, we do not exclude a priori nuclear
candidates. Given that, the intrusion of AGNs is unavoidable.
of the
detected SN candidates only. This is the main weakness of the work
presented here. On the other hand, we could verify the reliability of
our SN candidate selection criteria: out of the 29 candidates for
which we have obtained VLT spectra during the entire search project,
22 turned out to be SNe (45% type Ia and the other type II and Ib/c)
and 7 variable AGNs. We stress that our approach to candidate
selection was designed to avoid as much as possible any selection bias
and in particular, we do not exclude a priori nuclear
candidates. Given that, the intrusion of AGNs is unavoidable.
Even without spectroscopy, contamination by variable AGNs can be
reduced by looking at the long term variability history of the
candidates. With this aim we kept a database, powered by MySQL![]() , which is used to search
for multiple detections of the same source (Riello 2003). If the
source shows long-term, erratic variability, it is excluded from the
list of SN candidates. For the candidates that passed this selection
and that were centered on the host galaxy nucleus (
, which is used to search
for multiple detections of the same source (Riello 2003). If the
source shows long-term, erratic variability, it is excluded from the
list of SN candidates. For the candidates that passed this selection
and that were centered on the host galaxy nucleus (![]()
![]() )
we
found that
)
we
found that ![]() were actually SNe while the remaining ones were
still AGNs. To take this into account, in all the calculations nuclear
candidates were given a statistical weight of 0.4. Note that with
progression of the monitoring, AGN contamination will continue to be
reduced.
were actually SNe while the remaining ones were
still AGNs. To take this into account, in all the calculations nuclear
candidates were given a statistical weight of 0.4. Note that with
progression of the monitoring, AGN contamination will continue to be
reduced.
In the 5 fields discussed in this paper, we have detected 40 candidates. These are listed in Table 2 where we report the candidate designation (Col. 1), coordinates (Cols. 2-3), and apparent V magnitude at discovery (Col. 4), the apparent V magnitude of the host galaxy (Col. 5), the offset (in arcsec) from the host nucleus (Col. 6), the host photometric redshift (Col. 7), the number of individual exposures in which the object has been seen (Col. 8) and the epoch of first detection (Col. 9). In the last column we report the classification of the candidate. Candidates located in the host galaxy nuclear regions are labelled SNAGN and are given a smaller weight as described above.
For 9 of the candidates we obtained spectroscopic observations which were used to derive spectral classification and redshift (Table 3). Eight of these objects were confirmed as SNe, classified as type Ia (3), type II (4) and type Ic (1). One object was found to be a Seyfert 1 galaxy.
Table 3: SN candidates with spectroscopic classification.
The estimate of SN rates in the local Universe relies on the characterization of the galaxy sample that has been searched (Cappellaro et al. 1997). For each galaxy one needs to know the distance, which uses the computation of the surveillance time, and the integrated luminosity, which is used as a normalization factor. Indeed, it has been demonstrated that the SN rate scales with the size of the parent stellar population as measured from the integrated blue luminosity (Cappellaro et al. 1993). For nearby galaxies the relevant information can be readily retrieved from published catalogues, while this is not the case when one goes to larger distances.
In an attempt to follow the same approach for our intermediate redshift SN project, we exploited the B, V, R images obtained during the search to measure magnitudes and colors of the galaxies detected in our fields and we used them to derive distances and absolute luminosities through the SED fitting photometric redshift technique (Bolzonella et al. 2000).
With this aim we selected from the image archive, for each field and band,
the exposures obtained under the best conditions, in particular those
with seeing <
![]() ,
which were stacked together using the SWARP package by E. Bertin (cf. http://terapix.iap.fr/). This
produces a sensible gain in the S/N ratio: while the limiting
magnitude of a typical search image is
,
which were stacked together using the SWARP package by E. Bertin (cf. http://terapix.iap.fr/). This
produces a sensible gain in the S/N ratio: while the limiting
magnitude of a typical search image is ![]() ,
the same for the
stacked image is
,
the same for the
stacked image is ![]() (
(![]() point source).
point source).
From the V images, which compared to the other bands benefit from
longer cumulative exposure times, we built the galaxy catalogue
including all sources with SExtractor stellarity index ![]() 0.9 (Arnouts et al. 2001). A further selection is performed excluding galaxies
fainter than R=21.8. While this limit was originally chosen to
improve our confidence in the photometric redshifts (see next paragraphs), it has
also the advantage that up to this magnitude the S/N is good enough to
guarantee a clean star-galaxy separation and a good photometric
accuracy. For these selected galaxies, B and R magnitudes were
eventually measured adopting the same aperture as defined in the V image.
0.9 (Arnouts et al. 2001). A further selection is performed excluding galaxies
fainter than R=21.8. While this limit was originally chosen to
improve our confidence in the photometric redshifts (see next paragraphs), it has
also the advantage that up to this magnitude the S/N is good enough to
guarantee a clean star-galaxy separation and a good photometric
accuracy. For these selected galaxies, B and R magnitudes were
eventually measured adopting the same aperture as defined in the V image.
Photometric redshifts were estimated using the hyper-z code
(Bolzonella et al. 2000). This program searches for the best match between the
measured colors of galaxies and the values in a grid created from a
library of spectral energy distribution (SED) templates for different
redshifts. It has been shown that with a proper sampling of the SED,
even with broad band filters, galaxy redshifts can be measured with an
rms error as small as
![]() (Bolzonella et al. 2000). In our case,
however, with observations in only three bands we cannot match this
level of accuracy. In particular, we note that one of the most
significant features in the galaxy SED, the 4000 Å break, falls
redward of the R band for redshifts larger than z>0.8. This means
that the redshifts derived for more distant galaxies are very
uncertain.
(Bolzonella et al. 2000). In our case,
however, with observations in only three bands we cannot match this
level of accuracy. In particular, we note that one of the most
significant features in the galaxy SED, the 4000 Å break, falls
redward of the R band for redshifts larger than z>0.8. This means
that the redshifts derived for more distant galaxies are very
uncertain.
On the other hand we notice that, because of the observing strategy
and limiting magnitude, the SNe discovered in our search are all at
z<0.8 with a peak of the distribution at ![]() .
To remove as
much as possible the contamination of distant galaxies erroneously
estimated at low redshift, we removed from the sample galaxies fainter
than R=21.8. This roughly corresponds to the magnitude M* at a
redshift z=0.8 (Wolf et al. 2003), where M* is a parameter of the
Schechter function (Schechter 1976) which is used to fit the galaxy
luminosity function. With this choice, galaxies with redshift
.
To remove as
much as possible the contamination of distant galaxies erroneously
estimated at low redshift, we removed from the sample galaxies fainter
than R=21.8. This roughly corresponds to the magnitude M* at a
redshift z=0.8 (Wolf et al. 2003), where M* is a parameter of the
Schechter function (Schechter 1976) which is used to fit the galaxy
luminosity function. With this choice, galaxies with redshift ![]() 0.8 contribute about
0.8 contribute about ![]() of the total sample luminosity.
of the total sample luminosity.
At the same time, low luminosity galaxies at low redshift are removed
from the sample. However at ![]() ,
the average redshift of our
search, they contribute to only 1/4 of the total luminosity and they
are expected to give a small contribution to the SN productivity. Indeed we found that out of the 40 SN candidates, only 2 (AXAF-H and AFAX-A, which were not included in the computations) were discovered in
galaxies fainter than R=21.8.
,
the average redshift of our
search, they contribute to only 1/4 of the total luminosity and they
are expected to give a small contribution to the SN productivity. Indeed we found that out of the 40 SN candidates, only 2 (AXAF-H and AFAX-A, which were not included in the computations) were discovered in
galaxies fainter than R=21.8.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{1256fig1.eps}
\end{figure}](/articles/aa/full/2005/04/aa1256/Timg26.gif) |
Figure 1:
Distribution of
|
| Open with DEXTER | |
The final galaxy catalog, which contains about 11 300 galaxies,
was cross-checked with NED in order to assess the accuracy of the
photometric redshifts. We found that spectroscopic redshifts were
available for 324 galaxies (including 118 galaxies of the field J1888
for which spectroscopic redshifts were kindly provided by P.-A. Duc, in
advance of publication). With these data we built the histogram of
![]() ,
the differences between
spectroscopic and photometric redshifts, which is shown in Fig. 1 (dashed line). The average difference is
,
the differences between
spectroscopic and photometric redshifts, which is shown in Fig. 1 (dashed line). The average difference is
![]() with a rms error
with a rms error
![]() ,
which is
both consistent with our limited SED sampling and sufficient for our
statistical analysis. An independent check on the accuracy of our
photometric redshift was made possible by the fact that one of our
fields (AXAF) partially overlaps with the Chandra Deep Field South
covered by the COMBO-17 survey (Wolf et al. 2003). The distribution of
,
which is
both consistent with our limited SED sampling and sufficient for our
statistical analysis. An independent check on the accuracy of our
photometric redshift was made possible by the fact that one of our
fields (AXAF) partially overlaps with the Chandra Deep Field South
covered by the COMBO-17 survey (Wolf et al. 2003). The distribution of ![]() for 1375 galaxies which we have in common is also shown in
Fig. 1 (thick line). The average difference
for 1375 galaxies which we have in common is also shown in
Fig. 1 (thick line). The average difference
![]() with a rms error
with a rms error
![]() is very similar to
those measured in the comparison with spectroscopic redshifts.
is very similar to
those measured in the comparison with spectroscopic redshifts.
The redshift distribution of our galaxy sample is shown in Fig. 2. As expected, given the adopted limiting magnitude, the
number counts peak at about ![]() .
For comparison, in
Fig. 2 we have also plotted the redshift distribution of the
SN candidate host galaxies (dots) with their statistical errors.
.
For comparison, in
Fig. 2 we have also plotted the redshift distribution of the
SN candidate host galaxies (dots) with their statistical errors.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{1256fig2.eps}
\end{figure}](/articles/aa/full/2005/04/aa1256/Timg32.gif) |
Figure 2: Redshift distribution of our galaxy sample (line, left-side scale) and SNe host galaxies (dots, right-side scale). For the latter, candidates coincident with the host galaxy nucleus have been counted with a 0.4 weight. |
| Open with DEXTER | |
The computation of rates requires the definition of the time interval during which the events could be detected. We need to estimate the time during which a SN hosted in a given galaxy remains brighter than the search detection threshold which is usually referred to as control time. This depends on i) the search threshold and detection efficiency; ii) the SN absolute magnitude and luminosity evolution; iii) the distance.
There are several concurrent factors determining the detection efficiency. For a given instrument and fixed exposure time, the key factors are the observing conditions, in particular sky transparency and seeing. There is also some dependence on the characteristics of the particular sky field, due to the disturbing presence of bright stars and nearby galaxies. The position of the candidate within the parent galaxy plays also a role.
While the sky transparency of a specific observation is measured by
the photometric constants, the impact of other factors was evaluated
performing a number of artificial star experiments. In these
simulations we placed a number of synthetic stars with a given
magnitude m, and the PSF deduced from field stars, distributing them
in different galaxies of the field. The position of the artificial
stars within the host galaxy was chosen randomly, assuming a Gaussian
distribution centered on the galaxy nucleus and a FWHM equal to that
of the host galaxy. Then, the synthetic frames were processed through
our search pipeline and the detection efficiency
![]() was
computed as the ratio between recovered and injected stars.
was
computed as the ratio between recovered and injected stars.
In Fig. 3 we plot an example of detection efficiency function
for one of the observation of the field AXAF. As a result of these
numerical experiments, which will be described in detail in a
forthcoming paper (Riello et al. 2004), we found that the most
critical parameter is the seeing. In particular we found that, taking
as a reference the magnitude at which the detection efficiency is ![]() ,
this is
,
this is ![]() 1.2 mag fainter when the seeing is 0
1.2 mag fainter when the seeing is 0
![]() 65
compared with a seeing of 1
65
compared with a seeing of 1
![]() 3.
3.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1256fig3.eps}
\end{figure}](/articles/aa/full/2005/04/aa1256/Timg37.gif) |
Figure 3:
Example of SN detection efficiency curve, plotted as a function
of apparent magnitude for one of the epochs of field AXAF(seeing
|
| Open with DEXTER | |
The other factor entering the computation of the control time for a
given epoch is the SN luminosity evolution and its absolute
luminosity. The prescription we used in our calculations is described
in the following. The apparent V light curve for each SN was
computed taking into account the luminosity distance (estimated from
the photometric redshift of the host galaxy), the time dilation and
the K-correction according to the following relation:
Following Cappellaro et al. (1997), we considered four basic SN types, namely
Ia, IIP, IIL and Ib/c. Guided by the general theoretical
interpretation, type IIP, IIL, and Ib/c will be collectively called
later core collapse (CC) SNe. B absolute magnitudes and light
curves were also taken as in Cappellaro et al. (1997). The K
![]() -correction for each SN type at different phases was
calculated using a sample of spectra with good S/N ratio available
in the Asiago-Padova SN archive. Spectra were redshifted by the appropriate
amount and synthetic photometry was computed using the synphot
package in IRAF. The choice of the KBV correction is
motivated by the fact that, for the average redshift of our search,
-correction for each SN type at different phases was
calculated using a sample of spectra with good S/N ratio available
in the Asiago-Padova SN archive. Spectra were redshifted by the appropriate
amount and synthetic photometry was computed using the synphot
package in IRAF. The choice of the KBV correction is
motivated by the fact that, for the average redshift of our search,
![]() ,
this minimizes both the uncertainties and
the time dependence of the K-correction. Note that for the same
reason we use as a reference the B light curves of local SNe.
,
this minimizes both the uncertainties and
the time dependence of the K-correction. Note that for the same
reason we use as a reference the B light curves of local SNe.
We introduce here the effective control time defined, for each
observation of a given galaxy, as the control time weighted by the
galaxy luminosity in units of
![]() :
:
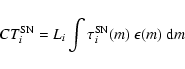 |
(2) |
Finally, for the given galaxy the total control time of the search
campaign,
![]() ,
is obtained by properly combining
the control time of individual observations (cf. Cappellaro et al. 1999).
,
is obtained by properly combining
the control time of individual observations (cf. Cappellaro et al. 1999).
For a given galaxy and SN type, the rates are derived by dividing the number of observed events by the total control time:
The average redshift of the SN search
![]() (i.e.
of the galaxy sample) is given by the average of the galaxy redshifts
weighted by the effective control time:
(i.e.
of the galaxy sample) is given by the average of the galaxy redshifts
weighted by the effective control time:
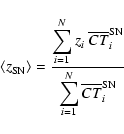 |
(4) |
Considering that we have a sample of galaxies with a wide spread in
redshift, to derive an estimate of the SN rates we have computed the
expected SN counts as a function of redshift, derived by summing the
contribution of individual SN types and using different assumptions
for the rate evolution with redshift. For the latter we assume a power
law dependence
![]() ,
where
,
where
![]() represents the local (z=0) rate for a given SN type
and
represents the local (z=0) rate for a given SN type
and ![]() is the evolution index (
is the evolution index (![]() indicates no
evolution). Using this model, the SN rate evolution parameters
can be derived from the best fit between the expected and observed
redshift distributions.
indicates no
evolution). Using this model, the SN rate evolution parameters
can be derived from the best fit between the expected and observed
redshift distributions.
In practice, we derive the total expected SN detection
![]() as the sum of
the expected number of Ia and CC events:
as the sum of
the expected number of Ia and CC events:
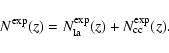 |
(5) |
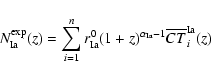 |
(6) |
As a first step, we have tested the null hypothesis that the SN rates
per unit blue luminosity do not change with redshift (
![]() and they are equal to the local values, namely
and they are equal to the local values, namely
![]() [h2 SNu]
[h2 SNu]![]() and
and
![]() [h2 SNu] (Cappellaro et al. 1999). Under this hypothesis, in our galaxy sample one would expect 13.2 events, which is significantly smaller than the 28.2 actually observed. This already points out that the global SN rate must
increase rapidly with redshift.
[h2 SNu] (Cappellaro et al. 1999). Under this hypothesis, in our galaxy sample one would expect 13.2 events, which is significantly smaller than the 28.2 actually observed. This already points out that the global SN rate must
increase rapidly with redshift.
In our case, since we do not have the spectroscopic classification for all the SN candidates, we cannot directly use Eq. (3) to derive individual SN rates. Unfortunately, with the limited statistics available to date and the incomplete spectroscopic classification, we cannot determine rates and evolutions of both SN Ia and CC SNe from our data alone and we need to use other data sets. For this purpose we have exploited the published measurements of SN Ia rate at different redshifts (Tonry et al. 2003; Blanc et al. 2004; Hardin et al. 2000; Pain et al. 2002; Madgwick et al. 2003) to fix the evolution of SN Ia and to derive the CC rate.
One further complication is that some of the high redshift SN Ia
measurements were given only per unit volume
(Tonry et al. 2003; Pain et al. 2002; Madgwick et al. 2003). To convert these numbers into rate per
unit luminosity (SNu scale), we need consistent estimates of the
luminosity density at different redshift. For this purpose we
collected from the literature recent measurements of the B luminosity density for the redshift range relevant for our SN search
(Fig. 4). As can be seen, the measurements show a
relatively high dispersion, particularly large at high redshift. The
best fit with a power law
![]() gives
gives
![]()
![]() and
and
![]() .
This has been used, in particular, to convert the rate per unit
volume of Pain et al. (2002) and Tonry et al. (2003).
.
This has been used, in particular, to convert the rate per unit
volume of Pain et al. (2002) and Tonry et al. (2003).
The published values of the SN Ia rate (in SNu) are plotted in
Fig. 5, which convincingly shows a redshift
evolution. This can be fitted with a power law relation with
![]() h2 SNu and
h2 SNu and
![]() .
.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{1256fig4.eps}
\end{figure}](/articles/aa/full/2005/04/aa1256/Timg78.gif) |
Figure 4:
Galaxy luminosity density ad different redshifts. Data are
from Norberg et al. (2002); Wolf et al. (2003); Madau et al. (1998); Blanton et al. (2003). The line
represents the best fit using a
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{1256fig5.eps}
\end{figure}](/articles/aa/full/2005/04/aa1256/Timg79.gif) |
Figure 5: Measurements of the SN Ia rate at different redshifts. References are as follows: filled triangle - Cappellaro et al. (1999), filled upside-down triangle - Blanc et al. (2004), filled square - Madgwick et al. (2003), empty square - Hardin et al. (2000), filled circle - Tonry et al. (2003), filled diamond - Pain et al. (2002), empty diamond - Gal-Yam et al. (2002). The line is a fit with the power law in (1+z) (see the text for details). Because of the large errorbars the Gal-Yam et al. estimates have not be used for the fit. |
| Open with DEXTER | |
Assuming that the SN Ia rate evolution is known, we can use the observed SN counts to constrain the evolution of core collapse rates. To this end, it is convenient to re-write Eq. (7) as follows:
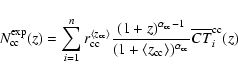 |
(9) |
By means of a maximum-likelihood method we search for the values of
![]() and
and
![]() which give the
best fit between observed and expected distributions as a function of
redshift. Resulting confidence levels are shown in Fig. 6.
We found that
which give the
best fit between observed and expected distributions as a function of
redshift. Resulting confidence levels are shown in Fig. 6.
We found that
![]() h2 SNu and
h2 SNu and
![]() where the quoted errors are the
1-
where the quoted errors are the
1-![]() confidence level. Clearly the parameter
confidence level. Clearly the parameter
![]() describing the CC-rate evolution is poorly confined by our data alone,
but the fair agreement with the measurement in the local Universe
(cf. Fig. 8) is conforting.
describing the CC-rate evolution is poorly confined by our data alone,
but the fair agreement with the measurement in the local Universe
(cf. Fig. 8) is conforting.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{1256fig6.eps}
\end{figure}](/articles/aa/full/2005/04/aa1256/Timg86.gif) |
Figure 6: Confidence level for the maximum-likelihood test. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{1256fig7.eps}
\end{figure}](/articles/aa/full/2005/04/aa1256/Timg87.gif) |
Figure 7: Observed (points with statistical errorbars) and expected (solid line) redshift distribution of SN counts. The short-dashed and long-dashed lines are the expected type Ia and CC SN counts respectively. |
| Open with DEXTER | |
The comparison between the observed and expected distribution for the best fit parameters is shown in Fig. 7. We notice that in our search about 2/3 of the observed SNe are expected to be CC and only 1/3 SN Ia. This is consistent with what we have found when spectroscopic confirmation was available (cf. Table 3).
The conclusion is that the CC SN rate at
![]() appears to be a factor 3 higher than in the local Universe.
appears to be a factor 3 higher than in the local Universe.
The errors quoted before for the rate and evolutionary index parameter are purely statistical. Even though they are large, systematics errors need also be considered. Indeed, although we do our best to exploit the significant observational efforts, this first estimate of the CC rate at z>0 should be regarded as preliminary in many respects. In the following we highlight what we believe are the most severe caveats. Note that we will not discuss here systematics which originate from the uncertainties on the SN properties (absolute magnitudes, light curves, intrinsic dispersion). For them we have made the same assumptions as for the computation of local rates (Cappellaro et al. 1999) and therefore they are expected to cancel out in the comparison. Also we do not address the uncertainties in the cosmological model adopted and we rather focus on other aspects.
As we mentioned above, the most severe concern is the lack of
spectroscopic classification for all candidates. In particular, we had
to account in a statistical manner for the expected contamination by AGNs, assigning a weight of 0.4 to the candidates coinciding with the
host galaxy nucleus. In order to evaluate the impact of this
assumption, we have computed the best fit for two extreme cases: a) all nuclear candidates are AGNs or b) ![]() of the nuclear
candidates are indeed SNe. The two extreme cases encompass the ranges:
of the nuclear
candidates are indeed SNe. The two extreme cases encompass the ranges:
![]() h2 SNu and
h2 SNu and
![]() for the two fit parameters respectively.
Therefore although important, this uncertainty is not likely to affect
our conclusions.
for the two fit parameters respectively.
Therefore although important, this uncertainty is not likely to affect
our conclusions.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{1256fig8.eps}
\end{figure}](/articles/aa/full/2005/04/aa1256/Timg91.gif) |
Figure 8: CC SN rate with redshift. The dot is the estimate of the local CC SN rate from Cappellaro et al. (1999) whereas the square is the new measurement derived in this paper. The solid line shows the deduced evolution with redshift. The dashed line shows the deduced type Ia rate evolution (see the text for details). The thick solid line is the CC SN rate evolution predicted by model M2 of Sadat et al. (1998). |
| Open with DEXTER | |
Of more concern is that in the current work we did not attempt to correct for the bias due to extinction in the host galaxies. This applies to all other estimates of SN rates at high redshift published so far. It is well known that in local SN searches there is a severe bias for SN detection in spiral galaxies which are not observed face-on (Cappellaro et al. 1999). This is attributed to the concentration of dust in the plane of the spiral galaxy disk which causes a higher average extinction for the inclined galaxies. Because of the wavelength dependence of extinction, it is expected that the blue photographic surveys which were used to derive the estimates of the local rates are heavily affected. For the same reason, it is sometimes claimed that CCD searches in nearby galaxies do not need to be corrected. This cannot be entirely true because the bias is seen even in the list of events discovered in the last few years mainly by CCD SN searches (Cappellaro et al. 2004). But even if we accept this claim, we stress that if high redshift galaxies have the same dust content as local ones then, just because of redshift, host galaxy extinction should cause a similar bias for blue band searches in nearby galaxies as for red searches in high redshift galaxies. Unfortunately, current data on high redshift SN searches do not allows to measure the size of this bias.
Any correction is likely to increase, possibly even significantly, the CC estimate reported here. None of the reported uncertainties, even if important, seems to undermine the main conclusion reached here, that a significant evolution of the CC rate must be present even for this short look back time.
When we compare our result with models we find that, in the redshift range we are exploring, the current predictions indicate a much shallower evolution of the CC rate (Madau et al. 1998; Sadat et al. 1998; Calura & Matteucci 2003; Kobayashi et al. 2000) than actually observed.
As an example, in Fig. 8 we show the predictions
of Sadat et al. (1998) in the most favorable case (model M2 which
corresponds to a higher SFR at high redshift). Although at a
2-![]() level the model is consistent with our measurement,taken
at face value the observed rate at z=0.26 is a factor
of 2 higher than the model. This becomes even more significant if we
consider that, due to the lack of extinction correction, our estimate
is expected to be a lower limit to the actual CC rate.
level the model is consistent with our measurement,taken
at face value the observed rate at z=0.26 is a factor
of 2 higher than the model. This becomes even more significant if we
consider that, due to the lack of extinction correction, our estimate
is expected to be a lower limit to the actual CC rate.
On the other hand, the CC rate evolution is directly
related to the adopted history of the SFR for which there are many new
estimates. Indeed, considering the short evolutionary time scale of
the CC SNe progenitors (<
![]() yr) and under the assumption
that the initial mass function (IMF) and the mass range of the CC progenitors do not change significantly in the redshift range of
interest, there is a simple direct relation between the SFR and the CC rate, namely:
yr) and under the assumption
that the initial mass function (IMF) and the mass range of the CC progenitors do not change significantly in the redshift range of
interest, there is a simple direct relation between the SFR and the CC rate, namely:
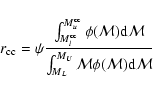 |
(10) |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1256fig9.eps}
\end{figure}](/articles/aa/full/2005/04/aa1256/Timg101.gif) |
Figure 9:
We compare our estimate of the SFR at redshift z=0.26 (big
filled dot) with the recent estimate of Fujita et al. (2003) based on
the H |
| Open with DEXTER | |
Recently, Fujita et al. (2003) have published an estimate of the SFR based on
the H![]() luminosity density at
luminosity density at
![]() .
This is shown in
Fig. 9 where are also reported other estimates of the SFR at
different redshifts (adapted from Fujita et al. 2003, see references
therein). As noted by Fujita et al. (2003) there is a systematic difference
in the SFR deduced from the H
.
This is shown in
Fig. 9 where are also reported other estimates of the SFR at
different redshifts (adapted from Fujita et al. 2003, see references
therein). As noted by Fujita et al. (2003) there is a systematic difference
in the SFR deduced from the H![]() luminosity density (filled
symbols) compared with that derived from the UV luminosity density not
corrected for extinction (empty symbols), with the former being
significantly smaller at all redshift. However, it has been shown that
this disagreement can be removed with a proper extinction correction
(Hippelein et al. 2003; Rosa-González et al. 2002).
luminosity density (filled
symbols) compared with that derived from the UV luminosity density not
corrected for extinction (empty symbols), with the former being
significantly smaller at all redshift. However, it has been shown that
this disagreement can be removed with a proper extinction correction
(Hippelein et al. 2003; Rosa-González et al. 2002).
As seen in Fig. 9, our measurement is in excellent agreement with the
value of Fujita et al. (2003) and in general with the rapid SFR evolution
deduced from the H![]() luminosity density. Our conclusion from the
evolution of the core collapse SN rate is that at at a redshift z=0.26, that is at a look back time of 2.8 Gyr with the adopted
cosmology, the SFR per unit comoving volume was three time higher than
in the local Universe. We stress again that, because our measurement of the CC SN rate
is not corrected for extinction, this is likely to be a lower limit (cf. Sect. 6)
luminosity density. Our conclusion from the
evolution of the core collapse SN rate is that at at a redshift z=0.26, that is at a look back time of 2.8 Gyr with the adopted
cosmology, the SFR per unit comoving volume was three time higher than
in the local Universe. We stress again that, because our measurement of the CC SN rate
is not corrected for extinction, this is likely to be a lower limit (cf. Sect. 6)![]() .
.
Acknowledgements
We would like to thank Michele Massarotti for the advice on the photometric redshift technique. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. A.C. acknowledges support from CONICYT, Chile, through grant FONDECYT 1000524. SV acknowledges support from the program "Promozione della ricerca scientifica Regione Campania'', Legge Regionale No. 5 del 28/03/2002.