D. E. Mkrtichian 1,2 - A. P. Hatzes3
1 - Astrophysical Research Center for the Structure and Evolution of the Cosmos,
Sejong University, Seoul 143-747, Korea
2 - Astronomical Observatory, Odessa National University, Shevchenko Park, Odessa
65014, Ukraine
3 - Thüringer Landessternwarte Tautenburg, Sternwarte 5, 07778 Tautenburg,
Germany
Received 21 October 2003 / Accepted 28 June 2004
Abstract
In this paper we present the first results from
a high-precision radial velocity (RV) study of the rapidly oscillating
Ap (roAp) star HR 1217. Data spanning a complete rotation period
were acquired on 9 nights in late 1997 and early
1998 using the Harlan J. Smith 2.7 m telescope at McDonald Observatory.
The RVs were measured using the wavelength range of each spectral
order (![]() 100 Å) of the "2dcoude'' echelle spectrograph. Most
of the pulsational modes can be seen in all spectral regions but the amplitude varies by factors of
ten or more between the different wavelength intervals.
A detailed analysis of the spectral order centered on 5825 Å, which
had the largest amplitudes, showed the presence of all published
photometric frequencies
100 Å) of the "2dcoude'' echelle spectrograph. Most
of the pulsational modes can be seen in all spectral regions but the amplitude varies by factors of
ten or more between the different wavelength intervals.
A detailed analysis of the spectral order centered on 5825 Å, which
had the largest amplitudes, showed the presence of all published
photometric frequencies ![]() -
-![]() .
The multi-mode oscillations were also found in the RV variations of
the high amplitude Nd III 5294 Å feature. Our RV data reveal two new excited modes at
frequencies
.
The multi-mode oscillations were also found in the RV variations of
the high amplitude Nd III 5294 Å feature. Our RV data reveal two new excited modes at
frequencies
![]() c d-1 (2585.3
c d-1 (2585.3 ![]() Hz) and
f-1 = 220.58 c d-1 (2553.0
Hz) and
f-1 = 220.58 c d-1 (2553.0 ![]() Hz) that follow the odd and even
alternative mode spacing with
Hz) that follow the odd and even
alternative mode spacing with
![]()
![]() Hz.
An analysis of individual nights shows strong amplitude and
phase modulation of all excited modes, including the two newly
discovered ones. The
amplitudes of the
Hz.
An analysis of individual nights shows strong amplitude and
phase modulation of all excited modes, including the two newly
discovered ones. The
amplitudes of the
![]() c d-1 (2652.9
c d-1 (2652.9 ![]() Hz) and
Hz) and
![]() c d-1 (2720.85
c d-1 (2720.85 ![]() Hz) modes are modulated
with the published magnetic field variations and reach their maximum and
minimum at magnetic extrema.
However, the phase variability is in disagreement with that expected from
the standard oblique pulsator model.
The phase jumps for the f2 mode occur exactly at
magnetic maximum and close to the phase of magnetic minimum,
while the f3 and f4 modes have a continuous change.
The peculiar phase variability is attributed to strong
vertical phase changes in the line-forming layers of atmosphere.
An echelle-diagram for all known excited modes in
HR 1217 is constructed. We interpret the
Hz) modes are modulated
with the published magnetic field variations and reach their maximum and
minimum at magnetic extrema.
However, the phase variability is in disagreement with that expected from
the standard oblique pulsator model.
The phase jumps for the f2 mode occur exactly at
magnetic maximum and close to the phase of magnetic minimum,
while the f3 and f4 modes have a continuous change.
The peculiar phase variability is attributed to strong
vertical phase changes in the line-forming layers of atmosphere.
An echelle-diagram for all known excited modes in
HR 1217 is constructed. We interpret the
![]() c d-1 (2805.7
c d-1 (2805.7 ![]() Hz) mode with the "peculiar'' spacing as due
to a mode of degree l = 4 that is the only observed member of
another system of equally-spaced frequencies. We predict
the existence of modes belonging to this system that should
be equally spaced at 68
Hz) mode with the "peculiar'' spacing as due
to a mode of degree l = 4 that is the only observed member of
another system of equally-spaced frequencies. We predict
the existence of modes belonging to this system that should
be equally spaced at 68 ![]() Hz with
Hz with ![]() .
.
Key words: techniques: radial velocities - techniques: spectroscopic - stars: chemically peculiar - stars: oscillations - stars: individual: HR 1217
Magnetic chemically-peculiar (Ap) stars are a class of late B through late A-type stars that
show strong magnetic fields with strengths of up
to several kiloGauss. These stars also exhibit strong surface
chemical peculiarities with many elements having a patchy
distribution across the stellar surface.
The photometric, spectroscopic, and magnetic variability in Ap
stars are due to rotational modulation. In the case of the
magnetic field variations these are due to
the inclination of the magnetic axis with respect to the
rotation axis.
The magnetic fields are also
believed to be responsible for the surface chemical inhomogeneities.
![\begin{figure}
\par\includegraphics[width=10.5cm,clip]{0547fig1.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg33.gif) |
Figure 1: The pulsational radial velocity curves of HR 1217. The solid lines are the nightly synthetic multifrequency fits. |
| Open with DEXTER | |
The rapid oscillations, both mono- and multi-periodic, with periods of 5 to 16 min and typical photometric amplitudes less then a few mmag were discovered in cool Ap stars by Kurtz (1978) and interpreted (Kurtz 1982) as due to high-overtone zonal dipole (l = 1, m = 0) p-modes with their axis of symmetry coinciding with the magnetic axis. The obliquity of the pulsation axis produces rotational modulation in both the phase and amplitude of the pulsations as predicted by the so-called "oblique pulsator model'' or OPM (Kurtz & Shibahashi 1986; Takata & Shibahashi 1995; Dziembowski & Goode 1996). We shall refer to this standard model and its revisions (Bigot & Dziembowski 2002) as the "two-dimensional oblique pulsator models'' (2D-OPM) because these are based on the assumption that the amplitudes and phases of stellar nonradial pulsation brightness and velocity fields depend only on the stellar latitude and longitude.
The relatively rich p-mode spectra of some roAp stars makes these
objects attractive for asteroseismic studies.The spacing of modes in
the multiperiodic roAp pulsators are well represented by the asymptotic
relationship for the frequency spacing of low l-degree high-overtone
(n>15) acoustic modes (Tassoul 1990).
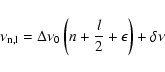 |
(1) |
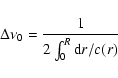 |
(2) |
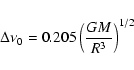 |
(3) |
The sharp-lined roAp star HR 1217 (HD 24712, DO Eri) is a typical member of
the cool group of Ap stars. It shows rotationally modulated
magnetic field variability with
a strength ranging from +0.4 kG to 1.5 kG (Preston 1972)
and has a
rotation period of 12.4572 days (Kurtz & Marang 1987).
Bangulo et al. (1995), using combined linear and circular
polarization data,
found a polar magnetic field of
![]() kG, an inclination
angle to the line-of-sight of
kG, an inclination
angle to the line-of-sight of
![]() ,
and an obliquity angle
(the angle between the rotation and magnetic axes) of
,
and an obliquity angle
(the angle between the rotation and magnetic axes) of
![]() .
The error in the angle determination is
2
.
The error in the angle determination is
2
![]() -3
-3
![]() .
Leroy et al. (1996), based on
linear polarization measurements, estimated
.
Leroy et al. (1996), based on
linear polarization measurements, estimated
![]() and
and
![]() ,
consistent with the
Bangulo et al. (1995) determinations.
,
consistent with the
Bangulo et al. (1995) determinations.
HR 1217 shows strong variations in the spectral lines of Eu with a maximum coinciding with magnetic maximum and Mg lines that vary antiphase with Eu (Preston 1972). The detailed abundance analysis of HR 1217 (Ryabchikova et al. 1997) shows an underabundance of most the iron-peak elements and an overabundance of rare earth elements and cobalt. The rare earth elements show large equivalent width variations over the rotation period and abundance variations of about 0.5 dex. Magnesium is at solar abundance, but is deficient by about 1.0 dex at magnetic minimum. These confirm the inhomogeneous distribution of some elements across the surface of this star.
The rapid and multimode pulsations in HR 1217 were discovered
by Kurtz (1982) and have been well studied (Kurtz & Seeman
1983; Kurtz et al. 1989). The frequency spectrum was
found to have 6 principal frequencies that show rotationally modulated
amplitude variations. The first five are spaced in frequency alternately
by 33.27 ![]() Hz and 34.75
Hz and 34.75 ![]() Hz.
Hz.
Shibahashi (1984) was the first to explain that the observed frequencies
are equally spaced due to alternative odd and even l-modes
with a principal spacing
![]()
![]() Hz.
However, the sixth mode at frequency 2806.2
Hz.
However, the sixth mode at frequency 2806.2 ![]() Hz was found at a
spacing of
Hz was found at a
spacing of
![]()
![]() Hz from the
Hz from the
![]()
![]() Hz
mode. This mode was termed "enigmatic" by Kurtz et al. (1989).
Hz
mode. This mode was termed "enigmatic" by Kurtz et al. (1989).
Mkrtichian & Hatzes (2000) gave a possible explanation of the
peculiar spacing of the 2806.2 ![]() Hz mode with respect to
Hz mode with respect to ![]() .
This is due to a higher degree l > 3 mode that is naturally
shifted in spacing relative to the sequence of l = 0, 2 (even)
and l = 1, 3 (odd) sequence
that form the equal spacing of the observed
.
This is due to a higher degree l > 3 mode that is naturally
shifted in spacing relative to the sequence of l = 0, 2 (even)
and l = 1, 3 (odd) sequence
that form the equal spacing of the observed ![]() -
-![]() modes.
modes.
Another possible explanation of the peculiar spacing of 2806.2 ![]() Hz
was suggested by Cunha (2001) who proposed that the mode
following the fifth mode was actually missing from observations due to
its coupling with Alfvenic waves at the surface of the star. The next
mode that is observed has its frequency diminished by the effect of the
magnetic field.
Hz
was suggested by Cunha (2001) who proposed that the mode
following the fifth mode was actually missing from observations due to
its coupling with Alfvenic waves at the surface of the star. The next
mode that is observed has its frequency diminished by the effect of the
magnetic field.
Recently, using a global multisite campaign on
HR 1217 with the Whole Earth Telescope,
Kurtz et al. (2002) found the "missing" mode
at a frequency
![]() Hz. This was separated from
f5 by 36.13
Hz. This was separated from
f5 by 36.13 ![]() Hz and thus followed the f1-
Hz and thus followed the f1-![]() alternative odd and even degree spacing. The
spacing of the 2806.2
alternative odd and even degree spacing. The
spacing of the 2806.2 ![]() Hz mode
remains unexplained.
Hz mode
remains unexplained.
The first spectroscopic detection of pulsations in HR 1217 were reported by Matthews et al. (1988) who found radial velocity (RV) variations with a peak-to-peak amplitude of 400 m s-1 on one night, but were unable to detect any significant variations on the previous night to a level of 130 m s-1. The first spectroscopic RV confirmation of the multimode pattern of oscillations in HR 1217 were found by Hatzes et al. (1999, 2002). In the preliminary analysis of their data they detected five of the six photometric modes known at that time and these showed strong amplitude variations from night to night. Balona & Zima (2002), based on high-resolution spectroscopy of HR 1217, found radial velocity variations with power in the 2.6-2.8 mHz range. However, the strong 1 c d-1 aliasing in the power spectrum and the low signal-to-noise ratio of the data did not permit the accurate discrimination of multi-mode oscillation frequencies.
Mkrtichian (1992, 1994) introduced for the study of the two-dimensional (l,m) structure of nonradial pulsations in roAp stars the concept of a "periodic spatial filter'' (hereafter 2D-PSF). The distribution of chemical elements on the surface of Ap stars is known to be patchy. Pulsational RV variations originating from an element concentrated in a localized region of the star will experience less cancellation effects allowing higher degree modes to be detected. Thus spectroscopic studies are more sensitive and have the potential of finding higher degree modes than are possible using photometric studies which measure a more "integrated'' quantity.
Table 1: Log of the 1997/1998 year spectroscopic observations. The rotation phases are given according to ephemeris of Kurtz et al. (1989). N is the number of RV points obtained per night.
In this paper we present preliminary results of our RV study of the
pulsations in HR 1217. The RV analysis is primarily performed
on a wavelength interval spanning each spectral order of the echelle
spectrograph employed for this study (![]() 100 Å). These are
termed "broad-band'' RV measurements as they represent an average RV
from many lines. Previous work (Kanaan & Hatzes 1998; Mkrtichian et al. 2003; Hatzes & Mkrtichian 2004) has shown that a more
complete understanding of the pulsational RV variations in roAp stars can
only come after an examination of the
RV variations of individual lines. This type of
study is a time consuming process and will be the subject of a
subsequent paper. In this work we concentrate on the broad-band RV
measurements and present a detailed analysis of only one spectral order
and one spectral feature of Nd III.
We show that even with these broad-band and single-line measurements we
are able to find the presence of additional excited modes.
100 Å). These are
termed "broad-band'' RV measurements as they represent an average RV
from many lines. Previous work (Kanaan & Hatzes 1998; Mkrtichian et al. 2003; Hatzes & Mkrtichian 2004) has shown that a more
complete understanding of the pulsational RV variations in roAp stars can
only come after an examination of the
RV variations of individual lines. This type of
study is a time consuming process and will be the subject of a
subsequent paper. In this work we concentrate on the broad-band RV
measurements and present a detailed analysis of only one spectral order
and one spectral feature of Nd III.
We show that even with these broad-band and single-line measurements we
are able to find the presence of additional excited modes.
Precise stellar radial velocity measurements were made using an iodine absorption cell placed just before the entrance slit of the spectrograph during each observation. A description of the use of this method can be found in Hatzes & Kürster (1994). This analysis did not take into account possible changes in the shape of the instrumental profile which is required if one wants to achieve the very highest RV precision (Valenti et al. 1995; Butler et al. 1996). This was not done because this is computationally intensive given the large number of observations. Furthermore, the expected RV variations are large (50-300 m s-1) and should not be influenced by subtle changes of the instrumental profile.
Molecular
iodine has useful lines in the wavelength range of 5000-6300 Å (14
spectral orders) which dictated the sub-framing of the CCD detector. The RV analysis with the iodine cell requires a high signal-to-noise
template spectrum of the star taken without iodine absorption lines. For
this we took a much longer exposure of HR 1217
without the cell. Figure 1 shows sample radial velocity curves from
a single spectral order at the observed rotation phases.
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{0547fig2.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg54.gif) |
Figure 2: The discrete Fourier transform (central wavelength shown at the top) as a function of rotation phase ( top to bottom, rotation phase values shown at the far right) for the first 7 spectral orders (wavelength interval 5590-6300 Å). Each spectral order spans approximately 100 Å. The dashed lines show the location of the published photometric frequencies from Kurtz et al. (1989). |
| Open with DEXTER | |
A time series analysis using discrete Fourier transforms (DFT) was
performed on the RV measurements.
Throughout the paper we follow the nomenclature of frequencies
![]() -
-![]() given in a recent paper of Kurtz et
al. (2002) that is different from earlier nomenclature f1-
given in a recent paper of Kurtz et
al. (2002) that is different from earlier nomenclature f1-![]() (Kurtz et al. 1989). The old
("enigmatic'')
(Kurtz et al. 1989). The old
("enigmatic'') ![]() is denoted as
is denoted as ![]() ,
while the
current
,
while the
current ![]() is the new photometric mode found
by Kurtz et al. (2002). With this convention the numerical subscript is
consistent with an increasing value of frequency.
Following this nomenclature we
denote the new spectroscopically detected frequencies as
is the new photometric mode found
by Kurtz et al. (2002). With this convention the numerical subscript is
consistent with an increasing value of frequency.
Following this nomenclature we
denote the new spectroscopically detected frequencies as ![]() and
and
![]() in order to compare with previous works.
Note that the negative subscript should not be confused with the
negative superscript normally used to denote rotational sidelobes.
Rather, it gives a relative frequency location with respect to
other published modes.
in order to compare with previous works.
Note that the negative subscript should not be confused with the
negative superscript normally used to denote rotational sidelobes.
Rather, it gives a relative frequency location with respect to
other published modes.
Our RV analysis software uses days as the time unit, so the results
of our DFT analysis produces frequencies as cycles per day. We relate these
frequencies to the more conventional ![]() Hz unit when
necessary.
Hz unit when
necessary.
Figures 2 and 3 show the discrete
Fourier transform of the RV variations for each of the 14 spectral orders
(left to right) as a function of rotation phase (top to bottom).
The number above each column of DFTs represents the central wavelength
of the spectral order. Each order spans approximately ![]() 50 Å from
the central wavelength.
Rotation phases were reckoned according to
50 Å from
the central wavelength.
Rotation phases were reckoned according to
There are strong amplitude variations both as a function of wavelength and rotation phase. The highest RV amplitudes can be found in the spectral region centered on 5825 Å where the amplitude can be as high as 200 m s-1. This is most likely due to the contribution of high-amplitude of rare earth element (REE) lines that lie inside the spectral order (for instance Nd III 5845.02 Å). Studies have shown that these can have the highest RV amplitudes (Savanov et al. 1999; Kochukhov & Ryabchikova 2001a,b; Balona & Zima 2002). The same is true for other spectral orders centered on 5056 Å and 5132 Å showing high amplitude RV variations (up to 100 m s-1). The lowest amplitude spectral regions are centered on 6253 Å and 5929 Å where the amplitude often does not exceed about 40 m s-1.
There are also very strong amplitude variations associated with
rotational modulation. The highest amplitudes occur in the phase
interval
![]() where the pulsational modes can
be seen in all spectral orders, with the possible exception of the one
centered on 6253 Å. The center of this phase
interval coincides with magnetic maximum.
The pulsational RV amplitude of all modes are
low, or non-detectable between the phase interval
where the pulsational modes can
be seen in all spectral orders, with the possible exception of the one
centered on 6253 Å. The center of this phase
interval coincides with magnetic maximum.
The pulsational RV amplitude of all modes are
low, or non-detectable between the phase interval
![]() which is coincident with the minimum of the magnetic field variations.
which is coincident with the minimum of the magnetic field variations.
The dominant mode in all the power spectra of the various spectral
orders appears to be
![]() c d-1 (2653
c d-1 (2653 ![]() Hz). To show the rotational
modulation of the pulsational phase and amplitude a least squares fit using
this single frequency was made to all the RV data.
Throughout this paper the pulsational phase,
Hz). To show the rotational
modulation of the pulsational phase and amplitude a least squares fit using
this single frequency was made to all the RV data.
Throughout this paper the pulsational phase, ![]() in fraction of a
pulsation cycle, is calculated according to the
sin-wave fit
in fraction of a
pulsation cycle, is calculated according to the
sin-wave fit
![]() with an arbitrary starting time,
with an arbitrary starting time,
![]() = HJD 2 450 000.
= HJD 2 450 000.
We chose not to fit all the modes for every spectral order as this is time consuming and of limited use for atmospheric diagnostics since more information can be gleaned from a RV analysis using single spectral lines. (Below we perform a detailed analysis of a single spectral order.) However, it would be instructive to see the amplitude and phase modulation for a single high-amplitude mode for all spectral regions since this provides the best comparison to very broad-band (compared to this study) photometric variations.
Figures 4 and 5 show the variations
of the phase and amplitude, respectively, of the ![]() mode as
a function of rotation phase. The reddest order (centered on 6253 Å)
is not shown because the pulsational amplitude and phase could not be
determined with sufficient accuracy due to a poor measurement precision
caused by two effects. First, the iodine
absorption lines are quite weak in this spectral order and they lose
their efficacy as a wavelength reference. Second, this region of the
spectrum was plagued by
many telluric absorption features which can add systematic
errors to the RV measurements.
mode as
a function of rotation phase. The reddest order (centered on 6253 Å)
is not shown because the pulsational amplitude and phase could not be
determined with sufficient accuracy due to a poor measurement precision
caused by two effects. First, the iodine
absorption lines are quite weak in this spectral order and they lose
their efficacy as a wavelength reference. Second, this region of the
spectrum was plagued by
many telluric absorption features which can add systematic
errors to the RV measurements.
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{0547fig3.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg63.gif) |
Figure 3: The same as in Fig. 2, but for the wavelength interval 5013-5590 Å (7 spectral orders). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm]{0547fig4.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg64.gif) |
Figure 4:
The rotational modulation of the amplitude of the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm]{0547fig5.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg65.gif) |
Figure 5:
The rotational modulation of the phase
of the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{0547fig6.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg66.gif) |
Figure 6:
The amplitude spectra of consecutive steps of a DFT analysis
for the entire RV data. The position of principal frequencies
from Kurtz et al. (1989) are indicated by dashed lines.
(Top) DFT of original RV data. (Middle) DFT of RV residuals after
removing contribution
from |
| Open with DEXTER | |
The amplitudes and phases of the various modes and their rotational sidelobes when analysing the complete data set does not give us direct information about the shape of the amplitude modulation and the rotational phases of pulsation phase jumps of the individual modes. The "averaged'' amplitudes of modes over a complete rotation cycle will be significantly lower than the maximum from an individual night. These averaged amplitudes might also miss some as yet undetected mode whose signal may be present at one rotation phase, but not another. For these reasons we divided our analysis into three steps.
First, the entire data set of one spectral order was studied in detail. We chose to perform this broad-band RV analysis on the high-amplitude order centered on wavelength 5825 Å. Second, we undertook this broad-band analysis separately for every night with the aim of studying the rotational variation of the amplitude and phase of individual modes. Finally, as a check of the broad-band results we analyzed the RVs for a single spectral feature, Nd III 5294.1 Å, that showed high pulsational amplitudes. The work on Nd III is a precursor to a complete line-by-line analysis of HR 1217 to published as part of our series in the RV study of roAp stars.
We performed a frequency analysis for the entire dataset of
the order centered on 5825 Å (5776-5873 Å) which contained 2075
data points spanning 48 days from the first to the last observation.
The top panel of Fig. 6 shows the amplitude spectrum of the
HJD 2 450 798-2 450 846 RV data. (For convenience we will refer
to the data from each night by the integer value of the Julian
Day for that night.)
Pulsation frequencies were found using the following
pre-whitening procedure.
A sine wave was fit
to the dominant frequency and this component was removed from the
data. An analysis was then performed on the pre-whitened data
and the contribution of the next dominant mode was then removed.
The steps of this analysis are shown in the top and middle panels of the
figure.
Through this sequential pre-whitening procedure
we were able
to find the principal photometric frequencies with their
sidelobes: ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and ![]() ,
where the symbols + or - denote the rotational sidelobes
(
,
where the symbols + or - denote the rotational sidelobes
(
![]() and
and
![]() )
The bottom panel of
Fig. 6 shows the DFT of the RV residuals. The highest
and approximately equal strength peaks occur at
frequencies of 241.29 and 242.29 c d-1 and have
amplitudes of 21.3 m s-1 and 21.6 m s-1, respectively.
The second frequency is clearly a 1 c d-1 alias of first.
The 241.29 c d-1 (2792.7
)
The bottom panel of
Fig. 6 shows the DFT of the RV residuals. The highest
and approximately equal strength peaks occur at
frequencies of 241.29 and 242.29 c d-1 and have
amplitudes of 21.3 m s-1 and 21.6 m s-1, respectively.
The second frequency is clearly a 1 c d-1 alias of first.
The 241.29 c d-1 (2792.7 ![]() Hz)
peak coincides with the mean position of
the new
Hz)
peak coincides with the mean position of
the new ![]() mode and is close to the
mode and is close to the ![]() mode.
These two modes could
not be safely resolved by our RV data due to their
close spacing and the 1 c d-1 pattern in
the spectral window function.
mode.
These two modes could
not be safely resolved by our RV data due to their
close spacing and the 1 c d-1 pattern in
the spectral window function.
There is also excess power above the 12 m s-1 noise level
(at surrounding frequencies) in the interval
219-220 c d-1 and 232-238 c d-1. In the interval 232-238 c d-1 this excess may be naturally explained by a combination of
the small-amplitude ![]() mode and its unresolved,
rotationally split sidelobes, along with the residual sidelobes of
mode and its unresolved,
rotationally split sidelobes, along with the residual sidelobes of ![]() and
and ![]() .
Because further attempts to resolve
the low-amplitude sidelobes in the interval 229-238 c d-1 could not
provide additional information we focus on the frequency interval
centered around 220 c d-1.
.
Because further attempts to resolve
the low-amplitude sidelobes in the interval 229-238 c d-1 could not
provide additional information we focus on the frequency interval
centered around 220 c d-1.
Table 2:
Photometric frequencies ![]() -
-![]() detected in
analysis of entire data of the spectral order centered on 5825 Å.
Also listed
are the new modes detected in different subsets of the RV data.
detected in
analysis of entire data of the spectral order centered on 5825 Å.
Also listed
are the new modes detected in different subsets of the RV data.
The RV noise peaks of our broad-band radial velocity data for the entire
data set is about 12 m s-1 in the frequency range of interest. This leads us
to suspect that the signal around frequency = 220 c d-1 is indeed
real. To show that this signal is not an artifact
we analysed the broad-band data in another way.
First, for every night we approximated the signal from the contribution of
high amplitude ![]() ,
,
![]() ,
and f4 modes using the simultaneous least square sine wave solution with
fixed frequencies, but with variable phases and amplitudes.
We removed this three-frequency fit from the RV measurements of each
night. This procedure automatically removed the
rotation sidelobes of the large amplitude modes from the DFT of the
data from the combined nights which
simplified the search for new low-amplitude modes. We merged
all the nightly residuals into the one residual data set for
a further search for periodicities.
The DFT analysis of this data set is shown in Fig. 7
and this gives approximately the same result as the consecutive prewhitening
procedure for the entire data set. The right arrow in the figure marks the
location of
,
and f4 modes using the simultaneous least square sine wave solution with
fixed frequencies, but with variable phases and amplitudes.
We removed this three-frequency fit from the RV measurements of each
night. This procedure automatically removed the
rotation sidelobes of the large amplitude modes from the DFT of the
data from the combined nights which
simplified the search for new low-amplitude modes. We merged
all the nightly residuals into the one residual data set for
a further search for periodicities.
The DFT analysis of this data set is shown in Fig. 7
and this gives approximately the same result as the consecutive prewhitening
procedure for the entire data set. The right arrow in the figure marks the
location of ![]() and the left arrow the new suspected mode with a
frequency = 219.9
and the left arrow the new suspected mode with a
frequency = 219.9 ![]() 1 c d-1 (2545.1
1 c d-1 (2545.1 ![]() Hz) and an amplitude = 17.8 m s-1.
The
Hz) and an amplitude = 17.8 m s-1.
The ![]() 1 c d-1 uncertainty is due to alias pattern of spectral
window function. This is consistent with the consecutive pre-whitening
procedure of the previous analysis.
1 c d-1 uncertainty is due to alias pattern of spectral
window function. This is consistent with the consecutive pre-whitening
procedure of the previous analysis.
| |
Figure 7:
The amplitude DFT spectra of merged nightly
residuals after removing the contribution of
|
| Open with DEXTER | |
The statistical significance of the two peaks in Fig. 7
(indicated by arrows)
was assessed using a bootstrap
randomization technique (e.g. Murdoch et al. 1993; Kürster et al.
1997). The measured RV values were randomly shuffled keeping
the observed times fixed. A Lomb-Scargle periodogram (Lomb 1976;
Scargle 1982) was then computed for each shuffled data set. The
fraction of the random-data periodograms having peak power greater than the
observed peak power in the frequency interval
![]() c d-1 was
taken as the false alarm probability (FAP) that random noise could
produce the observed signal. We should note that this is a very
conservative estimate for the FAP of signals known
to be present in the data (like f6 which has been found photometrically).
In this case one should determine the probability that random noise produces
a peak higher than the data periodogram at exactly this frequency and not
over the broad frequency range that we considered.
c d-1 was
taken as the false alarm probability (FAP) that random noise could
produce the observed signal. We should note that this is a very
conservative estimate for the FAP of signals known
to be present in the data (like f6 which has been found photometrically).
In this case one should determine the probability that random noise produces
a peak higher than the data periodogram at exactly this frequency and not
over the broad frequency range that we considered.
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{0547fig8.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg72.gif) |
Figure 8: DFT of the "broad-band'' RVs of the order centered on 5825 Å from the individual nights ( left panels, from top to bottom) and after subtracting a two-frequency solution ( right panels, from top to bottom). Note the different RV scale for the upper four panels. The vertical dashed lines shows the position of the photometric frequencies from Kurtz et al. (2002). The Julian dates and the corresponding mean rotation phases are given for each panel. |
| Open with DEXTER | |
Using 105 "shuffles'' we determined
FAP =
![]() for f6 and
FAP =
for f6 and
FAP =
![]() for the peak at 219.9 c d-1 (2545.1
for the peak at 219.9 c d-1 (2545.1 ![]() Hz,
termed f0).
The detection of f6 is highly significant and thus provides spectroscopic
confirmation of this new photometric mode. The detection of f0 is
marginally significant. (Our criterion for a statistically significant
signal in the data is that it must have FAP < 10-3). However,
in the next subsection we show that based on a single night analysis this
signal is most likely real and due to an additional excited mode.
Hz,
termed f0).
The detection of f6 is highly significant and thus provides spectroscopic
confirmation of this new photometric mode. The detection of f0 is
marginally significant. (Our criterion for a statistically significant
signal in the data is that it must have FAP < 10-3). However,
in the next subsection we show that based on a single night analysis this
signal is most likely real and due to an additional excited mode.
The analysis of whole data set shows that the all principal photometric
frequencies known for HR 1217 (Kurtz et al. 2002) are
also present in our high precision RV data, but the RV amplitude ratios
of the modes do not follow the photometric amplitude ratios. For
instance, the highest RV amplitude in our observations is at 229.21 c d-1
(2652.9 ![]() Hz =
Hz = ![]() )
whereas the highest photometric amplitude
was reported in 1986 at 232.2 c d-1 (2687.5
)
whereas the highest photometric amplitude
was reported in 1986 at 232.2 c d-1 (2687.5 ![]() Hz =
Hz = ![]() ,
Kurtz
et al. 1989), and 235.08 c d-1 (2720.8
,
Kurtz
et al. 1989), and 235.08 c d-1 (2720.8 ![]() Hz =
Hz = ![]() )
using data taken in 2000 during a Whole Earth Telescope campaign
(Kurtz et al. 2002). The differences in
photometric
amplitudes could be explained by temporal amplitude variability.
A different RV-to-photometric amplitude ratio of modes is also consistent with
suggestion that different acoustic modes will have different phase and
amplitude profiles across the atmosphere (Mkrtichian et al.
2003) and hence results in different amplitudes in the
continuum and line-forming layers.
)
using data taken in 2000 during a Whole Earth Telescope campaign
(Kurtz et al. 2002). The differences in
photometric
amplitudes could be explained by temporal amplitude variability.
A different RV-to-photometric amplitude ratio of modes is also consistent with
suggestion that different acoustic modes will have different phase and
amplitude profiles across the atmosphere (Mkrtichian et al.
2003) and hence results in different amplitudes in the
continuum and line-forming layers.
The analysis of all the data distributed over the whole rotation period can provide higher frequency resolution, but leads to loss of information regarding the shape of variability of the pulsational amplitudes and phases over a rotation cycle.
Knowing the exact photometric frequencies for modes will enable us to investigate the night-to-night amplitude and phase variability in RVs. Moreover, this analysis for the separate nights will help us to determine the nights with nearly constant pulsational phases. This will allow us to combine these into one data string in order to obtain a higher frequency resolution and a better signal-to-noise ratio for detecting low amplitude signals.
A least squares fit to a single night of observations using
seven fixed frequencies, but with variable amplitudes and phases
may in some cases give unrealistic and divergent solutions.
We thus chose to fit
the data from the individual nights simultaneously with the frequencies of
two highest
amplitude modes (usually ![]() and
and ![]() ).
The contribution of these were then subtracted and a simultaneous
one- or two-frequency solution was performed on the residuals using the
known (fixed) values of photometric frequencies.
Such a technique helps to avoid uncertain results that may arise
during the multi-frequency fitting of a short time series of data.
).
The contribution of these were then subtracted and a simultaneous
one- or two-frequency solution was performed on the residuals using the
known (fixed) values of photometric frequencies.
Such a technique helps to avoid uncertain results that may arise
during the multi-frequency fitting of a short time series of data.
Figure 8 shows the DFT of the nightly RV data using the spectral order centered
on 5825 Å.
Figure 9 shows a phase plot of the residual RVs after removing
a three-frequency fit (![]() ,
,
![]() ,
and
,
and ![]() )
to the data taken on JD 2 450 804 and phased to the
remaining best fit frequency 241.7 c d-1 (2797.5
)
to the data taken on JD 2 450 804 and phased to the
remaining best fit frequency 241.7 c d-1 (2797.5 ![]() Hz). This
signal is most
likely a doublet of two close frequencies (
Hz). This
signal is most
likely a doublet of two close frequencies (![]() and
and ![]() )
and has a semi-amplitude 56.2 m s-1.
)
and has a semi-amplitude 56.2 m s-1.
This procedure was then performed on data from all nights
to find the multi-frequency amplitude and phase solutions for residuals
as a function of rotation phase. We also checked some multi-frequency
solutions that were uncertain by combining two consecutive nights for
the DFT analysis and comparing these to results using only one night of
data.
The resulting rotational amplitude and phase variability of the highest
amplitude modes (![]() ,
,
![]() and
and ![]() )
is presented in panels of Fig. 10. These
will be discussed in
Sect. 4.1.
)
is presented in panels of Fig. 10. These
will be discussed in
Sect. 4.1.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0547fig9.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg75.gif) |
Figure 9:
The phase curve of residuals after removal of a
three frequency fit ( |
| Open with DEXTER | |
On the night of JD 2 450 845 (![]() )
the residual DFT (see the right
panel of Fig. 8) showed
significant power (amplitude of 40 m s-1) at 222.1 c d-1 (2570.6
)
the residual DFT (see the right
panel of Fig. 8) showed
significant power (amplitude of 40 m s-1) at 222.1 c d-1 (2570.6 ![]() Hz). This confirms our suspicion (see above)
regarding the presence of
additional modes excited with frequencies between 220-223 c d-1.
Hz). This confirms our suspicion (see above)
regarding the presence of
additional modes excited with frequencies between 220-223 c d-1.
To check the results of the previous subsections, we analysed the
RV measurements of a single spectral line, the
strong feature of Nd III at 5294 Å which was found to have
a high RV amplitude. Data were analyzed from several nights
centered on the selected rotation phases that did not show
significant pulsation phase and amplitude variations for ![]() and
and ![]() .
(This facilitates correctly
subtracting the contribution of these modes.)
The
.
(This facilitates correctly
subtracting the contribution of these modes.)
The ![]() mode had its maximum RV amplitude
of 322.9 m s-1 on the night JD = 2 450 804. A short time series of
the RV measurements for this Nd III spectral line is shown in Fig. 11.
An analysis of this night showed that the signal around
220 c d-1 was not detectable (possibly due to rotational
modulation).
mode had its maximum RV amplitude
of 322.9 m s-1 on the night JD = 2 450 804. A short time series of
the RV measurements for this Nd III spectral line is shown in Fig. 11.
An analysis of this night showed that the signal around
220 c d-1 was not detectable (possibly due to rotational
modulation).
We then analysed the RVs of the Nd III 5294.1 Å line from on
JD = 2 450 845.
Figure 12 (top panel) is the DFT of the original data.
The bottom panel show the DFT of residuals after
subtracting the fit to the ![]() from the data. This shows
a signal with amplitude = 76 m -1 at a frequency of 221.39 c d-1 -
approximately midway between the 220.4 and 223.3 c d-1 modes expected
from equally spaced p-modes in HR 1217. This is probably an unresolved
blend of these frequencies. The FAP of this peak using the bootstrap
randomization technique and
from the data. This shows
a signal with amplitude = 76 m -1 at a frequency of 221.39 c d-1 -
approximately midway between the 220.4 and 223.3 c d-1 modes expected
from equally spaced p-modes in HR 1217. This is probably an unresolved
blend of these frequencies. The FAP of this peak using the bootstrap
randomization technique and
![]() shuffles is FAP < 5
shuffles is FAP < 5 ![]() 10-6. This is statistically significant and confirms that
the signal found in broad-band RV analysis at frequencies shorter than f1 mode is indeed real. Figure 13 shows the RV residuals phased to a period of 6.477 min (
10-6. This is statistically significant and confirms that
the signal found in broad-band RV analysis at frequencies shorter than f1 mode is indeed real. Figure 13 shows the RV residuals phased to a period of 6.477 min (
![]() c d-1 = 2573.3
c d-1 = 2573.3 ![]() Hz). Each point
represents phased-averaged measurements using a bin size of 0.05
pulsation phases.
Hz). Each point
represents phased-averaged measurements using a bin size of 0.05
pulsation phases.
To check independently this detection and to resolve the blended peaks
by extending the time-base, we performed a DFT analysis on two
closely-spaced nights JD 2 450 843 and 2 450 845 that covered the
rotation phases ![]() -0.25. This
corresponds to the relatively stationary pulsation phase of
-0.25. This
corresponds to the relatively stationary pulsation phase of ![]() and
and ![]() modes (i.e. no jumps in the pulsational
phase occur from one night to the next).
modes (i.e. no jumps in the pulsational
phase occur from one night to the next).
The signals of the highest amplitude modes (![]() and
and ![]() )
were pre-whitened from the
nightly data and the residuals were merged into one data set for
analysis.
The top panel of Fig. 14 shows the DFT of these
residuals with two resolved peaks:
)
were pre-whitened from the
nightly data and the residuals were merged into one data set for
analysis.
The top panel of Fig. 14 shows the DFT of these
residuals with two resolved peaks:
![]() at
at
![]() c d-1 = 2553.0
c d-1 = 2553.0 ![]() Hz
(
Hz
(
![]() m s-1)
and
m s-1)
and ![]() at
at
![]() c d-1 = 2585.3
c d-1 = 2585.3 ![]() Hz
(
Hz
(
![]() m s-1). The f-1 peak is statistically significant
having FAP = 6.5
m s-1). The f-1 peak is statistically significant
having FAP = 6.5 ![]() 10-5 determined by 105 runs
of a bootstrap randomization scheme. The bottom panel of Fig. 14 shows the DFT of residuals
after the pre-whitening the
10-5 determined by 105 runs
of a bootstrap randomization scheme. The bottom panel of Fig. 14 shows the DFT of residuals
after the pre-whitening the
![]() signal.
The FAP of the
signal.
The FAP of the
![]() peak is
peak is
![]() .
The remaining low amplitude peaks in the 220-243 c d-1 interval corresponds
to the
.
The remaining low amplitude peaks in the 220-243 c d-1 interval corresponds
to the ![]() and
and ![]() modes.
modes.
![\begin{figure}
\par\includegraphics[width=12.2cm,clip]{0547fig10.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg87.gif) |
Figure 10:
Pulsation amplitude and phase for the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0547fig11.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg88.gif) |
Figure 11: The pulsation RV variations of the Nd III 5294.1 Å spectral line obtained on JD 2 450 804. |
| Open with DEXTER | |
One more statistically significant new peak (having the
broad alias sidelobes) in the DFT is at a frequency 244.07 c d-1
(2824.9 ![]() Hz). This has a maximum amplitude of 52.8 m s-1 and
a FAP =
Hz). This has a maximum amplitude of 52.8 m s-1 and
a FAP =
![]() (105 shuffles). The frequency of this
peak (which is probably a blend with the
(105 shuffles). The frequency of this
peak (which is probably a blend with the
![]() c d-1
(2805.6
c d-1
(2805.6 ![]() Hz) mode) is exactly at the expected position
(
Hz) mode) is exactly at the expected position
(
![]() c d-1) of the next equally spaced (with
c d-1) of the next equally spaced (with ![]() )
mode. However, it is a premature to conclude, based on
quality of available subset of RV data, about the existence of new
excited mode outside the interval of 220-243 c d-1.
)
mode. However, it is a premature to conclude, based on
quality of available subset of RV data, about the existence of new
excited mode outside the interval of 220-243 c d-1.
As a final check of the certainty of the detection of the two new modes
in the interval 220-223 c d-1 we carried out an analysis
of another subset of
ND III 5294.1 Å line RV data, namely those taken on the
consecutive nights
JD = 2 450 800 and 2 450 801. These nights correspond to another
rotation phase interval (
![]() -0.72) with relatively
constant (after
-0.72) with relatively
constant (after ![]() -switching) pulsation phases
for f2, f3, and f4.
Figure 15 shows the DFTs of raw data and the
residual RVs after application of the
consecutive pre-whitening procedure on the two highest amplitude
peaks of
-switching) pulsation phases
for f2, f3, and f4.
Figure 15 shows the DFTs of raw data and the
residual RVs after application of the
consecutive pre-whitening procedure on the two highest amplitude
peaks of ![]() and
and ![]() .
The residual DFT (bottom panel) shows a pattern of peaks with amplitudes
around 30 m s-1 at the positions of the
.
The residual DFT (bottom panel) shows a pattern of peaks with amplitudes
around 30 m s-1 at the positions of the ![]() ,
,
![]() ,
,
![]() and
and ![]() modes.
A peak at 221.5 c d-1 (2563.7
modes.
A peak at 221.5 c d-1 (2563.7 ![]() Hz) is exactly the position of the 1 c d-1 alias of 220.4 c d-1 (2550.9
Hz) is exactly the position of the 1 c d-1 alias of 220.4 c d-1 (2550.9 ![]() Hz, marked as
Hz, marked as
![]() )
which follows the equidistant spacing of the
)
which follows the equidistant spacing of the
![]() -
-![]() sequence.
The FAP of this peak is 9.1
sequence.
The FAP of this peak is 9.1 ![]() 10-3. We do not see
10-3. We do not see ![]() frequency which
is most likely a result of rotational modulation of the pulsational
amplitude.
frequency which
is most likely a result of rotational modulation of the pulsational
amplitude.
In summary, our analysis confirms the existence of the new photometric ![]() mode.
We have detected
with a high statistical significance two new pulsation
frequencies, 220.58 c d-1
(2553.0
mode.
We have detected
with a high statistical significance two new pulsation
frequencies, 220.58 c d-1
(2553.0 ![]() Hz) and 223.37 c d-1 (2585.3
Hz) and 223.37 c d-1 (2585.3 ![]() Hz), using RV
measurements from subsets of our "broad-band'' spectral data and from
a single spectral line (Nd III 5294.1 Å).
These follow
the
Hz), using RV
measurements from subsets of our "broad-band'' spectral data and from
a single spectral line (Nd III 5294.1 Å).
These follow
the ![]() -
-![]() equidistant spacing i.e. related to
the same odd and even l-degree sequences of p-modes.
equidistant spacing i.e. related to
the same odd and even l-degree sequences of p-modes.
The expected effect of a large global magnetic field is to modify the pure zonal mode of pulsation giving rise to magnetically perturbed components (Takata & Shibahashi 1995; Dziembowski & Goode 1996). The revised oblique pulsator model that includes the effects of the centrifugal force and the magnetic field was suggested by Bigot & Dziembowski (2002). For a dipole mode they developed a simple geometrical picture of non-axisymmetric pulsations in the presence of rotation and magnetic field that explained the observed pulsational amplitude modulation. This two-dimensional model is valid for polar magnetic field strengths greater than 1 kG and needs to be established by observations.
Recently, excitation of axisymmetric non-radial p-modes in the
presence of a magnetic field was investigated by Saio & Gautschy
(2004). They show that only high-overtone modes excited by classical
![]() -mechanism survive in the presence of a few kG magnetic field
and the amplitudes of the mainly dipole or quadrupole modes are strongly
confined to the magnetic axis.
The comparison of observed rotational RV modulation for different modes
with those predicted by different pulsator models may be a valuable tool
for checking which model is correct.
-mechanism survive in the presence of a few kG magnetic field
and the amplitudes of the mainly dipole or quadrupole modes are strongly
confined to the magnetic axis.
The comparison of observed rotational RV modulation for different modes
with those predicted by different pulsator models may be a valuable tool
for checking which model is correct.
We compared the observed and predicted pulsational amplitude variations
for HR 1217
for l = 1-3 zonal (m = 0) modes in the context of the
standard 2D-OPM model. This was done using the
SPOTNRP code (Mkrtichian 1992) written for
modeling line-profile variations and the spatial response functions for
2D-OPM in roAp stars with surface chemical anomalies.
Our simulations were carried out for the low-degree l = 1-3,
m = 0 modes that covered the complete rotational period of
HR 1217. Figure 16 shows the variations of
the modulus of the disc-integrated amplitudes for these modes
normalized by the maximum surface velocity amplitude. We assumed no
surface anomalies for these calculations in order to compare to the results
of our analysis of the 5825 Å spectral order which represents an
average RV of many spectral lines from a variety of atomic species. The
effect of the surface inhomogeneous distribution of elements
investigated by Mkrtichian (1994) and Mkrtichian et al.
(2000) should thus be nearly eliminated. In the oblique pulsator
model for HR 1217 we assume inclination angles for the rotation and
magnetic axes of
![]() ,
,
![]() ,
respectively, as determined from the linear
polarization data of Leroy et al. (1996).
,
respectively, as determined from the linear
polarization data of Leroy et al. (1996).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0547fig12.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg95.gif) |
Figure 12:
The frequency analysis of the RV measurements of the
Nd III 5294.1 Å line obtained on JD 2 450 845.
( Top panel) The DFT of original RV
data. ( Bottom panel) The DFT of the residual RV data after subtracting the
contribution due to
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0547fig13.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg96.gif) |
Figure 13:
The phase curve of JD 2 450 845 RV residuals after removing the
contribution due to
|
| Open with DEXTER | |
The amplitude and pulsation variations for the three high
amplitude modes ![]() ,
,
![]() ,
and
,
and ![]() are shown in Fig. 10.
The comparison of Figs. 16 with 10 shows that the shape of the
amplitude modulations for the
are shown in Fig. 10.
The comparison of Figs. 16 with 10 shows that the shape of the
amplitude modulations for the ![]() ,
,
![]() ,
modes are close to that expected from a
zonal l=1 mode having its highest amplitude
at magnetic maximum.
These show a maximum amplitude
centered
on rotation phase
,
modes are close to that expected from a
zonal l=1 mode having its highest amplitude
at magnetic maximum.
These show a maximum amplitude
centered
on rotation phase
![]() and a
minimum around
and a
minimum around
![]() .
Since magnetic maximum occurs at
.
Since magnetic maximum occurs at
![]() this is consistent with the 2D-OPM.
this is consistent with the 2D-OPM.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0547fig14.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg98.gif) |
Figure 14:
The amplitude spectra for two merged residual RV data
of the Nd III 5294.1 Å line from the nights
JD 2 450 843 and 2 450 845. This residual data results from two consecutive
steps of pre-whitening the data by the contribution of
|
| Open with DEXTER | |
On the other hand, the rotational modulation of the pulsational phase of
the
![]() ,
,
![]() and
and ![]() modes does not seem
to be consistent with any mode in the standard 2D-OPM.
The
modes does not seem
to be consistent with any mode in the standard 2D-OPM.
The ![]() mode shows a pulsational phase jump
exactly at magnetic maximum while the
mode shows a pulsational phase jump
exactly at magnetic maximum while the ![]() and
and ![]() modes show a
relatively monotonous change in phase
(see Fig. 10) around the rotation phase coincident
with the magnetic maximum.
modes show a
relatively monotonous change in phase
(see Fig. 10) around the rotation phase coincident
with the magnetic maximum.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0547fig15.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg99.gif) |
Figure 15:
DFT analysis of combined data for Nd III 5294.1 Å
spanning JD 2 450 800-2 450 801.
( Top) DFT of the original data. ( Middle) DFT of the
residuals after pre-whitening by the f2 mode.
( Bottom) DFT of the RV residuals after prewhitening by the
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0547fig16.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg100.gif) |
Figure 16:
The calculated rotational modulation of the
relative RV amplitudes (modulus of the
spatial response function) of pure l=1, 2 and 3 zonal (m=0) modes in a
standard OPM for HR 1217. The pulsation phase is positive
around the magnetic maximum ( |
| Open with DEXTER | |
The results of our modeling shown in Fig. 16 demonstrate that for
pulsations aligned with the magnetic axis
the l,m = 1, 0 mode does not show pulsational phase jumps, only the
zonal modes l = 2, 3 have approximately a ![]() phase jump
(hereafter "
phase jump
(hereafter "![]() -switching") during the rotation cycle. The pulsation
phase for HR 1217, according to the 2D-OPM, should be switched at
-switching") during the rotation cycle. The pulsation
phase for HR 1217, according to the 2D-OPM, should be switched at
![]() and
and
![]() for l = 2 modes, and at
for l = 2 modes, and at
![]() and
and
![]() for l = 3 modes (see
Fig. 16).
However, all l = 1-3 pure zonal modes cannot explain the observed
variability and phase jumps of
for l = 3 modes (see
Fig. 16).
However, all l = 1-3 pure zonal modes cannot explain the observed
variability and phase jumps of
![]() ,
,
![]() ,
and
,
and ![]() in HR 1217.
in HR 1217.
The pulsation phase "![]() -switching'' for the
-switching'' for the
![]() mode occurs exactly at magnetic and pulsation amplitude
maxima, i.e. between rotation phases
mode occurs exactly at magnetic and pulsation amplitude
maxima, i.e. between rotation phases
![]() and 0.09, and
then jumps back at rotation phases 0.33-0.48. This is
inconsistent with what is expected from the standard 2D-OPM.
For the
and 0.09, and
then jumps back at rotation phases 0.33-0.48. This is
inconsistent with what is expected from the standard 2D-OPM.
For the ![]() and f3 modes the phase variations are different
with respect to the
and f3 modes the phase variations are different
with respect to the ![]() mode.
The pulsational phase for both modes jumps at
mode.
The pulsational phase for both modes jumps at
![]() -0.48.
Over the rotational
phase interval
-0.48.
Over the rotational
phase interval
![]() -1.33 the pulsation phase
of f3 decreases while the phase of f4 increases almost linearly back to its previous values.
It is during this phase interval that the magnetic pole crosses the
line-of-sight.
The interpretation of the phases for
-1.33 the pulsation phase
of f3 decreases while the phase of f4 increases almost linearly back to its previous values.
It is during this phase interval that the magnetic pole crosses the
line-of-sight.
The interpretation of the phases for ![]() ,
,
![]() and
and ![]() in terms of any pure l = 1, 2 or 3 zonal mode
and the standard 2D-OPM thus encounters problems.
in terms of any pure l = 1, 2 or 3 zonal mode
and the standard 2D-OPM thus encounters problems.
An attempt to decompose the observed RV phase jumps and amplitude
modulation around the magnetic maximum for the ![]() and
and ![]() modes by a linear combination of correspondingly scaled
spherical harmonics can be productive if there is some realistic
theoretical predictions about the limits for a range of (l, m)
quantum numbers in the expansion. According to Dziembowski & Goode
(1996) and Cunha & Gough (2000) magnetically perturbed
l-degree eigenmodes will have strong
modes by a linear combination of correspondingly scaled
spherical harmonics can be productive if there is some realistic
theoretical predictions about the limits for a range of (l, m)
quantum numbers in the expansion. According to Dziembowski & Goode
(1996) and Cunha & Gough (2000) magnetically perturbed
l-degree eigenmodes will have strong ![]() components in their
expansions and could be misidentified with each other. The original
(l,m) = (2, 0) modes may have a strong l = 0 and (l,m) = (4, 0)
components, whereas the (l,m) = (1, 0) mode will have (l,m) = (3, 0)
components. Conversely, the (l,m) = (3, 0) modes have strong (l,m) = (1, 0)
and (l,m) = (5, 0) components. So, the modes of even and odd degrees are
expected to have odd and even terms in the expansion.
components in their
expansions and could be misidentified with each other. The original
(l,m) = (2, 0) modes may have a strong l = 0 and (l,m) = (4, 0)
components, whereas the (l,m) = (1, 0) mode will have (l,m) = (3, 0)
components. Conversely, the (l,m) = (3, 0) modes have strong (l,m) = (1, 0)
and (l,m) = (5, 0) components. So, the modes of even and odd degrees are
expected to have odd and even terms in the expansion.
However, it is clear from Fig. 10 that the phase
jump in ![]() at magnetic
maximum is not possible to represent as a combination axisymmetric
m=0 modes because all amplitude and phase changes of
l=1-4 zonal modes are symmetric with respect to the magnetic maximum.
There are difficulties if one attempts to explain the phase changes
between
at magnetic
maximum is not possible to represent as a combination axisymmetric
m=0 modes because all amplitude and phase changes of
l=1-4 zonal modes are symmetric with respect to the magnetic maximum.
There are difficulties if one attempts to explain the phase changes
between
![]() and 1.33 using a linear combinations of
magnetically distorted zonal l-components for the
and 1.33 using a linear combinations of
magnetically distorted zonal l-components for the ![]() and f4modes since during this time the magnetic pole crosses the line of sight.
and f4modes since during this time the magnetic pole crosses the line of sight.
It might seem that for the interpretation of the RV phase variability in the HR 1217 it will be better to include the non-axisymmetric components in distorted pulsations expansions as suggested by Takata & Shibahashi (1995) or as proposed by the revised OPM of Bigot & Dziembowski (2002). Again it is difficult to adjust simultaneously within the framework of the 2D-OPM model the maximum of pulsation RV amplitude and the RV phase switching and the constancy of the photometric phase around the magnetic maximum.
In retrospect, Mkrtichian et al. (2000) showed (see Figs. 3 and 4 in their paper) that the spotted distributions of chemical
elements in a standard 2D-OPM model may produce additional modulation
of the RV pulsation amplitudes for lines of individual elements. These
may introduce shifts in the rotational phase where the pulsational
![]() -switching occurs while the photometric phase might
show no anomalies. The magnitude of this effect for every mode
depends on the abundance, geometry, and location of spots on the
stellar disk with respect to pulsation axis. At some favorable
inclinations of the magnetic axis the contribution of the surface spots
may saturate the
-switching occurs while the photometric phase might
show no anomalies. The magnitude of this effect for every mode
depends on the abundance, geometry, and location of spots on the
stellar disk with respect to pulsation axis. At some favorable
inclinations of the magnetic axis the contribution of the surface spots
may saturate the ![]() -switching of pulsation phases for magnetically
reversive roAp stars. In turn, for some favourable geometry of spots and
inclinations of magnetic, rotation and pulsations axes, this effect may
lead to
-switching of pulsation phases for magnetically
reversive roAp stars. In turn, for some favourable geometry of spots and
inclinations of magnetic, rotation and pulsations axes, this effect may
lead to ![]() -switching of phases in the RV even for roAp stars that do
not show (like HR 1217) magnetic field reversals and pulsation phase
-switching of phases in the RV even for roAp stars that do
not show (like HR 1217) magnetic field reversals and pulsation phase
![]() -switching in the photometry. However, the similarities in
-switching in the photometry. However, the similarities in
![]() -switching in the "broad-band'' RV phases at magnetic maximum in
HR 1217 is seen to occur in the
-switching in the "broad-band'' RV phases at magnetic maximum in
HR 1217 is seen to occur in the ![]() mode (see
Fig. 5) and in all spectral orders covering the wavelength
range 5010-6300 Å. These regions include several tens of
spectral lines from many different chemical elements; any effects due to
abundance spots on the stellar surface will thus average out.
In the case of the
mode (see
Fig. 5) and in all spectral orders covering the wavelength
range 5010-6300 Å. These regions include several tens of
spectral lines from many different chemical elements; any effects due to
abundance spots on the stellar surface will thus average out.
In the case of the ![]() ,
,
![]() ,
and f4 modes we therefore cannot invoke abundance spots as a main cause of the
peculiar
rotational phase variations observed in HR 1217. The observed phase
variations are inconsistent with those predicted by the standard or
modified 2D-OPM. The origin of the phase variations must have another
physical nature.
,
and f4 modes we therefore cannot invoke abundance spots as a main cause of the
peculiar
rotational phase variations observed in HR 1217. The observed phase
variations are inconsistent with those predicted by the standard or
modified 2D-OPM. The origin of the phase variations must have another
physical nature.
The picture of atmospheric pulsation velocity amplitudes and phases in roAp stars, as follows from recent spectroscopic results (Kanaan & Hatzes 1998; Baldry & Bedding 2000; Mkrtichian et al. 2003; Kurtz et al. 2003), is more complicated. Mkrtichian et al. (2003) using the new technique of acoustic cross-sections found the existence of standing wave and running wave components in RV variations and oppositely pulsating layers in the atmosphere of 33 Librae. The hypothetical standing wave likely has two acoustic nodes - one close to continuum formation level and another in the superficial atmospheric layers. They predicted that the acoustic profiles across the atmosphere should be different for different modes. Independently, Kurtz et al. (2003) using the VLT spectroscopy found evidence of running wave component in the upper atmosphere of the roAp star HD 166473.
Any attempt to give a reasonable explanation of the rotational RV
phase and amplitude variability in HR 1217, or any other
roAp stars, should also reflect the existence of vertical acoustic waves
and nodes in atmosphere. Such complicated atmospheric
vertical amplitude and phase acoustic profiles should lead also to
strong line-profile variations especially in the case of vertical
stratifications of elements. In this case, during a pulsation cycle, the
layers contributing to the wings and core of spectral lines may have
opposite velocity shifts and these can introduce
strong line-profile variations even for slowly rotating roAp star.
In the framework of two-dimensional models of non-radial pulsations, such
line-profile
variations can be mis-interpreted as a non-axisymmetric sectoral or
tesseral mode oscillations as was suggested for the
line-profile variations in ![]() Equ (Kochukhov & Ryabchikova 2001a).
Equ (Kochukhov & Ryabchikova 2001a).
In this sense, the 2D-OPM
should be revised and we should
consider a three-dimensional oblique pulsation model (3D-OPM). That is,
a pulsational phase and amplitude that is a function of location on the stellar
surface and depth in the stellar atmosphere. This
picture would be consistent with the observed photometric and RV
variations in HR 1217. An attempt to understand such a 3D-OPM and
detailed analysis of observed line-by-line RV amplitude and phase
variations in HR 1217 is beyond the scope of the current work and
should be given in detail in one of the next papers on our series on RV
studies of roAp stars.
![\begin{figure}
\par\includegraphics[width=14.4cm,clip]{0547fig17.ps}
\end{figure}](/articles/aa/full/2005/04/aa0547-03/Timg110.gif) |
Figure 17:
Left panel: p-mode echelle-spectrum of HR 1217.
The
|
| Open with DEXTER | |
For completeness, we will give another possible,
but simple explanation of the non-equidistant spacing.
We would like to stress that all previous explanations
of the ![]() mode and its
probable breaking of
the equidistance spacing of modes
(Kurtz et al. 1989; Cunha 2001) were made under two
assumptions: i) that higher degree (l>3-degree) are not
detectable, and ii) that the
mode and its
probable breaking of
the equidistance spacing of modes
(Kurtz et al. 1989; Cunha 2001) were made under two
assumptions: i) that higher degree (l>3-degree) are not
detectable, and ii) that the ![]() mode belongs to the same
(l,m,n) sequences of odd and even l-degree modes which formed
mode belongs to the same
(l,m,n) sequences of odd and even l-degree modes which formed
![]() -
-![]() equally spaced modes.
However, these widely accepted assumptions about the photometric
"invisibility'' of high-degree modes due to surface cancellation effect
while correct for normal stars, may be not valid in the case of roAp
stars. Moreover, low-degree components of magnetically distorted
high-degree modes (Dziembowski & Goode 1996) may indeed be visible
in disk-integrated light.
In photometric studies of roAp stars, the
(probably) excited high-degree modes or their magnetically distorted
low degree components, may introduce a significant contribution to the
disk-integrated photometric variability and hence may be indeed be
detectable in disk-integrated measurements.
This may be due to the peculiar abundances
and their inhomogeneous distribution on the stellar surface which
can affect the local opacity, and possibly even a peculiar limb-darkening law.
For spectroscopic studies, Mkrtichian (1992, 1994) and
Mkrtichian et al. (2000) show that the surface chemical
inhomogeneities in roAp stars may act as a
2D-PSF for nonradial pulsations and allows us to detect in a slowly rotating
stars modes up to
equally spaced modes.
However, these widely accepted assumptions about the photometric
"invisibility'' of high-degree modes due to surface cancellation effect
while correct for normal stars, may be not valid in the case of roAp
stars. Moreover, low-degree components of magnetically distorted
high-degree modes (Dziembowski & Goode 1996) may indeed be visible
in disk-integrated light.
In photometric studies of roAp stars, the
(probably) excited high-degree modes or their magnetically distorted
low degree components, may introduce a significant contribution to the
disk-integrated photometric variability and hence may be indeed be
detectable in disk-integrated measurements.
This may be due to the peculiar abundances
and their inhomogeneous distribution on the stellar surface which
can affect the local opacity, and possibly even a peculiar limb-darkening law.
For spectroscopic studies, Mkrtichian (1992, 1994) and
Mkrtichian et al. (2000) show that the surface chemical
inhomogeneities in roAp stars may act as a
2D-PSF for nonradial pulsations and allows us to detect in a slowly rotating
stars modes up to
![]() -15.
-15.
Mkrtichian & Hatzes (2000), in their discussion on the
echelle-diagrams for roAp stars and of HR 1217 in particular, have
explained the non-equidistant spacing of 2791 ![]() Hz (the former
Hz (the former ![]() but the
present
but the
present ![]() ) mode as related to the
higher degree modes which may indeed be visible in the disk-integrated
light. This explanation is based on the fact that modes with
l > 3,
their (l, n) frequency pattern should be shifted relative to
the columns for l = 0 or 2 and l = 1 or 3 modes in the
echelle-diagram. In other words, if the
) mode as related to the
higher degree modes which may indeed be visible in the disk-integrated
light. This explanation is based on the fact that modes with
l > 3,
their (l, n) frequency pattern should be shifted relative to
the columns for l = 0 or 2 and l = 1 or 3 modes in the
echelle-diagram. In other words, if the ![]() mode is related
to another odd or even l-degree sequence (say l = 4 or l = 5) than
the one which are formed by
mode is related
to another odd or even l-degree sequence (say l = 4 or l = 5) than
the one which are formed by ![]() -
-![]() ,
then the
spacing of
,
then the
spacing of ![]() with respect
to
with respect
to ![]() mode should not be equal to
mode should not be equal to ![]() 34
34 ![]() Hz.
If true, then we predict another sequence of yet undetected
l=4 modes which should be spaced by 68
Hz.
If true, then we predict another sequence of yet undetected
l=4 modes which should be spaced by 68 ![]() Hz from
Hz from ![]() .
.
To elucidate this interpretation using a graphical form we show
in the left panel of Fig. 17 the
echelle-diagram for HR 1217 with the complete set of modes so far
detected. In the right panel for comparison is the constructed
echelle-diagram for the frequencies of l = 1-4, n = 33-37 overtone modes
from the theoretical model "L'' (
![]() ,
,
![]() /
/
![]() ,
,
![]() )
of Gautschy et al. (1998). Note, that this
model does not represent the theoretical spectrum of HR 1217 and is shown
only illustrative purposes.
The echelle-diagrams (ED) for high-overtone acoustic modes are
constructed by dividing the frequency range where the modes are present
on the frequency intervals by the value of the so called "large separation'',
)
of Gautschy et al. (1998). Note, that this
model does not represent the theoretical spectrum of HR 1217 and is shown
only illustrative purposes.
The echelle-diagrams (ED) for high-overtone acoustic modes are
constructed by dividing the frequency range where the modes are present
on the frequency intervals by the value of the so called "large separation'',
![]() ,
with the next frequency interval placed below
the previous one. An ED constructed in this
way has vertical columns, each corresponding to the
l quantum numbers of adjacent, consecutive overtone
modes that are equi-spaced in frequency.
We have used the
,
with the next frequency interval placed below
the previous one. An ED constructed in this
way has vertical columns, each corresponding to the
l quantum numbers of adjacent, consecutive overtone
modes that are equi-spaced in frequency.
We have used the
![]() Hz for HR 1217, and the
value 42
Hz for HR 1217, and the
value 42 ![]() Hz for model "L'' from Gautschy et al. (1998) which we give as an example of on
ED drawn simultaneously for low
and high degree-modes. The latter value, found on the direct spacing of
frequencies of consecutive overtones, gives a better approximation for
spacing onto the vertical columns for a given range of theoretical
frequencies than the value 45.34
Hz for model "L'' from Gautschy et al. (1998) which we give as an example of on
ED drawn simultaneously for low
and high degree-modes. The latter value, found on the direct spacing of
frequencies of consecutive overtones, gives a better approximation for
spacing onto the vertical columns for a given range of theoretical
frequencies than the value 45.34 ![]() Hz given for this model in the Table 1
from Gautschy et al. (1998).
Hz given for this model in the Table 1
from Gautschy et al. (1998).
As could be seen on the right panel of Fig. 17 the
theoretical echelle-diagram for the l = 4 modes form a vertical column that
is spaced between low degree odd (l = 1 or 3) and even (l = 2) columns of
consecutive overtone sequences in a manner that is qualitatively similar
to the spacing of ![]() mode in the echelle-diagram for HR 1217 (left panel). The
spacing between (l, n-1) = (4, n-1) and the closest (l, n) = (1, n)
and (l, n) = (2, n) modes
is indeed of order
mode in the echelle-diagram for HR 1217 (left panel). The
spacing between (l, n-1) = (4, n-1) and the closest (l, n) = (1, n)
and (l, n) = (2, n) modes
is indeed of order
![]() /4, but in fact the exact spacing of
columns depends on stellar models and frequency range of the analysed
modes. The l = 4 identification of the
/4, but in fact the exact spacing of
columns depends on stellar models and frequency range of the analysed
modes. The l = 4 identification of the ![]() mode
naturally explains the former "peculiar''
49.99
mode
naturally explains the former "peculiar''
49.99 ![]() Hz
Hz ![]() 3/4
3/4
![]() spacing between
spacing between ![]() and
and ![]() ,
as well
as the 14.72
,
as well
as the 14.72 ![]() Hz
Hz ![]()
![]() spacing between f7 and
spacing between f7 and ![]() .
.
The f3 and f4 modes showed obvious discrepancies in the phase
variability at rotation phases around magnetic maximum.
Here the pulsational phase continuously changed without ![]() -switching.
We conclude that the observed pulsational
phase changes cannot be explained within
the framework of the 2D-OPM which assumes that the amplitudes and phase
velocity fields and photometric variations depend only on the
stellar magnetic latitude and longitude.
-switching.
We conclude that the observed pulsational
phase changes cannot be explained within
the framework of the 2D-OPM which assumes that the amplitudes and phase
velocity fields and photometric variations depend only on the
stellar magnetic latitude and longitude.
We have constructed the echelle-diagram for p-mode spectrum of
HR 1217, we give a new, simple interpretation of the peculiar
spacing of ![]() as being related to l = 4 modes. We predict
the existence of another sequence of modes, yet undetected, that should
be equally spaced by 68
as being related to l = 4 modes. We predict
the existence of another sequence of modes, yet undetected, that should
be equally spaced by 68 ![]() Hz or 34
Hz or 34 ![]() Hz with respect to f7.
Hz with respect to f7.
Acknowledgements
D.E.M. acknowledges his work as a part of research activity of the Astrophysical Research Center for the Structure and Evolution of the Cosmos (ARCSEC) which is supported by the Korean Science and Engineering Foundation. D.E.M. is grateful to Alfred Gautschy for making available his models of roAp star and useful discussions. Part of this work was done under the US Civilian Research and Development Foundation (CRDF) grant UP2-317 and a grant by the German Academic Exchange Service (DAAD). A.P.H. acknowledges the support of grant 50OW0204 from the Deutsches Zentrum für Luft- und Raumfahrt e.V. (DLR).