A&A 429, L41-L45 (2005)
DOI: 10.1051/0004-6361:200400102

Gamma-ray bursts and other sources of giant lightning discharges in protoplanetary systems

B. McBreen1 - E. Winston1 - S. McBreen2 - L. Hanlon1


1 - Department of Experimental Physics, University College, Dublin 4, Ireland
2 - Astrophysics Missions Division, Research Scientific Support Department of ESA, ESTEC, Noordwijk, The Netherlands

Received 23 June 2004 / Accepted 6 November 2004

Abstract
Lightning in the solar nebula is considered to be one of the probable sources for producing the chondrules that are found in meteorites. Gamma-ray bursts (GRBs) provide a large flux of $\gamma $-rays that Compton scatter and create a charge separation in the gas because the electrons are displaced from the positive ions. The electric field easily exceeds the breakdown value of $\approx$1 V m-1 over distances of order 0.1 AU. The energy in a giant lightning discharge exceeds a terrestrial lightning flash by a factor of $\sim$1012. The predicted post-burst emission of $\gamma $-rays from accretion into the newly formed black hole or spin-down of the magnetar is sufficiently intense to cause a lightning storm in the nebula that lasts for days and is more probable than the GRB because the radiation is beamed into a larger solid angle. The giant outbursts from nearby soft gamma-ray repeater sources (SGRs) are also capable of causing giant lightning discharges. The total amount of chondrules produced is in reasonable agreement with the observations of meteorites. Furthermore in the case of GRBs most chondrules were produced in a few major melting events by nearby GRBs and lightning occurred at effectively the same time over the whole nebula, and provide accurate time markers to the formation of chondrules and evolution of the solar nebula. This model provides a reasonable explanation for the delay between the formation of calcium aluminium inclusions (CAIs) and chondrules.

Key words: gamma rays: bursts - solar system: formation - planetary systems: protoplanetary disks - planetary systems: formation

1 Introduction

Chondrules are typically millimetre-sized stony spherules that constitute the major component of most chondritic meteorites that originate in the region between Mars and Jupiter and which fall to Earth. They appear to have crystallised rapidly from free floating molten or partially molten drops. The large amount of chondrules present in chondritic meteorites and their possible crucial role in planet formation, highlights the importance of identifying the mechanism responsible for their formation. The heat source responsible for melting chondrules remains uncertain and proposed processes have been recently reviewed by Boss (1996) and Rubin (2000). One of the earliest proposals for the formation of chondrules is lightning caused by turbulence in the solar nebula (Whipple 1966; Cameron 1966). Lightning is a widespread phenomenon that is not restricted to terrestrial rainclouds (Uman 1987). Spacecraft have detected lightning on Jupiter and other planets. This model is not favoured for chondrule production for a number of reasons including the limitation to the build up of a large electrostatic potential by the gas conductivity, the breakdown potential of the gas and the available energy source (Desch & Cuzzi 2000; Gibbard et al. 1997; Eisenhour & Buseck 1995; Pilipp et al. 1998; Weidenschilling 1997; Love et al. 1995). It has also been pointed out that, if lightning were the mechanism responsible for chondrule formation, it would have to operate on a large scale comparable in size with the whole nebula (Pilipp et al. 1992).
Almost all the proposed heat sources are local to the solar nebula. One exception is that the precursor grains near the surface of the nebula were melted when they efficiently absorbed X-rays and $\gamma $-rays from a nearby GRB (McBreen & Hanlon 1999). This mechanism can produce a large amount of chondrules in the nebula ($\sim$30 Earth masses) but it has a low probability of occurrence (<0.1$\%$). X-ray melting of material has recently been demonstrated in the laboratory for the first time using a powerful synchrotron (Duggan et al. 2003,2002). The model of the X-ray melting of material by a GRB did not include lightning caused by Compton scattering of $\gamma $-rays by the gas in the nebula or the $\gamma $-rays from post-burst emission. The effect of this new process is to induce giant lightning discharges over the whole nebula.


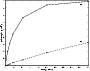 \begin{figure} \par\resizebox{8cm}{!}{\includegraphics{Gf232_f1.eps}} \par\end{figure} Figure 1: The path length of $\gamma $-rays a) and range of electrons b) as a function of energy in molecular hydrogen. The $\gamma $-ray data is taken from the compilation of Cullen et al. (1989) and the electron data from Berger & Seltzer (1964).
Open with DEXTER

2 Absorption of $\gamma $-rays in the nebula

The absorption of $\gamma $-rays in a gas with solar abundance is dominated by molecular hydrogen and it is sufficiently accurate here to consider only the absorption by H2. Compton scattering is the dominant process in H2 up to 70 MeV above which pair production and trident production overtake Compton scattering and only 27% of $\gamma $-rays with energy of 170 MeV and 5% at 1 GeV undergo Compton scattering. For $\gamma $-rays with energy above a few MeV, the kinematics of Compton scattering are such that most of the energy is taken by the electron, which is scattered in the forward direction. An incoming pulse of $\gamma $-rays in H2 is gradually transformed into electrons that move further into the nebula leaving a cloud of positive charge in its wake. Here we do not consider the scattered photons that also tend to move in the forward direction. The attenuation length of $\gamma $-rays and range of electrons in H2 is given in Fig. 1; the range of the latter in H2 is less than $\gamma $-rays with the same energy. As the energy increases, the range of the electrons become an increasing fraction of the $\gamma $-ray Compton attenuation length, thus facilitating a larger charge separation. This process has similarities to nuclear explosions in the atmosphere (Longmire 1978).

A charge separation will also occur with pair production because some positrons annihilate in flight creating a moving excess of negative charge that leaves behind a positive excess in the gas (Askaryan 1962; Jelley et al. 1966). The cross-section for positron annihilation is about 1 Barn/$\Gamma$ where $\Gamma = E/m_{0}c^{2}$. About 10% of the positrons with energy E = 400 MeV will annihilate in flight.

 \begin{figure} \resizebox{8.8cm}{!}{\includegraphics[clip]{Gf232_f2.eps}} \end{figure} Figure 2: The surface density, $\Sigma $, as a function of height above the midplane, H, in astronomical units (AUs) for two models with normalising values, $\Sigma _{0}$ and exponent n, with $\Sigma _{0} = 4250$ g cm-2 and n = -1.0 (solid line) and $\Sigma _{0} = 1700$ g cm-2 and n = -1.5 (dashed line)and for three radial distances of a) 1 AU, b) 3 AU and c) 5 AU. The diamonds and squares give path lengths of 150 and 300 g cm-2measured from the top of the nebula.
Open with DEXTER

In order to make progress with charge separation it is necessary to adopt a model of the nebula. There is a reasonably well developed theory of the solar nebula including the formation of terrestrial and gas giant planets. The discoveries of extrasolar planets and disks orbiting young stars are leading to the characterisation of protoplanetary disks around young stars. In most models of the solar nebula, after the early evolution of the Sun, accretion slows down and the nebula becomes essentially quiescent. We adopt the power law relationship for the surface density $\Sigma $ of the solar nebula as a function of radial distance r from the Sun given by

 \begin{displaymath}\Sigma = \Sigma_{0} [r/1~{\rm AU}]^{n} \end{displaymath} (1)

where $\Sigma _{0}$ has the normalising value of 4250 g cm-2at 1.0 AU and exponent n is -1.0 (Cameron 1995). The choice of $\Sigma _{0}$ and n varies between the models of the solar nebula. Hayashi et al. (1985) proposed $\Sigma _{0}$ = 1700 and n = -1.5 in the minimum-mass model of the solar nebula and these values are consistent with minimum-mass models of extrasolar nebula (Kuchner 2004).

In conventional models it is usually assumed that lightning occurs in the dusty midplane of the nebula (Horanyi et al. 1995; Love et al. 1995). However a GRB will preferentially interact with the outer region of the nebula that is in the direction of the GRB source. Therefore it is necessary to model the vertical structure of the nebula to obtain the surface density perpendicular to the midplane.

In the thin disk approximation the midplane isothermal pressure is given by (Cameron 1995)

 \begin{displaymath}P_{\rm c} = 0.25 ~ \Sigma ~ \Omega ~ c_{\rm s} \end{displaymath} (2)

where $c_{\rm s}$ is the speed of sound and $\Omega =(GM/r^{3})^{\frac{1}{2}}$ is the Keplerian angular velocity and M is the mass of the Sun. The vertical structure of the disk is given by

 \begin{displaymath}\rho = \rho_{0} ~ \exp (-z^{2}/H^{2}) \end{displaymath} (3)

where z is the vertical distance from the midplane. $\rho_{0}$and H are the density at the midplane and scale height of the nebula and are given by $\rho_{0} = 2.44 P_{\rm c}(NkT)^{-1}$ and $H = \pi c_{\rm s} (2 \Omega)^{-1}$ respectively where N is Avogadros number and k is the Boltzmann constant.

The surface density profile perpendicular to the midplane is plotted in Fig. 2 for r = 1, 3 and 5 AU using the two models. The surface density is reasonably constant in the midplane region and drops by only a factor of 2.7 in the first scale height and by the larger factor of 20 in the second scale height. Approaching the nebula from above the midplane, a path length of 300 g cm-2will reach the midplane at 5 AU, and 0.1 AU above the midplane at 3 AU using the minimum mass model (Figs. 2c and 2b).

3 Prompt GRB emission and charge separation

The rate of GRBs when averaged over the Hubble volume is $\sim$4 $\times$ 10-7 yr-1 galaxy-1 (Zhang & Meszaros 2004). The local GRB rate is smaller due to the drastic decrease in star formation at low redshifts and a value of 0.25 $\times$ 10-7yr-1 galaxy-1 is widely used at z = 0. We adopt a value of 10-7 yr-1 galaxy-1 for the GRB rate and $\sim$107 years for the lifetime of a protoplanetary disk. Hence there is a probability near 100% that any protoplanetary system will be irradiated by a GRB. The isotropic equivalent energy of GRBs is in the range 5 $\times$ 1051 to greater then 1054 erg. A GRB with an output of 1052 erg will deliver $\sim$106 erg cm-2 to a protoplanetary system that lies at a distance equal to a galactic radius of 10 kpc. The high energy emission extends to well above 100 MeV with a spectrum compatible with an extension of the electron synchrotron component (Dingus 2001). An anomalous radiation component in the energy band between $\sim$1-200 MeV was discovered in GRB 941017 (González et al. 2003). This component varies independently of the prompt GRB emission from 50 keV-1 MeV and contains three times more energy.

To model the charge separation and electric field in the nebula, we adopt a GRB that gives 106 erg cm-2 with 10% of the energy between 20 MeV and 100 MeV, which is assumed to be in 65 MeV $\gamma $-rays that yield Compton scattered electrons with energy of 50 MeV. The incident flux of $\gamma $-rays is $\approx$1013 photons m-2 and is attenuated exponentially in H2 using a mass absorption co-efficient of $\mu = 1.33 \times 10^{-2}$ cm2 g-1 (Fig. 3a (i)). The positive charge also declines exponentially in the same way because each Compton event creates a positive ion. The electrons travel on average an additional 10 g cm-2 into the nebula including only the ionization loss (Fig. 3a (ii)). The path length is further reduced by a retarding electric field of 1 V m-1 which is typical of the breakdown value (Fig. 3a (iii)). The charge excess is the difference between the two distributions (Fig. 3b). The net positive charge is confined to a layer of thickness 10 g cm-2 whereas the negative charge is distributed over a much wider range. The net positive or negative charge is 11% and has a value of $q \approx 10^{-7}$ C m-2. Two percent of the net negative charge is beyond 300 g cm2 and penetrates deeply into the nebula.

  \begin{figure} \par\includegraphics[width=8.5cm,clip]{Gf232_f3.eps}\par\end{figure} Figure 3: a) The number of $\gamma $-rays that Compton scatter and and the number of positive ions as a function of path length in H2 for an incident flux of 1013 photons m-2 (i). The number of electrons as a function of path length taking into account the ionization loss of 10 g cm-2 (ii) and also including a retarding electric field of 1 V m-1 (iii). b) The charge excess as a function of path length for the ionization loss (solid line) and also including the retarding electric field (broken line). The model used is for r = 3 AU and $\Sigma _{0} = 4250$ g cm-2 with n = -1.0.
Open with DEXTER

Electrical breakdown occurs when a normally insulating gas suddenly becomes conducting in a strong electric field. The gas pressure is particularly important because lower pressure reduces the voltage necessary for the discharge and increases the width of the discharge channel. Breakdown occurs when the electric field is strong enough that a free electron accumulates $\sim$1 eV of energy between successive collisions with gas molecules (Pilipp et al. 1992). This condition is given by $eE_{\rm s}(n\sigma)^{-1} \approx 1$ eV where $E_{\rm s}$ is the discharge electric field, n is the number density of gas molecules and $\sigma \sim 10^{-15}$ cm-2 is the collision cross section. $E_{\rm s}$ has a value of $\sim$ $2.4 \times 10^{6}$ V m-1 for air and $\sim$ $2.0 \times 10^{6}$ V m-1 for H2 at atmospheric pressure (Love et al. 1995). The measured value of $E_{\rm s}$ in thunderstorms is about a factor of 10 lower and this difference is often attributed to energetic runaway electrons from cosmic rays or radionuclides that prematurely trigger the discharge (Gurevich et al. 2001). The value of $E_{\rm s}$ scales with pressure and has a value of 20 V m-1 to 1 V m-1 at pressures between 10-5 and 5 $\times$10-7 of atmospheric pressure, typical of disks in planetary forming systems. $E_{\rm s}$ could have a higher value in dust loaded regions near the midplane (Gibbard et al. 1997). The Compton scattered electrons produce ions and electrons that increase the conductivity of the gas above that caused by cosmic rays and radionuclides (Desch & Cuzzi 2000; Love et al. 1995). The large scale and rapid formation of the charge separation prevents significant discharging by the gas conductivity.

The charge separation described in the nebula is analogous to a capacitor. The basic equation for a parallel plate capacitor yields the potential difference $V = qd(\epsilon_{\rm o})^{-1}$between the plates separated by a distance d. V attains a value of 1014 V for q = 10-7 C m-2 and a representative value of d = 0.1 AU. The electric field is $\sim$104 V m-1 and greatly exceeds $E_{\rm s}$ by a factor of at least 103 even for a GRB at a distance 10 kpc and $\sim$40 for a similar GRB at the distance to the Large Magellanic Cloud. As the GRB interacts with the nebula, the charge separation creates a strong electric field that exceeds $E_{\rm s}$ and triggers the discharge (Dwyer 2003). The duration of the discharge is estimated at 100 s (Pilipp et al. 1992). The average current in the channel is $\sim$1011 A if half of the excess charge from an area  $\sim d^{2}$ flows down the channel in 100 s. The width of the lightning channel depends on the gas pressure and has an estimated value of $\sim$105 cm assuming it is limited to a few thousand electron mean free paths (Pilipp et al. 1992).

The total energy in $\gamma $-rays, over an area comparable in size to the charge separation of 0.1 AU, gives an upper limit of 1029 erg to the energy dissipated in the channel and this exceeds a large terrestrial lightning flash by $\sim$1012. We cannot exclude the possibility of repeated strikes over the lightning channel, a situation that is somewhat analogous to the stepped leaders and return strokes in terrestrial lightning. Furthermore there is the possibility that the lightning may fragment into many channels (Uman 1987). The visible and ultraviolet radiation from the discharge heats and melts the precursor grains to form chondrules out to a distance of $\sim$109 cm from the discharge channel. The total amount of chondrules produced in the nebula within a radius of 5 AU is 5 $\times$ 1020 g assuming a GRB with 106 erg cm-2has 105 erg cm-2 in 65 MeV $\gamma $-rays, 2 $\times$1010 erg g-1 to heat and melt the precursor dustballs and an efficiency of 10-2 to convert the $\gamma $-ray energy to chondrules (Jones et al. 2000). The amount of chondrules produced is too small to account for the total mass of $\sim$ $3\times 10^{24}$ g in the asteroid belt and the value of $\sim$1027 g when the asteroid belt was 300 times larger than at present. The mass of chondrules can be increased by 3 $\times$104 to 1.5 $\times$ 1025 g for a GRB at a distance of 300 pc ($\times$103) with a higher isotropic luminosity of 1053 erg ($\times$10) and an anomalous MeV component as observed in GRB 941017 ($\times$3). This model is not sufficient because there is evidence from compound chondrules (Wasson 1993) and compositional gradients in chondrules (Wasson & Rubin 2003) that they were melted several times requiring a repeating process.

4 GRB post-burst emission and other sources

The afterglow continues for days and weeks after the GRB when the relativistic blast wave decelerates by sweeping up the external medium. Anomalies in the afterglow of some GRBs including the detection of GeV $\gamma $-rays that lasted for over 90 min after GRB 940217 (Hurley et al. 1994) can be accounted for by post-burst emission. After the GRB there could be a more extended period in which energy is injected into the remnant. This activity may be caused by continued drainage of matter left over from the explosion into the newly formed black hole or the spin-down of a super-pulsar or magnetar (Rees et al. 2000). The $\gamma $-ray post-burst emission has not been measured and we must rely on model computations (Ramirez-Ruiz 2004). The relativistic outflow from a super-pulsar interacts with photons from a binary companion or from the explosion. The emission is mostly in $\gamma $-rays and estimated at 1048 erg s-1immediately after the GRB that declines to 1047 erg s-1after 10 h and 1045 erg s-1 after 100 h. The emission is beamed into a large solid angle that is not well constrained by the model and we estimate it covers 10-1 of the sky. The prompt GRB fireball emission is collimated into a much smaller angle that is estimated on average to be 2 $\times$10-3 of the sky (Frail et al. 2001). The nebula is 50 times more likely to be irradiated by post-burst emission than by the GRB.

The model of GRB emission is not unique and in the case of a structured jet, where the energy density per unit solid angle falls away from the axis, the emission is beamed into a larger solid angle by a factor of about 5 (Zhang & Meszaros 2004). In this case the post-burst emission is ten times more likely to impinge on the nebula than the GRB. The post-burst emission of up to 1052 erg in $\gamma $-rays is sufficiently intense to cause a major lightning storm in the disk that lasts for days or even weeks and up to 50 such events may occur over the lifetime of the disk. These fifty events, occurring at a distance of 10 kpc, will produce 5 $\times$ 1023 g of chondrules assuming an efficiency of 10-2 for conversion of $\gamma $-ray energy to chondrules. The largest mass of chondrules is produced by the post-burst emission from the nearest GRB; a burst 100 pc distant will produce 1026 g within a radius of 5 AU in a disk. Strong dependence on the distance between the GRB and the protoplanetary disk results in a wide range in the mass of chondrules produced. In the above estimates we have assumed that the charge separation is not removed by the conductivity provided by the ions and electrons produced by the Compton scattered electrons, cosmic-rays and radionuclides. This will only be correct if the post burst emission is in short duration outbursts like the GRB emission. The post-burst emission is more likely to be highly variable in the case of continued and sporadic accretion into the newly formed Kerr black hole (McBreen et al. 2002).

Soft gamma-ray repeaters (SGRs) are also a possible source of lightning in the nebula. The energy that drives the giant flares (>1044 erg) such as the 1979 March 5 event from SNR N49 may be caused by a sudden large scale arrangement of the magnetic field which releases magnetic energy (Thompson & Duncan 1996). The extreme possibility is that the entire dipole moment is destroyed in a single event releasing $\sim$1047 erg (Eichler 2002). The rate of such events could be as high as the rate of magnetar production $\sim 10^{-3}$ yr-1 and $\sim$104 such events could occur over the lifetime of the nebula. About 10 to 100 of these SGR explosions should be close enough to generate lightning in the disk and each one produce a small amount of chondrules, but the overall contribution of SGRs is much smaller than that of GRBs.

Other nearby and less variable $\gamma $-ray sources such as quasars, microquasars and powerful X-ray binaries (Mirabel & Rodriguez 1999) might be expected to generate charge separation and lightning. They require a much longer time of $\sim$105 s to generate an electric field that can exceed $E_{\rm s}$, but the gas conductivity may limit the electric field to below this value. There is sufficient energy in these sources to produce large amounts of chondrules provided a method is found to limit the gas conductivity. The same limitation has been noted in other models of charge separation and lightning in the protoplanetary disk (Desch & Cuzzi 2000; Gibbard et al. 1997; Love et al. 1995).

5 Discussion

GRBs and other sources are capable of producing significant quantities of chondrules in protoplanetary systems anywhere in the disk of a galaxy. Stars form in giant molecular clouds of size about 100 pc and hence there is a higher than average probability it will contain massive stars that produce GRBs and SGRs and irradiate protoplanetary systems in the same cloud to form large amounts of chondrules.

Compound chondrules consist of a primary that solidified first and one or more secondaries attached to the primary (Wasson & Rubin 2003; Wasson 1993). Sibling compound chondrules have very similar textures and compositions and most, perhaps all, consist of chondrules melted in the same event. If this event is identified with a nearby GRB, the chondrules would have been produced all across the disk and should provide a simultaneous time marker between sibling chondrules in different meteorites. If the chondrules were produced by GRBs, the differences between the composition of meteorites are due to compositionally segmented regions of the nebula. The independent compound chondrules probably were produced in two separate events and it may be possible to determine the order and frequency of the GRB events from the meteorite record.

The magneto-rotational instability (MRI) provides an understanding of radial mixing and turbulence in the disk (Balbus & Hawley 1998). Turbulence can concentrate dust particles of a particular size to spatial densities well above their background values (Wood 1997; Cuzzi et al. 2001). A large amount of chondrules can then be produced by lightning and provide an explanation for the large quantity of compound chondrules in meteorites. The magnetic field in the nebula must be well coupled to matter for MRI to be effective and this condition was satisfied close to the Sun and beyond 10 AU where cosmic ray ionization may suffice to maintain a significant amount of ionization. The magnetic field during chondrule formation is not well constrained by the meteoritic evidence and seems to have a value between 1 and 10 Gauss (Jones et al. 2000; Sugiura et al. 1979). A magnetic field of this magnitude is significant because it would channel Compton scattered electrons into regions of enhanced magnetic field, such as MRIs, and possibly cause lightning between regions in the disk which is analogous to cloud to cloud lightning in the Earth's atmosphere.

The 26Al/27Al ratio of CAIs in meteorites has a value of 5 $\times$ 10-5 whereas in chondrules the ratio has a much smaller value (Cameron 1995; Jones et al. 2000). The simplest explanation is that there was an interval of at least a million years between the formation of CAIs and chondrules. Chondrules should have formed preferentially late in the development of the disk after the Sun had stripped away most of the gas and allowed the $\gamma $-rays to penetrate closer to the midplane. This effect is more important in models of the disk with more than the minimum mass as shown in Fig. 2. The penetration of the disk by $\gamma $-rays is easier beyond the snowline at about 5 AU because the disk is less massive. Chondrules produced beyond about 5 AU may have formed earlier and hence could contain 26Al.

GRBs in the galaxy affect the Earths atmosphere (Kurt & Zaidel 1996; Thorsett 1995; Scalo & Wheeler 2002) and these events may be responsible for mass extinctions (Thomas et al. 2004; Melott et al. 2004; Dar et al. 1998). Fortunately the rate of GRBs is very low in our galaxy. However a GRB can reveal protoplanetary systems in other galaxies by transient infrared emission from the melting chondrules and optical emission from the gas (McBreen & Hanlon 1999; Duggan et al. 2003). These events may be detectable for hundreds of years after the GRB when the expanding shell or cones of radiation interacts with protoplanetary systems.

References

 
Copyright ESO 2005