A&A 429, 1081-1092 (2005)
DOI: 10.1051/0004-6361:20041706
G. J. D. Petrie1,![]() -
K. Tsinganos
1 -
T. Neukirch
2
-
K. Tsinganos
1 -
T. Neukirch
2
1 - IASA and Section of Astrophysics, Astronomy and Mechanics,
Department
of Physics, University of Athens, Panepistimiopolis, 157 84 Zografos,
Athens, Greece
2 -
School of Mathematical and Computational Sciences,
University of St. Andrews, St. Andrews, KY16 9SS, Scotland, UK
Received 21 July 2004 / Accepted 9 September 2004
Abstract
An exact two-dimensional solution of the ideal magnetohydrodynamic (MHD) equations
with compressible flow in a uniform gravitational field is presented and applied to
solar prominences.
The solution is constructed via a systematic nonlinear separation of variables
method used to calculate several classes of MHD equilibria in Cartesian
geometry and uniform gravity. This simple model of steady plasma flow along the
dipped field lines of a solar prominence is the first 2D MHD model with a nonisothermal
temperature distribution which selfconsistently also examines the required heating.
Although the model is 2D, a third magnetic/velocity vector field component is
included and the highly sheared fields observed in prominences are reproduced.
A description is given of the balance of gas pressure gradient, gravity, Lorentz
and inertial forces acting along and across the prominence. It is found that the
flow may significantly influence the energy balance as in a similar application of this class of solutions to solar coronal
loops.
Key words: magnetohydrodynamics (MHD) - methods: analytical - Sun: corona - Sun: magnetic fields - Sun: filaments
Initially solar prominences (Priest 1989; Tandberg-Hanssen 1995, and references therein) were regarded as cool objects in hydrostatic equilibrium with the surrounding hot corona. However, soon it was realized that prominences require a support mechanism of the dense material against the solar gravitational field, some heating mechanism to compensate for their radiative cooling and a study of their observed mass motions. The first to argue that coronal magnetic fields could support prominences in static equilibrium were Bhatnagar et al. (1951), followed by other studies by Dungey (1953), Kippenhahn & Schlüter (1957), Brown (1958), Anzer (1972), Kuperus & Raadu (1974), Lerche & Low (1977), Anzer & Priest (1985), Hood & Anzer (1990), Low & Hundhausen (1995) and Low & Zhang (2004). In all these 1D or 2D magnetohydrostatic models the dense prominence material is supported against gravity mainly by the Lorentz force. Hence, because of the mathematical complexity of the full 3D magnetohydrostatic equations most modelling of prominence dynamics is 2D. However, important exact 3D magnetohydrostatic prominence models have also been calculated by Low (1982, 1984, 1992).
In 2D a prominence can be idealised as a flat vertical sheet of plasma embedded in a helically-structured configuration, a flux rope (Low & Hundhausen 1995; Low 2001; Low & Zhang 2004), embedded in a supporting magnetic structure. There are two basic kinds of magnetic configuration believed to support prominences in general, both readily modelled in 2D: the normal and inverse configurations (Tandberg-Hanssen 1995; Low & Hundhausen 1995; Low & Zhang 2004). Prominences are thus categorised according to whether the magnetic field threads the prominence in the same sense as the overarching arcade (normal configuration, Fig. 1, top left picture) or in the opposite sense (inverse configuration, Fig. 1, top right picture). The flux rope is represented by the closed curves in the profile views of the top pictures and its 3D structure is shown in the bottom picture, where a strong axial component parallel to the long axis of the prominence, usually found in observations (Leroy et al. 1984; Bommier et al. 1994), is shown. This sketch of the 2D spiralling field of a flux rope idealises long 3D spiralling field configurations which are anchored to the photosphere at each end. The flux rope is believed to be thermally isolated from the larger corona (Low 2001) by low cross-field thermal conductivity (Spitzer 1962) so that prominence temperatures of around 7000 K (Tandberg-Hanssen 1995) can be maintained in a corona of temperature around 1 MK.
![\begin{figure}
\par\includegraphics[width=7.15cm,clip]{1706normal.eps}\hspace*{1...
...ace*{1.8cm}\includegraphics[width=9.6cm,clip]{1706fluxrope.eps} }\end{figure}](/articles/aa/full/2005/03/aa1706/Timg6.gif) |
Figure 1: The two basic prominence types: the normal configuration ( top left picture) and the inverse configuration ( top right picture). The prominence is represented by the thick vertical line in each sketch, supported against gravity by the magnetic tension force of the concave upward lines of magnetic force in the lower half of the flux rope (closed curves in each of the two sketches). The flux rope is shown as a shaded sheet of dense plasma embedded in a flux rope in a 3D perspective sketch ( bottom picture) which shows the strong axial component of the magnetic field, the component parallel to the long axis of the prominence. |
| Open with DEXTER | |
The role of the observed (modest) plasma flows in prominences has received a rather limited theoretical attention, although flows in prominences have been observed already for a long time now (Athay et al. 1983; Engvold et al. 1985; Zirker et al. 1994). Thus, full steady MHD prominence models have rarely been attempted in the past. In an effort to investigate the effect of flows along the supporting prominence magnetic field lines, Tsinganos & Surlantzis (1992) analysed an exact polytropic 1D MHD solution in uniform gravity, which is an extension of the Kippenhahn & Schlüter (1957) model with compressible steady flows. The first study of 2D compressible steady MHD flows in Cartesian geometry was carried out by Tsinganos et al. (1993) who modelled planar coronal loops. Based on the theory from this paper, Del Zanna & Hood (1996) constructed a 2D MHD model of a prominence by matching (dynamically but not energetically) two isothermal regions modelling the hot corona and the cool prominence and extending the polarity prominence model of Hood & Anzer (1990). They also incorporated magnetic shear into their model by including a third magnetic (and velocity) field component. The MHD modelling of loops and prominences has developed in such an interconnected way because, although their geometrical structure and typical plasma parameter values are very different, they are both long-lived magnetic structures whose equilibrium states are described to zeroth order by the same MHD equations and they can both be modelled in Cartesian translational symmetry. However, in the models by Tsinganos & Surlantzis (1992), Tsinganos et al. (1993) and Del Zanna & Hood (1996) the emphasis is not on the interwoven interaction of plasma flows, prominence support and energetics. Petrie et al. (2002, hereafter Paper I) extended the Tsinganos et al. (1993) loop modelling technique to include non-isothermal temperatures, trans-Alfvénic flows and greater flexibility by developing a systematic solution construction method for 2D MHD modeling in Cartesian symmetry. Petrie et al. (2003, hereafter Paper II) further developed and refined this loop model by fitting example models to observational data sets and by adding a fully consistent model of the energetics. This allowed a combined study of the dynamics and energetics of coronal loops for the first time. In the present paper we present the first combined study of this type for prominences.
As well as support against gravity, or the effect of flows, the energy balance within a prominence is of great interest. The energy balance in prominences has been modelled using radiative transfer theory by many authors, e.g. Anzer & Heinzel (2000) and references therein. Both the dynamics and the energetics of prominences are crucial aspects to elucidate if the physics of prominences is to be understood. Both aspects remain poorly understood and, while it is widely acknowledged that the dynamical and energetic properties are likely to be highly interdependent, the separate challenges of modelling the dynamics and the energetics remain formidable in their own right. A combined study of the full steady MHD momentum balance and energetics of a prominence has never been achieved.
In the present paper we offer an extension of the dynamical (or static) studies by Bhatnagar et al. (1951), Kippenhahn & Schlüter (1957) and Brown (1958) as well as those by Tsinganos & Surlantzis (1992) and Del Zanna & Hood (1996) by including MHD flows in a nonisothermal atmosphere. We will focus on the basic macroscopic structure of a 2D MHD prominence. Petrie & Neukirch (1999) give a method for calculating 3D MHD equilibria with steady flow but the resulting solutions are incompressible and exclude gravity. While these are applicable to small loops and sunspots, for prominences (and coronal loops) we need compressibility and gravity because of the length scales involved. Since the full 3D MHD equations with compressibility and gravity are not amenable to analytical treatment we concentrate on modelling in 2D exploiting solutions calculated by the general method in Paper I, which allows us to include a third magnetic/velocity vector component. In a subsection we also use a simple a posteriori calculation of the energetics to check whether or not these flows might influence the heating as such flows do in coronal loops (Paper II). Our paper is thus organised as follows. The analytical modelling technique is outlined in Sect. 2. A model fitted to typical observed physical parameter values is presented in Sect. 3 and the results are briefly summarised in Sect. 4.
The dynamics of steady flows in solar atmospheric structures may be
described to zeroth order by the well known set of steady
(
![]() )
ideal hydromagnetic equations:
)
ideal hydromagnetic equations:
We represent ![]() by using a magnetic flux function
(per unit length in the
by using a magnetic flux function
(per unit length in the
![]() direction)
direction)
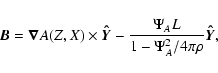 |
(3) |
where ![]() and L(A) are two of the familiar free integrals
(arbitrary functions of A) of the MHD equations (Tsinganos 1981). In fact, in our case with field-aligned flow
and L(A) are two of the familiar free integrals
(arbitrary functions of A) of the MHD equations (Tsinganos 1981). In fact, in our case with field-aligned flow
![]() is the ratio of the mass and magnetic fluxes,
is the ratio of the mass and magnetic fluxes,
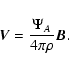 |
(4) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1706selfsim.ps}
\end{figure}](/articles/aa/full/2005/03/aa1706/Timg21.gif) |
Figure 2:
Illustration of the x-self-similarity of the solution:
two field lines defined by
|
| Open with DEXTER | |
![\begin{displaymath}{\vec B}= B_0 \alpha {\cal A}^{'}(\alpha) \left[{\vec{\hat{X}}}+F(x)
{\vec{\hat{Z}}}\right],
\end{displaymath}](/articles/aa/full/2005/03/aa1706/img25.gif) |
(7) |
It can be seen from Eq. (9) and Fig. 2 that two field lines defined by
![]() and
and
![]() differ from each other only by a vertical
translation, and that for any point (Z1 ,X) on the first field line,
the corresponding point on the second field line (Z2 ,X) can be found
from it by moving vertically a distance,
differ from each other only by a vertical
translation, and that for any point (Z1 ,X) on the first field line,
the corresponding point on the second field line (Z2 ,X) can be found
from it by moving vertically a distance,
Including a Y-component in the model we have found that the following
judicious choice of the free integrals
![]() and
and
![]() ,
,
Note that although these solutions are invariant in Y the inclusion of a Y-component in the model allows us to model the sheared magnetic and velocity fields which characterise prominences.
In the expression for the pressure Eq. (16) P0 = constant, while P1 and P2 satisfy the following two ODE's
| P1(x) | = | ||
| P2(x) | = | ||
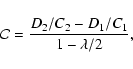 |
(23) |
By integrating this set of ODE's we obtain a complete solution. Note that this model belongs to the first family in Table 1 of Paper I generalising the models by Hood & Anzer (1990) and Del Zanna & Hood (1996), but not the models by Kippenhahn & Schlüter (1957) and Tsinganos & Surlantzis (1992) which are from the second family. For the first time, however, our solutions are non-adiabatic and non-isothermal so that a simple study of the effect of the flow on the thermodynamics of our solutions will be possible.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1706perline.eps}\hspace*{4mm}
\includegraphics[width=7.8cm,clip]{1706perlinebig.eps}
\end{figure}](/articles/aa/full/2005/03/aa1706/Timg69.gif) |
Figure 3:
Selection of periodic solutions. The right picture shows the same solutions as the left picture with the X-axis magnified. The solid line is
a solution whose physical parameter values at the bottom of each dip are as
follows: the temperature is 8000 K, the velocity is 10 km s-1, the magnetic
field strength is 2 G and the gas density is
|
| Open with DEXTER | |
Brown (1958) was able to describe analytically the distinction between the periodic and non-periodic cases in the solutions in the first magnetyhydrostatic model of Bhatnagar et al. (1951). For these one-dimensional solutions the second-order ODE for G(x) may be integrated to give solution curves in the G(x),F(x)=G'(x) phase space. Closed phase curves correspond to periodic solutions and open curves to non-periodic solutions. In our more general case such an explicit description is not possible. However it can be seen that if part of our expression for F'(x) has a single sign and dominates the expression, then F'(x) does not change sign and the solution is non-periodic. This depends on the relative size of the functions C1 (F2+1), D1/M2 and P1. If any of these quantities dominates in Eq. (20) for F'(x) then we have a single loop/dip. If two or three of these quantities are comparable then we may have periodically fluctuating parameters and a periodic solution. In our prominence case the dominant quantity is D1/M2, associated with the very large density. This causes F'(x) to be strictly positive and we have a dip, a field line which is concave upwards. A large decrease in density and increase in temperature would result in a dominant pressure function, strictly negative F'(x) and a loop/arcade solution as in Papers I and II. In the specific examples in Papers I and II the quantity D1/M2 that dominates but a combination of C1 (F2+1) and P1 in Paper I and P1 alone in the high-temperature, sub-Alfvénic examples of Paper II. If, however, C1 (F2+1) is much larger than D1/M2 and P1 we have a flow-dominated solution and negative F'(x). An arcade solution resembling the shape of a projectile's trajectory in uniform gravity results as pointed out by Tsinganos & Surlantzis (1992). The Kippenhahn & Schlüter (1957) case is the one where the density's influence is much larger than that of the flow, i.e. C1 (F2+1)/(D1/M2) < 1 so that D1/M2 dominates, F'(x) is positive and we have a dip.
Figure 3 shows a selection of periodic solutions. The solid line is
a solution whose physical parameter values at the bottom of each dip are as
follows: the temperature is 8000 K, the velocity is 10 km s-1, the magnetic
field strength is 2 G and the gas density is
![]() g/cm3.
This solution is clearly periodic with period about 10 Mm. The dotted line
is a solution with dip parameter values equal to those of the solid line
except that the magnetic field strength is only 1 G. The dashed line is a
solution with dip parameter values equal to those of the solid line except
that the velocity is 20 km s-1. Both the fast solution and the solution with
weak magnetic field have larger periods than
the first solution because the fluid does not change direction so much, either
because the inertial force is large in the case of the fast solution or
because the inertial force has less effective opposition in the case of the
solution with weak magnetic field. The solution with weak magnetic field has
a smaller amplitude than the other two because the weaker magnetic field does
not deviate the fluid as far from a straight path.
g/cm3.
This solution is clearly periodic with period about 10 Mm. The dotted line
is a solution with dip parameter values equal to those of the solid line
except that the magnetic field strength is only 1 G. The dashed line is a
solution with dip parameter values equal to those of the solid line except
that the velocity is 20 km s-1. Both the fast solution and the solution with
weak magnetic field have larger periods than
the first solution because the fluid does not change direction so much, either
because the inertial force is large in the case of the fast solution or
because the inertial force has less effective opposition in the case of the
solution with weak magnetic field. The solution with weak magnetic field has
a smaller amplitude than the other two because the weaker magnetic field does
not deviate the fluid as far from a straight path.
Of course in reality prominence structure is not periodic. We discuss now the models
that we calculate to reproduce observed features of prominences. We still
use periodic solutions but we model prominence dips using the lower part of a
single period.
From measurements of all four Stokes parameters and the Hanle effect the
magnetic vector field can be determined. A representative value for the field
strength is 8 G for quiescent prominences and 20 G for active region filaments
(Leroy et al. 1984). The magnetic field of the
prominence is generally far from perpendicular to the prominence sheet. The
angle between the magnetic field and the prominence long axis is quite small
and the magnetic field is highly sheared. Leroy et al. (1984) derive
statistical results from simultaneous observations of a sample of 256 prominences of low to medium latitude in two optically-thin lines. They find
that prominences lower than 30 000 km high are generally of normal
configuration and have shear angle (angle between field lines and prominence
long axis) of average
![]() while those higher than 30 000 km are of
inverse configuration and have average shear angle
while those higher than 30 000 km are of
inverse configuration and have average shear angle
![]() .
Computing
the complete 3D structure of a smaller sample of prominences
Bommier et al. (1994) calculated that the average angle between the
outgoing prominence field and the solar surface is
.
Computing
the complete 3D structure of a smaller sample of prominences
Bommier et al. (1994) calculated that the average angle between the
outgoing prominence field and the solar surface is ![]() .
.
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{1706promline.eps}\hspace*{...
...}\includegraphics[width=8.7cm,clip]{1706oblique.eps}\hspace*{2cm}}\end{figure}](/articles/aa/full/2005/03/aa1706/Timg73.gif) |
Figure 4: Prominence field line projection in X-Z plane ( left), X-Y plane ( right) and an oblique 3D perspective view ( bottom) with the prominence dip and polarity inversion line at X=0. Note the correspondence between these near-horizontal lines with strong axial component and the intersections of the flux rope magnetic field with the prominence sheet in Fig. 1, where the field also is nearly horizontal and has a strong axial component. |
| Open with DEXTER | |
The field line plots of our example model are shown in
Fig. 4. The field strength at the dip is fixed at 10 G.
The Y-axis points in the direction of the
prominence long axis, the X-axis is in the horizontal direction
perpendicular
to the Y-axis and the Z-axis points vertically upwards. The left
picture shows a plot of the magnetic field line of the prominence projected
onto the X - Z plane from the bottom of the prominence dip at X=0 Mm to
the edge of the prominence at about X=3 Mm. The right picture shows a
selection of field lines projected onto the X - Y plane showing the highly
sheared structure of these field lines. The model is invariant in the Y direction. The prominence polarity inversion line is also shown.
The prominence width is between 5000 and
6000 km, the height is around 20 000 km and the angle between the
prominence field and the long axis is
![]() .
The prominence field
has a shallow dip. The outgoing field makes an angle
with the solar surface of approximately
.
The prominence field
has a shallow dip. The outgoing field makes an angle
with the solar surface of approximately ![]() (field is horizontal).
(field is horizontal).
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{1706rho.eps}\hspace*{3mm}
...
...e*{4cm}\includegraphics[width=6.5cm,clip]{1706V.eps}\hspace*{4cm}}\end{figure}](/articles/aa/full/2005/03/aa1706/Timg74.gif) |
Figure 5: Plots of the gas density ( top left), temperature ( top right) and velocity ( bottom) plots inside the prominence. |
| Open with DEXTER | |
Because the prominence plasma is very dense and because the model is
non-isothermal and compressible, imposing a significant dip angle on the
prominence magnetic field vector causes the plasma at the bottom to become
greatly compressed and unrealistically hot. This is because there is so much
mass trapped in the dip and even a small slope in the field line can cause a
large pressure gradient. We were able to produce reasonable temperature
profiles for the prominence model only by imposing a very small dip angle such
as in the configuration shown in Fig. 4. This is in
agreement with the average dip angle for normal prominences observed by Leroy
et al. (1984) which is approximately ![]() (approximately horizontal).
The resulting density and velocity plots are very flat. This is because in
Eq. (19) for M2' the denominator is very large with the
small value of M2 while the numerator is small because of the factor F,
the slope, which is small in our model. Therefore we have a very small change
in M2 across the prominence and so
(approximately horizontal).
The resulting density and velocity plots are very flat. This is because in
Eq. (19) for M2' the denominator is very large with the
small value of M2 while the numerator is small because of the factor F,
the slope, which is small in our model. Therefore we have a very small change
in M2 across the prominence and so ![]() and
and ![]() change very little
as well. Meanwhile there is more variation in the pressure and therefore the
temperature across the prominence. The model temperature is greater at the
centre of the prominence than at the edges, in agreement with the
observations of Zhang et al. (1987).
change very little
as well. Meanwhile there is more variation in the pressure and therefore the
temperature across the prominence. The model temperature is greater at the
centre of the prominence than at the edges, in agreement with the
observations of Zhang et al. (1987).
We fix the shear angle
![]() via the free function
via the free function
![]() in Eq. (17). We choose the value
in Eq. (17). We choose the value
![]() which is typical of observed shear angles (Leroy et al. 1984; Bommier et al. 1994). Provided that the pressure function given by Eq. (16) is kept positive,
which is typical of observed shear angles (Leroy et al. 1984; Bommier et al. 1994). Provided that the pressure function given by Eq. (16) is kept positive, ![]() can be fixed at any value.
can be fixed at any value.
In our model plasma enters one side of the prominence and then exits the
other. The plasma density is almost undiminished from the centre to the
edges of the model. If the mass fluxes in and out of the model corresponding
to the observed velocities of approximately 5 km s-1 are much too large to be
matched by possible sinks and sources associated with cross-field diffusion
(see next subsection), we must have an ideal unidirectional flow through the
prominence magnetic flux tubes and we must account for the plasma entering
one side of the model and exiting the other. This is a complication that
arises in modelling steady flows in prominences and does not arise in
static modelling. In steady flow modelling this issue of the transition from
prominence flows to coronal flows has never been adequately addressed. In
Paper II we
found that we were unable to model the transition region part of coronal
loops. The same thing is true of this prominence model: we are unable to
include a transition region between the prominence and the much sparser
corona. In ideal MHD we know that the condition
![]() constant must
hold along any flux tube, where
constant must
hold along any flux tube, where
![]() and AF is the
cross-sectional area of the tube. It is therefore clear that in order for
the fluid to flow along such a flux tube from a region within the prominence
to a coronal region outside, a decrease in the density by a factor of 100 cannot be compensated by a corresponding increase in the velocity from 5 km s-1. Although the velocity is likely to increase in the coronal part it
is also likely that the flux tube width changes a great deal between the
prominence interior and exterior, much like the expansion of thin
photospheric flux tubes into much broader tubes in the corona. That
prominence magnetic field strengths are significantly larger than coronal
estimates seems to support this picture. It may be that the magnetic field inside the prominence is more sheared than the field external to the prominence and that this contributes to the large change in cross-sectional area. However we know from
Eq. (10) that neighbouring field lines differ by a vertical
translation in our solutions and so we are unable to reproduce this flux tube
expansion (as was also the case in Paper II). In models of prominences it is
not unusual for variation with height to be ignored (e.g. Kippenhahn &
Schlüter 1957; Low 1982; Anzer & Heinzel 2000) or else simplified by a
self-similarity assumption (Hood & Anzer 1990; Del Zanna & Hood 1996; the
present paper) as such assumptions are usually necessary to obtain an exact
solution. Del Zanna & Hood (1996) tried to model the transition from
prominence conditions to coronal conditions as an MHD shock conserving
momentum but not energy. When one tries to treat the energetics across such
a shock one encounters
unavoidable step-function behaviour in the total energy function due to
the thermal and kinetic energies. This carries over to delta functions
in the heating model (see next section). It is also difficult to explain why such a shock would not
propagate along the field lines in a real prominence. Modeling the sharp transition between prominences and the corona with tangential discontinuities has the advantage that
thermal conditions can differ greatly across tangential discontinuities in a reasonable physical
picture, while along field lines conditions are homogeneous in the absence
of dynamical shock fronts (Spitzer 1962; see also the introduction). This is why Fig. 1 shows the
prominences residing in a twisted flux tube distinct and
thermally isolated from the greater corona. An adequate model of the prominence-corona transition region including such discontinuities will
require a more complex, probably numerical solution.
and AF is the
cross-sectional area of the tube. It is therefore clear that in order for
the fluid to flow along such a flux tube from a region within the prominence
to a coronal region outside, a decrease in the density by a factor of 100 cannot be compensated by a corresponding increase in the velocity from 5 km s-1. Although the velocity is likely to increase in the coronal part it
is also likely that the flux tube width changes a great deal between the
prominence interior and exterior, much like the expansion of thin
photospheric flux tubes into much broader tubes in the corona. That
prominence magnetic field strengths are significantly larger than coronal
estimates seems to support this picture. It may be that the magnetic field inside the prominence is more sheared than the field external to the prominence and that this contributes to the large change in cross-sectional area. However we know from
Eq. (10) that neighbouring field lines differ by a vertical
translation in our solutions and so we are unable to reproduce this flux tube
expansion (as was also the case in Paper II). In models of prominences it is
not unusual for variation with height to be ignored (e.g. Kippenhahn &
Schlüter 1957; Low 1982; Anzer & Heinzel 2000) or else simplified by a
self-similarity assumption (Hood & Anzer 1990; Del Zanna & Hood 1996; the
present paper) as such assumptions are usually necessary to obtain an exact
solution. Del Zanna & Hood (1996) tried to model the transition from
prominence conditions to coronal conditions as an MHD shock conserving
momentum but not energy. When one tries to treat the energetics across such
a shock one encounters
unavoidable step-function behaviour in the total energy function due to
the thermal and kinetic energies. This carries over to delta functions
in the heating model (see next section). It is also difficult to explain why such a shock would not
propagate along the field lines in a real prominence. Modeling the sharp transition between prominences and the corona with tangential discontinuities has the advantage that
thermal conditions can differ greatly across tangential discontinuities in a reasonable physical
picture, while along field lines conditions are homogeneous in the absence
of dynamical shock fronts (Spitzer 1962; see also the introduction). This is why Fig. 1 shows the
prominences residing in a twisted flux tube distinct and
thermally isolated from the greater corona. An adequate model of the prominence-corona transition region including such discontinuities will
require a more complex, probably numerical solution.
However our more uniform model is a reasonable approximation in the more homogeneous interior of the prominence dip. Whether the prominence is embedded in a flux rope or a sheared arcade, flows of order 50-100 km s-1 along expanded coronal flux tubes could easily provide the necessary source/sink for this mass flux, given a flux tube expansion factor of order 5-10. From Paper II we know that such velocities are not only possible in coronal flux tubes but that they appear to be typical.
Landman (1986) calculated the line intensities to be expected under
non-LTE conditions and derived a value
![]() between 0.1 and 0.2. Previous results
obtained by Hirayama (see Hirayama 1985) were an order of magnitude higher.
Conditions in prominences are normally such that there are enough ions present
for the prominence to behave like a plasma and the ideal MHD equations are
valid. For a prominence H=25 000 km high we calculate that under gravity the
plasma would free-fall to the photosphere in just over 7 min. Meanwhile
even with the neutral and ion number densities equal to each other
between 0.1 and 0.2. Previous results
obtained by Hirayama (see Hirayama 1985) were an order of magnitude higher.
Conditions in prominences are normally such that there are enough ions present
for the prominence to behave like a plasma and the ideal MHD equations are
valid. For a prominence H=25 000 km high we calculate that under gravity the
plasma would free-fall to the photosphere in just over 7 min. Meanwhile
even with the neutral and ion number densities equal to each other
![]() ,
the magnetic diffusivity
,
the magnetic diffusivity ![]() differs from the fully-ionised
case by less than one part in 1000 (Priest 1982, p79): we
calculate
differs from the fully-ionised
case by less than one part in 1000 (Priest 1982, p79): we
calculate
![]() m2/s taking the average particle mass to be the mass
of a
m2/s taking the average particle mass to be the mass
of a
![]() and the temperature to be 8000 K. The time to diffuse
over 25 000 km is about 15 600 years. Free-fall times and diffusion times
are comparable over distances of around 20 m. This calculation is
sufficiently insensitive to ion:neutral ratios for our purposes. Neutrals
would have to be many orders of magnitude more populous than ions for diffusion
to become important over the distances and timescales of interest.
and the temperature to be 8000 K. The time to diffuse
over 25 000 km is about 15 600 years. Free-fall times and diffusion times
are comparable over distances of around 20 m. This calculation is
sufficiently insensitive to ion:neutral ratios for our purposes. Neutrals
would have to be many orders of magnitude more populous than ions for diffusion
to become important over the distances and timescales of interest.
Since the prominence plasma is only partially ionised and much denser than the ambient
coronal plasma, it is interesting to ask how well MHD describes the properties
of this prominence plasma. It is generally thought that prominences are supported
against the gravitational force by their magnetic field. Hence an especially important question is how
well the frozen-in condition of ideal MHD is satisfied by the partially ionised
plasma. In particular, the neutral species (mainly H and He) are not directly supported
by the magnetic field but only through collisional coupling to the ions and electrons.
This leads to a drainage of the neutral species from the prominence.
The time scales for this drainage have recently been calculated by Gilbert et al. (2002)
using a simplified model involving the Lorentz force for the species with nonvanishing
electric charge, the gravitational force and collisional forces.
The species taken into account by the model are electrons, protons (H+), singly charged
helium (He+), neutral hydrogen (H) and neutral helium (He).
Based on these assumptions and taking a temperature of 7000 K, assuming a plasma composed of 90% hydrogen, half-ionised, and 10% helium, 10% ionised (giving a mean particle mass of 0.96 proton masses), Gilbert et al. (2002) find that for a prominence with a number
density
of n=1010 cm-3 and a vertical extension of 7000 km (
![]() )
the
loss time scale for hydrogen is roughly 520 h (22 days). The loss time for helium is
actually much shorter and of the order of 1 day. These results were not sensitive to the ionisation fractions, temperature, helium abundance or magnetic field strength but varied linearly with the populations of neutrals. For our example with atom
density around 1010 cm-3 the Gilbert et al. (2002) model gives
neutral helium and neutral hydrogen cross-field velocities of
)
the
loss time scale for hydrogen is roughly 520 h (22 days). The loss time for helium is
actually much shorter and of the order of 1 day. These results were not sensitive to the ionisation fractions, temperature, helium abundance or magnetic field strength but varied linearly with the populations of neutrals. For our example with atom
density around 1010 cm-3 the Gilbert et al. (2002) model gives
neutral helium and neutral hydrogen cross-field velocities of
![]() and
and
![]() km s-1 respectively. Therefore
over the time scales of interest this cross-field diffusion of neutrals is
negligible. In one hour the helium atoms will drift about 200 km while the
hydrogen atoms, the larger category by far, would have travelled only about 10 km. Ideal MHD with field-aligned flow is therefore a reasonable
description.
km s-1 respectively. Therefore
over the time scales of interest this cross-field diffusion of neutrals is
negligible. In one hour the helium atoms will drift about 200 km while the
hydrogen atoms, the larger category by far, would have travelled only about 10 km. Ideal MHD with field-aligned flow is therefore a reasonable
description.
![\begin{figure}
\par {\hspace*{4mm}\includegraphics[width=6.7cm,clip]{1706momacro...
...hspace*{5mm}
\includegraphics[width=6.7cm,clip]{1706momacrossy.eps}
\end{figure}](/articles/aa/full/2005/03/aa1706/Timg89.gif) |
Figure 6: Shown is the momentum breakdown along and across the magnetic field. We graph components across the field line in the X-Z plane ( top pictures) on a larger ( left) and a smaller ( right) scale, along the field line ( bottom left) and across the field line in the Y-direction ( bottom right). In the field-aligned plots positive momentum means momentum directed from the left foot point to the right, in the X-Z-plane cross-field plots positive momentum is momentum directed from inside the structure outwards while in the Y-direction plots positive momentum is momentum in the direction of increasing Y. |
| Open with DEXTER | |
Figure 6 shows the momentum breakdown in the model. We graph components across the field line in the X - Z plane and in the Y direction and along the field line. The field-aligned magnetic forces cancel because the Lorentz force is perpendicular to the magnetic field line.
Across the prominence field line the largest forces are the downward
gravitational force, because of the high density of the prominence plasma,
and the magnetic tension force which is directed upward and largely balances
the weight.
The remaining forces all point upwards. The inertial force is much smaller
than the others because the flow velocity vector is
small, nearly straight and of a nearly constant size. The gas and magnetic
pressure gradient forces are approximately equal but significantly smaller
than the magnetic tension force. Along the field lines the inertial force is
negligible and the downward
gravitational force is mostly balanced by an upward gas pressure force.
In the Y-direction the magnetic and gas pressures are zero because the model
is invariant in this direction. Furthermore there is no gravitational force
component, so that the momentum balance in the Y-direction consists of the
inertial and magnetic tension forces. These forces are very small because
the field lines have little curvature in the Y - Z plane. The largest forces in the system are the weight and the magnetic tension force. The inertial force is the smallest force in the system. Although the mass of the prominence is great, the inertial force has negligible influence on the momentum balance for any reasonable flow velocity. As in the loop model in Paper II, the influence of the flow on the plasma parameters is very small indeed. The pressure, density and temperature distributions in the MHD parameters would change very little in the limit
![]() .
If magnetic field structure and plasma distribution are the sole topics of interest then the magnetohydrostatic approximation is a good one. However, we are interested also in the energetics of prominences. In the next section we investigate whether or not steady flows of magnitude comparable to observed flows in prominences are influential in the heating balance, as was found to be the case in the study of flows in coronal loops in Paper II.
.
If magnetic field structure and plasma distribution are the sole topics of interest then the magnetohydrostatic approximation is a good one. However, we are interested also in the energetics of prominences. In the next section we investigate whether or not steady flows of magnitude comparable to observed flows in prominences are influential in the heating balance, as was found to be the case in the study of flows in coronal loops in Paper II.
As we have seen the dynamics of flows in prominences is described by the MHD equations. Meanwhile, the energetics of the flow is governed by the first
law of thermodynamics:
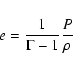 |
(25) |
The net heat in/out q is calculated from the MHD model using the
first law of thermodynamics Eq. (24). The model is
non-polytropic and non-adiabatic, as described in Sect. 2.1 of Paper II.
In our general case the pressure and density are not known as explicit
functions of each other. It is possible to calculate q along a field line
by exploiting the fact that functions of ![]() are constant and by using
the derivatives of the x-dependent functions associated with P and
are constant and by using
the derivatives of the x-dependent functions associated with P and ![]() in Eqs. (15) and (16).
in Eqs. (15) and (16).
![\begin{figure}
\par\hspace*{7mm}\includegraphics[width=6.5cm,clip]{1706energy.ep...
...s}\hspace*{6mm}
\includegraphics[width=6.8cm,clip]{1706heatbig.eps}
\end{figure}](/articles/aa/full/2005/03/aa1706/Timg101.gif) |
Figure 7:
Energy ( left pictures) and heating ( right pictures) profiles of the prominence.
The potential energy is the dominant energy of the prominence plasma because of the very
large density of this plasma. The thermal energy is much smaller while the kinetic energy
is much smaller still, barely visible on the graph. In the right picture, the radiative
losses |
| Open with DEXTER | |
If the ionisation is
dominated by collisional processes as in the corona then the assumption of
local thermodynamic equilibrium (LTE) is valid. This may not hold for prominences,
which consist of thin flux tubes of width
approximately 300-1000 km (Démoulin et al. 1987) which
are irradiated from the much hotter corona as well as the transition region
and the chromosphere (Tandberg-Hanssen 1995).
In most prominences the hydrogen and helium lines become optically
thick at 40 000 K and the optically thin approximation overestimates the
losses (Kuin & Poland 1991).
In our model we include non-LTE effects by incorporating the radiation model
of Kuin & Poland (1991) to calculate ![]() .
The thermal conduction
energy is calculated assuming that conduction is mainly along the field, using
the expression
.
The thermal conduction
energy is calculated assuming that conduction is mainly along the field, using
the expression
(Spitzer 1962) where subscripts || indicate values and derivatives along the field line, and the variation of the magnetic field strength along the field line is taken into account (Priest 1982, p. 86).
Since the plasma parameters P, ![]() and T are completely determined by the dynamics, the radiative losses
and T are completely determined by the dynamics, the radiative losses ![]() ,
the heat conduction
,
the heat conduction
![]() and the net heat in/out of the flow q are all determined. Hence we must satisfy Eq. (26) by calculating the heating function a posteriori (Low & Tsinganos 1986). Given the known functions
and the net heat in/out of the flow q are all determined. Hence we must satisfy Eq. (26) by calculating the heating function a posteriori (Low & Tsinganos 1986). Given the known functions ![]() ,
,
![]() and q we find
and q we find ![]() from Eq. (26).
from Eq. (26).
Figure 7 shows the breakdown of the total energy (left) and the heating balance (right) inside the prominence.
Because of the much larger density of the prominence suspended at such a large height most of the energy contained in the prominence is potential energy. The thermal energy is smaller in the prominence than in the corona because of the low temperature. This can be seen by comparing Fig. 7 (left) with the corresponding Figs. 5 and 8 (bottom left) of Paper II for the coronal loop model, i.e., in coronal loops at around 1 MK the thermal energy dominates the total energy with only a small contribution from the potential energy.
Figure 7 (right picture) shows that the radiative losses are dominant but
that the net heat in/out is not negligibly small. Temperature gradients, which are present
because of the compressibility of the flow and the great density of the plasma
in the dip, cause some conduction to take place. This conduction is
nevertheless small and is barely visible in the heating plot. The example plotted has flux tube
width 500 km and is typical. We only plot parameters for the central 3000 km because
the radiation model is only valid for temperatures greater than 7000 K.
This also avoids complications introduced by geometrical effects on external
irradiation not included in the radiation model.
The importance of the flow in the two plots of Fig. 7 mirrors
the situation existing in coronal loops despite the very different physical parameter values.
We can demonstrate the situation by using a dimensional calculation. If we take typical
prominence values for the gas density
![]() g/cm3 and temperature
T=8000 K, and a velocity of V=5 km s-1, and if we take as a length scale
Z0=3000 km (approximately equal to the half-width of the part of the prominence under
scrutiny and also the hydrostatic length scale along the field line) then we find that
the corresponding typical potential energy per unit mass is
g/cm3 and temperature
T=8000 K, and a velocity of V=5 km s-1, and if we take as a length scale
Z0=3000 km (approximately equal to the half-width of the part of the prominence under
scrutiny and also the hydrostatic length scale along the field line) then we find that
the corresponding typical potential energy per unit mass is
![]() ,
the kinetic energy per unit mass is
,
the kinetic energy per unit mass is
![]() and the enthalpy per unit
mass is
and the enthalpy per unit
mass is
![]() .
Thus the kinetic
energy is not significant compared to the other energies. Meanwhile the
radiative loss function is
.
Thus the kinetic
energy is not significant compared to the other energies. Meanwhile the
radiative loss function is
![]() erg cm-3 s-1, the conduction is
erg cm-3 s-1, the conduction is
![]() and the volumetric net heat in/out is
and the volumetric net heat in/out is
![]() .
Thus the difference
between the roles of the flow in
the energy and heating profiles is clear in both the modelling and
the magnitude calculations. In fact the net heat in/out q plays a
smaller role in our models than these numbers in the magnitude calculation indicate because q is a
derivative of an even function near the symmetry axis and is therefore
slightly smaller than the dimensional calculation suggests. The main
conclusion from the heating balance is that the heating roughly balances the
radiative losses while it may also be influenced by moderate steady flows.
In a static model the MHD parameters would change very
little in the limit
.
Thus the difference
between the roles of the flow in
the energy and heating profiles is clear in both the modelling and
the magnitude calculations. In fact the net heat in/out q plays a
smaller role in our models than these numbers in the magnitude calculation indicate because q is a
derivative of an even function near the symmetry axis and is therefore
slightly smaller than the dimensional calculation suggests. The main
conclusion from the heating balance is that the heating roughly balances the
radiative losses while it may also be influenced by moderate steady flows.
In a static model the MHD parameters would change very
little in the limit
![]() ,
but
,
but
![]() .
Then the heating function
would change visibly
by becoming symmetric and, since heat conduction is negligible, almost
exactly equal to minus the radiative losses. Thus the difference between the
energetics graphs in the static (
.
Then the heating function
would change visibly
by becoming symmetric and, since heat conduction is negligible, almost
exactly equal to minus the radiative losses. Thus the difference between the
energetics graphs in the static (
![]() )
and steady
(
)
and steady
(
![]() )
cases may be striking for even moderate flows which
leave the magnetic structure and the plasma distribution unchanged from the
static case. This corresponds perfectly with the situation in Paper II with
coronal loops.
)
cases may be striking for even moderate flows which
leave the magnetic structure and the plasma distribution unchanged from the
static case. This corresponds perfectly with the situation in Paper II with
coronal loops.
It is striking that in models constructed in this way, the flow breaks
the symmetry of the coronal heating function: although the radiative losses ![]() are symmetric the heating function
are symmetric the heating function ![]() is not (see also Paper II). We
can make sense of this by considering likely scenarios in magnetic structures
with steady unidirectional flows. The
coronal heating mechanism has been for several decades, and continues to be,
the subject of intense debate among solar physicists. The main
candidates are reconnection ("nanoflares'', Parker 1994) and wave dissipation
(resonant absorption or phase mixing, Heyvaerts & Priest 1983). The plasma in prominences (and loops)
is approximately symmetrically distributed and
so its radiative losses are symmetrically distributed. Meanwhile the heat
sources are likely not to be evenly distributed in general, whether they
are sites of reconnection or wave sources.
is not (see also Paper II). We
can make sense of this by considering likely scenarios in magnetic structures
with steady unidirectional flows. The
coronal heating mechanism has been for several decades, and continues to be,
the subject of intense debate among solar physicists. The main
candidates are reconnection ("nanoflares'', Parker 1994) and wave dissipation
(resonant absorption or phase mixing, Heyvaerts & Priest 1983). The plasma in prominences (and loops)
is approximately symmetrically distributed and
so its radiative losses are symmetrically distributed. Meanwhile the heat
sources are likely not to be evenly distributed in general, whether they
are sites of reconnection or wave sources.
We could have added to our model of a prominence dip a surrounding hot arcade model separated from the prominence by a discontinuity as in Del Zanna & Hood (1996). However, we refrain from doing so for the following reason. To satisfy mass and momentum conservation across a discontinuity between a cool, dense region and a hot, sparse region forces the enthalpy to change by a large factor across the discontinuity. Because the gravitational potential energy per unit mass is continuous across the boundary and the influence of the kinetic energy is minimal on each side for any realistic velocity, this change cannot be balanced. Point energy sources/sinks at such boundaries are implied and energy changes by factors of 10 or more, corresponding to delta-function behaviour in the heating function. For these reasons and for others discussed in Sect. 3.3 it is not possible to describe steady flows in prominences and their surrounding magnetic fields self-consistently using these solutions. This is why we confine ourselves to a local model describing steady flows in the dense, dipped part of the prominence. However it can be seen that the scenario of a narrow, dense prominence flux tube expanding into a broad, sparse coronal flux tube is reasonable from an energetic point of view as well as from the point of view of dynamics (Sect. 3.3) provided that the supporting arcade is of a similar temperature to the prominence, which is likely given that field-aligned heat conduction is very efficient (Spitzer 1962). In this scenario the potential energy would dominate the thermal and kinetic energies across the transition and the cool coronal flux tube would be separated from the hot corona by tangential discontinuities across which thermal conduction is very inefficient. A generalisation to such a global model would require a formidable numerical treatment and is outside the scope of this work which concentrates instead on the prominence interior.
We have modelled a prominence by using a two-dimensional compressible equilibrium solution of the full ideal steady MHD equations incorporating a consistent energetics model for the first time. Our model generalises known self-similar prominence models, such as those by Hood & Anzer (1990) and Del Zanna & Hood (1996) by including non-isothermal flows and a study of the heating balance. Although the model is 2D, third components of the magnetic and velocity vector fields allow us to model the highly sheared fields observed in prominences. This is therefore the first time that the sheared structure, fluid flow and energetics of prominences have been combined in a single model. We find on fitting our model to typical observed physical parameter values that, close to the centre of the prominence dip, the energetics may be influenced by a steady flow while the physical parameters of the dynamical model are almost completely unaffected by the flow. This striking conclusion is analogous to the finding in Paper II for coronal loops.
Both magnetic diffusion and cross-field diffusion of neutrals are found to be insignificant within the time scales of interest so that an ideal MHD description is reasonable. Many flows observed in prominences may be time-dependent but for persistent flows showing a high degree of organisation, as have been observed, the steady-state approximation is reasonable. It may also be the case that the observed flows are not field-aligned but are associated with motion of the supporting field lines themselves. It is impossible to establish this with the observations currently available. If the field lines or vertical structures are observed to be static then the flows can only be field-aligned.
The modelled prominence dip must be very shallow for the physical parameters to stay within reasonable bounds. This is consistent with the near-horizontal prominence fields found in observations. Within the prominence the magnetic tension force bears most of the burden of the prominence weight. We were unable to add self-consistently a surrounding magnetic field solution because of limitations of the self-similar assumptions which were necessary for us to obtain exact solutions. That our self-similar solutions cannot accommodate sharp boundaries between prominences and supporting fields should not be surprising since self-similarity does not allow a free choice in the prescription of boundary conditions. However there is no physical reason why such a solution should not be possible by other, probably numerical, means. Such a global prominence model remains a challenge for the future.
Acknowledgements
It is a pleasure to thank Christophe Sauty for helping to improve the paper and BC Low for useful comments about MHD shocks. The authors acknowledge support from the EC's human potential programme under contract HPRN-CT-2000-00153, PLATON.