A&A 429, 755-765 (2005)
DOI: 10.1051/0004-6361:20041517
On the spectrum of high-energy cosmic rays produced
by supernova remnants in the presence of strong cosmic-ray streaming instability and wave dissipation
V. S. Ptuskin1 - V. N. Zirakashvili1,2
1 - Institute for Terrestrial Magnetism, Ionosphere and Radiowave Propagation, 142190 Troitsk, Moscow Region, Russia
2 - Max-Planck-Institut für Kernphysik, 69029 Heidelberg, Postfach 103980, Germany
Received 23 June 2004 / Accepted 16 August 2004
Abstract
The cosmic-ray streaming instability creates strong magnetohydrodynamic turbulence in the precursor of a SN shock. The level of turbulence determines the maximum energy of cosmic-ray particles accelerated by the diffusive shock acceleration mechanism. In this paper we present the continuation of previous work (Ptuskin & Zirakashvili 2003). We assume that Kolmogorov type nonlinear wave interactions together with ion-neutral collisions restrict the amplitude of the random magnetic field. As a result, the maximum energy of the accelerated particles strongly depends on the age of a SNR. The average spectrum of cosmic rays injected in the interstellar medium in the course of the adiabatic SNR evolution (the Sedov stage) is approximately
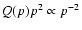 at energies larger than 10-30 GeV/nucleon and with a maximum particle energy that is close to the position of the knee in the cosmic-ray spectrum observed at
at energies larger than 10-30 GeV/nucleon and with a maximum particle energy that is close to the position of the knee in the cosmic-ray spectrum observed at 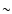
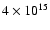 eV. At an earlier stage of SNR evolution - the ejecta-dominated stage described by the
Chevalier-Nadyozhin solution, the particles are accelerated to higher energies and have a rather steep power-law distribution. These results suggest that the knee may mark the transition from the ejecta-dominated to the adiabatic evolution of SNR shocks which accelerate cosmic rays.
eV. At an earlier stage of SNR evolution - the ejecta-dominated stage described by the
Chevalier-Nadyozhin solution, the particles are accelerated to higher energies and have a rather steep power-law distribution. These results suggest that the knee may mark the transition from the ejecta-dominated to the adiabatic evolution of SNR shocks which accelerate cosmic rays.
Key words: ISM: supernova remnants - ISM: cosmic rays
Diffusive shock acceleration is considered as the main mechanism of acceleration of galactic cosmic rays. The diffusion coefficient D(E), which is a function of energy, determines the maximum energy that particles can gain in the process of acceleration by the shock moving through the turbulent interstellar medium. The condition of efficient acceleration is
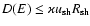 ,
where
,
where
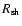 is the radius and
is the radius and
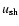 is the velocity of a spherical shock, and the constant
is the velocity of a spherical shock, and the constant
 (see Drury et al. 2001, and Malkov & Drury 2001 for a review). The Bohm value of the diffusion coefficient
(see Drury et al. 2001, and Malkov & Drury 2001 for a review). The Bohm value of the diffusion coefficient
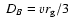 (v is the particle velocity, and
(v is the particle velocity, and
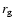 is the particle Larmor radius), which is a lower boundary of the diffusion along the average
magnetic field, gives the maximum particle energy
is the particle Larmor radius), which is a lower boundary of the diffusion along the average
magnetic field, gives the maximum particle energy
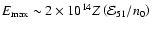 eV at the time of transition from the ejecta-dominated stage to the stage of adiabatic evolution of SNRs (the particle charge is Ze). Here we consider a SN burst with a kinetic energy of the ejecta
eV at the time of transition from the ejecta-dominated stage to the stage of adiabatic evolution of SNRs (the particle charge is Ze). Here we consider a SN burst with a kinetic energy of the ejecta
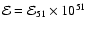 erg in a gas with density n0 cm-3 and an interstellar magnetic field B0=5
erg in a gas with density n0 cm-3 and an interstellar magnetic field B0=5 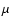 G . This value of
G . This value of 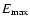 is close but somewhat less than the energy of the "knee'', the break in the total cosmic ray spectrum observed at
is close but somewhat less than the energy of the "knee'', the break in the total cosmic ray spectrum observed at 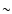
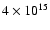 eV.
eV.
Analyzing the early stage of SNR evolution when the shock velocity is high,
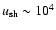 km s-1, Bell & Lucek (2001) found that the
cosmic-ray streaming instability in the shock precursor can be so strong that the amplified field
km s-1, Bell & Lucek (2001) found that the
cosmic-ray streaming instability in the shock precursor can be so strong that the amplified field
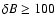
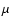 G far exceeds the interstellar value B0. The
maximum particle energy increases accordingly. The cosmic-ray streaming instability is less efficient as the shock velocity decreases with time, and the nonlinear wave interactions reduce the level of turbulence at the late Sedov stage (Völk et al. 1988; Fedorenko 1990). This leads to fast diffusion and to a corresponding decrease of
G far exceeds the interstellar value B0. The
maximum particle energy increases accordingly. The cosmic-ray streaming instability is less efficient as the shock velocity decreases with time, and the nonlinear wave interactions reduce the level of turbulence at the late Sedov stage (Völk et al. 1988; Fedorenko 1990). This leads to fast diffusion and to a corresponding decrease of 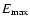 .
The effect is aggravated by possible wave damping produced by the ion-neutral collisions (Bell 1978; Drury et al. 1996). The acceleration of cosmic rays and their streaming instability in a wide range of shock velocities was considered in our previous paper (Ptuskin & Zirakashvili 2003, Paper I). The analytical expressions for the cosmic ray diffusion coefficient and for the instability growth rate were generalized to the case of an arbitrary strong random magnetic field,
.
The effect is aggravated by possible wave damping produced by the ion-neutral collisions (Bell 1978; Drury et al. 1996). The acceleration of cosmic rays and their streaming instability in a wide range of shock velocities was considered in our previous paper (Ptuskin & Zirakashvili 2003, Paper I). The analytical expressions for the cosmic ray diffusion coefficient and for the instability growth rate were generalized to the case of an arbitrary strong random magnetic field,
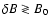 .
The rate of nonlinear wave interactions was assumed to correspond to the Kolmogorov nonlinearity of magnetohydrodynamic waves. The
collisional dissipation was also taken into account. The maximum energy of the accelerated particles was determined as a function of shock velocity and thus as a function of SNR age. The maximum energy of a particle with charge Ze can be as high as 1017Z eV in some very young SNRs and falls to about 1010Z eV at the end of the adiabatic (Sedov) stage. The widely accepted estimate of the cosmic ray diffusion coefficient at the strong shock that corresponds to the Bohm diffusion value calculated for the interstellar magnetic field strength turns out to be incorrect. This result may explain why SNRs with an age of more than a few thousand years are not prominent sources of very high energy gamma-rays (Buckley et al. 1998; Aharonian et al. 2002). The presence of a strongly amplified random magnetic field in young SNRs is evidently supported by the interpretation of data on synchrotron X-ray emission from young SNRs,
see e.g. Vink (2003) for a review.
.
The rate of nonlinear wave interactions was assumed to correspond to the Kolmogorov nonlinearity of magnetohydrodynamic waves. The
collisional dissipation was also taken into account. The maximum energy of the accelerated particles was determined as a function of shock velocity and thus as a function of SNR age. The maximum energy of a particle with charge Ze can be as high as 1017Z eV in some very young SNRs and falls to about 1010Z eV at the end of the adiabatic (Sedov) stage. The widely accepted estimate of the cosmic ray diffusion coefficient at the strong shock that corresponds to the Bohm diffusion value calculated for the interstellar magnetic field strength turns out to be incorrect. This result may explain why SNRs with an age of more than a few thousand years are not prominent sources of very high energy gamma-rays (Buckley et al. 1998; Aharonian et al. 2002). The presence of a strongly amplified random magnetic field in young SNRs is evidently supported by the interpretation of data on synchrotron X-ray emission from young SNRs,
see e.g. Vink (2003) for a review.
The main objective of the present work is the calculation of the average spectrum of cosmic rays ejected into the interstellar medium by a SNR in a course of its evolution. Some necessary results of Paper I are presented in Sect. 2, the evolution of SNR shocks is discussed in Sect. 3, the average cosmic-ray source spectrum is calculated in Sect. 4
followed by the discussion in Sect. 5, the conclusion is given in Sect. 6. Appendix A describes the thin shell approximation used in our calculations.
In the test particle approximation, the momentum distribution of accelerated particles
for high Mach number shocks has the canonical form
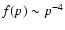 (Krymsky 1977; Bell 1978). In the case of efficient acceleration, the action of cosmic ray pressure on the shock structure causes a nonlinear modification of the shock that changes the shape of the particle spectrum, making it flatter at ultrarelativistic energies (Eichler 1984; Berezhko et al. 1996; Malkov & Drury 2001). Because of this effect, we assume that the distribution of ultrarelativistic particles at the shock is of the form
(Krymsky 1977; Bell 1978). In the case of efficient acceleration, the action of cosmic ray pressure on the shock structure causes a nonlinear modification of the shock that changes the shape of the particle spectrum, making it flatter at ultrarelativistic energies (Eichler 1984; Berezhko et al. 1996; Malkov & Drury 2001). Because of this effect, we assume that the distribution of ultrarelativistic particles at the shock is of the form
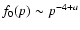 where 0<a<0.5; the value a=0.3 is used in the numerical estimates below. The normalization of f(p) is such that the integral
where 0<a<0.5; the value a=0.3 is used in the numerical estimates below. The normalization of f(p) is such that the integral
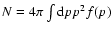 gives the number density of cosmic rays. The differential cosmic ray intensity is
I(E)=f(p)p2. We assume that
the cosmic ray pressure at the shock is some fraction
gives the number density of cosmic rays. The differential cosmic ray intensity is
I(E)=f(p)p2. We assume that
the cosmic ray pressure at the shock is some fraction
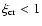 of
the upstream momentum flux entering the shock front, so that
of
the upstream momentum flux entering the shock front, so that
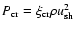 ,
and the equation for the distribution function of relativistic accelerated particles at the shock is
,
and the equation for the distribution function of relativistic accelerated particles at the shock is
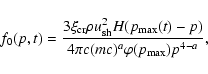 |
(1) |
where
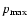 is the maximum momentum of the accelerated particles, H(p) is the step function, and
is the maximum momentum of the accelerated particles, H(p) is the step function, and
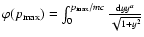 .
The
approximation
of the last integral at
.
The
approximation
of the last integral at
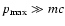 is
is
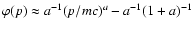 .
The value of
.
The value of
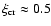 and
the total compression ratio at the shock close to 7 were found in the
numerical simulations of strongly modified SN shocks by Berezhko et al.
(1996). Here and below we mainly consider protons as the most
abundant cosmic ray component. For ions with charge Z, the equations should be written as functions of p/Z instead of p. In particular, the maximum momentum of nuclei with charge Z is a factor of Z larger than that of protons. We use the notation m for the proton mass. The acceleration in old SNRs (
and
the total compression ratio at the shock close to 7 were found in the
numerical simulations of strongly modified SN shocks by Berezhko et al.
(1996). Here and below we mainly consider protons as the most
abundant cosmic ray component. For ions with charge Z, the equations should be written as functions of p/Z instead of p. In particular, the maximum momentum of nuclei with charge Z is a factor of Z larger than that of protons. We use the notation m for the proton mass. The acceleration in old SNRs (
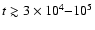 yr) when
yr) when
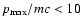 is not considered in the present paper because Eq. (1) is not applied at low Mach numbers, see Paper I for details. (Using the test particle approximation for a non-modified shock, Drury et al. (2003) found that the spectrum of the accelerated particles is somewhat steeper if the diffusion coefficient increases with time compared to the case of constant D. This effect is not included in our consideration.)
is not considered in the present paper because Eq. (1) is not applied at low Mach numbers, see Paper I for details. (Using the test particle approximation for a non-modified shock, Drury et al. (2003) found that the spectrum of the accelerated particles is somewhat steeper if the diffusion coefficient increases with time compared to the case of constant D. This effect is not included in our consideration.)
The following steady-state equation determines the energy density W(k) (k is the wave number) of the magnetohydrodynamic turbulence amplified by the streaming instability in the cosmic-ray precursor upstream of the supernova shock:
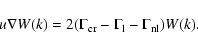 |
(2) |
Here the l.h.s. describes the advection of turbulence by a highly supersonic gas flow. The terms on the r.h.s. of the equation describe respectively the wave amplification by cosmic ray streaming, the linear damping of waves in the background plasma, and the nonlinear wave-wave interactions that may limit the amplitude of the turbulence. The equation for the wave growth rate at the shock
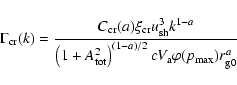 |
(3) |
was suggested in Paper I as the generalization of the equation derived for the case of a weak random field (Berezinskii et al. 1990). Here
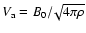 is the Alfvén velocity (
is the Alfvén velocity (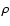 is the gas density),
is the gas density),
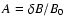 is the dimensionless wave amplitude, and
is the dimensionless wave amplitude, and
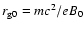 .
The ion-neutral and electron-ion collisions usually determine the linear damping processes in the thermal space plasma. The Kolmogorov-type nonlinearity with a simplified expression
.
The ion-neutral and electron-ion collisions usually determine the linear damping processes in the thermal space plasma. The Kolmogorov-type nonlinearity with a simplified expression
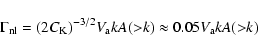 |
(4) |
at
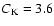 (as follows from the numerical simulations by Verma et al. 1996) was used in Paper I. The wave-particle interaction is of resonant character and the resonance condition is
(as follows from the numerical simulations by Verma et al. 1996) was used in Paper I. The wave-particle interaction is of resonant character and the resonance condition is
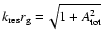 ,
where the Larmor radius
,
where the Larmor radius
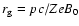 is defined through the regular field B0, and
is defined through the regular field B0, and
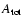 is the total amplitude of the random field. The particle scattering leads to a cosmic-ray diffusion with diffusion coefficient
is the total amplitude of the random field. The particle scattering leads to a cosmic-ray diffusion with diffusion coefficient
![$D=(1+A_{{\rm tot}
}^{2})^{1/2}vr_{{\rm g}}\left[ 3A^{2}(>k_{{\rm res}})\right] ^{-1}$](/articles/aa/full/2005/03/aa1517/img44.gif) .
.
Equation (2) allows finding the following approximate equation for the
dimensionless amplitude of the total random magnetic field produced by the
cosmic-ray streaming instability at the shock (Paper I):
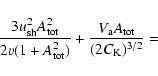 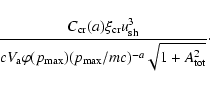 |
(5) |
To study the effect of nonlinear interactions, the term with linear damping in Eq. (2) was omitted in Eq. (5);
![$C_{{\rm cr}}(a)=27[4(5-a)(2-a)]^{-1}$](/articles/aa/full/2005/03/aa1517/img47.gif) .
The maximum particle
momentum satisfies the equation
.
The maximum particle
momentum satisfies the equation
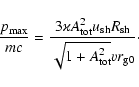 |
(6) |
In the high velocity limit, when
![$u_{{\rm sh}}\gg4aC_{{\rm cr}}
\xi_{{\rm cr}}c[9(2C_{{\rm K}})^{3/2}]^{-1}$](/articles/aa/full/2005/03/aa1517/img49.gif) and
and
![$u_{{\rm sh}}
\gg3V_{{\rm a}}[2aC_{{\rm cr}}\xi_{{\rm cr}}]^{-1}$](/articles/aa/full/2005/03/aa1517/img50.gif) ,
the advection term dominates over the nonlinear dissipation term in the l.h.s. of Eq. (5) and the wave amplitude is large,
,
the advection term dominates over the nonlinear dissipation term in the l.h.s. of Eq. (5) and the wave amplitude is large,
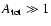 .
The maximum momentum of accelerated particles and the amplified magnetic field are then given by the approximate equations
.
The maximum momentum of accelerated particles and the amplified magnetic field are then given by the approximate equations
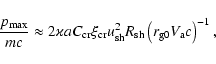 |
(7) |
and
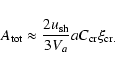 |
(8) |
Here the cosmic ray diffusion coefficient depends on the particle Larmor
radius as
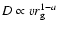 at
at
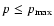 .
.
In the low velocity limit, when
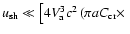
![$\left.\left.(2C_{{\rm K}}\right) ^{3}
\xi_{{\rm cr}})^{-1}\right] ^{1/5}$](/articles/aa/full/2005/03/aa1517/img57.gif) and
and
![$u_{{\rm sh}}\ll\left[
V_{{\rm a}}^{2}c\left( aC_{{\rm cr}}(2C_{{\rm K}})^{3/2}
\xi_{{\rm cr}}\right) ^{-1}\right] ^{1/3}$](/articles/aa/full/2005/03/aa1517/img58.gif) ,
the nonlinear dissipation term dominates over the advection term in the l.h.s. of Eq. (5) and the wave amplitude is small,
,
the nonlinear dissipation term dominates over the advection term in the l.h.s. of Eq. (5) and the wave amplitude is small,
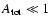 .
The maximum momentum of accelerated particles and the amplified magnetic field are then given by the approximate equations
.
The maximum momentum of accelerated particles and the amplified magnetic field are then given by the approximate equations
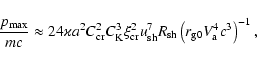 |
(9) |
and
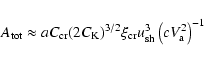 |
(10) |
assuming that this value of the amplified field exceeds the value of the random interstellar magnetic field. The cosmic ray diffusion coefficient depends on the particle Larmor radius as
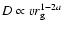 at
at
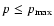 .
(Note the misprint in the numerical coefficient in the first equality of Eq. (19) in Paper I that is analogous to the present Eq. (9).)
.
(Note the misprint in the numerical coefficient in the first equality of Eq. (19) in Paper I that is analogous to the present Eq. (9).)
Figure 1 illustrates the results of calculations of 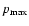 at the Sedov
stage of SNR evolution at
at the Sedov
stage of SNR evolution at
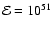 erg in the warm interstellar gas with temperature
erg in the warm interstellar gas with temperature
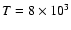 K, average density n0=0.4 cm-3, which includes small interstellar clouds, intercloud density n=0.1 cm-3, number density of ions
K, average density n0=0.4 cm-3, which includes small interstellar clouds, intercloud density n=0.1 cm-3, number density of ions
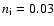 cm-3, interstellar magnetic field strength B0=5
cm-3, interstellar magnetic field strength B0=5 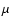 G, see Paper I. The time dependence of the shock radius and the shock velocity are given by the following equations (the Sedov solution; see e.g. Ostriker & McKee 1988):
G, see Paper I. The time dependence of the shock radius and the shock velocity are given by the following equations (the Sedov solution; see e.g. Ostriker & McKee 1988):
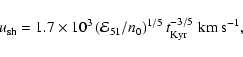 |
(11) |
where we assume that the ultrarelativistic gas of cosmic rays mainly
determines the pressure behind the shock. The value
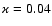 was
assumed in the calculations in Fig. 1.
was
assumed in the calculations in Fig. 1.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1517fig1.eps}
\end{figure}](/articles/aa/full/2005/03/aa1517/Timg71.gif) |
Figure 1:
The maximum momentum of accelerated protons 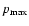 in units mc as a function of shock velocity
in units mc as a function of shock velocity
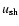 at the Sedov stage of
at the Sedov stage of 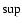 ernova remnant evolution in warm interstellar gas. The three solid lines correspond to three cases of wave dissipation considered separately: nonlinear wave interactions; damping by ion-neutral collisions at constant density of neutral atoms; damping by ion-neutral collisions when the diffuse neutral gas restores its density after complete ionization by the radiation from the supernova explosion. The dashed line represents the age of a supernova remnant t (plotted on the right ordinate) as a function of shock velocity. The dotted line shows the Bohm limit on maximum particle momentum calculated for the interstellar magnetic field strength. The dash-dot line gives the maximum particle
momentum when the wave dissipation is not taken into account. ernova remnant evolution in warm interstellar gas. The three solid lines correspond to three cases of wave dissipation considered separately: nonlinear wave interactions; damping by ion-neutral collisions at constant density of neutral atoms; damping by ion-neutral collisions when the diffuse neutral gas restores its density after complete ionization by the radiation from the supernova explosion. The dashed line represents the age of a supernova remnant t (plotted on the right ordinate) as a function of shock velocity. The dotted line shows the Bohm limit on maximum particle momentum calculated for the interstellar magnetic field strength. The dash-dot line gives the maximum particle
momentum when the wave dissipation is not taken into account. |
| Open with DEXTER |
The three solid lines correspond to the
three cases of wave dissipation considered separately: nonlinear wave
interactions; damping by ion-neutral collisions at constant gas density;
damping by ion-neutral collisions when the diffuse neutral gas restores
its density after complete ionization by the radiation from the SN burst.
For
the last two curves, the dissipation of waves due to the ion-neutral
collisions
with damping rate
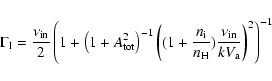 |
(12) |
was taken into account whereas the term
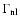 that
describes
nonlinear dissipation was omitted. Here
that
describes
nonlinear dissipation was omitted. Here
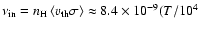 K
K
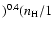 cm-3)s-1 for the temperature
cm-3)s-1 for the temperature
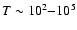 K is the frequency of ion-neutral collisions with cross section
K is the frequency of ion-neutral collisions with cross section 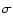 averaged over the velocity distribution of thermal particles,
averaged over the velocity distribution of thermal particles,
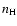 is the number density of neutral hydrogen. (Note a slight correction of the "collisional damping'' curve in Fig. 1 comparing to corresponding Fig. 2 in Paper I.) The maximum energy of protons accelerated by SN shocks at the early Sedov stage is close to
is the number density of neutral hydrogen. (Note a slight correction of the "collisional damping'' curve in Fig. 1 comparing to corresponding Fig. 2 in Paper I.) The maximum energy of protons accelerated by SN shocks at the early Sedov stage is close to
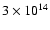 eV, which exceeds the Bohm limit calculated for the interstellar magnetic field value by one order of magnitude. The maximum energy decreases to about 1010 eV at the end of the Sedov stage, which is much less than the Bohm limit calculated for the interstellar magnetic field value. In particular, the particle energy is less than 1013 eV at
eV, which exceeds the Bohm limit calculated for the interstellar magnetic field value by one order of magnitude. The maximum energy decreases to about 1010 eV at the end of the Sedov stage, which is much less than the Bohm limit calculated for the interstellar magnetic field value. In particular, the particle energy is less than 1013 eV at
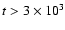 yr and this may explain the absence of a TeV
yr and this may explain the absence of a TeV 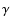 -ray signal from many SNRs (Buckley et al. 1998; Aharonian et al. 2002) where the gamma-rays could in principle be produced through
-ray signal from many SNRs (Buckley et al. 1998; Aharonian et al. 2002) where the gamma-rays could in principle be produced through 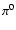 decays if sufficiently energetic cosmic rays were present.
decays if sufficiently energetic cosmic rays were present.
With the extreme choice of parameters of the rapidly expanding young SNR envelope, it was found (Bell & Lucek 2001, Paper I) that the maximum particle energy may reach ultra high energies. The estimate of the highest particle energy according to Paper I is
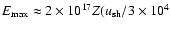 km s
km s
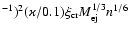 eV at the end of a free expansion stage which precedes the Sedov stage (here
eV at the end of a free expansion stage which precedes the Sedov stage (here
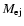 is the mass of the ejecta in
is the mass of the ejecta in 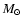 ). We shall see below that this promising estimate is in some sense devalued by the results of the calculations of the particle flux - the
flux turns out to be low at the highest energies which can be achieved in the process
of acceleration.
). We shall see below that this promising estimate is in some sense devalued by the results of the calculations of the particle flux - the
flux turns out to be low at the highest energies which can be achieved in the process
of acceleration.
A typical source of galactic cosmic rays is most probably associated with the core collapse supernova, type II SNe, that is the final stage of evolution for stars more massive than about 8 solar masses while on the main sequence. Before the explosion, the massive star goes through the Main Sequence O-star stage, the Red Supergiant stage, and, for the most massive progenitors (>
 ), which give rise to the rare type Ib/c SNe, through the Wolf-Rayet stage. The fast wind of a massive progenitor star on the main sequence produces a big bubble of hot rarefied gas with a temperature of about
106 K in the surrounding interstellar medium, see Weaver et al. (1977),
Lozinskaya (1992). The typical type II SN goes through the Red Super Giant
phase before the explosion and this process is accompanied by the flow of a low-velocity dense wind. Thus, immediately after the supernova burst, the shock propagates through the wind of a Red Super Giant star, then through the hot bubble, and finally it enters the interstellar medium. Our calculations will be done for an ejecta mass
), which give rise to the rare type Ib/c SNe, through the Wolf-Rayet stage. The fast wind of a massive progenitor star on the main sequence produces a big bubble of hot rarefied gas with a temperature of about
106 K in the surrounding interstellar medium, see Weaver et al. (1977),
Lozinskaya (1992). The typical type II SN goes through the Red Super Giant
phase before the explosion and this process is accompanied by the flow of a low-velocity dense wind. Thus, immediately after the supernova burst, the shock propagates through the wind of a Red Super Giant star, then through the hot bubble, and finally it enters the interstellar medium. Our calculations will be done for an ejecta mass
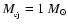 (the solar mass). The spherically symmetric distribution of gas density in the stellar wind is
(the solar mass). The spherically symmetric distribution of gas density in the stellar wind is
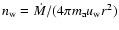 ,
where
,
where
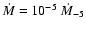 (solar mass)/yr is the mass loss rate,
(solar mass)/yr is the mass loss rate,
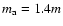 is the
mean interstellar atom mass per hydrogen nucleus, the wind velocity
is the
mean interstellar atom mass per hydrogen nucleus, the wind velocity
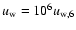 cm/s. The magnetic field in the stellar wind
has the shape of a Parker spiral similar to the interplanetary
magnetic field (Parker 1958). At the relatively large distances from the
surface of the star that are of interest here the magnetic field has a predominately
azimuthal structure and its value is
cm/s. The magnetic field in the stellar wind
has the shape of a Parker spiral similar to the interplanetary
magnetic field (Parker 1958). At the relatively large distances from the
surface of the star that are of interest here the magnetic field has a predominately
azimuthal structure and its value is
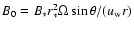 where
where 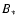 is the surface magnetic field
strength at the star radius
is the surface magnetic field
strength at the star radius 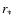 ,
,
 is the angular velocity of
star rotation, and
is the angular velocity of
star rotation, and 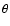 is the polar angle. Hence
is the polar angle. Hence
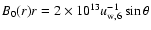 G
G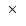 cm at
cm at
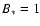 G,
G,
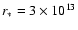 cm,
cm,
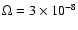 s-1 that gives
s-1 that gives
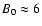
 G at the distance r=1 pc from the star.
G at the distance r=1 pc from the star.
Below we shall also use the following set of parameters of the medium surrounding the type II SN: the radius of the spherical Red Super Giant wind
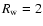 pc, the star mass loss
pc, the star mass loss
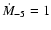 ,
and the wind velocity
,
and the wind velocity
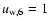 .
In addition, the radius of the spherical bubble of hot gas
.
In addition, the radius of the spherical bubble of hot gas
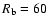 pc, the gas density in the bubble
pc, the gas density in the bubble
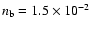 cm-3, the magnetic field
cm-3, the magnetic field
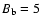
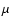 G. The gas density in the undisturbed interstellar medium around the bubble is assumed to be equal to n0=1 cm-3 (physically, the value of n0 determines
G. The gas density in the undisturbed interstellar medium around the bubble is assumed to be equal to n0=1 cm-3 (physically, the value of n0 determines
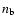 ,
see Weaver et al. 1977). The hot bubble is separated by a dense thin shell from the interstellar gas. The accepted parameters are close to those assumed by Berezhko & Völk (2000) in their analysis of gamma-ray production in SNRs. A lengthy discussion and additional references can be found there.
,
see Weaver et al. 1977). The hot bubble is separated by a dense thin shell from the interstellar gas. The accepted parameters are close to those assumed by Berezhko & Völk (2000) in their analysis of gamma-ray production in SNRs. A lengthy discussion and additional references can be found there.
A considerable fraction of cosmic rays is probably accelerated in type Ia SNe (their explosion rate in the Galaxy is about 1/4 of that of type II SN). These supernovae are caused by the thermonuclear explosions of compact white dwarfs following mass accretion. The characteristic masses of the progenitor star and ejecta are 1.4 solar mass. The progenitor stars do not appear to have an observable amount of mass loss nor do they emit
ionizing radiation that could modify the ambient medium. We assume that the SNR shock goes through the uniform weakly ionized interstellar medium with density 1 cm-3, and magnetic field 7 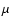 G.
G.
It is instructive to consider the asymptotic regimes of the propagation of SNR shock - the ejecta dominated stage and the adiabatic stage.
The adiabatic regime was mentioned earlier (see the Sedov solution (11) for the shock moving in a gas with constant density), and it refers to the stage of SNR evolution when the mass of swept-up gas significantly exceeds the mass of ejecta. This condition is fulfilled in the case of a medium with constant density at
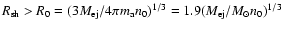 pc,
pc,
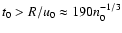 yr, where
yr, where
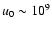 cm/s is the initial velocity of the ejecta. The adiabatic regime for the SNR shock moving through the progenitor star wind is described by the equations (at
cm/s is the initial velocity of the ejecta. The adiabatic regime for the SNR shock moving through the progenitor star wind is described by the equations (at
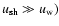 :
:
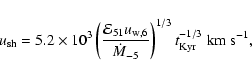 |
(13) |
see Ostriker & McKee (1988). As in Eq. (11), we assume that the ultrarelativistic gas of cosmic rays mainly determines the pressure behind the shock. Equation (13) is valid when the mass of swept-up gas is relatively large and
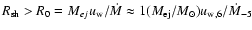 pc.
pc.
The quantity
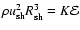 is conserved for the adiabatic shocks considered. The constant
is conserved for the adiabatic shocks considered. The constant
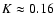 for solution (11), and
for solution (11), and
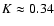 for solution (13). In the general case of a power-law gas distribution
for solution (13). In the general case of a power-law gas distribution
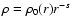 ,
s<5, the adiabatic shock evolution is described by the equations
,
s<5, the adiabatic shock evolution is described by the equations
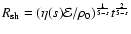 ,
and
,
and
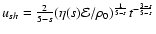 ,
where
,
where 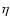 is constant at fixed s, which gives
the general formula
is constant at fixed s, which gives
the general formula
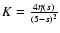 (the values of
(the values of 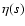 were given by Ostriker & McKee 1988).
were given by Ostriker & McKee 1988).
The ejecta-dominated stage precedes the adiabatic one. As long as the mass of the ejecta is large compared to the swept-up mass, the blast wave is moving with relatively weak deceleration. At this stage, shortly after the explosion, the structure of the rapidly expanding envelope of the presupernova star is important for the shock evolution. Actually, the blast wave consists of two shocks, the forward shock and the reverse shock, with the contact discontinuity surface between them. This surface separates the shocked wind or interstellar gas downstream of the forward shock from the shocked envelope
gas that fills the downstream region of the reverse shock. The reverse shock lags
behind the forward shock and enters the dense internal part of the exploding star by the time of the beginning of the Sedov stage. Though as an approximation for very young SNRs it cannot be well justified, we ignore below the cosmic ray acceleration at the reverse shock compared to the forward shock and use the notation
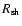 for the radius of forward shock (Berezinsky & Ptuskin 1989 considered the cosmic ray acceleration by both shocks; see also Yoshida & Yanagita 2001). The outer part of the star that freely expands after the SN explosion has a power law density profile
for the radius of forward shock (Berezinsky & Ptuskin 1989 considered the cosmic ray acceleration by both shocks; see also Yoshida & Yanagita 2001). The outer part of the star that freely expands after the SN explosion has a power law density profile
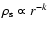 ,
see e.g. Chevalier & Liang (1989).
The value of k typically lies between 6 and 14. The value
,
see e.g. Chevalier & Liang (1989).
The value of k typically lies between 6 and 14. The value 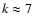 is characteristic of the SNe type Ia, and
is characteristic of the SNe type Ia, and
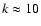 is typical of the SNe type II. A self similar solution for the blast wave at the ejecta-dominated stage was found by Chevalier (1982) and Nadyozhin (1981, 1985).
They showed that at an age larger than about one week, the evolution of the shock at the
ejecta-dominated stage can be approximately described by the power-law dependence
is typical of the SNe type II. A self similar solution for the blast wave at the ejecta-dominated stage was found by Chevalier (1982) and Nadyozhin (1981, 1985).
They showed that at an age larger than about one week, the evolution of the shock at the
ejecta-dominated stage can be approximately described by the power-law dependence
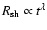 where the expansion parameter
where the expansion parameter
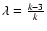 for the explosion in the uniform medium, and
for the explosion in the uniform medium, and
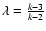 for the explosion in the wind of a presupernova
star
(for k>5 ejecta). In particular, using the results of the two papers mentioned above,
one can obtain the following equations
for the explosion in the wind of a presupernova
star
(for k>5 ejecta). In particular, using the results of the two papers mentioned above,
one can obtain the following equations
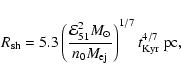
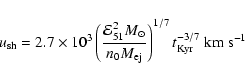 |
(14) |
for a type Ia SN explosion in an uniform interstellar medium at k=7;
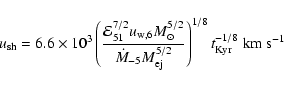 |
(15) |
for a type II SN explosion in the wind of a presupernova star at k=10.
Following the approach of Truelove & McKee (1999), one can describe the shock
produced by a type Ia SN using the continuous solution which coincides with the ejecta-dominated Eq. (14) until the moment
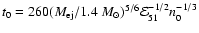 yr, and is given by the equations
yr, and is given by the equations
at a later time t>t0. It is evident from Eq. (16) that the adiabatic approximation (11) holds at
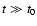 .
.
The evolution of a type II SN shock first follows the ejecta-dominated solution (15) in a presupernova wind and then, while still moving in the wind, it enters the adiabatic regime at the distance 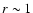 pc. The subsequent evolution proceeds in the medium with a complicated structure described above for a type II SN. The fairly accurate solution for the SNR evolution during this period can be obtained in the "thin-shell'' approximation, e.g. Ostriker & McKee (1988), Bisnovatyi-Kogan & Silich (1995).
Using this approximation for the strong shock and assuming a spherically symmetric distribution of the circumstellar gas density
pc. The subsequent evolution proceeds in the medium with a complicated structure described above for a type II SN. The fairly accurate solution for the SNR evolution during this period can be obtained in the "thin-shell'' approximation, e.g. Ostriker & McKee (1988), Bisnovatyi-Kogan & Silich (1995).
Using this approximation for the strong shock and assuming a spherically symmetric distribution of the circumstellar gas density 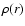 ,
we come to the following equations where the shock velocity
,
we come to the following equations where the shock velocity
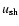 and the SNR age t are parameterized as functions of the shock radius
and the SNR age t are parameterized as functions of the shock radius
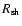 (see Appendix for the derivation of these equations):
(see Appendix for the derivation of these equations):
where
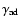 is the adiabatic index (
is the adiabatic index (
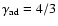 if the pressure downstream of the shock is determined by the
relativistic particles), and
if the pressure downstream of the shock is determined by the
relativistic particles), and
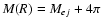
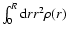 is
the mass of the swept-up gas. The self-similar solution by Chevalier and by Nadyozhin is not explicitly reproduced by Eqs. (17). The solutions (15) and (17) are fitted together at the transition from the ejecta-dominated regime to the adiabatic regime (at
is
the mass of the swept-up gas. The self-similar solution by Chevalier and by Nadyozhin is not explicitly reproduced by Eqs. (17). The solutions (15) and (17) are fitted together at the transition from the ejecta-dominated regime to the adiabatic regime (at 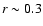 pc) in our numerical simulations of cosmic ray acceleration in the type II SNRs described below.
pc) in our numerical simulations of cosmic ray acceleration in the type II SNRs described below.
It is worth noting that the energy loss of SNRs in the form of escaping cosmic
rays is not taken into account in the solutions for shock evolution that
were
described in this section. In fact the shock evolution is only
approximately adiabatic.
At a given SNR age t, the cosmic rays are accelerated up to a maximum momentum
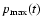 .
Also, particles with
.
Also, particles with
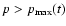 cannot be confined in the precursor of the shock even if they were accelerated earlier. Thus particles accelerated to the maximum energy escape from a SNR (see also Berezhko & Krymsky 1988). Let us estimate the flux of these run-away particles. We consider the simplified approach for the maximum energy of the accelerated particles and take the dependence of diffusion on momentum in the following simplified form:
cannot be confined in the precursor of the shock even if they were accelerated earlier. Thus particles accelerated to the maximum energy escape from a SNR (see also Berezhko & Krymsky 1988). Let us estimate the flux of these run-away particles. We consider the simplified approach for the maximum energy of the accelerated particles and take the dependence of diffusion on momentum in the following simplified form:
| D(p) |
= |
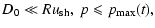 |
|
| D(p) |
= |
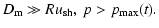 |
(18) |
The spectrum of the accelerated particles in this case has a very steep cut-off at
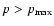 (cf. Eq. (1)) and the spectrum of run-away particles beyond
(cf. Eq. (1)) and the spectrum of run-away particles beyond
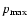 can be approximated by a
can be approximated by a  -function. To find the equation for these particles, let us integrate the equation for the momentum distribution function of cosmic rays
-function. To find the equation for these particles, let us integrate the equation for the momentum distribution function of cosmic rays
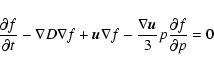 |
(19) |
on momentum p from
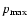 to
to
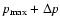 ,
where
,
where
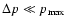 and larger than the width of the run-away particle
spectrum. Denoting
and larger than the width of the run-away particle
spectrum. Denoting
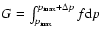 one
obtains from Eq. (19):
one
obtains from Eq. (19):
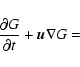 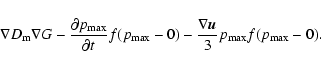 |
(20) |
Since the diffusion coefficient of the run-away particles is large, the advection
terms play no role in this equation and the last two terms can be considered
as a source of the particles. The total source of run-away particles is given by
the
volume integral of these terms. As a result, the source spectrum of the run-away
particles has the form
| q(p,t) |
= |
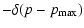 |
|
| |
|
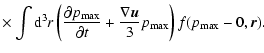 |
(21) |
The integration here is performed over the domain where the integrand is
negative. The integral
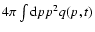 has dimensions number of
particles per unit time.
has dimensions number of
particles per unit time.
Below we consider the case of a spherically symmetric SN shock with linear
velocity profile at
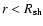 :
:
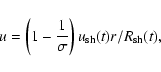 |
(22) |
where 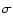 is the total shock compression ratio. It includes a thermal subshock and
a cosmic ray precursor. The linear velocity profile (22) is a good approximation of Sedov's solution and it can be considered as a very approximate one at the ejecta-dominated stage. Since the shock is partially modified in the
presence of cosmic rays, we should not assume any relation between the shock compression ratio
is the total shock compression ratio. It includes a thermal subshock and
a cosmic ray precursor. The linear velocity profile (22) is a good approximation of Sedov's solution and it can be considered as a very approximate one at the ejecta-dominated stage. Since the shock is partially modified in the
presence of cosmic rays, we should not assume any relation between the shock compression ratio 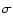 and the spectral index of accelerated particles 4-a (recall that
and the spectral index of accelerated particles 4-a (recall that
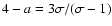 for unmodified shocks). We accept the value
for unmodified shocks). We accept the value 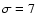 in our calculations. The preshock at
in our calculations. The preshock at
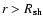 is created by the cosmic ray pressure gradient. Its width is small in comparison with the shock radius under the conditions
given by Eq. (18) and the plane shock approximation can be used. Since the cosmic ray
pressure dominates the gas pressure in the precursor region, its gradient is proportional to
the velocity gradient
is created by the cosmic ray pressure gradient. Its width is small in comparison with the shock radius under the conditions
given by Eq. (18) and the plane shock approximation can be used. Since the cosmic ray
pressure dominates the gas pressure in the precursor region, its gradient is proportional to
the velocity gradient
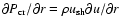 ,
where
,
where
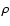 is the density of the circumstellar medium. We also use the assumption that
the cosmic
ray pressure at the shock is some fraction
is the density of the circumstellar medium. We also use the assumption that
the cosmic
ray pressure at the shock is some fraction
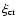 of the
upstream
momentum flux, see Eq. (1).
Now assuming that
of the
upstream
momentum flux, see Eq. (1).
Now assuming that
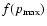 is proportional to the cosmic ray
pressure
the expression (21) for the run-away particle source takes the form
is proportional to the cosmic ray
pressure
the expression (21) for the run-away particle source takes the form
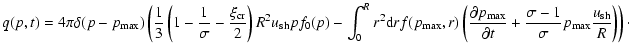 |
|
|
(23) |
The first term in this expression describes the particles
which runs away from the shock front, and the second term describes the
particles escaping from the shock interior.
In principle, the turbulence downstream from the strong shock might be
enhanced, which would result in a small cosmic ray diffusion coefficient. In
this case the particles do not run away from the
downstream and the second term
in Eq. (23) should be omitted. If the turbulence downstream is maintained
by the same process of cosmic ray streaming instability as in the
upstream region,
the downstream diffusion coefficient is comparable to the upstream diffusion
coefficient for particles with
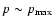 .
We shall further assume
that particles can run away both from upstream and downstream of the shock.
The uncertainty of the efficiency of the run-away process in the inner part of
SNR does not qualitatively change the conclusion about the average source
spectrum of cosmic rays calculated later in this section and shown in Fig. 2.
.
We shall further assume
that particles can run away both from upstream and downstream of the shock.
The uncertainty of the efficiency of the run-away process in the inner part of
SNR does not qualitatively change the conclusion about the average source
spectrum of cosmic rays calculated later in this section and shown in Fig. 2.
The distribution function of
particles
with
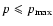 can be found using the solution of
transport Eq. (19) at
can be found using the solution of
transport Eq. (19) at
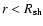 with the boundary condition
with the boundary condition
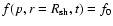 by the method of characteristics. This gives:
by the method of characteristics. This gives:
The expression in brackets in front of the integral in Eq. (24) should be
positive, which means that adiabatically the particles lose energy more slowly than
the maximum energy decreases. For the opposite sign, the adiabatic losses of
particles are faster than the decrease of maximum energy and the particles
do not run away from downstream of the shock. They can run away later
if at that time the decrease of the maximum momentum is faster.
The average source power Q(p) of run-away cosmic rays per unit volume in
the galactic disk is obtained by integrating q with respect to t
and by averaging over many SN explosions:
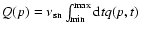 ,
where
,
where
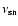 is the average frequency of SN
explosions per unit volume of the galactic disk. Changing the variable of
integration from t to
is the average frequency of SN
explosions per unit volume of the galactic disk. Changing the variable of
integration from t to
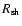 (
(
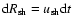 )
one can derive the following equation:
)
one can derive the following equation:
Here Eq. (1) for f0 with the approximation
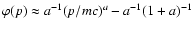 is used, and the condition
is used, and the condition
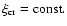 is assumed. The function
is assumed. The function
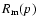 in Eq. (25)
is defined by the equation
in Eq. (25)
is defined by the equation
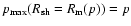 .
If
the last equation has multiple solutions at a given p, the summation on all
these solutions should be performed in Eq. (25). The physical meaning of
.
If
the last equation has multiple solutions at a given p, the summation on all
these solutions should be performed in Eq. (25). The physical meaning of
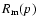 is as follows: it is the value of the shock radius when the maximum
momentum of accelerating particles is equal to p.
The second term in the r.h.s. of Eq. (25) should be omitted if the
expression
in parentheses in front of the integral is negative.
is as follows: it is the value of the shock radius when the maximum
momentum of accelerating particles is equal to p.
The second term in the r.h.s. of Eq. (25) should be omitted if the
expression
in parentheses in front of the integral is negative.
Let us assume that the maximum momentum is a power-law function of the shock
radius,
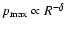 ,
the particles are
ultrarelativistic,
,
the particles are
ultrarelativistic,
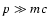 ,
and the compression ratio is constant,
,
and the compression ratio is constant,
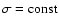 .
The
remarkable
feature of Eq. (25) is then that the expression in square brackets does not
depend on momentum at the adiabatic stage of SNR shock propagation in the
medium with a power-law distribution of the gas density, because
.
The
remarkable
feature of Eq. (25) is then that the expression in square brackets does not
depend on momentum at the adiabatic stage of SNR shock propagation in the
medium with a power-law distribution of the gas density, because
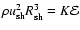 ,
,
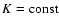 .
in this
case,
see Sect. 3. The average cosmic ray source power is now given by the
simple
equation
.
in this
case,
see Sect. 3. The average cosmic ray source power is now given by the
simple
equation
Q(p) = 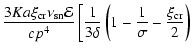 ![$\displaystyle \left.+ \frac{1}{\sigma}\frac{1-\frac{\sigma -1}{\sigma \delta}}
{1-\frac{1}{\sigma }+a\left( \delta-1+\frac{1}{\sigma }\right) }\right]\cdot$](/articles/aa/full/2005/03/aa1517/img202.gif) |
(26) |
Here the factors 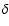 ,
and
,
and
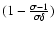 should
be
positive. The first term in the square brackets describes the particles
which
run away from the shock and the second term describes the particles which
run away from the SNR interior. Consequently, while in the adiabatic regime,
the SNR shock during its evolution produces run-away particles with the
universal power-law overall spectrum
should
be
positive. The first term in the square brackets describes the particles
which
run away from the shock and the second term describes the particles which
run away from the SNR interior. Consequently, while in the adiabatic regime,
the SNR shock during its evolution produces run-away particles with the
universal power-law overall spectrum
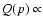 p-4, whereas the
instantaneous spectrum at the shock is more flat and not universal (see Eq. (1)) and the instantaneous spectrum of run-away particles has a
delta-function
form (see Eq. (24)).
p-4, whereas the
instantaneous spectrum at the shock is more flat and not universal (see Eq. (1)) and the instantaneous spectrum of run-away particles has a
delta-function
form (see Eq. (24)).
The total source power of ultrarelativistic particles calculated with the use of Eq. (26) is
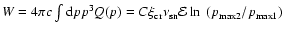 ,
where
,
where
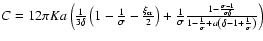 ;
;
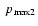 and
and
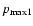 are the maximum momenta of
accelerated particles at the beginning and at the end of the adiabatic stage
respectively, thus typically
are the maximum momenta of
accelerated particles at the beginning and at the end of the adiabatic stage
respectively, thus typically
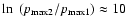 .
This leads to the estimate
.
This leads to the estimate
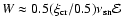 for the shock moving in the uniform interstellar
medium. Hence a considerable part of the total available mechanical energy
of SN explosion
for the shock moving in the uniform interstellar
medium. Hence a considerable part of the total available mechanical energy
of SN explosion
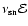 goes into cosmic rays at
goes into cosmic rays at
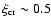 .
As is well known, the source spectrum
.
As is well known, the source spectrum
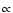 p-4or slightly steeper, and an efficiency of cosmic ray acceleration at the level 10-30% are needed to fit the cosmic ray data below the knee in the cosmic ray spectrum at about
p-4or slightly steeper, and an efficiency of cosmic ray acceleration at the level 10-30% are needed to fit the cosmic ray data below the knee in the cosmic ray spectrum at about
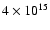 eV in the empirical model of cosmic ray origin (e.g. Ptuskin 2001, see also discussion below).
eV in the empirical model of cosmic ray origin (e.g. Ptuskin 2001, see also discussion below).
At the ejecta-dominated stage which precedes the adiabatic stage, the
average
spectrum of the run-away particles is different from p-4. Let us
consider
the general case and assume that
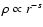 ,
,
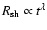 and hence
and hence
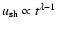 .
The maximum
momentum of accelerated particles in the high velocity limit (7) has the
scaling
.
The maximum
momentum of accelerated particles in the high velocity limit (7) has the
scaling
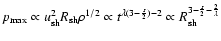 ,
so that
,
so that
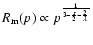 .
Now Eq. (25) at
.
Now Eq. (25) at
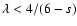 gives the
following shape of the average spectrum of run-away particles:
gives the
following shape of the average spectrum of run-away particles:
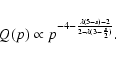 |
(27) |
A characteristic of the adiabatic regime is the relation
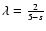 and therefore Eq. (27) gives
and therefore Eq. (27) gives
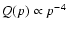 in agreement
with
Eq. (26). The Chevalier - Nadyozhin solution for the ejecta-dominated stage
has
in agreement
with
Eq. (26). The Chevalier - Nadyozhin solution for the ejecta-dominated stage
has
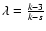 .
With the set of parameters excepted in
Section 3, we have then
.
With the set of parameters excepted in
Section 3, we have then
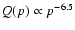 for the acceleration at the shock
produced by a type II SN in the presupernova star wind (s=2, k=10,
for the acceleration at the shock
produced by a type II SN in the presupernova star wind (s=2, k=10,
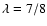 ), and
), and
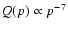 for the acceleration at the shock
produced by a type Ia SN in a uniform interstellar medium (s=0, k=7,
for the acceleration at the shock
produced by a type Ia SN in a uniform interstellar medium (s=0, k=7,
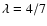 ). Thus the cosmic rays accelerated at the ejecta-dominated
stage
have higher energies than at the later adiabatic stage but the average
energy
spectrum of produced cosmic rays is rather steep at the "canonical'' choice
of presupernova star parameters.
). Thus the cosmic rays accelerated at the ejecta-dominated
stage
have higher energies than at the later adiabatic stage but the average
energy
spectrum of produced cosmic rays is rather steep at the "canonical'' choice
of presupernova star parameters.
The results of our numerical calculations of the average spectra for type II
and type Ia SNe are shown in Fig. 2. The parameter 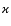 is equal to
0.1 in a high-velocity regime (7) and it is equal to 0.04 in a low-velocity
regime (9).
is equal to
0.1 in a high-velocity regime (7) and it is equal to 0.04 in a low-velocity
regime (9).
The calculations for type II SN are based on Eqs. (5), (6), (15), (17) and (25). For the set of parameters accepted in the present paper, the type II supernovae are able to accelerate cosmic ray protons to a maximum energy of the order
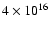 eV if the
acceleration starts one week after the SN explosion when
eV if the
acceleration starts one week after the SN explosion when
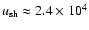 km s-1. The energy spectrum is close to p-4 at
energies less than about
km s-1. The energy spectrum is close to p-4 at
energies less than about
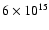 eV and it steepens above this energy. Thus the proton knee lies at about
eV and it steepens above this energy. Thus the proton knee lies at about
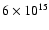 eV, in good agreement with the observational data. The sharp dip in the average proton spectrum at
eV, in good agreement with the observational data. The sharp dip in the average proton spectrum at
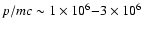 is caused by the assumed abrupt change
of the gas density at the boundary between the dense Red Super Giant wind
and the
low density bubble. We ran calculations up to the maximum shock radius 60
pc
(the corresponding SNR age is
is caused by the assumed abrupt change
of the gas density at the boundary between the dense Red Super Giant wind
and the
low density bubble. We ran calculations up to the maximum shock radius 60
pc
(the corresponding SNR age is
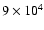 yr) when the Mach number
approaches
3 and the use of the particle spectrum (1) characteristic of the strongly
modified shocks can no longer be justified. The protons are accelerated to
about
20 GeV at this moment.
yr) when the Mach number
approaches
3 and the use of the particle spectrum (1) characteristic of the strongly
modified shocks can no longer be justified. The protons are accelerated to
about
20 GeV at this moment.
The calculations for type Ia SN in Fig. 2 are based on Eqs. (5), (6), (14), (16) and (25).
The calculations were made for a shock radius range from 0.2 to 30 pc
(SNR age from 4 yr to
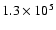 yr). The shock velocity
changes
during this period from
yr). The shock velocity
changes
during this period from
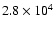 km s-1 to 91 km s-1. The protons are
accelerated from the maximum energy
km s-1 to 91 km s-1. The protons are
accelerated from the maximum energy
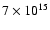 eV to about 10 GeV.
The approximate proton spectrum p-4 extends to the knee at about
eV to about 10 GeV.
The approximate proton spectrum p-4 extends to the knee at about
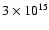 eV.
eV.
The average source spectrum produced by type Ia SNe is multiplied by 1/4 in Fig. 2, which corresponds to their relative explosion rate and hence reflects the relative contribution of this type of supernovae to the total production of cosmic
rays in the Galactic disk as compared to the contribution of type II SNe.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1517fig2.eps}\end{figure}](/articles/aa/full/2005/03/aa1517/Timg238.gif) |
Figure 2:
The solid line shows the average source spectrum
Q(p)p4c
(given in units
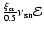 per
steradian) for protons released into the interstellar medium during SNR
evolution after SNII explosion in the wind of a RSG progenitor star. The
dashed line presents the case of a SNIa explosion in a uniform interstellar gas;
the average source spectrum is multiplied by 1/4. The dotted line shows the
shape of the proton source spectrum used by Hörandel (2003) to fit the KASCADE
data.
per
steradian) for protons released into the interstellar medium during SNR
evolution after SNII explosion in the wind of a RSG progenitor star. The
dashed line presents the case of a SNIa explosion in a uniform interstellar gas;
the average source spectrum is multiplied by 1/4. The dotted line shows the
shape of the proton source spectrum used by Hörandel (2003) to fit the KASCADE
data. |
| Open with DEXTER |
The spectrum of high-energy cosmic rays in the Galaxy is of the form
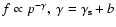 under the steady state
conditions
in which the action of cosmic ray sources (with source power
under the steady state
conditions
in which the action of cosmic ray sources (with source power
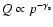 )
is balanced by the escape of energetic particles
from the Galaxy (with escape time
)
is balanced by the escape of energetic particles
from the Galaxy (with escape time
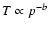 ).
The all-particle spectrum of cosmic rays observed at the Earth is close
to
).
The all-particle spectrum of cosmic rays observed at the Earth is close
to
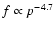 at
energies
at
energies
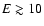 GeV/nucleon with a characteristic transition (the
knee, Kulikov & Khristiansen 1958) ranging over less than one decade in
the
vicinity of
GeV/nucleon with a characteristic transition (the
knee, Kulikov & Khristiansen 1958) ranging over less than one decade in
the
vicinity of
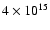 eV to the another power-law
eV to the another power-law
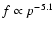 .
The latter extends to about
.
The latter extends to about
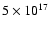 eV where the second knee with a
break
eV where the second knee with a
break
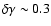 is seen in the cosmic ray spectrum, see
(Hörandel 2003) for a review. This structure is usually
associated with a
severe decrease of the efficiency of cosmic ray acceleration and/or
confinement in the Galaxy.The extragalactic component of cosmic rays
probably
dominates at
is seen in the cosmic ray spectrum, see
(Hörandel 2003) for a review. This structure is usually
associated with a
severe decrease of the efficiency of cosmic ray acceleration and/or
confinement in the Galaxy.The extragalactic component of cosmic rays
probably
dominates at
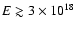 eV (Gaisser et al. 1993). In
the
alternative interpretation (Berezinsky et al. 2004),
the Galactic component
falls steeply (with
eV (Gaisser et al. 1993). In
the
alternative interpretation (Berezinsky et al. 2004),
the Galactic component
falls steeply (with
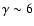 )
at
)
at
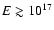 eV and the
extragalactic
component dominates from energy
eV and the
extragalactic
component dominates from energy 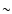
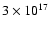 eV and above.
eV and above.
The exponent
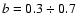 was obtained from the data on the abundance of
secondary nuclei at energies 109 to 1011 eV/nucleon. The secondary
nuclei are produced in cosmic rays in the course of nuclear fragmentation of
more heavier primary nuclei moving through the interstellar gas. The
uncertainty
in the value of b is mainly due to the choice of specific model of cosmic
ray transport in the Galaxy, see Ptuskin (2001). It
follows that the
source exponent below the first knee lies in the range
was obtained from the data on the abundance of
secondary nuclei at energies 109 to 1011 eV/nucleon. The secondary
nuclei are produced in cosmic rays in the course of nuclear fragmentation of
more heavier primary nuclei moving through the interstellar gas. The
uncertainty
in the value of b is mainly due to the choice of specific model of cosmic
ray transport in the Galaxy, see Ptuskin (2001). It
follows that the
source exponent below the first knee lies in the range
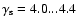 .
The value
.
The value
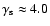 for the average
source
spectrum was obtained above in the consideration of particle acceleration by
SNR shocks during their adiabatic evolution (though smaller
for the average
source
spectrum was obtained above in the consideration of particle acceleration by
SNR shocks during their adiabatic evolution (though smaller 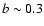 and
consequently larger
and
consequently larger
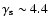 would be more favorable
for
the explanation of the high isotropy of cosmic rays observed at 1012 to
1014 eV). According to the results of Sect. 4 the calculated average
source spectrum p-4 for protons accelerated by a "typical'' type II
SNe
extends up to about
would be more favorable
for
the explanation of the high isotropy of cosmic rays observed at 1012 to
1014 eV). According to the results of Sect. 4 the calculated average
source spectrum p-4 for protons accelerated by a "typical'' type II
SNe
extends up to about
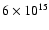 eV, which coincides with the
observed position of the knee
eV, which coincides with the
observed position of the knee 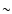
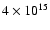 eV within the accuracy
of our analysis. The knee position at 3-5 PeV was determined in the recent
KASCADE
experiment (Ulrich et al. 2003).
The scaling
of the knee position in our model is
eV within the accuracy
of our analysis. The knee position at 3-5 PeV was determined in the recent
KASCADE
experiment (Ulrich et al. 2003).
The scaling
of the knee position in our model is
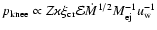 for explosion in the stellar wind and
for explosion in the stellar wind and
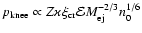 for explosion
in the uniform interstellar medium.
for explosion
in the uniform interstellar medium.
As was recalled earlier, the diffusive shock acceleration at the strong
nonmodified shock produces the spectrum
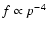 .
The back reaction
of efficiently accelerating particles modifies the shock structure, which
results in a
flatter particle spectrum (see references at the beginning of Sect. 2
and Eq. (1) where
.
The back reaction
of efficiently accelerating particles modifies the shock structure, which
results in a
flatter particle spectrum (see references at the beginning of Sect. 2
and Eq. (1) where 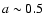 if the shock modification is very strong).
However, the numerical simulation of acceleration by SNR shocks under the
standard assumption of Bohm diffusion in the shock precursor (calculated for
the interstellar magnetic field strength) and with efficient confinement of
accelerated particles during the whole of the SNR evolution gives an overall source
spectrum
that is close to p-4 (Berezhko et al. 1996).
Berezhko & Völk (2000) pointed out that the last result is
in
some sense accidental. The late stages of SNR evolution are important
here
since a relatively weak
shock produces a steep particle spectrum, which has an effect on the overall
spectrum.
The situation is different in the model
discussed in the present paper because the diffusion coefficient
increases strongly with SNR age and the cosmic rays with energies larger
than
10-30 GeV/nucleon leave the supernova shell as run-away particles when
the shock remains strong. The final average source spectrum of high-energy
cosmic
rays with energies larger than 10-30 GeV/n is close to
p-4 provided that the shock evolution is approximately adiabatic and
the
efficiency of particle acceleration
if the shock modification is very strong).
However, the numerical simulation of acceleration by SNR shocks under the
standard assumption of Bohm diffusion in the shock precursor (calculated for
the interstellar magnetic field strength) and with efficient confinement of
accelerated particles during the whole of the SNR evolution gives an overall source
spectrum
that is close to p-4 (Berezhko et al. 1996).
Berezhko & Völk (2000) pointed out that the last result is
in
some sense accidental. The late stages of SNR evolution are important
here
since a relatively weak
shock produces a steep particle spectrum, which has an effect on the overall
spectrum.
The situation is different in the model
discussed in the present paper because the diffusion coefficient
increases strongly with SNR age and the cosmic rays with energies larger
than
10-30 GeV/nucleon leave the supernova shell as run-away particles when
the shock remains strong. The final average source spectrum of high-energy
cosmic
rays with energies larger than 10-30 GeV/n is close to
p-4 provided that the shock evolution is approximately adiabatic and
the
efficiency of particle acceleration
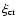 is roughly constant.
The source spectrum of particles with energies less than 10-30 GeV/n may
be
steeper because they are accelerated by not very strong shocks. In this
connection
it should be noted that the source
spectrum in the basic empirical model of cosmic ray propagation in the
Galaxy is of the form
is roughly constant.
The source spectrum of particles with energies less than 10-30 GeV/n may
be
steeper because they are accelerated by not very strong shocks. In this
connection
it should be noted that the source
spectrum in the basic empirical model of cosmic ray propagation in the
Galaxy is of the form
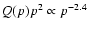 at E<30 GeV/n, and
at E<30 GeV/n, and
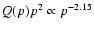 at E>30 GeV/n,
see Jones et al. (2001).
at E>30 GeV/n,
see Jones et al. (2001).
There are other important differences between the standard
models of cosmic-ray acceleration and the one presented here.
As noted before, our
model of cosmic ray acceleration with a strong increase in time of the
diffusion
coefficient and corresponding decrease of maximum particle energy may
naturally explain why the SNRs are generally not bright in very high energy
gamma-rays at an age larger than a few thousand years. At this period of
time, there are no particles with the energies needed to generate the very high
energy gamma-rays in a SNR shell. Another problem is the contribution of
gamma-ray emission from numerous unresolved SNRs with relatively flat
spectra
to the diffuse galactic background at very high energies. Working in the
standard model Berezhko & Völk (2003) took the maximum
possible energy of
protons accelerated in SNRs equal to 1014 eV, i.e. well below the knee
position, and this made it possible not to exceed the upper limits on the diffuse
gamma-ray
emission at
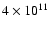 to 1013 eV obtained in the Whipple,
HEGRA,
and TIBET experiments. In the model considered in the present work even with
efficient proton acceleration that may go beyond the knee, the expected
gamma-ray emission from SNRs at
to 1013 eV obtained in the Whipple,
HEGRA,
and TIBET experiments. In the model considered in the present work even with
efficient proton acceleration that may go beyond the knee, the expected
gamma-ray emission from SNRs at
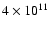 eV is an order of
magnitude smaller than in the model with Bohm diffusion. For a similar
reason,
the standard model compared with the present model predicts a larger ratio of
fluxes of
secondary and primary nuclei formed at very high energies through the
reacceleration of secondaries by strong shocks and through the direct
production of secondaries by primary nuclei with flat energy spectra inside
SNRs, see Berezhko et al. (2003).
eV is an order of
magnitude smaller than in the model with Bohm diffusion. For a similar
reason,
the standard model compared with the present model predicts a larger ratio of
fluxes of
secondary and primary nuclei formed at very high energies through the
reacceleration of secondaries by strong shocks and through the direct
production of secondaries by primary nuclei with flat energy spectra inside
SNRs, see Berezhko et al. (2003).
The interpretation of the energy spectrum beyond the knee in the present model
is
associated with the cosmic ray acceleration during the ejecta-dominated
stage
of SNR evolution when the protons gain
energy that is larger by an order of magnitude than at the
adiabatic stage but the number of particles involved in the
shock
acceleration is relatively small. The average source spectrum of accelerated
particles is not universal at this stage. It is power law
with an exponent
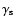 whose value is very
sensitive to the parameter k. The last is not well determined from the
observations but the typical values accepted in our calculations were k=10for a type II SN explosion in the wind of a Red Super Giant progenitor,
and
k=7 for a type Ia SN explosion in a uniform interstellar medium (see
Chevalier & Liang 1989) that give
whose value is very
sensitive to the parameter k. The last is not well determined from the
observations but the typical values accepted in our calculations were k=10for a type II SN explosion in the wind of a Red Super Giant progenitor,
and
k=7 for a type Ia SN explosion in a uniform interstellar medium (see
Chevalier & Liang 1989) that give
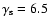 and
and
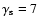 respectively; see Sect. 4. To illustrate
the range of possible uncertainty, it is worth noting that the value k=5.4was suggested for the type Ia SNe by Imshennik et al. (1981).
This value of
k results in
respectively; see Sect. 4. To illustrate
the range of possible uncertainty, it is worth noting that the value k=5.4was suggested for the type Ia SNe by Imshennik et al. (1981).
This value of
k results in
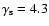 at the ejecta-dominated stage.
at the ejecta-dominated stage.
The breaks and cutoffs in the spectra of ions with different charges should
occur at the same magnetic rigidity as for protons, i.e. at the same ratio
p/Z (or E/Z for ultrarelativistic nuclei). The data of the KASCADE
experiment
(Ulrich et al. 2003) for the most abundant groups of nuclei
(protons, helium,
CNO group, and the iron group nuclei) are, in general, consistent with this
concept. According to Hörandel (2003) a good fit to the
observations is
reached if an individual constituent ion spectrum has a gradual steepening
by
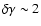 at energy
at energy
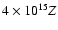 eV. Equation (27) shows that the
value
eV. Equation (27) shows that the
value
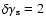 can be obtained at k=9, s=2 (the SN
explosion in the progenitor wind), or k=6.6, s=0 (the SN explosion in
the
uniform interstellar medium), which are not very different from our accepted
"typical'' values, see Fig. 2.
can be obtained at k=9, s=2 (the SN
explosion in the progenitor wind), or k=6.6, s=0 (the SN explosion in
the
uniform interstellar medium), which are not very different from our accepted
"typical'' values, see Fig. 2.
At present, the main problem of the data interpretation centers around the
second knee in the cosmic ray spectrum. The natural assumption that all
individual ions have only one knee at 
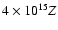 eV and that the
knee in the spectrum of iron (Z=26) expected at about 1017 eV
explains the second knee in the all-particle spectrum does not agree with
the
observed position of the second knee at
eV and that the
knee in the spectrum of iron (Z=26) expected at about 1017 eV
explains the second knee in the all-particle spectrum does not agree with
the
observed position of the second knee at
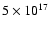 eV. One way out was
suggested by Hörandel (2003) who included all elements up to
Z=92 into
the consideration and assumed that
eV. One way out was
suggested by Hörandel (2003) who included all elements up to
Z=92 into
the consideration and assumed that
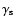 decreases with Z
to
raise the contribution of ultra heavy nuclei from Galactic sources to the
cosmic ray flux at
decreases with Z
to
raise the contribution of ultra heavy nuclei from Galactic sources to the
cosmic ray flux at  1017 eV. Of considerable promise is the
approach by Sveshnikova (2003) who took into account the
dispersion of
parameters of SN explosions in her calculations of the knee position and the
maximum particle energy. This leads to a widening of the energy interval
between the two knees in the overall all-particle spectrum. This analysis
should be supplemented by the account of different chemical compositions of
the
progenitor star winds that determine the composition of accelerated cosmic
rays (Silberberg et al. 1991). We plan future work on this
topic in the
framework of the model developed in the present paper and Paper I. It
should
be noted that the model by Berezinsky et al. (2004)
is quite consistent with
the decreasing of the flux from Galactic sources above 1017 eV
since the conjunction with the intergalactic cosmic ray flux in their model
occurs at relatively low energy.
1017 eV. Of considerable promise is the
approach by Sveshnikova (2003) who took into account the
dispersion of
parameters of SN explosions in her calculations of the knee position and the
maximum particle energy. This leads to a widening of the energy interval
between the two knees in the overall all-particle spectrum. This analysis
should be supplemented by the account of different chemical compositions of
the
progenitor star winds that determine the composition of accelerated cosmic
rays (Silberberg et al. 1991). We plan future work on this
topic in the
framework of the model developed in the present paper and Paper I. It
should
be noted that the model by Berezinsky et al. (2004)
is quite consistent with
the decreasing of the flux from Galactic sources above 1017 eV
since the conjunction with the intergalactic cosmic ray flux in their model
occurs at relatively low energy.
There is also a very different scenario which assumes the strong
reacceleration of cosmic rays
above the knee by the collective effect of multiple SNR shocks in
violent
regions of the Galactic disk (Axford 1994; Bykov & Toptygin
2001; Klepach et al. 2000)
or Galactic wind (Völk & Zirakashvili 2004).
Finally, it is worth noting that in principle the knee may
arise not in the sources but in the process of cosmic ray propagation in the
Galaxy,
e.g. as a result of interplay between ordinary and Hall diffusion
(Ptuskin et al. 1993; Roulet 2004).
However, this explanation requires the existence of a power-law source
spectrum
which extends without essential breaks up to about 1018 eV or even
further.
The accounting for non-linear effects which accompany the cosmic ray
streaming
instability raises the maximum energy of accelerated particles in young SNRs
above the standard Bohm limit by about two orders of magnitude. It also
considerably
reduces the maximum energy of particles that are present inside SNRs at the
late Sedov stage
if, as was assumed in our calculations in Sect. 4, the
cosmic ray diffusion coefficient downstream of the shock is not much smaller
than the diffusion coefficient in the cosmic ray
precursor of the shock and the
energetic particles with
 run away from the
SNR interior.
In the present paper we studied the effect of a strong time
dependence of the maximum particle momentum
run away from the
SNR interior.
In the present paper we studied the effect of a strong time
dependence of the maximum particle momentum
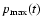 on the average
spectrum
of cosmic rays injected into interstellar space from many supernova remnants
over their lifetime. The instantaneous cosmic ray spectrum at a strongly
modified shock is flat (
on the average
spectrum
of cosmic rays injected into interstellar space from many supernova remnants
over their lifetime. The instantaneous cosmic ray spectrum at a strongly
modified shock is flat (
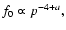 a>0, Eq. (1)) and the
particle energy density is mainly determined by the particles with maximum
momentum
a>0, Eq. (1)) and the
particle energy density is mainly determined by the particles with maximum
momentum
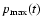 .
The instantaneous source spectrum of the run-away
particles is close to a delta function (
.
The instantaneous source spectrum of the run-away
particles is close to a delta function (
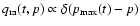 ,
Eq. (24)). At the same time, the assumption that a
constant fraction
,
Eq. (24)). At the same time, the assumption that a
constant fraction 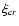 of incoming gas momentum flux goes into the
cosmic ray pressure at the shock, and the fact that the supernova remnant
evolution is adiabatic leads to an average
source spectrum for ultrarelativistic particles from the ensemble of SNRs
that is close to
of incoming gas momentum flux goes into the
cosmic ray pressure at the shock, and the fact that the supernova remnant
evolution is adiabatic leads to an average
source spectrum for ultrarelativistic particles from the ensemble of SNRs
that is close to
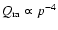 from energies 10-30 GeV/n up to the knee position in the observed
cosmic ray spectrum
independent of the value of a, (see Eq. (26) and Fig. 2). This source
spectrum is consistent with the
empirical model of cosmic ray propagation in the Galaxy. The acceleration at
the preceding ejecta-dominated stage of SNR evolution provides the steep
power-law
tail in the particle distribution at higher energies up to
from energies 10-30 GeV/n up to the knee position in the observed
cosmic ray spectrum
independent of the value of a, (see Eq. (26) and Fig. 2). This source
spectrum is consistent with the
empirical model of cosmic ray propagation in the Galaxy. The acceleration at
the preceding ejecta-dominated stage of SNR evolution provides the steep
power-law
tail in the particle distribution at higher energies up to
 1018 eV (if the iron nuclei dominate at these energies).
The knee in the observed energy spectrum of cosmic rays at
1018 eV (if the iron nuclei dominate at these energies).
The knee in the observed energy spectrum of cosmic rays at
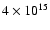 eV is explained in our model by the
transition from the ejecta-dominate stage to
the adiabatic stage of SNR shock evolution.
In spite of the approximate character of our consideration, the
suggested
scenario of particle acceleration can explain the energy spectrum of
Galactic
cosmic rays.
eV is explained in our model by the
transition from the ejecta-dominate stage to
the adiabatic stage of SNR shock evolution.
In spite of the approximate character of our consideration, the
suggested
scenario of particle acceleration can explain the energy spectrum of
Galactic
cosmic rays.
Acknowledgements
The authors are grateful to Evgenij Berezhko and
Heinz Völk for fruitful discussions. We thank the referee for
valuable comments. This work was supported by
an RFBR grant at IZMIRAN. VSP was also supported by a NASA grant
during his visit to the University of Maryland where part of this work was
carried out.
The thin-shell approximation can be used when the swept-up gas is
concentrated
in a thin layer behind the shock. In particular, it is applied to the case
of
a spherical adiabatic shock, see Ostriker & McKee
(1988) and
Bisnovatyi-Kogan & Silich (1995) for details. The total mass of the
gas shell
involved in the motion and confined by the shock of radius
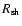 in the spherically symmetrical case is
in the spherically symmetrical case is
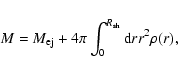 |
(A.1) |
where
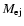 is the ejected mass,
is the ejected mass,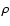 is the density of
ambient gas.
is the density of
ambient gas.
The equation of momentum conservation is
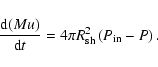 |
(A.2) |
Here u is the gas velocity behind the shock,
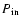 is the
pressure behind the shock, and P is the pressure of ambient gas. For the
adiabatic blastwave, u is related to the shock velocity
is the
pressure behind the shock, and P is the pressure of ambient gas. For the
adiabatic blastwave, u is related to the shock velocity
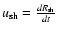 by the equation
by the equation
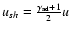 ,
where
,
where
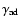 is the ratio of the
specific heats (adiabatic index). The energy of explosion
is the ratio of the
specific heats (adiabatic index). The energy of explosion
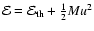 consists of the internal energy
consists of the internal energy
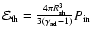 and the kinetic energy.
and the kinetic energy.
Now for a very strong shock where
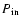 is
negligible compared to P, Eq. (A2) can be presented as:
is
negligible compared to P, Eq. (A2) can be presented as:
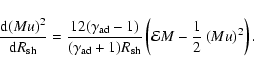 |
(A.3) |
The solution of Eq. (A3) allows finding the shock velocity and the shock age
as functions of the shock radius:
where
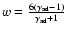 ,
which
coincides with Eq. (17) in the main text.
,
which
coincides with Eq. (17) in the main text.
- Aharonian, F. A.,
Akhperjanian, A. G., Beilicke, M. et al. 2002, A&A, 395,
803 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Axford, W. I. 1994,
ApJS, 90, 937 [NASA ADS] [CrossRef] (In the text)
- Bell, A. R. 1978,
MNRAS, 182, 147 [NASA ADS] (In the text)
- Bell, A. R., &
Lucek, S. G. 2001, MNRAS, 321, 433 [NASA ADS] [CrossRef] (In the text)
- Berezhko, E.
G., Ksenofontov, L. T., Ptuskin, V. S., Zirakashvili, V. N., &
Völk, H. J. 2003, A&A 410, 189
(In the text)
- Berezhko, E.
G., & Krymsky, G. F. 1988, Sov. Phys. Uspekhi, 31, 83 (In the text)
- Berezhko, E.
G., & Völk, H. J. 2000, A&A, 357, 283 [NASA ADS] (In the text)
- Berezhko, E.
G., & Völk, H. J. 2003, Proc. 28th Intern. Cosmic Ray
Conf., Tsukuba, 2433
- Berezhko, E.
G., Yelshin, V. K., & Ksenofontov, L. T. 1996, JETP, 82, 1 [NASA ADS] (In the text)
-
Berezinskii, V. S., Bulanov, S. V., Ginzburg, V. L, Dogiel, V. A.,
& Ptuskin, V. S. 1990, Astrophysics of Cosmic Rays, ed. V. L.
Ginzburg, Amsterdam, North Holland
(In the text)
- Berezinsky,
V. S., Grigorieva, S. I.,& Hnatyk, B. I. 2004, Astropart.
Phys., 21, 617 [NASA ADS] [CrossRef] (In the text)
- Berezinsky,
V. S., & Ptuskin, V. S. 1989, A&A 215, 399
(In the text)
- Bisnovatyi-Kogan, G. S.,
& Silich, S. A. 1995, Rev. Mod. Phys., 67, 661 [NASA ADS] [CrossRef] (In the text)
- Blandford, R. D.,
& Ostriker, J. P. 1980, ApJ, 237, 793 [NASA ADS] [CrossRef]
- Buckley, J. H.,
Akerlof, C. W., Carter-Lewis, D. A., et al. 1998, A&A, 329,
639 [NASA ADS] (In the text)
- Bykov, A. M., &
Toptygin, I. N. 2001, Astron. Lett., 27, 625 [NASA ADS] [CrossRef] (In the text)
- Chevalier, R.
A. 1982, ApJ, 259, 302 [NASA ADS] [CrossRef] (In the text)
- Chevalier, R.
A., & Liang, E. P. 1989, ApJ, 344, 332 [NASA ADS] [CrossRef] (In the text)
- Drury, L. O'C.,
Duffy, P., & Kirk, J. G. 1996, ApJ, 309, 1002 [NASA ADS] (In the text)
- Drury, L. O'C.,
Ellison, D. E., Aharonian, F. A., et al. 2001, Space Sci. Rev., 99,
329 [NASA ADS] [CrossRef] (In the text)
- Drury, L. O'C., van
der Swaluw, E., & Carroll, O. 2003,
[arXiv:astro-ph/0309820]
(In the text)
- Eichler, D. 1984,
ApJ, 277, 429 [NASA ADS] [CrossRef] (In the text)
- Fedorenko, V. N.
1990, Preprint 1442, A. F. Ioffe Phys. Tech. Inst., Leningrad
(In the text)
- Gaisser, T. K. et al.
1993, Phys. Rev. D47, 1919
(In the text)
- Hörandel, J.
R. 2003, Astroparticle Physics, 19, 193 [NASA ADS] [CrossRef] (In the text)
- Imshennik, V. S.,
Nadyozhin, D. K., & Utrobin, V. P. 1981, Ap&SS, 78,
105 [NASA ADS] (In the text)
- Jones, F. C., Lukasiak,
A., Ptuskin, V., & Webber, W. 2001, ApJ, 547, 264 [NASA ADS] [CrossRef] (In the text)
- Klepach, E. G.,
Ptuskin, V. S., & Zirakashvili, V. N. 2000, Astropart. Phys.,
13, 161 [NASA ADS] [CrossRef] (In the text)
- Krymsky, G. F. 1977,
Soviet Physics-Doklady, 22, 327 (In the text)
- Kulikov, G. V., &
Khristiansen, G. B. 1958, JETP 35, 441
(In the text)
- Lozinskaya, T.
A. 1992, Supernovae and Stellar Wind in the Interstellar Medium,
New York, American Institute of Physics
(In the text)
- Malkov, M. A., &
Drury, L. O'C. 2001, Rep. Prog. Phys., 64, 429 [NASA ADS] [CrossRef] (In the text)
- Nadyozhin, D.
K. 1981, Preprint ITEP, #1
(In the text)
- Nadyozhin, D.
K. 1985, Ap&SS, 112, 225 [NASA ADS] (In the text)
- Ostriker, J. P.,
& McKee, C. F. 1988, Rev. Mod. Phys., 60, 1 [NASA ADS] [CrossRef] (In the text)
- Parker, E. N. 1958,
ApJ, 128, 664 [NASA ADS] [CrossRef] (In the text)
- Ptuskin, V. S.
2001, Space Sci. Rev., 99, 281 [NASA ADS] [CrossRef] (In the text)
- Ptuskin, V. S., Rogovaya,
S. I., Zirakashvili, V. N., et al. 1993, A&A, 268, 726 [NASA ADS] (In the text)
- Ptuskin, V. S.,
& Zirakashvili, V. N. 2003, A&A, 403, 1 [EDP Sciences] [NASA ADS] [CrossRef] (Paper I)
(In the text)
- Roulet, E. 2004, Int.
J. Mod. Phys. A, 19, 1133 [NASA ADS] (In the text)
- Silberberg, R.,
Tsao, C. H., Shapiro, M. M., & Biermann, P. L. 1991, in Cosmic
Rays, Supernovae, Interstellar Medium, ed. M. M. Shapiro, R.
Silberberg, & J. P. Wefel (Kluwer Ac. Publ.), 97
(In the text)
- Sveshnikova,
L. G. 2003, A&A, 409, 799 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Truelove, J. K.,
& McKee, C. F. 1999, ApJS, 120, 299 [NASA ADS] [CrossRef] (In the text)
- Ulrich, H., Antonia,
T., Apel, W. D., et al. 2003, Nucl. Phys. B (Proc. Suppl.), 122,
218 [NASA ADS] (In the text)
- Verma, M. K., Roberts, D.
A., Goldstein, M. L., et al. 1996, JGR, 101, 21619 [NASA ADS] (In the text)
- Vink, J. 2003
[arXiv:astro-ph/0311406]
(In the text)
- Völk, H. J.,
& Zirakashvili, V. N. 2004, A&A, 417, 807 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Völk, H. J., Zank,
L. A., & Zank, G. P. 1988, A&A, 198, 274 [NASA ADS] (In the text)
- Weaver, R., McCray, R.,
Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [NASA ADS] [CrossRef] (In the text)
- Yoshida, T., &
Yanagita, S. 2001, Proc. 27th Intern. Cosmic Ray Conf., Hamburg,
OG3.3.11
(In the text)
Copyright ESO 2005
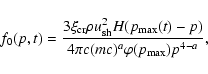
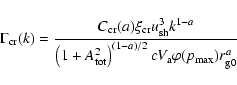
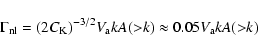
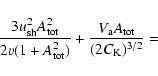
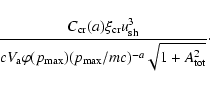
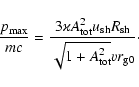
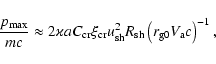
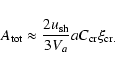
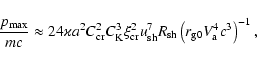
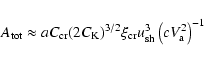
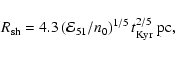
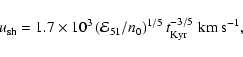
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1517fig1.eps}
\end{figure}](/articles/aa/full/2005/03/aa1517/Timg71.gif)
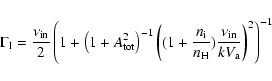
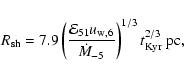
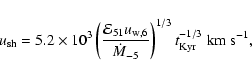
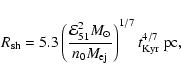
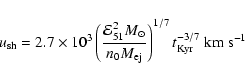
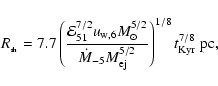
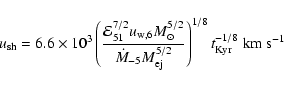
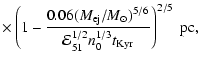
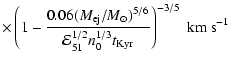
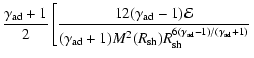
![$\displaystyle \left.\times \int_{0}^{R{\rm sh}}{\rm d}rr^{6\left(
\frac{\gamma_{{\rm ad}}-1}{\gamma_{{\rm ad}}+1}\right) -1}M(r)\right]
^{1/2},\;$](/articles/aa/full/2005/03/aa1517/img149.gif)
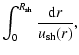
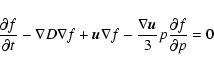
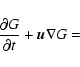
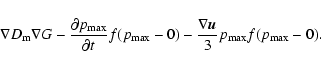
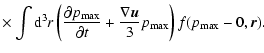
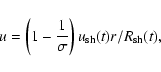
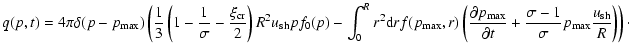
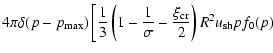
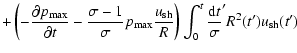
![$\displaystyle \left.\times f_{0}\left( p\left( \frac{R(t)}{R(t^{\prime})}\right...
...right) \left(
\frac{R(t)}{R(t^{\prime})}\right)
^{3-\frac 3\sigma }\right]\cdot$](/articles/aa/full/2005/03/aa1517/img186.gif)
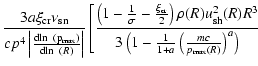
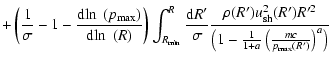
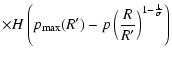
![$\displaystyle \left.\times \left( \frac{p}{p_{\max}(R^{\prime})}\right) ^{a}
\l...
...{R^{\prime}}\right) ^{(a-1)(\sigma -1)/\sigma }\right]
_{R=R_{{\rm m}}(p)}\cdot$](/articles/aa/full/2005/03/aa1517/img193.gif)
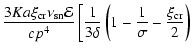
![$\displaystyle \left.+ \frac{1}{\sigma}\frac{1-\frac{\sigma -1}{\sigma \delta}}
{1-\frac{1}{\sigma }+a\left( \delta-1+\frac{1}{\sigma }\right) }\right]\cdot$](/articles/aa/full/2005/03/aa1517/img202.gif)
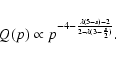
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1517fig2.eps}\end{figure}](/articles/aa/full/2005/03/aa1517/Timg238.gif)
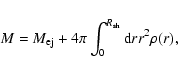
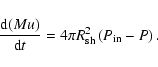
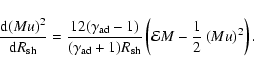
![$\displaystyle \frac{\gamma_{{\rm ad}}+1}{2}\left[
\frac{2w\mathcal{E}}{M^{2}(R_...
...h}})R_{{\rm sh}}^{w}}\int
_{0}^{R_{{\rm sh}}}{\rm d}rr^{w-1}M(r)\right] ^{1/2},$](/articles/aa/full/2005/03/aa1517/img283.gif)