A&A 429, 531-542 (2005)
DOI: 10.1051/0004-6361:200400082
Turbulence in circumstellar disks
F. Hersant1,2,3 - B. Dubrulle1 - J.-M. Huré4,5
1 - CNRS URA 2464 GIT/SPEC/DRECAM/DSM, CEA Saclay, 91191
Gif-sur-Yvette Cedex, France
2 -
LESIA CNRS UMR 8109, Observatoire de Paris-Meudon, Place Jules
Janssen, 92195 Meudon Cedex, France
3 -
Institut für Theoretische Astrophysik, Tiergartenstraße 15,
69121 Heidelberg, Germany
4 -
LUTh CNRS UMR 8102, Observatoire de Paris-Meudon, Place Jules
Janssen, 92195 Meudon Cedex, France
5 -
Université Paris 7 Denis Diderot, 2 Place Jussieu, 75251
Paris Cedex 05, France
Received 31 January 2003 / Accepted 16 August 2004
Abstract
We investigate the relationship between circumstellar disks and the
Taylor-Couette flow. Using the Reynolds similarity principle, this
results in a number of parameter-free predictions about stability of
the disks, and their turbulent transport properties, provided the
disk structure is available. We discuss how the latter can be deduced
from interferometric observations of circumstellar material. We use
the resulting disk structure to compute the molecular transport
coefficients, including the effect of ionization by the
central object. The resulting control parameter indicates that the
disk is well into the turbulent regime. The analogy is also used to
compute the effective accretion rate, as a
function of the disk
characteristic parameters (orbiting velocity, temperature and
density). These values are in very good agreement with experimental,
parameter-free predictions derived from the supposed relationship. The turbulent
viscosity is also computed and found to correspond to an
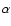 -parameter
-parameter
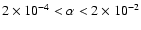 .
Predictions regarding fluctuations are also checked: luminosity
fluctuations
in disks do obey the same universal distribution as energy fluctuations
observed in a laboratory turbulent flow. Radial velocity
dispersion in the outer part of the disk is predicted to be of the
order of 0.1 km s-1,
in agreement with available observations.
All these issues provide
a proof of the turbulent character of
circumstellar disks, as well as a parameter-free theoretical
estimate of effective accretion rates.
.
Predictions regarding fluctuations are also checked: luminosity
fluctuations
in disks do obey the same universal distribution as energy fluctuations
observed in a laboratory turbulent flow. Radial velocity
dispersion in the outer part of the disk is predicted to be of the
order of 0.1 km s-1,
in agreement with available observations.
All these issues provide
a proof of the turbulent character of
circumstellar disks, as well as a parameter-free theoretical
estimate of effective accretion rates.
Key words: turbulence - Solar system: formation - stars: formation - accretion, accretion disks
1 Introduction
Stars form by gravitational collapse of molecular clouds. During this process,
proto-stars get surrounded and plausibly are fed by an
envelope/disk made of gas and dust, which can, under certain conditions,
coagulate to form planetary embryos. There is little doubt that gas motion,
usually considered as turbulent, plays a major role.
Turbulent motion enhances transport properties, thereby
accelerating the evolution of the temperature and density in the
envelope/disk. Also, turbulence may catalyze planet formation thanks to
the trapping of dust particle inside large-scale vortices (Barge &
Sommeria 1995; Tanga et al. 1996; Chavanis 2000).
As of now, the assertion that circumstellar disks are
turbulent (what we shall refer to as the "turbulent hypothesis'') has
never been properly checked. It mainly relies on the fact that
the luminosity produced by the disk interacting with the central
star is very
large (see e.g. Hartmann et al. 1998). In certain cases (FU
Orionis-type systems),
this luminosity is so high that it even supersedes the stellar
component.
The most widely accepted scenario so far to account for the abnormal
luminosities of young stellar
objects involves a magnetospheric
accretion for classical T Tauri stars. In this case, the matter in the inner
parts of the disk is coupled with the stellar magnetic field and falls onto
the stars along the field lines at the free fall velocity (see e.g. Gullbring
et al. 1998; Muzerolle et al. 1998). This entails an
accretion shock at the stellar surface in which almost all the visible
and UV excess is produced (veiling the stellar lines).
This scenario has shown many successes in interpreting spectral features
of T Tauri stars like sodium and hydrogen line profiles (see e.g. Muzerolle et al. 1998).
In the case of Fu Ori stars,
the currently
advocated picture involves a wide boundary layer
(see e.g. Popham et al. 1996).
One of the main weaknesses of this scenario is its
low predictive
power since it relies on an adjustable parameter (the accretion
rate) which must be postulated a posteriori by comparison with
observational data.
Indeed, in this framework, the luminosity is directly related
to the amount of
energy released by the disk.
The
necessity for turbulence comes from the hypothesis
that no laminar motions can produce the amount of energy
dissipated
required to explain observed luminosities (see e.g. Pringle 1981
and references therein). However, no attempt has been made to
substantiate this claim in a quantitative manner. The questions we address here
are: what are the luminosities produced by a laminar disk and by a
turbulent disk? How do these compare with observations?
These two questions are equally difficult to answer, but they hide
different levels of difficulties. One is of a theoretical nature: the
physical processes at work in this disk/star interaction region are
complex. A correct description should simultaneously include the
resolution of turbulence (with compressibility effects), radiative
transfer (accounting for UV-irradiation by the star), magnetic
processes, chemistry, the disk flaring, phase separation, time
evolution, etc. The second difficulty is of an observational nature. At
the present time,
information has been gathered about the temperature, density and
velocity distributions
in the outer parts of disks, at 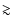 100 AU typically,
thanks to high resolution interferometry and clever data analysis
(Guilloteau & Dutrey 1998).
Unfortunately, basic parameters (mean free path, sound velocity and
viscosity) connected with the gas dynamics and dissipation are still
not known in the inner regions, and especially in the region
where the disk and the star interact.
100 AU typically,
thanks to high resolution interferometry and clever data analysis
(Guilloteau & Dutrey 1998).
Unfortunately, basic parameters (mean free path, sound velocity and
viscosity) connected with the gas dynamics and dissipation are still
not known in the inner regions, and especially in the region
where the disk and the star interact.
Because of these difficulties, we choose to adopt a
radically different approach than the classical model: instead of
trying to build a fully
"realistic'' circumstellar disk, we use a simplified hydrodynamic
model ("zero order model'') and study in detail its physical
properties.
In the future, we will slowly increase its complexity (and reality!) by adding
new ingredients like magnetic field, stratification, radiative
transfer. Here, we show that our zero order model is analogous to an
incompressible rotating shear flow. It is therefore amenable to
treatment as a
simple laboratory prototype, the Taylor-Couette flow. From theoretical and
experimental studies of the properties of this prototype, one can then
build general laws in circumstellar disks by a simple use of the
Reynolds similarity principle. Taylor-Couette flow is a classical
laboratory flow, and it has been the subject of many experiments. A
recent review about stability properties and transport properties for
use in astrophysical flows has been made by Dubrulle et al. (2004).
As a result, they derive critical conditions for stability, and
simple scaling laws
for transport properties, including the influence of stratification,
magnetic field, boundary conditions and aspect ratio. In the present
paper, we apply these results to circumstellar disks and derive the
expression of the characteristic
parameters of the model as a function of astrophysical observables. We
propose a procedure of quantitative estimation of the observables using
the observational results of Guilloteau & Dutrey (1998) and derive
parameter-free predictions about turbulence and turbulent transport
in circumstellar disks. These predictions are tested against
observational data from T Tauri and FU Ori stars.
2 Hydrodynamic model
2.1 Basic ideas
Observation of circumstellar disks suggests that they have sizes
between 100 and 1000 astronomical units. In the following, we will focus
only on the part of the disk expected to behave like an incompressible fluid.
An estimate of the importance of compressibility can be obtained via
the Mach number, the ratio of the typical velocity to thermal
velocities. It is generally admitted that compressibility effects
start playing a role when this number reaches values of unity. In the
outer part of the disk, this ratio has been estimated by Guilloteau
& Dutrey (1998) from CO line profiles. Its value is about
0.2-0.3. In the inner part of the disk (radius ranging from 1 to 30
astronomical units), we may use the disk structure inferred from
the D/H ratio measured in the Solar System
(Drouart et al. 1999; Hersant et al. 2001), which leads
to a Mach number of the order of 0.05 to 0.1. These figures
indicate that both the inner and the outer part can be treated
as
incompressible fluids. Closer to the star, the situation is less
clear. On the one hand, temperature tends to increase strongly, leading
to an increase of the sound velocity and a decrease of the Mach
number. On the other hand, as one gets closer to the boundary, one
may expect larger typical velocities induced by larger velocity
gradients, and thus an increase of the Mach number. There are no direct
observations supporting one scenario or the other. We shall then
consider two scenarios: one in which the Mach number Ma never exceeds
unity. In this case, the whole disk is incompressible, and connects
smoothly onto the star at the star radius. The inner boundary is thus
defined as
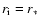 .
In the second scenario, the Mach number
reaches unity at some "interaction radius''
.
In the second scenario, the Mach number
reaches unity at some "interaction radius''
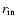 ,
leading to
an inner boundary at
,
leading to
an inner boundary at
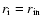 .
At this location, a shock
appears, in which all velocities are suddenly decreased to very small
values. In the shock, all the kinetic energy is transfered to the
thermal energy, thereby producing a strong temperature increase (by a
factor of
.
At this location, a shock
appears, in which all velocities are suddenly decreased to very small
values. In the shock, all the kinetic energy is transfered to the
thermal energy, thereby producing a strong temperature increase (by a
factor of
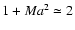 ). This
entails an increase of ionization and the matter gets more coupled to
the stellar magnetic field.
This second situation is considered in magnetospheric
accretion models (Hartmann et al. 1998; Hartmann et al.
2002), in which case
). This
entails an increase of ionization and the matter gets more coupled to
the stellar magnetic field.
This second situation is considered in magnetospheric
accretion models (Hartmann et al. 1998; Hartmann et al.
2002), in which case
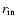 is the Alfven radius; see Schatzman (1962, 1989). Figure 1 summarizes these two possible
configurations. From a hydrodynamical point of view, in the first
situation the boundary is similar to a free-slip boundary (with
possible non-zero velocities in the direction tangential to the star
boundary), while in the second situation, the interaction radius acts
as a no-slip boundary (with all velocities becoming zero). This
difference may be reflected in the transport properties, see Dubrulle et al. (2004). In the following, the free-slip boundary condition will be
referred to as smooth, while the no-slip boundary will be
referred to as rough.
In the laboratory experiments reviewed in Dubrulle et al. (2004), the turbulent
transport depends on the boundary conditions.
Specifically, transport is enhanced (with respect to other
boundary conditions) for boundary
conditions of the rough or no-slip type.
In the astrophysical case, it is not quite clear whether these two
boundary conditions apply, or even whether different inner and outer
boundary conditions result in an intermediate transport enhancement.
We shall therefore devise observational tests using quantities
independent of boundary conditions via a suitable
non-dimensionalisation.
is the Alfven radius; see Schatzman (1962, 1989). Figure 1 summarizes these two possible
configurations. From a hydrodynamical point of view, in the first
situation the boundary is similar to a free-slip boundary (with
possible non-zero velocities in the direction tangential to the star
boundary), while in the second situation, the interaction radius acts
as a no-slip boundary (with all velocities becoming zero). This
difference may be reflected in the transport properties, see Dubrulle et al. (2004). In the following, the free-slip boundary condition will be
referred to as smooth, while the no-slip boundary will be
referred to as rough.
In the laboratory experiments reviewed in Dubrulle et al. (2004), the turbulent
transport depends on the boundary conditions.
Specifically, transport is enhanced (with respect to other
boundary conditions) for boundary
conditions of the rough or no-slip type.
In the astrophysical case, it is not quite clear whether these two
boundary conditions apply, or even whether different inner and outer
boundary conditions result in an intermediate transport enhancement.
We shall therefore devise observational tests using quantities
independent of boundary conditions via a suitable
non-dimensionalisation.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS3549f1.eps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg18.gif) |
Figure 1:
Two possible configurations considered in the present
model: a) the whole disk is incompressible and extends onto the
proto-star; and b) the disk is incompressible until an "interaction
radius'' imposed for instance by a magnetic field. |
| Open with DEXTER |
In either case,
the angular velocity 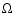 at the inner boundary is that of the star,
namely
at the inner boundary is that of the star,
namely
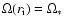 .
For
.
For
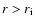 ,
the Mach number
of the flow is less than one by construction, i.e. pressure
fluctuations vary over a time scale short compared to the dynamical
time. In such a case, one can assume hydrostatic equilibrium in the
vertical direction, implying a decoupling of the vertical and
horizontal structure. It is then convenient to describe the disk by
its
"horizontal equations'', obtained by averaging the original equations of
motion in the vertical direction. The procedure is described e.g. in
Dubrulle (1992). It leads to:
,
the Mach number
of the flow is less than one by construction, i.e. pressure
fluctuations vary over a time scale short compared to the dynamical
time. In such a case, one can assume hydrostatic equilibrium in the
vertical direction, implying a decoupling of the vertical and
horizontal structure. It is then convenient to describe the disk by
its
"horizontal equations'', obtained by averaging the original equations of
motion in the vertical direction. The procedure is described e.g. in
Dubrulle (1992). It leads to:
Here,
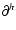 is the horizontal gradient (
is the horizontal gradient (
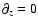 ), u and p are the
Favre average of the velocity and the pressure over the vertical
direction,
), u and p are the
Favre average of the velocity and the pressure over the vertical
direction, 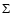 is the surface density,
is the surface density, 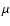 and
and 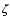 are
surface viscosity coefficients, G is the gravitational constant, M the mass of the
star, and r the distance to the star in
cylindrical coordinate, er is a unit vector in the radial
direction and H the vertical scale height. In the hydrostatic
approximation,
are
surface viscosity coefficients, G is the gravitational constant, M the mass of the
star, and r the distance to the star in
cylindrical coordinate, er is a unit vector in the radial
direction and H the vertical scale height. In the hydrostatic
approximation,
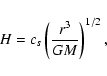 |
(2) |
where cs is the sound velocity.
This expression is only valid when self-gravity can be neglected, namely when:
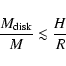 |
(3) |
where
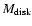 and M are the masses of the disk and the
star, respectively (see e.g. Huré 2000).
and M are the masses of the disk and the
star, respectively (see e.g. Huré 2000).
In the opposite case,
H will rather vary like the Jeans length in the vertical direction,
as:
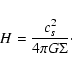 |
(4) |
These equations should be supplemented with an equation for the
surface energy
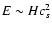 ,
but we shall not need it in the
sequel.
,
but we shall not need it in the
sequel.
Equation (1) admits simple basic state, under the
shape of stationary axi-symmetric solution. The mass conservation
then implies:
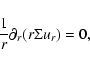 |
(5) |
or
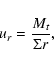 |
(6) |
where Mt is a constant, dimensionally equivalent to an accretion rate.
Plugging this into the radial and azimuthal component of Eq. (1), we obtain two equations:
The general solution of the second equation of (7) is:
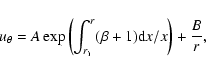 |
(8) |
where A and B are constants and
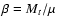 .
Plugging this
solution into the first equation of (7) then
defines the general pressure.
.
Plugging this
solution into the first equation of (7) then
defines the general pressure.
The basic state depends on three constants A, B and Mt, which
must be specified through some sort of boundary conditions. In the
case of astrophysical flows, the boundary conditions are not very
well known and it is less easy to constrain the parameters. The
condition that the rotation velocity of the disk matches the star
velocity at the interaction radius only provides one relation between
the three parameters:
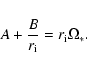 |
(9) |
An additional constraint comes from the hypothesis that the disk is geometrically thin.
This is consistent with our assumption that the Mach number is less
than unity. In that case, as soon as there is no dramatic variation of the thermodynamic variables, radial pressure gradients and terms involving the radial
velocity![[*]](/icons/foot_motif.gif) can be neglected compared to the
gravity, and the only way to satisfy the first equation of (7) is to set
can be neglected compared to the
gravity, and the only way to satisfy the first equation of (7) is to set
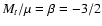 .
In this case, the disk is almost Keplerian and obeys:
.
In this case, the disk is almost Keplerian and obeys:
where
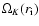 is the angular Keplerian velocity at
is the angular Keplerian velocity at
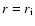 .
The corresponding solution is plotted in Fig. 2.
It is made of a Keplerian disk in the outer part, with a continuous
matching towards the star velocity at the interaction radius.
.
The corresponding solution is plotted in Fig. 2.
It is made of a Keplerian disk in the outer part, with a continuous
matching towards the star velocity at the interaction radius.
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{MS3549f2.ps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg50.gif) |
Figure 2:
Velocity profile in a circumstellar disk in the viscous
regime, with Keplerian velocity in the outer part, and smooth
matching onto the central object at the interaction radius. For this
example, the mass of the central star has been taken as a solar mass. |
| Open with DEXTER |
In the expression we derived for the velocity, we did not need to
specify anything about the condition at the outer boundary of the
disk. One may then wonder what determines this boundary, and whether
it is relevant in specifying the geometry of the problem.
One way to
answer this question is to note that stationary solutions of the
shape (10) are only possible provided the dynamical time
scales are short with respect to the viscous time scale. In the
vertical direction, the dynamical time scale to ensure hydrostatic
equilibrium is
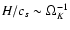 .
In the horizontal plane,
the two dynamical time scale are the radial time scale
.
In the horizontal plane,
the two dynamical time scale are the radial time scale
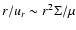 and the orbital time scale
and the orbital time scale
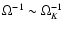 .
The radial time scale is comparable to the viscous
time scale. So the condition for stationarity is that the orbital
time scale is less than the viscous time scale, resulting in
.
The radial time scale is comparable to the viscous
time scale. So the condition for stationarity is that the orbital
time scale is less than the viscous time scale, resulting in
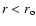 ,
with
,
with 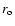 solution of the equation:
solution of the equation:
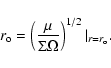 |
(11) |
This radius defines the outer geometrical limit within which
stationary solutions can reasonably exist. If in this formula one
considers the ordinary viscosity, then one typically obtains 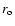 much larger than the observed disk outer radii. On the other hand,
one may argue that as soon as the disk is turbulent, the molecular
viscosity becomes irrelevant and one must consider a kind of
"turbulent viscosity'' in this formula. In this case, using the
formula we derive in Sect. 3.3, we find that
much larger than the observed disk outer radii. On the other hand,
one may argue that as soon as the disk is turbulent, the molecular
viscosity becomes irrelevant and one must consider a kind of
"turbulent viscosity'' in this formula. In this case, using the
formula we derive in Sect. 3.3, we find that 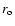 is of the order
of the disk scale height. In geometrically thin disks, it is not clear whether
this limit really exists or not.
Neither limits really match the observed disk radii. However, the
sharp observed edge of disks remains inconsistent with stationary models.
Stationary solutions, due to constant accretion rate in radius, are
indeed in
essence radially infinite. This suggests that the disk outer radii
may still be linked to some non-stationary effects. This is the
subject of a forthcoming paper (Mayer et al. 2004, in preparation).
is of the order
of the disk scale height. In geometrically thin disks, it is not clear whether
this limit really exists or not.
Neither limits really match the observed disk radii. However, the
sharp observed edge of disks remains inconsistent with stationary models.
Stationary solutions, due to constant accretion rate in radius, are
indeed in
essence radially infinite. This suggests that the disk outer radii
may still be linked to some non-stationary effects. This is the
subject of a forthcoming paper (Mayer et al. 2004, in preparation).
Astrophysical disks are (weakly) compressible and radially stratified.
It is however possible to build an incompressible analog of them,
using clever boundary conditions. This remark is at the heart of the
laboratory prototype. Consider an incompressible, unstratified
fluid, enclosed within a domain with cylindrical symmetry, bounded by
inner and outer radii 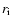 and
and 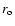 .
Its equations of motion
are given by the Navier-Stokes equations:
.
Its equations of motion
are given by the Navier-Stokes equations:
| |
|
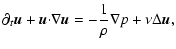 |
|
| |
|
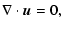 |
(12) |
where 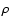 is the density,
is the density, 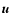 is the velocity,
is the velocity, 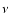 the
molecular viscosity and p is the pressure.
If we assume hydrostatic equilibrium in the vertical direction, we get:
the
molecular viscosity and p is the pressure.
If we assume hydrostatic equilibrium in the vertical direction, we get:
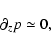 |
(13) |
so that p is a function of r only. In that case, Eq. (12) admits the basic state of
stationary solutions, with axial and translational symmetry along the
disk rotation axis (the velocity only depends on r). The
incompressibility condition then implies:
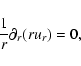 |
(14) |
or
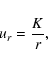 |
(15) |
where K is a constant, to be constrained later.
Plugging this into the radial and azimuthal component of
Eq. (12), we obtain two equations:
The second equation of Eq. (16) is homogeneous in r. It
only admits two power law solutions, with exponent -1 and
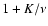 ,
so that the general solution is:
,
so that the general solution is:
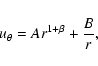 |
(17) |
where A and B are constants and
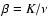 .
Plugging this
solution into the first equation of (16) then defines
the pressure.
.
Plugging this
solution into the first equation of (16) then defines
the pressure.
The basic state depends on three constants A, B and K, which
must be specified through boundary conditions. In laboratory flows,
these conditions are usually well defined and allow for a simple
determination of the constants once the rotation velocities at the
inner and outer boundaries are known (Bahl 1970):
| A |
= |
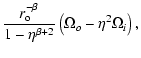 |
|
| B |
= |
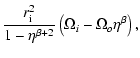 |
(18) |
where
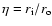 is the radius ratio,
is the radius ratio,
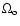 and
and
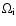 are the angular velocity at outer and inner radii and
are the angular velocity at outer and inner radii and
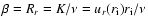 is the radial Reynolds number,
based on the radial velocity through the wall of the inner cylinder.
Note that it is positive for motions outwards from the axis of
rotation.
is the radial Reynolds number,
based on the radial velocity through the wall of the inner cylinder.
Note that it is positive for motions outwards from the axis of
rotation.
Comparing Eq. (10) with Eqs. (17) and (18), it is possible to see that the "laboratory'' analog
of Keplerian flow is such that:
This shows that this
basic state also describes laboratory incompressible flows, with
rigid boundaries and without gravity, in which angular momentum
distribution may be imposed by boundary conditions, and astrophysical
flows, without rigid boundaries, in which angular momentum
distribution is imposed by gravity. In other words, building a
prototype of astrophysical disks (within the approximations described
above) requires a (laboratory) flow with equivalent angular momentum
distribution, and equivalent control parameters. We now derive these
control parameters, in order to apply the Reynolds similarity
principle.
The shape of the basic state allows for the determination of the
control parameters of the flow. These parameters are essential in the
comparison with the laboratory prototype since the Reynolds
similarity principle states that the astrophysical disk will behave
like the laboratory prototype with same control parameters. These
control parameters are
the global Reynolds number:
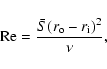 |
(20) |
the rotation number:
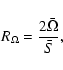 |
(21) |
the curvature number
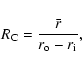 |
(22) |
the local radial Reynolds number:
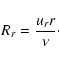 |
(23) |
The aspect ratio:
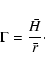 |
(24) |
Here,
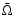 ,
,
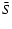 and
and 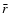 are the characteristic angular
velocity, shear and radius. Adopting the convention of Dubrulle et al.
(2004), we find:
are the characteristic angular
velocity, shear and radius. Adopting the convention of Dubrulle et al.
(2004), we find:
while 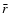 is fixed through the condition
is fixed through the condition
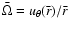 .
A simplification occurs in two
limiting cases, relevant to astrophysical disks:
.
A simplification occurs in two
limiting cases, relevant to astrophysical disks:
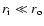 or
or
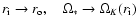 .
In both cases,
we have:
.
In both cases,
we have:
The control parameters then simplify into:
If the disk is stratified or magnetized, other control parameters
appear, like the Prandtl number
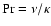 and the magnetic
Prandtl number
and the magnetic
Prandtl number
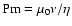 where
where 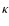 and
and 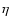 are the heat
diffusivity and the magnetic resistivity, and
are the heat
diffusivity and the magnetic resistivity, and 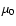 is the vacuum permeability.
is the vacuum permeability.
The computation of the control parameters requires an estimate of
molecular transport coefficients. These coefficients depend on the
ionization state of the gas. There are two sources of ionization.
Thermal ionization is efficient in the inner part of the disk. The
corresponding ionization fraction can be written as (Fromang et al.
2003):
| xeth |
= |
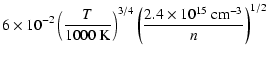 |
|
| |
|
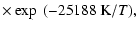 |
(28) |
where T and n are the temperature and the number density of
neutral species (hydrogen mainly), respectively. For temperature lower than 103 K (typically r>1 AU), thermal ionization is negligible. However,
X-ray
illumination from the central star
(or the magnetospheric accretion flow)
may induce a weak ionization in
some part of the disk (typically away from the mid-plane) (Feigelsson
& Montmerle 1999). A theoretical study has been
performed by Igea & Glassgold (1999). They found that at a given
radius from the source, the ionization fraction is a universal
function of the vertical column density 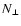 ,
independent of the
structural details of the disk. The role of cosmic rays in the disk
ionization is still a matter of debate (Sano et al. 2000) and will not be discussed here. For a typical young stellar object,
Igea and Glassgold's result can be approximated by:
,
independent of the
structural details of the disk. The role of cosmic rays in the disk
ionization is still a matter of debate (Sano et al. 2000) and will not be discussed here. For a typical young stellar object,
Igea and Glassgold's result can be approximated by:
where 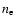 is the ion number density, and
is the ion number density, and
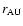 is the distance from the central star, in astronomical units.
is the distance from the central star, in astronomical units.
When the gas is neutral, the viscosity and heat diffusivity are given
by (Lang 1980):
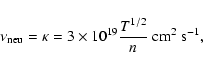 |
(31) |
where T is the disk temperature, and n the number density.
When the gas is weakly ionized (
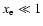 ), the transport
coefficient must be multiplied by a factor (Lang 1980):
), the transport
coefficient must be multiplied by a factor (Lang 1980):
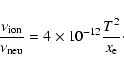 |
(32) |
This correction is valid as long as
 .
This sets a limit on
ionization fraction, below which the gas viscosity takes the neutral value:
.
This sets a limit on
ionization fraction, below which the gas viscosity takes the neutral value:
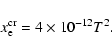 |
(33) |
The Prandtl number in this case is equal to 10-11 (Lang 1980).
The resistivity of an ionized gas can be written as the sum of the
resistivity induced by electron-neutral collisions and electron-ion collisions:
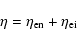 |
(34) |
where (Lang 1980)
| |
|
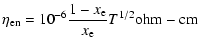 |
(35) |
| |
|
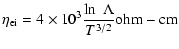 |
(36) |
where
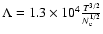 is the Coulomb
logarithm.
is the Coulomb
logarithm.
Table 1:
Observational parameters for T Tauri stars (from
Bouvier 1990; Hartmann et al. 1998)
and for FU Ori stars (from Popham et al. 1996)
considered in this study ( left) and disk physical
parameters
( right). The computation of the corotation radius requires the
knowledge of the stellar rotation velocity. In case this last quantity
is not available, the corotation radius has been set to
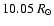 ,
the
solar value. Lower and upper bound on
,
the
solar value. Lower and upper bound on 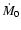 and Re have been
computed using either the star radius or the corotation radius
for
and Re have been
computed using either the star radius or the corotation radius
for 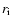 .
Accretion rates are in
.
Accretion rates are in 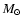 yr-1.
yr-1.
Various physical parameters are required to estimate the control
parameter.
Parameters associated with the disk are 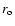 ,
,
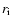 ,
,
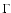 and
and 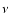 .
The disk inner
radius depends on whether the disk/star interaction is direct or
indirect. In the first case,
.
The disk inner
radius depends on whether the disk/star interaction is direct or
indirect. In the first case,
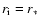 .
In the
second case,
.
In the
second case, 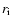 may not exceed the corotation radius at which the
disk velocity matches the star velocity. In the following, we will
consider variations of
may not exceed the corotation radius at which the
disk velocity matches the star velocity. In the following, we will
consider variations of 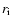 in between these two limits.
The disk outer radius
in between these two limits.
The disk outer radius 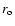 must be specified through the implicit
relation (11). Direct observations of the disk suggest that the
disk size is of the order of
must be specified through the implicit
relation (11). Direct observations of the disk suggest that the
disk size is of the order of
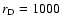 AU for the disk around T Tauri
and even smaller,
AU for the disk around T Tauri
and even smaller,
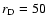 AU, for the disk around FU ORI (Kenyon
1999). Clearly,
AU, for the disk around FU ORI (Kenyon
1999). Clearly, 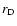 is thus the maximum size
is thus the maximum size 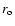 can achieve. For
practical reasons, we defer its discussion to the next section, after
computation of the temperature and density profile.
can achieve. For
practical reasons, we defer its discussion to the next section, after
computation of the temperature and density profile.
Parameters relative to
the proto-star have been measured in some T Tauri and FU Ori stars.
Table 1 gives the sample of stars we shall
use in the following. It is particularly convenient and illustrative
to scale all quantities in the problem with respect to values defined
at the distance of
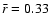 AU, which is the characteristic
radius corresponding to a disk with
AU, which is the characteristic
radius corresponding to a disk with
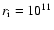 cm and
cm and
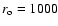 AU, the two extreme limits for
AU, the two extreme limits for 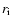 and
and 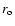 .
We also use, as a
reference, a rotation period of
the star of 8 days (typical T Tauri star), leading to
.
We also use, as a
reference, a rotation period of
the star of 8 days (typical T Tauri star), leading to
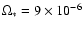 s-1.
s-1.
The temperature and number density in circumstellar disks are
not known due to the lack of
spatial resolution. However, their magnitude can
be deduced by short radii extrapolation of measurements made on the outer
disk. The inversion method of Guilloteau & Dutrey
(1998), based on 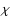 -square fitting of CO interferometric maps, yields
temperature and density profiles at
-square fitting of CO interferometric maps, yields
temperature and density profiles at
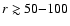 AU.
For instance, for the disk around DM Tau (
AU.
For instance, for the disk around DM Tau (
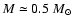 ),
their method predicts
),
their method predicts
where 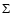 is the surface density of the disk (including gas and dust).
Error bars on the measurements are rather large, and could amount to
a possible variation by a factor of 5 to 10.
At r=1 AU, one finds
is the surface density of the disk (including gas and dust).
Error bars on the measurements are rather large, and could amount to
a possible variation by a factor of 5 to 10.
At r=1 AU, one finds
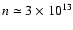 cm-3 and
cm-3 and
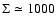 g cm-2, in agreement with values
obtained by
modeling the deuterium enrichment in the Solar System (Drouart et al. 1999; Hersant et al. 2001).
At the reference radius of 0.33 AU, the density is
g cm-2, in agreement with values
obtained by
modeling the deuterium enrichment in the Solar System (Drouart et al. 1999; Hersant et al. 2001).
At the reference radius of 0.33 AU, the density is
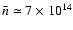 cm-3, the surface density is
cm-3, the surface density is
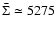 g cm-2, the height is
g cm-2, the height is
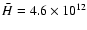 cm and the temperature
is
cm and the temperature
is 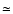 925 K.
In a more recent analysis of the disk around BP Tau, Dutrey et al.
(2003) found densities and temperature
corresponding to a value of
925 K.
In a more recent analysis of the disk around BP Tau, Dutrey et al.
(2003) found densities and temperature
corresponding to a value of
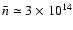 cm-3,
cm-3,
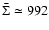 g cm-2,
g cm-2,
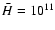 cm
and
cm
and
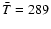 K. The difference between these figures and the
figures of DM Tau provide an illustration of the error bars
associated with our "typical values'', since the disk
around BP Tau seems much smaller, and corresponds to a more evolved
stage than the disk around DM Tau.
K. The difference between these figures and the
figures of DM Tau provide an illustration of the error bars
associated with our "typical values'', since the disk
around BP Tau seems much smaller, and corresponds to a more evolved
stage than the disk around DM Tau.
It is interesting to study the ionization state of the disk with
temperature and density observed in DM Tau. The ionization
fraction is plotted as a function of radius in
Fig. 3 for the thermal and X-ray contribution. One
sees that the thermal contribution dominates at r<1 AU, while the
X-ray contribution becomes important at larger radii. However,
comparing with the limiting ionization state Eq. (33), one
sees
that only the outer part of the disk r>100 AU is sufficiently
ionized to influence the molecular viscosity.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS3549f3.eps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg164.gif) |
Figure 3:
Midplane
ionization fraction due
to thermal contribution (dot-dashed line) and X-ray contribution
(dot-dotted line). The solid line is the limiting ionization
fraction, below which the ionization does not influence molecular
transport. The shaded area is the region whereionization has to be
taken into account in the computation of theviscosity. |
| Open with DEXTER |
The previous scaling allows for an estimate of the disk control
parameter, and, therefore, for an identification of the possible regimes.
A difficulty with respect to the laboratory experiment is that in
disks, the transport coefficients vary over across the disk due to
the radial stratification. To define the control parameter, one must
pick a typical value. In this context, it is logical to consider
their value at 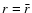 ,
since both the typical shear and radii at
this location have been used.
Using the values given in the previous section, we then obtain:
,
since both the typical shear and radii at
this location have been used.
Using the values given in the previous section, we then obtain:
The value of the rotation number indicates that the flow is
anti-cyclonic and belongs to the "globally sub-critical'' class
defined in Dubrulle et al. (2004). The radial Reynolds number is
negative, indicating an inward
radial circulation. Its value is close to unity. So its influence on transport
properties can be neglected as a first approximation, see Dubrulle et al. (2004). The curvature number depends on the interpretation of the
viscous time scale (see Sect. 2.9.2). In the case where the
interpretation is done with the molecular viscosity, one finds
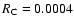 ,
that is, disks are in the wide gap limit. In the other
limiting case where the viscous time scale is computed using the
turbulent viscosity, one finds
,
that is, disks are in the wide gap limit. In the other
limiting case where the viscous time scale is computed using the
turbulent viscosity, one finds
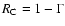 ,
that is, disks are in
the small gap limit.
The relevant
Reynolds parameter to be considered in studying transport properties
will be
,
that is, disks are in
the small gap limit.
The relevant
Reynolds parameter to be considered in studying transport properties
will be
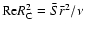 ,
see Dubrulle et al. (2004).
Finally, the aspect ratio is less than one. From the review of
Dubrulle et al, we infer that an additional correction
,
see Dubrulle et al. (2004).
Finally, the aspect ratio is less than one. From the review of
Dubrulle et al, we infer that an additional correction
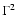 must be
included in the definition of the relevant Reynolds parameter, which
becomes:
must be
included in the definition of the relevant Reynolds parameter, which
becomes:
This is the expression one would naturally derive by
considering the "smallest'' length scale in the problem, see e.g.
Longaretti (2003).
The stability properties of circumstellar disks can be found by
comparing the physical Reynolds number Re
 with critical
Reynolds numbers
derived in laboratory experiments, in the anti-cyclonic non-linear
regime. These measurements are summarized in Dubrulle et al. (2004).
Disregarding any body forces, one finds a critical Reynolds number of
the order of 2300, well below the disk value. Taking into account the
possible stable vertical stratification observed e.g. in DM Tau (Dartois et al. 2003)
with critical
Reynolds numbers
derived in laboratory experiments, in the anti-cyclonic non-linear
regime. These measurements are summarized in Dubrulle et al. (2004).
Disregarding any body forces, one finds a critical Reynolds number of
the order of 2300, well below the disk value. Taking into account the
possible stable vertical stratification observed e.g. in DM Tau (Dartois et al. 2003)![[*]](/icons/foot_motif.gif) , one obtains a slightly larger
value of the order of 4000 (Dubrulle et al. 2005). The presence of
a vertical magnetic field may increase the critical Reynolds number,
due to the low magnetic Prandtl number prevailing in disks. Using the
scaling of Willis & Barenghi (2002), one finds a critical Reynolds
number
, one obtains a slightly larger
value of the order of 4000 (Dubrulle et al. 2005). The presence of
a vertical magnetic field may increase the critical Reynolds number,
due to the low magnetic Prandtl number prevailing in disks. Using the
scaling of Willis & Barenghi (2002), one finds a critical Reynolds
number
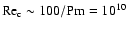 .
This is still well below the
observed Reynolds number. These numbers lead us to conclude that the
disk is turbulent.
.
This is still well below the
observed Reynolds number. These numbers lead us to conclude that the
disk is turbulent.
However, due to the huge variation of the transport coefficients
across the disk, one may wonder how strong this conclusion is. A way
to answer this question is to see how locally in the disk, the
stability criterion are satisfied using a "local'' non-dimensionalized
parameter, built by replacing 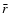 by r the distance to the
central object. The result of this procedure is plotted in Fig. 4. One sees that at any radius, such an effective
local Reynolds number is well above any critical Reynolds number due
to body forces.
This strengthens our conclusion.
by r the distance to the
central object. The result of this procedure is plotted in Fig. 4. One sees that at any radius, such an effective
local Reynolds number is well above any critical Reynolds number due
to body forces.
This strengthens our conclusion.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{MS3549f4.eps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg181.gif) |
Figure 4:
Physical local Reynolds number in circumstellar disks as a
function of radius (dotted-line with symbols). The dashed-dotted line
and the full line are the
critical Reynolds number deduced from laboratory experiments, see
Dubrulle et al. (2004). |
| Open with DEXTER |
3.2 Mean energy dissipation and accretion rate
The quantitative comparison between experimental
measurements and energy dissipated in
circumstellar disks first requires a relation linking
the torque and the disk luminosity 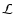 .
The total power dissipated in a Taylor-Couette experiment with same
control parameter as in a Keplerian disk is
.
The total power dissipated in a Taylor-Couette experiment with same
control parameter as in a Keplerian disk is
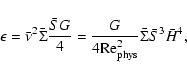 |
(39) |
where
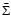 is the disk surface density, G the non-dimensional
torque and
is the disk surface density, G the non-dimensional
torque and 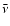 the viscosity.
In a stationary disk, this
power is dissipated under the form of heat, and thus coincides with
the disk luminosity, that is
the viscosity.
In a stationary disk, this
power is dissipated under the form of heat, and thus coincides with
the disk luminosity, that is
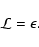 |
(40) |
In practice, observed luminosities are often expressed as a function
of an "effective mass accretion rate'', namely (Hartmann et al. 1998)
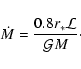 |
(41) |
From a theoretical point of view, the detailed computation of the
accretion luminosity is
not straightforward since it depends on the boundary conditions at the
interaction radius. For comparison with experimental data, we
therefore consider the quantity:
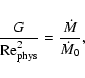 |
(42) |
where 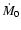 is an effective accretion rate given by
is an effective accretion rate given by
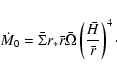 |
(43) |
The quantity
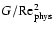 (the non-dimensional energy dissipation),
includes all the boundary condition dependence and only depends on
the Reynolds number.
(the non-dimensional energy dissipation),
includes all the boundary condition dependence and only depends on
the Reynolds number.
The results of Dubrulle et al. (2004) lead to an analytical
prediction for the function
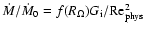 ,
where
,
where
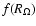 is a function
parameterizing the influence of rotation, and
is a function
parameterizing the influence of rotation, and 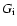 is the torque in
situation when only the inner cylinder is rotating. From the
experiments, we infer
is the torque in
situation when only the inner cylinder is rotating. From the
experiments, we infer
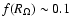 if the flow is turbulent, and 1 is the flow is laminar. Taking the
wide gap limit
if the flow is turbulent, and 1 is the flow is laminar. Taking the
wide gap limit
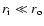 ,
,
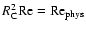 in the formulae of
Dubrulle et al. (2004), we obtain three possible regimes:
in the formulae of
Dubrulle et al. (2004), we obtain three possible regimes:
- in the laminar regime, for
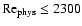
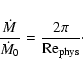 |
(44) |
- for smooth boundary conditions and
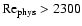
![\begin{displaymath}\frac{\dot M}{\dot M_{0}}\vert_{\rm smooth}
=0.06 \left[ \ln\...
...3\times 10^{-4}~ {\rm Re}_{\rm phys}^2
\right)\right]^{-3/2}.
\end{displaymath}](/articles/aa/full/2005/02/aa3549/img199.gif) |
(45) |
- for rough boundary conditions and
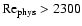
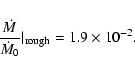 |
(46) |
In the other limit
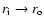 ,
the turbulent value follows a similar
expression, but must be multiplied by a factor
,
the turbulent value follows a similar
expression, but must be multiplied by a factor
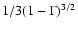 .
In astrophysical disks, the boundary conditions are not known a
priori. Moreover, given the huge physical difference between the
inner part and the outer part, it is unlikely that the boundary
conditions at the inner and outer part coincide, so that we are
probably more in a state of "mixed'' boundary conditions studied
experimentally by Van den Berg et al. (2003). In that case, the energy
dissipation is found to vary between the two limits set by
respectively the "pure'' smooth type (45) and the
pure "rough'' type (46), see Dubrulle et al. (2004). We
shall therefore adopt these formulae as a lower and upper limit of
the energy dissipation in disks.
.
In astrophysical disks, the boundary conditions are not known a
priori. Moreover, given the huge physical difference between the
inner part and the outer part, it is unlikely that the boundary
conditions at the inner and outer part coincide, so that we are
probably more in a state of "mixed'' boundary conditions studied
experimentally by Van den Berg et al. (2003). In that case, the energy
dissipation is found to vary between the two limits set by
respectively the "pure'' smooth type (45) and the
pure "rough'' type (46), see Dubrulle et al. (2004). We
shall therefore adopt these formulae as a lower and upper limit of
the energy dissipation in disks.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS3549f5.eps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg205.gif) |
Figure 5:
Comparison between the non-dimensional energy dissipation
predicted from laboratory measurements in the wide gap limit (
dotted lines) or in the small gap limit ( plain lines) and
observed in
circumstellar disks ( symbols), as a function of
the Reynolds number
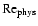 .
For an easier comparison, the mean
energy dissipation has been translated into the non-dimensional
accretion rate .
For an easier comparison, the mean
energy dissipation has been translated into the non-dimensional
accretion rate
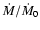 (computed using Eq. (45) and observationally
determined parameters reported in Table 1). The
symbols (computed using Eq. (45) and observationally
determined parameters reported in Table 1). The
symbols  report the value using
report the value using
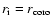 ,
which provides
an upper bound of the energy dissipation. The
circles
report the value using ,
which provides
an upper bound of the energy dissipation. The
circles
report the value using
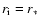 ,
which provides the lower
bound of the energy dissipation. All the quantities have been
computed using temperature and density estimated for the DM Tau
system using the results of Guilloteau & Dutrey (1998), so there is
no adjustable parameter in this plot. ,
which provides the lower
bound of the energy dissipation. All the quantities have been
computed using temperature and density estimated for the DM Tau
system using the results of Guilloteau & Dutrey (1998), so there is
no adjustable parameter in this plot. |
| Open with DEXTER |
3.2.3 Test against observational data
We find the following scaling for
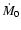 :
:
We are aware that these values are probably uncertain by a factor of 10 or even more. In the next decade, the results expected with ALMA
will greatly reduce the error bars.
At
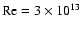 ,
our model (Eqs. (45) and (46) predicts that
,
our model (Eqs. (45) and (46) predicts that
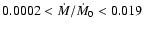 ,
resulting in
,
resulting in
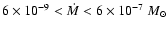 yr-1 for T Tauri stars. This is in good agreement with the observed values ranging
from
yr-1 for T Tauri stars. This is in good agreement with the observed values ranging
from
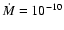 to
to
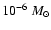 yr-1 (Hartmann et al. 1998). Disks around
FU Ori are characterized by a smaller disk radius, leading to higher
values of
yr-1 (Hartmann et al. 1998). Disks around
FU Ori are characterized by a smaller disk radius, leading to higher
values of 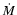 according to Eq. (47), by a factor 5. This is not quite
enough to reach values of up to
according to Eq. (47), by a factor 5. This is not quite
enough to reach values of up to
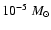 yr-1,
associated with
disks around
FU Ori stars (Kenyon 1994). Such values could be obtained if the
typical disk density is higher in disk around FU Ori, resulting in
more massive disks. This is plausible, since FU Ori stars are younger than
T-Tauri stars.
yr-1,
associated with
disks around
FU Ori stars (Kenyon 1994). Such values could be obtained if the
typical disk density is higher in disk around FU Ori, resulting in
more massive disks. This is plausible, since FU Ori stars are younger than
T-Tauri stars.
A graphical representation of this discussion can be obtained by
plotting the computed
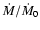 as a function of
as a function of
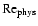 using the values listed in Table 1 as input
parameters. To remove the problem of our ignorance of the actual
value of
using the values listed in Table 1 as input
parameters. To remove the problem of our ignorance of the actual
value of 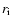 ,
we have used the relation
,
we have used the relation
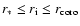 and computed the corresponding
and computed the corresponding
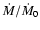 and
and
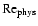 .
The actual dissipation lies in between the
two corresponding estimates. These estimates are plotted in
Fig. 5. For comparison, we have added the
theoretical predictions (Eqs. (45) and (46)) giving the minimum and the maximum expected values
in the turbulent case, as well as the laminar value. This last value
is very much lower than the turbulent values, and is never even
nearly approached by any stars we considered. This may be seen as a
proof of the turbulent character of these disks.
.
The actual dissipation lies in between the
two corresponding estimates. These estimates are plotted in
Fig. 5. For comparison, we have added the
theoretical predictions (Eqs. (45) and (46)) giving the minimum and the maximum expected values
in the turbulent case, as well as the laminar value. This last value
is very much lower than the turbulent values, and is never even
nearly approached by any stars we considered. This may be seen as a
proof of the turbulent character of these disks.
We also see that energy dissipation for disks around T Tauri stars has a
tendency to cluster between the minimal and maximal values allowed
by the theoretical predictions. The relative position of the cluster
of points is slightly better in the case where 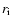 is computed
with
is computed
with
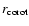 ,
which may be an indication that
,
which may be an indication that 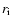 is actually
closer to the corotation radius than to the star radius. However,
given the error bars stressed above, this is probably not enough to
conclude that disks around T Tauri stars are connected through a
magneto-sphere, rather than through a boundary layer. In the case of
FU Ori, the points are clearly above the maximum allowed by our
choice of parameters. The discrepancy is slightly lower for the case
when
is actually
closer to the corotation radius than to the star radius. However,
given the error bars stressed above, this is probably not enough to
conclude that disks around T Tauri stars are connected through a
magneto-sphere, rather than through a boundary layer. In the case of
FU Ori, the points are clearly above the maximum allowed by our
choice of parameters. The discrepancy is slightly lower for the case
when
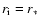 ,
a choice which should probably be favored by the
possible signatures of boundary layer in these objects (Kenyon
1994). In that case, an increase of the surface density by a factor 10 with respect to our values would be enough to solve the
discrepancy.
,
a choice which should probably be favored by the
possible signatures of boundary layer in these objects (Kenyon
1994). In that case, an increase of the surface density by a factor 10 with respect to our values would be enough to solve the
discrepancy.
Our estimate neglects the influence of the magnetic field. Laboratory
experiments using liquid metals have proved that this can potentially
change the intensity of the transport with respect to the pure
hydro-dynamical case. However, no experiment has been performed so
far to study the magnetic influence in regimes relevant to
astrophysical disks.
The turbulent viscosity in circumstellar disks can be predicted by
comparison with laboratory measurements, see Dubrulle et al. (2004).
We find:
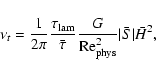 |
(48) |
where
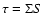 is proportional to the angular momentum, and
the index lam means laminar value. The ratio
is proportional to the angular momentum, and
the index lam means laminar value. The ratio
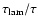 is a
function describing the radial variation of the turbulent transport.
In an incompressible laboratory flow with constant density, this
function is the ratio of the laminar shear profile to the
turbulent shear profile: the turbulence regulates itself through a
modification of the velocity profile. In Keplerian disks, the shear
profile is fixed (through the gravitational force), and the
regulation operates through the density. This function has been
measured in a number of laboratory experiments. At large Reynolds
number, it seems to approach a constant value of 4 predicted by Busse
(1970) using the argument of maximal momentum transport.
With
is a
function describing the radial variation of the turbulent transport.
In an incompressible laboratory flow with constant density, this
function is the ratio of the laminar shear profile to the
turbulent shear profile: the turbulence regulates itself through a
modification of the velocity profile. In Keplerian disks, the shear
profile is fixed (through the gravitational force), and the
regulation operates through the density. This function has been
measured in a number of laboratory experiments. At large Reynolds
number, it seems to approach a constant value of 4 predicted by Busse
(1970) using the argument of maximal momentum transport.
With
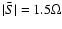 and
and
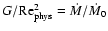 ,
this
defines a resulting typical turbulent viscosity as:
,
this
defines a resulting typical turbulent viscosity as:
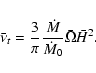 |
(49) |
This turbulent viscosity takes the shape of an 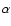 viscosity,
proposed by Shakura & Sunyaev (1973). The corresponding
viscosity,
proposed by Shakura & Sunyaev (1973). The corresponding 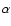 coefficient here is a function of the Reynolds number of the
circumstellar disk (through Eqs. (45) and (46)). At
coefficient here is a function of the Reynolds number of the
circumstellar disk (through Eqs. (45) and (46)). At
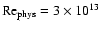 ,
its value is
typically
,
its value is
typically
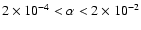 .
This range is in
good agreement with the range of values inferred from the D/H ratio
in the Solar System (Drouart et al. 1999; Hersant et al. 2001). More
generally, this range is compatible with the disk lifetime and the values
usually adopted in theories. Using this expression for the turbulent
viscosity, the viscous timescale is:
.
This range is in
good agreement with the range of values inferred from the D/H ratio
in the Solar System (Drouart et al. 1999; Hersant et al. 2001). More
generally, this range is compatible with the disk lifetime and the values
usually adopted in theories. Using this expression for the turbulent
viscosity, the viscous timescale is:
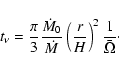 |
(50) |
3.4 Energy fluctuations
Up to now, we have considered only the mean energy dissipation and its
luminous counterpart, but we can also obtain interesting information from the
luminosity fluctuations which reflect the dynamics of the underlying
turbulent flow. In laboratory experiments with smooth boundary
conditions, turbulent fluctuations are
observed to follow a universal (i.e. Reynolds
number-independent), log-normal
distribution (Lathrop et al. 1992) with variance
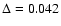 .
The universal distribution occurs
for variables normalized by their mean. Energy dissipation is
proportional to the wall shear stress squared. Since the functional
shape of the log-normal distribution is unchanged by squaring,
the distribution of energy dissipation should also be log-normal.
To check this prediction, we have computed the distribution of the
luminosity fluctuations observed from the disk around BP Tau and from
the disk around V1057 Cygni. The results are shown in Figs. 6
and 7. One sees that the
fluctuations in the disk around V1057 Cyg are very well fitted by a
log-normal distribution, with a variance similar to that of
laboratory experiments. In the case of BP Tau, however, the comparison
is not as good. This difference between the two systems may be traced
to different boundary conditions. If we accept that disks around
T Tauri stars follow the magnetospheric accretion scenario, while the disk
around FU Ori is connected to the star through a boundary layer, it may not be
surprising that only the disk around FU Ori follows the laboratory,
smooth boundary condition distribution. Since we do not have any
measurements for rough boundary conditions, we cannot say whether the
discrepancy comes from the different boundary conditions, or from the
presence of other physical effects, like accretion shock or a magnetic
field.
.
The universal distribution occurs
for variables normalized by their mean. Energy dissipation is
proportional to the wall shear stress squared. Since the functional
shape of the log-normal distribution is unchanged by squaring,
the distribution of energy dissipation should also be log-normal.
To check this prediction, we have computed the distribution of the
luminosity fluctuations observed from the disk around BP Tau and from
the disk around V1057 Cygni. The results are shown in Figs. 6
and 7. One sees that the
fluctuations in the disk around V1057 Cyg are very well fitted by a
log-normal distribution, with a variance similar to that of
laboratory experiments. In the case of BP Tau, however, the comparison
is not as good. This difference between the two systems may be traced
to different boundary conditions. If we accept that disks around
T Tauri stars follow the magnetospheric accretion scenario, while the disk
around FU Ori is connected to the star through a boundary layer, it may not be
surprising that only the disk around FU Ori follows the laboratory,
smooth boundary condition distribution. Since we do not have any
measurements for rough boundary conditions, we cannot say whether the
discrepancy comes from the different boundary conditions, or from the
presence of other physical effects, like accretion shock or a magnetic
field.
![\begin{figure}
\par\includegraphics[angle=270,width=7.9cm,clip]{MS3549f6.ps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg228.gif) |
Figure 6:
Distribution of
luminosity fluctuations observed disk around BP Tau (
symbols) compared with a log-normal distribution of various variance 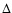 ( plain line). The value of
( plain line). The value of 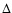 is indicated beside
each line.
is indicated beside
each line. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=7.8cm,clip]{MS3549f7.ps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg229.gif) |
Figure 7:
Distribution of luminosity fluctuations observed disk around V1057 Cyg (
symbols) compared with a log-normal distribution of variance
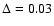 ( plain line).
( plain line). |
| Open with DEXTER |
Laboratory measurements provide interesting clues about the intensity
of velocity fluctuations. Since such fluctuations may be potentially
observable in disks using non-thermal line widening, they may be used
as additional constraints or observational tests of the analogy
between laboratory flows and circumstellar disks. From results of
Dubrulle et al. (2004), it appears that azimuthal velocity
fluctuations should be proportional to the mean azimuthal velocity,
with a proportionality factor depending weakly on the Reynolds
number, like
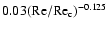 .
With
.
With
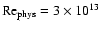 and
and
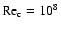 (see Sect. 3.1), the factor is of the
order of 0.01.
Using Eq. (10), we can compute the azimuthal velocity
dispersion for a typical circumstellar disk around a T Tauri.
The azimuthal velocity dispersion decreases from about 0.6 km s-1 in the
inner part, to 0.03 km s-1 in the outer part, at 100 AU The total velocity
dispersion depends on the anisotropy of the turbulence. In
laboratory experiments, the radial relative velocity dispersion is
observed to be about twice the azimuthal velocity dispersion. There
was no measure of the vertical velocity dispersion, but it can be
expected to be much smaller than the horizontal dispersion due to the
rotation-induced anisotropy (Dubrulle & Valdettaro 1992).
(see Sect. 3.1), the factor is of the
order of 0.01.
Using Eq. (10), we can compute the azimuthal velocity
dispersion for a typical circumstellar disk around a T Tauri.
The azimuthal velocity dispersion decreases from about 0.6 km s-1 in the
inner part, to 0.03 km s-1 in the outer part, at 100 AU The total velocity
dispersion depends on the anisotropy of the turbulence. In
laboratory experiments, the radial relative velocity dispersion is
observed to be about twice the azimuthal velocity dispersion. There
was no measure of the vertical velocity dispersion, but it can be
expected to be much smaller than the horizontal dispersion due to the
rotation-induced anisotropy (Dubrulle & Valdettaro 1992).
The velocity dispersion in disks has been measured by Guilloteau & Dutrey (1998)
at r>100 AU They obtain a value of
the order of 0.1 km s-1,
which would correspond to a value of about 0.05 km s-1 for the
azimuthal component. This is close to the values found from
comparison with laboratory flows.
In this paper, we have derived and studied the analogy between
circumstellar disks and the Taylor-Couette flow. This analogy results
in a number of parameter-free predictions about stability of the
disks, and their turbulent transport properties, provided an estimate
of the disk structure is available. We have proposed
to get this
estimate from interferometric observations of circumstellar disks,
and checked that the energy dissipation, the turbulent
transport, and the fluctuations in circumstellar disks all follow
behavior compatible with the prediction from the analogy. This check
can first be used as a clear proof of the turbulent character
of circumstellar disks. A second interesting application would be to
build from this analogy a parameter-free model of circumstellar
disks. In this respect, the proportionality between the turbulent
viscosity and the so-called "accretion rate'' (a quantity easily
accessible by observation) is very interesting because it opens the
possibility to infer the disk structure from the observation of
its luminosity. For this, a model has to be built linking the
turbulent transport and the disk structure. This is the subject of
ongoing work.
We note
finally that our model could also possibly apply to other types of
disks (e.g. around black holes, or in close binaries) given
minor adaptations.
Acknowledgements
We thank A. Dutrey for useful discussions and comments on the
manuscript. We are indebted to the anonymous referee whose
helpful remarks led us to clarify the paper and our thoughts.
This work has received support from the Programme
national de Planétologie. F.H. acknowledges support from an ESA
research
fellowship.
- D'Alessio, P.,
Canto, J., Calvet, N., & Lizano, S. 1998, ApJ, 500, 411 [CrossRef]
- Bahl, S. K. 1970, Def.
Sci. J., 20, 89 (In the text)
- Barge, P., &
Sommeria, J. 1995, A&A, 295, L1 (In the text)
- van den
Berg, T. H., Doering, C. R., Lohse, D., & Lathrop, D. P. 2003,
PRL, submitted
(In the text)
- Chavanis, P.-H.
2000, A&A, 356, 1089 (In the text)
- Bouvier, J. 1990,
AJ, 99, 946 [CrossRef] (In the text)
- Bouvier, J.,
Forestini, M., & Allain, S. 1997, A&A, 326, 1023
- Busse, F. H. 1970, J.
Fluid Mech., 47, 28 [MathSciNet] (In the text)
- Dartois, E.,
Dutrey, A., & Guilloteau, S. 2003, A&A, 399, 773 [EDP Sciences] [CrossRef] (In the text)
- Dutrey, A.,
Guilloteau, S., & Simon, M. 2003, A&A, 402, 1003 [EDP Sciences] [CrossRef] (In the text)
- Drouart, A.,
Dubrulle, B., Gautier, D., & Robert, F. 1999, Icarus, 140,
129 [CrossRef] (In the text)
- Dubrulle, B.
1992, A&A, 266, 592 (In the text)
- Dubrulle, B.,
& Valdettaro, L. 1992, A&A, 263, 387
- Dubrulle, B.,
Dauchot, O., Daviaud, F., Longaretti, P.-Y., Richard, D., &
Zahn, J.-P. 2004, Phys. Fluids, submitted
(In the text)
- Dubrulle, B.,
Marié, L., Normand, Ch., Hersant, F., Richard, D., & Zahn,
J.-P. 2005, A&A, 429, 1 [EDP Sciences] [CrossRef] (In the text)
- Feigelson,
E., & Montmerle, Th. 1999, ARA&A, 37, 363
- Ferreira, J.
1997, A&A, 319, 340
- Fromang, S.,
Terquem, C., & Balbus, S. 2002, MNRAS, 329, 18 [CrossRef]
- Dutrey, A.,
Guilloteau, S., & Simon, M. 2003, A&A, 402, 1003 [EDP Sciences] [CrossRef]
- Guilloteau,
S., & Dutrey, A. 1998, A&A, 339, 467 (In the text)
- Gullbring,
E., Hartmann, L., Briceño, C., & Calvet, N. 1998, ApJ,
492, 323 [CrossRef] (In the text)
- Hartmann, L.,
Calvet, N., Gullbring, E., & D'Alessio, P. 1998, ApJ, 495,
385 [CrossRef] (In the text)
- Hartmann, L.,
Calvet, N., Gullbring, E., & D'Alessio, P. 1998, ApJ, 495,
385 [CrossRef]
- Hartmann, L.
2002, ApJ, L29
(In the text)
- Hersant, F.,
Gautier, D., & Huré, J.-M. 2001, ApJ, 554, 391 [CrossRef] (In the text)
- Huré, J.-M. 2000,
A&A, 358, 378 (In the text)
- Igea, J., &
Glassgold, A. E. 1999, ApJ, 518, 848 [CrossRef] (In the text)
- Kenyon, S. 1994,
ASP Conf. Ser., 56, 63 (In the text)
- Kenyon, S. J. 1999,
OSPS conf., 613
(In the text)
- Lang, K. R.,
Astrophysical Formulae (Springer-Verlag), 1980
(In the text)
- Lathrop, D. P.,
Fineberg, J., & Swinney, H. L. 1992, Phys. Rev. A, 46
(In the text)
- Longaretti,
P.-Y. 2003, preprint
(In the text)
- Muzerolle,
J., Calvet, N., & Hartmann, L. 1998, ApJ, 492, 743 [CrossRef] (In the text)
- Popham, R. 1996,
ApJ, 467, 749 [CrossRef] (In the text)
- Popham, R.,
Kenyon, S., Hartmann, L., & Narayan, R. 1996, ApJ, 473,
422 [CrossRef]
- Pringle, J. E. 1981,
ARA&A, 19, 137
- Sano, T., Miyama, S.
M., Umebayashi, T., & Nakanon, T. 2000, ApJ, 543, 486 [CrossRef] (In the text)
- Shakura, N. I.,
& Sunyaev, R. A. 1973, A&A, 24, 337 (In the text)
- Schatzman, E.
1962, Ann. Astrophys., 25, 18
- Schatzman, E.
1989, in Turbulence and non-linear dynamics in MHD flows, ed. M.
Meneguzzi, A. Pouquet, & P. L. Sulem, North-Holland
- Tanga, P., Babiano,
A., Dubrulle, B., & Provenzale, A. 1996, Icarus, 121, 158 [CrossRef] (In the text)
- Willis, A. P.,
& Barenghi, C. F. 2002, A&A, 388, 688 [EDP Sciences] [CrossRef] (In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS3549f1.eps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg18.gif)
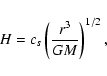
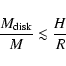
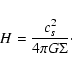
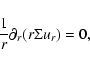
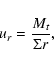
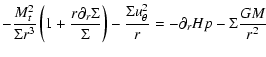
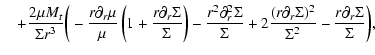
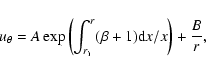
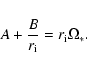
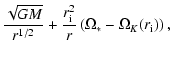
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{MS3549f2.ps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg50.gif)
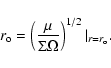
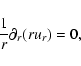
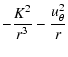
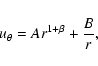
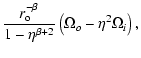
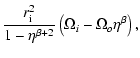
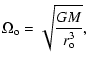
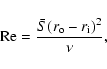
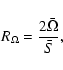
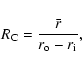
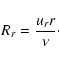
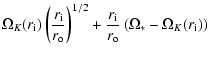
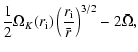
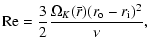
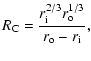
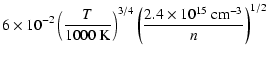
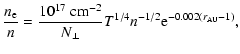
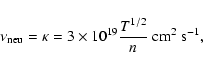
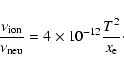
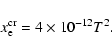
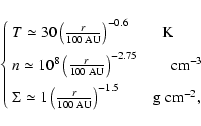
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{MS3549f3.eps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg164.gif)
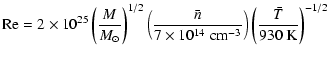
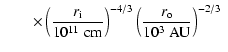
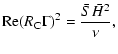
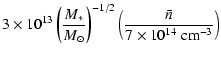
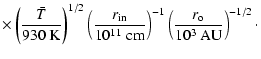
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{MS3549f4.eps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg181.gif)
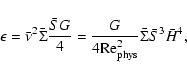
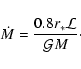
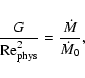
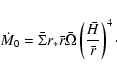
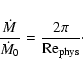
![\begin{displaymath}\frac{\dot M}{\dot M_{0}}\vert_{\rm smooth}
=0.06 \left[ \ln\...
...3\times 10^{-4}~ {\rm Re}_{\rm phys}^2
\right)\right]^{-3/2}.
\end{displaymath}](/articles/aa/full/2005/02/aa3549/img199.gif)
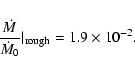
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{MS3549f5.eps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg205.gif)
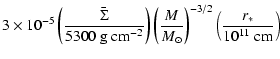
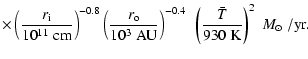
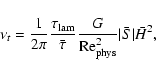
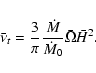
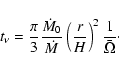
![\begin{figure}
\par\includegraphics[angle=270,width=7.9cm,clip]{MS3549f6.ps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg228.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.8cm,clip]{MS3549f7.ps}
\end{figure}](/articles/aa/full/2005/02/aa3549/Timg229.gif)