E. Covas1 - D. Moss 2 - R. Tavakol1
1 - Astronomy Unit, School of Mathematical Sciences,
Queen Mary, University of London, Mile End Road, London E1 4NS, UK
2 - School of Mathematics, The University of Manchester M13 9PL, UK
Received 28 July 2004 / Accepted 7 September 2004
Abstract
Increasing evidence is becoming available about not only
the surface differential rotation of rapidly rotating cool stars
but, in a small number of cases, also about temporal variations,
which possibly are analogous to the solar torsional oscillations.
Given the present difficulties in
resolving the precise nature of such variations,
due to both the short length and poor resolution of the available data,
theoretical input is vital to help assess the
modes of behaviour that might be expected, and will facilitate
interpretation of the observations.
Here we take a first step in this direction by
studying the variations in the
convection zones of such stars, using a two dimensional
axisymmetric mean field
dynamo model operating in a spherical shell in which
the only nonlinearity is the action
of the azimuthal component of the Lorentz force of the
dynamo generated magnetic field on the stellar
angular velocity. We consider three families of models with
different depths of dynamo-active regions. For moderately supercritical
dynamo numbers we find torsional oscillations that penetrate
all the way down to the
bottom of the convection zones, similar
to the case of the Sun.
For larger dynamo numbers we find
fragmentation in some cases and sometimes there are
other dynamical modes of behaviour,
including quasi-periodicity and chaos.
We find that the largest deviations in the angular velocity distribution
caused by the Lorentz force are of the order of few percent,
implying that the original assumed "background'' rotation field
is not strongly distorted.
Key words: magnetic fields - magnetohydrodynamics (MHD) - chaos - stellar dynamcis - stars: oscillations - stars: magnetic fields
A steadily increasing number of observations of the variations in the surface rotation of rapidly rotating cool stars is now becoming available (e.g. Collier Cameron & Donati 2002; Donati et al. 2003; Reiners & Schmitt 2003; Messina & Guinan 2003, amongst other papers too numerous to mention here). Using a variety of techniques including spot tracing and Doppler imaging, these observations parallel, at much lower resolution, determinations of variations in the solar surface rotation law.
For example, recent observations of the rapidly rotating K dwarf
AB Doradus (
![]() d), and of other rapidly rotating
late-type stars, show the presence of a
surface differential rotation generically
similar to that of the Sun, in that there is
equatorial acceleration, with a mean pole-equator variation of about
d), and of other rapidly rotating
late-type stars, show the presence of a
surface differential rotation generically
similar to that of the Sun, in that there is
equatorial acceleration, with a mean pole-equator variation of about ![]() .
In one way the differential rotation of AB Dor is remarkably solar-like
in spite of the very different rotational period, in that
the equator pulls one full
turn ahead of the pole every 110 days or so, compared to
a lap time of 120 days in the case of the Sun.
This differential rotation varies by about a factor of 2 (Collier et al. 2002; Donati et al. 2003b).
.
In one way the differential rotation of AB Dor is remarkably solar-like
in spite of the very different rotational period, in that
the equator pulls one full
turn ahead of the pole every 110 days or so, compared to
a lap time of 120 days in the case of the Sun.
This differential rotation varies by about a factor of 2 (Collier et al. 2002; Donati et al. 2003b).
LQ Hydrae is another well studied rapidly rotating dwarf, with
![]() d. Again there is equatorial acceleration,
with a mean latitudinal differential rotation of about
d. Again there is equatorial acceleration,
with a mean latitudinal differential rotation of about ![]() ,
but varying
with time by
a factor of about 10 (Donati et al. 2003b).
,
but varying
with time by
a factor of about 10 (Donati et al. 2003b).
A significant trend seems to be that surface differential rotation and rotational
period are positively correlated, so that the product
![]() does not depend strongly on rotational period (e.g. Hall 1991; Donahue 1993;
Messina & Guinan 2003; Reiners & Schmitt 2003), although it is clear from
the above that there are exceptions.
does not depend strongly on rotational period (e.g. Hall 1991; Donahue 1993;
Messina & Guinan 2003; Reiners & Schmitt 2003), although it is clear from
the above that there are exceptions.
In general, these rapid rotators appear to possess magnetic cycles (e.g. Donati et al. 2003a), in common with many of the cool stars in the Mount Wilson HK-project (e.g. Baliunas et al. 1995).
These observations raise a number of interesting questions, including the form of the surface rotation law and its variations. Of course, rotation laws and their variations in the interiors of these stars are quite unknown. Even at the surface, spatiotemporal variations are only beginning to be observed for a few objects. In particular, it is of considerable interest whether torsional oscillations of the type observed in the Sun are widespread in these stars - the observations of LQ Hyd and AB Dor give tantalising hints.
Here we examine these questions in the context of
non-linear mean field dynamo models in a spherical shell, which
include the
feedback of the Lorentz force of the large-scale magnetic field
on this rotation law as the nonlinearity.
This parallels our previous studies of solar torsional oscillations (see,
e.g., Covas et al. 2000;
Tavakol et al. 2002;
Covas et al. 2004,
and references therein).
We investigate the nature of variations in the
convection zones of rapidly rotating stars,
by considering three families of models with
different depths of dynamo-active regions ("convective envelopes'').
Specialisation to rapid rotation is made by choice of a
quasi-cylindrical zero order rotation law.
This is
subsequently modified as the dynamo saturates, via the feedback of
the azimuthal Lorentz force.
We study the effects of changing the
strengths of the zeroth order differential
rotation and of the ![]() -effect on the variations caused to the
zero order rotation profile.
By examining this range of models we aim to obtain
insight into the possible forms and
types of variation in their rotation that might be expected.
Such theoretical input is,
despite its obvious limitations, potentially of primary
importance given the scarcity and limited duration and resolution of
observations of rotational variations of these stars.
-effect on the variations caused to the
zero order rotation profile.
By examining this range of models we aim to obtain
insight into the possible forms and
types of variation in their rotation that might be expected.
Such theoretical input is,
despite its obvious limitations, potentially of primary
importance given the scarcity and limited duration and resolution of
observations of rotational variations of these stars.
Furthermore, theoretical stellar dynamo studies are in a fundamentally unsatisfactory state because there has only been one object, the Sun, against which to calibrate in anything but the grossest manner the unknown parameters occurring in mean field dynamo models. Modelling late-type stars with known surface rotation laws (and in a few cases, known temporal variations) has the potential to calibrate and test dynamo theory models and predictions against a range of observed systems.
It can be noted that these rapidly rotating stars with significant convective envelopes often display nonaxisymmetric features, such as photometric variability believed to be caused by large starspots. These features are conventionally associated with the presence of large-scale nonaxisymmetric magnetic fields. Here we only study axisymmetric fields as a first approximation, taking the viewpoint that the nonaxisymmetric components can be treated as higher order contributions to the field. Moss (2004a,b) has made a preliminary study of nonaxisymmetric field generation in these object, using a different (alpha-quenching) dynamo nonlinearity.
In the next section we outline our dynamo model. Section 3 contains our detailed results. In Sect. 4 we make a brief comparison of the results of our model with some observations and in Sect. 5 we summarise our results and draw some conclusions.
We shall assume that the gross features of the
large-scale magnetic field in such stars
can be described by a mean field dynamo
model, with the standard equation
Equations (1) and (2) were solved using the code
described in Moss & Brooke (2000) (see also
Covas et al. 2000) together with the boundary conditions given below,
over the range
![]() ,
,
![]() .
We consider three families of models with
dynamo-active shells ("convection zones'') of different thicknesses with
lower boundaries at fractional radii
r0= 0.2, 0.64 and 0.775. We associate these with physical "stellar
radii''
.
We consider three families of models with
dynamo-active shells ("convection zones'') of different thicknesses with
lower boundaries at fractional radii
r0= 0.2, 0.64 and 0.775. We associate these with physical "stellar
radii''
![]() cm,
cm,
![]() cm and
cm and
![]() cm respectively.
The stellar convection zone proper is thought to occupy the region
with fractional radius
cm respectively.
The stellar convection zone proper is thought to occupy the region
with fractional radius
![]() ,
where
,
where
![]() respectively and where the
regions
respectively and where the
regions
![]() ,
where
d=0.05, can be thought of as the
corresponding overshoot regions/tachoclines.
In the simulations discussed below we use a mesh resolution of
,
where
d=0.05, can be thought of as the
corresponding overshoot regions/tachoclines.
In the simulations discussed below we use a mesh resolution of
![]() points, uniformly distributed in radius and latitude respectively.
points, uniformly distributed in radius and latitude respectively.
In order to represent the expected form of the rotation law in rapidly
rotating stars with Rossby number ![]() ,
in
,
in
![]() we chose
we chose
![\begin{figure}
\par\includegraphics[width=8cm,clip]{contour_r=0.64.eps}
\end{figure}](/articles/aa/full/2005/02/aa1741/Timg58.gif) |
Figure 1:
Contours of the zero-order rotation profile
|
| Open with DEXTER | |
This choice is consistent also with the limited observations, which suggest that mean surface rotation laws are of the solar-like
form
![]() ,
where c and d are
constants and
,
where c and d are
constants and ![]() is the co-latitude.
This form of
is the co-latitude.
This form of
![]() means that the relevant dynamo number is
actually
means that the relevant dynamo number is
actually
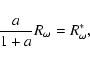 |
(4) |
If, to be definite, we choose
![]() when
when
![]() ,
,
![]() ,
then we obtain
,
then we obtain
![]() cm2 s-1.
Then, e.g., calculations with
cm2 s-1.
Then, e.g., calculations with
![]() ,
a=0.1 and
,
a=0.1 and
![]() (cf. LQ Hydrae), a=0.05 both have
(cf. LQ Hydrae), a=0.05 both have
![]() and so
will yield identical results in terms of dimensionless variables.
The basic arbitrariness in our nominal
value of
and so
will yield identical results in terms of dimensionless variables.
The basic arbitrariness in our nominal
value of ![]() should be remembered, especially when comparing our results
with observations (Sect. 4).
should be remembered, especially when comparing our results
with observations (Sect. 4). ![]() is rather difficult to estimate,
but values
is rather difficult to estimate,
but values
![]() seem acceptable.
seem acceptable.
Rather arbitrarily, we put
![]() ,
where
,
where
![\begin{displaymath}\alpha_r =\cases{0 ~~~~~~~~~~~~~~{\rm if}~~ r<r_1 \cr
1 ~~~~~...
...[3-2 \frac{(r-r_1)}{(r_2-r_1)}\right ] ~~{\rm elsewhere}.
\cr}
\end{displaymath}](/articles/aa/full/2005/02/aa1741/img73.gif)
Table 1: Values of model parameters as r0 varies.
Also, in order to take some notional account of the
likely decrease in the turbulent diffusion coefficient ![]() in the overshoot region, we took
in the overshoot region, we took
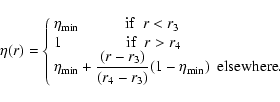
Throughout we take
![]() and
and
![]() and use a uniform density: our earlier work (Covas et al. 2004) illustrates the
effects of introducing a strongly radially dependent density - in brief, no
qualitatively new effects are found, although the radial distribution of
perturbations to the angular velocity can be altered. In particular, it tends
to increase (decrease) the strength of the torsional oscillations at the top (bottom) of the convection zone.
At the outer boundary r=1 we
impose vacuum boundary conditions, whereby
the interior poloidal field is
smoothly joined, by a matrix multiplication,
to an external vacuum solution;
the azimuthal field there satisfies B=0.
At the inner boundary r=r0 we use the same conditions as
Tavakol et al. (2002). The variable v' satisfies stress-free boundary conditions.
and use a uniform density: our earlier work (Covas et al. 2004) illustrates the
effects of introducing a strongly radially dependent density - in brief, no
qualitatively new effects are found, although the radial distribution of
perturbations to the angular velocity can be altered. In particular, it tends
to increase (decrease) the strength of the torsional oscillations at the top (bottom) of the convection zone.
At the outer boundary r=1 we
impose vacuum boundary conditions, whereby
the interior poloidal field is
smoothly joined, by a matrix multiplication,
to an external vacuum solution;
the azimuthal field there satisfies B=0.
At the inner boundary r=r0 we use the same conditions as
Tavakol et al. (2002). The variable v' satisfies stress-free boundary conditions.
Our dynamo model shares features with both "interface'' and "distributed'' models - the radial rotational shear is concentrated near a "tachocline'', whereas the alpha effect is more radially homogeneous. We adopted this model here partly because of the success of a similar model in studying solar torsional oscillations (Covas et al. 2004, and references therein), and also because of the repeated hints from observations that a distributed dynamo may be more appropriate for these stars (e.g. Donati et al. 2003a,b; Petit et al. 2004). Meridional circulation has been suggested to play a role in the solar dynamo. We did not include it in our model, choosing in this exploratory study to direct our attention to a simple, quasi-interface, dynamo model. An investigation of the effects of meridional circulation on torsional oscillations would certainly be welcome. However we note that, even for the Sun, the circulation in the deeper convection zone can only be estimated by plausible extrapolation from that of the near-surface regions. The situation with rapid rotators is more uncertain, and an investigation of such a dynamo model would entail considerable exploration of this additional degree of freedom.
For each value of r0 we assign a "stellar radius'', given above.
Using ![]() ,
we can then evaluate
,
we can then evaluate ![]() - see Table 1.
We chose nominal values
- see Table 1.
We chose nominal values
![]() ,
and
,
and
![]() for all models.
For each of these choices, we made a detailed study of dynamo action and the
associated variations in the rotation laws as the strength of the alpha-effect
and differential rotation (measured by
for all models.
For each of these choices, we made a detailed study of dynamo action and the
associated variations in the rotation laws as the strength of the alpha-effect
and differential rotation (measured by ![]() and a or
and a or
![]() respectively) was varied.
respectively) was varied.
Here we shall briefly discuss the different families of models separately:
![\begin{figure}
\par\includegraphics[width=6cm,clip]{TO.r0=0.2.Calpha=-1.4.a=0.1....
...cludegraphics[width=6cm,clip]{TO-butt.r0=0.2.Calpha=-1.4.a=0.1.eps}
\end{figure}](/articles/aa/full/2005/02/aa1741/Timg83.gif) |
Figure 2:
The radial r-t contours of the angular velocity
residuals
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{fragmentation.r=0.2.Calpha=-2.50.eps}
\end{figure}](/articles/aa/full/2005/02/aa1741/Timg84.gif) |
Figure 3: The r-t diagram for torsional oscillations showing spatiotemporal fragmentation. Note the contrast between the top of the dynamo region and the bottom, where the period is halved. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{TO.r0=0.2.Calpha=-8.a=0.01.e...
...ncludegraphics[width=6cm,clip]{TO-butt.r0=0.2.Calpha=-8.a=0.01.eps}
\end{figure}](/articles/aa/full/2005/02/aa1741/Timg85.gif) |
Figure 4:
As in Fig. 2
for a
dynamo region with r0=0.2, a=0.01 and
|
| Open with DEXTER | |
With differential rotation given by a=0.1 (
![]() ),
the onset of dynamo action occurs at
),
the onset of dynamo action occurs at
![]() .
The strongest torsional oscillations are found
to be around the bottom of the dynamo region.
As an example we show in Fig. 2
the radial (r-t) contours of the angular velocity
residuals
.
The strongest torsional oscillations are found
to be around the bottom of the dynamo region.
As an example we show in Fig. 2
the radial (r-t) contours of the angular velocity
residuals
![]() as a
function of time.
Also shown is
the corresponding butterfly diagram
(i.e. latitude-time plot) for the toroidal component
of the magnetic field
as a
function of time.
Also shown is
the corresponding butterfly diagram
(i.e. latitude-time plot) for the toroidal component
of the magnetic field ![]() near the surface and
the butterfly diagram of the torsional oscillations at surface.
near the surface and
the butterfly diagram of the torsional oscillations at surface.
For ![]() between -1.0 and -2.0 we obtain
torsional oscillations that extend all the way down
to the bottom of the dynamo region.
For
between -1.0 and -2.0 we obtain
torsional oscillations that extend all the way down
to the bottom of the dynamo region.
For ![]() between about -2.0 and -2.7
there is some fragmentation, in the sense that the
regimes at the top and bottom of the convection
zone are not the same and in particular
the latter has half the period of the former.
An example of such fragmentation
can be seen in
Fig. 3.
For still larger values of
between about -2.0 and -2.7
there is some fragmentation, in the sense that the
regimes at the top and bottom of the convection
zone are not the same and in particular
the latter has half the period of the former.
An example of such fragmentation
can be seen in
Fig. 3.
For still larger values of ![]() the regime becomes
noisy and then irregular.
the regime becomes
noisy and then irregular.
When the differential parameter is given by a=0.01 (
![]() ),
the marginal value of
),
the marginal value of
![]() ,
with the strongest torsional oscillations again
being found around the bottom of the dynamo region.
As an example we show in Fig. 4
analogous results to Fig. 2 for this case.
,
with the strongest torsional oscillations again
being found around the bottom of the dynamo region.
As an example we show in Fig. 4
analogous results to Fig. 2 for this case.
Around
![]() the regime becomes
quasi-periodic/ noisily periodic with
the butterfly diagram showing slight equatorial
asymmetry and the torsional oscillations
starting to break up,
as shown in Fig. 5.
For
the regime becomes
quasi-periodic/ noisily periodic with
the butterfly diagram showing slight equatorial
asymmetry and the torsional oscillations
starting to break up,
as shown in Fig. 5.
For ![]() between
between ![]() -12 and -14
the angular velocity and magnetic fields still show oscillations but
the migration towards the equator is lost.
-12 and -14
the angular velocity and magnetic fields still show oscillations but
the migration towards the equator is lost.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{butterfly.r=0.99.Calpha=-10....
...raphics[width=6cm,clip]{residuals.v.10.degrees.Calpha-10.r=0.2.eps}
\end{figure}](/articles/aa/full/2005/02/aa1741/Timg92.gif) |
Figure 5: An example of a noisy periodic regime before the onset of fully chaotic behaviour. The top panel shows the magnetic butterfly diagram close to the surface with the usual solar-type migration towards the equator, whilst also showing slight equatorial asymmetry. The bottom panel shows the r-t diagram for the torsional oscillations, again showing the onset of break-up of periodicity. |
| Open with DEXTER | |
With differential rotation defined by
a=0.1 (
![]() ), the marginal value of
), the marginal value of ![]() is about -2.0.
Solutions become noisily periodic for
is about -2.0.
Solutions become noisily periodic for
![]() .
.
With a=0.01, the onset of dynamo action is at
![]() ,
with the regime becoming quasi-periodic/noisily periodic around
,
with the regime becoming quasi-periodic/noisily periodic around
![]() .
.
As examples we show in Figs. 6 and 7 results analogous to those shown above, when a=0.1 and a=0.01 respectively.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{TO.r0=0.64.Calpha=-2.a=0.1.e...
...ncludegraphics[width=6cm,clip]{TO-butt.r0=0.64.Calpha=-2.a=0.1.eps}
\end{figure}](/articles/aa/full/2005/02/aa1741/Timg96.gif) |
Figure 6:
As in Fig. 2
for a
dynamo region with r0=0.64, a=0.1 and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{TO.r0=0.64.Calpha=-12.a=0.01...
...ludegraphics[width=6cm,clip]{TO-butt.r0=0.64.Calpha=-12.a=0.01.eps}
\end{figure}](/articles/aa/full/2005/02/aa1741/Timg97.gif) |
Figure 7:
As in Fig. 2
for a
dynamo region with r0=0.64, a=0.01 and
|
| Open with DEXTER | |
With a=0.01, the marginal
![]() ,
and the solutions start to become noisy, and eventually become
fragmented, at
,
and the solutions start to become noisy, and eventually become
fragmented, at
![]() .
.
As examples we show in Figs. 8 and 9 comparable results to those given previously, for a=0.1 and a=0.01 respectively.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{TO.r0=0.775.Calpha=-5.a=0.1....
...cludegraphics[width=6cm,clip]{TO-butt.r0=0.775.Calpha=-5.a=0.1.eps}
\end{figure}](/articles/aa/full/2005/02/aa1741/Timg103.gif) |
Figure 8:
As in Fig. 2
for a
dynamo region with
r0=0.775, a=0.1 and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{TO.r0=0.775.Calpha=-17.a=0...
...egraphics[width=6.2cm,clip]{TO-butt.r0=0.775.Calpha=-17.a=0.01.eps}
\end{figure}](/articles/aa/full/2005/02/aa1741/Timg104.gif) |
Figure 9:
As in Fig. 2
for a dynamo region with
r0=0.775, a=0.01 and
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{disruptionOmega.eps}
\end{figure}](/articles/aa/full/2005/02/aa1741/Timg106.gif) |
Figure 10:
The behaviour of
|
| Open with DEXTER | |
An important question
is the way and the extent to which the magnetic field
modifies the rotation profile.
In order to quantify the changes in the rotation profile
produced by this interaction,
we studied the mean changes in
![]() (normalised by
(normalised by
![]() )
as a function of
r and
)
as a function of
r and ![]() over a cycle.
In particular we considered the quantity
over a cycle.
In particular we considered the quantity
![\begin{displaymath}\langle\Delta\Omega(\Omega_0, r, \theta, t)\rangle
=\underbra...
...Omega_0(r,\theta)\right \vert}{\Omega_0(r,\theta)}\right]\cdot
\end{displaymath}](/articles/aa/full/2005/02/aa1741/img107.gif) |
(5) |
Briefly these results show that
in all cases, the effects are mainly concentrated
near the equator and the bottom of the dynamo region.
The strongest surface effects (i.e. largest
![]() )
are seen for the stars with the deepest dynamo region (r0=0.2).
The general shape of the contours is similar in all three cases, with
a band of strong contours
starting near r=r0 at the equator and
coming to the surface in mid latitudes.
)
are seen for the stars with the deepest dynamo region (r0=0.2).
The general shape of the contours is similar in all three cases, with
a band of strong contours
starting near r=r0 at the equator and
coming to the surface in mid latitudes.
To give quantitative estimates of
![]() ,
we show in
Fig. 10 its behaviour
as a function of
,
we show in
Fig. 10 its behaviour
as a function of ![]() for
models with different depths of the dynamo region.
The maximum values of
for
models with different depths of the dynamo region.
The maximum values of
![]() for the cases with a=0.1 are
for the cases with a=0.1 are
![]() ,
, ![]() and
and ![]() for r0=0.2, r0=0.64 and
r0=0.775 respectively, and when
a=0.01 they are
for r0=0.2, r0=0.64 and
r0=0.775 respectively, and when
a=0.01 they are ![]() ,
,
![]() and
and ![]() for r0=0.2, r0=0.64 and
r0=0.775 respectively.
for r0=0.2, r0=0.64 and
r0=0.775 respectively.
As can be seen,
the largest amplitudes of the deviations are
of the order of few percent.
The observation that the values of
![]() are small is interesting as
it implies that the underlying imposed angular velocity
are small is interesting as
it implies that the underlying imposed angular velocity ![]() is not very strongly distorted by its interaction with the magnetic field.
is not very strongly distorted by its interaction with the magnetic field.
To estimate the effects of the magnetic
field on the observable surface rotation profile, we also studied how well
the mean surface rotation law can be fitted
by the rotation law usually employed by observers
in fitting their data
Of course, in general both model and observed rotation laws vary with time, but such variations are only now beginning to be determined observationally. This aspect is addressed in Sect. 4.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{OmegaFullByOmegaStarAtSurfaceClean.eps}
\end{figure}](/articles/aa/full/2005/02/aa1741/Timg121.gif) |
Figure 11:
The fitting of our rotation profile by the parameterization (7).
The model parameters used are
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{BOXED.AVE.r=0.64.Calpha=-2.a=0.1.eps}
\end{figure}](/articles/aa/full/2005/02/aa1741/Timg122.gif) |
Figure 12:
The rectangular contours of the average
|
| Open with DEXTER | |
We also investigated the effects of changing the
sign of a in the definition of
the underlying rotation profile, whilst keeping
![]() .
This
is of potential relevance since
there are hints that such behaviour may occur in a minority of stars
(e.g. Messina & Guinan 2003).
.
This
is of potential relevance since
there are hints that such behaviour may occur in a minority of stars
(e.g. Messina & Guinan 2003).
We show a typical case in Fig. 13. Unsurprisingly perhaps, the major effect is that now the sense of migration of the torsional oscillations (and the magnetic field) is reversed.
For a small number of objects, notably AB Dor and LQ Hyd, observations
are of sufficiently high quality to allow determination of not only
the mean surface rotation law
![]() ,
but also its variation with time.
That is
,
but also its variation with time.
That is
For a dynamo region with r0=0.2 and
![]() ,
our solution with a=0.05 gave
,
our solution with a=0.05 gave
![]() ,
,
![]() ,
i.e.
,
i.e.
![]() .
When a=0.1,
.
When a=0.1,
![]() ,
and when a=0.2,
a*10=0.17,
a*11=0.004, so that
,
and when a=0.2,
a*10=0.17,
a*11=0.004, so that ![]() .
For the case r0=0.64 and
.
For the case r0=0.64 and
![]() ,
we found
,
we found
![]() and
and
![]() ,
i.e.
,
i.e.
![]() .
For a=0.1, we find
.
For a=0.1, we find
![]() ,
and when
a=0.2 we obtained
a*10=0.18,
a*11=0.026,
,
and when
a=0.2 we obtained
a*10=0.18,
a*11=0.026, ![]() .
When
.
When
![]() is increased above these values, solutions lose their regular,
coherent behaviour, although the departure from the zero-order angular velocity
distribution can become larger.
is increased above these values, solutions lose their regular,
coherent behaviour, although the departure from the zero-order angular velocity
distribution can become larger.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{butt.r=0.64_Calph=-3.00.a=-1...
...m}
\includegraphics[width=6cm,clip]{TO.r=0.64_Calph=-3.00.a=-1.eps}
\end{figure}](/articles/aa/full/2005/02/aa1741/Timg156.gif) |
Figure 13:
The butterfly diagrams of the near-surface magnetic field and torsional oscillations
for a dynamo region with r0=0.64, a=-0.1 and
|
| Open with DEXTER | |
We have made a detailed study of the variations in magnetic field and angular velocity that might be expected to occur in the convection zones of rapidly rotating cool stars, using a mean field dynamo model in which the only nonlinearity is the action of the azimuthal component of the Lorentz force of the dynamo generated magnetic field on the stellar angular velocity. This dynamo model, when applied to the Sun, yields results that have an encouraging agreement with the results from the helioseismic observations. Given the current difficulties in resolving the precise nature of such variations a theoretical understanding of the range of possible modes of behaviour is crucial in interpretation the observations.
We considered three families of models with
different depths of dynamo-active regions,
with bases at fractional radii
r0= 0.2, 0.64 and 0.775.
For moderately critical regimes we find
torsional oscillations to be present, qualitatively similar to
those found in the Sun, that in
all cases penetrate all the way down to the
bottom of the convection zone/dynamo-active region![]() .
In some cases, the surface amplitudes are small, and the oscillations are
concentrated deep down.
For larger values of
.
In some cases, the surface amplitudes are small, and the oscillations are
concentrated deep down.
For larger values of
![]() we found
fragmentation in some cases as well as
other dynamical modes of behaviour, including quasi-periodicity and
irregularity.
we found
fragmentation in some cases as well as
other dynamical modes of behaviour, including quasi-periodicity and
irregularity.
We have found that the values of
![]() ,
the averaged relative
deviations in
,
the averaged relative
deviations in ![]() ,
increase with
,
increase with
![]() as well as with increasing values of the strength of
the differential rotation parameter a or of
as well as with increasing values of the strength of
the differential rotation parameter a or of
![]() .
The largest values of
.
The largest values of
![]() (obtained
for a=0.1) are of the order
of a few percent for coherent non-chaotic regimes.
The fact that these are relatively small
is interesting as it implies that
the original angular velocity law is not very distorted - quite modest
changes from
(obtained
for a=0.1) are of the order
of a few percent for coherent non-chaotic regimes.
The fact that these are relatively small
is interesting as it implies that
the original angular velocity law is not very distorted - quite modest
changes from ![]() are enough to self-limit dynamo action (cf. also Moss &
Brooke 2000).
In this connection, we have also shown that the rotation profile can
be well represented by a rotation law of the form (7).
are enough to self-limit dynamo action (cf. also Moss &
Brooke 2000).
In this connection, we have also shown that the rotation profile can
be well represented by a rotation law of the form (7).
When we make a preliminary comparison with the observed behaviour of the late-type dwarfs AB Dor and LQ Hyd (Sect. 4), we can find models with variations in surface differential rotation that are not inconsistent with those observed for these stars, although we cannot produce anything as extreme as the episodes of almost uniform surface rotation as reported for LQ Hyd. In fact, our model cannot distinguish between the representations of these stars - this points to omissions in our modelling. For example, we do not directly represent absolute differences in angular velocity between different models, as these models depend only on differential rotation. Inter alia, the absolute value of the angular velocity might be expected to affect the structure of the alpha-tensor (here reduced to a scalar). However, we are encouraged; our very simple model is untuned, and there are a number of plausible modifications that could be made to it.
Our results all show butterfly diagrams which are
mainly concentrated around the equator (with dispersion
depending upon the parameters of the model.
This differs from the results recently obtained by Bushby (2003)
who, with a different ![]() -quenched dynamo model, used an
-quenched dynamo model, used an ![]() -profile concentrated near
the tachocline together with a quasi-cylindrical rotation profile
with
-profile concentrated near
the tachocline together with a quasi-cylindrical rotation profile
with
![]() (rather than
(rather than ![]()
![]() ,
as suggested by observations and used in our model).
We made a comparison,
using our code with
,
as suggested by observations and used in our model).
We made a comparison,
using our code with ![]() -quenching implemented together
with his
-quenching implemented together
with his ![]() and
and ![]() profiles, and
found agreement with his results. We, however,
did find that Bushby's results aresomewhat fragile,
in the sense that there seem to be two distinct regimes
distinguished by the strength of the differential rotation
parameter. In particular we found that increasing this
parameter from 0.0046 (as used by Bushby) to 0.01 changes the behaviour
of the butterfly diagrams from a pole to an equator dominated
regime. That choice (0.0046) was motivated by a desire
in an
profiles, and
found agreement with his results. We, however,
did find that Bushby's results aresomewhat fragile,
in the sense that there seem to be two distinct regimes
distinguished by the strength of the differential rotation
parameter. In particular we found that increasing this
parameter from 0.0046 (as used by Bushby) to 0.01 changes the behaviour
of the butterfly diagrams from a pole to an equator dominated
regime. That choice (0.0046) was motivated by a desire
in an ![]() -quenched
model with unchanging angular velocity, to have a rotation law that exerted zero
total rotational stress on the interior region.
We also find that these results are fragile with respect to the
choice of the
-quenched
model with unchanging angular velocity, to have a rotation law that exerted zero
total rotational stress on the interior region.
We also find that these results are fragile with respect to the
choice of the ![]() profile, specifically by changing
profile, specifically by changing
![]() to
to
![]() ,
as well as to the radial distribution of
,
as well as to the radial distribution of ![]() noted
by Bushby.
noted
by Bushby.