A&A 429, 477-487 (2005)
DOI: 10.1051/0004-6361:20041591

Abundances and kinematics of a candidate sub-damped Lyman$\alpha $ galaxy toward PHL 1226[*]

L. Christensen1 - R. E. Schulte-Ladbeck2 - S. F. Sánchez1 - T. Becker1 - K. Jahnke1 - A. Kelz1 - M. M. Roth1 - L. Wisotzki1,3


1 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
2 - Department of Physics & Astronomy, University of Pittsburgh, 3941 O'Hara Street, Pittsburgh, PA 15260, USA
3 - Institut für Physik, Universität Potsdam, Am Neuen Palais 10, 14469 Potsdam, Germany

Received 3 July 2004 / Accepted 8 September 2004

Abstract
The spectrum of the quasar PHL 1226 is known to have a strong Mg II and sub-damped Lyman$\alpha $ (sub-DLA) absorption line system with $N(H {\sc i})=(5\pm2)\times10^{19}$ cm-2 at z=0.1602. Using integral field spectra from the Potsdam Multi Aperture Spectrophotometer (PMAS) we investigate a galaxy at an impact parameter of 6 $.\!\!^{\prime\prime}$4 which is most probably responsible for the absorption lines. A fainter galaxy at a similar redshift and a slightly larger distance from the QSO is known to exist, but we assume that the absorption is caused by the more nearby galaxy. From optical Balmer lines we estimate an intrinsic reddening consistent with 0, and a moderate star formation rate of 0.5 M $_{\normalsize\odot}$ $\>\rm yr^{-1}$  is inferred from the H$\alpha $ luminosity. Using nebular emission line ratios we find a solar oxygen abundance $12+\log\textrm{(O/H)}=8.7\pm0.1$ and a solar nitrogen to oxygen abundance ratio $\log\textrm{(N/O)}=-1.0\pm0.2$. This abundance is larger than those of all known sub-DLA systems derived from analyses of metal absorption lines in quasar spectra. On the other hand, the properties are compatible with the most metal rich galaxies responsible for strong Mg II absorption systems. These two categories can be reconciled if we assume an abundance gradient similar to local galaxies. Under that assumption we predict abundances $12+\log\textrm{(O/H)}=7.1$ and $\log\textrm{(N/O)}=-1.9$ for the sub-DLA cloud, which is similar to high redshift DLA and sub-DLA systems. We find evidence for a rotational velocity of $\sim$200 km s-1 over a length of $\sim$7 kpc. From the geometry and kinematics of the galaxy we estimate that the absorbing cloud does not belong to a rotating disk, but could originate in a rotating halo.

Key words: galaxies: abundances - galaxies: kinematics and dynamics - quasars: individual: PHL 1226

1 Introduction

Metal absorption line systems in QSO spectra are frequently used to derive abundances of intervening neutral gas clouds of high column density. A classic definition divides strong QSO hydrogen absorption systems into different regimes: Lyman limit systems (LLS) with column densities of neutral hydrogen in the range $10^{17}<N(H {\sc i})<2\times10^{20}$ cm-2, and damped Lyman$\alpha $ systems (DLAs) having N(H I) $~>2\times10^{20}$ cm-2 (Wolfe et al. 1986). Sub-DLA systems with $10^{19}<N(H {\sc i})<2\times10^{20}$ cm-2 also show broad absorption line wings characteristic for DLAs and contain a large fraction of the neutral hydrogen at high redshifts (Péroux et al. 2003). Strong hydrogen absorption lines in QSO spectra are believed to arise in gas-rich (proto)-galaxies, but any relation between absorption line systems and the galaxies responsible for these is not well understood. Deep imaging studies of the fields around QSOs which exhibit strong Ly$\alpha $ absorption lines have revealed several absorbing galaxy candidates close to the line of sight (e.g. Le Brun et al. 1997). Follow-up spectroscopy is necessary to confirm the candidates as the corresponding absorbing galaxies.

Table 1: Log of the observations. $\sigma _{{\rm star}}$ denotes the standard deviation of flux in images of the guide star during each integration. Column 6 lists the signal to noise ratio of a one-dimensional spectrum within a 1 $^{\prime \prime }$ radius of the QSO.

To date only few (13) low-redshift DLAs and sub-DLA galaxies have been identified (Rao et al. 2003; Lacy et al. 2003; Turnshek et al. 2001; Chen & Lanzetta 2003, and references therein), while at high redshift even fewer confirmations exist (Møller et al. 2004; Djorgovski et al. 1996; Møller & Warren 1993; Fynbo et al. 1999; Møller et al. 2002; Christensen et al. 2004). Considering the difficulties of confirming the absorbing galaxies, alternative approaches have been carried out to determine which types of galaxies produce DLA systems. Through measurements of relative abundances of various elements, it has been suggested that DLA galaxies are likely dwarf galaxies (Dessauges-Zavadsky et al. 2003; Prochaska et al. 2003; Nissen et al. 2004; Pettini et al. 1999). Sub-DLAs show the same spread in metallicity as the DLA systems indicating a similar nature of the two samples (Péroux et al. 2003). Although metallicities of DLA and sub-DLA systems can be easily derived from the QSO spectra, the metallicity of the parent galaxy has only been determined for one DLA galaxy previously (Schulte-Ladbeck et al. 2004).

Studies have shown that Mg II absorption systems arise in halos of a wide range of galaxy types (Steidel et al. 1994; Bergeron & Boisse 1991) and are typically associated with LLS. Mg II systems have been suggested to be related to rotating disks (Charlton & Churchill 1998), while Steidel et al. (2002) found that Mg II systems cannot be explained by simple disk models and suggested that the absorption occurs in rotating halos.

The quasar PHL 1226 (Q0151+045 at z=0.404) has a strong Mg II absorption system at z=0.1602 (Bergeron et al. 1988, hereafter B88). A column density of $N(H {\sc i})=(5\pm2)\times10^{19}$ cm-2 was measured in a UV HST spectrum classifying the object as sub-DLA (Rao 2004, private communication). A bright $V=19.2\pm0.3$ galaxy at a projected angular separation of 6 $.\!\!^{\prime\prime}$4 to the west of the QSO was identified as being responsible for the absorption system by B88, who named this galaxy G4. For a flat cosmological model with $\Omega_{\Lambda}=0.7$ and H0=70 km s-1 Mpc-1, which we use throughout the paper, an impact parameter of 6 $.\!\!^{\prime\prime}$4 corresponds to 17.6 kpc. An additional fainter galaxy, G3 (V=20.5) at a similar redshift, was found at an impact parameter 10 $.\!\!^{\prime\prime}$9 to the north of the QSO. Either galaxy could be responsible for the absorption system considering the scaling-law between Mg II halo sizes and galaxy luminosities (Le Brun et al. 1993; Bergeron & Boisse 1991; Guillemin & Bergeron 1997). Optical spectroscopy of G3 and G4 is presented in Ellison et al. (2004).

In this paper we present a study of the galaxy G4 using integral field spectroscopy with the Potsdam Multi Aperture Spectrophotometer (PMAS) (Roth et al. 2000). We describe the data reduction in Sect. 2. Spectra and synthetic narrow-band emission line images are presented in Sect. 3 From the spectra we derive the intrinsic reddening, oxygen and nitrogen abundances, and star formation rate in Sect. 4. We analyse the kinematics of the galaxy itself in Sect. 5. A discussion is presented in Sect. 6, and the conclusions in Sect. 7.

   
2 Observations and data reduction

PMAS is an Integral Field Instrument developed at the Astrophysikalisches Institut Potsdam. It is currently installed at the Calar Alto Observatory 3.5 m Telescope in Spain and has been available as a common user instrument since July 1, 2002. Observations using integral field units have the advantage of combining imaging and spectroscopy information in one dataset. In 2002, we started a project to use PMAS for the study of sub-DLA and DLA galaxies. The great advantage of using integral field spectroscopy for the investigation of the very few currently known sub-DLA and DLA galaxies is that they allow us to obtain data on the galaxies' positions, velocity fields and star-forming properties all in one data cube. Such data are critical to derive the nature of the galaxies causing absorption systems in QSOs. It is our goal to use this new instrument to identify galaxies responsible for low- as well as high-redshift QSO absorbers, and to study their properties.

During the pilot observing run for this project, we observed two QSO fields. Observations for the DLA galaxy toward Q2233+131 revealed an extended Lyman-$\alpha $ emission nebula surrounding the galaxy responsible for the DLA; the analysis was presented in Christensen et al. (2004). A second object observed in the pilot study was PHL 1226 (Q0151+045). The $8\hbox {$^{\prime \prime }$ }\times 8\hbox {$^{\prime \prime }$ }$ PMAS field was targeted at the galaxy G4 because it is closer to the QSO than G3, and thus the more likely absorbing galaxy. An additional criterion was technical - G4 is more than a magnitude brighter than G3 which is farther than 8 $^{\prime \prime }$ away from PHL 1226; its observation would have required another set-up and a large amount of observing time. Here, we report in detail on the results which can be obtained from the PMAS data of G4.

We obtained $4\times1800$ s exposures of G4 divided over two nights on Sep. 5 and 8, 2002, using a grating with 300 lines mm-1 which resulted in a spectral resolution of 6.6 Å FWHM. The chosen grating angle allowed to cover the wavelength range 4575-7880 Å. The first night was photometric with a seeing of 1 $^{\prime \prime }$, while the seeing was varying during the second night and the conditions were not photometric. A log of the observations is presented in Table 1.

The PMAS instrument has two cameras; one for the spectrograph, and an additional camera used for acquisition and guiding (A and G camera) which is equipped with a 1k $\;\times\;1$k SITe CCD. Using data from the A and G camera, one can estimate the variations and the evolution of the sky quality during the night. Photometry of the guide star images taken during the spectral integrations, show variations with a standard deviation presented in Col. 5 of Table 1.

The spectrograph is coupled by 256 fibers to a $16\times16$ element micro-lens array. During the observations each lens covered 0 $\hbox{$.\!\!^{\prime\prime}$ }5\times0\hbox{$.\!\!^{\prime\prime}$ }5$ on the sky. The detector is a 2k $\;\times\;$4k SITe ST002A CCD which was read out in a $2\times2$ binned mode.


  \begin{figure} \par\resizebox{7.5cm}{!}{\includegraphics[clip]{1591_f1.eps}}\end{figure} Figure 1: Broad band image in the wavelength range $4500 < \lambda < 8000$ Å of the QSO at the position (0, 0) and the galaxy G4 at (-6.5,  -1.5) as indicated. Each spaxel represents a spectrum and the field of view is $8\hbox {$^{\prime \prime }$ }\times 8\hbox {$^{\prime \prime }$ }$. North is up and east is left. Coordinates are relative to the QSO position.
Open with DEXTER

Data reduction was performed with IDL based routines written specifically for PMAS data (Becker 2002). After bias subtraction the spectra were extracted using information of the location of the 256 spectra on the CCD obtained from a calibration frame obtained with an exposure of a continuum emission lamp immediately before or after each target exposure. In the extraction a Gaussian line profile was used to increase the signal-to-noise ratio of the extracted spectra. Wavelength calibration was done using calibration spectra of Hg-Ne emission line lamps also obtained following the science exposures. The accuracy of the wavelength calibration was checked using sky emission lines, showing a standard deviation of 0.3 Å. Corrections for varying fiber-to-fiber transmissions as a function of wavelength uses flat field spectra obtained from the twilight sky.

Cosmic rays were removed from the spectra using the L.A. Cosmic routine within IRAF (van Dokkum 2001). Each of the 4 exposures were corrected for an average extinction value appropriate for Calar Alto before combining them. The effect of differential atmospheric extinction was corrected using the theoretical approach described in Filippenko (1982). We checked whether the data cube was appropriately corrected for the differential atmospheric refraction by cross-correlating each monochromatic image with the broad-band image shown in Fig. 1. This showed that the relative shift with wavelength was smaller than 0 $.\!\!^{\prime\prime}$08, which was negligible for the further analysis. Subtraction of the sky background was done by creating an average sky spectrum by selecting spaxels (spatial elements) located between the QSO and the galaxy, uncontaminated by flux from any of these two. This sky spectrum was subtracted from all 256 spectra.

The method for combining the individual exposures was as follows. Firstly, monochromatic images were made from the data cube at some selected wavelength. Then we found a scale factor between the images, by calculating the total flux in the images. Because the spectra taken on Sep. 8 were of poorer quality than the first ones, the individual data cubes were scaled to the ones from Sep. 5, and the final combination took the varying seeing into account by applying a weighting scheme, where the weights were given from the signal to noise ratio of each spectrum. The signal-to-noise ratio was found from a 1D spectrum created by co-adding spectra within 1 $^{\prime \prime }$ radial aperture centered on the galaxy. These S/N ratios are listed in Col. 6 in Table 1. Finally, flux calibration was done the standard way by comparing the spectra obtained of the spectrophotometric standard, BD+28$^\circ$4211 observed on Sep. 5 with table values. After the data reduction the spectra are contained in a data cube of dimensions $16\times16\times1008$ pixels.

Further analysis of the reduced data cube was done using the Euro3D Visualization Tool (Sánchez 2004), while one-dimensional spectra were analysed using both IRAF and our own software (Sánchez et al., 2004, in prep.). Figure 1 presents a composed broad-band image, with dimensions $8\hbox {$^{\prime \prime }$ }\times 8\hbox {$^{\prime \prime }$ }$. To the east (left), the QSO is seen at the edge of the field. The absorbing galaxy G4, identified by B88, is the principal source in the field at the position (-6.5, -1.5) in agreement with the impact parameter of 6 $.\!\!^{\prime\prime}$4.

   
3 Galaxy and QSO spectra

In the dust maps of Schlegel et al. (1998) a Galactic reddening of EB-V = 0.051 is found in the direction toward PHL 1226. The reduced spectra were de-reddened using this value before deriving other quantities. From the reduced data cube, one can create spectra from chosen spaxels or monochromatic- and narrow band images in any wavelength region. A spectrum of the QSO created by co-adding 20 spaxels is shown in Fig. 2.

One sees that strong telluric absorption lines are present around 7600 Å which coincidentally corresponds to H$\alpha $ at the redshift of the absorber. When line fluxes are derived, this feature will skew the results towards lower values if not corrected for. Thus, to correct for this effect, a model for the telluric absorption line was created. The QSO spectrum was smoothed using a Gaussian function with $\sigma=10$ Å, normalised to 1 at 7580 Å and outside the region around 7600 Å the value was set to 1. Following, all spectra were divided by this model to correct for the absorption as demonstrated in in Fig. 4, which brought out the presence of the [N II] (6548 Å) line in the spectrum of G4 as explained in detail in Sect. 3.2.


  \begin{figure} \par\resizebox{8.4cm}{!}{\includegraphics[clip]{1591_f2.ps}}\end{figure} Figure 2: Spectrum of PHL 1226 created by co-adding 20 spaxels. The flux levels are relative since the QSO is located at the edge of the field of view. Broad emission lines from H$\gamma $ and H$\beta $ at z=0.404 can be seen at 6100 Å and 6820 Å, respectively.
Open with DEXTER

Table 2: List of emission lines in the galaxy spectrum and the corresponding redshifts. Line fluxes are derived after a correction for Galactic extinction and telluric absorption was applied. Fluxes and EWs are the observed ones.

Co-adding all spaxels (112 in an area of $4\hbox{$^{\prime\prime}$ }\times7\hbox{$^{\prime\prime}$ }$) corresponding roughly to the size of the galaxy in this dataset results in the spectrum presented in Fig. 3. This spectrum gives the total continuum flux from the galaxy with S/N = 6 and does not show strong emission lines, specifically not before the correction for telluric absorption is applied. One must note that co-adding 112 spaxels dilutes any emission line signal coming from a potentially smaller region. Additionally, residuals from the background subtraction can artificially enhance emission lines. This appears to be the case for the sulfur lines in Fig. 3, because they lie close to strong sky lines. In order to increase the signal to noise ratio of the emission line spectrum, and be less affected by sky subtraction residuals, a localization of the emission line region needs to be done.

To check the spectrophotometry, we convolved the galaxy spectrum with a transmission curve of the Bessell V band filter. We find $V=19.08\pm0.05$, corresponding to an absolute magnitude MV = -20.3 for the galaxy in agreement with the photometry in B88.


  \begin{figure} \par\resizebox{8.3cm}{!}{\includegraphics[clip,angle=90]{1591_f3.ps}}\end{figure} Figure 3: Spectrum of the galaxy created by co-addition of 112 spaxels. Any emission line present in the galaxy has been smeared out because many spaxels do not contribute to the line emission as shown in Sect. 3.1. The seemingly strong [S II] lines are partly caused by errors in sky subtraction.
Open with DEXTER


  \begin{figure} \par\resizebox{8.4cm}{!}{\includegraphics[clip,angle=90]{1591_f4.ps}}\end{figure} Figure 4: Zoom in of the spectrum in Fig. 6 in the region around [N II], H$\alpha $, and [S II]. This plot shows the effect of correcting for the telluric absorption feature around 7600 Å. The lower spectrum (thin line) is the uncorrected spectrum, and the gray line is the model of the telluric feature created from the QSO spectrum. The upper spectrum (thick line) has been corrected for the absorption feature and offset by $+3\times 10^{-17}$  erg cm-2 s-1 Å-1 for clarity.
Open with DEXTER

   
3.1 Emission line images

Emission line images are created by selecting appropriate narrow band filters from the data cube. These narrow band images are created in a wavelength range of $\pm$10 Å around the emission wavelength as shown in Fig. 5. The continuum emission is subtracted using narrow-band images in wavelengths adjacent to the emission lines. Compared to the broad band image in the lower right panel, one sees that most of the emission lines originate $\sim$1 $^{\prime \prime }$ to the south of the G4 centre. Furthermore, the strongest emission is located in a region within a $2\hbox{$^{\prime\prime}$ }\times2\hbox{$^{\prime\prime}$ }$ aperture. No other strong emission line regions are found in the field.


  \begin{figure} \par\resizebox{5cm}{!}{\includegraphics[clip]{1591_f5.ps}}\hspace... ...hspace*{6mm} \resizebox{5cm}{!}{\includegraphics[clip]{1591_f10.ps}}\end{figure} Figure 5: Emission line images of various emission lines where the continuum has been subtracted using images using adjacent wavelengths. For comparison a broad band image is included in the lower right hand panel. Smoothed contours of 2, 4, 6,...$\sigma $ levels are overlayed. The solid black line represent the 4$\sigma $ level.
Open with DEXTER

   
3.2 High surface brightness region

To create a spectrum with a higher signal to noise ratio relevant for deriving properties from the emission lines, we selected spaxels from Fig. 5 where the surface brightness of the emission lines is strongest, i.e. within a 1 $^{\prime \prime }$ radial aperture (corresponding to $\sim$15 spaxels) centered on (-6.5, -2.5). Several lines can be identified in the spectrum shown in Fig. 6. Observed line fluxes and equivalent widths (EW) are listed in Table 2. All emission line fluxes refer to the spectrum which has been corrected for the telluric absorption feature.


  \begin{figure} \par\resizebox{14cm}{!}{\includegraphics[angle=90,clip]{1591_f11.ps}}\end{figure} Figure 6: Spectrum of the galaxy created by co-adding 15 spaxels that appeared to be associated with the bright line emission region. Emission lines listed in Table 2 are indicated.
Open with DEXTER

The median redshift of the emission lines is $z_{{\rm em}}$ = $0.1595\pm0.0006$ in agreement with $z=0.1592\pm0.0020$ found by B88. The observed FWHM of emission lines are $7.2\pm0.5$ Å and $6.1\pm1.1$ Å for H$\alpha $ and H$\beta $, respectively, which implies that the lines are consistent with being unresolved given the spectral resolution. Line fluxes of the faint lines have been derived assuming a similar width as for the brighter lines. The velocity difference between the absorption system and the median emission redshift is 180 km s-1. In Sect. 5 we will return to further analysis of the kinematics involved in this system along with the implications.

To check if the correction for telluric absorption is appropriate we measure the line ratio [N II]$\lambda$6583/[N II]$\lambda$6548 which should theoretically be 3.0 (Wiese et al. 1966), while the derived ratio is $3.58\pm0.76$. Thus, we conclude that the correction does not introduce large errors of the derived line fluxes. Before application of the correction the line ratio is $\sim$2, however, it is uncertain as the continuum level is wrongly placed because of the telluric absorption.

Although unaffected by the correction for telluric absorption, the [O III]$\lambda$5007/[O III]$\lambda$4959 line ratio should be 2.87, while we measure the ratio $2.31\pm0.85$. Line ratios of the emission lines [O III]$\lambda$5007 vs. H$\beta $ and [N II]$\lambda$6583 vs. H$\alpha $ classify this object as an H II galaxy according to the classification scheme of Veilleux & Osterbrock (1987).

Using long slit spectroscopy B88 find a H$\beta $ line flux of $2.2\times10^{-16}$  erg cm-2 s-1, which is slightly below our measured line flux given in Table 2. Their long slit spectrum was obtained with a 1 $.\!\!^{\prime\prime}$5 slit, i.e. smaller than our 1 $^{\prime \prime }$ radial aperture for creating the spectrum. Therefore, our finding of a larger line flux can be explained by small slit-losses in their spectrum.

   
4 Derived properties

Using the strong emission lines observed in the galaxy spectrum we derive the dust reddening, abundances from the nebular emission lines in Table 2, and its star formation rate.

   
4.1 Dust reddening

From the observed Balmer decrement the dust content can be estimated. In the Case B Balmer recombination scenario the ratio of the emission lines is \(I(\mbox{H$\alpha$ })/I(\mbox{H$\beta$ })=2.85\), depending slightly on the temperature and density (Brocklehurst 1971), while the observed flux ratio is $F(\mbox{H$\alpha$ })/F(\mbox{H$\beta$ })=3.02\pm0.39$ which is consistent with no reddening.

Using the Milky Way extinction curve in Fitzpatrick (1999), we find the reddening EB-V  $=0.05\pm0.09$ or equivalently $A_V=0.16\pm0.28$ for a Galactic value of RV=3.1. Similarly, the theoretical ratio of $I(\mbox{H$\gamma$ })/I(\mbox{H$\beta$ })$is 0.46 in the case B scenario, while we measure $F(\mbox{H$\gamma$ })/F(\mbox{H$\beta$ })$ = $0.52\pm0.17$. This corresponds to EB-V = $0.25\pm0.88$which is in agreement with the reddening derived from the H$\alpha $/H$\beta $ line ratio.

Because the internal extinction in this system is consistent with 0, we do not correct the derived emission line fluxes for this effect. With integral field data one can in principle create dust maps by dividing the H$\alpha $-image with the H$\beta $-image, but in this case, the signal to noise ratio is not high enough to derive a reliable extinction map.

   
4.2 Chemical abundances

Using the line fluxes of strong emission lines we derive abundances of oxygen and nitrogen using various calibrations and diagnostics from the literature.

4.2.1 Oxygen
To determine the oxygen abundance of the galaxy we make use of the relation \({\rm O3N2}\equiv \log([O {\sc iii}]\lambda5007 / \mbox{H$\beta$ })/$ $ ( [N {\sc ii}]\lambda6583/\mbox{H$\alpha$ })\) recently calibrated in Pettini & Pagel (2004). Our data cover all the strong lines involved in the O3N2 calibration which for G4 yields $12+\log\textrm{(O/H)}=8.66\pm0.10$, while an additional error of 0.14 dex is due to the scatter in the calibration itself. The abundance corresponds to the solar oxygen abundance $8.66\pm0.05$ in Asplund et al. (2004). This solar oxygen abundance is lower than found in models previously[*], driving the derived oxygen abundance for G4 relative to solar towards higher values than reported in the literature for other Mg II galaxies. Taking instead the solar oxygen abundance $8.74\pm0.08$obtained by Holweger (2001), G4 has sub-solar metallicity (0.8 Z $_{\normalsize\odot}$), but still consistent with solar within 1$\sigma $ errors.

The O3N2 ratio benefits from the fact that the involved lines are not separated by long wavelength ranges, and thus the quantity is largely unaffected by dust obscuration. At any rate, the small intrinsic reddening inferred for G4 implies that the O3N2 ratio is affected little.

For comparison we also calculate oxygen abundances using line diagnostics calibrated by other authors. For example, the oxygen abundance can be estimated from the ratio N2 $~\equiv\log([N {\sc ii}]/\mbox{H$\alpha$ })$ using the calibration in Denicoló et al. (2002). These two strong emission lines are present in the G4 spectrum, and the calibration gives $12~+~\log\textrm{(O/H)}=8.77\pm0.06$. Applying instead the slightly different calibration of the N2 ratio in Pettini & Pagel (2004), we find $12~+~\log\textrm{(O/H)}=8.65\pm0.03$ in agreement with the O3N2 diagnostic. The intrinsic 1$\sigma $ scatter of this latter N2 calibration causes an additional uncertainty of 0.18 dex.

As another line of enquiry, we combine our data of G4 with those available in the literature. Oxygen abundances have frequently been determined using the \(R_{23}\equiv([O {\sc ii}]\lambda3727+[O {\sc iii}]\lambda4959+[O {\sc iii}]\lambda5007)/\mbox{H$\beta$ }\)intensity ratio (Pagel et al. 1979). Although the spectrum of G4 does not cover the wavelength of [O II], we can estimate roughly the value if it had been covered. If the flux reported in B88 ( $[O {\sc ii}]=4.1\times10^{-16}$ erg cm-2 s-1) is not corrected for Galactic extinction, the un-absorbed value will be $f_{{\rm obs}}=4.1\times10^{0.4E_{B-V}R(5963~{\rm\AA})}$, where EB-V is the Galactic extinction, and $R(5945~\textrm{{\AA}})=4.125$ is the value of the extinction curve at the wavelength of [O II] at z=0.1595. Furthermore, we correct the slit-loss present in their spectra by applying a scale factor between their H$\beta $ line flux and ours. We estimate the [O II] line flux $F([O {\sc ii}])=(6.7\pm0.4) \times 10^{-16}$  erg cm-2 s-1. Ellison et al. (2004) find an [O II] flux twice this value, but also their H$\beta $ and [O III] fluxes are twice the ones we measure.

Using the scaled B88 [O II] line flux we find $\log~R_{23}=0.48\pm0.18$, which according to the calibrations in Kobulnicky et al. (1999) gives $12+\log\textrm{(O/H)}=9.02\pm0.13$. This value agrees within the errors with the R23-based $12+\log\textrm{(O/H)}=8.9\pm0.2$ in Ellison et al. (2004) which justifies our assumption of applying a scaling factor of the [O II] flux.

All the derived abundances using the various diagnostics are summarised in Table 3. Kobulnicky et al. (1999) report that the calibration is very uncertain for line fluxes with lower signal to noise ratio than 8:1. Given such uncertainties of the latter abundance determination, combined with the fact that the O3N2 calibration involves emission lines detected in the data, and not a scaled [O II] flux derived from B88, we rely on the oxygen abundance derived from the O3N2 ratio. Thus, we find that the galaxy has a solar oxygen abundance.

Table 3: Oxygen abundance determinations. Diagnostics have been taken from following papers: (1) Pettini & Pagel (2004), (2) Denicoló et al. (2002), (3) Kobulnicky et al. (1999).

4.2.2 Nitrogen
Having derived a solar oxygen abundance for G4, this information can be used to estimate the electron temperature which in turn is used to determine the N abundance. Because oxygen is the main coolant of a gaseous nebula, one expects to see a correlation between the oxygen abundance and the electron temperature of an H II region. From a sample of extragalactic H II regions with a large range of O abundances van Zee et al. (1998b) derive $T_{\rm e}$. In their 39 regions with 8.56$\;<\;$12+log(O/H)$\;<\;$8.76, similar to the value of G4 within errors, we find an average $T_{\rm e}=7000\pm900$ K. This temperature estimate is in agreement within 1$\sigma $ errors with the relation between R23 and the [N II] temperature in Thurston et al. (1996), which yields $t_{[N {\sc ii}]}=7600\pm1000$ K. The uncertainty both reflects the calibration scatter (500 K) and the uncertainties of line fluxes (900 K).

Abundances of ionized nitrogen can then be derived using the relation between temperature and nitrogen to oxygen ratio (Pagel et al. 1992). Disregarding ionization corrections, the nitrogen abundance can be derived assuming (N/O) = (N+/O+), which is a valid approximation since the ionization potentials for O+ and N+ are similar. Furthermore, as shown by the models in Thurston et al. (1996), this approximation is accurate within 5%. For the emission lines from G4 we find $\log{\rm (N/O)}=-0.98\pm0.23$ using the average $T_{\rm e}$, i.e. sub-solar, but consistent within 1$\sigma $ with the solar value $\log{\rm (N/O)}\mbox{$_{\normalsize\odot}$ }=-0.81$ (Holweger 2001). A similar result is obtained from the [N II] temperature which gives $\log{\rm (N/O)}=-0.90\pm0.22$. A linear relation between the O and N abundance at high oxygen abundances is observed in extragalactic H II regions (van Zee et al. 1998a), thus a solar N/O abundance is expected for G4.

Ionic abundances can also be derived using software for analysis of emission line nebulae within the IRAF/STSDAS environment (Shaw & Dufour 1995). As inputs we use the [N II] temperature estimated above and a low density environment (n=10 cm-3) which is preferred from the observed [S II] $\lambda\lambda$6717,6731 line ratio. These values give $\log\textrm{(N/O)}=-0.98\pm0.13$ where the error mostly depends on the uncertainty of the temperature. Choosing instead a density of 100 cm-3only increases $\log\textrm{(N/O)}$ by 0.01 dex.

As a consistency check, we investigated whether the derived oxygen abundance is in agreement with calibrations to derive the (N/O) abundance ratio. Using the polynomial relations between the oxygen abundance and $\log$(N+/O+) in Kewley & Dopita (2002) yields $\log\textrm{(N/O)}=-0.90\pm0.08$ inferred from the oxygen abundance derived from the O3N2 diagnostics. The error includes the uncertainty of the chosen ionization parameter. However, as shown in Kewley & Dopita (2002) this diagnostic is relatively independent of the ionization parameter for metallicities larger than half solar, which is the case here. The derived abundance ratios using the various estimators are summarised in Table 4. From these values we conclude that the galaxy has $\log{\rm (N/O)}=-1.0\pm0.2$.

Table 4: Nitrogen abundance determinations using different diagnostics from following papers: (1) van Zee et al. (1998b); Pagel et al. (1992), (2) Pagel et al. (1992); Thurston et al. (1996), (3) Shaw & Dufour (1995), (4) Kewley & Dopita (2002).

   
4.3 Star formation rate

The derived line fluxes of emission lines can be used to derive an overall star formation rate (SFR) of the galaxy. A redshift of z=0.1595 corresponds to a luminosity distance of $2.35\times10^{27}$ cm (760 Mpc) for the given cosmological model. Thus, the H$\alpha $  line flux corresponds to a luminosity $L(\mbox{H$\alpha$ })=(6.25\pm0.20)\times10^{40}$ erg s-1. Using the relation

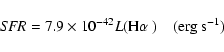\begin{displaymath}{\it SFR} = 7.9 \times 10^{-42} L( \mbox{H$\alpha$ }) \quad (\textrm{erg~s}^{-1}) \end{displaymath} (1)

in Kennicutt (1998) to convert the flux to a SFR we find SFR = $0.49\pm0.15$ M $_{\normalsize\odot}$ $\>\rm yr^{-1}$. The uncertainty includes the one from the line flux and a larger additional uncertainty from the intrinsic scatter of the calibration of the conversion factor of $\sim$30%.

The H$\alpha $ based SFR relies only on the data set of G4 presented here, while an alternative measure of the SFR can be estimated from the scaled [O II] line flux. At z=0.1595 the luminosity is $L([O {\sc ii}])=(4.67\pm0.28)\times10^{40}$ erg s-1, which, using the conversion in Kennicutt (1998), yields SFR = $0.43\pm0.12$ M $_{\normalsize\odot}$ $\>\rm yr^{-1}$. This value is furthermore in agreement with the calibration in Kewley et al. (2004), which yields SFR = $0.45\pm0.17$ M $_{\normalsize\odot}$ $\>\rm yr^{-1}$. The agreement between the SFR of the galaxy derived from different calibrations gives credibility to the inferred small internal reddening in the galaxy.

   
5 Kinematics

From the redshift difference between the sub-DLA cloud and the galaxy found from the one-dimensional spectrum of G4, we find that the relative velocity difference is 180 km s-1. Considering that the galaxy seems to be a fairly luminous galaxy, such a velocity difference over a distance of 17.6 kpc could be consistent with rotation of a massive disk, but the orientation of the galaxy with the major axis oriented roughly north-south, while the sub-DLA cloud lies to the north-east, does not support this hypothesis. We analyse here only radial velocities but note that the proper motion of the cloud could be significant.

By fitting the strongest H$\alpha $ emission lines with Gaussians we examine the dynamics of the galaxy G4. Because each individual spectrum is rather noisy, the fitting could only be done satisfactorily in the region around the strongest emission. In Fig. 7, velocity offsets relative to the systemic z=0.1595 are shown as contours overlayed an image of the H$\alpha $ emission intensity. Uncertainties of the centroids of the Gaussian fits to the strongest lines are of the order of one tenth of the spectral resolution, i.e. 0.6 Å corresponding to errors of 25 km s-1. We find evidence for a systematic velocity of ${\sim}{-}120$ to +160 km s-1 with the rotation axis oriented roughly east-west. The point of zero-level velocity is located roughly 0 $.\!\!^{\prime\prime}$5 to the south of the centre of the G4 continuum emission.

In this representation the absorbing cloud towards the QSO (at coordinates 0, 0) has a velocity offset of +180 km s-1 with respect to zero velocity of the H$\alpha $ emission. We conclude that it is unlikely that the absorbing cloud is participating in a disk rotation.


  \begin{figure} \par\resizebox{8.4cm}{!}{\includegraphics[clip]{1591_f12.ps}}\end{figure} Figure 7: The gray scale image shows the intensity of the H$\alpha $ emission line. Relative velocities in km s-1 inferred from H$\alpha $ emission lines are shown as contours. Grey contours (orange in the electronic edition) are positive velocities, and black (blue) contours are negative. Only regions showing H$\alpha $ emission have been included for clarity. In comparison, the relative velocity difference of absorption in the sub-DLA cloud is +180 km s-1 towards the QSO sight-line.
Open with DEXTER

In the integral field data we measure a velocity of 160 km s-1 relative to the zero velocity contour of H$\alpha $ at a distance of $\sim$2 $^{\prime \prime }$ corresponding to 5.5 kpc. However, if one takes the centre of the galaxy as the true reference point, the velocity difference is $\sim$200 km s-1over a distance of 2 $.\!\!^{\prime\prime}$5 (6.9 kpc) as indicated in Fig. 7. Assuming that the galaxy is viewed edge-on, the dynamical mass is \(M_{{\rm dyn}}=v_c r/G=(6\pm2)\times10^{10}\) M $_{\normalsize\odot}$, where the error is due to the uncertainty of the velocity. Because the inclination axis is not known, this value is a lower limit, while another uncertainty is due to the fact that we probably do not reach asymptotic values for the rotation curve. In any case, the estimate shows that the galaxy is a fairly massive one.

   
6 Discussion

Having derived various properties of the sub-DLA galaxy, we proceed by comparing them to those of other sub-DLA and DLA galaxies in the literature. We emphasize once again that there is another galaxy, G3, at the same redshift as G4 but having a larger impact parameter. G3 might contribute to the absorption seen in PHL 1226. No galaxy in Fig. 3 of B88, however, is closer to the QSO than G4, and we discuss in Sect. 6.3 that our data allow us to exclude an emission-line galaxy with a smaller impact parameter than G4 between G4 and the QSO. As is common practice in the literature on DLA galaxies, we proceed with the assumption that the absorbing cloud belongs to the galaxy with the smallest impact parameter.

6.1 Relationship with DLAs, sub-DLAs and Mg II systems

The derived oxygen abundance of the galaxy G4 is larger than abundances derived for high redshift sub-DLAs (Péroux et al. 2003; Dessauges-Zavadsky et al. 2003). Furthermore, compared to the nearby DLA absorber SBS 1543+594 (Schulte-Ladbeck et al. 2004), this galaxy has a higher abundance, but that goes in hand with its higher luminosity. In fact we calculate MB=-20.0 using the spectrum in Fig. 3 shifted to the rest frame and convolved with the Bessell B band transmission function. G4 exhibits values which are entirely consistent with the local luminosity-metallicity relation (Pilyugin et al. 2004; Kobulnicky & Koo 2000).

On the other hand, G4 has an oxygen abundance compatible with the upper end of abundances derived for the Mg II selected galaxies ( $-0.6<{\rm [O/H]}<-0.1$ derived in Guillemin & Bergeron 1997). For comparison, high resolution spectra of strong Mg II absorption systems towards a couple of QSOs at $z\sim1$ have indicated metallicities ranging from 0.1 to 1 times solar (Ding et al. 2003a,b). This could indicate a general agreement between metallicities derived using absorption lines and emission line diagnostics.

The kinematic investigation showed that the absorber is clearly not associated with a disk, but it could be part of a rotating halo as suggested for other Mg II absorbers (Steidel et al. 2002). The galaxy G4 and its sub-DLA system could thus be similar to the z=0.16377 sub-DLA towards Q0850+4400 (Lanzetta et al. 1997). They showed that the absorption arises at large galactocentric distance (17 kpc) and does not participate in a general disk rotation.

Alternatively, Bond et al. (2001) suggested that a substantial fraction of very strong Mg II systems arise in superwinds from galaxies. Along similar lines, expanding superbubbles were suggested to be the explanation for metal absorption line mirror symmetries seen in the strong Mg II absorber towards Q1331+17 (Ellison et al. 2003). A superwind from the galaxy G4 is unlikely at present time given the relatively small SFR. However, as it is comparable to an L* galaxy, a previous starburst could have expelled neutral gas clouds enriched by metals.

6.2 Abundance gradient effect

Metallicity studies of DLAs and sub-DLAs are trying to explain the question of what is the nature of the parent galaxy. Only in very few currently known cases, where the parent galaxy has been clearly identified, can such an investigation be carried out. Abundances derived from metal absorption lines associated with the DLAs can be compared to abundances based on emission line diagnostics for H II regions in the galaxy. The DLA galaxy SBS 1543+594 is one example, where the impact parameter is small - in fact, the sight line to the QSO goes through the disk of the dwarf galaxy. In such a case, the inferred metallicity of the DLA cloud and the galaxy is expected to be similar. However, in the case of the G4/sub-DLA system towards PHL 1226 where the impact parameter is larger and the sub-DLA cloud possibly does not belong to the disk of the galaxy, one would expect to find lower (O/H) and (N/O) abundances of the sub-DLA cloud due to abundance gradients.

Analysing abundances in extragalactic H II regions Vila-Costas & Edmunds (1992) and Zaritsky et al. (1994) found a large scatter in the abundance gradients for individual galaxies of a given Hubble type. They also found a tendency for more shallow gradients, expressed in dex/kpc, for early and late type spirals compared to intermediate type spirals. Locally, three face-on disk galaxies were found to have strong abundance gradients along the major axes in the outer regions of their disks (Ferguson et al. 1998, hereafter F98). Fewer studies have analysed the metallicity gradient along the minor axes of galaxies, but smaller metallicities have been found for extraplanar H II regions compared to the core of an edge-on galaxy (Tüllmann et al. 2003). The study of H II regions in face-on galaxies can therefore also be biased by projection effects.

The data presented here do not allow us to estimate the Hubble type of G4, making it difficult to predict an appropriate abundance gradient. If one takes the measured metallicity gradient from F98 with an average in $\log$(O/H) of -0.09 dex kpc-1, the abundance of the sub-DLA cloud at 17.6 kpc is expected to be $\sim$1.6 dex lower than what we find for the G4 disk. Similarly, the average gradient in $\log$(N/O) is -0.05 dex kpc-1 which implies an abundance ratio smaller by 0.9 dex. Thus one could expect 12+$\log$(O/H) = 7.1 and $\log$(N/O) = -1.9 for the sub-DLA abundances. We assume that the gradients are straight lines which may not be the case (Zaritsky et al. 1994). If a low abundance of the PHL 1226 sub-DLA cloud should be confirmed by future space based spectroscopy, these values would place the sub-DLA system toward PHL 1226 among the metallicities for the currently measured high redshift DLA and sub-DLA systems measured by several authors (Lopez et al. 2002; Pettini et al. 2002b; Lopez & Ellison 2003; Centurión et al. 2003).

These approximate cloud metallicities are crude estimates since the impact parameter is a lower limit due to the unknown inclination angle, and the individual abundance gradients in F98 vary within a factor of 2. Furthermore, the lowest metallicities observed by F98 reach 12+$\log$(O/H) = 7.95, thus we are extrapolating their metallicity gradient.

6.3 Sub-DLA cloud properties

Other properties of G4 such as H$\beta $ luminosity, EW of H$\beta $ , absolute magnitude, and oxygen abundance are compatible with those of emission line field galaxies at redshifts 0.26<z<0.82 (Kobulnicky et al. 2003). This apparently seems to be in contradiction with the spectroscopic analyses suggesting that sub-DLAs/DLAs are chemically less evolved than star forming galaxies at similar redshifts. Specifically, sub-DLAs/DLAs have sub-solar metallicity and element abundances suggesting low SFRs (Pettini et al. 2002a; Dessauges-Zavadsky et al. 2003; Péroux et al. 2003; Prochaska et al. 2003). On the other hand we can not, with the currently available data set, exclude the possibility that a galaxy less luminous than G4 closer to the line of sight towards PHL 1226 is responsible for the sub-DLA. In the integral field data presented here we find no evidence for line emission closer to the line of sight than 5 $^{\prime \prime }$ to the west of the QSO. With the presented single pointing towards the QSO we can not say anything about the other directions.

As argued, either galaxy G4 or G3 could be responsible for the sub-DLA cloud. If the cloud were associated with G3, it too has to be associated with a halo because of the orientation of the galaxy which suggests an elongation in the east-west direction (i.e. perpendicular to the direction toward PHL 1226). Assuming that the sub-DLA cloud indeed belongs to the galaxy G4, we find a velocity difference of 180 km s-1 from the sub-DLA cloud redshift to the H$\alpha $ velocity at the centre of G4, for which we estimate the galaxy mass $(6\pm2)\times10^{10}$ M $_{\normalsize\odot}$. In this case, the escape velocity at a distance of 17.6 kpc is $200\pm30$ km s-1 implying that the cloud could be gravitationally bound.

Yet another possibility for the location of the sub-DLA cloud is gravitational interaction between systems. Indeed the galaxies G4 and G3 have a distance of 12 $.\!\!^{\prime\prime}$6 from each other corresponding to 35 kpc, so it could be an interacting system, but with the currently available observations we can not test this scenario.

   
7 Conclusions

Using integral field spectroscopy with PMAS we have observed the absorber G4, previously identified by Bergeron et al. (1988), toward the QSO PHL 1226 at an impact parameter of 6 $.\!\!^{\prime\prime}$4. This galaxy is most probably responsible for a strong Mg II and sub-DLA absorption system at z=0.1602 in the QSO spectrum. At the same redshift another galaxy, G3, is present. We cannot determine whether the PHL 1226 absorber belongs to galaxy G4 or G3, but concentrate on G4. Their impact parameters of 6 $.\!\!^{\prime\prime}$4 and 10 $.\!\!^{\prime\prime}$9 correspond to 18 and 29 kpc, respectively, implying that either could be responsible for the absorption given the scaling-law of Mg II absorbers.

A strong emission line region is shown to be limited to an area of approximately 1 $^{\prime \prime }$ in radius within the galaxy. In the spectra we find emission lines from [O III], [N II], [S II] as well as Balmer lines H$\gamma $, H$\beta $  and H$\alpha $ at the redshift $0.1595\pm0.0006$. We do not find regions of emission at the same redshift closer to the QSO line of sight.

From the Balmer line ratios we find evidence of an intrinsic reddening of $\mbox{$E_{B-V}$ }=0.05\pm0.16$, i.e. consistent with 0. From the measured H$\alpha $ line flux we derive a SFR = 0.5 M $_{\normalsize\odot}$ yr-1.

Using the O3N2 line ratio diagnostics from Pettini & Pagel (2004) we derive a solar oxygen abundance \(12+\log\textrm{(O/H)}=8.7\pm0.1\). Also a solar value of the abundance ratio $\log$(N/O) = $-1.0\pm0.2$ is found implying a metallicity comparable to the upper-end of metallicities for the currently known sample of Mg II galaxies.

A kinematic analysis of the H$\alpha $ emission line showed that the galaxy has rotational velocities of -120 to +160 km s-1 relative to the systemic redshift with the rotational axis oriented roughly east-west. The sub-DLA cloud, on the other hand, has a velocity difference of 180 km s-1relative to the galaxy and an impact parameter of 17.6 kpc above the disk assuming that the disk is seen edge on. With such geometry and kinematics, the sub-DLA cloud is likely part of a rotating halo and possibly gravitationally bound. From relative velocity measurements we derive a kinematic mass of $6\times10^{10}$ M $_{\normalsize\odot}$, which corresponds to a fairly massive galaxy. The absolute magnitude is MV=-20.3 and MB=-20.0 which is consistent with the mass-luminosity relation for spiral galaxies (Forbes 1992).

With future UV space-based spectroscopy it will be possible to compare the metallicity of the sub-DLA cloud towards PHL 1226 with abundances derived for the galaxy, which is necessary in order to understand the relation between the absorption lines in QSO spectra and the galaxies responsible for them. If there is a difference in metallicity in line with the metallicity gradients observed in local disk galaxies, we expect that the properties of the sub-DLA cloud will be similar to those of high redshift DLA and sub-DLA systems. This is an intriguing prospect which could suggest that the specific sight line through the galaxy responsible for the DLA or sub-DLA cloud has important consequences on the derived properties of the cloud.

Acknowledgements
L. Christensen acknowledges support by the German Verbundforschung associated with the ULTROS project, grant No. 05AE2BAA/4. R. Schulte-Ladbeck is thankful for funding from HST archival grant No. 10282. S. F. Sánchez acknowledges the support from the Euro3D Research Training Network, grant No. HPRN-CT2002-00305. K. Jahnke and L. Wisotzki acknowledge a DFG travel grant under Wi 1389/12-1.

References

 
Copyright ESO 2004