A&A 429, 631-643 (2005)
DOI: 10.1051/0004-6361:20041527

The $\beta$ Cephei variable in the eclipsing binary HD 92024

I. Determination of the orbit[*]

L. M. Freyhammer1,2 - H. Hensberge 1 - C. Sterken 2,[*] - K. Pavlovski 3 - A. Smette 4,5,[*] - S. Ilijic 6


1 - Royal Observatory of Belgium, Ringlaan 3, 1180 Brussels, Belgium
2 - OBSS/WE, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussels, Belgium
3 - Department of Physics, University of Zagreb, Bijenicka 32, 10000 Zagreb, Croatia
4 - Institut d'Astrophysique et de Géophysique, Université de Liège, 17 Allée du 6 Août, 4000 Liège, Belgium
5 - European Southern Observatory, Casilla 19001, Alonso de Cordova 3107, Vitacura, Santiago, Chile
6 - Faculty of Electrical Engineering and Computing, Department of Applied Physics, University of Zagreb, Unska 3, 10000 Zagreb, Croatia

Received 24 June 2004 / Accepted 28 August 2004

Abstract
HD 92024 is a member of the open cluster NGC 3293; it is the only eclipsing binary system with a $\beta~{\rm Cephei}$ component known in the southern hemisphere. This paper presents the first spectroscopic analysis of the single-lined binary and provides an orbital analysis based on recent high-resolution spectroscopy and photometry. A procedure to derive orbital elements with minimal influence of the pulsational line-profile variations on the radial velocities is applied, and we find the stellar masses to be $15.0^{+3.0}_{-4.0}~M_\odot$ and $3.0\pm0.5~M_\odot$ respectively, and radii of $8.4\pm0.8~R_\odot$, $2.1\pm0.4~R_\odot$. The temperatures are $25~500\pm500$ K and $12~500\pm1000$ K. The surface gravity values of $\log g= 3.77\pm0.08$ and $4.27\pm0.18$ indicate that the binary consists of an evolved early B-type primary and a late-B main sequence companion. The resulting distance $2.8\pm0.3$ kpc and systemic velocity -16 km s-1 confirm cluster membership. Theoretical stellar models indicate an age of 10-13 Myr, somewhat higher than the literature value for the brightest members of NGC 3293.

Key words: stars: binaries: eclipsing - stars: binaries: spectroscopic - stars: early-type - techniques: spectroscopic

   
1 Introduction

$\beta$ Cephei stars are early B-type stars in an advanced state of core-hydrogen burning that pulsate in opacity-driven modes penetrating the whole interior (Dziembowski & Pamyatnykh 1993) with periods of 2-12 h and visual amplitudes typically below 0 $.\!\!^{\rm m}$1. They have spectral types between B0.5 and B3 and masses in the range 7 $M_\odot$ to 20 $M_\odot$. The multiperiodic oscillation patterns comprise low radial order pressure (p) and gravity (g) modes, which makes this class of variables a promising candidate for asteroseismological studies. A considerable fraction of the known $\beta~{\rm Cephei}$ stars are components of binary systems and even both components may be $\beta~{\rm Cephei}$ stars. The mechanisms behind tidal influence on a $\beta~{\rm Cephei}$ component in a binary are not well understood, but may suppress the $\beta~{\rm Cephei}$ pulsations, though not in all cases. Still, whenever an eclipsing companion is present, it becomes possible to obtain independent estimates of stellar masses and stellar densities, which will provide strong constraints on the asteroseismic tests. For reviews on $\beta~{\rm Cephei}$ stars we refer to Sterken & Jerzykiewicz (1993) and Aerts & De Cat (2003).

HD 92024 (V381 Car, SpT. B1 III, $m_V=9\hbox{$.\!\!^{\rm m}$ }02$) is the only known $\beta~{\rm Cephei}$ component in an eclipsing binary in the southern hemisphere. The star is a member of the young open cluster NGC 3293 where it was registered as #5 by Feast (1958). He determined the cluster's radial velocity to be -14$\;\pm\;$1.8  $~{\rm km}~{\rm s}^{-1}$ and identified the star as a radial velocity variable with a range of 52  $~{\rm km}~{\rm s}^{-1}$. The distance modulus to NGC 3293 is $V_0-M_V=12.2\pm0.2$ (=2750$\;\pm\;$250 pc, Baume et al. 2003) and the cluster shows differential reddening.

Balona (1977) discovered the $\beta~{\rm Cephei}$ light variations of HD 92024 and the eclipsing nature was found by Engelbrecht & Balona (1986, EB86 hereafter) who determined an ephemeris based on extensive photometric B-band observations relative to NGC 3293-20. They detected two oscillation frequencies, f1=5.640  $\;{\rm c}~{\rm d}^{-1}$ and f2=7.669  $\;{\rm c}~{\rm d}^{-1}$, but the f2 frequency is ambiguous due to a 1  $\;{\rm c}~{\rm d}^{-1}$ alias. Engelbrecht (1986) re-analysed the EB86 photometry and detected a third frequency f3=7.17  $\;{\rm c}~{\rm d}^{-1}$. Jerzykiewicz & Sterken (1992, JS92 hereafter) obtained uvby photometry over 5 years and confirmed the frequencies f1 and f3, or the latter's 1  $\;{\rm c}~{\rm d}^{-1}$ alias. By combining their observations with those of EB86 they derived an orbital period of $8\hbox{$.\!\!^{\rm d}$ }3245\pm0.0001$ with a primary minimum of light at HJD  $2~445~391.4005\pm0.001$.

The present paper deals with the orbital elements of the binary system using recent high-resolution spectroscopy and photometry including new eclipse observations. In Sect. 2 the observations and data reduction are described. Section 3 gives the ephemeris and the period analysis of the photometry, and Sect. 4 shows the spectroscopic analysis leading to the orbital elements. In Sect. 5 the photometric analysis with the Wilson-Devinney code is given. Finally, the stellar dimensions and evolutionary stage are presented and discussed in Sect. 6, before concluding in Sect. 7.

   
2 Observations and reduction

The observations cover spectroscopy and photometry (CCD and PMT) obtained during 2001-2003, supplemented with spectra from 1989. All observations were obtained at the ESO La Silla observatory. In addition, photometric data from the literature were added. Details on the collection and reduction of the data are given together with the fully reduced spectra in Hensberge et al. (2004).

2.1 Light-curve observations

A comprehensive set of mostly by-CCD frames of HD 92024 has been obtained using several telescopes in the last decade as part of the project Long-Term Photometry of Variables (Sterken 1983, 1994). More than 1100 Strömgren uvby PMT photometric measurements were obtained with the 50-cm Strömgren Automatic Telescope (SAT) on 15 nights distributed over Dec. 2002-Apr. 2003. Differential observations were done continuously around parts of the light minima. In order to cover complete pulsational cycles for the subsequent removal of pulsational light variations, the observations were made as continuous series of 4 h or longer whenever possible. Automatic centering within a circular diaphragm of 17 $^{\prime\prime}$ diameter was used throughout and all measurements were done at an air mass less than 2.1. We adopted three comparison stars (Table 1), NGC 3293-20 (=CPD-57$^$3523, C1), HD 92072 (C2), HD 91477 (C3), approximately matching the spectral type of the binary and positioned on the sky within a few degrees from it. The observations were done in C1-P-C2-P-C3-P-C1- etc. sequences, allowing accurate magnitude differences to be formed in case C1 was found to be variable. Each observation of a star in this sequence consisted of three integrations of max 120 s, and sky measurements were taken at least once per sequence at a fixed position close to the binary. The number of counts per program star observation is 150 000-400 000, depending on binary phase, passband and observing conditions, leading to rms contributions from photon statistics of about 2-3 mmag. The rms from the differential light curves is 4-8 mmag. Light curves for HD 92024 were made with procedures similar to those described in Clausen et al. (2001) and the data were kept in the instrumental system. Linear extinction coefficients were determined individually for each night from the observations of comparison stars and standard stars, though the latter were optimised for later-type stars in other programs on the SAT. Whenever appropriate, linear or quadratic corrections for drift during the night that was caused by changes in the sky transparency or temperature variations of the uncooled photomultipliers were also applied. The comparison stars were all found to be constant down to the level indicated in Table 2. In particular, a detailed frequency analysis of the difference light curve of C1 to C2, C3 showed no presence of cyclic frequencies down to the level of 3 mmag (0-50 $\;{\rm c}~{\rm d}^{-1}$). Light curves for HD 92024 were then formed using, for each HD 92024 observation, the two comparison star measurements closest in time. All C2 and C3 observations were first shifted to the level of C1.

Table 1: Photometric indices and data for HD 92024 (P) and comparison stars. Sources: Kaltcheva (2003) and Shobbrook (1983, for C1).

Table 2: rms scatter of the PMT magnitude differences (mmag) between comparison stars. N is the number of differential measurements.

An additional two hours of CCD observations were obtained in Apr 2001 (JD 2 452 009) using the Danish 1.54-m telescope with DFOSC (2k $\times$ 2k LORAL-LESSER CCD, 0 $\hbox{$.\!\!^{\prime\prime}$ }$40 pix-1). The observations were reduced using MOMF (Kjeldsen & Frandsen 1992), which applies a combination of aperture and PSF-fitting photometry. The photometry of HD 92024 was done differential to C1. The CCD and PMT data were then combined with photometry published by EB86 (B CCD-data) and JS92 (b,uvby PMT-data) by adding magnitude offsets determined from the available out-of-eclipse observations; for improving the ephemeris, a blue light curve (Fig. 1) was formed by combining all B and b data (2277 points), while for the binary model analysis a set with simultaneous uvby observations was composed (1617 points in uvby and 73 points more in b, Fig. 2).
  \begin{figure} \par\includegraphics[angle=90,width=15.9cm,clip]{1527fg01.ps} \end{figure} Figure 1: The blue light curve before ( top) and after ( bottom) prewhitening the frequencies f1,f2,f3. The four different datasets are indicated.
Open with DEXTER

A thorough pulsational analysis based on our spectra and a larger set of photometry will be the subject of a forthcoming publication. The full set of photometric data will be made available in a machine-readable data paper.

2.2 Echelle spectroscopy

Table 3: Logbook of the spectroscopic observations of HD 92024. Dates, incl. Julian date (=HJD-2 400 000), indicate start of night in UT. Column 3 lists the observers: Sterken (S), Hensberge (H) and Freyhammer (F). N is the number of spectra obtained that night, $\Delta t_{\rm exp}$ is the mean integration time (s), "Ins'' indicates instrument used (FEROS or ECHELEC) and S/N denotes the range of signal-to-noise at 4500 Å. The last column gives the orbital phase interval covered that night.

We obtained 103 high-resolution spectra with the FEROS echelle spectrograph at the ESO 1.52-m telescope during 9 nights in 2001-2002 (See observing log for all spectra in Table 3). FEROS is a fiber-fed (object+sky) spectrograph which provides a resolution R=48 000 and wavelength range 3700-8600 Å. It is equipped with a thinned and backside-illuminated 2k $\times$ 4k EEV CCD.

We intend in Paper II to study the $\beta~{\rm Cephei}$ oscillations by exploiting the full wavelength range in these spectra for information on line-profile variations. Therefore, a considerable effort was now put into improving the reduction of the FEROS spectra beyond the limitations of the standard FEROS pipeline. The main concern was to ensure consistency between all spectra by imposing a differential data reduction procedure, assuring correct order merging, removing time-dependent vignetting and blaze function variations before combining the orders, and by avoiding the introduction of time-dependent effects from the calibration unit into the spectra. Technical details are given in Hensberge (2001) and Hensberge et al. (2004). During the order-merging process, the spectra were rebinned to $\ln \lambda$, partly in anticipation of the cross-correlation velocity analysis.

23 spectra were obtained during five nights in 1989 with the ECHELEC spectrograph, also on the ESO 1.5-m, covering the range 4390-4715 Å. ECHELEC is a Littrow echelle spectrograph ( $R\sim25~000$) with a grism as cross disperser. It was equipped with a thinned backside-illuminated RCA CCD with 1024 $\;\times\;$640 pixels. In view of their long integration times, low S/N and small wavelength coverage, we reduced the ECHELEC spectra in the standard way using MIDAS routines. Instead of a reduction with more dedicated software (see Verschueren & Hensberge 1990; Verschueren et al. 1997, for details), an a posteriori correction derived from comparison to the FEROS spectra was then applied (see Hensberge et al. 2004) to minimise possible systematic errors from blemished CCD columns and improper order merging.

   
3 Ephemeris and period analysis

The light variability in HD 92024 caused by the primary's pulsations was removed from the light curves using the following procedure. 1290 out-of-eclipse data points were selected from the blue dataset; by calculating power spectra with Period98 (Sperl 1998) we sequentially searched for and removed the three most significant frequencies in the light curve. The resulting frequency solution is f1=5.6400  $\;{\rm c}~{\rm d}^{-1}$, f2=6.6613  $\;{\rm c}~{\rm d}^{-1}$, f3=7.1624  $\;{\rm c}~{\rm d}^{-1}$ with semi-amplitudes a1=7.4 mmag, a2=3.8 mmag, a3=4.2 mmag, as also found by Engelbrecht (1986). f2 and f3 are of very similar significance in the power spectrum. A final analysis of the complete light curve, with the eclipse model subtracted, confirmed all frequencies, with f3 being the least significant. For all light curves we then prewhitened f1,f2,f3, using appropriate amplitudes for each passband.

Some systematic variability remains in the light curves after prewhitening, so the frequency solution may be incomplete, but the residuals no longer critically obstruct analysis of the eclipses. The reduction of scatter by the prewhitening, inside as well as outside the eclipses, is apparent from Table 4 where our SAT data are compared to the EB86 measurements. It is seen that after prewhitening, the rms errors are comparable for data in- and outside of the eclipses as well as for the EB86 and the SAT data, indicating that the frequency analysis (based on out-of-eclipse data alone) predicts the pulsational light variations inside and outside the eclipses equally well. A closer look at the nightly light curves revealed that, as explained well by constructive interference of the frequencies, the EB86 data have higher pulsational amplitudes than the recent SAT observations. This explains the higher scatter in the EB86 data prior to the prewhitening.

Table 4: The effect of prewhitening frequencies in the SAT b light curve, with comparison to the B light curves by EB86. The statistical uncertainty in the errors ($\sigma $) is 10% as derived from observations.

Two additional full nights of SAT-observations in 2004 were perfectly reproduced by the used frequency solution.

In the prewhitened uvby light curves, Fig. 2, we notice a small orbital eccentricity because the secondary minimum occurs slightly later than half an orbital period after the primary. During secondary eclipse (full occultation by the $\beta~{\rm Cephei}$ primary) a minor blueing of the light is seen, clearest in u-b. The fact that Table 4 shows similar levels of scatter during the eclipses for light curves over 18 years, and that the old data fit nicely inside the secondary eclipse's shape as given by the recent SAT light curves, suggests absence of any significant apsidal motion. A test for apsidal motion from partly covered primary and secondary minima, using the SAT data and the EB86 and JS92 data, also showed that the timing, duration and depth of the eclipses are stable within the quality level of the available photometry. The light curves show that the centre of the secondary minimum is 1.4 h off from the half-period phase. Based on our SAT data alone, the change in orbital period needed to position the secondary eclipse exactly half a period from the primary is 0.11 days. Such a large change is discrepant with the period determined from the SAT data (even for their 120-days baseline). The large recent dataset on its own is thus incompatible with the circular orbit assumed by EB86. Their assumption at that time was logical, as they did only cover ingress of the secondary eclipse.

A refined ephemeris (Table 5) was then calculated from the blue light curve. Using the procedure by Lafler & Kinman (1965) for a fine grid of test periods centered on the period by EB86, the orbital period was improved to $8\hbox{$.\!\!^{\rm d}$ }32457\pm 0.00002$. With the method of Kwee & van Woerden (1956) applied on data in primary eclipse, our new ephemeris becomes

 \begin{displaymath}\begin{tabular}{@{$\;$ }r @{$\;$ }c @{$\;$ }r @{$\;$ }l } Mi... ...$ }32457& E \\ $\pm$0.0008 & & $\pm$0.00002.\\ \end{tabular}\end{displaymath} (1)

This ephemeris is within the errors of the result given in JS92 but more accurate. The phase of secondary mid-eclipse is 0.507$\;\pm\;$0.001.
  \begin{figure} \par\includegraphics[height=8.6cm,width=6.8cm,angle=90,clip]{1527fg02.ps} \end{figure} Figure 2: Prewhitened y and u-b light- and colour curves (see text). The binary model from Sect. 5 is superimposed.
Open with DEXTER


  \begin{figure} \par\includegraphics[height=11.3cm,width=8.1cm,angle=90,clip]{1527fg03.ps} \end{figure} Figure 3: The model orbit from RV differences (full line), compared with RVs from cross-correlations with a template (thick lines). For $\gamma =0$.
Open with DEXTER

   
4 Spectroscopic analysis

Superimposed on the stellar FEROS spectra is a number of faint emission lines from the surrounding H II region. They do not affect the cross-correlations in the wavelength region we selected and therefore we did not remove them, although this would be possible using the sky-fiber spectra. Guided by the list of Jenniskens & Désert (1994), diffuse interstellar bands (DIBs) were modelled and divided away from the spectra with the purpose of eliminating the adverse effect they would have on the cross-correlation analysis. Moreover, the spectra were inspected interactively and by means of an automated procedure in order to detect and remove remaining cosmic rays and quasi-static features due to bad pixels and other CCD blemishes. The noise in individual spectra was derived from pseudo-continuum windows in three spectral regions (4298-4402 Å, 4980-5597 Å and 6121-6977 Å), and nightly S/N-ranges are listed in Table 3.

The FEROS spectra reveal substantial line-profile variations (LPVs) despite the exposure time being one tenth of the pulsational cycle. In many cases the local line depth changes more than a factor of 2 within 70  $~{\rm km}~{\rm s}^{-1}$ from the line-centre during a pulsation cycle, while producing variable subcomponent line-structure. No secondary spectrum is seen.

To aid in the spectroscopic analysis, two composite spectra were made from FEROS spectra with orbital (model) shifts eliminated: a "103-spectrum composite'', made by averaging all FEROS spectra, and a "narrow-line spectrum composite'' averaged over 10 spectra having similar deep and narrow line profiles. The 103-spectrum composite has S/N = 1000 and is shown in its full extent with line identifications in Hensberge et al. (2004).

   
4.1 Radial-velocity amplitude

The FEROS and ECHELEC spectra were used to determine orbital parameters. As the ECHELEC spectra cover some of the FEROS spectra's orbital phases, they are also valuable for testing orbit stability over the 13-yrs baseline.

Figure 3 shows the final orbit with strings of nightly RVs superimposed with thick lines. These RVs were obtained by cross-correlating the FEROS spectra with an average spectrum constructed from all spectra compensated for nightly orbital shifts. While the orbital radial velocity at most changes 7  $~{\rm km}~{\rm s}^{-1}$ in a single night, the velocity fields may shift the RVs up to 14  $~{\rm km}~{\rm s}^{-1}$, which could bias the orbital parameter determination. The option to eliminate a large part of this bias by averaging over a single night, or a pulsation cycle, is not attractive since night-to-night bias remains due to the multi-periodicity, and only in the most recent observing run was the star monitored continuously.

Therefore, we decided to follow an alternative approach to minimise the impact of pulsational line-shifts. We refer to this method as matched-profile RV differences, because the orbit will be derived from the difference in radial velocity between pairs of spectra $S(\ln \lambda_n, t_i)$ and $S(\ln \lambda_n, t_j)$ for different times t selected to have similar line profiles. For all possible pairs of combinations ( $t_i, t_j ; i \leq j$), we compute correlations as:

 \begin{displaymath} {C}(i,j;k) = \frac{\displaystyle \sum_{n=1}^N(1-S(\ln \lamb... ...sum_{n=1}^N(1-S(\ln \lambda_{n+k}, t_j))^2\biggr]^\frac{1}{2}} \end{displaymath} (2)

where we sum over the pixels, n=1, ...,N for different velocity shifts k, expressed in pixels ( $\Delta\ln{\lambda}$), of the spectrum at tj. Assuming that the line profiles at the times ti and tj are not too different, the position of the maximum of C(i,j;k) estimates the difference in the RV of the star at ti and tj. To compare spectra, two parameters $I_{\rm SN}$ and $I_{\rm MM}$ were introduced. As indicator of S/N of each pair at ti, tj we used the square root of the product of the maxima of the corresponding auto-correlations: $I_{\rm SN}=[\max{{C}(i,i;k)}\times \max{{C}(j,j;k)}]^{\footnotesize {1/2}}$, where the maxima are determined with a 3rd degree polynomial fit to $C(i, i; 2\leq\vert k\vert)$. By excluding the 3 central cross-correlation values we avoid the auto-correlation unity value at k=0 and the adjacent values which are affected by substantial noise correlation introduced by the rebinning of the spectra. Finally, the mismatch $I_{\rm MM}$ of line profiles was expressed as the difference between $I_{\rm SN}$ (the case of identical profiles) and the fitted $\max{{C}(i, j; k)}$. For identical line profiles, $I_{\rm MM}=0$.


  \begin{figure} \par\includegraphics[height=6.7cm,width=7cm,clip]{1527fg04.ps} \end{figure} Figure 4: Selection of matching pairs (fat dots) among all combinations for the criteria (see text): linear cutoff (line), pair elements separated >4.5 h in time, $I_{\rm SN}>0.90$ and $I_{\rm MM}<0.00139$. Points along zero ordinate are auto-correlations and pairs with ECHELEC elements.
Open with DEXTER

For the correlations, we found after some tests that the RV information from the adopted region 4209-4733 Å could not be improved by adding data at other wavelengths. From the 5253 possible combinations of FEROS spectra, 80 pairs passed our test of line-profile similarity. Figure 4 (big symbols) shows the selected matches for the criteria: linear cutoff (dashed line), |ti-tj|>4.5 h, $I_{\rm SN}>0.90$ and $I_{\rm MM}<0.00139$. These criteria were optimised to eliminate spectral mismatch while preserving a good phase coverage. The difference of the two spectra in each matched pair (corrected for orbital shift) was below 5% in local line-profile mismatch for the He I  4471 Å line, and typically far less, while the mismatch for disordered pairs was above 30%. In order to include the ECHELEC spectra, suffering a larger smearing of the LPVs due to longer exposure time, we averaged up to three consecutive FEROS spectra as matching templates. The similarity was judged subjectively as it is evidently less stringent for the noisier ECHELEC spectra.

In total, we selected 101 RV differences for pairs of 107 different orbital phases. Using an iterative procedure, we optimised the four parameters: radial-velocity semi-amplitude $K_{\rm A}$, eccentricity e, time of periastron passage $t_{\rm peri}$, and periastron longitude $\omega$, by a least-squares fit to the differential RV measurements for an eccentric Keplerian orbit,

 \begin{displaymath} {\rm RV} = \gamma + K_{\rm A} (\cos(\omega + \nu) + e\cos ... ...;\; K_{\rm A}=\frac{2\pi a_{\rm A} \sin i} {P\sqrt{1-e^2}}, \end{displaymath} (3)

where P is the orbital period, $a_{\rm A} \sin i$ is the primary's projected major semi-axis, $\gamma$ is the systemic radial velocity and $\nu$ is the true anomaly. Because photometry more strongly constrains $\omega$, we optimised e and $\omega$ iteratively with light-curve fitting ($\omega$) and orbit fit (e). The resulting orbital elements $\omega, e, t_{\rm peri}, K_{\rm A}$ are given in Table 5, for the corresponding radial-velocity curve in Fig. 3 (line). The rms of this solution is 2.8  $~{\rm km}~{\rm s}^{-1}$ per pair element, assuming random errors. Errors for $\omega$ and e are from this optimisation procedure, while the error in inclination was evaluated in the dynamical analysis using WD (Sect. 5). The figure shows that the aforementioned average-template RVs match the fitted orbit. The spectroscopy confirms the orbital eccentricity.

Table 5: Orbital elements for HD 92024.

Table 6: Orbital elements from SBOP fitting to RVs made by cross-correlation of all spectra with the 103-spectrum composite (cf. Table 5). $P=8\hbox{$.\!\!^{\rm d}$ }32457$. The fitting was made for all RVs (Col. 2) and for nightly averages (Col. 3). In the last column $\sigma $ is rescaled to single velocity measurements for comparison purposes.

How reliable is the solution in Table 5 compared to classical orbit-fitting methods? The input RV differences could be seriously affected by pulsational velocity effects only if constructive interference would mimic a given line profile shape closely (98% of the RV difference pairs had already been rejected!) but produce a Doppler shift. In Table 6 two alternative orbit solutions are given for RVs from cross-correlation of the FEROS and ECHELEC spectra with the 103-spectrum composite. Solutions for all RVs (Col. 2) and for nightly RV averages (Col. 3) are found using SBOP (Etzel 1985). The FEROS data were given twice the weights of the ECHELEC data, and the number of spectra defining the nightly average was taken into account. The main difference of the SBOP solutions from our solution is the marginally higher velocity amplitude that would lead to a 15% increase in the mass function. The fact that the scatter of the solutions in Table 6 is markedly higher than for the RV differences ( $\sigma=2.6~\hbox{$~{\rm km}~{\rm s}^{-1}$ }$) gives support to our method and shows, a posteriori, that our reliability concern expressed above is unimportant.

Detection of the faint secondary spectrum may be feasible through spectral disentangling of the components as e.g. done by Holmgren et al. (1999). In view of the faintness of the secondary spectrum, for a B8V star according to the present analysis (see final results, Tables 11 and 12), its strong hydrogen lines offer the best chance for detection. Still, their signature will only be on the 1-1.5% level of the total flux. Clearly, detection attempts can only be efficient after proper consideration of line variability linked to the pulsations of the primary. Therefore, the spectroscopy presently only constrains the stellar masses through the mass function f(M)

 \begin{displaymath} P K_{\rm A}^3 1.0385\times10^{-7}\left(1-e^2\right)^\frac{3... ...}+M_{\rm B})^2} = \frac{q^3 M_{\rm A} \sin^3 i}{(1+q)^2}\cdot \end{displaymath} (4)

From the spectroscopic temperature estimate (Sect. 4.3) we can use theoretical evolutionary tracks through the $\beta~{\rm Cephei}$ instability strip to pin down the possible mass range to 11-18 $M_\odot$. Combining this with Eq. (4), the possible mass-ratio is $q=M_{\rm B}/M_{\rm A}=0.205\pm0.019$, or a mass of the secondary $M_{\rm B}=2.92\pm0.45~{M}_\odot$.

4.2 Projected rotational velocity

With static line-profile models (without velocity fields), spectral line-width only provides an upper limit on the rotation rate. Balona's (1975) value of 122  $~{\rm km}~{\rm s}^{-1}$ represents the straightforward interpretation of the average line width. Using our narrow-line spectrum composite results in a significantly lower estimate. From the $V_{\rm rot} \sin{i}$ - FWHM relation for B0.5-1.5III-IV stars by Slettebak (1975), the He I  4471 Å line indicates a projected rotational velocity $75\pm20$  $~{\rm km}~{\rm s}^{-1}$. Using synthetic line profiles, a similar value $70\pm20$  $~{\rm km}~{\rm s}^{-1}$ is found from the Si III triplet around 4568 Å. The uncertainty estimate of 20  $~{\rm km}~{\rm s}^{-1}$ reflects the influence from the LPVs as judged from the deviation of the narrow-line composite's line shape from a rotational profile. The stellar radius, determined from the duration of the eclipses, requires a rotational velocity of $V_{\rm sync} \sin{i} \equiv 51$  $~{\rm km}~{\rm s}^{-1}$, if synchronised with orbit. Synchronisation can therefore not be firmly excluded.

   
4.3 Atmospheric parameters

The LPVs hamper direct comparison of spectral lines to synthetic model profiles that do not include velocity fields. De Ridder (2001) quantified the effects from pulsations in spectra of $\beta~{\rm Cephei}$ stars: stars with effective temperatures of about $T_{\rm eff}= 25~500$ K may exhibit relative temperature variations of 1.5% during the pulsation cycles, while the relative equivalent width (EW) exhibits relative variations of 3-9% (Si III lines). These variations need not to be in phase for different lines.

Table 7: EW-measurements for HD 92024 FEROS spectra and in model lines for different temperatures and abundances. The second column lists helium abundance for the helium lines (using $\log g=3.8$) and metal abundance for selected metal lines ( $\log g=4.0$), while Cols. 3-5 give corresponding model EWs for three different temperatures. The last columns give EWs for the two composite spectra, combined from all 103, and from 10 similar spectra.

In the present case, the dynamical analysis of light curves and radial-velocity measurements (Sects. 4.1 and 5) gives a more precise estimate of $\log g$ than the Balmer lines do. While the dynamical analysis only constrains the temperature ratio for the two stars, the spectroscopic determination of $~T_{\rm eff}$ in an early-B giant profits from the occurrence of lines of different ions of the same species at visual wavelengths: He I, II; N II, III; C II, III and Si III, IV. Having the above mentioned limitations related to the usage of static atmosphere models in mind, we used synthetic NLTE line profiles only to constrain the effective temperature $T_{\rm eff,A}$.

Theoretical spectra, calculated using the non-LTE line-formation package DETAIL/SURFACE (Butler & Giddings 1985), were rotationally broadened through convolution with the rotation profile from Gray (1976) to 40-100  $~{\rm km}~{\rm s}^{-1}$ in steps of 10  $~{\rm km}~{\rm s}^{-1}$. These models, available from another investigation, were for: surface gravities $\log g=3.7$ and 4.0, $T_{\rm eff}=25~000{-}28~000$ K in steps of 1000 K, solar helium abundance, and metal abundances[*] $[{\rm m/H}]=-0.30, -0.15, 0.0, 0.15, 0.30$. Additional spectra were made with hydrogen and helium lines available for $\log g=3.83$, $T_{\rm eff}=25~000{-}27~000$and helium abundances $[{\rm He/H}]=-0.30$ and -0.15. A turbulence velocity of 2  $~{\rm km}~{\rm s}^{-1}$ was assumed.

In order to estimate the uncertainty introduced by using static models, the analysis was applied to the 103-spectrum composite, as well as to the narrow-line spectrum composite. Fortunately, the EW of these lines does not vary substantially in contrast to their profiles as seen in Table 7 that lists the most important lines used in the analysis. EWs were measured by integrating the average absorption over observed and synthetic profiles of selected lines.

The width of the Balmer lines is consistent with $\log g=3.77\pm0.10$ (Sect. 5), but their line cores are more shallow than those of the synthetic models, probably due to the broadening of the observed profiles by the LPVs. The determination of temperature involves to some extent the abundance of the species producing the temperature-sensitive lines. Mathys et al. (2002) reported normal abundances for six bright stars in NGC 3293. They find a marginal overabundance of helium (0.15) and, as is usual for early B-stars (e.g. Daflon et al. 2001), subsolar metal abundance with typically $[{\rm m/H}]= -0.4$ to -0.2. From ultraviolet IUE spectra, Daszynska et al. (2003) derived solar metallicity for a subsample of the cluster's $\beta~{\rm Cephei}$ stars.

In the temperature range of early B-stars, lines of ionised helium fade quickly with decreasing temperature, while lines of neutral helium slowly become stronger. The only detected He II line is 4686 Å. For solar helium abundance, ionised helium poses an upper limit to $~T_{\rm eff}$ which is at face value incompatible with the lower limit due to neutral helium. Therefore subsolar helium abundances were also tested and gave compatible temperature estimates for $[{\rm He/H}]\lesssim-0.1$ and $~T_{\rm eff}$ = 25 000-26 000 K (Table 7). This also applies for lines such as He I  4471 Å and He I  4713 Å for which EW measurements are not listed because of interfering weak blends. The marginally subsolar helium abundance is likely an artifact of the simplified modelling done, and verification is outside the scope of this paper.

The Si IV lines are quite temperature-sensitive at the current temperature range, as opposed to the insensitivity of the Si III lines. The 25 000-27 000 K range is acceptable for Si IV for a reasonable range in abundances (solar to $2\times$subsolar). We note that the Si III lines are somewhat stronger than expected from static models, again indicating the need for detailed modelling in Paper II. Carbon and nitrogen lines do not constrain the temperature more than helium and silicon do, and their relative strengths support the conclusions derived from these: $T_{\rm eff}=25~500\pm500$ K. We compared our narrow-line spectrum composite to ECHELEC spectra of the binary $\sigma $ Sco (HD 147165, SpT. B1 III), which has a $\beta~{\rm Cephei}$ primary with $T_{\rm eff}=26~150\pm1070$ K, $\log g=3.85\pm0.17$ (mean values, vander Linden & Butler 1988). The two stars showed almost identical spectra in the wavelength region 3900-4065 Å, having similar line widths and strengths. This indicates that they have essentially the same temperature.

4.4 Systemic velocity

The systemic radial velocity $\gamma$ was determined from our 103-spectrum composite, because the LPVs were averaged in it and it had no orbital shifts. Seven isolated lines of He I, O II, and Si III (Table 8) were selected. The oxygen and silicon lines gave the most consistent velocities. The wavelengths of these lines were estimated with IRAF's onedspec.splot task in three different ways: imposing line symmetry; allowing for asymmetry; allowing for asymmetry and a slightly inclined continuum. The consistency of the results (see rms of the three estimates per line in Table 8, Col. 4) compared to the scatter of $\Delta$RV for different lines indicates that the measuring method is not the dominant source of uncertainty: systematic line-to-line differences, possibly related to atmosphere structure, are apparently dominant. Taking all measurements together, the unweighted mean gives $\gamma=-16.0\pm2.0$  $~{\rm km}~{\rm s}^{-1}$, in agreement with Feast's (1958) value for the cluster velocity.

Table 8: Velocity shifts for selected lines in the 103-spectrum composite. Error estimates are deduced from fitting same profiles with different fitting parameters (see text), and the listed shifts are means of the three measurements. Laboratory wavelengths are from Martin et al. (1999). Last column: comments on line strength and profile.

   
4.5 Pulsation frequencies

The flux variation induced by pulsations can be studied for wavelength bins in the 103 FEROS spectra compensated for orbital shifts; each bin provides a monochromatic light curve. Temporal variability across line profiles is affected by e.g. position in the spectral line, line-blends and line-sensitivity to pressure and temperature. A complex model including velocity fields for line profiles is therefore required to extract the full information. But in order to detect oscillation frequencies, one may combine the frequency information in wavelength bins over the studied line profile. This was successfully demonstrated by Schrijvers et al. (2004) who combined power spectra for wavelength bins across a spectroscopic line, and improved the power of present frequencies. Phase differences of LPVs in different lines do not affect the frequencies and the periodograms can be summed directly. We anticipate that this method will be even more valuable for spectra covering a large wavelength range. For the FEROS spectra, more than 500 bins (5.5  $~{\rm km}~{\rm s}^{-1}$ bin width) in 27 spectral lines were identified[*] to have substantial pulsational information.
  \begin{figure} \par\includegraphics[height=6.4cm,width=4.1cm,clip]{1527fg05.ps}\... ...{2mm} \includegraphics[width=4.1cm,height=6.4cm,clip]{1527fg06.ps} \end{figure} Figure 5: Two-dimensional power spectra for wavelength regions centered on the Si III 4553 Å ( left) and O II  4596 Å ( right) lines. Owing to insufficient data sampling, strong aliasing makes the significant frequencies appear "smeared''. The three photometric frequencies are indicated ("-''). Note the similarity of the periodicities for the two lines.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.1cm,clip]{1527fg07.eps} \end{figure} Figure 6: Summed power spectrum from the combined O II  4596 Å and Si III  4553 Å regions ( top). The three photometric frequencies are indicated with dotted lines. The two lower panels show the power spectra with respectively one (7.1651  $\;{\rm c}~{\rm d}^{-1}$) and two (7.1651 and 6.6640 c/d) frequencies prewhitened. Note that power still is present at 5.6597, 6.6620 and 12.8655  $\;{\rm c}~{\rm d}^{-1}$, indicating an incomplete solution.
Open with DEXTER

As a quick test of the efficiency of combining more regions, we used the FEROS spectra shifted in wavelength to eliminate the orbital shifts. Two different, relatively strong lines O II  4596 Å and Si III  4553 Å, were selected and power spectra were computed with Period98 for bins corresponding in size to 5.5  $~{\rm km}~{\rm s}^{-1}$. With only 103 spectra, obtained in two short periods of 4-12 days duration and separated by one year, strong 1, 0.091, 0.003  $\;{\rm c}~{\rm d}^{-1}$ aliases are unavoidable and limit the usefulness of the dataset. As seen in Fig. 5, the three photometric frequencies f1, f2, f3 (indicated with bars) are prominent for both line regions. f1 is, however, not unambiguous due to aliasing from the other two frequencies. Contrary to the photometry, f3 has highest power. Also notice the higher power for the stronger Si-line, and that most information is contained inside $\Delta \lambda=1.5$ Å. Then, by summing the power spectra for regions with the highest power, we combine the information in both line-regions to obtain the summed one-dimensional periodogram in Fig. 6 (top). Significant periodicities for all photometric frequencies are seen, but the strong aliases make unique detections of frequencies impossible in spite of the strongly enhanced S/N in the periodogram.

We then successively prewhitened the detected frequencies f3=7.1651  $\;{\rm c}~{\rm d}^{-1}$ and f2=6.6640  $\;{\rm c}~{\rm d}^{-1}$, while keeping only frequency fixed during the calculations (as amplitude and phase vary among and in the lines). The results are inserted in the lower two panels in the figure. Due to the substructure of the window function related to the 1-year baseline, several alias frequencies (e.g. 7.159, 7.162 and 7.165  $\;{\rm c}~{\rm d}^{-1}$) appear with the same power, and any one of these leads to phase diagrams similar to the ones presented in Fig. 7. The bottom panel in Fig. 6 with the periodogram for both frequencies prewhitened still has power at 5.6597, 6.6620 and 12.8655  $\;{\rm c}~{\rm d}^{-1}$. The 5.6597  $\;{\rm c}~{\rm d}^{-1}$ frequency is probably an alias of f2, or f1 combined with the alias of the 6.6640  $\;{\rm c}~{\rm d}^{-1}$ frequency.

  \begin{figure} \par\includegraphics[width=8cm,clip]{1527fg08.ps} \end{figure} Figure 7: Integrated-flux variations, in units of normalised flux per pixel, inside a 5-bin wide core region of Si III  4553 Å. The panels show phase diagrams for each of the detected pulsational periods, each successive one after prewhitening for the previous one above. Sinusoidal fits are superimposed for the individual frequencies. The panels show the monochromatic input light curve phased with $f_3=7.1651~\hbox{$\;{\rm c}~{\rm d}^{-1}$ }$  a), then f3 is prewhitened and the light curve is phased with f2 b), and c) is for the light curve with f3 and f2 prewhitened and phased with a candidate frequency $f=12.8655~\hbox{$\;{\rm c}~{\rm d}^{-1}$ }$. Note the reduction of the scatter.
Open with DEXTER

The wavelength-dependent amplitudes and phases of the frequencies complicate the construction of phase plots corresponding to Fig. 6. As a simple demonstration of the phased pulsation modes, Fig. 7 shows phase diagrams for variations of the integrated normalised flux inside a 5-bin (0.34-Å) wide core region of Si III  4553 Å; the phases correspond to $f_3=7.1651~\hbox{$\;{\rm c}~{\rm d}^{-1}$ }$ (a) and, with f3 prewhitened, $f_2=6.6620~\hbox{$\;{\rm c}~{\rm d}^{-1}$ }$ (b). The residuals of f3, f2 prewhitened (panel c) have rms = 0.011, while a similar region in the continuum, 8 Å blue-ward of the Si-line, has 0.0051. This rms difference is partly due to the candidate frequencies seen in Fig. 6 (bottom panel), for which Fig. 7 (c) shows the phase of the 12.8655  $\;{\rm c}~{\rm d}^{-1}$ frequency. Including the latter candidate frequency and adding asymmetry terms in the fit to f3 and f2 only lowers the residual rms to 0.0010, while selecting the best alias peaks from the dataset itself results in an rms = 0.0079. The lower scatter in the continuum window suggests the presence of more low-amplitude pulsation modes. We emphasise that all frequencies other than f3 and f2 are ambiguous in the preliminary spectroscopic analysis presented here.

For the reasons mentioned we will not try to interpret the prewhitened periodogram further than f3 and f2. More important is the significant reduction of noise in the summed power spectrum, showing the feasibility of the method.

   
5 Photometric analysis

In order to take reflection and deformation effects into account, the Wilson-Devinney WD programme (Wilson & Devinney 1971; Wilson 1992) was applied. We used the version of Sept. 1993 in mode 2 throughout, i.e. detached system configuration. We recall that the model parameters ${\mathcal L}_{\rm A,B}$ are monochromatic 4$\pi$ steradian luminosities (in arbitrary units); ${\mathcal L}_{\rm B}$ is calculated from the input temperatures and radii.

The primary's temperature $T_{\rm eff,A}$ was fixed to the spectroscopic value. Bolometric limb darkening coefficients were interpolated in the tables of Van Hamme (1993): 0.620 (primary) and 0.699 (secondary). The linear limb darkening coefficients for each component and passband were fixed to the values calculated by Diaz-Cordoves et al. (1995):

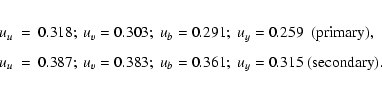
\begin{eqnarray*}u_u&=&0.318;~ u_v=0.303; ~ u_b=0.291;~ u_y=0.259~~({\rm primary... ...u&=&0.387;~ u_v=0.383;~ u_b=0.361; ~u_y=0.315~({\rm secondary}). \end{eqnarray*}


Reflection albedos and gravity-darkening coefficients were fixed to the theoretical (canonical) values for stars with radiative envelopes (1.0). Eccentric orbit, synchronous rotation of the components and no third light were assumed. As input photometry the uvby light curves were used. The blue dataset was also tested since it is more abundant and has better out-of-eclipse coverage, but both datasets were compatible. In order to let the spectroscopy constrain the analysis, we computed 107 model RVs corresponding to the phases of the observed spectra used in the RV-difference fitting.

   
5.1 Determination of the photometric elements

Using simple black-body atmosphere models, we first evaluated the solution space with DC, the differential correction part of WD, based on the initial parameters from EB86 and from our spectroscopic orbit analysis.

We tested for orbital eccentricity with the blue light curve and the RVs, however without weights the RVs had little influence on the solution (107:2262 points). By adjusting $e, \omega$ and phase shift d$\phi$ and then optimising the size of the orbital semi-major axis $a=a_{\rm A}+a_{\rm B}$ and the mass ratio q, we got a solution with slightly higher periastron longitude than from the spectroscopy but again with eccentricity. We then compared individual solutions for the 5 uvby and blue light curves, without the RV data but with the orbital parameters a, q fixed. The agreement was good with less than 2% differences in stellar potentials and same inclination (85 $.\!\!^\circ$6$\;\pm\;$0 $.\!\!^\circ$4). Because the uvby data gave results consistent with those from the blue (B+b) light curve, we did not use the latter in the following part of the photometric analysis.

The unknown mass ratio was evaluated with DC for a grid of different values of q while optimising the other parameters for each value. The minimum value of $\chi^2$ was then found at $q=0.200\pm0. 005$ by using second-degree polynomial interpolation along the q axis. This result is in agreement with all light curves and the mass ratio was fixed to this value in the further analysis. Direct confirmation from the spectrum of the secondary is required, though, before the formal accuracy of q can be determined. In view of the limited number of RV data compared to photometric data, appropriate weights were defined to recover with WD the $\omega$ and e values in Table 5. These weights were hereafter applied in the remaining analysis. The inclination value was slightly affected by the inclusion of weights and was optimised with the photometry to $i=85\hbox{$.\!\!^\circ$ }2$.

DC was then used to evaluate individual light curves with model RVs, keeping now also periastron longitude, eccentricity, and inclination fixed. The final adopted results of the WD analysis are listed in Table 9. Introduction of atmosphere models by Kurucz (1993) brought the u band results in line with those of the other bands; in particular $T_{\rm eff,B}$ was now the same to within 500 K for all passbands. The geometry, through the stellar potentials and the radii indicating absence of deformation, also agrees well. The model light curves, superimposed in Fig. 2, reproduce the colour change during secondary eclipse, and also reflection effects outside the eclipses seem required. The rms values of individual solutions given at the bottom of Table 9 are for the photometry, and the associated photometric residuals are shown in Fig. 8. Considering that the eclipse light changes are 2-8 times larger than the pulsations, it is satisfying that all residuals are smaller than half the pulsation amplitudes (worst case). Residuals for the spectroscopy were evaluated by subtracting the 101 measured RV differences from those predicted by the WD model. This indicated an rms of 2.6  $~{\rm km}~{\rm s}^{-1}$ per pair element.


  \begin{figure} \par\includegraphics[angle=90,width=8.4cm,clip]{1527fg09.ps} \end{figure} Figure 8: Residuals of the uvby light curves from the DC solution with the geometry free (Table 9). Dotted lines delimit the start and end of both eclipses. From top to bottom: y,b,v,u.
Open with DEXTER

Table 9: Wilson-Devinney binary model solutions for the 4 light curves and model RVs for HD 92024. $k=r_{\rm B}/r_{\rm A}$. Assumed were e=0.028, $\omega =64\hbox {$^\circ $ }$, q=0.20, $T_{\rm eff,A}=$25 500 K and $i=85\hbox{$.\!\!^\circ$ }2$. Stellar radii $r_{\rm A,B}$ are in units of the orbital semi-major axis a. ${\mathcal L}_{\rm A,B}(\phi_{0.25})$ are the normalised ( ${\mathcal L}_{\rm A}(\phi_{0.25})+ {\mathcal L}_{\rm B}(\phi_{0.25})\equiv 1$) light contributions at phase 0.25. Last row gives number of observations for light curves and RVs.

The errors listed in Table 9 are output from WD and should only serve as lower limits on the true errors. Errors for a subset of key parameters were therefore examined in more detail: $\Omega_{\rm A}$, $\Omega_{\rm B}$, i and $T_{\rm eff,B}$ were changed in turn in grids of test values, while for each value the other parameters were optimised. Acceptable parameter values are those occurring in the subspace of allowed $\chi^2<1.056~\chi_{\rm rand}^{2}+\chi_{\rm syst}^{2}$ (see Eq. (12) in Hensberge et al. 2000), where $\chi_{\rm rand}^{2}$ and $\chi_{\rm syst}^{2}$ are the random and systematic contributions. The factor 1.056 defines the 95% confidence level, assuming that the $\chi^2$ sum is built up from residuals due to random errors in the data as well as from systematic contributions, and that only the term due to random errors increases when there is a slight deviation from the best-fit solutions. In our case, systematic contributions are primarily due to the influence of the pulsations. Despite our carefulness, they strongly dominate the residuals in the photometry (Fig. 8). For the light curves, the residuals of the best-fit model have an rms of 5 mmag, while the expected (theoretical) random noise should only contribute an rms of 3 mmag (b-band). We note that the best-fit values for the individual potentials, contrary to their ratio, are strongly correlated with the inclination i. Hence, we list in Table 10 the large uncertainty in $\Omega_{\rm A}$ and $\Omega_{\rm B}$ from the corresponding uncertainty in i, as well as the small uncertainty in $\Omega_{\rm B}/\Omega_{\rm A}$. The ratio of the temperatures is reflected by the depth of the shallow total eclipse and may be sensitive to the systematic residuals after the prewhitening. Therefore, we computed the rms error in the depth when offsets for light curves from different nights are taken explicitly into account, and also performed WD solutions using only subsets of the same light curve. We conclude that the uncertainty in the eclipse depth is 2 mmag, or a change of 1000 K in temperature of the secondary, slightly higher than the 770 K indicated by the analysis of acceptable $\chi^2$ subspace (95% conf. level). Table 10 also lists the means of the relative radii, with WD errors.

Some of the advantages of a simultaneous solution for multiple passbands are that one avoids inconsistencies among solutions of individual light curves and that the number of free parameters is reduced. For comparison, we therefore also performed a simultaneous uvby and RV evaluation, made for two subsets $\{i$, $T_{\rm eff,B}$, $\Omega_{\rm A}\}$ and $\{{\mathcal L}_{\rm A}$, $\Omega_{\rm B}\}$ to avoid fitting correlated parameters. The resulting values $i=85\hbox{$.\!\!^\circ$ }2, T_{\rm eff,B}=12~360~{\rm K}$, $\Omega_{\rm A}=5.609$, $\Omega_{\rm B}=5.741$ and also the luminosities were all in good agreement with those of Table 9.

Consequently, we fix the geometry to the mean values in Table 9 and re-evaluate the temperature and luminosities to get the passband-dependent luminosity ratios. Table 11 presents the solution. There is good correspondence of the evaluated parameters for different passbands, seen both in potentials and sigma's for the solutions. The effective temperature range is now within 250 K, which is mainly caused by a changed temperature in the y passband.

Table 10: Mean elements for HD 92024. $T_{\rm eff,A}$ = 25 500.

Table 11: Wilson-Devinney binary model solution for HD 92024 for fixed mean geometry from Table 9. q = 0.20 and $T_{\rm eff,A}=25~500$ K. The resulting mean temperature is $\langle T_{\rm eff,B}\rangle =12~410\pm860$ K.

In addition to the relative radii $r_{\rm A,B}$ given in Table 9, WD gives as output the masses $M_{\rm A,B}$ and mean radii $R_{\rm A,B}$, expressed in solar units, the surface gravities (cgs units) and the bolometric magnitudes for both components. These results are given in Table 12. Errors are based on the accuracies of the radial velocity amplitude, the mass ratio, the relative radii and the inclination; errors in the masses are from Sect. 4.1.

   
6 Absolute dimensions and evolutionary status

Astrophysical data for the two components of HD 92024 are given in Table 12.

As shown by Sterken & Jerzykiewicz (1993), the Strömgren indices for the system correspond to MK type B1 III. The secondary star's temperature and surface gravity from the dynamical analysis (Table 12) correspond (Lester et al. 1986) to indices c0=0.658, m0=0.118, which, according to Crawford's (1978) average parameters are equivalent to MK type B8V. When taking the uncertainty in temperature and gravity into account, the possible types of the secondary are B7V-B9V.

Using bolometric corrections from Flower (1996), we derive the absolute magnitudes from the bolometric magnitudes output by WD. As given in the table, they correspond to a systemic distance of $2.8\pm0.3$ kpc, in excellent agreement with the cluster distance estimate by Baume et al. (2003).

Table 12: Astrophysical data for HD 92024. $M_{\rm bol,\odot } =4.75$ is assumed, and $M_{\odot } = 1.989\times 10^{30}$ kg and $G= 6.67259\times 10^{-11}$ m3 kg-1 s-2 are from Seidelmann (1992). Bolometric corrections are from Flower (1996).

   
6.1 Theoretical models, age

In Fig. 9, the components of HD 92024 are compared with evolutionary stellar models from Claret (1995) for the chemical composition (X=0.70, Z=0.02) with convective core overshooting. We recall from Sect. 4.5 that near-solar metallicity was appropriate. The model tracks for $\log L$ versus $\log T_{\rm eff}$ predict masses of $14\pm1.5$ and $3.2\pm0.5$ solar masses, in agreement with the results from the WD analysis. The evolutionary mass of HD 92024 appears to be more precise than our conservative estimate based on temperature and position of the instability strip in an evolutionary diagram. The position of HD 92024 in Fig. 9 confirms the evolved state of the primary being midway through the core hydrogen-burning phase. The superimposed isochrones indicate an age of 10-13 Myr, which is compatible with the other estimates for NGC 3293's brightest members of 6.5-10.0 Myr (Baume et al. 2003) and 8.9-9.3 Myr (Balona et al. 1997). The location of the faint component is in good agreement with a main-sequence star model of the right mass.
  \begin{figure} \par\includegraphics[width=7.7cm,clip]{1527fg10.ps} \end{figure} Figure 9: The positions of the components of HD 92024 in an evolutionary diagram for $\log L$ versus $\log T_{\rm eff}$ from Claret (1995). Error bars are included from Table 12. Dotted lines are isochrones with $\log age$ indicated while the solid lines are evolutionary tracks for different masses.
Open with DEXTER

7 Conclusions

We have used high-precision photometry and high-dispersion time-resolved spectroscopy in an orbital analysis of HD 92024 to determine the physical parameters of the components. A new method was applied to determine orbital elements from radial-velocity shifts in the presence of velocity fields. The analysis did not provide a spectroscopic detection of the much fainter secondary component, which strongly limits the accuracy of the mass ratio and thus also of the mass of the primary star. A binary model indicates a well-detached system without stellar deformations, a minor eccentricity and two eclipses (one being total). From spectroscopy, the primary's temperature was measured and found to agree with the photometric colour indices. The results are consistent with two stars of types B1 III and B8V, as suggested by Engelbrecht & Balona (1986). The spectrum was found to be nearly identical to that of $\sigma~$Sco. We successfully combined spectroscopic information from two different spectral line regions to detect two of the three photometric oscillation frequencies. With a baseline of more than 10 years, no indications of apsidal motion were found from either spectroscopy or photometry. We determine a distance to HD 92024 that together with the systemic velocity confirms membership of NGC 3293. Evolutionary models agree with the masses from the dynamical analysis. Isochrones indicate a somewhat high age of 10-13 Myr, as compared to results from photometric studies of the cluster. Improvement of these results requires the detection of the spectrum of the faint secondary.

Acknowledgements
Part of this research was carried out in the framework of the "IAP P5/36'' project of the Belgian Federal Science Policy, and was supported by the Belgian Fund for Scientific Research (FWO) and the Flemish Ministry for Foreign Policy, European Affairs, Science and Technology, under contract BIL 01/2. Support from the project "Structure and evolution of stars - new insight from eclipsing binaries and pulsating stars'' by the Danish National Science Research Council is acknowledged. We thank Jens Viggo Clausen, Erik Heyn Olsen and Bodil Helt for their invaluable guidance in planning and retrieving the SAT data, the ESO staff for assistance during the observations, and C. Papadaki and M. Y. Bouzid for some SAT observations obtained in a combined observing effort. We wish to thank the referee Prof. P. Harmanec for constructive criticism and useful comments which all improved the paper. We have made use of the Simbad database, operated by the CDS, Strasbourg, France, the ESO-MIDAS and NOAO-IRAF software, and the Wilson-Devinney code.

References

 
Copyright ESO 2004