A&A 429, 731-738 (2005)
DOI: 10.1051/0004-6361:20041173
On the dynamics of some resonances of Phobos in the future
T. Yokoyama - M. R. Mana
- C. do Nascimento - M. T. Santos - N.
Callegari Jr
Universidade Estadual Paulista, IGCE-DEMAC Caixa Postal 178,CEP 13.500-970
Rio Claro (São Paulo), Brasil
Received 28 April 2004 / Accepted 8 September 2004
Abstract
A probable capture of Phobos into an interesting resonance was
presented in our previous work.
With a simple model, considering Mars in a Keplerian and circular
orbit, it was shown that once captured in the resonance, the inclination of the satellite
reaches very high values. Here, the integrations are extended
to much longer times and escape situations are analyzed.
These escapes are due to the interaction of new additional resonances, which
appear as the inclination starts to increase reaching some specific
values. Compared to classical capture in mean motion resonances, we see
some interesting differences in this problem.
We also include the effect of Mars' eccentricity
in the process of the capture.
The role played by this eccentricity becomes important, particularly when
Phobos encounters a double resonance at
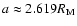 .
Planetary
perturbations acting on Mars and variation of its equator are
also included. In general, some possible scenarios of the future of Phobos are presented.
.
Planetary
perturbations acting on Mars and variation of its equator are
also included. In general, some possible scenarios of the future of Phobos are presented.
Key words: planets and satellites: general -
solar system: general
In Yokoyama (2002), hereafter PYO, we showed that in the future,
Phobos will face some interesting resonance because its semi major
axis a is continuously decreasing due to the action of tides. This means that the
frequencies associated with the longitude of the node (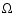 )
and the argument of the
pericenter (w)
are also varying, so that in the neighbourhood of a
specific value of the semi major axis, these frequencies can
satisfy resonant relations like
)
and the argument of the
pericenter (w)
are also varying, so that in the neighbourhood of a
specific value of the semi major axis, these frequencies can
satisfy resonant relations like
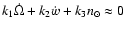 ,
where
,
where 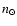 is the mean motion of the
Sun, ki are integers, and dots mean time derivatives. This
kind of commensurability
is rather different to usual mean motion resonances, since only
one mean longitude (the Sun) is involved. Moreover, this mean motion is not
affected by the tidal effects.
The current semimajor axis (a), eccentricity (e) and inclination (I) of Phobos
are:
is the mean motion of the
Sun, ki are integers, and dots mean time derivatives. This
kind of commensurability
is rather different to usual mean motion resonances, since only
one mean longitude (the Sun) is involved. Moreover, this mean motion is not
affected by the tidal effects.
The current semimajor axis (a), eccentricity (e) and inclination (I) of Phobos
are:
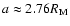 ,
,
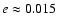 and
and
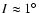 ,
where
inclination is referred to Mars'
equator and
,
where
inclination is referred to Mars'
equator and 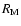 is the equatorial radius of Mars. In our previous work we
showed that Phobos can be
captured in the
is the equatorial radius of Mars. In our previous work we
showed that Phobos can be
captured in the
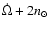 resonance in the neighbourhood of
resonance in the neighbourhood of
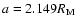 .
Even in the absence of tides, i.e., for the ordinary restricted three body
problem, the effect of this
resonance is clearly visible. Indeed, taking
.
Even in the absence of tides, i.e., for the ordinary restricted three body
problem, the effect of this
resonance is clearly visible. Indeed, taking
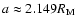 and
integrating the Cartesian Eqs. (1) as given in PYO (Mars
is in a Keplerian orbit), we get
Fig. 1. The
obliquity of the equator is artificially fixed to
and
integrating the Cartesian Eqs. (1) as given in PYO (Mars
is in a Keplerian orbit), we get
Fig. 1. The
obliquity of the equator is artificially fixed to
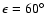 (Panels A, B).
For this high value of
(Panels A, B).
For this high value of 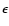 ,
the inclination varies up to
almost
,
the inclination varies up to
almost 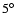 while for
while for
 (Panels C, D), the maximum inclination is
(Panels C, D), the maximum inclination is 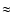
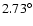 .
If however the semi major axis a is slightly changed to
a=2.145, the angle
.
If however the semi major axis a is slightly changed to
a=2.145, the angle
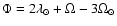 does not librate any more and the variation of the
inclination is negligible.
does not librate any more and the variation of the
inclination is negligible.
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{1173fig1.eps}} %
\end{figure}](/articles/aa/full/2005/02/aa1173/Timg55.gif) |
Figure 1:
Left panels: variation of the inclination for resonant semi
major
axes. Right panels: libration of the resonant argument:
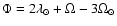 .
Initial conditions for the satellite: Top: .
Initial conditions for the satellite: Top:
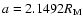 ,
e=0.015, ,
e=0.015,
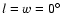 , ,
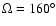 , ,
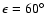 ,
Bottom: a=2.1498,
e=0.015, ,
Bottom: a=2.1498,
e=0.015,
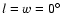 , ,
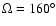 , ,
 .
Mars is assumed in a
Keplerian orbit with initial conditions: a=1.5236 AU, e=0.0933, .
Mars is assumed in a
Keplerian orbit with initial conditions: a=1.5236 AU, e=0.0933,
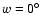 , ,
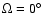 , ,
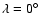 , ,
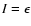 . .
|
| Open with DEXTER |
Now, let us suppose a case when the semi major axis of Phobos decreases secularly
due to tides and passes through
the resonant value (
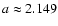 ). According to Szeto (1983)
the time rate variation of Phobos' semimajor axis is of the order
of 10-7 cm s-1.
The current obliquity of Mars
is
). According to Szeto (1983)
the time rate variation of Phobos' semimajor axis is of the order
of 10-7 cm s-1.
The current obliquity of Mars
is
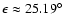 ,
but this value is chaotically
varying (Ward 1979; Touma & Wisdom 1993; Laskar & Robutel
1993) and over a long time scale it can sweep
a large interval. In particular, in a frequency analysis
over 45 Myr, Laskar & Robutel (1993) found a
chaotic zone of
,
but this value is chaotically
varying (Ward 1979; Touma & Wisdom 1993; Laskar & Robutel
1993) and over a long time scale it can sweep
a large interval. In particular, in a frequency analysis
over 45 Myr, Laskar & Robutel (1993) found a
chaotic zone of 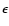 which can range from
which can range from
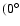 to
to
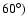 .
If at the moment when
.
If at the moment when
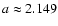 ,
the current value of
,
the current value of 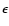 is larger than
is larger than
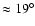 ,
then capture usually occurs and inclination
grows secularly to high values, much greater than the present value. As
mentioned in PYO, the reason for this large increase is due to
the continuous outward displacement of the libration center
(Fig. 2 in PYO) as Phobos' semi major axis decreases.
In PYO we always considered Mars in a circular orbit and integrations were
not long enough, so that no escape or possible rupture of the
resonance were presented. This time we want to explore some escape situations.
This problem was studied by many authors: Beaugé &
Ferraz-Mello (1994), Gomes
(1995a,b, 1997a,b,
1998), Liou & Zook (1997), Hamilton
(1994), Jancart et al. (2003),
etc.
In particular, Gomes has presented
a deep study of the phenomenon of resonance lock. He
also deduced some interesting formulae that govern the
evolution of the eccentricity, inclination and semi major axis
not only in the restricted three body problem but in the mutual
case as well. Gomes considers different kind of dissipative
forces; however in all cases the resonance is mainly due to the combination of
two mean longitudes. Therefore, for the restricted three body problem, in general,
once a capture takes place, the semi major axis of the particle must stop
its secular variation and remains librating around some
resonant value. Depending on the dissipative force, the amplitude of the
libration of the semi major can either
decrease to a stationary value (stable lock) or increase beyond some tolerable
limit (unstable lock), so that the escape is unavoidable and capture is only temporary
(Gomes 1995b). A noteworthy point in the
present problem is
the resonant angle: instead of two mean motions,
the resonance comes from Phobos' longitude of node and the mean
motion of the Sun. Therefore, in opposition to mean motion resonances,
in our problem, the satellite remains captured, even if
its semi major axis is decreasing (Sect. 3).
In PYO we list other similar resonances, e.g., the evection:
,
then capture usually occurs and inclination
grows secularly to high values, much greater than the present value. As
mentioned in PYO, the reason for this large increase is due to
the continuous outward displacement of the libration center
(Fig. 2 in PYO) as Phobos' semi major axis decreases.
In PYO we always considered Mars in a circular orbit and integrations were
not long enough, so that no escape or possible rupture of the
resonance were presented. This time we want to explore some escape situations.
This problem was studied by many authors: Beaugé &
Ferraz-Mello (1994), Gomes
(1995a,b, 1997a,b,
1998), Liou & Zook (1997), Hamilton
(1994), Jancart et al. (2003),
etc.
In particular, Gomes has presented
a deep study of the phenomenon of resonance lock. He
also deduced some interesting formulae that govern the
evolution of the eccentricity, inclination and semi major axis
not only in the restricted three body problem but in the mutual
case as well. Gomes considers different kind of dissipative
forces; however in all cases the resonance is mainly due to the combination of
two mean longitudes. Therefore, for the restricted three body problem, in general,
once a capture takes place, the semi major axis of the particle must stop
its secular variation and remains librating around some
resonant value. Depending on the dissipative force, the amplitude of the
libration of the semi major can either
decrease to a stationary value (stable lock) or increase beyond some tolerable
limit (unstable lock), so that the escape is unavoidable and capture is only temporary
(Gomes 1995b). A noteworthy point in the
present problem is
the resonant angle: instead of two mean motions,
the resonance comes from Phobos' longitude of node and the mean
motion of the Sun. Therefore, in opposition to mean motion resonances,
in our problem, the satellite remains captured, even if
its semi major axis is decreasing (Sect. 3).
In PYO we list other similar resonances, e.g., the evection:
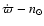 .
Although in our problem we are mostly interested in the
capture of inclination, it is instructive to comment briefly on some points
related to the dynamics of the
evection resonance. This commensurability might have been important in
the past of the Earth-Moon system (Touma & Wisdom 1998). Capture in this case
was possible only for the increasing semi major axis of the Moon.
The duration of this regime is interesting, since unlike our
problem, the increase of the eccentricity generates some consequences
for the evolution of the semi major axis: in the Touma & Wisdom problem, the eccentricity
grows rapidly,
and after some time, its value is high enough that
the Moon's semi major axis stops increasing.
This occurs because, when the orbit becomes very eccentric, at the pericenter, the
angular motion of the Moon becomes faster than the angular
rotation of the Earth. This is not the situation in our problem,
that is, the capture in inclination does not dampen the decay of Phobos' semi major axis.
In the Earth-Moon problem the dynamics of the evection is very
complex, but as pointed out by Touma & Wisdom (1998),
capture in this resonance is always temporary (for tidal
dissipative forces). Compared to problems involving two mean
motion resonance, or evection resonances, we show that the
dynamics of
our resonance presents some clear differences in the evolution during the capture.
.
Although in our problem we are mostly interested in the
capture of inclination, it is instructive to comment briefly on some points
related to the dynamics of the
evection resonance. This commensurability might have been important in
the past of the Earth-Moon system (Touma & Wisdom 1998). Capture in this case
was possible only for the increasing semi major axis of the Moon.
The duration of this regime is interesting, since unlike our
problem, the increase of the eccentricity generates some consequences
for the evolution of the semi major axis: in the Touma & Wisdom problem, the eccentricity
grows rapidly,
and after some time, its value is high enough that
the Moon's semi major axis stops increasing.
This occurs because, when the orbit becomes very eccentric, at the pericenter, the
angular motion of the Moon becomes faster than the angular
rotation of the Earth. This is not the situation in our problem,
that is, the capture in inclination does not dampen the decay of Phobos' semi major axis.
In the Earth-Moon problem the dynamics of the evection is very
complex, but as pointed out by Touma & Wisdom (1998),
capture in this resonance is always temporary (for tidal
dissipative forces). Compared to problems involving two mean
motion resonance, or evection resonances, we show that the
dynamics of
our resonance presents some clear differences in the evolution during the capture.
This work is organized in the following way: Sect. 2 shows
some situations of capture and escape. To explain
these escapes and to put the problem in a workable form,
we still keep Mars' equator as the reference
plane. The dynamics of the problem when Mars' eccentricity is
taken into account is described in Sect. 3. In Sect. 4 we include
the planetary perturbations acting on Mars and also the
precessional equations of Mars' equator. Section 5 is devoted to
conclusions.
As mentioned before, many authors have studied the phenomenon of
capture and escape in resonances involving mean motion
commensurability. Very roughly speaking, due to the dissipative
force, the semimajor axis of the perturbed body varies secularly
so that at some moment a particular orbital resonance involving
the mean motions can be satisfied. Then, provided that certain
conditions are fulfilled (see for instance, Henrard 1982; Peale 1989; Malhotra 1990; Gomes
1995a, 1997a, etc.) a capture takes place.
Usually, in this case, the ratio of semi major axes, or the semi
major axis of the perturbed body (restricted three body problem),
stops varying secularly. Also, under the capture, a specific angle
connected to the current resonance starts to librate, whereas the
eccentricity or inclination begins to vary secularly. Beaugé &
Ferraz-Mello (1994) showed that in the case of drag
forces, the eccentricity varies secularly during some time, but
after that, it has the tendency to stabilize around a specific
value which they called universal eccentricity. In
spite of this stabilization, the capture may not be permanent,
that is, if the temporal variation of the libration angle
increases in amplitude, an escape from the resonance will appear
and this rupture is essentially due to the unstable character of
the resonance lock. Therefore, according to Gomes (1995b), a resonance lock is stable or unstable and this
stability depends on the particular dissipative force involved. A
detailed study yielding analytical criteria about the permanency
in resonance trapping is given in his paper.
Similarly to universal eccentricity, the concept
of universal inclination was introduced by Gomes
(1997b) considering only one specific resonant
librating angle.
However, it seems that the existence of such
universal values is not completely clear, at least for arbitrary
dissipative forces or when it is not possible to define one
specific resonant angle in the libration regime. Actually, Gomes
(1997b) says: although the concept of a
universal inclination is presented here, I could not get any
example where this feature showed in an unequivocal way, with the
inclination coming to a value equal to the universal inclination.
In this section, we discuss the escapes in our problem. Even
though an analytical proof is not given, we show through numerical
experiments that all the escapes occur, without any previous
stabilization around some possible universal value. We put the
problem into the simplest workable form, so that we still keep a
simplified model taking Mars equator as the reference plane. The
Sun is in a Keplerian circular orbit, with
its current inclination with respect to Mars' equator.
Therefore, we consider Phobos disturbed by the Sun and the
oblateness of Mars. The coordinate system is fixed at the center
of the planet. Besides the mean motion of the Sun (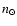 ),
the principal frequencies are:
),
the principal frequencies are:
where (
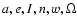 )
are respectively: semi major
axis, eccentricity, inclination, mean motion, argument of the
pericenter and longitude of the node. J2 is the oblateness
coefficient, k2, is the gravitational constant and
)
are respectively: semi major
axis, eccentricity, inclination, mean motion, argument of the
pericenter and longitude of the node. J2 is the oblateness
coefficient, k2, is the gravitational constant and 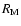 is
the equatorial radius of the planet. The complete disturbing
function of the problem is given in Eqs. (4) to (5) in PYO. We
integrate the averaged equations of the motion and the tidal
effect on the Phobos orbit is computed through the simplest model
for the semi major axis:
is
the equatorial radius of the planet. The complete disturbing
function of the problem is given in Eqs. (4) to (5) in PYO. We
integrate the averaged equations of the motion and the tidal
effect on the Phobos orbit is computed through the simplest model
for the semi major axis:
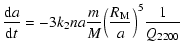 |
|
|
(1) |
![\begin{figure}
\par\resizebox{8.2cm}{!}{\includegraphics[clip]{1173fig2.eps}} \end{figure}](/articles/aa/full/2005/02/aa1173/Timg70.gif) |
Figure 2:
Left panels: evolution of the resonant angle (
top), eccentricity ( center), inclination ( bottom)
taking the Radau integrator with LL=12. Initial
conditions:
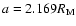 ,
e=0.01, ,
e=0.01,
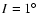 , ,
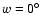 , ,
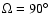 , ,
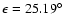 .Right panels:
similar but with .Right panels:
similar but with
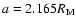 ,
e=0.02, ,
e=0.02,
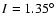 , ,
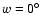 , ,
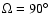 , ,
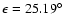 .
As the semi major axis and inclination evolve, new
resonances can appear. Whenever a new resonance is
encountered the dynamics of the libration of .
As the semi major axis and inclination evolve, new
resonances can appear. Whenever a new resonance is
encountered the dynamics of the libration of 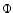 is clearly affected and either
an escape or a different mode of libration occurs. The passage through the new resonances
provokes some jumps in the eccentricity.
is clearly affected and either
an escape or a different mode of libration occurs. The passage through the new resonances
provokes some jumps in the eccentricity.
|
| Open with DEXTER |
where k2 is the second order Love number of Mars,
while Q2200 is the dissipation function (Szeto
1983; Yoder 1981).
Figure 2 shows two different capture/escapes in
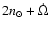 resonance. The panels on the left
correspond to the variation of the resonant angle, eccentricity
and inclination with respect to the semi major axis of a single
orbit starting with
resonance. The panels on the left
correspond to the variation of the resonant angle, eccentricity
and inclination with respect to the semi major axis of a single
orbit starting with
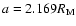 ,
e=0.01,
,
e=0.01,
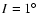 ,
,
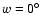 ,
,
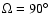 ,
,
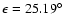 .
Similarly, on the right,
the initial conditions are:
.
Similarly, on the right,
the initial conditions are:
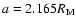 ,
e=0.02,
,
e=0.02,
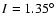 ,
,
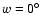 ,
,
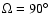 ,
,
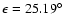 .
In these integrations, the precision
parameter LL in the Radau (Everhart 1985) integrator is fixed to be LL=12. Panel A shows the
evolution of the resonant angle
.
In these integrations, the precision
parameter LL in the Radau (Everhart 1985) integrator is fixed to be LL=12. Panel A shows the
evolution of the resonant angle
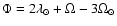 .
Once captured (at
.
Once captured (at
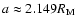 ), libration takes place and lasts until
), libration takes place and lasts until
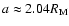 ,
when we have escape. In panel B, Phobos is
captured in the same way as before, but it does not escape when
,
when we have escape. In panel B, Phobos is
captured in the same way as before, but it does not escape when
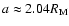 .
Instead,
.
Instead, 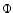 changes its libration mode, and
remains librating in this new mode until
changes its libration mode, and
remains librating in this new mode until
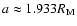 .
Again, as before, it acquires a new libration mode and it
continues until
.
Again, as before, it acquires a new libration mode and it
continues until
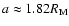 when it escapes definitively.
Connected to each of these mentioned semi major axes, the
eccentricity undergoes some clear jumps, although the inclination
seems to ignore such effects. Starting from different initial
conditions, the qualitative results are similar, i.e., at some
specific values of the semi major axis,
when it escapes definitively.
Connected to each of these mentioned semi major axes, the
eccentricity undergoes some clear jumps, although the inclination
seems to ignore such effects. Starting from different initial
conditions, the qualitative results are similar, i.e., at some
specific values of the semi major axis, 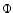 changes its
libration mode. In some cases, this change causes the escape from
resonance, so that inclination stops its secular variation. To
understand these dynamics, we simply calculate the values of the
semi major axis where different resonances
changes its
libration mode. In some cases, this change causes the escape from
resonance, so that inclination stops its secular variation. To
understand these dynamics, we simply calculate the values of the
semi major axis where different resonances
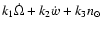 can occur. Of course, in the beginning,
for the current I of Phobos and
can occur. Of course, in the beginning,
for the current I of Phobos and
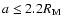 ,
only
,
only
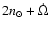 is
possible. Then capture takes place at
is
possible. Then capture takes place at
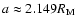 ,
however, after that, since I is increasing, we note
that other resonant
combination can be fulfilled. Considering each of the arguments of the cosines
given in PYO (Eq. (5)), the following additional resonances can occur together
with
,
however, after that, since I is increasing, we note
that other resonant
combination can be fulfilled. Considering each of the arguments of the cosines
given in PYO (Eq. (5)), the following additional resonances can occur together
with
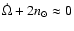 :
:
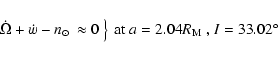
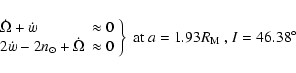

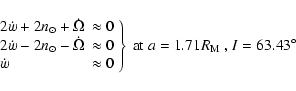
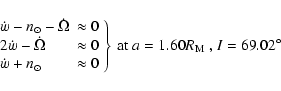
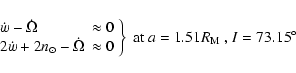
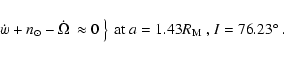
These values were obtained taking e=0.015, since
usually the variation of the eccentricity is very small (see Fig. 2) compared to the variation of the inclination. At
these solutions, two or more resonances occur simultaneously.
Actually the problem becomes a non-autonomous system with two
degree of freedom. Then, the adiabatic invariant theory should
break down in the neighbourhood of the double resonance when they
are of the same importance. Some numerical experiments
show that in this situation, the motion can become very
unstable. More precisely, in Sect. 4 we show a typical situation
that illustrates the existence of two different separatrices in
the case of two simultaneous resonances.
In the present situation, due to the interaction of these two
resonances, a chaotic motion appears, but it is temporary since
the semi major axis is varying and the double resonance occurs for
specific semi major axes given in the above equations. This
disturbs the original capture, so that the occurrence of an escape
or some change in the libration mode, shown in Fig. 2,
seems to be quite natural. However, so far, we are not able to
predict those encounters that provoke escapes.
![\begin{figure}
\par\resizebox{7.6cm}{!}{\includegraphics[clip]{1173fig3.eps}} \end{figure}](/articles/aa/full/2005/02/aa1173/Timg87.gif) |
Figure 3:
A) circles are solutions of Eq. (2), while the continuous curve
is obtained from direct integration of an orbit starting at
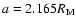 ,
e=0.01, ,
e=0.01,
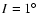 , ,
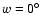 , ,
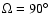 ,
LL=12, ,
LL=12,
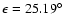 .
B)
circles are solution of Eq. (3), while the continuous
curve results from numerical integration of an orbit starting
at: .
B)
circles are solution of Eq. (3), while the continuous
curve results from numerical integration of an orbit starting
at:
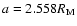 ,
e=0.01, ,
e=0.01,
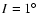 , ,
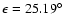 , ,
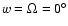 ,
LL=10. In both cases, analytical results match very
well the numerical integration. ( C)-D)): even considering only one resonant
term ( ,
LL=10. In both cases, analytical results match very
well the numerical integration. ( C)-D)): even considering only one resonant
term (
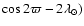 in
in 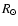 ,
both
inclination and eccentricity undergo large variations. Initial conditions:
a=1.98, e=0.01, ,
both
inclination and eccentricity undergo large variations. Initial conditions:
a=1.98, e=0.01,
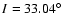 , ,
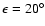 , ,
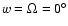 ,
LL=10. ( E)-F)): similar to ( C)-D)), but for ,
LL=10. ( E)-F)): similar to ( C)-D)), but for
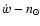 resonance.
This time inclination decreases. Initial conditions:
resonance.
This time inclination decreases. Initial conditions:
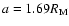 ,
e=0.01, ,
e=0.01,
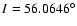 , ,
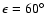 , ,
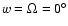 ,
LL=10. ,
LL=10.
|
| Open with DEXTER |
Assuming only one specific resonant librating angle, Gomes
(1997b) was able to find very interesting separate
expressions for the evolution of the eccentricity and inclination.
They are differential equations that give the variation of these
orbital elements in the case of capture. Through these relations,
the concepts of universal inclination and
eccentricity can be derived.
Here we can also obtain very simple relations giving the evolution
of I and e during the capture. On the other hand, the
existence of the universal inclination in this
problem seems to be not so clear. Jancart, Lemaître &
Letocart (2003) working with general dissipation
forces could not find a universal value for the inclination.
Again, the problem analyzed by these authors involved mean motion
resonances. In the present problem, the evolution of the capture
may present some particular features, since the resonance
relation and the dissipative force are different. In order to see
that, we make some simplified assumptions: instead of considering
the whole effect of the tidal dissipative force, we assume that
the tidal effect is simply given through Eq. (1), that
is, only semi major axis variation is taken. Therefore, if Phobos
is to be trapped in a specific resonance, the resonant relations
like
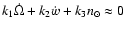 must remain valid all during the
capture. For instance, in the
must remain valid all during the
capture. For instance, in the
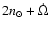 resonance, the following relation between eccentricity and
inclinations should hold:
resonance, the following relation between eccentricity and
inclinations should hold:
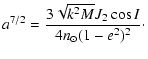 |
|
|
(2) |
Since this is an inclination type resonance, and
provided that the eccentricity variation is small, it is easy to
conclude that for a decreasing semi major axis, the inclination
can increase with no bounds.
In the present problem, if the initial eccentricity is small,
usually, its variation is also very small, so that
Eq. (2) is an analytical relation that gives the
inclination variation versus semi major axis. Unlike problems
involving orbital resonances (Gomes 1997b), in the
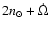 only one resonant angle is in the
libration regime. Therefore the theoretical variation of the
inclination given by Eq. (2) is always valid until an
escape occurs.
only one resonant angle is in the
libration regime. Therefore the theoretical variation of the
inclination given by Eq. (2) is always valid until an
escape occurs.
In Fig. 3, panel A, the continuous curve comes
from direct numerical integration. The circles are solutions of
Eq. (2) but we interrupted at
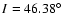 because the
numerical integration shows an escape at this point. The agreement
between the continuous and the circled curves is excellent.
because the
numerical integration shows an escape at this point. The agreement
between the continuous and the circled curves is excellent.
The situation is similar for the evection resonance:
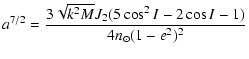 |
|
|
(3) |
where eccentricity increases when the satellite is
receding from the planet (the variation of the inclination is
assumed to be negligible). However, in a real and complete tidal
model, there will appear a kind of bound on the maximum
eccentricity, since as the orbit becomes more eccentric, the
angular motion of Phobos, at the pericenter, can be larger than
Mars' rotation. This will stop the secular variation of the semi
major axis and this is the typical scenario in the case of a more
complete tidal model (Touma & Wisdom 1998). In other
words, for increasing semi major axis and to study further
consequences in a eccentricity resonance capture, the tidal model
should be more complete than the simple one given in
Eq. (1). In the present problem, Phobos' semi major axis
is always decreasing, so that capture in evection resonance or
eccentricity type resonances is not expected. Even so, it is
instructive to test Eq. (3), since at least during some
time, the semi major axis increases until the orbit becomes very
eccentric. The theoretical variation of the eccentricity,
predicted in Eq. (3), can be compared against the
numerical integration. As before, in Fig. 3B the circled
curve is obtained from Eq. (3), while the continuous
curve corresponds to numerical integration. The inclination
remains almost constant (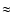
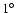 )
over all the integration
time (
)
over all the integration
time (
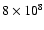 years). Again the agreement is quite good.
years). Again the agreement is quite good.
Therefore, provided that eccentricity (or inclination) does not
vary greatly, Eq. (2) (or Eq. (3)) gives the
variation of inclination (or eccentricity) with respect to a.
Note, however, that if the initial inclination is not small, we
have some cases where even in an eccentricity type resonance, the
inclination suffers large variation during the evolution of the
capture. Although Eq. (3) remains valid, both
inclination and eccentricity can undergo large variation. In
Fig. 3C-E we show the significant increase and decrease
of the inclination in the
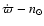 and
and
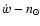 resonances respectively. Panel D shows the
variation of the eccentricity, and it is the corresponding pair of
panel C. Analogously, panel F is the corresponding pair of panel
E. In order to decouple and to get separate equations for
eccentricity and inclination, we need an extra relation, involving
a,e,I. In this sense, we consider, for instance, the action:
resonances respectively. Panel D shows the
variation of the eccentricity, and it is the corresponding pair of
panel C. Analogously, panel F is the corresponding pair of panel
E. In order to decouple and to get separate equations for
eccentricity and inclination, we need an extra relation, involving
a,e,I. In this sense, we consider, for instance, the action:
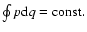 ,
where p is the canonical momentum associated
with the resonant librating angle q. Interesting interpretations
and geometric idea of this quantity are given by several authors (Henrard 1982;
Henrard & Lemaître 1986; Peale 1989; Gomes 1995a,b, etc.). Let
,
where p is the canonical momentum associated
with the resonant librating angle q. Interesting interpretations
and geometric idea of this quantity are given by several authors (Henrard 1982;
Henrard & Lemaître 1986; Peale 1989; Gomes 1995a,b, etc.). Let 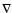 be the gradient operator
while J1 and J2 are the two first integrals of the motion.
If
be the gradient operator
while J1 and J2 are the two first integrals of the motion.
If
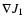 and
and
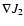 are not colinear vectors in the
(p, q) phase space, then we say that J1 and J2 are
independent integrals. With this reasoning, although
are not colinear vectors in the
(p, q) phase space, then we say that J1 and J2 are
independent integrals. With this reasoning, although
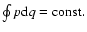 and Eq. (3) are not integrals of the motion,
separated equations for I and e could be obtained (provided
that the previous relations are independent). Usually, an explicit
analytical expression for
and Eq. (3) are not integrals of the motion,
separated equations for I and e could be obtained (provided
that the previous relations are independent). Usually, an explicit
analytical expression for
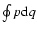 is not possible, and in
that case we have to resort to approximate numerical methods
(Henrard & Lemaître 1986).
is not possible, and in
that case we have to resort to approximate numerical methods
(Henrard & Lemaître 1986).
In the two previous sections we considered Mars in a circular orbit.
The current inclination of Phobos is 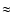
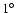 .
Under
normal conditions this value should remain almost unchanged, so
that capture of Phobos in the
.
Under
normal conditions this value should remain almost unchanged, so
that capture of Phobos in the
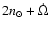 commensurability is almost certain (Yokoyama 2002),
provided that Mars' obliquity is not less than
commensurability is almost certain (Yokoyama 2002),
provided that Mars' obliquity is not less than 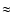
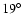 .
However before reaching this resonance, two previous
commensurabilities are encountered:
.
However before reaching this resonance, two previous
commensurabilities are encountered:
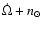 (N), and
(N), and
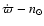 (E). They appear almost
simultaneously at
(E). They appear almost
simultaneously at
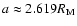 so that we called them
double resonance. The former, for a decreasing semi major axis, is
favorable for capture while the latter (evection), provides
capture only if a is increasing. Since they appear
simultaneously, capture in (N) resonance, for a decreasing
semi major axis, is not certain. Indeed, some numerical
experiments in our previous work (PYO), showed that for the
circular case, capture in the
so that we called them
double resonance. The former, for a decreasing semi major axis, is
favorable for capture while the latter (evection), provides
capture only if a is increasing. Since they appear
simultaneously, capture in (N) resonance, for a decreasing
semi major axis, is not certain. Indeed, some numerical
experiments in our previous work (PYO), showed that for the
circular case, capture in the
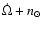 resonance
usually does not occur. However, a salient fact is noted: some
slight jumps in the inclination of Phobos were observed during the
passage through these resonances. In the circular case, these
jumps are not significant, and therefore, capture in the next
resonance,
resonance
usually does not occur. However, a salient fact is noted: some
slight jumps in the inclination of Phobos were observed during the
passage through these resonances. In the circular case, these
jumps are not significant, and therefore, capture in the next
resonance,
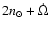 ,
should not be affected. But
if the height of these jumps becomes large, the post passage
inclination may exceed some threshold value so that the capture in
the next
,
should not be affected. But
if the height of these jumps becomes large, the post passage
inclination may exceed some threshold value so that the capture in
the next
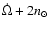 resonance may not be certain.
So, in this section we show the effect of Mars' eccentricity. It
can play an important role mainly in the presence of the double
resonance. Besides the resonances given in PYO, the following
additional combinations (of order
resonance may not be certain.
So, in this section we show the effect of Mars' eccentricity. It
can play an important role mainly in the presence of the double
resonance. Besides the resonances given in PYO, the following
additional combinations (of order 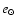 )
will appear for
)
will appear for
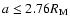 :
:
The remaining higher order terms are negligible. Notice
that
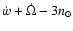 is just a linear combination
of evection (E) and (N) resonances. Therefore, at
is just a linear combination
of evection (E) and (N) resonances. Therefore, at
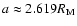 ,
we have only (N) and (E)
resonances. Moreover, both appear not only here, but also in the
circular case, so that it is clear that they are much more
important than the remaining resonances listed in Eq. (4).
Several numerical runs have shown that the consequences and
variations caused by these commensurabilities are very weak
compared to those caused by (N) and (E) resonances.
Therefore, we concentrate our investigation only on this point.
Figure 4 is the spectral analysis of the inclination
variable considering the interval
,
we have only (N) and (E)
resonances. Moreover, both appear not only here, but also in the
circular case, so that it is clear that they are much more
important than the remaining resonances listed in Eq. (4).
Several numerical runs have shown that the consequences and
variations caused by these commensurabilities are very weak
compared to those caused by (N) and (E) resonances.
Therefore, we concentrate our investigation only on this point.
Figure 4 is the spectral analysis of the inclination
variable considering the interval
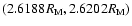 of
Phobos' semi major axis. A total of 120 initial conditions were
taken in this interval and the solutions were analyzed via FFT.
Due to the amount of computation time in obtaining this figure, we
considered only two cosines, corresponding to evection (E)
and (N) resonances, in the disturbing function. Moreover,
Mars was considered in a circular orbit. For each semi major axis,
the problem is integrated and the log of the fundamental
frequencies and their harmonics are shown in Fig. 4.
Those frequencies whose amplitudes are
of
Phobos' semi major axis. A total of 120 initial conditions were
taken in this interval and the solutions were analyzed via FFT.
Due to the amount of computation time in obtaining this figure, we
considered only two cosines, corresponding to evection (E)
and (N) resonances, in the disturbing function. Moreover,
Mars was considered in a circular orbit. For each semi major axis,
the problem is integrated and the log of the fundamental
frequencies and their harmonics are shown in Fig. 4.
Those frequencies whose amplitudes are 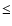 0.5% of
0.5% of
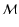 are discarded, where
are discarded, where
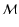 is the maximum value of
the amplitude for each integration (see Callegari et al. 2004). The curves show the behaviour of
the frequencies for different values of the semi major axis. In
the case of regular motion, their paths are well defined and vary
continuously with respect to a. In Fig. 4, we use E (or N) to identify the curve whose frequency is due
to E (or N) resonance. At about
is the maximum value of
the amplitude for each integration (see Callegari et al. 2004). The curves show the behaviour of
the frequencies for different values of the semi major axis. In
the case of regular motion, their paths are well defined and vary
continuously with respect to a. In Fig. 4, we use E (or N) to identify the curve whose frequency is due
to E (or N) resonance. At about
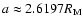 we see two well defined frequencies, almost symmetric with
respect to this value of a. Both correspond to the N
frequency although only the curve on the left is marked. The
remaining curves not labelled with these two letters correspond to
higher harmonics of the E frequency or linear combinations
between E and N frequencies. In particular, higher
harmonics of the N frequency have very small amplitudes, so
that they do not appear in the figure. At
we see two well defined frequencies, almost symmetric with
respect to this value of a. Both correspond to the N
frequency although only the curve on the left is marked. The
remaining curves not labelled with these two letters correspond to
higher harmonics of the E frequency or linear combinations
between E and N frequencies. In particular, higher
harmonics of the N frequency have very small amplitudes, so
that they do not appear in the figure. At
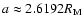 and
and
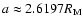 ,
it is clear that the two fundamental
frequencies fall to zero. At these points, the corresponding
periods of (E) resonance and (N) resonance go to infinity,
which characterizes the separatrices of both resonances. In the
neighbourhood and in the region where these separatrices overlap,
we have some chaotic motion. Since these two separatrices are very
close to each other, we expect the appearance of chaotic motion in
more the general case.
,
it is clear that the two fundamental
frequencies fall to zero. At these points, the corresponding
periods of (E) resonance and (N) resonance go to infinity,
which characterizes the separatrices of both resonances. In the
neighbourhood and in the region where these separatrices overlap,
we have some chaotic motion. Since these two separatrices are very
close to each other, we expect the appearance of chaotic motion in
more the general case.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{1173fig4.eps}} \end{figure}](/articles/aa/full/2005/02/aa1173/Timg116.gif) |
Figure 4:
Evolution of the log of the frequencies versus semi
major axis. At the point where the fundamental frequency goes
to zero we have the corresponding semi major of the separatrix.
Since these separatrices are close, they can overlap and we expect the
onset of chaos. Each integration was extended to 1 996 050
years, generating 216 outputs, sampled at every 30 years. Phobos initial
conditions: e=0.051,
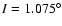 , ,
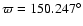 , ,
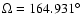 .
Mars initial conditions: e=0.0, .
Mars initial conditions: e=0.0,
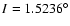 , ,
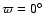 , ,
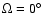 , ,
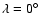 , ,
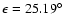 . . |
| Open with DEXTER |
We examine the dynamics when the semi major of Phobos varies,
passing through these two resonant values. This time, Mars'
eccentricity is considered (up to fourth order terms) and also all
cosines of the disturbing function given in Eq. (5) in PYO.
![\begin{figure}
\par\resizebox{8.2cm}{!}{\includegraphics[clip]{1173fig5.eps}} \end{figure}](/articles/aa/full/2005/02/aa1173/Timg117.gif) |
Figure 5:
Due to the action of the two simultaneous resonances in the neighbourhood
of
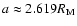 ,
the motion is very irregular (chaotic).
Depending on the input values, the inclination and
eccentricity are strongly excited during the passage through
the double resonance. The final stabilized values are
not predictable. On the left, the system leaves the double resonance with
inclination ,
the motion is very irregular (chaotic).
Depending on the input values, the inclination and
eccentricity are strongly excited during the passage through
the double resonance. The final stabilized values are
not predictable. On the left, the system leaves the double resonance with
inclination 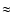 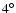 and eccentricity
and eccentricity 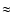 0.08. On
the right, these values are smaller than those used in the
input data. Initial conditions ( left panels):
a=2.625, e=0.015, 0.08. On
the right, these values are smaller than those used in the
input data. Initial conditions ( left panels):
a=2.625, e=0.015,
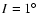 , ,
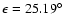 , ,
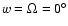 ,
( right panels):
a=2.630, e=0.015, ,
( right panels):
a=2.630, e=0.015,
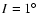 , ,
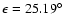 , ,
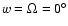 . . |
| Open with DEXTER |
Figure 5 shows the situation when Phobos encounters (E) and (N) resonances. As expected, it is clear that the
motion is quite irregular in the vicinity of
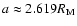 .
Because of this, in all integrations of this figure, we again
fixed high precision in the Radau integrator (LL=12). In
Fig. 5A the inclination goes through jumps during the
passage through the critical value of the semi major axis, but
after that it stabilizes at
.
Because of this, in all integrations of this figure, we again
fixed high precision in the Radau integrator (LL=12). In
Fig. 5A the inclination goes through jumps during the
passage through the critical value of the semi major axis, but
after that it stabilizes at
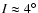 .
Also the eccentricity
is excited to
.
Also the eccentricity
is excited to
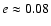 (Fig. 5C). This significant
increase in the inclination is important since unless some extra
damping occurs, the next resonance (
(Fig. 5C). This significant
increase in the inclination is important since unless some extra
damping occurs, the next resonance (
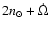 )
will be faced with an inclination so large that capture in this
resonance may not be possible. Indeed, certain capture is possible
only when the initial action
)
will be faced with an inclination so large that capture in this
resonance may not be possible. Indeed, certain capture is possible
only when the initial action
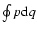 (see PYO, Eq. (9)), far
from the resonance, is less than the area inside of the separatrix
first formed, during the evolution of the semi major axis (Henrard 1982; Peale 1989). This means that
we cannot guarantee capture for an arbitrary initial inclination.
For instance, several numerical experiments show that for
(see PYO, Eq. (9)), far
from the resonance, is less than the area inside of the separatrix
first formed, during the evolution of the semi major axis (Henrard 1982; Peale 1989). This means that
we cannot guarantee capture for an arbitrary initial inclination.
For instance, several numerical experiments show that for
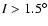 capture depends on the phase, while for
capture depends on the phase, while for
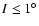 we
always can get capture no matter the initial values for w or
we
always can get capture no matter the initial values for w or 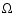 .
.
Figure 5B shows another interesting situation: as before,
the motion is also very complicated due to the double resonance
and the inclination is excited to high values. However, at the
end, it decreases back to about
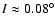 .
The final
eccentricity is also smaller than the initial value before
entering the critical region (Fig. 5D). Since the motion
is very irregular it seems that the precision parameter LL=12 in
the Radau integrator is important. In this sense, a curious case
appears if LL is relaxed to LL=9: we have a capture in the
.
The final
eccentricity is also smaller than the initial value before
entering the critical region (Fig. 5D). Since the motion
is very irregular it seems that the precision parameter LL=12 in
the Radau integrator is important. In this sense, a curious case
appears if LL is relaxed to LL=9: we have a capture in the
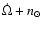 and inclination increases to high values
similar to those shown in Fig. 2. After a lot of
numerical experiments, we prefer to say that this capture is
improbable and that the percentage of initial conditions leading
to capture is very small. Moreover, tests showed that the general
dynamics is very sensitive to the starting point and to the
precision parameter LL used in the integrator. In particular,
the initial conditions we used to get the mentioned capture were:
and inclination increases to high values
similar to those shown in Fig. 2. After a lot of
numerical experiments, we prefer to say that this capture is
improbable and that the percentage of initial conditions leading
to capture is very small. Moreover, tests showed that the general
dynamics is very sensitive to the starting point and to the
precision parameter LL used in the integrator. In particular,
the initial conditions we used to get the mentioned capture were:
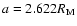 ,
e=0.015,
,
e=0.015,
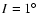 ,
,
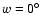 ,
,
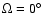 ,
,
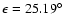 ,
with LL=9.
,
with LL=9.
We believe that the inclusion of
Mars' eccentricity enhances the effect of the double resonance.
The final value of the inclination when the semi major axis
crosses the region
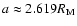 seems to be completely
uncertain.
seems to be completely
uncertain.
Up to now, the orbit of Mars was considered Keplerian with a fixed
equator. In a more realistic model, we should take into account
the planetary perturbations which will disturb not only Mars'
orbit but also its equator. However, an integration starting from
present data until Phobos semi major axis decreases to
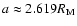 or
or
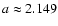 ,
needs an enormous and probably a
prohibitive computational effort (Hamilton 2002).
Without a reliable tidal model, and corresponding reliable
constants, we cannot be confident of the final result of this long
time integration. Usually tidal models demand knowledge of
important physical constants, but in general, the accuracy of
these values is always questionable: the dissipation function Q,
Love's number
,
needs an enormous and probably a
prohibitive computational effort (Hamilton 2002).
Without a reliable tidal model, and corresponding reliable
constants, we cannot be confident of the final result of this long
time integration. Usually tidal models demand knowledge of
important physical constants, but in general, the accuracy of
these values is always questionable: the dissipation function Q,
Love's number 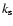 ,
mass satellite (Phobos) and also rigidity and
dissipation in Phobos. For the precession of Mars' equator, the
problem is the same and the important constants involved are: the
moment of inertia and spin rate. In spite of all these
difficulties we think it is interesting to have a rough
qualitative idea of the main effects when planetary perturbations
are included. To avoid the problem of computational time, we
artificially change the initial semi major of Phobos, and start
our integration in the neighbourhood of
,
mass satellite (Phobos) and also rigidity and
dissipation in Phobos. For the precession of Mars' equator, the
problem is the same and the important constants involved are: the
moment of inertia and spin rate. In spite of all these
difficulties we think it is interesting to have a rough
qualitative idea of the main effects when planetary perturbations
are included. To avoid the problem of computational time, we
artificially change the initial semi major of Phobos, and start
our integration in the neighbourhood of
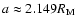 and
not
and
not
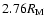 ,
which is the current value of Phobos' semi major
axis. In order to consider the perturbation of the planets on
Mars, we use Laskar's secular theory (Laskar 1988). We
also take the variation of Mars equator through the equations
(Woolard 1953):
,
which is the current value of Phobos' semi major
axis. In order to consider the perturbation of the planets on
Mars, we use Laskar's secular theory (Laskar 1988). We
also take the variation of Mars equator through the equations
(Woolard 1953):
where
| K0 |
= |
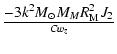 |
|
| K1 |
= |
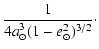 |
|
In the above equations, we take the Sun as the main disturber of
Mars equator (Woolard 1953).
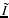 and
and
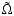 are the inclination and longitude of the node of Mars'
equator referred to an inertial reference plane (ecliptic of
2000). These equations are averaged with respect to the mean
anomaly of the Sun. The notation of the variables and constants
are the same as used in PYO, with two new constants: C=polar
moment of inertia, wz = spin rate. In this work we adopted
are the inclination and longitude of the node of Mars'
equator referred to an inertial reference plane (ecliptic of
2000). These equations are averaged with respect to the mean
anomaly of the Sun. The notation of the variables and constants
are the same as used in PYO, with two new constants: C=polar
moment of inertia, wz = spin rate. In this work we adopted
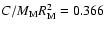 and the Mars rotation period was fixed to be
1.026 days.
and the Mars rotation period was fixed to be
1.026 days.
The Laskar secular theory (Laskar 1988) is given
through the series:
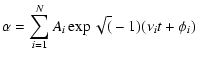 |
|
|
(6) |
where in general only 25 terms in the above series were
considered (we are interested only in the qualitative behaviour
of the solution). The frequencies (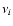 ), phases (
), phases (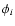 )
and
amplitudes (Ai) of each orbital element (
)
and
amplitudes (Ai) of each orbital element (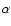 )
are given
in Laskar (1988), Table 9.
)
are given
in Laskar (1988), Table 9.
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[clip]{1173fig6.eps}} \end{figure}](/articles/aa/full/2005/02/aa1173/Timg144.gif) |
Figure 6:
A typical situation of capture in the
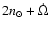 resonance including planetary perturbation
on Mars and variation of its equator. In panel A,
Phobos' inclination with respect to the ecliptic of 2000 is shown, while in
panel B, the same inclination is shown with respect to the
moving Mars equator. Panel C, shows the behaviour of
resonance including planetary perturbation
on Mars and variation of its equator. In panel A,
Phobos' inclination with respect to the ecliptic of 2000 is shown, while in
panel B, the same inclination is shown with respect to the
moving Mars equator. Panel C, shows the behaviour of
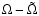 .
Initially these two nodes are almost
synchronous and after the capture, they start to diverge (
more details are given in the text). Panel D, exhibits the variation of the obliquity.
Initial conditions a=2.152, e=0.015, .
Initially these two nodes are almost
synchronous and after the capture, they start to diverge (
more details are given in the text). Panel D, exhibits the variation of the obliquity.
Initial conditions a=2.152, e=0.015,
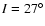 , ,
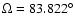 , ,
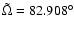 , ,
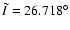 |
| Open with DEXTER |
The equations to be integrated are the same as before, but this
time the orbit of Mars is given through series 6
and we also add Eq. (5). As usual, the initial
conditions are chosen such that Phobos' inclination with respect
to Mars' equator is 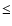
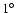 and
and
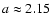 .
Figure
6 shows a case of a capture in the
.
Figure
6 shows a case of a capture in the
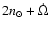 resonance, when planetary perturbations on
Mars and motion of its equator are considered.
resonance, when planetary perturbations on
Mars and motion of its equator are considered.
Panel A shows the variation of the inclination of Phobos with
respect to the ecliptic plane. A fast oscillation around the
initial inclination (
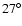 )
is noticed. The amplitude of this
oscillation starts to increase as the capture occurs. In fact,
this inclination may reach zero or values greater than
)
is noticed. The amplitude of this
oscillation starts to increase as the capture occurs. In fact,
this inclination may reach zero or values greater than
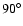 (Gomes 1997b), so that regularized variables are
needed in these cases. Panel B shows the corresponding inclination
referred to the equatorial plane. This time, once capture occurs,
instead of the fast oscillations of the previous case, we have the
well-known slow and secular increasing behaviour of the
inclination. Panel C shows the difference
(Gomes 1997b), so that regularized variables are
needed in these cases. Panel B shows the corresponding inclination
referred to the equatorial plane. This time, once capture occurs,
instead of the fast oscillations of the previous case, we have the
well-known slow and secular increasing behaviour of the
inclination. Panel C shows the difference
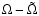 .
Its behaviour is very similar to the inclination in panel A.
Finally, the variation of the obliquity (
.
Its behaviour is very similar to the inclination in panel A.
Finally, the variation of the obliquity (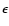 )
of Mars is
shown in panel D. A few tests have shown that sometimes capture
fails if the initial inclination with respect to the equator is
)
of Mars is
shown in panel D. A few tests have shown that sometimes capture
fails if the initial inclination with respect to the equator is
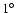 ,
while we always found successful capture when we took it as
,
while we always found successful capture when we took it as
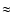
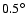 .
Therefore we see that even considering planetary
perturbations and the variation of the equator, capture still
occurs and the general path of the variation of the inclination
with respect to the equator is quite similar to the cases without
these two effects.
.
Therefore we see that even considering planetary
perturbations and the variation of the equator, capture still
occurs and the general path of the variation of the inclination
with respect to the equator is quite similar to the cases without
these two effects.
Considering the simplest tidal model for Phobos, we analyzed some
situations of escape from the
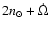 resonance.
The escapes are due to new resonances that appear as the
inclination reaches some specific values:
resonance.
The escapes are due to new resonances that appear as the
inclination reaches some specific values:
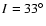 ,
,
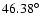 ,
,
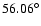 ,
,
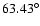 ,
,
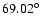 ,
,
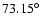 ,
,
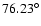 .
However, we
cannot predict the inclinations for which escapes will occur.
After several numerical simulations, we conclude that the
existence of a universal inclination is not clear
in this problem, since no stabilization of the inclination was
found.
Some
analytic equations that give the path followed by the inclination
during the capture are derived for each resonance. We also show
that for
.
However, we
cannot predict the inclinations for which escapes will occur.
After several numerical simulations, we conclude that the
existence of a universal inclination is not clear
in this problem, since no stabilization of the inclination was
found.
Some
analytic equations that give the path followed by the inclination
during the capture are derived for each resonance. We also show
that for
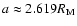 ,
the role played by the
eccentricity of Mars is decisive, since Phobos' inclination can be
excited to about
,
the role played by the
eccentricity of Mars is decisive, since Phobos' inclination can be
excited to about 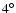 ,
so that capture in
,
so that capture in
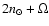 is
not possible any longer. Finally, including planetary
perturbations on Mars and precession equations for the motion of
its equator, we showed that capture of Phobos is still possible
and probably, the general features of the dynamics should be
similar to the simplified model.
is
not possible any longer. Finally, including planetary
perturbations on Mars and precession equations for the motion of
its equator, we showed that capture of Phobos is still possible
and probably, the general features of the dynamics should be
similar to the simplified model.
Acknowledgements
Part of this work was supported by FAPESP and FUNDUNESP.
An anonymous referee is gratefully thanked for very
important comments.
- Beaugé, C.,
& Ferraz-Mello, S. 1994, Icarus, 110, 239 [CrossRef] (In the text)
- Callegari Jr, N.,
Michtchenko, T. A., & Ferraz-Mello, S. 2004, Celest. Mech. Dyn.
Astron., in press
(In the text)
- Dobrovolskis,
R. A., & Steiman-Cameron, T. Y. 1989, Geophys. Res. Lett., 16,
8, 949
- Everhart, E. 1985, in
Dynamics of Comets: Their origin and Evolution, ed. A. Carusi,
& G. Valsechi (Dordrecht: Reidel Publishing Co), 185
(In the text)
- Gomes, R. S.
1995a, Celest. Mech. Dyn. Astron., 61, 97 (In the text)
- Gomes, R. S.
1995b, Icarus, 115, 47 [CrossRef] (In the text)
- Gomes, R. S.
1997a, A&A, 321, 960 (In the text)
- Gomes, R. S.
1997b, AJ, 114, 2166 [CrossRef] (In the text)
- Gomes, R. S. 1998,
AJ, 116, 997 [CrossRef] (In the text)
- Hamilton, D. P.
1994, Icarus, 109, 221 [CrossRef] (In the text)
- Hamilton, D. P.
2002, An explanation for the high inclinations of Thebe and
Amalthea (invited talk) In 11th Brazilian Colloquium on Orbital
Dynamics, 17, Universidade Federal de Viçosa, Viçosa,
Brasil
(In the text)
- Henrard, J. 1982,
Celest. Mech., 27, 3 [MathSciNet] (In the text)
- Henrard, J.,
& Lemaître, A. 1986, Celest. Mech., 39, 213 [MathSciNet] (In the text)
- Jancart, S.,
Lemaître, A., & Istace, A. 2002, Celest. Mech. Dyn.
Astron., 84, 197 [MathSciNet]
- Jancart, S.,
Lemaître, A., & Letocart,V. 2003, Celest. Mech. Dyn.
Astron., 86, 363 [MathSciNet] (In the text)
- Laskar, J. 1988,
A&A, 198, 341 (In the text)
- Laskar, J., &
Robutel, P. 1993, Nature, 361, 608 [CrossRef] (In the text)
- Liou, J. C., &
Zook, H. A. 1997, Icarus, 128, 354 [CrossRef] (In the text)
- Malhotra, R.
1990, Icarus, 87, 249 [CrossRef] (In the text)
- Peale, S. J. 1989, in
Satellites, ed. J. A. Burns, & M. S. Matthews (Univ. Arizona),
159
(In the text)
- Szeto, A. M. K. 1983,
Icarus, 55, 133 [CrossRef] (In the text)
- Touma, J., &
Wisdom, J. 1993, Science, 259, 1294 (In the text)
- Touma, J., &
Wisdom, J. 1993, AJ, 115, 1653 (In the text)
- Ward, W. R. 1979, J.
Geophys. Res., 84, 237 (In the text)
- Woolard, E. K.
1953, Astron. Papers of American Ephemeris, 15, 1 (In the text)
- Yoder, F. C. 1981,
Icarus, 49, 327 (In the text)
- Yokoyama, T.
2002, Planetary and Space Science, 50, 63 [CrossRef] (In the text)
Copyright ESO 2004
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[clip]{1173fig1.eps}} %
\end{figure}](/articles/aa/full/2005/02/aa1173/Timg55.gif)
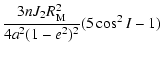
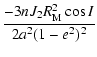
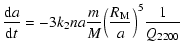
![\begin{figure}
\par\resizebox{8.2cm}{!}{\includegraphics[clip]{1173fig2.eps}} \end{figure}](/articles/aa/full/2005/02/aa1173/Timg70.gif)
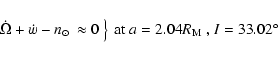
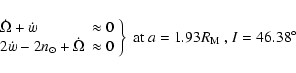

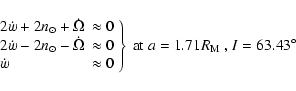
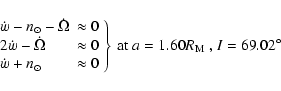
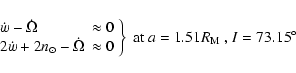
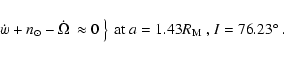
![\begin{figure}
\par\resizebox{7.6cm}{!}{\includegraphics[clip]{1173fig3.eps}} \end{figure}](/articles/aa/full/2005/02/aa1173/Timg87.gif)
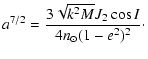
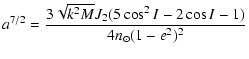
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{1173fig4.eps}} \end{figure}](/articles/aa/full/2005/02/aa1173/Timg116.gif)
![\begin{figure}
\par\resizebox{8.2cm}{!}{\includegraphics[clip]{1173fig5.eps}} \end{figure}](/articles/aa/full/2005/02/aa1173/Timg117.gif)
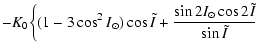
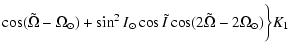
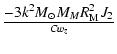
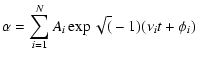
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[clip]{1173fig6.eps}} \end{figure}](/articles/aa/full/2005/02/aa1173/Timg144.gif)