A&A 429, 19-30 (2005)
DOI: 10.1051/0004-6361:20041656
Monte Carlo techniques for time-dependent radiative transfer in
3-D supernovae
L. B. Lucy
Astrophysics Group, Blackett Laboratory, Imperial College
London, Prince Consort Road, London SW7 2AZ, UK
Received 13 July 2004 / Accepted 7 September 2004
Abstract
Monte Carlo techniques based on indivisible energy packets are described for
computing light curves and spectra for 3-D supernovae. The radiative transfer is
time-dependent and includes all effects of O(v/c). Monte Carlo quantization
is achieved by discretizing the initial distribution of
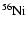 into
into 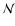 radioactive pellets. Each pellet decays with the emission of a
single energy packet comprising
radioactive pellets. Each pellet decays with the emission of a
single energy packet comprising  -ray photons
representing one line from either the
-ray photons
representing one line from either the
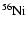 or the
or the
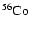 decay
spectrum. Subsequently, these energy packets propagate through the
homologously-expanding ejecta with
appropriate changes in the nature of their contained energy as they undergo
Compton scatterings and pure absorptions.
decay
spectrum. Subsequently, these energy packets propagate through the
homologously-expanding ejecta with
appropriate changes in the nature of their contained energy as they undergo
Compton scatterings and pure absorptions.
The 3-D code is tested by applying it to a spherically-symmetric
SN in which the transfer of optical radiation is treated with a grey
absorption coefficient. This 1-D problem is separately solved using
Castor's co-moving frame moment equations. Satisfactory agreement is obtained.
The Monte Carlo code is a platform onto which more advanced treatments
of the interactions of matter and radiation can be added. Some of
these have already been developed and tested in previous papers and are
summarized here.
Key words: stars: supernovae: general - radiative transfer - methods: numerical
In earlier papers, Monte Carlo (MC) methods were used to construct spectral
synthesis codes for SNe in their photospheric phases. Because the emphasis was on
coarse analyses of the spectra of newly-discovered SNe,
major simplifying approximations were made to minimize computing time and to
ensure robustness. Thus, in the first code (Lucy 1987; Mazzali & Lucy 1993),
the SN's atmosphere is spherically-symmetric and homologously expanding,
the radiation field is stationary (
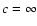 ), continuum
formation is confined to a sharply-defined lower boundary
(Schuster-Schwarzschild approximation), and line formation results from the
coherent scattering of this continuum as it propagates through the outer
layers. Moreover, the stratifications of temperature, ionization and excitation are
derived not from first principles but from formulae that approximate the effects of
dilution in the SN's extended atmosphere.
), continuum
formation is confined to a sharply-defined lower boundary
(Schuster-Schwarzschild approximation), and line formation results from the
coherent scattering of this continuum as it propagates through the outer
layers. Moreover, the stratifications of temperature, ionization and excitation are
derived not from first principles but from formulae that approximate the effects of
dilution in the SN's extended atmosphere.
In a subsequent paper (Lucy 1999b), two innovations significantly
improved this code. First, coherent scattering was replaced
by downward branching as the mechanism of line formation. Secondly, a
computed spectrum's sampling errors were greatly reduced by using the
formal integral for the emergent intensity instead of simply binning the
escaping photon packets.
Although these codes have proved their worth diagnostically,
they cannot compute spectra for explosion models, a challenge that
must be faced if explosion mechanisms and progenitor scenarios are to be confronted with
observed spectra and light curves. Evidently, simplifying assumptions
must be reconsidered in planning a more powerful and versatile code.
First, the assumption of stationarity must be abandoned. As Arnett
(1980, 1982) long ago demonstrated for SNe both of types I and II, the
luminosity L(t) at elapsed time t does not in general closely approximate the instantaneous
energy deposition rate by  -rays emitted in radioactive decays.
Accordingly, the time-dependent diffusion of radiant energy through the expanding ejecta
must be treated explicitly if we wish to compute the emergent luminosity
density
-rays emitted in radioactive decays.
Accordingly, the time-dependent diffusion of radiant energy through the expanding ejecta
must be treated explicitly if we wish to compute the emergent luminosity
density 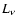 as a function of time.
as a function of time.
Similarly, artificially creating radiant energy by means of a continuum-emitting
lower boundary is no longer acceptable. The computational domain must
be the complete configuration, not just a "reversing layer''; and
continuum formation must be treated explicitly.
Escaping radiant energy then derives ultimately from radioactive decays or
from the energy content of the ejecta at t1, the time at which the
output from an explosion calculation is used to initiate the spectral
synthesis code.
Removal of the constraint of spherical symmetry is also
highly desirable in view of accumulating observational evidence and
theoretical arguments implying that most and perhaps all SN explosions
are significantly aspherical - see Wheeler (2004) for a recent review.
Of the assumptions in the earlier codes, the only
one retained is that of homologous expansion.
This requires that the explosion calculation, which of necessity includes
gas dynamics, be continued until all mass elements are to
a good approximation coasting ballistically.
With the assumptions to be dropped identified, the problem is
now defined: to solve the time-dependent, 3-D NLTE transfer problem for
UVOIR radiation in the homologously expanding ejecta of a SN, given the distribution of
mass and composition at an initial time t1. Of course, this problem is coupled to a corresponding 3-D transport problem for the  -rays emitted by radioactive isotopes. This coupling occurs via the equations describing the deposition and degradation of
-rays emitted by radioactive isotopes. This coupling occurs via the equations describing the deposition and degradation of  -ray
energy.
-ray
energy.
In view of the magnitude of this problem, this paper is restricted to
describing an exploratory MC code in which the UVOIR radiation's interaction with matter is governed by a grey absorption coefficient. This problem was previously treated by Pinto &
Eastman (2000) in order to explore the sensitivity of type Ia light
curves to parameters. Here the aim is to create a software platform onto which more realistic
physics can be subsequently added and with which numerical techniques can be tested.
Monte Carlo methods are a natural choice for this problem given
the experience with the earlier codes. Moreover, MC methods are
commonly favoured for transport phenomena in geometrically-complex configurations
with no symmetries. Nevertheless, the conventional approach in which
the derivatives in the time-dependent transfer equation (RTE) are
approximated by differences has already been partially implemented for 3-D SNe by
Höflich (2003). With regard to the application of MC methods, the most
advanced work seems to be that of Kasen et al. (2004) who carry out 2-D time-independent calculations to compute the observable characteristics
of a type Ia model with a conical hole.
In this section, after some preliminaries, recent developments in
MC technique that are relevant for a general spectral synthesis code are summarized. These remarks
are not restricted to the grey case considered in this paper.
Random numbers are obtained with a double precision version of
the routine ran2 of Press et al. (1992). Such numbers are always denoted by z, with each z denoting an independent call to ran2.
As in earlier codes, the MC quanta are energy
packets. In general, these are referred to as  -packets except when
specifying the nature of the contained energy (Paper I, Sect. 2). Thus
r-packets and
-packets except when
specifying the nature of the contained energy (Paper I, Sect. 2). Thus
r-packets and  -packets are monochromatic photon packets of UVOIR radiation and of
-packets are monochromatic photon packets of UVOIR radiation and of  -rays, respectively. On the other hand,
k-packets and i-packets contain not radiation but thermal kinetic energy
and ionization energy, respectively. In addition, a full treatment of
radioactive decay and
-rays, respectively. On the other hand,
k-packets and i-packets contain not radiation but thermal kinetic energy
and ionization energy, respectively. In addition, a full treatment of
radioactive decay and  -ray
deposition will require consideration of
-ray
deposition will require consideration of 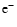 - and
- and 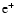 -packets
containing non-thermal electrons and positrons, respectively.
-packets
containing non-thermal electrons and positrons, respectively.
The SN is enclosed in a Cartesian grid containing I3 identical
cubic cells. This grid expands with the ejecta so that each
cell contains a fixed parcel of matter. Physical variables do not vary
spatially within cells.
The expansion itself is discretized into N time steps. Expansion occurs in
instantaneous jumps at times tn separated by a constant value of
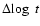 .
During every time interval (
tn,tn+1), the density
.
During every time interval (
tn,tn+1), the density 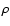 of each cell is held fixed at the value predicted by homologous expansion
at time
of each cell is held fixed at the value predicted by homologous expansion
at time
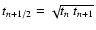 .
.
Here, and throughout the paper, t is the elapsed time since
explosion and is measured in the SN's centre-of-mass rest frame (rf).
With this time-stepping, the calculation is divided into N separate MC experiments,
each of which updates the radiation field throughout the
grid from time tn to tn+1 for
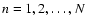 .
.
Given the modest accuracy with which we can currently treat many of the
physical processes in SN ejecta, all terms of O(v/c) in radiative transfer
could be neglected except for Doppler frequency shifts, which
are essential in line transfer. Nevertheless, looking forward to a time
when the relevant cross sections will be known to high precision, terms of O(v/c) are now included.
The basic transfer calculations are carried out in the rf, but
transformations to and from the local co-moving frame (cmf) are convenient
in treating interactions with matter. The motion of an  -packet is thus given by r(t), its position as a function of time t in the rf Cartesian coordinate system with origin at the SN's centre of mass. When the grid attached to the ejecta expands instantaneously at times tn, the coordinates
-packet is thus given by r(t), its position as a function of time t in the rf Cartesian coordinate system with origin at the SN's centre of mass. When the grid attached to the ejecta expands instantaneously at times tn, the coordinates 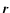 and direction vectors
and direction vectors  of the
of the  -packets remain unchanged.
-packets remain unchanged.
In the context of this discretization of space and time,
energy conservation implies I3N constraints that the solution must satisfy. Thus, for each cell
and every time step, the net emissivity of radiant energy per unit mass must be balanced by
energy created within the mass element after subtracting the increase 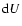 in its
internal energy and the
in its
internal energy and the 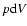 work done by gas pressure.
work done by gas pressure.
With conventional transfer techniques, a solution satisfying this
huge number of constraints - perhaps 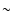 108 - has to be achieved
iteratively - and convergence is never rapid. In contrast,
if the quanta in a MC calculation are indestructible and
indivisible
108 - has to be achieved
iteratively - and convergence is never rapid. In contrast,
if the quanta in a MC calculation are indestructible and
indivisible  -packets, local
energy conservation is automatically and rigorously obeyed, even if physical
variables have not converged to their final values (Lucy 1999a).
-packets, local
energy conservation is automatically and rigorously obeyed, even if physical
variables have not converged to their final values (Lucy 1999a).
To a good approximation, energy conservation can be simplified to
the condition of thermal equilibrium
by neglecting the gas terms
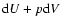 (Arnett 1980;
Pinto & Eastman 2000a).
With this simplification, the net emissivity for UVOIR radiation in the
cmf is equal to the rate of energy deposition by
(Arnett 1980;
Pinto & Eastman 2000a).
With this simplification, the net emissivity for UVOIR radiation in the
cmf is equal to the rate of energy deposition by  -rays.
-rays.
Thermal equilibrium is rigorously obeyed by the MC calculation because the effective cmf emissivity
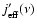 implied by using
indivisible
implied by using
indivisible  -packets is subject to the integral constraint
-packets is subject to the integral constraint
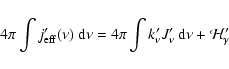 |
(1) |
where 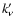 is the cmf absorption coefficient per unit volume,
is the cmf absorption coefficient per unit volume,
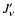 is the cmf mean intensity, and
is the cmf mean intensity, and
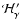 is the
cmf
is the
cmf  -ray energy deposition rate per unit volume.
In contrast, when the RTE is solved conventionally, the cmf
emissivity
-ray energy deposition rate per unit volume.
In contrast, when the RTE is solved conventionally, the cmf
emissivity 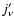 is given by the fundamental NLTE formulae relating the emission of photons
by bound-bound (b-b) and free-bound (f-b) transitions to the level
populations and the electron temperature. Equation (1) is then only satisfied asymptotically as the iterative procedure converges.
is given by the fundamental NLTE formulae relating the emission of photons
by bound-bound (b-b) and free-bound (f-b) transitions to the level
populations and the electron temperature. Equation (1) is then only satisfied asymptotically as the iterative procedure converges.
Note that, in contrast to 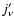 derived from first
priniples, the MC emissivity
derived from first
priniples, the MC emissivity
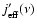 is not defined by mathematical formulae. Rather it is defined operationally by the rules governing the
re-emission of absorbed
is not defined by mathematical formulae. Rather it is defined operationally by the rules governing the
re-emission of absorbed  -packets (Papers I, II).
-packets (Papers I, II).
In addition to the constraints demanded by thermal equilibrium,
an even larger number of constraints are required by statistical equilibrium.
During each time step and for each cell, the number
of excitations of an atomic level must balance the number of de-excitations.
With accurate models for the atoms in the multi-species plasma,
the total number of levels might be 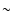 103. This is therefore the
number of constraints per cell per time step implied by statistical
equilibrium. Combining this with the earlier estimate of I3N, we see
that
103. This is therefore the
number of constraints per cell per time step implied by statistical
equilibrium. Combining this with the earlier estimate of I3N, we see
that 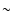 1011 constraints must be satisfied in the course of computing
NLTE light curves and spectra of a 3-D SN.
1011 constraints must be satisfied in the course of computing
NLTE light curves and spectra of a 3-D SN.
Indivisible  -packets allow the
constraint of statistical equilibrium to be
incorporated automatically and rigorously,
even when excitation and de-excitation rates computed from basic formulae
do not balance. This is achieved with the macro-atom formalism (Paper I),
according to which the rate of de-excitation of an excited state is not
determined by its level population but by the rates at which radiative
and collisional processes from all other levels populate the level in question, either
directly or through the internal transitions of the macro-atom.
-packets allow the
constraint of statistical equilibrium to be
incorporated automatically and rigorously,
even when excitation and de-excitation rates computed from basic formulae
do not balance. This is achieved with the macro-atom formalism (Paper I),
according to which the rate of de-excitation of an excited state is not
determined by its level population but by the rates at which radiative
and collisional processes from all other levels populate the level in question, either
directly or through the internal transitions of the macro-atom.
If the radiation field is computed from the RTE, errors in
level populations, such as those present prior to
convergence, result in the non-physical creation or
destruction of radiant energy. This problem is a consequence of the generality
of the RTE equation with the NLTE emissivity 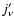 .
Because of this generality, the NLTE RTE could be used to follow the time-dependent relaxation to
statistical equilibrium. In contrast, with the macro-atom formalism,
spurious sources or sinks of radiant energy are
eliminated. This is achieved by effectively solving
a less general transfer
equation, namely one that incorporates the constraint of statistical
equilibrium and one, therefore, that cannot be used for a relaxation
calculation.
.
Because of this generality, the NLTE RTE could be used to follow the time-dependent relaxation to
statistical equilibrium. In contrast, with the macro-atom formalism,
spurious sources or sinks of radiant energy are
eliminated. This is achieved by effectively solving
a less general transfer
equation, namely one that incorporates the constraint of statistical
equilibrium and one, therefore, that cannot be used for a relaxation
calculation.
A consequence of computing de-excitation rates with the macro-atom
machinery is that these rates and the corresponding emissivity
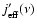 are
insensitive to errors in the populations of the emitting
levels (Paper I, Sect. 6). In contrast, with the RTE,
errors in level populations translate directly into errors in
are
insensitive to errors in the populations of the emitting
levels (Paper I, Sect. 6). In contrast, with the RTE,
errors in level populations translate directly into errors in 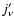 and therefore in the derived radiation field. Evidently, the
macro-atom approach is more tolerant of departures from the NLTE solution
than is the conventional approach.
and therefore in the derived radiation field. Evidently, the
macro-atom approach is more tolerant of departures from the NLTE solution
than is the conventional approach.
As thus far developed, the macro-atom approach imposes the
constraint of thermal equilibrium simultaneously with that of statistical
equilibrium. Thus when a k-packet is created (Paper II, Sect. 4.3.1),
it is instantaneously eliminated (Paper II, Sect. 4.3.2). Thus, there is
no net energy transfer to or from the thermal pool. Moreover, this holds
even if the electron temperature does not imply thermal equilibrium.
Note also that if a k-packet is created by the de-activation of a
macro-atom of one atomic species, it may be eliminated by the activation of
a macro-atom of another species.
For SNe ejecta at late times, the assumptions of ionization and
thermal equilibrium break down (Fransson & Kozma 1993). But this does not
preclude the use of indivisible  -packets, since these are
fundamentally a means of tracking energy. Departures from equilibrium can be
modelled by allowing for the
finite life time of a non-radiative
-packets, since these are
fundamentally a means of tracking energy. Departures from equilibrium can be
modelled by allowing for the
finite life time of a non-radiative  -packet before it converts back
into an r-packet. Thus a b-f process creates a k-packet or
an i-packet, but neither should be immediately
eliminated if the recombination time is not short compared to the elapsed
time t. Moreover, while awaiting elimination, the k-packet's energy
declines due to
-packet before it converts back
into an r-packet. Thus a b-f process creates a k-packet or
an i-packet, but neither should be immediately
eliminated if the recombination time is not short compared to the elapsed
time t. Moreover, while awaiting elimination, the k-packet's energy
declines due to
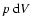 work.
work.
If, during such non-equilibrium phases, statistical equilibrium
remains a good approximation for the excited levels of each ion separately,
then this constraint can be imposed by introducing macro-ions
adapting the procedures of Paper I.
The above remarks strongly suggest that non-equilibrium phases
can be treated with closely similar techniques. Nevertheless, this must
be confirmed with test problems as in Paper I.
The robustness of the emissivities derived with the macro-atom
formalism suggests that useful predictions of
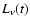 may be obtained
without converging to the exact NLTE solution. Instead,
estimates of the excitation, ionization and temperature in each cell
could be derived using the characteristics of the local MC radiation field
as in Abbott & Lucy (1985) and in the previous diagnostic codes (Sect. 1).
The accuracy of this approach in computing ionization fractions has been
confirmed by Springmann & Puls (1998) for an O-star wind.
may be obtained
without converging to the exact NLTE solution. Instead,
estimates of the excitation, ionization and temperature in each cell
could be derived using the characteristics of the local MC radiation field
as in Abbott & Lucy (1985) and in the previous diagnostic codes (Sect. 1).
The accuracy of this approach in computing ionization fractions has been
confirmed by Springmann & Puls (1998) for an O-star wind.
Nevertheless, for definitive results, the NLTE solution
must be obtained. Fortunately, the use of indivisible  -packets
and the macro-atom formalism facilitate this task. Because the thermal and
statistical equilibrium constraints are directly incorporated into the
MC calculation,
convergence to the NLTE solution can be achieved with geometry-independent
-packets
and the macro-atom formalism facilitate this task. Because the thermal and
statistical equilibrium constraints are directly incorporated into the
MC calculation,
convergence to the NLTE solution can be achieved with geometry-independent
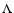 -iterations (Lucy 1999a; Paper II). Thus, by simply repeating the
process of bringing matter into thermal and statistical equilibrium with
the MC radiation field and then recomputing the latter, the solution
converges to the required equilibria. Moreover, convergence is rapid.
-iterations (Lucy 1999a; Paper II). Thus, by simply repeating the
process of bringing matter into thermal and statistical equilibrium with
the MC radiation field and then recomputing the latter, the solution
converges to the required equilibria. Moreover, convergence is rapid.
With regard to thermal equilibrium, this success with
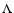 -iterations
was initially demonstrated for a 1-D problem (Lucy 1999a). Recently,
the geometric independence of the technique has been demonstrated with
its successful application to demanding 3-D problems (Harries et al. 2004;
Kurosawa et al. 2004). With regard to thermal and statistical
equilibrium, experience is
thus far limited to a simple 1-D problem (Paper II).
-iterations
was initially demonstrated for a 1-D problem (Lucy 1999a). Recently,
the geometric independence of the technique has been demonstrated with
its successful application to demanding 3-D problems (Harries et al. 2004;
Kurosawa et al. 2004). With regard to thermal and statistical
equilibrium, experience is
thus far limited to a simple 1-D problem (Paper II).
A NLTE calculation requires the radiative rates of excitation,
ionization and heating. With the RTE, these are obtained by
numerical integration. But computing these quantities in
a MC simulation is not so straightforward. The obvious
approach is simply to count the relevant events - e.g,
photoionizations - in each cell in time 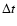 ,
thereby deriving
the rate empirically. This is akin to a physics experiment in which
detectors are distributed throughout an apparatus to record
events. But, though appealing, this
fails to make full use of the MC radiation field.
For example, even if no photoionizations occur in a cell, a non-zero
ionization rate must surely be derivable if it was traversed by
r-packets containing ionizing photons.
,
thereby deriving
the rate empirically. This is akin to a physics experiment in which
detectors are distributed throughout an apparatus to record
events. But, though appealing, this
fails to make full use of the MC radiation field.
For example, even if no photoionizations occur in a cell, a non-zero
ionization rate must surely be derivable if it was traversed by
r-packets containing ionizing photons.
To derive MC estimators of radiative rates, a summation procedure
based on volume elements is preferred (Lucy 1999) to the more obvious
choice of reference surfaces.
The basic building block from which the required estimators are
derived will now be stated in a more general form than in earlier papers
(Lucy 1999; Paper II).
If, at a given position and time,
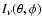 is the
specific intensity at frequency
is the
specific intensity at frequency 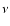 of a pencil of radiation propagating in direction
of a pencil of radiation propagating in direction
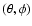 ,
then
,
then
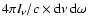 is the
instantaneous energy density of radiation in the frequency interval
is the
instantaneous energy density of radiation in the frequency interval
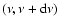 propagating within solid angle
propagating within solid angle
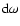 about the
specified direction. This basic formula allows the MC radiation field to be converted into the conventional description in terms of
about the
specified direction. This basic formula allows the MC radiation field to be converted into the conventional description in terms of 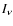 .
.
If, during 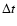 ,
an r-packet of energy
,
an r-packet of energy
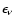 with
with
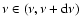 propagates in a cell of volume V, and if for a time
propagates in a cell of volume V, and if for a time
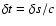 its trajectory
is in the solid angle element
its trajectory
is in the solid angle element
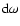 ,
then
,
then
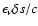 is the packet's contribution to the cell's time-integrated radiant energy
in
is the packet's contribution to the cell's time-integrated radiant energy
in
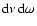 .
Accordingly, the volume- and time-averaged
estimator of the specific intensity is given by
.
Accordingly, the volume- and time-averaged
estimator of the specific intensity is given by
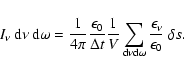 |
(2) |
Here
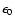 is the reference value for the energy of the
is the reference value for the energy of the  -packets (Sect. 3.2).
-packets (Sect. 3.2).
Equation (2), when multiplied by the appropriate weight functions
and integrated over 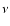 and
and 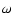 ,
yields MC estimators for
any required property of the radiation field. Estimators of this type
were used initially to compute integrated mean intensities and
absorption rates in a 1-D non-grey atmosphere in LTE (Lucy 1999a). Similar
applications to dusty circumstellar envelopes
have been reported by Wolf (2003) and by Niccolini et al. (2003).
Estimators for the radiative rates
needed for NLTE calculations can also be derived (Paper II).
,
yields MC estimators for
any required property of the radiation field. Estimators of this type
were used initially to compute integrated mean intensities and
absorption rates in a 1-D non-grey atmosphere in LTE (Lucy 1999a). Similar
applications to dusty circumstellar envelopes
have been reported by Wolf (2003) and by Niccolini et al. (2003).
Estimators for the radiative rates
needed for NLTE calculations can also be derived (Paper II).
The class of MC estimators derived from Eq. (2) can be described as
optimum and non-parametric. Optimum because they use all the MC information and non-parametric because no assumption is made about the radiation field. These
estimators are appropriate when the simulation is large enough that
in each 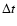 every cell is traversed by many
every cell is traversed by many  -packets.
If not, a functional form can be assumed for
-packets.
If not, a functional form can be assumed for 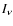 or
or 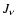 - e.g.,
a dilute black body - and its parameters estimated from the limited number
of trajectories in V. This functional form can then be multiplied by the
appropriate weight functions to derive an estimate of the required quantity
by numerical integration.
This second procedure dampens the effects of sampling errors but,
insofar as the functional form is inexact, yields biased
estimators - i.e., ones that do not converge to their exact values as
- e.g.,
a dilute black body - and its parameters estimated from the limited number
of trajectories in V. This functional form can then be multiplied by the
appropriate weight functions to derive an estimate of the required quantity
by numerical integration.
This second procedure dampens the effects of sampling errors but,
insofar as the functional form is inexact, yields biased
estimators - i.e., ones that do not converge to their exact values as
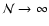 ,
where
,
where 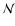 is the number of packets in
the simulation.
is the number of packets in
the simulation.
An application where the extra generality provided by Eq. (2)
is essential is in constructing an estimator for
the source function in a medium with non-isotropic scattering.
The emergent rf spectrum for a MC simulation can be derived simply by
counting escaping r-packets into frequency bins, with light travel-time taken into
account as in Sect. 4.2. But even in the spherical case,
large 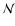 is then required to keep sampling errors small enough
to allow a useful comparison with observed spectra. The solution
is to extract the source function from the simulation and
then calculate the emergent flux from the formal integral (Lucy 1999b).
In a particular 1-D case, the errors in the resulting spectrum correspond to
those of a binned spectrum from a simulation with
is then required to keep sampling errors small enough
to allow a useful comparison with observed spectra. The solution
is to extract the source function from the simulation and
then calculate the emergent flux from the formal integral (Lucy 1999b).
In a particular 1-D case, the errors in the resulting spectrum correspond to
those of a binned spectrum from a simulation with 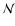 increased by
a factor of
increased by
a factor of  320. For a 3-D SN, where spectra for multiple
lines-of-sight must be computed, the binning option is almost useless,
and the already large gain
factor with the formal integral will be vastly increased.
320. For a 3-D SN, where spectra for multiple
lines-of-sight must be computed, the binning option is almost useless,
and the already large gain
factor with the formal integral will be vastly increased.
In a previous paper (Paper II) on the NLTE transfer of UVOIR radiation in a
SN envelope, the  -packets were all created at the lower boundary, thus
implicitly representing the outward diffusion of the energy released by
radioactive decays in the deeper interior.
But with the computational domain now being the entire ejecta,
the creation and transport of
-packets were all created at the lower boundary, thus
implicitly representing the outward diffusion of the energy released by
radioactive decays in the deeper interior.
But with the computational domain now being the entire ejecta,
the creation and transport of  -rays must be treated explicitly. In
this section, therefore, the concept of indivisible
-rays must be treated explicitly. In
this section, therefore, the concept of indivisible  -packets
is extended to
cover this aspect of the general spectral synthesis problem for SNe.
-packets
is extended to
cover this aspect of the general spectral synthesis problem for SNe.
In a very recent paper, Milne et al. (2004) have compared results
with various  -ray transport codes and reviewed the physical processes
that must be treated. Their emphasis is on the prediction of
-ray transport codes and reviewed the physical processes
that must be treated. Their emphasis is on the prediction of  -ray
spectra rather on the powering of optical emission.
-ray
spectra rather on the powering of optical emission.
The radioactive decays
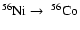 and
and
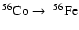 each occur with the emission of
a spectrum of
each occur with the emission of
a spectrum of  -ray lines - see Table 1 in Ambwani & Sutherland (1988). Gamma-rays
of energy El are emitted with probability
-ray lines - see Table 1 in Ambwani & Sutherland (1988). Gamma-rays
of energy El are emitted with probability
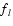 when a parent nucleus decays. The total energy emitted per decay is
therefore
when a parent nucleus decays. The total energy emitted per decay is
therefore
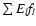 ,
giving
,
giving
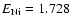 and
and
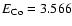 MeV for the
MeV for the
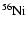 and
and
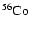 nuclei, respectively.
The e-folding times for these decays are
nuclei, respectively.
The e-folding times for these decays are
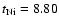 and
and
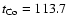 days.
days.
The total  -ray energy emitted by the decay sequence
-ray energy emitted by the decay sequence
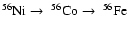 in the limit
in the limit
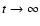 is
is
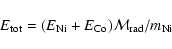 |
(3) |
where
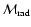 is the initial mass of
is the initial mass of
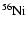 ,
and
,
and
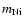 is the mass of the
is the mass of the
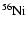 nucleus.
nucleus.
The initial mass of radioactive matter
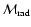 is quantized into
is quantized into 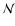 pellets, where
pellets, where
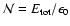 .
These pellets have the
following property: they emit a single
.
These pellets have the
following property: they emit a single
 -packet with cmf energy
-packet with cmf energy
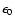 and containing
and containing  -rays
whose cmf photon energy
-rays
whose cmf photon energy
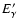 corresponds to
one of the lines emitted in the decay sequence
corresponds to
one of the lines emitted in the decay sequence
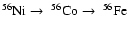 .
Following this
event, a pellet is permanently inert.
.
Following this
event, a pellet is permanently inert.
As
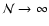 ,
this model must yield
the correct time-dependent
,
this model must yield
the correct time-dependent  -ray line emissivities.
To achieve this, we first identify two kinds of pellet: a fraction
-ray line emissivities.
To achieve this, we first identify two kinds of pellet: a fraction
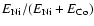 are Ni pellets that collectively emit the
are Ni pellets that collectively emit the
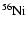 spectrum, while the remainder are Co pellets, and they account for the
spectrum, while the remainder are Co pellets, and they account for the
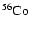 spectrum.
spectrum.
If a pellet is designated as a Ni pellet, its decay time is
randomly chosen as
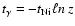 ;
and the emitted
;
and the emitted  -packet is assigned to line lfrom the
-packet is assigned to line lfrom the
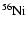 spectrum with probability
spectrum with probability
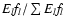 .
On the other hand, a Co pellet's decay time is
.
On the other hand, a Co pellet's decay time is
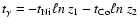 ,
where z1 and z2 are independent random numbers from (0,1). Two terms are
required for the Co pellets since each
,
where z1 and z2 are independent random numbers from (0,1). Two terms are
required for the Co pellets since each
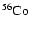 nucleus is created in the
decay of
nucleus is created in the
decay of
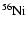 nucleus. Having thus selected
nucleus. Having thus selected
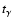 for a Co pellet,
we select a line from the
for a Co pellet,
we select a line from the
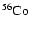 spectrum as with
spectrum as with
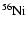 .
.
When a pellet decays, the emitted  -packet is assigned
a cmf direction vector
-packet is assigned
a cmf direction vector  ' in accordance with
isotropic emission. Thus
' in accordance with
isotropic emission. Thus

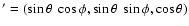 ,
with
,
with
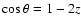 and
and
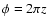 .
The
corresponding rf vector
.
The
corresponding rf vector  is obtained with
the exact aberration formula - e.g., Castor (1972, Eq. (5)). The
is obtained with
the exact aberration formula - e.g., Castor (1972, Eq. (5)). The
 -packet's initial rf energy is then
-packet's initial rf energy is then
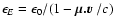 ,
where the local rf velocity
,
where the local rf velocity
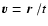 .
.
The positions of the pellets at t1 are obtained by sampling
the distribution of
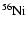 predicted by the explosion model. Their
positions when they decay are then given by the assumption of homologous
expansion.
predicted by the explosion model. Their
positions when they decay are then given by the assumption of homologous
expansion.
The  -packets emitted in the
interval
(tn,tn+1) are added to the
-packets emitted in the
interval
(tn,tn+1) are added to the  - and r-packets
still propagating in the ejecta at time tn to form a list of
active
- and r-packets
still propagating in the ejecta at time tn to form a list of
active  -packets
whose trajectories are up-dated during this time step.
-packets
whose trajectories are up-dated during this time step.
In propagating through the ejecta,  -rays
create cascades of non-thermal electrons in multiple Compton
scatterings off free and bound electrons as well as being absorbed in
photoionizations. This redistribution of the energy of the emitted
-rays
create cascades of non-thermal electrons in multiple Compton
scatterings off free and bound electrons as well as being absorbed in
photoionizations. This redistribution of the energy of the emitted
 -ray into numerous channels over a substantial volume can nevertheless
be modelled with indivisible
-ray into numerous channels over a substantial volume can nevertheless
be modelled with indivisible  -packets in such a way that the correct
physics emerges as
-packets in such a way that the correct
physics emerges as
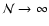 .
.
As a  -packet propagates, it undergoes events, both
numerical and physical. The numerical events are: escaping from the grid,
reaching the surface of a cell, or coming to the end of the current time step
at
t = tn+1. The currently-included physical events are Compton scattering and
photoelectric absorption.
-packet propagates, it undergoes events, both
numerical and physical. The numerical events are: escaping from the grid,
reaching the surface of a cell, or coming to the end of the current time step
at
t = tn+1. The currently-included physical events are Compton scattering and
photoelectric absorption.
In describing how a  -packet's trajectory is computed, it
suffices to explain how to find the next event along the trajectory of one
packet (cf. Paper II, Sect. 5).
-packet's trajectory is computed, it
suffices to explain how to find the next event along the trajectory of one
packet (cf. Paper II, Sect. 5).
Given the rf position r and direction vector
 following an event,
the next event is identified by computing the distances along
the trajectory to all possible events and then selecting the event
reached first. Since calculating distances to the numerical events is trivial, we here treat only the physical events.
following an event,
the next event is identified by computing the distances along
the trajectory to all possible events and then selecting the event
reached first. Since calculating distances to the numerical events is trivial, we here treat only the physical events.
If E is the rf energy of photons in a  -packet,
the cmf energy is
-packet,
the cmf energy is
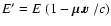 .
Accordingly, in the cmf the
.
Accordingly, in the cmf the  -packet sees Compton scattering coefficient
-packet sees Compton scattering coefficient
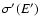 and absorption coefficient k'(E').
But in the rf these transform to
and absorption coefficient k'(E').
But in the rf these transform to
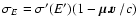 and
and
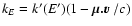 .
Thus, when the radiative transport is carried out in the rf, the
absorption, scattering (and emission) coefficients are direction-dependent - e.g., Castor (1972, Eqs. (2) and (3)).
.
Thus, when the radiative transport is carried out in the rf, the
absorption, scattering (and emission) coefficients are direction-dependent - e.g., Castor (1972, Eqs. (2) and (3)).
With these rf coefficients determined, we select the distance 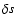 along the trajectory at which a physical event will occur from
the standard MC formula
along the trajectory at which a physical event will occur from
the standard MC formula
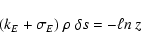 |
(4) |
and this event happens if 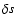 is smaller than the distances to the
numerical events. Morever, when a physical event happens, it is a Compton scattering if
is smaller than the distances to the
numerical events. Morever, when a physical event happens, it is a Compton scattering if
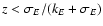 and a photoelectic absorption if not.
and a photoelectic absorption if not.
If 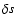 is the distance to the selected event, the updated
space-time rf coordinates are r
is the distance to the selected event, the updated
space-time rf coordinates are r
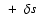
 and
and
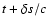 .
.
Starting with numerical events, we now describe subsequent actions.
If the  -packet exits the grid, it escapes to
-packet exits the grid, it escapes to 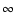 ,
and attention then
turns to the next
,
and attention then
turns to the next  -packet in the list of those active during the
current time step.
But if the
-packet in the list of those active during the
current time step.
But if the  -packet exits only the current cell and not the grid,
then it enters the
neighbouring cell and the search for the next event proceeds as above.
Finally, if the event is the end of the time step at tn+1,
computation of the trajectory is suspended, and the
-packet exits only the current cell and not the grid,
then it enters the
neighbouring cell and the search for the next event proceeds as above.
Finally, if the event is the end of the time step at tn+1,
computation of the trajectory is suspended, and the  -packet's current
rf data string r, t,
-packet's current
rf data string r, t,  ,
,
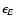 ,
Eis stored to await the next time step.
,
Eis stored to await the next time step.
With regard to physical events, the following actions are taken:
in the event of a photoelectric absorption, the  -packet's
trajectory as a
-packet's
trajectory as a  -packet terminates. It now becomes a k- or
i-packet (cf. Sect. 2.7) with the same cmf energy
-packet terminates. It now becomes a k- or
i-packet (cf. Sect. 2.7) with the same cmf energy
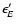 as the absorbed
as the absorbed
 -packet. Then, since energy storage in the gas is neglected (Sect. 2.4), this
k- or i-packet converts immediately to an r-packet. In a general code,
the frequency
-packet. Then, since energy storage in the gas is neglected (Sect. 2.4), this
k- or i-packet converts immediately to an r-packet. In a general code,
the frequency 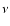 of photons in this r-packet are determined by
continuum emission (f-b or f-f) or line emission following collisional
excitation, and these are treatable with the macro-atom formalism
(Papers I and II). But here, with grey transport for UVOIR radiation, the
emitted r-packet
can be regarded as bolometric. Its cmf energy is
of photons in this r-packet are determined by
continuum emission (f-b or f-f) or line emission following collisional
excitation, and these are treatable with the macro-atom formalism
(Papers I and II). But here, with grey transport for UVOIR radiation, the
emitted r-packet
can be regarded as bolometric. Its cmf energy is
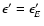 and its
cmf direction vector
and its
cmf direction vector  ' is selected according to
isotropic emission. The rf direction vector
' is selected according to
isotropic emission. The rf direction vector  then follows from the
aberration formula, and the rf energy is
then follows from the
aberration formula, and the rf energy is
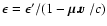 .
These
quantities together with r and t comprise the data string required to initiate the r-packet's trajectory in the 3-D code for UVOIR radiation (Sect. 4).
.
These
quantities together with r and t comprise the data string required to initiate the r-packet's trajectory in the 3-D code for UVOIR radiation (Sect. 4).
In the event of a Compton scattering, we first
find the scattering angle 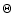 by randomly selecting
by randomly selecting
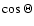 from a look-up table of the percentiles of the
from a look-up table of the percentiles of the
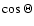 probability distribution as functions of the incident
probability distribution as functions of the incident
 -ray energy. A
-ray energy. A  -ray scattered through angle
-ray scattered through angle 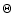 has its incident
energy
has its incident
energy
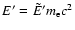 reduced to
reduced to
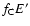 ,
where
,
where
![$f_{\rm C} = 1/[1+ \tilde{E}' ~ (1-\cos \Theta)]$](/articles/aa/full/2005/01/aa1656/img99.gif) ,
with the remaining energy transferred to a Compton electon. Thus the
energy is divided in the ratio
,
with the remaining energy transferred to a Compton electon. Thus the
energy is divided in the ratio
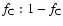 .
Accordingly, since
.
Accordingly, since
 -packets are indivisible, the
-packets are indivisible, the  -packet continues as a
-packet continues as a
 -packet if
-packet if
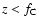 .
If not, it becomes an
.
If not, it becomes an 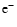 packet.
packet.
If the packet continues as a  -packet, its cmf energy
remains
-packet, its cmf energy
remains
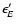 but it now contains
but it now contains  -rays of cmf energy
-rays of cmf energy
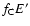 .
To derive the rf values of these quantities, we must select a new direction vector. In the cmf, the incident
.
To derive the rf values of these quantities, we must select a new direction vector. In the cmf, the incident  '1 and emergent
'1 and emergent  ' direction vectors are such that
' direction vectors are such that  '1
'1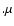 '
'
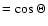 .
The combination of this with azimuthal angle
.
The combination of this with azimuthal angle
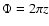 ,
where azimuth is defined with respect to polar direction
,
where azimuth is defined with respect to polar direction  '1, determines
'1, determines  '.
The aberration formula then gives
'.
The aberration formula then gives  and so, in the rf,
the emergent
and so, in the rf,
the emergent  -packet has energy
-packet has energy
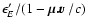 and contains
and contains
 -rays with photon energies
-rays with photon energies
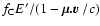 .
The next event for
this
.
The next event for
this  -packet is now searched for as described in Sect. 3.3.1.
-packet is now searched for as described in Sect. 3.3.1.
On the other hand, if the  -packet converts to an
-packet converts to an 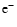 packet,
we assume in situ degradation into a bolometric r-packet with cmf energy
packet,
we assume in situ degradation into a bolometric r-packet with cmf energy
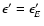 .
The rf data string needed to initiate its subsequent trajectory is now computed as for an r-packet created by photoelectric absorption - see
above.
.
The rf data string needed to initiate its subsequent trajectory is now computed as for an r-packet created by photoelectric absorption - see
above.
The above treatment is a straightforward extension of the indivisible  -packet idea to
-packet idea to
 -ray transport. Nevertheless, it should still be tested against the
traditional MC treatment in which the MC quanta are photons
(e.g. Colgate et al. 1980; Ambwani & Sutherland 1988). Such a test
has been carried out by computing
-ray transport. Nevertheless, it should still be tested against the
traditional MC treatment in which the MC quanta are photons
(e.g. Colgate et al. 1980; Ambwani & Sutherland 1988). Such a test
has been carried out by computing  -ray
deposition in a spherical SN. For simplicity, effects of O(v/c) are
neglected and photoelectric absorption acts only as a guillotine when E drops below 100 keV.
-ray
deposition in a spherical SN. For simplicity, effects of O(v/c) are
neglected and photoelectric absorption acts only as a guillotine when E drops below 100 keV.
In one calculation, the pellets emit a single  -packet as described above. In the comparison
calculation, each pellet emits multiple photon packets with photon energies El and weights
-packet as described above. In the comparison
calculation, each pellet emits multiple photon packets with photon energies El and weights
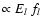 ,
thus representing the appropriate
,
thus representing the appropriate  -ray line
spectrum. Each such packet then undergoes several Compton scatterings,
at each of which the energy of the Compton electron is deposited in situ.
This continues until a photoelectric absorption deposits the remaining
energy. The two deposition profiles converge to one another as
-ray line
spectrum. Each such packet then undergoes several Compton scatterings,
at each of which the energy of the Compton electron is deposited in situ.
This continues until a photoelectric absorption deposits the remaining
energy. The two deposition profiles converge to one another as
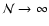 .
.
In the present code, an explicit determination of
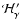 ,
the heating rate due to the deposition of
,
the heating rate due to the deposition of  -ray energy,
is not required. The assumption of local thermal
equilibrium implies that absorbed
-ray energy,
is not required. The assumption of local thermal
equilibrium implies that absorbed  -packets are immediately
re-emitted as r-packets (Sect. 3.3.2) and their subsequent propagation
is through matter with a temperature-independent grey absorption coefficient.
But in a more general code, the thermal history of the ejecta must be
calculated, and this requires
-packets are immediately
re-emitted as r-packets (Sect. 3.3.2) and their subsequent propagation
is through matter with a temperature-independent grey absorption coefficient.
But in a more general code, the thermal history of the ejecta must be
calculated, and this requires
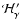 .
In any case, this
quantity is needed here for the solution with moment equations (Sect. 5).
.
In any case, this
quantity is needed here for the solution with moment equations (Sect. 5).
In Sect. 3.3, two deposition processes are considered. First there is
the loss of energy to Compton electrons, which occurs at the rate
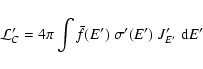 |
(5) |
where
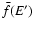 is the expected fraction of E' transferred to
the Compton electron and J'E' is the cmf mean intensity at photon energy E'.
Second, there is the loss in photoionizations, which occurs at the rate
is the expected fraction of E' transferred to
the Compton electron and J'E' is the cmf mean intensity at photon energy E'.
Second, there is the loss in photoionizations, which occurs at the rate
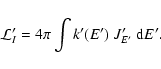 |
(6) |
Estimators for these rates can be derived by applying Eq. (2)
in the cmf. But note that the transport of packets is carried out in the rf.
If 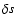 is the distance between consecutive events for a
is the distance between consecutive events for a
 -packet propagating in the rf, then, to O(v/c), in the cmf,
-packet propagating in the rf, then, to O(v/c), in the cmf,
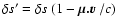 .
Accordingly,
since we also have
.
Accordingly,
since we also have
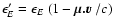 ,
the reqired estimators are
,
the reqired estimators are
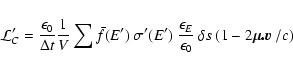 |
(7) |
and
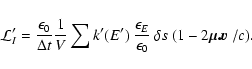 |
(8) |
These summations are over all trajectory segments 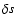 in V. Thus there is no restriction to packets that undergo Compton scatterings (Eq. (7)) or
photoelectric absorptions (Eq. (8)) in V.
Accordingly, the resulting deposition rate
in V. Thus there is no restriction to packets that undergo Compton scatterings (Eq. (7)) or
photoelectric absorptions (Eq. (8)) in V.
Accordingly, the resulting deposition rate
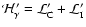 is more accurate than the crude estimate obtained by summing
the cmf energies of
is more accurate than the crude estimate obtained by summing
the cmf energies of  -packets that terminate their trajectories in V.
-packets that terminate their trajectories in V.
A by-product of this 3-D time-dependent treatment of  -ray transport
is the prediction of
-ray transport
is the prediction of  -ray spectra, observations of which have
potential for detecting asymmetries in SN explosions (Höflich 2002; Hungerford et al.
2003). Crude spectra can be obtained simply by binning escaping
-ray spectra, observations of which have
potential for detecting asymmetries in SN explosions (Höflich 2002; Hungerford et al.
2003). Crude spectra can be obtained simply by binning escaping  -packets according to their rf energies E. But for high quality results, especially for the orientation-dependent
spectra of an asymmetric SN, the formal integral should be used (Sect. 2.10).
-packets according to their rf energies E. But for high quality results, especially for the orientation-dependent
spectra of an asymmetric SN, the formal integral should be used (Sect. 2.10).
Additional physical processes can be readily incorporated into this  -packet treatment of
-packet treatment of
 -ray transport.
-ray transport.
Following Ambwani & Sutherland (1988, Table 1), positrons emitted in
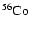 are here assumed to annihilate in situ. But at late times,
the transport of positrons should be followed until they
escape or deposit their rest and kinetic energies in the ejecta. This
requires that we allow the Co pellets to emit
are here assumed to annihilate in situ. But at late times,
the transport of positrons should be followed until they
escape or deposit their rest and kinetic energies in the ejecta. This
requires that we allow the Co pellets to emit 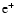 packets instead
of the
packets instead
of the  -packets with E = 0.511 MeV.
-packets with E = 0.511 MeV.
In treating Compton scattering, we assume
that Compton electrons degrade in situ. The basis for this is
the short stopping distance of MeV electrons compared to MeV
 -rays (Colgate et al. 1980).
Nevertheless, we may eventually wish to follow
the motion of the
-rays (Colgate et al. 1980).
Nevertheless, we may eventually wish to follow
the motion of the 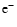 -packets, especially at late epochs.
-packets, especially at late epochs.
In addition to Compton scattering and photoelectric absorption,
a  -ray with
-ray with
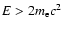 can tranform to an
can tranform to an
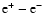 pair as it passes an atomic nucleus - see, e.g., Ambwani & Sutherland (1988) - with each of the pair having kinetic energy (ke)
pair as it passes an atomic nucleus - see, e.g., Ambwani & Sutherland (1988) - with each of the pair having kinetic energy (ke)
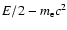 .
In stopping, the
positron releases energy
.
In stopping, the
positron releases energy
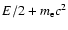 ,
comprising its ke plus the rest energy
,
comprising its ke plus the rest energy
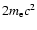 radiated when the positron annihilates with an ambient
electron. In contrast, stopping the electron releases only its ke.
radiated when the positron annihilates with an ambient
electron. In contrast, stopping the electron releases only its ke.
Accordingly, when treated with indivisible  -packets, pair
production converts a
-packets, pair
production converts a  -packet into an e+-packet with
probability 1/2+q or into an
-packet into an e+-packet with
probability 1/2+q or into an 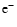 -packet with probability
1/2-q, where
-packet with probability
1/2-q, where
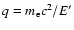 .
In either case, the cmf
energy of the packet is that of the incident
.
In either case, the cmf
energy of the packet is that of the incident  -packet
-packet
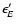 .
If in situ deposition is not assumed, the selected packet's motion is then
followed to escape or deposition. Note that a return to the pair production event
to follow the other member of the pair is not required (cf. Paper I,
Sect. 1).
.
If in situ deposition is not assumed, the selected packet's motion is then
followed to escape or deposition. Note that a return to the pair production event
to follow the other member of the pair is not required (cf. Paper I,
Sect. 1).
If the evolution of the ejecta is followed to late epochs (>1000 days),
then rare but long-lived radioactive isotopes such as
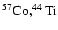 and
and
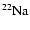 must be included (e.g., Woosley et al.
1989). This just requires additional types of pellet.
must be included (e.g., Woosley et al.
1989). This just requires additional types of pellet.
In a previous paper (Paper II) the NLTE transfer of UVOIR radiation in
a SN envelope of pure H was treated using and extending the macro-atom
formalism (Paper I). Here, given the emphasis on time dependence and 3-D,
we simplify to a grey absorption coefficient.
As with  -packets, the transport of r-packets is carried out in a
sequence of MC simulations for the time steps
-packets, the transport of r-packets is carried out in a
sequence of MC simulations for the time steps
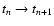 .
Each
of these simulations directly follows the corresponding one for
.
Each
of these simulations directly follows the corresponding one for
 -packets (Sect. 3.3).
-packets (Sect. 3.3).
The r-packets that propagate in the ejecta in the time interval (
tn,tn+1) have several sources. First are those that did not escape during the previous time step. For these,
we have the rf data string (r, t,  ,
,
 ), and so their trajectories can be continued from time tn. Second are those created
during the current time step as
), and so their trajectories can be continued from time tn. Second are those created
during the current time step as  -packets are eliminated.
This occurs either by photoelectric absorption or by the stopping of Compton electrons
(Sect. 3.3.2). In either case, the
-packets are eliminated.
This occurs either by photoelectric absorption or by the stopping of Compton electrons
(Sect. 3.3.2). In either case, the  transport routine provides the
rf data string (r, t,
transport routine provides the
rf data string (r, t,  ,
,
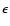 )
needed to initiate their trajectories as r-packets.
)
needed to initiate their trajectories as r-packets.
A third source is specific to the first time step.
Radiant energy emitted by pellets that decay at times prior to t1must be accounted for. An approximate treatment is as follows:
A  -packet emitted at
-packet emitted at
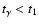 and position r
and position r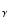 is assumed to have converted to
an r-packet by time t1 but to have diffused negligibly relative to
matter (position coupling) in the time interval (
is assumed to have converted to
an r-packet by time t1 but to have diffused negligibly relative to
matter (position coupling) in the time interval (
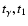 )
so that at t1 its rf position is r
)
so that at t1 its rf position is r
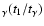 .
This is justified by the short mean
free paths of photons in these early, high-density phases. The rf direction vector at t1 is computed on the assumption of isotropic emission in the cmf.
.
This is justified by the short mean
free paths of photons in these early, high-density phases. The rf direction vector at t1 is computed on the assumption of isotropic emission in the cmf.
The energies of these packets must also be specified.
Although position coupled, they still do work on the expanding
ejecta. An r-packet's energy at t1 is therefore
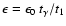 .
.
An additional source of r-packets at t1 is the radiation
generated by shock heating during the explosion.
The explosion model's prediction of this radiation can be discretized into
r-packets of energy
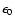 ,
the same quantum of energy as for
the radioactive pellets (Sect. 3.2). However, such r-packets are
neglected in this test code.
,
the same quantum of energy as for
the radioactive pellets (Sect. 3.2). However, such r-packets are
neglected in this test code.
As an r-packet propagates, it undergoes numerical
and physical events. The numerical events are identical to those for
 -packets (Sect. 3.3.1). The physical events are absorptions.
-packets (Sect. 3.3.1). The physical events are absorptions.
In describing how a r-packet's trajectory is computed, it
suffices to explain how to find the next event along the trajectory of one
packet. Given the rf data string (r, t,  ,
,
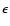 ),
the next event is identified by computing the distances along
the trajectory to all possible events and then selecting the event
reached first. As with
),
the next event is identified by computing the distances along
the trajectory to all possible events and then selecting the event
reached first. As with  -packets, we treat only physical events.
-packets, we treat only physical events.
Because the transport of r-packets is also carried out in the rf,
the anisotropy of the rf absorption coefficient must again be allowed
for, as it was for  -packets in Sect. 3.3.1. If the grey
absorption coefficient per unit volume in the cmf is k', the effective
value in the rf is
-packets in Sect. 3.3.1. If the grey
absorption coefficient per unit volume in the cmf is k', the effective
value in the rf is
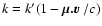 ,
and so the distance
,
and so the distance 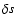 to the absorption event is given by
to the absorption event is given by
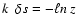 .
This event happens if this is smaller than the distance to any numerical
event. With
.
This event happens if this is smaller than the distance to any numerical
event. With 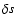 thus determined, the coordinates (r,t) are updated as for
thus determined, the coordinates (r,t) are updated as for  -packets (Sect. 3.3.1).
-packets (Sect. 3.3.1).
For numerical events, the subsequent actions
correspond to those for  -packets (Sect. 3.3.2).
-packets (Sect. 3.3.2).
If the event is an absorption, we assume instantaneous isotropic
re-emission in the cmf. Accordingly, the new rf direction vector  is
calculated as it was for emitted
is
calculated as it was for emitted  -packets in Sect. 3.2.
-packets in Sect. 3.2.
The energy content of the bolometric r-packet must also be updated.
If the incident packet has rf energy
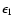 and
direction vector
and
direction vector  1, its cmf energy is
1, its cmf energy is
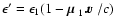 .
Since this is conserved by the absorption-emission event, the updated rf energy is
.
Since this is conserved by the absorption-emission event, the updated rf energy is
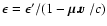 .
Calculation of the post-event data string (r, t,
.
Calculation of the post-event data string (r, t,  ,
,
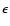 )
is now complete, and the search for the next event can begin.
)
is now complete, and the search for the next event can begin.
Consider an r-packet with post-event data string (r, t,  ,
,
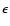 )
that is an escapee from the grid. A distant observer at rest in the rf who detects this packet records its arrival at what he perceives to be a time
)
that is an escapee from the grid. A distant observer at rest in the rf who detects this packet records its arrival at what he perceives to be a time
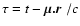 after the explosion. Thus the
pairs
after the explosion. Thus the
pairs
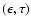 detected by one such observer is the
data set from which he can construct the bolometric light curve of the
3-D SN as seen from his orientation.
detected by one such observer is the
data set from which he can construct the bolometric light curve of the
3-D SN as seen from his orientation.
In this paper, the 3-D code is tested by applying it to a
spherically-symmetric SN. Accordingly, we use all pairs
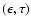 to construct its orientation-averaged bolometric light curve (Sect. 6.3).
to construct its orientation-averaged bolometric light curve (Sect. 6.3).
In order to test the 3-D code described in Sects. 3 and 4, we apply it
in Sect. 6 to a spherically-symmetric SN. This allows the code to be tested
against a solution of the same problem obtained
by numerical integration of the time-dependent RTE.
Castor (1972) has given a general treatment, accurate to O(v/c),
of radiative transfer in spherically-symmetric flows. In particular, he
derives the zeroth and first frequency-integrated moment equations in the cmf. These two equations, applied to a homologously expanding flow with grey absorption, are the basis of the comparison calculation.
If we again neglect the contributions of the gas to energy balance
(Sect. 2.4), the zeroth moment equation is
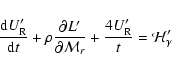 |
(9) |
where the dependent variables are
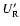 ,
the cmf energy density
of radiation, and L', the cmf luminosity variable. The independent
variables are elapsed time t and the mass coordinate
,
the cmf energy density
of radiation, and L', the cmf luminosity variable. The independent
variables are elapsed time t and the mass coordinate
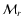 .
Note
that time derivatives in the moment equations are Lagrangian.
.
Note
that time derivatives in the moment equations are Lagrangian.
The first moment equation is
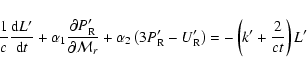 |
(10) |
where
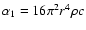 ,
,
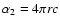 ,
and the third dependent variable
,
and the third dependent variable
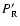 is the cmf radiation pressure.
is the cmf radiation pressure.
To make this system determinate, an approximate formula
relating the three moments must be imposed. Here we adopt Eddington's
approximation,
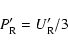 |
(11) |
which is used to eliminate
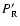 from Eq. (10). This leaves two
partial differential equations (PDEs) in the two variables
from Eq. (10). This leaves two
partial differential equations (PDEs) in the two variables
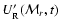 and
and
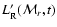 .
.
The PDEs must be solved subject to appropriate boundary conditions.
Clearly, at the SN's centre,
|
<tex2htmlcommentmark>
L'(0,t) = 0
|
(12) |
while, at the surface, Eddington's boundary condition
F(0) = 2 J(0) gives
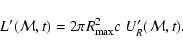 |
(13) |
Here
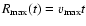 ,
and
,
and 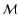 is the total mass of the ejecta.
is the total mass of the ejecta.
In addition, initial conditions are required at t = t1.
As in the MC code (Sect. 4.1.1), we assume that
diffusion of radiation relative to matter is still negligible (Sect. 4.1.1)
at t1, and so
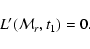 |
(14) |
An initial condition for
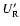 is derived as follows:
For t < t1, negligible relative diffusion of
is derived as follows:
For t < t1, negligible relative diffusion of  -rays implies
in situ deposition, so that
-rays implies
in situ deposition, so that
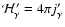 ,
the integrated
,
the integrated  -ray emissivity in the cmf. Accordingly, from Eq. (9),
the required initial condition is given by integrating the ordinary
differential equation (ODE)
-ray emissivity in the cmf. Accordingly, from Eq. (9),
the required initial condition is given by integrating the ordinary
differential equation (ODE)
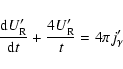 |
(15) |
which can be done analytically.
If
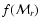 is the mass fraction of
is the mass fraction of
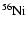 in the mass shell
in the mass shell
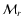 at t = 0, then
at t = 0, then
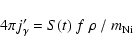 |
(16) |
where S(t), the energy released per
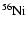 nucleus, is given by
nucleus, is given by
 |
(17) |
Since each term in Eq. (17) has the same form and Eq. (15) is
linear, we consider a single exponential - i.e.,
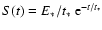 ,
and we note also that homologous
expansion implies that
,
and we note also that homologous
expansion implies that
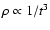 .
Integration of Eq. (15) then gives
.
Integration of Eq. (15) then gives
![\begin{displaymath}%
U'_{\rm R} = E_{*} ~
\left( ~ \frac{t_{*}}{t} - \left[1+ \...
...t] {\rm e}^{-t/t_{*}} \right)
~ f ~ \rho ~ / ~ m_{{\rm Ni}}.
\end{displaymath}](/articles/aa/full/2005/01/aa1656/img158.gif) |
(18) |
This solution can be applied to each term in Eq. (17) to construct the
complete solution. But with
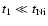 ,
the first (
,
the first (
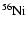 ) term suffices.
) term suffices.
Note that, in deriving Eq. (18), we assumed
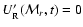 at t = 0. This is consistent with the
neglect of shock heating in the MC code (Sect. 4.1.1).
at t = 0. This is consistent with the
neglect of shock heating in the MC code (Sect. 4.1.1).
Equations (9) and (10) are solved in the same way as are the equations of stellar
evolution when the 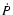 and
and 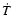 terms are included in
the energy equation (e.g., Schwarzschild 1958, p. 100).
Thus, the time derivatives of
terms are included in
the energy equation (e.g., Schwarzschild 1958, p. 100).
Thus, the time derivatives of
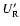 and L' are replaced by backward difference formulae. Then, since
the solution at earlier time steps is known, the PDE problem is
effectively simplified to a two-point boundary value problem for
ODEs. When the space derivatives in the ODEs
are approximated by difference formulae, the resulting algebraic system can
be solved with an
elimination procedure (Henyey method). Here, a slight generalization
of the procedure described
by Richtmyer (1957, pp. 101-104) has been followed.
and L' are replaced by backward difference formulae. Then, since
the solution at earlier time steps is known, the PDE problem is
effectively simplified to a two-point boundary value problem for
ODEs. When the space derivatives in the ODEs
are approximated by difference formulae, the resulting algebraic system can
be solved with an
elimination procedure (Henyey method). Here, a slight generalization
of the procedure described
by Richtmyer (1957, pp. 101-104) has been followed.
In stellar evolution codes, it is still current practice
(A. Weiss, private communication) to approximate the time derivative of a
variable Q at time tn with the formula
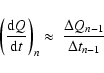 |
(19) |
where 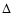 denotes the forward difference operator, so that
denotes the forward difference operator, so that
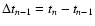 .
This formula is not
centred and thus has error
.
This formula is not
centred and thus has error
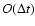 .
But higher accuracy can be achieved by using more than one
previous model - e.g, Richtmyer (1957, p. 94, item 9).
If the two previous models at tn-1 and tn-2 are used,
the appropriate difference approximation is obtained by fitting a
parobola and then evaluating its derivative at tn. The resulting
formula is
.
But higher accuracy can be achieved by using more than one
previous model - e.g, Richtmyer (1957, p. 94, item 9).
If the two previous models at tn-1 and tn-2 are used,
the appropriate difference approximation is obtained by fitting a
parobola and then evaluating its derivative at tn. The resulting
formula is
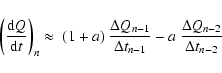 |
(20) |
where
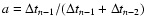 .
Thus, with
constant time steps, a = 1/2. The gain in accuracy is investigated in Sect. 6.2.
.
Thus, with
constant time steps, a = 1/2. The gain in accuracy is investigated in Sect. 6.2.
In starting the integration of the PDEs, the theory of Sect. 5.4
is used to provide the previous solutions required by
Eqs. (19) and (20) as well as initial estimates of
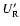 and L'for the first Henyey iteration.
and L'for the first Henyey iteration.
The solution of the PDEs yields the two functions
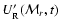 and
and
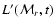 .
Thus we directly get the bolometric
light curve L'(t) seen by a cmf observer at
.
Thus we directly get the bolometric
light curve L'(t) seen by a cmf observer at
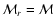 ,
the surface of the SN. But the quantity of interest is the
light curve seen by a distant observer at rest in the rf. This can be
calculated using
,
the surface of the SN. But the quantity of interest is the
light curve seen by a distant observer at rest in the rf. This can be
calculated using  -packets as follows:
-packets as follows:
In a small interval 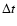 at t, the surface emits Nr-packets at random times tn in
at t, the surface emits Nr-packets at random times tn in 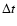 .
These all have cmf energy
.
These all have cmf energy
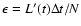 ,
and their direction cosines are
,
and their direction cosines are
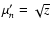 ,
corresponding to zero limb-darkening, an assumption
consistent with Eddington's approximations. Their direction cosines
,
corresponding to zero limb-darkening, an assumption
consistent with Eddington's approximations. Their direction cosines 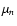 in the rf are given by the aberration formula, and their rf energies are then
in the rf are given by the aberration formula, and their rf energies are then
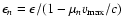 .
The distant observer
perceives the nth packet as having been emitted at elapsed time
.
The distant observer
perceives the nth packet as having been emitted at elapsed time
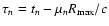 ,
and so the N pairs
(
,
and so the N pairs
(
 )
represent the contribution of the interval
)
represent the contribution of the interval  to the bolometric light curve seen by this observer. Summing over all intervals
to the bolometric light curve seen by this observer. Summing over all intervals  then gives the complete light curve (cf. Sect. 4.2).
then gives the complete light curve (cf. Sect. 4.2).
After first investigating the accuracy of bolometric light curves for
spherical SN obtained
with the cmf moment equations, this section uses such a light
curve to check the 3-D MC code described in Sects. 3 and 4.
The model SN is closely similar to that used by Pinto & Eastman (2000) to
investigate the parameter sensitivity of type Ia light curves. The ejecta has
uniform density and its basic parameters
are:
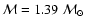 ,
,
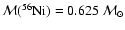 ,
and
,
and
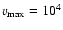 km s-1.
The
km s-1.
The
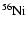 is assumed to be stongly concentrated in the central core. Thus,
is assumed to be stongly concentrated in the central core. Thus,
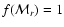 for
for
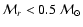 and then drops linearly
to zero at
and then drops linearly
to zero at
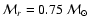 .
.
The grey absorption coefficient for UVOIR radiation is
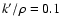 cm2 g-1, and the photoelectric absorption
coefficient k'E for
cm2 g-1, and the photoelectric absorption
coefficient k'E for  -rays is derived from Eq. (3)
of Ambwani & Sutherland (1988) with nuclear charge Z = 14.
-rays is derived from Eq. (3)
of Ambwani & Sutherland (1988) with nuclear charge Z = 14.
Numerical solutions of Castor's equations have been obtained in order
to test the MC code against an RTE treatment accurate to O(v/c). But
the neglect of higher order terms in v/c is not the only source of error
in the RTE solutions.
Larger errors may arise due to the closure
approximation (Sect. 5.2) and the difference approximation of time
derivatives (Sect. 5.5).
The moment equations are solved on a uniformly-spaced grid
with 400 grid points, the innermost at
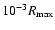 .
The energy deposition rate
.
The energy deposition rate
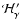 in Eq. (9) is derived with a 1-D version of the MC code
described in Sect. 3 using the estimators given in Eqs. (7) and (8).
The number of radioactive pellets is
in Eq. (9) is derived with a 1-D version of the MC code
described in Sect. 3 using the estimators given in Eqs. (7) and (8).
The number of radioactive pellets is
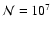 .
.
To investigate sensitivity to the approximation of time derivatives,
two sequences of light curves are computed,
one using Eq. (19) to evaluate
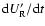 and
and
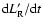 ,
the other using Eq. (20). Along each sequence,
,
the other using Eq. (20). Along each sequence,
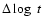 varies, thereby determining the rate of convergence as
varies, thereby determining the rate of convergence as
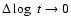 .
For each light curve,
.
For each light curve,
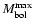 ,
the peak rf bolometric
magnitude, is obtained by parabolic fitting.
,
the peak rf bolometric
magnitude, is obtained by parabolic fitting.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1656fig1.ps}\end{figure}](/articles/aa/full/2005/01/aa1656/Timg191.gif) |
Figure 1:
Bolometric magnitude at maximum as function of time step
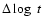 .
Time derivatives are approximated with Eq. (19)
( open circles) or Eq. (20) ( filled circles). The extrapolation to
vanishingly small time step is shown ( star) as are .
Time derivatives are approximated with Eq. (19)
( open circles) or Eq. (20) ( filled circles). The extrapolation to
vanishingly small time step is shown ( star) as are 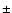 0.05 mag
error bands. 0.05 mag
error bands. |
| Open with DEXTER |
The values of
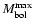 as a function of
as a function of
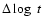 are plotted in Fig. 1, together with the value
are plotted in Fig. 1, together with the value
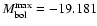 obtained by extrapolating to infinitesimal time step. Error bands
of
obtained by extrapolating to infinitesimal time step. Error bands
of  0.05 mag. are also drawn.
0.05 mag. are also drawn.
Figure 1 shows, as expected, that errors grow linearly with Eq. (19)
and quadratically with Eq. (20).
From this plot, we find that accuracy <0.05 mag. requires
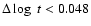 with Eq. (20) but
with Eq. (20) but
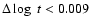 with Eq. (19). Clearly,
for high precision, Eq. (20) is preferred and is indeed used in Sect. 6.3.
with Eq. (19). Clearly,
for high precision, Eq. (20) is preferred and is indeed used in Sect. 6.3.
Although this test refers to the cmf moment equations, it is surely
relevant generally to numerical solutions of the time-dependent RTE.
Accurate difference
approximations for time derivatives are necessary to limit the
accumulation of errors as one integrates forward in time. And of course the
same remark applies to stellar evolution codes.
In Fig. 2, the rf bolometric light curve computed with the 3-D MC code
is compared with that derived from the cmf moment equations.
The MC light curve is from a simulation in which the initial
distribution of radioactive matter is represented by
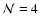
 106 pellets, with the resulting
106 pellets, with the resulting  - and
r-packets propagating in a 1003 grid. The calculation starts at
- and
r-packets propagating in a 1003 grid. The calculation starts at
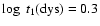 ,
and the time steps are
,
and the time steps are
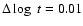 .
The rf light curve is derived from escaping r-packets as described in
Sect. 4.2. Thus, for packets with arrival
times
.
The rf light curve is derived from escaping r-packets as described in
Sect. 4.2. Thus, for packets with arrival
times 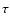 in the interval
(tn,tn+1), the values of
in the interval
(tn,tn+1), the values of 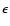 are summed to obtain an estimate of Ln+1/2.
are summed to obtain an estimate of Ln+1/2.
The rf light curve derived from the PDEs of Sect. 5.1 is also plotted
in Fig. 2. This is derived from the cmf light curve L'(t) as described
in Sect. 5.6. As for the calculations of Sect. 6.2, the spherical SN is
modelled with 400 shells, and
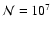 in the 1-D
in the 1-D  -ray
code.
-ray
code.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1656fig2.ps}\end{figure}](/articles/aa/full/2005/01/aa1656/Timg200.gif) |
Figure 2:
Comparison of bolometric light curves. The light curve obtained
with the 3-D Monte Carlo code ( filled circles) compared to that
obtained from the moment equations ( solid line). The corresponding
 -ray deposition curves are also plotted. -ray deposition curves are also plotted. |
| Open with DEXTER |
Figure 2 shows that the two bolometric light curves are in good
agreement over an extended time interval, from well before to long after
maximum light at t = 15.3 days. This implies
a corresponding degree of agreement in the  -ray energy deposition
rates. Nevertheless, these are also plotted in Fig. 2.
For the 3-D code, the deposition rate is calculated simply by summing
the energies of
-ray energy deposition
rates. Nevertheless, these are also plotted in Fig. 2.
For the 3-D code, the deposition rate is calculated simply by summing
the energies of  -packets as they convert to r-packets. But for
the 1-D code, the estimators defined by Eqs. (7) and (8) are used to
calculate
-packets as they convert to r-packets. But for
the 1-D code, the estimators defined by Eqs. (7) and (8) are used to
calculate
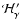 ,
which is then summed over shells.
,
which is then summed over shells.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1656fig3.ps}\end{figure}](/articles/aa/full/2005/01/aa1656/Timg201.gif) |
Figure 3:
Light curve residuals. The differences between the bolometric light
curves plotted in Fig. 2 as a function of elapsed time t. Residuals for
3-D MC calculations with 1003 ( filled circles) and 203
( open circles) grids are shown. |
| Open with DEXTER |
To investigate the precision of the 3-D light curve in more detail,
the residuals relative to the PDE solution are plotted in Fig. 3.
This plot reveals large systematic residuals at early times on the rising
branch of the light curve but that these decrease with time becoming quite
small for 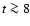 dys. For the interval 10-50 days, the mean residual
is -0.008 mag. A residual of this order may reflect errors in the
PDE solution since this relies on Eddington's approximations.
dys. For the interval 10-50 days, the mean residual
is -0.008 mag. A residual of this order may reflect errors in the
PDE solution since this relies on Eddington's approximations.
The large residuals on the rising branch have been traced to
inadequate spatial resolution of the distribution of
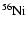 in the 3-D code, despite the 1003 grid. Because
in the 3-D code, despite the 1003 grid. Because
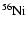 is uniformly
distributed within each cubical cell, the function
is uniformly
distributed within each cubical cell, the function
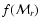 (Sect. 6.1) is slightly broadened relative to its more accurate
representation in the
1-D calculation. This results in some released radioactive energy reaching
the surface slightly early, giving a brighter MC light curve. This explanation
is confirmed by finding that these residuals become larger with a
coarser grid. To illustrate this, Fig. 3 includes the residuals for
t < 10 days with a 203 grid.
(Sect. 6.1) is slightly broadened relative to its more accurate
representation in the
1-D calculation. This results in some released radioactive energy reaching
the surface slightly early, giving a brighter MC light curve. This explanation
is confirmed by finding that these residuals become larger with a
coarser grid. To illustrate this, Fig. 3 includes the residuals for
t < 10 days with a 203 grid.
This comparison with the PDE solution shows that, with a fine enough
grid, the MC code described in Sects. 3 and 4 is capable of carrying out high precision
transport calculations accurate to O(v/c) for  -rays and UVOIR
radiation propagating in a 3-D SN.
-rays and UVOIR
radiation propagating in a 3-D SN.
Among the merits of using  -packets is conservation of energy to high
precision and the ready monitoring of energy transformations within the
configuration.
-packets is conservation of energy to high
precision and the ready monitoring of energy transformations within the
configuration.
Energy conservation for the ejecta implies that
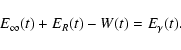 |
(21) |
Here
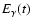 is the total energy released by radioactive decays in
the time interval (0,t),
is the total energy released by radioactive decays in
the time interval (0,t),
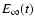 is the total energy lost through
the surface in (0,t), and ER(t) is the radiant energy stored in the ejecta at
time t, all these quantities being evaluated in the rf. Finally,
W(t) is the total work done in (0,t) by radiation interacting with the
expanding ejecta.
is the total energy lost through
the surface in (0,t), and ER(t) is the radiant energy stored in the ejecta at
time t, all these quantities being evaluated in the rf. Finally,
W(t) is the total work done in (0,t) by radiation interacting with the
expanding ejecta.
Estimators for the quantities in Eq. (21) are sums over packets. Thus,
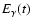 is the sum of the initial rf energies
is the sum of the initial rf energies
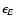 of
of
 -packets emitted by radioactive pellets (Sect. 3.2);
-packets emitted by radioactive pellets (Sect. 3.2);
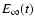 is the sum of the rf energies
is the sum of the rf energies
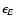 and
and 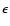 of
of  - and r-packets that escape the grid in (0,t); and
- and r-packets that escape the grid in (0,t); and
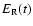 is the sum of the rf energies of packets still propagating within
the ejecta at time t. Finally, W(t) is the sum
over all physical events in (0,t) of
is the sum of the rf energies of packets still propagating within
the ejecta at time t. Finally, W(t) is the sum
over all physical events in (0,t) of
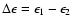 ,
where
,
where
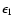 and
and
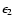 are an
are an  -packet's incident and
emergent rf energies, respectively.
-packet's incident and
emergent rf energies, respectively.
At all time steps in the calculation of Sect. 6.3,
the left- and right-hand sides of Eq. (21) agree to better than 1 part in 1012.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{1656fig4.ps}\end{figure}](/articles/aa/full/2005/01/aa1656/Timg209.gif) |
Figure 4:
Energy fractions as functions of elapsed time t. Quantities
plotted are
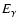 ,
the integrated energy released by radioactive
decays, ,
the integrated energy released by radioactive
decays,
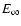 ,
the integrated energy emitted to ,
the integrated energy emitted to 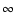 ,
W, the work done on the expanding ejecta, and ,
W, the work done on the expanding ejecta, and 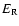 ,
the radiant energy stored in the ejecta. The unit of energy is ,
the radiant energy stored in the ejecta. The unit of energy is
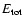 - see Eq. (3) - so that - see Eq. (3) - so that
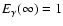 . . |
| Open with DEXTER |
The time variations of the quantities in Eq. (21) are plotted in Fig. 4,
where the unit of energy is
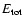 from Eq. (3). For the adopted
parameters,
from Eq. (3). For the adopted
parameters,
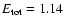
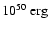 .
.
Figure 4 illustrates the strong departures from stationarity.
In the early dense phases (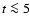 days), energy released by radioactive
decays is trapped within the ejecta, resulting in increasing
days), energy released by radioactive
decays is trapped within the ejecta, resulting in increasing
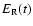 while
while
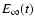 remains close to zero. This continues until
remains close to zero. This continues until
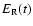 reaches a maximum of 0.085 at t = 9.6 days. Thereafter,
the dropping density allows the trapped radiation to be released, resulting
in a sharp increase in
reaches a maximum of 0.085 at t = 9.6 days. Thereafter,
the dropping density allows the trapped radiation to be released, resulting
in a sharp increase in
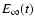 and concomitant decrease in
and concomitant decrease in
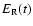 .
For
.
For 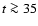 days, energy storage is inconsequential (
days, energy storage is inconsequential (
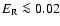 ); stationarity then becomes a good approximation, as is evident from the closely similar slopes of
); stationarity then becomes a good approximation, as is evident from the closely similar slopes of
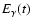 and
and
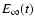 .
.
The maximum of
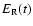 is a rough measure of the highest fraction
of
is a rough measure of the highest fraction
of  -packets active at one time and for which, therefore, storage
space must be allocated. In fact, because many of the packets trapped
at t = 9.6 days have lost energy by doing work on the expanding ejecta,
the active fraction is larger. In the calculation reported here, the
peak active number is 7.2
-packets active at one time and for which, therefore, storage
space must be allocated. In fact, because many of the packets trapped
at t = 9.6 days have lost energy by doing work on the expanding ejecta,
the active fraction is larger. In the calculation reported here, the
peak active number is 7.2  105 at t = 9.2 days - i.e.,
105 at t = 9.2 days - i.e.,
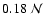 .
.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1656fig5.ps}\end{figure}](/articles/aa/full/2005/01/aa1656/Timg216.gif) |
Figure 5:
Residence times
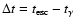 plotted
against
plotted
against
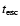 .
Escaping r packets ( open circles) and .
Escaping r packets ( open circles) and
 -packets ( filled circles) are indicated. -packets ( filled circles) are indicated. |
| Open with DEXTER |
Non-stationarity is also illustrated by Fig. 5, which plots
residence against escape times for  -packets in a small simulation
with
-packets in a small simulation
with
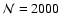 .
For
.
For 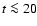 days, we see that it is not uncommon
for escaping r-packets to have residence times close to the age of the SN.
Thereafter, the lowered density allows packets to escape readily and
typical residence times drop to
days, we see that it is not uncommon
for escaping r-packets to have residence times close to the age of the SN.
Thereafter, the lowered density allows packets to escape readily and
typical residence times drop to  a few days. Note also that no
a few days. Note also that no
 -packets escape until
-packets escape until 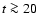 days.
days.
In stationary problems, or this problem with
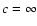 ,
a MC simulation must continue until all packets have escaped. This limits the
usefulness of MC methods for optically thick media. But here a packet
initially at large optical depth escapes when that depth has dropped to
,
a MC simulation must continue until all packets have escaped. This limits the
usefulness of MC methods for optically thick media. But here a packet
initially at large optical depth escapes when that depth has dropped to  1 because of expansion. Figure 5 illustrates this effect.
1 because of expansion. Figure 5 illustrates this effect.
For this problem, the difficulty with an unacceptably large number
of events before escape would reappear if
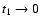 were
necessary for accuracy.
Fortunately, the position coupling assumption (Sect. 4.1.1) is well
justified for
were
necessary for accuracy.
Fortunately, the position coupling assumption (Sect. 4.1.1) is well
justified for 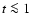 day.
day.
The aim of this paper has been to initiate a MC approach to computing
light curves and spectra for 3-D SN explosions.
The adopted procedure is based on indestructible and indivisible
 -packets as the MC quanta. Although
not called upon for this test problem, the attraction of this
approach in the long-term for this and other multi-dimensional NLTE problems
is that it allows the constraints of thermal and
statistical equilibrium to be incorporated into the scheme via the concept
of macro-atoms. Moreover, the iterations required to achieve full
self-consistency between radiation, level populations and the electron
temperature can be carried out with
geometry-independent
-packets as the MC quanta. Although
not called upon for this test problem, the attraction of this
approach in the long-term for this and other multi-dimensional NLTE problems
is that it allows the constraints of thermal and
statistical equilibrium to be incorporated into the scheme via the concept
of macro-atoms. Moreover, the iterations required to achieve full
self-consistency between radiation, level populations and the electron
temperature can be carried out with
geometry-independent  -iterations.
-iterations.
The calculations reported in Sect. 6 demonstrate that high
photometric precision can be achieved with MC methods for time-dependent
transport calculations in 3-D. Contributing strongly to maintaining accuracy
are the radioactive pellets introduced in Sect. 3.2 since they
result in a seamless transition from energy transport by  -rays to
that by UVOIR radiation. This avoids the loss of accuracy that might arise
if the
-rays to
that by UVOIR radiation. This avoids the loss of accuracy that might arise
if the  -ray deposition profile were separately calculated and then
randomly sampled to create UVOIR radiation. An incidental benefit is
simplified coding.
-ray deposition profile were separately calculated and then
randomly sampled to create UVOIR radiation. An incidental benefit is
simplified coding.
In Sect. 1, this investigation was described as providing a
platform onto which more detailed treatments of matter-radiation
interactions can be added. Thus the already detailed modelling of
 -ray transport can be further improved as discussed in Sect. 3.7.
Also
-ray transport can be further improved as discussed in Sect. 3.7.
Also
 ,
the rate of energy deposition in the form of Compton
electrons,
is available from Eq. (7) as the source term for a Spencer-Fano
calculation of the rates at which non-thermal electrons lose energy to
thermal electrons and in ionizing and exciting atoms. Finally, the NLTE transfer of UVOIR radiation can be implemented following the successful
test for a pure H envelope in Paper II.
,
the rate of energy deposition in the form of Compton
electrons,
is available from Eq. (7) as the source term for a Spencer-Fano
calculation of the rates at which non-thermal electrons lose energy to
thermal electrons and in ionizing and exciting atoms. Finally, the NLTE transfer of UVOIR radiation can be implemented following the successful
test for a pure H envelope in Paper II.
An encouraging aspect of this agenda is that the physics missing
from the present code is well understood, even though many relevant
cross sections are still poorly known. But a discouraging aspect is
that the demands on computer power are such that useful results for a physically-
realistic 3-D model are not feasible at present with a single workstation.
Nevertheless, as argued in Paper II, an attractive option is to implement
these methods on a computer with numerous parallel processors. But even then, it is probably desirable and necessary to approach the full problem
via simplified versions that are less demanding on computer time and storage
space. Specifically, as in previous diagnostic codes, the iterations required
at each time step for full
self-consistency should initially be omitted in favour of approximate formulae
relating gas characteristics to the local MC radiation field.
Acknowledgements
I am grateful to S. A. Sim for detailed comments on the manuscript.
- Abbott, D. C., &
Lucy, L. B. 1985, ApJ, 288, 679 [CrossRef] (In the text)
- Ambwani, K., &
Sutherland, P. 1988, ApJ, 325, 820 [CrossRef] (In the text)
- Arnett, W. D. 1980, ApJ,
237, 541 [CrossRef] (In the text)
- Arnett, W. D. 1982, ApJ,
253, 785 [CrossRef] (In the text)
- Castor, J. I. 1972, ApJ,
178, 779 [CrossRef] (In the text)
- Colgate, S. A., Petschek,
A. G., & Kriese, J. T. 1980, ApJ, 237, L81 [CrossRef] (In the text)
- Eastman, R. G., &
Pinto, P. A. 1993, ApJ, 412, 731 [CrossRef]
- Fransson, C., &
Kozma, C. 1993, ApJ, 408, L25 [CrossRef] (In the text)
- Harries, T. J., Monnier,
J. D., Symington, N. H., & Kurosawa, R. 2004, MNRAS, 350,
565 [CrossRef] (In the text)
- Höflich, P. 2002,
New Astron. Rev., 46, 475 [CrossRef] (In the text)
- Höflich, P. 2003, in
Stellar Atmosphere Modeling, ASP Conf. Proc., 28, 185
(In the text)
- Kasen, D., Nugent, P.,
Thomas, R. C., & Wang, L. 2004, ApJ, in press
[arXiv:astro-ph/0311009]
(In the text)
- Kurosawa, R., Harries, T.
J., Bate, M. R., & Symington, N. H. 2004, MNRAS, in press
[arXiv:astro-ph/0403582]
(In the text)
- Lucy, L. B. 1987, in ESO
Workshop on SN 1987A, ed. I. J. Danziger, 417
(In the text)
- Lucy, L. B. 1999a,
A&A, 344, 282 (In the text)
- Lucy, L. B. 1999b,
A&A, 345, 211 (In the text)
- Lucy, L. B. 2002,
A&A, 384, 725 [EDP Sciences] [CrossRef] (Paper I)
- Lucy, L. B. 2003,
A&A, 403, 261 [EDP Sciences] [CrossRef] (Paper II)
- Mazzali, P. A., &
Lucy, L. B. 1993, A&A, 279, 447 (In the text)
- Meyerott, R. E. 1978,
ApJ, 221, 975 [CrossRef]
- Milne, P. A., Hungerford,
A. L., Fryer, C. L., et al. 2004, ApJ, in press
[arXiv:astro-ph/0406173]
(In the text)
- Niccolini, G., Woitke,
P., & Lopez, B. 2003, A&A, 399, 703 [EDP Sciences] [CrossRef] (In the text)
- Pinto, P. A., &
Eastman, R. G. 2000a, ApJ, 530, 744 [CrossRef] (In the text)
- Pinto, P. A., &
Eastman, R. G. 2000b, ApJ, 530, 757 [CrossRef]
- Press, W. H., Teukolsky,
S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical
Recipes (Cambridge: Cambridge Univ. Press)
(In the text)
- Richtmyer, R. D. 1957,
Difference Methods for Initial-Value Problems (New York:
Interscience Publishers)
(In the text)
- Schwarzschild, M. 1958,
Structure and Evolution of the Stars (Princeton University
Press)
(In the text)
- Springmann, U., &
Puls, J. 1998, in Boulder-Munich II: Properties of Hot, Luminous
Stars, ed. I. D. Howarth, ASP Conf. Ser., 131, 286
(In the text)
- Wheeler, J. C. 2004, in
Cosmic Explosions in Three Dimensions: Asymmetries in Supernovae
and Gamma-Ray Bursts, ed. P. Höflich, P. Kumar, & J. C.
Wheeler (Cambridge University Press)
(In the text)
- Wolf, S. 2003, ApJ, 582,
859 [CrossRef] (In the text)
- Woosley, S. E., Pinto, P.
A., & Hartmann, D. 1989, ApJ, 346, 395 [CrossRef] (In the text)
Copyright ESO 2004
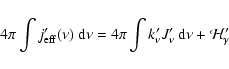
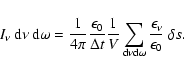
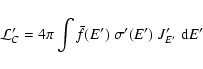
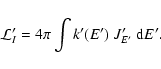
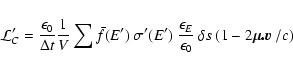
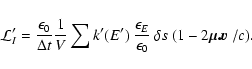
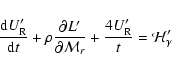
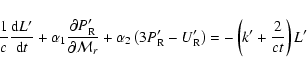
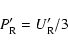
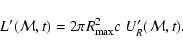
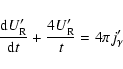
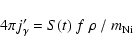
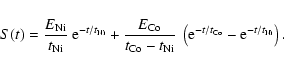
![\begin{displaymath}%
U'_{\rm R} = E_{*} ~
\left( ~ \frac{t_{*}}{t} - \left[1+ \...
...t] {\rm e}^{-t/t_{*}} \right)
~ f ~ \rho ~ / ~ m_{{\rm Ni}}.
\end{displaymath}](/articles/aa/full/2005/01/aa1656/img158.gif)
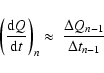
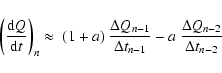
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1656fig1.ps}\end{figure}](/articles/aa/full/2005/01/aa1656/Timg191.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1656fig2.ps}\end{figure}](/articles/aa/full/2005/01/aa1656/Timg200.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1656fig3.ps}\end{figure}](/articles/aa/full/2005/01/aa1656/Timg201.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{1656fig4.ps}\end{figure}](/articles/aa/full/2005/01/aa1656/Timg209.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1656fig5.ps}\end{figure}](/articles/aa/full/2005/01/aa1656/Timg216.gif)