A. Vögler1
-
S. Shelyag1 -
M. Schüssler1 -
F. Cattaneo2 -
T. Emonet3,![]() -
T. Linde3
-
T. Linde3
1 - Max-Planck-Institut für Sonnensystemforschung![]() ,
Max-Planck-Strasse 2,
37191 Katlenburg-Lindau, Germany
,
Max-Planck-Strasse 2,
37191 Katlenburg-Lindau, Germany
2 -
Department of Mathematics, University of Chicago,
5734 South University Avenue, Chicago, IL 60637, USA
3 -
Department of Astronomy and Astrophysics, University of Chicago,
5640 South Ellis Avenue, Chicago, IL 60637, USA
Received 22 June 2004 / Accepted 23 August 2004
Abstract
We have developed a 3D magnetohydrodynamics
simulation code for applications
in the solar convection zone and
photosphere. The code includes a non-local
and non-grey radiative transfer module and takes into account
the effects of partial ionization.
Its parallel design is based on domain decomposition,
which makes it suited for use on parallel
computers with distributed memory architecture.
We give a description of the equations and numerical
methods and present the results of the simulation
of a solar plage region.
Starting with a uniform vertical field of 200 G,
the processes of flux expulsion and convective
field amplification lead to a dichotomy of strong,
mainly vertical fields
embedded in the granular
downflow network
and weak, randomly oriented fields filling
the hot granular upflows.
The strong fields form a magnetic network with
thin, sheet-like structures extending along downflow lanes
and micropores with diameters of up to 1000 km
which form occasionally at vertices where several downflow
lanes merge.
At the visible surface around optical depth unity, the strong
field concentrations are in pressure balance with their
weakly magnetized surroundings and reach field strengths
of up to 2 kG, strongly exceeding the values corresponding
to equipartition with the kinetic energy density of
the convective motions.
As a result of the
channelling of radiation, small flux concentrations
stand out as bright features, while the larger micropores
appear dark in brightness maps owing to the suppression
of the convective energy transport.
The overall shape of the magnetic
network changes slowly on a timescale much larger than the
convective turnover time, while the magnetic flux is
constantly redistributed within the network leading
to continuous formation and dissolution of flux
concentrations.
Key words: magnetohydrodynamics (MHD) - Sun: magnetic fields - Sun: photosphere - Sun: granulation - Sun: faculae, plages
The interaction between convective flows and magnetic fields in the solar photosphere and the uppermost layers of the convection zone gives rise to a number of processes which are of interest both in a solar and in a general astrophysical context. These include flux expulsion and convective field amplification, which lead to highly evacuated flux concentrations with superequipartition field strength, the modification or suppression of convective energy transport by strong fields, and the dynamics resulting from wave excitation and magnetic reconnection. In the context of the magnetic connectivity of the entire solar atmosphere, information on the structure and dynamics of the photospheric fields represents a crucial input.
While the progress in observational techniques (e.g. infrared spectroscopy, speckle polarimetry, adaptive optics) has greatly improved our knowledge of photospheric magnetic fields, observations provide information about the variation of physical quantities along the line of sight in a structured atmosphere only in highly convoluted form, which does usually not allow an unambiguous interpretation, while subphotospheric layers are entirely inaccessible to direct observations. Numerical simulations of MHD processes in the photosphere, on the other hand, provide a way to obtain information on the full three-dimensional structure of magnetic field configurations, as well as on spatial scales which are not resolved by current observations, thus helping to develop consistent models of the physical processes underlying the observed phenomena. In order to approximate solar conditions, comprehensive simulations of magneto-convection in the photosphere and convection zone include elaborate physics: radiative transfer, which is the main driver of convection and has an important influence on the temperature structure and brightness of magnetic field concentrations, and partial ionization, which strongly affects the efficiency of convective energy transport. With continuum, spectral line and polarization diagnostics, realistic numerical models can be directly compared with observations.
Following the work by Nordlund (1983), fully three-dimensional simulations of photospheric magneto-convection (e.g. Nordlund & Stein 1990; Bercik 2002; Stein & Nordlund 2003b) have provided valuable insight into the spatial structure and time evolution of magnetic field concentrations. A different approach was taken by Grossmann-Doerth et al. (1998) and Steiner et al. (1998) who carried out two-dimensional simulations of magnetic structures in Cartesian geometry. While geometrically constrained, these simulations achieved relatively high spatial resolution at affordable computational cost, thus permitting a more realistic modelling of small-scale magnetic structures, boundary layers and shocks. Comprehensive reviews of realistic simulations of solar magneto-convection have been given by Schüssler (2001) and Schüssler & Knölker (2001). Following the lines of more idealized models, Cattaneo (1999), Emonet & Cattaneo (2001) and Cattaneo et al. (2003) have carried out simulations of thermal magneto-convection in the Boussinesq approximation which highlighted the possibility that a substantial fraction of the magnetic field in the quiet photosphere is generated locally by fast dynamo action associated with the granular and supergranular flows.
In this paper we present MURaM![]() ,
a newly developed
3D MHD simulation code for applications in the solar
photosphere and convection zone
which meets the requirements of realistic simulations
(Vögler 2003; Vögler et al. 2003).
It includes non-local
and non-grey radiative transfer and takes into account
partial ionization effects.
The code is parallelized by means of domain decomposition,
which allows to make full use of the computational
capabilities of large, massively parallel computers
with distributed memory architecture.
We give a detailed description of the code and
discuss simulation results obtained with it.
Early other results already obtained with the MURaM
code have been presented by Vögler & Schüssler (2003),
Schüssler (2003), Schüssler et al. (2003), and
Keller et al. (2004).
The paper is organized as follows.
In Sect. 2 we describe the physical model, including the
basic equations and the boundary conditions. The numerical
methods are addressed in Sect. 3. In Sect. 4 we present
the simulation of a typical solar plage region with an
average field strength of 200 G. We discuss morphology, time
evolution and statistical properties of the magnetic field
as well as the relation between field strength and brightness
of magnetic structures. Our conclusions are given
in Sect. 5.
,
a newly developed
3D MHD simulation code for applications in the solar
photosphere and convection zone
which meets the requirements of realistic simulations
(Vögler 2003; Vögler et al. 2003).
It includes non-local
and non-grey radiative transfer and takes into account
partial ionization effects.
The code is parallelized by means of domain decomposition,
which allows to make full use of the computational
capabilities of large, massively parallel computers
with distributed memory architecture.
We give a detailed description of the code and
discuss simulation results obtained with it.
Early other results already obtained with the MURaM
code have been presented by Vögler & Schüssler (2003),
Schüssler (2003), Schüssler et al. (2003), and
Keller et al. (2004).
The paper is organized as follows.
In Sect. 2 we describe the physical model, including the
basic equations and the boundary conditions. The numerical
methods are addressed in Sect. 3. In Sect. 4 we present
the simulation of a typical solar plage region with an
average field strength of 200 G. We discuss morphology, time
evolution and statistical properties of the magnetic field
as well as the relation between field strength and brightness
of magnetic structures. Our conclusions are given
in Sect. 5.
We solve the equations of (non-ideal) MHD in three spatial dimensions
in an inertial frame of
reference with
constant gravitational acceleration,
using Cartesian coordinates. Rotation of the Sun is not
accounted for since the Coriolis force is negligible
on typical length-scales of solar granulation of the order
of 1000 km. An estimate for the Rossby number gives
![]() ,
whereas the Coriolis
force becomes dominant for
,
whereas the Coriolis
force becomes dominant for ![]() .
We write the system of magnetohydrodynamic equations in
conservative form in terms of density,
.
We write the system of magnetohydrodynamic equations in
conservative form in terms of density, ![]() ,
momentum density,
,
momentum density,
![]() ,
total energy per volume, e, and
magnetic field strength,
,
total energy per volume, e, and
magnetic field strength, ![]() ,
as the independent variables.
The system consists of the continuity equation,
,
as the independent variables.
The system consists of the continuity equation,
In our code, the diffusive terms are implemented in two alternative
ways.
One version assumes constant scalar diffusion
coefficients, ![]() (the dynamic viscosity), K and
(the dynamic viscosity), K and ![]() .
In this case, the components of the vicous stress tensor
.
In this case, the components of the vicous stress tensor
![]() are given by
are given by
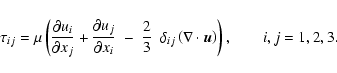 |
(5) |
The system of MHD Eqs. (1)-(4) is
completed by the equation of state, which describes the relations
between the thermodynamical quantities of the fluid.
At temperatures typically encountered in the uppermost few Mm of
the convection zone, the solar plasma is partly ionized and
the simple thermodynamical relations for an ideal
gas do not apply. As hydrodynamical calculations
have shown, changes in the thermodynamical properties
due to partial ionization have considerable consequences for the
character of convection. In the hydrogen ionization zone,
about 2/3 of the enthalpy flux is transported by latent
heat. Buoyancy driving is strongly enhanced since partial
ionization reduces the adiabatic gradient
![]() ,
and the increase in specific heat tends to suppress
the radiative damping of temperature fluctuations
(Rast & Toomre 1993).
For our equation of state, we take into account the first
ionization of the eleven most
abundant elements.
Since we write the MHD equation
with
,
and the increase in specific heat tends to suppress
the radiative damping of temperature fluctuations
(Rast & Toomre 1993).
For our equation of state, we take into account the first
ionization of the eleven most
abundant elements.
Since we write the MHD equation
with ![]() and
and
![]() as
the fundamental thermodynamical quantities whose
time development is explicitly described,
the system is closed by relations specifying the dependence
of T and p on
as
the fundamental thermodynamical quantities whose
time development is explicitly described,
the system is closed by relations specifying the dependence
of T and p on ![]() and
and
![]() :
:
The photosphere is the region where radiation takes over from
convection as the dominant energy transport mechanism
and where the plasma becomes transparent for radiation in the
visible wavelength range.
The energy exchange between gas and radiation determines
the outgoing radiation intensity as well as the temperature structure
of the photosphere and is
responsible for the strong entropy gradient which acts as
the main driver of convection. Therefore, an accurate
representation of the radiative energy exchange
rate,
![]() ,
is crucial both for the dynamics and
temperature structure as well as
for the
diagnostics of magneto-convection.
Since the mean free path of photons becomes large as
the atmosphere becomes transparent in the photosphere,
radiative transfer at this height is essentially non-local,
rendering the diffusion approximation of radiative energy
transport inadequate.
Hence, an accurate calculation of
,
is crucial both for the dynamics and
temperature structure as well as
for the
diagnostics of magneto-convection.
Since the mean free path of photons becomes large as
the atmosphere becomes transparent in the photosphere,
radiative transfer at this height is essentially non-local,
rendering the diffusion approximation of radiative energy
transport inadequate.
Hence, an accurate calculation of
![]() requires the solution of the (time-independent)
radiative transfer equation (RTE hereafter)
requires the solution of the (time-independent)
radiative transfer equation (RTE hereafter)
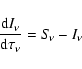 |
(7) |
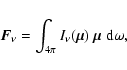 |
(8) |
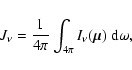 |
(9) |
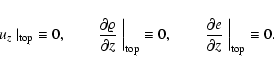 |
(11) |
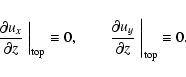 |
(12) |
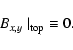 |
(13) |
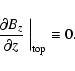 |
(14) |
The lower boundary of the computational domain is located in the convectively unstable upper layers of the convection zone which are characterized by bulk fluid motions. Ideally, an implementation of an open lower boundary should allow free motions across the boundary without interfering with the fluid. Some degree of interference is unavoidable, though, since in principle any formulation of an open boundary condition requires knowledge of the physical conditions outside the domain, which is not available. The missing information has to be replaced with reasonable assumptions regarding the physical properties of the incoming fluid at the boundary.
The first assumption we make is that the total pressure
![]() is uniform across the
lower boundary:
is uniform across the
lower boundary:
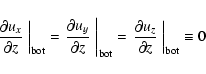 |
(16) |
Owing to the strong stratification of the convection zone, upflows
undergo a strong adiabatic expansion which tends
to smooth out any initial or subsequent fluctuation during
their rise. Therefore, one expects
upflows entering the computational domain to be quite uniform.
In our implementation, the internal energy density per unit mass,
![]() ,
in upflows is assumed to be uniform across the
lower boundary and set to a global value,
,
in upflows is assumed to be uniform across the
lower boundary and set to a global value,
![]() .
We assume that all inflows are vertical with
a smooth vertical profile of uz:
.
We assume that all inflows are vertical with
a smooth vertical profile of uz:
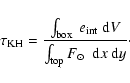 |
(19) |
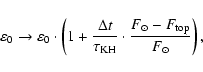 |
(20) |
Since our numerical simulations are carried out in a rather small
computational box containing a limited
number of convective flow cells, statistical fluctuations
of the total mass in the simulated volume can become
significant if no measures are taken
to control the mass flux across the lower boundary.
We use the total pressure at the bottom,
![]() ,
as
control parameter in order to preserve the total mass of the system.
Let
,
as
control parameter in order to preserve the total mass of the system.
Let ![]() be the (relative) mass deficit inherited from
the previous timestep,
be the (relative) mass deficit inherited from
the previous timestep,
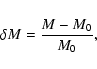 |
(21) |
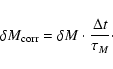 |
(22) |
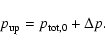 |
(23) |
The MURaM code solves the system of MHD equations on a three-dimensional uniform Cartesian grid. For the spatial discretization of the partial derivatives, centered, fourth-order accurate, explicit finite differences are used for both first and second derivatives. The code is parallelized using a domain-decomposition scheme. The computational domain is divided into a three-dimensional array of rectangular subdomains, each of which is assigned to a separate process on the computer. Parallelization is done with MPI and follows the distributed-memory concept, i.e. each process only possesses knowledge of the variables in its own subdomain. In order to apply the 5-point stencil of the fourth-order scheme to grid cells bordering on subdomain boundaries, knowledge of two layers of cells outside the subdomain is required. Therefore each subdomain is endowed with two layers of "ghost'' cells on each subdomain boundary. The required information is communicated between the neighbouring subdomains and stored in the ghost layers before the numerical derivatives are evaluated. If the subdomain boundary coincides with a global boundary, the ghost cells are assigned values according to the boundary conditions. The numerical solution of the system is advanced in time with an explicit, fourth-order accurate Runge-Kutta scheme. The centered-difference operators and the time-stepping scheme are described in Appendices B and C, respectively.
For each physical quantity subject to diffusion and for each
coordinate direction, a separate diffusion coefficient,
consisting of a shock-resolving and a hyperdiffusive part, is defined:
The shock-resolving part is designed to have significant values only
in those regions where converging flows with strong cell-to-cell velocity
jumps lead to the build-up of strong gradients in advected quantities.
The rate at which gradients grow in converging flows
is determined by the local value of the flow divergence.
Following Caunt & Korpi (2001), we define
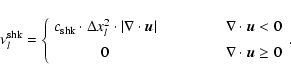 |
(25) |
The hyperdiffusive part is defined on cell interfaces normal to the
direction of diffusion.
For a physical quantity u and direction l, we define, following
Stein & Nordlund (1998):
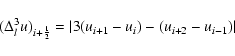 |
(27) |
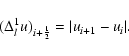 |
(28) |
The maximum allowed timestep,
![]() ,
is determined
by a criterion which ensures that in a single timestep flow velocities,
wave speeds, and diffusion transport information across distances
not larger than the mesh width.
When the artificial diffusion terms are used, the timestep criterion
in our code reads
,
is determined
by a criterion which ensures that in a single timestep flow velocities,
wave speeds, and diffusion transport information across distances
not larger than the mesh width.
When the artificial diffusion terms are used, the timestep criterion
in our code reads
| (29) |
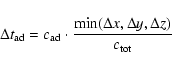 |
(30) |
| (31) |
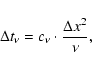 |
(32) |
In the case of constant scalar diffusion coefficients, a more strigent timestep criterion, based on the analysis of linear advection-diffusion equations discretized with fourth-order centered differences (e.g. Hirsch 1988), is used:
| (33) |
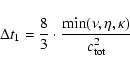 |
(34) |
![\begin{displaymath}\Delta t_{2} = \frac{2}{3} \left[
{\rm max}(\nu,\eta,\kappa...
...\Delta y^2} + \frac{1}{\Delta z^2}
\right)
\right]^{-1}\cdot
\end{displaymath}](/articles/aa/full/2005/01/aa1507/img106.gif) |
(35) |
In order to set a quantity u to value u0 on the upper
or lower boundary,
the values in the two layers of ghost cells are fixed in such a way that
the difference, u-u0, is antisymmetric
with respect to the boundary,
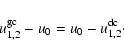 |
(36) |
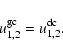 |
(37) |
![\begin{displaymath}\left[\frac{\partial p}{\partial z}\right]^{\rm dc}_1
= \fr...
...rm dc}_2
= \frac{p_1^{\rm dc}-p_3^{\rm dc}}{2\Delta z}\cdot
\end{displaymath}](/articles/aa/full/2005/01/aa1507/img113.gif) |
(38) |
We use the multigroup method (Nordlund 1982; Ludwig 1992;
see also Stein & Nordlund 2003a)
in order to account
for the frequency dependence of the radiative transfer.
The underlying idea of this approach is to sort frequencies into
a small number of groups according to the height at which they
mainly contribute to the radiative heating rate.
As the sorting criterion we use the geometrical depth
in a 1D reference atmosphere at which optical depth
![]() is reached.
For each frequency group, an average opacity is defined
and a transfer equation
for the group-integrated intensity
with a group-integrated source function is solved.
For the simulation described in Sect. 4 we have used
four opacity groups. We took the opacity distribution
functions and continuum opacities from the ATLAS9 stellar atmosphere
package of Kurucz (1993) as the basis for the multigroup sorting
and averaging procedure.
A comprehensive description of our multigroup implementation
is given by Vögler et al. (2004).
is reached.
For each frequency group, an average opacity is defined
and a transfer equation
for the group-integrated intensity
with a group-integrated source function is solved.
For the simulation described in Sect. 4 we have used
four opacity groups. We took the opacity distribution
functions and continuum opacities from the ATLAS9 stellar atmosphere
package of Kurucz (1993) as the basis for the multigroup sorting
and averaging procedure.
A comprehensive description of our multigroup implementation
is given by Vögler et al. (2004).
Since the computation of the radiative source term is usually the most
time-consuming part of a realistic simulation, efficiency
considerations have high priority in the choice
of numerical methods. Furthermore, the domain decomposition
scheme used in our code
demands a solver which is local and reduces the communication overhead
to a minimum. Given these requirements, the method of choice is
the short-characteristics formal solver (Mihalas et al. 1978; Olson & Kunasz 1987;
Kunasz & Olson 1988; Kunasz & Auer 1988).
It is based on the
discretized form of the formal solution of the radiative transfer equation.
In order to calculate the intensity for a certain direction and frequency on a given
grid point, the transfer equation is solved along the ray segment (short
characteristic) between
the grid point and the nearest upwind intersection of the ray with
a cell boundary.
The grid on which we solve the radiative transfer coincides with the
cell corners of the grid used by the MHD solver. The values of T, p and
![]() on the radiative grid are interpolated from the adjacent
MHD grid cells.
An example for a short characteristic within a grid cell is shown in Fig. 1.
Applying the formal solution to the short characteristic between the points F and E,
the intensity at point F is given by
on the radiative grid are interpolated from the adjacent
MHD grid cells.
An example for a short characteristic within a grid cell is shown in Fig. 1.
Applying the formal solution to the short characteristic between the points F and E,
the intensity at point F is given by
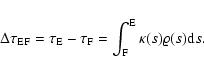 |
(40) |
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{1507f1.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg122.gif) |
Figure 1:
The intensity at gridpoint F is obtained by solving the
transfer equation along the short characteristic
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5cm,clip]{1507f2.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg123.gif) |
Figure 2: The walking order of the short-characteristics method in a 2D grid for a ray direction pointing into the upper right quadrant. Black circles represent gridpoints on the upwind boundaries, where the intensity values are assumed to be given. |
| Open with DEXTER | |
At the global top and bottom boundaries of the computational domain, the incoming
intensity must be specified in order to start the short-characteristics
scheme.
As long as the medium is optically thin at the top
of the box for
a given frequency group ![]() ,
the incoming radiation from outside the computational
domain is negligible and the boundary condition
,
the incoming radiation from outside the computational
domain is negligible and the boundary condition
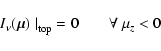 |
(41) |
In the simulations discussed here, this assumption
is valid for all frequency groups
except the one representing the strongest line opacities.
For this group, the
![]() level is close to the top of the box and
setting the incoming radiation to zero would lead to artificial
cooling of the uppermost layers. In order to derive a
more realistic boundary condition, we assume that above the computational
domain there is a isothermal plane-parallel
layer with temperature
level is close to the top of the box and
setting the incoming radiation to zero would lead to artificial
cooling of the uppermost layers. In order to derive a
more realistic boundary condition, we assume that above the computational
domain there is a isothermal plane-parallel
layer with temperature
![]() ,
whose optical thickness in
the most opaque group is
,
whose optical thickness in
the most opaque group is
![]() .
According to the formal solution of the RTE,
the radiation entering the box from such a layer is given by
.
According to the formal solution of the RTE,
the radiation entering the box from such a layer is given by
The bottom of the simulation box is located in the optically thick regions
where the diffusion approximation holds. At the bottom, incoming radiation
is set to the local value of the source function:
| (43) |
Once the angular integration has been performed,
the radiative heating rate for frequency group ![]() can be derived
from the two equivalent expressions
can be derived
from the two equivalent expressions
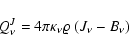 |
(44) |
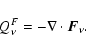 |
(45) |
As pointed out by Bruls et al. (1999), ![]() suffers from severe
accuracy problems in the optically thick regime, since then
suffers from severe
accuracy problems in the optically thick regime, since then ![]() approaches
approaches ![]() ,
and the difference of these two
almost equal quantities is amplified by a factor
,
and the difference of these two
almost equal quantities is amplified by a factor
![]() which grows exponentially with depth.
On the other hand,
which grows exponentially with depth.
On the other hand, ![]() is
less accurate than
is
less accurate than ![]() in the optically thin
layers of the upper photosphere
since small inaccuracies
in the orientation of the flux vector can lead to significant
errors when the divergence of the nearly constant radiative flux
is determined, while the
difference
in the optically thin
layers of the upper photosphere
since small inaccuracies
in the orientation of the flux vector can lead to significant
errors when the divergence of the nearly constant radiative flux
is determined, while the
difference
![]() is only slightly affected.
Following a suggestion
of Bruls et al. (1999), we make a smooth transition from
is only slightly affected.
Following a suggestion
of Bruls et al. (1999), we make a smooth transition from ![]() to
to ![]() for each
frequency group separately, depending on the local
optical depth scale for the group considered,
using
for each
frequency group separately, depending on the local
optical depth scale for the group considered,
using ![]() in regions with
in regions with
![]() and
and ![]() otherwise.
The total (frequency-integrated) radiative heating rate is then given by
otherwise.
The total (frequency-integrated) radiative heating rate is then given by
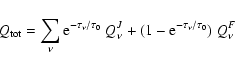 |
(46) |
| |
Figure 3:
Geometrical setup of the simulation run. The vector
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{1507f4.eps}\hspace*{4mm}\i...
...07f6.eps}\hspace*{4mm}\includegraphics[width=7.7cm,clip]{1507f7.eps}\end{figure}](/articles/aa/full/2005/01/aa1507/Timg152.gif) |
Figure 4: Map of (frequency-integrated) brightness ( lower right) and horizontal cuts at the the average geometrical height corresponding to optical depth unity of (clockwise from bottom left) temperature, vertical magnetic field and vertical velocity. The "mesoscale'' network of magnetic field structures is embedded in the network of granular downflows. Larger field concentrations appear dark while the brightness of small magnetic structures occasionally exceeds the brightness of granules. Most of the domain exhibits "abnormal'' granulation with small granules (compared to the "normal'' granules in the upper right corner). See also the movies provided as supplementary online material. |
| Open with DEXTER | |
The simulation results show that within a few minutes
(approximately one turnover time of the convection)
after the magnetic field has been introduced,
the convective motions transport most of the magnetic
flux into the intergranular downflow regions. During this
initial phase, the magnetic field forms a network structure
with maximum field strengths around 2000 G at height z=0.
(It should be noted that the average
![]() level
of the fully developed convection in its statistically
steady state is shifted upwards by approximately 80-100 km
as a result of the turbulent pressure of the convective
flow (see e.g. Stein & Nordlund 1998).
The magnetic network is organized on a larger scale, which
typically comprises 2-6 granules.
As the simulation develops in time, the network on this scale turns out
to be long-lived with a typical timescale of hours.
Similar large-scale organization also appears in other convection
simulations (e.g., Cattaneo et al. 2001). However, since the
horizontal box size is comparable to the length scale of the
pattern, it cannot be ruled out that it is an artifact.
level
of the fully developed convection in its statistically
steady state is shifted upwards by approximately 80-100 km
as a result of the turbulent pressure of the convective
flow (see e.g. Stein & Nordlund 1998).
The magnetic network is organized on a larger scale, which
typically comprises 2-6 granules.
As the simulation develops in time, the network on this scale turns out
to be long-lived with a typical timescale of hours.
Similar large-scale organization also appears in other convection
simulations (e.g., Cattaneo et al. 2001). However, since the
horizontal box size is comparable to the length scale of the
pattern, it cannot be ruled out that it is an artifact.
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{1507f8.eps}\hspace*{4mm}\i...
...10.eps}\hspace*{4mm}\includegraphics[width=6.1cm,clip]{1507f11.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg155.gif) |
Figure 5:
Statistical properties of a layer of 100 km
thickness around optical depth unity. Upper left:
probability density function (PDF) of the field strength, signed with
the vertical orientation of the field vector. Upper right: joint PDF of field strength and the inclination angle of |
| Open with DEXTER | |
Figure 4 shows a map of the frequency-integrated emergent intensity (brightness) together with horizontal slices of temperature, vertical magnetic field, and vertical velocity at z=0 for a snapshot taken about two hours of simulated solar time after the start of the magnetic phase. The magnetic field forms elongated, sheet-like structures that extend along intergranular lanes as well as larger structures with a size of up to 1000 km ("micropores''), which are located at vertices where several downflow lanes merge. The micropores appear dark in the intensity picture, while smaller structures are usually brighter than the non-magnetic downflow lanes, their brightness occasionally exceeding the brightness of granules. A large part of the simulated area shows "abnormal'' granulation (Dunn & Zirker 1973; Title et al. 1992) with reduced granule sizes compared to the "normal'' granules in the upper right corner of the intensity map. The micropores are far from homogeneous; they show considerable small scale intensity fluctuations, which are related to localized upflows in regions of reduced field strength. While the overall shape of the magnetic network is stable, the magnetic features show a strong time dependence on small scales as magnetic flux is incessantly redistributed within the network. Consequently, the typical lifetime of the micropores is smaller than the timescale associated with the magnetic network and is comparable to the granule lifetime. The magnetic network itself is embedded in the network of granular downflows. While convective motions are effectively supressed inside strong field features, downflows occur at their edges. Basically, this result is consistent with earlier MHD simulations (e.g. Deinzer et al. 1984a,b; Knölker et al. 1991) which showed that the influx of radiation into a magnetic element drives a baroclinic flow in form of a strong downflow at its edge. It is also consistent with the observational finding that observed Stokes-V profiles in plage regions show a distinct area asymmetry (Stenflo et al. 1984; Grossmann-Doerth et al. 1989; Solanki 1989; Sigwarth et al. 1999).
Figure 5 shows some
statistical properties of a layer of 100 km thickness around
![]() .
The probability density function (PDF) for the magnetic field,
multiplied with the sign of its vertical component is shown in the
upper left panel. There appears to be a superposition of two components.
Most of the volume considered is occupied by weak field, the
probability density dropping off approximately exponentially
with increasing field strength.
The distribution reveals a pronounced local minimum at B=0, indicating that
magnetic fields, albeit mostly weak, permeate the whole volume,
and strictly field free regions are avoided.
Superimposed on this exponential distribution is a Gaussian "bulge''
(the high field strength wing shows the characteristic
parabolic shape on a logarithmic scale)
with a maximum around 1500 G, which reflects the sheet and micropore
structures in the network of concentrated magnetic field.
The joint probability density function (joint PDF) of magnetic field strength
and inclination angle of the field vector with respect to the
horizontal plane given in the upper right panel of Fig. 5
shows that most of the
strong field (above the kilogauss level) is vertical and
upward directed (which is the orientation
of the initial field), presumably as the result of
buoyancy acting on the partially evacuated magnetic structures.
The inclination angle of weak fields is much more evenly distributed.
With decreasing field strength, a slight preference for
upward directed fields is observed.
The joint PDF of the vertical magnetic field and the flow
velocity multiplied with the sign of the vertical velocity component in the
lower left panel of Fig. 5 (positive velocities correspond to upflows) shows the effect of strong fields on the fluid motions:
while flow velocities up to
.
The probability density function (PDF) for the magnetic field,
multiplied with the sign of its vertical component is shown in the
upper left panel. There appears to be a superposition of two components.
Most of the volume considered is occupied by weak field, the
probability density dropping off approximately exponentially
with increasing field strength.
The distribution reveals a pronounced local minimum at B=0, indicating that
magnetic fields, albeit mostly weak, permeate the whole volume,
and strictly field free regions are avoided.
Superimposed on this exponential distribution is a Gaussian "bulge''
(the high field strength wing shows the characteristic
parabolic shape on a logarithmic scale)
with a maximum around 1500 G, which reflects the sheet and micropore
structures in the network of concentrated magnetic field.
The joint probability density function (joint PDF) of magnetic field strength
and inclination angle of the field vector with respect to the
horizontal plane given in the upper right panel of Fig. 5
shows that most of the
strong field (above the kilogauss level) is vertical and
upward directed (which is the orientation
of the initial field), presumably as the result of
buoyancy acting on the partially evacuated magnetic structures.
The inclination angle of weak fields is much more evenly distributed.
With decreasing field strength, a slight preference for
upward directed fields is observed.
The joint PDF of the vertical magnetic field and the flow
velocity multiplied with the sign of the vertical velocity component in the
lower left panel of Fig. 5 (positive velocities correspond to upflows) shows the effect of strong fields on the fluid motions:
while flow velocities up to
![]() can be found in regions
of weak field, the velocities are reduced in magnetic
structures with field strengths above 1000 G. Fluid motions are not
completely supressed, however, since the predominantly vertical fields
permit vertical flows. Downflows are preferred inside strong field features.
The lower right panel of Fig. 5 shows the joint PDF of
the inclination angles of magnetic field vector and flow vector with
respect to the horizontal plane.
The pronounced diagonal feature indicates that
flow field and magnetic field are roughly aligned in most of the volume
considered. In addition to this component, there is a clear correlation
of (strong) vertical magnetic field with downflows.
The picture obtained here
exhibits some similarities with simulations
of idealized Boussinesq magneto-convection (Emonet & Cattaneo 2001),
which also show a preferentially vertical
orientation of strong fields embedded in downdrafts and a
decrease of the velocity amplitude with increasing field strength.
can be found in regions
of weak field, the velocities are reduced in magnetic
structures with field strengths above 1000 G. Fluid motions are not
completely supressed, however, since the predominantly vertical fields
permit vertical flows. Downflows are preferred inside strong field features.
The lower right panel of Fig. 5 shows the joint PDF of
the inclination angles of magnetic field vector and flow vector with
respect to the horizontal plane.
The pronounced diagonal feature indicates that
flow field and magnetic field are roughly aligned in most of the volume
considered. In addition to this component, there is a clear correlation
of (strong) vertical magnetic field with downflows.
The picture obtained here
exhibits some similarities with simulations
of idealized Boussinesq magneto-convection (Emonet & Cattaneo 2001),
which also show a preferentially vertical
orientation of strong fields embedded in downdrafts and a
decrease of the velocity amplitude with increasing field strength.
![\begin{figure}
\includegraphics[width=12.2cm,clip]{1507f12.eps}\hspace*{2mm}\includegraphics[width=5cm,clip]{1507f13.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg158.gif) |
Figure 6: Left: face-on view of a thin magnetic sheet. The spreading of the field lines in the upper photosphere is clearly visible. At a depth of approximately 300 km below the surface, the sheet is disrupted. The grey, horizontal plane in dicates the height z=0. Right: magnetic map of the sheet at z=0. The arrow shows the viewing direction of the field line plot on the left. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12.2cm,clip]{1507f14.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg159.gif) |
Figure 7:
The same sheet as in Fig. 6, from a different
angle. The isosurface
|
| Open with DEXTER | |
The three-dimensional field line plot given in
Fig. 6 (left panel) shows a face-on view
of a thin magnetic sheet (cf. magnetic map at z=0 on the
right panel). The structure appears coherent around
the visible surface. At a depth of 200-300 km below z=0 the sheet is disrupted by vigorous convective flows,
the coherence is lost and a large part of the flux
appears in form of turbulent, more or less randomly
oriented field lines. We find this to be a typical property
of thin magnetic flux concentrations in our simulation.
Figure 7 shows the same flux sheet from a
different viewing angle. The depression of the visible surface
(
![]() )
associated with the magnetic sheet
is clearly visible. The field lines appear to be systematically
twisted, possibly as a result of a horizontal shear
near the surface.
In contrast, the micropore shown
in Fig. 8 appears much more coherent
over the whole simulated height range.
While the field undergoes fragmentation and forms more
concentrated strands of flux underneath the surface,
a significant part of the flux remains more or less vertical
in the sub-surface layers.
)
associated with the magnetic sheet
is clearly visible. The field lines appear to be systematically
twisted, possibly as a result of a horizontal shear
near the surface.
In contrast, the micropore shown
in Fig. 8 appears much more coherent
over the whole simulated height range.
While the field undergoes fragmentation and forms more
concentrated strands of flux underneath the surface,
a significant part of the flux remains more or less vertical
in the sub-surface layers.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{1507f15.eps}\hspace*{2mm}\includegraphics[width=5cm,clip]{1507f16.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg160.gif) |
Figure 8: Three-dimensional field line plot ( left) and corresponding magnetic map ( right) of a micropore. The translucent plane shows the field strength at z=0; strong fields appear white. |
| Open with DEXTER | |
The upper panel of Fig. 9
shows that the total (gas + magnetic)
pressure inside strong field concentrations
(here defined as fields exceeding
a height-dependent critical value,
![]() ;
at a given height z,
;
at a given height z,
![]() is defined such that the fields with
is defined such that the fields with
![]() comprise 70% of the total flux at that height)
is over a large
height range in balance with the external gas pressure.
So, despite of the dynamic time evolution of the strong
fields in the downflow network and although the
typical diameters of flux concentrations are not necessarily
small compared against other relevant length scales like e.g. the pressure
scale height, the pressure conditions are largely consistent
with the simple picture of a thin flux tube or flux sheet in horizontal
magnetohydrostatic pressure balance with its surroundings.
The deviations become significant in the uppermost 300 km
of the computational domain where the total pressure inside
strong fields clearly exceeds the external pressure.
This is plausible since the field concentrations
spread out with height and become nearly vertical close to the
upper boundary, thus giving rise to an inwards directed magnetic
curvature force which is balanced by an outwards directed
magnetic pressure force. Correspondingly, the actual average field strength
of the field concentrations shown in the lower
panel of Fig. 9, exceeds the value predicted
by the thin flux-tube approximation in the height range above
comprise 70% of the total flux at that height)
is over a large
height range in balance with the external gas pressure.
So, despite of the dynamic time evolution of the strong
fields in the downflow network and although the
typical diameters of flux concentrations are not necessarily
small compared against other relevant length scales like e.g. the pressure
scale height, the pressure conditions are largely consistent
with the simple picture of a thin flux tube or flux sheet in horizontal
magnetohydrostatic pressure balance with its surroundings.
The deviations become significant in the uppermost 300 km
of the computational domain where the total pressure inside
strong fields clearly exceeds the external pressure.
This is plausible since the field concentrations
spread out with height and become nearly vertical close to the
upper boundary, thus giving rise to an inwards directed magnetic
curvature force which is balanced by an outwards directed
magnetic pressure force. Correspondingly, the actual average field strength
of the field concentrations shown in the lower
panel of Fig. 9, exceeds the value predicted
by the thin flux-tube approximation in the height range above
![]() km.
km.
Owing to the strong decrease in
gas pressure with height, the plasma-![]() in strong flux
concentrations shown in Fig. 10
drops by more than three orders of magnitude across
the vertical extent of the simulation
box. While it is of the order of unity near the visible
surface
in strong flux
concentrations shown in Fig. 10
drops by more than three orders of magnitude across
the vertical extent of the simulation
box. While it is of the order of unity near the visible
surface
![]() (
(
![]() km),
it drops below 0.1 near the top of the box, which shows
that the gas pressure is largely irrelevant for the
internal force balance of magnetic flux concentrations
in the uppermost parts of the domain.
km),
it drops below 0.1 near the top of the box, which shows
that the gas pressure is largely irrelevant for the
internal force balance of magnetic flux concentrations
in the uppermost parts of the domain.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1507f17.eps}\par\vspace*{3mm}
\hspace*{1.5mm}\includegraphics[width=8.3cm,clip]{1507f18.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg166.gif) |
Figure 9: Upper panel: horizontally averaged gas pressure inside (solid) and outside (dashed) strong field regions, and total (gas + magnetic) pressure in strong field regions (dotted). (See the text for the definition of strong fields used here.) Lower panel: average (rms) field strength inside (solid) and outside (dotted) strong fields as a function of height. The dashed line shows the field strength which would balance the difference between the inside and outside gas pressures. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1507f19.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg167.gif) |
Figure 10:
Average plasma- |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1507f20.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg168.gif) |
Figure 11: Horizontally averaged (rms) horizontal velocity in regions of strong and weak magnetic field as function of height. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1507f21.eps}\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{1507f22.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg170.gif) |
Figure 12:
Detailed view of the flow and magnetic structure of a flux
concentration. Upper panel: vectors of horizontal velocity superimposed on
a greyscale map of the vertical magnetic field at a height of 550 km above
the visible surface. Lower panel: the same at
a height of 100 km. The longest arrows correspond to a velocity of
|
| Open with DEXTER | |
In the upper part of the computational domain, the structure
of horizontal flows undergoes a characteristic change with height.
This is illustrated by Fig. 11, which shows
horizontally averaged (root-mean-square) velocities of horizontal flows
as a function of height, in strong-field and
weak-field regions, respectively.
Horizontal flows are stronger outside
magnetic field concentrations than inside below z=400 km and reach a
maximum around z=200 km, where the granular upflows turn over
and converge horizontally towards the downflow lanes.
Above z=400 km, a different picture is obtained:
the rms horizontal velocity inside magnetic structures
increases with height, while the velocities
outside decrease significantly.
As a result, horizontal flows have larger amplitudes
inside magnetic fields.
As the example shown in Fig. 12 illustrates,
there is a correlation between flows inside magnetic
structures at large heights and
converging granular flows immediately outside magnetic structures
at deeper levels near the visible surface around
![]() .
The anticlockwise whirl flow at z=550 km (upper panel)
corresponds to a net circulation of granular flows around
the magnetic element
with the same orientation at z=100 km (lower panel).
It is conceivable that the shear due to such surrounding flows
excites torsional Alfvén waves propagating
upward along field concentrations. While
such waves in the uppermost parts
of the computational domain cannot
be described realistically with the present closed upper boundary
conditions, future versions of our code with a
transmitting upper boundary will allow us to
thoroughly analyze
this potentially important mechanism of mechanical energy
transport and assess its relevance for the energy
balance in the upper layers of the solar atmosphere.
.
The anticlockwise whirl flow at z=550 km (upper panel)
corresponds to a net circulation of granular flows around
the magnetic element
with the same orientation at z=100 km (lower panel).
It is conceivable that the shear due to such surrounding flows
excites torsional Alfvén waves propagating
upward along field concentrations. While
such waves in the uppermost parts
of the computational domain cannot
be described realistically with the present closed upper boundary
conditions, future versions of our code with a
transmitting upper boundary will allow us to
thoroughly analyze
this potentially important mechanism of mechanical energy
transport and assess its relevance for the energy
balance in the upper layers of the solar atmosphere.
It is a well established observational fact that the brightness of magnetic structures in the photosphere strongly depends on their size (Topka et al. 1997). While small field concentrations appear as bright points in continuum-intensity pictures, larger structures like pores and sunspots are dark as a result of the reduced convective energy transport in their interior (see e.g. Zwaan 1987, for an overview of the hierarchy of magnetic elements). A particular case is the brightening of magnetic concentrations in molecular lines like the CH lines in the "G band''. Schüssler et al. (2003) and Shelyag et al. (2004) have shown that the G-band brightening is caused by a depletion of CH molecules in the partially evacuated magnetic structures.
![\begin{figure}
\par {\includegraphics[width=7.5cm,clip]{1507f23.eps}\hspace*{6mm}}
\par\vspace*{2mm}
\includegraphics[width=8cm,clip]{1507f24.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg173.gif) |
Figure 13:
Upper panel: joint probability distribution of magnetic field
strength and frequency-integrated brightness.
The grey-shading indicates
the probability density, with level-intervals of 0.5 on the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{1507f25.eps}\par\vspace*{2mm}
\includegraphics[width=7cm,clip]{1507f26.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg174.gif) |
Figure 14: Vertical field strength at z=0 ( upper panel) and intensity map ( lower panel) for a sheet-like magnetic structure. The vertical lines indicate the position of the cuts shown in Fig. 15. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{1507f27.eps}\par\vspace*{2mm}
\includegraphics[width=7.7cm,clip]{1507f28.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg175.gif) |
Figure 15:
Vertical cut through the sheet-like magnetic structure shown in Fig. 14. Left panel:
density (grey-scaled) and magnetic field vectors projected on the veertical
plane. The longest vector correponds to a field strength of 2000 G.
Right panel: temperature structure and radiative
flux vectors. The solid lines indicate the level
|
| Open with DEXTER | |
Figures 14 and 15 provide a
detailed view of a typical sheet-like structure in an intergranular
lane which
illustrates the connection between brightness and
field strength.
Figure 14 shows magnetic field and
intensity maps. The vertical line marks
the position of the vertical cuts through this structure
shown in Fig. 15.
As Fig. 15 illustrates,
the partial evacuation and lower temperature
of the magnetic structure leads to
a depression of the visible surface inside the sheet (the bold solid
lines, indicating the level
![]() ).
This results in radiation flowing in from the hot neighbouring
granules through the sidewalls, heating up the interior
of the sheet. This horizontal heating is balanced
by cooling due to radiative losses in the vertical direction.
The resulting net radiative heating rate in the interiour of the
sheet is very small which indicates that
it is nearly in radiative equilibrium and convective energy
transport is not relevant.
The bright appearance of the sheet is, in turn, a direct
consequence of the increased temperature around the (depressed)
visible surface corresponding to this radiative equilibrium.
).
This results in radiation flowing in from the hot neighbouring
granules through the sidewalls, heating up the interior
of the sheet. This horizontal heating is balanced
by cooling due to radiative losses in the vertical direction.
The resulting net radiative heating rate in the interiour of the
sheet is very small which indicates that
it is nearly in radiative equilibrium and convective energy
transport is not relevant.
The bright appearance of the sheet is, in turn, a direct
consequence of the increased temperature around the (depressed)
visible surface corresponding to this radiative equilibrium.
This example confirms the basic mechanism for brightness enhancement due to channelling of radiation which was already found in earlier, more simplified models of photospheric magnetic elements (e.g. Spruit 1976; Deinzer et al. 1984a,b; Knölker et al. 1991) and demonstrates that results of idealized, two-dimensional models are indeed relevant for the explanation of some aspects of three-dimensional magneto-convection. The nature of facular brightenings close to the solar limb was studied by Keller et al. (2004) whose analysis of photospheric MHD simulations showed that faculae originate from a thin layer within granules immediately below largely transparent magnetic flux concentrations.
It should be noted that radiative heating is not the only mechanism
which could affect the temperature structure of magnetic
structures.
In principle, Joule dissipation near the
edges of the magnetic sheet, where the gradients
in field strength are large, can also heat the interior of the
sheet.
In the solar photosphere, this effect is expected to be
small compared with the radiative heat influx because of the
high electric conductivity of the plasma. Since the value of the conductivity
in simulations of this kind is unrealistically low -
an inevitable consequence of the limited spatial resolution -
Joule heating tends to be overestimated (Schüssler 1986;
Hirayama 1992).
However, as Fig. 16 shows, the contribution of Joule
dissipation to the total heating around ![]() is negligible,
indicating that
the effects of limited grid resolution do not
seriously affect the temperature structure obtained from the simulation.
is negligible,
indicating that
the effects of limited grid resolution do not
seriously affect the temperature structure obtained from the simulation.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1507f29.eps} \end{figure}](/articles/aa/full/2005/01/aa1507/Timg176.gif) |
Figure 16: Radiative and joule heating across a flux sheet. The solid line shows the heating rate due to horizontal influx of radiation energy into the sheet along the cut indicated in Fig. 14, at a depth of 80 km below z=0. The dashed line shows the joule heating occuring at the sheet boundaries at the same depth. |
| Open with DEXTER | |
Figure 17 illustrates the formation of a micropore. At the beginning of the time sequence shown, a small granule is surrounded by magnetic field, which is embedded in a complex structure of downflows and forms a ring around the granule. Subsequently, the initially bright granule shrinks and becomes darker as the upflow velocity in the granule decreases; the surrounding magnetic flux converges to form a dark micropore with a diameter of approximately 1000 km. In its interior, vertical motions are strongly reduced, which implies that convective energy transport is almost completely supressed. The micropore is, however, punctuated by small, non-magnetic upwellings, which penetrate it from below and carry hot plasma to the surface. While the shape of the micropore changes continuously, it more or less retains its position. Roughly 15 min after the end of the sequence shown, most of the magnetic flux of the micropore has been transported away into the magnetic network and the pore has dissolved. Apparently, the size (amount of magnetic flux) of the micropores which form in this simulation is too small to structure the convective flow around them in a way that would stabilize them and extend their lifetime beyond about 1-2 convective turnover times. The micropore formation process shown in Fig. 17 is reminiscent of the result reported by Hirzberger (2003), who observed several bright points immediately before the appearance of a micropore at the same position. It is also in qualitative agreement with the magneto-convection simulations of Bercik (2002) (see also Stein et al. 2002).
![\begin{figure}
\par\includegraphics[width=14cm,clip]{1507f30.eps}
\end{figure}](/articles/aa/full/2005/01/aa1507/Timg177.gif) |
Figure 17: Time series of vertical magnetic field ( left; light shades indicate strong fields), intensity ( middle), and vertical velocity ( right; light and dark shades indicate up- and downflows, respectively) during the formation of a micropore. An initially bright, small granule shrinks, while the magnetic field surrounding it forms a small pore which appears dark in the intensity picture. |
| Open with DEXTER | |
The first results obtained with this code are promising. The simulation of a solar plage region with an average field strength of 200 G is in agreement with the basic picture of solar magneto-convection derived from previous simulations. But the results also suggest that a wealth of new information can be obtained by combining full three-dimensionality with high spatial resolution: while the sizes, lifetimes, and field strengths of micropores found in our simulations are consistent both with observations (Topka et al. 1997; Hirzberger 2003) and simulations (Stein et al. 2002), they appear as internally highly structured features which show significant fluctuations of brightness and field strength around the mean values and are penetrated by hot, weakly magnetized upflows. The near-surface structure of the quasi two-dimensional flux sheets in the intergranular lanes is consistent with earlier two-dimensional models (e.g. Deinzer et al. 1984a,b; Knölker et al. 1991). Our simulations, however, show that slender flux sheets which appear as coherent features around optical depth unity, get disrupted by turbulent downflows beneath the surface and are, in fact, shallow phenomena. The occurrence of strong vortical flows inside magnetic structures in the upper photosphere, which are triggered by the advection of vorticity towards the footpoints of the field concentrations in the surface layers, suggests that important information about the transport of mechanical energy in the upper layers of the solar atmosphere can be obtained from simulations of this kind.
Acknowledgements
This work has been supported by the Deutsche Forschungsgemeinschaft under grant SCHU 500/7 in the framework of the Priority Research Program "Analysis and Numerics of Conservation Laws''. A.V. and S.S. were supported by the Max-Planck-Institute for Aeronomy through doctoral stipends. A.V. would like to thank the colleagues from the University of Chicago for their hospitality and financial support during a stay at the Department of Astronomy and Astrophysics at UofC.
In the following, a brief outline is given how temperature
and pressure are derived from
![]() and
and ![]() if the first ionization of a number of elements is
taken into account. For the simulations presented here, the
eleven most abundant elements in the solar photosphere were included.
The internal energy per mass
unit
if the first ionization of a number of elements is
taken into account. For the simulations presented here, the
eleven most abundant elements in the solar photosphere were included.
The internal energy per mass
unit
![]() is given by
is given by
Table A.1: Relative abundances and ionization energies of first ionization for the eleven most abundant elements in the solar photosphere.
Choosing i as the index denoting the grid position
along a particular spatial direction,
the first and second spatial derivatives of quantity u are given by
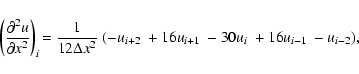 |
(B.2) |
For partial differential equations corresponding to a conservation law,
the centered difference scheme is equivalent
to a finite volume scheme
with the numerical flux
In a multidimensional domain, mixed derivatives are calculated by straightforward successive application of Eq. (B.1) in different coordinate directions.
The numerical solution of the system is advanced in time with an explicit
fourth-order Runge-Kutta scheme. Defining
![]() as the vector which
describes the state of the system for time t0, i.e.
as the vector which
describes the state of the system for time t0, i.e.
| (C.1) |
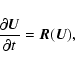 |
(C.2) |
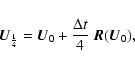
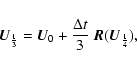
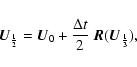
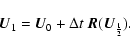 |
(C.3) |
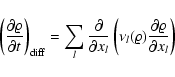 |
(D.1) |
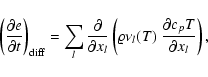 |
(D.2) |
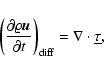 |
(D.3) |
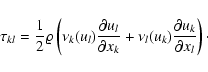 |
(D.4) |
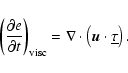 |
(D.5) |
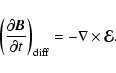 |
(D.6) |
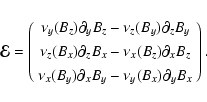 |
(D.7) |
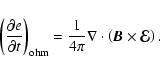 |
(D.8) |
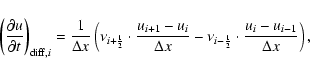 |
(D.9) |
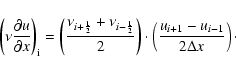 |
(D.10) |