V. F. Cardone1 - E. Piedipalumbo2 - C. Tortora2
1 - Dipartimento di Fisica "E.R. Caianiello'', Università di Salerno, and INFN, Sez. di Napoli, Gruppo Coll. di Salerno, Via S. Allende, 84081 Baronissi (Salerno), Italy
2 -
Dipartimento di Scienze Fisiche, Università di Napoli, and INFN, Sez. di Napoli, Complesso Universitario di Monte S. Angelo, Via Cinthia, Edificio G, 80126 Napoli, Italy
Receveid 11 March 2004 / Accepted 30 July 2004
Abstract
Recently, Rasia et al. (2004, MNRAS, 531, 237) proposed a new dynamical model for the mass density profile of clusters of galaxies as a result of a set of high resolution hydrodynamical simulations of structure formation. We investigate the lensing properties of this model evaluating the deflection angle, the lensing potential and the amplification of the images. We give particular attention to the structure and position of the critical curves to see whether this model is able to produce radial and tangential arcs. With this aim we also investigate the effect of taking into account the brightest cluster galaxy in the lensing potential and the deviations from spherical symmetry mimicked by an external shear. We also analyze the implication of the gas density and temperature profiles of the Rasia et al. (2004) model for the properties of the X-ray emission and the comptonization parameter that determines the CMBR temperature decrement due to the Sunyaev-Zel'dovich effect.
Key words: galaxies: clusters: general - gravitational lensing - dark matter
To first order, galaxy clusters may be described as large dark matter haloes since this component represents up to ![]() of the cluster mass. Cluster properties may thus be investigated by means of numerical simulations performed in the standard framework of hierarchical CDM structure formation. The impressive growth in processing speeds of computers in recent years has allowed us to make a detailed investigation of this fundamental topic. While there is a general consensus that relaxed galaxy clusters exhibit a density profile that is well described by a double power law with outer asymptotic slope -3, there is still controversy about the value of the inner asymptotic slope
of the cluster mass. Cluster properties may thus be investigated by means of numerical simulations performed in the standard framework of hierarchical CDM structure formation. The impressive growth in processing speeds of computers in recent years has allowed us to make a detailed investigation of this fundamental topic. While there is a general consensus that relaxed galaxy clusters exhibit a density profile that is well described by a double power law with outer asymptotic slope -3, there is still controversy about the value of the inner asymptotic slope ![]() with proposed values mainly in the range
with proposed values mainly in the range ![]() 1.0-1.5 (Power et al. 2003; Navarro et al. 2004,1997; Jing & Suto 2002; Tormen et al. 1997; Moore et al. 1998). A similar controversy has arisen over the question whether such cusps are indeed observed in galaxies (see, e.g., Simon et al. 2003, and references therein). However, on galaxy scales, the effect of baryonic collapse and astrophysical feedback processes (such as supernova explosions) may alter significantly the dark halo structure, thus complicating the interpretation of the observations.
1.0-1.5 (Power et al. 2003; Navarro et al. 2004,1997; Jing & Suto 2002; Tormen et al. 1997; Moore et al. 1998). A similar controversy has arisen over the question whether such cusps are indeed observed in galaxies (see, e.g., Simon et al. 2003, and references therein). However, on galaxy scales, the effect of baryonic collapse and astrophysical feedback processes (such as supernova explosions) may alter significantly the dark halo structure, thus complicating the interpretation of the observations.
Strongly lensed arcs in galaxy clusters probe the gravitational potential on scales (
![]() )
large enough to avoid baryonic contamination and are thus an ideal tool for investigating this puzzling question. In particular, radial arcs probe the slope of the mass profile at their positions, while tangential arcs constrain the total mass within their radial distance from the cluster centre. Moreover, a measurement of the velocity dispersion essentially fixes the mass divided by the radius though this estimate is reliable only for relaxed clusters. These observables can then be combined to obtain a powerful method for extracting information on the cluster structure.
)
large enough to avoid baryonic contamination and are thus an ideal tool for investigating this puzzling question. In particular, radial arcs probe the slope of the mass profile at their positions, while tangential arcs constrain the total mass within their radial distance from the cluster centre. Moreover, a measurement of the velocity dispersion essentially fixes the mass divided by the radius though this estimate is reliable only for relaxed clusters. These observables can then be combined to obtain a powerful method for extracting information on the cluster structure.
Note that the second most important component of a galaxy cluster, namely the gaseous intracluster medium (ICM), is often neglected in numerical simulations. In the usual approach, the ICM distribution is determined a posteriori from the dark matter density profile imposing hydrodynamical equilibrium and assuming an isothermal or polytropic equation of state for the gas (Ascasibar et al. 2003; Komatsu & Seljak 2001). However, such an approach is somewhat biased since it relies on hypotheses (isothermality and hydrodynamical equilibrium) that do not hold in real galaxy clusters. On the other hand, it is also possible to determine the radial mass profile of both dark matter and ICM directly from simulations explicitly taking into account the gas component. This is the approach followed in a recent paper by Rasia et al. (2004). Using an extended set of high resolution non-radiative hydrodynamic simulations and assuming spherical symmetry, these authors have first derived the phase space density of the dark matter particles and then given fitting formulae for the density profile and the velocity dispersion, thus allowing them to verify the dynamical equilibrium of the system. Turning then to the hot gas component, they have derived analytic expressions for the density structure, the temperature profile and the velocity dispersion of the ICM without imposing any a priori hypotheses on the gas dynamical status or its equation of state. In particular, Rasia et al. have shown that the isothermality hypothesis breaks down at distances from the centre larger than ![]()
![]() ,
with
,
with ![]() the virial radius of the cluster. The Rasia et al. model (hereafter RTM model) presents some peculiarities that make it different from the other models available in literature. Moreover, all the relevant quantities of both the dark matter and gas have been derived in a self-consistent way free of any bias induced by aprioristic hypotheses on the dynamical state of the system.
the virial radius of the cluster. The Rasia et al. model (hereafter RTM model) presents some peculiarities that make it different from the other models available in literature. Moreover, all the relevant quantities of both the dark matter and gas have been derived in a self-consistent way free of any bias induced by aprioristic hypotheses on the dynamical state of the system.
In particular, the knowledge of the gas profile allows one to resort to a completely different (and complementary) observable. With temperature of the order of few keV, the ICM gas is dense and hot enough that clusters are luminous X-ray sources with the bulk of the X-rays being produced as bremsstrahlung radiation (Sarazin 1998). Electrons in the ICM are not only scattered by ions, but may themselves Compton scatter photons of the cosmic microwave background radiation (CMBR) giving rise to the Sunyaev-Zel'dovich (SZ) effect (see Birkinshaw 1999 for a comprehensive review). The temperature decrement due to the SZ effect is able to provide information on the cluster structure, on the motions of galaxy clusters relative to the Hubble flow and on the Hubble flow itself and the cosmological constants that characterize it (Sereno 2003; Reese et al. 2002).
In order to investigate if the RTM model is viable, a direct comparison with the main cluster observables (both from lensing and SZ effect) is needed. As a first step, one has to study the lensing properties of the RTM model and calculate the SZ effect taking care of the peculiar temperature profile. This is the aim of the present paper.
In Sect. 2 we evaluate the deflection angle and the lensing potential of the spherically symmetric RTM model. Radial and tangential arcs form near the position of the critical curves. Therefore, Sect. 3 is devoted to a detailed investigation of the structure of the critical curves of the model with a particular emphasis on how these properties depend on the model parameters. The effect of taking into account the contribution of the brightest cluster galaxy to the lensing potential is investigated in Sect. 4, while the impact of deviations from spherical symmetry or tidal perturbations from nearby clusters are mimicked by an external shear and discussed in Sect. 5. Having been proposed recently, the RTM model has to be compared with existing models. In particular, in Sect. 6, we compare some of its lensing properties with those of the NFW model investigating possible systematic errors in the virial mass estimate. The computation of the SZ effect due to the distribution of the ICM in the RTM model is presented in Sect. 7, while the results are compared with the prediction of both the ![]() model and the NFW model in Sect. 8 where we also discuss the detectability of RTM clusters in a SZ survey. The details of the numerical simulations on which the RTM model is based may induce systematic errors in the main results. Some qualitative comments on this topic are presented in Sect. 9. We summarize and conclude in Sect. 10.
model and the NFW model in Sect. 8 where we also discuss the detectability of RTM clusters in a SZ survey. The details of the numerical simulations on which the RTM model is based may induce systematic errors in the main results. Some qualitative comments on this topic are presented in Sect. 9. We summarize and conclude in Sect. 10.
Let us adopt a rectangular coordinate system (x, y, z) with its origin in the cluster centre and let
![]() be the usual spherical coordinates. The mass density profile of the RTM model is (Rasia et al. 2004):
be the usual spherical coordinates. The mass density profile of the RTM model is (Rasia et al. 2004):
![\begin{displaymath}\rho_0 = \frac{(1 - f_{\rm b}) \Delta_{\rm v}}{6 \left[ (1 + 2 x_{\rm p})/(1 + x_{\rm p})^{1/2} - 2 x_{\rm p}^{1/2} \right]}
\end{displaymath}](/articles/aa/full/2005/01/aa0426-04/img53.gif) |
(2) |
The RTM model is fully characterized by two parameters, namely the dimensionless scale radius ![]() (or the concentration
(or the concentration
![]() )
and the virial radius
)
and the virial radius ![]() .
However, it is more convenient to express
.
However, it is more convenient to express ![]() in terms of the virial mass (i.e. the total cluster mass)
in terms of the virial mass (i.e. the total cluster mass) ![]() using the following relation:
using the following relation:
As a first step to investigate the lensing properties of the RTM model, we have to evaluate the corresponding surface mass density. Starting from the definition:
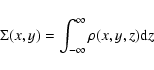
Having obtained the surface mass density, it is now straightforward to compute the deflection angle. Because of the circular symmetry in the lens plane, the deflection angle is purely radial and its amplitude is (Schneider et al. 1992):
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0426fig1.eps} %
\end{figure}](/articles/aa/full/2005/01/aa0426-04/Timg85.gif) |
Figure 1:
The scaled deflection angle
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0426fig2.eps} %\end{figure}](/articles/aa/full/2005/01/aa0426-04/Timg86.gif) |
Figure 2:
The deflection angle at the virial radius
|
| Open with DEXTER | |
This qualitative discussion also explains the behaviour of
![]() with
with ![]() that is shown in Fig. 2. A comment is in order here to understand how this plot has been obtained. Equation (9) shows that
that is shown in Fig. 2. A comment is in order here to understand how this plot has been obtained. Equation (9) shows that
![]() depends on the cluster parameters
depends on the cluster parameters
![]() ,
the lens and source redshift
,
the lens and source redshift
![]() and the background cosmological model. We adopt a flat
and the background cosmological model. We adopt a flat ![]() CDM model with
CDM model with
![]() giving
giving
![]() (Eke et al. 1996). We set
(Eke et al. 1996). We set
![]() as for the real cluster lens MS2137-23 (Sand et al. 2002, 2004). Unless otherwise stated, the same values for the cosmological parameters and the lens and source redshift will be used throughout the paper. To obtain the plot in Fig. 2, we have fixed
as for the real cluster lens MS2137-23 (Sand et al. 2002, 2004). Unless otherwise stated, the same values for the cosmological parameters and the lens and source redshift will be used throughout the paper. To obtain the plot in Fig. 2, we have fixed
![]() ,
but the results for other values of
,
but the results for other values of ![]() may be easily scaled observing that
may be easily scaled observing that
![]() .
.
Let us now derive the lensing potential ![]() for the RTM model. To this end, one should solve the two dimensional Poisson equation (Schneider et al. 1992):
for the RTM model. To this end, one should solve the two dimensional Poisson equation (Schneider et al. 1992):
The most spectacular effect of lensing by a galaxy cluster is the formation of giant arcs (see, e.g., Kneib et al. 1996 for the textbook example of A2218). These are very luminous and highly distorted images of a source galaxy whose position is near one of the critical curves of the lensing potential. The position of the arcs in a given lensing system makes it possible to strongly constrain the cluster mass distribution and can also be used to determine the cosmological parameters (Sereno 2002). Moreover, arc statistics is a promising and efficient tool to discriminate among different cosmological models and theories of structure formation. It is thus quite interesting to investigate the number (and the type) of arcs the RTM model may form.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0426fig3.eps}
\end{figure}](/articles/aa/full/2005/01/aa0426-04/Timg122.gif) |
Figure 3:
Contours of equal Einstein radius |
| Open with DEXTER | |
To this end, let us first remember the expression for the magnification ![]() of a source due to the lensing effect. It is (Schneider et al. 1992):
of a source due to the lensing effect. It is (Schneider et al. 1992):
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0426fig4.eps}
\end{figure}](/articles/aa/full/2005/01/aa0426-04/Timg137.gif) |
Figure 4:
Contours of equal radial critical curve distance
|
| Open with DEXTER | |
Figure 3 shows that highly concentrated clusters (i.e., with small values of ![]() )
give rise to tangential critical curves that are more distant from the cluster centre. Thus, one could qualitatively conclude that only RTM models with lower values of
)
give rise to tangential critical curves that are more distant from the cluster centre. Thus, one could qualitatively conclude that only RTM models with lower values of ![]() are able to produce tangential arcs. However, one should also take into account that, as expected, for a fixed
are able to produce tangential arcs. However, one should also take into account that, as expected, for a fixed ![]() the Einstein radius increases with
the Einstein radius increases with ![]() .
Therefore, RTM models with high values of
.
Therefore, RTM models with high values of ![]() could still produce tangential arcs with large radii provided that the mass is large enough and that it is possible to extrapolate the RTM model outside the mass range probed by the simulations.
could still produce tangential arcs with large radii provided that the mass is large enough and that it is possible to extrapolate the RTM model outside the mass range probed by the simulations.
As said above, radial critical curves are implicitly defined by the condition
![]() .
Inserting Eqs. (4) and (8) into Eq. (21), we get
.
Inserting Eqs. (4) and (8) into Eq. (21), we get
![]() ,
the radial critical curve distance from the cluster centre. To investigate how
,
the radial critical curve distance from the cluster centre. To investigate how
![]() depends on the model parameters, we plot in Fig. 4 the contours of equal
depends on the model parameters, we plot in Fig. 4 the contours of equal
![]() in the
in the
![]() plane. The behaviour of
plane. The behaviour of
![]() with
with
![]() is qualitatively similar to that of the Einstein radius
is qualitatively similar to that of the Einstein radius ![]() ,
but the opposite holds for the dependence on
,
but the opposite holds for the dependence on ![]() .
For a given value of
.
For a given value of
![]() ,
,
![]() increases with
increases with ![]() ,
while
,
while ![]() decreases. As a result, highly concentrated RTM models (i.e. models with small
decreases. As a result, highly concentrated RTM models (i.e. models with small ![]() and henceforth high
and henceforth high
![]() )
give rise to tangential arcs situated at large distances from the cluster centre, but the radial arc lies in the very inner regions of the cluster.
)
give rise to tangential arcs situated at large distances from the cluster centre, but the radial arc lies in the very inner regions of the cluster.
As a simple application of these results, we consider the case of the real cluster lens MS2137-23 in which both a tangential and a radial arc have been observed with
![]() arcsec and
arcsec and
![]() arcsec (Sand et al. 2002, 2004). An easy way to derive the values of the RTM model parameters able to fit the arc positions in MS2137-23 is to draw the contour levels in the plane
arcsec (Sand et al. 2002, 2004). An easy way to derive the values of the RTM model parameters able to fit the arc positions in MS2137-23 is to draw the contour levels in the plane
![]() for
for ![]() and
and
![]() equal to the values quoted above and look for the intersection point between these two curves. It turns out that the best fit parameters are
equal to the values quoted above and look for the intersection point between these two curves. It turns out that the best fit parameters are
![]() ,
i.e.
,
i.e.
![]() and
and
![]() .
As a further test, we also consider the case of the real cluster lens RX J1133 at redshift
.
As a further test, we also consider the case of the real cluster lens RX J1133 at redshift
![]() (Sand et al. 2004). Both a radial and a tangential arc are observed with
(Sand et al. 2004). Both a radial and a tangential arc are observed with
![]() and
and
![]() that may be obtained by describing the cluster with a RTM model with best fit parameters
that may be obtained by describing the cluster with a RTM model with best fit parameters
![]() ,
i.e.
,
i.e.
![]() and
and
![]() .
The values of the concentration are quite high if compared to
.
The values of the concentration are quite high if compared to
![]() found by Rasia et al. (2004) for their sample of simulated clusters. However, this could not be considered evidence against the RTM model. Actually, we have only considered the spherical case, while it is well known that a small cluster ellipticity also changes significantly the position of the critical curves (see, e.g., Bartelmann & Meneghetti 2003). Moreover, one should also take into account the impact on the critical curves of the galaxy lying at the centre of the cluster gravitational potential and of other eventual substructures. That is why we do not speculate further on the high
found by Rasia et al. (2004) for their sample of simulated clusters. However, this could not be considered evidence against the RTM model. Actually, we have only considered the spherical case, while it is well known that a small cluster ellipticity also changes significantly the position of the critical curves (see, e.g., Bartelmann & Meneghetti 2003). Moreover, one should also take into account the impact on the critical curves of the galaxy lying at the centre of the cluster gravitational potential and of other eventual substructures. That is why we do not speculate further on the high
![]() values needed to reproduce the arc positions in MS2137-23 and RX J1133, while a detailed comparison with observations will be presented elsewhere.
values needed to reproduce the arc positions in MS2137-23 and RX J1133, while a detailed comparison with observations will be presented elsewhere.
Some recent studies have highlighted the importance of considering the brightest cluster galaxy (hereafter BCG) when investigating the lensing properties of a cluster (Sand et al. 2004; Meneghetti et al. 2003). It is thus interesting to study how the critical curves of the RTM model are affected by the addition of a BCG. To this end, we place the galaxy exactly at the centre of the cluster and model it using the Hernquist profile whose mass density is (Hernquist 1990):
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0426fig5.eps}
\end{figure}](/articles/aa/full/2005/01/aa0426-04/Timg168.gif) |
Figure 5:
Zero level curves of the denominator in
Eq. (28) in the plane
|
| Open with DEXTER | |
To study where the critical curves form, we plot in Fig. 5 the loci in the
![]() plane where the total magnification formally diverges having arbitrarily fixed
plane where the total magnification formally diverges having arbitrarily fixed
![]() and
and
![]() kpc as for the BCG in MS2137-23 (Sand et al. 2004). The solid line refers to the case with no BCG, while the dashed one shows how the curves are modified by the addition of a BCG with total mass
kpc as for the BCG in MS2137-23 (Sand et al. 2004). The solid line refers to the case with no BCG, while the dashed one shows how the curves are modified by the addition of a BCG with total mass![]()
![]() .
The number of critical curves is still two, but their position is affected by the presence of BCG with the distance between them increased with respect to the case with no BCG. In particular, while
.
The number of critical curves is still two, but their position is affected by the presence of BCG with the distance between them increased with respect to the case with no BCG. In particular, while
![]() is slightly smaller or larger depending on the ratio between the mass of galaxy and that of the cluster, the Einstein radius
is slightly smaller or larger depending on the ratio between the mass of galaxy and that of the cluster, the Einstein radius ![]() significantly increases. This is expected since
significantly increases. This is expected since ![]() is proportional to the total mass within the tangential critical curve so that if the BCG mass is added
is proportional to the total mass within the tangential critical curve so that if the BCG mass is added ![]() ,
gets obviously higher.
,
gets obviously higher.
Figure 6 is similar to Fig. 5, but now the cluster mass is set at
![]() and we let
and we let ![]() change, while the BCG parameters are fixed as before. The increase of
change, while the BCG parameters are fixed as before. The increase of ![]() is still visible, but what is most noteworthy is the possibility to have radial and critical curves with higher values of
is still visible, but what is most noteworthy is the possibility to have radial and critical curves with higher values of ![]() .
From Fig. 6 one sees that, when there is no BCG, RTM models with
.
From Fig. 6 one sees that, when there is no BCG, RTM models with
![]() are unable to produce radial arcs (i.e.
are unable to produce radial arcs (i.e.
![]() ), while the radial critical curve appears when the BCG is taken into account in the total lensing potential even for less concentrated clusters (i.e. with larger
), while the radial critical curve appears when the BCG is taken into account in the total lensing potential even for less concentrated clusters (i.e. with larger ![]() ).
).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0426fig6.eps} %
\end{figure}](/articles/aa/full/2005/01/aa0426-04/Timg176.gif) |
Figure 6:
Same as Fig. 5 but now the
value of |
| Open with DEXTER | |
| |
Figure 7:
Constraints in the
|
| Open with DEXTER | |
Finally, we investigate qualitatively how the constraints on the RTM model parameters are changed by the presence of a BCG. To this end, we plot in Fig. 7 the constraints imposed by the presence of a radial arc at
![]() or a tangential arc at
or a tangential arc at
![]() as observed for the real cluster lens MS2137-23 (Sand et al. 2002, 2004). The results in the right panel are easy to explain qualitatively. Adding a BCG pushes up the curve in the
as observed for the real cluster lens MS2137-23 (Sand et al. 2002, 2004). The results in the right panel are easy to explain qualitatively. Adding a BCG pushes up the curve in the
![]() plane so that a tangential arc at a given distance may be produced by less concentrated and less massive clusters than in the case with no BCG. As already noted,
plane so that a tangential arc at a given distance may be produced by less concentrated and less massive clusters than in the case with no BCG. As already noted, ![]() is proportional to the total projected mass within
is proportional to the total projected mass within ![]() itself. Since now the BCG provides part of this mass, less mass has to be contributed by the cluster and thus less massive and concentrated models are needed to obtain a given value of
itself. Since now the BCG provides part of this mass, less mass has to be contributed by the cluster and thus less massive and concentrated models are needed to obtain a given value of ![]() .
Note, however, that the deviations from the case with no BCG are quite small, as expected given the high mass ratio between the cluster and the galaxy. On the other hand, the left panel shows that adding a BCG requires more concentrated and massive clusters to produce a radial arc at a given
.
Note, however, that the deviations from the case with no BCG are quite small, as expected given the high mass ratio between the cluster and the galaxy. On the other hand, the left panel shows that adding a BCG requires more concentrated and massive clusters to produce a radial arc at a given
![]() than in the case with no BCG. It is also worth noting that the constraints from the position of the radial arc are more sensitive to the presence (or absence) of the BCG (see, e.g., the distance between the solid and dashed line in the left panel compared to the same in the right one). This is expected since the radial critical curve is innermost and thus probes a range that is more sensitive to the inner structure of the cluster where the BCG plays a more significant role.
than in the case with no BCG. It is also worth noting that the constraints from the position of the radial arc are more sensitive to the presence (or absence) of the BCG (see, e.g., the distance between the solid and dashed line in the left panel compared to the same in the right one). This is expected since the radial critical curve is innermost and thus probes a range that is more sensitive to the inner structure of the cluster where the BCG plays a more significant role.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0426fig8.eps}
\end{figure}](/articles/aa/full/2005/01/aa0426-04/Timg181.gif) |
Figure 8:
Critical curves (solid) and caustics (dashed) for
the RTM model with the addition of external shear. Upper panels
are for
|
| Open with DEXTER | |
Up to now, we have investigated the lensing properties of the RTM model (with and without a central BCG) assuming spherical symmetry of the mass distribution. However, real clusters are moderately elliptical and it is well known that even small ellipticities may alter significantly the lensing properties of a given model. In particular, taking into account deviations from spherical symmetry is very important when trying to extract constraints on the model parameters from the position of the lensed arcs in real systems (as clearly demonstrated, for instance, in Bartelmann & Meneghetti 2003; Dalal & Keeton 2003). On the other hand, even when assuming spherical symmetry, it is important to take into account also the effect of substructures in the cluster mass distribution and possible tidal deformations due to nearby clusters. Finally, the large scale structure as a whole could also have a non-negligible effect (Keeton et al. 1997).
To the lowest order, all these effects may be mimicked by adding an external shear to the lensing potential which is now written as:
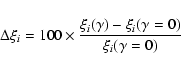
In the case with no shear (upper left panel), the two critical curves are spherical, while the tangential caustic is the origin and the radial one is a circle. The effect of the shear is to deform the critical curves into ellipses, while the inner caustic (corresponding to the tangential critical curve) becomes diamond-shaped and the external one becomes elliptical. In particular, the radial critical curve is more and more elongated along the major axis![]() as the shear strength increases. Quantitatively, this could be seen in Table 1 where
as the shear strength increases. Quantitatively, this could be seen in Table 1 where
![]() is positive and increases with
is positive and increases with ![]() ,
while
,
while
![]() is negative and different from
is negative and different from
![]() .
This is what corresponds graphically to an ellipse more and more elongated along the major axis as
.
This is what corresponds graphically to an ellipse more and more elongated along the major axis as ![]() increases. On the other hand, the tangential critical curve may also deviate from elliptical symmetry and acquire a dumbbell shape as
increases. On the other hand, the tangential critical curve may also deviate from elliptical symmetry and acquire a dumbbell shape as ![]() gets higher. As a consequence, the higher
gets higher. As a consequence, the higher ![]() ,
the higher the the radial arc distance (measured along the major axis),
,
the higher the the radial arc distance (measured along the major axis),
![]() ,
from the cluster centre for fixed values of the RTM model parameters. A similar result holds for
,
from the cluster centre for fixed values of the RTM model parameters. A similar result holds for ![]() .
Note that these effects are qualitatively the same whatever the value of
.
Note that these effects are qualitatively the same whatever the value of ![]() ,
but are more pronounced (i.e.
,
but are more pronounced (i.e.
![]() is larger) for lower values of
is larger) for lower values of ![]() (i.e. higher concentrations) as can be seen from Table 1.
(i.e. higher concentrations) as can be seen from Table 1.
Table 1:
The impact of shear on the length along the major an minor axes of the tangential and radial critical curves. The upper half of the table refers to the RTM model with
![]() ,
while for the lower half
,
while for the lower half
![]() .
In both cases, the virial mass is set to
.
In both cases, the virial mass is set to
![]() .
.
It is interesting to compare the lensing properties of the RTM model with those of the model proposed by Navarro et al. (1997, hereafter NFW) and mostly used in the literature. Using the same normalization as in Rasia et al. (2004), the density profile of the NFW model is:
Using Eqs. (8), (9), (32) and (33) and the definition of virial radius, we get the following expression for the ratio between the deflection angle of the NFW and RTM model:
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0426fig9.eps}
\end{figure}](/articles/aa/full/2005/01/aa0426-04/Timg216.gif) |
Figure 9:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0426fig10.eps}
\end{figure}](/articles/aa/full/2005/01/aa0426-04/Timg217.gif) |
Figure 10:
|
| Open with DEXTER | |
| |
Figure 11:
Contour plot in the
|
| Open with DEXTER | |
The NFW model is used in most of the studies of the structure of dark matter haloes in galaxy clusters. It is therefore interesting to investigate the error induced by using the NFW model to describe a cluster that is actually better described by the RTM model. As a straightforward example, we consider the estimate of the virial mass from the size of the Einstein radius. To this aim, let us look at Fig. 11 where we plot the contour level curves in the
![]() plane for the Einstein radius of the NFW model corresponding to values of
plane for the Einstein radius of the NFW model corresponding to values of ![]() evaluated for RTM models. Let us consider, for instance, the RTM model with
evaluated for RTM models. Let us consider, for instance, the RTM model with
![]() for which one obtains the fourth line (from the left) in the left panel of Fig. 11. If one assumes that Eq. (35) holds, then one should estimate the NFW model parameters from the intersection point of the dashed curve with the fourth line, thus grossly underestimating the mass. Actually, even if one does not use Eq. (35),
for which one obtains the fourth line (from the left) in the left panel of Fig. 11. If one assumes that Eq. (35) holds, then one should estimate the NFW model parameters from the intersection point of the dashed curve with the fourth line, thus grossly underestimating the mass. Actually, even if one does not use Eq. (35), ![]() turns out to be underestimated for the values of
turns out to be underestimated for the values of
![]() in the plot. To get the correct value of
in the plot. To get the correct value of ![]() ,
one should select a value of
,
one should select a value of
![]() that is unrealistically low for a galaxy cluster. We thus conclude that using the NFW model to study a cluster that is intrinsically described by the RTM model leads to underestimating the virial mass by an amount that depends on the concentration of both the NFW and the RTM model.
that is unrealistically low for a galaxy cluster. We thus conclude that using the NFW model to study a cluster that is intrinsically described by the RTM model leads to underestimating the virial mass by an amount that depends on the concentration of both the NFW and the RTM model.
In principle, one should compare the lensing properties of the NFW and of the RTM models by also including the effects of the brightest cluster galaxy and of shear. However, this would increase the number of parameters to eight: two for the NFW model, two for the RTM model, the BCG mass and scale radius and the shear strength and orientation. It is likely that some degeneracies could occur among parameters, rendering a comparison between the NFW and the RTM model meaningless in this case so that we prefer to not perform this test.
At the beginning of 70's, Sunyaev & Zel'dovich (1972,1970) suggested that the cosmic microwave background radiation (CMBR) can be scattered by the trapped hot intracluster electrons giving rise to a measurable distortion of its spectrum. This (inverse) Compton scattering (now referred to as Sunyaev-Zel'dovich effect, hereafter SZE) has been recognized in the last two decades as an important tool for cosmological and astrophysical studies (Birkinshaw 1999). More recently, the SZE has been used to investigate several physical properties of the gas with much attention devoted to the geometry of its density profile as well as its thermodynamical status. In particular, it has been shown that the canonical hypotheses of spherical symmetry and isothermal temperature profile may induce errors (of order ![]() )
in the estimated values of different parameters such as the Hubble constant (Piffaretti et al. 2003; Roettiger et al. 1997).
)
in the estimated values of different parameters such as the Hubble constant (Piffaretti et al. 2003; Roettiger et al. 1997).
The physics of the SZE is quite simple to understand. A gas of electrons in hydrostatic equilibrium within the gravitational potential of a cluster will have a temperature
![]() ,
with M and
,
with M and
![]() typical values of the total mass and size of a cluster. At this temperature, the thermal emission in X-rays is composed of thermal bremsstrahlung and line radiation. Electrons in the intracluster gas are not only scattered by ions, but can themselves scatter photons of the CMBR giving rise, on average, to a slight change in the photon energy. Because of this inverse Thomson scattering, an overall change in brightness of the CMBR is observed. As a consequence, the SZE is localized and visible in and towards clusters of galaxies having X-ray emission strong enough to be detectable.
typical values of the total mass and size of a cluster. At this temperature, the thermal emission in X-rays is composed of thermal bremsstrahlung and line radiation. Electrons in the intracluster gas are not only scattered by ions, but can themselves scatter photons of the CMBR giving rise, on average, to a slight change in the photon energy. Because of this inverse Thomson scattering, an overall change in brightness of the CMBR is observed. As a consequence, the SZE is localized and visible in and towards clusters of galaxies having X-ray emission strong enough to be detectable.
In the non-relativistic limit, the scattering process can be described by the Kompaneets equation
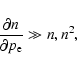 |
(38) |
In the following, we analyze the implications of the gas density and temperature profile of the RTM model for the SZE. Contrary to the lensing applications, we limit our analysis to the spherically symmetric case, without considering any ellipticity in the profiles. The reason for this choice is the fact that the gas profiles have been deduced by means of hydrodynamical (and not simply N-body) simulations, so that the hypothesis of axial symmetry for the density profile is not enough to assure a similar elliptical temperature profile.
The radial dependence of cluster profiles is becoming a testing ground for models of structure formation and for our understanding of gas dynamics in galaxy clusters. Actually, the formation of structures is believed to be driven by some hierarchical development, which leads to the prediction of self-similar scalings between systems of different masses and at different epochs. Moreover, the intracluster gas is generally assumed to be isothermal and in hydrostatical equilibrium. From the observational point of view, however, the situation is rather controversial and yet undetermined: X-ray observations of poor clusters fall below the self similar expectations, and even if the isothermal distribution is often a reasonable approximation to the actual observed clusters, some clusters do not show isothermal distribution (Puy et al. 2000). It turns out that the emerging temperature profile is one where the temperature increases from the center to some characteristic radius, and then decreases again. The central temperature decrement has been much discussed in terms of cooling flows, while the outer temperature decrement seems to be confirmed both observationally and numerically. On the other hand, the temperature profile described in Eq. (44) reproduces quite well some of these observational features: it shows an isothermal core up to
![]() ,
followed by a steep decrease that reaches a factor two lower around the virial radius; the density profiles are self-similar roughly for s > 0.06, while the gas density becomes flatter in the inner region. However, these non-trivial clusters profiles need to be observationally tested. The observations of the SZE, which are becoming increasingly accurate, can be used to probe these properties. Here we analyze the radial dependence of the SZE observables, deferring the comparison with the observational data in the X-ray and SZE domain to a forthcoming paper.
,
followed by a steep decrease that reaches a factor two lower around the virial radius; the density profiles are self-similar roughly for s > 0.06, while the gas density becomes flatter in the inner region. However, these non-trivial clusters profiles need to be observationally tested. The observations of the SZE, which are becoming increasingly accurate, can be used to probe these properties. Here we analyze the radial dependence of the SZE observables, deferring the comparison with the observational data in the X-ray and SZE domain to a forthcoming paper.
The temperature shift may be evaluated inserting Eqs. (43) and (44) into Eqs. (42) and (37) thus obtaining:
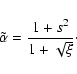
| |
Figure 12:
The structure integral |
| Open with DEXTER | |
Let us now investigate in more detail how the peculiarities of the model affect the structure integral (and hence the comptonization parameter and the temperature shift). First, we consider the effect of the finite extension of the RTM model. To this end, in Fig. 12 we plot the structure integral ![]() as function of
as function of ![]() with the upper (lower) curve obtained assuming l = 1 (
with the upper (lower) curve obtained assuming l = 1 (
![]() )
in Eq. (47). It is worth noting that the usual hypothesis of infinite extension may lead to a significant underestimate of the SZE effect of the model by an amount that depends on the value of
)
in Eq. (47). It is worth noting that the usual hypothesis of infinite extension may lead to a significant underestimate of the SZE effect of the model by an amount that depends on the value of ![]() .
However, since what is usually measured is the temperature shift at the cluster centre, the relative error is not dramatic, being less than
.
However, since what is usually measured is the temperature shift at the cluster centre, the relative error is not dramatic, being less than ![]()
![]() for
for ![]() as shown in Fig. 13. Note, however, that the error due to the finite cluster extension for the RTM model is lower than the corresponding one for the standard
as shown in Fig. 13. Note, however, that the error due to the finite cluster extension for the RTM model is lower than the corresponding one for the standard ![]() model (Puy et al. 2000).
model (Puy et al. 2000).
| |
Figure 13:
The relative error
|
| Open with DEXTER | |
The temperature profile of the RTM model is approximately isothermal up to ![]()
![]() .
Moreover, the isothermality hypothesis is often used in SZE computations. It is thus interesting to investigate what is the systematic error induced by the simplifying assumption
.
Moreover, the isothermality hypothesis is often used in SZE computations. It is thus interesting to investigate what is the systematic error induced by the simplifying assumption
![]() for the RTM model. In this case, the structure integral may be analytically expressed in terms of hypergeometric functions:
for the RTM model. In this case, the structure integral may be analytically expressed in terms of hypergeometric functions:
The peculiar non-isothermal temperature profile of the RTM model makes it different from most of the parametrizations used to describe the gas properties in galaxy clusters. It is thus particularly interesting to compare the SZE signal for the RTM model with that from more standard gas profiles. As interesting examples, we will consider the ![]() and the NFW models.
and the NFW models.
The X-ray surface brightness in galaxy clusters is commonly fitted using the so called ![]() -model (Cavaliere & Fusco Femiano 1976) whose density profile is:
-model (Cavaliere & Fusco Femiano 1976) whose density profile is:
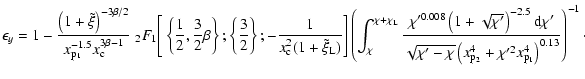 |
(54) |
| |
Figure 14:
The structure integral |
| Open with DEXTER | |
| |
Figure 15:
The relative error in the SZE signal induced by
using the best fit |
| Open with DEXTER | |
Actually, the most interesting implications of the non-isothermal temperature profile for the RTM model with respect to the standard ![]() -model concerns the detectability of a cluster SZE signal, and therefore the statistics of the Sunyaev-Zeldovich clusters in different cosmological models. Even if all of the physics of the effect is coded in the Compton y parameter, it is the total flux density from the cluster that is requested from the observational point of view. This is found by integrating the comptonization parameter over the whole cluster face obtaining:
-model concerns the detectability of a cluster SZE signal, and therefore the statistics of the Sunyaev-Zeldovich clusters in different cosmological models. Even if all of the physics of the effect is coded in the Compton y parameter, it is the total flux density from the cluster that is requested from the observational point of view. This is found by integrating the comptonization parameter over the whole cluster face obtaining:
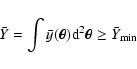 |
(57) |
If the gas temperature profile is isothermal, the integrated SZE flux calculated according to Eq. (55) may be simply related to the temperature-weighted mass of the cluster divided by
![]() ,
where
,
where ![]() is the angular diameter distance. Actually, in an isothermal regime, where d
is the angular diameter distance. Actually, in an isothermal regime, where d
![]() ,
Eq. (55) becomes:
,
Eq. (55) becomes:
| |
Figure 16:
Dependence of
|
| Open with DEXTER | |
However, for the RTM model, the temperature profile is approximately isothermal only in the inner regions (
![]() )
so that the question of the detectability has to be revisited. As a first step, let us compare
)
so that the question of the detectability has to be revisited. As a first step, let us compare
![]() ,
the exact (i.e. computed using the correct temperature profile) integrated SZE flux for the RTM model, with
,
the exact (i.e. computed using the correct temperature profile) integrated SZE flux for the RTM model, with
![]() that is evaluated under the isothermal approximation. These quantities are given as:
that is evaluated under the isothermal approximation. These quantities are given as:
As a consequence, an RTM cluster is also detectable at lower mass regimes than a ![]() -model cluster, as shown from a direct comparison. To this aim, we first recall that the integrated SZE flux for a
-model cluster, as shown from a direct comparison. To this aim, we first recall that the integrated SZE flux for a ![]() -model is:
-model is:
![\begin{displaymath}Y_{\beta} \propto \frac{\xi^2}{3} \times {_2F_1}\left [ \left...
...ac{5}{2} \right \}, - \frac{\xi^2}{x_{\rm c}^2} \right ] \cdot
\end{displaymath}](/articles/aa/full/2005/01/aa0426-04/img336.gif) |
(63) |
Even if the NFW model is mostly used to describe the dark matter rather than the gas distribution in galaxy clusters, it is nonetheless interesting to compare the SZE predictions for the RTM model with the same quantities evaluated for this popular model.
| |
Figure 17:
Comparison of the integrated SZE flux of a |
| Open with DEXTER | |
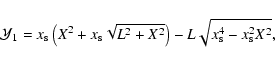 |
(65) |
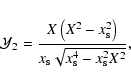 |
(66) |
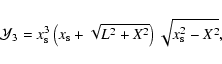 |
(67) |
| |
Figure 18: Relative discrepancy between the Componization parameter for an RTM model and its best fitting NFW model. |
| Open with DEXTER | |
There is a caveat about the RTM model that could affect the main results we have discussed so far. The simulations that have been considered by Rasia et al. (2004) in developping the model are based non-radiative hydrodynamics so that cooling flows and cold blobs that may be on the line of sight are not reproduced. Taking into account these effects is a difficult task, but we expect, qualitatively, that cooling flows and conduction should lower the central temperature and thus increase the SZE signal at the centre. However, we stress that detailed simulations, that also take into account star formation and feedback processes, are needed to investigate how the gas temperature profile (and thus the SZE signal) is affected. Some preliminary results have been presented (Dolag et al. 2004), but the effect on the SZE flux has still to be investigated.
As a final remark, note that merging of clusters has not been considered, but it is likely that this does not affect the main results. Actually, the sample of simulated clusters analyzed by Rasia et al. (2004) comprises both relaxed, unrelaxed and post-merging systems and the RTM model turns out to be a good fit to the full sample which strongly suggests that merging effects do not alter the cluster structure significantly. As a result, the lensing properties of the model are likely to be affected only when the merging is in progress in which case external shear could mimic to first order the deviations from spherical symmetry of the outer regions of the dark matter halo. A stronger effect is expected for the impact of merging on the SZE signal and the X-ray emission, since they depend on
![]() and
and
![]() respectively. Although further detailed simulations are needed to quantitatively address this question, some partial analytical results have already been obtained for some special mergers regimes, when the presence of cold fronts marks the late merging stages: namely the transonic and the subsonic mergers. It turns out that in the transonic regime the frequency spectrum of the SZE signal g(p) changes, due to a shock particle re-acceleration mechanism, depending on the concentration, which induces a new electron population. As net effect, the crossover changes by up to
respectively. Although further detailed simulations are needed to quantitatively address this question, some partial analytical results have already been obtained for some special mergers regimes, when the presence of cold fronts marks the late merging stages: namely the transonic and the subsonic mergers. It turns out that in the transonic regime the frequency spectrum of the SZE signal g(p) changes, due to a shock particle re-acceleration mechanism, depending on the concentration, which induces a new electron population. As net effect, the crossover changes by up to ![]()
![]() .
In the subsonic case, instead, g(p) remains unchanged, but the amplitude of the SZE signal is enhanced in a non-negligible way, mainly in the interior regions of the cluster where it also reaches
.
In the subsonic case, instead, g(p) remains unchanged, but the amplitude of the SZE signal is enhanced in a non-negligible way, mainly in the interior regions of the cluster where it also reaches ![]()
![]() (Koch & Jetzer 2004). Moreover, it is well known (Torri et al. 2004) that the X-ray luminosity overall increases during merging so that it is likely that, as net effect, the SZE signal is enhanced during cluster merging events.
(Koch & Jetzer 2004). Moreover, it is well known (Torri et al. 2004) that the X-ray luminosity overall increases during merging so that it is likely that, as net effect, the SZE signal is enhanced during cluster merging events.
| |
Figure 19: Relative discrepancy between the integrated SZE fluxes for an RTM model and its best fitting NFW model. |
| Open with DEXTER | |
Being detectable at high redshift, galaxy clusters are promising tools for determining cosmological parameters and testing theories of structure formation. Hydrodynamical simulations are able to predict not only the dark matter mass distribution, but also the density law and the temperature profile of the gas component, thus allowing a study of both the lensing properties and the Sunyaev-Zel'dovich effect due to the cluster. This has been the aim of the present paper where we have applied this study to the RTM model, recently proposed by Rasia et al. (2004) on the basis of the results of a large set of high resolution hydrodynamical simulations.
Assuming spherical symmetry in the density profile, we have derived the main lensing properties of the RTM model evaluating the deflection angle and the lensing potential that allows us to write down the lens equations. Most of the work has been devoted to a detailed investigation of the structure of the critical curves of the RTM model since it is the position of radial and tangential arcs (that form just near the critical curves) that gives the most useful constraints on the cluster parameters. The main results are summarized below.
One of the most interesting features of the RTM model is that the temperature profile is approximately isothermal only up to
![]() .
We have investigated the implications for the SZE of the RTM model for the intracluster gas evaluating the structure integral that determines the temperature decrement. We have thus taken into account both the finite extent of the model and its peculiar temperature profile, estimating the errors induced by the usually adopted simplifications of infinite extent and isothermal temperature. The main results are as follows.
.
We have investigated the implications for the SZE of the RTM model for the intracluster gas evaluating the structure integral that determines the temperature decrement. We have thus taken into account both the finite extent of the model and its peculiar temperature profile, estimating the errors induced by the usually adopted simplifications of infinite extent and isothermal temperature. The main results are as follows.
Acknowledgements
We thank Elena Rasia for the interesting discussions on the RTM model characteristics and the impact of merging and cooling flows on the SZE signal. P. Koch is acknowledged for the interesting discussion about the transonic and subsonic merger regimes. We are also grateful to G. Longo, C. Rubano and M. Sereno for a careful reading of the manuscript. Finally, the authors are indebted with the referee, Percy Gomez, for his constructive report that has helped to improve the paper.