A&A 428, 781-791 (2004)
DOI: 10.1051/0004-6361:20041182
Effects of thermal fluctuations in the SPOrt experiment
E. Carretti1 -
M. Zannoni2 -
C. Macculi1 -
S. Cortiglioni1 -
C. Sbarra1
1 - IASF/CNR Bologna, via Gobetti 101, 40129 Bologna, Italy
2 -
IASF/CNR Milano, via Bassini 15, 20133 Milano, Italy
Received 29 April 2004 / Accepted 20 August 2004
Abstract
The role of systematic errors induced by thermal fluctuations is analyzed for the SPOrt experiment with the aim at estimating their impact on the measurement of the
Cosmic Microwave Background Polarization (CMBP). The transfer functions of the antenna devices
from temperature to data fluctuations are computed, by writing them in terms of both instrument and thermal environment parameters. In addition, the corresponding contamination maps are estimated,
along with their polarized power spectra, for different behaviours of the
instabilities. The result is that thermal effects are at a negligible level even for fluctuations
correlated with the Sun illumination provided their frequency
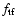 is larger than that of the Sun illumination (
is larger than that of the Sun illumination (
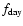 )
by a factor
)
by a factor
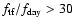 ,
which defines
a requirement for the statistical properties of the temperature behaviour.
The analysis with actual SPOrt operative parameters shows that the instrument is only weakly sensitive to temperature instabilities, the main contribution coming from the cryogenic stage.
The contamination on the E-mode spectrum does not significantly pollute the CMBP signal and no specific data cleaning seems to be needed.
,
which defines
a requirement for the statistical properties of the temperature behaviour.
The analysis with actual SPOrt operative parameters shows that the instrument is only weakly sensitive to temperature instabilities, the main contribution coming from the cryogenic stage.
The contamination on the E-mode spectrum does not significantly pollute the CMBP signal and no specific data cleaning seems to be needed.
Key words: polarization - cosmology: cosmic microwave background -
instrumentation: polarimeters - methods: data analysis
The tiny level of the Cosmic Microwave Background Polarization (CMBP)
requires a careful understanding and estimate of
all systematic effects, which, if not kept under control,
can jeopardize the measurement of the signal.
In the last years several works have been published on this topic, witnessing an increasing interest
in systematics (e.g. Piat et al. 2000; Carretti et al. 2001;
Leahy et al. 2002; Kaplan & Delabrouille 2002;
Mennella et al. 2002; Hu et al. 2003; Page et al. 2003;
Franco et al. 2003; Carretti et al. 2004).
Among others, thermal fluctuations can seriously affect the data
and many teams have studied the impact on their CMB experiments
(e.g. Piat et al. 2000; Mennella et al. 2002; Page et al. 2003).
The importance of thermal fluctuations depends on the receiver scheme and,
in some cases, can be crucial. An example is the total power architecture, where the variations induced onto the data are only slightly dumped with respect to the
primary temperature fluctuations, making the detection
of a 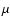 K signal a real challenge even in a very stable thermal environment.
Thus, besides a quiet environment, receivers with a
low sensitivity to temperature are necessary to weaken thermal fluctuations effects.
Having a low offset generation, correlators minimize the thermal disturbance.
K signal a real challenge even in a very stable thermal environment.
Thus, besides a quiet environment, receivers with a
low sensitivity to temperature are necessary to weaken thermal fluctuations effects.
Having a low offset generation, correlators minimize the thermal disturbance.
In this work we present an estimate of the thermal contamination for the SPOrt![[*]](/icons/foot_motif.gif) experiment (Cortiglioni et al. 2004),
a set of four correlation radio-polarimeters devoted to measure the Stokes parameters Q and U of CMBP with an angular resolution of FWHM
experiment (Cortiglioni et al. 2004),
a set of four correlation radio-polarimeters devoted to measure the Stokes parameters Q and U of CMBP with an angular resolution of FWHM 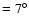 from the International Space
Station (ISS). The ISS environment is not optimal from the thermal point of view. In fact, thermal
simulations show that the Sun illumination modulation due to the motion around the Earth induces
orbit-synchronous temperature fluctuations with
from the International Space
Station (ISS). The ISS environment is not optimal from the thermal point of view. In fact, thermal
simulations show that the Sun illumination modulation due to the motion around the Earth induces
orbit-synchronous temperature fluctuations with 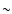 3 K amplitude in case no active temperature control is used. Thus, a careful analysis of thermal effects is mandatory.
3 K amplitude in case no active temperature control is used. Thus, a careful analysis of thermal effects is mandatory.
In the following we derive the transfer functions from temperature to data fluctuations to evaluate
the sensitivity of the SPOrt radiometers to thermal instabilities. In addition,
we study the contamination on the E-mode signal as a function of the statistical properties of the temperature instabilities, aiming at estimating its impact on the cosmological signal.
We show that the SPOrt correlation receivers are naturally an optimal architecture to keep
under control the noise induced by temperature variations, thanks to their low sensitivity to temperature. In fact, the contamination on the E-mode is close to the cosmological signal
already in case of free temperature fluctuations without thermal control, even though not sufficiently low to allow a clean detection. The adoption of an active
control for the horn section further reduces the spurious signal at a comfortably negligible level,
leaving the CMBP signal uncontaminated.
The paper is organized as follows: the computation of the transfer functions is presented in Sect. 2, whereas the effects of the fluctuation statistics and the SPOrt scanning strategy are presented in Sect. 3. The transfer functions and the contamination on the E-mode specific to the SPOrt experiment are given in Sect. 4 and, finally, the conclusions are summarized in Sect. 5.
2 Transfer functions
Thermal fluctuation effects can be evaluated starting from the offset generation equation.
In SPOrt-like correlation polarimeters the offset is mainly generated by horn, polarizer and orthomode transducer (OMT), according to the equation![[*]](/icons/foot_motif.gif) (Carretti et al. 2001)
(Carretti et al. 2001)
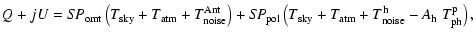 |
|
|
(1) |
where
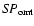 and
and
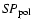 are
are
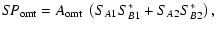 |
|
|
(2) |
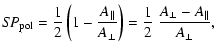 |
|
|
(3) |
SA1, SB2 the transmission parameters of the two OMT arms,
SA2, SB1 their isolation terms, 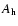 ,
,
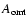 the attenuations of the horn and the OMT, respectively, and
the attenuations of the horn and the OMT, respectively, and 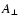 ,
,
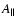 the attenuations of the polarizer along its two main polarizations. The offset sources are thus
the physical temperature of the polarizer
the attenuations of the polarizer along its two main polarizations. The offset sources are thus
the physical temperature of the polarizer
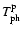 and the signals propagating in the antenna system: the signal collected from the sky (
and the signals propagating in the antenna system: the signal collected from the sky (
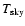 ,
in antenna temperature), the
atmosphere emission (
,
in antenna temperature), the
atmosphere emission (
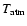 )
and the noise temperatures of the horn alone (
)
and the noise temperatures of the horn alone (
 )
and of the whole antenna system
)
and of the whole antenna system
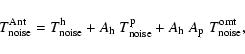 |
(4) |
with 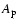 the mean attenuation of the two polarizer arms.
A complete description of derivation
and implications of Eq. (1) is given in
Carretti et al. (2001). Here we
just point out that the offset is generated by OMT and polarizer
that partially correlate the antenna noise
as well as the sky and atmosphere emissions.
the mean attenuation of the two polarizer arms.
A complete description of derivation
and implications of Eq. (1) is given in
Carretti et al. (2001). Here we
just point out that the offset is generated by OMT and polarizer
that partially correlate the antenna noise
as well as the sky and atmosphere emissions.
Practically, all the terms are sensitive to thermal fluctuations:
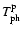 by definition;
by definition;
 ,
,
 and
and
 according to the equations
(e.g. see Kraus 1986)
according to the equations
(e.g. see Kraus 1986)
with
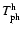 ,
,
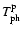 ,
,
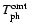 the physical temperatures of horn, polarizer and OMT. Finally,
also attenuations A and coefficients
the physical temperatures of horn, polarizer and OMT. Finally,
also attenuations A and coefficients
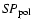 and
and
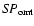 are functions of
the temperature through the relations
(see Appendix A for a detailed derivation)
are functions of
the temperature through the relations
(see Appendix A for a detailed derivation)
Using Eqs. (1)-(8) we can write the
offset variations as a function of those of the
physical temperatures as
where the transfer functions H of the three devices are defined by
with the corrective terms h, p, O given by
These corrective terms, dominated by (A-1) terms, are in general much lower than 1.
Slightly different is 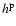 ,
which can be as high as
,
which can be as high as
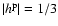 when
when
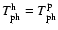 ,
but which, anyway, reduces the instability effects.
,
but which, anyway, reduces the instability effects.
The dumping factors with respect to the thermal fluctuations
are thus given by noise generation terms (A-1) and by
the extra-terms (
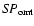 ,
,
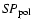 )
typical of the correlation
architecture. Actually,
the offsets for total power outputs are directly given by
)
typical of the correlation
architecture. Actually,
the offsets for total power outputs are directly given by
 (Eq. (4))
and the corresponding transfer functions are
(Eq. (4))
and the corresponding transfer functions are
where the extra terms are not present.
Considering that
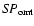 and
and
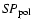 can be as low as
10-3 (see Carretti et al. 2001 for an evaluation of the SPOrt case)
the advantages of correlation architectures become obvious.
can be as low as
10-3 (see Carretti et al. 2001 for an evaluation of the SPOrt case)
the advantages of correlation architectures become obvious.
3 Effects of fluctuation statistics and SPOrt scanning strategy
The transfer functions provide the instantaneous response
to thermal fluctuations. The relevant effects, however,
have to be evaluated on the final maps, which means also
the scanning strategy and
the behaviour of the thermal fluctuations must be
accounted for.
First, we will estimate the dumping factors by an
approximate analytical analysis.
It is a worst case analysis which does not
provide a complete description of the effects - as how the
contamination is spread on the various angular scales -
but it will help us have an insight into the mechanisms dumping the
thermal contaminations.
Then, we will face the exact treatment by simulations which will
provide us with the real contamination maps and
allow us to estimate the contamination on the signal
power spectra.
In this section, we will consider
unit offset fluctuations only (arbitrary units),
to better evaluate the pure effects irrespective of the
real offsets generated by the SPOrt receivers.
The scanning strategy of SPOrt consists in observing
toward the Zenith of the International Space Station
while orbiting in
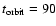 min
around the Earth along a
min
around the Earth along a
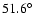 inclination orbit.
The latter is a circle precessing in
inclination orbit.
The latter is a circle precessing in
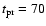 days, so that
the observation of the sky within declinations
days, so that
the observation of the sky within declinations
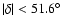 is performed in the same time
(see Cortiglioni et al. 2004 for details).
is performed in the same time
(see Cortiglioni et al. 2004 for details).
The precession moves the trajectory by the 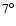 of the beam-size along the Celestial Equator in
of the beam-size along the Celestial Equator in
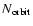
 22 orbits,
during which SPOrt observes the same pixel stripe.
22 orbits,
during which SPOrt observes the same pixel stripe.
The map-making procedure consists in averaging
all the data collected in a pixel (see Sbarra et al. 2003 for details).
Thus the error
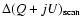 on the maps after
on the maps after
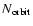 observations is given by
observations is given by
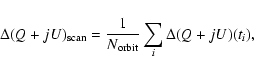 |
(15) |
where ti is the time at the 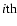 of the
of the
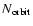 passages.
passages.
The result depends on the behaviour of the fluctuations.
With no loss of generality, we can consider sinusoidal
variations for the temperature of each device
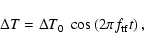 |
(16) |
since a generic function can always be expanded
by Fourier transform (
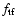 is the fluctuation frequency).
The linear relationship between temperature and offset variations
(Eq. (9)) leads to the same behaviour of
the offset fluctuations
is the fluctuation frequency).
The linear relationship between temperature and offset variations
(Eq. (9)) leads to the same behaviour of
the offset fluctuations
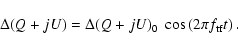 |
(17) |
From a statistical point of view, fluctuations
can be divided in three different types:
- 1.
- Thermal fluctuations synchronous with the Sun illumination
(i.e. the ISS day). In this case the fluctuation
frequency
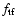 is that of the ISS day
is that of the ISS day
i.e. the orbit frequency
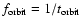 properly corrected for the ISS precession (
properly corrected for the ISS precession (
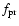 )
and the Sun revolution (
)
and the Sun revolution (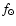 ).
This is the natural behaviour when no active temperature control
is in operation, with
the maximum expected under Sun illumination and the minimum
when in the Earth shadow.
In this case no dumping over the
).
This is the natural behaviour when no active temperature control
is in operation, with
the maximum expected under Sun illumination and the minimum
when in the Earth shadow.
In this case no dumping over the
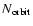 orbits
occurs since, when the instrument is observing toward the
same sky pixel during these consecutive orbits,
the fluctuation has the same phase and the averaging does not
dump the effects on the pixel map (see Mennella et al. 2002).
In this case dumping is simply by a unit factor
orbits
occurs since, when the instrument is observing toward the
same sky pixel during these consecutive orbits,
the fluctuation has the same phase and the averaging does not
dump the effects on the pixel map (see Mennella et al. 2002).
In this case dumping is simply by a unit factor
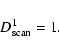 |
(19) |
- 2.
- Thermal fluctuations synchronous with the Sun illumination, but with a
frequency which is an integer multiple of the ISS day
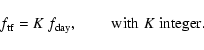 |
(20) |
This situation can occur when an active control is in operation, but
without enough strength to decorrelate the period with respect to
the Sun illumination.
In this case again no dumping occurs over the
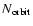 orbits, and
the corresponding dumping factor is
orbits, and
the corresponding dumping factor is
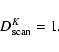 |
(21) |
- 3.
- Thermal fluctuations asynchronous with the night-day cycle
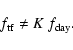 |
(22) |
This situation is typical of cryogenic sections with closed
loop control, where the stabilized temperature
has a behaviour imposed by
the control electronics and in general is independent
of the outer temperature fluctuations.
In this case the situation is better: as described by Mennella et al. (2002) there is a dumping by a factor
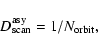 |
(23) |
which greatly reduces the effects on the final maps.
We would like to add only that, differing from the others,
the value of this dumping factor is a conservative estimate,
since it represents the
envelope of actual K values
(see Mennella et al. 2002 for a detailed discussion).
Table 1 reports the worst case
fluctuations on the final maps
after a precession time (in arbitrary units
relative to the amplitude in a single orbit)
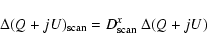 |
(24) |
with x=K or
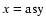 ,
and shows the advantage to be asynchronous with the Sun illumination.
,
and shows the advantage to be asynchronous with the Sun illumination.
Table 1:
Fluctuations on the map after 1 precession time for 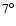 pixels. Values for both synchronous and asynchronous thermal instabilities are reported (see text for details).
pixels. Values for both synchronous and asynchronous thermal instabilities are reported (see text for details).
Actually, in one precession each pixel
is visited twice: once during the first 35 days and a
second time after about half a precession (see Fig. 1).
Since the combination of these two sets of observations does not
play a relevant role in our worst case analysis,
we will discuss it at the end of Sect. 3.2.
![\begin{figure}
\par\includegraphics[angle=90,width=8.6cm,clip]{1182f1.ps}\end{figure}](/articles/aa/full/2004/48/aa1182/Timg103.gif) |
Figure 1:
Sky coverage of two orbits separated by 35 days (dark and light gray).
The 180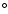 -shift is due to the precession. The central pixel is observed during both orbits.
The map is a mollview projection in Celestial coordinates. -shift is due to the precession. The central pixel is observed during both orbits.
The map is a mollview projection in Celestial coordinates. |
| Open with DEXTER |
3.2 Contamination in the lifetime
So far we have analyzed dumping after just one sky coverage.
As described above, SPOrt observes the whole of the accessible
sky every 70 days and the final map comes
from the combination of these coverages.
The thermal effects on the final map thus
depend on how the contamination maps of each
coverage combine with each other.
In the simple case
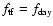 the
fluctuations depend on the Sun illumination and show the maximum temperature
when in presence of the Sun and the minimum when in the Earth shadow.
Over a precession period, SPOrt observes each pixel for
the
fluctuations depend on the Sun illumination and show the maximum temperature
when in presence of the Sun and the minimum when in the Earth shadow.
Over a precession period, SPOrt observes each pixel for
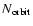 consecutive orbits.
70 Earth-days later, when the precession allows SPOrt to observe the same pixel again,
the illumination conditions are different due to the new position
of the Sun with respect to the Earth. Thus, each pixel will be observed when
temperature fluctuations are in different phases
depending on the observing season, which provides some cancellation effects.
As an example, if a pixel is observed during the day (Sun above the
horizon) with a positive temperature fluctuation, 6 months later it
is observed at night with a negative temperature variation.
consecutive orbits.
70 Earth-days later, when the precession allows SPOrt to observe the same pixel again,
the illumination conditions are different due to the new position
of the Sun with respect to the Earth. Thus, each pixel will be observed when
temperature fluctuations are in different phases
depending on the observing season, which provides some cancellation effects.
As an example, if a pixel is observed during the day (Sun above the
horizon) with a positive temperature fluctuation, 6 months later it
is observed at night with a negative temperature variation.
In fact, as in Eq. (15), the error on the final map is the average of the offset
variations in each observation time:
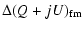 = = 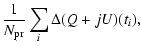 |
(25) |
where
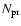 is the number of precessions and tj the observing time.
Two different observations of the same pixel differ for a multiple
of both the orbit time
is the number of precessions and tj the observing time.
Two different observations of the same pixel differ for a multiple
of both the orbit time
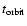 and the precession time
and the precession time
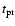 .
Thus, the
.
Thus, the 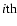 observation of a pixel happens at the time
observation of a pixel happens at the time
where i is the 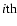 precession, ni the number of orbits at this
precession and
precession, ni the number of orbits at this
precession and
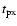 the time when the first observation of the pixel
occurred. Using these expressions for valid ti, Eq. (25) becomes
the time when the first observation of the pixel
occurred. Using these expressions for valid ti, Eq. (25) becomes
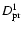 is the dumping factor related to the precession
with respect to the instantaneous offset amplitude
is the dumping factor related to the precession
with respect to the instantaneous offset amplitude
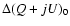 .
It depends not only on the orbital parameters, but also on the pixel
position (by
.
It depends not only on the orbital parameters, but also on the pixel
position (by
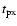 ). In order to evaluate the effects we consider the worst case, i.e. the maximum value of
). In order to evaluate the effects we consider the worst case, i.e. the maximum value of
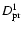 .
Table 2 reports its value
for different mission lifetimes.
.
Table 2 reports its value
for different mission lifetimes.
Table 2:
Dumping factors due to the precession of the SPOrt orbit. The cases of thermal behaviour
synchronous with the Sun illumination with K=1
(
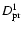 ), K=10 (
), K=10 (
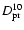 )
and K=30
(
)
and K=30
(
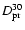 )
are displayed. The asynchronous case (
)
are displayed. The asynchronous case (
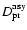 )
is shown as well.
)
is shown as well.
It is worth noting that the best situation corresponds
to 12, 24 and 36 months, during which the mission benefits from complete Sun revolutions.
To understand this, one has to bear in mind that
the phase of the fluctuation at a given pixel
depends on the season and performs
a whole 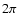 cycle in one year. When the lifetime is
close to a complete Sun revolution (12, 24, 36 months),
the phases taken at the various precessions sample well
the whole cycle and the net effect is a cancellation of
the thermal contributions. On the other hand, when the lifetime is 18 or 30 months,
the last half of a year covers just a half of the whole cycle and the cancellation is not optimal.
cycle in one year. When the lifetime is
close to a complete Sun revolution (12, 24, 36 months),
the phases taken at the various precessions sample well
the whole cycle and the net effect is a cancellation of
the thermal contributions. On the other hand, when the lifetime is 18 or 30 months,
the last half of a year covers just a half of the whole cycle and the cancellation is not optimal.
Moving to the second kind of fluctuations -
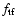 =
=
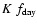 - similar considerations can be done and the errors on the final maps
- similar considerations can be done and the errors on the final maps
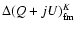 are given by:
are given by:
The worst case is again the maximum value of the dumping factor
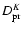 and is reported in Table 2 for different lifetimes and a couple
of K values (namely,
K = 10, 30). While for K=1 the phase
does a complete
and is reported in Table 2 for different lifetimes and a couple
of K values (namely,
K = 10, 30). While for K=1 the phase
does a complete 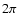 period in one Sun revolution, for K>1 the cycle is closed in 1/K years and, for each pixel, the phase sampling may not be complete and well
distributed over the whole period. Thus, the K>1 case is less predictable and in some pixels
(Table 2 is only the worst case in the whole map)
the fluctuations may be only slightly
dumped, as occurs for K=10 and lifetime = 12 months.
On the other hand, in a few cases (as for K=30, lifetime = 18 months)
even the worst pixel shows a large dumping.
Anyway, in general, the maximum fluctuations
are worse than in the simplest K=1 case.
period in one Sun revolution, for K>1 the cycle is closed in 1/K years and, for each pixel, the phase sampling may not be complete and well
distributed over the whole period. Thus, the K>1 case is less predictable and in some pixels
(Table 2 is only the worst case in the whole map)
the fluctuations may be only slightly
dumped, as occurs for K=10 and lifetime = 12 months.
On the other hand, in a few cases (as for K=30, lifetime = 18 months)
even the worst pixel shows a large dumping.
Anyway, in general, the maximum fluctuations
are worse than in the simplest K=1 case.
Finally, in the case of asynchronous fluctuations the same
situation as the
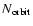 consecutive asynchronous scans occurs,
resulting in a dumping factor by the number of precessions
consecutive asynchronous scans occurs,
resulting in a dumping factor by the number of precessions
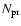
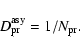 |
(29) |
Results for various lifetimes are again reported in Table 2.
The total reduction on the final map includes the actions
of both the first
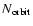 scans and the precession, and
is given by the product
scans and the precession, and
is given by the product
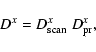 |
(30) |
with x = K or x = asy. It represents the total efficiency with which the
scanning strategy is able to dump the signal fluctuations generated by the system.
The corresponding offset fluctuations
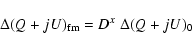 |
(31) |
are reported in Table 3 for two different lifetimes.
Table 3:
Fluctuations on the final map due to both the first
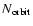 scans and the precession. The values are reported for the four cases described in Table 2 treated in the text and for two different lifetimes. All the fluctuations are in arbitrary units considering
scans and the precession. The values are reported for the four cases described in Table 2 treated in the text and for two different lifetimes. All the fluctuations are in arbitrary units considering
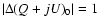 the maximum offset fluctuation in one orbit.
the maximum offset fluctuation in one orbit.
However, these values represent the residual pixel fluctuation only for
the worst pixel. Accounting
for neither the statistical nor angular distribution of the deviations,
they do not provide a complete description
of the impact of thermal fluctuations.
As a final consideration, we recall that in one precession the pixels
are in general visited twice:
once during the first 35 days and a second time after about
half a precession (the exact delay depends on the distance of the
pixel from the Equator).
These two sets of observations can be treated as observations of
two different pixels and
combined only at the end to evaluate the total dumping factor.
They are characterized by two different parallactic
angles and their combination
can lead to some cancellation. In fact,
when the difference between the parallactic angles
is 0 no cancellation occurs;
when the difference is
no cancellation occurs;
when the difference is  ,
the offset is
cancelled out. For the SPOrt scanning strategy, this difference runs
between
,
the offset is
cancelled out. For the SPOrt scanning strategy, this difference runs
between 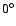 (at the top and bottom edges of the orbit)
and
(at the top and bottom edges of the orbit)
and
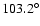 ,
i.e. twice the orbit inclination (at the Equator).
Thus, in our worst case analysis no further cancellation
has to be considered.
,
i.e. twice the orbit inclination (at the Equator).
Thus, in our worst case analysis no further cancellation
has to be considered.
Anyway, a complete treatment of the SPOrt case must be done via simulations,
that, reproducing the real scanning strategy and map-making,
account for all the details.
A complete description of thermal fluctuation effects is
provided by the angular power spectra of the contamination maps.
To estimate these power spectra we simulate
the experiment assuming the offset fluctuations of
Eq. (17) and generating
the final Q, U maps using the SPOrt map-making procedure (Sbarra et al. 2003),
which also accounts for pixel observations at different parallactic angles.
We adopt a unit fluctuation
amplitude
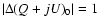 (arbitrary units) to evaluate relative effects.
(arbitrary units) to evaluate relative effects.
Figure 2 reports the results for a 12-month lifetime.
Clearly, the best case is the asynchronous one where the
fluctuations are well dumped on all the scales of interest for SPOrt
(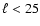 )
reaching values 3.5-5 orders of magnitude lower than the instantaneous fluctuation amplitude (
)
reaching values 3.5-5 orders of magnitude lower than the instantaneous fluctuation amplitude (
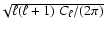 is a fair estimate of the signal).
is a fair estimate of the signal).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1182f2a.ps}\vspace*{5mm}
\includegraphics[width=8cm,clip]{1182f2b.ps}\end{figure}](/articles/aa/full/2004/48/aa1182/Timg137.gif) |
Figure 2:
Top: E-mode power spectra of the contamination of the thermal fluctuations
featuring a unit amplitude
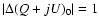 .
A lifetime of 12 months is assumed.
The spectra are presented for four different configurations: synchronous
with the Sun illumination ( .
A lifetime of 12 months is assumed.
The spectra are presented for four different configurations: synchronous
with the Sun illumination (
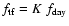 with
K = 1, 10, 30),
and asynchronous. For synchronous cases we plot the average of realizations with different polarization angles of
with
K = 1, 10, 30),
and asynchronous. For synchronous cases we plot the average of realizations with different polarization angles of
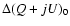 .
The asynchronous case, instead, is the average of many realizations with K in the [30.2, 30.8] range centred on 30.5. Ranges with other central frequencies provide similar results. Bottom: the same but for a 36-month lifetime. .
The asynchronous case, instead, is the average of many realizations with K in the [30.2, 30.8] range centred on 30.5. Ranges with other central frequencies provide similar results. Bottom: the same but for a 36-month lifetime. |
| Open with DEXTER |
The synchronous case with K=1 reduces the contamination as well,
but the dumping is limited to about 2.5 orders of magnitude.
The synchronous case with K > 1 is interesting: dumping is relevant up to a critical 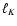 at which the fluctuations dramatically increase at a level much higher than
those for K=1. This confirms the results of the analytical
analysis (see Table 2), where we find
that cases with K>1 can show maximum deviations larger than for K=1.
But much more interesting is the relation between the critical
at which the fluctuations dramatically increase at a level much higher than
those for K=1. This confirms the results of the analytical
analysis (see Table 2), where we find
that cases with K>1 can show maximum deviations larger than for K=1.
But much more interesting is the relation between the critical 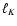 and
the fluctuation frequency: the higher K, the higher
and
the fluctuation frequency: the higher K, the higher 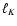 .
That is, the high frequency of the thermal fluctuations brings the power of the contamination
to small angular scales: approximately, a K=1 behaviour generates dipole-like patterns, while,
for a generic K, the dominant structures are approximately on
.
That is, the high frequency of the thermal fluctuations brings the power of the contamination
to small angular scales: approximately, a K=1 behaviour generates dipole-like patterns, while,
for a generic K, the dominant structures are approximately on
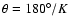 scale.
This is confirmed by the spectral shapes of Fig. 2 where the peak of the spectra
are at
scale.
This is confirmed by the spectral shapes of Fig. 2 where the peak of the spectra
are at
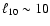 for K=10 and at
for K=10 and at
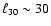 for K=30.
for K=30.
The cleanliness of the K=30 configuration for 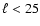 is appealing: all the
is appealing: all the 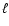 -range accessible to SPOrt has
low contamination (about 1-2 orders of magnitude lower than the case with K = 1),
making the condition K>30 an interesting option for the experiment.
-range accessible to SPOrt has
low contamination (about 1-2 orders of magnitude lower than the case with K = 1),
making the condition K>30 an interesting option for the experiment.
The maps in Fig. 3, reporting the polarized intensity
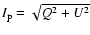 of the contamination with 12-month lifetime,
support this view giving an insight from the pixel-space point of view.
The patterns look different depending on the K value and show
that the higher K, the smaller the size of the dominant structures. Thus,
a K value large enough to make the dominant structures on scales
smaller than
of the contamination with 12-month lifetime,
support this view giving an insight from the pixel-space point of view.
The patterns look different depending on the K value and show
that the higher K, the smaller the size of the dominant structures. Thus,
a K value large enough to make the dominant structures on scales
smaller than  (SPOrt's FWHM) allows the minimization of the thermal fluctuation impact in the angular-scale range of interest for SPOrt.
(SPOrt's FWHM) allows the minimization of the thermal fluctuation impact in the angular-scale range of interest for SPOrt.
It is worth noting that the maximum values of the fluctuations in Fig. 3
are close to those of Table 2, in agreement with the analytical analysis.
The results for a longer lifetime (36 months) are shown in Fig. 2
as well, and their comparison with 12-month spectra gives us
a hint to the time behaviour.
The case K=1 is practically unchanged, confirming
that a longer experiment does not provide a benefit in case of
synchronous fluctuations with K=1 (see Table 2).
![\begin{figure}
\par\includegraphics[angle=90,width=10.6cm,clip]{1182f3aa.eps}\vs...
...ce*{5mm}
\includegraphics[angle=90,width=10.6cm,clip]{1182f3cc.eps} \end{figure}](/articles/aa/full/2004/48/aa1182/Timg143.gif) |
Figure 3:
Polarized intensity
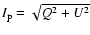 map of the thermal contamination for a 12-month lifetime. The cases K=1 ( top), K=10 ( mid) and K=30 ( bottom) are presented. All fluctuations are in arbitrary units considering
map of the thermal contamination for a 12-month lifetime. The cases K=1 ( top), K=10 ( mid) and K=30 ( bottom) are presented. All fluctuations are in arbitrary units considering
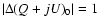 the amplitude in one orbit.
the amplitude in one orbit. |
| Open with DEXTER |
The cases K>1, instead, show a decrement of the thermal fluctuation
contamination, confirming that this configuration is
good for the SPOrt case, at least for K>30.
Finally, the asynchronous case does not show any improvement, in contrast
with the prediction of Table 2.
The numerical error limit is likely to have already been reached.
4 E-mode contamination in the SPOrt case
The SPOrt experiment has two well defined thermal environments
(see also Table 4):
- the horn location with temperature
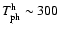 K.
Simulations considering the ISS environment show that the natural
thermal fluctuations, with no thermal control,
are synchronous with the Sun illumination
(
K.
Simulations considering the ISS environment show that the natural
thermal fluctuations, with no thermal control,
are synchronous with the Sun illumination
(
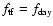 )
with amplitude
)
with amplitude
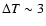 K.
However, the adoption of an active control performed through heaters
ensures a stability
within
K.
However, the adoption of an active control performed through heaters
ensures a stability
within
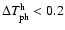 K and
breaks the correlation with the Sun modulation, moving the
fluctuations to shorter periods with frequencies
K and
breaks the correlation with the Sun modulation, moving the
fluctuations to shorter periods with frequencies
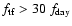 for all the SPOrt radiometers. This
occurs already for the 22 GHz, which,
having the larger heat capacity, is the slowest. In addition, the
fluctuations are decoupled from the Sun illumination modulation
showing an asynchronous behaviour.
for all the SPOrt radiometers. This
occurs already for the 22 GHz, which,
having the larger heat capacity, is the slowest. In addition, the
fluctuations are decoupled from the Sun illumination modulation
showing an asynchronous behaviour.
- the cryogenic part, including polarizer and OMT,
with temperature
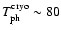 K
and thermal stability within
K
and thermal stability within
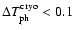 K
provided by a closed-loop cryo-cooler.
These fluctuations are intrinsically
uncorrelated with the Sun illumination.
K
provided by a closed-loop cryo-cooler.
These fluctuations are intrinsically
uncorrelated with the Sun illumination.
Table 4:
Temperature and fluctuations (maximum amplitude)
of the SPOrt antenna devices.
The presence of two thermal environments suggests to rewrite
Eq. (9) as
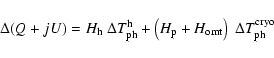 |
(32) |
and to discuss their effects separately.
The offset fluctuations induced by the horn alone are
given by
![$\displaystyle %
\Delta(Q+jU) = {3\over 2}~(A_{\rm h} - 1)
\;\left[S\!P_{\rm omt...
...t) + S\!P_{\rm pol}\left(1+h^{\rm p}\right)\right]
\;\Delta T_{\rm ph}^{\rm h}.$](/articles/aa/full/2004/48/aa1182/img154.gif) |
|
|
(33) |
Table 5 lists the values computed
for the SPOrt receivers at 22 and 90 GHz,
representing the best and worst cases, respectively.
Table 5:
Maximum offset fluctuation
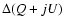 in one orbit (90 min) induced by the horn temperature instabilities for the SPOrt experiment. The cases of the 22 and 90 GHz channels are reported, representing the best and worst cases among the SPOrt receivers. Details about horn temperature fluctuations (
in one orbit (90 min) induced by the horn temperature instabilities for the SPOrt experiment. The cases of the 22 and 90 GHz channels are reported, representing the best and worst cases among the SPOrt receivers. Details about horn temperature fluctuations (
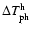 )
and antenna characteristics are also listed: horn attenuation (
)
and antenna characteristics are also listed: horn attenuation (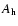 ), OMT isolation (
|SB1|2), polarizer differential attenuation (
), OMT isolation (
|SB1|2), polarizer differential attenuation (
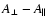 ),
),
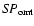 and
and
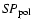 coefficients, and the
coefficients, and the 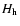 transfer function.
transfer function.
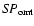 has been estimated with the approximation
has been estimated with the approximation
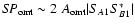 as described in Carretti et al. (2001). The case of a 3 K variation is also shown, that is the natural horn temperature fluctuation without active control.
as described in Carretti et al. (2001). The case of a 3 K variation is also shown, that is the natural horn temperature fluctuation without active control.
A low sensitivity is clearly shown by the
transfer functions, whose levels reduce the impact of
thermal instabilities by 4-5 orders of magnitude.
The offset fluctuations are directly related to the values of
the OMT isolation and the differential attenuation between the
two main polarizations of the polarizer
(see Eqs. (2) and (3)).
Such low offset fluctuations are due to
the improvements in performances of passive devices
obtained by the SPOrt team (Cortiglioni et al. 2004; Peverini et al. 2003).
In fact, state-of-the-art OMTs available at the beginning of the project
had isolations worse than 40 dB, while the device developed for this experiment, with
about 60 dB isolation, leads to a decrease of the offset fluctuations
by a factor about 10.
As described in Sect. 3, the evaluation of the thermal
instability impact has to be performed in the
multipole space, where the contamination
on different angular scales can be estimated and compared to the
expected cosmological signal.
First of all we consider what happens in the case of no
active control, corresponding to a synchronous behaviour
with K=1. The contamination-map power spectra
are shown in Fig. 4, along with the
expected polarized sky emission (E-mode)
as from WMAP best-fit cosmological model
(Spergel et al. 2003; Kogut et al. 2003).
The cosmological signal appears significantly contaminated
even when the optical depth of the reionized medium is
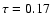 .
This means that the free thermal fluctuations induced by the ISS environment
are too large for such a measurement, calling for a reduction of the thermal disturbances.
.
This means that the free thermal fluctuations induced by the ISS environment
are too large for such a measurement, calling for a reduction of the thermal disturbances.
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{1182f4.ps}\end{figure}](/articles/aa/full/2004/48/aa1182/Timg164.gif) |
Figure 4:
E-mode power spectra of the contamination induced by thermal fluctuations of the horn
in case of no temperature control. Spectra are corrected for the smearing effects of the beam window function. A lifetime of 36 months is considered. The E-mode spectrum expected
for the cosmological signal is also reported for comparison for two
cosmological models: the concordance model as from WMAP's first-year results with
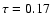 (Spergel et al. 2003); a similar model but with a lower
(Spergel et al. 2003); a similar model but with a lower
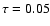 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{1182f5a.ps}\vspace*{5mm}
\includegraphics[width=7.35cm,clip]{1182f5b.ps}\end{figure}](/articles/aa/full/2004/48/aa1182/Timg165.gif) |
Figure 5:
Top: E-mode power spectra of the contamination due to horn thermal fluctuations
with active temperature control. Spectra are corrected for the smearing effects of the beam window function. The 90 GHz receiver and a lifetime of 12 months are assumed. The E-mode spectrum expected for the cosmological signal is also reported for comparison for two cosmological models: that from WMAP first-year results with
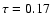 (Spergel et al. 2003); a similar model but with a lower
(Spergel et al. 2003); a similar model but with a lower
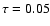 .
Bottom: the same for a 36-month lifetime. .
Bottom: the same for a 36-month lifetime. |
| Open with DEXTER |
Table 6:
As for Table 5, but for the cryo-stage of the SPOrt radiometers.
As a worst case, we assume
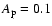 dB and
dB and
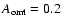 dB the attenuations of
polarizer and OMT, respectively. Anyway, the offset fluctuations are
marginally dependent on their values,
dB the attenuations of
polarizer and OMT, respectively. Anyway, the offset fluctuations are
marginally dependent on their values,
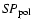 being
the dominant term.
being
the dominant term.
The active control adopted for SPOrt allows temperature fluctuations with
amplitude
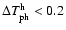 K and
with frequency
K and
with frequency
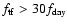 ,
which satisfies the condition identified
in Sect. 3. The power spectrum of the contamination for this configuration
is reported in Fig. 5, where the worst case
(90 GHz receiver) is shown for two different lifetimes (12 and 36 months).
Here we consider both a synchronous behaviour with K=30
and the case of asynchronous fluctuations.
The main result is that already for K=30 and a 12-month lifetime
the contamination is well below the signal, not only for
,
which satisfies the condition identified
in Sect. 3. The power spectrum of the contamination for this configuration
is reported in Fig. 5, where the worst case
(90 GHz receiver) is shown for two different lifetimes (12 and 36 months).
Here we consider both a synchronous behaviour with K=30
and the case of asynchronous fluctuations.
The main result is that already for K=30 and a 12-month lifetime
the contamination is well below the signal, not only for
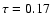 ,
but even for
a lower optical depth
,
but even for
a lower optical depth
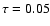 .
A 36-month lifetime provides even better
results. However, the 12-month lifetime already provides a very comfortable scenario which does not need any specific data cleaning.
.
A 36-month lifetime provides even better
results. However, the 12-month lifetime already provides a very comfortable scenario which does not need any specific data cleaning.
The cryo-stage induces offset fluctuations according to the formula
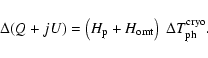 |
(34) |
The values for the 22 and 90 GHz receivers are reported
in Table 6.
In this case the dominant term is related to the polarizer and
only
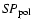 acts to dump the fluctuation, without
contributions from (A-1) terms. As already mentioned
by Carretti et al. (2001), the leading offset due to the
polarizer is a polarized noise generated by the device itself,
rather than the correlation of an unpolarized noise generated by the antenna.
This is why only one dumping factor is in action (
acts to dump the fluctuation, without
contributions from (A-1) terms. As already mentioned
by Carretti et al. (2001), the leading offset due to the
polarizer is a polarized noise generated by the device itself,
rather than the correlation of an unpolarized noise generated by the antenna.
This is why only one dumping factor is in action (
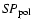 ),
leading to the quite unexpected result that the cryo-stage generates the most
relevant contamination, larger than the horn contribution,
even though the latter is in a warm section.
),
leading to the quite unexpected result that the cryo-stage generates the most
relevant contamination, larger than the horn contribution,
even though the latter is in a warm section.
The behaviour is determined by the cooler electronics, which, performing
an active control to anchor the temperature to a fixed set-point, induces
fluctuations not related with the external environment.
This is true only as a first approximation, since
a small correlation can arise due to the coupling between the
cryo-stage and the feed horn. In fact, these are connected through a
transition waveguide whose aim is to thermally separate the two
environments while allowing the passage of electromagnetic waves.
However, the thermal separator filters the fluctuations
and only a small fraction is transmitted to the cold-stage.
As an example, tests performed during the integration phases
on the BaR-SPOrt receiver, an instrument similar to SPOrt (Cortiglioni et al. 2003),
show that fluctuations of the cold-stage induced by the horn
are a few percent of those of the horn itself. Therefore,
considering a 0.2 K horn temperature variation,
the fluctuations correlated to the warm part are
expected to be no more than few hundredths of Kelvin.
Anyway, should a coupling with the horn arise,
the fluctuations would have a statistics similar to that of the
horn, leading to, as worst case, a periodic behaviour with
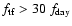 .
.
As for the horn section, we study the
contamination impact through the analysis of the power spectrum.
We perform the analysis for two configurations: the
asynchronous behaviour and the synchronous one with K=30, the latter
representing the worst condition, especially if all the 0.1 K variation
is considered of such a kind. The spectra are reported in Fig. 6
for two different mission durations. Although higher than that
from the horn section, the contamination is again well below the sky signal already for a 12-month
mission and synchronous fluctuations with K=30.
Also this contribution, thus, is unlikely to require any
data cleaning. It is worth noting that even the low
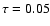 model
is free from contaminations in the
model
is free from contaminations in the 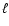 -range where most of the cosmological signal resides (
-range where most of the cosmological signal resides (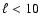 ).
).
5 Summary and conclusions
In this work the importance of the errors induced by thermal instabilities
has been evaluated for the SPOrt experiment.
In particular we have computed and analyzed
- 1.
- The transfer functions of the front-end passive devices (horn, OMT, polarizer)
describing how the temperature fluctuations are reflected on the signal.
- 2.
- The dumping effects on the final sky maps due to both the
SPOrt scanning strategy and the behaviour of the fluctuations.
The main results can be summarized as follows:
- The correlation scheme of SPOrt has a low sensitivity
to temperature instabilities. In fact, the transfer functions
are the products between (A-1) terms, common to total power
architectures, and
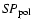 and
and
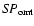 coefficients,
specific to correlators. Thus, these benefit from extra-terms
which further reduce the impact of thermal fluctuations,
making correlators a suitable solution for measurements
of weak signals.
coefficients,
specific to correlators. Thus, these benefit from extra-terms
which further reduce the impact of thermal fluctuations,
making correlators a suitable solution for measurements
of weak signals.
- The 70-day precession of the ISS orbit allows cancellation
effects in the case of fluctuations synchronous with
the Sun illumination (K=1). The dumping is more than 2 orders of magnitude.
- Fluctuations with shorter periods (K > 1) show stronger
dumping, but only on angular scales larger than
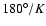 .
In fact,
they move the contamination to multipoles
.
In fact,
they move the contamination to multipoles
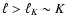 ,
leaving
the range
,
leaving
the range
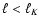 much cleaner than in the
case with K=1. As a consequence,
the condition K>30 is enough to minimize the contamination on
the angular scales accessible to SPOrt (
much cleaner than in the
case with K=1. As a consequence,
the condition K>30 is enough to minimize the contamination on
the angular scales accessible to SPOrt (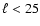 ).
).
- Fluctuations uncorrelated with the Sun illumination represent
the best condition, although their contamination level is not so far
from the synchronous case with K>30;
We would like to point out that the results for K=1 are mainly due to different Sun illumination conditions during the different precession periods.
Therefore, in case of no changes in the thermal conditions during different scans,
this dumping effect would not be present.
An example of such a condition is the Lagrangian point L2
of the Earth-Sun system, where the same
pixel is observed every 6 months with similar
illumination conditions (Sun in the back
of the spacecraft). L2 enjoys an optimal environment stability,
much better than that in the low-orbit of ISS.
However, no dumping effects due to different Sun illumination conditions can be expected, so that
the impact of scan synchronous fluctuations must be carefully evaluated,
especially when dealing with the weak CMBP signal. In this case relevant benefits
can only be obtained from a proper scanning strategy with several crossing
at different angles among the scans, as that of WMAP.
The analysis of the actual antenna system of SPOrt shows a low sensitivity to
thermal instabilities, achieved thanks to both the correlation scheme and
new devices developed by the SPOrt team to minimize systematic effects.
In spite of this, the fluctuations induced by the ISS orbit would be too large to allow a clean detection of CMBP in absence of an active thermal control of the horns.
On the other hand, the active control adopted for the horns
leads to fluctuations featuring an amplitude within 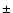 0.2 K (instead of
0.2 K (instead of 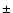 3 K) and a frequency
3 K) and a frequency
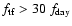 .
Our analysis shows that the resulting contamination is well
below the expected cosmological signal, leaving
the E-mode spectrum of the CMBP uncontaminated.
.
Our analysis shows that the resulting contamination is well
below the expected cosmological signal, leaving
the E-mode spectrum of the CMBP uncontaminated.
The thermal fluctuations of the cold-stage
generate a contamination low enough to allow again
a clean detection of
the CMBP signal, although this is - surprisingly -
the most contaminant source, even larger than that of the warm stage.
The cold stage contribution, being much larger than that from the warm section,
in practice represents the total contamination for the SPOrt experiment,
which thus, in spite of an unfriendly environment, appears to be robust
against systematics induced by thermal fluctuations.
Acknowledgements
This work has been carried out in the frame of the SPOrt experiment,
a programme of the Italian Space Agency (Agenzia Spaziale Italiana: ASI).
We thank Riccardo Tascone for useful discussions and the referee for useful comments.
M.Z., C.M. and C.S. acknowledge ASI grants. Some results of this paper have been derived using the
HEALPix![[*]](/icons/foot_motif.gif) (Górski et al. 1999). We acknowledge the use of the CMBFAST package.
(Górski et al. 1999). We acknowledge the use of the CMBFAST package.
Appendix A: Temperature dependence of attenuation,
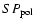 and
and
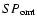
In general, the attenuation A of passive devices like feed horns, polarizers and OMTs
dependes on the electric resistivity in a fashion (e.g. see Collin 1996)
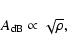 |
(A.1) |
where
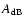 is expressed in dB unit.
In the temperature range of interest for SPOrt (80-300 K), the resistivity
is expressed in dB unit.
In the temperature range of interest for SPOrt (80-300 K), the resistivity 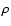 has a linear behaviour with respect to the temperature T for
most of the materials the devices are made of (e.g. Al, Au, Ag), so that
has a linear behaviour with respect to the temperature T for
most of the materials the devices are made of (e.g. Al, Au, Ag), so that
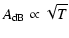 |
|
|
(A.2) |
that means the linear attenuation follows
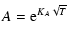 |
|
|
(A.3) |
where KA is a proper constant.
At lower temperature, the linear behaviour of 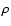 is no more valid and a proper function of T has to be used.
However, this dependence weekens (
is no more valid and a proper function of T has to be used.
However, this dependence weekens (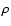 is going to be constant toward T = 0 K) and the variations we derive below
can be considered as a worst case estimate.
is going to be constant toward T = 0 K) and the variations we derive below
can be considered as a worst case estimate.
For devices with low attenuation (A = 1+x, with 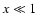 )
a linear approximation
can be applied. In this limit the simple relation
)
a linear approximation
can be applied. In this limit the simple relation
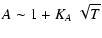 |
|
|
(A.4) |
holds and the variations with respect to T of the attenuations and
the
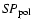 ,
,
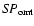 coefficients
can be easily computed. In particular we have the following
results:
coefficients
can be easily computed. In particular we have the following
results:
- 1.
- Attenuations: expanding to the first order of
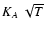 one
gets
one
gets
Alternatively, starting from the first row of the previous equation,
one can also write
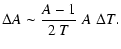 |
|
|
(A.6) |
In this paper we use both of them.
- 2.
- A-1: in similar way, it can be written
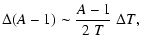 |
|
|
(A.7) |
or, equivalently,
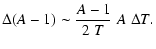 |
|
|
(A.8) |
- 3.
-
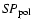 coefficient: Eq. (3) can be written as
coefficient: Eq. (3) can be written as
where 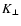 and
and
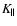 are the KA coefficients of
are the KA coefficients of 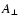 and
and
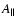 ,
respectively. Therefore, the variation of
,
respectively. Therefore, the variation of
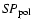 writes
writes
- 4.
-
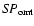 coefficient: this contains not only attenuation terms,
but also the isolations SA2, SB1 between the two OMT arms.
The latter mainly depends on the geometry of the device rather than
on resistive effects, so that, as a first approximation,
they can be considered constant with respect
to the temperature. Equation (2) can be written as
coefficient: this contains not only attenuation terms,
but also the isolations SA2, SB1 between the two OMT arms.
The latter mainly depends on the geometry of the device rather than
on resistive effects, so that, as a first approximation,
they can be considered constant with respect
to the temperature. Equation (2) can be written as
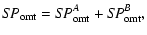 |
|
|
(A.11) |
with
| |
|
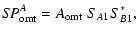 |
|
| |
|
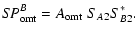 |
(A.12) |
Reminding that the attenuations along the OMT arms are given by
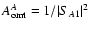 ,
,
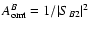 ,
one can
write
,
one can
write
The OMT attenuation
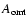 is the average of those along the two arms,
for which, in general, the relation
is the average of those along the two arms,
for which, in general, the relation
 holds. Thus, we can write
holds. Thus, we can write
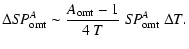 |
|
|
(A.14) |
A similar relation holds for the other term
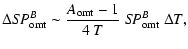 |
|
|
(A.15) |
so that the variation of
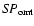 is given by
is given by
- Carretti, E., Tascone, R.,
Cortiglioni, S., Monari, J., & Orsini, M. 2001, New Astron., 6,
173 [NASA ADS] [CrossRef] (In the text)
- Carretti, E., Cortiglioni,
S., Sbarra, C., & Tascone, R. 2004, A&A, 420, 437 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Collin, R. E. 1996,
Foundation for Microwave Engineering (McGrawHill)
(In the text)
- Cortiglioni, S., Bernardi,
G., Carretti, E., et al. 2003, Proc. of the 16th ESA Symp. on
European Rocket and Balloon Programmes and Related Research, ESA
Proc., SP-530, 271
(In the text)
- Cortiglioni, S., Bernardi,
G., Carretti, E., et al. 2004, New Astron., 9, 297 [NASA ADS] [CrossRef] (In the text)
- Franco, G., Fosalba, P.,
& Tauber, J. A. 2003, A&A, 405, 349 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Górski, K. M., Hivon,
E., & Wandelt, B. D. 1999, in Proc. of the MPA/ESO Cosmology
Conference Evolution of Large-Scale Structure, ed. A. J. Banday, R.
S. Sheth, & L. da Costa, Print Partners Ipskamp, NL, 37
[arXiv:astro-ph/9812350]
(In the text)
- Hu, W., Hedman, M. M.,
& Zaldarriaga, M. 2003, PRD, 67, id. 043004
(In the text)
- Kaplan, J., &
Delabrouille, J. 2002, Astrophysical Polarized Backgrounds, ed. S.
Cecchini, S. Cortiglioni, R. Sault, & C. Sbarra, AIP Conf.
Proc., 609, 209
(In the text)
- Kogut, A., Spergel, D. N.,
Barnes, C., et al. 2003, ApJS, 148, 161 [NASA ADS] [CrossRef] (In the text)
- Kraus, J. D. 1986, Radio
Astronomy (Cygnus-Quasar Books)
(In the text)
- Leahy, J. P., Yurchenko,
V., Hastie, M. A., Bersanelli, M., & Mandolesi, N. 2002,
Astrophysical Polarized Backgrounds, ed. S. Cecchini, S.
Cortiglioni, R. Sault, & C. Sbarra, AIP Conf. Proc., 609,
215
(In the text)
- Mennella, A., Bersanelli,
M., Burigana, C., et al. 2002, A&A, 384, 736 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Page, L., Jackson, C.,
Barnes, C., et al. 2003, ApJ, 585, 566 [NASA ADS] [CrossRef] (In the text)
- Peverini, O. A., Tascone,
R., Baralis, M., et al. 2003, in International Conference on
Electromagnetics in Advanced Applications ICEAA '03, Torino 8-12
September 2003, Proceedings of ICEAA '03, 363
(In the text)
- Piat, M., et al. 2000,
Proceedings of LTD-9, NIMA, 444, 413
(In the text)
- Sbarra, C., Carretti, E.,
Cortiglioni, S., et al. 2003, A&A, 401, 1215 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Spergel, D. N., Verde, L.,
Peiris, H. V., et al. 2003, ApJS, 148, 175 [CrossRef] (In the text)
Copyright ESO 2004
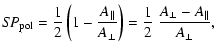
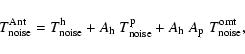
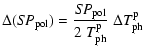
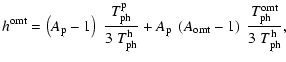
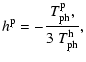
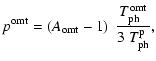
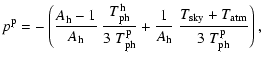
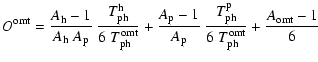
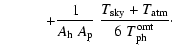
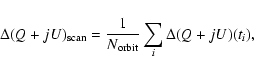
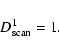
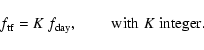
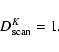
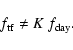
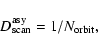
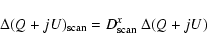
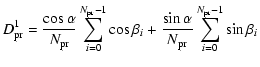
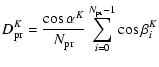
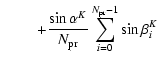
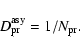
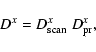
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1182f2a.ps}\vspace*{5mm}
\includegraphics[width=8cm,clip]{1182f2b.ps}\end{figure}](/articles/aa/full/2004/48/aa1182/Timg137.gif)
![\begin{figure}
\par\includegraphics[angle=90,width=10.6cm,clip]{1182f3aa.eps}\vs...
...ce*{5mm}
\includegraphics[angle=90,width=10.6cm,clip]{1182f3cc.eps} \end{figure}](/articles/aa/full/2004/48/aa1182/Timg143.gif)
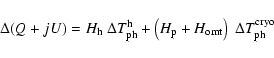
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{1182f4.ps}\end{figure}](/articles/aa/full/2004/48/aa1182/Timg164.gif)
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{1182f5a.ps}\vspace*{5mm}
\includegraphics[width=7.35cm,clip]{1182f5b.ps}\end{figure}](/articles/aa/full/2004/48/aa1182/Timg165.gif)
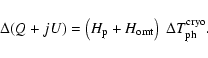
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{1182f6a.ps}\vspace*{5mm}
\includegraphics[width=7.35cm,clip]{1182f6b.ps} \end{figure}](/articles/aa/full/2004/48/aa1182/Timg176.gif)
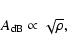
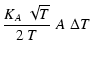
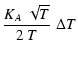
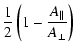
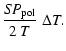
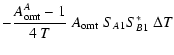
![$\displaystyle \left[ \left(A_{\rm omt}-1\right) -
{1\over 2}\; \left(A_{\rm omt}^A-1\right)\right]\;
{S\!P_{\rm omt}^A \over 2~T}\;\Delta T.$](/articles/aa/full/2004/48/aa1182/img214.gif)