A&A 428, 757-779 (2004)
DOI: 10.1051/0004-6361:20041087
1 - Department of Physics, Tokyo Metropolitan University,
1-1 Minami-osawa, Hachioji, Tokyo 192-0397, Japan
2 -
Institute of Space and Astronautical Science, Japan Aerospace Exploration Agency, 3-1-1 Yoshinodai, Sagamihara, Kanagawa 229-8510, Japan
Received 14 April 2004 / Accepted 22 July 2004
Abstract
We present a uniform analysis of the ROSAT HRI and
the ASCA GIS/SIS data for 79 distant clusters of galaxies
in the redshift range
0.1 < z < 0.82 to study the global
structures of the intracluster medium. We have constructed an
X-ray catalog consisting of the largest sample of clusters in the
redshift range for which pointed X-ray observations were carried
out with both the observatories. We determined the
emission-weighted X-ray temperatures of the clusters with ASCA, while we studied surface brightness distribution with
the ROSAT HRI utilizing the isothermal ![]() model. We
investigated the statistical properties and trends for redshift
evolution of the X-ray parameters including the temperature, the
density profile of the intracluster gas and the gas-mass fraction
within r500. We also present correlations of the
cluster parameters with the X-ray temperature and with the core
radius and compare them with the predictions of the self-similar
model, from which we discuss the possible origin of the double
structure discovered in the core radius distribution.
model. We
investigated the statistical properties and trends for redshift
evolution of the X-ray parameters including the temperature, the
density profile of the intracluster gas and the gas-mass fraction
within r500. We also present correlations of the
cluster parameters with the X-ray temperature and with the core
radius and compare them with the predictions of the self-similar
model, from which we discuss the possible origin of the double
structure discovered in the core radius distribution.
Key words: galaxies: clusters: general - galaxies: intergalactic medium - X-rays: galaxies - cosmology: observations - cosmology: dark matter - catalogs
Clusters of galaxies are the largest collapsed systems known in the universe. Because the time scale of evolution of clusters is a significant fraction of the age of the Universe, the clusters may preserve information about the early universe and thus are considered to be excellent tracers of the formation and evolution of structures. They are considered to continue to grow into larger systems through complex interaction between smaller systems, namely merging process. It is possible that the clusters that we see are in different stages of evolution.
For the understanding of cluster structure and evolution, we believe it is important to analyze systematically a large number of clusters at various redshifts. After the ASCA (Tanaka et al. 1994) and the ROSAT (Trümper 1993) X-ray observatories were put into orbit, it became possible to study relatively distant clusters at X-ray energies. During 7-10 years of observations, more than one hundred clusters were recorded with both observatories. Since ASCA has a high sensitivity to measure the X-ray spectrum in the wide energy band while ROSAT is good at imaging in the soft X-ray band, the two observatories are an excellent combination to study properties of the intracluster medium (ICM). At present the XMM-Newton and the Chandra satellites are in orbit and generate much cluster data with higher sensitivities. However, as we will mention below, the data set used in the present paper will be one of the best existing to construct the largest sample of distant clusters and study global X-ray structures.
X-ray observations bring us valuable information on not only the physical
state of the ICM but also the underlying potential structure of the
clusters. Statistical studies are very powerful in exposing
the physical nature of the clusters. In particular, nearby clusters
have been extensively studied at X-ray wavelengths. As to the low
redshift samples (![]() ), Mohr et al. (1999) performed a
systematic analysis on the ROSAT PSPC data of 45 clusters and
utilizing the published ICM temperatures, they investigated the
correlation between the ICM mass and the temperature, namely the
), Mohr et al. (1999) performed a
systematic analysis on the ROSAT PSPC data of 45 clusters and
utilizing the published ICM temperatures, they investigated the
correlation between the ICM mass and the temperature, namely the
![]() relation. They found that the slope of the relation is
significantly steeper than that predicted from the self-similar model
(Kaiser 1986). The observed luminosity-temperature (
relation. They found that the slope of the relation is
significantly steeper than that predicted from the self-similar model
(Kaiser 1986). The observed luminosity-temperature (
![]() )
relation is also known to be steeper than the expectation of the
self-similar model (e.g. David et al. 1993). The inconsistency
between the observations and the simple theoretical model has been
debated for many years and various possibilities such as
non-gravitational heating (e.g. Evrard & Henry 1991; Cavaliere et al. 1997) and dependence of gas mass or gas-mass fraction
on the temperature have been proposed
(e.g. David et al. 1993; Neumann & Arnaud 2001). For higher
redshift samples, however, the number of clusters that were uniformly
analyzed was limited compared to the nearby clusters. The ASCA
spectroscopic data of distant clusters were compiled by
Mushotzky & Scharf (1997) (38 clusters with z>0.14),
White (2000) (41 clusters with z>0.1 and 65 clusters with
z<0.1), and Novicki et al. (2002) (32 clusters with 0.3<z<0.6 and 53 clusters with z<0.3), while the combined (i.e. spectral and
imaging) analyses of the distant clusters were separately published
in Allen (1998) (13 clusters with
0.1<z<0.45),
Hashimotodani (1999) (27 clusters with
0.1<z<0.78),
Ettori & Fabian (1999) (36 clusters at z>0.05),
Schindler (1999) (11 clusters at z>0.3),
Lewis et al. (1999) (14 clusters with
0.14<z<0.55) and
Vikhlinin et al. (2002) (22 clusters at z>0.4). Recently,
Ettori et al. (2004) reported the Chandra analysis of 28
clusters at 0.4<z<1.3 and observed the steeper slopes in the L-T and the
)
relation is also known to be steeper than the expectation of the
self-similar model (e.g. David et al. 1993). The inconsistency
between the observations and the simple theoretical model has been
debated for many years and various possibilities such as
non-gravitational heating (e.g. Evrard & Henry 1991; Cavaliere et al. 1997) and dependence of gas mass or gas-mass fraction
on the temperature have been proposed
(e.g. David et al. 1993; Neumann & Arnaud 2001). For higher
redshift samples, however, the number of clusters that were uniformly
analyzed was limited compared to the nearby clusters. The ASCA
spectroscopic data of distant clusters were compiled by
Mushotzky & Scharf (1997) (38 clusters with z>0.14),
White (2000) (41 clusters with z>0.1 and 65 clusters with
z<0.1), and Novicki et al. (2002) (32 clusters with 0.3<z<0.6 and 53 clusters with z<0.3), while the combined (i.e. spectral and
imaging) analyses of the distant clusters were separately published
in Allen (1998) (13 clusters with
0.1<z<0.45),
Hashimotodani (1999) (27 clusters with
0.1<z<0.78),
Ettori & Fabian (1999) (36 clusters at z>0.05),
Schindler (1999) (11 clusters at z>0.3),
Lewis et al. (1999) (14 clusters with
0.14<z<0.55) and
Vikhlinin et al. (2002) (22 clusters at z>0.4). Recently,
Ettori et al. (2004) reported the Chandra analysis of 28
clusters at 0.4<z<1.3 and observed the steeper slopes in the L-T and the
![]() relations, which provided hints of
negative evolution in their relations at high redshift.
relations, which provided hints of
negative evolution in their relations at high redshift.
On the other hand, Ota (2001) and Ota & Mitsuda (2002) have
attempted to construct the largest X-ray sample of distant clusters
with z>0.1 based on the combined analysis of the ROSAT HRI and
the ASCA GIS/SIS data. The data set used in the analysis is one
of the best suited for the purpose of the present systematic study for
the following reasons: the largest cluster sample of the pointed
observations were stored in the ROSAT and the ASCA
archival database, which enable us to cover the widest redshift range
up to ![]() .
The focal plane instruments, the ROSAT HRI and
the ASCA GIS/SIS have sufficient sensitivities to study the
global properties of the ICM spatial structure with a typical
resolution of
.
The focal plane instruments, the ROSAT HRI and
the ASCA GIS/SIS have sufficient sensitivities to study the
global properties of the ICM spatial structure with a typical
resolution of
![]() and spectral features such as the ICM
temperature and the luminosity, respectively. In
addition, the instruments' responses were well calibrated and the use
of the same detectors for all the clusters will reduce systematic
effects when comparing their results. Our sample covers the
intermediate redshift range of 0.1-0.8 between those of Mohr et al.'s
sample (z<0.1) and Ettori et al.'s sample (0.4<z<1.3), thus
combining our data with the other two samples is
helpful in discussing the
evolution of internal structure of the ICM directly from the
observational point of views.
and spectral features such as the ICM
temperature and the luminosity, respectively. In
addition, the instruments' responses were well calibrated and the use
of the same detectors for all the clusters will reduce systematic
effects when comparing their results. Our sample covers the
intermediate redshift range of 0.1-0.8 between those of Mohr et al.'s
sample (z<0.1) and Ettori et al.'s sample (0.4<z<1.3), thus
combining our data with the other two samples is
helpful in discussing the
evolution of internal structure of the ICM directly from the
observational point of views.
In this paper we describe a uniform analysis of the ROSAT HRI and
the ASCA SIS/GIS data of 79 clusters performed in
Ota (2001) and Ota & Mitsuda (2002) and thus provide
an X-ray database of ICM structure with the widest
redshift range of
0.1<z<0.82. In order to perform a reliable
parameter determination we paid special attention to evaluating all
possible systematic errors in the spatial and the spectral
analyses. We determined the spectral and spatial properties of the
intracluster gas in terms of the temperature, the core radius and the
central electron density etc. for all of the clusters. In the image
analysis we found that the sample can be naturally classified into
regular and irregular clusters according to the X-ray surface
brightness distribution. We present the statistical properties of the
X-ray parameters and the relations to the double-![]() nature of the
clusters discovered in the core radius distribution. We also estimated
the cluster total mass, the gas mass and the gas-mass fraction within
a radius corresponding to a fixed overdensity of 500. We further
studied the redshift dependency of the parameters and their
correlations, where we considered a systematic error due mainly to the
limited sensitivity of the instruments and some assumptions used in
the estimations.
nature of the
clusters discovered in the core radius distribution. We also estimated
the cluster total mass, the gas mass and the gas-mass fraction within
a radius corresponding to a fixed overdensity of 500. We further
studied the redshift dependency of the parameters and their
correlations, where we considered a systematic error due mainly to the
limited sensitivity of the instruments and some assumptions used in
the estimations.
This paper is organized in the following manner. In the next section, we describe the characteristics of our samples. In Sects. 3 and 4, we explain the methods of spatial analysis with ROSAT and spectral analysis with ASCA in detail. In Sect. 5, we derive the X-ray parameters to describe the global structure of clusters and investigate their redshift dependence. In Sect. 6 we study correlations of the parameters and discuss the properties of the ICM. In Sect. 7 we summarize our results.
We use
![]() ,
,
![]() and
and
![]() .
The quoted errors are the
90% confidence range throughout the paper except where noted.
.
The quoted errors are the
90% confidence range throughout the paper except where noted.
We have selected distant clusters with
![]() for which
pointed X-ray observation data with both ASCA and ROSAT/HRI are available. Though there are 83 clusters which meet
the criteria, we rejected three (A222,
A223, A1758S) because of the large (>210'')
pointing off-axis angles in the ROSAT observations. We did not
include a high-redshift cluster, AXJ2016+112 at z=1(Hattori et al. 1997) because the Chandra observation showed
that the X-ray emission from the direction of AXJ2016+112 can be
resolved into point sources and the cluster diffuse emission is not
prominent (Chartas et al. 2001). The final sample comprises 79
clusters. Among them, three clusters (#1 PKS 0745-19, #6
A2204, and #13 A1689) overlap with
Mohr et al. (1999)'s nearby cluster sample and thirty are known to
have strong gravitational lensing signals
(e.g. Hattori et al. 1999). The observation logs are summarized
in Table 1,
where the clusters were sorted according to the
redshift and numbered from 1 to 79. The redshift distribution of the
sample is shown in Fig. 1a. The clusters with
for which
pointed X-ray observation data with both ASCA and ROSAT/HRI are available. Though there are 83 clusters which meet
the criteria, we rejected three (A222,
A223, A1758S) because of the large (>210'')
pointing off-axis angles in the ROSAT observations. We did not
include a high-redshift cluster, AXJ2016+112 at z=1(Hattori et al. 1997) because the Chandra observation showed
that the X-ray emission from the direction of AXJ2016+112 can be
resolved into point sources and the cluster diffuse emission is not
prominent (Chartas et al. 2001). The final sample comprises 79
clusters. Among them, three clusters (#1 PKS 0745-19, #6
A2204, and #13 A1689) overlap with
Mohr et al. (1999)'s nearby cluster sample and thirty are known to
have strong gravitational lensing signals
(e.g. Hattori et al. 1999). The observation logs are summarized
in Table 1,
where the clusters were sorted according to the
redshift and numbered from 1 to 79. The redshift distribution of the
sample is shown in Fig. 1a. The clusters with
![]() ,
,
![]() and
and
![]() make up 58%, 32%, and
10% of the sample, respectively. The average redshift is 0.30.
make up 58%, 32%, and
10% of the sample, respectively. The average redshift is 0.30.
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1087f1a.eps}\vspace*{1mm}
\par\includegraphics[width=7.2cm,clip]{1087f1b.eps}
\end{figure}](/articles/aa/full/2004/48/aa1087/Timg49.gif) |
Figure 1: a) Redshift distribution of 79 distant clusters. b) Redshift distribution of the 45 regular clusters (open) and the 34 irregular clusters (hatched). |
Because our analysis targets were collected from the proposal observations and the sensitivities for high-redshift clusters are limited, we have to carefully consider possible selection bias. In the first step, we compare the sample with other unbiased cluster samples. We show temperature distributions of our sample and the nearby X-ray flux-limited 55 cluster sample constructed by Edge et al. (1990) in Fig. 2. Our sample covers the equivalent temperature range, but has a higher average temperature of 6.8 keV. The Kolmogorov-Smirnov (K-S) test gave the probability that the two samples are from the same temperature distribution as 0.06 (the K-S parameter, D = 0.24). Observation bias will be discussed in Sects. 5.1.1 and 5.2.2 in more detail.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{1087f2.eps}
\end{figure}](/articles/aa/full/2004/48/aa1087/Timg50.gif) |
Figure 2: Comparison of the temperature distribution of our 79 distant clusters (open) to the nearby flux limited 55 sample of Edge et al. (1990) (hatched). |
We have retrieved the event lists of the ROSAT HRI detector from
the ROSAT Data Archive of the Max-Plank-Institut für
extraterrestrische Physik (MPE) at Garching, Germany. We used the
EXSAS analysis package (Zimmermann et al. 1992) to produce X-ray
images from the event lists. The raw HRI data has a 0
![]() 5 spatial
resolution. However, since the half power diameter of the X-ray
telescope is 4
5 spatial
resolution. However, since the half power diameter of the X-ray
telescope is 4
![]() 8 at the optical axis and the photon counting
statistics of the present data are limited, it is not worth
oversampling the telescope point spread function (PSF). We thus
rebinned the image into
8 at the optical axis and the photon counting
statistics of the present data are limited, it is not worth
oversampling the telescope point spread function (PSF). We thus
rebinned the image into
![]() bins, within whose diameter about
70% of photons from a point source are included.
bins, within whose diameter about
70% of photons from a point source are included.
If there were multiple pointings for a cluster, and the pointing
offset angles between them are smaller than
![]() ,
we superpose the
event lists in the sky coordinate. The PHA channel of 1-10, which
corresponds to 0.2-2 keV, was used to avoid particle background
events.
,
we superpose the
event lists in the sky coordinate. The PHA channel of 1-10, which
corresponds to 0.2-2 keV, was used to avoid particle background
events.
Next we searched for foreground/background sources in the field of view with the standard source detection program in the EXSAS. We created lists of all the sources detected by the maximum likelihood technique and having a likelihood of >8. We used the lists to exclude those sources from the analysis.
![\begin{figure}
\par\includegraphics[width=10.7cm,clip]{1087f3.eps}
\end{figure}](/articles/aa/full/2004/48/aa1087/Timg57.gif) |
Figure 3:
Centroid determination and classification of X-ray
morphology. #13 A1689 and #19 A2163 are
shown in the left and right panels, respectively. From top to bottom:
a) the HRI image in the pixel coordinates. b) The centroids
determined in circles of radii
|
We apply a method to determine cluster centroids and classify the
morphology of clusters. A similar technique to find the cluster
center was first introduced by Mohr et al. (1993). We extended the
method to evaluate the systematic errors of the centroid
determination for distant clusters and found that the analysis can
also be used to determine the regularity of the X-ray distribution. The
cluster emission is typically extended about
![]() from the
optical axis of the telescope. In this image region, the position
dependence of the telescope vignetting is known to be less than 2%
(Briel et al. 1997). The position dependence of the background
intensity is also small up to
from the
optical axis of the telescope. In this image region, the position
dependence of the telescope vignetting is known to be less than 2%
(Briel et al. 1997). The position dependence of the background
intensity is also small up to
![]() .
Thus they do not affect
the centroid determination.
.
Thus they do not affect
the centroid determination.
The analysis consists of two major steps. First we estimate the 0th order center position and a parameter which represents the extent of the X-ray image, utilizing 1-dimensional image projections and Gaussian fits to them. Then, starting from the 0th order initial value, we determine the center from the center of gravity of the photon distribution.
First, we extracted a
![]() image that contains the
central region of the cluster emission. Then we projected along the x-
and y-axes to get one-dimensional intensity profiles. We fit these
with Gaussian functions, and determined the mean,
(xG,0, yG,0)and the width,
image that contains the
central region of the cluster emission. Then we projected along the x-
and y-axes to get one-dimensional intensity profiles. We fit these
with Gaussian functions, and determined the mean,
(xG,0, yG,0)and the width,
![]() .
To determine
these values with higher accuracy, we extracted an image of size
.
To determine
these values with higher accuracy, we extracted an image of size
![]() whose center is at
(xG,0,
yG,0) and performed the one-dimensional Gaussian fitting again to
derive the next set of
(xG,1, yG,1) and
whose center is at
(xG,0,
yG,0) and performed the one-dimensional Gaussian fitting again to
derive the next set of
(xG,1, yG,1) and
![]() .
The procedure was iterated i times
until the mean position converged within 0.1 pixels i.e.
|(xG,i,
yG,i) - (xG,i-1, yG,i-1)| < (0.1, 0.1) or the number of
iterations reached i=20. We then define a parameter
.
The procedure was iterated i times
until the mean position converged within 0.1 pixels i.e.
|(xG,i,
yG,i) - (xG,i-1, yG,i-1)| < (0.1, 0.1) or the number of
iterations reached i=20. We then define a parameter
![]() as
as
![]() ,
which is a
measure of the image extent for further analysis.
,
which is a
measure of the image extent for further analysis.
Next we determine the cluster center from the center of gravity of the
photon distribution in an aperture circle of radius, R. Then if
the X-ray image is circularly symmetric and the center of the circle is
at the X-ray center, the center of gravity of the photon distribution
should coincide with the center of the circle. For a given value of
R, we can determine the center position,
![]() ,
where
,
where ![]() represents the position
of the photon, and
represents the position
of the photon, and ![]() sums all the photons over the circular
area of the radius R. Then starting with the mean position
determined in the previous paragraph,
sums all the photons over the circular
area of the radius R. Then starting with the mean position
determined in the previous paragraph,
![]() ,
we extract a circular image of the radius R centered at
,
we extract a circular image of the radius R centered at ![]() ,
and calculate the centroid position
,
and calculate the centroid position ![]() .
We continue the
iteration until
.
We continue the
iteration until
![]() becomes less than 0.1
pixels. If there were contaminating sources in the circle, we
excluded the region centered at the sources and the region symmetric
to them so as not to affect the centroid determination. We changed
the aperture radius R from 2
becomes less than 0.1
pixels. If there were contaminating sources in the circle, we
excluded the region centered at the sources and the region symmetric
to them so as not to affect the centroid determination. We changed
the aperture radius R from 2
![]() to 9
to 9
![]() to
study the R dependence of the results. As a result, while some
clusters showed constant centroids almost independent of the radius,
others exhibited systematic behavior. Two representative cases are
shown in Fig. 3.
to
study the R dependence of the results. As a result, while some
clusters showed constant centroids almost independent of the radius,
others exhibited systematic behavior. Two representative cases are
shown in Fig. 3.
The dependence of the center of gravity on the aperture radius may
indicate some asymmetry or substructures of the cluster. However,
because the results with different R are not statistically
independent, the Poisson fluctuations may produce systematic
deviations. To estimate this effect, we performed
Monte-Carlo simulations and generated a number of simulation images
assuming the isothermal ![]() -model as the X-ray image distribution.
We calculated the RMS value of the distance between the center of
gravity and the true center,
-model as the X-ray image distribution.
We calculated the RMS value of the distance between the center of
gravity and the true center,
![]() ,
for various
combinations of parameters, the cluster core radius
,
for various
combinations of parameters, the cluster core radius ![]() ,
the number
of photons N and the size of the aperture R, while
,
the number
of photons N and the size of the aperture R, while ![]() was
fixed to the typical value of 0.67.
was
fixed to the typical value of 0.67.
If the displacement of the center of gravity with different values of the
aperture radius R is larger than the standard deviation determined
from the simulation, we can conclude that there is asymmetry or
substructures. In Fig. 3, we show the deviation of the
center of gravity from that determined for
![]() normalized by the standard deviation. For some clusters the deviation
is well within the
normalized by the standard deviation. For some clusters the deviation
is well within the
![]() level; however, for others it is not.
We define criteria for irregularity of clusters as follows: (1) more
than 1 data point whose deviation exceeds
level; however, for others it is not.
We define criteria for irregularity of clusters as follows: (1) more
than 1 data point whose deviation exceeds
![]() ,
and/or
(2) deviations (
,
and/or
(2) deviations (
![]() )
seen in more than a few
consecutive points. Accordingly, we classified our sample into regular
and irregular clusters. The results are listed in Table 2.
The ratio of regular to irregular is 45:34 and
the redshift distributions of the two subgroups are shown in Fig.
1b.
)
seen in more than a few
consecutive points. Accordingly, we classified our sample into regular
and irregular clusters. The results are listed in Table 2.
The ratio of regular to irregular is 45:34 and
the redshift distributions of the two subgroups are shown in Fig.
1b.
We derive azimuthally-averaged radial profiles of the X-ray surface
brightness centered at the cluster centroids that were determined
within the
![]() aperture radii for both the regular and
irregular clusters. We have chosen the centroids because they are less
affected by the Poisson fluctuations in the outer image regions. The
bin size of the radial profile is 5
aperture radii for both the regular and
irregular clusters. We have chosen the centroids because they are less
affected by the Poisson fluctuations in the outer image regions. The
bin size of the radial profile is 5
![]() .
We excluded the
contaminating sources from the integration area with a circle of radius
5 times the FWHM of the PSF at position.
.
We excluded the
contaminating sources from the integration area with a circle of radius
5 times the FWHM of the PSF at position.
We study the effect of the choice of the center on the results of
the radial profile fits, by shifting the center positions determined
for R between
![]() and
and
![]() .
We found the
.
We found the
![]() -model parameters (Sect. 3.4) constant
within the statistical errors for all the regular clusters and many of
the irregular clusters. For 30% of the irregular clusters, the resulting core
radius increases typically by a factor of 2 as R increases from
-model parameters (Sect. 3.4) constant
within the statistical errors for all the regular clusters and many of
the irregular clusters. For 30% of the irregular clusters, the resulting core
radius increases typically by a factor of 2 as R increases from
![]() to
to
![]() .
.
In the following two subsections, we analyze the X-ray radial profile
under the isothermal ![]() -model (Cavaliere & Fusco-Femiano 1976). The
single
-model (Cavaliere & Fusco-Femiano 1976). The
single ![]() -model fitting function is written as
-model fitting function is written as
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1087f4a.eps}\par\includegraphics[width=8cm,clip]{1087f4b.eps}
\end{figure}](/articles/aa/full/2004/48/aa1087/Timg82.gif) |
Figure 4:
Radial X-ray surface brightness profile of #13
A1689 fitted with the single |
It is crucial for reliable determination of the model parameters to
estimate the background level correctly. The HRI background is
dominated by the particle background (Briel et al. 1997) and the
detailed calibration by Snowden (1998) showed that it can be
modeled by a constant image within ![]() from the detector
center. The counting rate of the particle background depends strongly
on the satellite orbit and time, and typically ranges from 1 to 10
from the detector
center. The counting rate of the particle background depends strongly
on the satellite orbit and time, and typically ranges from 1 to 10
![]() over the entire detector. Thus the background counting rate
needs to be determined observation by observation. We determined the
background level from the radial profile including the background as
one of the fitting parameters as Eq. (1). Since
we do not know the true extent of the cluster emission and also
over the entire detector. Thus the background counting rate
needs to be determined observation by observation. We determined the
background level from the radial profile including the background as
one of the fitting parameters as Eq. (1). Since
we do not know the true extent of the cluster emission and also ![]() and
and ![]() are strongly coupled (Fig. 5), the background
level and the model parameters depend on the outer radius of the
fitting area,
are strongly coupled (Fig. 5), the background
level and the model parameters depend on the outer radius of the
fitting area,
![]() .
Particularly when
.
Particularly when
![]() is too
small, the background level determined from the fit tends to be over-
or under-estimated and results in uncertain
is too
small, the background level determined from the fit tends to be over-
or under-estimated and results in uncertain ![]() and
and ![]() .
However, as shown in Fig. 6, the best-fit parameters
converge to constants if
.
However, as shown in Fig. 6, the best-fit parameters
converge to constants if
![]() is large enough, typically
is large enough, typically
![]() .
For all the clusters, we confirmed that the
parameters converge at
.
For all the clusters, we confirmed that the
parameters converge at
![]() .
Thus we decided to
adopt this value for all clusters, within which the background can be
regarded as constant. Finally the background level we obtained from
fits are reasonable background levels.
.
Thus we decided to
adopt this value for all clusters, within which the background can be
regarded as constant. Finally the background level we obtained from
fits are reasonable background levels.
![\begin{figure}
\par\includegraphics[width=5.8cm,clip]{1087f5.eps}
\end{figure}](/articles/aa/full/2004/48/aa1087/Timg87.gif) |
Figure 5:
|
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{1087f6.eps}
\end{figure}](/articles/aa/full/2004/48/aa1087/Timg91.gif) |
Figure 6:
Effect of the outer cut off radius in the single |
Because the effective area of the X-ray telescope decreases with
off-axis angle, the cluster image may be affected by the
vignetting. However since the off-axis angle of the cluster centroid
of the present data is smaller than
![]() ,
and the typical
spatial extent of the present clusters is
,
and the typical
spatial extent of the present clusters is
![]() ,
the
vignetting effect is at most 3% at the rim of the clusters (the HRI
vignetting function is given in Briel et al. (1997)). Although we
performed fits with the
,
the
vignetting effect is at most 3% at the rim of the clusters (the HRI
vignetting function is given in Briel et al. (1997)). Although we
performed fits with the ![]() -model fitting function with and
without the correction of the vignetting function, the results showed
no difference.
-model fitting function with and
without the correction of the vignetting function, the results showed
no difference.
The ![]() -model function needs to be convolved with the X-ray
telescope PSF, then integrated over the image bin. However, since the
present image bin size is larger than the extent of the PSF, the
convolution with the PSF is not important. Also, the
-model function needs to be convolved with the X-ray
telescope PSF, then integrated over the image bin. However, since the
present image bin size is larger than the extent of the PSF, the
convolution with the PSF is not important. Also, the ![]() -model
function varies slowly within the
-model
function varies slowly within the
![]() bins in most cases, so
integration within the image bin can be replaced by the value at the
center of the bin. We confirmed these with simulations by comparing
two cases with and without convolution in the fitting model. As
shown in Fig. 7, we find the difference of the two cases to be
negligibly small as long as the core radius is larger than the bin
size,
bins in most cases, so
integration within the image bin can be replaced by the value at the
center of the bin. We confirmed these with simulations by comparing
two cases with and without convolution in the fitting model. As
shown in Fig. 7, we find the difference of the two cases to be
negligibly small as long as the core radius is larger than the bin
size,
![]() .
We also confirmed that both cases well
reproduce the assumed
.
We also confirmed that both cases well
reproduce the assumed ![]() value of 0.6 within reasonable
statistical errors. Thus in order to make the computation time
shorter, we skip the convolution with the PSF and the integration over
the bin. If the best-fit value (and the error domain) of the core
radius is smaller than the bin size, we regard it as an upper limit.
value of 0.6 within reasonable
statistical errors. Thus in order to make the computation time
shorter, we skip the convolution with the PSF and the integration over
the bin. If the best-fit value (and the error domain) of the core
radius is smaller than the bin size, we regard it as an upper limit.
In Fig. 5, we showed a ![]() contour map on the
contour map on the
![]() plane where the other free parameters, S0 and C, are
optimized at each point of the plane. The two parameters are strongly
coupled and the allowed parameter range exists in an elongated
region. We quote the 90% confidence intervals on the best-fit
parameters. Table 2
lists the results of single
plane where the other free parameters, S0 and C, are
optimized at each point of the plane. The two parameters are strongly
coupled and the allowed parameter range exists in an elongated
region. We quote the 90% confidence intervals on the best-fit
parameters. Table 2
lists the results of single ![]() -model
fitting. For #43 A1758 and #79 MS1054.5-0321,
because the fitting parameters did not converge properly, we optimized
the parameters within the range of
-model
fitting. For #43 A1758 and #79 MS1054.5-0321,
because the fitting parameters did not converge properly, we optimized
the parameters within the range of
![]() .
.
We compared the results of ![]() -model fitting with
Hashimotodani (1999) for 27 ROSAT/HRI clusters with
0.1<z<0.78 and Ettori et al. (2004) for 10 high redshift Chandra clusters with constrained model parameters. We found that
there is a good agreement for
-model fitting with
Hashimotodani (1999) for 27 ROSAT/HRI clusters with
0.1<z<0.78 and Ettori et al. (2004) for 10 high redshift Chandra clusters with constrained model parameters. We found that
there is a good agreement for ![]() and
and ![]() measurements between
our and Hashimotodani samples within their statistical
errors. Furthermore for 8 of the 10 high redshift clusters, there is a
good agreement between our and the Ettori et al. samples within the 90%
statistical errors. For the two highest redshift samples, #70
RX J1347.5-1145 (z=0.451) and #71 3C 295
(z=0.4641),
measurements between
our and Hashimotodani samples within their statistical
errors. Furthermore for 8 of the 10 high redshift clusters, there is a
good agreement between our and the Ettori et al. samples within the 90%
statistical errors. For the two highest redshift samples, #70
RX J1347.5-1145 (z=0.451) and #71 3C 295
(z=0.4641), ![]() is systematically smaller by about 40% compared
to the Chandra measurements.
is systematically smaller by about 40% compared
to the Chandra measurements. ![]() is also systematically
smaller with the mean ratio of 0.93 for 10 high redshift samples,
although the difference is the
is also systematically
smaller with the mean ratio of 0.93 for 10 high redshift samples,
although the difference is the
![]() effect. We consider that
the limited sensitivity of the HRI for the outer part of the cluster
emission may cause the underestimation of
effect. We consider that
the limited sensitivity of the HRI for the outer part of the cluster
emission may cause the underestimation of ![]() for the highest
redshift (z>0.4) samples.
for the highest
redshift (z>0.4) samples.
As a result, the fractions of clusters with ![]() values exceeding
the 90% and 99% confidence levels are 25/79 (=0.32) and 11/79
(=0.14), respectively. The fractions are larger than expected only by
the statistical errors. Thus there may be some systematic errors that
are not well explained by the single
values exceeding
the 90% and 99% confidence levels are 25/79 (=0.32) and 11/79
(=0.14), respectively. The fractions are larger than expected only by
the statistical errors. Thus there may be some systematic errors that
are not well explained by the single ![]() -model. For some
clusters, systematic deviations from the current model are
particularly seen in the central regions (e.g. #13 A1689),
which will be discussed in the next subsection.
-model. For some
clusters, systematic deviations from the current model are
particularly seen in the central regions (e.g. #13 A1689),
which will be discussed in the next subsection.
We also evaluated an X-ray significance radius, ![]() ,
representing
the extension of the observed cluster X-ray emission at which the
best-fit
,
representing
the extension of the observed cluster X-ray emission at which the
best-fit ![]() -model surface brightness becomes equal to the
-model surface brightness becomes equal to the
![]() background level. The results are also listed in Table 5.
background level. The results are also listed in Table 5.
For some clusters, systematic residuals are seen in the results of
single ![]() -model fitting. As often seen in nearby clusters, this
may be attributed to the presence of central excess emission. The
excess component is often represented by an additional
-model fitting. As often seen in nearby clusters, this
may be attributed to the presence of central excess emission. The
excess component is often represented by an additional ![]() -model
component (Jones & Forman 1984), whose core radius is
-model
component (Jones & Forman 1984), whose core radius is
![]() kpc, and on average
60 h50-1 kpc
(Mohr et al. 1999). This corresponds to only several bins of the
present analysis even at z=0.1. It is not easy to constrain such
central emission in the distant clusters. To evaluate
the statistical significance of the central emission, we attempted two
methods. We restrict this analysis to the 45 regular clusters because
the irregular clusters are often accompanied by substructures, which
can cause artificial double structures in their radial profiles.
kpc, and on average
60 h50-1 kpc
(Mohr et al. 1999). This corresponds to only several bins of the
present analysis even at z=0.1. It is not easy to constrain such
central emission in the distant clusters. To evaluate
the statistical significance of the central emission, we attempted two
methods. We restrict this analysis to the 45 regular clusters because
the irregular clusters are often accompanied by substructures, which
can cause artificial double structures in their radial profiles.
In the first analysis, we exclude central bins from the fit and
investigate the variation of single ![]() -model parameters against
the inner cutoff radius,
-model parameters against
the inner cutoff radius,
![]() .
We test the improvement in the
.
We test the improvement in the
![]() value of the fit with the F-test compared to the case of
value of the fit with the F-test compared to the case of
![]() (Fig. 8). We define the value of F as
(Fig. 8). We define the value of F as
![]() ,
where
,
where
![]() and
and ![]() are the minimum
are the minimum ![]() value and the degrees of
freedom, and the suffix "1'' and "2'' correspond to the case of
value and the degrees of
freedom, and the suffix "1'' and "2'' correspond to the case of
![]() and
and
![]() pixels, respectively (
pixels, respectively (
![]() ). For nine clusters, we find that the probability of exceeding
the F value, P, rises at a certain
). For nine clusters, we find that the probability of exceeding
the F value, P, rises at a certain
![]() .
For seven such cases, the
core radius also starts increasing at the same inner cutoff
radius. This indicates that the nine clusters have significant two
core sizes. Moreover for the seven of the nine the core radius of the
inner component at which the significant improvement of
.
For seven such cases, the
core radius also starts increasing at the same inner cutoff
radius. This indicates that the nine clusters have significant two
core sizes. Moreover for the seven of the nine the core radius of the
inner component at which the significant improvement of ![]() starts is roughly
starts is roughly ![]() .
.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1087f8.eps}
\end{figure}](/articles/aa/full/2004/48/aa1087/Timg105.gif) |
Figure 8:
Effect of the inner cutoff radius in the single |
In the second analysis, we assumed the double ![]() -model composed of
different core radii (
r1 < r2),
-model composed of
different core radii (
r1 < r2),
We have plotted the two core radii against the core radius derived by
the single ![]() -model for the nine "double-
-model for the nine "double-![]() '' clusters in
Fig. 9a. It is remarkable that one of the two cores is
nearly consistent with the core of the single
'' clusters in
Fig. 9a. It is remarkable that one of the two cores is
nearly consistent with the core of the single ![]() -model, namely
-model, namely
![]() or
or
![]() .
This indicates that the single
.
This indicates that the single
![]() -model tends to detect the one of the two components that is more
dominant. We also show the ratio of two cores versus the ratio of two
normalization factors in Fig. 9b. r2/r1 is
-model tends to detect the one of the two components that is more
dominant. We also show the ratio of two cores versus the ratio of two
normalization factors in Fig. 9b. r2/r1 is ![]() on
average, while S2/S1 ranges from 0.01 to 1. These are
consistent with nearby clusters (Mohr et al. 1999). We can
classify them into two groups: inner core dominated clusters (
on
average, while S2/S1 ranges from 0.01 to 1. These are
consistent with nearby clusters (Mohr et al. 1999). We can
classify them into two groups: inner core dominated clusters (
![]() )
and outer core dominated clusters (
)
and outer core dominated clusters (
![]() ). For the inner core dominant clusters, the single
). For the inner core dominant clusters, the single ![]() -model
fit picks up the inner
-model
fit picks up the inner ![]() -model component, while for the outer
core dominant clusters, the outer component is picked up. In Table 2
the inner/outer core dominant clusters are denoted with W(1)/W(2).
-model component, while for the outer
core dominant clusters, the outer component is picked up. In Table 2
the inner/outer core dominant clusters are denoted with W(1)/W(2).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1087f9a.eps}\vspace*{1mm}
\par\includegraphics[width=7.8cm,clip]{1087f9b.eps}
\end{figure}](/articles/aa/full/2004/48/aa1087/Timg114.gif) |
Figure 9:
Core radii derived by the double |
We then investigated the reproducibility of the best-fit parameters of
the double ![]() -model utilizing Monte-Carlo simulations. We made
ten simulation clusters for each set of model parameters described
below and fitted them with the double
-model utilizing Monte-Carlo simulations. We made
ten simulation clusters for each set of model parameters described
below and fitted them with the double ![]() -model. We assumed
-model. We assumed
![]() as a typical core radius of the inner
component and several different values of r2 between 6 and 24
pixels. We fixed
as a typical core radius of the inner
component and several different values of r2 between 6 and 24
pixels. We fixed
![]() .
For the intensity
ratio, we checked two typical cases, i.e. S2/S1 = 0.1 and 1.0. We
then generated 75 000 events within a radius of
.
For the intensity
ratio, we checked two typical cases, i.e. S2/S1 = 0.1 and 1.0. We
then generated 75 000 events within a radius of
![]() ,
which are
typical total counts for double-
,
which are
typical total counts for double-![]() clusters including
background. We confirmed that the two core radii are well determined
as long as
clusters including
background. We confirmed that the two core radii are well determined
as long as
![]() .
Thus,
at least for the nine double-
.
Thus,
at least for the nine double-![]() clusters we detected, we can
conclude that the model parameters are well-determined by the model
fitting.
clusters we detected, we can
conclude that the model parameters are well-determined by the model
fitting.
We also find that the double-![]() clusters are found only at
z<0.3 and the ratio to the regular clusters at z<0.3 is
32%. However we have to take into account the fact that such double
structures are difficult to find at higher (z>0.3) redshifts because
of the low surface brightness. In order to constrain the double
structure at higher redshifts, we estimated the upper limits of the
possible additional
clusters are found only at
z<0.3 and the ratio to the regular clusters at z<0.3 is
32%. However we have to take into account the fact that such double
structures are difficult to find at higher (z>0.3) redshifts because
of the low surface brightness. In order to constrain the double
structure at higher redshifts, we estimated the upper limits of the
possible additional ![]() -model component. For this purpose we
fitted the radial profile with double
-model component. For this purpose we
fitted the radial profile with double ![]() -model with the ratio of
the two cores fixed at the average of nine double-
-model with the ratio of
the two cores fixed at the average of nine double-![]() clusters,
r2/r1=4. We need to consider two cases: (1) the inner
component is dominant, namely the inner core radius is approximately
the core radius of the single
clusters,
r2/r1=4. We need to consider two cases: (1) the inner
component is dominant, namely the inner core radius is approximately
the core radius of the single ![]() -model,
-model,
![]() ,
and
(2) the outer component is dominant,
,
and
(2) the outer component is dominant,
![]() .
We thus
performed the fit with
.
We thus
performed the fit with
![]() or
or
![]() as the
initial value. For some cases, the fit converged to certain best-fit
values or upper limits of the fitting parameters. However in some
cases the fit did not converge. In such cases we fixed r1 or
r2 at the value of
as the
initial value. For some cases, the fit converged to certain best-fit
values or upper limits of the fitting parameters. However in some
cases the fit did not converge. In such cases we fixed r1 or
r2 at the value of ![]() obtained from the single
obtained from the single ![]() -model
fitting.
-model
fitting.
We find that in addition to the nine double-![]() clusters, there
are several other clusters that may contain a second
component. In case (1) the outer component is marginally detected for
seven clusters at the 90% confidence level. For other 17 clusters,
the upper limit of the surface brightness of the outer component is
within the range
(0.01 - 0.1)S1 which is comparable to the range
for the seven inner-core dominant double-
clusters, there
are several other clusters that may contain a second
component. In case (1) the outer component is marginally detected for
seven clusters at the 90% confidence level. For other 17 clusters,
the upper limit of the surface brightness of the outer component is
within the range
(0.01 - 0.1)S1 which is comparable to the range
for the seven inner-core dominant double-![]() clusters. In case (2)
the inner component is marginally detected for three clusters, and
the upper limit is consistent with the two double-
clusters. In case (2)
the inner component is marginally detected for three clusters, and
the upper limit is consistent with the two double-![]() clusters for the
other 16. In Table 2
the clusters with marginal
inner/outer component are denoted with S(1)/S(2).
clusters for the
other 16. In Table 2
the clusters with marginal
inner/outer component are denoted with S(1)/S(2).
We finally obtain the fraction of clusters with marginal
double-![]() structure at z>0.3 to be 35%. It is comparable to
the occurrence of the double structures in the lower redshift systems
within the Poisson errors. Thus we cannot conclude that there is
significant evolution of the fraction of the double-
structure at z>0.3 to be 35%. It is comparable to
the occurrence of the double structures in the lower redshift systems
within the Poisson errors. Thus we cannot conclude that there is
significant evolution of the fraction of the double-![]() clusters
in the regular clusters within the observed redshift range. On the
other hand, Ettori et al. (2004) noted based on the
clusters
in the regular clusters within the observed redshift range. On the
other hand, Ettori et al. (2004) noted based on the ![]() -model
analysis that their high redshift (z>0.4) samples do not show any
significant double structure in the surface brightness
distribution. Thus there might be a trend of evolution in the core
structure of the ICM distribution starting around
-model
analysis that their high redshift (z>0.4) samples do not show any
significant double structure in the surface brightness
distribution. Thus there might be a trend of evolution in the core
structure of the ICM distribution starting around ![]() .
We
suggest that this should be confirmed by further observations.
.
We
suggest that this should be confirmed by further observations.
The GIS was operated in the PH-nominal mode during observations. The SIS has several choices between the CCD data modes (FAINT or BRIGHT) and the CCD clocking modes (1CCD or 2CCD or 4CCD). For observations done in a mixture of the FAINT and BRIGHT modes, we can combine converted BRIGHT (on-board FAINT) and on-board BRIGHT mode data.
First we extacted the X-ray images in the 0.7-10 keV for the GIS and
the 0.5-10 keV for the SIS, respectively. The two sensors in the
same system, namely GIS-2, -3 and SIS-0, -1 are added together. We
fitted the projected images to Gaussian functions and determined the
peak positions. We accumulate spectra from a circular region centered
on the Gaussian peak, where the extraction radii are
![]() and
and
![]() for the GIS and the SIS, respectively. We will discuss the
effect of the contamination from foreground/background point sources
in the next subsection. We select a larger integration area for the
GIS because the FWHM of the point spread function of the GIS detector
alone depends on the incident photon energy E keV, and is given by
for the GIS and the SIS, respectively. We will discuss the
effect of the contamination from foreground/background point sources
in the next subsection. We select a larger integration area for the
GIS because the FWHM of the point spread function of the GIS detector
alone depends on the incident photon energy E keV, and is given by
![]() (The ASCA Data Reduction Guide 2002). The FWHM for soft photons is
wider than for hard photons; the smaller integration radius would make
the spectrum harder, resulting in a systematically higher temperature.
This is a serious effect for a distant cluster with apparent core size
larger than
(The ASCA Data Reduction Guide 2002). The FWHM for soft photons is
wider than for hard photons; the smaller integration radius would make
the spectrum harder, resulting in a systematically higher temperature.
This is a serious effect for a distant cluster with apparent core size
larger than
![]() when the GIS integration radius is smaller than
when the GIS integration radius is smaller than
![]() .
Note that
.
Note that
![]() corresponds to
corresponds to ![]() Mpc at
z=0.1, and it mostly covers the cluster region corresponding to
Mpc at
z=0.1, and it mostly covers the cluster region corresponding to
![]() (see Sect. 5.2.1 for definition). The
systematic error in estimating the bolometric luminosity due to the
fixed integration radii will be discussed in the next subsection.
(see Sect. 5.2.1 for definition). The
systematic error in estimating the bolometric luminosity due to the
fixed integration radii will be discussed in the next subsection.
We subtract background spectra that were obtained during blank-sky observations. Because the ASCA background has a detector position dependency, we extract them from the same region as the cluster in the detector coordinates.
The instrument response can be split into two parts: a redistribution matrix (RMF), which specifies the channel probability distribution for a photon of given energy, and an effective area curve (ARF), which specifies the telescope area and window absorption. We utilized the latest version of the GIS RMFs, gis2v4_0.rmf and gis3v4_0.rmf, while we generate the SIS RMF using the FTOOL sisrmg. We built the ARF files with the ASCAARF program appropriate for the cluster extended emission, summing the ARFs for each bin in the cluster image region according to the weight of the photon counts.
In order to measure the average, emission-weighted X-ray temperature of the gas, we fitted the SIS and GIS spectra simultaneously with a thin-thermal plasma emission model from Raymond & Smith (1977). There are four parameters in the spectral model, the temperature kT, the metallicity relative to the solar abundance Z, the redshift z, and the normalization factor. The redshift of each object was fixed at the cataloged value in the NASA/IPAC Extragalactic Database (NED). The fitting function was convolved with the telescope and detector response functions. In the spectral fitting, we used the XSPEC version 9.0 analysis software (Arnaud 1996). We rebinned the spectral channels so that each bin contains at least 40 photons.
Yaqoob (1999) pointed out that fitting with fixed ![]() result in a systematically high temperature because of the serious
decrease of the low-energy efficiency of the SIS since early 1994. To
avoid the problem, the absorption column density
result in a systematically high temperature because of the serious
decrease of the low-energy efficiency of the SIS since early 1994. To
avoid the problem, the absorption column density ![]() was
allowed to vary. Note that in the observation of #57 A402,
which was done during the AO7 phase, a serious reduction in the
efficiency below 1 keV was seen in the SIS spectra, so we used only
the GIS data for this cluster.
was
allowed to vary. Note that in the observation of #57 A402,
which was done during the AO7 phase, a serious reduction in the
efficiency below 1 keV was seen in the SIS spectra, so we used only
the GIS data for this cluster.
We checked the contribution of foreground/background contaminating
sources in the ASCA spectra. We picked up the point sources
whose photon counts are greater than 10% of the cluster from the HRI
source lists. Excluding regions of
![]() circles around the
sources, we recalculate the spectra, responses and backgrounds to
determine the temperature by the Raymond-Smith model fitting. Note
that Energy Encircled Function at
circles around the
sources, we recalculate the spectra, responses and backgrounds to
determine the temperature by the Raymond-Smith model fitting. Note
that Energy Encircled Function at
![]() is approximately
is approximately
![]() for the GIS and
for the GIS and
![]() for the SIS, respectively. We
estimated the difference of the best-fit temperatures with and without
point sources excluded relative to the
for the SIS, respectively. We
estimated the difference of the best-fit temperatures with and without
point sources excluded relative to the ![]() error of the
measurement, and found that the contribution of the point-like sources
does not affect the temperature measurement for most cases, except
for #56 CL0500-24, #66 CL0024+17, #76 3C 220.1, and
A963. For #20 A963, we excluded one nearby source from
the spectral region of the GIS and the SIS. More specific analyses
are described in Ota et al. (1998) for CL0500-24,
Soucail et al. (2000) for CL0024+17, Ota et al. (2000)
for 3C 220.1. In the case of CL0500-24 and
CL0024+17, only the SIS data were used. Table 4
lists the results of the spectral analysis.
error of the
measurement, and found that the contribution of the point-like sources
does not affect the temperature measurement for most cases, except
for #56 CL0500-24, #66 CL0024+17, #76 3C 220.1, and
A963. For #20 A963, we excluded one nearby source from
the spectral region of the GIS and the SIS. More specific analyses
are described in Ota et al. (1998) for CL0500-24,
Soucail et al. (2000) for CL0024+17, Ota et al. (2000)
for 3C 220.1. In the case of CL0500-24 and
CL0024+17, only the SIS data were used. Table 4
lists the results of the spectral analysis.
We compared our results with values published in White (2000) (there are 26 clusters in common) to find a good agreement between the two measurements with a mean temperature ratio of 1.04. We also compared 6 high redshift clusters with constrained ASCA temperature with Ettori et al. (2004). The temperatures for 5 clusters are statistically consistent between the two results, while there is systematic difference for #71 3C 295. As for 3C 295, Ettori et al. (2004) excluded the central emission associated with the AGN, thus our temperature measurement may be affected by the AGN.
We estimated the X-ray luminosity in the 2-10 keV band from the GIS
flux,
![]() ,
and converted it into the bolometric
luminosity,
,
and converted it into the bolometric
luminosity,
![]() ,
using the emissivity of the
Raymond-Smith plasma model. In order to check the systematic error of
the luminosity estimation, we calculated the bolometric luminosity by
integrating the
,
using the emissivity of the
Raymond-Smith plasma model. In order to check the systematic error of
the luminosity estimation, we calculated the bolometric luminosity by
integrating the ![]() -model surface brightness distribution
determined with the ROSAT HRI within the same integration area,
to find that two estimations are consistent within about 15%. Then
we derived the bolometric luminosity within r500 (see Sect. 5.2.1),
-model surface brightness distribution
determined with the ROSAT HRI within the same integration area,
to find that two estimations are consistent within about 15%. Then
we derived the bolometric luminosity within r500 (see Sect. 5.2.1),
![]() ,
by multiplying
,
by multiplying
![]() with the ratio of the luminosities within r500 to
6' using the
with the ratio of the luminosities within r500 to
6' using the ![]() -model. In Table 4
we listed
-model. In Table 4
we listed
![]() ,
,
![]() ,
and
,
and
![]() .
.
In Sect. 3 we analyzed the cluster surface
brightness distribution under the assumption that the gas is
isothermal, and the spatial distribution is described by the single
![]() -model or the double
-model or the double ![]() model. In Sect. 4, we
determined the average X-ray temperature with the ASCA spectral
data. The X-ray images and the fitting results of individual clusters
are shown in Fig. C.1.
We will derive some physical
quantities of the clusters from the X-ray parameters obtained from the
analysis and investigate the redshift dependence of these parameters
and the histograms.
model. In Sect. 4, we
determined the average X-ray temperature with the ASCA spectral
data. The X-ray images and the fitting results of individual clusters
are shown in Fig. C.1.
We will derive some physical
quantities of the clusters from the X-ray parameters obtained from the
analysis and investigate the redshift dependence of these parameters
and the histograms.
We show the spectral parameters obtained with the Raymond-Smith fittings as a function of redshift in Fig. 10. In the plot of the temperature, we quoted the results of nearby clusters (Mohr et al. 1999) for comparison. There is no significant change in the temperature over a wide redshift range, particularly in z<0.5. On the other hand, some clusters with z>0.5 resulted in very high temperatures, though their errors are not well-constrained due to the limited photon statistics and the error range overlaps with the high temperature clusters in z<0.5.
![\begin{figure}
\par\includegraphics[width=13.4cm,clip]{1087f10.eps}\end{figure}](/articles/aa/full/2004/48/aa1087/Timg132.gif) |
Figure 10:
X-ray temperature a), metal abundance b), the 2-10 keV
flux c) and the 2-10 keV luminosity within
|
As indicated from Fig. 10a, it is hard to detect a cluster
whose X-ray flux is below
![]() due to the
detection limit of ASCA. This flux corresponds to
due to the
detection limit of ASCA. This flux corresponds to
![]() at z=0.5 and to
at z=0.5 and to ![]() keV from the
keV from the
![]() relation. Thus at z>0.5, clusters with temperature lower than 2.5
keV are barely detected. We consider that this can account for the
higher average temperature at z>0.5.
relation. Thus at z>0.5, clusters with temperature lower than 2.5
keV are barely detected. We consider that this can account for the
higher average temperature at z>0.5.
In Fig. 11 we plot the number of occurrence of each spectral parameter to study how the samples are distributed in the parameter space, regardless of the redshift. We show the distributions of the regular and the irregular clusters separately as well as the distributions of all the clusters. As a result, there is no clear difference between the distributions of the regular and irregular clusters. In Table 8 we summarize the mean and the standard deviation of the spectral parameters.
| Parameter | Regular (45) | Irregular (34) | All (79) | |||
| Mean | Standard deviation | Mean | Standard deviation | Mean | Standard deviation | |
| kT [keV] | 6.3 | 2.8 | 7.2 | 2.7 | 6.8 | 2.8 |
| Z [solar] | 0.33 | 0.22 | 0.24 | 0.15 | 0.29 | 0.19 |
|
|
|
|
|
|
|
|
| 0.56 | 0.11 | 0.73 | 0.61 | 0.64 | 0.32 | |
| 0.076 | 0.060 | 0.273 | 0.259 | 0.163 | 0.202 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4 | 4.6 | 15.6 | 8.1 | 9.4 | 8.5 |
| r500 [ h70-1 Mpc] | 0.96 | 0.22 | 1.1 | 0.4 | 1.0 | 0.3 |
| M500 [
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.20 | 0.08 | 0.18 | 0.07 | 0.20 | 0.07 |
![\begin{figure}
\par\includegraphics[width=13cm,clip]{1087f12.eps}\end{figure}](/articles/aa/full/2004/48/aa1087/Timg182.gif) |
Figure 12:
Results from |
![\begin{figure}
\par\includegraphics[width=13.4cm,clip]{1087f13.eps}\end{figure}](/articles/aa/full/2004/48/aa1087/Timg186.gif) |
Figure 13:
r500, M500,
|
We plot the ![]() -model parameters, and the parameters derived from
those X-ray parameters as functions of redshift in Fig. 12. We show the results of
double-
-model parameters, and the parameters derived from
those X-ray parameters as functions of redshift in Fig. 12. We show the results of
double-![]() model fits, and their inner and outer components are
distinguished by different symbols. In the figures we also plotted the
parameters taken from Mohr et al. (1999) for clusters with z <
0.1.
model fits, and their inner and outer components are
distinguished by different symbols. In the figures we also plotted the
parameters taken from Mohr et al. (1999) for clusters with z <
0.1.
We do not see in those figures any clear redshift dependence in the distributions of the X-ray parameters except for the parameters related to r500 shown in Fig. 13. We will go back to these parameters in Sect. 5.2.3 and focus on the parameters that do not involve the overdensity radius.
From Fig. 12b, we notice that the core radius shows an
apparent redshift dependence. As noted in Ota & Mitsuda (2002),
the core radius shows a remarkably large cluster-to-cluster
dispersion, spanning over two orders of magnitude. The core radii of
the irregular clusters are systematically larger than those of the
regular clusters, and there seems to be a gap in the ![]() distribution at around
0.1 h70-1 Mpc.
The regular clusters also show a similar bimodal
distribution in
distribution at around
0.1 h70-1 Mpc.
The regular clusters also show a similar bimodal
distribution in ![]() but the fraction of the larger
but the fraction of the larger ![]() group
decreases with increasing z.
group
decreases with increasing z.
To investigate the selection effect, we created simulation
clusters with the Monte-Carlo method and performed the analysis on the
simulation clusters. We scale the count rate of
MS0906.5+1110 at z=0.18 to estimate the expected total
counts for a 40 ksec observation of a cluster at z=0.5 with a
typical luminosity
![]() .
The expected
cluster counts are about 600 counts. We simulated a series of cluster
images with various core sizes and found that the signal-to-noise
ratio is quite low for clusters with large cores of
.
The expected
cluster counts are about 600 counts. We simulated a series of cluster
images with various core sizes and found that the signal-to-noise
ratio is quite low for clusters with large cores of
![]() kpc at z>0.5. Based on the results we estimated the sensitivity of
the current HRI observation to be
kpc at z>0.5. Based on the results we estimated the sensitivity of
the current HRI observation to be
![]() .
We show the sensitivity curve in Fig. 12b. Thus the redshift dependencies of the core radius can be
explained by a selection effect.
.
We show the sensitivity curve in Fig. 12b. Thus the redshift dependencies of the core radius can be
explained by a selection effect.
Therefore we conclude that the X-ray parameters, temperature, core
radius, ![]() ,
and the central electron density are consistent with
showing no significant trend of evolution at
,
and the central electron density are consistent with
showing no significant trend of evolution at ![]() .
.
Although the X-ray parameters that are directly determined from
observation do not show strong redshift-dependence, we find a weak
redshift dependence in the overdensity radius, which
approximately follows
![]() (Fig. 13a). The dependence is likely to be introduced when
we define r500 by Eq. (8), i.e.
(Fig. 13a). The dependence is likely to be introduced when
we define r500 by Eq. (8), i.e.
![]() .
In other words, the redshift dependency
is introduced by the assumption,
.
In other words, the redshift dependency
is introduced by the assumption,
![]() .
We confirmed that such a negative dependence disappears when we
assume a constant
.
We confirmed that such a negative dependence disappears when we
assume a constant
![]() independently of
independently of
![]() ,
for
example
,
for
example
![]() .
.
In Fig. 13d, we show the gas-mass fraction inside r500determined with
![]() .
We do not see a clear
dependence on the redshift in our own data. We then obtain the average
gas-mass fraction of our sample of 79 distant clusters to be
.
We do not see a clear
dependence on the redshift in our own data. We then obtain the average
gas-mass fraction of our sample of 79 distant clusters to be
(1) We have defined the cluster limiting radius with
![]() and the resultant value is typically
and the resultant value is typically
![]() Mpc for the current sample. On the other hand, the extent of the
observed X-ray emission,
Mpc for the current sample. On the other hand, the extent of the
observed X-ray emission, ![]() ,
is found to be larger for most of
the clusters (Fig. C.1)
and
,
is found to be larger for most of
the clusters (Fig. C.1)
and
![]() on average.
Thus we do not need to worry about the effect of extrapolation in the
current
on average.
Thus we do not need to worry about the effect of extrapolation in the
current
![]() estimation. The average gas-mass fraction
within
estimation. The average gas-mass fraction
within ![]() is derived as
is derived as
![]() ,
which
agrees with Eq. (10) within the errors.
,
which
agrees with Eq. (10) within the errors.
(2) Since the determination of the gas-mass fraction requires absolute
calibrations of the X-ray telescope/detector systems of ROSAT
and ASCA, we carefully examined the calibrational errors and found
that they can cause at maximum 25% errors in
![]() (see
Appendix B for details).
(see
Appendix B for details).
(3) The assumption of
![]() may be a source of uncertainty in
may be a source of uncertainty in
![]() .
We can infer
.
We can infer
![]() from the condition that the central mass density should be
higher than the average mass density, namely
from the condition that the central mass density should be
higher than the average mass density, namely
![]() .
Since the observed range of
.
Since the observed range of ![]() is
is
![]() ,
we obtain
,
we obtain
![]() ,
where the smaller (larger) value corresponds
to the clusters with large (small) core radii. Thus it is likely that
the clusters with large
,
where the smaller (larger) value corresponds
to the clusters with large (small) core radii. Thus it is likely that
the clusters with large ![]() were formed at
were formed at
![]() .
.
We then vary the formation redshift,
![]() for which
we calculate the critical density,
for which
we calculate the critical density,
![]() and find the radius where the measured matter density
is 500 times
and find the radius where the measured matter density
is 500 times
![]() .
If we simply assume a fixed formation redshift for all the clusters,
ranging from 0.5 to 1.5, and calculate the mean gas-mass fractions
within r500 in the same manner as Eq. (10),
.
If we simply assume a fixed formation redshift for all the clusters,
ranging from 0.5 to 1.5, and calculate the mean gas-mass fractions
within r500 in the same manner as Eq. (10),
![]() varies from 0.18 to 0.12 with a typical
standard error of 0.05.
Thus the
varies from 0.18 to 0.12 with a typical
standard error of 0.05.
Thus the
![]() estimation
largely depends on the assumption of
estimation
largely depends on the assumption of
![]() .
However such an effect is expected to be more serious for the low-redshift clusters,
whose average gas-mass fraction was measured to be
.
However such an effect is expected to be more serious for the low-redshift clusters,
whose average gas-mass fraction was measured to be
![]() (Sanderson et al. 2003; Mohr et al. 1999).
Thus we may not attribute the systematic error in measuring
(Sanderson et al. 2003; Mohr et al. 1999).
Thus we may not attribute the systematic error in measuring
![]() for the distant sample
to the assumption of
for the distant sample
to the assumption of
![]() .
.
(4) The emission-weighted temperature reflects the temperature of the
cluster core region. Then, if there is a significant temperature drop
at the center, it may cause an overestimation of the gas-mass fraction
because the cluster hydrostatic mass estimation is more
sensitive to the temperature profile than the gas
mass. Such temperature drops were usually found in cluster cores with
short (![]() a few Gyr) cooling timescales. The spectral analysis of
the cooling flow clusters with the XMM-Newton and the Chandra satellites showed that the temperature drops typically by a
factor of 3 over the central
a few Gyr) cooling timescales. The spectral analysis of
the cooling flow clusters with the XMM-Newton and the Chandra satellites showed that the temperature drops typically by a
factor of 3 over the central ![]() kpc region
(e.g. Tamura et al. 2001; Schmidt et al. 2001). We then
estimated the emission-weighted temperature within 1.5 Mpc
(corresponding to the typical integration radius for the GIS spectra)
assuming the radial temperature profile of
kpc region
(e.g. Tamura et al. 2001; Schmidt et al. 2001). We then
estimated the emission-weighted temperature within 1.5 Mpc
(corresponding to the typical integration radius for the GIS spectra)
assuming the radial temperature profile of
![]() (from
Fig. 1 of Tamura et al. 2001) and the
(from
Fig. 1 of Tamura et al. 2001) and the ![]() -model surface
brightness distribution with
-model surface
brightness distribution with
![]() kpc and
kpc and ![]() to find that
it is lower by about 30% than that of the outer(r>0.1 Mpc)
region. On the other hand, we obtained the mean gas-mass fraction for
the 26 regular clusters with
to find that
it is lower by about 30% than that of the outer(r>0.1 Mpc)
region. On the other hand, we obtained the mean gas-mass fraction for
the 26 regular clusters with
![]() Gyr to be
Gyr to be
![]() ,
which is larger by 20%
than that of the rest of the sample. Thereby we consider that, for at
most 1/3 of the samples,
,
which is larger by 20%
than that of the rest of the sample. Thereby we consider that, for at
most 1/3 of the samples,
![]() may be overestimated to some
extent, depending on the degree of the temperature gradient. However,
considering the fact that the correlation between
may be overestimated to some
extent, depending on the degree of the temperature gradient. However,
considering the fact that the correlation between
![]() and
and
![]() is weak as well as that the ranges of
is weak as well as that the ranges of
![]() for
clusters with short and long cooling timescales are not very
different, the effect of the temperature gradient in estimating the
mean gas-mass fraction for all the samples is suggested to be not
large compared to the cluster-cluster variation.
For more accurate measurements of
for
clusters with short and long cooling timescales are not very
different, the effect of the temperature gradient in estimating the
mean gas-mass fraction for all the samples is suggested to be not
large compared to the cluster-cluster variation.
For more accurate measurements of
![]() ,
we need to constrain the temperature profiles
for the individual clusters and reduce the measurement uncertainties.
,
we need to constrain the temperature profiles
for the individual clusters and reduce the measurement uncertainties.
Since we found no significant evolution in the X-ray parameters, we
will investigate the distribution of X-ray parameters obtained from
the ![]() -model analysis without distinguishing the clusters by
redshift. In Fig. 14, we show the histograms of the X-ray
parameters. We find that both kT and
-model analysis without distinguishing the clusters by
redshift. In Fig. 14, we show the histograms of the X-ray
parameters. We find that both kT and ![]() are distributed in
ranges smaller than 1 order of magnitude, while
are distributed in
ranges smaller than 1 order of magnitude, while ![]() and
and
![]() are
distributed over almost two orders of magnitude.
are
distributed over almost two orders of magnitude.
![\begin{figure}
\par\includegraphics[width=10.3cm,clip]{1087f15.eps}\end{figure}](/articles/aa/full/2004/48/aa1087/Timg227.gif) |
Figure 15:
Histograms of r500, M500,
|
While the mean value of ![]() for all the clusters is
for all the clusters is
![]() Mpc, if we treat the regular and the
irregular clusters separately, we obtain
Mpc, if we treat the regular and the
irregular clusters separately, we obtain
![]() Mpc and
Mpc and
![]() Mpc for the regular and the irregular clusters (see
Table 8).
Thus these are different by a factor of 3. We also
notice that the distributions of the irregular and regular clusters
are not separated. Instead, the distribution of the regular clusters
has a double-peaked structure, whose core radii corresponding to the
two peaks are
50 h70-1 kpc and
200 h70-1 kpc
respectively. Thus there is about a factor of four difference. The
peak of the larger core radius coincides with that of the irregular
clusters. One may consider that the regular clusters with a large core
radius were classified as regular because the counting statistics were
not very good. However, we find that the statistics of irregular and
regular clusters with a large core are not very different. Thus it
is difficult to explain this coincidence just by statistics. The core
radius distribution when the nearby
Mohr et al. (1999) samples and the our distant samples were added
together was shown in Ota & Mitsuda (2002).
Mpc for the regular and the irregular clusters (see
Table 8).
Thus these are different by a factor of 3. We also
notice that the distributions of the irregular and regular clusters
are not separated. Instead, the distribution of the regular clusters
has a double-peaked structure, whose core radii corresponding to the
two peaks are
50 h70-1 kpc and
200 h70-1 kpc
respectively. Thus there is about a factor of four difference. The
peak of the larger core radius coincides with that of the irregular
clusters. One may consider that the regular clusters with a large core
radius were classified as regular because the counting statistics were
not very good. However, we find that the statistics of irregular and
regular clusters with a large core are not very different. Thus it
is difficult to explain this coincidence just by statistics. The core
radius distribution when the nearby
Mohr et al. (1999) samples and the our distant samples were added
together was shown in Ota & Mitsuda (2002).
In Fig. 14b, we also show the distributions of the core
radii of the double-![]() clusters. We notice that the double-peaked
structure of the core radius of the regular clusters seems related to
the double-
clusters. We notice that the double-peaked
structure of the core radius of the regular clusters seems related to
the double-![]() structure because the core radius of the
smaller-core component is distributed around the lower peak of the
regular-cluster core radius distribution, while the larger-core is
around the higher peak.
structure because the core radius of the
smaller-core component is distributed around the lower peak of the
regular-cluster core radius distribution, while the larger-core is
around the higher peak.
![\begin{figure}
\par\includegraphics[width=13.3cm,clip]{1087f16.eps}\end{figure}](/articles/aa/full/2004/48/aa1087/Timg231.gif) |
Figure 16:
Relations of the metallicity a), the bolometric luminosity
b), |
In Sect. 3.5, we have shown that about 20% of
regular clusters have significant double-![]() structures, and for
about 60% of regular clusters, the existence of a similar structure
cannot be rejected. We have also shown that there are inner-core
dominant and outer-core dominant cases and that a single
structures, and for
about 60% of regular clusters, the existence of a similar structure
cannot be rejected. We have also shown that there are inner-core
dominant and outer-core dominant cases and that a single ![]() -model
fit picks up the core radius of the dominant core (Fig. 9).
Thus we consider that the correspondence between the core radius
distribution of all the regular clusters and the distribution of
double-
-model
fit picks up the core radius of the dominant core (Fig. 9).
Thus we consider that the correspondence between the core radius
distribution of all the regular clusters and the distribution of
double-![]() clusters is not just a coincidence but that it is
related to the double core nature of the regular clusters.
clusters is not just a coincidence but that it is
related to the double core nature of the regular clusters.
The electron density, the dark matter density and the cooling time at the cluster center show similar double-peaked distributions. On the other hand, as shown in Fig. 15, r500 and the other three parameters evaluated within r500 are distributed in ranges smaller than 1 order of magnitude. We will discuss the correlations between the parameters in the next section in more detail. We list the mean and the standard deviation for all the parameters in Table 8.
|
|
|||
| Relation |
|
|
|
|
|
|
|
|
| M-T |
|
|
|
|
|
|
|
|
|
|
0.28+0.09-0.06(kT)-0.08+0.14-0.14 | 0.33+0.10-0.08(kT)-0.11+0.15-0.15 | 0.47+0.16-0.15(kT)-0.19+0.20-0.16 |
|
|
|
|
|
| EzM-T |
|
|
|
|
|
|
|
|
We investigate correlations of various cluster parameters with the
X-ray temperature, kT in Sect. 6.1 and also with the
core radius, ![]() in Sect. 6.2, which showed the
distinct double-peaked distribution and thus may provide a clue to
understand the structures of clusters. Possible
systematic errors will be considered in each subsection.
in Sect. 6.2, which showed the
distinct double-peaked distribution and thus may provide a clue to
understand the structures of clusters. Possible
systematic errors will be considered in each subsection.
In the following analysis, we first calculate the Pearson's
correlation coefficient,
![]() ,
to measure the strength of the correlation. We take
the logarithm of the two measured parameters, x and y, namely
,
to measure the strength of the correlation. We take
the logarithm of the two measured parameters, x and y, namely
![]() and
and ![]() ,
except for the case of the Z-T and the
,
except for the case of the Z-T and the
![]() relations. Then if
relations. Then if
![]() ,
we derive the
best-fit relation between the two parameters assuming the power-law
function. In order to take into account the statistical uncertainties
of both the x and y axes, we performed the
,
we derive the
best-fit relation between the two parameters assuming the power-law
function. In order to take into account the statistical uncertainties
of both the x and y axes, we performed the ![]() minimization
in the linear (Y=aX+b) fit by defining
minimization
in the linear (Y=aX+b) fit by defining
![]() ,
where
,
where
![]() and
and
![]() are the
are the ![]() errors for the
parameter Xi and Yi, respectively. Because in all the cases
below the fits were not statistically acceptable due to large
scatters of the data at the 90% confidence level, the error ranges of the
coefficients a and b were estimated from the dispersions of the
data points around the model functions rather than the photon
statistics. We excluded two irregular clusters, #43 A1758
and #79 MS1054.5-0321, in the analysis except for the Z-T and the
errors for the
parameter Xi and Yi, respectively. Because in all the cases
below the fits were not statistically acceptable due to large
scatters of the data at the 90% confidence level, the error ranges of the
coefficients a and b were estimated from the dispersions of the
data points around the model functions rather than the photon
statistics. We excluded two irregular clusters, #43 A1758
and #79 MS1054.5-0321, in the analysis except for the Z-T and the
![]() relations because their
relations because their ![]() -model
parameters were not well constrained (Sect. 3.4),
although they are plotted in Figs. 16 and 18. We
then compare some of the resulting relations with the predictions of
the self-similar model.
-model
parameters were not well constrained (Sect. 3.4),
although they are plotted in Figs. 16 and 18. We
then compare some of the resulting relations with the predictions of
the self-similar model.
In Figs. 16a-h, we show eight parameters derived from the
spectral and the image analysis, the gas mass, and the gas-mass
fraction etc. as a function of X-ray temperature. We mainly show the
relations derived for
![]() below.
In Table 7,
we show the cluster parameters of the individual clusters
for the overdensities of
below.
In Table 7,
we show the cluster parameters of the individual clusters
for the overdensities of
![]() and
and
![]() (Nakamura & Suto 1997)
and in Table 9
the scaling relations
with and without consideration of the cosmological factor,
Ez=Hz/H0 as noted by Ettori et al. (2004).
Since we did not find any strong redshift
evolution in the observed X-ray properties, we first derive the
parameter correlations regardless of their redshifts. We will discuss
the correlations in the case where we take into account the sample
redshifts later. Note that kT and
(Nakamura & Suto 1997)
and in Table 9
the scaling relations
with and without consideration of the cosmological factor,
Ez=Hz/H0 as noted by Ettori et al. (2004).
Since we did not find any strong redshift
evolution in the observed X-ray properties, we first derive the
parameter correlations regardless of their redshifts. We will discuss
the correlations in the case where we take into account the sample
redshifts later. Note that kT and ![]() are in
units of [keV] and [
h70-1 Mpc], respectively.
are in
units of [keV] and [
h70-1 Mpc], respectively.
The large error in the normalization factor in Eq. (11) is affected by the intrinsic scatter around the
best-fit relation. We found from Fig. 16b that the
normalization factors of the
![]() relation are
significantly different between the regular and the irregular
clusters: for a fixed temperature, the regular clusters tend to have a
larger luminosity in comparison to the irregular clusters. The
difference becomes more evident if we divide the sample into two
subgroups according to the core radius ranges of
relation are
significantly different between the regular and the irregular
clusters: for a fixed temperature, the regular clusters tend to have a
larger luminosity in comparison to the irregular clusters. The
difference becomes more evident if we divide the sample into two
subgroups according to the core radius ranges of
![]() Mpc and
Mpc and
![]() Mpc (see
also Ota & Mitsuda 2002). If we fit them separately, fixing
the slope at the best-fit value of 3.08, we obtain
Mpc (see
also Ota & Mitsuda 2002). If we fit them separately, fixing
the slope at the best-fit value of 3.08, we obtain
| (12) | |||
| (13) |
![\begin{displaymath}M_{500}~\left[h_{70}^{-1}~{M_{\odot}}\right]
=1.64^{+0.35}_{-0.26}\times10^{13} (kT)^{1.68^{+0.10}_{-0.11}},
\end{displaymath}](/articles/aa/full/2004/48/aa1087/img278.gif) |
(15) |
We compare the M500-T relation with those derived for two
samples of nearby clusters (Table 1 of Finoguenov et al. 2001).
Because they calculated it under a different cosmology:
![]() and
and
![]() ,
we calculate the relation using the same set
of cosmological parameters and obtain
,
we calculate the relation using the same set
of cosmological parameters and obtain
![]() for
the distant clusters. In comparison to their flux-limited sample
(HIFLUGCS) and the sample with temperature profiles, the slope is in
a good agreement within the errors but
it should be noted that the best-fit normalization is
about 30% smaller for the distant sample. This may be attributed
to the significant redshift dependency of the critical density
and will be worth further investigation in the light of the cluster formation redshift.
for
the distant clusters. In comparison to their flux-limited sample
(HIFLUGCS) and the sample with temperature profiles, the slope is in
a good agreement within the errors but
it should be noted that the best-fit normalization is
about 30% smaller for the distant sample. This may be attributed
to the significant redshift dependency of the critical density
and will be worth further investigation in the light of the cluster formation redshift.
We also showed the Ez M-T relation calculated for
![]() in Table 9.
The result is
within a range consistent with the relation for z>0.4(Ettori et al. 2004).
in Table 9.
The result is
within a range consistent with the relation for z>0.4(Ettori et al. 2004).
![\begin{displaymath}M_{\rm gas}~\left[h_{70}^{-5/2}{~M_{\odot}}\right]
=2.88^{+0.93}_{-0.64}\times10^{12} (kT)^{1.85^{+0.14}_{-0.15}},
\end{displaymath}](/articles/aa/full/2004/48/aa1087/img283.gif) |
(16) |
For nearby clusters, Mohr et al. (1999) obtained the relation
to be
![]() under
under
![]() and
and
![]() ,
which is significantly steeper than the theoretically expected slope
of 1.5. On the other hand, Vikhlinin et al. (1999) reported
based on the ROSAT PSPC data analysis of nearby regular
clusters, a flatter relation in the form of
,
which is significantly steeper than the theoretically expected slope
of 1.5. On the other hand, Vikhlinin et al. (1999) reported
based on the ROSAT PSPC data analysis of nearby regular
clusters, a flatter relation in the form of
![]() ,
utilizing a different method in determining the
limiting radius (they defined the baryon overdensity radius of
R1000, corresponding to the dark matter overdensity of
,
utilizing a different method in determining the
limiting radius (they defined the baryon overdensity radius of
R1000, corresponding to the dark matter overdensity of
![]() ).
).
If we calculate the distant
![]() relation within r500using the same set of cosmological parameters,
relation within r500using the same set of cosmological parameters,
![]() .
The
relation is slightly flatter than that derived by
Mohr et al. (1999) but within a range consistent with the
result of either Mohr et al. (1999) or
Vikhlinin et al. (1999) under the current measurement errors.
.
The
relation is slightly flatter than that derived by
Mohr et al. (1999) but within a range consistent with the
result of either Mohr et al. (1999) or
Vikhlinin et al. (1999) under the current measurement errors.
As shown above, although the relation within r500 obtained for our
distant sample is consistent with the local relations, it is found to
be less steep than that found for z>0.4,
![]() (Ettori et al. 2004), which is not conflict with
the view that the lower redshift clusters contain more gas
for a fixed temperature, as pointed by Ettori et al. (2004).
(Ettori et al. 2004), which is not conflict with
the view that the lower redshift clusters contain more gas
for a fixed temperature, as pointed by Ettori et al. (2004).
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{1087f17.eps}\end{figure}](/articles/aa/full/2004/48/aa1087/Timg297.gif) |
Figure 17:
Venn diagrams which illustrate the relation between the X-ray
morphology and the optical morphology a) and the X-ray core radius
and the optical morphology b) (see
Sect. 6.2 for definition of the cD cluster).
In the panel b), we divided the sample into three subgroups: small
core (
|
![\begin{figure}
\par\includegraphics[width=12.95cm,clip]{1087f18.eps}\end{figure}](/articles/aa/full/2004/48/aa1087/Timg300.gif) |
Figure 18:
Relations of |
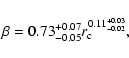 |
(18) |
![\begin{displaymath}n_{\rm e0}~\left[h_{70}^{1/2}~{\rm cm^{-3}}\right]
= 0.89^{+0.30}_{-0.23}\times 10^{-3}r_{\rm c}^{-1.29^{+0.10}_{-0.11}}.
\end{displaymath}](/articles/aa/full/2004/48/aa1087/img306.gif) |
(19) |
| (20) | |||
| (21) |
| (22) | |||
| (23) | |||
| (24) |
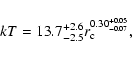 |
(25) |
From the above discussion, it seems difficult to explain the small
core size that we discovered in the histogram either by the potential
structure of the cD galaxy or the cooling radius. As long as we rely
on the hydrostatic assumption and the ![]() model, the X-ray surface
brightness distributions are likely to represent the gravitational
potential structures of the clusters. If this is the case, the
double-
model, the X-ray surface
brightness distributions are likely to represent the gravitational
potential structures of the clusters. If this is the case, the
double-![]() nature of the X-ray emission profile reflects the shape
of the gravitational potential of the dark matter, which is likely to
have two preferable scales of
nature of the X-ray emission profile reflects the shape
of the gravitational potential of the dark matter, which is likely to
have two preferable scales of ![]() kpc and
kpc and
![]() kpc.
kpc.
In an effort to constrain the physical status of ICM in the dark matter
potential, comparing the high-resolution X-ray observations to
gravitational lensing observations will provide another powerful test
(e.g. Hattori et al. 1997). Thanks to the improvement of
spatial resolution achieved by Chandra, now measurements on the
cluster mass profile down to ![]() 5 kpc scale are possible at
such high redshifts (
5 kpc scale are possible at
such high redshifts (![]() )
and several authors have measured
the dark matter distribution in the lensing clusters under the
hydrostatic hypothesis (e.g. Ota et al. 2004; Xue & Wu 2002; Arabadjis et al. 2002). For example, Ota et al. (2004)
showed from the high-resolution Chandra data of
CL0024+17 (z=0.395) and the comparison with the detailed
lens modeling by Tyson et al. (1998) that the cluster density
profile is well reproduced by the double-
)
and several authors have measured
the dark matter distribution in the lensing clusters under the
hydrostatic hypothesis (e.g. Ota et al. 2004; Xue & Wu 2002; Arabadjis et al. 2002). For example, Ota et al. (2004)
showed from the high-resolution Chandra data of
CL0024+17 (z=0.395) and the comparison with the detailed
lens modeling by Tyson et al. (1998) that the cluster density
profile is well reproduced by the double-![]() model and the inner
core also reflects the underlying dark matter potential. They also
noted that the core structure may be related to the past merging event
as inferred from the optical observations (Czoske et al. 2001,2002).
model and the inner
core also reflects the underlying dark matter potential. They also
noted that the core structure may be related to the past merging event
as inferred from the optical observations (Czoske et al. 2001,2002).
Recently Hayakawa et al. (2004) estimated the dark matter
distribution in a nearby non-cD, regular cluster, Abell 1060, from
the Chandra data analysis, without explicitly using the double
![]() -model, and found a central mass concentration at r<
50 kpc. Their result also supports the idea that dark matter may
preferentially be accumulated within a radius of
-model, and found a central mass concentration at r<
50 kpc. Their result also supports the idea that dark matter may
preferentially be accumulated within a radius of ![]() kpc. On
the other hand, Ettori et al. (2004) suggested that no significant
double structure is seen in the high redshift sample. Thus
considering from the above, the double-
kpc. On
the other hand, Ettori et al. (2004) suggested that no significant
double structure is seen in the high redshift sample. Thus
considering from the above, the double-![]() nature of the ICM
discovered in the present sample may be much related to the history of
the past merging and the relaxation process.
The small core component might be attributed
to the presence of dark matter subhalos due to the cluster mergers or
the internal structures in clusters (e.g. Fujita et al. 2002).
nature of the ICM
discovered in the present sample may be much related to the history of
the past merging and the relaxation process.
The small core component might be attributed
to the presence of dark matter subhalos due to the cluster mergers or
the internal structures in clusters (e.g. Fujita et al. 2002).
Furthermore, since there is clearly a tight coupling between the core
radius and the radiative cooling time as shown in Sect. 6.2, the detailed treatment of the thermal evolution
of the ICM will also be important. A number of numerical simulations
including non-gravitational effects such as radiative cooling and
galaxy feedback have been carried out and thus provide a clue
to the underlying physics in the cluster core regions. However, the
authors pointed out difficulties in regulating the central over-cooling
and produce a constant-density core (e.g. Pearce et al. 2000).
Masai & Kitayama (2004) recently proposed a quasi-hydrostatic
model, which predicts a characteristic temperature profile with an
asymptotic temperature for the central region being ![]() of the
non-cooling outer region, as observed in nearby "cooling flow''
clusters. Thus detailed comparison of the X-ray data with their model
regarding the temperature and density profiles will be important to
understand the evolution of the ICM structure. We need further
investigations to put a stronger constraint on the origin of the
double nature of the cluster structures, which is however beyond the
scope of the present paper and will be discussed in a separate paper.
of the
non-cooling outer region, as observed in nearby "cooling flow''
clusters. Thus detailed comparison of the X-ray data with their model
regarding the temperature and density profiles will be important to
understand the evolution of the ICM structure. We need further
investigations to put a stronger constraint on the origin of the
double nature of the cluster structures, which is however beyond the
scope of the present paper and will be discussed in a separate paper.
Acknowledgements
We are grateful to S. Sasaki, T. Kitayama and K. Masai for their helpful comments and discussions. N.O. is supported by a Research Fellowship for Young Scientists from the JSPS. This research has made use of the ROSAT HRI data obtained through the ROSAT Data Archive of MPE at Garching, Germany and the ASCA data through the DARTS Online Service provided by ISAS (ISAS/JAXA) and the HEASARC Online Service provided by NASA/Goddard Space Flight Center. We also thank the anonymous referee for helpful comments.
| ASCA GIS/SIS | ROSAT HRI | ||||||||
| ID | Cluster | z |
|
Seq. | X-ray centroid |
|
Seq. | ||
| SIS | GIS | RA (J2000) | Dec (J2000) | ||||||
| 1 | PKS 0745-19 | 0.1028 | 23 995 | 79 739 | 81 016 000 | 07 47 31.4 | -19 17 46.2 | 23 386 | 800398h |
| 2 | A2811 | 0.1086 | 88 632 | 93 838 | 84 003 000 | 00 42 07.3 | -28 32 01.3 | 9345 | 800773h |
| 3 | A1068 | 0.1375 | 63 674 | 70 871 | 84 064 000 | 10 40 44.8 | +39 57 11.9 | 17 669 | 800748h, 800630h |
| 4 | A1413 | 0.1427 | 51 212 | 75 012 | 81 008 000 | 11 55 18.0 | +23 24 26.1 | 18 858 | 800871h |
| 5 | A990 | 0.144 | 128 830 | 148 150 | 84 070 000 | 10 23 40.5 | +49 08 26.0 | 6745 | 800866h |
| 6 | A2204 | 0.1523 | 35 730 | 40 141 | 82 045 010 | 16 32 47.0 | +05 34 33.0 | 15 489 | 800750h |
| 7 | A2104 | 0.1554 | 95 089 | 105 570 | 84 072 000 | 15 40 07.8 | -03 18 22.4 | 43 680 | 800828h-1, 800828h |
| 8 | RX J1050.5-0236 | 0.1645 | 55 889 | 57 608 | 84 036 000 | 10 50 36.8 | -02 36 18.6 | 34 836 | 800703h-1, 800703h |
| 9 | A586 | 0.171 | 21 669 | 18 326 | 81 009 010 | 07 32 20.5 | +31 37 57.5 | 23 020 | 800668h |
| 10 | A2218 | 0.1756 | 63 431 | 74 648 | 80 001 000 | 16 35 52.6 | +66 12 35.3 | 35 809 | 800588h-1, 800588h |
| 11 | MS0906.5+1110 | 0.18 | 44 627 | 46 250 | 83 034 000 | 09 09 12.5 | +10 58 36.0 | 84 294 | 800801h-1, 800801h, 800664h |
| 12 | A665 | 0.1819 | 131 730 | 152 440 | 85 033 000 | 08 30 57.5 | +65 51 15.0 | 99 305 | 800900h, 800774h |
| 13 | A1689 | 0.1832 | 60 444 | 70 671 | 80 005 000 | 13 11 29.6 | -01 20 33.1 | 22 722 | 800445h, 800445h-1 |
| 14 | MS0440.5+0204 | 0.19 | 18 291 | 74 158 | 82 026 000 | 04 43 10.2 | +02 10 20.3 | 27 229 | 800457h-1, 800457h |
| 15 | A1246 | 0.1902 | 84 866 | 81 675 | 83 007 000 | 11 23 58.3 | +21 29 11.6 | 15 500 | 800732h |
| 16 | MS0839.8+2938 | 0.194 | 57 171 | 74 553 | 82 011 000 | 08 42 55.7 | +29 27 25.2 | 19 075 | 800159h |
| 17 | A115 | 0.1971 | 65 025 | 73 741 | 82 034 000 | 00 55 50.3 | +26 24 36.0 | 50 719 | 800633h-1, 800633h |
| 18 | MS0451.5+0250 | 0.199 | 35 565 | 36 180 | 82 041 000 | 04 54 10.2 | +02 55 39.2 | 12 790 | 800460h |
| 19 | A2163 | 0.203 | 57 576 | 62 750 | 80 024 000 | 16 15 46.3 | -06 08 37.1 | 36 194 | 800593h-1, |
| 20 | A963 | 0.206 | 57 366 | 60 613 | 80 000 000 | 10 17 03.7 | +39 02 56.2 | 20 616 | 800004h-1, 800004h |
| 21 | ZW2701 | 0.214 | 56 613 | 62 541 | 86 076 000 | 09 52 49.3 | +51 53 05.3 | 17 581 | 800729h-1, 800729h |
| 22 | A1851 | 0.2149 | 38 762 | 71 979 | 82 007 000 | 14 00 05.2 | +72 07 25.8 | 29 209 | 800670h |
| 23 | MS0735.6+7421 | 0.216 | 22 860 | 31 466 | 83 035 000 | 07 41 44.3 | +74 14 35.5 | 27 164 | 800204h |
| 24 | A773 | 0.217 | 75 824 | 81 940 | 82 001 000 | 09 17 52.4 | +51 43 34.7 | 22 854 | 800653h, 800618h |
| 25 | A1704 | 0.2205 | 40 084 | 39 196 | 81 007 000 | 13 14 24.9 | +64 34 37.3 | 41 291 | 800667h |
| 26 | MS1006+1202 | 0.221 | 37 960 | 42 471 | 86 057 000 | 10 08 47.5 | +11 47 57.1 | 87 310 | 800880h, 800807h-1, 800807h |
| 27 | A2261 | 0.224 | 38 965 | 40 466 | 84 062 000 | 17 22 27.0 | +32 07 54.5 | 30 079 | 801084h |
| 28 | A1942 | 0.224 | 67 409 | 68 631 | 83 000 000 | 14 38 22.0 | +03 40 04.8 | 44 515 | 800711h |
| 29 | A2219 | 0.2256 | 31 009 | 71 527 | 82 037 000 | 16 40 20.2 | +46 42 31.2 | 13 342 | 800408h |
| 30 | A1895 | 0.2257 | 44 102 | 48 679 | 83 033 000 | 14 14 02.5 | +71 17 08.4 | 39 628 | 800800h-1, 800800h |
| 31 | A2390 | 0.228 | 10 782 | 17 620 | 82 032 000 | 21 53 36.5 | +17 41 45.2 | 35 573 | 800346h, 800178h-1, 800178h-0, 800117h |
| 32 | A1763 | 0.2284 | 74 407 | 78 447 | 83 044 000 | 13 35 20.0 | +40 59 53.8 | 18 197 | 801049h |
| 33 | A2111 | 0.229 | 71 711 | 82 790 | 85 065 000 | 15 39 41.7 | +34 25 01.6 | 62 288 | 800666h |
| 34 | A267 | 0.23 | 70 323 | 75 400 | 85 048 000 | 01 52 41.7 | +01 00 39.1 | 15 850 | 800731h |
| 35 | A2667 | 0.23 | 59 099 | 77 198 | 85 028 000 | 23 51 39.4 | -26 05 02.8 | 45 469 | 800659h, 800612h-1, 800612h |
| 36 | A1682 | 0.2339 | 73 103 | 78 656 | 84 075 000 | 13 06 51.8 | +46 33 30.2 | 18 304 | 800616h |
| 37 | RX J2129.3+0005 | 0.235 | 61 213 | 67 219 | 85 029 000 | 21 29 39.9 | +00 05 22.2 | 20 940 | 800835h-1, 800835h |
| 38 | MS1910+6736 | 0.246 | 44 444 | 54 448 | 86 058 000 | 19 10 28.2 | +67 41 26.0 | 25 258 | 800808h |
| 39 | A1835 | 0.2532 | 31 071 | 35 677 | 82 052 000 | 14 01 20.0 | +02 52 38.9 | 2835 | 800409h |
| 40 | RX J1023.8-2715 | 0.2533 | 38 484 | 40 505 | 85 044 000 | 10 23 50.4 | -27 15 23.8 | 45 207 | 800911h, 800598h |
| 41 | A68 | 0.255 | 70 733 | 77 645 | 86 061 000 | 00 37 06.1 | +09 09 28.3 | 17 266 | 801046h |
| 42 | MS1455.0+2232 | 0.2578 | 47 759 | 60 774 | 82 053 000 | 14 57 15.0 | +22 20 37.3 | 14 886 | 800198h, 800198h-1, 800198h-2 |
| 43 | A1758 | 0.279 | 35 906 | 40 180 | 83 013 010 | 13 32 43.8 | +50 32 48.4 | 29 444 | 800579h |
| 44 | A483 | 0.28 | 71 358 | 75 804 | 82 031 000 | 04 15 57.0 | -11 32 45.2 | 17 700 | 800709h |
| 45 | A697 | 0.282 | 110 750 | 130 120 | 84 031 000 | 08 42 58.1 | +36 21 55.0 | 28 128 | 800854h |
| 46 | 1E0657-56 | 0.296 | 74 130 | 101 260 | 86 075 000 | 06 58 29.4 | -55 56 42.0 | 59 569 | 800665h, 800443h |
| 47 | MS1008.1-1224 | 0.301 | 35 183 | 36 948 | 82 056 000 | 10 10 32.4 | -12 39 24.9 | 69 220 | 800434h |
| 48 | MS1147.3+1103 | 0.303 | 54 515 | 56 143 | 84 060 000 | 11 49 52.4 | +10 46 44.2 | 57 338 | 800674h-2, 800674h-1 |
| 49 | RX J1131.9-1955 | 0.3072 | 90 244 | 94 126 | 84 067 000 | 11 31 55.9 | -19 55 51.9 | 10 864 | 800597h-1, 800597h |
| 50 | AC118 | 0.308 | 71 094 | 137 540 | 82 000 000 | 00 14 17.1 | -30 23 02.6 | 34 203 | 800608h |
| 51 | MS0811.6+6301 | 0.312 | 49 606 | 56 128 | 84 061 000 | 08 15 59.7 | +62 53 07.7 | 68 408 | 800675h |
| 52 | MS1241.5+1710 | 0.312 | 39 144 | 39 392 | 83 067 000 | 12 44 01.4 | +16 53 44.9 | 18 562 | 800673h-1 |
| 53 | AC114 | 0.312 | 73 467 | 73 521 | 83 019 010 | 22 58 49.2 | -34 48 27.0 | 23 179 | 800342h-1, 800342h |
| 54 | MS2137.3-2353 | 0.313 | 32 276 | 32 221 | 81 022 000 | 21 40 15.2 | -23 39 41.0 | 15 661 | 800245h-1, 800245h |
| 55 | A1995 | 0.3186 | 47 129 | 56 164 | 82 005 000 | 14 52 59.5 | +58 02 58.1 | 37 876 | 800707h-1, 800707h, 800581h |
| 56 | CL0500-24 | 0.32 | 81 122 | - | 83 017 000 | 05 01 06.2 | -24 25 20.3 | 37 756 | 800682h |
| 57 | A402 | 0.3224 | - | 93 794 | 87 062 000 | 02 57 41.7 | -22 09 11.0 | 22 198 | 800876h |
| 58 | MS1224.7+2007 | 0.327 | 31 949 | 30 981 | 82 043 000 | 12 27 13.4 | +19 50 56.8 | 54 856 | 800435h-3, 800435h-2, 800435h-1, 800435h |
| 59 | A1722 | 0.3275 | 66 380 | 85 119 | 81 013 000 | 13 20 07.6 | +70 04 40.7 | 27 894 | 800580h |
| 60 | CL1358+6245 | 0.328 | 71 765 | 75 814 | 81 032 000 | 13 59 50.5 | +62 31 02.6 | 29 456 | 800110h-1, 800110h |
| 61 | CL2244-02 | 0.33 | 89 054 | 78 066 | 83 016 000 | 22 47 13.4 | -02 05 38.0 | 33 700 | 800829h |
| 62 | RX J1532.9+3021 | 0.345 | 70 463 | 80 462 | 86 067 000 | 15 32 53.8 | +30 21 00.2 | 22 320 | 800855h |
| 63 | A959 | 0.3533 | 43 968 | 60 784 | 82 006 000 | 10 17 39.2 | +59 33 49.5 | 80 986 | 800785h-1, 800785h, 800669h-1, 800669h |
| 64 | MS1512.4+3647 | 0.372 | 38 774 | 38 202 | 83 066 000 | 15 14 22.4 | +36 36 17.8 | 35 218 | 800672h |
| 65 | A370 | 0.375 | 28 975 | 64 078 | 80 010 000 | 02 39 52.0 | -01 34 33.6 | 22 016 | 801066h |
| 66 | CL0024+17 | 0.39 | 91 111 | - | 84 046 000 | 00 26 35.9 | +17 09 40.0 | 121 912 | 800694h-2, 800694h-1, 800694h, 800589h-1, 800589h |
| 67 | A851 | 0.4069 | 69 281 | 88 012 | 83 068 000 | 09 42 59.5 | +46 59 36.1 | 45 610 | 800819h |
| 68 | MS0302.7+1658 | 0.424 | 73 650 | 60 371 | 87 055 000 | 03 05 31.7 | +17 10 04.0 | 34 005 | 800683h |
| 69 | MS1621.5+2640 | 0.426 | 68 557 | 73 073 | 85 051 000 | 16 23 35.7 | +26 34 19.0 | 78 447 | 800888h, 800461h |
| 70 | RX J1347.5-1145 | 0.451 | 66 018 | 81 376 | 83 050 000 | 13 47 30.9 | -11 45 08.6 | 36 458 | 800681h-2, 800681h-1, 800681h |
| 71 | 3C 295 | 0.4641 | 42 242 | 69 125 | 71 003 000 | 14 11 20.2 | +52 12 12.2 | 29 579 | 800678h-1, 800678h |
| 72 | CL0016+16 | 0.541 | 106 000 | 117 020 | 84 016 000 | 00 18 33.5 | +16 26 12.8 | 76 593 | 800677h-1, 800677h |
| 73 | MS0451.6-0305 | 0.55 | 43 174 | 55 729 | 81 025 000 | 04 54 11.7 | -03 00 52.2 | 46 208 | 800660h-1, 800660h |
| 74 | CL2236-04 | 0.56 | 73 163 | 68 577 | 83 018 000 | 22 39 32.7 | -04 29 32.8 | 47 120 | 800908h |
| 75 | MS2053.7-0449 | 0.583 | 66 067 | 72 115 | 85 052 000 | 20 56 20.7 | -04 37 51.6 | 95 458 | 800889h, 800810h-1 |
| 76 | 3C 220.1 | 0.61 | 79 909 | 84 684 | 86 034 000 | 09 32 39.9 | +79 06 27.1 | 36 607 | 701727h |
| 77 | MS1137.5+6625 | 0.782 | 78 405 | 97 362 | 85 046 010 | 11 40 22.2 | +66 08 15.0 | 100 035 | 800784h, 800662h |
| 78 | RX J1716.6+6708 | 0.813 | 100 230 | 115 780 | 84 059 000 | 17 16 49.8 | +67 08 23.3 | 172 521 | 800891h |
| 79 | MS1054.5-0321 | 0.8231 | 124 650 | 132 210 | 83 065 000 | 10 56 58.4 | -03 37 38.6 | 190 754 | 800937h-1, 800937h, 800783h-1, 800783h |
| ID | Cluster | R/I | S/W | S0 |
|
BM | |||
|
|
[arcsec] | [ h70-1 Mpc] | |||||||
| 1 | PKS 0745-19 | R | W(1) |
|
|
|
|
0.97 | - |
| 2 | A2811 | R | S |
|
|
|
|
1.24 | I-II |
| 3 | A1068 | R | S |
|
|
|
|
1.00 | I |
| 4 | A1413 | R | W(2) |
|
|
|
|
1.36 | I |
| 5 | A990 | R | S |
|
|
|
|
1.18 | III |
| 6 | A2204 | R | W(1) |
|
|
|
|
1.06 | II |
| 7 | A2104 | R | S(1) |
|
|
|
|
0.97 | III |
| 8 | RX J1050.5-0236 | R | S |
|
|
|
|
1.14 | III |
| 9 | A586 | R | W(2) |
|
|
|
|
1.10 | I |
| 10 | A2218 | I | S |
|
|
|
|
0.92 | II |
| 11 | MS0906.5+1110 | I | S |
|
|
|
|
1.17 | - |
| 12 | A665 | I | S |
|
|
|
|
1.35 | III |
| 13 | A1689 | R | W(1) |
|
|
|
|
1.04 | II-III |
| 14 | MS0440.5+0204 | R | S(1) |
|
|
|
|
0.89 | - |
| 15 | A1246 | R | S |
|
|
|
|
1.12 | II-III |
| 16 | MS0839.8+2938 | R | S |
|
|
|
|
1.12 | - |
| 17 | A115 | I | S |
|
|
|
|
1.33 | III |
| 18 | MS0451.5+0250 | I | S |
|
|
|
|
0.97 | III |
| 19 | A2163 | I | S |
|
|
|
|
1.07 | - |
| 20 | A963 | R | S |
|
|
|
|
0.94 | I-II |
| 21 | ZW2701 | R | W(1) |
|
|
|
|
0.88 | - |
| 22 | A1851 | I | S |
|
|
|
|
1.01 | II-III |
| 23 | MS0735.6+7421 | R | W(1) |
|
|
|
|
1.16 | - |
| 24 | A773 | R | S |
|
|
|
|
1.07 | II-III |
| 25 | A1704 | R | S(1) |
|
|
|
|
0.99 | II |
| 26 | MS1006+1202 | I | S |
|
|
|
|
1.19 | - |
| 27 | A2261 | R | S(2) |
|
|
|
|
1.09 | - |
| 28 | A1942 | I | S |
|
|
|
|
1.26 | III |
| 29 | A2219 | R | S |
|
|
|
|
1.10 | III |
| 30 | A1895 | I | S |
|
|
|
|
1.31 | III |
| 31 | A2390 | R | W(1) |
|
|
|
|
1.61 | - |
| 32 | A1763 | I | S |
|
|
|
|
0.98 | III |
| 33 | A2111 | I | S |
|
|
|
|
1.06 | II-III |
| 34 | A267 | R | S |
|
|
|
|
1.05 | - |
| 35 | A2667 | R | W(1) |
|
|
|
|
1.25 | I |
| 36 | A1682 | I | S |
|
|
|
|
1.02 | II |
| 37 | RX J2129.3+0005 | R | S(1) |
|
|
|
|
1.03 | - |
| 38 | MS1910+6736 | I | S |
|
|
|
|
1.27 | - |
| 39 | A1835 | R | S |
|
|
|
|
1.14 | - |
| 40 | RX J1023.8-2715 | R | S |
|
|
|
|
0.92 | II-III |
| 41 | A68 | R | S |
|
|
|
|
1.16 | II-III |
| 42 | MS1455.0+2232 | R | S |
|
|
|
|
1.40 | - |
| 43 | A1758 | I | S |
|
|
|
|
1.16 | III |
| 44 | A483 | I | S |
|
|
|
|
1.01 | III |
| 45 | A697 | I | S |
|
|
|
|
0.83 | II-III |
| 46 | 1E0657-56 | I | S |
|
|
|
|
1.37 | - |
| 47 | MS1008.1-1224 | I | S |
|
|
|
|
0.94 | - |
| 48 | MS1147.3+1103 | R | S |
|
|
|
|
1.29 | - |
| 49 | RX J1131.9-1955 | I | S |
|
|
|
|
1.11 | - |
| 50 | AC118 | I | S |
|
|
|
|
1.04 | III |
| 51 | MS0811.6+6301 | R | S |
|
|
|
|
0.94 | - |
| 52 | MS1241.5+1710 | R | S(2) |
|
|
|
|
1.07 | - |
| 53 | AC114 | I | S |
|
|
|
|
1.18 | II-III |
| 54 | MS2137.3-2353 | R | S |
|
|
|
|
0.76 | - |
| 55 | A1995 | R | S |
|
|
|
|
1.09 | - |
| 56 | CL0500-24 | I | S |
|
|
|
|
0.97 | III |
| 57 | A402 | R | S(1) |
|
|
|
|
1.09 | - |
| 58 | MS1224.7+2007 | R | S |
|
|
|
|
1.30 | - |
| 59 | A1722 | I | S |
|
|
|
|
0.81 | III |
| 60 | CL1358+6245 | R | S |
|
|
|
|
1.26 | - |
| 61 | CL2244-02 | I | S |
|
|
|
|
1.14 | - |
| 62 | RX J1532.9+3021 | R | S(1) |
|
|
|
|
1.01 | - |
| 63 | A959 | I | S |
|
|
|
|
1.13 | III |
| 64 | MS1512.4+3647 | R | S |
|
|
|
|
1.06 | - |
| 65 | A370 | I | S |
|
|
|
|
1.02 | II-III |
| 66 | CL0024+17 | I | S |
|
|
|
|
1.24 | - |
| 67 | A851 | I | S |
|
|
|
|
1.03 | - |
| 68 | MS0302.7+1658 | R | S |
|
|
|
|
0.92 | - |
| 69 | MS1621.5+2640 | I | S |
|
|
|
|
1.12 | - |
| 70 | RX J1347.5-1145 | R | S |
|
|
|
|
1.06 | - |
| 71 | 3C 295 | R | S(1) |
|
|
|
|
1.10 | - |
| 72 | CL0016+16 | I | S |
|
|
|
|
1.00 | - |
| 73 | MS0451.6-0305 | I | S |
|
|
|
|
0.96 | - |
| 74 | CL2236-04 | R | S |
|
|
|
|
1.34 | III |
| 75 | MS2053.7-0449 | R | S |
|
|
|
|
1.30 | - |
| 76 | 3C 220.1 | R | S(2) |
|
|
|
|
1.02 | - |
| 77 | MS1137.5+6625 | R | S |
|
|
|
|
1.15 | - |
| 78 | RX J1716.6+6708 | I | S |
|
|
|
|
1.20 | - |
| 79 | MS1054.5-0321 | I | S |
|
|
|
|
1.11 | - |
| ID | Cluster | S1 | r1 | r1 | S2 | r2 | r2 |
|
|
|
|
[arcsec] | [ h70-1 Mpc] |
|
[arcsec] | [ h70-1 Mpc] | ||||
| 1 | PKS 0745-19 |
|
|
|
|
|
|
|
0.90 |
| 4 | A1413 |
|
|
|
|
|
|
|
1.30 |
| 6 | A2204 |
|
|
|
|
|
|
|
0.99 |
| 9 | A586 |
|
|
|
|
|
|
|
1.05 |
| 13 | A1689 |
|
|
|
|
|
|
|
0.93 |
| 21 | ZW2701 |
|
|
|
|
|
|
|
0.84 |
| 23 | MS0735.6+7421 |
|
|
|
|
|
|
|
0.90 |
| 31 | A2390 |
|
|
|
|
|
|
|
1.22 |
| 35 | A2667 |
|
|
|
|
|
|
|
1.15 |
| ID | Cluster | kT | Z | Normalization | Flux |
|
|
|
||
| [
|
[keV] | [solar] | [
|
[
|
[
|
[
|
||||
| 1 | PKS 0745-19 |
|
|
|
|
|
|
|
|
865.9/716 |
| 2 | A2811 |
|
|
|
|
|
|
|
|
504.3/466 |
| 3 | A1068 |
|
|
|
|
|
|
|
|
470.2/368 |
| 4 | A1413 |
|
|
|
|
|
|
|
|
527.3/504 |
| 5 | A990 |
|
|
|
|
|
|
|
|
563.3/454 |
| 6 | A2204 |
|
|
|
|
|
|
|
|
496.9/487 |
| 7 | A2104 |
|
|
|
|
|
|
|
|
468.7/476 |
| 8 | RX J1050.5-0236 |
|
|
|
|
|
|
|
|
213/172 |
| 9 | A586 |
|
|
|
|
|
|
|
|
130.8/137 |
| 10 | A2218 |
|
|
|
|
|
|
|
|
391.4/370 |
| 11 | MS0906.5+1110 |
|
|
|
|
|
|
|
|
240/223 |
| 12 | A665 |
|
|
|
|
|
|
|
|
729.6/570 |
| 13 | A1689 |
|
|
|
|
|
|
|
|
618.2/566 |
| 14 | MS0440.5+0204 |
|
|
|
|
|
|
|
|
140.6/125 |
| 15 | A1246 |
|
|
|
|
|
|
|
|
361.4/294 |
| 16 | MS0839.8+2938 |
|
|
|
|
|
|
|
|
202.2/181 |
| 17 | A115 |
|
|
|
|
|
|
|
|
392.7/348 |
| 18 | MS0451.5+0250 |
|
|
|
|
|
|
|
|
214.6/220 |
| 19 | A2163 |
|
|
|
|
|
|
|
|
563.2/547 |
| 20 | A963 |
|
|
|
|
|
|
|
|
238.2/257 |
| 21 | ZW2701 |
|
|
|
|
|
|
|
|
246.5/201 |
| 22 | A1851 |
|
|
|
|
|
|
|
|
158.6/126 |
| 23 | MS0735.6+7421 |
|
|
|
|
|
|
|
|
103/134 |
| 24 | A773 |
|
|
|
|
|
|
|
|
323.4/327 |
| 25 | A1704 |
|
|
|
|
|
|
|
|
160.7/158 |
| 26 | MS1006+1202 |
|
|
|
|
|
|
|
|
125.9/140 |
| 27 | A2261 |
|
|
|
|
|
|
|
|
255.6/280 |
| 28 | A1942 |
|
|
|
|
|
|
|
|
147.8/155 |
| 29 | A2219 |
|
|
|
|
|
|
|
|
462.5/400 |
| 30 | A1895 |
|
|
|
|
|
|
|
|
120/137 |
| 31 | A2390 |
|
|
|
|
|
|
|
|
185.1/175 |
| 32 | A1763 |
|
|
|
|
|
|
|
|
368.1/362 |
| 33 | A2111 |
|
|
|
|
|
|
|
|
219.9/233 |
| 34 | A267 |
|
|
|
|
|
|
|
|
304.2/254 |
| 35 | A2667 |
|
|
|
|
|
|
|
|
454.2/410 |
| 36 | A1682 |
|
|
|
|
|
|
|
|
255.3/250 |
| 37 | RX J2129.3+0005 |
|
|
|
|
|
|
|
|
314.5/324 |
| 38 | MS1910+6736 |
|
|
|
|
|
|
|
|
110.5/107 |
| 39 | A1835 |
|
|
|
|
|
|
|
|
377.6/334 |
| 40 | RX J1023.8-2715 |
|
|
|
|
|
|
|
|
252.2/250 |
| 41 | A68 |
|
|
|
|
|
|
|
|
291/262 |
| 42 | MS1455.0+2232 |
|
|
|
|
|
|
|
|
242.9/253 |
| 43 | A1758 |
|
|
|
|
|
|
|
|
213.4/175 |
| 44 | A483 |
|
|
|
|
|
|
|
|
145.2/136 |
| 45 | A697 |
|
|
|
|
|
|
|
|
542.6/415 |
| 46 | 1E0657-56 |
|
|
|
|
|
|
|
|
631.3/511 |
| 47 | MS1008.1-1224 |
|
|
|
|
|
|
|
|
92.9/78 |
| 48 | MS1147.3+1103 |
|
|
|
|
|
|
|
|
64.5/83 |
| 49 | RX J1131.9-1955 |
|
|
|
|
|
|
|
|
321.2/340 |
| 50 | AC118 |
|
|
|
|
|
|
|
|
411.6/425 |
| 51 | MS0811.6+6301 |
|
|
|
|
|
|
|
|
69.1/64 |
| 52 | MS1241.5+1710 |
|
|
|
|
|
|
|
|
47.4/51 |
| 53 | AC114 |
|
|
|
|
|
|
|
|
300.1/227 |
| 54 | MS2137.3-2353 |
|
|
|
|
|
|
|
|
116.3/130 |
| 55 | A1995 |
|
|
|
|
|
|
|
|
171/159 |
| 56 | CL0500-24 |
|
|
|
|
|
|
|
24.5/26 | |
| 57 | A402 |
|
|
|
|
|
|
|
|
124.9/140 |
| 58 | MS1224.7+2007 |
|
|
|
|
|
|
|
|
37.7/45 |
| 59 | A1722 |
|
|
|
|
|
|
|
|
203.2/188 |
| 60 | CL1358+6245 |
|
|
|
|
|
|
|
|
182.6/177 |
| 61 | CL2244-02 |
|
|
|
|
|
|
|
72.2/58 | |
| 62 | RX J1532.9+3021 |
|
|
|
|
|
|
|
|
379.3/305 |
| 63 | A959 |
|
|
|
|
|
|
|
|
107.9/110 |
| 64 | MS1512.4+3647 |
|
|
|
|
|
|
|
|
53.2/47 |
| 65 | A370 |
|
|
|
|
|
|
|
118.4/124 | |
| 66 | CL0024+17 |
|
|
|
|
|
|
3.6/5 | ||
| 67 | A851 |
|
|
|
|
|
|
|
|
131.8/118 |
| 68 | MS0302.7+1658 |
|
|
|
|
|
|
|
|
89.1/73 |
| 69 | MS1621.5+2640 |
|
|
|
|
|
|
|
|
121.6/101 |
| 70 | RX J1347.5-1145 |
|
|
|
|
|
|
|
|
508.2/406 |
| 71 | 3C 295 |
|
|
|
|
|
|
|
|
114.3/103 |
| 72 | CL0016+16 |
|
|
|
|
|
|
|
|
263.9/236 |
| 73 | MS0451.6-0305 |
|
|
|
|
|
|
|
|
107.5/114 |
| 74 | CL2236-04 |
|
|
|
|
|
|
|
|
30.1/41 |
| 75 | MS2053.7-0449 |
|
|
|
|
|
|
|
|
62.7/61 |
| 76 | 3C 220.1 |
|
|
|
|
|
|
|
18.2/33 | |
| 77 | MS1137.5+6625 |
|
|
|
|
|
|
|
|
46.8/39 |
| 78 | RX J1716.6+6708 |
|
|
|
|
|
|
|
|
54.1/44 |
| 79 | MS1054.5-0321 |
|
|
|
|
|
|
|
|
168/163 |
|
|
||||||||||
| ID | Cluster |
|
|
|
rX |
|
|
|
|
|
|
|
|
[Gyr] | [Gyr] |
|
|
|
|
[h70-3/2] | ||
| 1 | PKS 0745-19 |
|
|
|
12.2 | 1.43 |
|
|
|
|
| 2 | A2811 |
|
|
|
12.1 | 0.89 |
|
|
|
|
| 3 | A1068 |
|
|
|
11.8 | 1.37 |
|
|
|
|
| 4 | A1413 |
|
|
|
11.7 | 1.64 |
|
|
|
|
| 5 | A990 |
|
|
|
11.7 | 0.93 |
|
|
|
|
| 6 | A2204 |
|
|
|
11.6 | 2.11 |
|
|
|
|
| 7 | A2104 |
|
|
|
11.5 | 1.42 |
|
|
|
|
| 8 | RX J1050.5-0236 |
|
|
|
11.4 | 1.09 |
|
|
|
|
| 9 | A586 |
|
|
|
11.4 | 0.97 |
|
|
|
|
| 10 | A2218 |
|
|
|
11.3 | 1.51 |
|
|
|
|
| 11 | MS0906.5+1110 |
|
|
|
11.3 | 1.90 |
|
|
|
|
| 12 | A665 |
|
|
|
11.3 | 2.11 |
|
|
|
|
| 13 | A1689 |
|
|
|
11.2 | 1.99 |
|
|
|
|
| 14 | MS0440.5+0204 |
|
|
|
11.2 | 0.96 |
|
|
|
|
| 15 | A1246 |
|
|
|
11.2 | 1.47 |
|
|
|
|
| 16 | MS0839.8+2938 |
|
|
|
11.1 | 0.85 |
|
|
|
|
| 17 | A115 |
|
|
|
11.1 | 3.37 |
|
|
|
|
| 18 | MS0451.5+0250 |
|
|
|
11.1 | 1.12 |
|
|
|
|
| 19 | A2163 |
|
|
|
11.0 | 2.00 |
|
|
|
|
| 20 | A963 |
|
|
|
11.0 | 1.83 |
|
|
|
|
| 21 | ZW2701 |
|
|
|
10.9 | 1.28 |
|
|
|
|
| 22 | A1851 |
|
|
|
10.9 | 1.08 |
|
|
|
|
| 23 | MS0735.6+7421 |
|
|
|
10.9 | 2.08 |
|
|
|
|
| 24 | A773 |
|
|
|
10.9 | 1.33 |
|
|
|
|
| 25 | A1704 |
|
|
|
10.8 | 2.06 |
|
|
|
|
| 26 | MS1006+1202 |
|
|
|
10.8 | 1.18 |
|
|
|
|
| 27 | A2261 |
|
|
|
10.8 | 2.05 |
|
|
|
|
| 28 | A1942 |
|
|
|
10.8 | 1.34 |
|
|
|
|
| 29 | A2219 |
|
|
|
10.8 | 1.86 |
|
|
|
|
| 30 | A1895 |
|
|
|
10.8 | 1.24 |
|
|
|
|
| 31 | A2390 |
|
|
|
10.8 | 3.31 |
|
|
|
|
| 32 | A1763 |
|
|
|
10.8 | 2.01 |
|
|
|
|
| 33 | A2111 |
|
|
|
10.8 | 2.04 |
|
|
|
|
| 34 | A267 |
|
|
|
10.7 | 1.10 |
|
|
|
|
| 35 | A2667 |
|
|
|
10.7 | 2.56 |
|
|
|
|
| 36 | A1682 |
|
|
|
10.7 | 1.21 |
|
|
|
|
| 37 | RX J2129.3+0005 |
|
|
|
10.7 | 1.95 |
|
|
|
|
| 38 | MS1910+6736 |
|
|
|
10.6 | 1.30 |
|
|
|
|
| 39 | A1835 |
|
|
|
10.5 | 1.37 |
|
|
|
|
| 40 | RX J1023.8-2715 |
|
|
|
10.5 | 2.28 |
|
|
|
|
| 41 | A68 |
|
|
|
10.5 | 1.15 |
|
|
|
|
| 42 | MS1455.0+2232 |
|
|
|
10.5 | 1.16 |
|
|
|
|
| 43 | A1758 |
|
|
|
10.3 | 1.03 |
|
|
|
|
| 44 | A483 |
|
|
|
10.3 | 0.79 |
|
|
|
|
| 45 | A697 |
|
|
|
10.2 | 1.90 |
|
|
|
|
| 46 | 1E0657-56 |
|
|
|
10.1 | 1.57 |
|
|
|
|
| 47 | MS1008.1-1224 |
|
|
|
10.1 | 1.34 |
|
|
|
|
| 48 | MS1147.3+1103 |
|
|
|
10.0 | 1.50 |
|
|
|
|
| 49 | RX J1131.9-1955 |
|
|
|
10.0 | 1.69 |
|
|
|
|
| 50 | AC118 |
|
|
|
10.0 | 1.66 |
|
|
|
|
| 51 | MS0811.6+6301 |
|
|
|
10.0 | 1.13 |
|
|
|
|
| 52 | MS1241.5+1710 |
|
|
|
10.0 | 0.62 |
|
|
|
|
| 53 | AC114 |
|
|
|
10.0 | 1.95 |
|
|
|
|
| 54 | MS2137.3-2353 |
|
|
|
10.0 | 1.04 |
|
|
|
|
| 55 | A1995 |
|
|
|
9.9 | 1.23 |
|
|
|
|
| 56 | CL0500-24 |
|
|
|
9.9 | 0.97 |
|
|
|
|
| 57 | A402 |
|
|
|
9.9 | 1.41 |
|
|
|
|
| 58 | MS1224.7+2007 |
|
|
|
9.8 | 1.26 |
|
|
|
|
| 59 | A1722 |
|
|
|
9.8 | 1.52 |
|
|
|
|
| 60 | CL1358+6245 |
|
|
|
9.8 | 1.99 |
|
|
|
|
| 61 | CL2244-02 |
|
|
|
9.8 | 0.48 |
|
|
|
|
| 62 | RX J1532.9+3021 |
|
|
|
9.7 | 1.52 |
|
|
|
|
| 63 | A959 |
|
|
|
9.6 | 1.88 |
|
|
|
|
| 64 | MS1512.4+3647 |
|
|
|
9.4 | 1.06 |
|
|
|
|
| 65 | A370 |
|
|
|
9.4 | 1.45 |
|
|
|
|
| 66 | CL0024+17 |
|
|
|
9.3 | 1.99 |
|
|
|
|
| 67 | A851 |
|
|
|
9.1 | 1.75 |
|
|
|
|
| 68 | MS0302.7+1658 |
|
|
|
9.0 | 1.05 |
|
|
|
|
| 69 | MS1621.5+2640 |
|
|
|
9.0 | 1.86 |
|
|
|
|
| 70 | RX J1347.5-1145 |
|
|
|
8.8 | 2.11 |
|
|
|
|
| 71 | 3C 295 |
|
|
|
8.7 | 0.71 |
|
|
|
|
| 72 | CL0016+16 |
|
|
|
8.2 | 2.01 |
|
|
|
|
| 73 | MS0451.6-0305 |
|
|
|
8.1 | 1.65 |
|
|
|
|
| 74 | CL2236-04 |
|
|
|
8.0 | 0.86 |
|
|
|
|
| 75 | MS2053.7-0449 |
|
|
|
7.9 | 0.44 |
|
|
|
|
| 76 | 3C 220.1 |
|
|
|
7.7 | 0.35 |
|
|
|
|
| 77 | MS1137.5+6625 |
|
|
|
6.7 | 1.20 |
|
|
|
|
| 78 | RX J1716.6+6708 |
|
|
|
6.6 | 1.01 |
|
|
|
|
| 79 | MS1054.5-0321 |
|
|
|
6.5 | 0.92 |
|
|
|
|
|
|
||||||||||
| ID | Cluster |
|
|
|
|
r500 | M500 |
|
|
|
|
|
[Gyr] |
|
[Gyr] |
|
|
|
|
[h70-3/2] | ||
| 1 | PKS 0745-19 |
|
|
|
|
|
|
|
|
|
| 4 | A1413 |
|
|
|
|
|
|
|
|
|
| 6 | A2204 |
|
|
|
|
|
|
|
|
|
| 9 | A586 |
|
|
|
|
|
|
|
|
|
| 13 | A1689 |
|
|
|
|
|
|
|
|
|
| 21 | ZW2701 |
|
|
|
|
|
|
|
|
|
| 23 | MS0735.6+7421 |
|
|
|
|
|
|
|
|
|
| 31 | A2390 |
|
|
|
|
|
|
|
|
|
| 35 | A2667 |
|
|
|
|
|
|
|
|
|
Suppose that the density distribution of intracluster gas is
characterized by superposition of the two ![]() -model gas profiles.
-model gas profiles.
| S(r) | = | 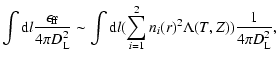 |
|
| = | ![$\displaystyle \sum_{i=1}^{2}S_i\left[1+\left(\frac{r}{r_i}\right)^2\right]^{-3\beta_i+1/2}\cdot$](/articles/aa/full/2004/48/aa1087/img2622.gif) |
(A.2) |
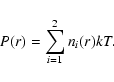 |
(A.3) |
The gas-mass fraction is determined from the parameters, T, ![]() ,
,
![]() ,
and
,
and
![]() ,
and
,
and
![]() is further determined from the central
surface brightness
is further determined from the central
surface brightness
![]() ,
T,
,
T, ![]() ,
and
,
and ![]() .
Among those
parameters, a possible systematic effect for
.
Among those
parameters, a possible systematic effect for ![]() was investigated in
Sect. 3.4, and was found to be less than the pixel
size of the X-ray image.
was investigated in
Sect. 3.4, and was found to be less than the pixel
size of the X-ray image. ![]() is strongly coupled to
is strongly coupled to ![]() and its
systematic error is determined by the systematic error of
and its
systematic error is determined by the systematic error of ![]() .
On
the other hand,
.
On
the other hand,
![]() requires the absolute calibration of the
X-ray telescope/detector effective area, which usually contains large
systematic errors. The temperature, T, requires a calibration of
the effective area as a function of X-ray energy. Thus we will
investigate the systematic errors in
requires the absolute calibration of the
X-ray telescope/detector effective area, which usually contains large
systematic errors. The temperature, T, requires a calibration of
the effective area as a function of X-ray energy. Thus we will
investigate the systematic errors in
![]() and T below.
and T below.
Systematic errors in the electron density mainly come from the
calibration of the ROSAT HRI. Because the gain of the HRI
continuously decreased from the launch to the end of the mission, the
conversion factor from the photon energy to pulse height is time
dependent. Thus the errors in the gain determination cause
significant error in the absolute flux. The possible range of the
gain variations over the lifetime of ROSAT was measured by
Prestwitch et al. (1998). Thus we tried the response matrices for
the two extreme gain values in calculating Eq. (3) to estimate the maximum systematic errors.
Taking into account that the result also depends on the cluster
emission spectrum, the effect is ![]() % in the worst case. The
calibration of the effective area of the X-ray telescope and the HRI
system is also reported by the ROSAT Science Data Center, from
which we estimate that the systematic errors in
% in the worst case. The
calibration of the effective area of the X-ray telescope and the HRI
system is also reported by the ROSAT Science Data Center, from
which we estimate that the systematic errors in
![]() is
is ![]() 10%.
10%.
Systematic errors in the temperature come from the calibration of ASCA. The response functions of the ASCA XRT/GIS and XRT/SIS
are well calibrated for point sources. However, for the extended
sources, there still are significant systematic errors. In
particular we found that the derived temperature is dependent on the
spectrum integration region on the detector if the integration radius
is too small. In the spectral analysis, we determined the radius so
that the dependence becomes insignificant. However, we still consider
there is some systematic effect related to this problem and estimate
that it will affect
![]() by about 5% (notice T affects
both M500 and
by about 5% (notice T affects
both M500 and
![]() ).
).
In total, the systematic error due to the instrument calibrations is
estimated to be ![]() %.
%.