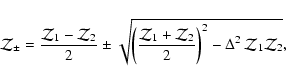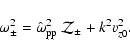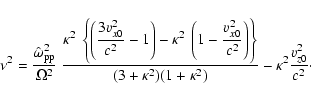A&A 428, 365-371 (2004)
DOI: 10.1051/0004-6361:20041882
Magnetic field generation in relativistic shocks
An early end of the exponential Weibel instability in
electron-proton plasmas
J. Wiersma - A. Achterberg
Sterrenkundig Instituut, Universiteit Utrecht, PO Box 80000,
3508 TA Utrecht, The Netherlands
Received 21 April 2004 / Accepted 26 August 2004
Abstract
We discuss magnetic field generation by the proton Weibel
instability in relativistic shocks, a situation that applies to the
external shocks in the fireball model for Gamma-ray Bursts, and possibly
also to internal shocks.
Our analytical estimates show that the linear phase of the instability ends
well before it has converted a significant fraction of the energy in the
proton beam into magnetic energy: the conversion efficiency is much smaller
(of order
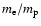 )
in electron-proton plasmas than in pair
plasmas.
We find this estimate by modelling the plasma in the shock transition zone
with a waterbag momentum distribution for the protons and with a background
of hot electrons.
)
in electron-proton plasmas than in pair
plasmas.
We find this estimate by modelling the plasma in the shock transition zone
with a waterbag momentum distribution for the protons and with a background
of hot electrons.
For ultra-relativistic shocks we find that the wavelength of the most
efficient mode for magnetic field generation equals the electron skin depth,
that the relevant nonlinear stabilization mechanism is magnetic trapping,
and that the presence of the hot electrons limits the typical magnetic field strength generated by this mode so that it does not
depend on the energy content of the protons.
We conclude that other processes than the linear Weibel instability must
convert the free energy of the protons into magnetic fields.
Key words: plasmas - magnetic fields - instabilities - shock waves -
gamma rays: bursts
1 Introduction
Magnetic field generation in relativistic shocks in a hydrogen
(electron-proton) plasma is important for the fireball model for Gamma-ray
Bursts (Rees & Mészáros 1992).
This model proposes that the non-thermal radiation we observe in the prompt
and afterglow emission from the Gamma-ray Burst is synchrotron radiation
from collisionless relativistic shocks.
To explain the observed intensity of the afterglows as synchrotron emission,
the models need a magnetic field strength B of at least ten per cent of the equipartition
field strength (Panaitescu & Kumar 2002; Gruzinov & Waxman 1999).
This means that the magnetic energy density must contribute about one to
ten per cent to the total energy density of the plasma behind the shock:
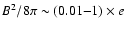 ,
with e the post-shock thermal
energy density.
In electron-proton plasmas this implies a much stronger magnetic field than
in pair plasmas because the energy density in an ultra-relativistic shock
propagating into a cold medium (where
,
with e the post-shock thermal
energy density.
In electron-proton plasmas this implies a much stronger magnetic field than
in pair plasmas because the energy density in an ultra-relativistic shock
propagating into a cold medium (where
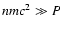 ,
with n the number
density, m the rest mass and P the thermal pressure)
is roughly proportional to the rest mass m of the particles.
In this paper, we look at what happens in a plasma consisting of particles of widely different mass.
,
with n the number
density, m the rest mass and P the thermal pressure)
is roughly proportional to the rest mass m of the particles.
In this paper, we look at what happens in a plasma consisting of particles of widely different mass.
In collisionless shocks, plasma instabilities can generate magnetic fields.
Within the shock transition layer the relative motion of the mixing
pre- and post-shock plasma produces very anisotropic velocity
distributions for all particle species concerned.
Fluctuating electromagnetic fields deflect the incoming charged particles
and act as the effective collisional process needed to complete the shock
transition (e.g., Hoshino et al. 1992).
These fluctuating fields occur naturally because anisotropic velocity
distributions are unstable against several plasma instabilities, such as
the electrostatic two-stream instability and the electromagnetic Weibel
instability.
The first is an instability of (quasi-)longitudinal charge density
perturbations and leads to fluctuating electric fields satisfying
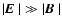 where
where
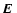 and
and
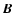 are the fluctuating electric and
magnetic fields.
The second is an instability of the advection currents (proportional to the
beam velocity) that result from charge bunching in the beams, and leads to
spontaneously growing transverse waves (Weibel 1959) with
are the fluctuating electric and
magnetic fields.
The second is an instability of the advection currents (proportional to the
beam velocity) that result from charge bunching in the beams, and leads to
spontaneously growing transverse waves (Weibel 1959) with
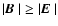 .
In a relativistic shock, where the relative velocity of the pre- and
post-shock plasma approaches the velocity of light, the Weibel instability
dominates because it has the largest growth rate (Califano et al. 2002).
.
In a relativistic shock, where the relative velocity of the pre- and
post-shock plasma approaches the velocity of light, the Weibel instability
dominates because it has the largest growth rate (Califano et al. 2002).
As both analytical estimates and numerical simulations show, the Weibel
instability in pair plasmas can produce a magnetic field of
near-equipartition strength (Yang et al. 1994; Medvedev & Loeb 1999; Fonseca et al. 2003; Haruki & Sakai 2003; Kazimura et al. 1998).
In numerical simulations, the magnetic field generation always undergoes an
exponentially growing phase that agrees with the estimates from linear
analytical theory, and enters a nonlinear phase after that.
Yang et al. (1994) have shown that in pair plasmas, the magnetic field
strength reaches its maximum value at the end of the linear phase of the
instability.
The question arises whether the same holds true for the Weibel instability
operating in an electron-proton plasma (Medvedev & Loeb 1999).
Numerical simulations (Frederiksen et al. 2004) show that the
nonlinear phase may be more important in electron-ion plasmas.
In this paper we present an analytical estimate that shows that the
linear phase of the instability ends much earlier for proton beams
in a hydrogen plasma than for electron(-positron) beams in a pair plasma.
We do not present a full self-consistent shock model: rather we consider
the plasma processes that could generate a magnetic field in a plasma with
properties such as one expects near the front of a collisionless
relativistic shock.
The paper is organised as follows.
In Sect. 2 we define a model for the shock situation in terms
of the momentum distributions of the particles.
We calculate the conditions for the instability in Sect. 3.1 and
the magnetic field strength at the end of the linear phase of the
instability in Sect. 3.2.
In Sect. 3.3, we compare the energy density associated with this
magnetic field strength with the total available energy density associated
with the beams.
Section 4 contains the discussion and Sect. 5
the conclusions.
2 A simple model for a relativistic shock transition
In an electron-proton plasma, the protons dominate the shock energetics
because they have a much larger rest mass than the electrons.
Therefore, we will study the proton-driven Weibel instability.
In this section we present a simple model for the plasma in the
transition layer at the front of the shock.
The plasma in an astrophysical relativistic shock does not necessarily
behave as a single fluid.
Coulomb collisions between electrons and protons are not sufficiently fast
to create thermal equilibrium between the protons and electrons.
This problem of the non-equilibration of the electron and ion energies
already exists in the much slower ( 1000 km s-1) shocks associated with
Supernova Remnants (Draine & McKee 1993; Vink 2004).
1000 km s-1) shocks associated with
Supernova Remnants (Draine & McKee 1993; Vink 2004).
We assume that scattering by plasma waves is far more
efficient for the light electrons than for the heavy ions so that
when the trajectories of the incoming protons start to become significantly
perturbed, the electrons have already undergone the fast-growing
electron Weibel instability (Medvedev & Loeb 1999; Frederiksen et al. 2004),
which has converted the kinetic energy of their bulk motion into the thermal
energy of a relativistically hot electron plasma with an (almost) isotropic
thermal velocity distribution.
The incoming protons form, seen from the rest frame of the hot electrons, a
relativistic beam.
We also assume that part of the protons are reflected further downstream
although that assumption is not critical for our final
conclusions (see Appendix A).
The electron-driven Weibel instability produces a weak fluctuating magnetic
field with
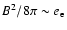 ,
with
,
with 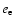 the energy density
of the shocked electrons.
We ignore this magnetic field in the calculations for proton beams, but it
could serve as a seed perturbation for the proton-driven Weibel instability.
the energy density
of the shocked electrons.
We ignore this magnetic field in the calculations for proton beams, but it
could serve as a seed perturbation for the proton-driven Weibel instability.
2.1 The proton velocity distribution
A simple model for the anisotropic proton velocity distribution within the shock transition
layer is a waterbag distribution (Yoon & Davidson 1987; Silva et al. 2002).
We consider a similar situation as in Fig. 6 of Frederiksen et al. (2004): we take two
counter-streaming proton beams moving along the x-direction, with a small
velocity spread in the z-direction to model thermal motions:
![$\displaystyle F(\vec{p}) = {\frac{n_{\rm p}}{4 p_{z0}}} \:
\left[ \delta(p_x-p_...
...x0}) \right]
\delta(p_y) \left[\Theta(p_z+p_{z0}) - \Theta(p_z-p_{z0}) \right].$](/articles/aa/full/2004/47/aa1882/img15.gif) |
|
|
(1) |
Here 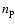 is the total proton density, px0 is the bulk
momentum of the proton beams, pz0 is the maximum momentum in thermal
motions and
is the total proton density, px0 is the bulk
momentum of the proton beams, pz0 is the maximum momentum in thermal
motions and
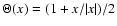 is the Heavyside step function.
The assumption of two beams of equal strength is mathematically convenient,
but not essential (see Appendix A).
is the Heavyside step function.
The assumption of two beams of equal strength is mathematically convenient,
but not essential (see Appendix A).
This is a simple model that mimics the properties of non-relativistic
collisionless shocks (see the Microstructure Section
in Tsurutani & Stone 1985) in which (partial) reflection of the ions occurs as a
result of deflection by an electrostatic potential jump in the shock
transition, or by "overshoots'' in the strong magnetic field in the wake of
the shock.
In addition, the waterbag model accounts for partial ion heating by
including a velocity dispersion in the direction perpendicular to both the
beam direction and the wave magnetic field.
This direction lies along the wave vector of the unstable modes (the
z-direction in our configuration).
2.2 The shock conditions for the electrons
We assume that the electrons have (almost) completed the shock transition so
that their properties obey the relativistic shock conditions (Blandford & McKee 1976),
which follow from the generally valid conservation laws for particle
number, energy and momentum.
Here and below, we will label properties of the post-shock electron plasma
with subscript 2, and those of the pre-shock plasma with subscript 1.
We will assume that the pre-shock plasma is cold in the sense that
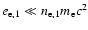 .
Then the shock conditions for the proper density
.
Then the shock conditions for the proper density 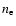 and the
proper energy density
and the
proper energy density 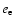 for the electrons are:
for the electrons are:
where
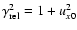 is the Lorentz factor of the relative
velocity between the pre- and post-shock plasma (with
is the Lorentz factor of the relative
velocity between the pre- and post-shock plasma (with
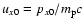 ).
).
We neglect the dynamical influence of a pre-shock magnetic field on the
electron-fluid jump conditions.
This influence will be small if
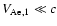 where
where
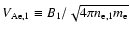 is the Alfvén speed based on
the electron mass (instead of the proton mass).
We also neglect any large-scale electrostatic field in the shock that might
accelerate the electrons to higher energies while decelerating the
incoming protons.
is the Alfvén speed based on
the electron mass (instead of the proton mass).
We also neglect any large-scale electrostatic field in the shock that might
accelerate the electrons to higher energies while decelerating the
incoming protons.
3 The Weibel instability
3.1 The dispersion relation
We consider the instability of a purely transverse electromagnetic wave with
wave vector
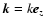 and frequency
and frequency 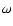 .
The instability will grow with a rate equal to the imaginary part of the
wave frequency:
.
The instability will grow with a rate equal to the imaginary part of the
wave frequency:
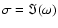 .
.
The Weibel instability for the model of the previous section obeys a
dispersion relation of the form
(e.g., Silva et al. 2002)
![\begin{displaymath}
k^2 c^2 - \omega^{2} \left[ \: 1 + \chi _{xx}(\omega, k) \: \right] = 0,
\end{displaymath}](/articles/aa/full/2004/47/aa1882/img31.gif) |
(3) |
where
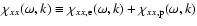 is the xx-component of the plasma susceptibility
tensor, which contains contributions of both the electrons and the protons.
is the xx-component of the plasma susceptibility
tensor, which contains contributions of both the electrons and the protons.
Since the electrons have a relativistically hot thermal velocity
distribution their contribution is
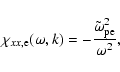 |
(4) |
where
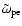 is the electron plasma frequency (in Gaussian units):
is the electron plasma frequency (in Gaussian units):
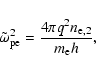 |
(5) |
with
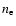 the electron proper density, q the electron charge,
the electron proper density, q the electron charge,
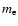 the
electron mass and
the
electron mass and
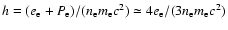 the electron enthalpy per
unit rest energy for the relativistically hot electrons with
the electron enthalpy per
unit rest energy for the relativistically hot electrons with
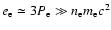 .
If we assume that the electrons are fully shocked, the shock conditions
(2) enable us to express
.
If we assume that the electrons are fully shocked, the shock conditions
(2) enable us to express
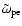 in terms of the pre-shock
electron number density:
in terms of the pre-shock
electron number density:
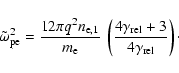 |
(6) |
The factor between brackets approaches unity in ultra-relativistic
shocks with
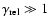 .
.
The proton contribution to dispersion relation (3) is
(see Silva et al. 2002)
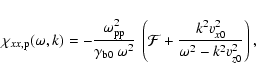 |
(7) |
with
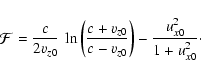 |
(8) |
Here
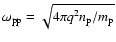 is the (non-relativistic) proton
plasma frequency based on the density in the lab frame,
is the (non-relativistic) proton
plasma frequency based on the density in the lab frame,  is the proton
rest mass,
is the proton
rest mass,
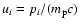 ,
,
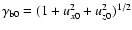 and
and
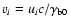 .
To ensure quasi-neutrality of the plasma we must have
.
To ensure quasi-neutrality of the plasma we must have
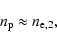 |
(9) |
and the associated plasma frequency is
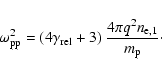 |
(10) |
For what follows it is convenient to introduce the frequency
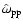 defined by
defined by
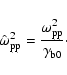 |
(11) |
If the velocity dispersion in the beam is small, which is always true
for a Weibel-unstable proton distribution (see the end of this section), we
have
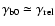 so that
so that
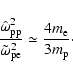 |
(12) |
Note that one can get the equations for an electron-positron beam in an
electron-positron plasma (see also Yang et al. 1994; Silva et al. 2002) by replacing 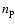 and
and  with the beam density and electron mass respectively.
We will use this in what follows to compare results for electron-proton
plasmas with those for electron-positron plasmas.
In those cases we assume that the density of the electron-positron beams is
comparable to the density of the background electron-positron plasma.
with the beam density and electron mass respectively.
We will use this in what follows to compare results for electron-proton
plasmas with those for electron-positron plasmas.
In those cases we assume that the density of the electron-positron beams is
comparable to the density of the background electron-positron plasma.
Substituting the contributions (4) and (7) in (3) we
can write the dispersion relation as a biquadratic equation for 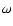 :
:
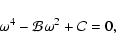 |
(13) |
with
where
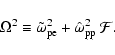 |
(16) |
Since
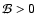 the wave is unstable for
the wave is unstable for
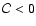 with
with
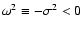 where
the growth rate
where
the growth rate 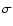 follows from
follows from
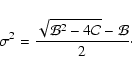 |
(17) |
For a given set of shock parameters (
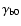 ,
vz0, n0), the growth
rate is a function of the wave number (Fig. 1).
,
vz0, n0), the growth
rate is a function of the wave number (Fig. 1).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1882fig1.eps}
\end{figure}](/articles/aa/full/2004/47/aa1882/Timg66.gif) |
Figure 1:
Growth rate as a function of wave number for
a shock with
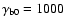 and
vz0= 0.001 c.
The solid line is for proton beams in a background of hot electrons; the
dashed line is for electron-positron beams in an electron-positron plasma.
and
vz0= 0.001 c.
The solid line is for proton beams in a background of hot electrons; the
dashed line is for electron-positron beams in an electron-positron plasma. |
| Open with DEXTER |
Anticipating our results for a proton beam in a background of
(relativistically) hot electrons, we will assume that the growth rate of the
unstable modes satisfies
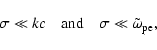 |
(18) |
and that the characteristic plasma frequencies satisfy
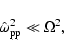 |
(19) |
see Eq. (27) below.
Under these assumptions we can approximate the solution of the dispersion relation with
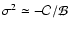 ,
which leaves the instability criterion (
,
which leaves the instability criterion (
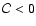 )
unchanged.
We will also make the approximation of a small beam velocity
dispersion:
)
unchanged.
We will also make the approximation of a small beam velocity
dispersion:
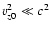 .
Then the dispersion relation
reduces to
.
Then the dispersion relation
reduces to
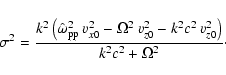 |
(20) |
For further analysis we introduce the following dimensionless quantities:
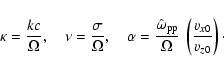 |
(21) |
Expressed in these quantities the dispersion relation (20) reads
where we have eliminated vz0 using the definition
of 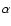 and we define
and we define
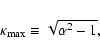 |
(23) |
which is the limiting wavenumber of the Weibel instability: the instability
condition is satisfied for
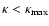 .
The parameter
.
The parameter 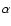 is a measure for the range of unstable wave numbers.
The Weibel instability occurs only if
is a measure for the range of unstable wave numbers.
The Weibel instability occurs only if 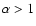 .
This condition poses a restriction on the velocity spread vz0:
.
This condition poses a restriction on the velocity spread vz0:
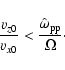 |
(24) |
The quantity 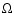 depends on vz0 through Eqs. (16) and (8), but
a quick inspection shows that
depends on vz0 through Eqs. (16) and (8), but
a quick inspection shows that 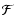 and
and 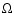 are
increasing functions of vz0 so if condition (24) holds,
then we also have
are
increasing functions of vz0 so if condition (24) holds,
then we also have
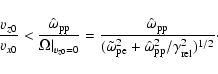 |
(25) |
It follows that for relativistic shocks with
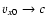 the proton-driven
instability requires
the proton-driven
instability requires
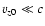 so that
so that
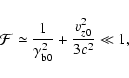 |
(26) |
and
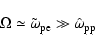 |
(27) |
(see Eq. (12)).
The largest growth rate occurs for a mode with wave number
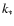 ,
which
follows from
,
which
follows from
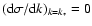 .
Using the approximated dispersion relation (22) we find that
this wavenumber equals
.
Using the approximated dispersion relation (22) we find that
this wavenumber equals
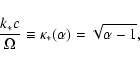 |
(28) |
with the corresponding growth rate
In the last equality we have used the definition of 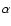 .
For a strong, relativistic shock we find
.
For a strong, relativistic shock we find
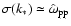 .
.
In view of this fact and Eq. (27), conditions (18)
and (19) automatically hold for the proton-driven Weibel
instability.
3.2 Stabilization of the Weibel instability
The linear phase of the Weibel instability (during which perturbations grow
exponentially with time) ends when the generated electromagnetic fields
significantly perturb the trajectories of the particles taking part in the
instability.
Because the magnetic fields generated by the instability are inhomogeneous,
the particles will quiver under the influence of the Lorentz force.
When the amplitude of these quiver motions exceeds the wavelength of the
instability, the linear theory breaks down.
Yang et al. (1994) give a full treatment of these quiver motions and show that
this criterion agrees with the magnetic trapping argument, which says that
the instability will stop when the wave magnetic field becomes so strong
that it traps the beam particles.
The linearized equation describing the quiver motions in the z-direction
for a beam particle in a magnetic field
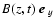 reads:
reads:
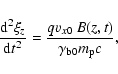 |
(30) |
where 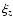 is the displacement.
In the linear stage of the instability the wave magnetic field varies as
is the displacement.
In the linear stage of the instability the wave magnetic field varies as
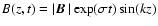 for a wave with wave number k and
growth rate
for a wave with wave number k and
growth rate 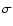 ,
so the amplitude of the quiver motion is
,
so the amplitude of the quiver motion is
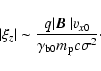 |
(31) |
The trapping criterion
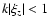 corresponds to
corresponds to
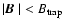 with
with
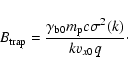 |
(32) |
This corresponds to Eq. (18) of Yang et al. (1994).
Assuming that trapping saturates the Weibel instability at all
wavelengths we get the typical field amplitude as
a function of wavenumber (Fig. 2).
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{1882fig2.eps}
\end{figure}](/articles/aa/full/2004/47/aa1882/Timg105.gif) |
Figure 2:
Saturation magnetic field as a function of wave number
for a proton-driven instability and for an
instability in an electron-positron plasma, using the same parameters as in
Fig. 1 with
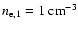 . . |
| Open with DEXTER |
The maximum field amplitude is reached at those wave numbers where
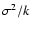 has the maximum value.
For dispersion relation (22) this maximum is reached at a
wavenumber
has the maximum value.
For dispersion relation (22) this maximum is reached at a
wavenumber 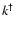 that follows from
that follows from
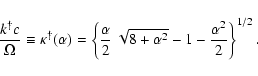 |
(33) |
If the instability is strong, so that
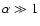 ,
we find that this wavenumber and the
associated growth rate are
,
we find that this wavenumber and the
associated growth rate are
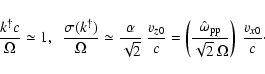 |
(34) |
Note that the trapping criterion predicts the largest field amplitude at a
wavenumber
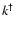 ,
which is not equal to the wavenumber
,
which is not equal to the wavenumber 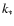 of
the fastest growing mode (Eq. (28)):
of
the fastest growing mode (Eq. (28)):
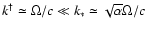 for
for
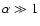 .
Eventually, this slower growing long-wavelength mode reaches a higher
magnetic field than the faster growing mode
(see also the discussion in Yang et al. 1994).
If
.
Eventually, this slower growing long-wavelength mode reaches a higher
magnetic field than the faster growing mode
(see also the discussion in Yang et al. 1994).
If
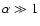 the saturation field strength due to trapping at
the saturation field strength due to trapping at
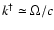 is
is
where we have used Eqs. (12) and (27) to eliminate
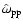 and
and 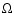 .
.
For parameters typical for the external shock associated with Gamma-ray
Bursts we have
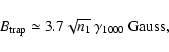 |
(36) |
with
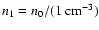 and
and
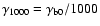 .
.
We should note that Medvedev & Loeb (1999) use a different method for estimating B: they propose that the instability saturates when the beam ions become
magnetized.
This happens when the Larmor radius
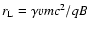 of the beam
particles in the generated magnetic field becomes smaller than the
wavelength of the fastest growing mode of the instability.
This criterion
of the beam
particles in the generated magnetic field becomes smaller than the
wavelength of the fastest growing mode of the instability.
This criterion
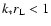 corresponds to
corresponds to
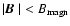 with
with
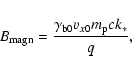 |
(37) |
with 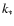 given by Eq. (28).
However, the trapping argument predicts the smallest saturation
amplitude
given by Eq. (28).
However, the trapping argument predicts the smallest saturation
amplitude
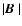 .
In particular, we have
.
In particular, we have
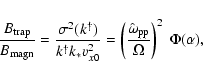 |
(38) |
where
 |
(39) |
To derive this relation we have used definition (21) to write
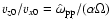 .
For a proton beam in a hot electron background we have
.
For a proton beam in a hot electron background we have
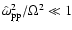 and
and
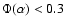 for all
for all
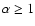 .
For a strong instability with
.
For a strong instability with
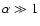 we have
we have
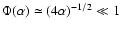 .
Therefore, trapping occurs well before the field can totally magnetize a
proton beam with a density comparable to the density of the hot background
electrons.
In view of this we will use
.
Therefore, trapping occurs well before the field can totally magnetize a
proton beam with a density comparable to the density of the hot background
electrons.
In view of this we will use
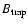 as an estimate of the saturation
magnetic field strength.
as an estimate of the saturation
magnetic field strength.
The criteria (32) and (37) predict the typical
amplitude of the magnetic field as one particular wave mode k saturates.
In a realistic situation the instability will involve a superposition of
wave modes and one should interpret B as the amplitude that
follows from the power spectrum
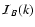 of the field
fluctuations:
of the field
fluctuations:
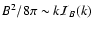 with
with
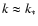 for magnetization and
for magnetization and
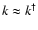 for
trapping.
The total magnetic energy in the unstable modes is
for
trapping.
The total magnetic energy in the unstable modes is
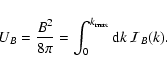 |
(40) |
3.3 The equipartition parameter
A measure of the strength of the magnetic field is the equipartition
parameter, which compares the energy density in the magnetic field with the
total energy density.
The protons dominate the energy budget, and the total available energy
density is
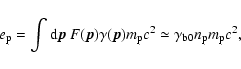 |
(41) |
where the approximation is valid for
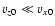 .
.
We define the proton equipartition parameter as
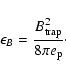 |
(42) |
Using Eq. (35) for the magnetic field, with
the definition (11) for
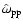 and the approximation
and the approximation
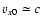 for relativistic shocks we get
for relativistic shocks we get
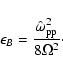 |
(43) |
Then from Eqs. (12) and (27) we have
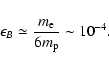 |
(44) |
4 Discussion
The small value of the equipartition parameter (44) implies that the
proton-driven Weibel instability in a background of relativistically hot
electrons saturates long before the magnetic field reaches equipartition
with the available proton free energy.
Equation (25) demonstrates that the proton-driven Weibel
instability in a hydrogen plasma is not a suitable candidate for the
mechanism responsible for "thermalization'' of the incoming protons in the
shock layer.
In electron(-positron) beams in a hot pair background the instability
condition, 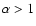 ,
allows a large beam velocity dispersion:
,
allows a large beam velocity dispersion:
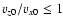 if the number densities in the beam and in the hot background are of
similar magnitude (see also Yoon & Davidson 1987).
Therefore, the Weibel instability is in principle capable of randomizing a
significant fraction of the beam momentum of an electron(-positron) beam, as
asserted in Sect. 2, whereas this is not true for a proton beam in
a hydrogen plasma.
if the number densities in the beam and in the hot background are of
similar magnitude (see also Yoon & Davidson 1987).
Therefore, the Weibel instability is in principle capable of randomizing a
significant fraction of the beam momentum of an electron(-positron) beam, as
asserted in Sect. 2, whereas this is not true for a proton beam in
a hydrogen plasma.
In the limit of a cold, relativistic proton beam the properties of the
electrons and not those of the protons determine many of the results.
The electron plasma frequency determines the wave number (33) of
the mode with the maximum magnetic field so that the electron skin depth
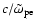 sets the length scale of the dominant mode.
This happens because the low inertia of the electrons makes them very
responsive to the perturbations of the protons.
The dispersion relation for the Weibel modes (Fig. 1), also
supports this view: the plateau around the maximum growth rate starts
roughly at a wave number
sets the length scale of the dominant mode.
This happens because the low inertia of the electrons makes them very
responsive to the perturbations of the protons.
The dispersion relation for the Weibel modes (Fig. 1), also
supports this view: the plateau around the maximum growth rate starts
roughly at a wave number
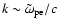 .
Studies that do not include the response of the background electrons
(by treating the protons as an isolated system) miss this point.
The peak magnetic field (35) does not contain any parameters
connected with the protons.
Therefore, proton beams in a hydrogen plasma generate nearly the same
magnetic field strength as electron(-positron) beams in an electron-positron
plasma (Fig. 2) despite the larger kinetic energy of the
protons.
.
Studies that do not include the response of the background electrons
(by treating the protons as an isolated system) miss this point.
The peak magnetic field (35) does not contain any parameters
connected with the protons.
Therefore, proton beams in a hydrogen plasma generate nearly the same
magnetic field strength as electron(-positron) beams in an electron-positron
plasma (Fig. 2) despite the larger kinetic energy of the
protons.
Gruzinov (2001) anticipated this when he excluded the case where a small
parameter in the theory might be important in his analysis of the Weibel
instability: our analysis shows that the relevant small parameter is
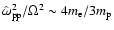 .
The result is a small equipartition parameter (44).
In this respect our result is similar to the one found by
Sagdeev (1966, p. 88), who argued for the Weibel instability in a
non-relativistic plasma that the electrons have a quenching
effect on the ion instability.
.
The result is a small equipartition parameter (44).
In this respect our result is similar to the one found by
Sagdeev (1966, p. 88), who argued for the Weibel instability in a
non-relativistic plasma that the electrons have a quenching
effect on the ion instability.
In our analysis we have excluded electrostatic waves, which
could also play an important role in the shock transition zone
(Schlickeiser et al. 2002).
In that case electrostatic Bremsstrahlung could be an alternative
explanation for the Gamma-ray Burst afterglow emission (Schlickeiser 2003),
relaxing the need in synchrotron models for a high magnetic field strength.
5 Conclusions
We have presented an analytical estimate of the magnetic field produced at
the end of the linear phase of the Weibel instability at the front of an
ultra-relativistic shock propagating into a cold hydrogen plasma, a
situation that applies to the external shocks that produce gamma-ray burst afterglows
in the fireball model (Rees & Mészáros 1992).
The magnetic field strength that we find is too weak to explain the observed
synchrotron radiation (Gruzinov & Waxman 1999): the equipartition
parameter (Eq. (44)) is at least two orders of magnitude too
small.
This is radically different from the results for the Weibel instability in
pair plasmas.
The reason is that the contribution of the electrons to the electromagnetic
response of the plasma inhibits the instability of the protons.
The saturation magnetic field (35) which this low equipartition
parameter corresponds to is the magnetic field at the point where the
linear approximation breaks down and where non-linear trapping effects start
to limit the growth of the unstable Weibel mode.
After this happens, it is likely that the instability enters a nonlinear
phase or that another type of instability takes over: numerical
simulations (Frederiksen et al. 2004) of similar plasmas show near-equipartition
magnetic fields behind the Weibel-unstable region in the shock transition.
The nonlinear phase would then be the dominant phase in electron-ion plasmas
and deserves further study to determine the physical mechanism and
the properties of the resulting magnetic field.
Acknowledgements
This research is supported by the Netherlands Research School for Astronomy
(NOVA).
Appendix A: Asymmetric beams
We consider asymmetric proton beams and show that we can neglect
the effect of the asymmetry for typical parameters.
We replace the proton distribution (1) by
![$\displaystyle F(\vec{p}) = {\frac{n_{\rm p}}{2 p_{z0}}} \:
\left[ \frac{1 + \De...
...0}) \right]\delta(p_y) \left[\Theta(p_z+ p_{z0}) - \Theta(p_z- p_{z0}) \right],$](/articles/aa/full/2004/47/aa1882/img148.gif) |
|
|
(A.1) |
with
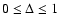 the parameter measuring the asymmetry between
the two beams.
This asymmetry changes the dispersion relation of the waves to
(e.g., Akhiezer et al. 1975):
the parameter measuring the asymmetry between
the two beams.
This asymmetry changes the dispersion relation of the waves to
(e.g., Akhiezer et al. 1975):
![\begin{displaymath}
k^2 c^2 - \omega^{2} \left[ \: 1 + \chi _{xx}(\omega,\: k) ...
...{2}(\omega,\: k)}{1 + \chi _{zz}(\omega,\: k)}\: \right]
= 0.
\end{displaymath}](/articles/aa/full/2004/47/aa1882/img150.gif) |
(A.2) |
The extra term
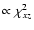 appears in relation (A.2)
because the waves are no longer transverse: the charge bunching of the
asymmetric beams produces a net charge density, leading to a component of
the wave electric field along the wave vector.
appears in relation (A.2)
because the waves are no longer transverse: the charge bunching of the
asymmetric beams produces a net charge density, leading to a component of
the wave electric field along the wave vector.
We will give the extra components of the susceptibility tensor and
publish a derivation elsewhere (Achterberg & Wiersma, in
preparation).
The proton contribution to
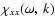 is the same as in the
symmetric case.
For a thermal electron background with an isotropic momentum distribution,
only the two proton beams contribute to the off-diagonal components of the
susceptibility tensor so that
is the same as in the
symmetric case.
For a thermal electron background with an isotropic momentum distribution,
only the two proton beams contribute to the off-diagonal components of the
susceptibility tensor so that
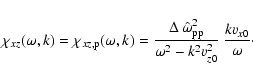 |
(A.3) |
This off-diagonal component vanishes in the symmetric case (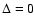 ).
The longitudinal response of the beam-plasma system is contained in
).
The longitudinal response of the beam-plasma system is contained in
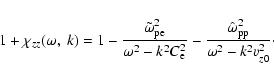 |
(A.4) |
Here
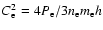 is the effective sound speed
in the hot electron gas.
In the ultra-relativistic case one has
is the effective sound speed
in the hot electron gas.
In the ultra-relativistic case one has
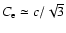 .
For proton beams in a hot electron background one has
.
For proton beams in a hot electron background one has
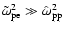 and
and
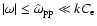 for the Weibel
instability (see Sect. 3.1).
This implies that
for the Weibel
instability (see Sect. 3.1).
This implies that
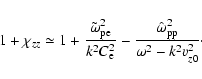 |
(A.5) |
The resulting dispersion relation can
be written in terms of the dimensionless variable
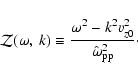 |
(A.6) |
One finds
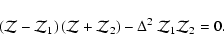 |
(A.7) |
Here
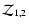 are defined by
are defined by
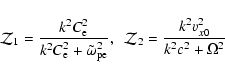 |
(A.8) |
with
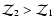 for the parameters considered here.
The solution of this quadratic equation,
for the parameters considered here.
The solution of this quadratic equation,
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{1882fig3.eps}
\end{figure}](/articles/aa/full/2004/47/aa1882/Timg166.gif) |
Figure A.1:
The growth rate as a function of wavenumber for
asymmetric proton beams in a relativistically hot electron background with sound
speed
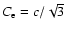 .
Different lines correspond to different values of the parameter .
Different lines correspond to different values of the parameter 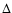 ,
which measures the asymmetry between the beams. ,
which measures the asymmetry between the beams. |
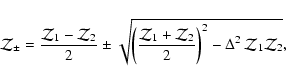 |
(A.9) |
determines the frequency through
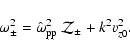 |
(A.10) |
The Weibel-unstable branch corresponds to the solution branch
 as
as
 .
In the symmetric case (
.
In the symmetric case (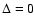 )
one has
)
one has
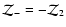 which follows from Eq. (A.7),
and one recovers dispersion relation (20).
The stable branch
which follows from Eq. (A.7),
and one recovers dispersion relation (20).
The stable branch
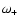 is a modified (largely electrostatic) ion-acoustic wave.
is a modified (largely electrostatic) ion-acoustic wave.
Although the asymmetry decreases the range of unstable wave numbers
(Fig. A.1) and lowers the growth rate with respect to the symmetric
case 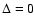 ,
the change is small unless
,
the change is small unless
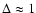 :
the case
where there is almost no reflection. For a single beam,
:
the case
where there is almost no reflection. For a single beam, 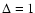 ,
one has
,
one has
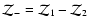 ,
which
gives the following dispersion relation for
,
which
gives the following dispersion relation for
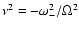 in the ultra-relativistic limit with
in the ultra-relativistic limit with
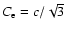 and
and
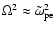 :
:
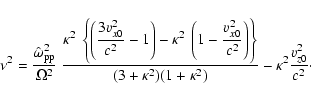 |
(A.11) |
- Akhiezer, A. I.,
Akhiezer, I. A., Polovin, R. V., Sitenko, A. G.,
& Stepanov, K. N. 1975, International series of monographs
in natural philosophy, Vol. 68, Plasma Electrodynamics, v. 1.
Linear theory (Oxford: Pergamon Press)
(In the text)
- Blandford, R. D.,
& McKee, C. F. 1976, Phys. Fluids, 19, 1130 [NASA ADS] [CrossRef] (In the text)
- Califano, F., Cecchi, T.,
& Chiuderi, C. 2002, Phys. Plasmas, 9, 451 [NASA ADS] [CrossRef] (In the text)
- Draine, B. T.,
& McKee, C. F. 1993, ARA&A, 31, 373 [NASA ADS]
- Fonseca, R. A.,
Silva, L. O., Tonge, J. W., Mori, W. B., &
Dawson, J. M. 2003, Phys. Plasmas, 10, 1979 [NASA ADS] [CrossRef] [MathSciNet]
- Frederiksen,
J. T., Hededal, C. B., Haugbølle, T., &
Nordlund, Å. 2004, ApJ, 608, L13 [NASA ADS] [CrossRef] (In the text)
- Gruzinov, A. 2001, ApJ,
563, L15 [NASA ADS] [CrossRef] (In the text)
- Gruzinov, A., &
Waxman, E. 1999, ApJ, 511, 852 [NASA ADS] [CrossRef]
- Haruki, T., &
Sakai, J.-I. 2003, Phys. Plasmas, 10, 392 [NASA ADS] [CrossRef]
- Hoshino, M., Arons, J.,
Gallant, Y. A., & Langdon, A. B. 1992, ApJ, 390,
454 [NASA ADS] [CrossRef] (In the text)
- Kazimura, Y., Sakai,
J. I., Neubert, T., & Bulanov, S. V. 1998, ApJ, 498,
L183 [NASA ADS] [CrossRef]
- Medvedev, M. V.,
& Loeb, A. 1999, ApJ, 526, 697 [NASA ADS] [CrossRef]
- Panaitescu, A., &
Kumar, P. 2002, ApJ, 571, 779 [NASA ADS] [CrossRef]
- Rees, M. J., &
Mészáros, P. 1992, MNRAS, 258, 41 [NASA ADS] (In the text)
- Sagdeev, R. Z.
1966, Rev. Plasma Phys., 4, 23 (In the text)
- Schlickeiser, R. 2003,
A&A, 410, 397 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Schlickeiser, R.,
Vainio, R., Böttcher, M., et al. 2002, A&A, 393,
69 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Silva, L. O.,
Fonseca, R. A., Tonge, J. W., Mori, W. B., &
Dawson, J. M. 2002, Phys. Plasmas, 9, 2458 [NASA ADS] [CrossRef]
- Tsurutani, B. T.,
& Stone, R. G., ed. 1985, Geophysical Monograph,
Vol. 35, Collisionless Shocks in the Heliosphere: Reviews of
Current Research (American Geophysical Union)
(In the text)
- Vink, J. 2004, Adv.
Space Res., 33, 356 [NASA ADS] [CrossRef]
- Weibel, E. S.
1959, Phys. Rev. Lett., 2, 83 [NASA ADS] [CrossRef] (In the text)
- Yang, T.-Y. B.,
Arons, J., & Langdon, A. B. 1994, Phys. Plasmas, 1,
3059 [NASA ADS] [CrossRef]
- Yoon, P. H., &
Davidson, R. C. 1987, Phys. Rev. A, 35, 2718 [NASA ADS] [CrossRef], brief
report
Copyright ESO 2004
![\begin{displaymath}
k^2 c^2 - \omega^{2} \left[ \: 1 + \chi _{xx}(\omega, k) \: \right] = 0,
\end{displaymath}](/articles/aa/full/2004/47/aa1882/img31.gif)
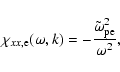
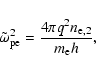
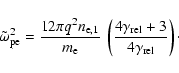
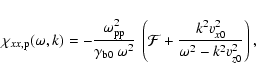
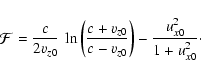
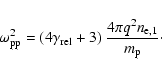
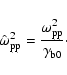
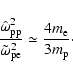
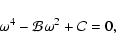
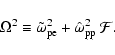
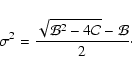
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{1882fig1.eps}
\end{figure}](/articles/aa/full/2004/47/aa1882/Timg66.gif)
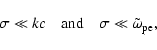
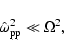
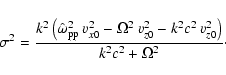
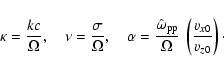
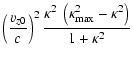
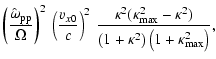
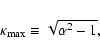
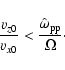
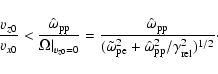
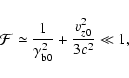
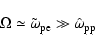
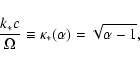
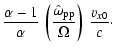
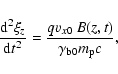
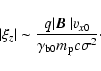
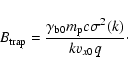
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{1882fig2.eps}
\end{figure}](/articles/aa/full/2004/47/aa1882/Timg105.gif)
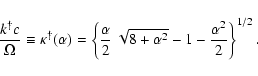
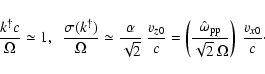
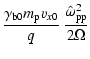
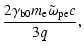
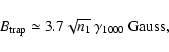
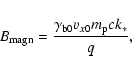
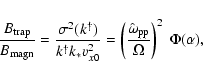

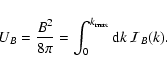
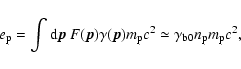
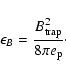
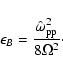
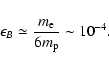
![$\displaystyle F(\vec{p}) = {\frac{n_{\rm p}}{2 p_{z0}}} \:
\left[ \frac{1 + \De...
...0}) \right]\delta(p_y) \left[\Theta(p_z+ p_{z0}) - \Theta(p_z- p_{z0}) \right],$](/articles/aa/full/2004/47/aa1882/img148.gif)
![\begin{displaymath}
k^2 c^2 - \omega^{2} \left[ \: 1 + \chi _{xx}(\omega,\: k) ...
...{2}(\omega,\: k)}{1 + \chi _{zz}(\omega,\: k)}\: \right]
= 0.
\end{displaymath}](/articles/aa/full/2004/47/aa1882/img150.gif)
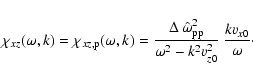
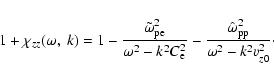
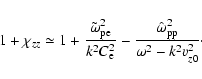
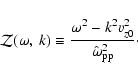
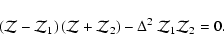
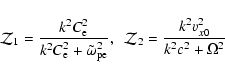
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{1882fig3.eps}
\end{figure}](/articles/aa/full/2004/47/aa1882/Timg166.gif)