P. Koten 1 - J. Borovicka 1 - P. Spurný 1 - H. Betlem 2 - S. Evans3
1 - Astronomical Institute, Ondrejov Observatory,
Fricova 298, 25165 Ondrejov, Czech Republic
2 -
Dutch Meteor Society, Leiden, The Netherland
3 -
British Astronomical Association, Haverhill, UK
Received 17 June 2004 / Accepted 5 August 2004
Abstract
Double station data on 496 meteors belonging to several meteor showers
were obtained within the program of the video meteor observations during
years 1998-2001. Analyzed meteors cover a range of photometric masses
from 10-7 to 10-4 kg with a corresponding range of maximum
brightness from +4.7 to -2.1 absolute magnitude. Atmospheric
trajectories of Perseid, Orionid and Leonid meteors are analysed. These typical
cometary high velocity meteors are compared to Geminid meteors with
probable asteroidal origin and Taurid meteors - another cometary shower
with significantly lower entry velocity. The light curves of the studied meteors vary
widely, but generally are nearly symmetrical with the point of maximum brightness
located close the to middle of the luminous trajectory. Small differences between
showers are reported. We found that the height data are in good agreement
with the dust-ball model predictions. The only difference is the beginning height
behaviour. The beginning heights of cometary meteors increase with increasing
photometric mass. These meteoroids probably contain a volatile part which starts
to ablate before we are able to detect the meteors. The Geminid meteors are
a different case. They start to ablate suddenly and their beginning height is
almost constant in the whole range of studied meteoroid masses. In this case we
observe real beginnings of meteor ablation.
Key words: meteors, meteoroids - solar system: general - comets: general
The study of meteor interaction with the Earth's atmosphere may provide an insight into the physical structure of meteoroids and their parent bodies, i.e. comets and asteroids. Several spacecrafts made close observations of such objects in recent years and other experiments are running or are in development. However for return of material samples we still have to wait several more years. Fortunately, the atmosphere of our planet can be used as a detector of the small particles originating from these bodies. Although these particles are destroyed during the interaction with the atmosphere, this process provides some information about their composition and structure. This is why we study atmospheric trajectories and light curve shapes of the meteors.
The photographic observation of meteors has a long tradition at the Ondrejov Observatory, Czech Republic. As well as this long-standing program, a systematic double station observation of faint meteors belonging to major meteor showers by means of sensitive videotechnique was started several years ago. This enabled us to expand the range of studied meteor masses. The limiting sensitivity of our instrumentation is about +5.5m, significantly below the photographic limit. We are able to detect meteors down to masses of 10-8 kg. However, video data are of a lower precision in comparison with photographic data.
The classical theory of meteors shows good agreement with the photographic observation of bright meteors (e.g. Ceplecha et al. 1998). For fainter meteors Hawkes & Jones (1975) proposed a quantitative model of the dust-ball meteoroids. These are assumed to be conglomerates of small grains bound together by a glue of a lower boiling point. Light is produced only by ablation of the grains. Beginning, maximum light and terminal heights of smaller meteoroids are approximately mass-independent, because all grains are released above the radiation ceiling. For bigger meteoroids the model predicts behaviour similar to the classical theory of compact meteors. Detachment of the grains continues even below the radiation ceiling simultaneously with ablation, which results in mass dependence of both maximum light and terminal heights. The threshold value between both cases is called the critical mass.
Hapgood et al. (1982) found that the height data of the Perseid meteors are in good agreement with the predictions of this model. They also calculated the energy required for disintegration of the dust-ball meteoroid. The resulting value was lower than the model assumed, which suggests weaker meteoroid material. Beech (1984) obtained similar results for southern Taurid, Geminid and Perseid meteors and again for Draconid meteors (Beech 1986).
Several authors described the light curve shape of the faint meteors using the so-called F parameter. Fleming et al. (1993) found that light curves of sporadic meteors are nearly symmetrical with only a few cases of flares. Perseid meteors do not differ from other shower meteors or from sporadic ones and also produce light curves close to symmetrical (Hawkes et al. 1998). Campbell et al. (1999) fitted the light curve by a parabola, which was rotated through some angle about the maximum brightness point. Also in this representation the light curves of Leonid and Perseid meteors are on average symmetrical and there is no significant difference between the showers. Grains of masses in the range from 10-12 kg to 10-6 kg are needed to model Leonid and Perseid meteors.
Series of Leonid storms in recent years provided us opportunity to collect large sets of data for more detailed studies of meteoroid structure. NASA's multi-instrument aircraft campaigns (for more details see http://leonid.arc.nasa.gov) as well as many ground-based expeditions recorded several storms originating from different filaments of the Leonid meteor stream. Thus investigators were able to compare meteoroids with different times since ejection from the parent comet. Murray et al. (1999, 2000) found differences between 1998 and 1999 Leonid meteors. Light curves of 1998 meteors were skewed to the beginning of their luminous trajectories, while those recorded in 1999 to the end. This fact was explained by a different morphological structure caused by different times of exposure to the harsh cosmic environment. Similar differences also were found by Koten et al. (2003), who moreover expanded this analysis to the 2000 Leonid shower, and found that the light curve shape described using the parameter F is not proportional to the age of the filament.
Koschny et al. (2002) developed a fragmentation model using Poisson
statistics. The fragmentation is modeled using only one number, the Poisson number,
which describes the size distribution of the particles. Beech & Murray (2003)
modeled the light curves and compared them with observational data recorded during
the 1998 to 2001 Leonid storms. They assumed a power-law distribution of the form
![]() for the fundamental grain mass distribution and found that the value
for the fundamental grain mass distribution and found that the value
![]() provides a good description of the typical Leonid meteor light
curve. They also recognized there is no correlation between Leonid light curve shape
and meteoroid age. Finally, Campbell-Brown & Koschny (2004) presented
another model of faint meteor ablation built on the classical model and added a thermal
fragmentation mechanism. Using both Gaussian and power-law distribution of particles,
they modeled light curves of meteors and succesfully compared them to three observed
Leonid meteors.
provides a good description of the typical Leonid meteor light
curve. They also recognized there is no correlation between Leonid light curve shape
and meteoroid age. Finally, Campbell-Brown & Koschny (2004) presented
another model of faint meteor ablation built on the classical model and added a thermal
fragmentation mechanism. Using both Gaussian and power-law distribution of particles,
they modeled light curves of meteors and succesfully compared them to three observed
Leonid meteors.
Table 1:
Details of the observed meteor showers. Geocentric velocities ![]() are taken from Cook (1973). For each shower the number of double station
meteors used for this analysis is given as well as ranges of both their photometric
masses
are taken from Cook (1973). For each shower the number of double station
meteors used for this analysis is given as well as ranges of both their photometric
masses ![]() and maximum brightnesses
and maximum brightnesses
![]() ,
average zenith
distance of the radiant
,
average zenith
distance of the radiant ![]() ,
average parameter
,
average parameter ![]() and a meteor
class according to this parameter (Ceplecha 1988).
and a meteor
class according to this parameter (Ceplecha 1988).
The analyzed data were taken within the double-station observation program,
which is currently running at the Ondrejov Observatory. Within this program,
the most active meteor showers are regularly observed. For some of them a
sufficient amount of data was not collected, partially because of unfavourable weather
conditions in Central Europe during some parts of the year.
Observations are usually made on the base Ondrejov
(14![]() 46' 48.8'' E, 49
46' 48.8'' E, 49![]() 54' 36.8'' N, 524 m)
- Kunzak (15
54' 36.8'' N, 524 m)
- Kunzak (15![]() 12' 2.8'' E, 49
12' 2.8'' E, 49![]() 6' 27.2'' N, 652 m) with a separation of 92.5 km and the azimuth of the second station 340
6' 27.2'' N, 652 m) with a separation of 92.5 km and the azimuth of the second station 340![]() (
(
![]() ). Both stations are equipped with S-VHS commercial Panasonic
camcorders connected to second generation Dedal-41 image intensifiers and Arsat 1.4/50 mm lenses. The diameter of the field of view (FOV) is about 25
). Both stations are equipped with S-VHS commercial Panasonic
camcorders connected to second generation Dedal-41 image intensifiers and Arsat 1.4/50 mm lenses. The diameter of the field of view (FOV) is about 25![]() .
Another system with the same intensifier and Zenitar 2.8/16 mm lens giving a wider FOV (
.
Another system with the same intensifier and Zenitar 2.8/16 mm lens giving a wider FOV (![]()
![]() )
has been used at the Kunzak station since 2001. Whereas the
limiting sensitivity of the basic systems is about +5.5m, for the wider system it
decreases to about +3.8m.
)
has been used at the Kunzak station since 2001. Whereas the
limiting sensitivity of the basic systems is about +5.5m, for the wider system it
decreases to about +3.8m.
Leonid observations were made on the
base Curica (2![]() 25' 53.8'' W, 37
25' 53.8'' W, 37![]() 51' 26.6'' N, 1007 m) - Lucainena de las Torres (2
51' 26.6'' N, 1007 m) - Lucainena de las Torres (2![]() 13' 58.4'' W, 37
13' 58.4'' W, 37![]() 2' 13.7'' N, 707 m) in the
south-eastern part of Spain in 2001. The configuration of the stations was very
similar to that used in the Czech Republic. The distance and azimuth of the
southern station were 92.7 km and 349
2' 13.7'' N, 707 m) in the
south-eastern part of Spain in 2001. The configuration of the stations was very
similar to that used in the Czech Republic. The distance and azimuth of the
southern station were 92.7 km and 349![]() .
The same instruments
were used. Both stations used cameras with 1.4/50 mm lenses. Moreover the
Lucainena station was equipped with another system using the second generation
intensifier and 1.8/28 mm lens giving a FOV of about 36
.
The same instruments
were used. Both stations used cameras with 1.4/50 mm lenses. Moreover the
Lucainena station was equipped with another system using the second generation
intensifier and 1.8/28 mm lens giving a FOV of about 36![]() ,
operated by
Stephen Evans.
,
operated by
Stephen Evans.
The records stored on S-VHS tapes were inspected using the recognition software
MetRec (Molau 1999) and digitalized with a PC framegrabber. The PAL
standard gives the time resolution of 0.04 s. Each frame was transformed into
![]() pixel, 8-bit monochrome image. All meteors were stored as a sequence
in non-compressed AVI format. Later, each meteor was measured by our original
software MetPho and subsequent trajectory computation was done by means of
our standard procedures. The well-known Southworth-Hawking D-criterion
(Southworth & Hawkins 1967) was used for the determination of the
meteor shower membership. Reference orbits of the meteor streams were taken
from Cook (1973). More details about the processing are given in
Koten (2002).
pixel, 8-bit monochrome image. All meteors were stored as a sequence
in non-compressed AVI format. Later, each meteor was measured by our original
software MetPho and subsequent trajectory computation was done by means of
our standard procedures. The well-known Southworth-Hawking D-criterion
(Southworth & Hawkins 1967) was used for the determination of the
meteor shower membership. Reference orbits of the meteor streams were taken
from Cook (1973). More details about the processing are given in
Koten (2002).
Records of more than 1500 meteors taken from 1998 to 2001 were measured
and their heliocentic orbits and atmosperic trajectories computed (Koten et al. 2003).
496 of them belonging to Perseid, Orionid, Leonid, Geminid and Taurid showers were
used for this analysis. The Taurid shower has two branches - southern and northern.
Both have similar entry velocity and the same origin, so both branches were analyzed
altogether. Members of other meteor showers were also recorded, but their number
is not sufficient for this kind of statistical analysis. Basic data of all studied meteors are
shown in Table 1. The zenith distance of the radiant can affect the
beginning height of the meteor. Nevertheless the table shows that all showers were
observed in a similar range of zenith distances, with the average value for each
shower just below 45![]() .
We can therefore conclude that the beginning
heights are not affected by systematic differences in radiant zenith distance. The
covered range of meteoroid masses is approximately 10-7 to 10-4 kg.
There is a lack of small meteoroids in low velocity showers. This is because small and
slow meteoroids produce meteors that are too faint for our instrumentation.
.
We can therefore conclude that the beginning
heights are not affected by systematic differences in radiant zenith distance. The
covered range of meteoroid masses is approximately 10-7 to 10-4 kg.
There is a lack of small meteoroids in low velocity showers. This is because small and
slow meteoroids produce meteors that are too faint for our instrumentation.
The brightness of the meteor changes during its passage through the atmosphere. Since there is no significant deceleration of meteors in the studied range of masses, the produced light is directly proportional to the rate of ablation.Using our instrumentation we are able to measure the meteor brightness with a time resolution of 0.04 s.
The integration of the meteor light curve results in the initial photometric
mass of the meteoroid ![]() according to the formula
(Ceplecha 1988)
according to the formula
(Ceplecha 1988)
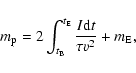 |
(1) |
For the purpose of our analysis we use only complete or almost complete light curves. Meteors with a portion of the luminous trajectory well outside the field of view were excluded from the analysed sample as were meteors that enter the field of view and their real beginning heights are actually higher than observed.
The meteor light curve shape can be described by the set of F-parameters
(Fleming et al. 1993):
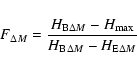 |
(2) |
Parameter F describes the location of the maximum brightness of the meteor along
its luminous trajectory. Light curves for which F=0.5 are perfectly symmetrical
with the point of the maximum exactly at the middle of the trajectory. Meteors
with F<0.5 reach the maximum brightness during the early part of the trajectory.
F>0.5 means that the light curve is skewed to the terminal point. Single-body
meteors described by the classical meteor theory should have ![]() .
The
dust-ball model predicts that the light curves should be nearly symmetrical (Hawkes
& Jones 1975).
.
The
dust-ball model predicts that the light curves should be nearly symmetrical (Hawkes
& Jones 1975).
For each meteor, the average value ![]() of individual
of individual
![]() was calculated. We found that the light curves vary much, but the majority
tend to be symmetrical with the point of maximum brightness close to the
middle of the luminous trajectory. Despite the broad range of values for each
shower, small differences between particular showers are obvious. The distribution
of this parameter for the Perseid shower is shown in Fig. 1.
was calculated. We found that the light curves vary much, but the majority
tend to be symmetrical with the point of maximum brightness close to the
middle of the luminous trajectory. Despite the broad range of values for each
shower, small differences between particular showers are obvious. The distribution
of this parameter for the Perseid shower is shown in Fig. 1.
The mean F-values for each meteor shower are given in Table 2. If we consider that higher F means a more compact body (more similar to a classical meteoroid) we can conclude that Geminids are the most compact meteoroids in our sample and Leonids the most fragile. For other showers we get almost the same value of this parameter, which lies between limits given by Leonid and Geminid meteors.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1485fig1.ps}
\end{figure}](/articles/aa/full/2004/47/aa1485/Timg31.gif) |
Figure 1: Distribution of the F-values for the Perseid shower. Total number of meteors included in this plot is 170. |
| Open with DEXTER | |
In addition to the general characterization of each shower we also investigated
the F values for individual meteors within each meteor shower. We found that
there is no direct relation between the photometric mass of a meteor and its light
curve shape described using the F parameter. Figure 2 shows the value
of this parameter for each Perseid meteor against its photometric mass. Similar results
were obtained for other showers. There are two areas in this plot without any (or
almost any) meteors. Area No. I lies in the lower right part of the plot. It means
that bigger meteors (
![]() kg) produce light curves which are skewed
to the end of their luminous trajectory. However, only a few of them reach values
greater than 0.8. A detailed look at these meteors with extreme values of F shows
that their luminous trajectories terminate suddenly after reaching the maximum
brightness. For several such meteors it is even not possible to compute the F value
and these meteors are not included in this analysis. On the other hand, smaller
meteors (with
kg) produce light curves which are skewed
to the end of their luminous trajectory. However, only a few of them reach values
greater than 0.8. A detailed look at these meteors with extreme values of F shows
that their luminous trajectories terminate suddenly after reaching the maximum
brightness. For several such meteors it is even not possible to compute the F value
and these meteors are not included in this analysis. On the other hand, smaller
meteors (with
![]() kg) almost uniformly cover the range of values
between 0.2 and 0.8. With the exception of the extreme meteors mentioned above,
parameter F does not exceed 0.8 (empty area No. II). There are also no meteors
with parameter F<0.2.
kg) almost uniformly cover the range of values
between 0.2 and 0.8. With the exception of the extreme meteors mentioned above,
parameter F does not exceed 0.8 (empty area No. II). There are also no meteors
with parameter F<0.2.
Table 2: Average F for each meteor shower.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1485fig2.ps}
\end{figure}](/articles/aa/full/2004/47/aa1485/Timg35.gif) |
Figure 2: F-values against the meteor photometric mass for the Perseid shower. Two areas without meteors can be found in this plot. Moreover, there is no meteor with F<0.2. |
| Open with DEXTER | |
We can conclude that smaller meteoroids produce meteors with a broad variety of light curve shapes; many of them are close to symmetrical with the maximum brightness located close to the middle of their luminous trajectory. This behaviour is in agreement with the predictions of the dust-ball model. Light curves of the bigger meteoroids are different, they reach the maximum brightness in the second half of the trajectory. Thus light curves of these meteors look like the light curves of the meteors described by the classical theory of meteors. Among the fainter meteors we can find both fragile and more compact bodies while among the brighter meteors only compact ones.
Table 3:
Average beginning heights ![]() ,
heights of maximum brightness
,
heights of maximum brightness ![]() and terminal heights
and terminal heights ![]() for all studied meteor showers.
for all studied meteor showers.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1485fig3.ps}
\end{figure}](/articles/aa/full/2004/47/aa1485/Timg37.gif) |
Figure 3: Beginning height, height of maximum brightness and terminal height of 188 Perseid meteors as a function of their photometric mass. |
| Open with DEXTER | |
In addition to the light curves the heights of meteors, especially the beginning heights,
give us clues about the morphology of meteoroids. The dustball model provides some
predictions for the heights at which meteors produce light. For that reason we investigated
the beginning heights ![]() ,
heights of the maximum light
,
heights of the maximum light ![]() and the
terminal heights
and the
terminal heights ![]() of our sample of meteors.
of our sample of meteors.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1485fig4.ps}
\end{figure}](/articles/aa/full/2004/47/aa1485/Timg38.gif) |
Figure 4: Beginning heights of five meteor showers as a function of the meteor photometric mass. From the top, the Leonid (Leo), Orionid (Ori), Perseid (Per), Taurid (Tau) and Geminid (Gem) showers are plotted. |
| Open with DEXTER | |
Basic data of heights ![]() ,
, ![]() and
and ![]() for each meteor shower
are given in Table 3. A plot of height data against the photometric
mass of Perseid meteors is shown in Fig. 3. This plot suggests
that the values are almost constant up to a certain value of photometric mass.
After reaching this value, both the height of maximum light and terminal height start
to decrease with increasing photometric mass, as the dust-ball model predicts.
Comparable results were obtained also for other showers. Only the value of the
critical mass slightly differs for all studied cometary showers. Because of the special
interest in beginning heights, other plots of those values for each shower are given in
Fig. 4. The beginning heights appear to be constant up to the critical
mass for Perseid meteors and increase with increasing mass above this value. The
other cometary showers show an increase of the beginning height over the whole range
of photometric masses. The Geminid shower is different. The beginning height is almost
constant. The difference between the highest and lowest beginning height is only 7.5 km,
a value that is several times smaller than for other showers. On the other hand, the height
of maximum light and the terminal height decrease over whole range of masses. This suggests
that in the context of the dust-ball model we are above the critical mass. However the
faintest meteors are not contained in our sample.
for each meteor shower
are given in Table 3. A plot of height data against the photometric
mass of Perseid meteors is shown in Fig. 3. This plot suggests
that the values are almost constant up to a certain value of photometric mass.
After reaching this value, both the height of maximum light and terminal height start
to decrease with increasing photometric mass, as the dust-ball model predicts.
Comparable results were obtained also for other showers. Only the value of the
critical mass slightly differs for all studied cometary showers. Because of the special
interest in beginning heights, other plots of those values for each shower are given in
Fig. 4. The beginning heights appear to be constant up to the critical
mass for Perseid meteors and increase with increasing mass above this value. The
other cometary showers show an increase of the beginning height over the whole range
of photometric masses. The Geminid shower is different. The beginning height is almost
constant. The difference between the highest and lowest beginning height is only 7.5 km,
a value that is several times smaller than for other showers. On the other hand, the height
of maximum light and the terminal height decrease over whole range of masses. This suggests
that in the context of the dust-ball model we are above the critical mass. However the
faintest meteors are not contained in our sample.
Because the plots in Fig. 4 are not so illustrative, we adopted
the method used by Hapgood et al. (1982). For each shower, all meteors were
sorted by their photometric masses and divided into several groups. For each
group the average photometric mass and ![]() ,
, ![]() and
and ![]() were computed and
plotted. Trends of height data are better observable in
this representation (Fig. 5). Linear fits were applied to the data
obtained in this way. The slope of such a line is different for each shower. Only in the
case of Perseid shower were used different fits for smaller and bigger masses.
Beginning heights of fainter Perseid meteors seem to be mass-independent.
Figure 5 shows the slope of the linear fit of the beginning heights of each
shower. The range of photometric masses for each shower is also evident from
this plot. Values of the slope and the quality of the fits are given in Table 4.
The quality is expressed as the correlation coefficient
were computed and
plotted. Trends of height data are better observable in
this representation (Fig. 5). Linear fits were applied to the data
obtained in this way. The slope of such a line is different for each shower. Only in the
case of Perseid shower were used different fits for smaller and bigger masses.
Beginning heights of fainter Perseid meteors seem to be mass-independent.
Figure 5 shows the slope of the linear fit of the beginning heights of each
shower. The range of photometric masses for each shower is also evident from
this plot. Values of the slope and the quality of the fits are given in Table 4.
The quality is expressed as the correlation coefficient
![]() .
For a perfect fit
.
For a perfect fit
![]() .
For the Geminid shower, the beginning height increases only very slightly
with increasing photometric mass. Moreover the low value of the correlation coefficient
means no relation between beginning height and photometric mass. The increase of the
Leonid shower is the steepest. The slope of line for other showers lies between these
two extreme cases.
.
For the Geminid shower, the beginning height increases only very slightly
with increasing photometric mass. Moreover the low value of the correlation coefficient
means no relation between beginning height and photometric mass. The increase of the
Leonid shower is the steepest. The slope of line for other showers lies between these
two extreme cases.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1485fig5.ps}
\end{figure}](/articles/aa/full/2004/47/aa1485/Timg40.gif) |
Figure 5: Beginning heights of meteors as a function of their photometric mass. Lines represent linear fits through the grouped values for each shower (see detailed explanation in the text). |
| Open with DEXTER | |
The fact that the beginning heights increase with increasing mass is in apparent disagreement with the dust-ball model, which predicts mass-independent beginning heights for a given entry velocity. It could be some kind of instrumentation effect. The almost constant beginning heights of the Geminid shower speaks against this idea, however. Also it is not possible that this is caused by a lower entry velocity of Geminids, because the even slower Taurids show increased beginning height. It seems that this fact is really given by the different structure of the meteoroid material. Nevertheless, possible relations between such parameters as the beginning height, the photometric mass, the zenith distance of the radiant and the distance of the meteor beginning from the station were checked. No relation which could explain this apparent discrepancy with the model predictions was found. The increase of beginning height with mass in cometary showers is therefore a real observed effect. This conclusion is in agreement with the results of Jacchia et al. (1967), who analyzed trajectories of 413 photographic meteors.
To explain this fact, it is necessary to clarify the meteor beginning we observe.
Our abilities are limited by the sensitivity limit of the detectors used. Figure 6
shows the plots of the apparent beginning brightness
![]() of the Orionid meteors
vs. their photometric mass during four different nights. No trend with mass was found.
The average value
of the Orionid meteors
vs. their photometric mass during four different nights. No trend with mass was found.
The average value
![]() is marked by the dashed line. The sensitivity limit is
slightly different for each night, because of the different atmospheric conditions,
adjustment of the intensification etc. This results in values of
is marked by the dashed line. The sensitivity limit is
slightly different for each night, because of the different atmospheric conditions,
adjustment of the intensification etc. This results in values of
![]() between 5.30
and 5.55 within these four nights. A similar analysis was done for the other showers and
the conclusion is that the sensitivity limit of the basic instrumentation used
(i.e. lenses 1.4/50 mm) lies around +5.5m.
between 5.30
and 5.55 within these four nights. A similar analysis was done for the other showers and
the conclusion is that the sensitivity limit of the basic instrumentation used
(i.e. lenses 1.4/50 mm) lies around +5.5m.
Table 4:
Slope of the line k fitted through the beginning heights of shower
meteors, the correlation coefficient
![]() and the relative error of this fit.
and the relative error of this fit.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1485fig6.ps}
\end{figure}](/articles/aa/full/2004/47/aa1485/Timg43.gif) |
Figure 6: Apparent beginning brightness of Orionid meteors as a function of their photometric mass. The dashed line marks the average value +5.46m. |
| Open with DEXTER | |
For the faint meteors it is possible to neglect the deceleration term and use the classical
luminous equation (Ceplecha et al. 1998):
Equations (3) and (4) together with the assumption that
there are several constant parameters for each shower (included in
the constant C) results in
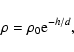 |
(7) |
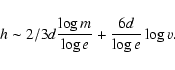 |
(8) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1485fig7.ps}
\end{figure}](/articles/aa/full/2004/47/aa1485/Timg60.gif) |
Figure 7: Light curves and beginning heights of Leonid and Geminid meteors with different photometric masses of meteoroids. Light curves of all Geminid meteors start at the same height level, whereas the Leonid meteors we can observe just when their brightness exceeds the limiting magnitude of the camera. |
| Open with DEXTER | |
Light curves and atmospheric trajectories of almost 500 meteors belonging to five major meteor showers were studied in this paper. We especially analysed the light curve shapes and heights of meteors and found that there are differences in all these characteristics among meteors of all showers studied.
The variability of meteor light curves was previously reported in several papers. We also found similar behaviour in our sample of data. We described light curve shapes using the traditional parameter F. Although values of this parameter lie in a broad range, we can determine typical values of this parameter for all showers. The highest value was found for the Geminids, the lowest for the Leonid 2000 shower. In terms of meteoroid structure the Geminid meteors seems to be the strongest and the Leonid meteors the most fragile.
Investigation of height data shows even more significant diffences between Geminids and other showers. Beginning heights of Leonid, Orionid, Perseid and Taurid meteors increase with increasing photometric mass. We interpret this as evidence that gradual ablation starts before we are able to detect the meteors. These cometary meteoroids probably contain a volatile part which is released at very high altitudes. The Geminids, on the other hand, start to ablate suddenly at a height of about 100 km. This is probably due to reaching the melting temperature of silicates, which may or may not be preceded by meteoroid fragmentation.
Acknowledgements
This work was supported by the Grant Agency of the Czech Republic, grants 205/02/P038 and No. 205/02/0982, and by the Academy of Sciences of Czech Republic scientific project AV0Z1003909. We would like to express our gratitude to students Jirí Palek, Petr Zasche and Stanislav Poddaný for their help with the meteor records reduction, which is a time consuming activity and to our colleague Rostislav Stork for his participation in observations, records recognition and meteors cataloging. We thank also on other colleagues Zdenek Ceplecha and Petr Pecina for their valuable comments and suggestions.