We present a statistical model for estimating the effects of stellar encounters on orbits in the outer Solar System, focussing on the scattered disk at
H. Rickman1 - Ch. Froeschlé2 - Cl. Froeschlé2 - G. B. Valsecchi3
1 - Uppsala Astronomical Observatory, Box 515, 75120 Uppsala, Sweden
2 -
Observatoire de la Côte d'Azur, BP 4229, 06304 Nice, France
3 -
INAF-IASF, via Fosso del Cavaliere 100, 00133 Roma, Italy
Received 16 April 2004 / Accepted 25 August 2004
Abstract
We present a statistical model for
estimating the effects of stellar encounters on orbits in the outer
Solar System, focussing on the scattered disk at ![]() 103 AU from
the Sun. We describe a Monte Carlo simulation using those results and
apply it to the evolution of the scattered disk over 4 Gyr, finding
that a final perihelion distance distribution with an extended tail
reaching to very large values is to be expected. This would likely
result from a single close stellar encounter, in agreement with the
conclusion by Morbidelli & Levison (2004). We estimate that the
newly discovered minor planet (90377) Sedna may be a typical
representative of such an extended scattered disk and that a few
more objects of the same size may reside at similar heliocentric
distances. There is a possibility that the bulk of the population,
which should have smaller perihelion distances, contains some very
large objects that may have contributed to sculpting the
Kuiper Belt.
We also find that the creation of an extended scattered disk by a
stellar encounter should have been accompanied by a huge influx of
large objects into the inner Solar System, but the timing of the
encounter is constrained by the fact that the scattered disk must
still have been quite massive. Thus it likely happened long before
the purported late heavy bombardment of the terrestrial planets.
103 AU from
the Sun. We describe a Monte Carlo simulation using those results and
apply it to the evolution of the scattered disk over 4 Gyr, finding
that a final perihelion distance distribution with an extended tail
reaching to very large values is to be expected. This would likely
result from a single close stellar encounter, in agreement with the
conclusion by Morbidelli & Levison (2004). We estimate that the
newly discovered minor planet (90377) Sedna may be a typical
representative of such an extended scattered disk and that a few
more objects of the same size may reside at similar heliocentric
distances. There is a possibility that the bulk of the population,
which should have smaller perihelion distances, contains some very
large objects that may have contributed to sculpting the
Kuiper Belt.
We also find that the creation of an extended scattered disk by a
stellar encounter should have been accompanied by a huge influx of
large objects into the inner Solar System, but the timing of the
encounter is constrained by the fact that the scattered disk must
still have been quite massive. Thus it likely happened long before
the purported late heavy bombardment of the terrestrial planets.
Key words: comets: general - Kuiper Belt - minor planets, asteroids
The discovery of minor planet (90377) Sedna was recently reported (Brown
et al. 2004). This is a very large object, whose absolute magnitude H=1.7and limits to its thermal radiation indicate a diameter intermediate between
(50000) Quaoar and Pluto. Orbital elements determined on the basis of
observations from Sep. 2001 until early 2004 include a perihelion
distance of ![]() AU and a semimajor axis of
AU and a semimajor axis of
![]() AU
(Marsden 2004), and the object is currently at
AU
(Marsden 2004), and the object is currently at ![]() AU inbound.
AU inbound.
Both the size and the orbit of Sedna are remarkable and came quite
unexpected. The closest analogue among previous transneptunian objects
is 2000 CR105 with ![]() AU and
AU and
![]() AU, whose
H=6.1 indicates a diameter around 300 km. Both these objects belong
to the "extended scattered disk'' according to the terminology of
Gladman et al. (2002), as Morbidelli & Levison (2004) note
in their analysis of formation scenarios. The orbit of Sedna is of
special importance in that it accentuates very clearly the need for
an efficient mechanism to raise the perihelion distances from the range
accessible by interactions with Neptune (Gladman et al. 2002; Gomes 2003);
at variance with other trans-Neptunian objects, Sedna is really the
propotype of what we will call, in the rest of this paper, the ETNOs,
the Exterior Trans-Neptunian Objects.
AU, whose
H=6.1 indicates a diameter around 300 km. Both these objects belong
to the "extended scattered disk'' according to the terminology of
Gladman et al. (2002), as Morbidelli & Levison (2004) note
in their analysis of formation scenarios. The orbit of Sedna is of
special importance in that it accentuates very clearly the need for
an efficient mechanism to raise the perihelion distances from the range
accessible by interactions with Neptune (Gladman et al. 2002; Gomes 2003);
at variance with other trans-Neptunian objects, Sedna is really the
propotype of what we will call, in the rest of this paper, the ETNOs,
the Exterior Trans-Neptunian Objects.
Let us briefly recapitulate some current ideas about the scattered disk. It is a structure that arises naturally from the accretion of the giant planets. Gravitational scattering sends a large population of planetesimals and planetary embryos both inward (toward the Sun) and outward to orbits with larger semimajor axes. The latter have perihelia locked to the vicinity of the scattering planet's orbit, and aphelia reaching out to hundreds or thousands of AU. The orbital inclinations are small to moderate. At the time the planetary accretion reaches and passes its maximum rate, the mass of this exterior disk may be comparable to the final mass of the planet. Afterwards it gradually subsides, mainly through repeated encounters with the planet, which either eject the objects into hyperbolic orbits or increase their semimajor axes beyond the range where external perturbers take control of the perihelion distances. Today's scattered disk - even though perhaps comparable in population size to the Kuiper Belt (Morbidelli & Brown 2004) - is hence but a bleak shadow of what it was, when the giant planets accreted.
Brown et al. (2004) discussed modes of origin for Sedna, concentrating
on three mechanisms - scattering by an unseen planet at ![]() AU,
a single stellar encounter, and formation of the Solar System in a
stellar cluster. They did not exclude any of these scenarios, but found
a preference for the third one. The main argument against the unseen
planet was that in fact it should likely have been seen, while the stellar
encounter was deemed too unlikely based on statistical results by
Fernández (1997). The stellar cluster scenario was found credible on
the basis of an investigation by Fernández & Brunini (2000). Let us note,
however, that this scenario may suffer from a time scale problem. Galactic
clusters tend to disperse within
AU,
a single stellar encounter, and formation of the Solar System in a
stellar cluster. They did not exclude any of these scenarios, but found
a preference for the third one. The main argument against the unseen
planet was that in fact it should likely have been seen, while the stellar
encounter was deemed too unlikely based on statistical results by
Fernández (1997). The stellar cluster scenario was found credible on
the basis of an investigation by Fernández & Brunini (2000). Let us note,
however, that this scenario may suffer from a time scale problem. Galactic
clusters tend to disperse within ![]() 108 yr, as evidenced by the main
sequence turnoff points of most observed clusters, and it is not certain
that the nascent Solar System could form a scattered disk exterior
to Neptune's orbit and extending to 103 AU within such a short time
interval. For a relevant set of preliminary results, see Dones et al. (2004).
108 yr, as evidenced by the main
sequence turnoff points of most observed clusters, and it is not certain
that the nascent Solar System could form a scattered disk exterior
to Neptune's orbit and extending to 103 AU within such a short time
interval. For a relevant set of preliminary results, see Dones et al. (2004).
Morbidelli & Levison (2004) considered an early high eccentricity of
Neptune's orbit, massive planetary embryos in the transneptunian region,
tidal effects of an early, massive transneptunian disk, and stellar
encounters. Their conclusion, based on actual simulations, was that only
the stellar encounter scenario gave satisfactory results. An important
finding was that too close an encounter, at 500 AU or less, would yield
too many objects with semimajor axes much less than the two discovered
objects (2000 CR105 and Sedna) in the extended scattered disk.
Their preferred distance was 800 AU. The stellar velocity employed in
their simulation (0.2 AU/yr ![]() km s-1) is conspiciously small compared
to the distribution of Galactic field stars in the solar neighbourhood
(cf. Table 1) - instead it is suggestive of the velocity that a member
of the Sun's hypothetical stellar cluster would have.
km s-1) is conspiciously small compared
to the distribution of Galactic field stars in the solar neighbourhood
(cf. Table 1) - instead it is suggestive of the velocity that a member
of the Sun's hypothetical stellar cluster would have.
Thus, except if viewed in the stellar cluster scenario, the very puffed-up q distribution resulting from the Morbidelli & Levison simulation (their Fig. 5c) may not be realistic. We are currently performing Monte Carlo simulations of stellar perturbations on comets of the Oort cloud, aiming to use a distribution of stellar parameters (velocities, masses, relative encounter frequencies) that is as realistic as possible. Upon the discovery of Sedna, by the time of the submission of the above-cited papers by Brown et al., and Morbidelli & Levison, we decided to check the apparently promising stellar encounter scenario on the basis of our own simulation procedure. The model developed for this case is a slight modification of the one we use for the Oort cloud and focuses on a scattered disk component with perihelia slightly outside Neptune's orbit and aphelia extending to 103 AU - we refer to such hypothetical objects as "proto-ETNOs''.
In Sect. 2 we describe this model, in Sect. 3 we present the results, and in Sect. 4 we discuss their relevance and implications for the structure of the extended scattered disk, judging that indeed a stellar encounter is a likely scenario without excluding the possibility of a stellar cluster. Speculations about effects on the classical Kuiper belt and a discussion relating to the late heavy bombardment are also offered. Finally, Sect. 5 summarizes our conclusions.
We simulate stellar perturbations in the following manner. First we
create impulse samples for objects placed at certain standard
heliocentric distances ![]() .
In the present investigation we use
.
In the present investigation we use
![]() ,
200, 500 and 1000 AU. Each sample involves
,
200, 500 and 1000 AU. Each sample involves
![]() stellar passages within 40 000 AU from the Sun, assumed to occur
at random with an isotropic distribution of distance and direction with
respect to the position of the object. For convenience the calculations
are done with the star passing in the z direction of a cartesian
coordinate system centered on the Sun such that the star cuts the
(x, y) plane on the positive x axis, while the object is placed
at a random position on a sphere of radius
stellar passages within 40 000 AU from the Sun, assumed to occur
at random with an isotropic distribution of distance and direction with
respect to the position of the object. For convenience the calculations
are done with the star passing in the z direction of a cartesian
coordinate system centered on the Sun such that the star cuts the
(x, y) plane on the positive x axis, while the object is placed
at a random position on a sphere of radius ![]() around the Sun.
around the Sun.
We use the classical impulse approximation, i.e., the star moves along
a straight line with constant speed v*, and the object remains fixed.
The heliocentric impulse imparted to the object, i.e., the differential
impulse of the object with respect to the Sun, is hence:
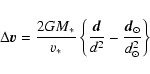 |
(1) |
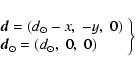 |
(2) |
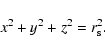 |
(3) |
Table 1:
Stellar parameters. Categories 1-11 refer to MK types for
main sequence stars, category 12 is white dwarfs, and category 13 is
giant stars. Values of the solar apex velocities ![]() and
encounter frequencies
and
encounter frequencies
![]() (the latter in number per Myr
within 1 pc) have been taken from Table 8 of García-Sánchez
et al. (2001), while the velocity dispersions
(the latter in number per Myr
within 1 pc) have been taken from Table 8 of García-Sánchez
et al. (2001), while the velocity dispersions ![]() are
one-dimensional and correspond to those listed by García-Sánchez
et al. divided by
are
one-dimensional and correspond to those listed by García-Sánchez
et al. divided by ![]() .
Stellar masses are taken from Allen (1985).
.
Stellar masses are taken from Allen (1985).
We consider the same 13 categories of stars as in García-Sánchez
et al. (2001) with the values of solar apex velocities, internal velocity
dispersions and encounter frequencies listed by these authors (see their
Table 8) as derived from classical stellar statistics investigations. For the
stellar masses we take values listed by Allen (1985). In Table 1 we list
all stellar parameters used in our work. To calculate the encounter speed
of a certain star, we first determine the category from the fractional
contributions to the total encounter frequency of 10.525 Myr-1within ![]() pc.
pc.
We compute the peculiar velocity ![]() of the star with respect to
the velocity centroid of its category, such that
of the star with respect to
the velocity centroid of its category, such that
![]() is found from a combination of three Gaussian components, each with the
dispersion listed in Table 1. We then combine this with the apex velocity
is found from a combination of three Gaussian components, each with the
dispersion listed in Table 1. We then combine this with the apex velocity
![]() assuming a random direction of
assuming a random direction of ![]() :
:
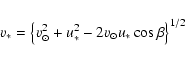 |
(4) |
The four impulse samples are used as input to a Monte Carlo
simulation of stellar encounters for orbits like that of a "proto-ETNO''.
To this end we first determine a minimum impulse modulus
![]() such that only impulses larger than this
are taken into account. This determination is described below, and the
aim is to find a balance such that
such that only impulses larger than this
are taken into account. This determination is described below, and the
aim is to find a balance such that
![]() can safely
be disregarded, and encounters with
can safely
be disregarded, and encounters with
![]() are in general
close enough for the classical impulse approximation to be valid. Thus,
for each perturbation sample we only save the entries with
are in general
close enough for the classical impulse approximation to be valid. Thus,
for each perturbation sample we only save the entries with
![]() ,
and we note
the measure of this subsample compared to the total sample size of
,
and we note
the measure of this subsample compared to the total sample size of
![]() .
We could have reached a somewhat higher accuracy of our
simulation results, if we had used more than four impulse samples.
However, as illustrated by Table 2 below, the four samples are not
dramatically different, and we judge this loss of accuracy to be no
more severe than that caused by using the classical impulse approximation.
.
We could have reached a somewhat higher accuracy of our
simulation results, if we had used more than four impulse samples.
However, as illustrated by Table 2 below, the four samples are not
dramatically different, and we judge this loss of accuracy to be no
more severe than that caused by using the classical impulse approximation.
Each test object in our simulation is initially placed on an orbit with
perihelion distance q0=35 AU and aphelion distance Q0=1000 AU at a
time 4 Gyr ago. By this we aim to represent a scattered disk object that
was ejected by Neptune and had its perihelion distance raised until it almost
decoupled from the planet's gravitational influence. The simulation runs
for 4 Gyr with a time step
![]() yr. This is exactly 1% of the average interval between consecutive stellar passages within
40 000 AU for the above choice of the encounter frequency, i.e., the
probability for a random encounter to occur during time
yr. This is exactly 1% of the average interval between consecutive stellar passages within
40 000 AU for the above choice of the encounter frequency, i.e., the
probability for a random encounter to occur during time ![]() is
1%. For each time step we decide by means of a random number
is
1%. For each time step we decide by means of a random number ![]() if
a stellar passage occurs or not.
if
a stellar passage occurs or not.
If a passage occurs, we calculate the exact time
![]() by a random number
by a random number ![]() ,
i.e.,
,
i.e.,
![]() ,
and we solve Kepler's
equation to find the eccentric anomaly and the heliocentric distance rof the object. We then associate the encounter with one of the four
standard distances
,
and we solve Kepler's
equation to find the eccentric anomaly and the heliocentric distance rof the object. We then associate the encounter with one of the four
standard distances ![]() according to limits placed at the geometric
means of consecutive
according to limits placed at the geometric
means of consecutive ![]() values: if r<141.4 we take
values: if r<141.4 we take
![]() ,
else
if r<316.2 we take
,
else
if r<316.2 we take
![]() ,
else if r<707.1 we take
,
else if r<707.1 we take
![]() ,
and
otherwise we take
,
and
otherwise we take
![]() .
With the above combination of q0 and
Q0 we get likelihoods of 3.0%, 6.3%, 26.2% and 64.5% for the four
representative values of
.
With the above combination of q0 and
Q0 we get likelihoods of 3.0%, 6.3%, 26.2% and 64.5% for the four
representative values of ![]() .
.
We first check by means of a random number ![]() if the encounter yields
a significant impulse, and if it does, we pick a random entry from the
corresponding file. These entries contain both
if the encounter yields
a significant impulse, and if it does, we pick a random entry from the
corresponding file. These entries contain both
![]() and the direction cosine
and the direction cosine
![]() with respect to the radial direction (the hats denote
unit vectors). In addition we pick at random the direction cosine Ctof the non-radial component with respect to the transverse direction in
the orbital plane. We can hence compute the perturbations
with respect to the radial direction (the hats denote
unit vectors). In addition we pick at random the direction cosine Ctof the non-radial component with respect to the transverse direction in
the orbital plane. We can hence compute the perturbations
![]() and
and
![]() of both in-plane velocity components as well as the
out-of-plane component
of both in-plane velocity components as well as the
out-of-plane component
![]() .
.
By applying all these we recompute the orbital energy and angular
momentum, and thus, we get the new perihelion distance q and inverse
semimajor axis 1/a. We take another time step ![]() and repeat
the whole process, until the total time elapsed reaches
and repeat
the whole process, until the total time elapsed reaches
![]() yr.
yr.
As a supplement to this investigation we have also developed a routine to compute the effect of a single close stellar encounter on a population of objects like the scattered disk. We still use the classical impulse approximation, and we let the star travel parallel to the z-axis as in the above-described calculation of the impulse samples. The disk is formed by a large number of test objects with uniform distributions of a and q within prechosen limits. The orbits have inclinations to the midplane that are confined below a given maximum value, and the orbital position of a given object is chosen at random, uniformly in mean anomaly. The perturbations of q and a for all the disk objects are computed and recorded. Finally, the orientation of the disk can be chosen such that the axis of symmetry is either the x, y or z coordinate axis. This means that the star can cross the disk perpendicular to its plane (the z-disk) or along a chord in the midplane (the y-disk), or it may pass close to the disk parallel to its plane without crossing it (the x-disk).
Let us first check the validity of the classical impulse approximation
for our study. In fact, the reliability of the simulation results is not
critically dependent on a high accuracy of the estimates of
![]() .
It should be enough to check against total breakdown of the underlying
assumptions. To this end we compute the time spent by the star along
the inner part of its track, where most of the interaction occurs, and
compare it with the orbital period of a typical "proto-ETNO'' - the
latter being a little more than 10 000 yr.
.
It should be enough to check against total breakdown of the underlying
assumptions. To this end we compute the time spent by the star along
the inner part of its track, where most of the interaction occurs, and
compare it with the orbital period of a typical "proto-ETNO'' - the
latter being a little more than 10 000 yr.
| |
Figure 1:
Encounter geometry and illustration of the
interaction length. For the upper stellar track the latter is
|
| Open with DEXTER | |
We compute the interaction time as:
T* = D*/v*, where the interaction
length D* is estimated by
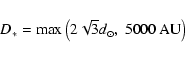 |
(5) |
![\begin{figure}
\par\includegraphics[width=85mm]{1109fi2a.eps}\\
\includegraphics[width=85mm]{1109fi2b.eps}\end{figure}](/articles/aa/full/2004/47/aa1109/Timg70.gif) |
Figure 2:
Interaction time distributions for impulses
larger than
|
| Open with DEXTER | |
Figure 2 shows histograms of T* for encounter subsamples with
![]() ,
where the reference
speed is arbitrarily chosen as
,
where the reference
speed is arbitrarily chosen as
![]() AU/yr, i.e., the circular
speed at
AU/yr, i.e., the circular
speed at
![]() AU. For comparison, the aphelion velocity of Sedna
for Q=1000 AU is 0.0742 AU/yr, and if the perihelion were displaced to
35 AU it would be 0.0517 AU/yr. For both the smaller sample
size with
AU. For comparison, the aphelion velocity of Sedna
for Q=1000 AU is 0.0742 AU/yr, and if the perihelion were displaced to
35 AU it would be 0.0517 AU/yr. For both the smaller sample
size with
![]() AU and the larger one with
AU and the larger one with
![]() AU, the vast
majority of the encounters have
AU, the vast
majority of the encounters have
![]() yr and only a very small
fraction have T*>5000 yr. The latter is close to half the orbital period
of Sedna and may be taken as the interaction time where the impulse
approximation breaks down.
yr and only a very small
fraction have T*>5000 yr. The latter is close to half the orbital period
of Sedna and may be taken as the interaction time where the impulse
approximation breaks down.
Table 2:
Numbers of big impulses (
![]() )
and of those that take an
interaction time larger than 5000 yr (
)
and of those that take an
interaction time larger than 5000 yr (
![]() ). The ratio of the
latter to the former is
). The ratio of the
latter to the former is
![]() .
The impulse limit
.
The impulse limit
![]() denotes the ratio
denotes the ratio
![]() .
The
experiment in each case involves
.
The
experiment in each case involves
![]() random encounters.
random encounters.
From the values listed in Table 2 we see that the fraction of the encounters
that are too slow does not reach beyond about 6% even for
![]() and
and
![]() AU
(Fig. 2b), and is smaller for larger
AU
(Fig. 2b), and is smaller for larger
![]() or smaller
or smaller ![]() .
We deem that this is good enough and that the use of
.
We deem that this is good enough and that the use of
![]() is thus warranted,
but we would hesitate to use smaller values of
is thus warranted,
but we would hesitate to use smaller values of
![]() .
.
In order to estimate the size of a typical perturbation
![]() caused by
caused by
![]() ,
we take
,
we take
![]() and
use:
and
use:
![]() ,
where
,
where
![]() AU2 yr-1for an orbit with q=35 AU and Q=1000 AU. We get a
AU2 yr-1for an orbit with q=35 AU and Q=1000 AU. We get a
![]() that increases from 0.16 AU at r=100 AU to 1.6 AU at r=1000 AU. This
means that neglecting smaller impulses may imply the neglect of an important
small-scale scatter of q. We will return to this point below.
that increases from 0.16 AU at r=100 AU to 1.6 AU at r=1000 AU. This
means that neglecting smaller impulses may imply the neglect of an important
small-scale scatter of q. We will return to this point below.
![\begin{figure}
\par\includegraphics[width=85mm]{1109fi3a.eps}\\
\includegraphics[width=85mm]{1109fi3b.eps}\end{figure}](/articles/aa/full/2004/47/aa1109/Timg83.gif) |
Figure 3:
Encounter speed vs. minimum distance for impulses
larger than
|
| Open with DEXTER | |
In Fig. 3 we show scatter diagrams of v* vs. ![]() for the samples of significant impulses at
for the samples of significant impulses at
![]() and 1000 AU. As
explained below, these samples contain many more stellar encounters than
we can expect over the age of the Solar System, for the simple reason
that we need good statistics. Note the wide range
of encounter velocities that contribute in both cases, and the presence
of an extended tail of the distribution of minimum distances for
and 1000 AU. As
explained below, these samples contain many more stellar encounters than
we can expect over the age of the Solar System, for the simple reason
that we need good statistics. Note the wide range
of encounter velocities that contribute in both cases, and the presence
of an extended tail of the distribution of minimum distances for
![]() AU (Fig. 3b). These are due to the inclusion of a small
fraction
of massive stars into our material (mainly B stars and giants, see Table
1). However, the entries peak around
AU (Fig. 3b). These are due to the inclusion of a small
fraction
of massive stars into our material (mainly B stars and giants, see Table
1). However, the entries peak around
![]() km s-1 and
km s-1 and
![]() AU for
AU for
![]() AU (
AU (
![]() AU for
AU for
![]() AU).
Note that a
AU).
Note that a ![]() star that passes the Sun or the object at a
distance of 1000 AU with a speed of 30 km s-1
star that passes the Sun or the object at a
distance of 1000 AU with a speed of 30 km s-1
![]() AU/yr imparts
an impulse of 0.006 AU/yr
AU/yr imparts
an impulse of 0.006 AU/yr
![]() ,
while much more
distant encounters will yield a significant impulse only if they are
slow and the stars are massive. But for
,
while much more
distant encounters will yield a significant impulse only if they are
slow and the stars are massive. But for
![]() AU the impulses to the
object and the Sun from a
AU the impulses to the
object and the Sun from a
![]() AU encounter will largely
cancel out, so closer encounters are needed for significant net impulses
to result.
AU encounter will largely
cancel out, so closer encounters are needed for significant net impulses
to result.
We need to emphasize that the samples of 107 encounters are much larger
than the number of stellar passages within 40 000 AU expected during
4 Gyr. The latter is close to 1600, so the ratio is about 6250. Thus
our samples correspond to a time interval of
![]() Gyr
Gyr
![]() yr. In particular, for an object spending 64.5%
of 4 Gyr in the range of
yr. In particular, for an object spending 64.5%
of 4 Gyr in the range of
![]() AU we expect
AU we expect
![]() stellar encounters within 40 000 AU, and for a sample size of
6952 in Fig. 3b (see Table 2b)
we should hence expect
stellar encounters within 40 000 AU, and for a sample size of
6952 in Fig. 3b (see Table 2b)
we should hence expect
![]() significant impulses to occur. The contribution from the
range of
significant impulses to occur. The contribution from the
range of
![]() AU is similarly:
AU is similarly:
![]() ,
while the contributions from
,
while the contributions from
![]() and 200 AU are much smaller.
The expectation is thus a little less than one significant impulse per object
during 4 Gyr.
and 200 AU are much smaller.
The expectation is thus a little less than one significant impulse per object
during 4 Gyr.
![\begin{figure}
\par\includegraphics[width=85mm]{1109fi4a.eps}\\
\includegraphics[width=85mm]{1109fi4b.eps}\end{figure}](/articles/aa/full/2004/47/aa1109/Timg97.gif) |
Figure 4:
Distribution of stellar categories (cf. Table 1)
for large impulses suffered by an object at
|
| Open with DEXTER | |
Figure 4a shows how the significant impulses are distributed over the 13 stellar categories. Comparing with the relative contributions to the encounter frequency in Table 1, we note that - as expected - the massive star types are overrepresented in the statistics of big impulses. Even so, M dwarfs yield the dominant contribution. But if we concentrate on very big impulses, as shown in Fig. 4b, the contributions are actually rather evenly distributed over all categories.
![\begin{figure}
\par\includegraphics[width=85mm]{1109fi5.eps}\end{figure}](/articles/aa/full/2004/47/aa1109/Timg98.gif) |
Figure 5:
Impulse modulus vs. radial direction cosine,
limited to impulses larger than
|
| Open with DEXTER | |
Figure 5 shows how the radial direction cosine of the
impulse vector is
distributed with respect to the modulus of the vector for the
![]() AU
sample. An isotropic distribution of impulse directions would yield a
uniform distribution of Cr. We note that this is nearly the case for
all ranges of
AU
sample. An isotropic distribution of impulse directions would yield a
uniform distribution of Cr. We note that this is nearly the case for
all ranges of
![]() ,
even though there is a slight
concentration to intermediate values of Cr of both positive and
negative sign.
,
even though there is a slight
concentration to intermediate values of Cr of both positive and
negative sign.
We have performed one principal Monte Carlo simulation involving 10 000test objects whose starting orbits are characterized by: q0=35 AU; Q0=1000 AU. During the 4 Gyr covered by the simulation, 4148 objects received no significant impulse at all - though, as we have seen above, the smaller impulses that we neglected could amount to perturbations of several AU in q. The majority of the rest (almost 3000) suffered only one significant impulse, while close to 1000 suffered two, about 300 suffered three and less than 50 suffered four or five. These numbers show clearly that the large perturbations experienced by our test objects mainly result from one close stellar encounter, not a random walk of smaller steps.
A total of 28 objects, i.e., 0.28% of the sample, were ejected on hyperbolic orbits during a very close stellar encounter. A large fraction of the objects had their perihelion distances decreased by significant amounts, and we have deemed that an orbit with q<31 AU is unstable against planetary perturbations so that the object will become ejected rapidly from the Solar System. The number of objects thus excluded was 1510.
![\begin{figure}
\par\includegraphics[width=85mm]{1109fi6.eps}\end{figure}](/articles/aa/full/2004/47/aa1109/Timg99.gif) |
Figure 6: Distribution of perihelion distances acquired by objects that received significant impulses in a 4 Gyr simulation but stayed at q>31 AU. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=85mm]{1109fi7.eps}\end{figure}](/articles/aa/full/2004/47/aa1109/Timg100.gif) |
Figure 7: Distribution of perihelion distances for all objects that received significant impulses in a 4 Gyr simulation, independent of how q evolved. |
| Open with DEXTER | |
Figure 6 shows a histogram of final q values for the 4314 objects that left our principal simulation having suffered significant perturbations. The cut of the abscissa at q=200 AU is artificial, and the tail in fact extends to 800 AU. Interpretations and implications of this diagram will be presented in the next section. Figure 7 shows the result of an additional simulation, including the orbits that were perturbed to q<31 AU. We note that a significant percentage of the test objects entered the Saturn-Uranus region and some were even injected directly into Jupiter-crossing orbits.
![\begin{figure}
\par\includegraphics[width=85mm]{1109fi8a.eps}\\
\includegraphic...
...th=85mm]{1109fi8b.eps}\\
\includegraphics[width=85mm]{1109fi8c.eps}\end{figure}](/articles/aa/full/2004/47/aa1109/Timg101.gif) |
Figure 8:
Semimajor axes and perihelion distances acquired
at a stellar passage with
|
| Open with DEXTER | |
Given that the far tails of the q-distribution in Fig. 7
are expected
to originate in one close stellar encounter, we computed the response
of x-, y- and z-disks with 10 000 test objects to an encounter
with a 1 ![]() star moving at 30 km s-1. The minimum approach distance
was 800 AU. In each case the disk had orbital inclinations below
star moving at 30 km s-1. The minimum approach distance
was 800 AU. In each case the disk had orbital inclinations below ![]() and perihelion distances from 32 to 36 AU. Figure 8 shows the
resulting distribution of a and q for x-, y- and z-disks with
initial semimajor axes between 100 and 600 AU. Note the appearance of a
wide scatter in q that starts at
and perihelion distances from 32 to 36 AU. Figure 8 shows the
resulting distribution of a and q for x-, y- and z-disks with
initial semimajor axes between 100 and 600 AU. Note the appearance of a
wide scatter in q that starts at
![]() AU for the y-disk and
somewhat closer in for the z-disk, while the x-disk remains much less
perturbed over the entire range of a. The reason is that the y- and
z-disks are penetrated by the star, while the x-disk is situated on
average 800 AU from the stellar track. Thus close encounters between
the star and disk objects occur in the former cases but not in the latter.
AU for the y-disk and
somewhat closer in for the z-disk, while the x-disk remains much less
perturbed over the entire range of a. The reason is that the y- and
z-disks are penetrated by the star, while the x-disk is situated on
average 800 AU from the stellar track. Thus close encounters between
the star and disk objects occur in the former cases but not in the latter.
![\begin{figure}
\par\includegraphics[width=85mm]{1109fi9a.eps}\\
\includegraphic...
...th=85mm]{1109fi9b.eps}\\
\includegraphics[width=85mm]{1109fi9c.eps}\end{figure}](/articles/aa/full/2004/47/aa1109/Timg104.gif) |
Figure 9: Perihelion distances acquired through the same stellar passage as in Fig. 8 by 10 000 objects forming a disk with a0between 400 and 600 AU, for the same disk axis orientations as in Fig. 8. |
| Open with DEXTER | |
We also made computations for disks confined to initial a between 400 and 600 AU to get better statistics of the resulting q distribution for Sedna-type orbits. The results are shown in Fig. 9. We see that, while an encounter with the x-disk orientation is unable to produce a distribution like that in Fig. 7, both the y- and z-disk encounters give results that bear a qualitative resemblance to the result of our long-term Monte Carlo simulation.
Thus, from Figs. 8 and 9 we find a useful confirmation of the simulation, in the sense that an explicit stellar encounter that matches the expectations for the closest ones that ever occurred may indeed reproduce the same scatter of perihelion distances that the simulation yielded. But we also note that different encounter geometries - just like different stellar masses, velocities and distances - yield results that differ to some extent. Therefore we cannot claim to know what the q distribution of the extended scattered disk looks like in detail, but for want of the required detailed knowledge, we can take the simulation results in Figs. 6 and 7 as the best current estimate.
To discuss this further, Fig. 6 should be interpreted as a
probability density distribution for the results of stellar perturbations
over any 4 Gyr period during the
![]() yr that our impulse
samples cover. It is not immediately obvious that this represents the
true history of the Solar System, however. In particular, even though
the closest encounter distance statistically expected should be a little
less than 1000 AU from the Sun, we cannot be sure that such an encounter
has actually occurred. If the closest real encounter was at, e.g., 1500 AU
(this would not be too unlikely, if the present encounter frequency is
larger than the average in the past), then the whole tail of large
q values including the orbit of Sedna would likely be absent. On the other
hand, the present encounter frequency might also be smaller than it
used to be in the past, so that even closer passages could have occurred.
In fact, all encounter distances are possible a priori, but Morbidelli
& Levison (2004) did indicate a likely minimum value, as we shall
discuss below.
yr that our impulse
samples cover. It is not immediately obvious that this represents the
true history of the Solar System, however. In particular, even though
the closest encounter distance statistically expected should be a little
less than 1000 AU from the Sun, we cannot be sure that such an encounter
has actually occurred. If the closest real encounter was at, e.g., 1500 AU
(this would not be too unlikely, if the present encounter frequency is
larger than the average in the past), then the whole tail of large
q values including the orbit of Sedna would likely be absent. On the other
hand, the present encounter frequency might also be smaller than it
used to be in the past, so that even closer passages could have occurred.
In fact, all encounter distances are possible a priori, but Morbidelli
& Levison (2004) did indicate a likely minimum value, as we shall
discuss below.
Indeed, we can only make statements about probabilities, and it is evident
that, based on the belief that the current encounter frequency is not an
overestimate, an encounter to within 1000 AU or less is not at all
unlikely. And when it happened, as verified by Figs. 8b,c
and 9b,c, a hypothetical population of proto-ETNOs might
have been affected according to a distribution similar to that in
Fig. 7, given that the objects would have had random positions at
![]() AU.
AU.
Now, can the existence of one roughly Pluto-sized object in the Sedna orbit be used to infer the existence of a much larger population of such large objects with a q distribution like that in Fig. 6? A tentative answer to this question can be obtained by asserting that, currently, there is no such object at r<50 AU (otherwise it would be bright enough to have been detected long ago) and only one (i.e., Sedna) at 50<r<100 AU. The former seems a safer assumption than the latter, and we shall return to this point below. We have computed the fraction of the time spent at 50<r<100 AU by each object contributing to Fig. 6 plus the 4148 ones remaining in the initial orbit, and formed the sum of all these fractions. This turned out to be about 106, so according to our second assertion we have to scale down our simulated population by a factor 106. As a result, the number of objects expected to be at r<50 AU is only about 1/2.
The result of this exercise is a population of 80 objects, of which
1 has q>90 AU, 2 have 60<q<90 AU, 11 have 40<q<60 AU, and 66 have
q<40 AU. Each object except the first has a roughly equal chance of
being the one that currently has r<100 AU, so it does not appear too
unlikely for Sedna to be the one. However, from Fig. 8 we
see that the
picture just described cannot be complete. If the very large population
with ![]() AU has survived until the present time, so should also
the fraction of the initial scattered disk with
AU has survived until the present time, so should also
the fraction of the initial scattered disk with ![]() AU, whose
perihelion distances have remained small. If that were the case, we
should have another, even larger population of large objects with
AU, whose
perihelion distances have remained small. If that were the case, we
should have another, even larger population of large objects with
![]() AU and
AU and ![]() AU, and it would be unbelievable that none
have been observed.
AU, and it would be unbelievable that none
have been observed.
Obviously, our discussion has missed two unmodelled sources of perturbations
of q: the field of more distant, or in any case less efficient, stellar
encounters, and the gravitational influence of the planets. As to the
first one, we have seen that the effects may amount to a cumulative
![]() AU. Gladman et al. (2002) found that interactions
with Neptune may raise q to 36 AU, and thus the inverse is also possible.
The combination of the two mechanisms may yield an efficient erosion
of the scattered disk so that, effectively, no Sedna-sized objects
remain today with
AU. Gladman et al. (2002) found that interactions
with Neptune may raise q to 36 AU, and thus the inverse is also possible.
The combination of the two mechanisms may yield an efficient erosion
of the scattered disk so that, effectively, no Sedna-sized objects
remain today with ![]() AU.
AU.
We are thus led to conjecture that the decisive stellar encounter occurred early on, before the erosion had time to occur and the scattered disk may have been very massive. Morbidelli & Levison (2004) argue that the encounter must have occurred before the Oort cloud was created - and thus at an early epoch - because otherwise the cloud would have been disrupted. We note that this is natural in the cluster scenario for which Morbidelli and Levison's simulation is relevant, because on the one hand the stellar encounter is expected to be very slow and thus able to disrupt the Oort cloud, and on the other hand it must have occurred very early, before the cluster was disrupted. Hence there should have been time to rebuild the Oort cloud afterwards.
But even so, we believe that an early stellar encounter is necessary, since if it occurred too late, it would have been impossible to create the above number of objects the size of Sedna in the extended scattered disk. The current mass of the extended scattered disk is very uncertain, being dependent both on the actual number of Sedna-sized objects and the slope of the size distribution (Morbidelli, priv. comm.). The mass of the primordial scattered disk is uncertain too, as is the "erosional'' half life against ejection by Neptune. Further research is needed in order to say exactly how early an epoch is required, and whether a connection to a stellar cluster where the Sun was born (Brown et al. 2004) is indeed likely. If the scattered disk was strongly perturbed by an encounter with a cluster member, and if that is the main reason that the ETNO population exists, we still expect our results from encounters with random field stars to be valid for the remaining part of the disk until the present time.
In any case, with the scenario proposed we may assume that essentially
the whole population with q<40 AU in Fig. 6 has been stripped
away, and only the part with q>40 AU exists today. Repeating thus the
above analysis to find the size of such an ETNO population on the
assumption that only one or two currently have 50<r<100 AU, we get
![]() 5-10 objects with q>90 AU,
5-10 objects with q>90 AU, ![]() 10-20 objects with 60<q<90 AU,
and
10-20 objects with 60<q<90 AU,
and ![]() 50-100 objects with 40<q<60 AU. In fact there is no special
justification for that assumption. Judging from the sky coverage of
present surveys, Brown et al. (2004) estimate a likely number of
50-100 objects with 40<q<60 AU. In fact there is no special
justification for that assumption. Judging from the sky coverage of
present surveys, Brown et al. (2004) estimate a likely number of ![]() 6,
for which case the quoted numbers will have to be scaled upward by a
factor of
6,
for which case the quoted numbers will have to be scaled upward by a
factor of ![]() 4.
4.
To summarize, we find that our simulation has borne out Morbidelli and
Levison's suggestion of an early, close stellar encounter as a likely
mechanism to explain the Sedna orbit. In addition, we are led to expect
the existence of a large number of similar-sized or larger objects with
perihelion distances from ![]() 40 AU outward. If the total number is
40 AU outward. If the total number is
![]() 80, it is likely that Sedna is currently alone in the
50<r<100 AU range. More likely, the total number is several hundred,
and Sedna has several as yet undiscovered colleagues of comparable
brightness in the same range of r. A comment on the circumstance that
the first discovered object belongs to a minority of
80, it is likely that Sedna is currently alone in the
50<r<100 AU range. More likely, the total number is several hundred,
and Sedna has several as yet undiscovered colleagues of comparable
brightness in the same range of r. A comment on the circumstance that
the first discovered object belongs to a minority of ![]() 10% with
very large q is in order. We do not believe this minority to be so
small as to call for a special explanation. Moreover, even though a
stellar encounter distance less than 800 AU might have stirred up the
scattered disk more efficiently, we noted in the Introduction that
Morbidelli & Levison (2004) give a strong argument against such a
scenario in that the inner part of the scattered disk would also have
been excited and the non-discovery of Sedna-like objects with much
smaller semimajor axes would thus be difficult to explain.
10% with
very large q is in order. We do not believe this minority to be so
small as to call for a special explanation. Moreover, even though a
stellar encounter distance less than 800 AU might have stirred up the
scattered disk more efficiently, we noted in the Introduction that
Morbidelli & Levison (2004) give a strong argument against such a
scenario in that the inner part of the scattered disk would also have
been excited and the non-discovery of Sedna-like objects with much
smaller semimajor axes would thus be difficult to explain.
It is tempting to speculate that one or a few objects with
![]() AU,
where a large part of the population should be, may even be much larger than
Sedna, and may thus offer an alternative to the
"rogue planet'' scenario
for explaining the apparent edge of the Kuiper belt at
AU,
where a large part of the population should be, may even be much larger than
Sedna, and may thus offer an alternative to the
"rogue planet'' scenario
for explaining the apparent edge of the Kuiper belt at ![]() 50 AU
(Brunini & Melita 2002). Each such object might have made hundreds of
thousands of perihelion passages since they were emplaced. We find it
very interesting to investigate the possible sculpting effect of those
passages on a population in the 50-60 AU range, as well as the "heating''
effect on the orbital distribution at somewhat smaller distances.
50 AU
(Brunini & Melita 2002). Each such object might have made hundreds of
thousands of perihelion passages since they were emplaced. We find it
very interesting to investigate the possible sculpting effect of those
passages on a population in the 50-60 AU range, as well as the "heating''
effect on the orbital distribution at somewhat smaller distances.
Let us now discuss the implications of Figs. 7 and 9.
If indeed the scattered disk was massive enough for the close stellar
encounter to have transferred hundreds of objects the size of Sedna
or larger with ![]() AU into large values of q, then a large number
of such objects would also have been injected into planet-crossing orbits.
For any reasonable size distribution, the number of
objects with diameters of
AU into large values of q, then a large number
of such objects would also have been injected into planet-crossing orbits.
For any reasonable size distribution, the number of
objects with diameters of ![]() 100 km or smaller would have been enormous.
Thus a huge population of large objects would have invaded the inner Solar
System. One may wonder whether this is a possible scenario for explaining
the late heavy bombardment of the terrestrial planets and the Moon
(Hartmann et al. 2000), along the lines discussed by Levison et al. (2001).
However, the stellar encounter that created the ETNO population
must likely have occurred much earlier. A more attractive scenario might
be that this encounter happened very early (possibly within a stellar
cluster) and that later on a random field star passed very close about
4 Gyr ago with relatively little effect on the ETNO population but
injecting an important gust of objects into the inner Solar System.
100 km or smaller would have been enormous.
Thus a huge population of large objects would have invaded the inner Solar
System. One may wonder whether this is a possible scenario for explaining
the late heavy bombardment of the terrestrial planets and the Moon
(Hartmann et al. 2000), along the lines discussed by Levison et al. (2001).
However, the stellar encounter that created the ETNO population
must likely have occurred much earlier. A more attractive scenario might
be that this encounter happened very early (possibly within a stellar
cluster) and that later on a random field star passed very close about
4 Gyr ago with relatively little effect on the ETNO population but
injecting an important gust of objects into the inner Solar System.
Acknowledgements
HR gratefully acknowledges the hospitality of the Observatoire de Nice during a stay there as visiting scientist in Nov.-Dec. 2003, when the basic work on computer codes used in this paper was done. Research grants from the Swedish National Space Research Board and the Swedish Council of Science were also very beneficial for this work.