A&A 428, 545-554 (2004)
DOI: 10.1051/0004-6361:20040325
The influence of rotation in radiation driven winds from hot stars
II. CAK topological analysis
M. Curé 1 - D. F. Rial 2
1 - Departamento de Física y Meteorología, Facultad de Ciencias,
Universidad de Valparaíso, Valparaíso, Chile
2 - Departamento de Matemáticas, Facultad de Ciencias Exactas y Naturales,
Universidad de Buenos Aires, Argentina
Received 24 February 2004 / Accepted 26 August 2004
Abstract
The topological analysis from Bjorkman (1995) for the standard model that describes the winds from hot stars by Castor et al. (1975) has been extended to include the effect of stellar rotation and changes in the ionization of the wind.
The differential equation for the momentum of the wind is non-linear and transcendental for the velocity gradient. Due to this non-linearity the number of solutions that this equation possess is not known. After a change of variables and the introduction of a new physically meaningless independent variable, we manage to replace the non-linear momentum differential equation by a system of differential equations where all the derivatives are explicitely given. We then use this system of equations to study the topology of the rotating-CAK model. For the particular case when the wind is frozen in ionization (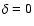 )
only one physical solution is found, the standard CAK solution, with a X-type singular point. For the more general case (
)
only one physical solution is found, the standard CAK solution, with a X-type singular point. For the more general case (
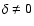 ), besides the standard CAK singular point, we find a second singular point which is focal-type (or attractor). We find also, that the wind does not adopt the maximal mass-loss rate but almost the minimal.
), besides the standard CAK singular point, we find a second singular point which is focal-type (or attractor). We find also, that the wind does not adopt the maximal mass-loss rate but almost the minimal.
Key words: hydrodynamics - methods: analytical - stars: early-type - stars: mass-loss - stars: rotation - stars: winds, outflows
Since the launch of the first satellite with a telescope on board, it has been established the widespread presence of stellar winds from hot stars. These winds are driven by the transfer of momentum of the radiation field to the gas by scattering of radiation in spectral lines (Lucy & Solomon 1970). The theory of radiation driven stellar winds is the standard tool to describe the observed properties of the winds from these stars. Castor et al. (1975, hereafter "CAK'') obtained an analytical hydrodynamic model for these winds, based in the Sobolev approximation.
The CAK model has been improved by Friend & Abbott (1986, "FA'') and Pauldrach
et al. (1986, "PPK''), giving a general agreement with the observations. For a extended review see
Kudritzki & Puls (2000, "KP'') and references therein.
This agreement with the observations led to the development of a new method to
determine galactic distances using Supergiants as targets, namely the Wind Momentum Luminosity relationship ("WML'', Kudritzki et al. 1999; KP, and references therein).
More detailed studies from Puls et al. (1996) and Lamers & Leitherer (1993) came to the conclusion that the line-driven wind theory shows a systematic discrepancy with the observations. Lamers & Leitherer (1993) suggest that this discrepancy may arise due to an inadequate treatment of multiple scattering. Abbott & Lucy (1985), Puls (1987) and Gayley et al. (1995) have shown that multiple scattering can provide an enhancement of the wind momentum over that from single scattering only by a factor of two - three for O stars (Abbott & Lucy 1985, found a factor of 3.3 for the wind of 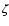 Pup).
Pup).
Vink et al. (2000) calculate, including the multiple scattering effects, mass-loss rates for a grid of wind models that covers a wide range of stellar parameters. They found a much better agreement between theory and observation, concluding that the inclusion of multiple scattering increases the confidence of the WML relationship to derive extragalactic distances.
In all the calculations involved in the WML relationship, the solution of the improved (or modified) CAK wind (hereafter m-CAK) is not used. Instead an ad hoc 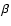 -field velocity profile is utilized (see KP; Vink et al. 2000).
-field velocity profile is utilized (see KP; Vink et al. 2000).
The unsatisfactory results of the velocity field obtained from the m-CAK model
when applied in the WML relationship could come from the complex structure of this
non-linear transcendental equation for the velocity gradient and its solution
schema. Due to this non-linearity in the momentum differential equation, there exist many
solution branches in the integration domain. A physical solution that describes the observed
winds must start at the stellar photosphere, satisfying certain boundary condition and reach infinity. There is no solution branch that covers the whole integration domain, thus a solution must pass through a singular point in order to match a second solution branch. Therefore, the solution in this second solution branch reaches infinity. To find the location of singular points is one of the most difficult aspects of topological analysis of non-linear differential equations.
Bjorkman (1995) performed a topological analysis of the CAK differential equation. He showed that
the original solution from CAK, which passes through a X-type critical point and has a monotonically
increasing velocity field, is the only physical solution that satisfies the condition of
zero pressure at infinite radius. In this study Bjorkman did not include the influence of
the star's rotational speed.
Although it is known that the line-force parameters (see below) are not constant through in the wind (Abbott 1982), the standard m-CAK model still uses these parameters as constant. For the particular case of extreme low metalicities, Kudritzki (2002) introduced a new treatment of the line-force with depth dependent radiative force multipliers. As a test, he applied this new treatment for the most massive and most luminous O stars in the Galaxy and in the Magellanic Clouds (due to the lower metalicity) finding an acceptable agreement between theory and observations. Then, it was used to understand the influence of stellar winds on the evolution of very massive stars in the early universe and on the interstellar medium in the early stages of galaxy formation.
On the other hand, it is known from observations, that all early type stars have moderate to large rotational speeds (Hutchings et al. 1979; Abt et al. 2002) and for Oe and
Be stars, their rotational speed is a large fraction of their break-up speed (Slettebak 1976; Chauville et al. 2001).
The incorporation of rotation in the CAK and m-CAK models has been studied by Castor (1979),
Marlborough & Zamir (1984), FA and PPK, concluding that the effect of the centrifugal force
results in a downstream-shift of the position of the singular point, a slightly lower terminal
velocity and a slightly larger mass loss rate as a result of an increasing in the star's
rotational speed.
Maeder (2001) studied the influence of the stellar rotation in the WML relationship, finding just
a very small effect on it.
A revision of the influence of the stellar rotation in radiation driven winds has been done by
Curé (2004) finding that there exists a second singular point in these winds. He studied the
case when the stellar rotational speed is high and found numerical solutions, that pass through
this second singular point, and which are denser and slower than the standard m-CAK solution.
In view of these results, it is crucial to understand the solution topology of the standard
model, forall when one wants to incorporate other physical processes into the theory.
The purpose of this article is to study the topology of the rotating-CAK model. In
Sect. 2 we give a brief exposition of the radiation driven winds theory and
the non-linear differential equation for the momentum, including rotation, is shown.
In Sect. 3 after a coordinate transformation, we develop a general method
that allows to replace the non-linear momentum equation in a simple and
straightforward manner by a system of ordinary differential equations, where all
the derivatives are explicitely given. In Sect. 4 a general condition for
the eigenvalue of the problem is developed. This condition allows to classify the
topology of the singular point (Saddle or Focal) and constrains the location of it
in the integration domain. Section 5 is devoted to the application of the
criteria developed in Sect. 4 for the rotating-CAK model. In
Sect. 6 we show numerical results of this topological analysis, first for
a wind frozen in ionization (setting the 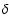 parameter of the line-force to
zero) and compare our results with Bjorkman`s (1995) for the non-rotating CAK model
and the rotating-CAK model from Marlborough & Zamir (1984). Furthermore,
Sect. 6 shows the results of the influence of changes in the wind`s ionization
structure (
parameter of the line-force to
zero) and compare our results with Bjorkman`s (1995) for the non-rotating CAK model
and the rotating-CAK model from Marlborough & Zamir (1984). Furthermore,
Sect. 6 shows the results of the influence of changes in the wind`s ionization
structure (
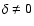 )
on the topology and discuss the rotating-CAK wind model.
Conclusion are in Sect. 7.
)
on the topology and discuss the rotating-CAK wind model.
Conclusion are in Sect. 7.
2 The non-linear differential equation
The standard stationary model for radiation driven stellar winds treats an one-component
isothermal radial flow, ignoring the influence of heat conduction, viscosity and magnetic
fields (see e.g., Kudritzki et al. 1989, "KPPA'').
For a star with mass M, radius 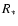 ,
effective temperature T and
luminosity L, the momentum equation with the inclusion of the centrifugal force due to star's
rotation, reads:
,
effective temperature T and
luminosity L, the momentum equation with the inclusion of the centrifugal force due to star's
rotation, reads:
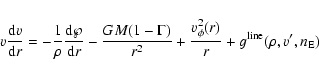 |
(1) |
where
v is the fluid velocity,
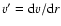 is the velocity gradient,
is the velocity gradient, 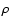 is the
mass density,
is the
mass density, 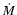 is the star's mass loss rate,
is the star's mass loss rate, 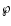 is the fluid pressure,
is the fluid pressure,
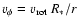 ,
where
,
where
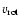 is the star's
rotational speed at the equator,
is the star's
rotational speed at the equator, 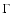 represents the ratio of the radiative
acceleration due to the continuous flux mean opacity,
represents the ratio of the radiative
acceleration due to the continuous flux mean opacity,
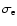 ,
relative to
the gravitational acceleration, i.e.,
,
relative to
the gravitational acceleration, i.e.,
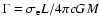 and
the last term
and
the last term
 represents the acceleration due to the lines.
represents the acceleration due to the lines.
The standard parameterization of the line-force (Abbott 1982) reads:
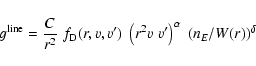 |
(2) |
W(r) is the dilution factor and
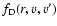 is the finite disk correction factor. The
line force parameters are:
is the finite disk correction factor. The
line force parameters are: 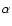 ,
,
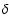 and k (the last has been incorporated in the
constant C), typical values of these parameter from LTE and non-LTE calculations are
summarized in Lamers & Cassinelli (1999, Chap. 8, "LC'').
We have not used the absolute value of the velocity gradient in the line-force
term, because we are interested in monotonic velocity laws.
and k (the last has been incorporated in the
constant C), typical values of these parameter from LTE and non-LTE calculations are
summarized in Lamers & Cassinelli (1999, Chap. 8, "LC'').
We have not used the absolute value of the velocity gradient in the line-force
term, because we are interested in monotonic velocity laws.
The constant C represents the
eigenvalue of the problem (see below) and is given by:
 |
(3) |
where
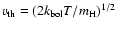 is the hydrogen thermal speed,
is the hydrogen thermal speed, 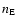 is the electron number density in units of
is the electron number density in units of
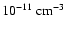 (Abbott 1982), while the meaning
of all other quantities is standard (see, e.g., LC).
(Abbott 1982), while the meaning
of all other quantities is standard (see, e.g., LC).
Together with the momentum Eq. (1), the continuity equation reads:
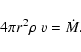 |
(4) |
Introducing the following change of variables:
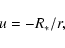 |
(5) |
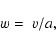 |
(6) |
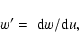 |
(7) |
where a is the isothermal sound speed, i.e.,
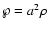 .
Replacing the
density
.
Replacing the
density 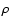 from Eq. (4), the m-CAK momentum Eq. (1) with the line force (2), we obtain:
from Eq. (4), the m-CAK momentum Eq. (1) with the line force (2), we obtain:
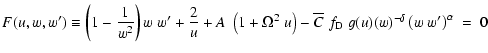 |
|
|
(8) |
here the constants A,
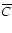 and
and 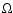 are:
are:
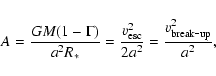 |
(9) |
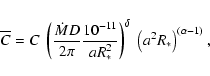 |
(10) |
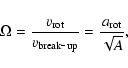 |
(11) |
where
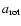 is defined by:
is defined by:
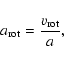 |
(12) |
here
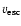 is the escape velocity and
is the escape velocity and
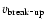 is the
"break-up'' velocity. The function g(u) is defined as:
is the
"break-up'' velocity. The function g(u) is defined as:
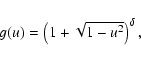 |
(13) |
and the constant D is:
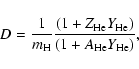 |
(14) |
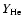 is the helium abundance relative to the hydrogen,
is the helium abundance relative to the hydrogen,
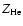 is the amount of free electrons provided by helium,
is the amount of free electrons provided by helium,
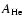 is the atomic
mass number of helium and
is the atomic
mass number of helium and 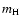 is the mass of the proton.
is the mass of the proton.
The standard solution, from this non-linear differential Eq. (8), starts at the stellar surface and after crossing the
singular point reaches infinity. At the stellar surface the differential
equation must satisfy a boundary condition, namely the monochromatic
optical depth integral (see Kudritzki 2002, Eq. (48)):
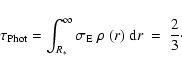 |
(15) |
A numerically equivalent boundary condition is to set the density at the stellar surface to a specific value,
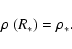 |
(16) |
When the singularity condition,
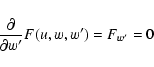 |
(17) |
is satisfied, its location (
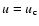 )
corresponds to a singular (or critical) point, and in order to get a physical solution, the regularity condition must be imposed, namely:
)
corresponds to a singular (or critical) point, and in order to get a physical solution, the regularity condition must be imposed, namely:
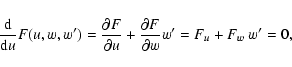 |
(18) |
hereafter, all partial derivatives are written in a shorthand form, i.e.
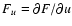 .
.
In order to satisfy simultaneously Eqs. (8), (17), (18) and (15)
or (16), the value of the constant
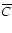 is not arbitrary, i.e.,
the constant
is not arbitrary, i.e.,
the constant
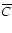 is the eigenvalue of this non-linear problem.
is the eigenvalue of this non-linear problem.
3 Coordinate transformation and system of equations
In this section we will apply another coordinate transformation and introduce a new independent variable, 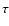 ,
without physical meaning. This will allow us to transform the non-linear differential equation for the momentum (8) into a system of coupled differential equations, which is numerically integrable.
,
without physical meaning. This will allow us to transform the non-linear differential equation for the momentum (8) into a system of coupled differential equations, which is numerically integrable.
Defining
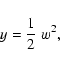 |
(19) |
and
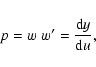 |
(20) |
the momentum
Eq. (8) can be written in a general form as:
Differentiating this function and using
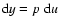 ,
we obtain:
,
we obtain:
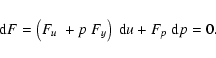 |
(22) |
We introduce now a new independent variable, 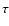 ,
defined implicitely by:
,
defined implicitely by:
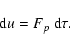 |
(23) |
Because u and 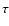 are independent variables, they have to be related between them.
While
are independent variables, they have to be related between them.
While
 ,
we can write
,
we can write 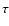 as function of u as:
as function of u as:
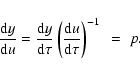 |
(24) |
We can transform from Eq. (22) to the following system of ordinary differential equations:
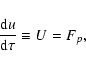 |
(25) |
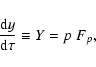 |
(26) |
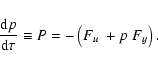 |
(27) |
A solution of this system of differential equations is also a solution of the original momentum equation, since if any initial condition
(u0,y0,p0) satisfies
F(u0,y0,p0) =0, then a solution of Eqs. (25)-(27) verifies that
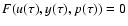 .
.
An advantage of this equation system (25)-(27) over the CAK momentum differential Eq. (8) is that all the derivatives are explicitely given, therefore there is no need to use root-finding algorithms to find the value of the velocity-gradient. Also, standard numerical methods (e.g., Runge-Kutta) can be used to integrate this system.
4 Linearization and eigenvalue criteria
All critical points of the system (25)-(27) satisfy simultaneously F=0, U=0 and P=0. Thus, in order to study the behavior of the solution in the neighborhood of a singular point we linearise this system of differential equations, using the Groebman-Hartman theorem
("GH'', see appendix; For more details see Amann 1990), we obtain:
| |
|
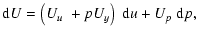 |
(28) |
| |
|
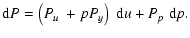 |
(29) |
We have not included 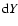 because U and Y are dependent (Y=pU, Eq. (26)).
The GH theorem indicates that the eigenvalues (and the eigenvectors) of the partial derivative matrix B, defined by:
because U and Y are dependent (Y=pU, Eq. (26)).
The GH theorem indicates that the eigenvalues (and the eigenvectors) of the partial derivative matrix B, defined by:
![\begin{displaymath}B=\left(
\begin{array}[c]{cc}
U_{u}+p~U_{y} & U_{p}\\
P_{u}+p~P_{y} & P_{p}%
\end{array}\right) ,
\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img81.gif) |
(30) |
provide the information concerning the topology structure of the critical (singular) points.
On the other hand, if we consider the eigenvalue 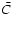 as a free paramenter, the critical points are the
solution of the following system of equations:
as a free paramenter, the critical points are the
solution of the following system of equations:
In this case the number of incognits is greater than the number of equations, then we can only solve for the incognits in terms of one of them (implicit function theorem).
If
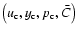 satisfies the previous system and furthermore,
satisfies the previous system and furthermore,
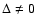 at the singular point, we can solve for
at the singular point, we can solve for 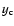 ,
,
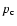 and
and
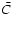 and its derivatives as a function of
and its derivatives as a function of 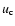 .
We obtain for the gradient of
.
We obtain for the gradient of 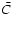 :
:
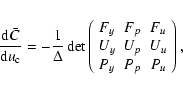 |
(34) |
where the determinant 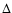 is defined by:
is defined by:
![\begin{displaymath}\Delta=\det\left(
\begin{array}[c]{ccc}%
F_{y} & F_{p} & F_{\...
...U_{\bar{C}}\\
P_{y} & P_{p} & P_{\bar{C}}
\end{array}\right),
\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img93.gif) |
(35) |
Considering that at the critical point: Fp=0 and
Fu=-pFy,
Eq. (34) transforms to:
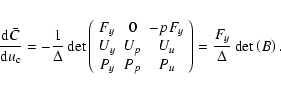 |
(36) |
The GH theorem establishes that the singular point topology is determined by the sign of the
eigenvalues of the matrix B. A critical point is of X-type (Saddle) when the eigenvalues
are both real and have opposite sign, or equivalently,
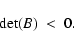 |
(37) |
Applying this to the rotating-CAK model (see next section for details) it is verified that,
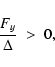 |
(38) |
then a X-type singular point corresponds to the condition:
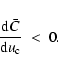 |
(39) |
Therefore any X-type physically relevant singular point, is related to the behavior of the
eigenvalue 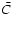 ,
specifically when condition (39) holds.
,
specifically when condition (39) holds.
5 The topology of the rotating-CAK model
The analysis we have shown in the last section (up to Eq. (37)) is valid for the general radiation driven stellar winds theory, i.e., including the finite-disk correction factor.
In the remainder of this paper we will study the original CAK model, i.e.
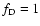 .
The topological study of the m-CAK model will be the scope of a future article.
.
The topological study of the m-CAK model will be the scope of a future article.
The non-linear momentum Eq. (8) for the rotational-CAK model (including 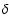 ),
in (u, y, p) coordinates reads:
),
in (u, y, p) coordinates reads:
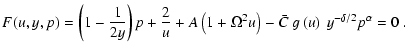 |
|
|
(40) |
From this equation, after a straightforward calculation, the corresponding system of differential equations U and P, (Eqs. (25) and (27), respectively) are:
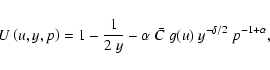 |
(41) |
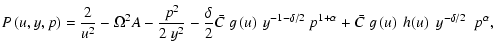 |
|
|
(42) |
where
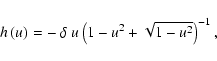 |
(43) |
Fy and 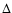 are:
are:
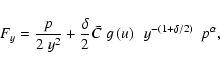 |
(44) |
It is easy to verify that both,
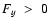 and
and
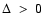 .
.
Once the location of the critical point, 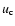 ,
is known, we can solve
,
is known, we can solve 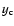 ,
,
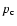 and
and 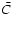 from Eqs. (40)-(42), obtaining:
from Eqs. (40)-(42), obtaining:
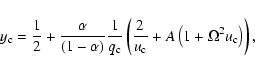 |
(46) |
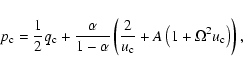 |
(47) |
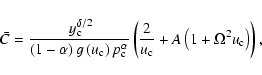 |
(48) |
where 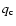 is the positive solution of the quadratic equation
is the positive solution of the quadratic equation
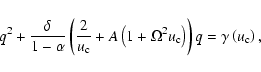 |
(49) |
with
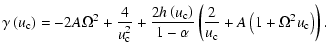 |
|
|
(50) |
Equations (46)-(48) are generalizations
of the Eqs. (49)-(51) from Marlborough & Zamir (1984),
including now the effect of the line-force term
 .
.
Since the eigenvalue 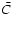 must be positive, we have:
must be positive, we have:
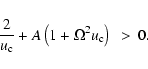 |
(51) |
This last inequality imposes a restriction in the position (furthest from the stellar surface in the radial coordinate r) of the singular point, namely:
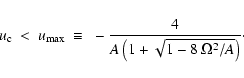 |
(52) |
6 Topology of the rotating CAK wind
In this section we show the results of our topological analysis. Following Bjorkman (1995), we choose a typical B2 V star with stellar parameters summarized in Table 1. We have adopted the line-force multiplier parameters k and 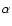 from Abbott (1982) and the
from Abbott (1982) and the 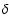 parameter is from LC, these values are summarized in Table 2.
parameter is from LC, these values are summarized in Table 2.
Table 1:
B2 V stellar parameters.
Table 2:
Line-force parameters.
The factor
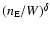 in the line-force takes into account the changes in the
ionization of the wind. As a first step to understand the topology of the rotating-CAK model
we set
in the line-force takes into account the changes in the
ionization of the wind. As a first step to understand the topology of the rotating-CAK model
we set 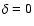 .
.
This case is simpler because we can obtain analytically from
Eqs. (46)-(48)
the variable y as function of u and p, i.e.:
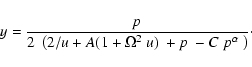 |
(53) |
Bjorkman (1995) obtained the same result (see his Eq. (13)) for the
non-rotational case, 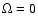 .
Moreover,
.
Moreover, 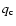 can be expressed by:
can be expressed by:
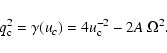 |
(54) |
As we mentioned in previous sections, qc must be positive. This gives an
additional
restriction for the location of the singular point (nearest to the stellar
surface in the radial coordinate r). The value of
 is defined when
is defined when
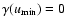 and is given by:
and is given by:
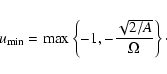 |
(55) |
Therefore, 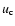 is restricted to the interval
is restricted to the interval
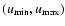 .
A similar result which
restricts the location of the critical point to an interval has been found by
Marlborough & Zamir (1984) see their Eq. (65)).
.
A similar result which
restricts the location of the critical point to an interval has been found by
Marlborough & Zamir (1984) see their Eq. (65)).
Figure 1a shows the behavior of 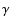 (Eq. (54)) versus
(Eq. (54)) versus
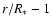 for different values of the rotational parameter
for different values of the rotational parameter 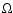 .
For the non-rotational case
.
For the non-rotational case
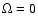 ,
the function
,
the function 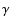 is positive for almost the whole integration domain, therefore the singular point can be placed anywhere. Thus, is the lower boundary condition which fixes the position of the singular point. For the rotational case, the second term in the RHS of Eq. (54) is the dominant term for almost any value of
is positive for almost the whole integration domain, therefore the singular point can be placed anywhere. Thus, is the lower boundary condition which fixes the position of the singular point. For the rotational case, the second term in the RHS of Eq. (54) is the dominant term for almost any value of 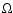 .
Therefore the larger is
.
Therefore the larger is 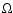 the larger is the value of
the larger is the value of
 (
(
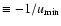 )
as the different curves in Fig. 1a show.
)
as the different curves in Fig. 1a show.
On the other hand, the value of the term
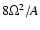 in Eq. (52) is almost negligible
and consequently the value of
in Eq. (52) is almost negligible
and consequently the value of
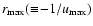 is almost constant at
is almost constant at
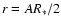 .
Table 3 shows the interval
.
Table 3 shows the interval
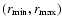 for different values of the parameter
for different values of the parameter 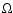 .
It is clear from this table that from a very low value of
.
It is clear from this table that from a very low value of
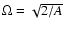 (=0.038 for our test star) the location of
(=0.038 for our test star) the location of
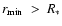 and the critical point,
and the critical point,
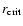 ,
is strongly shifted downstream in the wind. Once
,
is strongly shifted downstream in the wind. Once
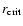 (or
(or 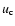 )
is fixed, the value of
)
is fixed, the value of
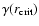 is inserted in Eq. (54) and
is inserted in Eq. (54) and 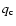 and
and 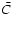 are obtained. Figure 1b shows
are obtained. Figure 1b shows 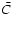 from Eq. (48) against
from Eq. (48) against
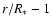 for the same values of
for the same values of 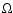 of Fig. 1a (same type of lines too). The value of the derivative,
of Fig. 1a (same type of lines too). The value of the derivative,
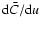 is always negative indicating that the critical point is an X-type.
is always negative indicating that the critical point is an X-type.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{0325fig1.eps}
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg136.gif) |
Figure 1:
a) The function 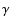 versus
versus
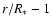 (Eq. (54)) for
different values of the rotational parameter
(Eq. (54)) for
different values of the rotational parameter 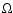 . .
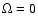 ,
continuous-line; ,
continuous-line;
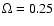 ,
dashed-line; ,
dashed-line;
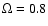 ,
dotted-line. The horizontal line is for ,
dotted-line. The horizontal line is for 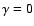 .
b) The eigenvalue from Eq. (48) as a function of .
b) The eigenvalue from Eq. (48) as a function of
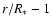 for the same values of
for the same values of 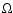 as a).
Note that
as a).
Note that
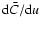 is always negative in the interval
is always negative in the interval
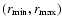 . . |
| Open with DEXTER |
Table 3:
Analytical approximation and numerical results for the rotational-CAK model with 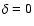 .
Note: the mass loss rate is given in units of
.
Note: the mass loss rate is given in units of
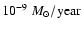 and the terminal velocity is in km s-1.
and the terminal velocity is in km s-1.
The matrix of linearization B (Eq. (30)) is given by:
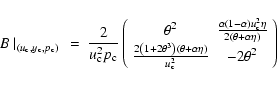 |
(56) |
where 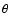 and
and 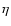 are given by:
are given by:
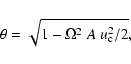 |
(57) |
and
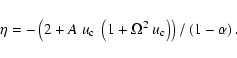 |
(58) |
The eigenvalues of the B-matrix are:
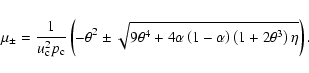 |
(59) |
It is easy to check that the product of the eigenvalues
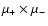 is negative, i.e., the topology of the singular point
is saddle or X-type as the GH theorem establishes. We can write the associated eigenvectors as
is negative, i.e., the topology of the singular point
is saddle or X-type as the GH theorem establishes. We can write the associated eigenvectors as
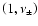 ,
where
,
where
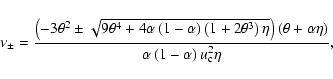 |
(60) |
where 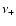 (
(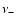 )
corresponds to the unstable (stable) manifold.
The maximum value of
)
corresponds to the unstable (stable) manifold.
The maximum value of 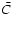 ,
that accounts for the minimum mass loss rate,
occurs when
,
that accounts for the minimum mass loss rate,
occurs when
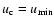 ,
Eq. (48) becomes:
,
Eq. (48) becomes:
![\begin{displaymath}\begin{array}[l]{lll}
\bar{C}_{\max} =&\frac{A~(1-\Omega^{2})...
...ight) ^{1-\alpha} &, \;if\; \Omega ~> ~ \sqrt{2/A}.
\end{array}\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img151.gif) |
(61) |
In order to obtain a numerical solution for the wind, we need an approximation for the location of
the critical point. We use the value of
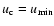 as a first guess of the critical point
and use this value of
as a first guess of the critical point
and use this value of 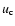 to calculate
to calculate
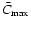 as our first guest for the eigenvalue
as our first guest for the eigenvalue 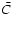 .
Table 3 shows
the values of
.
Table 3 shows
the values of
 ,
,
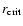 and
and
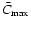 ,
,
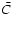 confirming that this is a very good approximation.
Now using standard numerical algorithms we integrate our system of equations
(Eqs. (25)-(27)) from the singular point up and downstream to obtain the numerical solution.
confirming that this is a very good approximation.
Now using standard numerical algorithms we integrate our system of equations
(Eqs. (25)-(27)) from the singular point up and downstream to obtain the numerical solution.
As Bjorkman (1995) pointed out, it is insightfull to study the solution topology in
a p versus
 diagram. Figure 2 shows this phase diagram.
diagram. Figure 2 shows this phase diagram.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0325fig2.eps}
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg154.gif) |
Figure 2:
The topology of the freeze in ionization rotating-CAK model (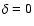 ), p versus ), p versus
 for
for
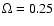 .
The unique curve that starts at the stellar surface and reaches infinity is the CAK original solution (continuous-line). .
The unique curve that starts at the stellar surface and reaches infinity is the CAK original solution (continuous-line). |
| Open with DEXTER |
If we start to integrate at the singular point, we cannot leave this point because all the equations,
U=0, Y=0 and P=0 are simultaneously satisfied at this point.
Therefore we have to move slightly up and downstream along the direction of the unstable manifold. After this, we can integrate obtaining the different solutions showed in
Fig. 2.
From this figure, it is clear that the only solution that reaches the stellar surface
(
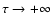 ,
in the direction of
,
in the direction of
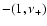 )
and also reaches infinite (
)
and also reaches infinite (
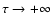 ,
in the direction of
,
in the direction of
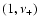 )
is the original CAK solution (continuous-line). The results from Table 3 for the non-rotational case are the same one obtained by Bjorkman (1995).
)
is the original CAK solution (continuous-line). The results from Table 3 for the non-rotational case are the same one obtained by Bjorkman (1995).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0325fig3.eps}\par
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg158.gif) |
Figure 3:
The velocity profile v(r) (in km s-1) as function of
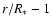 for the non rotating case (continuous-line) and for the
rotational cases:
for the non rotating case (continuous-line) and for the
rotational cases:
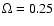 dashed-line;
dashed-line;
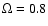 dotted-line. The location of the singular points is indicated by a larger-dot.
dotted-line. The location of the singular points is indicated by a larger-dot. |
| Open with DEXTER |
Figure 3 shows the velocity profile, v (in km s-1) versus
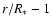 for our
B2 V test star. We have chosen this value of
for our
B2 V test star. We have chosen this value of
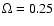 from the study of Abt
et al. (2002),
that concluded that B-stars rotate at a
from the study of Abt
et al. (2002),
that concluded that B-stars rotate at a 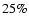 of their break-up speed. The values
of their break-up speed. The values
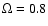 accounts for a fast rotator, e.g., a typical Be-Star (Chauville et al. 2001). We see from this figure that neglects the rotational speed always overpredicts the value of the terminal velocity.
accounts for a fast rotator, e.g., a typical Be-Star (Chauville et al. 2001). We see from this figure that neglects the rotational speed always overpredicts the value of the terminal velocity.
We conclude that the rotational speed shifts the location of the critical point downstream and reduces the terminal velocity, but has almost no influence on the value of the eigenvalue (mass loss rate).
Furthermore, we can see from our approximate and numerical results summarized in
Table 3 that the CAK wind do not have the
maximum mass-loss rate as Feldmeier et al. (2002) and
Owocki & ud-Doula (2004) concluded for a non-rotating CAK model with zero sound speed. Contrary to expectation, the rotating-CAK wind critical solution corresponds to an almost minimum mass-loss rate (maximum eigenvalue).
Abbott (1982) studied the indirect influence of the density in the line-force through the
dependence of the ionization balance in the electron density. He found that this dependency
modifies the force-multiplier and therefore the line-force by a factor
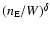 ,
where
,
where 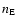 is the electron density (in units of
is the electron density (in units of
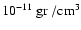 )
and W is the
dilution factor.
)
and W is the
dilution factor.
Although this is a weak influence, because 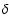 ranges between 0.0 and 0.2, it is
important to study how its inclusion in the momentum equation modifies the topology of the
rotating CAK model.
ranges between 0.0 and 0.2, it is
important to study how its inclusion in the momentum equation modifies the topology of the
rotating CAK model.
As we pointed out in Sect. 5, the existence of
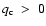 implies
implies
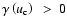 .
.
The behavior of 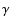 (Eq. (50)) versus
(Eq. (50)) versus
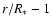 is shown in
Fig. 4a for the same values of
is shown in
Fig. 4a for the same values of 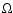 of Fig. 1. We can
interpret from this figure, that
of Fig. 1. We can
interpret from this figure, that 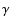 in
in
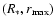 is a decreasing function in the
neighborhood of
is a decreasing function in the
neighborhood of
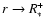 and an increasing function in the neighborhood
of
and an increasing function in the neighborhood
of
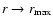 .
Furthermore, the function
.
Furthermore, the function 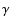 posses only one minimum in the
integration domain located at
posses only one minimum in the
integration domain located at
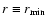 .
The value of
.
The value of
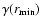 decreases as
decreases as 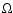 increases. For small values of
increases. For small values of 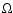 ,
,
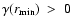 and the location of the singular
point
and the location of the singular
point
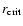 can be anywhere in the integration domain
can be anywhere in the integration domain
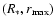 .
For larger values
of
.
For larger values
of 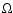 ,
,
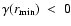 and
and
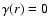 has two roots, at
has two roots, at
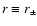 where
r- < r+ (or
u- < u+). Thus,
where
r- < r+ (or
u- < u+). Thus,
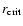 can be located now in
two different intervals, i.e.,
can be located now in
two different intervals, i.e.,
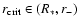 or
or
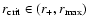 .
For the particular case where
.
For the particular case where
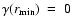 ,
the value of the rotational speed parameter is
,
the value of the rotational speed parameter is
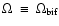 ,
where the subscript "bif'' accounts for the bifurcation in the wind solution topology.
,
where the subscript "bif'' accounts for the bifurcation in the wind solution topology.
Figure 4b shows 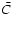 (Eq. (48)) against
(Eq. (48)) against
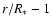 for different
values of
for different
values of 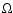 .
When
.
When 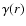 is positive,
is positive, 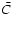 exhibits now a different behavior
compared with the
exhibits now a different behavior
compared with the 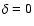 case. As long as
case. As long as
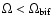 ,
,
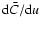 is positive
in the interval
is positive
in the interval
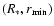 ,
i.e., any singular point in this interval is an attractor. Furthermore,
,
i.e., any singular point in this interval is an attractor. Furthermore,
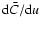 reaches its maximum, when
reaches its maximum, when 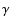 is minimum, i.e., in the neighborhood of
is minimum, i.e., in the neighborhood of
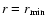 ,
from this point up to
,
from this point up to
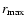 ,
,
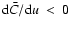 and any singular point in
and any singular point in
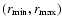 is X-type. When
is X-type. When
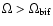 ,
the minimum
of
,
the minimum
of 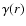 is
negative and the intervals are reduced to:
is
negative and the intervals are reduced to:
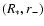 for the attractor type singular point
and
for the attractor type singular point
and
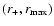 for the X-type singular point.
for the X-type singular point.
The behavior of 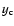 ,
,
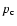 and
and 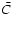 (Eqs. (46)-(48)) in the neighborhood of
(Eqs. (46)-(48)) in the neighborhood of
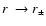 ,
in the inverse radial coordinate u, is as follows:
,
in the inverse radial coordinate u, is as follows:
This divergent behavior of 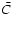 in the neighborhood of
in the neighborhood of 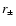 ,
is shown in the curves for
,
is shown in the curves for
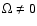 in Fig. 4. The almost constant value of
in Fig. 4. The almost constant value of 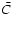 explains why a slightly change in the eigenvalue cause an enormous change in the location in the
singular point.
explains why a slightly change in the eigenvalue cause an enormous change in the location in the
singular point.
Tables 4 and 5 summarise the numerical calculation for our test star with
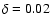 and
and
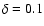 respectively. The data of the
respectively. The data of the 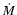 column (see also
the
column (see also
the 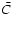 column) show that the effect of the rotation on
column) show that the effect of the rotation on 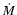 (
(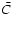 )
is almost negligible.
Figure 5 shows the velocity profile for three different values of
)
is almost negligible.
Figure 5 shows the velocity profile for three different values of 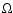 (
0.0;0.25;0.8), panel a) for
(
0.0;0.25;0.8), panel a) for
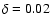 and panel b) for
and panel b) for
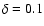 .
A large dot shows the respective positions of the critical points. The effect of shifting the position of the critical point is stronger for low rotational speeds and decreases when
.
A large dot shows the respective positions of the critical points. The effect of shifting the position of the critical point is stronger for low rotational speeds and decreases when 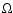 increases as a comparison between Figs. 3 and 5 clearly shows.
The terminal velocity, is a decreasing function of the rotational speed and has almost the same behavior as in the
increases as a comparison between Figs. 3 and 5 clearly shows.
The terminal velocity, is a decreasing function of the rotational speed and has almost the same behavior as in the 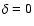 case. But for high rotational speeds, the influence of
case. But for high rotational speeds, the influence of 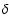 in
in
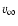 is
negligible/small as a comparison between Tables 3 and 4/5 shows.
is
negligible/small as a comparison between Tables 3 and 4/5 shows.
We conclude from that the factor
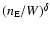 strongly shifts outwards the location of the critical
point and produces a bifurcation in the solution topology.
strongly shifts outwards the location of the critical
point and produces a bifurcation in the solution topology.
Table 4:
Numerical results for the rotation-CAK model with
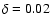 .
Note: the mass loss rate is given in units of
.
Note: the mass loss rate is given in units of
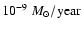 and
the terminal velocity is in km s-1.
and
the terminal velocity is in km s-1.
Table 5:
Same as Table 4 but for
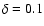 .
.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0325fig5.eps}
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg194.gif) |
Figure 5:
The velocity profile v(r) (in km s-1) as function of
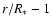 for the non rotating case (continuous-line) and for
the rotational cases:
for the non rotating case (continuous-line) and for
the rotational cases:
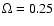 dashed-line;
dashed-line;
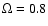 dotted-line.
dotted-line. |
| Open with DEXTER |
6.2.1 Bifurcation rotational speed
In order to have an analytical approximation for the value of
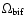 ,
we can approximate for the function h(u), Eq. (43):
,
we can approximate for the function h(u), Eq. (43):
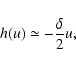 |
(65) |
then the minimum of 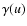 is achieved at:
is achieved at:
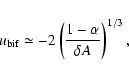 |
(66) |
and the minimum value of
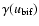 is
is
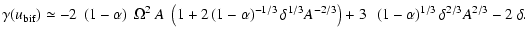 |
|
|
(67) |
From
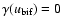 ,
we can obtain the bifurcation value of
,
we can obtain the bifurcation value of
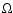 given by
given by
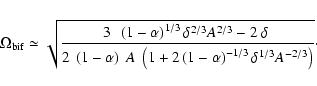 |
(68) |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0325fig6.eps}
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg203.gif) |
Figure 6:
The curves
 and
and 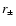 are shown with continuous lines as function
of
are shown with continuous lines as function
of 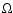 .
These curves represent the boundaries for the type of the singular point topology.
The numerical results for the location of the singular point is also shown in dashed-line.
a) is for .
These curves represent the boundaries for the type of the singular point topology.
The numerical results for the location of the singular point is also shown in dashed-line.
a) is for
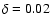 and b) for
and b) for
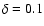 .
See text for details. .
See text for details. |
| Open with DEXTER |
Figure 6 show the curves
 and
and 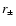 as function of
as function of 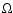 .
The intersection point for all the curves (in continuous-line) is at
.
The intersection point for all the curves (in continuous-line) is at
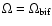 .
Critical
points can not be located between the curves r+ and r- (filled region). In addition, we show
curves for the location of the critical point from numerical calculations (dashed-lines), with the
lower boundary condition,
.
Critical
points can not be located between the curves r+ and r- (filled region). In addition, we show
curves for the location of the critical point from numerical calculations (dashed-lines), with the
lower boundary condition,
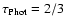 .
.
We can clearly see from this figure, that the position of the critical point is shifted outwards from
the stellar surface and the greater is 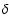 the further is the position of this critical point.
It can be inferred from this figure, that the location of the singular point remains almost constant as long as
the further is the position of this critical point.
It can be inferred from this figure, that the location of the singular point remains almost constant as long as
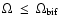 ,
but from values of
,
but from values of
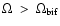 the position of
the position of
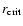 grows almost linear with
grows almost linear with 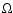 .
.
This behavior of the solution topology can be applied for the winds of Be-Stars. At polar latitudes, i.e., slow rotational speed, the wind behaves as the standard CAK wind, but as the latitude approaches to the equator, the rotational speed is larger than
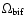 and the wind is slower and denser. This transition from polar to equatorial latitudes seems to have a similar behavior described by Curé (2004) for the more general rotating m-CAK wind. The study of the influence of this bifurcation in the winds of Be stars will be the scope of a forthcoming article.
and the wind is slower and denser. This transition from polar to equatorial latitudes seems to have a similar behavior described by Curé (2004) for the more general rotating m-CAK wind. The study of the influence of this bifurcation in the winds of Be stars will be the scope of a forthcoming article.
6.2.2 Phase diagram with
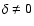
Figure 7 shows the phase diagram p versus
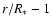 for
for
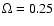 and
and
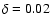 for our test star. The solution topology seems to be similar to the
for our test star. The solution topology seems to be similar to the 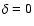 case. Here the shallow and steep curves are in continuous line and dashed line respectively. The shallow solution is the CAK solution while the steep solution correspond to accretion flows or for radiation driven disk winds (Feldmeier et al. 2002). As we mentioned in previous section, we move slightly from the singular point in the unstable manifold in the directions
case. Here the shallow and steep curves are in continuous line and dashed line respectively. The shallow solution is the CAK solution while the steep solution correspond to accretion flows or for radiation driven disk winds (Feldmeier et al. 2002). As we mentioned in previous section, we move slightly from the singular point in the unstable manifold in the directions
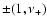 and then integrate outwards and inwards, obtaining the solution topology of Fig. 7.
Figure 8 shows both shallow and steep solutions, but here we have started from the singular point but with different values of the eigenvalue
and then integrate outwards and inwards, obtaining the solution topology of Fig. 7.
Figure 8 shows both shallow and steep solutions, but here we have started from the singular point but with different values of the eigenvalue 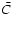 .
The almost horizontal dotted curves correspond to
.
The almost horizontal dotted curves correspond to 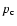 from Eq. (47) and is not a continuous curve because of the bifurcation in the solution topology. The left-most shallow curve that start at a X-type singular point do not reach stellar surface, but is trapped by the attractor singular point. This result implies that there is a shorter window of locations of singular points, that fixes the eigenvalues
from Eq. (47) and is not a continuous curve because of the bifurcation in the solution topology. The left-most shallow curve that start at a X-type singular point do not reach stellar surface, but is trapped by the attractor singular point. This result implies that there is a shorter window of locations of singular points, that fixes the eigenvalues 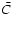 and can reach infinity passing through the X-type critical point.
This feature is not present when
and can reach infinity passing through the X-type critical point.
This feature is not present when 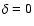 .
.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0325fig7.eps}
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg209.gif) |
Figure 7:
The topology of the rotating-CAK model, p versus
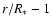 for
for
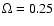 and
and
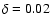 .
The unique curve that starting at the stellar surface
and reaches infinity is the CAK original solution (continuous-line). .
The unique curve that starting at the stellar surface
and reaches infinity is the CAK original solution (continuous-line). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0325fig8.eps}
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg210.gif) |
Figure 8:
The topology of the rotating-CAK model, p versus
 for
for
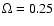 .
The different curves correspond to different values of the eigenvalues.
The left-most curve starts at the "normal'' critical point and is trapped by the attractor. See text for details. .
The different curves correspond to different values of the eigenvalues.
The left-most curve starts at the "normal'' critical point and is trapped by the attractor. See text for details. |
| Open with DEXTER |
7 Conclusions
In this article we have examined the topology of the rotating-CAK wind non-linear differential equation.
After the introduction of an additional physically meaningless independent variable (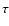 )
we transform the momentum equation to a set of equations where all the derivatives are explicitly given. This formalism permitted us to linearise the equations in the neighborhood of the critical points. This linearization let us to define a condition for the derivative of the eigenvalue that defines the topology of the critical point, i.e, X-type or attractor.
)
we transform the momentum equation to a set of equations where all the derivatives are explicitly given. This formalism permitted us to linearise the equations in the neighborhood of the critical points. This linearization let us to define a condition for the derivative of the eigenvalue that defines the topology of the critical point, i.e, X-type or attractor.
We have applied our results to the case of a point star (CAK) for a frozen in ionization rotating wind, recovering and generalizing the results of previous studies (Bjorkman 1995; Marlborough & Zamir 1984). The most significant result (with
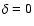 )
is that the wind does not assume the maximum mass-loss rate but almost the minimum.
)
is that the wind does not assume the maximum mass-loss rate but almost the minimum.
For the more general case, where changes in the wind ionization are taken into account, our analysis shows the existence of a bifurcation in the solution topology, where two critical points exist.
The first critical point (closer to the star's surface) is an attractor while the second is the standard CAK critical point. Besides the known fact that the rotational speed shifts the location of the critical point outwards in the wind, the inclusion of the term
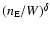 produces the same effect, reinforcing this displacement.
produces the same effect, reinforcing this displacement.
The bifurcation topology seems to explain the results from Curé (2004) that there exist two regions in the wind of a fast rotating hot star, one where the wind is the one from the standard solution (fast wind) and the other with a new solution that is slower and denser. This result shows us the necessity to perform a topological analysis of the rotating m-CAK wind. This study is currently underway.
Acknowledgements
This work has been possible thanks to the research cooperation agreement UBA/UV and DIUV project 15/2003. M.C. wants to thank the hospitality of the colleges from the mathematics department from the UBA during his stay in Buenos Aires.
Considering the system of differential equations given by:
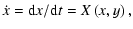 |
|
|
|
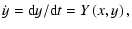 |
|
|
(A.1) |
where x and y are the dependent variables and t is the independent variable.
The point
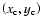 is singular (critical) if and only if
verifies that:
is singular (critical) if and only if
verifies that:
In order to understand the topological behavior of the solutions close to
a singular point, we expand this system using Taylor series at
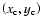 ,
obtaining:
,
obtaining:
Neglecting superior order terms and using that
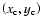 is a singular point, we have, in matrix form:
is a singular point, we have, in matrix form:
![\begin{displaymath}\left(
\begin{array}[c]{c}%
\dot{x}\\
\dot{y}%
\end{array}\r...
...n{array}[c]{c}%
x-x_{\rm c}\\
y-y_{\rm c}%
\end{array}\right)
\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img216.gif) |
(A.2) |
where B is the Jacobian matrix at
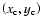 ,
i.e.,
,
i.e.,
![\begin{displaymath}B=\left. \left(
\begin{array}[c]{cc}%
X_{x} & X_{y}\\
Y_{x} ...
...ray}\right) \right\vert _{\left( x_{\rm c},y_{\rm c}\right) }.
\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img217.gif) |
(A.3) |
For a 3-dimensional system case:
with a constraint
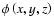 satisfying:
satisfying:
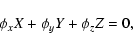 |
(A.5) |
the surface defined by:
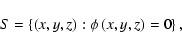 |
(A.6) |
is invariant for the differential equation system evolution.
From the Eq. (A.6), we can solve for z (using the implicit function theorem) obtaining
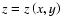 and reduce the system (A.4) to:
and reduce the system (A.4) to:
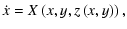 |
|
|
|
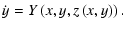 |
|
|
(A.7) |
If
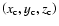 is a singular point of Eq. (A.7),
the Jacobian matrix B is
given by:
is a singular point of Eq. (A.7),
the Jacobian matrix B is
given by:
![\begin{displaymath}B=\left. \left(
\begin{array}[c]{cc}%
X_{x}+z_{x}X_{z} & X_{y...
...y}\right) \right\vert _{\left( x_{\rm c},y_{\rm c}\right) } .%
\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img228.gif) |
(A.8) |
Since
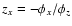 and
and
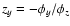 ,
we have
,
we have
![\begin{displaymath}B=\frac{1}{\phi_{z}}\left. \left(
\begin{array}[c]{cc}%
\phi_...
...y}\right) \right\vert _{\left( x_{\rm c},y_{\rm c}\right) } .%
\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img231.gif) |
(A.9) |
For 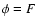 ,
X=U and Y=P, we obtain Eq. (30).
,
X=U and Y=P, we obtain Eq. (30).
- Abbott, D. C. 1982,
ApJ, 259, 282 [NASA ADS] [CrossRef] (In the text)
- Abbott, D. C.,
& Lucy, L. B. 1985, ApJ, 288, 679 [NASA ADS] [CrossRef] (In the text)
- Abt, H. A., Levato, H.,
& Grosso, M. 2002, ApJ, 573, 359 [NASA ADS] [CrossRef] (In the text)
- Amann, H. 1990, Ordinary
differential equations: an introduction to nonlinear analysis.
Gruyter studies in mathematics 13 (Berlin: Ed. Walter de
Gruyter)
- Bjorkman, J. E.
1995, ApJ, 453, 369 [NASA ADS] [CrossRef] (In the text)
- Castor, J. I.,
Abbott, D. C., & Klein, R. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] (In the text)
- Castor, J. I. 1979,
Mass Loss and Evolution of O-Type Stars, ed. P. S. Conti, & C.
W. de Loore (Dordrecht: Reidel), IAU Symp., 83, 175
(In the text)
- Chauville,
J., Zorec, J., Ballereau, D., et al. 2001, A&A, 378, 861 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Curé, M. 2004,
ApJ, 614, 929 [NASA ADS] [CrossRef] (In the text)
- Friend, D., &
Abbott, D. C. 1986, ApJ, 311, 701 [NASA ADS] [CrossRef] (In the text)
- Feldmeier,
A., Shlosman, I., & Hamann, W.-R. 2002, A&A, 566, 392 [NASA ADS] (In the text)
- Gayley, K. G.,
Owocki, S. P., & Cranmer, S. R. 1995, ApJ, 442, 296 [NASA ADS] [CrossRef] (In the text)
- Hutchings, J.
B., Nemec, J. M., & Cassidy, J. 1979, PASP, 91, 313 [NASA ADS] [CrossRef] (In the text)
- Kudritzki, R.
P., Pauldrach, A., Puls, J., & Abbott, D. C. 1989, A&A,
219, 205 [NASA ADS] (In the text)
- Kudritzki, R.
P., Puls, J., Lennon, D. J., et al. 1999, A&A, 350, 970 [NASA ADS] (In the text)
- Kudritzki, R.
P., & Puls, J. 2000, ARA&A, 38, 613 [NASA ADS] (In the text)
- Kudritzki, R.
P. 2002, ApJ, 577, 389 [NASA ADS] [CrossRef] (In the text)
- Lamers, H. J. G. L.
M., & Leitherer, C. 1993, ApJ, 412, 771 [NASA ADS] [CrossRef] (In the text)
- Lamers, H. J. G. L.
M., & Cassinelli, J. 1999, Introduction to stellar winds
(Cambridge: Cambridge University Press)
(In the text)
- Lucy, L. B., &
Solomon, P. M. 1970, ApJ, 159, 879 [NASA ADS] [CrossRef] (In the text)
- Maeder, A. 2001,
A&A, 373, 122 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Marlborough, J. M., & Zamir, M. 1984, ApJ, 276, 706 [NASA ADS] [CrossRef] (In the text)
- Owocki, S. P.,
& ud-Doula, A. 2004, ApJ, 600, 1004 [NASA ADS] [CrossRef] (In the text)
- Pauldrach,
A., Puls, J., & Kudritzki, R. P. 1986, A&A, 164, 86 [NASA ADS] (In the text)
- Puls, J. 1987, A&A,
184, 227 [NASA ADS] (In the text)
- Puls, J., Kudritzki,
R.-P., Herrero, A., et al. 1996, A&A, 305, 171 [NASA ADS] (In the text)
- Slettebak, A.
1976, in Be and Shell Stars, ed. Arne Slettebak (Dordrecht: D.
Reidel Pub. Co.), IAU Symp., 70, 123
(In the text)
- Vink, J. S., de Koter,
A., & Lamers, H. J. G. L. M. 2000, A&A, 362, 295 [NASA ADS] (In the text)
Copyright ESO 2004
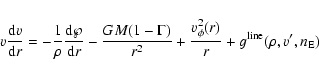
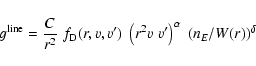

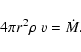
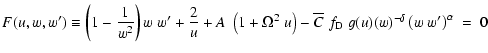
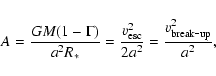
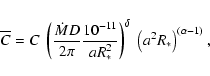
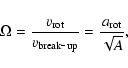
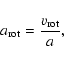
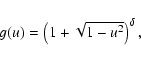
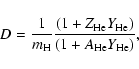
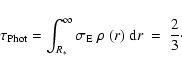
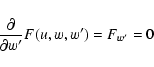
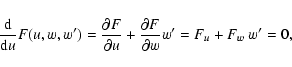
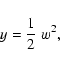
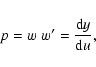
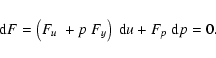
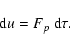
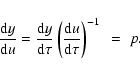
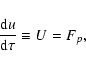
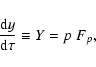
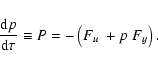
![\begin{displaymath}B=\left(
\begin{array}[c]{cc}
U_{u}+p~U_{y} & U_{p}\\
P_{u}+p~P_{y} & P_{p}%
\end{array}\right) ,
\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img81.gif)
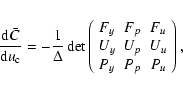
![\begin{displaymath}\Delta=\det\left(
\begin{array}[c]{ccc}%
F_{y} & F_{p} & F_{\...
...U_{\bar{C}}\\
P_{y} & P_{p} & P_{\bar{C}}
\end{array}\right),
\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img93.gif)
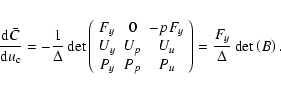
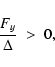
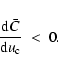
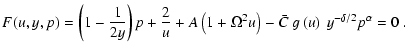
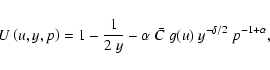
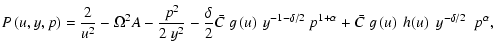
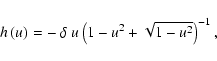
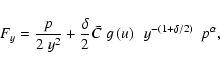
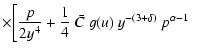
![$\displaystyle \times \left( (4\alpha+\delta)~y^{\delta/2}~ + 2~\alpha~\delta~\bar{C}~g(u)~y\;p^{\alpha } \right) \bigg].$](/articles/aa/full/2004/47/aa0325-04/img107.gif)
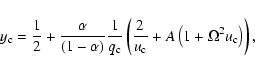
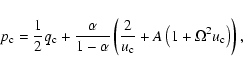
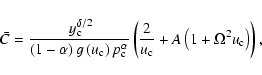
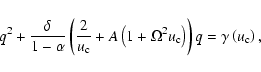
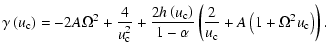
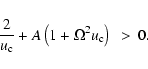
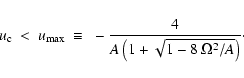
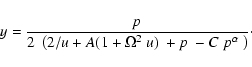
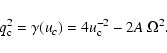
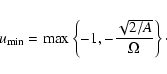
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{0325fig1.eps}
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg136.gif)
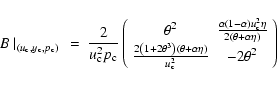
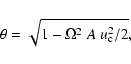
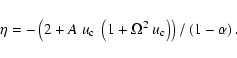
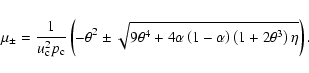
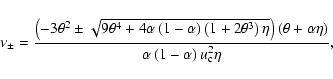
![\begin{displaymath}\begin{array}[l]{lll}
\bar{C}_{\max} =&\frac{A~(1-\Omega^{2})...
...ight) ^{1-\alpha} &, \;if\; \Omega ~> ~ \sqrt{2/A}.
\end{array}\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img151.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0325fig2.eps}
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg154.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0325fig3.eps}\par
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg158.gif)
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{0325fig4.eps}
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg163.gif)
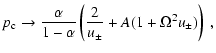
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0325fig5.eps}
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg194.gif)
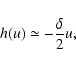
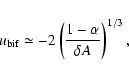
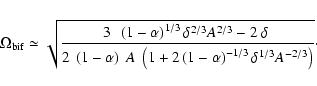
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0325fig6.eps}
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg203.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{0325fig7.eps}
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg209.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0325fig8.eps}
\end{figure}](/articles/aa/full/2004/47/aa0325-04/Timg210.gif)
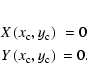
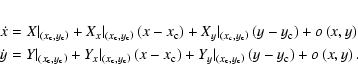
![\begin{displaymath}\left(
\begin{array}[c]{c}%
\dot{x}\\
\dot{y}%
\end{array}\r...
...n{array}[c]{c}%
x-x_{\rm c}\\
y-y_{\rm c}%
\end{array}\right)
\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img216.gif)
![\begin{displaymath}B=\left. \left(
\begin{array}[c]{cc}%
X_{x} & X_{y}\\
Y_{x} ...
...ray}\right) \right\vert _{\left( x_{\rm c},y_{\rm c}\right) }.
\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img217.gif)
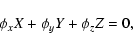
![\begin{displaymath}B=\left. \left(
\begin{array}[c]{cc}%
X_{x}+z_{x}X_{z} & X_{y...
...y}\right) \right\vert _{\left( x_{\rm c},y_{\rm c}\right) } .%
\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img228.gif)
![\begin{displaymath}B=\frac{1}{\phi_{z}}\left. \left(
\begin{array}[c]{cc}%
\phi_...
...y}\right) \right\vert _{\left( x_{\rm c},y_{\rm c}\right) } .%
\end{displaymath}](/articles/aa/full/2004/47/aa0325-04/img231.gif)