A. Pasquali1,![]() - G. De Marchi2,
- G. De Marchi2,![]() - L. Pulone3 - M. S. Brigas1,4
- L. Pulone3 - M. S. Brigas1,4
1 - ESO/ST-ECF, Karl-Schwarzschild-Strasse 2, 85748 Garching
bei München, Germany
2 -
ESA, Space Telescope Operations Division, 3700 San Martin
Drive, Baltimore, MD 21218, USA
3 -
INAF, Osservatorio Astronomico di Roma, Via di Frascati 33,
00040 Monte Porzio Catone (RM), Italy
4 -
Osservatorio Astronomico di Cagliari,
Strada 54, Poggio dei Pini, 09012 Capoterra, Cagliari, Italy
Received 14 August 2003 / Accepted 21 July 2004
Abstract
Data obtained with the NICMOS instrument on board the Hubble
Space Telescope (HST) have been used to determine the H-band luminosity
function (LF) and mass function (MF) of three stellar fields in the
globular cluster M 15, located ![]()
![]() from the cluster
centre. The data confirm that the cluster MF has a characteristic mass
of
from the cluster
centre. The data confirm that the cluster MF has a characteristic mass
of ![]() 0.3
0.3 ![]() ,
as obtained by Paresce & De Marchi (2000)
for a stellar field at
,
as obtained by Paresce & De Marchi (2000)
for a stellar field at
![]() from the centre. By combining the
present data with those published by other authors for various radial
distances (near the centre, at
from the centre. By combining the
present data with those published by other authors for various radial
distances (near the centre, at
![]() and at
and at
![]() ),
we have studied the radial variation of the LF due to the effects of
mass segregation and derived the global mass function (GMF) using the
Michie-King approach. The model that simultaneously best fits the LF
at various locations, the surface brightness profile and the velocity
dispersion profile suggest that the GMF should resemble a segmented
power-law with the following indices:
),
we have studied the radial variation of the LF due to the effects of
mass segregation and derived the global mass function (GMF) using the
Michie-King approach. The model that simultaneously best fits the LF
at various locations, the surface brightness profile and the velocity
dispersion profile suggest that the GMF should resemble a segmented
power-law with the following indices:
![]() for stars more
massive than 0.8
for stars more
massive than 0.8 ![]() ,
,
![]() for
for
![]() and
and
![]() at smaller masses (Salpeter's IMF
would have x=1.35). The best fitting model also suggests that the
cluster mass is
at smaller masses (Salpeter's IMF
would have x=1.35). The best fitting model also suggests that the
cluster mass is ![]()
![]() and that the
mass-to-light ratio is on average
and that the
mass-to-light ratio is on average
![]() ,
with
,
with
![]() in the core. A large amount of mass (
in the core. A large amount of mass (![]()
![]() )
is found
in the cluster core in the form of stellar heavy remnants, which may be
sufficient to explain the mass segregation in M 15 without invoking the
presence of an intermediate-mass black hole.
)
is found
in the cluster core in the form of stellar heavy remnants, which may be
sufficient to explain the mass segregation in M 15 without invoking the
presence of an intermediate-mass black hole.
Key words: globular clusters: general - globular clusters: individual: M 15
Table 1: Log of the observations.
Further evidence of mass segregation in the central regions of M 15 comes from the detection of colour gradients whereby (U-B) and (B-V) colours get bluer towards the cluster centre (Bailyn et al. 1989; Cederbloom et al. 1992). They have been justified in terms of either a core concentration of blue stars due to binary-single star interactions or the central lack of low mass main-sequence stars. In either case, mass segregation is likely to be the driving mechanism. De Marchi & Paresce (1994) have resolved with HST/FOC a large number of bright blue stars in the core of M 15, the majority of which can be classified as blue stragglers. Nevertheless, the rest appear to belong to a new, as yet unidentified class of very blue stars. Amongst several possibilities (such as Early-Post AGB, subdwarfs and well-mixed single stars), De Marchi & Paresce (1994, 1996) have suggested that dynamical interactions and close encounters could have stripped off the envelope of red giant stars, enhancing their mass loss and heading their evolution towards the late stage of helium white dwarf and CO white dwarf.
Because of minimal interactions with the Galaxy, the outskirts of M 15
have been observed to constrain the cluster initial MF (IMF) of low
mass stars. For example, De Marchi & Paresce (1995) performed deep
HST/WFPC2 photometry of a field
![]() NW of the centre and derived
the Luminosity Function (LF) of main-sequence stars down to
NW of the centre and derived
the Luminosity Function (LF) of main-sequence stars down to
![]() ,
or two
magnitudes fainter than the LF peak. The mass distribution that Paresce
& De Marchi (2000) have subsequently inferred from this LF shows that
the characteristic mass of M 15 is
,
or two
magnitudes fainter than the LF peak. The mass distribution that Paresce
& De Marchi (2000) have subsequently inferred from this LF shows that
the characteristic mass of M 15 is ![]() 0.30
0.30 ![]() and that
the number of stars less massive than
and that
the number of stars less massive than
![]() quickly drops
off. This appears to be a common feature of all Galactic globular
clusters for which deep LFs are available, regardless as to their
metallicity, position in the Galaxy and dynamics (Piotto et al. 1997;
Paresce & De Marchi 2000). This MF is believed to be representative of
the IMF of globular clusters, however the true IMF can be reliably
established only by disentangling the cluster dynamical evolution from
the observed MF. This is best achieved when MFs are available at
several distances from the cluster centre. For M 15, MFs are found in
the literature near the core (De Marchi & Paresce 1996; Sosin & King
1997) and for the above mentioned field at
quickly drops
off. This appears to be a common feature of all Galactic globular
clusters for which deep LFs are available, regardless as to their
metallicity, position in the Galaxy and dynamics (Piotto et al. 1997;
Paresce & De Marchi 2000). This MF is believed to be representative of
the IMF of globular clusters, however the true IMF can be reliably
established only by disentangling the cluster dynamical evolution from
the observed MF. This is best achieved when MFs are available at
several distances from the cluster centre. For M 15, MFs are found in
the literature near the core (De Marchi & Paresce 1996; Sosin & King
1997) and for the above mentioned field at
![]() NW of the cluster
centre. Deep images taken by HST/NICMOS Camera 3 (NIC3) during the
1998 parallel campaign have allowed us to derive the MF in three, outer
fields at 7' NE of the centre. We have used this mass distribution
together with those published previously to constrain the Global Mass
Function (GMF) of M 15. If the interaction of M 15 with the
Galactic tidal field has been as weak as recent works indicate (Gnedin
& Ostriker 1997; Dauphole et al. 1996), then the GMF should reflect
the IMF.
NW of the cluster
centre. Deep images taken by HST/NICMOS Camera 3 (NIC3) during the
1998 parallel campaign have allowed us to derive the MF in three, outer
fields at 7' NE of the centre. We have used this mass distribution
together with those published previously to constrain the Global Mass
Function (GMF) of M 15. If the interaction of M 15 with the
Galactic tidal field has been as weak as recent works indicate (Gnedin
& Ostriker 1997; Dauphole et al. 1996), then the GMF should reflect
the IMF.
The NIC3 observations are presented in Sect. 2 and the data reduction is described in Sect. 3. The LF of the NIC3 fields in the H band and its corresponding MF are discussed in Sect. 4 and compared with other literature measurements in Sect. 5. We derive the GMF in Sect. 6 and our conclusions follow in Sect. 7.
M 15 has been observed with the NIC3 camera of HST/NICMOS on 1998
July 7th and 18th, during the parallel observations campaign. Three
overlapping fields have been imaged at about ![]() NE from the
centre of the cluster, at a distance of 7 times the half-light radius
(
NE from the
centre of the cluster, at a distance of 7 times the half-light radius
(![]() ;
Trager et al. 1995). Multiple exposures have been taken of
each field through both the F110W and F160W filters, centered at
;
Trager et al. 1995). Multiple exposures have been taken of
each field through both the F110W and F160W filters, centered at
![]() m and
m and ![]() m, respectively. The coordinates of the
fields and the names, filters, and total exposure times of the image
data-sets are given in Table 1. Hereafter we refer to the F110W and F160W bands as J and H, respectively.
m, respectively. The coordinates of the
fields and the names, filters, and total exposure times of the image
data-sets are given in Table 1. Hereafter we refer to the F110W and F160W bands as J and H, respectively.
The images were reduced using the NICMOS standard calibration pipeline: they were first processed with CALNICA for bias subtraction, dark-count correction and flat-fielding. Images belonging to the same field were then associated by means of the IRAF routine MAKEASSOCIATION and combined with CALNICB, to remove cosmic rays and to increase the signal-to-noise ratio.
Photometry was performed on each of the three combined images with
the DAOPHOT package. Stars were identified with DAOFIND, by
setting the detection threshold at ![]() above the local
background. We traced the radial profile of each identified object
and discarded those with full width at half maximum (FWHM) larger than
2.5 pixels, since the typical FWHM of a well defined point source in
our frames is 1.5 pixels. Moreover, we compared images of the same
association in order to identify bad pixels not flagged by the
calibration pipeline. In this way we selected a sample of 539 stars imaged in both J and H bands. Because of the highly variable
background, we decided to measure stellar count-rates in small fixed
apertures of 2 pixels in radius (equivalent to
above the local
background. We traced the radial profile of each identified object
and discarded those with full width at half maximum (FWHM) larger than
2.5 pixels, since the typical FWHM of a well defined point source in
our frames is 1.5 pixels. Moreover, we compared images of the same
association in order to identify bad pixels not flagged by the
calibration pipeline. In this way we selected a sample of 539 stars imaged in both J and H bands. Because of the highly variable
background, we decided to measure stellar count-rates in small fixed
apertures of 2 pixels in radius (equivalent to
![]() ), and the
corresponding background values in a fixed annulus with a radius of 5 pixels and a width of 2 pixels. After background subtraction and before
applying any aperture correction, we corrected the count-rates for
the NIC3 intra-pixel sensitivity, using the equations computed by
Storrs et al. (1999; see Table 2) in the case of out-of-focus campaign
data.
), and the
corresponding background values in a fixed annulus with a radius of 5 pixels and a width of 2 pixels. After background subtraction and before
applying any aperture correction, we corrected the count-rates for
the NIC3 intra-pixel sensitivity, using the equations computed by
Storrs et al. (1999; see Table 2) in the case of out-of-focus campaign
data.
The aperture correction was determined in three steps:
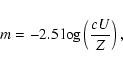 |
(1) |
Table 2: Estimated photometric errors.
We estimated the internal uncertainty of our photometry by comparing
the resulting magnitudes of those stars in common to two different
fields: Fields 1 and 2 overlap nearly over two quadrants sharing 83
stars, whilst Fields 1 and 3 have in common only 12 stars. As a
measure of the uncertainty, we used the difference between the
magnitudes measured in each field and the weighted mean of the two
values, with the weight given by the square root of the exposure time.
The resulting errors, for Field 2, are shown in Table 2 for three
magnitude ranges. We associate an uncertainty of 0.05 mag to stars
brighter than magnitude 22 and a photometric error >0.1 to fainter
objects. As regards Field 1, errors are usually twice as large, since
the exposure time is ![]() 3.5 times shorter in both bands. For
Field 3 we adopted the same uncertainty scale as for Field 2.
3.5 times shorter in both bands. For
Field 3 we adopted the same uncertainty scale as for Field 2.
We used the ADDSTAR routine in DAOPHOT to determine the completeness of
our photometry. We tested each frame separately in both the J and H band, by adding about ![]() of the total number of detected stars in
order not to increase the crowding in the images. We performed four
runs for several magnitude bins. The results are shown in Table 3 for
all the observed fields. Since NIC3 is less sensitive in the H band,
the completeness in H significantly affects our subsequent data
analysis. In the case of Field 1, for which only short exposures are
available, the completeness rapidly decreases to
of the total number of detected stars in
order not to increase the crowding in the images. We performed four
runs for several magnitude bins. The results are shown in Table 3 for
all the observed fields. Since NIC3 is less sensitive in the H band,
the completeness in H significantly affects our subsequent data
analysis. In the case of Field 1, for which only short exposures are
available, the completeness rapidly decreases to ![]()
![]() at
at
![]() .
Fields 2 and 3, on the other hand, reach a completeness of
.
Fields 2 and 3, on the other hand, reach a completeness of ![]()
![]() and
and ![]()
![]() ,
respectively, at
,
respectively, at
![]() .
.
Table 3: Completeness factors.
We have corrected the observed magnitudes of our sample for reddening by assuming E(B-V) = 0.1 from Durrell & Harris (1993). This implies AJ = 0.1 and AH = 0.06.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0192fig1.ps}
\end{figure}](/articles/aa/full/2004/47/aa0192-03/Timg33.gif) |
Figure 1: De-reddened CMD of each observed field and all of the fields combined. Stars common to two fields have been removed from each field but are included in the CMD of the whole sample, with averaged magnitudes and colours. |
| Open with DEXTER | |
The de-reddened colour-magnitude diagram (CMD) is plotted for each of
the three fields and for the whole sample in Fig. 1. For the stars
in common to more than one field, we have adopted the mean magnitudes
and colours computed as above. Similar levels of photometric
completeness are reached for all three fields at magnitudes brighter
than
![]() ,
so that their CMDs can be directly compared to
one another. In all the three cases the main sequence is well defined
down to
,
so that their CMDs can be directly compared to
one another. In all the three cases the main sequence is well defined
down to
![]() and spreads out for
-0.4 < (J-H)0 < 1.8 at
fainter magnitudes due to our photometric uncertainty. The few stars
brighter than H0 = 18 are probably foreground objects. Indeed,
Durrell & Harris (1993) determined the turn-off for M 15 at
V0 =
19.4 which corresponds to
H0 = 18.4 from the theoretical track of
Baraffe et al. (1997) at the metallicity of M 15 ([Fe/H] = -2.15).
This implies that the stars at
and spreads out for
-0.4 < (J-H)0 < 1.8 at
fainter magnitudes due to our photometric uncertainty. The few stars
brighter than H0 = 18 are probably foreground objects. Indeed,
Durrell & Harris (1993) determined the turn-off for M 15 at
V0 =
19.4 which corresponds to
H0 = 18.4 from the theoretical track of
Baraffe et al. (1997) at the metallicity of M 15 ([Fe/H] = -2.15).
This implies that the stars at
![]() are either cluster
objects evolved off the main sequence or simply foreground stars.
are either cluster
objects evolved off the main sequence or simply foreground stars.
The bright tip of the main sequence shows up at
![]() for
Fields 1 and 2 while it falls at
for
Fields 1 and 2 while it falls at
![]() for Field 3. This
apparently fainter turn-off magnitude is likely due to statistical
fluctuations in our small sample.
for Field 3. This
apparently fainter turn-off magnitude is likely due to statistical
fluctuations in our small sample.
In order to reduce the contamination from foreground and background
stars, we applied to the CMD of each field a
![]() clipping
selection around the average colour of the main sequence. The resulting
three decontaminated samples were merged onto the CMD of Fig. 2
where the stars in common are represented with averaged magnitudes and
colours. Using the predictions of Ratnatunga & Bahcall (1985), we have
estimated the field-star contamination to be about 4 stars for each
NICMOS field in the direction of M 15. This estimate is valid for a
limiting magnitude of H = 23 (i.e. 0.2
clipping
selection around the average colour of the main sequence. The resulting
three decontaminated samples were merged onto the CMD of Fig. 2
where the stars in common are represented with averaged magnitudes and
colours. Using the predictions of Ratnatunga & Bahcall (1985), we have
estimated the field-star contamination to be about 4 stars for each
NICMOS field in the direction of M 15. This estimate is valid for a
limiting magnitude of H = 23 (i.e. 0.2 ![]() in Fig. 2),
which corresponds to
in Fig. 2),
which corresponds to
![]() in the evolutionary tracks of
Baraffe et al. (1997), and is integrated over the whole (B-V) colour
range taken into account by Ratnatunga & Bahcall (1985). Therefore, we
do not expect the CMD to change significantly after the
in the evolutionary tracks of
Baraffe et al. (1997), and is integrated over the whole (B-V) colour
range taken into account by Ratnatunga & Bahcall (1985). Therefore, we
do not expect the CMD to change significantly after the
![]() -clipping is applied. The photometric errors are also indicated
on the left-hand side of Fig. 2: in the range
-clipping is applied. The photometric errors are also indicated
on the left-hand side of Fig. 2: in the range
![]() the (J-H)0 colours are known with an accuracy of
the (J-H)0 colours are known with an accuracy of ![]() 0.07 mag, at
0.07 mag, at
![]() they increase to
they increase to ![]() 0.13 mag and for H0 >
23 the photometric accuracy is as poor as
0.13 mag and for H0 >
23 the photometric accuracy is as poor as ![]() 0.24 mag.
0.24 mag.
Superposed on the observed CMD distribution is the theoretical track
obtained from the models of Baraffe et al. (1997) for a metallicity of
![]() ,
which closely matches the
,
which closely matches the
![]() value of M 15. This track is scaled by the distance modulus of 15.11 mag
(Durrell & Harris 1993). The stellar masses actually defining the
theoretical track are listed on the right-hand side of Fig. 2 for
decreasing H0 magnitudes. The main sequence spans a mass range
between 0.8
value of M 15. This track is scaled by the distance modulus of 15.11 mag
(Durrell & Harris 1993). The stellar masses actually defining the
theoretical track are listed on the right-hand side of Fig. 2 for
decreasing H0 magnitudes. The main sequence spans a mass range
between 0.8 ![]() and 0.2
and 0.2 ![]() .
.
The LF observed for the external fields of M 15 is plotted in
Fig. 3 (solid line) corrected for incompleteness. The stars in the
CMD were grouped into magnitude bins (each 0.5 mag wide) between
H0 = 18 and H0 = 24, where completeness drops to less than ![]() .
Since the completeness of the three fields is nearly the same
at H0 < 23, we have assumed a mean completeness factor with which we
have corrected the star counts of bins brighter than 23. At H0 > 23,
Fields 2 and 3 are the major contributors to the observed LF, since
they are deeper. In this magnitude range we have, therefore, ignored
the stars in Field 1 not contained in Fields 2 or 3 and
rescaled the total number of objects in these two latter fields to
match the total area of the survey. Therefore we computed a mean
completeness factor between these two fields and used the resulting
value to correct the star counts of bins fainter than H0 = 23. Given
the shallower photometric depth of Field 1, having ignored its
contribution to the LF for H0 > 23 is not likely to affect the
statistical significance of our results.
.
Since the completeness of the three fields is nearly the same
at H0 < 23, we have assumed a mean completeness factor with which we
have corrected the star counts of bins brighter than 23. At H0 > 23,
Fields 2 and 3 are the major contributors to the observed LF, since
they are deeper. In this magnitude range we have, therefore, ignored
the stars in Field 1 not contained in Fields 2 or 3 and
rescaled the total number of objects in these two latter fields to
match the total area of the survey. Therefore we computed a mean
completeness factor between these two fields and used the resulting
value to correct the star counts of bins fainter than H0 = 23. Given
the shallower photometric depth of Field 1, having ignored its
contribution to the LF for H0 > 23 is not likely to affect the
statistical significance of our results.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0192fig2.ps}
\end{figure}](/articles/aa/full/2004/47/aa0192-03/Timg45.gif) |
Figure 2:
De-reddened CMD of the whole sample on which the
theoretical track of Baraffe et al. (1997), computed for the
metallicity of M 15 (
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0192fig3.ps}
\end{figure}](/articles/aa/full/2004/47/aa0192-03/Timg46.gif) |
Figure 3:
Luminosity function (solid curve) of the whole sample, corrected for
photometric completeness. Poissonan errors have been associated to the
observed star counts. The dashed distribution is the best fitting LF,
computed under the assumption of a log-normal mass distribution with a
characteristic mass of 0.3 |
| Open with DEXTER | |
The LF of Fig. 3 extends over the range
![]() ,
peaking
at MH = 7.1 (corresponding to MI = 8.5; Baraffe et al. 1997) and
is characterised by a quite sharp drop to fainter magnitudes due to a
lack of progressively less massive stars. Moreover, this LF confirms
the general behaviour found by Paresce & De Marchi (2000) for a dozen
Galactic globular clusters: their average LF, computed from stars below
1
,
peaking
at MH = 7.1 (corresponding to MI = 8.5; Baraffe et al. 1997) and
is characterised by a quite sharp drop to fainter magnitudes due to a
lack of progressively less massive stars. Moreover, this LF confirms
the general behaviour found by Paresce & De Marchi (2000) for a dozen
Galactic globular clusters: their average LF, computed from stars below
1 ![]() near the half-light radius, rises to a maximum value at
near the half-light radius, rises to a maximum value at
![]() and then drops for fainter magnitudes
(this applies
regardless of the cluster position and orbit in the Galaxy and of its
internal dynamical state).
and then drops for fainter magnitudes
(this applies
regardless of the cluster position and orbit in the Galaxy and of its
internal dynamical state).
The MF of the observed fields was derived from the LF of Fig. 3.
Instead of deriving the MF by inverting the LF, we followed the
approach of Paresce & De Marchi (2000), so as to treat separately
observational and theoretical uncertainties. We assumed a model MF of
log-normal type, i.e. one of the type:
![\begin{displaymath}\ln\left(\frac{{\rm d}N}{{\rm d}\log(m)}\right) = A -
\left[\frac{\log(m/m_{\rm c})}{\sqrt{2}\sigma}\right]^2
\end{displaymath}](/articles/aa/full/2004/47/aa0192-03/img49.gif) |
(2) |
As mentioned in the Introduction, M 15 has been extensively studied for it is at a relatively large distance from the Galactic plane and, consequently, not severely affected by dynamical interactions with the Galaxy.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0192fig4.ps}
\end{figure}](/articles/aa/full/2004/47/aa0192-03/Timg53.gif) |
Figure 4:
Spatial distribution of the stellar fields observed within the
half-light radius of M 15 ( |
| Open with DEXTER | |
Figure 4 spatially visualises the stellar fields observed in the core
of M 15 by De Marchi & Paresce (1996; DMP96) and Sosin & King (1997;
SK97-1, SK97-2) in order to derive the central MF. The DMP96 and SK97-1
fields are at the centre, whilst the SK97-2 field is
![]() away from it. All fields are well within the
half-light radius of M 15 (
away from it. All fields are well within the
half-light radius of M 15 (
![]() ;
Trager et al. 1995).
Both studies detect a substantial amount of mass segregation, although
the LFs differ for MV > 4.8. The two luminosity distributions are
plotted in Fig. 5: the LF of De Marchi & Paresce (1996) has been
here translated from the original FOC F346M band magnitudes to standard
Johnson V values using Baraffe et al.'s tracks (private
communication).
;
Trager et al. 1995).
Both studies detect a substantial amount of mass segregation, although
the LFs differ for MV > 4.8. The two luminosity distributions are
plotted in Fig. 5: the LF of De Marchi & Paresce (1996) has been
here translated from the original FOC F346M band magnitudes to standard
Johnson V values using Baraffe et al.'s tracks (private
communication).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0192fig5.ps}
\end{figure}](/articles/aa/full/2004/47/aa0192-03/Timg55.gif) |
Figure 5: Luminosity functions as derived by De Marchi & Paresce (1996; solid curve) and Sosin & King (1997; dashed distribution) for their field positioned at the centre of M 15. Poisson errors have been associated with the plotted star counts. |
| Open with DEXTER | |
Both LFs have been normalised to the peak star count. An interesting point is that at MV > 4.8 the LF of De Marchi & Paresce (1996) dramatically drops, whilst the LF derived by Sosin & King (1997) is flat. We believe that this discrepancy is due to photometric incompleteness and to the colour extrapolation from the UV to the V band.
Whilst mass segregation affects the innermost region of globular clusters, dynamical interactions with the Galaxy act predominantly on their outermost regions inducing stellar evaporation and stripping. Thus, clusters as rich as M 15 are likely to be dynamically unperturbed at their half-light radius (Richer et al. 1991) and stars at this distance can be used to constrain the IMF. Table 4 lists the observations available in the literature which cover the outskirts of M 15. Their corresponding fields are plotted in Fig. 6 together with the cluster centre and half-light radius.
Table 4: M 15 surveys.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0192fig6.ps}
\end{figure}](/articles/aa/full/2004/47/aa0192-03/Timg59.gif) |
Figure 6:
Spatial distribution of the fields observed at distance larger
than the cluster half-light radius. DH93 labels the field imaged by
Durrell & Harris (1993) at |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=13.5cm,clip]{0192fig7.ps}
\end{figure}](/articles/aa/full/2004/47/aa0192-03/Timg62.gif) |
Figure 7: The LFs computed by Durrell & Harris (1993, DH93) and De Marchi & Paresce (1995, DMP95) are compared with the distribution obtained from the NIC3 data. All of the luminosity distributions have been translated into MI values and scaled to the peak star-counts of the NIC3 luminosity function. |
| Open with DEXTER | |
Having derived the spatially resolved LF for M 15, we can now study
its radial changes and address the issue as to whether they are
consistent with mass segregation ensuing from two body relaxation. To
study the dynamical properties of the cluster, we employed the
multi-mass Michie-King models originally developed by Meylan (1987,
1988) and later suitably modified by Pulone et al. (1999) and De Marchi
et al. (2000) for the general case of clusters with a set of radially
varying LFs. Each model run is characterised by a MF in the form of
a power-law
![]() ,
with a variable index x, and by four structural parameters describing, respectively, the
scale radius (
,
with a variable index x, and by four structural parameters describing, respectively, the
scale radius (![]() ), the scale velocity (
), the scale velocity (![]() ), the
central value of the dimensionless gravitational potential
), the
central value of the dimensionless gravitational potential ![]() ,
and the anisotropy radius (
,
and the anisotropy radius (![]() ). (After having suggested,
in Sect. 3, a rather general description of the functional form of
the MF, namely a log-normal distribution, it might seem inappropriate
to adopt a variable power-law as the basis for the MF in our dynamical
model. In fact, as we show below, the resulting MF is
indistinguishable, for any practical purposes, from a log-normal
distribution.)
). (After having suggested,
in Sect. 3, a rather general description of the functional form of
the MF, namely a log-normal distribution, it might seem inappropriate
to adopt a variable power-law as the basis for the MF in our dynamical
model. In fact, as we show below, the resulting MF is
indistinguishable, for any practical purposes, from a log-normal
distribution.)
From the parameter space defined in this way, we selected those models
that simultaneously fit both the observed surface brightness profile
(SBP) and velocity dispersion profile (VDP) of the cluster as measured,
respectively, by Guhathakurta et al. (1996; for
![]() )
and Trager et al. (1995; for
)
and Trager et al. (1995; for
![]() )
and by Gebhardt et al. (2000). However, even requiring good fits to both the SBP and VDP can, by itself, only constrain
)
and by Gebhardt et al. (2000). However, even requiring good fits to both the SBP and VDP can, by itself, only constrain ![]() ,
, ![]() ,
, ![]() ,
and
,
and ![]() ,
whilst still allowing the MF to take on a variety of
shapes. To break this degeneracy, we further imposed the condition that
the model MF agree with the observed LF at all radial distances offered
by the data.
,
whilst still allowing the MF to take on a variety of
shapes. To break this degeneracy, we further imposed the condition that
the model MF agree with the observed LF at all radial distances offered
by the data.
Since Michie-King modeling only provides a "snapshot'' of the current dynamical state of the cluster, it is useful to refer to the GMF, i.e. the mass distribution of all cluster stars at present, or, in other words, the MF that the cluster would have simply as a result of stellar evolution (i.e. ignoring any local modifications induced by internal dynamics and/or the interaction with the Galactic tidal field). Clearly, in this case the IMF and GMF of main sequence (unevolved) stars is the same. For practical purposes, the GMF has been divided into sixteen different mass classes, covering main sequence stars, white dwarfs and heavy remnants, precisely as described in Pulone et al. (1999).
Our parametric modelling approach assumes energy equipartition amongst
stars of different masses. Thus, we ran a large number of trials to see
whether we could find a set of parameters for the GMF (i.e. a suitable
GMF "shape'') such that the local MFs produced by mass segregation
would locally fit the observations. We note here that, rather than
converting the observed LFs into MFs for comparison with the
predictions of the model, we prefer to keep observational errors and
theoretical uncertainties separate. Therefore, we convert the model MFs
to LFs using for all the same M-L relation, namely that of Baraffe et al. (1997), precisely as we did in Fig. 3. Not surprisingly, our
exercise confirms what we had already shown in that figure and
described above: as long as a single value of the index x is used
for the GMF over the mass range 0.2-0.8 ![]() ,
none of the
predicted local LFs can be fitted to our data. In fact, a change
of slope is needed at
,
none of the
predicted local LFs can be fitted to our data. In fact, a change
of slope is needed at
![]()
![]() so that both the rising
and dropping portions of the local LF can be simultaneously reproduced.
If we then allow the MF to take on more than one slope, the GMF that
best fits the observations is one with x=0.9 for stars in the range
so that both the rising
and dropping portions of the local LF can be simultaneously reproduced.
If we then allow the MF to take on more than one slope, the GMF that
best fits the observations is one with x=0.9 for stars in the range
![]() and x=-2.2 at smaller masses. The shape of
this GMF is, thus, very similar to the log-normal distribution shown in
Fig. 3.
and x=-2.2 at smaller masses. The shape of
this GMF is, thus, very similar to the log-normal distribution shown in
Fig. 3.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0192fig8.ps}
\end{figure}](/articles/aa/full/2004/47/aa0192-03/Timg71.gif) |
Figure 8:
The best fits of the Michie-King models to the LF observed
at |
| Open with DEXTER | |
Although stars more massive than ![]()
![]() have evolved and
are no longer visible, the shape of the IMF in this mass range has
strong implications on the fraction of heavy remnants in the cluster
and, as such, on the central velocity dispersion. We find that the
best fit to the data and to the cluster's structural parameters, as
given above, requires a value of x=0.8 for stars in the range
have evolved and
are no longer visible, the shape of the IMF in this mass range has
strong implications on the fraction of heavy remnants in the cluster
and, as such, on the central velocity dispersion. We find that the
best fit to the data and to the cluster's structural parameters, as
given above, requires a value of x=0.8 for stars in the range
![]() .
It should be noted that the global cluster MF is thus
slightly shallower than Salpeter's IMF, which would have x=1.35.
The total implied cluster mass is
.
It should be noted that the global cluster MF is thus
slightly shallower than Salpeter's IMF, which would have x=1.35.
The total implied cluster mass is ![]()
![]() and
the mass-to-light ratio is on average
and
the mass-to-light ratio is on average
![]() ,
with
,
with
![]() in the core. The total cluster luminosity LV has been
estimated by integrating the best-fitting SBP (solid line in
Fig. 9), properly normalised to match the observed central surface
brightness. The best fitting models suggest that a large
fraction of mass (of order
in the core. The total cluster luminosity LV has been
estimated by integrating the best-fitting SBP (solid line in
Fig. 9), properly normalised to match the observed central surface
brightness. The best fitting models suggest that a large
fraction of mass (of order ![]()
![]() )
is trapped in heavy remnants,
namely stellar black holes, neutron stars and white dwarfs. However, the
presence of an intermediate mass black hole is not required.
)
is trapped in heavy remnants,
namely stellar black holes, neutron stars and white dwarfs. However, the
presence of an intermediate mass black hole is not required.
Interestingly, the rather shallow GMF that we obtain for stars above
![]() ,
which, in turn, results in a large fraction of heavy
remnants, is also dictated by the central enhancement seen in the SBP.
The excellent fit that our model offers to the radial surface density
of TO-mass stars (Fig. 9) would not be otherwise possible. A steeper
MF index would result in a shallower central profile which would fail
to reproduce the central density enhancement. It should also be noted
that, since a canonical King-type profile does not reproduce the SBP of M 15 (see, e.g., Trager et al. 1995), the value of
,
which, in turn, results in a large fraction of heavy
remnants, is also dictated by the central enhancement seen in the SBP.
The excellent fit that our model offers to the radial surface density
of TO-mass stars (Fig. 9) would not be otherwise possible. A steeper
MF index would result in a shallower central profile which would fail
to reproduce the central density enhancement. It should also be noted
that, since a canonical King-type profile does not reproduce the SBP of M 15 (see, e.g., Trager et al. 1995), the value of ![]() that we obtain
does not correspond with the canonical definition of core radius,
namely that at which the surface density falls to one-half its central
value. The latter definition only applies to the profile of the
original King model with a single mass component (see Kent & Gunn
1982). In our case,
that we obtain
does not correspond with the canonical definition of core radius,
namely that at which the surface density falls to one-half its central
value. The latter definition only applies to the profile of the
original King model with a single mass component (see Kent & Gunn
1982). In our case, ![]() simply represents a scale radius.
simply represents a scale radius.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0192fig9.ps}
\end{figure}](/articles/aa/full/2004/47/aa0192-03/Timg76.gif) |
Figure 9:
Model fit to the surface brightness profile. The solid line
corresponds to the profile of stars of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{0192fig10.ps}
\end{figure}](/articles/aa/full/2004/47/aa0192-03/Timg77.gif) |
Figure 10: Model fit to the velocity dispersion profile. |
| Open with DEXTER | |
Contrary to what we have concluded here, in their analysis of the
radial variation of the LF of M 15, Sosin & King (1997) concluded that
a multi-mass Michie-King model is unable to reproduced the
observations. As their Fig. 12 shows, the variation predicted by
their multi-mass model is larger than that observed when comparing the
centre of the cluster and the region at
![]() .
We have
identified three reasons that might have led Sosin & King (1997) to
this conclusion and we discuss them here briefly.
.
We have
identified three reasons that might have led Sosin & King (1997) to
this conclusion and we discuss them here briefly.
The first is mostly related to the approach used and, as such, should only affect the uncertainty of the results. Sosin & King (1997) decided to transform the observed LFs into MFs, not necessarily using the same M-L relation for all data, and to compare the predictions of their multi-mass models to these MFs. The advantage of our approach, in which the LF predicted by the model is compared with the observed LF, is that we ensure that observational errors and theoretical uncertainty (in the model and M-L relation) are kept separate and that only one M-L relation is used throughout the process.
Secondly, it appears that their dynamical model is unable to reproduce
at all the observed velocity dispersion profile, as the authors
themselves point out. Conversely, ours is in excellent agreement with
the observations.
As a result, Sosin & King (1997) predict a fraction of heavy
remnants (![]()
![]() )
well below the current estimates for this
cluster.
)
well below the current estimates for this
cluster.
Most importantly, however, we believe that their inability to reproduce
the observed radial variation of the LF stems from the functional form
of the MF that they adopt. As we describe in Sect. 4, we have made a
general assumption about the shape of the GMF, in the form of a
log-normal distribution, based on what was learnt from the observation
of a large number of halo GCs (Paresce & De Marchi 2000). We then let
our procedure find the parameter values that simultaneously fit all
available data. Since the number of independent measurements is larger
than that of the unknowns, the procedure is bound to converge. On the
other hand, Sosin & King (1997) adopt the MF determined by Piotto et al. (1996) at
![]() as the basis for their dynamical
model, but the MF predicted by it for the cluster core fails to match
the data. The origin of the mismatch seems to lie predominantly in the
assumed shape of the MF, which is flat in the range
as the basis for their dynamical
model, but the MF predicted by it for the cluster core fails to match
the data. The origin of the mismatch seems to lie predominantly in the
assumed shape of the MF, which is flat in the range
![]() and then sharply rises at lower masses. This results in
a MF in the central cluster regions that sharply drops in the range
and then sharply rises at lower masses. This results in
a MF in the central cluster regions that sharply drops in the range
![]() .
It appears that having adopted a
model MF with a more gentle rise from
.
It appears that having adopted a
model MF with a more gentle rise from
![]() all the way
through to
all the way
through to
![]() (which still fits the data at
(which still fits the data at ![]() equally well) would have produced a MF in considerably better agreement
with the observations in the central cluster region.
equally well) would have produced a MF in considerably better agreement
with the observations in the central cluster region.
Table 5: Parameters of the Michie-King models used for M 15.
We have analysed HST/NICMOS parallel data available for three fields in
the Galactic globular cluster M 15 located at ![]() NE of the
cluster centre. Their total LF extends over the range
NE of the
cluster centre. Their total LF extends over the range
![]() and peaks at MH = 7.1 (or
and peaks at MH = 7.1 (or
![]() ). It also shows a
sharp drop towards fainter magnitudes, which is a typical signature of
the lack of progressively less massive stars. We have fitted this LF
with a log-normal mass distribution and obtained a characteristic mass
of
). It also shows a
sharp drop towards fainter magnitudes, which is a typical signature of
the lack of progressively less massive stars. We have fitted this LF
with a log-normal mass distribution and obtained a characteristic mass
of
![]() ,
with a standard deviation of 0.28. These
values agree well with the characteristic mass and standard deviation
derived for a dozen Galactic globular clusters by Paresce & De Marchi
(2000), thus supporting the ubiquity of the log-normal mass
distribution for globular clusters.
,
with a standard deviation of 0.28. These
values agree well with the characteristic mass and standard deviation
derived for a dozen Galactic globular clusters by Paresce & De Marchi
(2000), thus supporting the ubiquity of the log-normal mass
distribution for globular clusters.
The H-band LF obtained at ![]() from the centre of M 15 has been
compared with the LFs derived by Durrell & Harris (1993) and De Marchi
& Paresce (1995) at
from the centre of M 15 has been
compared with the LFs derived by Durrell & Harris (1993) and De Marchi
& Paresce (1995) at ![]() NW and
NW and
![]() NW of the cluster
centre, respectively. The comparison has required the translation of
all original observed magnitudes into the I band. The overlap among
these three LFs is excellent, indicating that the distribution of the
stars at distances larger than the half-light radius (
NW of the cluster
centre, respectively. The comparison has required the translation of
all original observed magnitudes into the I band. The overlap among
these three LFs is excellent, indicating that the distribution of the
stars at distances larger than the half-light radius (![]()
![]() ;
Trager et al. 1995) may not be significantly perturbed in M 15,
as expected from its Galactocentric distance (
;
Trager et al. 1995) may not be significantly perturbed in M 15,
as expected from its Galactocentric distance (
![]() Kpc;
Gnedin & Ostriker 1997) and the small ellipticity of its orbit (e =
0.32; Dinescu et al. 1999). Indeed, calculations by Gnedin &
Ostriker (1997) show that the time to destruction of M 15, due to the
combined effects of internal dynamical evolution and interaction with
the Galaxy, is as large as 50 Gyr. Therefore, if correct, this
time-scale would suggest that the outermost fields observed in M 15
have not been significantly perturbed by tidal stripping and
evaporation and that their content should likely represent the
initial stellar mass distribution. In other words, the high
degree of similarity between the LFs (and hence the MFs) of the fields
at
Kpc;
Gnedin & Ostriker 1997) and the small ellipticity of its orbit (e =
0.32; Dinescu et al. 1999). Indeed, calculations by Gnedin &
Ostriker (1997) show that the time to destruction of M 15, due to the
combined effects of internal dynamical evolution and interaction with
the Galaxy, is as large as 50 Gyr. Therefore, if correct, this
time-scale would suggest that the outermost fields observed in M 15
have not been significantly perturbed by tidal stripping and
evaporation and that their content should likely represent the
initial stellar mass distribution. In other words, the high
degree of similarity between the LFs (and hence the MFs) of the fields
at
![]() and
and ![]() from the centre would imply that
these are very close to be the cluster IMF and there are no significant
radial variations in the cluster IMF.
from the centre would imply that
these are very close to be the cluster IMF and there are no significant
radial variations in the cluster IMF.
We have used the LF measured for M 15 at ![]() (this work),
(this work),
![]() (De Marchi & Paresce 1995), and
(De Marchi & Paresce 1995), and
![]() (Sosin & King 1997) from the cluster centre and in the core (De Marchi
& Paresce 1996; Sosin & King 1997) to study the effects of mass
segregation. We have fitted Michie-King models to the observed surface
brightness and velocity dispersion profiles in order to estimate the
cluster structural parameters and to the observed LF to constrain the
shape of the cluster GMF. The latter turns out to be characterised by
two slopes, x=0.9 for stars in the range
(Sosin & King 1997) from the cluster centre and in the core (De Marchi
& Paresce 1996; Sosin & King 1997) to study the effects of mass
segregation. We have fitted Michie-King models to the observed surface
brightness and velocity dispersion profiles in order to estimate the
cluster structural parameters and to the observed LF to constrain the
shape of the cluster GMF. The latter turns out to be characterised by
two slopes, x=0.9 for stars in the range
![]() and x=-2.2 at smaller masses, and is thus very close to the log-normal
distribution obtained directly from our NIC3 data near the cluster's
half-light radius.
and x=-2.2 at smaller masses, and is thus very close to the log-normal
distribution obtained directly from our NIC3 data near the cluster's
half-light radius.
The values of the cluster structural parameters that best fit the
observations imply a cluster total mass of ![]()
![]() and a mass-to-light ratio of
and a mass-to-light ratio of
![]() on
average, with
on
average, with
![]() in the cluster core. In addition, the
best-fitting Michie-King model parameters suggest a slope of x=0.8for the IMF in the range
in the cluster core. In addition, the
best-fitting Michie-King model parameters suggest a slope of x=0.8for the IMF in the range
![]() ,
which supports the
presence of a large fraction of heavy remnants (
,
which supports the
presence of a large fraction of heavy remnants (![]()
![]() )
in the
core. If such a high fraction of heavy remnants is present, as
originally suggested by Illingworth & King (1977), it would
rule out the need for an intermediate-mass black hole to explain the
mass segregation and velocity dispersions observed in the core of M 15.
)
in the
core. If such a high fraction of heavy remnants is present, as
originally suggested by Illingworth & King (1977), it would
rule out the need for an intermediate-mass black hole to explain the
mass segregation and velocity dispersions observed in the core of M 15.
Acknowledgements
We are very grateful to Carlton Pryor, the referee of this paper, for comments that have substantially strengthened the presentation of our work. It is a pleasure to thank Isabelle Baraffe and France Allard for providing us the theoretical tracks for the HST/FOC filters F253M and F346M and Francesco Paresce for useful discussions. M.S.B. acknowledges support from the Osservatorio Astronomico di Cagliari and from the Director General's Discretionary Fund at ESO.