A&A 428, 241-246 (2004)
DOI: 10.1051/0004-6361:20041398

Some features of Geminid meteoroid disintegration in the Earth's atmosphere

P. B. Babadzhanov - N. A. Konovalova

Institute of Astrophysics, Tajik Academy of Sciences, and Isaac Newton Institute of Chile, Tajikistan Branch; Bukhoro Str. 22, Dushanbe 734042, Tajikistan

Received 3 June 2004 / Accepted 13 July 2004

Abstract
Among 11 bright Geminid meteors photographed at the Institute of Astrophysics, Tajik Academy of Sciences (Dushanbe, Tajikistan), 3 displayed distinct high-frequency (more than 100 Hz) pulsations of brightness, or flickering. As a rule, for these Geminids, pulsations of brightness begin at the middle of their photographed path, at the height of about 75 km, and last until the end of the visible trajectory. Different possible meteoroid ablation mechanisms causing the flickering of the bright Geminids are discussed. The obtained results allow us to conclude that the observed high-frequency flickering of Geminid fireballs may be explained by an autofluctuating mechanism of the meteoroid ablation, i.e. by melting and cyclic ablation of the surface-layer of meteoric matter with the period corresponding to the observed period of the flickering.

Key words: meteors, meteoroids

1 Introduction

The Geminid meteor shower, reaching the peak activity on 13 December, is one of the strongest annual meteor phenomena, with the shortest orbital period (1.6 years) and the shortest perihelion distance (0.14 AU). During previous decades the astronomers investigating the Geminids usually came to the conclusion that meteoroids of this shower are more dense than meteoroids of others showers. According to the data of photographic observations of fireballs and taking into account "gross fragmentation'' of meteoroids in the atmosphere, Ceplecha & McCrosky (1992) concluded that the bulk density of Geminid meteoroids is equal to 3-4 g/cm3. Using high-performance observations of 41 Geminid meteors, Spurny (1993) has obtained the same estimation of the density of Geminid meteoroids and concluded that probably they have an asteroidal origin. Gustafson (1989) suggested that the Geminids are flakes of a relative high density porous material, pieces of a very thin mantle that may have formed on Phaethon. Our determination of the bulk density of meteoroids producing bright photographic meteors, based on the analysis of the light curves of meteors and taking into account the quasi-continuous fragmentation of meteoroids in the Earth's atmosphere, has shown that the mean bulk density of Geminid meteoroids is equal to 2.9 g/cm3 (Babadzhanov 2002). It is possible that the high density of Geminid meteoroids in comparision with other meteoroids is due to the small perihelion distance of the Geminid orbit, i.e. repeated transit of Geminid meteoroids very close to the Sun.

Except for high density, another distinctive feature of bright Geminids are high-frequency (up to several hundreds Hz) pulsations of brightness seen since the first years of systematic photographic observations of meteors. For example, according to the data of Astapovich (1958), bright flickering Geminids were photographed in the Harward observatory (USA) in 1933 (December 14) and 1934 (December 12). The pulsations of brightness were observed for 6 of 12 Geminid fireballs photographed according to the Meteoroid Observation and Recovery Program (MORP) of Canada (Halliday 1988). In scientific publications there are examples of meteors whose flickering frequency varies from several Hz up to hundreds of Hz (low-frequency pulsations) (Kramer 1966; Getman 1993; Beech & Brown 2000; Konovalova 2003), but the flickering frequency of Geminids is almost ten times as much, the flickering starts suddenly, approximately from the middle of a meteor trajectory and remain steady down to its end. Thus the frequency of flickerings increases in the process of penetration of the meteoroid into the atmosphere, and the amplitude of flickering remains practically nearly constant during the whole visible path.

In the papers devoted to investigation of the meteor flickering phenomenon (see, for example, Kramer 1966) it has been underlined that the appearance of meteor flickering may be expected only for meteors produced by massive meteoroids penetrating deeply into the Earth's atmosphere. However, the analysis of light curves of 566 meteors photographed in 1957-1983 in Dushanbe shows that not all the meteors produced by massive meteoroids and deeply penetrating into the Earth's atmosphere display regular pulsations of brightness. So, even for the brightest meteors of Perseids, $\alpha$-Capricornids, Orionids and the majority of bright sporadic meteors produced by meteoroids of masses similar to masses of Geminids, the high-frequency pulsations of brightness are not observed. The presence of one or several strong flares of brightness is typical creating the effect of low-frequency pulsations as in the case of Taurids (Konovalova 2003). Pulsations of brightness for Leonids and $\delta$-Aquarids are not observed at all, although the meteors of these showers are very bright.

The appearance of high-frequency flickering for Geminids and low-frequency ones for the above-mentioned showers and sporadic meteors is apparently connected to the ablation mechanism of meteoroids, which in turn directly depend on the physical properties of meteoroids, mainly on their composition, structure and strength.

Oleak (1964) lists the following main mechanisms of meteor flickering:

1.
rotation of the meteoroid;

2.
vibration of the meteoroid;

3.
successive detachment of fragments (wreckages);

4.
autofluctuating character of the evaporation process.
For the first and second mechanisms we expect the pulsation of brightness both for bright and weak meteors. This is not observed, although the changes of brightness, caused by rotation or vibration of meteoroids, may take place (Astapovich 1958; Beech & Brown 2000; Beech 2001, 2002).

Successive detachment of wreckages, i.e. the "gross fragmentation'' of meteoroids can cause low frequence pulsations of the meteor brightness (Bronshten 1981; Getman 1993; Konovalova 2003). Below, at first we consider the rotation of meteoroids and the consequences of its development, and then the autofluctuating character of the evaporation process of meteoroids.

2 Observational data on Geminid fireballs

In the periods of maximum activity of the Geminid meteor shower, with small cameras (D:F = 1:2.5, F = 250 mm) of the meteor patrol of the Institute of Astrophysics of Tajik Academy of Sciences (Dushanbe), photos were taken of three flickering fireballs belonging to this shower and designated 643881, 761683 and 821691. The photographs of the Geminids were obtained in the guiding camera and in undriven ones with a rotating shutter at the Gissar observatory and the corresponding station Kipchak, located 34 km away. The Geminid 821691 was also photographed by the long-focus camera MK-75 (D:F = 1:3.5, F = 750 mm) using the method of instantaneous exposure ( $\tau_{\rm exp} = 5.6 \times 10^{-4}$ s) and 29 instantaneous images of the meteor were obtained at 0.02 s intervals. For the photography of meteors highly sensitive panchromatic films of $30 \times 30$ cm size were used.

The data of radiants, zenith angles, velocities, heights, masses and orbital elements were published earlier (Babadzhanov et al. 1998). The photographic photometry was conducted on meteor negatives obtained from undriven cameras. The visual magnitudes of Geminids were determined in comparision with diurnal star trails, then the transition from visual magnitudes to absolute ones was performed by the technique described by Ivanikov (1957). The initial mass of the meteoroids was calculated with the formula:

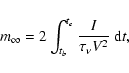\begin{displaymath}m_\infty = 2 \int_{t_b}^{t_e}\frac{I}{\tau_{\nu} V^2}~{\rm d}t, \end{displaymath} (1)

where tb and te are the times of appearance and disappearance of the meteor; I is the observed meteor luminosity determined as $\log I = 9.72 - 0.4 M$; $\tau_\nu = \tau_0 V$ is the luminous efficiency, where $\log \tau_0 = -9.28$ and V is the meteoroid velocity in cm/s. The data on meteors under study are presented in Table 1, where we give: the number N of the meteor; year, month and day (UT); the right ascention $\alpha_{\rm R}$ and the declination $\delta_{\rm R}$ of radiant; $\cos z_{\rm R}$ - cosine of the zenith distance of the radiant; the initial velocity $V_\infty$; the heights of beginning $h_{\rm b}$, maximum luminocity $h_{\max}$ and end $h_{\rm e}$ of the meteor; the theoretical height h0 of the beginning of intensive evaporation of the meteoroid; the maximum absolute (100 km distance) magnitude $M_{\max}$ of the meteor; the duration t of the meteor; the initial mass $m_\infty$ and radius $r_\infty$ of the meteoroid.

In our paper (Babadzhanov & Konovalova 1986, 1987) the preliminary results of the analysis of radiation features of three bright Geminids, showing regular high-frequency ( $\nu_{{\rm obs}} \geq 100$ Hz) pulsations of brightness were given. The observed light curves of these Geminids are shown in Fig. 1. In Fig. 2 for the Geminid 821691 we show the variation of velocity V versus height h.


  \begin{figure} \par\includegraphics{1398fig1.eps}\end{figure} Figure 1: Observed light curves of Geminids: a) 643881; b) 761683; c) 821691.
Open with DEXTER


  \begin{figure} \par\includegraphics{1398fig2.eps}\end{figure} Figure 2: Velocity versus height variations for the Geminid 821691.
Open with DEXTER

As seen from the light curves of the three Geminids, the high-frequency flickering arises suddenly, approximately from the middle of the visible trajectory. The amplitude of the brightness pulsations varies from 0.25 up to 1.0 mag thus with no dependence on height. In the first half of the meteor path no flickering is observed, although the meteor brightness is sufficient: for example at the height of 80 km the brightness of the Geminid meteors 643881, 761683 and 821691 is -3.0, -2.6 and -3.8 mag (the photographic camera system has a limiting magnitude of about 0 mag). The frequency of the pulsations $\nu_{{\rm obs}.}$measured on the photos obtained with a rotating shutter continuously grows with penetration of the meteoroids deep into the atmosphere for all the three Geminids, approximately from a hundred Hz up to several hundreds Hz at the end of the visible trajectory. The graphs of variations of observable pulsations frequency $\nu_{{\rm obs}.}$versus height h are shown in Fig. 3, where the circles mark the values of $\nu_{{\rm obs}.}$ obtained as a result of measurement of the distance between the two adjacent pikes of pulsations as a function of time, which is known with high accuracy for each end of the meteor shutter break.


  \begin{figure} \par\includegraphics[width=8cm,clip]{1398fig3.eps}\end{figure} Figure 3: Observed (circles) and calculated (solid line) frequency of flickering versus height variations for the Geminids: a) 643881; b) 761683; c) 821691.
Open with DEXTER

Table 1: Observed and calculated data of the Geminid meteors.

The analysis of photos of about 200 bright meteors (brighter than absolute magnitude -2.5) from the Dushanbe archive has shown that only 3 meteors with high-frequency pulsations of brightness of more than 100 Hz (flickering) are revealed, and all of them are Geminids. Thus, from 11 photographed Geminids of brighter than -2.5 mag, the flickering fireballs form 27%. Here the Geminids are not included that have some flares along the meteor trajectory. Halliday (1963) showed data of flickering bright -8 mag Geminids photographed on December 13, 1960 in Canada. Halliday (1963, 1988) interpreted the flickering of Geminids as an oscillation of a relative thin meteoroid in flight.

The high-frequency pulsations (flickering) of meteors is rather infrequent. According to Ashgabad datas from 1942-1945 such meteors form 1% (Astapovich 1958). On the data of photographic observations of meteors in Dushanbe in 1957-1983 the high-frequency pulsating meteors form 1.5% of all meteors brighter -2.5 mag photographed by the meteor patrol. Meteors with low-frequency pulsations of brightness (from several Hz up to several tens of Hz) are observed more often and they belong mainly to Orionids, Perseids, Taurids or $\alpha$-Capricornids showers and to the sporadic background. This implies that the flickering of the Geminids is a distinctive feature of this shower, probably connected to the ablation mechanism of the meteoroids. This is confirmed by the Geminid fireball photos obtained by the method of instantaneous exposure on the long-focus cameras MK-75. The instantaneous images of Geminids have a drop-shaped form with a well-marked wake reaching from 90 up to 385 m in length. Babadzhanov & Kramer (1965), Babadzhanov (1983), Babadzhanov & Konovalova (1983) have shown that such instantaneous images of meteors may be a result of separation of fragments or drops melting from the surface of the meteoroid, which represents a kind of quasi-continuous fragmentation of meteoroids (Lebedinets 1980).

3 On the rotation mechanisms of meteoroids and their consequences

A. Analysis of mechanisms producing rotation of meteoroids both in interplanetary space and in the Earth's atmosphere has been carried out by many researchers. Opik (1958), Dolginov (1968), Paddack (1969), Bronshten (1981), Olsson-Steel (1987), Kruchinenko (1995), Beech & Brown (2000), Beech (2001, 2002) assume that owing to mutual collisions in inteplanetary space or under the solar "windmill'' mechanism the majority of meteoroids generating meteors of optical and radar ranges, up to the entrance in the Earth's atmosphere have fast rotation. Confirmation of meteoroid rotation in the Earth's atmosphere is given by meteorites' tracks of rotation, which are impressed on their crust as a curved stream of melted matter (Krinov 1963). Assuming that flickering Geminids are produced by meteoroids which were spun even before entry into the Earth's atmosphere and gained some angular rate of rotation in space, Beech (2002) estimated the time since separation of these meteoroids from the near-Earth object 3200 Phaeton, which is associated with the Geminid stream (Babadzhanov & Obrubov 1993).

Having conducted the analysis of mechanisms producing the rotation of meteoroids, Kruchinenko (1995) came to the conclusion that owing to mutual collisions in interplanetary space, the majority of meteoroids producing meteors of optical and radar ranges have fast rotation at the Earth entry, but large bodies having small geocentric velocities and producing meteorites possess a slow rotation. But Dolginov (1968) showed that for particles of meteoric range the effect of this mechanism is vanishingly small, so that for acquisition of noticeable rotation by a meteoroid even of mass 10 -3 g the period required is more than the lifetime of the Metagalaxy. However, if the particle, which already had a rotation acquired in inteplanetary space, enters the atmosphere, then because of the great deceleration in dense atmosphere, it does not gain stationary rotation (Dolginov 1968).

Beech & Brown (2000) and Beech (2002) explain the observed high-frequency brightness pulsations of Geminids also by meteoroid rotation acquired in space because of collisional fragmentation, since the effect of the "solar windmill'' (Radzievsky 1954; Paddack 1969) can result in negligible rotation rates of bodies of centimetre size.

Levin (1956), Bronshten (1981), Adolfsson & Gustafson (1994), Kruchinenko (1995) showed that the difference in the height of appearance of meteors produced by non-rotating and highly-rotating meteoroids is approximately equal to 10 km, i.e. the meteors produced by a rotating meteoroid appear 10 km lower. To make the concrete conclusion about rotation of the three Geminids under consideration we calculate the theoretical heights of their appearance. For that we use the equation describing atmosphere density $\rho(h_0)$ at the height of the beginning h0 of intensive evaporation of the surface for non-rotating meteoroids defined from the solution of the problem of meteoroid heating in the high atmosphere in the preablation period (Levin 1956; Bronshten 1981):

$\displaystyle \rho (h_{0}) = \frac{2\lambda (T_{{\rm a}} - T_0)}{\Lambda x_0 V_\infty^3},$     (2)

where x0 is the warming-up depth at which temperature is e times less than the surface temperature and is determined according to the formula:
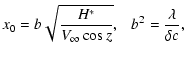$\displaystyle x_0 = b \sqrt {\frac{H^\ast}{V_\infty \cos z}}, ~~~ b^2 = \frac{\lambda}{\delta c},$     (3)

$\lambda$ is the coefficient of thermal conductivity; $\delta$, $V_\infty$ are the density and the initial velocity of the meteoroid; $H^\ast = 7 \times 10^5$ cm is the atmospheric scale height; c is the specific heat; $\Lambda$ is the heat transfer coefficient; $z_{\rm R}$ is the zenith distance of the meteor radiant; $T_{\rm a} = 2000~{\rm K}$ is the surface temperature of the meteoroid at the beginning of intensive evaporization; $T_0 = 280~{\rm K}$ is the initial temperature of the meteoroid, with which it enters the Earth's atmosphere and which corresponds to the equilibrium temperature of a meteoroid at the distance of 1 AU from the Sun.

In the calculations of $\rho(h_0)$ the following values of quantities from the Eqs. (2) and (3) were assumed for the case of a stony meteoroid (Levin 1956): $\lambda = 3 \times 10^5$ erg/cm s deg; c = 107 erg/g deg; $\Lambda = 0.15$ at the height of beginning of intensive vaporization for the cm-size meteoroids and $\delta = 2.9$ g/cm3for Geminid meteoroids (Babadzhanov 2002).

The values of the warming-up depth x0calculated according to formula (3) are in the range of 0.044-0.060 cm. The theoretical heights of the appearance h0 of Geminid meteors, corresponding to the calculated atmospheric densities $\rho(h_0)$, according to formula (2), are presented in Table 1, from which we see that the mean value of the theoretical beginning height h0 of Geminids under investigation is 90.7 km, very close to the mean value of their observable beginning height, $h_{{\rm b}} = 91.4~{\rm km}$. The result allows us to conclude that the given Geminid meteoroids when entering in atmosphere do not rotate.

B. The possibility of rotation for Geminid meteoroids in the Earth's atmosphere can be considered under the following scheme too: a non-rotating meteoroid enters the atmosphere and gains angular rotation with rate $\omega$ under the action of the molecular flow of air (Dolginov 1968; Obrubov & Konovalova 1982; Kruchinenko 1995):

$\displaystyle \omega = \frac{2.1 V}{m_\infty} \left[\frac{\rho (h) H^\ast m_{\rm m}}{\cos z_{\rm R}}\right]^{1/2},$     (4)

where $m_\infty$ is the meteoroid mass, $m_{\rm m} = 4.8 \times 10^{-23}$ g is the mass of air molecule, $z_{\rm R}$ is the zenith angle of the meteor radiant and V is the meteoroid velocity.

The meteoroid is considered rotating if its rotation period $P = 2 \pi / \omega$is much less than the typical ablation time $T_{\rm a}$:

$\displaystyle P \ll T_{{\rm a}} = \frac{H^\ast}{V \cdot \cos z_{\rm R}}\cdot$     (5)

From Eqs.(4) and (5) we obtain the following inequality:
$\displaystyle \left( \frac{0.33}{m_\infty} \right) \left( \frac{H^\ast}{\cos z_{\rm R}} \right)^{3/2} [\rho (h) m_{\rm m} ]^{1/2} \gg 1.$     (6)


For heights of the Geminids under investigation where the pulsations of brightness are clearly observed (i.e. $h \approx 75$ km and $\rho (h) = 4.34\times 10^{-8}$ g/cm3), the condition (5) is realized for particles of masses $m_\infty \ll 6 \times 10^{-7}$ g. This means that under the action of "fluctuation'' only very small-sized meteoroids with masses of $m_\infty \ll 6 \times 10^{-7}$ g can start to rotate in the Earth's atmosphere. Such particles produce meteors registered only by radar observations. But cm-meteoroids of some grammes producing the Geminid meteoroids under consideration cannot begin rotation in the Earth's atmosphere owing to the irregularity of striking of air molecules on the different parts of the meteoroid centre of mass. Thus, the observed flickering of Geminids cannot be explained by meteoroid rotation gained in the Earth's atmosphere.

Considering meteoroid rotation as the cause of fireball flickering, Novikov & Sokolov (2001) and Beech (2001) obtained the equations describing the light curve of the meteor. In these equations it is assumed that a rotating meteoroid of elipsoidal or cubic form modulates its head-on cross-section during its flight in the atmosphere. From the figures given in these papers (Novikov & Sokolov 2001, Fig. 2; Beech 2001, Figs. 1 and 2) it is visible, that a) theoretically, the pulsations of brightness arise from the very beginning of the visible meteor trajectory, and b) the amplitude of pulsations decreases monotonically. On the photographs of the three Geminids under investigation the steady, clearly discernible pulsations of brightness arise "suddenly'', almost from the middle of the meteor trajectory and this "suddenness'' is not connected to poor brightness of meteors in prior parts of trajectories.

The observable amplitude of flickering does not vary during the penetration of Geminid meteoroids into the atmosphere, remaining within the limits of 0.25-1 mag. These changes have no systematic character which could indicate meteoroid rotation with a variable cross-sectional area.

All these facts, together with the results of analyses of the capability of rotation of Geminid meteoroids in the Earth's atmosphere, allow us to suggest an explanation of the observable high-frequency flickering of Geminids: the autofluctuation mechanism of ablation of the meteoroid.

4 The autofluctuation mechanism of ablation

The autofluctuation mechanism occurs when the pressure of saturated vapours of meteor matter and the outer pressure regulate each other automatically (Oleak 1964). For this purpose it is necessary to solve the heat conduction equation

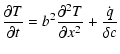$\displaystyle \frac{\partial T}{\partial t} = b^2 \frac{\partial ^2 T}{\partial x^2} + \frac{\dot q}{\delta c}$     (7)

at the boundary conditions on meteoroid surface
$\displaystyle T(x = 0, ~ t = 0) = T_{{\rm m}}, ~~~~ T(x = 0, ~ t = \Delta t) = T_{{\rm b}},$     (8)

where $b^2 = \frac{\lambda}{\delta c}$ is the parameter describing the thermal properties of meteoroid matter, $\dot q$ is the quantity of heat per unit of time and per unit volume (i.e. power of heat, brought to the meteoroid); $T_{\rm m}$ and $T_{\rm b}$ are the melting and boiling temperatures.

During the passage through the atmosphere, for a unit of time per unit surface the meteoroid receives the heat $W = \frac{1}{2} \Lambda \rho V^3$. Considering the atmospheric density equal to $\rho = \rho_0 {\rm e}^{kt}$, where $k = \frac{V \cos z_{\rm R}}{H^\ast}$, we have:

$\displaystyle \dot q = \frac {1}{2} \Lambda \rho_0 {\rm e}^{k t} V^3 \Delta (x),$     (9)

where $\Delta (x)$ is the usual Dirac delta-function.

Taking into account Eq. (9), it is possible to find the following solution of the Eq. (7) at boundary conditions (8) (Levin 1956; Kramer 1966; Bronshten 1981):

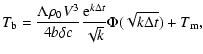$\displaystyle T_{{\rm b}} = \frac {\Lambda \rho_0 V^3} {4 b \delta c} \frac{{\rm e}^{k \Delta t}}{\sqrt {k}} \Phi (\sqrt {k \Delta t}) + T_{\rm m},$     (10)

where $\Phi (y)$ is the integral of the probability, $\Delta t$is the period of flickering.

For the Geminids under investigation, the quantity $k \Delta t$ is small enough $(0.006 < k \Delta t \sol 0.01)$, so it may be supposed that ${\rm e}^{k \Delta t} \approx 1$ and $\Phi (\sqrt {k \Delta t}) \approx \frac{2}{\sqrt {\pi}} \sqrt {k \Delta t}$. Then from the Eq. (10) it is possible to find the following expression for the period of flickering $\Delta t$:

$\displaystyle \Delta t = \frac{4 \pi \lambda \delta c} {\Lambda^2 \rho^2 V^6} (T_{\rm b} - T_{\rm m})^2,$     (11)

where $ T_{\rm b} = \frac{A}{B - \lg \rho V^2 }$; A and B are some constants describing the chemical composition of meteoric matter (Bronshten 1981).

According to Eq. (11), for several points of the meteor trajectories with known $\rho$ and V we calculated the theoretical periods of the Geminid fireball flickering. For calculations the following values of quantities included in Eq. (11) were used for stony matter (Levin 1956; Bronshten 1981): $\lambda = 3 \times 10^5$ erg/cm s deg, $A = 21~000^\circ$, B = 12.5, $T_{\rm m} = 1700^\circ$, c = 107 erg/g deg and $\delta = 2.9$ g/cm3. At the beginning of flickering the calculated values of the flickering periods are in good accordance with the observed ones for the following values of the heat transfer coefficient: $\Lambda = 0.04$ for the meteor 643881, $\Lambda = 0.02$ for the meteor 761683 and $\Lambda = 0.035$ for the meteor 821691. But for these values of $\Lambda$, a close coincidence of the calculated and observed frequency of flickering is found only for the meteor 643881 (Fig. 3a, solid line), which is probably related to the lower increase in the flickering frequency (approximately from 120 Hz to 320 Hz) than in the case of the two other Geminids. For the meteors 761683 and 821691 the discrepancy between calculated and observed values of flickering frequency become more and more considerable as a meteoroids penetrate deep into the atmosphere.

It is possible to assume that this discrepancy is connected to the change of the heat transfer coefficient along the path of the meteors 761683 and 821691. Bronshten (1981) holds that for bright fireballs the rise of $\Lambda$ at the end of the meteor trajectory is caused by substantial deceleration of a meteoroid at the end part of its trajectory. This increases the heat transfer coefficient because when the velocity is lost, shielding of the meteoroid by vapours is decreased.

Representing the variation of the heat transfer coefficient $\Lambda$ versus the height h of a meteor by the exponent dependence:

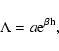\begin{displaymath}\Lambda = a {\rm e}^{\beta {\rm h}}, \end{displaymath} (12)

where a = 19.8 and $\beta = -0.10$ for the meteor 761683, and a = 0.82 and $\beta = -0.05$ for the meteor 821691 we determined the theoretical relation of flickering period $\Delta t$ versus height h(or flickering frequency $\nu_{{\rm fl}}= 1/\Delta t $ versus height h). Obtained theoretical flickering frequency-height relations are presented in Figs. 3b and 3c by solid lines, which show that they conform satisfactorily with observations (circles).

The correspondence of the calculated flickering frequency to the observed ones and their rise as the Geminid meteoroids penetrate deep in the atmosphere allows us to conclude that high-frequency ( $\nu_{{\rm fl}} \geq 100$ Hz) pulsations of Geminid brightness i.e. the flickering of the bright Geminids may be explained by the autofluctuation mechanism of meteoroid ablation in the Earth's atmosphere.

5 Conclusion

An analysis is carried out of observed features of radiation of three bright Geminid meteors manifested as regular high-frequency pulsations of brightness (flickering). The high-frequency flickering phenomenon was observed in 1.5 % of all meteors brighter than -2.5 mag photographed in Dushanbe.

The Geminid heights of appearance were calculated for the case of non-rotating meteoroids. As is known (Levin 1956; Bronshten 1981; Adolfsson & Gustafson 1994; Kruchinenko 1995), the appearance heights of meteors produced by non-rotating meteoroids are approximately 10 km higher than those produced by rotating ones. The calculated mean value of the beginning heights of the three Geminids equal to 90.7 km is very close to the mean value of their observed heights of appearance, equal to 91.4 km. The obtained results allow us to conclude that the Geminids under consideration did not rotate when entering the Earth's atmosphere.

The possibility is examined meteoroids gaining of rotation in the Earth's atmosphere owing to the fluctuating action of oncoming air molecules on different sides of the meteoroid centre of mass. It is derived that at the heights where the flickering of the Geminid fireballs were observed, the condition of "fluctuation" rotation is realized for the particles of mass $m \ll 6 \times 10^{-7}$ g. Such particles produce the meteors recorded by radar observations, but meteoroids of centimetre sizes producing bright Geminid fireballs cannot gain rotation in this way.

To explain the observed flickering phenomenon of three bright Geminids the autofluctuating mechanism of meteoroid ablation is supposed where the saturated vapors emitted and the outer pressure regular each other automatically.

The results obtained permit us to conclude that the observed high-frequency pulsations ( $\nu_{{\rm fl}} \geq 100$ Hz ) of brightness of three Geminid fireballs may be explained by an autofluctuating drop of the melting surface layer of a meteoroid, which has a cyclic character with a period corresponding to the observed period of the fireball flickering.

Acknowledgements
The authors would like to express their gratitude to the anonymous reviewer for useful comments. The annotation of the Language editor of the A&A Dr. Martine Ustin is also appreciated.

References

 
Copyright ESO 2004