A&A 428, 1-19 (2004)
DOI: 10.1051/0004-6361:20034208
Covariant gyrokinetic description of relativistic plasmas
A. Beklemishev 1 - M. Tessarotto 2
1 - Budker Institute of Nuclear Physics, 630090 Novosibirsk, Russia
2 - Department of Mathematical Sciences, University of Trieste, 34127 Trieste, Italy
Received 18 August 2003 / Accepted 20 July 2004
Abstract
A fundamental aspect of many plasma-related
astrophysical problems is the kinetic description of magnetized
relativistic plasmas in intense gravitational fields, such as in
accretion disks around compact gravitating bodies. The goal of
this paper is to formulate a gyrokinetic description for a
Vlasov-Maxwell plasma within the framework of general relativity.
A closed set of relativistic gyrokinetic equations, consisting of
the collisionless gyrokinetic equation and corresponding
expressions for the four-current density, is derived for an
arbitrary four-dimensional coordinate system. General relativity
effects are taken into account via the tetrad formalism. The
guiding-center dynamics of charged particles and the gyrokinetic
transformation are obtained accurate to the second order of the
ratio of the Larmor radius to the nonuniformity scale length. The
wave terms with arbitrary wavelength
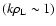 are described in the second-order (nonlinear) approximation with
respect to the amplitude of the wave. The same approximations are
used in the derivation of the gyrophase-averaged Maxwell
equations. The derivation is based on the perturbative Lagrangian
approach with a fully relativistic, four-dimensional covariant
formulation. Its results improve on existing limitations of the
gyrokinetic theory.
are described in the second-order (nonlinear) approximation with
respect to the amplitude of the wave. The same approximations are
used in the derivation of the gyrophase-averaged Maxwell
equations. The derivation is based on the perturbative Lagrangian
approach with a fully relativistic, four-dimensional covariant
formulation. Its results improve on existing limitations of the
gyrokinetic theory.
Key words: plasmas - relativity - gravitation
The gyrokinetic theory is an adequate, yet simplified, description of
collisionless magnetized plasmas. It strives to utilize the conservation of
the magnetic moment to reduce the number of effective degrees of freedom of
charged particles. In this respect it is similar to the drift-kinetic
approximation. However, it goes further than the drift approximation, since
it allows short-wavelength (comparable to the Larmor radius,
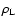 )
perturbations of the background fields.
)
perturbations of the background fields.
From the mathematical viewpoint, the dynamics of Hamiltonian systems can be
expressed, in principle, in arbitrary hybrid (i.e., non-canonical) state
variables. The search of phase-space transformations yielding "simpler''
equations of motion has long motivated theoretical research in physics and
mathematical physics. Among such transformations, a particular case is
provided by the gyrokinetic transformation, yielding hybrid variables
defined in such a way that one of them, the so-called gyrophase angle, is
ignorable. This transformation can only be introduced when particles move in
a sufficiently strong magnetic field.
For a certain class of problems in plasma physics and astrophysics, the
existing limitations of the standard gyrokinetic theory
(Hahm et al. 1988; Brizard & Chan 1999; Cooper 1997; Littlejohn 1979,1984; Boozer 1996) make its use difficult or impossible. In
particular, this involves the description of experiments in which the
electric field may become comparable in strength to the magnetic field (so
that the drift velocity becomes relativistic), and the study of relativistic
plasma flows in gravitational fields, which are observed or assumed to exist
in accretion disks and related plasma jets around neutron stars, black
holes, and active galactic nuclei (Frank et al. 1992). The finite Larmor radius
effects and the influence of short wavelength electromagnetic perturbations
are also expected to play a fundamental role in particle dynamics. The
present paper aims at extending the applicability range of gyrokinetic
theory to include these features, and at providing an effective tool for use
in plasma-physics-related problems in astrophysics.
The conventional non-relativistic gyrokinetic theory (Hahm et al. 1988; Littlejohn 1979) has
been generalized to include only some relativistic effects, which are
essential for the description of the confinement of fusion products in
thermonuclear reactors (Brizard & Chan 1999; Cooper 1997; Littlejohn 1984; Boozer 1996), namely, the particle itself is
considered relativistic, while its drift velocity is not. This deficiency
has been pointed out by Pozzo & Tessarotto (1998), who attempted to write the theory in the
reference frame moving with the fluid velocity, where all drifts should be
first order in the expansion parameter, and the question about relativistic
drifts should disappear. However, it proved to be more rewarding to create
the covariant theory (Beklemishev & Tessarotto 1999), as it makes use of the term
"relativistic'', i.e., with relation to any reference frame, in its
full sense. This approach is inherently more general and symmetric than the
non-relativistic treatment and its "relativistic'' generalizations. As a
result, even the non-relativistic limit of the theory is found to have a
broader applicability range than the standard derivation. In particular,
covariant formulation allows self-consistent inclusion of the gravitational
field, which makes the theory suitable for astrophysical applications.
In our previous paper (Beklemishev & Tessarotto 1999) the development of the covariant theory
(derivation of the gyrokinetic transformation) was carried out through first
order in the expansion parameter, and without the wave fields. It has been
shown that the fundamental adiabatic invariant of a particle, i.e., its
magnetic moment, as well as the ignorable gyrophase, can be defined as
Lorentz invariant, independent of the reference frame. Also, the derivation
itself becomes algebraically simple due to the internal symmetry of the
electromagnetic field in the four-dimensional formulation. Covariant
formulation allows the derived equations to be easily rendered for any
coordinate system in four-dimensional Riemann space-time. It is important
for astrophysics applications, as well as for problems where description in
curvilinear magnetic coordinates is convenient. Although we do not use
canonical variables, any coordinate system compatible with canonical
variables can be imposed on the final result. Here it is necessary to note
that the so-called relativistic drift Hamiltonian (Boozer 1996), and the
gyrokinetic theories based on it (Cooper 1997), are limited by the
applicability range of the drift equations given by Northrop (1963), i.e., assume
non-relativistic drifts. The covariant drift equations require no such
assumptions.
Covariant descriptions of guiding center dynamics have been published
earlier, in the most complete form by Fradkin (1978). He first used the
decomposition of motion of a charged particle into two quasi-independent
motions in orthogonal invariant planes of the electromagnetic field tensor.
Equations of motion were derived in the first order in inhomogeneity,
without the wave fields. However, explicit use of the proper time for
parameterization of the trajectory makes his expressions difficult to adapt
to the gyrokinetic description, where parameterization should be applicable
to the guiding center trajectory. Later, Beklemishev & Tessarotto (1999) showed that without such
parameterization the choice of the decomposition planes becomes a matter of
convenience rather than necessity.
The goal of the present work is two-fold. First, adopting the covariant
gyrokinetic approach developed earlier (Beklemishev & Tessarotto 1999) we intend to describe
particle dynamics in the presence of non-uniform and strong electromagnetic (EM) and gravitational fields, accurate to second order in the Larmor
radius, and treating consistently the effect of short-wavelength EM
perturbations. The basic features of the approach, allowing the relativistic
drifts typical of many astrophysical plasmas, are the assumption of a
non-vanishing parallel electric field and the description of particle
dynamics in the field-related basis tetrad, which allows a simpler
formulation of the relativistic equations of motion. Second, the
perturbative theory is employed to derive the relativistic Vlasov-Maxwell
equations expressed in gyrokinetic variables accurate through second order
in
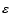 (which is the ratio of the gyro-radius/gyrotime to the
equilibrium gradient length/time) while the wave fields are taken into
account in the second order in the amplitude. The gyrophase-averaged
expression of the four-current density appearing in Maxwell equations is
evaluated with the same accuracy.
(which is the ratio of the gyro-radius/gyrotime to the
equilibrium gradient length/time) while the wave fields are taken into
account in the second order in the amplitude. The gyrophase-averaged
expression of the four-current density appearing in Maxwell equations is
evaluated with the same accuracy.
In contrast to non-covariant formulations, since the space and time
variables are treated in a parallel fashion, the applicability limits of
gyrokinetic theory are extended - the wave fields can be fast oscillating in
time (
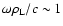 ), as well as in space (
), as well as in space (
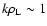 ), while the customary assumption
), while the customary assumption
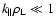 is not required. As a result, we find a contribution to the magnetic
moment which is proportional to the usually neglected parallel component of
the wave-field. An important feature of this work is its relative
simplicity, which allows us to present results with the gyrophase-averaging
performed explicitly. (The usual way of doing this is by leaving the
averaging along the particle trajectory to the reader's computer;
see, for example, Brizard & Chan 1999.) However, currently there is also a limitation linked
to our approach, namely, in the case of a vanishing background parallel
electric field, only certain polarizations of the wave field are allowed.
Namely, the wave field should be describable by just two components of the
vector potential, both orthogonal to the magnetic field (in the reference
frame where the electric field vanishes), or have a large wavelength, to be
described as part of the main field. We intend to eliminate this restriction
in the future.
is not required. As a result, we find a contribution to the magnetic
moment which is proportional to the usually neglected parallel component of
the wave-field. An important feature of this work is its relative
simplicity, which allows us to present results with the gyrophase-averaging
performed explicitly. (The usual way of doing this is by leaving the
averaging along the particle trajectory to the reader's computer;
see, for example, Brizard & Chan 1999.) However, currently there is also a limitation linked
to our approach, namely, in the case of a vanishing background parallel
electric field, only certain polarizations of the wave field are allowed.
Namely, the wave field should be describable by just two components of the
vector potential, both orthogonal to the magnetic field (in the reference
frame where the electric field vanishes), or have a large wavelength, to be
described as part of the main field. We intend to eliminate this restriction
in the future.
Another work dealing with the covariant representation of the gyrokinetic
theory (for a flat space-time) is the Ph.D. Thesis of Boghosian (1987). It extends
the covariant description of charged particle guiding center motion
developed by Fradkin (1978). In line with non-covariant treatments Boghosian
assumes a vanishing parallel component of the electric field and the usual
gyrokinetic ordering for admissible wave forms, and thus has to modify
Maxwell equations to maintain the assumed properties. His derivation is also
conducted only to first-order both in nonuniformity and in the
wave-amplitude.
The structure of the paper is as follows: The hybrid Hamilton variational
principle is formulated in Sect. 2. In Sect. 3 we present the definition of
the basis tetrad and its link to the Faraday tensor. In Sect. 4 the
relativistic gyrokinetic transformation is derived to second order in
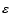 ,
and in the wave amplitude. The Euler equations for the
gyrocenter trajectories are formulated in Sect. 5. Maxwell equations with
the current and charge densities, expressed in terms of the distribution
function as a function of the gyrokinetic variables, and integrated in the
gyrophase, are presented in Sect. 6. In the Conclusion the results of the
paper are summarized.
,
and in the wave amplitude. The Euler equations for the
gyrocenter trajectories are formulated in Sect. 5. Maxwell equations with
the current and charge densities, expressed in terms of the distribution
function as a function of the gyrokinetic variables, and integrated in the
gyrophase, are presented in Sect. 6. In the Conclusion the results of the
paper are summarized.
Construction of the gyrokinetic transformation for the one-particle
Hamiltonian system requires a description of the particle dynamics in
phase-space. It is possible to redefine the Hamilton variational principle
in such a way that it becomes suitable for the phase-space description of
motion in non-canonical variables (Cary & Littlejohn 1983). We refer to this as "the
hybrid Hamilton variational principle''. In the framework of general
relativity the four-dimensional formulation of the Hamilton variational
principle is well known (Landau & Lifshits 1975). It makes it possible to describe the
particle trajectory (or its world-line) as a four-dimensional extremal
curve. In this section a hybrid form of this variational principle, suitable
for the description of particle dynamics in the seven-dimensional
phase-space (Beklemishev & Tessarotto 1999), is recalled.
The relevant tensor notations are standard. Thus,
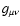 denotes the
metric tensor components, characterizing the coordinate system (and the
underlying space-time structure). It also provides the connection between
the co- and countervariant components of four-vectors (henceforth referred
to as 4-vectors)
denotes the
metric tensor components, characterizing the coordinate system (and the
underlying space-time structure). It also provides the connection between
the co- and countervariant components of four-vectors (henceforth referred
to as 4-vectors)
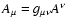 .
The signature of
.
The signature of
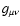 is assumed to be
is assumed to be
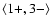 ,
while the invariant interval
,
while the invariant interval 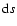 is
defined as
is
defined as
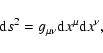 |
(1) |
where the Greek indices are assumed to go through
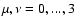 .
.
The four-velocity 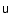 is then defined in terms of its countervariant
components according to
is then defined in terms of its countervariant
components according to
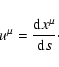 |
(2) |
The scalar product of any 4-vector 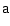 by itself, or its square
length,
by itself, or its square
length,
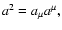 is not sign-definite. If its sign is
negative, we shall call the 4-vector "space-like'', while if it is
positive, the 4-vector is "time-like''. Unit 4-vectors are those with
square lengths equal to
is not sign-definite. If its sign is
negative, we shall call the 4-vector "space-like'', while if it is
positive, the 4-vector is "time-like''. Unit 4-vectors are those with
square lengths equal to 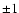 .
In these terms, because of (1)
.
In these terms, because of (1)
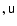 is the unit, time-like 4-vector
is the unit, time-like 4-vector
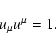 |
(3) |
The motion or the world-line of a particle with rest-mass ma and charge qa in prescribed fields in phase space can be found from the Hamilton
variational principle
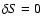 ,
as the extremal of the functional
,
as the extremal of the functional
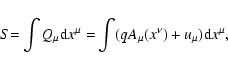 |
(4) |
where
q=qa/mac2. Ideally, a variational principle in phase space
should yield the standard relativistic equation of motion of the particle,
plus the relationship between velocity and displacement, Eq. (2). As
shown by Beklemishev & Tessarotto (1999), this is indeed the case for the functional (4),
but only for variations of 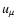 occurring on the hypersurface
occurring on the hypersurface
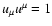 .
In this sense the phase space is only seven-dimensional. The
above variational principle is independent of the parameterization of the
world lines.
.
In this sense the phase space is only seven-dimensional. The
above variational principle is independent of the parameterization of the
world lines.
Finally, we note that the above variational principle, as any Lagrangian
variational principle, is gauge invariant, i.e., any change of the
generating differential 1-form of the type
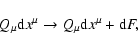 |
(5) |
where F is an arbitrary smooth function of coordinates 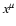 and zi, does not change the extremal curve.
and zi, does not change the extremal curve.
The use of a tetrad of four-vectors is a well-known type of description of
curved space-time (Landau & Lifshits 1975), which makes it possible to replace complex
derivatives of the metric tensor by derivatives of the tetrad components. We
adopt this approach below, while also finding it convenient to link our
tetrad to properties of the electromagnetic field, or the Faraday tensor,
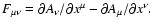
We first introduce an orthogonal basis of unit 4-vectors
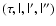 so that the last three
4-vectors are space-like, and
so that the last three
4-vectors are space-like, and
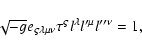 |
(6) |
where
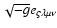 is the purely antisymmetric
tensor. This last requirement is necessary for distinguishing between the
left and right basis configurations. As long as the orientation of
is the purely antisymmetric
tensor. This last requirement is necessary for distinguishing between the
left and right basis configurations. As long as the orientation of
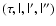 is arbitrary, it can be constructed
with 6 free parameters (3 pure space rotations and 3 space-time rotations).
The choice of orientation is assumed to depend only on
is arbitrary, it can be constructed
with 6 free parameters (3 pure space rotations and 3 space-time rotations).
The choice of orientation is assumed to depend only on 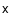 .
.
A special choice of orientation links the basis
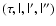 to the electromagnetic field tensor,
to the electromagnetic field tensor,
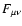 .
We shall refer to this choice of basis as
field-related and use it henceforth. With this choice the
.
We shall refer to this choice of basis as
field-related and use it henceforth. With this choice the
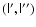 -plane coincides with the
space-like invariant plane of the antisymmetric tensor
-plane coincides with the
space-like invariant plane of the antisymmetric tensor
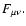 In
some sense this corresponds to the magnetic
coordinates of non-relativistic treatments. Fradkin (1978)
used these invariant planes of the electromagnetic field tensor for the
decomposition of motion of a charged particle.
In
some sense this corresponds to the magnetic
coordinates of non-relativistic treatments. Fradkin (1978)
used these invariant planes of the electromagnetic field tensor for the
decomposition of motion of a charged particle.
Any non-degenerate antisymmetric tensor of rank 4,
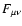 in
particular, has two orthogonal invariant planes. In our case one of them is
space-like, i.e., any vector belonging to it has negative length, while the
other contains both time-like and space-like vectors. Each of the invariant
planes has an associated eigenvalue. This means that if
in
particular, has two orthogonal invariant planes. In our case one of them is
space-like, i.e., any vector belonging to it has negative length, while the
other contains both time-like and space-like vectors. Each of the invariant
planes has an associated eigenvalue. This means that if
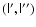 is the first invariant plane, then
is the first invariant plane, then
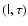 is the
other, and if H and E are the eigenvalues of
is the
other, and if H and E are the eigenvalues of
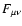 ,
then
,
then
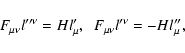 |
(7) |
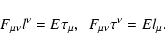 |
(8) |
(Both equalities in the second line have the same sign due to the
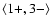 signature of the metric tensor. The physical meaning is that H and E are
the magnetic and electric field strengths in the reference frame where the
electric and the magnetic fields are parallel. The signs are chosen in such
a way that in this frame
signature of the metric tensor. The physical meaning is that H and E are
the magnetic and electric field strengths in the reference frame where the
electric and the magnetic fields are parallel. The signs are chosen in such
a way that in this frame
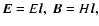 if
if
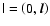 is a pure-space vector. For this reason the sign
of H is opposite to that in our previous paper (Beklemishev & Tessarotto 1999), consequently
the sign of the magnetic moment is also the opposite.) With this choice one
can assume
is a pure-space vector. For this reason the sign
of H is opposite to that in our previous paper (Beklemishev & Tessarotto 1999), consequently
the sign of the magnetic moment is also the opposite.) With this choice one
can assume 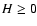 ,
without loss of generality, while the sign of E is
determined by the invariance of the scalar product
,
without loss of generality, while the sign of E is
determined by the invariance of the scalar product
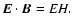
Due to these properties of the basis, the Faraday tensor can be fully
expressed via its components as
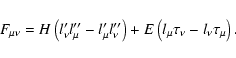 |
(9) |
The bivector combinations entering the above expression
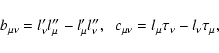 |
(10) |
can be viewed as linear operators, which combine projection on an
invariant plane with an orthogonal turn in it, i.e., each carries full
information about an oriented plane. Then
while the pure projection operators
 introduced by Fradkin (1978) can be expressed as
introduced by Fradkin (1978) can be expressed as
Since
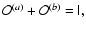 and
and
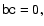 it is easy to check that the inverse of the Faraday tensor,
it is easy to check that the inverse of the Faraday tensor,
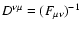 is
is
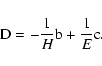 |
(11) |
It exists, provided that
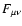 is not degenerate, i.e.,
is not degenerate, i.e., 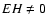 .
This inverse of the Faraday tensor can also be expressed via its dual,
namely,
.
This inverse of the Faraday tensor can also be expressed via its dual,
namely,
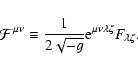 |
(12) |
Indeed,
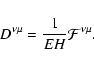 |
(13) |
The object of gyrokinetics is to introduce a new set of phase-space
variables (called the gyrokinetic
variables) such that the variable describing the rotation
angle along the Larmor orbit (i.e., the gyrophase  )
becomes
ignorable. This happens, by definition, when the Lagrangian (or, more
generally, the functional) is independent of
)
becomes
ignorable. This happens, by definition, when the Lagrangian (or, more
generally, the functional) is independent of  .
Once an ignorable
variable is found, the number of corresponding Euler equations is reduced by
one, and the new variables allow simplified numerical calculations, as the
motion is effectively integrated over the fast Larmor rotation. The
one-to-one transformation from the original set of phase-space variables
.
Once an ignorable
variable is found, the number of corresponding Euler equations is reduced by
one, and the new variables allow simplified numerical calculations, as the
motion is effectively integrated over the fast Larmor rotation. The
one-to-one transformation from the original set of phase-space variables
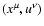 to the gyrokinetic variables is called the
gyrokinetic transformation. In what
follows to find these variables we use the Lagrangian perturbative approach,
which is equivalent (in broad terms) to the Lie-transform method, though
more direct.
to the gyrokinetic variables is called the
gyrokinetic transformation. In what
follows to find these variables we use the Lagrangian perturbative approach,
which is equivalent (in broad terms) to the Lie-transform method, though
more direct.
Indeed, we can search for the necessary transformation, representing it as a
Taylor-series expansion in small parameters (inhomogeneity and wave
amplitude). Then, in each order we can require the transformed functional to
be independent of the gyrophase (the ignorable variable), and thus find the
transformation and the new phase-independent functional order by order. For
this we should be sure that 1) the solution in the necessary order exists;
and 2) that the procedure converges. The existence of the solution depends
on the choice of the expansion form and is proven operationally, i.e., by
direct construction. Then the true dynamical system becomes replaced by the
new artificial one, described by the phase-independent Lagrangian of that
order. There is also the problem of convergence, i.e., how accurate the
gyrokinetic description is. This problem is common to all gyrokinetic (and
drift) theories and has not yet been explored in detail. From the physical
viewpoint, the artificial system has no cyclotron resonances, while the real
one has them, but their width decreases with the small parameters. The
gyrokinetic approach cannot work within this thin but possibly interlinking
Arnold web of resonances, where the adiabatic invariants are not conserved.
Outside the resonances one can claim that since the difference between the
real and the artificial Lagrangians is limited and tends to zero within some
suitable measure, the behaviour of the gyrokinetic system is similar to that
of the real systems.
We begin the search for the gyrokinetic transformation by a suitable
definition of the small parameters, i.e., we assume that the curvature
radius of the space-time and the gradient lengths of the background
electromagnetic fields are much larger than the Larmor radius characterizing
the particle path. However, we allow for the existence of wave fields with
sharp gradients [
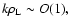 including
including
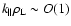 ], and rapidly varying in time [
], and rapidly varying in time [
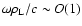 ], while such fields are assumed suitably smaller in strength than the
background field. (We stress that, unlike in conventional formulations of
gyrokinetic theory, this type of ordering is required in a covariant theory
due to the reference-frame dependence of the ordering assumptions involving
space and time scale lengths of the perturbations.) For this purpose we
introduce the ordering scheme following the notation of Littlejohn (1984):
], while such fields are assumed suitably smaller in strength than the
background field. (We stress that, unlike in conventional formulations of
gyrokinetic theory, this type of ordering is required in a covariant theory
due to the reference-frame dependence of the ordering assumptions involving
space and time scale lengths of the perturbations.) For this purpose we
introduce the ordering scheme following the notation of Littlejohn (1984):
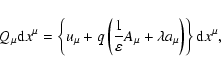 |
(14) |
where
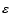 and
and 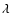 are formal small parameters (they should
be set to 1 in the final results) allowing distinction between the
large-scale background field
are formal small parameters (they should
be set to 1 in the final results) allowing distinction between the
large-scale background field 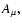 and the wave fields given by
and the wave fields given by 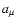 .
We search for the gyrokinetic transformation
.
We search for the gyrokinetic transformation
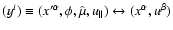 in the form of an expansion in powers of
in the form of an expansion in powers of
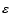 :
:
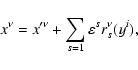 |
(15) |
where  is the ignorable phase variable (gyrophase),
is the ignorable phase variable (gyrophase), 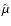 and
and
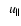 represent two more independent velocity characteristics
(to be defined later),
represent two more independent velocity characteristics
(to be defined later),
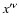 is the 4-vector
guiding center position,
is the 4-vector
guiding center position,
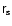 are
arbitrary 4-vector functions of the new variables (yi) to be
determined. We require that
are
arbitrary 4-vector functions of the new variables (yi) to be
determined. We require that
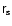 are purely oscillatory
in
are purely oscillatory
in  ,
i.e., the
,
i.e., the  -averages of
-averages of
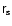 are zero,
as part of the
are zero,
as part of the
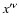 - definition. Note that the above
descriptions of the new variables
- definition. Note that the above
descriptions of the new variables
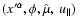 will acquire precise mathematical meaning only as a
result of the search for the gyrokinetic transformation.
will acquire precise mathematical meaning only as a
result of the search for the gyrokinetic transformation.
This search consists in applying the expansion (15) to the fundamental
1-form (14), and imposing the requirement that it is independent of  in each order. Since the 1-form itself depends on
in each order. Since the 1-form itself depends on 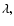 expansion
in this parameter will also appear.
expansion
in this parameter will also appear.
Since the difference between
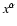 and
and
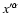 is assumed
small compared to the gradient lengths, the background field components
(unlike the wave terms) can be expanded in the Taylor series
is assumed
small compared to the gradient lengths, the background field components
(unlike the wave terms) can be expanded in the Taylor series
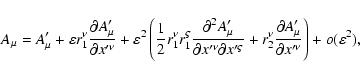 |
(16) |
where
 Furthermore, we assume
that the gravitational field and the metric coefficients
Furthermore, we assume
that the gravitational field and the metric coefficients
 have
the same order of the gradient length, and thus can also be expanded around
have
the same order of the gradient length, and thus can also be expanded around
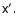 However, it is not necessary. It is sufficient to use
the primed metric tensor for lifting and lowering indexes of primed tensor
components. Finally, the
However, it is not necessary. It is sufficient to use
the primed metric tensor for lifting and lowering indexes of primed tensor
components. Finally, the
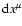 vector components in the new
variables (yi) look like
vector components in the new
variables (yi) look like
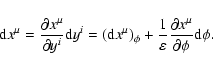 |
(17) |
Here
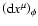 means the differential of
means the differential of 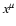 with respect to all other variables of the set
with respect to all other variables of the set
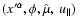 keeping
keeping  constant. As usual, the
factor
constant. As usual, the
factor
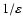 is introduced to denote the fast dependence
characterizing the Larmor rotation.
is introduced to denote the fast dependence
characterizing the Larmor rotation.
Equation (15) define only four out of seven transformation rules for
the gyrokinetic transformation
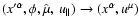 .
The rest are chosen in the
following way.
.
The rest are chosen in the
following way.
First, we express the four-velocity in the new variables as
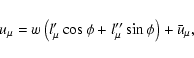 |
(18) |
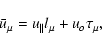 |
(19) |
which can be also regarded as the definition for the gyrophase  :it is defined as an angle in the velocity subspace,
where we introduce the cylindrical coordinate system. This definition is
covariant with respect to transformations of the space-time coordinate
system, which may change the vector components, but not the vectors
themselves. Note that the tetrad is linked to the position of the particle, x, rather than
:it is defined as an angle in the velocity subspace,
where we introduce the cylindrical coordinate system. This definition is
covariant with respect to transformations of the space-time coordinate
system, which may change the vector components, but not the vectors
themselves. Note that the tetrad is linked to the position of the particle, x, rather than
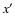 ,
so that its components
should be transformed to
,
so that its components
should be transformed to
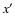 as well.
as well.
Furthermore, we assume that
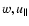 and uo are independent
of
and uo are independent
of  .
The validity of this assumption is justified by the existence of
the solution (at least for a non-degenerate Faraday tensor). Then, the
.
The validity of this assumption is justified by the existence of
the solution (at least for a non-degenerate Faraday tensor). Then, the  -independent part of the 4-velocity
-independent part of the 4-velocity
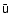 is not completely
arbitrary, but satisfies certain restrictions following from the requirement
is not completely
arbitrary, but satisfies certain restrictions following from the requirement
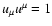 for all
for all  :
:
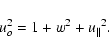 |
(20) |
Any two of three scalar functions w,uo or
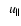 can be
considered independent characteristics of velocity, while the third can be
expressed via Eq. (20).
can be
considered independent characteristics of velocity, while the third can be
expressed via Eq. (20).
Let us substitute expressions (15), (17) into (14) and
drop terms of order
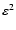 or smaller:
or smaller:
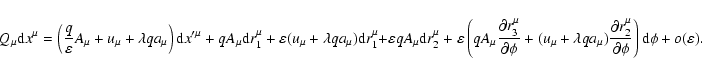 |
(21) |
Following Beklemishev & Tessarotto (1999) we construct the gauge-modified functional
so that after using Eq. (16) to represent 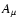 and
and
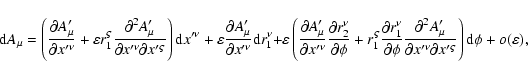 |
(23) |
we get
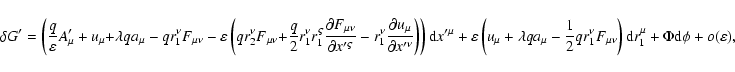 |
(24) |
where
![\begin{displaymath}\Phi =\varepsilon \left( r_{1}^{\nu }\frac{\partial u_{\mu }}...
...{\nu }^{\prime }}{\partial x^{\prime {\mu }}}\right]
\right) ,
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img102.gif) |
(25) |
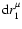 is given by Eq. (17), and
is given by Eq. (17), and
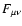 is the tensor of the electromagnetic field at
is the tensor of the electromagnetic field at
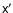 :
:
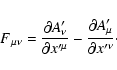 |
(26) |
We also decomposed the tetrad vectors around
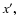
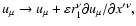 in Eqs. (24), (25), so that the definition of
in Eqs. (24), (25), so that the definition of 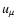 is shifted to that point.
is shifted to that point.
Now it is straightforward to eliminate from
 terms
oscillating in
terms
oscillating in  by properly defining displacements
by properly defining displacements
 We carry out the calculations for each order in
We carry out the calculations for each order in
 and
and 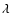 .
.
Initially we drop all terms in Eq. (24), which are of order
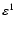 or higher, while retaining contributions of order
or higher, while retaining contributions of order 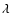 .
The conditions for
.
The conditions for  to be ignorable for the gauge-modified
functional
to be ignorable for the gauge-modified
functional
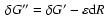 ,
where R is an arbitrary Gauge function look like
,
where R is an arbitrary Gauge function look like
| |
|
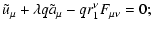 |
(27) |
| |
|
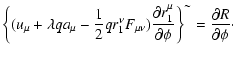 |
(28) |
Here 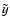 denotes the oscillating part of y, namely
denotes the oscillating part of y, namely
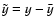 ,
where
,
where
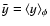 is the
is the  -independent part of y. By a proper choice of the gauge-function R one
can always satisfy Eq. (28). This means that
-independent part of y. By a proper choice of the gauge-function R one
can always satisfy Eq. (28). This means that
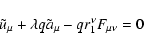 |
(29) |
yields the only essential requirements. The physical meaning of Eq.( In the text
29
) is the relationship between the first-order gyro-radius
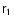 and the velocity
and the velocity
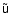 along the Larmor orbit. The time-like
component describes changes in energy due to displacements of charge in the
electric field.
along the Larmor orbit. The time-like
component describes changes in energy due to displacements of charge in the
electric field.
If the above requirements (27) and (28) are satisfied and  is ignorable, the phase-space variational principle in our
approximation can be expressed as
is ignorable, the phase-space variational principle in our
approximation can be expressed as
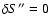 with
with
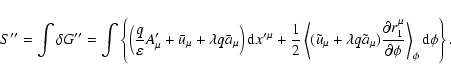 |
(30) |
Equation (29) can be formally solved for
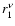 to yield
to yield
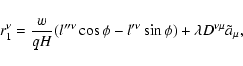 |
(31) |
where
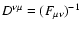 is given by Eq. (11), provided that
is given by Eq. (11), provided that
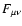 is not degenerate. As a result, the
is not degenerate. As a result, the  -independent functional
-independent functional
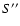 becomes
becomes
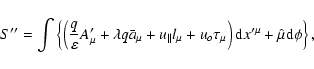 |
(32) |
where 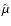 is the wave-field-modified magnetic moment, accurate to
order
is the wave-field-modified magnetic moment, accurate to
order
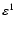 ,
,
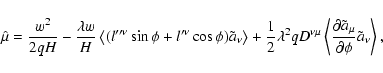 |
(33) |
and
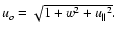
If the Faraday tensor is degenerate but the magnetic field is non-zero,
i.e., E=0, 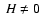 ,
a solution of Eq. (29) exists for a special
choice of the wave potential satisfying
,
a solution of Eq. (29) exists for a special
choice of the wave potential satisfying
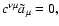 i.e., when the
i.e., when the
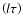 projection of
projection of 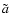 is zero.
Then the above expressions are valid with the replacement
is zero.
Then the above expressions are valid with the replacement
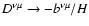 .
For other choices of the wave potential
there is no solution, meaning that we need to modify our representation of
the gyrokinetic transformation, Eqs. (15) and (18). This case
will be discussed elsewhere.
.
For other choices of the wave potential
there is no solution, meaning that we need to modify our representation of
the gyrokinetic transformation, Eqs. (15) and (18). This case
will be discussed elsewhere.
The evaluation of the gyrophase averages involving the wave field 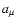 is, of course, the difficult part. The reason for this is the necessity of
transforming the given function of space-time coordinates
is, of course, the difficult part. The reason for this is the necessity of
transforming the given function of space-time coordinates
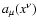 into a function of new variables, while the transformation rule (15), (31) is itself dependent on
into a function of new variables, while the transformation rule (15), (31) is itself dependent on 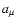 .
A solution of the equation
.
A solution of the equation
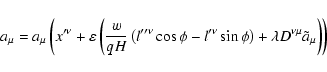 |
(34) |
can only be obtained by expanding in powers of 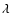 .
.
The solution of the problem in the limit
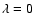 has already been
published by Beklemishev & Tessarotto (1999). By varying the functional (32) with respect to
has already been
published by Beklemishev & Tessarotto (1999). By varying the functional (32) with respect to  ,
we find
,
we find
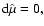 i.e.,
i.e.,
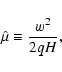 |
(35) |
the magnetic moment calculated in the reference frame where 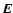 and
and 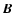 are parallel is the first integral of motion in our approximation.
are parallel is the first integral of motion in our approximation.
Now it is possible to rewrite the functional (32) using Eq. (19) and
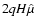 in place of w2:
in place of w2:
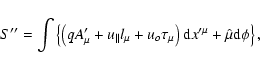 |
(36) |
with
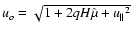 .
.
Using the  -independent functional (36) in the variational
principle,
-independent functional (36) in the variational
principle,
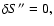 defines the particle trajectory in
terms of the new gyrokinetic variables
defines the particle trajectory in
terms of the new gyrokinetic variables
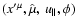 .
This set is non-canonical, but further
transformations of the variables (not involving
.
This set is non-canonical, but further
transformations of the variables (not involving  )
also lead to
)
also lead to  -independent functionals, and thus can be used to transform to canonical
variables, if necessary.
-independent functionals, and thus can be used to transform to canonical
variables, if necessary.
We return to the approximation (24) with
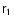 determined by
the lower-order requirement (29). This yields
determined by
the lower-order requirement (29). This yields
Choosing the independent velocity variables to be 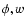 and
and
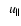 ,
and noting that
,
and noting that
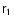 is independent of
is independent of
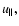 we can write
we can write
 |
(37) |
Inserting this into
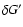 leads to the following conditions
for the gauge-modified functional,
leads to the following conditions
for the gauge-modified functional,
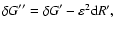 with arbitrary
with arbitrary 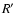 ,
to be
independent of
,
to be
independent of  :
:
| |
|
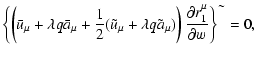 |
(38) |
| |
|
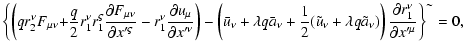 |
(39) |
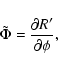 |
(40) |
where 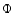 is given by Eq. (25). The last equation can always be
satisfied by a suitable choice of
is given by Eq. (25). The last equation can always be
satisfied by a suitable choice of 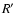 ,
Eqs. (39) define the
second-order displacement
,
Eqs. (39) define the
second-order displacement
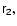 while Eq. (38) can be regarded as a solvability
condition. Using the solution for
while Eq. (38) can be regarded as a solvability
condition. Using the solution for
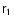 it can also be rewritten as
it can also be rewritten as
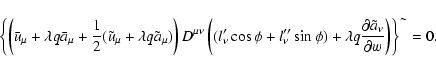 |
(41) |
With
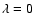 ,
and in view of the antisymmetric properties of
,
and in view of the antisymmetric properties of
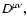 Eq. (41) becomes
Eq. (41) becomes
which is satisfied identically if the
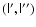 -plane is the invariant plane of
-plane is the invariant plane of
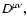 since it is
orthogonal to
since it is
orthogonal to
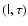 .
Thus the
field-related choice of the basis vectors
(see Eqs. (7), (8)) is sufficient for the solvability of the second-order
problem.
.
Thus the
field-related choice of the basis vectors
(see Eqs. (7), (8)) is sufficient for the solvability of the second-order
problem.
In the current approximation,
Then, Eq. (39) can be rewritten as
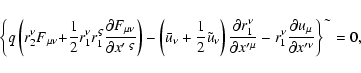 |
(42) |
while the  -independent functional becomes
-independent functional becomes
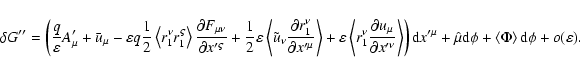 |
(43) |
The average
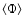 is zero, and we get
is zero, and we get
as in the lower order approximation, i.e.,
there are no second-order (in
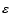 )
corrections to the magnetic moment. Thus, the second order modifications to
the Lagrangian can be described as inhomogeneity contributions to the
effective electromagnetic potential, while the form of the adiabatic
invariant remains unchanged.
)
corrections to the magnetic moment. Thus, the second order modifications to
the Lagrangian can be described as inhomogeneity contributions to the
effective electromagnetic potential, while the form of the adiabatic
invariant remains unchanged.
Using the explicit expression for
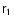 it is possible to evaluate averages, so that
it is possible to evaluate averages, so that
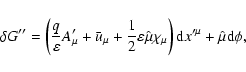 |
(44) |
where
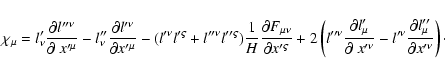 |
(45) |
Describes the inhomogeneity of the electromagnetic field.
As one can see, it is not necessary to actually solve for
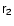 to find the transformed Lagrangian. It is only necessary to be sure that the
solution exists, which is true for the "field-related'' choice of the basis.
to find the transformed Lagrangian. It is only necessary to be sure that the
solution exists, which is true for the "field-related'' choice of the basis.
We proceed by considering the linear approximation in the wave-field
amplitude without high order curvature effects. As noted above, the main
problem here is the transformation of the highly-local wave field
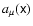 ,
where
,
where 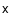 is the particle position, to the guiding-center
coordinates
is the particle position, to the guiding-center
coordinates
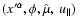 .
The
Taylor-expansion procedure used above for the transformation of the
equilibrium field fails if the wavelength is sufficiently short. To avoid
this problem, Eq. (34) is solved using Fourier analysis and
expansion in powers of
.
The
Taylor-expansion procedure used above for the transformation of the
equilibrium field fails if the wavelength is sufficiently short. To avoid
this problem, Eq. (34) is solved using Fourier analysis and
expansion in powers of 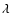 .
.
Assume that the wave field is given in terms of its Fourier components
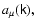 then Eq. (34) becomes
then Eq. (34) becomes
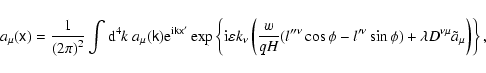 |
(46) |
where only the second exponential factor depends on  .
.
Here the ordering of the wave-vector 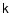 is such that
is such that
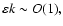 as usual (Littlejohn 1984) , except that the time-like component of
as usual (Littlejohn 1984) , except that the time-like component of 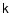 is proportional to the wave frequency, and the ordering for it is
equivalent to
is proportional to the wave frequency, and the ordering for it is
equivalent to
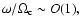 where
where
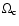 is the
cyclotron frequency, and not
is the
cyclotron frequency, and not
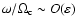 as in
conventional approaches; besides, the above ordering is also applicable to
as in
conventional approaches; besides, the above ordering is also applicable to
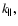 i.e.,
i.e.,
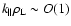 is assumed in
place of the usual ordering
is assumed in
place of the usual ordering
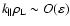 .
Therefore, our approach in this respect has a wider applicability range.
This is inevitable, for the reference frame may move with relativistic
velocity across the short-wavelength wave field, so that fast oscillations
in time may result anyway. However, the particle, drifting across the wave
field, will experience a quite definite oscillation frequency as well as the
wavelength, which is taken into account by our definition of
.
Therefore, our approach in this respect has a wider applicability range.
This is inevitable, for the reference frame may move with relativistic
velocity across the short-wavelength wave field, so that fast oscillations
in time may result anyway. However, the particle, drifting across the wave
field, will experience a quite definite oscillation frequency as well as the
wavelength, which is taken into account by our definition of
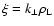 ,
introduced below.
,
introduced below.
We can calculate the required averages in Eqs. (32) and (33) by
using the expansion of Eq. (46) into a Fourier series in  .
We
use the following identity (Abramovits & Stegun 1972)
.
We
use the following identity (Abramovits & Stegun 1972)
![\begin{displaymath}\exp \left[ {\rm i}\zeta \sin \psi \right] =\sum_{n=-\infty }...
...
}J_{n}\left( \zeta \right) \exp \left( {\rm i}n\psi \right) ,
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img180.gif) |
(47) |
to get
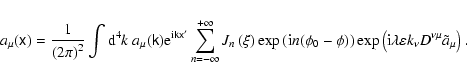 |
(48) |
Here
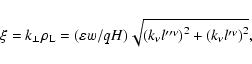 |
(49) |
where
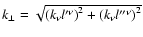 is the length of
is the length of
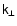 , which is the projection of
, which is the projection of 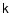 on the
on the
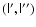 -plane;
-plane;
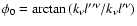 is the angle of
is the angle of
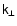 with respect to the
with respect to the
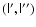 -basis,
-basis,
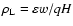 is the Larmor radius.
is the Larmor radius.
To the order
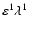 ,
,
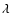 in the expression (48) can be set
to 0, so that its zero-order solution is just
in the expression (48) can be set
to 0, so that its zero-order solution is just
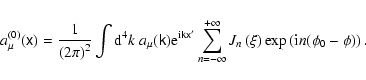 |
(50) |
Note that neglecting the last exponent in Eq. (48) or solving by
expansion in powers of 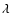 is possible only if the particle
displacement from the equilibrium orbit due to the wave field is much
smaller than the wavelength.
is possible only if the particle
displacement from the equilibrium orbit due to the wave field is much
smaller than the wavelength.
Now the averages, present in expressions (32), (33), become
| |
|
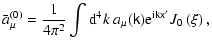 |
(51) |
| |
|
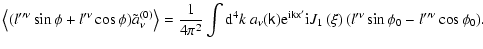 |
(52) |
So that to the order
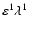
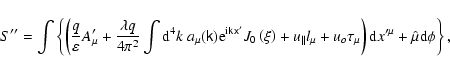 |
(53) |
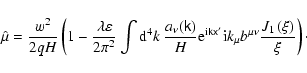 |
(54) |
Note that this definition of 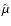 is invariant under gauge
transformations of
is invariant under gauge
transformations of 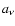 ,
and the adiabatic invariant can also be
rewritten in terms of Fourier components of the electromagnetic field tensor
of the wave
,
and the adiabatic invariant can also be
rewritten in terms of Fourier components of the electromagnetic field tensor
of the wave
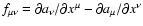 :
:
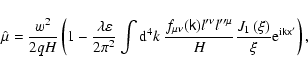 |
(55) |
where
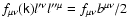 is essentially the parallel component of the wave
field. This effect is usually neglected in the standard gyrokinetic
ordering, so that the first order contribution to the magnetic moment
vanishes.
is essentially the parallel component of the wave
field. This effect is usually neglected in the standard gyrokinetic
ordering, so that the first order contribution to the magnetic moment
vanishes.
The second-order nonlinear corrections are responsible, in particular, for
three-wave interactions. Calculating them for a general Fourier-decomposed
wave field would allow subsequent construction of a weak-turbulence theory.
For other effects, such as the estimate of the Miller force of the
high-frequency field on a particle, just the eikonal representation of the
wave is sufficient. Below we adopt the first, more complete description.
In this approximation we can use the  -independent variational principle (32) with properly defined parameters. Indeed, besides
-independent variational principle (32) with properly defined parameters. Indeed, besides
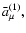 which is added to the effective vector potential,
which is added to the effective vector potential,
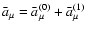 ,
there is one other significant contribution to the Lagrangian from the wave terms.
It enters into the definition of the adiabatic invariant
,
there is one other significant contribution to the Lagrangian from the wave terms.
It enters into the definition of the adiabatic invariant 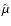 via Eq. (33),
so that
via Eq. (33),
so that
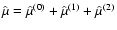 ,
where
,
where
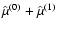 is given by Eq. (54).
is given by Eq. (54).
The second order contribution to the adiabatic invariant is given by
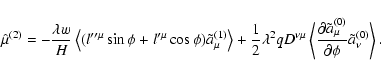 |
(56) |
The second term in this expression can be found using the zero-order
solution (50), while the first involves the first-order correction,
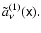
Expanding the last exponent in Eq. (48) in powers of 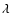 we
get
we
get
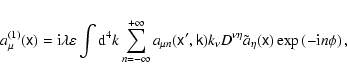 |
(57) |
where
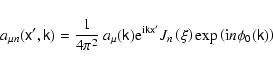 |
(58) |
by definition. The average of Eq. (57) then looks like
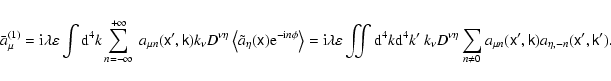 |
(59) |
The sum of the Bessel-function products in the above expression can be
simplified using the Graf addition theorem for Bessel functions (Abramovits & Stegun 1972).
This theorem can be cast in the form
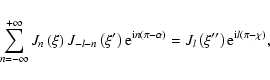 |
(60) |
where l is arbitrary, while
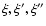 are proportional to the sides of a triangle,
are proportional to the sides of a triangle, 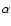 being the angle
between
being the angle
between 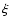 and
and
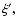 while
while 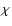 is the angle opposite to
is the angle opposite to 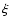 .
These conditions are satisfied in our case (due to the interpretation
of
.
These conditions are satisfied in our case (due to the interpretation
of 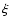 as proportional to the length of
as proportional to the length of
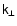 ,
(49))
with
,
(49))
with
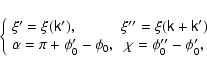 |
(61) |
where
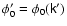 ,
,
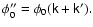 The
triangle is formed by four-vectors
The
triangle is formed by four-vectors
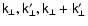 in the
in the
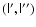 -plane.
-plane.
Using the definition of
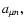 and taking into account the identity
(60) with l=0, we reduce the first-order correction to
and taking into account the identity
(60) with l=0, we reduce the first-order correction to
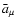 to the following expression
to the following expression
![\begin{displaymath}%
\bar{a}_{\mu}^{(1)}=\frac{{\rm i}\lambda\varepsilon}{\left(...
...{0}\left(
\xi\right) J_{0}\left( \xi^{\prime}\right) \right] .
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img218.gif) |
(62) |
Then, seeking the oscillating part of the first-order correction as a series
and using Eq. (57), we find that the coefficients
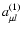 satisfy
satisfy
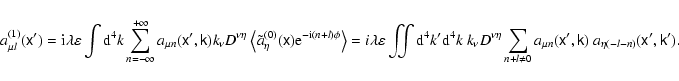 |
(63) |
The sum under the integral can be found using the identity (60) as
Fortunately, knowledge of the first harmonics
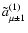 is sufficient for the evaluation of
is sufficient for the evaluation of
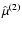 .
Indeed, the necessary
average can be calculated as
.
Indeed, the necessary
average can be calculated as
After substituting the definitions of
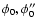 the above expression becomes
the above expression becomes
![\begin{displaymath}%
\left\langle (l^{\prime \prime \mu }\sin \phi +l^{\prime \m...
...ight)
\frac{J_{1}\left( \xi \right) }{\xi }k_{\zeta }\right] ,
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img232.gif) |
(64) |
where
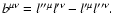
Proceeding now to calculation of the second term in Eq. (56) we note
that
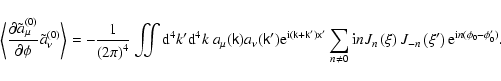 |
(65) |
Using again the addition theorem for Bessel functions (60) with l=0and Eq. (61) we get
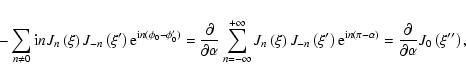 |
(66) |
with
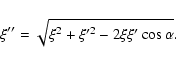 |
(67) |
Then
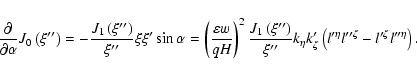 |
(68) |
Finally, incorporating the above averages into Eq. (56), the
second-order correction to the adiabatic invariant (magnetic moment) becomes
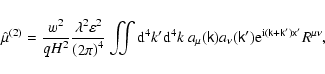 |
(69) |
where
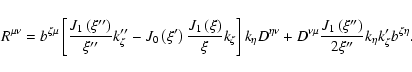 |
(70) |
The above results, Eqs. (62), (69), look complicated because of the presence of general
three-wave interactions. Indeed, they show that contributions to the
particle parameters with the wave vector
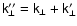 come from all pairs of
electromagnetic perturbations with the same sum of the wave vector
come from all pairs of
electromagnetic perturbations with the same sum of the wave vector
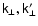 .
If we are interested in the average
Miller force only, it is sufficient to retain only the zero-sum pairs,
.
If we are interested in the average
Miller force only, it is sufficient to retain only the zero-sum pairs,
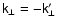 ,
so that
,
so that
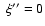 ,
which simplifies the expressions significantly.
,
which simplifies the expressions significantly.
As one can see, the above results are not gauge invariant with respect to
gauge transformations of the wave potential 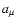 .
This problem can be
resolved using gauge-invariance of the variational principle (4), (14). Indeed, any transformation of the potential
.
This problem can be
resolved using gauge-invariance of the variational principle (4), (14). Indeed, any transformation of the potential
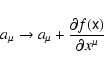 |
(71) |
can be compensated by
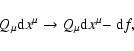 |
(72) |
so that the functional remains the same. Conversely, any transformation of
type (72) leads to an equivalent variational principle, while the
difference can be hidden in 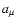 .
.
The above program of calculating the gyrokinetic transformation and the  -independent description of motion can be carried out for an arbitrary
gauge function f. This means that expressions obtained in the above
subsections should also be valid for
-independent description of motion can be carried out for an arbitrary
gauge function f. This means that expressions obtained in the above
subsections should also be valid for
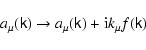 |
(73) |
with an arbitrary function
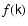 .
Thus, any gauge transformations of
the wave potential
.
Thus, any gauge transformations of
the wave potential 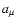 lead to different, but still valid expressions.
lead to different, but still valid expressions.
Finally, we summarize the results of this section by presenting the
transformed variational principle valid through the second order in 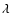 and second order in
and second order in
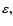 i.e., with terms of the order
i.e., with terms of the order
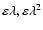 and
and
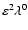 retained:
retained:
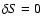 yields the particle phase-space trajectory with
yields the particle phase-space trajectory with
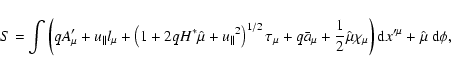 |
(74) |
where
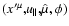 or
or
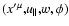 are the new gyrokinetic variables with
are the new gyrokinetic variables with
where
q=qa/mac2 is the signed charge-to-mass ratio,
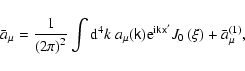 |
(75) |
![$\xi =k_{\bot }\rho _{{\rm L}}=\left( 2\hat{\mu}\left[ \left( k_{\nu
}l^{\prime ...
...^{2}+\left( k_{\nu }l^{\prime \prime \nu }\right)
^{2}\right] /qH\right) ^{1/2}$](/articles/aa/full/2004/46/aa0208-03/img255.gif) ,
and the second-order corrections
,
and the second-order corrections
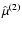 and
and
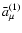 are given by Eqs. (69) and (62), respectively. The orthogonal basis
are given by Eqs. (69) and (62), respectively. The orthogonal basis
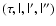 is chosen in such a way that
is chosen in such a way that
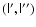 coincides with the space-like invariant plane of the
antisymmetric tensor of the electromagnetic field
coincides with the space-like invariant plane of the
antisymmetric tensor of the electromagnetic field
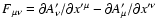 ,
with H being the corresponding eigenvalue.
,
with H being the corresponding eigenvalue.
The single-particle distribution function can be written in general
relativity either in the eight-dimensional phase space
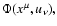
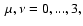 or in the seven-dimensional phase
space
or in the seven-dimensional phase
space
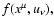 where only 3 components of the 4-velocity
where only 3 components of the 4-velocity 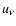 are independent, so that
are independent, so that
The 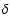 -function here reflects the fact that
-function here reflects the fact that
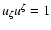 is the first integral of motion in the case of the eight-dimensional
representation. However, the collisionless kinetic equation in both cases
retains the same form, namely
is the first integral of motion in the case of the eight-dimensional
representation. However, the collisionless kinetic equation in both cases
retains the same form, namely
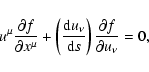 |
(76) |
although in the 7-dimensional case
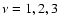 only, while u0 is the
dependent variable. Here
only, while u0 is the
dependent variable. Here
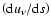 is a function of the
independent variables
is a function of the
independent variables
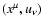 found as the right-hand side of
the single-particle dynamics equations. The kinetic equation can be
multiplied by
found as the right-hand side of
the single-particle dynamics equations. The kinetic equation can be
multiplied by 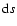 and thus represented in the
parameterization-independent form as
and thus represented in the
parameterization-independent form as
where the differentials are tangent to the particle orbit.
Because of the general properties of variable transformations it is obvious
that any non-degenerate transformation of the phase-space variables
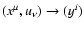 will lead to the same form of the
kinetic equation
will lead to the same form of the
kinetic equation
where the differentials are tangent to the particle orbit. In particular,
this property is useful for the transformation to the gyrokinetic variables.
Let
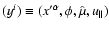 ,
then the kinetic equation becomes
,
then the kinetic equation becomes
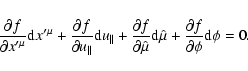 |
(77) |
By definition of the gyrokinetic variables the dynamic equations should be
independent of  ,
i.e., expressions for
,
i.e., expressions for
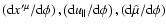 are independent of
are independent of  ,
while
,
while
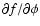 is periodic in
is periodic in  .
It follows that
.
It follows that
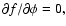 and, if
and, if 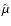 is the integral of motion,
is the integral of motion,
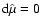 ,
we
get the kinetic equation expressed in the gyrokinetic variables as
,
we
get the kinetic equation expressed in the gyrokinetic variables as
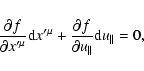 |
(78) |
which we shall call the gyrokinetic
equation. Here the coefficients
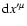 and
and
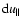 must be determined from the equations of
motion in the gyrokinetic variables.
must be determined from the equations of
motion in the gyrokinetic variables.
While the above derivation seems simple, there is a trick. Even if we prove
that there is no  -dependence in all orders, this does not mean
that there is no such dependence at all. In fact, this is what happens close
to the cyclotron resonances - the exponentially small (and thus having zero
expansion coefficients) resonant factor destroys the conservation of the
magnetic moment, rendering the gyrokinetic theory invalid. It should always
be kept in mind that the approximation works well for particles far from the
low-order cyclotron resonances.
-dependence in all orders, this does not mean
that there is no such dependence at all. In fact, this is what happens close
to the cyclotron resonances - the exponentially small (and thus having zero
expansion coefficients) resonant factor destroys the conservation of the
magnetic moment, rendering the gyrokinetic theory invalid. It should always
be kept in mind that the approximation works well for particles far from the
low-order cyclotron resonances.
Another question is: why is it so important to have
parameterization-independent equations of motion? Would it be possible to
use, say, Fradkin's drift equations with the proper-time parameterization to
construct the gyrokinetic equation in an alternative way? The answer follows
from the transformation of the Liouville Eq. (76) with the
transformation of the phase-space variables. Since its meaning is the
conservation of world lines, the form is retained for canonical-like
transformations (with a constant Jacobian). Otherwise, for an arbitrary set
of non-canonical drift equations of motion, one has to prove that the
Jacobian is at least independent of the gyrophase, in order to exclude this
variable from the gyrokinetic equation. In other terms, kinetic Eq. (77) (with coefficients
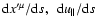 independent of
independent of  )
cannot
be transformed into the gyrokinetic equation, unless
)
cannot
be transformed into the gyrokinetic equation, unless
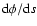 is also independent of
is also independent of  .
This
requirement is not fulfilled for Fradkin's equations, since the proper time s depends on the gyrophase with periodic corrections due to changes of
velocity along the orbit.
.
This
requirement is not fulfilled for Fradkin's equations, since the proper time s depends on the gyrophase with periodic corrections due to changes of
velocity along the orbit.
The equations of motion, or the relationships between differentials tangent
to the particle orbit, can be obtained as Euler equations of the transformed
variational principle (74). Let us find the first variation of Sassuming
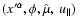 to be
independent:
to be
independent:
Here we introduced a new tensor notation
![\begin{displaymath}d_{\nu \mu }\equiv {\rm Rot}_{\nu }\left[ u{_{\parallel }}l_{...
...mu }+q\bar{a}_{\mu }+\frac{1}{2}\hat{\mu}\chi _{\mu }\right] ,
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img286.gif) |
(79) |
where the operator
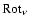 is defined by
is defined by
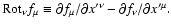
Extrema of the functional are achieved for world lines where
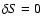 for all variations of independent variables. This yields the Euler equations
as
for all variations of independent variables. This yields the Euler equations
as
The first equation here confirms that 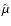 is an integral of motion,
the second equation determines the rate of rotation along the Larmor orbit
and is not needed for our purposes here. By multiplying the 4-vector
Eq. (83) by
is an integral of motion,
the second equation determines the rate of rotation along the Larmor orbit
and is not needed for our purposes here. By multiplying the 4-vector
Eq. (83) by
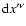 and taking the sum
in
and taking the sum
in 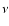 one can recover the third scalar Eq. (82) multiplied
by
one can recover the third scalar Eq. (82) multiplied
by
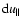 ,
i.e., out of five equations for four
unknown functions
,
i.e., out of five equations for four
unknown functions
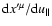 only four are independent, as should be the case for solvability. This
allows us to determine the non-trivial solutions (at least formally) and use
them as coefficients of the gyrokinetic equation.
only four are independent, as should be the case for solvability. This
allows us to determine the non-trivial solutions (at least formally) and use
them as coefficients of the gyrokinetic equation.
It is convenient to rewrite the 4-vector Eq. (83) through its
projections on the orthogonal vectors of the basis
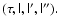 Taking scalar products with
Taking scalar products with
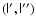 we get
we get
| |
|
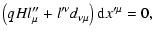 |
(84) |
| |
|
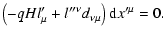 |
(85) |
These two equations determine the drift velocity. Taking the scalar product
with 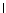 ,
we recover the following equation governing the
acceleration parallel to the magnetic field
,
we recover the following equation governing the
acceleration parallel to the magnetic field
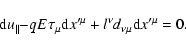 |
(86) |
Simplification occurred since the
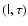 -plane for the
field-related choice of the basis coincides with the second invariant plane
of the electromagnetic field tensor, so that
-plane for the
field-related choice of the basis coincides with the second invariant plane
of the electromagnetic field tensor, so that
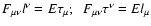 (see Eqs. (7), (8)). Then, the last equation looks like
(see Eqs. (7), (8)). Then, the last equation looks like
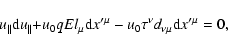 |
(87) |
which is the energy conservation law. However, as shown above, in its place
one can use another, equivalent but much more compact Eq. (82).
It describes the relationship between
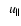 and the
differentials of the guiding-center position
and the
differentials of the guiding-center position
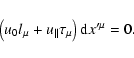 |
(88) |
It is possible to formally solve Eqs. (84)-(88) in terms of
the basis vectors. To do this we introduce new notations,
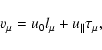 |
(89) |
and
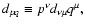 for arbitrary four-vectors
for arbitrary four-vectors
 .
Note that
.
Note that
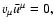 i.e.,
i.e., 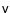 is
orthogonal to the particle world-velocity, and thus is orthogonal to the
drift velocity too, as expressed by Eq. (88).
is
orthogonal to the particle world-velocity, and thus is orthogonal to the
drift velocity too, as expressed by Eq. (88).
Searching for the solution in the form
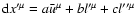 ,
and substituting it into
Eqs. (84), (85), we get
,
and substituting it into
Eqs. (84), (85), we get
![\begin{displaymath}{\rm d}{x^{\prime \mu }=}\left[ \bar{u}^{\mu }+\frac{l^{\prim...
...-d_{l^{\prime
}l^{\prime \prime }}}\right] {\rm d}s^{\prime },
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img311.gif) |
(90) |
![\begin{displaymath}{\rm d}u{_{\parallel }=}\left[ \left( qE-d_{l\tau }\right) u_...
...-d_{l^{\prime }l^{\prime \prime }}}\right] {\rm d}s^{\prime }.
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img312.gif) |
(91) |
Note that here
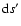 is just an arbitrary scalar function,
which can be chosen as convenient. It means that the above equations
determine just the direction of the world line of the gyrocenter in the
phase space, but do not define its parameterization.
is just an arbitrary scalar function,
which can be chosen as convenient. It means that the above equations
determine just the direction of the world line of the gyrocenter in the
phase space, but do not define its parameterization.
Consider a coordinate system chosen in such a way that the dependence of all
functions on
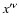 (with some particular
(with some particular 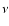 )
vanishes:
)
vanishes:
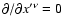 .
Then
.
Then
and the 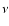 -component of the Euler Eq. (83) becomes
-component of the Euler Eq. (83) becomes
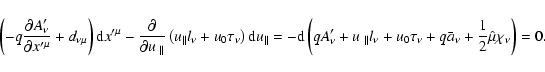 |
(92) |
Here the conservation of the magnetic moment, Eq. (80), and the
absence of any dependence on  are taken into account.
are taken into account.
This means that
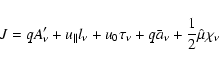 |
(93) |
is the integral of motion corresponding to the symmetry with respect to
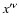 .
.
In general, the kinetic description of plasmas involves a combination of the
kinetic equation and Maxwell equations, which describe the evolution of the
collective (Hartree-Fock) electromagnetic fields. The same is true for the
gyrokinetic theory. However, since the gyrokinetic equation is written in
specific gyrokinetic variables, and thus yields the distribution function in
terms of these variables, one should have a special procedure of integration
in velocity space to calculate the source terms of Maxwell equations. This
procedure is presented below. Fortunately, the Jacobian of the gyrokinetic
transformation in the present formulation is simple enough to allow
integration in the gyrophase, so that expressions for the charge and current
densities via the gyrokinetic distribution function are found explicitly.
The general form of Maxwell equations in the presence of an arbitrary
gravitational field is well known (Landau & Lifshits 1975). The first pair of equations
can be written as
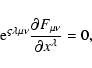 |
(94) |
and the second as
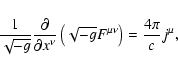 |
(95) |
where
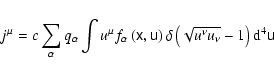 |
(96) |
is the current density, expressed via the distribution function of particle
species 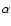 ,
and the signed particle charge
,
and the signed particle charge
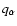 .
The
.
The 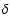 -function under the integral makes it possible to do a partial integration,
for example over u0, and arrive at a more widely used form
-function under the integral makes it possible to do a partial integration,
for example over u0, and arrive at a more widely used form
However, in the gyrokinetic transformation the four-velocity is expressed
via Eqs. (18)-(20) as
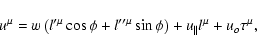 |
(97) |
so that
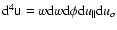 (the sign is positive due to Eq. (6)), while the partial integration over
(the sign is positive due to Eq. (6)), while the partial integration over
 leads to
leads to
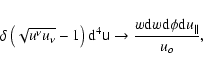 |
(98) |
where
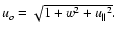 As a result, the
expression for the components of the current density can be rewritten as
As a result, the
expression for the components of the current density can be rewritten as
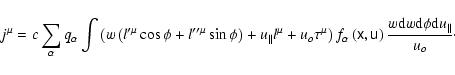 |
(99) |
In Eq. (99) the particle position  rather than its
gyrocenter position
rather than its
gyrocenter position
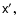 is kept constant while
integrating over the particle velocity. This means, that if the distribution
function
is kept constant while
integrating over the particle velocity. This means, that if the distribution
function
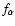 is given as a function of the gyrokinetic variables
is given as a function of the gyrokinetic variables
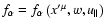 ,
it
is necessary to transform it to particle coordinates via the inverse
transformation
,
it
is necessary to transform it to particle coordinates via the inverse
transformation
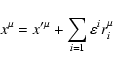 |
(100) |
before integrating. Furthermore, here we assumed that the distribution
function is defined in terms of the orbital velocity w rather than the
magnetic moment
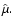 The two representations are roughly equivalent,
but integration in
The two representations are roughly equivalent,
but integration in 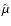 would be much more difficult, since its
relationship to w is defined via the electromagnetic field tensor at the
gyrocenter position, which would also require transformation before
integrating.
would be much more difficult, since its
relationship to w is defined via the electromagnetic field tensor at the
gyrocenter position, which would also require transformation before
integrating.
The gyrokinetic transformation has been found by expansion in orders of
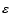 and
and 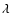 ,
and this expansion has to be exploited here
again:
,
and this expansion has to be exploited here
again:
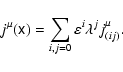 |
(101) |
The distribution function may have short-wavelength wave contributions,
which can be separated from the slowly changing background by using the
ordering scheme
![\begin{displaymath}%
f_{\alpha }\left( x^{\prime \mu },w,u_{\parallel }\right) =...
...ft[ {\rm i}k_{\mu }x^{\prime \mu }\right] {\rm
d}^{4}\tens{k}.
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img335.gif) |
(102) |
In these terms the zero-order current and charge density
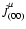 is easy to find:
is easy to find:
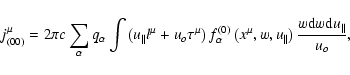 |
(103) |
while other orders require expansion.
The background distribution function
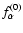 is slowly changing
on the Larmor-radius/gyrotime-scale, and thus can be expanded into a
Taylor series around the particle position. Note that the displacements
is slowly changing
on the Larmor-radius/gyrotime-scale, and thus can be expanded into a
Taylor series around the particle position. Note that the displacements
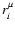 are given by the gyrokinetic transformation as functions of
are given by the gyrokinetic transformation as functions of
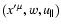 and thus should be expanded
as well. Keeping terms of the order of
and thus should be expanded
as well. Keeping terms of the order of
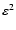 and larger, we
find
and larger, we
find
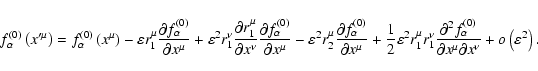 |
(104) |
Here all functions on the right-hand side can be regarded as functions of
the particle position 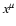 .
Meanwhile, due to dependence of the tetrad
in the velocity representation on
.
Meanwhile, due to dependence of the tetrad
in the velocity representation on 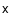 ,
and due to the use of winstead of
,
and due to the use of winstead of 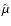 ,
all other functions under the integral in Eq. (99) do not require transformation.
,
all other functions under the integral in Eq. (99) do not require transformation.
The first order displacement of the gyrocenter is given by
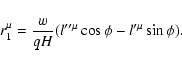 |
(105) |
Using it, we find the first-order current density as
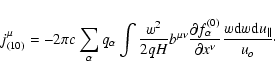 |
(106) |
Its structure corresponds to the usual
diamagnetic current.
Similarly, it is necessary to solve Eq. (42) for
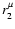 in
order to calculate the second-order current density. The form of this
equation (for
in
order to calculate the second-order current density. The form of this
equation (for
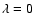 )
is such that
)
is such that
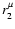 may have components
proportional to first and second powers of trigonometric functions of
may have components
proportional to first and second powers of trigonometric functions of 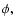 namely,
namely,
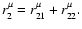 It is multiplied by
the velocity, which has terms with the zero and first powers of the same, so
that a range of first- to third-power terms are produced. However, of that
range only the second-power terms can produce a non-zero contribution after
integrating in
It is multiplied by
the velocity, which has terms with the zero and first powers of the same, so
that a range of first- to third-power terms are produced. However, of that
range only the second-power terms can produce a non-zero contribution after
integrating in  ,
so that in the following we ignore other terms. The
same argument applies to the expansion (104) as a whole.
,
so that in the following we ignore other terms. The
same argument applies to the expansion (104) as a whole.
First we solve for
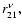 which satisfies
which satisfies
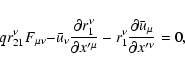 |
(107) |
then we find
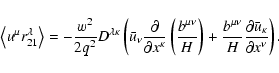 |
(108) |
The next combination of terms is
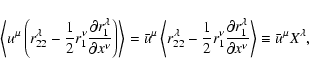 |
(109) |
where
 satisfies
satisfies
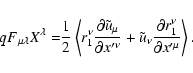 |
(110) |
After substitutions we find
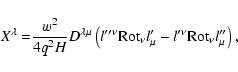 |
(111) |
where
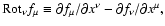 as before.
as before.
The last remaining terms in Eq. (104) contribute to the current via
combination
![\begin{displaymath}\left\langle r_{1}^{\nu }\frac{\partial }{\partial x^{\nu }}\...
...rtial f_{\alpha }^{(0)}}{\partial x^{{\mu }}}\right] \right) .
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img354.gif) |
(112) |
As a result, we can get the second-order
current density as
 where
where
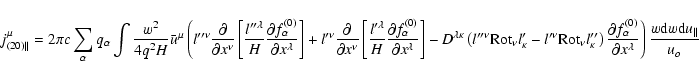 |
(113) |
belongs to the
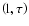 -plane, while
-plane, while
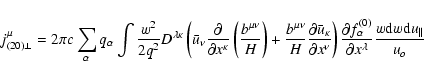 |
(114) |
has no
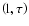 components.
components.
The parallel component,
 ,
represents the FLR corrections to the charge density and the parallel
current density. It is rarely used, since it is two orders smaller than
,
represents the FLR corrections to the charge density and the parallel
current density. It is rarely used, since it is two orders smaller than
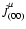 and has the same direction. The
perpendicular component,
and has the same direction. The
perpendicular component,
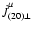 ,
describes currents caused by the drifts in inhomogeneous fields.
,
describes currents caused by the drifts in inhomogeneous fields.
First we calculate the transformation to the particle position variables
![\begin{displaymath}%
f_{\alpha }^{(1)}\left( \tens{x},w,u_{\parallel },\phi \rig...
...u }{\sum_{s}}\varepsilon ^{s}r_{s}^{\mu }\right]
{\rm d}^{4}k.
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img361.gif) |
(115) |
Retaining in the exponent terms of order
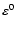 only [while
only [while
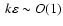 ], we get
], we get
![\begin{displaymath}%
f_{\alpha }^{(1)}\left( \tens{x}\right) =\frac{1}{4\pi ^{2}...
...mbda D^{\mu \nu }\tilde{a}_{\nu }\right) \right] {\rm d}^{4}k.
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img364.gif) |
(116) |
The last term in the exponent can be neglected in this order, and the rest
can be expanded into the Fourier series using Eq. (47) as
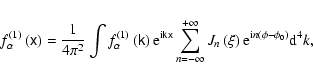 |
(117) |
where
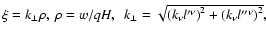 as before,
as before,
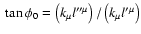 .
Then,
.
Then,
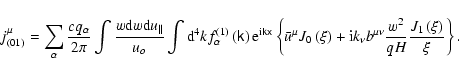 |
(118) |
Note that the above expression describes the parallel current due to the
wave, as well as the corresponding diamagnetic contribution.
The nonlinear corrections follow while the formerly neglected last term in
the exponent of Eq. (116) is taken into account. The resulting
first-order correction to
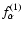 looks like
looks like
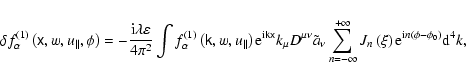 |
(119) |
where
 is taken at the particle position.
is taken at the particle position.
In principle, 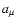 is a prescribed function of the particle position,
but its oscillating part is not. It is
necessary to transform the zero-order solution, Eq. (50),
is a prescribed function of the particle position,
but its oscillating part is not. It is
necessary to transform the zero-order solution, Eq. (50),
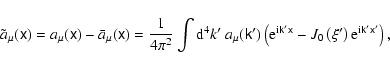 |
(120) |
back to particle position coordinates via the inverse transformation (100) . Then
![\begin{displaymath}\tilde{a}_{\mu }(\tens{x})=\frac{1}{4\pi ^{2}}\int {\rm d}^{4...
...\right) {\rm e}^{{\rm i}m(\phi -\phi _{0}^{\prime })}\right] .
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img373.gif) |
(121) |
Thus the combination appearing in Eq. (119) can be rewritten as
![\begin{displaymath}%
\tilde{a}_{\nu }\sum_{n=-\infty }^{+\infty }J_{n}\left( \xi...
... {\rm e}^{{\rm i}n(\phi -\phi _{0}^{\prime \prime })}\right] ,
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img374.gif) |
(122) |
where we have used the addition theorem for Bessel functions, Eq. (60), again, so that
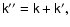 etc.
etc.
Now we can calculate
where
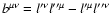 as before.
as before.
One can see that the nonlinear correction to the current density is due to
the interaction of the perturbation of the distribution function with the
perturbation of the particle motion, satisfying the three-wave interaction
criteria.
A closed set of relativistic gyrokinetic equations, consisting of the
collisionless gyrokinetic equation and the averaged Maxwell equations, is
derived for an arbitrary four-dimensional coordinate system.
The basic features of the approach are as follows:
- the guiding-center dynamics of charged particles and the gyrokinetic
transformation are obtained in the second order in terms of the ratio of the
Larmor radius to the inhomogeneity scale;
- the wave terms with arbitrary
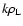 are described in the second-order approximation in the amplitude of the wave;
are described in the second-order approximation in the amplitude of the wave;
- the present description is closed, in the sense that it includes the
gyrophase-averaged expression for the four-current density, which is used
with Maxwell equations;
- the perturbative Lagrangian approach with a fully relativistic,
four-dimensional covariant formulation allows us to improve on the existing
limitations of the gyrokinetic theory: in comparison to equations derived by
other authors it is now possible to consider relativistic drift velocities,
i.e.,
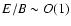 ,
and the wave field is no longer limited in frequency
and wavelength, i.e.,
,
and the wave field is no longer limited in frequency
and wavelength, i.e.,
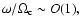
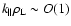 ,
so that the class of admissible waves is broader than
the usual drift-Alfvén
perturbations and can include magneto-sonic waves, for
example;
,
so that the class of admissible waves is broader than
the usual drift-Alfvén
perturbations and can include magneto-sonic waves, for
example;
- the covariant description of the gyro-dynamics of charged particles in
a strong magnetic field allows for the possibility of the gravitation
influencing the space-time metrics, and thus is suitable for the
investigation of astrophysical objects such as accretion disks and
relativistic jets.
The applicability of the present gyrokinetic equations to modelling
accretion disks can be assessed using the following scheme. If one is
interested in quasi-equilibrium structures without short-wave perturbations,
then the equations can be significantly simplified by throwing out the wave
terms. The other requirements are as follows:
- The plasma should be magnetized, and the Larmor radius should be
smaller than both characteristic scales: the Keplerian orbit radius, and the
inverse gradient of the electromagnetic field across the accretion disc. The
second scale is likely to be smaller for thin disks. Thus, significant FLR
(finite-Larmor-radius) corrections are likely to arise when the disk
thickness is comparable to the Larmor radius.
- Collisions, and the cyclotron/synchrotron radiation should not change
the particle energy too much during the time scale of the processes under
investigation. The second limitation is less severe if the plasma is
optically thick, i.e., the cyclotron emission is collective.
- One can describe plasmas even within the last stable orbit, but no
closer than one Larmor radius from the events horizon of the black hole.
For problems involving turbulence and dynamo effects, the Larmor radius
should be compared with the typical wavelength of the perturbation. Then,
besides the above two items, one should consider the following:
- If the wavelength is smaller than the Larmor radius, one can still
throw out the gyrokinetic wave terms and use the zero-order theory.
Otherwise, the FLR-corrections given by the wave terms are significant.
The important role of the FLR-corrections indicates when one should prefer
the gyrokinetic theory to the (possible) covariant drift theory. However, in
the opposite case these two should be equivalent (in results as well as in
complexity). Non-relativistic gyrokinetic/drift equations can be applied if
both the plasma temperature and the orbital velocity are non-relativistic,
or, if one is working locally, in a moving reference frame. Finally, the
generally preferred MHD (magnetohydrodynamic) approach is directly
applicable for cold collisional plasmas of the outer reaches of the
accretion disk, or just for fast MHD perturbations. The interesting subject of the covariant gyrofluid equations,
which combine the relative simplicity of the MHD with explicit conservation
of the magnetic moment in the collisionless plasmas, will be addressed in
our subsequent papers.
Acknowledgements
This work has been conducted via the cooperation
program between the Trieste University, Italy, and the Budker Institute of
Nuclear Physics, Novosibirsk, Russia.
- Abramowitz, M., & Stegun, I. A.
(ed.) 1972, Handbook of Mathematical Functions (New York: Dover)
In the text
- Beklemishev, A., & Tessarotto, M.
1999, Phys. Plasmas, 6, 4487
In the text
- Boghosian, B. M. 1987, Covariant Lagrangian
methods of relativistic plasma theory, University of California, Davis
In the text
- Boozer, A. H. 1996, Phys. Plasmas, 3,
3297
In the text
- Brizard, A. J., & Chan, A. A. 1999, Phys.
Plasmas, 6, 4548
In the text
- Cary, J. R., & Littlejohn, R. G. 1983,
Ann. Phys., 151, 1
In the text
- Cooper, W. A. 1997, Plasma Phys. Control. Fusion,
39, 931
- Fradkin, D. M. 1978, J. Physics A, 11, 1069
In the text
- Frank, J., King, A., & Raine, D. 1992,
Accretion Power in Astrophysics, Cambridge Astrophysics Series, 20, 2nd ed.
(Cambridge University Press)
In the text
- Hahm, T. S., Lee, W. W., &
Brizard, A. 1988, Phys. Fluids, 31, 1940
In the text
- Landau, L. D., & Lifshits, E. M. 1975,
The Classical Theory of Fields, 4th ed. (Oxford: Pergamon)
In the text
- Littlejohn, R. G. 1979, J. Math. Phys.,
20, 2445
In the text
- Littlejohn, R. G. 1984, Phys. Fluids, 27, 976
In the text
- Northrop, T. G. 1963, The Adiabatic Motion of
Charged Particles (New York: Interscience), 27
In the text
- Pozzo, M., & Tessarotto, M. 1998, Phys.
Plasmas, 5, 2232
In the text
Copyright ESO 2004
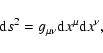
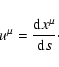
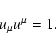
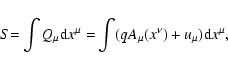
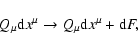
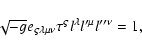
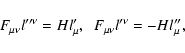
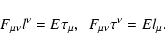
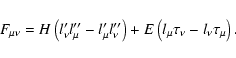
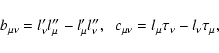
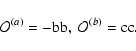
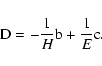
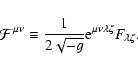
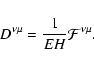
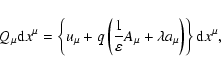
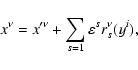
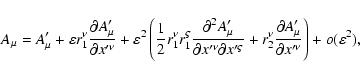
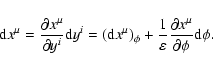
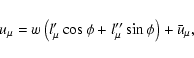
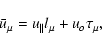
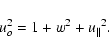
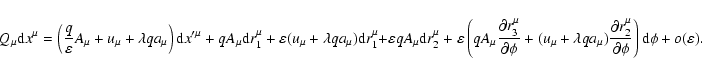
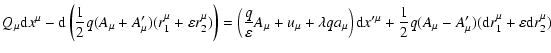
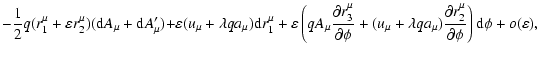
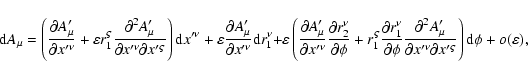
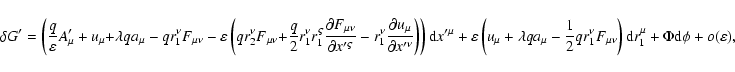
![\begin{displaymath}\Phi =\varepsilon \left( r_{1}^{\nu }\frac{\partial u_{\mu }}...
...{\nu }^{\prime }}{\partial x^{\prime {\mu }}}\right]
\right) ,
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img102.gif)
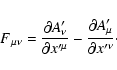
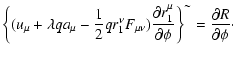
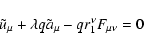
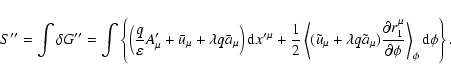
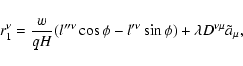
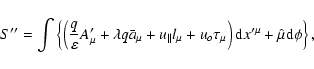
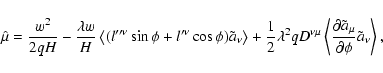
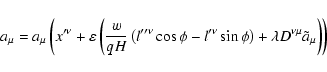
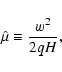
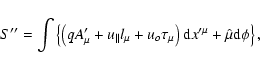
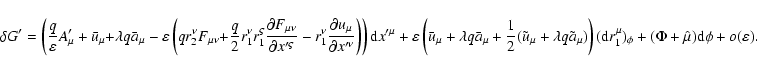

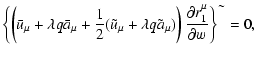
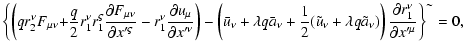
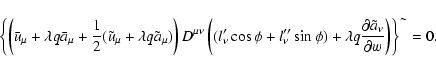
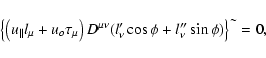
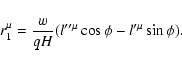
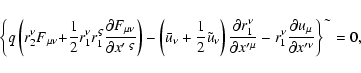
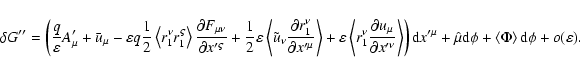
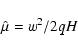
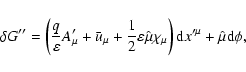
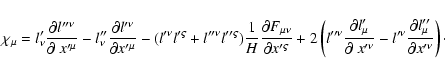
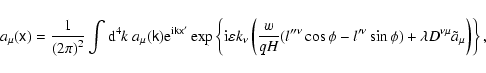
![\begin{displaymath}\exp \left[ {\rm i}\zeta \sin \psi \right] =\sum_{n=-\infty }...
...
}J_{n}\left( \zeta \right) \exp \left( {\rm i}n\psi \right) ,
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img180.gif)
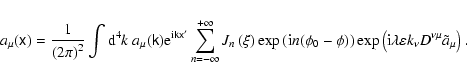
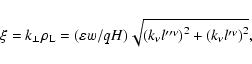
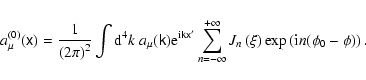
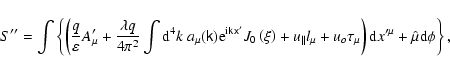
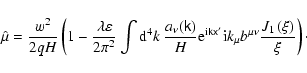
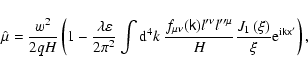
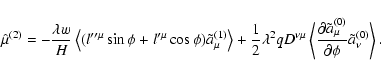
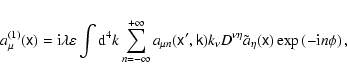
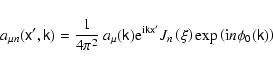
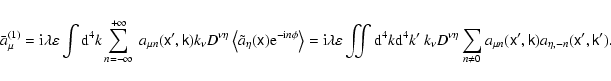
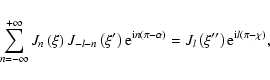
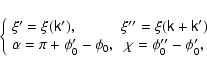
![\begin{displaymath}%
\bar{a}_{\mu}^{(1)}=\frac{{\rm i}\lambda\varepsilon}{\left(...
...{0}\left(
\xi\right) J_{0}\left( \xi^{\prime}\right) \right] .
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img218.gif)
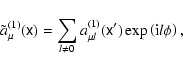
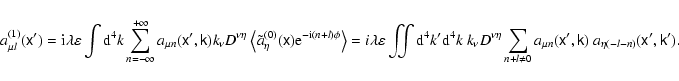
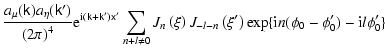
![$\displaystyle \frac{a_{\mu }(\tens{k})a_{\eta }(\tens{k}^{\prime })}{\left( 2\p...
...me }\right) J_{l}\left( \xi \right) {\rm e}^{{\rm i}l(\pi -\phi _{0})}\right] .$](/articles/aa/full/2004/46/aa0208-03/img224.gif)
![\begin{displaymath}%
\left\langle (l^{\prime \prime \mu }\sin \phi +l^{\prime \m...
...ight)
\frac{J_{1}\left( \xi \right) }{\xi }k_{\zeta }\right] ,
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img232.gif)
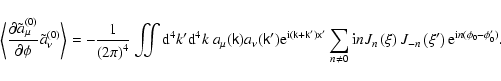
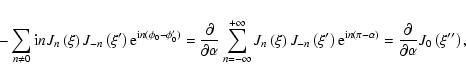
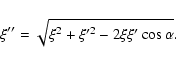
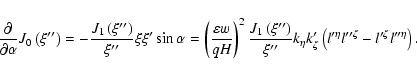
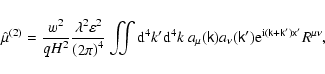
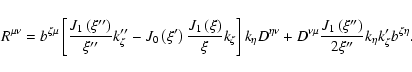
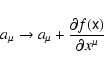
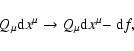
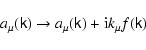
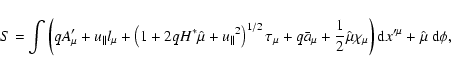
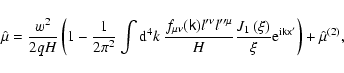
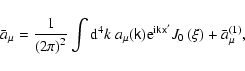
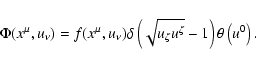
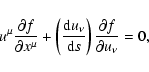
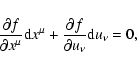
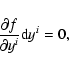
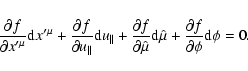
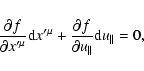
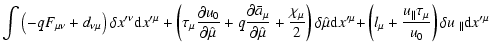
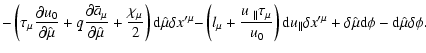
![\begin{displaymath}d_{\nu \mu }\equiv {\rm Rot}_{\nu }\left[ u{_{\parallel }}l_{...
...mu }+q\bar{a}_{\mu }+\frac{1}{2}\hat{\mu}\chi _{\mu }\right] ,
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img286.gif)
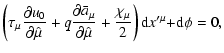
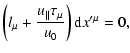
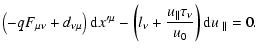
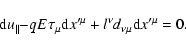
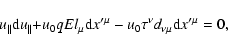
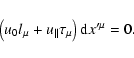
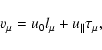
![\begin{displaymath}{\rm d}{x^{\prime \mu }=}\left[ \bar{u}^{\mu }+\frac{l^{\prim...
...-d_{l^{\prime
}l^{\prime \prime }}}\right] {\rm d}s^{\prime },
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img311.gif)
![\begin{displaymath}{\rm d}u{_{\parallel }=}\left[ \left( qE-d_{l\tau }\right) u_...
...-d_{l^{\prime }l^{\prime \prime }}}\right] {\rm d}s^{\prime }.
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img312.gif)
![\begin{displaymath}F_{\mu \nu }=\frac{\partial A_{\nu }^{\prime }}{\partial x^{\...
...u }+q\bar{a}_{\nu }+\frac{1}{2}\hat{\mu}
\chi _{\nu }\right] ,
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img315.gif)
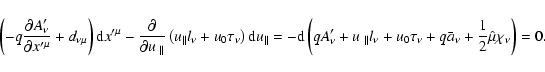
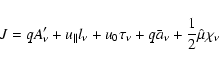
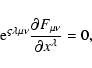
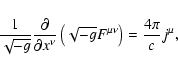
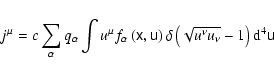
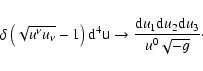
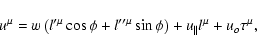
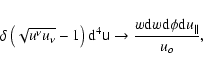
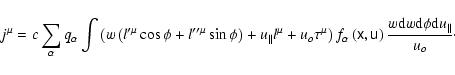
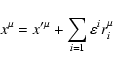
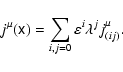
![\begin{displaymath}%
f_{\alpha }\left( x^{\prime \mu },w,u_{\parallel }\right) =...
...ft[ {\rm i}k_{\mu }x^{\prime \mu }\right] {\rm
d}^{4}\tens{k}.
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img335.gif)
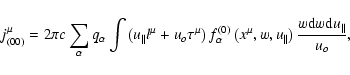
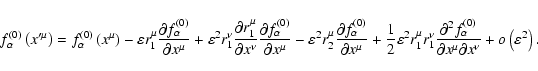
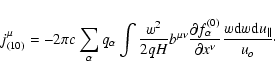
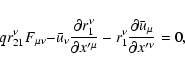
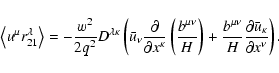
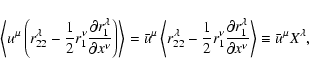
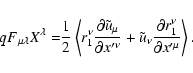
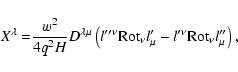
![\begin{displaymath}\left\langle r_{1}^{\nu }\frac{\partial }{\partial x^{\nu }}\...
...rtial f_{\alpha }^{(0)}}{\partial x^{{\mu }}}\right] \right) .
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img354.gif)
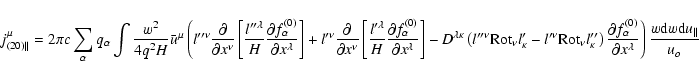
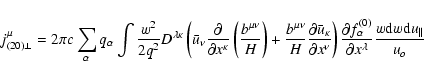
![\begin{displaymath}%
f_{\alpha }^{(1)}\left( \tens{x},w,u_{\parallel },\phi \rig...
...u }{\sum_{s}}\varepsilon ^{s}r_{s}^{\mu }\right]
{\rm d}^{4}k.
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img361.gif)
![\begin{displaymath}%
f_{\alpha }^{(1)}\left( \tens{x}\right) =\frac{1}{4\pi ^{2}...
...mbda D^{\mu \nu }\tilde{a}_{\nu }\right) \right] {\rm d}^{4}k.
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img364.gif)
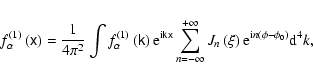
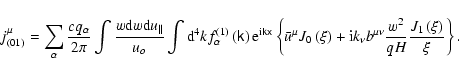
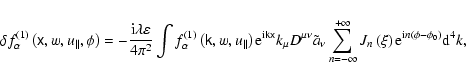
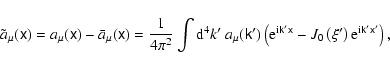
![\begin{displaymath}\tilde{a}_{\mu }(\tens{x})=\frac{1}{4\pi ^{2}}\int {\rm d}^{4...
...\right) {\rm e}^{{\rm i}m(\phi -\phi _{0}^{\prime })}\right] .
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img373.gif)
![\begin{displaymath}%
\tilde{a}_{\nu }\sum_{n=-\infty }^{+\infty }J_{n}\left( \xi...
... {\rm e}^{{\rm i}n(\phi -\phi _{0}^{\prime \prime })}\right] ,
\end{displaymath}](/articles/aa/full/2004/46/aa0208-03/img374.gif)
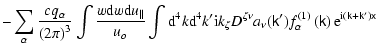
![$\displaystyle \times \left[ \bar{u}^{\mu }\left( J_{0}(\xi )-J_{0}\left( \xi ^{...
...1}\left( \xi
^{\prime \prime }\right) }{\xi ^{\prime \prime }}\right) \right] ,$](/articles/aa/full/2004/46/aa0208-03/img378.gif)