1 - Department of Astronomy, Peking University, Beijing 100871, PR China
2 - Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK

Abstract
We present a comparison of electron densities derived from optical forbidden line diagnostic ratios for a sample of over a hundred nebulae. We consider four density indicators, the [O II] $\lambda 3729/\lambda 3726$ , [S II] $\lambda 6716/\lambda 6731$ , [Cl III] $\lambda 5517/\lambda 5537$ and [Ar IV] $\lambda 4711/\lambda 4740$ doublet ratios. Except for a few H II regions for which data from the literature were used, diagnostic line ratios were derived from our own high quality spectra. For the [O II] $\lambda 3729/\lambda 3726$ doublet ratio, we find that our default atomic data set, consisting of transition probabilities from Zeippen (1982) and collision strengths from Pradhan (1976), fit the observations well, although at high electron densities, the [O II] doublet ratio yields densities systematically lower than those given by the [S II] $\lambda 6716/\lambda 6731$ doublet ratio, suggesting that the ratio of transition probabilities of the [O II] doublet, $A(\lambda3729)/A(\lambda3726)$ , given by Zeippen (1982) may need to be revised upwards by approximately 6 per cent. Our analysis also shows that the more recent calculations of [O II] transition probabilities by Zeippen (1987) and collision strengths by McLaughlin & Bell (1998) are inconsistent with the observations at the high and low density limits, respectively, and can therefore be ruled out. We confirm the earlier result of Copetti & Writzl (2002) that the [O II] transition probabilities calculated by Wiese et al. (1996) yield electron densities systematically lower than those deduced from the [S II] $\lambda 6716/\lambda 6731$ doublet ratio and that the discrepancy is most likely caused by errors in the transition probabilities calculated by Wiese et al. (1996). Using our default atomic data set for [O II], we find that $N_{\rm e}([\mbox{O {\sc ii}}]) \la N_{\rm e}([\mbox{S {\sc ii}}]) \approx N_{\rm e}([\mbox{Cl {\sc iii}}])< N_{\rm e}([\mbox{Ar {\sc iv}}])$ .

Key words: atomic data - ISM: lines and bands - ISM: planetary nebulae: general

Electron density, $N_{\rm e}$ , is one of the key physical parameters characterizing an ionized gaseous nebula. Accurate measurement of $N_{\rm e}$ is a prerequisite to the determination of nebular chemical abundances and calculation of the mass of ionized gas. Information on $N_{\rm e}$ can also be used to estimate the distance to a nebula. The electron density in an ionized gaseous nebula can be measured by observing the effects of collisional de-excitation on nebular (forbidden) emission lines. This is usually achieved by comparing the observed intensities of lines emitted from two different energy levels of nearly equal excitation energy from the same ion, such that their intensity ratio is insensitive to electron temperature ( $T_{\rm e}$ ). If the two levels have very different radiative transition probabilities, then the relative populations of the two levels will vary with electron density, as will the intensity ratio of transitions emitted from them.

In the optical wavelength region, the most commonly used density-diagnostic ratios are [O II] $\lambda 3729/\lambda 3726$ and [S II] $\lambda 6716/\lambda 6731$ . The two doublets are intrinsically strong and easy to observe from an ionized gaseous nebula. O⁰ and S⁰ have similar ionization potentials, thus one expects [O II] and [S II] lines to arise from similar ionization regions. The [O II] and [S II] doublet ratios should therefore yield comparable values of electron density for a given nebula. Other density-diagnostic ratios observable in the optical include [Cl III] $\lambda 5517/\lambda 5537$ and [Ar IV] $\lambda 4711/\lambda 4740$ . These lines are in general weaker than the [O II] and [S II] lines and are most useful for high excitation nebulae, in particular for planetary nebulae (PNe). [Cl III] and [Ar IV] trace regions of higher ionization degree, thus depending on the density structure of a nebula, densities from them need not be the same as those derived from the low excitation [O II] and [S II] lines. Owing to differences in their critical densities, diagnostic lines of different ions and emitted from different pairs of energy levels are useful for different density regimes - [O II] and [S II] lines are sensitive to density variations for $N_{\rm e} \sim 10^3$ cm^-3, [Cl III] for $N_{\rm e} \sim 10^4$ cm^-3 and [Ar IV] for $N_{\rm e} \sim 10^4{-}10^5$ cm^-3. Lines with relatively low critical densities, such as the [O II] and [S II] doublets, are suppressed in high density regions by collisional de-excitation. Thus in a highly stratified nebula containing dense ionized clumps, [O II] and [S II] emission will be biased towards regions of lower densities, electron densities derived from the [O II] and [S II] doublet ratios should therefore be lower than those yielded by the [Cl III] and [Ar IV] doublet ratios. The above simple reasoning is in consistence with the conclusion of the numerical analysis demonstrated by Rubin (1989) about how and to what extent does the $N_{\rm e}$ variations within a nebula affect the results of empirical $N_{\rm e}$ -diagnostics, which show a progression in inferred values of $N_{\rm e}$ with the same sequence of $N_{\rm c}$ changing from the lowest to the highest.

The low transition probabilities of nebular forbidden lines and the low impact energies involved in a photoionized gaseous nebula imply that the atomic data needed for the calculation of level populations and line intensity ratios as a function of $N_{\rm e}$ (and $T_{\rm e}$ ), including Einstein spontaneous transition probabilities and collision strengths, have to rely on sophisticated multi-electron quantum mechanics calculations. Validating the accuracy of those theoretical calculations through comparison with observations is thus an important aspect of nebular studies. The comparison of electron densities derived from various diagnostics of different characteristics, such as ionization potential, critical density and excitation energy, can provide valuable information about nebular structure.

In an earlier study of electron densities in PNe, Stanghellini & Kaler (1989) compared electron densities derived from the above four optical diagnostic ratios for a large sample using measurements published in the literature. They found that on average the [O II] doublet ratio yielded densities 16 per cent lower than values determined from the [S II] doublet ratio, and about 35 per cent lower than deduced from the [Cl III] doublet ratio. They also found that densities deduced from the [Cl III] and [Ar IV] doublet ratios were well correlated, although the latter tended to yield slightly lower values. They concluded that the atomic data for these diagnostic ratios were in good shape. Using the double-beam spectrograph mounted on the ANU 2.3 m telescope, Kingsburgh & English (1992) measured the [O II] and [S II] ratios simultaneously for a large sample of Galactic PNe and found that electron densities derived from the two ratios were in excellent agreement. On the other hand, a very different result was obtained by Meatheringham & Dopita (1991) who found that for a sample of 44 PNe in the Magellanic Clouds, [S II] densities were systematically lower than those determined from the [O II] doublet ratio. Using high resolution spectroscopic data obtained with an echelle spectrograph, mostly by the group led by Aller (Aller & Hyung 1995; Aller et al. 1996; Feibelman et al. 1994, 1996; Hyung 1994; Hyung & Aller 1995a,b, 1996, 1997a,b, 1998; Hyung et al. 1993, 1994a,b,c, 1995, 1997, 1999a,b, 2000, 2001; Keyes et al. 1990; Keenan et al. 1993, 1996, 1997) they determined simultaneously electron densities and temperatures using a number of plasma diagnostic lines in the optical and ultraviolet and found that overall the data yielded compatible and consistent results. More recently, Copetti & Writzl (2002), using data published in the literature, compared the observed line ratios for a number of density-diagnostics, instead of densities deduced from them, thus avoiding discarding measurements that yield ratios close to or beyond the the low- or high- $N_{\rm e}$ limits. They concluded that in general $N_{\rm e}([\mbox{N {\sc i}}]) \le N_{\rm e}([\mbox{O {\sc ii}}]) < N_{\rm e}([\mbox{S {\sc ii}}]$ , $[\mbox{Cl {\sc iii}}], [\mbox{Ar {\sc iv}}])$ as well as $N_{\rm e}([\mbox{S {\sc ii}}]) \simeq N_{\rm e}([\mbox{Cl {\sc iii}}]) \simeq N_{\rm e}([\mbox{Ar {\sc iv}}])$ and interpreted the results in terms of nebular inhomogeneities and possible errors in atomic parameters, in particular those of $[\mbox{O {\sc ii}}]$ .

At low plasma densities, each collisional excitation by electron impact leads to the emission of a photon. Therefore at low densities, the doublet flux ratio of an $N_{\rm e}$ -diagnostic, such as [O II] $\lambda 3729/\lambda 3726$ , is given by the ratio of collision strengths from the ground ⁴S_3/2 level to the corresponding upper levels ²D_5/2 and ²D_3/2 of the $\lambda3729$ and $\lambda3726$ lines, respectively. It has been commonly assumed that LS-coupling is a valid approximation for low excitation spectral terms of ground electron configurations of light element ions such as [O II]. Under this assumption, the ratio of collision strengths from ⁴S_3/2 to ²D_5/2 and ²D_3/2 is simply given by the ratio of the statistical weights of the upper two levels, i.e. 1.50 in this case. Employing the largest set of base functions hitherto, McLaughlin & Bell (1998) recently recalculated collision strengths for [O II] using the R-matrix method at the Breit-Pauli approximation level, and found that their results differ significantly from previous work such as those of Pradhan (1976). Most surprisingly, they find that the ratio of collision strengths from the ⁴S_3/2 level to the ²D_5/2and ²D_3/2 levels is not 1.50, but is about 1.93. McLaughlin & Bell attributed the result to departure from LS-coupling occurring in their calculations due to relativistic effects. This result, if confirmed, would have a profound significant effect on nebular studies, especially $N_{\rm e}$ determinations for low surface brightness H II regions which typically have very low electron densities. The extensive literature survey by Copetti & Writzl (2002) failed to find evidence in support of the result of McLaughlin & Bell (1998).

In this paper, we present measurements of intensity ratios of the four optical $N_{\rm e}$ -diagnostics for a large sample of >100 PNe. All measurements were derived from our own high quality spectra taken with a long-slit spectrograph equipped with a CCD detector. In Sect. 2 we describe the new observations and data reduction procedures and present the results in Sect. 3. The new measurements are analyzed and discussed in Sect. 4. In order to better constrain the low- $N_{\rm e}$ limit of the [O II] doublet ratio, we have included in our analysis the Galactic and Magellanic Cloud H II regions studied by Tsamis et al. (2003) and the extragalactic giant H II regions studied by Esteban et al. (2002). Diffuse galactic emission from low- $N_{\rm e}$ ionized gas offers the best medium to constrain observationally the low- $N_{\rm e}$ limit of the [O II] and [S II] doublet ratios. Measurements of such diffuse emission available in the literature are therefore discussed as well.

2 Observation and data reduction

Most of the observations were obtained with the ESO 1.52 m telescope using the Boller & Chivens (B&C) long-slit spectrograph in three observing runs in 1995, 1996 and 2001. In 1995, the spectrograph was equipped with a Ford $2048 \times2048$ $15~\mu{\rm m}\times 15~\mu$ m CCD, which was superseded in 1996 by a UV-enhanced Loral $2048 \times2048$ $15~\mu{\rm m}\times 15~\mu{\rm m}$ chip and in 2001 by a Loral $2688\times 2688$ $15~\mu{\rm m}\times 15~\mu{\rm m}$ chip.

A number of northern hemisphere PNe were later observed with the 2.5 m Isaac Newton Telescope (INT) using the Intermediate Dispersion Spectrograph (IDS) and the 235 mm camera equipped with an EEV CCD. The spectral wavelength coverage, slit width and FWHM resolution for each observing run are listed in Table 1.

Typical exposure times were about 5 min for low resolution spectra which had a FWHM of about 4.5 Å and about 20 to 30 min for spectra of higher resolution. Most nebulae were observed with a fixed position long-slit, sampling the brightest parts of the nebulae, normally passing through the nebular centre. For a few nebulae, such as NGC 6153, scanned spectra were also obtained by uniformly driving a long slit across the nebular surface, thus yielding average spectra for the entire nebula.

All spectra were reduced using the LONG92 package in MIDAS following the standard procedure. Spectra were bias-subtracted, flat-fielded and cosmic-rays removed, and then wavelength calibrated using exposures of a calibration lamp.

Given that in the current work, we are interested only in intensity ratios of two lines close in wavelength, the effects of any uncertainties in flux calibration and corrections for interstellar dust extinction on our results are minimal and can be safely neglected. Uncertainties in the observed doublet ratios are therefore dominated by the photon counting noise for the lines involved. The [S II] $\lambda\lambda$ 6716, 6731 and [O II] $\lambda\lambda$ 3726, 3729 lines are generally quite strong and easy to measure, except for some optically thin, high excitation PNe. The [Cl III] $\lambda\lambda$ 5517, 5537 lines are intrinsically much weaker, given the lower chlorine abundance. The[Ar IV] $\lambda\lambda$ 4711, 4740 lines can also be quite weak, especially in low excitation PNe. In our spectra, the [Ar IV] 4711.37 Å line was partially blended with the He I 4713.17 Å line even for those spectra taken with a spectral resolution of 1.5 Å FWHM. In PNe of very high excitation class, the [Ne IV] $\lambda\lambda$ 4714.25, 4715.61 lines may also contribute to the observed flux of the 4712 Å feature. On the other hand, in such cases, the intensities of the $\lambda\lambda$ 4714.25, 4715.61 lines can be well constrained using the other two [Ne IV] lines at 4724.15 and 4725.62 Å arising from the same upper level ²P _1/2,3/2. Using this, together with the fact that the laboratory wavelengths of all these lines are well known, we found that in most cases, the intensity of the [Ar IV] $\lambda$ 4711 line can be retrieved using Gaussian line profile fitting. The formal errors as given by the line fitting program were then propagated into the line ratios and electron densities deduced from them following standard procedures. The uncertainties could be underestimated or overestimated, depending on the relative intensities of the blending [Ar IV] $\lambda$ 4711 and He I $\lambda$ 4713 lines.

As a further check of the reliability and accuracy of our line profile fitting technique, we have compared for a number of sample PNe (e.g. Cn 2-1, He 2-118) line fluxes derived from the current data set with those measured on spectra newly obtained under a higher resolution ( $\sim$ 0.9 Å FWHM). The agreement between the two sets of measurement were found to be quite satisfactory, with typical differences of less than 3% when I( $\lambda4713$ )/ $I(\lambda4711$ ) ratio is about 2, and about 0.2% when the ratio is about 0.5. The errors introduced by line profile fitting procedures are therefore well within the photon counting noise limits.

For two sample PNe (M 2-24 and IC 4406), only low resolution spectra ( ${\it FWHM} = 4.5$ Å) were available. For these two nebulae contributions from the He I $\lambda$ 4713 line and the [Ne IV] $\lambda\lambda$ 4714, 4716 lines (as in the case of the high excitation PN IC 4406) to the $\lambda$ 4711 feature were estimated from the observed intensities of the He I $\lambda$ 4471 and [Ne IV] $\lambda\lambda$ 4724, 4726, respectively, and subtracted. Further observations of better spectral resolution should be useful.

The [Cl III] $\lambda\lambda$ 5517, 5537 lines were only marginally detected in Sn 1 and NGC 6072, resulting fairly large uncertainties in the line fluxes and their ratio.

Table 2: Line ratios and electron densities derived using the default atomic parameters described in Table 3.

3 Results

Intensity ratios for the four optical $N_{\rm e}$ -diagnostic doublets, derived from our new observations, are presented in Table 2, along with their uncertainties. Electron densities deduced from the ratios are also given in the table, all derived using EQUIB, a Fortran code to solve level populations for a multi-level atom, assuming a nominal electron temperature of 10 000 K. A five level atomic model was assumed for the four ions of interest here. References for our default atomic data set, including collision strengths and transition probabilities, are listed in Table 3. Also given in the table are ionization potentials for the ions and their predecessors.

In Figs. 1-6 we plot against each other the observed $N_{\rm e}$ -diagnostic ratios, [O II] $\lambda 3729/\lambda 3726$ , [S II] $\lambda 6716/\lambda 6731$ , [Cl III] $\lambda 5517/\lambda 5537$ and [Ar IV] $\lambda 4711/\lambda 4740$ against one another. Lines over-plotted in each graph show loci tracing variations of one diagnostic ratio as a function of another, assuming that both ions arise from identical ionization regions of uniform density, for the cases of $T_{\rm e}$ of 5000, 10 000 and 15 000 K. To further expand our sample into the low density regime, we have included in our analysis measurements of several Galactic and Magellanic Cloud H II regions observed by Tsamis et al. (2003) and extragalactic giant H II regions observed by Esteban et al. (2002). The default atomic parameters described in Table 3 were used. The rectangle in each diagram delineates the region of allowed values of the diagnostic line ratios between their low- density(top right) and high- $N_{\rm e}$ (bottom left) limits.

In Fig. 7, the [O II] $\lambda 3729/\lambda 3726$ ratio is plotted against the [S II] $\lambda 6716/\lambda 6731$ ratio and compared to theoretical predictions for various atomic data sets for O⁺, including the more recent collision strengths of McLaughlin & Bell (1998) who found that the ratio of collision strengths from the ground ⁴S_3/2level to the ²D_5/2 and ²D_3/2 levels deviates significantly from the LS-coupling value. Again, we assume here that the [O II] and [S II] lines arise from identical ionization regions and that there are no significant density inhomogeneities.

Electron densities derived from the four optical $N_{\rm e}$ -diagnostics using the default atomic parameters listed in Table 3 are compared against each other in Figs. 8-13. In all cases, a constant nominal $T_{\rm e}$ of 10 000 K is assumed in calculating the densities. In each diagram, nebulae that deviate significantly from the loci are labelled.

4 Discussion

$\begin{figure} \par\includegraphics[width=6.4cm,clip]{1470fig1.ps} \end{figure}$

Figure 1: The observed [O II] $\lambda 3729/\lambda 3726$ ratio is plotted against the [S II] $\lambda 6716/\lambda 6731$ ratio for 37 nebulae. Triangles are H II regions from Tsamis et al. (2003) and Esteban et al. (2002). The dotted, solid and dashed lines delineate the theoretical variations of the [O II] ratio as a function of the [S II] ratio, assuming that both ions arise from identical ionization regions of uniform density, for an $T_{\rm e}$ of 5000 K, 10 000 K and 15 000 K, respectively. Along the lines, $N_{\rm e}$ increases from top right to bottom left, and the six filled circles denote densities of 10⁰, 10², 10³, 10⁴, 10⁵, 10⁶ cm^-3, respectively. The dotted-dashed rectangle indicates the region of allowed values of the two diagnostic ratios between the low- and high-density limits.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=6.4cm,clip]{1470fig2.ps} \end{figure}$	Figure 2: Same as Fig. 1 but for [Ar IV] $\lambda 4711/\lambda 4740$ against [Cl III] $\lambda 5517/\lambda 5537$ . Observed values for a total of 59 nebulae are plotted.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=6.4cm,clip]{1470fig3.ps} \end{figure}$	Figure 3: Same as Fig. 1 but for [Ar IV] $\lambda 4711/\lambda 4740$ against [S II] $\lambda 6716/\lambda 6731$ . 62 nebulae are plotted.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=6.4cm,clip]{1470fig4.ps} \end{figure}$	Figure 4: Same as Fig. 1 but for [Ar IV] $\lambda 4711/\lambda 4740$ plotted against [O II] $\lambda 3729/\lambda 3726$ for 36 nebulae.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=6.4cm,clip]{1470fig5.ps} \end{figure}$	Figure 5: Same as Fig. 1 but for [Cl III] $\lambda 5517/\lambda 5537$ against [S II] $\lambda 6716/\lambda 6731$ for 74 nebulae. Note that in this digram the two filled circles at the top-right representing $N_{\rm e} = 10^0$ and 10² cm^-3 fall almost on top of each other.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=6.4cm,clip]{1470fig6.ps} \end{figure}$	Figure 6: Same as Fig. 1 but for [Cl III] $\lambda 5517/\lambda 5537$ against [O II] $\lambda 3729/\lambda 3726$ for 36 nebulae.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=6.4cm,clip]{1470fig7.ps} \end{figure}$

Figure 7: Same as Fig. 1 except that the loci delineating variations of the [O II] ratio as a function of the [S II] ratio for a homogeneous nebula were derived using combinations of atomic parameters tabulated in Table 4, where the different line types are described. A constant electron temperature of 10 000 K was assumed. The six circles denoting different electron densities are not plotted here.

Open with DEXTER

At low densities ( $N_{\rm e} \ll N_{\rm c}(\lambda; T_{\rm e})$ , where $N_{\rm c}(\lambda; T_{\rm e})$ is the critical density of the diagnostic line; cf. Osterbrock 1989), each collisional excitation by an electron leads to the emission of a photon. Given the small wavelengths interval, the energy difference can be ignored, thus the intensity ratio of an $N_{\rm e}$ -diagnostic doublet, such as [O II] $\lambda 3729/\lambda 3726$ , is given by the ratio of collision strengths from the ground ⁴S_3/2 level to the corresponding ²D_5/2 and ²D_3/2 upper levels. Since the ground term ⁴S has only one fine-structure level, under LS-coupling, this ratio is given by the ratio of the statistical weights of the upper levels and equals 1.50. Similar relations hold for the [S II], [Cl III] and [Ar IV] doublet ratios. Note that the two [O II] ²D fine-structure levels are inverted, but those of [S II], [Cl III] and [Ar IV] are not. Hence for the latter three ions, the ratio of the intensity of the shorter wavelength line to that of the longer wavelength line is 1.5, not the reverse as in the case of [O II].

At high electron densities [ $N_{\rm e} \gg N_{\rm c}(\lambda; T_{\rm e})$ ], collisional processes dominate over radiative decays and the upper two ²D _3/2,5/2 fine-structure levels are thermalized and populated according to their statistical weights, leading to a doublet intensity ratio that is given by the ratio of statistical weight ( $\omega$ ) times transition probability (A-value). For example, in the case of [O II], at high densities,

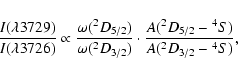
Measurements of doublet ratios near low- and high- $N_{\rm e}$ limits can therefore be used to constrain and test the accuracy of theoretical calculations of the relative collision strengths and spontaneous transition probabilities of $N_{\rm e}$ -diagnostic ratios. In the following, we will discuss each of the optical doublets and compare densities derived from them. Kolmogorov-Smirnov two-sample tests are carried out to test the null hypothesis that densities derived from individual $N_{\rm e}$ -diagnostics are consistent with each (densities derived from two diagnostic ratios are drawn from the same sample).

4.1 [O II] and [S II]

O⁰ and S⁰ have comparable ionization potentials. In addition, the [O II] and [S II] doublet lines have very similar critical densities and are therefore sensitive to $N_{\rm e}$ variations over a similar density regime. Figures 1 and 8 show that under the reasonable assumption that [O II] and [S II] lines arise from similar ionization regions, and that the nebula is more or less homogeneous, then for our default atomic data set the measured [O II] and [S II] ratios are consistent with each other over a wide $N_{\rm e}$ range, from less than 100 cm^-3 to over 10⁴ cm^-3. At densities higher than $\sim$ 10⁴ cm^-3, there is however some evidence that the [O II] doublet ratio indicates densities systematically lower than implied by the [S II] ratio. Our result thus differs slightly from the earlier [O II] and [S II] density survey by Kingsburgh & English (1992). From the integrated [O II] and [S II] doublet ratios measured from a homogeneous spectral data set for 64 Galactic PNe, Kingsburgh & English found that ${\rm log}~N_{\rm e}$ ([S II] $)= -0.31 + 1.08\times {\rm log}~N_{\rm e}$ ([O II]) and concluded that the result was consistent with a slope of unity, indicating equality between the two densities for their sample PNe. For [S II], Kingsburgh & English used the collision strengths and level energies from Mendoza (1983). We have recalculated [S II] densities from their published line ratios using our default atomic data whereby we have adopted the more recent calculations by Keenan et al. (1996) for [S II]. The results lead to revised relation between the [O II] and [S II] densities, ${\rm log}~N_{\rm e}$ ([S II] $)= -0.38 + 1.11\times {\rm log}~N_{\rm e}$ ([O II]). For comparison, our sample PNe yield ${\rm log}~N_{\rm e}$ ([S II] $)= -0.49 + 1.16\times {\rm log}~N_{\rm e}$ ([O II]). The slopes of the latter two relations are almost identical. We therefore conclude that the two spectroscopic surveys for the [O II] and [S II] doublet ratios are consistent with each other.

4.1.1 Low density limit

Table 4: References for O⁺ atomic data used to generate the loci plotted in Fig. 7.

$\begin{figure} \par\includegraphics[width=6.4cm,clip]{1470fig8.ps} \end{figure}$	Figure 8: Electron densities derived from the [S II] $\lambda 6716/\lambda 6731$ ratio plotted against value derived from the [O II] $\lambda 3729/\lambda 3726$ ratio. The dotted and dashed diagonal lines represent [S II] to [O II] $N_{\rm e}$ ratios of 2.5 and 0.625, respectively.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=6.4cm,clip]{1470fig9.ps} \end{figure}$	Figure 9: Same as Fig. 8 but for densities derived from the [Cl III] and [O II] doublet ratios, respectively.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=6.6cm,clip]{1470fig10.ps} \end{figure}$	Figure 10: Same as Fig. 8 but for densities derived from the [Ar IV] and [O II] doublet ratios, respectively.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=6.6cm,clip]{1470fig11.ps} \end{figure}$	Figure 11: Same as Fig. 8 but for densities derived from the [Cl III] and [S II] doublet ratios, respectively.
Open with DEXTER

Copetti & Writzl (2002) compared the observed [O II] $\lambda$ 3729/ $\lambda$ 3726 doublet ratios and the [S II] $\lambda$ 6716/ $\lambda$ 6731 ratios for a large sample of PNe and found that the locus calculated using the [O II] collision strengths of McLaughlin & Bell (1998) disagrees with observations near the low- $N_{\rm e}$ limit. Based on this, they concluded that the results of McLaughlin & Bell (1998) are probably spurious. A similar plot is shown in Fig. 7 using our own data. As noted by Copetti & Writzl (2002), the locus calculated using the [O II] collision strengths of McLaughlin & Bell deviates from observations at low densities. [S II] has a larger atomic mass number, and has a larger fine-structure splitting than [O II], thus one would expect [S II] to be affected more by relativistic effects. Consequently the [S II] doublet ratio ought to show an even larger deviation from the ratio of statistical weights should the effects invoked by McLaughlin & Bell (1998) apply. Were there to be a comparable deviation of the [S II] doublet ratio from its LS-coupling value as in the case of [O II] found by McLaughlin & Bell (1998), then the dash-dotted line in Fig. 7 can in principle be brought into agreement with observations. Thus the apparent disagreement noticed by Copetti & Writzl (2002) and shown here in Fig. 7 is not sufficient to reject the results of McLaughlin & Bell (1998). Alternatively, if relativistic effects are important for [S II] but not for [O II], then the dotted long-dashed locus in Fig. 7 will curve downwards as the low- $N_{\rm e}$ limit is approached (top-right corner of the graph) - a prediction not supported by the observations as well.

The key evidence against the results of McLaughlin & Bell (1998) remains the fact that none of the nebulae in our sample, including PNe and H II regions, shows a line ratio in excess of 1.5 (Fig. 1). The largest $\lambda$ 3729/ $\lambda$ 3726 ratio determined for a PN in our sample is $1.23\pm0.01$ (M 1-64, cf. Table 1), and that for an H II region is 1.43 (SMC N66, Tsamis et al. 2003). Amongst the 64 Galactic PNe observed by Kingsburgh & English (1992), IC 5148-50 has the largest $\lambda$ 3729/ $\lambda$ 3726 ratio, $1.45\pm0.04$ . Similarly, none of the nebulae in the extensive literature survey by Copetti & Writzl (2002) shows a ratio approaching 1.92.

$\begin{figure} \par\includegraphics[width=6.6cm,clip]{1470fig12.ps} \end{figure}$	Figure 12: Same as Fig. 8 but for densities derived from the [Ar IV] and [S II] doublet ratios, respectively.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=6.6cm,clip]{1470fig13.ps} \end{figure}$	Figure 13: Same as Fig. 8 but for densities derived from the [Ar IV] and [Cl III] doublet ratios, respectively.
Open with DEXTER

The best medium from which to determine observationally the low- $N_{\rm e}$ limit for [O II] $\lambda$ 3729/ $\lambda$ 3726 is the low- $N_{\rm e}$ plasma responsible for the diffuse galactic emission. Monk et al. (1990) obtained deep long-slit spectra centered on and around the PN IC 418 and symbiotic star RX Pup with the Anglo-Australian Telescope (AAT). [O II] $\lambda\lambda$ 3729, 3726 doublet emission was detected all the way out to an angular distance of 180 arcsec from the center of IC 418. The $\lambda3729$ / $\lambda3726$ ratio was found to change from a minimum $0.339\pm0.028$ to a maximum $1.78\pm0.67$ , both values remain consistent with the theoretical high- and low- $N_{\rm e}$ limits of 0.350 and 1.50, respectively, when taking into account the observational uncertainties. Similar results were found for RX Pup. There are also some other published observations near the density limits, yet none of them show clear evidence of inconsistency with the standard value when taking error bars into account. In Table 5 we list all the recent measurements we are aware of that yield an [O II] $\lambda$ 3729/ $\lambda$ 3726 ratio in excess of 1.4. Clearly the collision strengths of Pradhan (1976) are widely supported by observations; that is to say, LS-coupling is a good approximation for the five lowest levels of [O II]. To our knowledge, there are no direct observations of PNe and H II regions in favor of the collision strengths of McLaughlin & Bell (1998).

Similarly for [S II], none of the recent high quality measurements for a PN or an H II region of the $\lambda 6716$ / $\lambda 6731$ doublet ratio yield an value in excess of the canonical value of 1.5 under LS-coupling. For our sample PNe, the largest ratio recorded is $1.21\pm0.03$ whereas for those observed by Kingsburgh & English (1992) the maximum value is $1.35\pm0.04$ . In 23 of their long-slit PN spectra, Kingsburgh & English detected [S II] $\lambda\lambda6716,6731$ emission extending all along the slit length. Ten of the those extended emission regions show a $\lambda 6716$ / $\lambda 6731$ ratio in excess of 1.4 and these are listed in Table 6. Again, no values exceed the canonical value when taking error bars into account.

Table 5: [O II] $\lambda 3729/\lambda 3726$ intensity ratios of low- $N_{\rm e}$ plasmas from literature.

We note that for the very low surface brightness diffuse emission regions around PNe observed by Kingsburgh & English (1992), [S II] densities tend to be lower compared to [O II] values. Given that none of the measured [O II] and [S II] doublet ratios exceeds 1.5 when taking error bars into account, it seems unlikely this is caused by effects of possible departure from LS-coupling. A plausible explanation is that the low density Galactic diffuse gas, ionized by soft diffuse background radiation, emits more strongly in [S II] than in [O II] because of the lower ionization potential of neutral sulfur (10.4 eV compared to 13.6 eV for O⁰). Alternatively, the diffuse emission can be contaminated by scattered light from the main nebula of higher densities, and because the [O II] doublet falls in the near UV wavelength region, the contamination has a larger effect on [O II] than on [S II] (Monk et al. 1990).

To further explore this problem, we have also carried out a thorough literature survey of measurements of the [S II] $\lambda 6716$ / $\lambda 6731$ doublet ratio amongst ionized gaseous nebulae, emphasizing in particular those expected to have very low electron densities, such as diffuse ionized gas (DIG), extragalactic H II regions and supernova remnants (SNRs). The survey however does yield some evidence pointing to a $\lambda 6716$ / $\lambda 6731$ ratio in excess of 1.5. Deep spectroscopy of H II regions in NGC 55 by Tüllmann et al. (2003) revealed DIG emission which yields a [S II] $\lambda 6716/\lambda 6731$ ratio of $1.5\pm0.3$ . The error bars were estimated from their measured flux uncertainties, which were claimed to be less than 14 per cent. Galarza et al. (1999) presented spectroscopic observations of discrete emission-line nebulae and regions of DIG in M 31, including roughly 46 H II regions and 16 SNRs. In total 15 H II regions and 4 SNRs have a $\lambda 6716/\lambda 6731$ ratio larger or equal to 1.5, with a maximum of 3.9_2.0^5.8 (K 536, an H II region). While the uncertainties were large for most of the individual measurements, the ratios determined for two H II regions exceed 1.5 by more than $2\sigma$ , 2.3_2.2^2.4 in K 772 and 2.7_2.5^2.9 in K 70 (Position b; but for "K 70 mean'', the ratio is 1.7_1.6^1.8).

The observations of Galarza et al. (1999) of H II regions and SNRs in M 31 thus potentially pose a challenge to the validity of LS-coupling for the [S II] doublet. Given the very low surface brightness of such emission regions, measurements are always difficult. Any new independent measurements to corroborate these results will be invaluable. Similar observation for the [O II] $\lambda\lambda$ 3729, 3726 doublet ratio should also be attempted, although in this case it is even more difficult than for the [S II] lines, given the small wavelength difference between the two [O II] lines.

Table 6: Extended diffuse emission regions around PNe that give a [S II] $\lambda 6716$ / $\lambda 6731$ ratio larger than 1.4 (from Kingsburgh & English 1992).

Finally, we note that in a recent effort to detect the [¹³C III] 2s² ¹_1/2S₀-2s2p ³_1/2P⁰₀ $\lambda$ 1910 line, Rubin et al. (2004) reanalyzed all high resolution spectra of PNe available from the IUE Final Data Archive. They find that out of 41 PNe for which the [C III] 2s² ¹S₀-2s2p ³P⁰₂ $\lambda$ 1907 to C III] 2s² ¹S₀-2s2p ³P⁰₁ $\lambda$ 1909 ratio is determinable, 8 nebulae, most of thempreviously known low density PNe, show values in excess of its low density limit of 1.51 for pure ¹²C and 1.65 for pure ¹³C for $T_{\rm e} = 10~000$ K. Not all of the discrepancies can be explained by measurement uncertainties. As they point out, this current theoretical low density limit is fixed simply by the statistical weights of the energy levels giving rise to the lines, under the assumption of LS-coupling. Note that the [C III] 2s² ¹S₀-2s2p ³P⁰₂ $\lambda$ 1907 line and the C III] 2s² ¹S₀-2s2p ³P⁰₁ $\lambda$ 1909 line have very high critical densities of $7.4\times 10^4$ and $9.0\times 10^8$ cm^-3. Thus a PN with a typical electron density of $\la$ 10 000 cm^-3 is already approaching the low density limit of the $\lambda$ 1907/ $\lambda$ 1909 ratio.

In a related but probably of different nature problem, Rubin (2004) find that for roughly half of the PNe for which the $N_{\rm e}$ -sensitive [Ne V] 14.3/24.3 $\mu$ m ratio has been determined using ISO SWS spectra, the observed ratios are out of the low density bound. Since these fine-structure lines arise within a single spectral term, i.e. the 2p² ³P ground term of [Ne V], the problem here is probably caused by uncertainties in the relevant collision strengths, rather than related to the coupling scheme and the validity of the LS-coupling for these particular transitions.

4.1.2 High density limit

As described earlier, at high electron densities, the [O II] $\lambda 3729/\lambda 3726$ doublet ratio is determined entirely by the ratio of the Einstein transition probabilities, Thus measurements of the doublet ratio at the high- $N_{\rm e}$ limit can be used to observationally constrain the $A(\lambda3729)/A(\lambda3726)$ ratio. Similar relations hold for the [S II], [Cl III] and [Ar IV] doublet ratios.

In their analysis, Copetti & Writzl (2002) adopted the transition probabilities for [O II] tabulated by Wiese et al. (1996), which yield a very low high- $N_{\rm e}$ limit of 0.26 for the $\lambda 3729/\lambda 3726$ doublet ratio. Copetti & Writzl find that the locus for the $\lambda 3729/\lambda 3726$ ratio as a function of the [S II] $\lambda 6716/\lambda 6731$ ratio is incompatible with observations and conclude that the $A(\lambda3729)/A(\lambda3726)$ ratio for [O II] given by Wiese et al. (1996) needs to be revised upwards by approximately 25-50 per cent. A similar trend is seen in the current data set - the long-dashed line in Fig. 7, generated using the transition probabilities of Wiese et al. (1996), deviate significantly from the observations.

Similar, but to a lesser degree, a discrepancy exists between observations and the theoretical predictions for the radiative transition probabilities of [O II] given by Zeippen (1987), and originally calculated Butler & Zeippen by (1984) using the SUPER-STRUCTURE code. In their calculations, a configuration basis set was selected, which yielded satisfactory agreement with MC HF-BP (Multi-configuration Hartree-Fock method with Breit-Pauli relativistic effects) calculations. The effects of semi-empirical term energy corrections (TEC) and of relativistic corrections to the magnetic dipole transition operator were fully taken into account. Loci generated using the [O II] transition probabilities of Zeippen (1987) are shown as short-dashed and dotted-dotted-dashed lines in Fig. 7. They deviate from the observations by approximately 20 per cent at the high- $N_{\rm e}$ limit.

Overall, Fig. 7 shows that amongst the existing atomic parameters for the [O II] forbidden lines, our default set consisting of the transition probabilities from Zeippen (1982) and collision strengths from Pradhan (1976) fit the observations best. Close scrutiny of Fig. 7 reveals, however, that even this atomic data set shows some small deviations from the observations at high densities. An upward revision of the [O II] $A(\lambda3729)/A(\lambda3726)$ transition probability ratio by approximately 6 per cent would improve agreement with observation.

The above discussion is based on the assumption that the transition probabilities for [S II] are accurate, and that those of [O II] are to blame for any discrepancies shown in Fig. 7 between the observations and theoretical predictions. Evidence in favour of this interpretation will be discussed later in the paper.

4.2 [Cl III] and [Ar IV]

Cl⁺ and Cl²⁺ have ionization potentials of 23.8 and 39.6 eV, respectively. The corresponding values for Ar²⁺ and Ar³⁺ are 40.7 and 59.8 eV. Thus [Cl III] and [Ar IV] emission lines normally arise from inner regions of higher ionization degrees compared to [S II] and [O II] lines. In addition, the [Cl III] $\lambda$ 5517 and $\lambda$ 5537 lines have critical densities of $6.4~\times~ 10^3$ and $3.4\times 10^4$ cm^-3 at $T_{\rm e} = 10\ 000$ K and the corresponding values for the [Ar IV] $\lambda$ 4711 and $\lambda$ 4740 lines are $1.4\times 10^4$ and $1.3\times 10^5$ cm^-3. These values are much higher than those of the [S II] and [O II] doublet lines. In this section, we will first compare electron densities derived from the [Cl III] and [Ar IV] doublet ratios as well as from the [S II] and [O II] doublet ratios. This is followed by a brief discussion of the low density limits for the [Cl III] and [Ar IV] doublet ratios. Given the weakness of the [Cl III] and [Ar IV] lines, the low density limits of their doublet ratios are much less well constrained by the current observational data set compared to those for the [S II] and [O II] doublet ratios. On the other hand, given the higher critical densities of the [Cl III] and [Ar IV] lines, their low density limits are much easier to achieve than in the cases of the [S II] and [O II] doublet ratios.

4.2.1 [Cl III]

On the whole, densities deduced from the [Cl III] doublet ratios are similar to those deduced from the [O II] and [S II] doublet ratios. The agreement between the densities derived from the [S II] ratio and from the [Cl III] ratio is particularly good (cf. Fig. 11). At densities higher than $\ga$ $6\times10^3$ cm^-3, there is evidence that the [O II] doublet ratio yields densities slightly lower than those given by the [S II] ratio and by the [Cl III] ratio, when using our default atomic data set (cf. Figs. 8, 9). Note that S⁰ and S⁺have ionization potentials of 10.4 and 23.3 eV, respectively, compared to the corresponding values of 13.6 and 35.1 eV for O⁰ and O⁺, and 23.8 and 39.6 eV for Cl⁺ and Cl²⁺, respectively. Thus the O⁺ ionization zone is expected to have a larger overlap with that of Cl²⁺. This fact, combined with the realization that the [O II] and [S II] doublets have comparable critical densities which are smaller than those for the [Cl III] doublet, suggests that the systematically lower densities found from the [O II] doublet compared to those found from the [S II] and [Cl III] doublets at densities higher than $\ga$ $6\times10^3$ cm^-3 is unlikely to be caused by density inhomogeneities or ionization stratification. The discrepancy is more likely caused by uncertainties in the transition probabilities for the [O II] forbidden lines; as estimated in the previous section, the [O II] $A(\lambda3729)/A(\lambda3726)$ ratio given by Zeippen (1982) may need to be revised upwards by $\approx$ 6 per cent.

4.2.2 [Ar IV]

Figures 8-13, where we compare densities derived from the four optical $N_{\rm e}$ diagnostics, are arranged in such a way that for each pair of diagnostic ratios, $N_{\rm e}$ derived from the diagnostic of lower critical density is used as the abscissa. The [S II] and [O II] doublets have comparable critical densities; here we have chosen the [O II] $N_{\rm e}$ as the abscissa.

Plotted in this way, Figs. 10, 12 and 13, where densities derived from [Ar IV] are compared to those resulting from the other three diagnostic ratios, show a common feature - a rise in the data points as the high $N_{\rm e}$ limit is approached, suggesting densities derived from the [Ar IV] doublet are systematically higher than those derived from the other three $N_{\rm e}$ indicators, and that the deviation increases with increasing $N_{\rm e}$ . Adopting the earlier collision strengths of Zeippen et al. (1987) would lead to even higher densities being determined from the [Ar IV] doublet, although the increase is less than 0.1 dex except for densities lower than 10³ cm^-3 (Keenan et al. 1997). At such low densities, the [Ar IV] doublet ratio is however no longer a sensitive $N_{\rm e}$ -diagnostic.

Using the Long Wavelength Spectrometer (LWS) on board the Infrared Space Observatory (ISO), Liu et al. (2001) determined electron densities for a sample of bright Galactic PNe from the [O III] 52 $\mu$ m/88 $\mu$ m fine-structure line ratio and found that they are systematically lower than those derived from the optical [Cl III] and [Ar IV] doublet ratios. Considering the much lower critical densities of these [O III] lines ( $\sim$ a few $\times 10^3$ cm^-3) compared to those of the [Cl III] and [Ar IV] optical lines and the fact that the [Cl III] and [Ar IV] ratios yielded comparable densities consistent with each other, they argued that the discrepancy is unlikely to be caused by ionization stratification. Liu et al attributed it to the presence of modest $N_{\rm e}$ inhomogeneities. Emission of the [O III] fine-structure lines is suppressed by collisional de-excitation by electron impacts in high $N_{\rm e}$ regions. Our current optical study for a much larger sample of PNe however shows some evidence that the [Ar IV] doublet ratio tends to yield densities systematically higher than those deduced from the [Cl III] (and [O II] or [S II]) doublet ratio. The deviation is most profound at densities $\ga$ 10⁴ cm^-3 and increases as $N_{\rm e}$ increases (cf. Fig. 12). Since Ar²⁺ has an ionization potential of 40.7 eV, much higher than 23.8 eV of Cl⁺, it is possible that part of the discrepancy between the [Cl III] and [Ar IV] densities shown in Fig. 13 is caused by ionization stratification, where the inner, higher ionization Ar³⁺ zone has a higher $N_{\rm e}$ than the outer, lower ionization Cl²⁺ zone. Alternatively, nebulae with densities exceeding $\sim$ 10⁴ cm^-3 may contain ionized condensations with $N_{\rm e}$ exceeding the critical density for [Cl III], [O II] and [S II], with the [Ar IV] emission is less suppressed by collisional de-excitation.

4.2.3 Low density limit

The [Cl III] $\lambda 5517/\lambda 5537$ and [Ar IV] $\lambda 4711/\lambda 4740$ doublet ratios have low density limits of 1.44 and 1.42, respectively at $T_{\rm e} = 10\ 000$ K. For the [Cl III], only two nebulae in our sample have $\lambda 5517/\lambda 5537$ measured ratios in excess of its low density limit, $1.51\pm0.28$ in NGC 6072 and $1.46\pm0.22$ in NGC 5307. In both cases, the results remain consistent with the low density limit within 1 $\sigma$ measurement uncertainty. As described in Sect. 2 the [Cl III] doublet lines from NGC 6072 are very weak, and the high $\lambda 5517/\lambda 5537$ ratio measured for this nebula is most likely caused by observational uncertainties.

Similarly, two PNe in our sample have their measured [Ar IV] $\lambda 4711/\lambda 4740$ doublet ratios in excess of the low density limit, $2.39\pm 0.65$ in NGC 6781 and $1.64\pm 0.12$ in NGC 6072. In both cases, the uncertainties are large. Accurate measurements of the $\lambda 4711/\lambda 4740$ doublet ratio in these nebulae were further hampered by the serious contamination of the [Ar IV] $\lambda4711$ line by the nearby strong He I $\lambda4713$ line.

To conclude, amongst the PNe in our current sample, no credible cases can be established that the [Cl III] $\lambda 5517/\lambda 5537$ and [Ar IV] $\lambda 4711/\lambda 4740$ doublet ratios have a measured value in excess of their low density limit. Further high signal-to-noise ratio and high spectral resolution measurements of these two doublet ratios in low density nebulae should be useful.

Finally we note that Peimbert (2003) has recently obtained deep echelle spectrum of the Giant H II region 30 Doradus using the Ultraviolet Visual Echelle Spectrograph (UVES) mounted on the VLT Kueyen Telescope, at a spectral resolution of $\lambda/\Delta\lambda\sim 8800$ . The region he observed is found to have a very low $N_{\rm e}$ of just a few hundred cm^-3. The spectrum yields a [Cl III] $\lambda 5517/\lambda 5537$ and [Ar IV] $\lambda 4711/\lambda 4740$ doublet ratio of 1.33 and 1.35, respectively. Again both values are well within the low- $N_{\rm e}$ limits of the two doublet ratios.

4.3 Kolmogorov-Smirnov test

In order to investigate whether the four optical $N_{\rm e}$ -diagnostics yield electron densities compatible to each other, the Kolmogorov-Smirnov Two-sample Test has been carried out on the densities derived from each pair of diagnostic ratio, with the Null Hypothesis that densities derived from the two diagnostics of the pair are drawn from the same sample. Results from the tests are listed in Table 7. The table shows that except for the case of densities derived from [O II] versus those deduced from [Ar IV], the Null Hypothesis cannot be rejected at a high confidence level. In the case of [O II] versus [Ar IV] the Hypothesis can be rejected at a confidence level of 90 per cent, i.e. there is good evidence suggesting densities derived from the [O II] ratio differ systematically from those yielded by the [Ar IV] ratio. There is also some evidence, albeit quite weak, that densities yielded by the [S II] and [Cl III] ratios differ from those derived from the [Ar IV] doublet - the Null Hypothesis can be rejected with a risk possibility no more than 51 per cent. The evidence becomes more apparent if we restrict our analysis to high $N_{\rm e}$ nebulae. In fact, visual inspection of Figs. 8-13 suggests that in general,

Table 7: Results of Kolmogorov-Smirnov Two-sample Test on densities deduced from the four optical $N_{\rm e}$ -diagnostic ratios. X and Y denote the two density samples for the test, D is the Kolmogorv-Smirnov D statistic of the samples, P₀(>|D|) gives the probability of exceeding |D| under the Null Hypothesis and is equal to 1 minus confidence factor, n is the size of the samples and $D(\alpha _{0.10})$ is the critical D value for a confidence factor of 0.10.

5 Summary

In this paper we have presented measurements of the four optical $N_{\rm e}$ -diagnostic ratios for a sample of >100 Galactic PNe. We show that by adopting the default atomic parameters listed in Table 3, we obtain densities from the four diagnostics that are generally in good agreement. The agreement between the [S II] and [Cl III] densities is particularly good. We show that, under the assumption that the [O II] and [S II] lines arise from similar ionization zones (and would then yield comparable densities), the transition probabilities of Zeippen (1982) combined with the collision strengths of Pradhan (1976) for O⁺ give the best fit to observations. The more recent calculations of [O II] transition probabilities by Zeippen (1987) give a poor fit to the measurements at high densities and therefore can be ruled out. We confirm the earlier result of Copetti & Writzl (2002) that when using the [O II] transition probabilities listed in Wiese et al. (1996), electron densities derived from the [O II] doublet ratio are systematically lower than those deduced from the [S II] lines and that the discrepancies are most likely caused by uncertainties in the [O II] transition probabilities of Wiese et al.

At high electron densities, the [O II] doublet ratio is found to yield slightly lower densities compared to those derived from the [S II] and [Cl III] lines. The discrepancy can be removed by increasing the [O II] $\lambda$ 3729 to $\lambda$ 3726 transition probability ratio of Zeippen (1982) by approximately 6 per cent.

We also find that at high nebular densities, electron densities derived from the [Ar IV] ratio are systematically higher than deduced from the other three diagnostic ratios, and that the deviations increase with increasing density. While it is difficult to rule out that this is not caused by uncertainties in the [Ar IV] transition probabilities, modest density inhomogeneities, as pointed out by Liu et al. (2001), are probably to blame for the deviations.

Amongst the large number of PNe observed here as well as PNe and H II regions studied in the literature, no credible measurements, when measurement uncertainties are taken into account, can be established that yield an [O II] $\lambda 3729/\lambda 3726$ doublet ratio that exceeds the standard low- $N_{\rm e}$ limit of 1.5 under the assumption of LS-coupling. Thus we find no evidence in support of the more recent calculations of the [O II] collision strengths by McLaughlin & Bell (1998) who found a much higher low density limit of 1.93. Their result was attributed to departures from pure LS-coupling owing to relativistic effects. On the other hand, a thorough literature survey reveals a few measurements of the [S II] doublet in diffuse ionized gas in extragalactic H II regions and SNRs that produce a [S II] doublet ratio in excess of its low- $N_{\rm e}$ limit of 1.5 by more than a 2 $\sigma$ measurement uncertainty. Further observations to verify these results will be valuable.

A reexamination of electron density diagnostics for ionized gaseous nebulae

1 Introduction