A&A 427, 887-893 (2004)
DOI: 10.1051/0004-6361:20041464

Multiply-deuterated species in prestellar cores

D. R. Flower¹ - G. Pineau des Forêts^2,3 - C. M. Walmsley⁴

1 - Physics Department, The University, Durham DH1 3LE, UK
2 - IAS, Université de Paris-Sud, 92405 Orsay Cedex, France
3 - LUTH, Observatoire de Paris, 92195 Meudon Cedex, France
4 - INAF, Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy

Received 14 June 2004 / Accepted 5 August 2004

Abstract
We have studied the ortho, para, and, in the case of D₃⁺, meta forms of the multiply-deuterated isotopes of H₃⁺, under physical conditions believed to be appropriate to pre-protostellar cores. As deuterons have integral nuclear spin, I = 1, Bose-Einstein statistical laws apply. Having extended the network of chemical reactions used in our previous study (Walmsley et al. 2004), we have calculated the population densities of ortho- and para-D₂H⁺ and of ortho- and meta-D₃⁺. In the former case, comparison is made with the recent observations of para-D₂H⁺ in the prestellar core 16293E (Vastel et al. 2004). Using radiative transition probabilities computed by Ramanlal & Tennyson (2004), we have predicted the intensities of the near infrared vibrational transitions of the deuterated isotopes of H₃⁺. Many of these transitions can be observed, in absorption, only from above the Earth's atmosphere, but some might be detectable through atmospheric windows.

Key words: stars: formation - astrochemistry - ISM: clouds

1 Introduction

Recent observations of H₂D⁺ (Caselli et al. 2003; Ceccarelli et al. 2004) and additionally of D₂H⁺ (Vastel et al. 2004) have provided striking evidence of the extent of deuteration of H₃⁺ in the cold, dense gas of the interstellar medium. The removal of "heavy'' molecules, i.e. molecules containing elements heavier than helium, is believed to occur at high densities ( $n_{\rm H} \ga 10^5$ cm^-3) and low temperatures ($T \la 10$ K) by adsorption on to grains. It is accompanied by deuteration reactions with HD along the exothermic sequence H $_3^+ \rightarrow$ H₂D $^+ \rightarrow$ D₂H $^+ \rightarrow$ D₃⁺ (Roberts et al. 2003; Walmsley et al. 2004). Observations of the deuterated forms of H₃⁺, in conjunction with models of the deuteration process, enable information to be obtained on the conditions in media where stars are beginning to form, through gravitational contraction.

All four of the molecular ions H₃⁺, H₂D⁺, D₂H⁺ and D₃⁺ have "ortho'' and "para'' (and, in the case of D₃⁺, "meta'') forms, corresponding to the spin states of the protons (in H₃⁺ and H₂D⁺) or the deuterons (in D₂H⁺ and D₃⁺). Models of the deuteration process should distinguish between these forms, not only because the observations relate to specific modifications (ortho-H₂D⁺ and para-D₂H⁺) but also because the exo/endothermicities of the forwards and reverse reactions involved in deuteration depend on the forms of the reactants and products. The ortho:para ratios of the species H₃⁺ and H₂D⁺ are linked to the ratio of ortho- to para-H₂ (which are produced in grain-surface reactions), through the proton-exchanging reaction of H₃⁺ with H₂ and the formation of H₂D⁺ in the reaction H₃⁺(HD, H₂)H₂D⁺. On the other hand, the abundances of the ortho and para forms of D₂H⁺, and the ortho, para and meta forms of D₃⁺ are determined by reactions (principally with HD, which is also produced on grains) which modify the overall spin symmetry of the deuterons. Deuterons, unlike protons, have spin I = 1 and hence obey Bose-Einstein statistical laws.

Table 1: Statistical properties of the ortho and para forms of D₂ (Herzberg 1950). The ortho nuclear spin states are associated with even values of the rotational quantum number, J, and the para states with odd J. Only the lowest rotational level of each modification was included in the model. For D₂⁺ and D₂H⁺, the statistical properties of the lowest ortho and para levels are the same as in the case of D₂; but the lowest para level lies 42.0 K and 50.2 K, respectively, above the lowest ortho level, which is the ground level (Polyansky & Tennyson 1999; Ramanlal & Tennyson 2004).

Table 2: Statistical properties of the energy levels of D₃⁺ with J = 0 and J = 1. J is the rotational quantum number and K its projection on the molecular symmetry axis; g_I is the nuclear spin statistical weight. Only the two lowest energy levels, of A1 and E symmetry, were included in the model. The energies were computed by Polyansky & Tennyson (1999). Note that 1 cm $^{-1} \equiv 1.4388$ K.

In the present paper, we build on and extend our previous study of complete depletion in pre-protostellar cores by considering explicitly the ortho and para forms of D₂H⁺ and other species containing two deuterons, and the ortho and meta forms of D₃⁺. We determine their dependence on the physical conditions in the medium, including the properties of the grains. As defined in Sect. 2 of our previous paper, "complete depletion'' implies gas-phase fractional abundances of species such as CO much less than 10^-6.

2 Chemical model

The multiply-deuterated species D₂, D₂⁺, D₂H⁺ and D₃⁺ have been incorporated already in our previous model (Walmsley et al. 2004). However, we assumed that the chemical reactions implicated only their lowest energy states, of ortho symmetry. We now extend our study by considering the other modifications of these multiply-deuterated species. We discuss first those species containing two deuterons, and then D₃⁺ separately.

2.1 Species containing two deuterons

The template in this case is D₂, whose spectroscopic properties were discussed by Herzberg (1950). A deuteron has a spin quantum number I = 1 and a spin statistical weight  2I + 1 = 3. The total spin statistical weight of D₂ is $\prod _{i=1}^2 (2I_i + 1) = 9$, where the deuterons are labelled "1'' and "2''. Of the three possible values of the resultant nuclear spin, $I_{\rm tot} = 0, 1, 2,$ two ( $I_{\rm tot} = 0, 2$) are associated with states which are symmetric under exchange of the (identical) deuterons, whereas $I_{\rm tot} = 1$ is associated with states which are antisymmetric under deuteron exchange. The symmetric states, which are $\sum (2I_{\rm tot} + 1) = 6$ in number, are denoted "ortho'', whereas the 3 antisymmetric states are denoted "para''. These facts are summarized in Table 1.

When Bose-Einstein statistical laws apply, as here, the total (nuclear) wave function, which is a product of the spin and the rotational components, must be symmetric under exchange of identical bosons. As the rotational wave function has symmetry (-1)^J under exchange of the nucleons, where J is the rotational quantum number, it follows that the lowest rotational level, J = 0, must have ortho symmetry, and the first excited level, J = 1, must have para symmetry. Thus, the total statistical weight of the ground rotational level is 6, whereas that of the first excited rotational level is 9 (cf. Table 1). The first excited level lies at an energy E_J=1/k = 86.0 K above the J = 0 ground level (Herzberg 1950). We neglect levels $J \ge 2$, taking J = 0 to represent the ortho levels and J = 1 to represent the para levels. In the case of D₂⁺, the J = 1 level lies 42.0 K above J = 0 (using the spectroscopic constants of Herzberg (1950) for H₂⁺ and allowing for the different reduced mass of D₂⁺). In D₂H⁺, the lowest para level lies 50.2 K above the lowest ortho (ground) level (Polyansky & Tennyson 1999; Ramanlal & Tennyson 2004).

2.2 D₃⁺

The triply deuterated form of H₃⁺ (D₃⁺), needs separate consideration. Polyansky & Tennyson (1999) computed the energies of the rovibrational levels of H₃⁺ and all its deuterated isotopes, including D₃⁺, to spectroscopic accuracy. Ramanlal & Tennyson (2004) have recently provided the corresponding radiative transition probabilities.

In Table 2 are shown the lowest energy states of D₃⁺, together with their computed energies. Following the presentation by Townes & Schawlow (1955; see their Table 3-6), we deduce that: the lowest (ground) level, of A1 symmetry, has a nuclear spin statistical weight, g_I = 10; the first excited state, of E symmetry, has g_I = 8; and the second excited state, of A2 symmetry, has g_I = 1. The statistical weights and associated energies are listed in Table 2. We neglect the second excited state, of A2 symmetry, which has the lowest statistical weight. The ground state, which has the highest statistical weight (10), is denoted "ortho'', and the first excited state is denoted "meta''; the second excited state, which we neglect, is denoted "para''. Although the use of terms such as "ortho'' and "para'' is not strictly appropriate in this case, it serves to distinguish the energy levels. Thus, the "ortho'' level is again the lowest, with a total statistical weight (the product of the nuclear spin statistical weight, g_I, with (2J + 1)) of 10. The "meta'' level has a total statistical weight of 24.

3 Results

Our previous study (Walmsley et al. 2004) was directed towards understanding the observation of ortho-H₂D⁺ in L1544; the "ortho'', "para'' and "meta'' forms of multiply-deuterated species were not distinguished in those calculations. We have since found that the introduction of the distinction between the modifications has only modest effects on the results which we obtained and presented previously. Figure 1 illustrates this close similarity; it should be compared with Fig. 2 of Walmsley et al. (2004) and applies to the "reference'' model: a grain radius $a_{\rm g} = 0.1$ $\mu$m, a kinetic temperature T = 10 K, and a cosmic ray ionization rate $\zeta = 3$ $\times$ 10^-17 s^-1. As previously, the fractional abundances which we plot are those in steady state.

	Figure 1: Steady-state abundances of major ions and electrons in the standard model ($a_{\rm g}$ = 0.1 $\mu$m, T = 10 K, $\zeta = 3$ $\times$ 10-17 s-1) as functions of the density of molecular hydrogen.
Open with DEXTER

We now turn our attention to the multiply-deuterated species and, in particular, their modifications. We shall consider variations with respect to the gas density and temperature and the grain radius.

3.1 Dependence on n(H₂)

In Fig. 2, we plot the ratios para/ortho D₂H⁺, meta/ortho D₃⁺, and para/ortho D₂ as functions of the molecular hydrogen density. It should be recalled that "ortho'' refers to the lowest (ground) state and "para'' or "meta'' to the first excited state of these multiply-deuterated species. Results are given for the reference model ( $a_{\rm g} = 0.1$ $\mu$m, T = 10 K, and $\zeta = 3$ $\times$ 10^-17 s^-1).

In all three cases (D₂H⁺, D₃⁺, and D₂), the ratio of the excited to the ground state population density decreases with $n_{\rm H}$, owing to the enhanced rates of deuteron exchange reactions, which interconnect the modifications. The para/ortho D₂H⁺ and meta/ortho D₃⁺ ratios are determined principally by deuteron-exchanging reactions with HD, whose fractional abundance, n(HD)/n(H₂), is almost independent of n(H₂), as may be seen from Fig. 3. (Most of the deuterium in the medium is present in the form of HD, and of hydrogen in the form of H₂, and hence n(HD)/n(H₂)  $\approx 2n_{\rm D}/n_{\rm H} = 3.2 \times 10^{-5}$.)

In local thermodynamic equilibrium (LTE) at T = 10 K, the ratios of the excited to ground state densities are 0.045, 0.010, and 2.8 $\times$ 10^-4 for D₃⁺, D₂H⁺, and D₂, respectively. Thus, even at n(H₂) = 10⁷ cm^-3, none of these ratios has reached its LTE value. The para/ortho D₂ ratio is determined by dissociative recombination of D₃⁺ with electrons in the gas phase and on the surfaces of negatively charged grains and, at high densities, by deuteron-exchanging reactions with D₃⁺, which becomes the major ion (cf. Fig. 1). The fact that reactions involving five deuterons should assume significance is indicative of the very particular conditions which prevail in pre-protostellar cores. These same deuteron-exchanging reactions of D₂ with D₃⁺ also have some influence on the meta/ortho D₃⁺ ratio, and the corresponding reactions of D₂ with D₂H⁺ modify the para/ortho D₂H⁺ ratio. However, the fractional abundance of D₂, [D₂] < [HD], as Fig. 3 shows, and so the meta/ortho D₃⁺ and para/ortho D₂H⁺ ratios are determined principally by deuteron-exchanging reactions with HD, as already mentioned. As may be seen from Fig. 3, the fractional abundance of atomic D approaches that of H at high density.

	Figure 2: Steady-state values of the para/ortho D2 and D2H+ ratios and the meta/ortho D3+ ratio, as functions of the molecular hydrogen density ($a_{\rm g}$ = 0.1 $\mu$m, T = 10 K, $\zeta = 3$ $\times$ 10-17 s-1).
Open with DEXTER

	Figure 3: Steady-state fractional abundances of HD and D2, as functions of the molecular hydrogen density. The fractional abundances of atomic H and D are also plotted ($a_{\rm g}$ = 0.1 $\mu$m, T = 10 K, $\zeta = 3$ $\times$ 10-17 s-1).
Open with DEXTER

3.2 Dependence on T

As the temperature of the gas increases, the degree of deuteration of H₃⁺ is expected to fall, owing to the reverse sequence D $_3^+ \rightarrow$ D₂H $^+ \rightarrow$ H₂D $^+ \rightarrow$ H₃⁺; these reactions, with H₂, are endothermic (Ramanlal et al. 2003) and their rates increase rapidly with the kinetic temperature, T. Furthermore, the ratios of the excited to ground state population densities of the multiply-deuterated species might be expected to increase as T increases. These points are illustrated in Figs. 4 and 5, where the ratios n(para-H₂D⁺)/n(para-H₃⁺) and n(para-D₂H⁺)/n(ortho-D₂H⁺), n(meta-D₃⁺)/n(ortho-D₃⁺) are plotted against T. Also plotted in these Figures are the values of the ratios corresponding to LTE.

	Figure 4: The ratio n(H2D+)/n(H3+), computed for $n_{\rm H} = 2$ $\times$ 106 cm-3 and $a_{\rm g} = 0.1$ $\mu$m, as a function of the gas kinetic temperature, T. The value of the ratio in LTE is also plotted.
Open with DEXTER

	Figure 5: The the para/ortho D2H+ and meta/ortho D3+ ratios, computed for $n({\rm H_2}) = 10^6$ cm-3 and $a_{\rm g} = 0.1$ $\mu$m, as functions of the gas kinetic temperature, T. The values of the ratios in LTE are also plotted.
Open with DEXTER

	Figure 6: The the ortho/para H3+ and H2D+ ratios, computed for $n_{\rm H} = 2$ $\times$ 106 cm-3 and $a_{\rm g} = 0.1$ $\mu$m, as functions of the gas kinetic temperature, T. The values of the ratios in LTE are also plotted.
Open with DEXTER

Under conditions of thermodynamic equilibrium, when the rates per unit volume of forwards and reverse reactions are equal, the reaction para-H₃⁺(HD, para-H₂) para-H₂D⁺, which is exoergic by 232 K in the forwards direction, would give rise to an abundance ratio

$$\frac {n\left({\rm H_2D^+}\right)}{n\left({\rm H_3^+}\right)}... ... exp}(232/T) \frac {n({\rm HD})}{n\left({\rm H_2}\right)}\cdot$$

Taking k_f = 1.17 $\times$ 10^-10 cm³ s^-1, k_r = 1.40 $\times$ 10^-10 cm³ s^-1, and n(HD)/n(para-H₂) = 3.2 $\times$ 10^-5, we obtain

$$\frac {n\left({\rm H_2D^+}\right)}{n\left({\rm H_3^+}\right)} = 2.7 \times 10^{-5} {\rm exp}(232/T).$$

Figure 4 shows that the calculated abundance ratio tends towards its LTE value as T increases, although only slowly because of the large energy defect involved in the para-H₃⁺(HD, para-H₂)para-H₂D⁺ reaction. The para/ortho D₂H⁺ and meta/ortho D₃⁺ ratios also approach their LTE values with increasing T, as may be seen in Fig. 5. However, the para/ortho D₂H⁺ ratio has still not reached its LTE value at T = 50 K. Furthermore, the meta/ortho D₃⁺ ratio does not attain its LTE value, owing to reactions other than those (with HD) which interconvert the ortho and meta forms. Both the para/ortho ratio of D₂H⁺ and the meta/ortho ratio of D₃⁺ are superthermal at low T. The exoergicities of the deuteration reactions H₂D⁺(HD, H₂)D₂H⁺ and D₂H⁺(HD, H₂)D₃⁺ are sufficient to give rise to overpopulation of the excited (para and meta) levels at low temperatures, where the reactions are strongly favoured in the forwards (deuteration) direction (see Appendix B, where we derive an approximate expression for the meta/ortho D₃⁺ ratio at low temperatures).

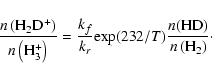
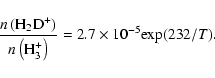
For completeness, the ortho/para H₃⁺ and H₂D⁺ ratios are plotted in Fig. 6; these ratios also are superthermal at low T. Note that the ortho/para H₃⁺ ratio does not reach its LTE value until T approaches 20 K. Thus, the assumption that the gas kinetic temperature may be derived from the observed value of this ratio, assuming LTE, is not valid at low T. In fact, the calculated values of the ratios plotted in Fig. 6 are double-valued: within certain ranges, the observed values of these ratios can correspond to either low-temperature non-LTE or higher temperature LTE solutions.

Vastel et al. (2004) have measured the column densities of ortho-H₂D⁺ and para-D₂H⁺ in the prestellar core 16293E, obtaining a ratio N(para-D₂H⁺)/N(ortho-H₂D⁺) = 0.75 for an excitation temperature $T_{\rm ex} = 10$ K (and assuming that the source is more extended that the observing beam). The calculated value of the ratio n(para-D₂H⁺)/n(ortho-H₂D⁺), as a function of T, is shown in Fig. 7. It may be seen from Fig. 7 that the value calculated at T = 10 K is consistent with that "observed''. However, we have just shown that neither the para/ortho D₂H⁺ nor the ortho/para H₂D⁺ ratio is in LTE at T = 10 K, and so this apparently good agreement should be viewed with circumspection. Moreover, the work of Mizuno et al. (1990) and Stark et al. (2004) suggests that a temperature in the range $12 \le T \le 16$ K may be more appropriate to 16293E.

The ortho/para H₂D⁺ and para/ortho D₂H⁺ ratios are superthermal at low T. Thermalization (with increasing T) leads to an initial decrease in both ratios, with the first decreasing faster than the second owing to the larger ortho:para separation in H₂D⁺ (86 K, as compared with 50 K in D₂H⁺). Thus, the ratio n(para-D₂H⁺)/n(ortho-H₂D⁺) tends to increase with T at low T. As LTE is approached, these trends are reversed, with ortho/para H₂D⁺ increasing faster than para/ortho D₂H⁺, and hence n(para-D₂H⁺)/n(ortho-H₂D⁺) decreases as T increases further, as may be seen in Fig. 7.

3.3 Dependence on a_g

In our calculations, we have assumed all the grains to have the same size, but we have investigated the dependence of the results on the grain radius, $a_{\rm g}$. We recall that it is the grain surface area per hydrogen nucleus which is relevant to the rates of gas-grain reactions.

	Figure 7: The ratio n(para-D2H+)/n(ortho-H2D+), computed for $n_{\rm H} = 2$ $\times$ 106 cm-3 and $a_{\rm g} = 0.1$ $\mu$m, as a function of the gas kinetic temperature, T. (Vastel et al. (2004) have reported a value of 0.75 for this ratio in the prestellar core 16293E (see text, Sect. 3.2).)
Open with DEXTER

As in our previous paper (Walmsley et al. 2004), we present results with reference to a model with the grain parameters $a_{\rm g} = 0.1$  $\mbox{$\mu$ m}$ and $\rho_{\rm g} = 2$ g cm^-3, where  $\rho_{\rm g}$ is the mean density of the grain material (core and ice mantle). To these parameters corresponds a grain surface area per hydrogen nucleus $n_{\rm g}~ \sigma _{\rm g}/n_{\rm H} = 1.1$ $\times$ $10^{-21}~ (0.10/a_{\rm g}$($\mu$m)) cm².

	Figure 8: The fractional abundances of the major ions and the free electron abundance plotted against the grain radius, $a_{\rm g}$, for a density of $n_{\rm H} = 2$ $\times$ 106 cm-3, T = 10 K, and $\zeta = 3$ $\times$ 10-17 s-1.
Open with DEXTER

	Figure 9: The ortho/meta ratio of D3+ and the ortho/para ratios of D2H+ and D2 plotted against the grain radius, $a_{\rm g}$, for a density of $n_{\rm H} = 2$ $\times$ 106 cm-3, T = 10 K, and $\zeta = 3$ $\times$ 10-17 s-1.
Open with DEXTER

In Fig. 8, we plot the fractional abundances of the major ions and the free electron abundance against $a_{\rm g}$, for a density of $n_{\rm H} = 2$ $\times$ 10⁶ cm^-3 and T = 10 K. As the grain size increases, the number density of grains (more specifically, of negatively charged grains) decreases, and so the free electron fraction increases, as may be seen in Fig. 8. Polyatomic ions recombine rapidly (dissociatively) with free electrons and on the surfaces of negatively charged grains. On the other hand, H⁺ recombines only slowly (radiatively) with free electrons but rapidly on the surfaces of negatively charged grains (which act as a third body and effectively catalyse the recombination reaction). Hence, the fraction of H⁺ increases with $a_{\rm g}$, and H⁺ becomes the major ion (when $a_{\rm g} \ga 0.1$ $\mu$m, for n(H₂) = 10⁶ cm^-3 and T = 10 K). The fraction of polyatomic ions first increases with the grain radius, as the number density of negatively charged grains decreases, then decreases as recombination with free electrons takes over. Thus, [D₃⁺] has a maximum in the vicinity of $a_{\rm g} = 0.1$ $\mu$m. Referring now to Fig. 9, we see that the maximum in [D₃⁺] is reflected in the variation of the ortho/para D₂ ratio. The ortho/para D₂H⁺ and ortho/meta D₃⁺ ratios, on the other hand, are approximately constant: they are determined by deuteron exchange with HD, whose fractional abundance is independent of $a_{\rm g}$ (as well as being independent of $n_{\rm H}$).

Table 3: Requisite column densities for unit optical depth in the absorption line centre for the deuterated forms of H₃⁺. Spectroscopic data from Ramanlal & Tennyson (2004).

4 Observational perspectives

We consider in this Section the prospects of observing directly either the ortho/para (ortho/meta) ratios or the relative abundances of the different deuterated forms of H₃⁺. Some pertinent observations have already been made. Vastel et al. (2004) have shown that H₂D⁺ and D₂H⁺ have comparable column densities, of the order of 10¹³ cm^-2, in the prestellar core 16293E; this observational result is compatible with the models discussed above. At densities in excess of 10⁶ cm^-3, the most abundant ion is likely to be either D₃⁺ or H⁺, depending on the grain size. It follows that the total number density of positive ions is considerably larger than the sum of the abundances of H₂D⁺ and D₂H⁺. In particular, a measurement of the fractional abundance of H₂D⁺ provides only a lower limit to the degree of ionization.

H₂D⁺ has been detected recently in the outer parts of the circumstellar disk surrounding the T Tauri star DM Tau (Ceccarelli et al. 2004), and the discussion in the present paper may be relevant to such objects. Once again, the determination of the ionization degree from the observations is complicated by our ignorance of the grain size in the relevant disk layer.

Whilst H₂D⁺ and D₂H⁺ can be (and have been) observed at sub-mm wavelengths, H₃⁺ and D₃⁺ lack a permanent dipole moment and consequently do not emit detectable rotational transitions. However, vibrational transitions are allowed in both species, and H₃⁺ has been observed, in the near infrared, in absorption towards strong background sources (e.g. McCall et al. 1999). Therefore, we have considered the observability, in the near infrared, of the deuterated forms of H₃⁺, assuming that the conditions are similar to those under which H₃⁺ itself has been detected. The sub-mm detections of H₂D⁺ and D₂H⁺ yield fractional abundances of the order of 10^-10, assuming a hydrogen column density of the order of 10²³ cm^-2; this value is typical of some prestellar cores (Bacmann et al. 2000) and corresponds to 50 mag of visual extinction, or approximately 2 mag at the wavelengths (around 5 $\mu$m) of the lines in Table 3. In this table are given, for several relevant transitions, the computed column density, $N_{\tau =1}$, for absorption from the lower level of a line for which the optical depth at the line centre, $\tau = 1$ (see, for example, Eq. (B12) of Tielens & Hollenbach 1985). We adopted a line width of 1 km s^-1. In Table 3 we give also the excitation energy, $E_{\rm l}$, of the lower level of the transition, relative to the ground level, and the transition wavelength. The A-values and quantum numbers have been taken from Ramanlal & Tennyson (2004): ( $J, K_{\rm a}, K_{\rm c}$) in the case of H₂D⁺ and D₂H⁺; and ( $\nu _{1}, \nu _{2}, J, G, U$) in the case of D₃⁺. We see that the computed column densities are of the order of 10¹⁴ cm^-2, and so several lines of the deuterated forms of H₃⁺ might be detectable, with optical depths at the line centre of the order of 0.1 (depending on the line width). Most of the transitions fall outside the M and L windows and would be observable only from above the atmosphere. Such observations may be the best way of determining the abundances of the ortho, para and (in the case of D₃⁺) meta forms of the isotopes of H₃⁺.

Appendix A: Additional chemical reactions and their rate coefficients

In this appendix are specified the additional reactions included to allow for the consequences of Bose-Einstein statistics on the abundances of multiply-deuterated species, as determined by our chemical model. As the abundance of D in the gas-phase can become comparable with that of H, the formation of para- and ortho-D₂ on grain surfaces is included in the reaction set, in addition to the formation of para- and ortho-H₂ and of HD.

Appendix B: A simplified analysis of the meta/ortho D₃⁺ abundance ratio

Meta-D₃⁺ and ortho-D₃⁺ are produced with approximately equal probability in the reactions D₂H⁺(HD, H₂)D₃⁺, as may be seen from Appendix A; let us denote the rate coefficient for formation of meta- or ortho-D₃⁺ in this reaction by k₁. In addition, there is interchange between the meta and ortho forms in the forwards (and reverse) reactions meta-D₃⁺(HD, HD)ortho-D₃⁺. At low kinetic temperatures, T, the reverse reaction, which is endoergic by 46.5 K, may be neglected; the rate coefficient for the forwards reaction is k₂ = 2.8 $\times$ 10^-10 cm³ s^-1.

Both meta-D₃⁺ and ortho-D₃⁺ are destroyed in dissociative recombination with electrons or on the surfaces of grains. We neglect the latter process (an assumption whose validity increases with the grain size); for the former process, we have k₃ = 2.7 $\times$ 10^-8 (T/300)^-0.52 cm³ s^-1 (cf. Appendix A). Furthermore, meta-D₃⁺ can be removed even at low T by the reaction meta-D₃⁺(ortho-H₂, HD)ortho-D₂H⁺; the rate coefficient is k₄ = 5.0 $\times$ 10^-10exp(-18.0/T). In steady state, the density of ortho-D₃⁺ is determined by

$$\left[k_1n\left({\rm D_2H^+}\right) + k_2n\left({\rm meta~D_3... ...ight]n({\rm HD}) = k_3n_{\rm e}n\left({\rm ortho~D_3^+}\right)$$

and that of meta-D₃⁺ by

$$\begin{eqnarray*}k_1n\left({\rm D_2H^+}\right)n({\rm HD}) &=& \left[k_3n_{\rm e}... ...eft({\rm ortho~H_2}\right)\right]n\left({\rm meta~D_3^+}\right). \end{eqnarray*}$$

Eliminating n(D₂H⁺) between these relations yields

$$\frac {n\left({\rm meta~D_3^+}\right)}{n\left({\rm ortho~D_3^... ... e} + 2k_2n({\rm HD}) + k_4n\left({\rm ortho~H_2}\right)}\cdot$$

Taking T = 10 K, n(H₂) = 10⁶ cm^-3, $a_{\rm g}$ = 0.1 $\mu$m, as in the reference model, we have n(HD) = 3.2 $\times$ 10^-5n(H₂), $n_{\rm e} \approx 10^{-8}n$(H₂), $n({\rm ortho~H_2}) = 5$ $\times$ 10^-5n(H₂) and hence $n({\rm meta~D_3^+})/n({\rm ortho~D_3^+}) \approx 0.07$, which is in reasonable agreement with the results presented in Fig. 5.

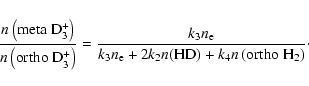
Thus, at low temperatures, the meta/ortho D₃⁺ ratio is expected to be less than 1, by an amount which depends on the degree of ionization and the ortho/para H₂ ratio. The analogous derivation of the para/ortho D₂H⁺ ratio would yield a qualitatively similar result.

Acknowledgements

It is a pleasure to thank Eric Herbst for informative discussions relating directly to the subject of the present study and Jonathan Tennyson for very helpful e-mail correspondence and providing results in advance of publication. We are also grateful to Paola Caselli, for her comments on the original version of our paper, and to Tom Millar, who was a helpful referee.

References

• Bacmann, A., André, P., Puget, J.-L., et al. 2000, A&A, 361, 555 [NASA ADS] (In the text)
• Caselli, P., van der Tak, F. F. S., Ceccarelli, C., & Bacmann, A. 2003, A&A, 403, L37 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Ceccarelli, C., Dominik, C., Lefloch, B., Caselli, P., & Caux, E. 2004, ApJ, 607, L51 [NASA ADS] [CrossRef] (In the text)
• Herzberg, G. 1950, Spectra of Diatomic Molecules (Princeton, NJ: D. Van Nostrand) (In the text)
• McCall, B. J., Geballe, T. R., Hinkle, K. H., & Oka, T. 1999, ApJ, 522, 338 [NASA ADS] [CrossRef] (In the text)
• Mizuno, A., Fukui, Y., Iwata, T., Nozawa, S., & Takano, T. 1990, ApJ, 356, 184 [NASA ADS] [CrossRef] (In the text)
• Polyansky, O. L., & Tennyson, J. 1999, J. Chem. Phys., 110, 5056 [NASA ADS] [CrossRef] (In the text)
• Ramanlal, J., & Tennyson, J. 2004, MNRAS, 354, 161 [NASA ADS] [CrossRef] (In the text)
• Ramanlal, J., Polyansky, O. L., & Tennyson, J. 2003, A&A, 406, 383 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Roberts, H., Herbst, E., & Millar, T. J. 2003, ApJ, 591, L41 [NASA ADS] [CrossRef] (In the text)
• Stark, R., Sandell, G., Beck, S. C., et al. 2004, ApJ, 608, 341 [NASA ADS] [CrossRef] (In the text)
• Townes, C. H., & Schawlow, A. L. 1955, Microwave Spectroscopy (London: McGraw-Hill) (In the text)
• Vastel, C., Phillips, T. G., & Yoshida, H. 2004, ApJ, 606, L127 [NASA ADS] [CrossRef] (In the text)
• Walmsley, C. M., Flower, D. R., & Pineau des Forêts, G. 2004, A&A, 418, 1035 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)

 

  
Online Material

Table A.1: Rate coefficients adopted in our chemical model for the reactions relating to the meta, ortho and para forms of multiply-deuterated species. The parameters $\alpha$, $\beta$, and $\gamma$ define the rate coefficients k (cm³ s^-1) at temperature T through the relation k = J $(a_{\rm g}, T)\gamma (T/300)^{\alpha } {\rm exp}(-\beta /T)$; J allows for Coulomb focusing in reactions of positive ions and negatively charged grains (Draine & Sutin 1987, Eq. (3.4)); $a_{\rm g}$ = 0.1 $\mu$m is adopted in the table. The rates (s^-1) of reactions induced directly by cosmic rays (crp) are given by  $\gamma \zeta$, where $\zeta$ is the rate of cosmic ray ionization of H₂. "g'' denotes "grain'', "m'', "o'' and "p'' denote "meta'', "ortho'' and "para'', respectively. Key reactions are in bold face. Numbers in parentheses are powers of 10. (The present table is complementary to that in Appendix A of Walmsley et al. 2004.)