A&A 427, 907-922 (2004)
DOI: 10.1051/0004-6361:20041227
T. Böhm 1 - C. Catala2 - L. Balona3 - B. Carter4
1 - Laboratoire d'Astrophysique, CNRS, Observatoire Midi-Pyrénées, 14 Ave. E. Belin,
31400 Toulouse Cedex, France
2 -
Observatoire de Paris-Meudon, CNRS, Paris Cedex, France
3 -
South African Astronomical Observatory, Capetown, South Africa
4 -
Center for Astronomy, Solar Radiation and Climate, University of Southern Queensland, Australia
Received 4 May 2004 / Accepted 15 July 2004
Abstract
We present the results of multisite observations spanning two years of the pre-main-sequence Herbig Ae star HD 104237. The star was observed in high resolution spectroscopy (R ![]() 35 000) for a total of 157.3 h of effective exposure time, over 42 nights, corresponding to a data base of 1888 individual echelle spectra.
We confirm that the HD 104237 system includes a spectroscopic binary, whose primary component HD 104237 A is pulsating. The resulting high quality radial velocity curve allows us to detect for the first time by spectroscopic means multiperiodic oscillations in a pre-main sequence star.
Five different modes are detected with very high confidence, with frequencies ranging between 28.5 and 35.6 d-1,
typical of
35 000) for a total of 157.3 h of effective exposure time, over 42 nights, corresponding to a data base of 1888 individual echelle spectra.
We confirm that the HD 104237 system includes a spectroscopic binary, whose primary component HD 104237 A is pulsating. The resulting high quality radial velocity curve allows us to detect for the first time by spectroscopic means multiperiodic oscillations in a pre-main sequence star.
Five different modes are detected with very high confidence, with frequencies ranging between 28.5 and 35.6 d-1,
typical of ![]() Scuti pulsations; an additional 3 frequencies have been extracted from the data, but with
a lower level of confidence. The pattern of frequencies indicates that at least some of the detected modes are non-radial.
The precise orbit determination and the measurement of the double line spectroscopic binary observed around periastron enabled us to determine a mass ratio of 1.29
Scuti pulsations; an additional 3 frequencies have been extracted from the data, but with
a lower level of confidence. The pattern of frequencies indicates that at least some of the detected modes are non-radial.
The precise orbit determination and the measurement of the double line spectroscopic binary observed around periastron enabled us to determine a mass ratio of 1.29 ![]() 0.02 between the primary and the secondary; based on the primary mass of 2.2
0.02 between the primary and the secondary; based on the primary mass of 2.2 ![]() 0.1
0.1 ![]() we conclude that the spectroscopic secondary HD 104237 b should have a mass of 1.7
we conclude that the spectroscopic secondary HD 104237 b should have a mass of 1.7 ![]() 0.1
0.1 ![]() and lie outside the pre-main sequence instability strip towards later spectral
types. A search for pulsations in the radial velocity curve of the much weaker secondary component was not conclusive at this stage. The location of the primary in the HR diagram and its position with respect to recent pre-main
sequence evolutionary tracks and isochrones implies a location of the secondary indicative of spectral type K3.
and lie outside the pre-main sequence instability strip towards later spectral
types. A search for pulsations in the radial velocity curve of the much weaker secondary component was not conclusive at this stage. The location of the primary in the HR diagram and its position with respect to recent pre-main
sequence evolutionary tracks and isochrones implies a location of the secondary indicative of spectral type K3.
Key words: stars: pre-main-sequence - stars: oscillations - stars: individual: HD 104237 - stars: binaries: spectroscopic
The Herbig Ae/Be stars are pre-main sequence (PMS) objects of intermediate
mass (2-8 ![]() )
(Herbig 1960; Strom et al. 1972; Finkenzeller
& Mundt 1984; Finkenzeller & Jankovitcz 1984).
They all show signs of intense stellar activity and strong stellar winds
(Praderie et al. 1982; Catala et al. 1986; Catala & Kunasz
1987; Böhm & Catala 1995; Böhm et al. 1996).
Many variable emission lines are present in their spectrum,
in particular H
)
(Herbig 1960; Strom et al. 1972; Finkenzeller
& Mundt 1984; Finkenzeller & Jankovitcz 1984).
They all show signs of intense stellar activity and strong stellar winds
(Praderie et al. 1982; Catala et al. 1986; Catala & Kunasz
1987; Böhm & Catala 1995; Böhm et al. 1996).
Many variable emission lines are present in their spectrum,
in particular H![]() shows strong variations in profile and in intensity.
The are recurrent observations of strong infrared excesses due to the presence of
circumstellar (CS) dust, either in the form of a spherical halo or in the form of a CS disk, or both.
shows strong variations in profile and in intensity.
The are recurrent observations of strong infrared excesses due to the presence of
circumstellar (CS) dust, either in the form of a spherical halo or in the form of a CS disk, or both.
The dusty environment and the active atmospheres and winds can explain photometric and spectroscopic variability on very different time scales and wavelength domains. Variable amounts of extinction by irregularly dispatched and gravitating circumstellar dust (Bibo & Thé 1991; van den Ancker et al. 1998) might explain photometric variations reaching several magnitudes in the visual domain and occurring on time scales of weeks to years; clumpy accretion (Pérez et al. 1992) could be responsible for lower amplitude photometric variations with time scales from hours to days. Rotational modulation of magnetically structured and active photospheres and chromospheres generate spectroscopic and photometric variability on time scales of from hours to days (Catala et al. 1999).
In massive protostars (
![]() ), the core evolution has a shorter
time scale than mass accretion, so that core hydrogen burning is
already present during the mass accretion phase. As a result, massive
protostars appear directly on the ZAMS. For lower-mass protostars,
the hydrostatic core evolution takes longer than the mass accretion phase, so
that mass accretion ends before the star reaches the ZAMS (the T Tauri stage
of PMS evolution). The Herbig Ae/Be stars occupy the intermediate case.
Their position in the HR diagram indicates that they are in the
radiative phase of their contraction towards the main sequence (Iben 1965;
Gilliland 1986), and should in principle not possess any outer convective
zone; therefore, if the young stellar evolutionary theory is correct, the classical
magnetic dynamo mechanism could not be responsible for the observed phenomena.
Finding the origin of this paradoxical activity is a major concern for young stellar
evolution. Obtaining a better understanding of the internal structure of these objects
is therefore a major goal of the current research.
), the core evolution has a shorter
time scale than mass accretion, so that core hydrogen burning is
already present during the mass accretion phase. As a result, massive
protostars appear directly on the ZAMS. For lower-mass protostars,
the hydrostatic core evolution takes longer than the mass accretion phase, so
that mass accretion ends before the star reaches the ZAMS (the T Tauri stage
of PMS evolution). The Herbig Ae/Be stars occupy the intermediate case.
Their position in the HR diagram indicates that they are in the
radiative phase of their contraction towards the main sequence (Iben 1965;
Gilliland 1986), and should in principle not possess any outer convective
zone; therefore, if the young stellar evolutionary theory is correct, the classical
magnetic dynamo mechanism could not be responsible for the observed phenomena.
Finding the origin of this paradoxical activity is a major concern for young stellar
evolution. Obtaining a better understanding of the internal structure of these objects
is therefore a major goal of the current research.
Stellar pulsations, if observed, can provide an excellent tool for analyzing the internal
stellar structure and its evolution. Breger et al. (1972) discovered the
first two pulsating intermediate mass PMS stars in the young cluster NGC 2264 (V 588 Mon and V 589 Mon). The existence of ![]() Scuti type pulsation amongst this category of stars
stars was later confirmed by photometric observations of the Herbig Ae star HR 5999
(Kurtz & Marang 1995) and radial velocity measurements of HD 104237
(Donati et al. 1997) based on
high resolution echelle spectroscopy.
Motivated by these interesting results Marconi & Palla (1998) investigated the
pulsation characteristics of HR 5999 theoretically, and predicted the existence of a pre-main-sequence instability strip, which is being
crossed by most of the intermediate mass PMS objects for a significant fraction
of their evolution to the main sequence. This strip covers approximately the same
area in the HR diagram as the
Scuti type pulsation amongst this category of stars
stars was later confirmed by photometric observations of the Herbig Ae star HR 5999
(Kurtz & Marang 1995) and radial velocity measurements of HD 104237
(Donati et al. 1997) based on
high resolution echelle spectroscopy.
Motivated by these interesting results Marconi & Palla (1998) investigated the
pulsation characteristics of HR 5999 theoretically, and predicted the existence of a pre-main-sequence instability strip, which is being
crossed by most of the intermediate mass PMS objects for a significant fraction
of their evolution to the main sequence. This strip covers approximately the same
area in the HR diagram as the ![]() Scuti variables.
Today, approximately thirteen intermediate-mass PMS stars have revealed to be
pulsating at timescales typical of
Scuti variables.
Today, approximately thirteen intermediate-mass PMS stars have revealed to be
pulsating at timescales typical of ![]() Scuti variables: HR 5999 (Kurtz & Marang
1995; Kurtz & Catala 2001), HD 104237 (Donati et al. 1997;
Kurtz & Muller 1999, hereafter KM), as well as eleven other candidates (Kurtz & Müller 2001; Marconi et al. 2001; Marconi et al. 2002;
Ripepi & Marconi 2003; Zwintz & Weiss 2003).
Typical pulsation periods range from half an hour (V 346 Ori, Pinheiro et al.
2003) to almost 5 h (HR 5999, Kurtz & Marang 1995). A recent review
by Catala (2003) presents the status of observational studies of pulsations in these stars.
Scuti variables: HR 5999 (Kurtz & Marang
1995; Kurtz & Catala 2001), HD 104237 (Donati et al. 1997;
Kurtz & Muller 1999, hereafter KM), as well as eleven other candidates (Kurtz & Müller 2001; Marconi et al. 2001; Marconi et al. 2002;
Ripepi & Marconi 2003; Zwintz & Weiss 2003).
Typical pulsation periods range from half an hour (V 346 Ori, Pinheiro et al.
2003) to almost 5 h (HR 5999, Kurtz & Marang 1995). A recent review
by Catala (2003) presents the status of observational studies of pulsations in these stars.
Marconi & Palla's models represent a first interesting approach to explaining the observed pulsation frequencies by radial oscillation models based on linear non-adiabatic calculations. However, it is likely that the asteroseismic behaviour of PMS stars has to take into account non-radial pulsations, as observed for instance in
roAp stars, ![]() Scuti stars, or
Scuti stars, or ![]() Dor stars (for a recent review, see e.g.
Telting 2003).
Dor stars (for a recent review, see e.g.
Telting 2003).
The aim of our study was to provide a first set of asteroseismic constraints for forthcoming non-radial pulsation models by determining unambiguously a higher number of periodicities with their corresponding amplitude and phase values: to achieve this goal, we decided to perform high resolution spectroscopic observations on a large time basis and with optimized time coverage.
Section 2 reviews previous related work, Sect. 3 describes the observations and data reduction, Sect. 4 summarizes results of the orbit determination, Sect. 5 presents results of the frequency analysis and in Sect. 6 the results are discussed in a more general context.
HD 104237 is a particularly interesting object and suitable target, as it belongs to this new category of pulsating PMS stars. First of all, this star is among the brightest Herbig Ae stars of the southern hemisphere (mV = 6.6), which enables short-exposure high-resolution spectroscopy on an extended time-base with 2 m class telescopes. The membership of the group of Herbig Ae/Be stars has been established by Hu et al. (1989).
Donati et al. (1997) observed this star in 1993 and 1995 in high resolution spectroscopy at AAT/UCLES; they reported that the spectrum of this A4V star features numerous spectral lines with relatively sharp profiles (![]() = 12
= 12 ![]() 2 km s-1) and concluded that the star is either viewed pole-on or moderately rotating. Moreover, they unambiguously discovered in their very small data set (each set spanning less than 40 min) a peak-to-peak 1.3 km s-1 modulation
with a period of 37.5 min, corresponding to 38.4 d-1 (38.6
2 km s-1) and concluded that the star is either viewed pole-on or moderately rotating. Moreover, they unambiguously discovered in their very small data set (each set spanning less than 40 min) a peak-to-peak 1.3 km s-1 modulation
with a period of 37.5 min, corresponding to 38.4 d-1 (38.6 ![]() 1 and 36.4
1 and 36.4 ![]() 1 min respectively for the 1993 and 1995 data sets), and attributed it to stellar pulsations. The spectropolarimetric study of HD 104237 marginally revealed a magnetic structure, which still needs to be confirmed.
1 min respectively for the 1993 and 1995 data sets), and attributed it to stellar pulsations. The spectropolarimetric study of HD 104237 marginally revealed a magnetic structure, which still needs to be confirmed.
Kurtz & Müller (2001) confirmed the ![]() Scuti type pulsational variability in
HD 104237 by photometric observations at the SAAO 0.5 m telescope in 1998. Their observations
revealed the existence of two close frequencies at 33.29 (f1) and 36.61 d-1 (f2), with
a mmag amplitude ratio of approximately 3.3. Moreover, they concluded that the ratio of amplitudes of the radial velocity and light variations is
not anomalous for a typical
Scuti type pulsational variability in
HD 104237 by photometric observations at the SAAO 0.5 m telescope in 1998. Their observations
revealed the existence of two close frequencies at 33.29 (f1) and 36.61 d-1 (f2), with
a mmag amplitude ratio of approximately 3.3. Moreover, they concluded that the ratio of amplitudes of the radial velocity and light variations is
not anomalous for a typical ![]() Scuti star. Taking the fundamental stellar parameters as reported by van den Ancker et al. (1998),
namely
Scuti star. Taking the fundamental stellar parameters as reported by van den Ancker et al. (1998),
namely
![]() ,
,
![]() and
and
![]() ,
or
,
or
![]() ,
they calculated small pulsation contants, Q, for the detected frequencies, suggesting high-overtone pulsation.
,
they calculated small pulsation contants, Q, for the detected frequencies, suggesting high-overtone pulsation.
Feigelson et al. (2003) showed recently that HD 104237 is in fact a multiple system (at least a quintet) formed by the Herbig Ae star itself and four low-mass PMS companions; two of the low-mass members of the group are actively accreting classical T Tauri stars, one of the components lies very close to the primary object and is thought to contribute to the spectrum as a K or M-type spectroscopic binary companion (called hereafter HD 104237 b).
Based on HST/STIS observation, Grady et al. (2004) very recently reported a bipolar microjet driven by HD 104237, which fits in the picture of a magnetically structured stellar atmosphere - and adds significance to the marginal magnetic
field detection by Donati et al. (1997). They also derive a new, significantly cooler, spectral type of A7.5Ve-A8Ve for the star, and a
![]() .
In addition to its IR excess (see e.g. Hu et al. 1989), HD 104237 shows a conspicuous UV/FUV excess, an indicator for active accretion.
.
In addition to its IR excess (see e.g. Hu et al. 1989), HD 104237 shows a conspicuous UV/FUV excess, an indicator for active accretion.
The most important parameters of HD 104237 are summarized in Table 1 and the previously determined pulsation frequencies are listed in Table 2.
Table 1: Parameters of HD 104237. References: [1] van den Ancker et al. (1998), [2] Donati et al. (1997), [3] Grady et al. (2004), [4] Hagen (1970), [5] van den Ancker et al. (1997).
Table 2: Previous pulsation frequency determinations for HD 104237. The first column indicates the year of observation, the second column the frequency; the corresponding period is shown in Col. 3; Col. 4 indicates spectroscopic or photometric oscillation amplitudes; the Col. 5 indicates the reference: [1] Donati et al. (1997), the 0.65 km s-1 amplitude in this table is calculated as half of the 1.3 km s-1 peak-to-peak amplitude stated in the paper; [2] Kurtz & Müller (2001).
The analysis presented in this paper is based on two distinct observing runs in 1999 and 2000. In April 1999 we observed HD 104237 during 7 nights with a maximum time coverage at the 1.9 m Radcliffe telescope of the South African Astronomical Observatory (SAAO).
In April 2000 we observed the same star in a bi-site campaign, involving in addition to the 1.9 m SAAO telescope, the Australian 74 inch Mt. Stromlo (MSSSO) telescope; this yielded a quasi-continuous time coverage
during more than 7 nights. Before and after the two-site campaign, we observed the
star extensively at SAAO. For 6 nights prior to the joint campaign
we obtained quasi-continuous single-site observations of the target star. Also, during 2 weeks in May the data base was enlarged by several
additional observations. The star was observed in high resolution spectroscopy (R ![]() 35 000 at SAAO, R
35 000 at SAAO, R ![]() 55 000 at Mt. Stromlo) for a total of 157.3 h of observations over 42 allocated nights, corresponding to a data base of 1888 individual echelle spectra. Table 3 summarizes the log of the observations.
The general observing strategy was to obtain as many 5 min observations of the target
during the night as possible. In order to be able to calibrate potential spectral shifts we decided to interleave one Th/Ar spectrum every hour. At the beginning and at the end of the night we
performed several series of tungsten calibration lamp flatfields through the fiber, and with
individual photon levels close to the signal levels of the spectroscopic observations.
55 000 at Mt. Stromlo) for a total of 157.3 h of observations over 42 allocated nights, corresponding to a data base of 1888 individual echelle spectra. Table 3 summarizes the log of the observations.
The general observing strategy was to obtain as many 5 min observations of the target
during the night as possible. In order to be able to calibrate potential spectral shifts we decided to interleave one Th/Ar spectrum every hour. At the beginning and at the end of the night we
performed several series of tungsten calibration lamp flatfields through the fiber, and with
individual photon levels close to the signal levels of the spectroscopic observations.
Spectroscopic observations at SAAO were obtained using the GIRAFFE fiber-fed echelle
spectrograph at the 1.9 m telescope. This instrument is a copy of the MUSICOS spectrograph
at the Telescope Bernard Lyot of the Pic du Midi Observatory, France (Baudrand & Böhm
1992). Its resolving power is about
![]() per resolved element, corresponding roughly to 2 pixels on the CCD in the dispersion direction. The 1k
per resolved element, corresponding roughly to 2 pixels on the CCD in the dispersion direction. The 1k ![]() 1k TEK CCD
is read by two amplifiers in parallel, decomposing the final image in two subfields of 0.5k
1k TEK CCD
is read by two amplifiers in parallel, decomposing the final image in two subfields of 0.5k ![]() 1k; this needs to be taken into account in the data reduction.
The wavelength range we ususally covered was 426-688 nm, spread over 50 orders in 1999,
and 436-688 nm, spread over 47 orders in 2000. The highest S/N (pixel-1) values we obtained reached 110 in April 2000, corresponding to more than 150 per resolved element (2 pixels); typical values of S/N (pixel-1) ranged around 50-70 in this run.
Since one of the interesting by-products of the HD 104237 observations concerned non-photospheric
line profile formation (future work), we decided to make use of the very good weather conditions
of April 15th and 17th 2000 to gather several spectra of the star
with a wavelength domain shifted to the blue (down to 375 nm), and to the red (up to 1020 nm).
Due to vacuum leakage of the camera in April 2000 we had to refill the dewar up to twice a
night, leading in the worst case to 3 distinct sub-series of observations for a given night; more details on the consequences for the data reduction are provided in Sect. 3.3.
1k; this needs to be taken into account in the data reduction.
The wavelength range we ususally covered was 426-688 nm, spread over 50 orders in 1999,
and 436-688 nm, spread over 47 orders in 2000. The highest S/N (pixel-1) values we obtained reached 110 in April 2000, corresponding to more than 150 per resolved element (2 pixels); typical values of S/N (pixel-1) ranged around 50-70 in this run.
Since one of the interesting by-products of the HD 104237 observations concerned non-photospheric
line profile formation (future work), we decided to make use of the very good weather conditions
of April 15th and 17th 2000 to gather several spectra of the star
with a wavelength domain shifted to the blue (down to 375 nm), and to the red (up to 1020 nm).
Due to vacuum leakage of the camera in April 2000 we had to refill the dewar up to twice a
night, leading in the worst case to 3 distinct sub-series of observations for a given night; more details on the consequences for the data reduction are provided in Sect. 3.3.
In April 2000 simultaneous observations were carried out at the Mt. Stromlo 74'' telescope using
the coude echelle spectrograph and a 2k ![]() 4k CCD. The adopted resolving power was
4k CCD. The adopted resolving power was
![]() .
Binning was used to project the resolved element on approximately 2 superpixels, providing finally a 0.5k
.
Binning was used to project the resolved element on approximately 2 superpixels, providing finally a 0.5k ![]() 2k frame (binning factor 2 in the dispersion direction parallel to the orders, and a binning factor of 4 in the direction perpendicular to the orders). The covered wavelength domain was 487 to 704 nm spread over 35 orders. Typical S/N (pixel-1) values were of the order of 30-60, rather similar to the SAAO results when taking into account the difference in spectral resolution (i.e. comparable S/N
2k frame (binning factor 2 in the dispersion direction parallel to the orders, and a binning factor of 4 in the direction perpendicular to the orders). The covered wavelength domain was 487 to 704 nm spread over 35 orders. Typical S/N (pixel-1) values were of the order of 30-60, rather similar to the SAAO results when taking into account the difference in spectral resolution (i.e. comparable S/N ![]() ). However, the spectral stability of the coude spectrograph at Mt. Stromlo was significantly worse than that of Giraffe at SAAO; this implied some differences in the data reduction procedure, as described below.
). However, the spectral stability of the coude spectrograph at Mt. Stromlo was significantly worse than that of Giraffe at SAAO; this implied some differences in the data reduction procedure, as described below.
Most of the data reduction was carried out following standard reduction procedures using the "ESPRIT'' spectroscopic data reduction package (Donati et al. 1997). This package also makes use of the "optimal extraction algorithm'' (Horne 1986). Heliocentric velocity correction was performed. The intrinsic wavelength calibration accuracy achieved with the "ESPRIT'' 2D-polynomial fit procedure is better than 0.7 pm mean rms (i.e. 7 m![]() ,
corresponding to 380 ms-1 at 5500
,
corresponding to 380 ms-1 at 5500 ![]() )
for the SAAO data sets, and better
than 0.5 pm mean rms (i.e. 5 m
)
for the SAAO data sets, and better
than 0.5 pm mean rms (i.e. 5 m![]() ,
corresponding to 300 ms-1 at 5500
,
corresponding to 300 ms-1 at 5500 ![]() )
for the Mt. Stromlo data set. However, the intrinsic
calibration precision is only one prerequisite for the optimized radial velocity calibration over time required for asteroseismic studies: Giraffe at the SAAO, a copy of the MUSICOS
spectrograph (Baudrand & Böhm 1992), is traditionally not an instrument dedicated
to this kind of studies, since it contains a high number of moving elements, and its light
conducting fiber does not contain any fiber-scrambler redistributing the light within the fiber before injection in the collimator of the spectrograph. This remark applies similarly to the echelle coude spectrograph at Mt. Stromlo and its mirror train.
)
for the Mt. Stromlo data set. However, the intrinsic
calibration precision is only one prerequisite for the optimized radial velocity calibration over time required for asteroseismic studies: Giraffe at the SAAO, a copy of the MUSICOS
spectrograph (Baudrand & Böhm 1992), is traditionally not an instrument dedicated
to this kind of studies, since it contains a high number of moving elements, and its light
conducting fiber does not contain any fiber-scrambler redistributing the light within the fiber before injection in the collimator of the spectrograph. This remark applies similarly to the echelle coude spectrograph at Mt. Stromlo and its mirror train.
As a consequence, the 2D-wavelength polynomical evolves strongly with time due to the instability of the spectrograph and its acquisition environment, and this even within minutes. The observed spectral instability within one night could reach up to 3.5 km s-1, in the form of a slowly evolving trend combined with some rapid shifts on small time and amplitude scales. The search for stellar pulsations requires taking this evolution into account, and finding a time-dependent correction to the initial wavelength calibration based on the Th/Ar arc lamp spectrum acquired at the beginning of each night.
Eventually, and after comparing different methods, we decided to adopt the following wavelength calibration strategy: we call "block of spectra'' a group of spectra obtained with the same instrumental set-up, without any mobile part of the spectrograph changing position and without refilling of the dewar. Whenever any change in setup or refilling of the camera's dewar had to take place, a new block of spectra was started. Therefore, due to the camera vacuum leakage at SAAO in 2000, we had to subdivide the nights into up to 3 blocks (see Table 3). Each block of spectra was calibrated in wavelength with respect to a reference Th/Ar arc lamp spectrum at the beginning of the block, which had to be acquired only a few minutes before the first stellar exposure. As a result, the 2D polynomial yielded a first reliable wavelength calibration for all spectra of the block. In a second step, we made use of the fact that our spectra contain many telluric water vapor lines, which are extremely narrow (spectral resolution), and positioned at the laboratory wavelength in the earth's frame. More than 100 of these lines with different intensities were contained in the observed wavelength domain. The wavelength position of these lines were moving with the instability of the spectrograph, since all spectra of one given observing block were calibrated with respect to the same initial arc spectrum; a global correction shift of each entire spectrum was therefore calculated using the very powerful technique of least-squares deconvolution ("LSD'', Donati et al. 1997), which combines the information contained in different spectral lines in order to increase the S/N. Using this LSD-technique on all telluric lines available in our spectra we calculated a reference velocity shift for every individual spectrum, and corrected for it. This procedure intrinsically assumes that all different areas of the CCD and all different wavelength domains are affected by the same velocity shift, which of course is only a first order approximation.
The precision of the crosscorrelation of LSD-profiles of telluric lines is orders of magnitudes higher than the intrinsic absolute calibration precision of the Th/Ar arc spectrum (values as mentioned above). In fact, the precision of the above correction is around 50 ms-1, based on a calculation similar to Appendix A in Böhm & Hirth (1997).
Once the correction is applied, it can therefore be assumed that every stellar spectrum is finally wavelength-calibrated with the same absolute precision as determined from the arc lamp spectra. The Mt. Stromlo spectra unfortunately could not be reduced to the same level of precision due to the absence of intense telluric lines; Mt. Stromlo data were therefore only corrected with respect to the initial arc spectrum of the night.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{1227orb.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg26.gif) |
Figure 1:
Orbital fit based on 2 years of bi-site spectroscopic observations of HD104237. HJD = 2 450 000 + |
| Open with DEXTER | |
The next step of the data reduction was to calculate for all 1888 stellar spectra photospheric LSD-profiles, using a mask corresponding to spectral type A4, and to fit a Gaussian to these residual profiles in order to measure their centroid. The measurement of the Gaussian centroid gives the radial velocity of the star's photosphere in the heliocentric wavelength frame. The accuracy of the radial velocity determinations increases, to first order, with the square root of the multiplex-number of lines, the large spectral domain of our echelle spectrograph set-up containing more than 290 photospheric lines. We estimate the finally achieved precision in radial velocity to be around 100 ms-1 for the SAAO data sets.
The Mt. Stromlo data could not be reduced to similar radial velocity precisions. For this data set, the radial velocity shift between the beginning and the end of the night could reach up to 1.5 km s-1. However, the general trend is a rather smooth evolution during the night, which, in this particular case, can be well fitted with a 2nd degree polynomial and does not significantly affect the subsequent frequency analysis, taking into account the rather short oscillation periods of this star (see Sect. 5). The residual error with respect to this general trend has a standard deviation of approximately 200 ms-1, as determined by the shifts of the arc spectra taken every hour. Any kind of vibration and resulting radial velocity shift occuring on time scales smaller than an hour cannot be measured by this method based on hourly arc spectra.
As described in the frequency analysis section (Sect. 5), we still decided to include these badly corrected radial velocity data in order to lower the aliases of the overall window function. Subsequent data reduction procedures are described in the individual analysis sections.
HD 104237 is a complex multiple system (Feigelson et al. 2003), with one component (HD 104237 b) very close (less than 2 marcsec) to the primary star and causing its spectroscopic binary behaviour. It was important for the oscillation frequency analysis (Sect. 5) to subtract the main orbital movement which has a peak-to-peak amplitude of approximately 35 km s-1, as can be seen in Fig. 1.
In fact, the overall radial velocity curve is the sum of a high-amplitude orbital movement and an almost 2 dex smaller stellar oscillation. Before determining the orbital parameters, we translated dates into HJD, heliocentric Julian date. We tried to fit the multiple object orbit with a binary approximation, which provided acceptable results despite its inherent error.
Figure 1 summarizes the orbital parameters determined by the binary fit on 2 year's data. The radial velocity corresponding to the orbital movement of the primary component was subtracted from the data, resulting in a residual radial velocity curve on which the subsequent frequency analysis was performed. It has to be noted, however, that except close to the periastron when both components are clearly separated (see Fig. 3 and section below), the primary profile suffers pollution by the 7 times weaker secondary profile (in the case of an A4 mask), which has not been subtracted for several reasons: i) the orbital timescale is much longer than the typical oscillation period, a small additional profile adds only low frequency contributions to the periodogram; ii) a subtraction of the profile adds additional method-dependent errors to the result; and iii) if the secondary profile should vary itself, there is no way at all to subtract its contribution, unless the variations are known.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{1227evol.eps}\end{figure}](/articles/aa/full/2004/45/aa1227/Timg27.gif) |
Figure 2:
Location of the HD 104237 primary (A) and spectroscopic secondary component HD 104237 b (location B) in the HR diagram. The luminosity and effective temperature pairs reported in van den Ancker et al. (1998) (VA) and Grady et al. (2004) (GR) are shown in the diagram, including error bars. Evolutionary tracks
(1.5, 2.0 and 2.5 |
| Open with DEXTER | |
As expected, the residual spectrum contains
errors due to the binary assumption and its subsequent orbital velocity subtraction, but also due to
the pollution by the unsubtracted secondary LSD profile. This can be seen most clearly
in the third nights of the 1999 and 2000 run, respectively, corresponding to
the 3rd panel from the top, left column, of Figs. 13 (![]() Julian date 1291.2-1291.6,
22nd April 1999) and 14 (
Julian date 1291.2-1291.6,
22nd April 1999) and 14 (![]() Julian date 1648.3-1648.7, 13 April 2000); in both
panels there subsists a clear diagonal trend of the radial velocity residual. In those nights, the radial velocity of the primary component, and therefore also of the secondary component, is close to the systemic velocity, implying a secondary profile travelling through the primary profile, from the red to the blue, explaining the direction of the radial velocity trend as observed.
Julian date 1648.3-1648.7, 13 April 2000); in both
panels there subsists a clear diagonal trend of the radial velocity residual. In those nights, the radial velocity of the primary component, and therefore also of the secondary component, is close to the systemic velocity, implying a secondary profile travelling through the primary profile, from the red to the blue, explaining the direction of the radial velocity trend as observed.
In some LSD residual spectra close to the periastron it was clearly possible to identify the secondary profile. In order to improve the contrast between the primary and this secondary profile,
we recalculated LSD profiles using a colder (
![]() = 7000 K) star mask, thereby
enhancing the intrinsic profile of the significantly
less luminous secondary (HD 104237 b) with respect to the primary. Figure 3 shows the double line cold mask LSD profile on two different nights around periastron in 1999, namely on
= 7000 K) star mask, thereby
enhancing the intrinsic profile of the significantly
less luminous secondary (HD 104237 b) with respect to the primary. Figure 3 shows the double line cold mask LSD profile on two different nights around periastron in 1999, namely on
![]() = 1289.4032 (continuous) and 1290.4893 (dot-dashed). Based on several measures of the radial velocities of both profiles with respect to the systemic velocity, and for different orbital positions, we calculated a mass ratio of
= 1289.4032 (continuous) and 1290.4893 (dot-dashed). Based on several measures of the radial velocities of both profiles with respect to the systemic velocity, and for different orbital positions, we calculated a mass ratio of
![]() = 1.29
= 1.29 ![]() 0.02.
0.02.
The mass of the primary has not yet been determined with high accuracy, and relies strongly on
the adopted stellar evolutionary model, the determination of the stellar luminosity and the spectral class. In the literature we find different estimates of the stellar mass
ranging from
![]() (Hagen 1970) to M = 2.5
(Hagen 1970) to M = 2.5 ![]()
![]() (van den Ancker et al. 1997). In a subsequent paper, van den Ancker et al. (1998)
announced corrected values (see Table 1) of the previously overestimated luminosity and effective temperature, which, placed in the latest HR diagrams by Palla & Stahler (2001), indicate a lower stellar mass of
M = 2.3
(van den Ancker et al. 1997). In a subsequent paper, van den Ancker et al. (1998)
announced corrected values (see Table 1) of the previously overestimated luminosity and effective temperature, which, placed in the latest HR diagrams by Palla & Stahler (2001), indicate a lower stellar mass of
M = 2.3 ![]()
![]() .
By placing the recently announced values of the stellar luminosity
.
By placing the recently announced values of the stellar luminosity
![]() and spectral class A7.5Ve-A8Ve from Grady et al. (2004) on these same tracks by Palla & Stahler we can infer a very similar value of the stellar mass of M = 2.2
and spectral class A7.5Ve-A8Ve from Grady et al. (2004) on these same tracks by Palla & Stahler we can infer a very similar value of the stellar mass of M = 2.2 ![]()
![]() .
In any case, the very different values of effective temperature and luminosity announced in the literature show the need for a clear determination of these parameters by means of high-resolution spectroscopy (work in progress).
.
In any case, the very different values of effective temperature and luminosity announced in the literature show the need for a clear determination of these parameters by means of high-resolution spectroscopy (work in progress).
Assuming the latter value of the mass of the primary,
i.e.
![]()
![]()
![]() ,
we estimated the mass of the close
companion HD 104237 b to be
,
we estimated the mass of the close
companion HD 104237 b to be
![]()
![]()
![]() .
Figure 2 shows the position of the primary and the secondary star in the HR diagram. The represented evolutionary tracks and isochrones are the result of recent modeling by Palla & Stahler (2001). The values of luminosity and spectral class as announced by Grady et al. (2004) place HD 104237 (A) right within the pre-main sequence instability strip calculated by Marconi & Palla (1998). However,
this result must be seen in the light of a persisting uncertainty in the effective temperature,
and also of a determination of the instability strip based solely on the first radial modes
(and not taking into account non-radial pulsations), and is therefore not very conclusive.
.
Figure 2 shows the position of the primary and the secondary star in the HR diagram. The represented evolutionary tracks and isochrones are the result of recent modeling by Palla & Stahler (2001). The values of luminosity and spectral class as announced by Grady et al. (2004) place HD 104237 (A) right within the pre-main sequence instability strip calculated by Marconi & Palla (1998). However,
this result must be seen in the light of a persisting uncertainty in the effective temperature,
and also of a determination of the instability strip based solely on the first radial modes
(and not taking into account non-radial pulsations), and is therefore not very conclusive.
Most likely, the age of HD 104237 is very close to 2 Myr, according to the interpolation of the
isochrones in the HR diagram (the star is located between the 1 Myr and 3 Myr isochrone).
Assuming the same age for both components, i.e. assuming that both stars are located on the same (here interpolated) isochrone, we find that the luminosity ratio should be approximately
![]() and that the effective temperature of the secondary should be
and that the effective temperature of the secondary should be
![]() ,
corresponding to the spectral class K3. The mass of the primary being only roughly known at this stage, another important piece of information is provided by the presence of a conspicuous
Li I 6707.8
,
corresponding to the spectral class K3. The mass of the primary being only roughly known at this stage, another important piece of information is provided by the presence of a conspicuous
Li I 6707.8 ![]() line at the velocity of the secondary, indicative of a spectral class later than F0, and a sign of youth; this confirms the pre-main sequence nature of both components of the spectroscopic binary. However, a clear analysis of the secondary spectrum and more precisely the line strength of the Li I 6707.8
line at the velocity of the secondary, indicative of a spectral class later than F0, and a sign of youth; this confirms the pre-main sequence nature of both components of the spectroscopic binary. However, a clear analysis of the secondary spectrum and more precisely the line strength of the Li I 6707.8 ![]() line is difficult to perform due to the strong continuum and line contribution of the primary star. A thorough analysis of this line will be presented in a subsequent paper. Further, more detailed studies are required to firmly establish the spectral classification of both stars.
line is difficult to perform due to the strong continuum and line contribution of the primary star. A thorough analysis of this line will be presented in a subsequent paper. Further, more detailed studies are required to firmly establish the spectral classification of both stars.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{1227bin.eps}\end{figure}](/articles/aa/full/2004/45/aa1227/Timg35.gif) |
Figure 3:
LSD profiles obtained before and after the periastron at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1227w99.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg36.gif) |
Figure 4: Spectral window of the SAAO 1999 data set. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1227wtot.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg37.gif) |
Figure 5: Spectral window of the total 2000 data set. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1227w00t.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg38.gif) |
Figure 6: Spectral window of the SAAO 2000 data set only. |
| Open with DEXTER | |
Before analyzing the stellar oscillation in the different data sets, we decided to correct for a residual trend in each observation run, by shifting each night by its mean radial velocity (shift only applied when a night contained more than 5 consecutive measurements).
As can be directly seen by comparing Fig. 13 (data set 1999) and Figs. 14-16 (data set 2000), the pulsation amplitudes changed significantly between 1999 and 2000, i.e. on a typical time-scale of one year. A global analysis of the total data set (SAAO 1999, SAAO 2000 and Mt. Stromlo 2000) did not therefore improve the result of the frequency analysis. We opted for a separate analysis of the 1999 and 2000 data sets, respectively. It has to be mentioned at this stage that we attributed the same weight to all radial velocity measurements, and did not attribute weights as a function of S/N or calibration precision.
The pulsation frequency analysis was performed using the PERIOD98 package (available at www.astro.univie.ac.at/~dsn/, Sperl 1998), which uses Fourier as well as multiple-least-squares algorithms. The latter technique fits a number of simultaneous sinusoidal variations in the radial velocity - time domain and does not rely on prewhitening. For the purpose of presentation only, however, low amplitudes are exhibited using the prewhitening technique. The various amplitude spectra are therefore presented as a series of panels, each with additional frequencies removed relative to the panel above.
We deliberately limited our frequency search to an area between 15 d-1 and 50 d-1 in the frequency domain; any lower frequency signal could not be considered as reliable because of poor continuum subtraction, as e.g. a consequence of the binary approximation. Frequencies higher than 50 d-1 were investigated, up to some artificial Nyquist frequency of 150 d-1, but no significant signal was present.
For a better understanding of the periodograms, we have as a first step calculated the spectral window function for the 1999 and 2000 data sets. The results are shown in Figs. 4 and 5; any real frequency should display the same alias pattern as the respective spectral window function.
As described in the data reduction section, we managed to achieve a much higher precision of radial velocity calibration for the SAAO data than for the Mt. Stromlo data of the year 2000 observing run. Therefore, we used two distinct approaches for the periodicity analysis: in a first step we performed periodicity analysis separately for the two data sets (SAAO 2000 and Mt. Stromlo 2000), and in a second step we proceeded to a global analysis of the complete 2000 data set. We found that the global analysis yielded a much clearer periodogram, since the corresponding window function shows significantly smaller sidelobes than the SAAO 2000 window function by itself (Figs. 6 versus 5); the gain in window function quality seems to dominate the loss in global calibration precision.
One of the most important questions in the study of multiperiodicity concerns the decision whether a peak correspond to a real physical variation intrinsic to the star, or only to statistical noise or sampling and data reduction contributions. Therefore, and in addition to the window function criterion, an amplitude criterion was needed to identify the last significant periodicity in the data sets. As of today, the most commonly accepted criterion for unevenly sampled astronomical data sets is based on empirical studies by Breger et al. (1993), and refined later by numerical studies by Kuschnig et al. (1997): 99.9% of all peaks due to noise are below a level of 4.0 times the mean noise amplitude level (respectively 99% below a level of 3.6 times the mean noise amplitude). These estimators have to be applied to the amplitude spectrum, not to the power spectrum. We adopted the following practical procedure: to estimate the confidence in a peak we calculated a sliding mean of the amplitude spectrum, with a box size of 10 d-1, and compared the peak with this sliding mean. We decided to perform this evaluation on the amplitude spectrum before any prewhitening of the analyzed oscillation frequency. By doing it this way, the result represents a certainly overestimated upper limit for the calculated mean, since most likely some real signal is included in the sliding box (see Figs. 8 and 10). Therefore, any peak exceeding 4.0 times the sliding mean amplitude curve and showing the same alias pattern as the corresponding spectral window function is certain to more than 99.9% (respectively 99% for the 3.6 mean amplitude curve). In order to illustrate the spectral window function criterion, we show in Fig. 7 the overplot of the 6th frequency of the SAAO 1999 data set with the periodogram of an artificial curve corresponding to its determined sinusoidal parameters calculated at the specific time grid. It can be seen that the sidelobes/aliases of this amplitude peak do exist in the observed periodogram, therefore the corresponding frequency is very likely to be really present in the observed data set.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{1227aF6.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg40.gif) |
Figure 7: f6 from the SAAO 1999 data set. Overplotted (dotted) is the periodogram corresponding to an artificial radial velocity curve with the frequency, amplitude and phase of this frequency calculated at the SAAO 1999 time grid, i.e. a convolution of the window function with the results of the frequency analysis for the 6th frequency. |
| Open with DEXTER | |
Table 4:
Frequencies, amplitudes and phases derived from the Fourier analysis of the SAAO 1999 data.
The uncertainty of the frequency is less than 0.04 d-1. Phase is relative to T0 = 1289.3706 (
![]() ).
).
![\begin{figure}
\par\includegraphics[width=12.6cm,clip]{1227p99.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg42.gif) |
Figure 8: Periodograms of the radial velocity oscillations in HD 104237 observed at SAAO in 1999. The sequence from top to bottom shows the change of the amplitude periodogram pre-whitened by f1, f2, f3, f4 and f5, respectively. The 99.9% confidence level is plotted (continuous), as well as the 99% level (dotted) and the 90% level (dashed). These levels correspond to a 4.0, 3.6 and 3.2-mean-amplitude-level calculated on 10 d-1 (cycles/day) sliding windows before prewhitening with the tested frequency (see text). |
| Open with DEXTER | |
Table 5:
Frequencies, amplitudes and phases derived from the Fourier analysis of the 2000 data set,
including the bi-site Mt. Stromlo/SAAO observations in April and May 2000. The uncertainty of the frequency is less than 0.006 d-1. Phase is relative to T0 = 1646.3040 (
![]() ).
).
Another important question concerns the precision that is obtained for the determined
pulsation frequencies. Ripepi et al. (2003) suggest estimating the error by measuring
the FWHM of the main lobe of the spectral window function. In our case these FWHMs
are 0.311 d-1 and 0.0866 d-1 for the 1999 and 2000 data sets respectively. However, if
we calculate the difference in frequency between identical modes in the two different data sets, we
find -0.006 d-1 for f1 (SAAO 1999, 33.289 d-1), +0.003 d-1 for f2 (SAAO 1999, 35.609 d-1), +0.018 d-1 for f3 (SAAO 1999, 28.503 d-1) and +0.058 d-1 for f4 (SAAO 1999, 30.954 d-1). It is obvious that the precision of the frequency determination does not only depend on the
total time-base of the observation (6.18 d in 1999, 40.1 d in 2000), but also on the sampling
rate, the signal to noise of the spectra (which in our case is strongly improved due to the multiplex gain of the LSD method), the intrinsic spectral stability depending on instrumental shifts and inherent calibration errors, as well as the time coverage, amongst others. It is certain that the data set for the year
2000 is of much higher quality than the 1999 data set, regarding all the facts cited above.
We therefore expect the typical error to be smaller than the calculated differences given above,
of the order of 3 ![]() 10-3 d-1 for the strong amplitude
frequencies f1 and f2 (2000), slightly higher for the lower amplitude
frequencies f3, f4 and f5. Kurtz & Müller (KM) estimate the uncertainty in the
frequency to be approximately 1/(4
10-3 d-1 for the strong amplitude
frequencies f1 and f2 (2000), slightly higher for the lower amplitude
frequencies f3, f4 and f5. Kurtz & Müller (KM) estimate the uncertainty in the
frequency to be approximately 1/(4![]() ), where
), where ![]() is the time span of the data set.
In our case this would yield 0.04 d-1 for the 1999 data set and 0.006 d-1 for the 2000 data set, values which are close to our estimation.
is the time span of the data set.
In our case this would yield 0.04 d-1 for the 1999 data set and 0.006 d-1 for the 2000 data set, values which are close to our estimation.
![\begin{figure}
\par\includegraphics[width=12.6cm,clip]{1227p99r.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg44.gif) |
Figure 9: Periodograms of the radial velocity oscillations in HD 104237 observed in 1999, showing the frequencies f7, f8, and the residual. Figure 8, continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12.6cm,clip]{1227ptot.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg45.gif) |
Figure 10: Periodograms of the radial velocity oscillations in HD 104237 observed in 2000, including the April/May 2000 bi-site campaign. The sequence from top to bottom shows the change of the amplitude periodogram pre-whitened by f1, f2, f3, f4 and f5, respectively. The 99.9% confidence level is plotted (continuous), as well as the 99% level (dotted) and the 90% level (dashed). These levels correspond to a 4.0, 3.6 and 3.2-mean-amplitude-level calculated on 10 cycles/day sliding windows before prewhitening with the tested frequency (see text). |
| Open with DEXTER | |
The adopted sinusoidal fit function of the PERIOD98 program to the data is as follows:
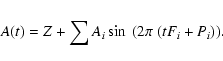
Figures 8 and 10 show the periodograms of the SAAO 1999 and SAAO/Mt. Stromlo 2000 data sets, the panels from top to bottom shows the change of the amplitude periodogram pre-whitened by f1, f2, f3, f4 and f5, respectively.
The SAAO 1999 data set reveals the presence of at least 6 distinct frequencies (f1 to f6 of Table 5), satisfying the double criteria based on the mean noise level and the presence of the window function pattern. Frequencies f4 to f6 have amplitudes between the 99.0% and the 99.9% level; we still consider the noise level criterion to be fulfilled. Frequencies f7 and f8 satisfy the noise level criterion, but no clear idenfication of the window function pattern can be achieved; we therefore consider these frequencies as uncertain. For the sake of completeness they are shown in Fig. 9.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1227aF50.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg47.gif) |
Figure 11: f5 from the global 2000 data set. Overplotted (dotted) is the periodogram corresponding to an artificial radial velocity curve with the frequency, amplitude and phase of this frequency calculated on the time grid for the year 2000, i.e. a convolution of the window function with the results of the frequency analysis for the 6th frequency. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1227comp.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg48.gif) |
Figure 12: f6 from the 1999 data set (continuous line) versus f5 from the global 2000 data set (dotted). Most likely the two frequencies are identical. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{1227ts99.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg49.gif) |
Figure 13:
Pulsations of HD 104237 during the SAAO 1999 run. Superimposed
(continuous line) is the result of the frequency analysis (Table 4).
Time is expressed in HJD = 2 450 000 + |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{1227ts0a.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg50.gif) |
Figure 14:
Pulsations of HD 104237 during the SAAO April 2000 run. Superimposed
(continuous line) is the result of the frequency analysis (Table 5), based
on all observations obtained in 2000, including the Mt. Stromlo April 2000 observations.
Time is expressed in HJD = 2 450 000 + |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.5cm,clip]{1227ts0b.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg51.gif) |
Figure 15:
Pulsations of HD 104237 during the SAAO May 2000 run. Superimposed
(continuous line) is the result of the frequency analysis (Table 5), based
on all observations obtained in 2000, including the April 2000 observations.
Time is expressed in HJD = 2 450 000 + |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.15cm,clip]{1227tsms.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg52.gif) |
Figure 16:
Pulsations of HD 104237 during the Mt. Stromlo 2000 run (filled circles), and SAAO 2000 run (diamonds). Superimposed (continuous line) is the result of the global frequency analysis (Table 5), based on all observations obtained in 2000. Time is expressed in HJD = 2 450 000 + |
| Open with DEXTER | |
It is clear that after prewhitening with f8 additional signal is contained in the residual amplitude spectrum, but any kind of reliable frequency determination is not reasonable at this stage.
The Mt. Stromlo and SAAO year 2000 observations unambiguously reveal the presence of 5 frequencies (f1 to f5 of Table 5), all satisfying both selection criteria. Figure 11 shows the last clearly selected (5th) frequency of the Mt. Stromlo/SAAO 2000 data set. After prewhitening with this frequency, the residual amplitude spectrum does not reveal significant additional signal at this stage, as can be seen in the lowest panel of Fig. 10.
It is obvious that frequencies f1, f2, f3 and f4 of the SAAO 1999 data set correspond to frequencies f2, f1, f4, f3 of the 2000 data set. Their existence is therefore established beyond any doubt. Frequency f5 (1999) was not found in the 2000 data set, but frequency f6 (1999) is very likely to be identical to f5 (2000), despite a frequency difference of 0.24 d-1; the latter is in fact largely blended, most likely due to a mode coupling (Fig. 12).
At this stage we want to mention that the periodicity analysis programs kindly provided by Don Kurtz gave exactly the same results for the 5 frequencies with the highest peak in the amplitude spectrum of 1999 and 2000. The three weakest frequencies of 1999 were also found in the amplitude spectrum, despite a different priority selection by the program.
After having performed the PERIOD98 frequency analysis we calculated for both SAAO 1999 and SAAO 2000 data sets artificial time series (with frequencies f1 to f6 and f1 to f5, respectively), which we subtracted from the original data. In both cases the residuals had
a standard deviation of
![]() ms-1. Due to the bad radial velocity correction and the low intrinsic quality of the Mt. Stromlo data, the residuals of the total year 2000 data set (SAAO and Mt. Stromlo) had a standard deviation of
ms-1. Due to the bad radial velocity correction and the low intrinsic quality of the Mt. Stromlo data, the residuals of the total year 2000 data set (SAAO and Mt. Stromlo) had a standard deviation of
![]() ms-1. These residuals should not be confounded with
the intrinsic radial velocity calibration precision we obtained. In fact, they contain orbital residuals due to the approximated orbital fit (binary approximation), secondary pollution in the LSD profiles of the primary (when the primary velocity is close to the systemic velocity), measurement errors of the centroid of the primary
LSD profile, but also remaining unextracted signal, as can be seen in the prewhitened amplitude spectra of Figs. 9 and 10.
ms-1. These residuals should not be confounded with
the intrinsic radial velocity calibration precision we obtained. In fact, they contain orbital residuals due to the approximated orbital fit (binary approximation), secondary pollution in the LSD profiles of the primary (when the primary velocity is close to the systemic velocity), measurement errors of the centroid of the primary
LSD profile, but also remaining unextracted signal, as can be seen in the prewhitened amplitude spectra of Figs. 9 and 10.
Figures 13-16 show the pulsations of HD 104237 in 1999 and 2000. Superimposed are artificial data corresponding to the results of the frequency analysis as described in Tables 4 and 5. A very nice agreement between observations and fitted data can be observed.
Motivated by the results of the orbital analysis (Sect. 4) and in order to better constrain the
location of the secondary component within the HR diagram, we decided to investigate in more
detail the radial velocity variations of the secondary component, HD 104237 b. According to the mass relation we determined and on the assumption that the two stars are coeval,
the secondary component should in fact lie outside the Marconi & Palla instability
strip. To do so, we extracted the secondary LSD profile of the SAAO 2000 observations around the periastron (April 11th and 12th), when both components were well separated. The proximity to the periastron implies strong orbital velocity changes for the secondary; we therefore corrected the radial velocity
measurements of the two nights by individually adjusted low order polynomia. The resulting residual
secondary radial velocity movements were subsequently analyzed: the standard deviation of the 2-day
series was
![]() 230 ms-1, similar to the value we measured on the residual curves of the primary, after having subtracted the fitted curve from the original data. We believe at this stage that any periodicity analysis of these secondary movements might be noise-limited, i.e. that no reliable periodicity measurement is possible on this data set. However, for the sake
of completeness, we show in Fig. 17 the amplitude spectrum of the secondary component
HD 104237 b. Potential pulsation frequencies might lie around 20, 25 and 31 d-1, but their existence in this data set is likely to be completely spurious since the corresponding amplitude levels are far below the 99.0% confidence level.
230 ms-1, similar to the value we measured on the residual curves of the primary, after having subtracted the fitted curve from the original data. We believe at this stage that any periodicity analysis of these secondary movements might be noise-limited, i.e. that no reliable periodicity measurement is possible on this data set. However, for the sake
of completeness, we show in Fig. 17 the amplitude spectrum of the secondary component
HD 104237 b. Potential pulsation frequencies might lie around 20, 25 and 31 d-1, but their existence in this data set is likely to be completely spurious since the corresponding amplitude levels are far below the 99.0% confidence level.
On the basis of two years of spectroscopic echelle observations, we clearly establish for the first time that HD 104237 A is a multiperiodic pre-main sequence pulsator. Five oscillation frequencies between 32.37 and 35.60 d-1 have clearly been observed in 1999 and in 2000, but with different amplitudes and amplitude ratios. Their existence is therefore firmly established. An additional 3 frequencies are reported based on the 1999 observations, but have not been found in the year 2000 observations. Since amplitudes change dramatically from one year to the next, it is not surprising that some modes are seen at one epoch and not seen at another.
The pulsation frequency identified by Donati et al. (1997) (see Table 2) is very probably identical to f1 by Kurtz & Müller (KM) and our 1999 observations (f2 of the 2000 data set); f2 (KM) has a frequency of 36.61 d-1, but the authors (KM) conclude on a potential alias ambiguity to the +1 d-1 alias; on the contrary, our unambiguous determination of f1 (2000) reveals that in fact the frequency ambiguity for f2 (KM) was with respect to the - 1 d-1 alias instead to the +1 d-1 alias.
When comparing the individual oscillation amplitudes and their ratios corresponding to data sets obtained in different years (our 1999 and 2000 observations,
but also the observations in 1993 and 1995 reported by Donati et al. 1997) one observes important variations. This phenomenon is typical of ![]() Scuti stars.
Scuti stars.
The observations of April/May 2000 reveal very narrow and unresolved peaks (width of the window function peaks) in the amplitude spectra, witness of a high degree of coherence of the modes, at least on the time scale of the 2-month's observations.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1227sec.eps} \end{figure}](/articles/aa/full/2004/45/aa1227/Timg56.gif) |
Figure 17: Amplitude spectrum of the secondary component HD 104237 b, based on SAAO 2000 observations of April 11th and 12th. The continuous envelope indicates the 99.9% probability level (99.0% for the dashed line), the dot-dashed line correspond to an artificial profile with parameters of the main frequency and window function distribution. Probability levels have been calculated based on a sliding 20 cd-1 window. |
| Open with DEXTER | |
The precise orbit determination and the measurement of the double lined spectroscopic binarity
observed around periastron enabled us to determine a mass ratio of
![]() = 1.29
= 1.29 ![]() 0.02, which indicates that the secondary spectroscopic
companion HD 104237 b should have a spectral class around K3 and a luminosity of
0.02, which indicates that the secondary spectroscopic
companion HD 104237 b should have a spectral class around K3 and a luminosity of
![]() ,
i.e. ten times weaker than the primary.
A search for pulsation of the secondary did not yield any conclusive result, but
further observations around the periastron are required to establish a clear
radial velocity analysis of the secondary. Moreover, the exact spectral type and mass of the two major components of HD 104237 have to be established by detailed spectroscopic studies; the mere
fact that we see a conspicuous Li I 6707.8
,
i.e. ten times weaker than the primary.
A search for pulsation of the secondary did not yield any conclusive result, but
further observations around the periastron are required to establish a clear
radial velocity analysis of the secondary. Moreover, the exact spectral type and mass of the two major components of HD 104237 have to be established by detailed spectroscopic studies; the mere
fact that we see a conspicuous Li I 6707.8 ![]() line at the velocity of the secondary
indicates a spectral class later than F0 for this object and confirms the pre-main sequence nature
of the secondary component of the spectroscopic binary.
line at the velocity of the secondary
indicates a spectral class later than F0 for this object and confirms the pre-main sequence nature
of the secondary component of the spectroscopic binary.
Based on preliminary rough modeling by Goupil, Lebreton & Samadi (private communication), the large separation of the oscillations in our primary star HD 104237 A should be
![]() Hz,
corresponding to 3.45-3.88 d-1. By calculating the frequency difference of adjacent frequencies in the amplitude spectrum (observations of the year 2000), we find frequency separations of 2.49, 1.36, 0.91, 2.32 d-1 between f4-f3, f3-f5, f5-f2 and f2-f1, respectively.
These separations are significantly smaller than the calculated value of the large separation;
this indicates that several nonradial pulsation modes must be present in our data of
HD 104237 (A). However, since the radial pulsation modes are separated by the large separation, and since the gap of 7.08 d-1 between f4 and f1 corresponds roughly to twice the large separation, there is a potential existence of 1 to 3 radial pulsation modes at most among the 5 observed frequencies in 2000 (5(8) in 1999).
Still, the frequency difference f1-f5 and f5 to f4 is not identical and
corresponds to 3.23 and 3.85 d-1, respectively. Three radial modes would be separated by exactly the same value, corresponding to the large separation. Despite the associated uncertainty in the frequency determination,
it is therefore unlikely that there are 3 radial modes amongst our detected frequencies.
Hz,
corresponding to 3.45-3.88 d-1. By calculating the frequency difference of adjacent frequencies in the amplitude spectrum (observations of the year 2000), we find frequency separations of 2.49, 1.36, 0.91, 2.32 d-1 between f4-f3, f3-f5, f5-f2 and f2-f1, respectively.
These separations are significantly smaller than the calculated value of the large separation;
this indicates that several nonradial pulsation modes must be present in our data of
HD 104237 (A). However, since the radial pulsation modes are separated by the large separation, and since the gap of 7.08 d-1 between f4 and f1 corresponds roughly to twice the large separation, there is a potential existence of 1 to 3 radial pulsation modes at most among the 5 observed frequencies in 2000 (5(8) in 1999).
Still, the frequency difference f1-f5 and f5 to f4 is not identical and
corresponds to 3.23 and 3.85 d-1, respectively. Three radial modes would be separated by exactly the same value, corresponding to the large separation. Despite the associated uncertainty in the frequency determination,
it is therefore unlikely that there are 3 radial modes amongst our detected frequencies.
The next step of our work will consist in a detailed modeling of radial and non-radial pulsations of this star, and also of a detailed spectroscopic study of both binary components, including individual line profile variations.
Acknowledgements
We would like to thank Stephen Marsden (USQ) for kindly participating in the Mt. Stromlo observations. It is a pleasure to thank Jean-Francois Donati for allowing us to use his excellent "ESPRIT'' software package, for instructing us on it and for fruitful discussions. We also want to especially thank Don Kurtz for interesting discussions and for providing his periodicity analysis package. The authors thank M. Breger and Eric Michel for discussions on frequency selection criteria. We are also indebted to M. J. Goupil, Y. Lebreton and D. R. Samadi for calculating a first rough asteroseismic model of the star. We are grateful to the referee for his very valuable comments. Finally, we want to thank the staff of the Mt. Stromlo and the SAAO observatories for supporting us during the different observing runs. The work made intensive use of the PERIOD98 periodicity analysis program provided by the Institute of Astronomy at the University of Vienna, as well as the Simbad and ADS database operated at CDS, Strasbourg, France.
Table 3: Log of the observations. Columns 4) and (5): Julian date (2 450 000+); Col. (6): number of high resolution HD 104237 spectra; Col. (7): typical range of S/N (pixel-1) at 550 nm (center of V band); Col. (8): "blocks'': the night has been subdivided in n distinct blocks with individual wavelength calibration (see text), "extd. R [B]'': not the usual wavelength domain, but shifted towards the red [blue].