A&A 427, 1097-1104 (2004)
DOI: 10.1051/0004-6361:20040514
P. Thébault1 - F. Marzari2 - H. Scholl3 - D. Turrini2 - M. Barbieri1,2
1 - Observatoire de Paris, Section de Meudon,
92195 Meudon Cedex, France
2 -
Dipartimento di Fisica, Universita di Padova, via Marzolo 8, 35131
Padova, Italy
3 -
Observatoire de la Côte d'Azur, Dept. Cassiopée, BP 4229,
06304 Nice, France
Received 24 March 2004 / Accepted 4 August 2004
Abstract
We numerically investigate under which conditions the
planet detected at 2.1 AU from ![]() Cephei could form through
the core-accretion scenario despite the perturbing presence
of the highly eccentric companion star.
We first show that the initial stage of runaway accretion
of kilometer-sized planetesimals is possible within
2.5 AU from the central star only if
large amounts of gas are present. In this case, gaseous
friction induces periastron alignment of the orbits which
reduces the otherwise high mutual impact velocities due
to the companion's secular perturbations.
The following stage of mutual accretion of large embryos
is also modeled. According to our
simulations, the giant impacts among the embryos
always lead to a core of 10
Cephei could form through
the core-accretion scenario despite the perturbing presence
of the highly eccentric companion star.
We first show that the initial stage of runaway accretion
of kilometer-sized planetesimals is possible within
2.5 AU from the central star only if
large amounts of gas are present. In this case, gaseous
friction induces periastron alignment of the orbits which
reduces the otherwise high mutual impact velocities due
to the companion's secular perturbations.
The following stage of mutual accretion of large embryos
is also modeled. According to our
simulations, the giant impacts among the embryos
always lead to a core of 10
![]() within
10 Myr, the average lifetime of gaseous discs. However,
the core always ends up within 1.5 AU from the central
star. Either the core grows more quickly in the inner region
of the disc, or it migrates inside by scattering the
residual embryos.
within
10 Myr, the average lifetime of gaseous discs. However,
the core always ends up within 1.5 AU from the central
star. Either the core grows more quickly in the inner region
of the disc, or it migrates inside by scattering the
residual embryos.
Key words: planets and satellites: formation - stars: binaries: general
Among the 15 presently known binary star systems harbouring
extra-solar planets, ![]() Cephei is that with the closest companion
star (with the
exception of Gliese 86, where the possible companion is believed to be
a brown dwarf, Els et al. 2001).
According to Hatzes et al. (2003), the secondary star has an orbit with a semimajor
axis of
Cephei is that with the closest companion
star (with the
exception of Gliese 86, where the possible companion is believed to be
a brown dwarf, Els et al. 2001).
According to Hatzes et al. (2003), the secondary star has an orbit with a semimajor
axis of
![]() AU and an eccentricity of
AU and an eccentricity of
![]() .
The planet detected around the primary K0 III giant star
has a mass of
.
The planet detected around the primary K0 III giant star
has a mass of
![]() Jupiter masses and an orbital
semimajor axis of 2.13 AU. The planet is located
inside a stable region with a dynamical
lifetime of at least 1 Gyr. This region extends to about 4 AU
from the central star (Holman & Wiegert 1999; Dvorak et al. 2003).
Jupiter masses and an orbital
semimajor axis of 2.13 AU. The planet is located
inside a stable region with a dynamical
lifetime of at least 1 Gyr. This region extends to about 4 AU
from the central star (Holman & Wiegert 1999; Dvorak et al. 2003).
Giant planets orbiting one of the stars in a binary system offer the possibility to test the core-accretion model for giant planet formation (Pollack et al. 1996) in a complex dynamical environment. The vicinity of a companion star in a highly eccentric orbit may prevent planetary formation because the companion reduces the size of the accretion disc, and it excites high relative velocities between colliding planetesimals.
In this paper we study the in situ formation of the giant
planet in the ![]() Cephei system by numerically investigating
both the stage of planetary embryo accretion from planetesimals
and the following stage
of high velocity collisions between large embryos
which form the core of the giant planet.
This last stage precedes that of rapid gas accretion which
sets on after sufficient accumulation of mass onto the
core.
Cephei system by numerically investigating
both the stage of planetary embryo accretion from planetesimals
and the following stage
of high velocity collisions between large embryos
which form the core of the giant planet.
This last stage precedes that of rapid gas accretion which
sets on after sufficient accumulation of mass onto the
core.
A critical parameter for the initial stage of
planetesimal accretion is the
relative impact velocity ![]() .
This velocity
determines whether accretion or erosion
dominates the planetesimal collisional
evolution. In a binary star system, the
secular perturbations of the closeby companion star may play
a critical role by exciting the relative velocities among the
planetesimals. Too large
.
This velocity
determines whether accretion or erosion
dominates the planetesimal collisional
evolution. In a binary star system, the
secular perturbations of the closeby companion star may play
a critical role by exciting the relative velocities among the
planetesimals. Too large ![]() prevent planetesimals
from growing by accretion and
the initial planetesimal population may even be ground down to dust.
We explored the distribution of collisional relative velocities of a
planetesimal population surrounding the primary star of the
prevent planetesimals
from growing by accretion and
the initial planetesimal population may even be ground down to dust.
We explored the distribution of collisional relative velocities of a
planetesimal population surrounding the primary star of the ![]() Cephei system
by using a deterministic code that includes the effect of gas drag.
This latter mechanism might indeed play a crucial role since
gas drag might force periastron and eccentricity
alignment of the perturbed planetesimal orbits and thus
reduce the large
Cephei system
by using a deterministic code that includes the effect of gas drag.
This latter mechanism might indeed play a crucial role since
gas drag might force periastron and eccentricity
alignment of the perturbed planetesimal orbits and thus
reduce the large ![]() induced by the companion's perturbations
(e.g. Marzari & Scholl 2000).
induced by the companion's perturbations
(e.g. Marzari & Scholl 2000).
We also investigated the late stage of core formation by following a
population of large planetary embryos
with a numerical model based on Chambers' Mercury code (Chambers et al. 2002)
which takes into account all mutual gravitational forces among
the embryos as well as mutual collisions. Our main concern is here
to see if mutual accretion of embryos can lead to a final planet at the
right place, i.e. ![]() 2.1 AU, and within 10 7 years, i.e. the
typical survival time for circumstellar discs (e.g. Armitage et al. 2003).
2.1 AU, and within 10 7 years, i.e. the
typical survival time for circumstellar discs (e.g. Armitage et al. 2003).
The dynamical conditions for accretion within a
planetesimal swarm perturbed by the companion of ![]() Cephei and affected by
gas drag are investigated in Sect. 2.
Section 3 is devoted to the study
of the final accumulation of massive embryos into a core.
In Sect. 4 we discuss the results.
Cephei and affected by
gas drag are investigated in Sect. 2.
Section 3 is devoted to the study
of the final accumulation of massive embryos into a core.
In Sect. 4 we discuss the results.
Planetesimal accretion in a circumstellar disc occurs when
mutual encounter velocities are lower than the
escape velocity
![]() of the mutually colliding bodies
(corrected by a factor that accounts for the
energy dissipation in the impact). In the absence of external perturbations,
average eccentricities and inclinations in a planetesimal swarm are small,
and relative velocities are always low enough to allow fast
runaway accretion of larger bodies on timescales of the
order of 104-105 years (e.g. Lissauer 1993).
When the planetesimal population
surrounds a star in a binary system, the gravitational pull of the
companion star excites large eccentricities and the impact velocities
may in some regions exceed by far the mutual escape velocity. In these regions
the swarm would erode to dust rather than form a planet.
of the mutually colliding bodies
(corrected by a factor that accounts for the
energy dissipation in the impact). In the absence of external perturbations,
average eccentricities and inclinations in a planetesimal swarm are small,
and relative velocities are always low enough to allow fast
runaway accretion of larger bodies on timescales of the
order of 104-105 years (e.g. Lissauer 1993).
When the planetesimal population
surrounds a star in a binary system, the gravitational pull of the
companion star excites large eccentricities and the impact velocities
may in some regions exceed by far the mutual escape velocity. In these regions
the swarm would erode to dust rather than form a planet.
A first step to test whether planetary formation is possible around ![]() Cephei
is thus to estimate the relative velocities between
planetesimals orbiting within the dynamically stable region
around the star. We have used a numerical code already adopted
in similar studies (see Thébault et al. 2002, and references therein).
This code computes the orbits of a
swarm of massless particles under the influence of one (or
several) gravitational perturbers. The particles can also be subjected
to gas drag forces. During the orbital computations, the relative velocities
of all mutual encounters are recorded. These velocities approximate
with a satisfying degree of precision the impact velocities during
planetesimal collisions.
Their distribution tells us whether planetesimals accrete into
larger bodies or erode into smaller pieces.
Cephei
is thus to estimate the relative velocities between
planetesimals orbiting within the dynamically stable region
around the star. We have used a numerical code already adopted
in similar studies (see Thébault et al. 2002, and references therein).
This code computes the orbits of a
swarm of massless particles under the influence of one (or
several) gravitational perturbers. The particles can also be subjected
to gas drag forces. During the orbital computations, the relative velocities
of all mutual encounters are recorded. These velocities approximate
with a satisfying degree of precision the impact velocities during
planetesimal collisions.
Their distribution tells us whether planetesimals accrete into
larger bodies or erode into smaller pieces.
In all our simulations we integrate the orbits of 2500 test
particles initially
distributed in the 0.3-5 AU region. The initial eccentricities and
inclinations satisfy the relation i=e/2 and are chosen such that
the average encounter
velocity is
![]() m s-1.
We stop our simulations after
m s-1.
We stop our simulations after
![]() years, a typical timescale
for the formation of planetary embryos (Lissauer 1993).
years, a typical timescale
for the formation of planetary embryos (Lissauer 1993).
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0514fig1.ps}
\end{figure}](/articles/aa/full/2004/45/aa0514-04/Timg23.gif) |
Figure 1: Distribution of particle eccentricity vs. semimajor axis after t=50 000 years for a simulation where the gas drag is not included. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0514fig2.ps}
\end{figure}](/articles/aa/full/2004/45/aa0514-04/Timg27.gif) |
Figure 2:
Plot of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{0514fig3.ps}
\end{figure}](/articles/aa/full/2004/45/aa0514-04/Timg31.gif) |
Figure 3:
Evolution of the average encounter velocity
distribution, at 5 different epochs, for the
gravitational model without gas drag in a disc initially truncated at 4 AU.
|
| Open with DEXTER | |
We performed a first test simulation where only
the gravitational forces of the two stars are taken into account.
Figure 1 shows the major secular perturbations of the
companion star on the planetesimal population. At the beginning
of the simulation eccentricities progressively increase but the
periastra of these forced orbits are almost aligned.
As time goes on, however,
there is a progressive dephasing process due to the different
values of semimajor
axis of the planetesimals in the swarm. This dephasing leads to the wavy
pattern observed in Fig. 1. The planetesimals
orbiting close to the outer limit of the disc
at ![]() 4.5 AU
are more strongly perturbed by the secondary star and they reach very
high eccentricities. They also survive over 105 years
and they cross the orbits of inner planetesimals in the 0-3 AU region
at high
4.5 AU
are more strongly perturbed by the secondary star and they reach very
high eccentricities. They also survive over 105 years
and they cross the orbits of inner planetesimals in the 0-3 AU region
at high ![]() (hence the wide "wing'' of high
(hence the wide "wing'' of high
![]() that is superimposed on the main swarm of lower relative velocities
in Fig. 2).
The contribution of these scattered planetesimals is critical since
they increase relative velocities far beyond the accumulation threshold
everywhere in the inner disc.
However, it is a matter of debate whether planetesimals could indeed form
in the outer edge of the stability region around the primary star.
Moreover, theoretical calculations of binary-disc interactions predict that
companions might truncate circumstellar discs at an outer radius of
0.2-0.5 times the binary semimajor axes (Artymowicz & Lubow 1994).
The grain coagulation process and the first impacts between the
proto-planetesimals would in any case have been highly energetic,
because of the companion's perturbations, possibly halting
any further growth. For this reason, we performed an additional
simulation with the planetesimal disc truncated beyond 4 AU.
In Fig. 3 we show the distribution of the impact
velocities at different evolutionary times in this truncated disc.
At the beginning, the secular oscillations do not induce a significant
increase of
that is superimposed on the main swarm of lower relative velocities
in Fig. 2).
The contribution of these scattered planetesimals is critical since
they increase relative velocities far beyond the accumulation threshold
everywhere in the inner disc.
However, it is a matter of debate whether planetesimals could indeed form
in the outer edge of the stability region around the primary star.
Moreover, theoretical calculations of binary-disc interactions predict that
companions might truncate circumstellar discs at an outer radius of
0.2-0.5 times the binary semimajor axes (Artymowicz & Lubow 1994).
The grain coagulation process and the first impacts between the
proto-planetesimals would in any case have been highly energetic,
because of the companion's perturbations, possibly halting
any further growth. For this reason, we performed an additional
simulation with the planetesimal disc truncated beyond 4 AU.
In Fig. 3 we show the distribution of the impact
velocities at different evolutionary times in this truncated disc.
At the beginning, the secular oscillations do not induce a significant
increase of ![]() among planetesimals because of the strong phasing
of all neighbouring orbits. Nevertheless, the oscillations
get narrower with time, and e and periastron
among planetesimals because of the strong phasing
of all neighbouring orbits. Nevertheless, the oscillations
get narrower with time, and e and periastron ![]() gradients between
adjacent regions keep increasing. At some point the orbital phasing is no
longer strong enough to prevent orbital crossing
between bodies with different semimajor axis.
The inner limit for the region where orbit crossing occurs is very sharp,
with
gradients between
adjacent regions keep increasing. At some point the orbital phasing is no
longer strong enough to prevent orbital crossing
between bodies with different semimajor axis.
The inner limit for the region where orbit crossing occurs is very sharp,
with
![]() increasing from 10 m s-1 to
increasing from 10 m s-1 to
![]() 1 km s-1 in less than 0.2 AU (Fig. 3).
Furthermore, this limit evolves inwards
with time, so that the 2.1 AU region is reached in less than
1 km s-1 in less than 0.2 AU (Fig. 3).
Furthermore, this limit evolves inwards
with time, so that the 2.1 AU region is reached in less than
![]() years (Fig. 3).
As a consequence, the timespan during which accretion
of km-sized objects is possible within 2.1 AU from the star,
assuming that the swarm was
initially aligned, is typically of the order of 104 years.
Numerical accretion models predict that this time span is
in principle enough
to allow the formation of 100 to 1000 km-sized bodies
(e.g. Wetherill & Stewart 1993; Weidenschilling et al. 1997; Barge & Pellat 1993). However, the large relative velocities
that build up after 104 years might halt any further growth
of the accreted objects. It is even
possible that the planetesimal formation process from the
dust of the circumstellar disc does not necessarily lead to
orbits that are initially aligned. In this case, the planetesimals
would have high relative
velocities from the beginning of their evolution. This might be the case if
we suppose that the binary forms by direct stellar-like gravitational
instabilities. The companion
star would reach its present mass well before the onset of planetesimal
accretion in the inner disc.
Thus, the formation of large embryos in the 2 AU
region probably requires the presence of some additional mechanism.
years (Fig. 3).
As a consequence, the timespan during which accretion
of km-sized objects is possible within 2.1 AU from the star,
assuming that the swarm was
initially aligned, is typically of the order of 104 years.
Numerical accretion models predict that this time span is
in principle enough
to allow the formation of 100 to 1000 km-sized bodies
(e.g. Wetherill & Stewart 1993; Weidenschilling et al. 1997; Barge & Pellat 1993). However, the large relative velocities
that build up after 104 years might halt any further growth
of the accreted objects. It is even
possible that the planetesimal formation process from the
dust of the circumstellar disc does not necessarily lead to
orbits that are initially aligned. In this case, the planetesimals
would have high relative
velocities from the beginning of their evolution. This might be the case if
we suppose that the binary forms by direct stellar-like gravitational
instabilities. The companion
star would reach its present mass well before the onset of planetesimal
accretion in the inner disc.
Thus, the formation of large embryos in the 2 AU
region probably requires the presence of some additional mechanism.
Frictional drag by the gas of the protoplanetary disc is an important factor in early planetary formation. It affects planetesimal orbits in two ways:
| (1) |
K = 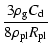 |
(2) |
We take as a reference
value for the gas density that of Bodenheimer et al. (2000) who
modeled the in situ formation of a giant planet around
47 UMa at 2 AU. Of course, the two systems
are not exactly comparable, the planet around 47 UMa being
![]()
![]() more
massive whereas the star is
more
massive whereas the star is ![]()
![]() less massive. While these two values
might compensate one another it is difficult to quantitatively
estimate how much exactly. However, the Bodenheimer et al. (2000) study
gives a good reference value for the in-situ formation of a giant planet
in an inner orbit.
According to these authors, this formation requires a
local gas density
less massive. While these two values
might compensate one another it is difficult to quantitatively
estimate how much exactly. However, the Bodenheimer et al. (2000) study
gives a good reference value for the in-situ formation of a giant planet
in an inner orbit.
According to these authors, this formation requires a
local gas density
![]() g cm-3,
about an order of magnitude higher than the value deduced from the
Hayashi (1981) minimum mass solar nebula.
We here use this value for
g cm-3,
about an order of magnitude higher than the value deduced from the
Hayashi (1981) minimum mass solar nebula.
We here use this value for
![]() and adopt the classical
and adopt the classical
![]() radial profile
of Hayashi (1981).
Different values of
radial profile
of Hayashi (1981).
Different values of
![]() are taken in independent simulations
to explore the parameter space.
The initial parameters adopted for our reference runs
are summarized in Table 1.
are taken in independent simulations
to explore the parameter space.
The initial parameters adopted for our reference runs
are summarized in Table 1.
Table 1: Initial parameters for the reference gas drag runs.
| |
Figure 4: Eccentricities vs. semi-major axis at t=2500 years for 200 m-sized planetesimals. The gas density is taken from Bodenheimer et al. (2000) with a nominal Hayashi (1981) radial profile. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0514fig5.ps}
\end{figure}](/articles/aa/full/2004/45/aa0514-04/Timg52.gif) |
Figure 5: Eccentricity vs. semimajor axis plot after t=50 000 years for 10 km-sized planetesimals. The dashed line is the corresponding average encounter velocity distribution as a function of the distance to the star. Gas density is the same as in Fig. 4. |
| Open with DEXTER | |
For planetesimal accretion to occur,
a balance between different competing mechanisms
is needed. For too small planetesimals, there is the
risk that a too strong gaseous friction leads to a
fast inward drift that prevents accretion of larger
bodies far from the star.
This is illustrated in Fig. 4: a
population of 200 m-sized bodies migrates towards the
star in less than
![]() years, leaving the region
beyond 2 AU totally depleted of material.
On the other hand, large planetesimals, that are less
affected by gas drag, do not significantly migrate
but their periastron alignment is weaker.
If it gets too weak, then
encounter velocities may not be reduced below the value that
allows accretion into larger bodies.
years, leaving the region
beyond 2 AU totally depleted of material.
On the other hand, large planetesimals, that are less
affected by gas drag, do not significantly migrate
but their periastron alignment is weaker.
If it gets too weak, then
encounter velocities may not be reduced below the value that
allows accretion into larger bodies.
In between these two accretion-inhibiting cases, there is a planetesimal
size-range where periastron alignment and eccentricity damping are efficient
enough to reach very low ![]() without removing bodies
from the system on a short timescale. As an example, for 10 km bodies
the periastron alignment keeps the
impact velocities below 10 m s-1 within 2.5 AU from the star (Fig. 5)
and the drift rate is also slow enough not to deplete this
region of the disc within 105 years. Figure 6
shows the limiting case, i.e. the run with the biggest
without removing bodies
from the system on a short timescale. As an example, for 10 km bodies
the periastron alignment keeps the
impact velocities below 10 m s-1 within 2.5 AU from the star (Fig. 5)
and the drift rate is also slow enough not to deplete this
region of the disc within 105 years. Figure 6
shows the limiting case, i.e. the run with the biggest
![]() (50 km) in which accretion is still possible at 2.1 AU.
Beyond 2.2 AU the collision velocities begin to grow quickly as the
secular perturbations are dephased.
(50 km) in which accretion is still possible at 2.1 AU.
Beyond 2.2 AU the collision velocities begin to grow quickly as the
secular perturbations are dephased.
As the planetesimal accretion proceeds, larger bodies are formed and
they still collide with the smaller ones that possibly still
make up most of the
mass of the swarm. It is relevant to verify whether the impact velocities
between large and small planetesimals still favour accretion rather than
fragmentation. The perihelion alignment is indeed different depending on
the size of the body. Smaller bodies tend to align their perihelia towards
![]() (Marzari & Scholl 2000) while larger planetesimals,
less affected by the drag force,
align to larger values. At the orbital crossing the impact velocities may
thus be higher compared to those of equal-size bodies. We performed
additional simulations where we include different size planetesimals.
Figure 7 shows the relative velocities between populations
of different size planetesimals. For
50 km target objects, colliding speeds significantly increase when the
impactor sizes get smaller, especially in the otherwise low
(Marzari & Scholl 2000) while larger planetesimals,
less affected by the drag force,
align to larger values. At the orbital crossing the impact velocities may
thus be higher compared to those of equal-size bodies. We performed
additional simulations where we include different size planetesimals.
Figure 7 shows the relative velocities between populations
of different size planetesimals. For
50 km target objects, colliding speeds significantly increase when the
impactor sizes get smaller, especially in the otherwise low ![]() region
below 2.5 AU. The
region
below 2.5 AU. The ![]() might reach
might reach ![]() 300 m s-1 when
10 km impactors are considered, and even
300 m s-1 when
10 km impactors are considered, and even
![]() 700 m s-1 for 1 km objects.
However, it can be shown that such impact velocities still lead to
accretion. Adopting the collisional
algorithm described in Petit & Farinella (1993), we find that a collision
between a 50 km and a 10 km object at 300 m s-1 leads
to net accretion of
700 m s-1 for 1 km objects.
However, it can be shown that such impact velocities still lead to
accretion. Adopting the collisional
algorithm described in Petit & Farinella (1993), we find that a collision
between a 50 km and a 10 km object at 300 m s-1 leads
to net accretion of ![]()
![]() of the impactor's mass, and
that a collision
between a 50 km and a 1 km object at 700 m s-1 leads
to net accretion of
of the impactor's mass, and
that a collision
between a 50 km and a 1 km object at 700 m s-1 leads
to net accretion of ![]()
![]() of the impactor's mass.
of the impactor's mass.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{0514fig6.ps}
\end{figure}](/articles/aa/full/2004/45/aa0514-04/Timg57.gif) |
Figure 6: Same as Fig. 5 but for 50 km-sized bodies. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0514fig7.ps}
\end{figure}](/articles/aa/full/2004/45/aa0514-04/Timg58.gif) |
Figure 7:
Mutual relative velocities, at t=30 000 years,
for a disc with 3 different
populations of objects: 1 km, 10 km and 50 km in sizes. The solid line
stands for |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{0514fig8.ps}
\end{figure}](/articles/aa/full/2004/45/aa0514-04/Timg59.gif) |
Figure 8: Same as Fig. 6 (50 km bodies at t=50 000 years) for a planetesimal disc initially truncated at 3 AU. The gas density decreases radially as r-1.5. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0514fig9.ps}
\end{figure}](/articles/aa/full/2004/45/aa0514-04/Timg60.gif) |
Figure 9:
Impact velocities, at t=15 000 years,
on 500 km bodies for 50 km (continuous
line), 10 km (dased line) and 1 km (dotted line) impactors.
Same high density truncated disc as in Fig. 8.
The absence of |
| Open with DEXTER | |
Conditions slightly more favourable to planetary formation, i.e.
allowing accretion of objects bigger than 50 km, are met if
we adopt a flatter gas density profile or if we truncate the
disc closer to the star. In Fig. 8 we show the relative
velocity distribution in a disc of 50 km radius planetesimals
cut at 3 AU from the central star and
a gas density profile in r-1.5 giving a
stronger drag force between 2 and 3 AU. Additional simulations
show that under these conditions low ![]() are maintained for bodies up to
are maintained for bodies up to ![]() 200 km, while the
inner limit of the low
200 km, while the
inner limit of the low ![]() region never extends beyond 2.5 AU.
region never extends beyond 2.5 AU.
For bodies in the 200-1000 km range, higher ![]() are obtained
in the a<2.5 AU region, especially for
collisions with smaller planetesimals, which are probably the
most frequent impactors on these bigger objects (Fig. 9).
However, such high
are obtained
in the a<2.5 AU region, especially for
collisions with smaller planetesimals, which are probably the
most frequent impactors on these bigger objects (Fig. 9).
However, such high ![]() impacts still lead to net
mass accretion. Using again the Petit & Farinella (1993) algorithm
for velocities obtained on a 500 km target (Fig. 9), one gets
that 95% of the impactor's mass is reaccreted after a 1200 m s-1
collision with a 50 km impactor, 97% for a 1400 m s-1 impact
with a 10 km body and 98% for a 1700 m s-1
collision with a 1 km impactor.
So even considering the large uncertainties in collision and
reaccretion physics, it seems that we are far below the accretion threshold
for 500 km bodies in our "extreme'' gas disc case,
i.e. high gas density in the outer regions (flat radial distribution)
and cut-off at 3 AU for the planetesimal swarm.
impacts still lead to net
mass accretion. Using again the Petit & Farinella (1993) algorithm
for velocities obtained on a 500 km target (Fig. 9), one gets
that 95% of the impactor's mass is reaccreted after a 1200 m s-1
collision with a 50 km impactor, 97% for a 1400 m s-1 impact
with a 10 km body and 98% for a 1700 m s-1
collision with a 1 km impactor.
So even considering the large uncertainties in collision and
reaccretion physics, it seems that we are far below the accretion threshold
for 500 km bodies in our "extreme'' gas disc case,
i.e. high gas density in the outer regions (flat radial distribution)
and cut-off at 3 AU for the planetesimal swarm.
Furthermore, even with lower gas densities, the final accretion phase of objects in the 200-1000 km range can be favoured by additional mechanisms that cannot be taken into account in our N-body simulations. Dynamical friction produced by the gravitational interactions between planetesimals tends to produce equipartition of energy (Wetherill & Stewart 1989). As a consequence, larger bodies have lower random velocities favouring softer impacts. Self-gravity of planetesimals may also restore periastron alignment, as recently showed by Kokubo (personal communication). The scenario that comes out in our simulations can thus be summarized as follows: small to medium size planetesimals are strongly affected by gas drag and their relative velocities are kept low by the periastron alignment. When the gas drag weakens, additional dynamical mechanisms, such as dynamical friction and self-gravity, are still active and help large planetesimals to continue their growth. In the case of massive protoplanetary discs gas drag may be able to do the whole job, allowing the growth of planetesimals until they are big enough to sustain high velocity impacts.
It should also be noted that the
high gas densities required to maintain the periastron alignment up to
large-size planetesimals might not be unrealistic in the case of the
![]() Cephei system. It is reasonable to expect that accretion discs surrounding
F2 stars, which are progenitors of K III giant stars
like
Cephei system. It is reasonable to expect that accretion discs surrounding
F2 stars, which are progenitors of K III giant stars
like ![]() Cephei are massive compared
to the minimum mass solar nebula. Even the density value for the gas
adopted by Bodenheimer et al. (2000) for the disc surrounding 47 UMa, a G0V star,
may be a lower limit for discs around F2 stars.
Cephei are massive compared
to the minimum mass solar nebula. Even the density value for the gas
adopted by Bodenheimer et al. (2000) for the disc surrounding 47 UMa, a G0V star,
may be a lower limit for discs around F2 stars.
An additional conundrum for planetary formation in ![]() Cephei is
whether planetesimals could form in the outer regions of the
disc perturbed by the gravity of a secondary star. How
sensitive is the dust sticking mechanism to the
gravitational pull of the star? It seems reasonable to assume
that the sticking mechanism was more efficient
in the inner disc, where the perturbations of
the secondary star were weaker. The truncation of the
planetesimal disc beyond a few AU from the star might thus be supported
by the physics of planetesimal formation. At which radial distance
did the truncation in the planetesimal population become significant?
Only detailed models of planetesimal formation that include the
gravitational effects of the companion star can answer this
question.
Cephei is
whether planetesimals could form in the outer regions of the
disc perturbed by the gravity of a secondary star. How
sensitive is the dust sticking mechanism to the
gravitational pull of the star? It seems reasonable to assume
that the sticking mechanism was more efficient
in the inner disc, where the perturbations of
the secondary star were weaker. The truncation of the
planetesimal disc beyond a few AU from the star might thus be supported
by the physics of planetesimal formation. At which radial distance
did the truncation in the planetesimal population become significant?
Only detailed models of planetesimal formation that include the
gravitational effects of the companion star can answer this
question.
On the other hand, we should not forget that for too high gas
densities, small bodies would spiral towards the star on
a short timescale. The question is then:
did accretion proceed fast enough to prevent such
a loss of small bodies where a large fraction of the
mass lies?
Planetesimal accretion in the ![]() Cephei system thus requires
a delicate balance between perihelia alignment at large sizes, fast
spiralling for small bodies, and proper values of the impact probability.
Cephei system thus requires
a delicate balance between perihelia alignment at large sizes, fast
spiralling for small bodies, and proper values of the impact probability.
A numerical model that includes all these effects at once is, at present, beyond computer capabilities. The main result of this section is that gaseous friction opens a window for starting planetesimal accretion within 2.5 AU from the star.
In this section, we shall assume that planetesimal accretion could take place and lead to the formation of planetary embryos. This embryo formation could have followed the scenario described by Kortenkamp et al. (2001). These authors have modeled planetesimal accretion in systems with a massive external perturber showing that the combination of gas drag, collisions, and secular perturbations of a massive external body favours orderly growth in the initial phases of planetary accretion followed by a phase of "type II'' runaway growth.
We here investigate whether giant impacts
between such massive embryos in ![]() Cephei can lead to the formation
of a planetary core whose orbit resembles that of the
observed planet and whose mass is at least
Cephei can lead to the formation
of a planetary core whose orbit resembles that of the
observed planet and whose mass is at least
![]() ,
the mass required to trigger the final phase where the core
accretes the remaining gas through rapid infall and forms
a giant planet (Pollack et al. 1996).
We also evaluate how the timescale of
the core formation depends on the initial mass of the
embryos, on their number, and on their spatial distribution.
,
the mass required to trigger the final phase where the core
accretes the remaining gas through rapid infall and forms
a giant planet (Pollack et al. 1996).
We also evaluate how the timescale of
the core formation depends on the initial mass of the
embryos, on their number, and on their spatial distribution.
We have simulated, within a full N-body model, the evolution of a population of protoplanets into a massive core by integrating the orbits of a swarm of planetary embryos distributed between 1 and 2.5 AU where, according to the previous computations, planetesimal accretion is mostly efficient. The orbital evolution of the embryos and their collisions are computed with Chambers' Mercury code (Chambers et al. 2002) which we modified to account for the large perturbations of the binary companion. The number and initial masses of the embryos are derived assuming a reference surface density of solid material at 2.1 AU ranging from 50 to 100 g cm-2. As in the previous section, these values are derived from the Bodenheimer et al. (2000) estimates for the formation of the planetary companion of 47 UMa. The initial masses of the embryos range from a few Lunar mass to the mass of Mars, depending on the adopted value of the disc density. In all the simulations we assume that only a fraction of the mass of the solids in the disc has accumulated into planetary embryos while the remaining mass is still in smaller planetesimals. This percentage varies from 50% to 75% of the total mass in different models. We also adopted three different distributions of the protoplanets as a function of the distance from the star. This is motivated by the uncertainty about the details of the planetesimal accretion process. Runaway growth, type II runaway growth, orderly growth, or even oligarchic growth can occur depending on the delicate balance between the mass and the velocity distribution. Kortenkamp et al. (2001) have shown that, for a particular binary system, type II runaway growth is to be preferred. However, the type of growth strongly depends on the binary orbital and physical properties, and on the disc parameters like the density and mass distribution. We prefer to cover a large spectrum of possibilities by assuming in our simulations different but equally possible initial conditions for the protoplanets:
1) A population of embryos whose number and location is computed
according to a superficial density ![]() constant on average
between 1 and 2.5 AU. 2)
A
constant on average
between 1 and 2.5 AU. 2)
A ![]() that decreases as 1 / r giving a constant
mass for the embryos
populating annular portions of the disc surrounding the star.
3) A fixed initial radial distance between the planetary
embryos expressed in Hill's radii.
In some of the simulations we even include a "proto-core'',
an embryo with an Earth mass located at 2.1 AU.
Initially, all embryos have eccentricities
lower than 0.04 and inclinations lower than
that decreases as 1 / r giving a constant
mass for the embryos
populating annular portions of the disc surrounding the star.
3) A fixed initial radial distance between the planetary
embryos expressed in Hill's radii.
In some of the simulations we even include a "proto-core'',
an embryo with an Earth mass located at 2.1 AU.
Initially, all embryos have eccentricities
lower than 0.04 and inclinations lower than
![]() with
respect to the orbital plane of the binary system.
with
respect to the orbital plane of the binary system.
Our simulations with an initial total embryo mass
of 25
![]() ,
about 50% of the solid mass
in a disc with
,
about 50% of the solid mass
in a disc with
![]() g cm-2,
fail to create a core of 10
g cm-2,
fail to create a core of 10
![]() within 10 Myr,
the typical lifetime of a gaseous disc.
The maximum mass of the core achieved in these simulations
is 6
within 10 Myr,
the typical lifetime of a gaseous disc.
The maximum mass of the core achieved in these simulations
is 6
![]() ,
which
might not be enough to trigger the final gas accretion phase.
If we increase the total embryo mass to
35
,
which
might not be enough to trigger the final gas accretion phase.
If we increase the total embryo mass to
35
![]() ,
a core of 8-10
,
a core of 8-10
![]() can form in a few cases. All simulations with an initial mass ranging from 50 to 75
can form in a few cases. All simulations with an initial mass ranging from 50 to 75
![]() ,
compatible with
,
compatible with
![]() g cm-2,
lead to the formation of a core with
a mass up to 20
g cm-2,
lead to the formation of a core with
a mass up to 20
![]() within 10 Myr.
However, our simulations all show that the core always ends up
within 1.5 AU from the primary star, while the observed
planet is at about 2.1 AU. Even when including in the
initial protoplanet population a bigger "proto-core'' of
1 Earth mass at 2.1 AU, the final accreted core always ends up
between 1 and 1.5 AU.
Two distinct mechanisms might account for this outcome:
1) in some cases a core might begin to form in the outer regions
but migrate inwards
due to planetesimal scattering reinforced by the
gravitational forces exerted by the binary star which excites the embryos'
eccentricities (Fig. 10).
2) In some other cases a core begins to form at
around 1 AU. It grows at a faster rate because
of the shorter Keplerian orbital period of bodies in inner
orbits. This core is able to accrete large protoplanets in outer orbits,
since the orbital eccentricity is large due to
the companion's perturbations, and the final result is a core around
1.5 AU and almost no remaining material beyond this position. This result
holds even when a large "proto-core'' is initially placed in the outer
disc (Fig. 11).
These two mechanisms are a peculiarity of
protoplanetary accretion in binary star systems, where large
eccentricities among the embryos are excited by the
gravitational pull of the secondary star.
In a few simulations the "proto-core'' is ejected out of the system
before it reaches 10
within 10 Myr.
However, our simulations all show that the core always ends up
within 1.5 AU from the primary star, while the observed
planet is at about 2.1 AU. Even when including in the
initial protoplanet population a bigger "proto-core'' of
1 Earth mass at 2.1 AU, the final accreted core always ends up
between 1 and 1.5 AU.
Two distinct mechanisms might account for this outcome:
1) in some cases a core might begin to form in the outer regions
but migrate inwards
due to planetesimal scattering reinforced by the
gravitational forces exerted by the binary star which excites the embryos'
eccentricities (Fig. 10).
2) In some other cases a core begins to form at
around 1 AU. It grows at a faster rate because
of the shorter Keplerian orbital period of bodies in inner
orbits. This core is able to accrete large protoplanets in outer orbits,
since the orbital eccentricity is large due to
the companion's perturbations, and the final result is a core around
1.5 AU and almost no remaining material beyond this position. This result
holds even when a large "proto-core'' is initially placed in the outer
disc (Fig. 11).
These two mechanisms are a peculiarity of
protoplanetary accretion in binary star systems, where large
eccentricities among the embryos are excited by the
gravitational pull of the secondary star.
In a few simulations the "proto-core'' is ejected out of the system
before it reaches 10
![]() ,
since it is close
to the border of the stability region.
,
since it is close
to the border of the stability region.
In Fig. 12
we show the outcome of a simulation with an intermediate
value for the total embryo mass (75
![]() )
and a proto-core
initially located at 2.3 AU. The
proto-core grows faster than nearby protoplanets
but it migrates inward due to the scattering of the other
bodies. It settles at about 1.4 AU and its
mass reaches almost 10
)
and a proto-core
initially located at 2.3 AU. The
proto-core grows faster than nearby protoplanets
but it migrates inward due to the scattering of the other
bodies. It settles at about 1.4 AU and its
mass reaches almost 10
![]() .
The final giant planet
is then expected to orbit closer to the primary star than
the observed planet in
.
The final giant planet
is then expected to orbit closer to the primary star than
the observed planet in ![]() Cephei.
Cephei.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{0514fig10.ps}
\end{figure}](/articles/aa/full/2004/45/aa0514-04/Timg66.gif) |
Figure 10:
Migration of the growing core due to scattering of protoplanets. The
initial disc extends from 1.5 to 2.5 AU and has a total mass of 75
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{0514fig11.ps}
\end{figure}](/articles/aa/full/2004/45/aa0514-04/Timg68.gif) |
Figure 11:
Evolution, in the (M, a) plane, of a
|
| Open with DEXTER | |
The previous results show that planetesimal accretion in
![]() Cephei depends on a delicate balancing between gas drag and
secular perturbations by the secondary star. If this balancing
is met, then type II runaway growth (Kortenkamp et al. 2001) might possibly
lead to the formation of massive planetary embryos within 2.5 AU
from the central star. In the subsequent phase when
giant impacts between the embryos build up a massive
core, the major problem is not the timescale
but the final location of the planet, which is always well inside
the actual position of the observed planet.
Several explanations might be proposed to account for
this discrepancy.
A first hypothesis involves the evolution of the whole system.
It is possible that the distance between the two
stars was larger when
the planet formed and that after the planet formation
additional mechanisms pushed the secondary star on
into a closer orbit. This could be the case if the
Cephei depends on a delicate balancing between gas drag and
secular perturbations by the secondary star. If this balancing
is met, then type II runaway growth (Kortenkamp et al. 2001) might possibly
lead to the formation of massive planetary embryos within 2.5 AU
from the central star. In the subsequent phase when
giant impacts between the embryos build up a massive
core, the major problem is not the timescale
but the final location of the planet, which is always well inside
the actual position of the observed planet.
Several explanations might be proposed to account for
this discrepancy.
A first hypothesis involves the evolution of the whole system.
It is possible that the distance between the two
stars was larger when
the planet formed and that after the planet formation
additional mechanisms pushed the secondary star on
into a closer orbit. This could be the case if the ![]() Cephei system
was born in a clustered
environment, where close encounters with other young stars may cause
perturbations of the binary orbit that tend to shrink it (Heggie 1985).
A different way to reduce the orbit of a binary system is related
to the possibility that, originally, the system was triple or more.
The ejection of one or more stars causes a transfer of binding energy
and an eventual reduction of the binary separation (Reipurth 2000).
A more complex mechanism is related to the formation
of more than one giant planet around
Cephei system
was born in a clustered
environment, where close encounters with other young stars may cause
perturbations of the binary orbit that tend to shrink it (Heggie 1985).
A different way to reduce the orbit of a binary system is related
to the possibility that, originally, the system was triple or more.
The ejection of one or more stars causes a transfer of binding energy
and an eventual reduction of the binary separation (Reipurth 2000).
A more complex mechanism is related to the formation
of more than one giant planet around ![]() Cephei.
If the circumstellar disc around the main star was significantly
more massive, with a superficial density of solids higher
than 100 g cm-2, it is possible that two or more giant planets
formed around the main star.
Mutual scattering among these planets ejected one, two or more of them
out of the system leaving a single planet in the observed orbit
(Marzari et al. 2004).
Another and more radical solution would be to renounce
the core-accretion model in favour of the alternative
disc instability scenario (Boss 2001), but this scenario
remains to be quantitatively tested for the
Cephei.
If the circumstellar disc around the main star was significantly
more massive, with a superficial density of solids higher
than 100 g cm-2, it is possible that two or more giant planets
formed around the main star.
Mutual scattering among these planets ejected one, two or more of them
out of the system leaving a single planet in the observed orbit
(Marzari et al. 2004).
Another and more radical solution would be to renounce
the core-accretion model in favour of the alternative
disc instability scenario (Boss 2001), but this scenario
remains to be quantitatively tested for the ![]() Cephei system.
Cephei system.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{0514fig12.ps}
\end{figure}](/articles/aa/full/2004/45/aa0514-04/Timg69.gif) |
Figure 12:
Snapshots of protoplanet accretion in the |
| Open with DEXTER | |