A&A 427, 1065-1074 (2004)
DOI: 10.1051/0004-6361:20040503
Transition region small-scale dynamics as seen by SUMER on SOHO
L. Teriaca1 - D. Banerjee2 - A. Falchi3 -
J. G. Doyle4 - M. S. Madjarska1,5
1 - Max-Planck-Institut für
Sonnensystemforschung![[*]](/icons/foot_motif.gif) , Max-Planck-Str. 2,
37191 Katlenburg-Lindau, Germany
, Max-Planck-Str. 2,
37191 Katlenburg-Lindau, Germany
2 -
Indian Institute of Astrophysics, Koramangala, Bangalore 560034, India
3 -
INAF - Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5,
50125 Firenze, Italy
4 -
Armagh Observatory, College Hill, Armagh BT61 9DG, UK
5 -
Department of Solar Physics, Royal Observatory of
Belgium, Av. Circulaire 3, 1180 Bruxelles, Belgium
Received 24 March 2004 / Accepted 10 August 2004
Abstract
High spectral, spatial and temporal resolution UV observations
of the quiet Sun transition region show a highly structured and dynamical
environment where transient supersonic flows are commonly observed.
Strongly non-Gaussian line profiles are the spectral signatures of these flows
and are known in the literature as explosive events.
In this paper we present a high spatial resolution ( 1'')
spectroheliogram of a
1'')
spectroheliogram of a
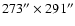 area of the quiet
Sun acquired with SUMER/SOHO in the O VI spectral line at
area of the quiet
Sun acquired with SUMER/SOHO in the O VI spectral line at
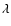 103.193 nm.
The extremely high quality of these observations allows us to identify
tens of explosive events from which we estimate an average size of 1800 km and
a birthrate of 2500 s-1 over the entire Sun. Estimates of the kinetic
and enthalpy fluxes associated with these events show that explosive events
are not important as far as solar coronal heating is concerned.
The relationship with the underlying photospheric magnetic field is also
studied, revealing that explosive events generally occur in regions with
weak (and, very likely, mixed polarity) magnetic flux.
By studying the structure of upward and downward flows exceeding those
associated to average quiet Sun profiles, we find a clear correlation between
the "excess'' flows and the magnetic network. However, although explosive events
are always associated with flow patterns often covering areas larger than the
explosive event itself, the contrary is not true. In particular, almost all
flows associated with the stronger concentrations of photospheric magnetic flux
do not show non-Gaussian line profiles.
In some cases, non-Gaussian line profiles are associated with supersonic
flows in small magnetic loops. The case of a small loop showing a supersonic
siphon-like flow of
103.193 nm.
The extremely high quality of these observations allows us to identify
tens of explosive events from which we estimate an average size of 1800 km and
a birthrate of 2500 s-1 over the entire Sun. Estimates of the kinetic
and enthalpy fluxes associated with these events show that explosive events
are not important as far as solar coronal heating is concerned.
The relationship with the underlying photospheric magnetic field is also
studied, revealing that explosive events generally occur in regions with
weak (and, very likely, mixed polarity) magnetic flux.
By studying the structure of upward and downward flows exceeding those
associated to average quiet Sun profiles, we find a clear correlation between
the "excess'' flows and the magnetic network. However, although explosive events
are always associated with flow patterns often covering areas larger than the
explosive event itself, the contrary is not true. In particular, almost all
flows associated with the stronger concentrations of photospheric magnetic flux
do not show non-Gaussian line profiles.
In some cases, non-Gaussian line profiles are associated with supersonic
flows in small magnetic loops. The case of a small loop showing a supersonic
siphon-like flow of  130
130
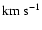 is studied in detail.
This is, to our knowledge, the first detection of a supersonic siphon-like flow
in a quiet Sun loop. In other cases, the flow patterns associated with explosive
events may suggest a relation with UV spicules.
is studied in detail.
This is, to our knowledge, the first detection of a supersonic siphon-like flow
in a quiet Sun loop. In other cases, the flow patterns associated with explosive
events may suggest a relation with UV spicules.
Key words: Sun: transition region - Sun: UV radiation - line: profiles
Extreme-UltraViolet (EUV) spectroscopy of plasmas at Transition Region (TR)
temperatures reveals the existence of different kinds of transient phenomena.
Highly non-Gaussian line profiles showing strong Doppler shifts are
frequently observed in quiet Sun areas and within coronal holes in lines
formed between
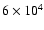 K and
K and
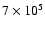 K.
First observed by Brueckner & Bartoe (1983) in HRTS spectra, they are known
as UV explosive events (EEs). Their birthrate on the quiet Sun was
estimated to be around
K.
First observed by Brueckner & Bartoe (1983) in HRTS spectra, they are known
as UV explosive events (EEs). Their birthrate on the quiet Sun was
estimated to be around
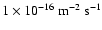 by Dere
et al. (1989). EEs are characterised by spatial scales of
by Dere
et al. (1989). EEs are characterised by spatial scales of  1600 km,
average lifetime of about 60 s and line profiles showing Doppler shifts up to
225
1600 km,
average lifetime of about 60 s and line profiles showing Doppler shifts up to
225
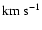 (Dere et al. 1989).
EEs are generally observed along the magnetic network at the boundaries of
the super-granulation cells but away from the larger flux concentrations (Porter
& Dere 1991), in regions with weak and mixed polarity fluxes (Chae et al.
1998) and in association with episodes of photospheric magnetic flux
cancellation (Dere et al. 1991; Chae et al. 1998; Ryutova & Tarbell 2000).
Furthermore, the spectral signature of EEs shows enhancements in both the red
and blue wings of the profile, implying high velocity flows similar to a
bi-directional jet associated with magnetic reconnection (Innes et al. 1997).
Hence, EEs are believed to be the product of magnetic reconnection, a
magnetic cancellation of the photospheric fields with emerging flux (Dere et al. 1991) or the interaction between separate flux elements driven together
by convective motions (Porter & Dere 1991).
The large velocities associated with EEs suggest that kinetic and
enthalpy flows could be relevant to the coronal energy budget.
Winebarger et al. (2002) estimated the global energy release associated
with explosive events through an analysis of the velocity differential
emission measure. They show that EEs can provide an energy flux
(Dere et al. 1989).
EEs are generally observed along the magnetic network at the boundaries of
the super-granulation cells but away from the larger flux concentrations (Porter
& Dere 1991), in regions with weak and mixed polarity fluxes (Chae et al.
1998) and in association with episodes of photospheric magnetic flux
cancellation (Dere et al. 1991; Chae et al. 1998; Ryutova & Tarbell 2000).
Furthermore, the spectral signature of EEs shows enhancements in both the red
and blue wings of the profile, implying high velocity flows similar to a
bi-directional jet associated with magnetic reconnection (Innes et al. 1997).
Hence, EEs are believed to be the product of magnetic reconnection, a
magnetic cancellation of the photospheric fields with emerging flux (Dere et al. 1991) or the interaction between separate flux elements driven together
by convective motions (Porter & Dere 1991).
The large velocities associated with EEs suggest that kinetic and
enthalpy flows could be relevant to the coronal energy budget.
Winebarger et al. (2002) estimated the global energy release associated
with explosive events through an analysis of the velocity differential
emission measure. They show that EEs can provide an energy flux
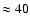 W m-2, implying that the EEs themselves
are not energetically significant to the solar atmosphere.
W m-2, implying that the EEs themselves
are not energetically significant to the solar atmosphere.
More recently another class of transient events, named blinkers (e.g.,
Harrison 1997; Harrison et al. 1999; Bewsher et al. 2002), was
discovered and studied with the CDS spectrometer (Harrison et al. 1995)
aboard SOHO. Blinkers are defined as enhancements of the radiance of lines
formed at mid-TR temperatures (e.g., O V 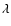 62.97 nm,
formation temperature of
62.97 nm,
formation temperature of
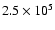 K)
primarily occurring at network boundaries (Harrison et al. 1999; Bewsher et al. 2002), although they have been also observed in the internetwork
(Brkovic et al. 2001). Due to the lower spatial and spectral resolution
of CDS with respect to SUMER, it has been a matter of debate whether blinkers are
EEs seen at lower resolution or whether they are different phenomena. Although
it seems very likely that some events, classified as short-duration blinkers,
could just be large EEs, recent studies seem to support the idea that blinkers
and EEs are different phenomena (Chae et al. 2000; Peter & Brkovic 2003;
Madjarska & Doyle 2003). The latter study, in particular, shows that blinkers
as seen in SUMER data have at most flows of
K)
primarily occurring at network boundaries (Harrison et al. 1999; Bewsher et al. 2002), although they have been also observed in the internetwork
(Brkovic et al. 2001). Due to the lower spatial and spectral resolution
of CDS with respect to SUMER, it has been a matter of debate whether blinkers are
EEs seen at lower resolution or whether they are different phenomena. Although
it seems very likely that some events, classified as short-duration blinkers,
could just be large EEs, recent studies seem to support the idea that blinkers
and EEs are different phenomena (Chae et al. 2000; Peter & Brkovic 2003;
Madjarska & Doyle 2003). The latter study, in particular, shows that blinkers
as seen in SUMER data have at most flows of  25
25
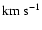 .
.
Although EEs can be observed up to 2''-3'' above the visible limb (Dere 1992),
both EEs and blinkers are essentially observed on the disk. Going off-limb,
UV observations reveal another type of dynamic transients: UV spicules.
UV spicules are elongated structures extending above the solar limb up to
 15 Mm (
15 Mm ( 21'', at the SOHO-Sun distance
21'', at the SOHO-Sun distance
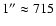 km)
(Withbroe 1983; Cook et al. 1984), showing variations indicative of apparent
motions around 30
km)
(Withbroe 1983; Cook et al. 1984), showing variations indicative of apparent
motions around 30
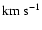 (Wilhelm 2000). Whether UV spicules are cospatial or the
extension of the long known H
(Wilhelm 2000). Whether UV spicules are cospatial or the
extension of the long known H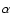 spicules (extensively reviewed by
Beckers 1968, 1972; Bray & Loughhead 1974; Athay 1976; Suematsu 1998)
is still uncertain, although there are strong indications that a close
relation may exist (see Wilhelm 2000, and references therein).
Moreover, it is still not known
whether they have any relation with other UV dynamic events.
Wilhelm (2000) suggested that EEs and spicules may be closely related,
outlining a mechanism where EEs could be the first stage of a sequence of events
leading to the formation of a spicule.
spicules (extensively reviewed by
Beckers 1968, 1972; Bray & Loughhead 1974; Athay 1976; Suematsu 1998)
is still uncertain, although there are strong indications that a close
relation may exist (see Wilhelm 2000, and references therein).
Moreover, it is still not known
whether they have any relation with other UV dynamic events.
Wilhelm (2000) suggested that EEs and spicules may be closely related,
outlining a mechanism where EEs could be the first stage of a sequence of events
leading to the formation of a spicule.
In this paper we present high spatial resolution observations of a large
quiet Sun area in the mid-transition region line O VI
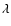 103.193 nm (
103.193 nm (
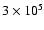 K).
These observations allow us to identify tens of explosive events and to
investigate their dynamical characteristics and their relationship with the
magnetic network. The birthrate and the typical size of these events are also
found.
From our results we make an estimation of the total energy (kinetic energy
plus enthalpy) flux associated with EEs.
A detailed analysis of the mass flows exceeding those associated to average
quiet Sun profiles is performed and a possible link between EEs and spicules
is explored. The first, to our knowledge, detection of a supersonic flow
in a small loop in the quiet Sun is also studied in detail. The
relevance of our results to the understanding of the structuring of the solar
TR is discussed.
K).
These observations allow us to identify tens of explosive events and to
investigate their dynamical characteristics and their relationship with the
magnetic network. The birthrate and the typical size of these events are also
found.
From our results we make an estimation of the total energy (kinetic energy
plus enthalpy) flux associated with EEs.
A detailed analysis of the mass flows exceeding those associated to average
quiet Sun profiles is performed and a possible link between EEs and spicules
is explored. The first, to our knowledge, detection of a supersonic flow
in a small loop in the quiet Sun is also studied in detail. The
relevance of our results to the understanding of the structuring of the solar
TR is discussed.
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{0503fig1.eps}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg17.gif) |
Figure 1:
Logarithmically-scaled image of the quiet Sun obtained by integrating
over the O VI 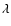 103.193 nm line ( 103.193 nm line (
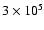 K) after
subtracting the continuum. The minimum and the maximum of the image correspond
to radiances around 14 and 4654 mW m-2 sr-1, respectively. Levels of
the longitudinal magnetic flux of 10 G, 25 G and 40 G are shown with white
(positive) and black (negative polarity) solid lines.
The locations where non-Gaussian line profiles were found are marked with
a black +. K) after
subtracting the continuum. The minimum and the maximum of the image correspond
to radiances around 14 and 4654 mW m-2 sr-1, respectively. Levels of
the longitudinal magnetic flux of 10 G, 25 G and 40 G are shown with white
(positive) and black (negative polarity) solid lines.
The locations where non-Gaussian line profiles were found are marked with
a black +. |
| Open with DEXTER |
A raster of a
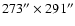 quiet region around Sun
centre (see Fig. 1) was obtained on 30 January 1996 by the
SUMER spectrograph (Wilhelm et al. 1995) aboard SOHO in the O VI
quiet region around Sun
centre (see Fig. 1) was obtained on 30 January 1996 by the
SUMER spectrograph (Wilhelm et al. 1995) aboard SOHO in the O VI
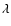 103.193 nm line. The capabilities of the SUMER experiment are
extensively described by Wilhelm et al. (1997) and Lemaire et al. (1997).
The raster starts at 04:38:01 and ends at 04:57:03 UTC. It consists of a
series of spectra obtained exposing for 3 s the central part of detector A.
After each exposure only 50 of the 1024 spectral pixels of the detector
were transmitted to the ground. This, with a spectral resolution of
103.193 nm line. The capabilities of the SUMER experiment are
extensively described by Wilhelm et al. (1997) and Lemaire et al. (1997).
The raster starts at 04:38:01 and ends at 04:57:03 UTC. It consists of a
series of spectra obtained exposing for 3 s the central part of detector A.
After each exposure only 50 of the 1024 spectral pixels of the detector
were transmitted to the ground. This, with a spectral resolution of
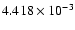 nm per pixel, corresponds to a spectral window of
nm per pixel, corresponds to a spectral window of
 0.22 nm.
The observed area was covered by stepping the
0.22 nm.
The observed area was covered by stepping the
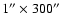 slit
westward 0.76'' a total of 360 times. The reduction of SUMER data
requires several stages. After correcting for dead time and local gain
depression, data were flat-fielded and destretched using the provided software.
Radiometrically calibrated spectral and line radiances have been
obtained by using the RADIOMETRY.PRO routine. To give an indication
of the noise level, spectral and line radiances are also shown in total
count per pixel.
slit
westward 0.76'' a total of 360 times. The reduction of SUMER data
requires several stages. After correcting for dead time and local gain
depression, data were flat-fielded and destretched using the provided software.
Radiometrically calibrated spectral and line radiances have been
obtained by using the RADIOMETRY.PRO routine. To give an indication
of the noise level, spectral and line radiances are also shown in total
count per pixel.
Around 25 min later, 15 full disk magnetograms were acquired with MDI
(Scherrer et al. 1995) from 05:22 to 05:38 UTC. No relevant variation is
observed during the 16 min separing the first and the last magnetogram.
After correcting for the solar rotation, an average of the 15 frames was
obtained, allowing us to build a good signal-to-noise magnetogram to superpose
to the O VI observations.
The resulting magnetogram was aligned to the
SUMER raster by cross-correlating the absolute magnetic flux and the SUMER
continuum around 103.08 nm, which forms in the middle chromosphere (around
1.1 Mm above
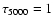 ,
according to model C of Vernazza et al. 1981).
At each spatial location, the continuum
level was obtained by averaging the spectral radiances over the 10 spectral
pixels between 103.062 and 103.106 nm. The latter point is away from the
O VI line centre by
,
according to model C of Vernazza et al. 1981).
At each spatial location, the continuum
level was obtained by averaging the spectral radiances over the 10 spectral
pixels between 103.062 and 103.106 nm. The latter point is away from the
O VI line centre by  4 times the average FWHM of the line.
The alignement is estimated to be precise within 3''.
4 times the average FWHM of the line.
The alignement is estimated to be precise within 3''.
A logarithmically-scaled image of the observed area obtained by integrating
over the O VI 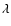 103.193 nm line is shown in Fig. 1.
Levels of the longitudinal magnetic flux of (10, 25 and 40) G are shown with
white (positive polarity) and black (negative polarity) solid lines.
The structures visible in Fig. 1 and
their relationship with the underlying longitudinal magnetic flux have been
discussed in detail by Warren & Winebarger (2000). Here, we want to focus
on a detailed analysis of the line profiles in order to study the small-scale
dynamics of the transition region plasma. In this way we further exploit the
potentials of one of the best raster sequences taken by the SUMER
spectrograph aboard SOHO.
103.193 nm line is shown in Fig. 1.
Levels of the longitudinal magnetic flux of (10, 25 and 40) G are shown with
white (positive polarity) and black (negative polarity) solid lines.
The structures visible in Fig. 1 and
their relationship with the underlying longitudinal magnetic flux have been
discussed in detail by Warren & Winebarger (2000). Here, we want to focus
on a detailed analysis of the line profiles in order to study the small-scale
dynamics of the transition region plasma. In this way we further exploit the
potentials of one of the best raster sequences taken by the SUMER
spectrograph aboard SOHO.
The profile of a line emitted by an optically-thin plasma is only determined
by the dynamics of the emitting ions (neglecting the small atomic broadening). Motions on scales larger than the
instrumental spatial resolution will lead to the shift of the entire line
profile, while thermal and non-thermal motions on scales smaller than the
spatial resolution will determine the shape of the profile. Moreover,
different structures with different dynamics may be present along the line
of sight (LOS) over which the line is integrated. However, quiet Sun profiles
are generally well represented by a single Gaussian (although a combination
of two Gaussians may represent better the "quiet'' TR line profile; see, e.g.,
Peter 2001), indicating that the small-scale thermal and non-thermal motions
both follow a Maxwellian distribution in most of the cases.
In this framework, the triggering of high-speed flows will lead to the
non-Gaussian line profiles characterising the explosive events.
It should be noted that flows on scales larger than the spatial
resolution may also lead to non-Gaussian line profiles when their
emission is combined with that from other structures along the LOS.
To identify explosive event profiles, a single Gaussian has been fitted to
all the  105 spectra forming the raster. All line profiles, for
which at least one of the fitted parameters (or the
105 spectra forming the raster. All line profiles, for
which at least one of the fitted parameters (or the 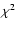 )
was diverging
by more than 3
)
was diverging
by more than 3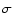 from the average of its distribution, were first
selected. All the profiles forming this sub-sample were, hence, visually
inspected and all profiles for which at least three to four contiguous pixels
were consistently diverging by a Gaussian profile (by more than their Poissonian
uncertainties) were flagged as explosive events.
The positions of the flagged profiles are indicated by black +
marks on the radiance image displayed in Fig. 1.
from the average of its distribution, were first
selected. All the profiles forming this sub-sample were, hence, visually
inspected and all profiles for which at least three to four contiguous pixels
were consistently diverging by a Gaussian profile (by more than their Poissonian
uncertainties) were flagged as explosive events.
The positions of the flagged profiles are indicated by black +
marks on the radiance image displayed in Fig. 1.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0503fig2.eps}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg23.gif) |
Figure 2:
Spectral radiances,
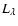 ,
at the centre of three of the explosive
events identified in Fig. 1. The profile obtained by averaging the
entire dataset is shown by the dotted lines. ,
at the centre of three of the explosive
events identified in Fig. 1. The profile obtained by averaging the
entire dataset is shown by the dotted lines. |
| Open with DEXTER |
It is clearly visible that the selected points are not randomly distributed,
but appear to form small patches. Considering all contiguous points as
belonging to the same event, it is possible to count around
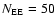 explosive events in the observed area with an average size of
explosive events in the observed area with an average size of
 1800 km. As representative examples
we show in Fig. 2 single-pixel line profiles from three
locations marked as E1, E2, and E3 in Fig. 1. The majority
(
1800 km. As representative examples
we show in Fig. 2 single-pixel line profiles from three
locations marked as E1, E2, and E3 in Fig. 1. The majority
( 2/3) of the profiles show a stronger blue wing with average bulk
velocities
2/3) of the profiles show a stronger blue wing with average bulk
velocities 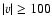
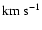 .
The average radiance L at the EEs locations
is 1.08 W m-2 sr-1, compared to a value of 0.37 W m-2 sr-1
obtained by averaging over the whole dataset.
.
The average radiance L at the EEs locations
is 1.08 W m-2 sr-1, compared to a value of 0.37 W m-2 sr-1
obtained by averaging over the whole dataset.
Once all the explosive events were identified, it is possible to estimate
their rate of occurrence. The explosive events birthrate, R, is
given by
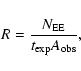 |
(1) |
where
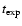 is the exposure time,
is the exposure time,
 the rastered
area and
the rastered
area and
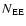 is the number of observed explosive events. Given an area
of
is the number of observed explosive events. Given an area
of
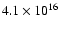 m2 (
m2 (
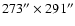 ),
),
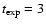 s and
s and
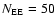 ,
we obtain an event birthrate
,
we obtain an event birthrate
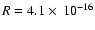 m-2 s-1 (
m-2 s-1 (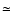 2500 s-1 over the
whole Sun).
2500 s-1 over the
whole Sun).
Although explosive events leave a weak signature in chromospheric lines
(Teriaca et al. 2002; Madjarska & Doyle 2002), no change is observable
in lines formed at 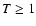 MK (Teriaca et al. 2002; Doyle et al. 2004).
This suggests that, at sites of strong velocities, the plasma is not heated
to coronal temperatures, indicating that energy is mostly used to accelerate
it. The presence of upward velocities
MK (Teriaca et al. 2002; Doyle et al. 2004).
This suggests that, at sites of strong velocities, the plasma is not heated
to coronal temperatures, indicating that energy is mostly used to accelerate
it. The presence of upward velocities
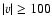
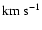 would,
within this framework, suggest a possible role for kinetic and enthalpy energy
fluxes associated with explosive events in heating the quiet Sun corona.
would,
within this framework, suggest a possible role for kinetic and enthalpy energy
fluxes associated with explosive events in heating the quiet Sun corona.
An (order of magnitude) estimate of the kinetic energy associated with an
explosive event, can be written as:
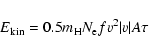 |
(2) |
where 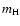 is the mass of the hydrogen atom,
is the mass of the hydrogen atom, 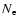 the
electron density (
the
electron density (
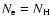 ,
fully ionised plasma of pure H)
and v, A and
,
fully ionised plasma of pure H)
and v, A and 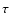 are the typical speed, area and lifetime of explosive
events, respectively. The volumetric filling factor, f, accounts for the
filamentary structure of the transition region and is estimated to be
around 0.01 (Feldman et al. 1979). However, for a large explosive event, Dere
(1992) found a value of 10-4 by comparing the electron density derived
from the ratio of density sensitive lines within the
are the typical speed, area and lifetime of explosive
events, respectively. The volumetric filling factor, f, accounts for the
filamentary structure of the transition region and is estimated to be
around 0.01 (Feldman et al. 1979). However, for a large explosive event, Dere
(1992) found a value of 10-4 by comparing the electron density derived
from the ratio of density sensitive lines within the 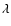 140 nm
O IV multiplet with that obtained from the volumetric emission
measure.
Applying the same technique to another explosive event observed in the same
O IV multiplet by Teriaca et al. (2001), we find a value
140 nm
O IV multiplet with that obtained from the volumetric emission
measure.
Applying the same technique to another explosive event observed in the same
O IV multiplet by Teriaca et al. (2001), we find a value
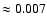 for f. These values also show that EE-like line profiles
are due to motions on scales much smaller than the actual spatial resolution.
Let us consider
for f. These values also show that EE-like line profiles
are due to motions on scales much smaller than the actual spatial resolution.
Let us consider
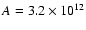 m2(
m2(
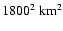 )
and |v|=100
)
and |v|=100
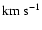 from
the present analysis,
from
the present analysis, 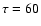 s (Dere et al. 1989) and the value
0.007 for the filling factor f. Teriaca et al. (2001)
find values around
s (Dere et al. 1989) and the value
0.007 for the filling factor f. Teriaca et al. (2001)
find values around
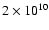 cm-3 for the electron density
during EEs observed in O IV lines (formed around
cm-3 for the electron density
during EEs observed in O IV lines (formed around
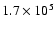 K).
Assuming constant pressure through the TR, we obtain an electron density of
K).
Assuming constant pressure through the TR, we obtain an electron density of
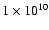 cm-3 for the plasma around
cm-3 for the plasma around
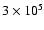 K. Adopting
this value of
K. Adopting
this value of 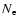 ,
Eq. (2) yields a kinetic energy
,
Eq. (2) yields a kinetic energy
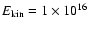 J for a typical event.
J for a typical event.
Similarly, the enthalpy energy flux is:
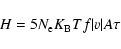 |
(3) |
where 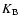 is the Boltzmann constant and T the line formation
temperature. Considering
is the Boltzmann constant and T the line formation
temperature. Considering
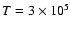 K (O VI), we obtain
K (O VI), we obtain
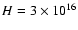 J. Finally, the total energy flux associated with
explosive events is obtained by multiplying the typical energy for one event
and the birthrate:
J. Finally, the total energy flux associated with
explosive events is obtained by multiplying the typical energy for one event
and the birthrate:
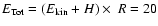 W m-2.
This value (provided f is correctly estimated) is at least one order
of magnitude smaller than the quiet Sun radiative losses for all plasmas
hotter than
W m-2.
This value (provided f is correctly estimated) is at least one order
of magnitude smaller than the quiet Sun radiative losses for all plasmas
hotter than
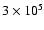 K (
K ( 400 W m-2)
calculated by Dere & Mason (1993). Furthermore, the energy flux should be
further reduced by considering that not all the explosive events show a
dominant blueshifted (upward directed) component.
400 W m-2)
calculated by Dere & Mason (1993). Furthermore, the energy flux should be
further reduced by considering that not all the explosive events show a
dominant blueshifted (upward directed) component.
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0503fig3.eps}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg54.gif) |
Figure 3:
Radiance image as in Fig. 1. Solid dark-grey and
light-grey (red and light-blue in the electronic version) isocontours show the
downward and upward mass fluxes, respectively. The contours are traced for
levels of
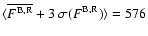 (count1/2 (count1/2
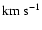 ).
Levels of the longitudinal magnetic flux of (10, 25 and 40) G are shown with
white (positive polarity) and black (negative polarity) solid lines.
The locations where non-Gaussian line profiles were found are marked with
a black +. ).
Levels of the longitudinal magnetic flux of (10, 25 and 40) G are shown with
white (positive polarity) and black (negative polarity) solid lines.
The locations where non-Gaussian line profiles were found are marked with
a black +. |
| Open with DEXTER |
From the analysis of Fig. 1 it appears that the observed events
outline the network (as seen in O VI) but generally do not appear in
the brightest regions. Moreover, they seem to avoid the areas where the
longitudinal magnetic flux is stronger.
In fact, for all but two of these events, the average
absolute longitudinal flux in the underlying area is below 6 G.
Although a vector magnetogram with higher spatial resolution would be
necessary to measure the true magnetic flux, these observations indicate
explosive events to occur in regions away from the strong magnetic
field concentrations.
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{0503fig4.eps}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg55.gif) |
Figure 4:
Detailed view of box A in
Fig. 1 together with the line profiles at the indicated locations.
a) Logarithmically-scaled radiance image. Isocontours of the negative
polarity of the longitudinal magnetic flux at (-10, -25 and -40) G are
shown with black solid lines (no positive flux above 10 G is present in
the displayed area).
Locations where non-Gaussian line profiles were found are marked with
a black +. The dashed dark-grey (red) line indicates the projection
(on the plane perpendicular to the LOS) of a semi-circular loop with a
diameter of 13''. The loop is inclined by 18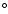 with respect to
the LOS and the footpoint line rotated by 12.5
with respect to
the LOS and the footpoint line rotated by 12.5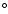 clockwise. The
black dots indicate the measured position of the observed loop. b)
Line profile at a location on the northern leg of the loop.
The bars indicate the data points. The thin solid lines show the three
components used to fit the data while the resulting fitting profile is
represented by the thick solid line. c) Line profile at the top of the
loop. The dotted line shows the profile obtained averaging over the whole
raster times 4.9. d) The same as for panel b) but for the
southern leg of the loop.
clockwise. The
black dots indicate the measured position of the observed loop. b)
Line profile at a location on the northern leg of the loop.
The bars indicate the data points. The thin solid lines show the three
components used to fit the data while the resulting fitting profile is
represented by the thick solid line. c) Line profile at the top of the
loop. The dotted line shows the profile obtained averaging over the whole
raster times 4.9. d) The same as for panel b) but for the
southern leg of the loop. |
| Open with DEXTER |
However, at the pressure characteristic of the network mid-transition region
(
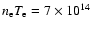 cm-3 K, Teriaca et al. 2001), the
low-
cm-3 K, Teriaca et al. 2001), the
low-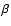 assumption holds also for magnetic fields of a few gauss and the
plasma is forced to move along the magnetic field lines. In this framework,
the study of plasma flows can provide information about the structuring of
the transition region and the configuration of the magnetic field also well
above the photosphere, where direct measurements are, thus far, not feasible.
assumption holds also for magnetic fields of a few gauss and the
plasma is forced to move along the magnetic field lines. In this framework,
the study of plasma flows can provide information about the structuring of
the transition region and the configuration of the magnetic field also well
above the photosphere, where direct measurements are, thus far, not feasible.
In the previous section only the clearly non-Gaussian line profiles were
marked as belonging to explosive events. Profiles characterised by large
broadenings and/or line shifts but still retaining a Gaussian shape were
not considered.
However, these profiles could still indicate relevant mass flows and/or
small-scale motions that exceed those generally observed on the quiet Sun.
To identify these "excess motions'' the following quantity was calculated
for each spectrum of coordinates (i, j) forming the raster.
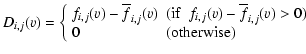 |
|
|
(4) |
where
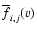 is the spectrum obtained averaging
over the whole dataset and scaled to match the observed peak amplitude at
position (i, j).
is the spectrum obtained averaging
over the whole dataset and scaled to match the observed peak amplitude at
position (i, j).
The mass flux of a plasma of density 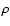 moving through an area A,
with a velocity v normal to A, is given by
moving through an area A,
with a velocity v normal to A, is given by
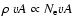 .
Assuming the pixel size as the unit area and considering that for an
allowed transition in an optically thin plasma
.
Assuming the pixel size as the unit area and considering that for an
allowed transition in an optically thin plasma  is proportional
to the square-root of the line radiance L, the
mass flux can be written as
is proportional
to the square-root of the line radiance L, the
mass flux can be written as 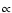
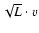 .
For each spectrum of the raster (of coordinates i, j), the upward and
downward directed mass fluxes (
.
For each spectrum of the raster (of coordinates i, j), the upward and
downward directed mass fluxes (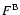 and
and 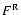 ,
respectively)
were computed as:
,
respectively)
were computed as:
where
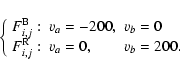 |
(5) |
The value of the speed in the blue and red wings, 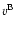 and
and 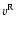 ,
can be easily calculated as the first moment of the difference spectrum
Di,j(v).
For both distributions the average
,
can be easily calculated as the first moment of the difference spectrum
Di,j(v).
For both distributions the average
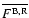 and the standard
deviation
and the standard
deviation
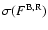 were also calculated. The quantities
were also calculated. The quantities
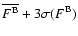 and
and
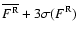 are
quite similar being equal to 611 and 541 (count1/2
are
quite similar being equal to 611 and 541 (count1/2
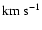 ), respectively.
Finally, the speed and the mass flux are considered as reliable
only at those locations were the radiance of the difference spectrum is 2.3
times larger than the uncertainties in the radiance of the wing itself.
In Fig. 3, the isocontours at the
), respectively.
Finally, the speed and the mass flux are considered as reliable
only at those locations were the radiance of the difference spectrum is 2.3
times larger than the uncertainties in the radiance of the wing itself.
In Fig. 3, the isocontours at the
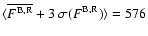 level are shown with dark-grey
(
level are shown with dark-grey
(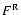 )
and light-grey (
)
and light-grey (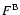 )
thick solid lines (red and light-blue in the
electronic version).
From the analysis of Fig. 3 several facts appear evident.
First, a good correlation between the "excess'' mass flows and the magnetic
field is clearly present. However, the flow patterns associated with
the stronger concentrations of the magnetic flux generally does not show any
non-Gaussian (or EE-like) line profile.
Second, EEs are associated with flow patterns often covering areas larger than
those showing strongly non-Gaussian line profiles and occur in areas with weak
(and, very likely, mixed polarity) magnetic flux.
)
thick solid lines (red and light-blue in the
electronic version).
From the analysis of Fig. 3 several facts appear evident.
First, a good correlation between the "excess'' mass flows and the magnetic
field is clearly present. However, the flow patterns associated with
the stronger concentrations of the magnetic flux generally does not show any
non-Gaussian (or EE-like) line profile.
Second, EEs are associated with flow patterns often covering areas larger than
those showing strongly non-Gaussian line profiles and occur in areas with weak
(and, very likely, mixed polarity) magnetic flux.
This seems to indicate a different structure of the transition region at the
locations of stronger flux concentration than in the remaining network.
The large flux concentrations could be the roots of coronal funnels either open
or forming the base of large coronal loops, while the remaining
network is dominated by small TR loops (Dowdy et al. 1986; Peter 2001).
At the regions of strong magnetic flux and large flows, a single Gaussian
provides a good fit of the line profiles showing bulk velocities either
downwards ( 30
30
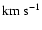 around X=-140, Y=-60) or upwards
(
around X=-140, Y=-60) or upwards
( -17
-17
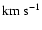 around X=-60, Y=-10). Heating/pressure imbalances
can easily explain subsonic flows in large coronal loops (see later in the
text).
The EEs would, instead, be typical of small loops that do not reach coronal
temperatures, in agreement with Teriaca et al. (2002) and Doyle et al. (2004)
who report that EEs are not seen in lines formed at coronal temperatures.
In this context it is interesting to note that the energy flux associated
with EEs (20 W m-2), although small with respect to the energy requirements
of the whole corona, it is comparable to the average energy radiated in the
O VI 103.193 nm line during EEs:
around X=-60, Y=-10). Heating/pressure imbalances
can easily explain subsonic flows in large coronal loops (see later in the
text).
The EEs would, instead, be typical of small loops that do not reach coronal
temperatures, in agreement with Teriaca et al. (2002) and Doyle et al. (2004)
who report that EEs are not seen in lines formed at coronal temperatures.
In this context it is interesting to note that the energy flux associated
with EEs (20 W m-2), although small with respect to the energy requirements
of the whole corona, it is comparable to the average energy radiated in the
O VI 103.193 nm line during EEs:
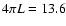 W m-2.
W m-2.
Now we focus our attention on the flows associated with EEs. It is important to
underline here that the EEs profiles and the "excess'' mass flows were
studied in a different manner. The EEs were identified by their strongly
non-Gaussian line profiles while the "excess'' flows were determined by the
moments of the difference spectra as in Eq. (5). This means that the
"excess'' flows with no corresponding EE-like profiles are due to a shift
and/or broadening of the entire line profile, while the sign of the mass flow
at the location of EEs gives information on the spatial characteristics and
extension of the enhanced wings characterising such events.
The majority of the EEs are dominated by upward flows, confirming
that the majority of these events, when observed in O VI, show a
prevalent blue wing emission, although it should be also noted the existence of
few EEs showing only the red wing.
In some of the cases the topology of the "excess'' flows could indicate
siphon-like flows in closed magnetic structures, while in other cases
blue and red patches seem to originate from the same EE but extend beyond it,
and the more extended blue pattern may be indicative of an association with
spicules.
A particularly interesting example of flows in a closed magnetic structure is
outlined by box A in Fig. 3.
Figure 4a shows an enlarged view of this region, revealing a small
isolated loop. Three line profiles corresponding to the
two legs (panels b and d) and the top (panel c) of the loop are also shown.
Note that the line profile in Fig. 4b indicates the presence
of downflows with velocities  100
100
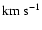 in correspondence with one
of the legs of the loop. Whereas the line profile in Fig. 4d,
corresponding to the other leg, shows the presence of upflows with velocities
in correspondence with one
of the legs of the loop. Whereas the line profile in Fig. 4d,
corresponding to the other leg, shows the presence of upflows with velocities
 -100
-100
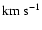 .
Furthermore, the line profile corresponding to the top portion of the loop
(Fig. 4c) shows a profile very close in shape to the average
quiet Sun profile, indicating no shifts at all. This is clearly a LOS
effect and represents a case of supersonic flows within a magnetic loop
(
.
Furthermore, the line profile corresponding to the top portion of the loop
(Fig. 4c) shows a profile very close in shape to the average
quiet Sun profile, indicating no shifts at all. This is clearly a LOS
effect and represents a case of supersonic flows within a magnetic loop
(
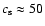
 ). To test this hypothesis further, the loop position
was found by determining the positions of the maxima along horizontal cuts in
the radiance image (black dots in Fig. 4a).
A semi-circular geometrical loop of 13'' diameter was then considered
and it was inclined with respect to the LOS, and its footpoint line rotated
until its projection on the plane perpendicular to the LOS (dashed
dark-grey/red line in Fig. 4a) matched the position of the observed
loop.
The match was obtained for an inclination of 18
). To test this hypothesis further, the loop position
was found by determining the positions of the maxima along horizontal cuts in
the radiance image (black dots in Fig. 4a).
A semi-circular geometrical loop of 13'' diameter was then considered
and it was inclined with respect to the LOS, and its footpoint line rotated
until its projection on the plane perpendicular to the LOS (dashed
dark-grey/red line in Fig. 4a) matched the position of the observed
loop.
The match was obtained for an inclination of 18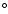 with respect to the
LOS and a rotation of 12.5
with respect to the
LOS and a rotation of 12.5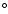 clockwise of the footpoint line.
clockwise of the footpoint line.
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[clip]{0503fig5.eps}}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg76.gif) |
Figure 5:
In the top panel the line radiance, L, along the loop (following the
dotted line in Fig. 4a) is shown. The distance along the loop is
reckoned from the southern extreme of the loop. In the bottom panel we show the
speeds obtained by the moment analysis ( + symbols) together with the
measurements obtained by the multi-Gaussian fitting (triangles).
Negative values indicate blueshifts (upflows). For the sake of clarity, the two
sets of measurements are slightly shifted with respect to each other in abscissa.
A single Gaussian fit (square) and the first moment (asterisk) of the line
profile at the loop top are also shown. The solid line indicate the LOS
component for a 130
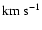 flow along the semi-circular geometrical loop
whose projection on the plain perpendicular to the LOS is shown by the dark-grey
(red) dashed line in Fig. 4a. The dotted lines are obtained for
velocities of 90 and 170
flow along the semi-circular geometrical loop
whose projection on the plain perpendicular to the LOS is shown by the dark-grey
(red) dashed line in Fig. 4a. The dotted lines are obtained for
velocities of 90 and 170
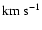 . . |
| Open with DEXTER |
The top panel of Fig. 5 shows
the line radiance along the loop. It is interesting to note that the top of
the loop is brighter than both the two legs. The lower panel of Fig. 5
shows the value of the wing speed along the loop (plus sign). Negative
values indicate blueshifts (upflows).  (upflows) is shown when
(upflows) is shown when
 while
while 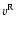 (downflows) is shown when
(downflows) is shown when
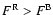 .
.
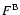 is much larger than
is much larger than 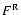 for the southern leg of the loop while the
contrary holds for the northern leg. To verify the values obtained from the
moment analysis of the difference spectra, a triple Gaussian fit was also
performed at the locations on the legs of the loop and the results for the
dominant wing are shown in the bottom panel of Fig. 5 by triangles.
An example of the applied fitting is shown in Fig. 4b
and 4d. In the lower panel of Fig. 5, the speed
measurements at the top of the loop were obtained from a single Gaussian fit
(square) and from the first moment (asterisk) of the line profile at that
location.
Finally, the speed component along the LOS was calculated
at each point along the geometrical loop for a flow of 130
for the southern leg of the loop while the
contrary holds for the northern leg. To verify the values obtained from the
moment analysis of the difference spectra, a triple Gaussian fit was also
performed at the locations on the legs of the loop and the results for the
dominant wing are shown in the bottom panel of Fig. 5 by triangles.
An example of the applied fitting is shown in Fig. 4b
and 4d. In the lower panel of Fig. 5, the speed
measurements at the top of the loop were obtained from a single Gaussian fit
(square) and from the first moment (asterisk) of the line profile at that
location.
Finally, the speed component along the LOS was calculated
at each point along the geometrical loop for a flow of 130
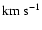 and the
results were compared with the measured values. The agreement is remarkably good
and represents (to our knowledge) the first detection of a supersonic flow in a
quiet Sun loop. Other indications
of similar flows can be seen in Fig. 3 around coordinates
(30, -95) and (-160, 55). It is interesting to note that all these three
cases concern loop structures oriented in the north-south direction, i.e. such
that the time to scan through the structure was minimum. This may be an
indication that these supersonic flows are of short duration. However,
observations extended in time are necessary to confirm it.
and the
results were compared with the measured values. The agreement is remarkably good
and represents (to our knowledge) the first detection of a supersonic flow in a
quiet Sun loop. Other indications
of similar flows can be seen in Fig. 3 around coordinates
(30, -95) and (-160, 55). It is interesting to note that all these three
cases concern loop structures oriented in the north-south direction, i.e. such
that the time to scan through the structure was minimum. This may be an
indication that these supersonic flows are of short duration. However,
observations extended in time are necessary to confirm it.
![\begin{figure}
\par\includegraphics[width=11.4cm,clip]{0503fig6.eps}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg79.gif) |
Figure 6:
Detailed view of the region marked as B in
Fig. 3. On the radiance image on the left panel isocontours
are defined as in Fig. 3.
The locations where non-Gaussian line profiles were found are marked with
a black +. On the right panel the line profile corresponding to one of
the marked pixels is shown (solid line) together with the average profile over
the whole raster (dotted line). |
| Open with DEXTER |
High-speed flows (50 to 100
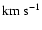 )
in cold loops (
)
in cold loops (
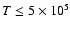 K) have
been so far observed only in active regions with both CDS (Brekke et al. 1997;
Kjeldseth-Moe & Brekke 1998) and SUMER (Wilhelm 1997). Our observations show
such phenomenon to exist also in the quiet Sun.
The short time in which the loop in Fig. 4 was rastered
(
K) have
been so far observed only in active regions with both CDS (Brekke et al. 1997;
Kjeldseth-Moe & Brekke 1998) and SUMER (Wilhelm 1997). Our observations show
such phenomenon to exist also in the quiet Sun.
The short time in which the loop in Fig. 4 was rastered
( 15 s) makes our observations much similar to a snapshot and allows
direct comparison with numerical models of flows along loops. Flows can be
driven by asymmetries (such as heating or pressure imbalances) between the
two legs of the loop (Boris & Mariska 1982; Mariska & Boris 1983;
McClymont & Craig 1987; Mariska 1988; McClymont 1989; Spadaro et al. 1991;
Thomas & Montesinos 1991; Robb & Cally 1992; Orlando et al. 1995a,b) or by
radiatively-cooling condensations (Reale et al. 1996, 1997; Müller et al.
2003).
In the majority of the cases the derived flows are very small, of the order of
few kilometers per second. However, short duration supersonic flows may also be
obtained (see, e.g. Orlando et al. 1995a,b; Robb & Cally 1992). It should be
noted that a footpoint pressure imbalance would lead to a flow arising from
the footpoint with the higher pressure. If we assume the ambient pressure being
equal at the two footpoints, then the stronger magnetic concentration
corresponds to a smaller gas pressure and the flow will be directed upwards at
the footpoint where the magnetic flux is weaker and downwards at the footpoint
with stronger flux concentration, as predicted by Thomas & Montesinos (1991).
This is exactly what we observe in the case illustrated in Figs. 4
and 5. This finding qualitatively resembles the siphon
flow observed by Rüedi et al. (1992) in the infrared.
A similar scenario may also characterise the case at (30, -95).
15 s) makes our observations much similar to a snapshot and allows
direct comparison with numerical models of flows along loops. Flows can be
driven by asymmetries (such as heating or pressure imbalances) between the
two legs of the loop (Boris & Mariska 1982; Mariska & Boris 1983;
McClymont & Craig 1987; Mariska 1988; McClymont 1989; Spadaro et al. 1991;
Thomas & Montesinos 1991; Robb & Cally 1992; Orlando et al. 1995a,b) or by
radiatively-cooling condensations (Reale et al. 1996, 1997; Müller et al.
2003).
In the majority of the cases the derived flows are very small, of the order of
few kilometers per second. However, short duration supersonic flows may also be
obtained (see, e.g. Orlando et al. 1995a,b; Robb & Cally 1992). It should be
noted that a footpoint pressure imbalance would lead to a flow arising from
the footpoint with the higher pressure. If we assume the ambient pressure being
equal at the two footpoints, then the stronger magnetic concentration
corresponds to a smaller gas pressure and the flow will be directed upwards at
the footpoint where the magnetic flux is weaker and downwards at the footpoint
with stronger flux concentration, as predicted by Thomas & Montesinos (1991).
This is exactly what we observe in the case illustrated in Figs. 4
and 5. This finding qualitatively resembles the siphon
flow observed by Rüedi et al. (1992) in the infrared.
A similar scenario may also characterise the case at (30, -95).
Although the majority of the EEs visible in Fig. 3 are located in
areas away from strong magnetic flux concentrations, a remarkable exception is
indicated by the region within box B in Fig. 3.
The left panel of Fig. 6 represents an enlarged view of this
region. The white and black contours represent the positive and
negative longitudinal magnetic flux, respectively. Thick solid dark-grey and
light-grey (red and light-blue) contours show the downwards and upwards directed
mass fluxes, respectively. Finally, the black + mark the location of
highly non-Gaussian line profiles, an example of which is provided in the right
panel. A closer inspection of Fig. 6 (left panel) reveals that the
non-Gaussian profiles are located in what appears to be the intersection of two
systems of loops, one connecting the positive polarity P1 to the negative
polarity N1 and the other connecting P2 and N2. The flow pattern seems to be
also organised along the same directions. The flow pattern and magnetic field
configuration seem shifted a few second of arc with respect to the other but
this may well be a residual error in superposing the magnetic field. This is a
clear example of a small-scale magnetic reconnection between two loop systems.
The reconnection site is indicated by the patch of non-Gaussian line
profiles at the centre of which the largest radiance of the entire dataset
was recorded (see Fig. 6, right panel).
Our careful spectroscopic analysis of a large quiet area around Sun centre
in the mid-transition region line O VI 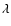 103.193 nm has revealed
substantial mass flows (exceeding those associated with the average quiet Sun
profiles) to be strongly correlated to the magnetic network.
Line profiles from the regions of high magnetic flux concentration are Gaussian
in shape and show bulk flows of the order of (10 to 30)
103.193 nm has revealed
substantial mass flows (exceeding those associated with the average quiet Sun
profiles) to be strongly correlated to the magnetic network.
Line profiles from the regions of high magnetic flux concentration are Gaussian
in shape and show bulk flows of the order of (10 to 30)
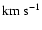 ,
either upwards or
downwards directed. This seems to indicate mass flows on scales larger than the
instrumental spatial resolution (
,
either upwards or
downwards directed. This seems to indicate mass flows on scales larger than the
instrumental spatial resolution ( 1.5'').
1.5'').
The non-Gaussian line profiles typical of the explosive events (EEs) testify,
on the other hand, the presence of flows on scales smaller than the spatial
resolution. Several explosive events were, hence, found in the observed
area through a search for the non-Gaussian line profiles. We have estimated
an event rate of  2500 s-1 over the whole Sun.
We find that the kinetic energy and enthalpy fluxes associated with EEs
do not play a significant role in the energy budget of the outer solar
atmosphere.
EEs are associated with mass flow patterns often larger than the area
characterised by the non-Gaussian line profiles. However, although they are
located along the network, EEs seem to avoid regions with strong magnetic flux
concentrations. Regions that, although often characterised by relevant
mass flows, show nearly Gaussian line profiles. These results could support
the idea of a multi-component transition region characterised by large coronal
funnel rooted at the strong flux concentrations and by a series of small cold
loop that outline the magnetic network (as depicted by Dowdy et al. 1986).
The majority of the coronal funnels would be the bases of large coronal loops,
as also sketched by Peter (2001).
2500 s-1 over the whole Sun.
We find that the kinetic energy and enthalpy fluxes associated with EEs
do not play a significant role in the energy budget of the outer solar
atmosphere.
EEs are associated with mass flow patterns often larger than the area
characterised by the non-Gaussian line profiles. However, although they are
located along the network, EEs seem to avoid regions with strong magnetic flux
concentrations. Regions that, although often characterised by relevant
mass flows, show nearly Gaussian line profiles. These results could support
the idea of a multi-component transition region characterised by large coronal
funnel rooted at the strong flux concentrations and by a series of small cold
loop that outline the magnetic network (as depicted by Dowdy et al. 1986).
The majority of the coronal funnels would be the bases of large coronal loops,
as also sketched by Peter (2001).
Mass flows seem to be present in all these structures, with those in the larger
loops being characterised by subsonic speeds (at least close to the footpoints)
and scales larger than the spatial resolution.
In the smaller loops, small-scale supersonic flows (witnessed by the EE-like
line profiles) seem instead a frequent feature. In, at least, one case
(see Fig. 4) we find evidence that EE-like line profiles are
clearly associated to a supersonic siphon-like flow in a loop structure.
Another two possible cases have also been found. These flows seem to be
triggered by pressure imbalances at the footpoints of small
( 10''-15'') TR loops.
However, only perhaps three such cases (3 couples of EEs locations) could be
found out of
10''-15'') TR loops.
However, only perhaps three such cases (3 couples of EEs locations) could be
found out of  50, thus siphon-like flows are likely to explain only
a minority of the observed EEs.
50, thus siphon-like flows are likely to explain only
a minority of the observed EEs.
As discussed in Sect. 1, EE-like profiles are believed to be the
spectral signature of bi-directional jets generated by magnetic reconnection
between oppositely directed magnetic field lines (Innes et al. 1997).
Chae et al. (2000) considered bi-directional jets to occur as a result of a
collision of a network and an internetwork flux thread. At the intersection
point, the two flux threads are almost anti-parallel, forming an angle that
is greater than 90 .
An alternative model (Chae 1999)
involves a two-step reconnection process. According to this model, the
initial reconnection occurs low in the atmosphere with the formation of
magnetic islands. These islands are observed as H
.
An alternative model (Chae 1999)
involves a two-step reconnection process. According to this model, the
initial reconnection occurs low in the atmosphere with the formation of
magnetic islands. These islands are observed as H up-flow events.
The magnetic islands are annihilated by over-lying magnetic field lines
through a second reconnection that, being a fast reconnection process,
produces the bi-directional jets. Such a model could explain the
observation (Madjarska & Doyle 2002) that EEs are first
observed in chromospheric lines then in TR lines.
It may also be consistent with the observed three to five minute recurrence rate
of explosive events (Chae et al. 1998; Ning et al. 2004). The latter authors
noted that this period is very close to the period of chromospheric and TR
oscillations and suggested that initial reconnection low in the atmosphere
could be triggered at a particular phase of a wave or oscillation.
up-flow events.
The magnetic islands are annihilated by over-lying magnetic field lines
through a second reconnection that, being a fast reconnection process,
produces the bi-directional jets. Such a model could explain the
observation (Madjarska & Doyle 2002) that EEs are first
observed in chromospheric lines then in TR lines.
It may also be consistent with the observed three to five minute recurrence rate
of explosive events (Chae et al. 1998; Ning et al. 2004). The latter authors
noted that this period is very close to the period of chromospheric and TR
oscillations and suggested that initial reconnection low in the atmosphere
could be triggered at a particular phase of a wave or oscillation.
EEs have some common aspects with spicules. In fact, spicules, like
EEs, are related to the chromospheric network (Beckers 1968, 1972; Athay 1976;
Suematsu 1998). The number of observed H spicules present on the Sun
at any time is around
spicules present on the Sun
at any time is around
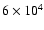 ,
if only spicules higher than 5 Mm are
considered (observed heights are between 6.5 and 9.5 Mm).
The number increases by one order of magnitude if smaller spicules
are also considered (Beckers 1972). An average lifetime of
,
if only spicules higher than 5 Mm are
considered (observed heights are between 6.5 and 9.5 Mm).
The number increases by one order of magnitude if smaller spicules
are also considered (Beckers 1972). An average lifetime of  600 s
(Beckers 1972) yields a birthrate between
600 s
(Beckers 1972) yields a birthrate between
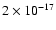 and
and
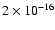 m-2 s-1, indicating that between 2 and 20
(0.7 and 6.7 s-1) spicules should be present in our observed FOV (compared
to around 50 EEs).
Finally, we note that the upward directed mass fluxes in
Fig. 3 cover about the 1.6% of the observed area. This value is
very close to the
m-2 s-1, indicating that between 2 and 20
(0.7 and 6.7 s-1) spicules should be present in our observed FOV (compared
to around 50 EEs).
Finally, we note that the upward directed mass fluxes in
Fig. 3 cover about the 1.6% of the observed area. This value is
very close to the  1% of the solar surface covered by spicules
(Beckers 1968, 1972; Athay 1976).
1% of the solar surface covered by spicules
(Beckers 1968, 1972; Athay 1976).
![\begin{figure}
\par\resizebox{7.5cm}{!}{\includegraphics[clip]{0503fig7.eps}}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg83.gif) |
Figure 7:
Close-up of the area within box C in Fig. 3.
Isocontours are defined as in Fig. 3.
The locations where non-Gaussian line profiles were found are marked with
a black +. |
| Open with DEXTER |
Wilhelm (2000) hypothesised that the rearrangement of the magnetic field
lines following a reconnection process (shown by the EE-like profiles) could
lead to the lifting of plasma, thus generating a spicule. In this case, an EE
could be the first stage in the formation of a spicule.
In most of our cases, blue and red patches seem to originate from a given EE
location but with the blue pattern generally more extended. This means that the
reconnection process affects an area much larger than that characterised by
non-Gaussian line profiles.
Figure 7 is a close-up of the area within box C in
Fig. 3 and shows several examples of flow patterns associated
to EEs. Particularly interesting is the velocity structure around (X=-8,
Y=20).
In this case the explosive event is located at the base of a  15''long blueshifted structure that could be related to the upward apparent motions
observed in spicules. The red contour could be directly related
to the plasma accelerated downward from the EE location while the more
extended blue pattern could be due to the upward accelerated plasma only at the
base of the pattern (where the EE-like profiles are observed), while at larger
distances it could be due to plasma lifted by the reconnecting field lines as
suggested by the spicule model outlined by Wilhelm (2000) in his Fig. 8a-d.
Another example of a flow pattern associated to a spicule could be that shown
on the right panel of Fig. 6.
15''long blueshifted structure that could be related to the upward apparent motions
observed in spicules. The red contour could be directly related
to the plasma accelerated downward from the EE location while the more
extended blue pattern could be due to the upward accelerated plasma only at the
base of the pattern (where the EE-like profiles are observed), while at larger
distances it could be due to plasma lifted by the reconnecting field lines as
suggested by the spicule model outlined by Wilhelm (2000) in his Fig. 8a-d.
Another example of a flow pattern associated to a spicule could be that shown
on the right panel of Fig. 6.
From a general comparison of the properties of these two types of events,
we feel that our results indicate a possible link between the occurrence
of the EEs and the formation of spicules.
However, further high spectral and spatial resolution UV space observations
in TR and, possibly, chromospheric lines (of a quality comparable to the data
presented here), combined with simultaneous high spatial resolution images at
several wavelengths across the H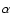 line are necessary to give a
definitive answer on whether or not EEs and spicules are effectively related
phenomena.
line are necessary to give a
definitive answer on whether or not EEs and spicules are effectively related
phenomena.
Acknowledgements
The authors thank D. E. Innes for fruitful discussion and K. Wilhelm for
careful reading of the manuscript and for useful comments and suggestions.
Many thanks also to the referee, V. Hansteen, for his comments that improved
the manuscript.
D.B. is grateful to the CPA, K. U. Leuven University for providing facilities
during his stay at Leuven. D.B.'s work is partially supported by the ESA PRODEX
project (ESA/Contract No. 14815/00/NL/SFe(IC)).
Research at Armagh Observatory is grant-aided by the N. Ireland Dept. of
Culture, Arts and Leisure.
The SUMER project is financially supported by DLR, CNES, NASA, and
PRODEX. SOHO is a mission of international cooperation between ESA
and NASA.
- Athay, R. G. 1976,
The Solar Chromosphere and Corona: Quiet Sun (Dordrecht:
Reidel)
(In the text)
- Beckers, J. M.
1968, Sol. Phys., 3, 367 [NASA ADS] (In the text)
- Beckers, J. M.
1972, ARA&A, 10, 73 [NASA ADS] (In the text)
- Bewsher, D.,
Parnell, C. E., & Harrison, R. A. 2002, Sol. Phys., 206,
21 [NASA ADS] [CrossRef] (In the text)
- Boris, J. P., &
Mariska, J. T. 1982, ApJ, 258, L49 [NASA ADS] [CrossRef] (In the text)
- Bray, R. J., &
Loughhead, R. E. 1974, The Solar Chromosphere (London: Chapman and
Hall)
(In the text)
- Brekke, P.,
Kjeldseth-Moe, O., & Harrison, R. A. 1997, Sol. Phys. 175,
511
(In the text)
- Brkovic, A.,
Solanki, S. K., & Rüedi, I. 2001, A&A, 373, 1056 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Brueckner, G.
E., & Bartoe, J.-D. F. 1983, ApJ, 272, 329 [NASA ADS] [CrossRef] (In the text)
- Chae, J. 1999, in High
Resolution Solar Physics: Theory, Observations and Techniques, ed.
T. R. Rimmele, K. S. Balasubramaniam, & R. R. Radick, Provo,
ASP Conf. Ser., ASP, 183, 375
(In the text)
- Chae, J., Wang, H.,
Lee, C.-Y., Goode, P. R., & Schühle, U. 1998, ApJ, 497,
L109 [NASA ADS] [CrossRef] (In the text)
- Chae, J., Wang, H.,
Goode, P. R., Fludra, A., & Schühle, U. 2000, ApJ, 528,
L119 [NASA ADS] [CrossRef] (In the text)
- Cook, J. W., Brueckner,
G. E., Bartoe, J.-D. F., & Socker, D. G. 1984, Adv. Space Res.,
4, 59 [NASA ADS] (In the text)
- Dere, K. P. 1992, in
Solar Wind Seven: Proc. of the 3rd COSPAR Coll., ed. E. Marsch,
& R. Schwenn, 11
(In the text)
- Dere, K. P., &
Mason, H. E. 1993, Sol. Phys., 144, 217 [NASA ADS] (In the text)
- Dere, K. P., Bartoe,
J.-D. F., & Brueckner, G. E. 1989, Sol. Phys., 123, 41 [NASA ADS] [CrossRef] (In the text)
- Dere, K. P., Bartoe,
J.-D. F., Brueckner, G. E., et al. 1991, J. Geophys. Res., 96,
9399 [NASA ADS] (In the text)
- Dowdy, J. F. Jr.,
Rabin, D., & Moore, R. L. 1986, Sol. Phys., 105, 35 [NASA ADS] [CrossRef] (In the text)
- Doyle, J. G.,
Madjarska, M. S., Dzifcáková, E., & Dammasch, I. E.
2004, Sol. Phys., 221, 51 [NASA ADS] [CrossRef] (In the text)
- Feldman, U.,
Doschek, G. A., & Mariska, J. T. 1979, ApJ, 229, 369 [NASA ADS] [CrossRef] (In the text)
- Harrison, R. A.
1997, Sol. Phys., 175, 467 [NASA ADS] [CrossRef] (In the text)
- Harrison, R.
A., Sawyer, E. C., Carter, M. K., et al. 1995, Sol. Phys., 162,
233 [NASA ADS] (In the text)
- Harrison, R.
A., Lang, J., Brooks, D. H., & Innes, D. E. 1999, A&A, 351,
1115 [NASA ADS] (In the text)
- Innes, D. E.,
Inhester, B., Axford, W. I., & Wilhelm, K. 1997, Nature, 386,
811 [NASA ADS] [CrossRef] (In the text)
-
Kjeldseth-Moe, O., & Brekke, P. 1998, Sol. Phys., 182, 73 [NASA ADS] [CrossRef] (In the text)
- Lemaire, P.,
Wilhelm, K., Curdt, W., et al. 1997, Sol. Phys., 170, 105 [NASA ADS] [CrossRef] (In the text)
- Madjarska, M.
S., & Doyle, J. G. 2002, A&A, 382, 319 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Madjarska, M.
S., & Doyle, J. G. 2003, A&A, 403, 731 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Mariska, J. T.
1988, ApJ, 334, 489 [NASA ADS] [CrossRef] (In the text)
- Mariska, J. T.,
& Boris, J. P. 1983, ApJ, 267, 409 [NASA ADS] [CrossRef] (In the text)
- McClymont, A.
N. 1989, ApJ, 347, L47 [NASA ADS] [CrossRef] (In the text)
- McClymont, A.
N., & Craig, I. J. D. 1987, ApJ, 312, 402 [NASA ADS] [CrossRef] (In the text)
- Müller, D. A.
N., Hansteen, V. H., & Peter, H. 2003, A&A, 411, 605 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Ning, Z., Innes, D. E.,
& Solanki, S. K. 2004, A&A, 419, 1141 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Orlando, S.,
Peres, G., & Serio, S. 1995a, A&A, 294, 861 [NASA ADS] (In the text)
- Orlando, S.,
Peres, G., & Serio, S. 1995b, A&A, 300, 549 [NASA ADS]
- Peter, H. 2001,
A&A, 374, 1108 [EDP Sciences] [NASA ADS] (In the text)
- Peter, H., &
Brkovic, A. 2003, A&A, 403, 287 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Porter, J. G.,
& Dere, K. P. 1991, ApJ, 370, 775 [NASA ADS] [CrossRef] (In the text)
- Reale, F., Peres, G.,
& Serio, S. 1996, A&A, 316, 215 [NASA ADS] (In the text)
- Reale, F., Peres, G.,
& Serio, S. 1997, A&A, 318, 506 [NASA ADS] (In the text)
- Robb, T. D., &
Cally, P. S. 1992, ApJ, 397, 329 [NASA ADS] [CrossRef] (In the text)
- Rüedi, I.,
Solanki, S. K., & Rabin, D. 1992, A&A, 261, L21 [NASA ADS] (In the text)
- Ryutova, M. P.,
& Tarbell, T. D. 2000, ApJ, 541, L29 [NASA ADS] [CrossRef] (In the text)
- Scherrer, P.
H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162,
129 (In the text)
- Spadaro, D.,
Antiochos, S. K., & Mariska, J. T. 1991, ApJ, 382, 338 [NASA ADS] [CrossRef] (In the text)
- Suematsu, Y.
1998, in Solar Jets and Coronal Plumes, ed. T.-D. Guyenne
(Noordwijk: ESA Publication Division), ESA SP-421, 19
(In the text)
- Teriaca, L.,
Madjarska, M. S., & Doyle, J. G. 2001, Sol. Phys., 200, 91 [NASA ADS] [CrossRef] (In the text)
- Teriaca, L.,
Madjarska, M. S., & Doyle, J. G. 2002, A&A, 392, 309 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Thomas, J. H.,
& Montesinos, B. 1991, ApJ, 375, 404 [NASA ADS] [CrossRef] (In the text)
- Vernazza, J.
E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] (In the text)
- Warren, H. P.,
& Winebarger, A. R. 2000, ApJ, 535, L63 [NASA ADS] [CrossRef] (In the text)
- Winebarger,
A. R., Emslie, A. G., Mariska, J. T., & Warren, H. P. 2002, ApJ
565, 1298
(In the text)
- Wilhelm, K. 1997,
in Fifth SOHO workshop: the Corona and Solar Wind Near Minimum
Activity, ed. A. Wilson (Noordwijk: ESA Publication Division), ESA
SP-404, 17
(In the text)
- Wilhelm, K. 2000,
A&A, 360, 351 [NASA ADS] (In the text)
- Wilhelm, K.,
Curdt, W., Marsch, E., et al. 1995, Sol. Phys., 162, 189 [NASA ADS] (In the text)
- Wilhelm,
K., Lemaire, P., Curdt, W., et al. 1997, Sol. Phys., 170, 75 [NASA ADS] [CrossRef]
- Withbroe, G. L.
1983, ApJ, 267, 825 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{0503fig1.eps}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg17.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{0503fig2.eps}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg23.gif)
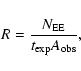
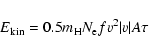
![\begin{figure}
\par\includegraphics[width=13cm,clip]{0503fig3.eps}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg54.gif)
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{0503fig4.eps}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg55.gif)
![$\displaystyle F_{i,j}^{\rm B,R}=\frac{\int_{v_{a}}^{v_{b}}v D_{i,j}(v){\rm d}v}
{\left[\int_{v_{a}}^{v_{b}}D_{i,j}(v){\rm d}v\right]^{1/2}}$](/articles/aa/full/2004/45/aa0503-04/img66.gif)
![\begin{figure}
\par\resizebox{8.5cm}{!}{\includegraphics[clip]{0503fig5.eps}}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=11.4cm,clip]{0503fig6.eps}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg79.gif)
![\begin{figure}
\par\resizebox{7.5cm}{!}{\includegraphics[clip]{0503fig7.eps}}\end{figure}](/articles/aa/full/2004/45/aa0503-04/Timg83.gif)