A&A 427, 923-932 (2004)
DOI: 10.1051/0004-6361:20040416
A. H. Córsico1,2,![]() - E. García-Berro3,4 - L. G.
Althaus1,2,3,
- E. García-Berro3,4 - L. G.
Althaus1,2,3,![]() - J. Isern3,5
- J. Isern3,5
1 - Facultad de Ciencias Astronómicas y Geofísicas,
Universidad Nacional de La Plata, Paseo del Bosque, s/n,
(1900) La Plata, Argentina
2 -
Instituto de Astrofísica La Plata, IALP,
CONICET, Argentina
3 -
Departament de Física Aplicada, Universitat
Politècnica de Catalunya, Av. del Canal Olímpic, s/n,
08860 Castelldefels, Spain
4 -
Institut d'Estudis Espacials de Catalunya, Ed. Nexus,
c/Gran Capità 2, 08034 Barcelona, Spain
5 -
Institut de Ciències de l'Espai (CSIC)
Received 10 March 2004 / Accepted 16 July 2004
Abstract
We explore the adiabatic pulsational properties of massive
white dwarf stars with hydrogen-rich envelopes and oxygen/neon and
carbon/oxygen cores. To this end, we compute the cooling of massive
white dwarf models for both core compositions taking into account the
evolutionary history of the progenitor stars and the chemical
evolution caused by time-dependent element diffusion. In particular,
for the oxygen/neon models we adopt the chemical profile resulting
from repeated carbon-burning shell flashes expected in very massive
white dwarf progenitors. For carbon/oxygen white dwarfs we consider
the chemical profiles resulting from phase separation upon
crystallization. For both compositions we also take into account the
effects of crystallization on the oscillation eigenmodes. We find
that the pulsational properties of oxygen/neon white dwarfs are
noticeably different from those made of carbon/oxygen, thus making
asteroseismological techniques a promising way to distinguish between
the two types of stars and, hence, to obtain valuable information about
their progenitors.
Key words: stars: evolution - stars: white dwarfs - stars: oscillations
White dwarfs are the most common end-product of stellar evolution.
Most of the presently observed white dwarfs are post-Asymptotic Giant
Branch (AGB) remnants, the core of which consists of the main ashes of
helium burning, basically a mixture of carbon and oxygen. However,
there is growing theoretical evidence suggesting that white dwarfs
with masses larger than ![]()
![]() could have cores
composed primarily of oxygen and neon (García-Berro & Iben 1994;
Ritossa et al. 1996; D'Antona & Mazzitelli 1996; García-Berro
et al. 1997; Iben et al. 1997). In particular, García-Berro
et al. (1997) found that when the core mass of the
could have cores
composed primarily of oxygen and neon (García-Berro & Iben 1994;
Ritossa et al. 1996; D'Antona & Mazzitelli 1996; García-Berro
et al. 1997; Iben et al. 1997). In particular, García-Berro
et al. (1997) found that when the core mass of the
![]() white
dwarf progenitor exceeds
white
dwarf progenitor exceeds ![]()
![]() ,
and before the star reaches
the thermally pulsing phase at the AGB tip, carbon is ignited
off-center in semidegenerate conditions. As a result of repeated
carbon-burning shell flashes that eventually give rise to carbon
exhaustion in the degenerate core, it is found that at the end of the
carbon burning phase the star would be left with an oxygen/neon core
with trace amounts of carbon and other heavier chemical species.
After mass-loss episodes, the progenitor remnant is
expected to evolve into the central star of a planetary nebula and
ultimately into a white dwarf with an oxygen/neon core of mass
,
and before the star reaches
the thermally pulsing phase at the AGB tip, carbon is ignited
off-center in semidegenerate conditions. As a result of repeated
carbon-burning shell flashes that eventually give rise to carbon
exhaustion in the degenerate core, it is found that at the end of the
carbon burning phase the star would be left with an oxygen/neon core
with trace amounts of carbon and other heavier chemical species.
After mass-loss episodes, the progenitor remnant is
expected to evolve into the central star of a planetary nebula and
ultimately into a white dwarf with an oxygen/neon core of mass ![]()
![]() .
A possible observational counterpart of these
massive white dwarfs could be the single massive white dwarf LHS 4033,
which has a mass of
.
A possible observational counterpart of these
massive white dwarfs could be the single massive white dwarf LHS 4033,
which has a mass of ![]()
![]() (Dahn et al. 2004). Other
possible massive white dwarfs hosting oxygen/neon cores could be the
magnetic white dwarf PG 1658+441 (Schmidt et al. 1992; Dupuis et al.
2003) - with a mass of
(Dahn et al. 2004). Other
possible massive white dwarfs hosting oxygen/neon cores could be the
magnetic white dwarf PG 1658+441 (Schmidt et al. 1992; Dupuis et al.
2003) - with a mass of ![]()
![]() - and the highly
magnetic white dwarf RE J0317-853 (Barstow et al. 1995; Ferrario
et al. 1997), which has a mass of
- and the highly
magnetic white dwarf RE J0317-853 (Barstow et al. 1995; Ferrario
et al. 1997), which has a mass of ![]()
![]() .
It should be
noted, however, that there are alternative evolutionary channels that
could eventually lead to massive white dwarfs with carbon/oxygen
cores. These scenarios involve the merging of two otherwise
light-weight ordinary white dwarfs. It has been shown (Segretain
et al. 1997; Guerrero et al. 2004) that in this case nuclear reactions
are not able to modify greatly the composition of the core of the
remnant.
.
It should be
noted, however, that there are alternative evolutionary channels that
could eventually lead to massive white dwarfs with carbon/oxygen
cores. These scenarios involve the merging of two otherwise
light-weight ordinary white dwarfs. It has been shown (Segretain
et al. 1997; Guerrero et al. 2004) that in this case nuclear reactions
are not able to modify greatly the composition of the core of the
remnant.
Many white dwarfs exhibit multiperiodic luminosity variations caused
by gravity-modes of low harmonic degree (
![]() )
and with periods
ranging from roughly 100 s to approximately 1200 s. Over the years,
the study of the pulsational patterns of variable white dwarfs through
asteroseismological techniques has become a very powerful tool for
probing the inner regions that would be otherwise unaccessible to
direct observations. In particular, for hydrogen-rich variable DA
white dwarfs - also known as ZZ Ceti stars - such a technique has
proved to be very successful in providing independent valuable
constraints to their fundamental properties, such as their core
composition, the outer layer chemical stratification or the
stellar mass - see, for instance, Pfeiffer et al. (1996), and
Bradley (1998, 2001). Very recently, increasing
attention has been paid to the study of the asteroseismological properties of
massive ZZ Ceti stars, since it opens the interesting possibility of
probing the physical mechanisms operating in their very dense
interiors and, particularly, to obtain useful information about the
crystallization process that occurs in their cores (Montgomery &
Winget 1999). This has been motivated by the discovery of pulsations
in the star BPM 37093 (Kanaan et al. 1992), a massive ZZ Ceti star
which has a stellar mass of
)
and with periods
ranging from roughly 100 s to approximately 1200 s. Over the years,
the study of the pulsational patterns of variable white dwarfs through
asteroseismological techniques has become a very powerful tool for
probing the inner regions that would be otherwise unaccessible to
direct observations. In particular, for hydrogen-rich variable DA
white dwarfs - also known as ZZ Ceti stars - such a technique has
proved to be very successful in providing independent valuable
constraints to their fundamental properties, such as their core
composition, the outer layer chemical stratification or the
stellar mass - see, for instance, Pfeiffer et al. (1996), and
Bradley (1998, 2001). Very recently, increasing
attention has been paid to the study of the asteroseismological properties of
massive ZZ Ceti stars, since it opens the interesting possibility of
probing the physical mechanisms operating in their very dense
interiors and, particularly, to obtain useful information about the
crystallization process that occurs in their cores (Montgomery &
Winget 1999). This has been motivated by the discovery of pulsations
in the star BPM 37093 (Kanaan et al. 1992), a massive ZZ Ceti star
which has a stellar mass of ![]()
![]() and an effective
temperature
and an effective
temperature
![]() K, and that, therefore, should
have a sizeable crystallized core (Winget et al. 1997). It is
interesting to note at this point that this mass is very close to the
theoretical lower limit (
K, and that, therefore, should
have a sizeable crystallized core (Winget et al. 1997). It is
interesting to note at this point that this mass is very close to the
theoretical lower limit (![]()
![]() )
for an oxygen/neon
white dwarf to be formed (Salaris et al. 1997; Gil-Pons et al.
2003). Indeed, Gil-Pons et al. (2003) find that for carbon burning
to take place in the corresponding progenitor, its mass on the main
sequence should be
)
for an oxygen/neon
white dwarf to be formed (Salaris et al. 1997; Gil-Pons et al.
2003). Indeed, Gil-Pons et al. (2003) find that for carbon burning
to take place in the corresponding progenitor, its mass on the main
sequence should be ![]()
![]() ,
leaving a massive oxygen/neon
white dwarf of
,
leaving a massive oxygen/neon
white dwarf of ![]()
![]() .
Hence, BPM 37093 could be
either a carbon/oxygen or an oxygen/neon white dwarf, depending on the
precise value of its mass.
.
Hence, BPM 37093 could be
either a carbon/oxygen or an oxygen/neon white dwarf, depending on the
precise value of its mass.
We do not intend to perform a detailed modelling of the pulsational characteristics of BPM 37093, since we consider it to be beyond the scope of the paper. Instead, the aim of the present paper is to assess the adiabatic pulsational properties of massive white dwarfs with carbon/oxygen (CO) and oxygen/neon (ONe) cores. More specifically, our main goal is to explore the possibility of using white dwarf asteroseismology to distinguish between the two types of star. To this end, we compute the cooling of massive white dwarf models for both core compositions taking into account the evolutionary history of their progenitors and the chemical evolution caused by time-dependent element diffusion during the evolution. The paper is organized as follows. In Sect. 2 we describe the main characteristics of our CO and ONe model white dwarfs. Special emphasis is given to the formation of the core chemical profile during the pre-white dwarf evolutionary stages. The pulsational predictions for t both types of white dwarf sequences are described in Sect. 3. Finally, in Sect. 4 we briefly summarize our main findings and draw our conclusions.
In this work we compute the evolution and the pulsational properties of massive white dwarfs with ONe cores. In pursuing this goal we adopt the chemical profiles obtained by García-Berro et al. (1997) - see Sect. 2.2 for a detailed discussion. Additionally, since a major aim of our work is to compare the theoretical pulsational spectra of our ONe white dwarf models with those of their CO analogs, we also compute the evolution of a white dwarf with a CO core of similar mass. The most relevant results of this calculation are presented in Sect. 2.1 below. An important aspect of the present study common to both sequences concerns the evolution of the chemical abundance distribution caused by diffusion once the white dwarfs are formed. This is particularly relevant for the study of the pulsational properties of white dwarfs. Indeed, element diffusion turns out to be a key ingredient as far as mode trapping in pulsating stratified white dwarfs is concerned (Córsico et al. 2001, 2002). We have used a time-dependent treatment for multicomponent gases (Burgers 1969) which considers gravitational settling and chemical and thermal diffusion for 1H, 3He, 4He, 12C, and 16O species, the dominant constituents outside the core of our white dwarf models - see Althaus et al. (2001a,b) for additional details. In this way, the trace element approximation usually invoked in most ZZ Ceti studies is avoided.
Our massive white dwarf models with a CO core have been computed with
the evolutionary code described at length in Althaus et al. (2003).
The code is based on an up-to-date and detailed physical description.
Briefly, the code uses OPAL radiative opacities for arbitrary
metallicity from Iglesias & Rogers (1996) and from Alexander &
Ferguson (1994) for the low-temperature regime. The equation of state
for the low-density regime comprises partial ionization for hydrogen
and helium compositions, radiation pressure and ionic contributions.
For the high-density regime, partially degenerate electrons and
Coulomb interactions are also considered. Under degenerate conditions
we use an updated version of the equation of state of Magni &
Mazzitelli (1979). Neutrino emission rates and high-density
conductive opacities are taken from the work of Itoh and
collaborators - see Althaus et al. (2002). A nuclear network of 34
thermonuclear reaction rates and 16 isotopes has been considered to
describe hydrogen (proton-proton chains and CNO bi-cycle) and helium
burning. Nuclear reaction rates were taken from Caughlan & Fowler
(1988) except for the 12C(
![]() O reaction rate,
for which we adopted that of Angulo et al. (1999).
O reaction rate,
for which we adopted that of Angulo et al. (1999).
The treatment of the change of the abundances during the pre-white
dwarf evolution is an important aspect. In
particular, our code uses a time-dependent scheme for the simultaneous
treatment of chemical changes caused by nuclear burning and
convective, salt finger and overshoot mixing, which are described as
diffusion processes (Althaus et al. 2003). We have used the
Schwarzschild criterion for convective stability. However, the
occurrence of additional mixing beyond what is predicted by this
criterion is suggested by both theoretical and observational evidence.
In particular, extra mixing episodes (particularly mechanical
overshooting and/or semiconvection) taking place beyond the formally
convective boundary towards the end of central helium burning have a
large influence on the carbon and oxygen distribution in the core of
white dwarfs - see Straniero et al. (2003) for a recent discussion.
Such mixing episodes leave strong signatures on the
theoretical period spectrum of massive ZZ Ceti stars (Althaus
et al. 2003). Therefore, we have allowed for some mechanical overshooting
by following the formalism of Herwig (2000). Our mixing scheme allows
for a self-consistent treatment of diffusive overshooting in the
presence of nuclear burning. In particular, we have considered
exponentially decaying diffusive overshooting above and below any
convective region, including the convective core (main sequence and
central helium burning phases), the external convective envelope and
the short-lived helium-flash convection zone which develops during the
thermal pulses. Finally, convection is treated according to the
mixing length theory for fluids with composition gradients (Grossman
& Taam 1996) that applies in the convective, semiconvective, and salt
finger instability regimes. The mass of the resulting CO white dwarf
is ![]()
![]() .
However, in oder to perform a direct
comparison with the ONe white dwarf model previously mentioned we have
artificially scaled the stellar mass of the CO model to
.
However, in oder to perform a direct
comparison with the ONe white dwarf model previously mentioned we have
artificially scaled the stellar mass of the CO model to
![]() - approximately the mass of BPM 37093 - but taking into
account the core chemical distribution expected for a progenitor star
with a stellar mass correspondingly larger.
- approximately the mass of BPM 37093 - but taking into
account the core chemical distribution expected for a progenitor star
with a stellar mass correspondingly larger.
Crystallization in the core of our ZZ Ceti models and its effects on
their pulsational pattern constitute an central point of this paper.
Crystallization sets in when
![]() ,
where
,
where
![]() is the radius of the
Wigner-Seitz sphere. In addition, the chemical redistribution in the
fluid above the solid core induced by phase separation upon
crystallization (García-Berro et al. 1988; Segretain et al.
1994) has been taken into account by adopting the phase diagram of
Segretain & Chabrier (1993) and following the procedure described in
Salaris et al. (1997) - see, also, Montgomery et al. (1999).
Nevertheless, for the sake of completeness we have also computed a
cooling sequence in which phase separation has been neglected.
is the radius of the
Wigner-Seitz sphere. In addition, the chemical redistribution in the
fluid above the solid core induced by phase separation upon
crystallization (García-Berro et al. 1988; Segretain et al.
1994) has been taken into account by adopting the phase diagram of
Segretain & Chabrier (1993) and following the procedure described in
Salaris et al. (1997) - see, also, Montgomery et al. (1999).
Nevertheless, for the sake of completeness we have also computed a
cooling sequence in which phase separation has been neglected.
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{0416fig1.eps}\end{figure}](/articles/aa/full/2004/45/aa0416-04/Timg23.gif) |
Figure 1:
The internal chemical profile corresponding to a
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[clip,width=8.8cm,clip]{0416fig2.eps}\end{figure}](/articles/aa/full/2004/45/aa0416-04/Timg24.gif) |
Figure 2: Same as Fig. 1, but in the case in which chemical rehomogenization induced by crystallization has been taken into account. |
| Open with DEXTER | |
In our evolutionary sequence, the CO white dwarf model begins to
crystallize at
![]() K. In Fig. 1
we show the chemical profile of a CO white dwarf model at the
ZZ Ceti stage, in which the chemical redistribution due to phase separation
has been neglected. The effective temperature of the model is
K. In Fig. 1
we show the chemical profile of a CO white dwarf model at the
ZZ Ceti stage, in which the chemical redistribution due to phase separation
has been neglected. The effective temperature of the model is
![]() K and their its mass fraction amounts to
0.63 (the crystallized core is shown as a gray zone). Note the
presence of a pronounced step at
K and their its mass fraction amounts to
0.63 (the crystallized core is shown as a gray zone). Note the
presence of a pronounced step at
![]() in the oxygen profile. This feature, which reflects the occurrence of
overshoot episodes prior to the formation of the white dwarf, leaves
strong imprints on the theoretical period spectrum (Althaus et al.
2003). Note also that the external chemical interfaces, including
the He-core transition, are very smooth as consequence of the element
diffusion processes acting during the evolution.
in the oxygen profile. This feature, which reflects the occurrence of
overshoot episodes prior to the formation of the white dwarf, leaves
strong imprints on the theoretical period spectrum (Althaus et al.
2003). Note also that the external chemical interfaces, including
the He-core transition, are very smooth as consequence of the element
diffusion processes acting during the evolution.
Figure 2 displays the chemical profiles of a CO ZZ Ceti
model in which chemical redistribution due to phase separation has
been considered at
![]() K. In this case the
crystallized mass fraction amounts to 0.55, a slightly smaller value
than that of the case in which phase separation was neglected
(Fig. 1). This is due to the larger abundance of
carbon in the overlying fluid layers resulting from the oxygen
enhancement in the crystallized core of the model. Note that, as a
consequence of the mixing resulting from phase separation, the
overshoot-induced step in the innermost oxygen profile has been
completely wiped out. Consequently, the theoretical period spectrum
for this model should have much fewer strong features when compared with
that of
the case in which chemical rehomogenization has been neglected. This
feature will be discussed in depth in Sect. 3.
K. In this case the
crystallized mass fraction amounts to 0.55, a slightly smaller value
than that of the case in which phase separation was neglected
(Fig. 1). This is due to the larger abundance of
carbon in the overlying fluid layers resulting from the oxygen
enhancement in the crystallized core of the model. Note that, as a
consequence of the mixing resulting from phase separation, the
overshoot-induced step in the innermost oxygen profile has been
completely wiped out. Consequently, the theoretical period spectrum
for this model should have much fewer strong features when compared with
that of
the case in which chemical rehomogenization has been neglected. This
feature will be discussed in depth in Sect. 3.
![\begin{figure}
\par\includegraphics[clip,width=8.7cm]{0416fig3.eps}\end{figure}](/articles/aa/full/2004/45/aa0416-04/Timg28.gif) |
Figure 3: The internal chemical profile corresponding to our initial ONe white dwarf model in terms of the outer mass fraction. |
| Open with DEXTER | |
The evolutionary stages - from the zero-age main sequence, through
helium burning and off-center carbon ignition and burning in partially
degenerate conditions up to the thermally pulsing AGB - leading to
the formation of ONe white dwarfs, as well as the input physics
employed in the calculations are described in García-Berro et al.
(1997) and references therein. Here, we restrict ourselves to
summarizing the main characteristics of the models and, particularly,
their internal composition. When the carbon burning phase is
finished, the star is left with a ![]()
![]() core
primarily composed of 16O and 20Ne, with trace amounts of
12C, 23Na and 24Mg. Surrounding the core there is a
buffer composed mainly of a mixture of 12C and 16O and, on
top of it, the overlying hydrogen- and helium-rich envelope layer.
The initial chemical profile of the envelope - which, after diffusion,
turns into a pure hydrogen layer - is shown in
Fig. 3. We have obtained an initial
configuration for our ONe white dwarf model by simply scaling the
internal chemical profiles built up during the pre-white dwarf
evolution to the structure of the massive, hot CO white dwarf model
considered previously. In this way we obtain a good starting
configuration with a mass close to that of BPM 37093 and the
appropriate chemical profile. Because we are interested in the
comparison of the pulsational properties of highly-evolved CO and ONe
ZZ Ceti models with the same stellar mass, this procedure is adequate
for our purposes.
core
primarily composed of 16O and 20Ne, with trace amounts of
12C, 23Na and 24Mg. Surrounding the core there is a
buffer composed mainly of a mixture of 12C and 16O and, on
top of it, the overlying hydrogen- and helium-rich envelope layer.
The initial chemical profile of the envelope - which, after diffusion,
turns into a pure hydrogen layer - is shown in
Fig. 3. We have obtained an initial
configuration for our ONe white dwarf model by simply scaling the
internal chemical profiles built up during the pre-white dwarf
evolution to the structure of the massive, hot CO white dwarf model
considered previously. In this way we obtain a good starting
configuration with a mass close to that of BPM 37093 and the
appropriate chemical profile. Because we are interested in the
comparison of the pulsational properties of highly-evolved CO and ONe
ZZ Ceti models with the same stellar mass, this procedure is adequate
for our purposes.
![\begin{figure}
\par\includegraphics[clip,width=8.7cm]{0416fig4.eps}\end{figure}](/articles/aa/full/2004/45/aa0416-04/Timg29.gif) |
Figure 4: Same as Fig. 3, but for an ONe white dwarf model in the ZZ Ceti instability strip. The crystallized region is displayed as a gray area. |
| Open with DEXTER | |
In our evolutionary sequence, the ONe white dwarf model begins to
crystallize at
![]() K, long before reaching the
ZZ Ceti instability strip. Figure 4 shows the resulting
chemical structure when the model has reached the ZZ Ceti instability
strip. At this point of the evolution, the crystallized
mass fraction amounts to
K, long before reaching the
ZZ Ceti instability strip. Figure 4 shows the resulting
chemical structure when the model has reached the ZZ Ceti instability
strip. At this point of the evolution, the crystallized
mass fraction amounts to ![]()
![]() .
Two important points deserve
additional comment. First, as is the case for CO white dwarfs,
the effects of chemical diffusion in the external chemical abundance
distribution are noteworthy. Indeed, the outer chemical
interfaces are markedly smoothed out by diffusion. Second, a
rehomogenization process induced by Rayleigh-Taylor instabilities has
led to a plateau in the innermost chemical profile by the time the ZZ
Ceti stage is reached. Note that as a result, a strong step in the
chemical profile at
.
Two important points deserve
additional comment. First, as is the case for CO white dwarfs,
the effects of chemical diffusion in the external chemical abundance
distribution are noteworthy. Indeed, the outer chemical
interfaces are markedly smoothed out by diffusion. Second, a
rehomogenization process induced by Rayleigh-Taylor instabilities has
led to a plateau in the innermost chemical profile by the time the ZZ
Ceti stage is reached. Note that as a result, a strong step in the
chemical profile at
![]() has arisen
after rehomogenization, a feature expected to be the most important
ingredient in determining the structure of the period pattern of the
model. It is also important to mention here that ONe white dwarf
models do not experience a significant chemical redistribution due to
phase separation because the charge ratio of Ne to O is much
smaller than that of O and C and, hence, the phase diagrams of
Segretain & Chabrier (1993) do not predict a sizeable enrichment in
Ne in the solid phase. Moreover, the evolutionary calculations of
Ritossa et al. (1996), García-Berro et al. (1997) and
Iben et al. (1997) predict that after the carbon burning phase and when the
thermally pulsing phase ensues there is a non-negligible fraction of
unburnt carbon in the oxygen/neon core. The mass fraction of unburnt
carbon in the ONe core can be as high as
has arisen
after rehomogenization, a feature expected to be the most important
ingredient in determining the structure of the period pattern of the
model. It is also important to mention here that ONe white dwarf
models do not experience a significant chemical redistribution due to
phase separation because the charge ratio of Ne to O is much
smaller than that of O and C and, hence, the phase diagrams of
Segretain & Chabrier (1993) do not predict a sizeable enrichment in
Ne in the solid phase. Moreover, the evolutionary calculations of
Ritossa et al. (1996), García-Berro et al. (1997) and
Iben et al. (1997) predict that after the carbon burning phase and when the
thermally pulsing phase ensues there is a non-negligible fraction of
unburnt carbon in the oxygen/neon core. The mass fraction of unburnt
carbon in the ONe core can be as high as
![]() -
see Fig. 3. The same happens when a merger of two
light-weight white dwarfs is involved (Guerrero
et al. 2004). Hence, the calculation of the effects of Ne
sedimentation upon crystallization would require a ternary phase
diagram (Segretain 1996) which, at present, is not yet well known and,
moreover, is beyond the scope of this paper.
-
see Fig. 3. The same happens when a merger of two
light-weight white dwarfs is involved (Guerrero
et al. 2004). Hence, the calculation of the effects of Ne
sedimentation upon crystallization would require a ternary phase
diagram (Segretain 1996) which, at present, is not yet well known and,
moreover, is beyond the scope of this paper.
We have carried out an adiabatic pulsational analysis of our white
dwarf models with the help of the same Newton-Raphson pulsational code
employed in Córsico et al. (2001; 2002) and described in detail in
Córsico (2003). This code is coupled to the evolutionary code
previously described. However, for the purposes of this work, we have
made appropriate modifications to the pulsational code in order to handle
properly the effects of crystallization on the oscillation
eigenmodes. Briefly, the boundary conditions at the stellar center
(when crystallization has not yet set in) and surface are those given
by Osaki & Hansen (1973). However, when the core of the white dwarf
undergoes crystallization we switch the fluid internal boundary
conditions to the so-called "hard sphere'' boundary conditions
(Montgomery & Winget 1999). Within this approximation, there is
an inhibition on the propagation of the nonradial
eigenfunctions in the crystallized region
of the core. Following previous studies of white dwarf pulsations,
the normalization condition adopted is
![]() at the
stellar surface, where
at the
stellar surface, where
![]() the radial component of the
displacement. The oscillation kinetic energy (
the radial component of the
displacement. The oscillation kinetic energy (
![]() )
is
computed according to Eq. (1) of Córsico et al. (2002), whereas the
weight function is computed as in Kawaler et al. (1985). Finally, we
derive the asymptotic spacing of periods (
)
is
computed according to Eq. (1) of Córsico et al. (2002), whereas the
weight function is computed as in Kawaler et al. (1985). Finally, we
derive the asymptotic spacing of periods (
![]() )
as in
Tassoul et al. (1990):
)
as in
Tassoul et al. (1990):
where N is the Brunt-Väisälä frequency, and r1
and r2 are, respectively, the radii of the inner and outer
boundaries of the propagation region of the modes. Hence, when the
core is already partially crystallized r1 coincides with the radius
of the crystallization front,
![]() .
It is important to
realize that the turning point r1 is no longer a fixed value but,
instead, it is a function of the crystallized mass
.
It is important to
realize that the turning point r1 is no longer a fixed value but,
instead, it is a function of the crystallized mass ![]() and
hence of the temperature of the (nearly) isothermal core. As a
result, as the white dwarf cools down, the internal boundary at r1moves outward, so the integral
and
hence of the temperature of the (nearly) isothermal core. As a
result, as the white dwarf cools down, the internal boundary at r1moves outward, so the integral
![]() decreases,
and consequently the period spacing increases and so do the periods
themselves - see Figs. 7 and 8 of Montgomery & Winget (1999).
decreases,
and consequently the period spacing increases and so do the periods
themselves - see Figs. 7 and 8 of Montgomery & Winget (1999).
The Brunt-Väisälä frequency is computed according to the
procedure of Brassard et al. (1991). This numerical treatment
takes explicit account of the contribution to N from any change in
composition in the white dwarf models by means of the Ledoux term B.
This is an important aspect in connection with the phenomenon of mode
trapping and mode confining (Brassard et al. 1992; Córsico et al.
2002). Specifically, the Brunt-Väisälä frequency is given by:
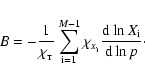 |
(3) |
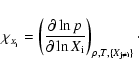 |
(4) |
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{0416fig5.eps}\end{figure}](/articles/aa/full/2004/45/aa0416-04/Timg50.gif) |
Figure 5:
The squared Brunt-Väisälä frequency (N2) - solid
line - in terms of the outer mass fraction, corresponding to the
same CO white dwarf model shown in Fig. 1. Inset: the
Ledoux term B. For the sake of completeness, we also show using a
dotted line the acoustic (Lamb) frequency corresponding to |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[clip,width=8.8cm,clip]{0416fig6.eps}\end{figure}](/articles/aa/full/2004/45/aa0416-04/Timg51.gif) |
Figure 6: Same as in Fig. 5, but for the CO white dwarf model analyzed in Fig. 2. |
| Open with DEXTER | |
When phase separation upon crystallization is taken into account for
the CO white dwarf models, chemical redistribution in the overlying
fluid layers is expected to take place as a consequence of the O
enhancement in the solid phase. Consequently, the chemical abundances
(an their distribution throughout the fluid layer) of both C and O are
expected to be significantly different from those of the previous
model. The Brunt-Väisälä frequency corresponding to a CO white
dwarf model in which the chemical profile has been computed
consistenly with the predictions of chemical rehomogenization
(Fig. 2) is shown in Fig. 6. Note that at
this stage the CO white dwarf models have a significant percentage of
its interior crystallized (![]() ), in such a way that the chemical
step produced by core overshooting during the pre-white dwarf
evolution has been wiped out by the ongoing chemical redistribution.
Because the external chemical transition regions have been smoothed by
diffusion, the shape of the Brunt-Väisälä frequency has no any
abrupt feature capable of strongly pertubating the period spectrum of
the model. Hence, the period spacing distribution should be more or
less uniform, at least in the asymptotic limit of large overtones
(long periods).
), in such a way that the chemical
step produced by core overshooting during the pre-white dwarf
evolution has been wiped out by the ongoing chemical redistribution.
Because the external chemical transition regions have been smoothed by
diffusion, the shape of the Brunt-Väisälä frequency has no any
abrupt feature capable of strongly pertubating the period spectrum of
the model. Hence, the period spacing distribution should be more or
less uniform, at least in the asymptotic limit of large overtones
(long periods).
![\begin{figure}
\par\includegraphics[clip,width=250pt]{0416fig7.eps}\end{figure}](/articles/aa/full/2004/45/aa0416-04/Timg54.gif) |
Figure 7:
Same as Fig. 6, but for the ONe white dwarf model
analyzed in Fig. 4. Dashed lines correspond to the case
in which the Ledoux term B is neglected in the region
|
| Open with DEXTER | |
Now we examine the Brunt-Väisälä frequency characterizing a
typical ONe white dwarf model at the ZZ Ceti stage. In
Fig. 7 we plot the profile of N2 for the same model
analyzed in Fig. 4. Clearly, the dominant feature is
the one located at
![]() (see
the Ledoux term B in the inset of the figure). As we shall see in
the next section, this feature is responsible for strong
non-uniformities in the period spectrum of this model.
(see
the Ledoux term B in the inset of the figure). As we shall see in
the next section, this feature is responsible for strong
non-uniformities in the period spectrum of this model.
We have computed adiabatic, nonradial, spheroidal g(gravity)-modes
with ![]() covering the period range of pulsations observed in ZZ
Ceti stars. We have not considered torsional modes, since these
modes, characterized by very short periods - of up to 20 s
(Montgomery & Winget 1999) - have not been detected in ZZ Ceti
stars so far.
covering the period range of pulsations observed in ZZ
Ceti stars. We have not considered torsional modes, since these
modes, characterized by very short periods - of up to 20 s
(Montgomery & Winget 1999) - have not been detected in ZZ Ceti
stars so far.
![\begin{figure}
\par\includegraphics[clip,width=8.8cm]{0416fig8.eps}\end{figure}](/articles/aa/full/2004/45/aa0416-04/Timg56.gif) |
Figure 8:
Asymptotic period spacing,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[clip,width=16cm]{0416fig9.eps}\end{figure}](/articles/aa/full/2004/45/aa0416-04/Timg57.gif) |
Figure 9:
The forward period spacing ( upper panels) and the kinetic
energy ( lower panels) in terms of the periods of |
| Open with DEXTER | |
We begin by examining Fig. 8, where the asymptotic period
spacing as a function of the effective temperature is shown for the
two CO and the ONe white dwarf models previously discussed, and for
two additional models in which crystallization has been completely
disregarded. These two additional models are only computed for the
sake of comparison and in order to exemplify the effects of
crystallization in spite of the fact that they are not physically
sound. The thick lines correspond to our fiducial models. That is,
the thick solid line corresponds to an ONe model in which
crystallization has been taken into account, whereas the thick dashed
line corresponds to the CO white dwarf model in which both
crystallization and phase separation were taken into account. The
thin dashed line corresponds to a CO model in which crystallization
but no phase separation was considered. The thin dotted
line corresponds to a CO model in which neither crystallization nor
phase separation were taken into account. Finally, the thin solid line
indicates the results for an ONe model in which crystallization was
completely disregarded. The results presented in Fig. 8
deserve several comments. Firstly, for all the cases considered
![]() is an increasing function of
is an increasing function of
![]() ,
as
expected from the fact that the Brunt-Väisälä frequency
decreases as the white dwarf cools down -
,
as
expected from the fact that the Brunt-Väisälä frequency
decreases as the white dwarf cools down -
![]() decreases as degeneracy increases, see Eq. (2). Secondly, it
is noteworthy that if crystallization is neglected
decreases as degeneracy increases, see Eq. (2). Secondly, it
is noteworthy that if crystallization is neglected
![]() is smaller for the ONe models than for the
CO ones. This trend is understood in terms of N2 having noticeably
larger values at the core region in the ONe models than in the CO
models. Thus, the integral of Eq. (1) turns out to be larger
for ONe models and, consequently, the asymptotic period
spacing is smaller.
is smaller for the ONe models than for the
CO ones. This trend is understood in terms of N2 having noticeably
larger values at the core region in the ONe models than in the CO
models. Thus, the integral of Eq. (1) turns out to be larger
for ONe models and, consequently, the asymptotic period
spacing is smaller.
![\begin{figure}
\par\includegraphics[clip,width=11.5cm]{0416fi10.eps}\end{figure}](/articles/aa/full/2004/45/aa0416-04/Timg59.gif) |
Figure 10: Same as Fig. 9, but for the case of an ONe white dwarf. |
| Open with DEXTER | |
In contrast, for the cases in which crystallization has been
considered, the values of
![]() of the ONe models are
always larger than those of the CO ones. In part, this can be
understood from the fact that the ONe model is characterized by a larger
crystallized mass fraction than the CO one for a fixed
of the ONe models are
always larger than those of the CO ones. In part, this can be
understood from the fact that the ONe model is characterized by a larger
crystallized mass fraction than the CO one for a fixed
![]() .
This in turn implies that the integral of N/r in
Eq. (1) is smaller and the resulting asymptotic period spacing
in the ONe model is larger. With regard to the CO models, we note
that when chemical rehomogenization is considered the asymptotic
period spacing is slightly greater than in the situation in
which rehomogenization is neglected. This can be understood on the
basis that, when rehomogenization is not allowed to
operate, the integral in Eq. (1) has an extra contribution
from the overshoot-induced step via the strong peak at
.
This in turn implies that the integral of N/r in
Eq. (1) is smaller and the resulting asymptotic period spacing
in the ONe model is larger. With regard to the CO models, we note
that when chemical rehomogenization is considered the asymptotic
period spacing is slightly greater than in the situation in
which rehomogenization is neglected. This can be understood on the
basis that, when rehomogenization is not allowed to
operate, the integral in Eq. (1) has an extra contribution
from the overshoot-induced step via the strong peak at
![]() in the the Brunt-Väisälä frequency (see
Fig. 1).
in the the Brunt-Väisälä frequency (see
Fig. 1).
We now examine the forward period spacing, defined as
![]() (k being the radial overtone). This quantity, which is
particularly sensitive to the details of the internal chemical structure
of the white dwarf models, is usually employed to infer the mode
trapping properties of ZZ Ceti stars. In addition, the theoretical
period spacing can be directly compared with the observed one in a
given star, whenever a sufficient number of consecutive periods (with
the same harmonic degree
(k being the radial overtone). This quantity, which is
particularly sensitive to the details of the internal chemical structure
of the white dwarf models, is usually employed to infer the mode
trapping properties of ZZ Ceti stars. In addition, the theoretical
period spacing can be directly compared with the observed one in a
given star, whenever a sufficient number of consecutive periods (with
the same harmonic degree ![]() )
can be measured. Here we restrict
ourselves to present pulsational results corresponding to the same
models analyzed in Figs. 5-7. We recall that these models are characterized by an
effective temperature of
)
can be measured. Here we restrict
ourselves to present pulsational results corresponding to the same
models analyzed in Figs. 5-7. We recall that these models are characterized by an
effective temperature of ![]() 11 800 K, which is representative of
ZZ Ceti stars. Figure 9 shows the
11 800 K, which is representative of
ZZ Ceti stars. Figure 9 shows the ![]() period spacing
distribution (top panels) and the kinetic energy of oscillation
(bottom panels) as a function of the period for a CO white dwarf in
which crystallization has been ignored (left panels), for a CO white
dwarf in which crystallization was taken into account but no phase
separation was considered (middle panels) and for the case in which
both crystallization and phase separation were properly taken into
account (right panels).
period spacing
distribution (top panels) and the kinetic energy of oscillation
(bottom panels) as a function of the period for a CO white dwarf in
which crystallization has been ignored (left panels), for a CO white
dwarf in which crystallization was taken into account but no phase
separation was considered (middle panels) and for the case in which
both crystallization and phase separation were properly taken into
account (right panels).
Clearly, when crystallization is considered the period spacing
distribution is much less featured. Similar behavior has been
reported by Montgomery & Winget (1999) in calculations
in which the crystallized mass fraction is considered as a free
parameter. When crystallization is ignored, the internal boundary
condition remains fixed at the center of the star. The resulting
eigenspectrum is composed of some core-confined modes, some modes
trapped in the outer layers, and the remainder normal modes (Córsico
et al. 2002; Althaus et al. 2003). In this case the modes nearly
preserve their character during the evolution. In contrast, when
crystallization is considered (middle panels) the inner boundary
condition moves together with the crystallization front, and the
eigenfunctions of all modes are pulled out to the surface of the
model. Under these circumstances, the resonance conditions
determining which modes are trapped or confined are strongly modified
as the degree of crystallization increases. This is clearly shown in
the top middle panel of Fig. 9, which corresponds to a
model in which the crystallization front is located at
![]() .
Note that for the high- and intermediate-overtone modes
the strong minima (associated with core-trapped modes) characterizing
the
.
Note that for the high- and intermediate-overtone modes
the strong minima (associated with core-trapped modes) characterizing
the
![]() distribution of the model for which crystallization
was ignored (left panel), are not present in the case in which
crystallization is considered (middle panel). A look at the lower
panels of Fig. 9 also shows that when crystallization
is taken into account the differences between the kinetic energies of
trapped, normal and confined modes are smaller. Another interesting
point is that the mean period spacing increases when crystallization
is considered, in agreement with the predictions of the asymptotic
theory of pulsations and with the results of Montgomery & Winget
(1999).
distribution of the model for which crystallization
was ignored (left panel), are not present in the case in which
crystallization is considered (middle panel). A look at the lower
panels of Fig. 9 also shows that when crystallization
is taken into account the differences between the kinetic energies of
trapped, normal and confined modes are smaller. Another interesting
point is that the mean period spacing increases when crystallization
is considered, in agreement with the predictions of the asymptotic
theory of pulsations and with the results of Montgomery & Winget
(1999).
We now examine the more realistic case in which phase separation is
included in addition to crystallization (right panels). In view of
the above considerations, we expect a smooth period spacing
distribution. We note that the period spacing distribution (upper
right panel) has a fairly clean structure for periods longer than
![]() 300 s. In fact, the forward period spacing for modes with
k> 12 becomes very close to 20.6 s, the value predicted by the
asymptotic theory and given by Eq. (1). As already discussed,
this is due mostly to the absence of any abrupt feature in the profile
of the Brunt-Väisälä frequency. In fact, the model is
characterized by a crystallized mass fraction of
300 s. In fact, the forward period spacing for modes with
k> 12 becomes very close to 20.6 s, the value predicted by the
asymptotic theory and given by Eq. (1). As already discussed,
this is due mostly to the absence of any abrupt feature in the profile
of the Brunt-Väisälä frequency. In fact, the model is
characterized by a crystallized mass fraction of ![]() 0.55, which
is large enough for the ongoing chemical rehomogenization processes
to erase the overshoot-induced step in the chemical profile (see
Figs. 1 and 2).
0.55, which
is large enough for the ongoing chemical rehomogenization processes
to erase the overshoot-induced step in the chemical profile (see
Figs. 1 and 2).
As previously stated, the major aim of this work is to explore the
possibility of using white dwarf asteroseismology to distinguish
massive CO white dwarfs from those having ONe cores. In the right
panels of Fig. 10 we show the distributions of
![]() and
and
![]() that correspond to our fiducial ONe model at
that correspond to our fiducial ONe model at
![]() K (which corresponds to a crystallized
mass
K (which corresponds to a crystallized
mass
![]() ). For the sake of completeness in
the left panels of this figure we also show the same distributions for
the case in which crystallization was ignored. We note that,
irrespective of the assumptions regarding crystallization for both
types of models (CO or ONe), the period spacing diagrams of ONe models
are noticeably different from those of the CO models. In particular, for
the case in which crystallization was disregarded (left panels), the
period spacing diagram of the ONe model shows strong and abundant
features linked with mode trapping and confining, mostly driven by the
structure at
). For the sake of completeness in
the left panels of this figure we also show the same distributions for
the case in which crystallization was ignored. We note that,
irrespective of the assumptions regarding crystallization for both
types of models (CO or ONe), the period spacing diagrams of ONe models
are noticeably different from those of the CO models. In particular, for
the case in which crystallization was disregarded (left panels), the
period spacing diagram of the ONe model shows strong and abundant
features linked with mode trapping and confining, mostly driven by the
structure at
![]() in the
Brunt-Väisälä frequency profile (see Fig. 7). When
crystallization is taken into account, the period spacing distribution
of the ONe model still has a complex structure but with a noticeably
lower strength (right upper panel of Fig. 10). In
particular, we note the presence of three minima at
in the
Brunt-Väisälä frequency profile (see Fig. 7). When
crystallization is taken into account, the period spacing distribution
of the ONe model still has a complex structure but with a noticeably
lower strength (right upper panel of Fig. 10). In
particular, we note the presence of three minima at ![]() 300,
600 and 900 s. However, the comparison of the period spacing
diagrams in the right panels of Figs. 9 and
10 indicates that two models with the same stellar mass
and effective temperature but differing in core composition (one
having a core rich in carbon and oxygen, and the other mainly composed
of oxygen and neon) should be characterized by a quite different
pulsational spectrum.
300,
600 and 900 s. However, the comparison of the period spacing
diagrams in the right panels of Figs. 9 and
10 indicates that two models with the same stellar mass
and effective temperature but differing in core composition (one
having a core rich in carbon and oxygen, and the other mainly composed
of oxygen and neon) should be characterized by a quite different
pulsational spectrum.
An additional difference in the pulsational properties between the two
types of models is found when the kinetic energies of the modes are
compared. In fact, all the modes of the ONe model have lower
energies than those of their counterparts of the CO model. Two facts
help to clarify this issue. We recall that
![]() is
proportional to the density and to the squared radial and horizontal
eigenfunctions. Firstly, the propagation regions in which the
eigenmodes are allowed to oscillate have different sizes.
Specifically, for the ONe white dwarf at
is
proportional to the density and to the squared radial and horizontal
eigenfunctions. Firstly, the propagation regions in which the
eigenmodes are allowed to oscillate have different sizes.
Specifically, for the ONe white dwarf at
![]() K, we find that
K, we find that ![]() of the stellar mass has already
crystallized. Hence, in this high-density region nonradial g-modes
are excluded. Therefore, the modes are able to propagate only in
the remaining external, low-density region. In the case of the
CO model at the same
of the stellar mass has already
crystallized. Hence, in this high-density region nonradial g-modes
are excluded. Therefore, the modes are able to propagate only in
the remaining external, low-density region. In the case of the
CO model at the same
![]() ,
the crystallized mass fraction is
aproximately 0.55, and so the modes can propagate in regions
characterized by considerably quite high densities. Secondly, we have found
that for the case of ONe models the amplitudes of the eigenfunctions
are considerably smaller than those of their counterparts in the CO
models. As a final remark we note that the mean period spacing of
the pulsation modes corresponding to ONe white dwarfs is slightly
larger than that of the CO models. This is again in agreement with
the predictions of the asymptotic theory, as shown in
Fig. 8.
,
the crystallized mass fraction is
aproximately 0.55, and so the modes can propagate in regions
characterized by considerably quite high densities. Secondly, we have found
that for the case of ONe models the amplitudes of the eigenfunctions
are considerably smaller than those of their counterparts in the CO
models. As a final remark we note that the mean period spacing of
the pulsation modes corresponding to ONe white dwarfs is slightly
larger than that of the CO models. This is again in agreement with
the predictions of the asymptotic theory, as shown in
Fig. 8.
![\begin{figure}
\par\includegraphics[clip,width=250pt]{0416fi11.eps}\end{figure}](/articles/aa/full/2004/45/aa0416-04/Timg65.gif) |
Figure 11:
Same as the upper-right panel of Fig. 10, but for
the case in which the effect of the strong step in the chemical
profile at
|
| Open with DEXTER | |
In closing, we stress that the main differences in the pulsational
spectrum between ONe and CO models are due to the presence of a strong
step in the core chemical profile of the ONe model. As mentioned, this
step marks the outer edge of the mixing zone induced by the negative
molecular weight of the ONe white dwarf progenitor. However, additional
mixing episodes beyond this external
border may wipe out the chemical step. In that case we would
expect the period pattern to be modified to a considerable
extent. This is indeed borne out by Fig. 11, in which
the period spacing is computed under the assumption that B= 0 in the
region at
![]() and the
resulting run of the Brunt-Väisälä frequency is that displayed
by a dashed line in Fig. 7. We are aware that this
procedure does not eliminate completely the effects of the strong
chemical feature on the period spectrum, because the change in density
associated with this chemical interface is still present in the
computation of N (see Eq. (2)). However, we consider this
approximation reliable enough for our purposes here. Note that the
forward period spacing becomes much less pronounced than when the
Brunt-Väisälä frequency is computed
self-consistently (right panel of Fig. 10), and instead,
it is reminiscent to the results obtained for the CO model (see right
panel of Fig. 9). This aspect would render the current
asteroseismological techniques much less able to yield the actual
core composition of the massive white dwarfs. We note however, that the
average period spacing remains virtually unchanged even in the presence of such
extra mixing episode.
and the
resulting run of the Brunt-Väisälä frequency is that displayed
by a dashed line in Fig. 7. We are aware that this
procedure does not eliminate completely the effects of the strong
chemical feature on the period spectrum, because the change in density
associated with this chemical interface is still present in the
computation of N (see Eq. (2)). However, we consider this
approximation reliable enough for our purposes here. Note that the
forward period spacing becomes much less pronounced than when the
Brunt-Väisälä frequency is computed
self-consistently (right panel of Fig. 10), and instead,
it is reminiscent to the results obtained for the CO model (see right
panel of Fig. 9). This aspect would render the current
asteroseismological techniques much less able to yield the actual
core composition of the massive white dwarfs. We note however, that the
average period spacing remains virtually unchanged even in the presence of such
extra mixing episode.
In this work we have computed the evolution of massive white dwarfs with hydrogen-rich envelopes and carbon/oxygen and oxygen/neon cores with the major aim of comparing their adiabatic pulsational properties. Particular attention was given to the formation of the core chemical profile during the pre-white dwarf evolutionary stages and to the evolution of the chemical abundance distribution caused by element diffusion during the white dwarf regime. In addition, the chemical rehomogenization induced by phase separation upon crystallization as well as the effects of crystallization on the oscillation eigenmodes have been fully taken into account.
Our results show that because the chemical interfaces in the envelope are markedly smoothed by diffusion, the chemical structure of the core mostly determines the structure of the period spectrum. This result reinforces the conclusions arrived at in Córsico et al. (2001, 2002) and Althaus et al. (2003) about the role of time-dependent element diffusion in pulsatng calculations. Moreover, we find that, in contrast with their carbon/oxygen core counterparts, oxygen/neon white dwarfs are characterized by strong non-uniformities in their period spacing distribution. The lack of a featured period spacing distribution characterizing white dwarfs with carbon/oxygen cores arises from the fact that the mixing episode induced by phase separation as crystallization proceeds completely wipes out any feature in the shape of the innermost chemical profile built up during the evolutionary stages prior to the white dwarf formation. In addition, we found that the average period spacing characterizing our oxygen/neon models is appreciably larger than that of the carbon/oxygen counterparts having the same stellar mass and effective temperature. This is true even in the presence of extra mixing episodes that could eventually remove the sharp abundance discontinuity left in the oxygen/neon models. Finally, we also find quite different kinetic energy spectra for the two types of models.
Hence, it turns out that the asteroseismological techniques usually
employed in variable white dwarf studies constitute, in principle, a powerful
tool for distinguishing massive carbon/oxygen white dwarfs from those
having oxygen/neon cores. In this regard, the most massive ZZ Ceti
star presently known, BPM 37093, is of particular interest since the
value of its stellar mass of ![]()
![]() places it close to
the theoretical lower limit for an oxygen/neon white dwarf to be
formed. Nonetheless, the scarcity of detected periods (eight periods) in
the light curve of BPM 37093 renders conclusive asteroseismological inferences
in this case very difficult. However, since the
average period spacing is larger for the oxygen/neon ones, a comparison with
the observed value would help to get a clear insight into the actual
core composition of this massive white dwarf. We feel that this aspect would
deserve to be explored in the frame of a set of white dwarf models with
various stellar masses. Ongoing attempts to constrain
the fundamental properties of BPM 37093 using asteroseismological data
should allow us to shed new light on the scenarios leading to the
formation of single massive white dwarfs and on the nature of their
progenitors.
places it close to
the theoretical lower limit for an oxygen/neon white dwarf to be
formed. Nonetheless, the scarcity of detected periods (eight periods) in
the light curve of BPM 37093 renders conclusive asteroseismological inferences
in this case very difficult. However, since the
average period spacing is larger for the oxygen/neon ones, a comparison with
the observed value would help to get a clear insight into the actual
core composition of this massive white dwarf. We feel that this aspect would
deserve to be explored in the frame of a set of white dwarf models with
various stellar masses. Ongoing attempts to constrain
the fundamental properties of BPM 37093 using asteroseismological data
should allow us to shed new light on the scenarios leading to the
formation of single massive white dwarfs and on the nature of their
progenitors.
Acknowledgements
This work was partially supported by the Instituto de Astrofísica La Plata, by the MCYT grants AYA04094-C03-01 and 02, by the European Union Feder funds, and by the CIRIT. L.G.A. also acknowledges the Spanish MCYT for a Ramón y Cajal Fellowship.