A&A 427, 393-396 (2004)
DOI: 10.1051/0004-6361:20040374
H. Asada1,2
1 - GReCO, Institute for Astrophysics at Paris,
98bis boulevard Arago, 75014 Paris, France
2 -
Faculty of Science and Technology,
Hirosaki University, Hirosaki 036-8561, Japan
Received 3 March 2004 / Accepted 28 July 2004
Abstract
We study the effect of the core radius of an isothermal
ellipsoidal gravitational lens on the caustics and
the critical curves.
We derive an analytic expression of the caustics for an isothermal
ellipsoidal gravitational lens via a sixth-order algebraic equation.
Since the expression is too long, by using another method
we obtain a parametric representation of the critical curves
in order to show analytically that there exist three cases:
there are two curves for a small core radius, one
for a quite large one, and no curves appear for an extremely large one,
though the latter two cases are not realistic. The caustics are
represented also by the same parameter.
Key words: gravitational lensing - galaxies: general - cosmology: theory
The caustics are curves on the source plane perpendicular to the line of sight. They are important to understand the gravitational lensing, particularly when estimating its probability. Furthermore, the number of images changes if a source crosses the caustics. Similarly, critical curves located on the lens plane play a crucial role; giant arcs are observed near these critical curves.
Analytic expressions for the caustics and critical curves were found for a singular isothermal ellipsoidal lens (Asada et al. 2003) during an algebraic study of the gravitational lens (Asada 2002; Asada et al. 2002). However, a cored isothermal ellipsoidal lens, which is more important and realistic than a singular one, seemed beyond an analytic approach, because the equation for a cored isothermal ellipsoidal lens is of much higher order and thus more complicated from an algebraic point of view (Asada et al. 2003). The existence of a core makes a crucial difference even if the core is small. For instance, the number of images for a singular isothermal ellipsoid is two or four, while it is one, three or five for a cored isothermal one (Asada et al. 2003). The main purpose of the present paper is to study the effect of the core radius on the caustics and the critical curves.
This paper is organized as follows. In Sect. 2, the lens equation for a cored isothermal ellipsoid is given in the form of a single sixth-order algebraic equation. The discriminant for this algebraic equation is also discussed. A parametric representation of the critical curves and caustics are obtained in Sect. 3. Section 4 provides our conclusion.
We consider an isothermal ellipsoidal lens with ellipticity
![]() and the angular core radius c.
The surface mass density projected onto the lens plane must be
non-negative everywhere. This puts a constraint as
and the angular core radius c.
The surface mass density projected onto the lens plane must be
non-negative everywhere. This puts a constraint as
![]() .
A tighter constraint
.
A tighter constraint
![]() comes from the requirement
that the density contour must be convex, which is reasonable
for an isolated relaxed system.
The lens equation is expressed as
comes from the requirement
that the density contour must be convex, which is reasonable
for an isolated relaxed system.
The lens equation is expressed as
| |
= | 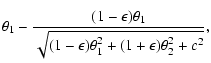 |
(1) |
| = | 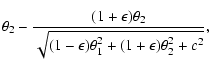 |
(2) |
where
![]() and
and
![]() denote
the positions of the source and images, respectively.
denote
the positions of the source and images, respectively.
For simplicity, we introduce variables as
![]() ,
,
![]() ,
,
![]() and
and
![]() ,
so that the lens equation
can be rewritten as
,
so that the lens equation
can be rewritten as
By the discriminant for polynomial equations, we can determine a location where the number of real solutions changes (e.g., van der Waerden 1966), which corresponds to a change in the number of images in the context of the lensing. The discriminant for the sixth-order Eq. (5) is computed for instance by using the software Mathematica (Wolfram 2000). The result is a lengthy polynomial of 656 terms, which is not tractable. Hence we employ another method to obtain a parametric representation of the caustics and critical curves in a much shorter and thus more practical form.
We will find allowed regions among r, c and e, which is
due to
![]() in Eq. (8).
In short, Eq. (8) implies
in Eq. (8).
In short, Eq. (8) implies
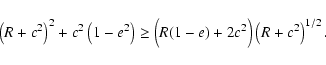 |
(11) |
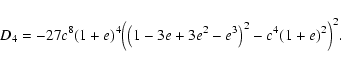 |
(13) |
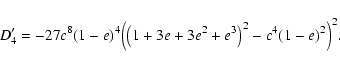 |
(21) |
It is convenient to consider Eq. (8)
as an r-parameter representation of the critical curves,
because we must solve Eq. (8) with respect to
r to obtain a ![]() -parameter representation.
This r-representation becomes
-parameter representation.
This r-representation becomes
![\begin{figure}
\par\includegraphics[width=8cm]{0374fig1.eps}\end{figure}](/articles/aa/full/2004/44/aa0374-04/Timg59.gif) |
Figure 1: Caustics for a cored isothermal ellipsoidal lens for e=0.1 and c=0.2. Sources are located at (0, 0.1), (0, 0.5) and (0, 0.7), denoted by the triangle, filled disk and square, respectively. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm]{0374fig2.eps}\end{figure}](/articles/aa/full/2004/44/aa0374-04/Timg60.gif) |
Figure 2: Critical curves for a cored isothermal ellipsoidal lens for e=0.1 and c=0.2. The images correspond to the sources in Fig. 1. |
| Open with DEXTER | |
We must perform numerical computations for various values of the parameters in order to obtain the caustics and critical curves. The present expression is analytic. Hence, it enables us to save time and reach more accurate results, for instance in rapid and accurate estimations of a lensing event rate, fittings to observational data, etc.
Acknowledgements
The author would like to thank M. Bartelmann, Y. Mellier and M. Kasai for useful conversations. He would like to thank L. Blanchet for hospitality at the Institute for Astrophysics at Paris. This work was supported by a fellowship for visiting scholars from the Ministry of Education of Japan.