M. Perucho1 - J. M. Martí1 - M. Hanasz2
1 - Departamento de Astronomía y Astrofísica,
Universidad de Valencia, 46100 Burjassot, Spain
2 - Torun Centre for
Astronomy, Nicholas Copernicus University, 97-148
Piwnice k.Torunia, Poland
Received 27 February 2004 / Accepted 11 July 2004
Abstract
In this paper we continue our study of the Kelvin-Helmholtz (KH)
instability in relativistic planar jets following the long-term
evolution of the numerical simulations which were introduced
in Paper I. The models have been classified into four classes (I to
IV) with regard to their evolution in the nonlinear phase,
characterized by the process of jet/ambient mixing and momentum
transfer. Models undergoing qualitatively different non-linear
evolution are clearly grouped in well-separated regions in a jet
Lorentz factor/jet-to-ambient enthalpy diagram. Jets with a low Lorentz
factor and small enthalpy ratio are disrupted by a strong shock after
saturation. Those with a large Lorentz factor and enthalpy ratio are
unstable although the process of mixing and momentum exchange proceeds
to a longer time scale due to a steady conversion of kinetic
to internal energy in the jet. In these cases, the high value of the
initial Lorentz seems to prevent transversal velocity from growing far
enough to generate the strong shock that breaks the slower jets.
Finally, jets with either high Lorentz factors and small enthalpy
ratios or low Lorentz factors and large enthalpy ratios appear as the
most stable.
In the long term, all the models develop a distinct transversal structure (shear/transition layers) as a consequence of KH perturbation growth. The properties of these shear layers are analyzed in connection with the parameters of the original jet models.
Key words: galaxies: jets - hydrodynamics - instabilities
In the previous paper (Perucho et al. 2004), hereafter
is Paper I, we have performed several simulations and characterized
the effects of relativistic dynamics and thermodynamics in the
development of KH instabilities in planar, relativistic jets. We
performed a linear stability analysis and numerical simulations for the
most unstable first reflection modes in the temporal approach, for
three different values of the Lorentz factor ![]() (5, 10 and 20)
and a few different values of specific internal energy of the jet
matter (from 0.08 to 60.0 c2; c is the light speed in vacuum).
(5, 10 and 20)
and a few different values of specific internal energy of the jet
matter (from 0.08 to 60.0 c2; c is the light speed in vacuum).
In Paper I we focused on the linear and postlinear regime, especially on the comparison of the results of the linear stability analysis and numerical simulations in the linear range of KH instability.
We demonstrated first that, with the appropriate numerical
resolution, a high convergence could be reached between the growth
rate of perturbed modes in the simulations and the results of a linear
stability analysis performed in the vortex sheet approximation. A 20%
accuracy has been determined for the full set of simulated models, on
average. The agreement between the linear stability analysis and
numerical simulations of KH instability in the linear range has been
achieved for a very high radial resolution of 400 zones/![]() (
(![]() is the jet radius), which
appears to be especially relevant for hot jets. The verified high
accuracy of the simulations made it possible to extend the analysis up
to nonlinear phases of the evolution of KH instability. We identified
several phases in the evolution of all the models: linear, saturation
and mixing phases. The further analysis of the mixing process,
operating during the long-term evolution, will be performed in the
present paper.
is the jet radius), which
appears to be especially relevant for hot jets. The verified high
accuracy of the simulations made it possible to extend the analysis up
to nonlinear phases of the evolution of KH instability. We identified
several phases in the evolution of all the models: linear, saturation
and mixing phases. The further analysis of the mixing process,
operating during the long-term evolution, will be performed in the
present paper.
We have found that in each of the examined cases the linear phase always ends when the longitudinal velocity perturbation departs from linear growth. Then the longitudinal velocity saturates at a value close to the speed of light. This limitation (inherent to relativistic dynamics) is easily noticeable in the jet reference frame. We also noted a saturation of the transversal velocity perturbation, measured in the jet reference frame, at the level of about 0.5 c. The transversal velocity saturates later than the longitudinal velocity at a moment which is close to the peak value of pressure perturbation.
Therefore we concluded that the relativistic nature of the examined flow is responsible for the departure of the system from linear evolution, which manifests as the limitation of velocity components. This behaviour is consistent with the one deduced by Hanasz (1995, 1997) with the aid of analytical methods.
Our simulations, performed for the most unstable first reflection
modes, confirm the general trends resulting from the linear stability
analysis: the faster (larger Lorentz factor) and colder jets have
smaller growth rates. As we mentioned in the Introduction of Paper I,
Hardee et al. (1998) and Rosen et al. (1999) note an exception which
occurs for the hottest jets. These jets appear to be the most stable
in their simulations (see also the simulations in Martí et al. 1997). They suggest that this behaviour is caused by the lack of
appropriate perturbations to couple to the unstable modes. This could
be partially true as fast, hot jets do not generate overpressured
cocoons that let the jet run directly into the nonlinear regime.
However, from the point of view of our results in Paper I, the high
stability of hot jets may have been caused by the lack of radial
resolution that leads to a damping in the perturbation growth
rates. Finally, one should keep in mind that the simulations performed
in the aforementioned papers only covered about one hundred time units
(
![]() ), well inside the linear regime of the corresponding models
for small perturbations. In this paper, the problem of the stability
of relativistic cold, hot, slow and fast jets is analyzed on the basis
of long-term simulations extending over the fully nonlinear evolution
of KH instabilities.
), well inside the linear regime of the corresponding models
for small perturbations. In this paper, the problem of the stability
of relativistic cold, hot, slow and fast jets is analyzed on the basis
of long-term simulations extending over the fully nonlinear evolution
of KH instabilities.
Table 1:
Equilibrium parameters of different simulated jet models
along with solutions of the dispersion relation (23) in Paper I,
corresponding to fastest growing first reflection mode, taken as input
parameters for numerical simulations. The primes are used to assign
wavenumber and complex frequency in the reference frame comoving with
jet. The listed equilibrium parameters are: ![]() - jet Lorentz
factor,
- jet Lorentz
factor,
![]() - rest mass density,
- rest mass density,
![]() and
and
![]() - specific internal energies of jet and ambient
medium,
- specific internal energies of jet and ambient
medium,
![]() ,
,
![]() - the sound speeds in jet and ambient
medium, p - pressure,
- the sound speeds in jet and ambient
medium, p - pressure, ![]() ,
, ![]() - relativistic density and
enthalpy contrasts and
- relativistic density and
enthalpy contrasts and ![]() - the jet Mach number. All the quantities
in the table, except the last column, are expressed in units of the
ambient density,
- the jet Mach number. All the quantities
in the table, except the last column, are expressed in units of the
ambient density,
![]() ,
the speed of light, c, and the jet
radius,
,
the speed of light, c, and the jet
radius, ![]() .
Parameters for the new set of simulations are shown in
the lower part of the table.
.
Parameters for the new set of simulations are shown in
the lower part of the table.
Finally, we found in Paper I that the structure of the pertubation does not change much accross the linear and saturation phases, except that the oblique sound waves forming the perturbation became steep due to their large amplitude. In this paper we show that the similarity of all models at the saturation time, found in Paper I, will lead to different final states in the course of the fully nonlinear evolution.
The plan of this paper is as follows: in Sect. 2 we recall the parameters of the simulations discussed in Paper I and in this paper along with a new complementary set of simulations introduced here with the aim of making the analysis more general. In Sect. 3 we describe our new results concerning the long-term nonlinear evolution of KH modes and we discuss our results and conclude in Sect. 4.
In this paper we continue the analysis of simulations presented in
Paper I. The parameters of the simulations are listed in
Table 1. The values of the parameters
were chosen to be close to those used in some simulations by Hardee et al.
(1998) and Rosen et al. (1999) and to span a wide range in
thermodynamical properties as well as jet flow Lorentz factors. In all
the simulations of Paper I, the density in the jet and ambient gases
are
![]() ,
,
![]() respectively and the adiabatic
exponent
respectively and the adiabatic
exponent
![]() .
.
Since the internal rest mass density is fixed, there are two free
parameters characterizing the jet equilibrium: Lorentz factor and jet
specific internal energy displayed in Cols. 2 and 3 of
Table 1. Models whose names start with the same letter
have the same thermodynamical properties. Jet (and ambient) specific
internal energies grow from models A to D. Three different values of
the jet flow Lorentz factor have been considered for models B, C and
D. The other dependent parameters are displayed in Cols. 5-11 of
Table 1. Note that given our choice of
![]() ,
the
ambient media associated with hotter models are also hotter. The next
three columns show the longitudinal wavenumber together with
oscillation frequency and the growth rate of the most unstable first
reflection (body) mode. The following three columns display the same
quantities in the the jet reference frame. The next two columns show the
transversal wavenumbers of linear sound waves in jet and ambient
medium respectively. The last column shows the linear growth rate of
KH instability in the jet reference frame expressed in dynamical time
units, i.e. in which time is scaled to
,
the
ambient media associated with hotter models are also hotter. The next
three columns show the longitudinal wavenumber together with
oscillation frequency and the growth rate of the most unstable first
reflection (body) mode. The following three columns display the same
quantities in the the jet reference frame. The next two columns show the
transversal wavenumbers of linear sound waves in jet and ambient
medium respectively. The last column shows the linear growth rate of
KH instability in the jet reference frame expressed in dynamical time
units, i.e. in which time is scaled to
![]() .
All other
quantities in the table are expressed in units of the ambient
density,
.
All other
quantities in the table are expressed in units of the ambient
density,
![]() ,
the speed of light, c, and the jet radius,
,
the speed of light, c, and the jet radius,
![]() .
.
In order to extend our conclusions to a wider region in the initial parameter space, we have performed a new set of simulations, which will be discussed only in some selected aspects. The initial data for these new simulations are compiled and shown in the lower part of Table 1. The external medium in all cases is that of model A05. From models F to H, internal energy in the jet is increased and rest-mass density decreased in order to keep pressure equilibrium, whereas the jet Lorentz factor is kept equal to its value in model A05.
The initial momentum density in the jet decreases along the sequence A05, F, G, H. Simulations I and J have the same thermodynamical values as models F and G, respectively, but have increasing jet Lorentz factors to keep the same initial momentum density as model A05. Finally, in simulations K and L we exchange the values of the Lorentz factor with respect to those in runs I and J.
The numerical setup for the simulations described in this paper is the
same as in Paper I. We only simulate half of the jet
(x>0) due to the assumed symmetry of perturbations. Reflecting
boundary conditions are imposed on the symmetry plane of the flow,
whereas periodical conditions are settled on both upstream and
downstream boundaries. The applied resolution of
![]() grid
zones per jet radius is chosen for all simulations listed in
Table 1, following the tests described in the Appendix
of Paper I. In the Appendix of this paper we present a discussion of
the influence of different longitudinal resolutions on the simulation
results during the long-term nonlinear evolution. Other details of the
numerical setup are described in Paper I.
grid
zones per jet radius is chosen for all simulations listed in
Table 1, following the tests described in the Appendix
of Paper I. In the Appendix of this paper we present a discussion of
the influence of different longitudinal resolutions on the simulation
results during the long-term nonlinear evolution. Other details of the
numerical setup are described in Paper I.
The steady model is then perturbed according to the selected mode
(the most unstable first reflection mode), with an absolute value of
the pressure perturbation amplitude inside the jet of
![]() .
This means that those models with the smallest
pressure, like model A, have relative perturbations in pressure three
orders of magnitude larger than those with the highest pressures,
D. However this difference seems not to affect the linear and
postlinear evolution (see footnote in Sect. 3).
.
This means that those models with the smallest
pressure, like model A, have relative perturbations in pressure three
orders of magnitude larger than those with the highest pressures,
D. However this difference seems not to affect the linear and
postlinear evolution (see footnote in Sect. 3).
Following the behaviour of simulated models, we found in Paper I that the evolution of the perturbations can be divided into the linear phase, saturation phase and mixing phase. This section is devoted to describing the fully nonlinear evolution of the modes described in Paper I. Our description shares many points with the framework developed by Bodo et al. (1994) for the case of classical jets.
In order to illustrate the growth of perturbations and determine the duration of the linear and saturation phases in our simulations, we plotted in Fig. 1 of Paper I the amplitudes of the perturbations of the longitudinal and transversal velocities inside the jet and in the jet reference frame, together with the pressure oscillation amplitude. We also plotted the growth of the imposed eigenmodes resulting from the linear stability analysis. Both velocity perturbations are transformed from the ambient rest frame to the unperturbed jet rest frame using the Lorentz transformation rules for velocity components.
In Paper I we defined the characteristic times
![]() and
and
![]() as the end of the linear and saturation phases
respectively. At the saturation time, the perturbation structure is
still close to the structure of the initial perturbation, except that
the oblique sound waves forming the perturbation became steeper,
leading to the formation of shock waves. Finally, nearly all the
simulations lead to a sharp peak of the pressure oscillation
amplitude. The times at which this peak appears,
as the end of the linear and saturation phases
respectively. At the saturation time, the perturbation structure is
still close to the structure of the initial perturbation, except that
the oblique sound waves forming the perturbation became steeper,
leading to the formation of shock waves. Finally, nearly all the
simulations lead to a sharp peak of the pressure oscillation
amplitude. The times at which this peak appears,
![]() ,
are
equal to or slightly larger than the saturation times for different
models. The definition of
,
are
equal to or slightly larger than the saturation times for different
models. The definition of
![]() ,
,
![]() and
and
![]() has been illustrated in Fig. 1 of Paper I. Table 2 collects the times of the linear and
saturation phases in the different models (Cols. 2-4) along with
other characteristic times (defined in the table caption and in
Sect. 3.1).
has been illustrated in Fig. 1 of Paper I. Table 2 collects the times of the linear and
saturation phases in the different models (Cols. 2-4) along with
other characteristic times (defined in the table caption and in
Sect. 3.1).
Table 2:
Times for the different phases in the evolution of the
perturbed jet models.
![]() :
end of linear phase (the
amplitudes of the different quantities are not constant any
longer).
:
end of linear phase (the
amplitudes of the different quantities are not constant any
longer).
![]() :
end of saturation phase (the amplitude of the
transverse speed perturbation reaches its maximum).
:
end of saturation phase (the amplitude of the
transverse speed perturbation reaches its maximum).
![]() :
the
tracer starts to spread.
:
the
tracer starts to spread.
![]() :
the peak in the amplitude of
the pressure perturbation is reached.
:
the peak in the amplitude of
the pressure perturbation is reached.
![]() :
external
material reaches the jet axis.
:
external
material reaches the jet axis.
![]() :
the jet has transferred
to the ambient a 1% of its initial momentum.
:
the jet has transferred
to the ambient a 1% of its initial momentum.
![]() :
longitudinal momentum in the jet and the ambient reach
equipartition.
:
longitudinal momentum in the jet and the ambient reach
equipartition.
![]() :
relative value of pressure
oscillation amplitude at the peak (see Fig. 1 of Paper I). Note that,
as a general trend,
:
relative value of pressure
oscillation amplitude at the peak (see Fig. 1 of Paper I). Note that,
as a general trend,
![]() .
.
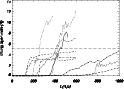 |
Figure 1:
Evolution of the mean width of the jet/ambient mixing layer
with time for all the simulations. Different types of lines are used
for models with different internal energies: Continuous line: model
A; dotted line: model B; dashed line: model C; dashed-dotted line:
model D. Line thickness increases with Lorentz factor (from 5,
thinest line, to 20 thickest one). A value of 5 |
| Open with DEXTER | |
The beginning of the mixing phase can be detected by the spreading
of the tracer contours. This can be seen in Fig. 1,
where the evolution with time of the mean width of the layer with
tracer values between 0.05 and 0.95 is shown. The times at which the
mixing phase starts (
![]() )
are shown in
Table 2. Consistently with the width of the initial
shear layer in our simulations (around 0.1
)
are shown in
Table 2. Consistently with the width of the initial
shear layer in our simulations (around 0.1 ![]() ), we have
defined
), we have
defined
![]() as the time at which the mixing layer exceeds a
width of 0.1
as the time at which the mixing layer exceeds a
width of 0.1 ![]() .
.
For models with the same thermodynamical properties, those with
smaller Lorentz factors start to mix earlier (see
Table 2). Moreover, according to
Fig. 1, the models can be sampled in two (or perhaps
three) categories. Models A05, B05, B10 and D10 have wide (>
![]() )
shear layers which are still in a process of widening at the end
of the simulation. The rest of the models have thiner shear layers
(<
)
shear layers which are still in a process of widening at the end
of the simulation. The rest of the models have thiner shear layers
(<
![]() wide) which are inflating at smaller speeds (
wide) which are inflating at smaller speeds (
![]() ,
in the case of models C05, D05 and C10;
,
in the case of models C05, D05 and C10;
![]() ,
in the case of models B20, C20, and D20). A deeper
analysis of the process of widening of the shear layers as a function
of time shows that all the models undergo a phase of exponential
growth extending from
,
in the case of models B20, C20, and D20). A deeper
analysis of the process of widening of the shear layers as a function
of time shows that all the models undergo a phase of exponential
growth extending from
![]() to soon after
to soon after
![]() .
.
We note that those models developing wider mixing layers are those
in which the peak in the maxima of the pressure perturbation as a
function of time,
![]() ,
reach values of the order of
70-100, with the exception of model B20 that has a thin mixing layer
at the end of the simulation but has
,
reach values of the order of
70-100, with the exception of model B20 that has a thin mixing layer
at the end of the simulation but has
![]() ,
and model D10, which does develop a wide shear layer but for which
,
and model D10, which does develop a wide shear layer but for which
![]() remains small. We also note that (with the
exception of model D10) the models developing wide mixing layers are
those with smaller internal energies and also relatively smaller
Lorentz factors.
remains small. We also note that (with the
exception of model D10) the models developing wide mixing layers are
those with smaller internal energies and also relatively smaller
Lorentz factors.
There are two basic mechanisms that contribute to the process of mixing between ambient and jet materials. The first one is the deformation of the jet surface by large amplitude waves during the saturation phase. This deformation favors the transfer of momentum from the jet to the ambient medium and, at the same time, the entrainment of ambient material in the jet. From Table 2, it is seen that the process of mixing and momentum exchange overlap during the saturation phase.
 |
Figure 2: Evolution of the jet particle fraction showing the development of mixing in two representative models. Left column (model B05): the ambient material carves its way through the jet difficulting the advance of the jet material which is suddenly stopped. Right column (model D05): the amount of ambient matter hampering the jet material is smaller and matter from the jet at the top of the jet crests is ablated by the ambient wind. |
| Open with DEXTER | |
The second mechanism of mixing starts during the transition to the
full non-linear regime and seems to act mainly in those models with
large
![]() .
As we shall see below, this large value of
.
As we shall see below, this large value of
![]() is associated with the generation of a shock at
the jet/ambient interface at
is associated with the generation of a shock at
the jet/ambient interface at
![]() ,
which appears to be the
responsible of the generation of wide mixing layers in those
models. Figure 2 shows a sequence of models with the
evolution of mixing in two characteristic cases, B05 and D05, during
the late lapse of the saturation phase. The evolution of model B05 is
representative of models A05, B05 and B10. Models B20, C05, C10, C20
and D10 have evolutions closer to model D05. As it is seen in
Fig. 2, in the case of model B05 (left column panels), the
ambient material carves its way through the jet difficulting the
advance of the jet material which is suddenly stopped. The result is
the break-up of the jet. In model D05, (right column panels), matter
from the jet at the top of the jet crests is ablated by the
ambient wind forming vortices of mixed material filling the valleys.
,
which appears to be the
responsible of the generation of wide mixing layers in those
models. Figure 2 shows a sequence of models with the
evolution of mixing in two characteristic cases, B05 and D05, during
the late lapse of the saturation phase. The evolution of model B05 is
representative of models A05, B05 and B10. Models B20, C05, C10, C20
and D10 have evolutions closer to model D05. As it is seen in
Fig. 2, in the case of model B05 (left column panels), the
ambient material carves its way through the jet difficulting the
advance of the jet material which is suddenly stopped. The result is
the break-up of the jet. In model D05, (right column panels), matter
from the jet at the top of the jet crests is ablated by the
ambient wind forming vortices of mixed material filling the valleys.
 |
Figure 3:
Pressure distribution at the onset of the jet/ambient surface
distortion at the end of the saturation phase for models A05, B05,
B10 and B20. The corresponding times are 355, 190, 370 and 765
|
| Open with DEXTER | |
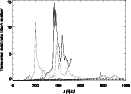 |
Figure 4:
Time evolution of the maxima of the transversal Mach number
of the jet with respect to the unperturbed ambient medium,
|
| Open with DEXTER | |
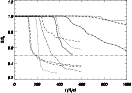 |
Figure 5: Evolution of the total longitudinal momentum in the jet as a function of time for all the simulations. Lines represent the same models than in Fig. 1. The long-dashed horizontal line serves us to identify those models tranferring more than 50% of the initial jet momentum to the ambient. |
| Open with DEXTER | |
The large amplitude of
![]() reached in models A05,
B05 and B10 is clearly associated with a local effect occurring in the
jet/ambient interface (see second panel in the left column of
Figs. 2 and 3) that leads to the jet
disruption. The sequence of events preceding the jet disruption
includes the formation of oblique shocks at the end of the
linear/saturation phase, the local effect in the jet/ambient
interface just mentioned and then a supersonic transversal expansion
of the jet that leads to i) a planar contact discontinuity (see last
panels in the left column of Fig. 2), and ii) the
formation of a shock (see below) that propagates traversally (see
Sect. 3.4). It appears that contrary to the velocity
perturbations in the jet reference frame (see Fig. 1 of Paper I), the
maximum relative amplitudes of pressure perturbation are strongly
dependent on physical parameters of simulations
reached in models A05,
B05 and B10 is clearly associated with a local effect occurring in the
jet/ambient interface (see second panel in the left column of
Figs. 2 and 3) that leads to the jet
disruption. The sequence of events preceding the jet disruption
includes the formation of oblique shocks at the end of the
linear/saturation phase, the local effect in the jet/ambient
interface just mentioned and then a supersonic transversal expansion
of the jet that leads to i) a planar contact discontinuity (see last
panels in the left column of Fig. 2), and ii) the
formation of a shock (see below) that propagates traversally (see
Sect. 3.4). It appears that contrary to the velocity
perturbations in the jet reference frame (see Fig. 1 of Paper I), the
maximum relative amplitudes of pressure perturbation are strongly
dependent on physical parameters of simulations![]() . The origin of the shock in models
with
. The origin of the shock in models
with
![]() ,
that enhances the turbulent
mixing of the jet and ambient fluids, can be found in the nonlinear
evolution of Kelvin-Helmholtz instability that leads to significant
changes of local flow parameters at the end of saturation phase. For
instance, the oblique shock front resulting from the steepening of
sound waves, during the linear and saturation phases (see Figs. 3-6 of
Paper I), crosses the initial shear layer at the interface of jet and
ambient medium. The formation of such oblique shock implies a sudden
and local growth of gradients of all the dynamical quantities at the
jet boundary. The local conditions changed by these oblique shocks may
become favourable for the development of other instabilities like
those discussed by Urpin (2002).
,
that enhances the turbulent
mixing of the jet and ambient fluids, can be found in the nonlinear
evolution of Kelvin-Helmholtz instability that leads to significant
changes of local flow parameters at the end of saturation phase. For
instance, the oblique shock front resulting from the steepening of
sound waves, during the linear and saturation phases (see Figs. 3-6 of
Paper I), crosses the initial shear layer at the interface of jet and
ambient medium. The formation of such oblique shock implies a sudden
and local growth of gradients of all the dynamical quantities at the
jet boundary. The local conditions changed by these oblique shocks may
become favourable for the development of other instabilities like
those discussed by Urpin (2002).
The generation of the shock wave at the jet/ambient interface
is reflected in the evolution of the maxima of
![]() (
(
![]() and
and
![]() being the Lorentz factors
associated with
being the Lorentz factors
associated with
![]() and
and
![]() ,
respectively) representing
the transversal Mach number of the jet with respect to the
unperturbed ambient medium. This quantity becomes larger than 1 around
,
respectively) representing
the transversal Mach number of the jet with respect to the
unperturbed ambient medium. This quantity becomes larger than 1 around
![]() in those models with
in those models with
![]() (see Fig. 4) pointing toward a supersonic expansion of
these jets at the end of the saturation phase. The fact that in all
our simulations the ambient medium surrounding colder models (i.e., A,
B) are also colder (see Sect. 2) favors the generation
of shocks in the jet/ambient interface in these models. On the other
hand, in the case of models with the highest Lorentz factors (B20,
C20, D20) the transversal velocity can not grow far enough to generate
the strong shock which breaks the slower jets.
(see Fig. 4) pointing toward a supersonic expansion of
these jets at the end of the saturation phase. The fact that in all
our simulations the ambient medium surrounding colder models (i.e., A,
B) are also colder (see Sect. 2) favors the generation
of shocks in the jet/ambient interface in these models. On the other
hand, in the case of models with the highest Lorentz factors (B20,
C20, D20) the transversal velocity can not grow far enough to generate
the strong shock which breaks the slower jets.
In order to extend our conclusions to a wider region in the initial parameter space, we have performed supplementary simulations (namely F, G, H, I, J, K, L) with the aim of clarifying the effect of the ambient medium in the development of the disruptive shock appearing after saturation. In all the cases, the external medium is that of model A05.
From models F to H, internal energy in the jet is increased and
rest-mass density decreased in order to keep pressure equilibrium,
whereas the jet Lorentz factor is kept constant to its value in model
A05. The transversal Mach numbers at the peak in these models reach
values very similar to that of model A05 (![]() 14). In fact, the
formation of a shock at the end of the saturation phase is observed in
these models as it is in model A05.
14). In fact, the
formation of a shock at the end of the saturation phase is observed in
these models as it is in model A05.
The initial momentum density in the jet has decreased along the sequence A05, F, G, H. Simulations I and J have the same thermodynamical values as models F and G, respectively, but have increasing jet Lorentz factors to keep the same initial momentum density as model A05. In the case of model I we find the same behavior as in previous ones: large transversal Mach number, shock and disruption. On the contrary, model J behaves much more like model B20, with a value of transversal Mach number slightly larger than one, strong expansion and almost no mixing. Finally, in order to know to which extent this change in behavior was caused by the increase in Lorentz factor or in specific internal energy, in simulations K and L we cross these values with respect to those in I and J. The results from these last simulations show that the evolution of model M is very close to that of model I: the large value of the transversal Mach number at the peak, shock and strong mixing; and that the evolution of model K is close to that of model J: a weaker shock, expansion and no mixing.
In the models developing a shock, mixing is associated with vorticity
generated after the shock formation and, in the case of models A05,
B05, B10 as well as F, G, H, I and L matter from the ambient
penetrates deep into the jet as to reach the jet axis (jet
break-up). The times at which this happens for the different models
are displayed in Table 2. Note that in models A05 and
B05 the entrainment of ambient matter up to the axis occurs just after
![]() ,
whereas in model B10 occurs later, probably because
the shock in this model is weaker. The process of mixing can be
affected by resolution, as small resolutions may suppress the
development of turbulence. We have analyzed this in the Appendix in
which we focus on the influence of longitudinal resolution.
,
whereas in model B10 occurs later, probably because
the shock in this model is weaker. The process of mixing can be
affected by resolution, as small resolutions may suppress the
development of turbulence. We have analyzed this in the Appendix in
which we focus on the influence of longitudinal resolution.
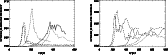 |
Figure 6: Evolution of the total transversal momentum in the jet as a function of time for all the simulations. Lines represent the same models than in Fig. 1. Left panel: models A05, B05, B10, C05, D05. Right panel: B20, C10, C20, D10, D20. Note the change in both horizontal and vertical scales between the two panels. |
| Open with DEXTER | |
 |
Figure 7: Snapshot in the mixing phase of logarithmic maps of pressure, jet mass fraction and specific internal energy and non-logarithmic Lorentz factor for model A05. Only the top half of the jet is shown. |
| Open with DEXTER | |
Let us now analyze the evolution of the longitudinal momentum in the jets as a function of time. Figure 5 shows the evolution of the total longitudinal momentum in the jet for the different models. Jets in models B05, C05, D05 and D10 (also D20) transfer more than 50% of their initial longitudinal momentum to the ambient, whereas models A05, B10 and C10 (also B20) seem to have stopped the process of momentum transfer retaining higher fractions of their respective initial momenta. Models C20 and D20 continue the process of momentum exchange at the end of the simulations but at a remarkable slower rate (specially C20).
 |
Figure 8: Same as Fig. 7 for models B05 ( upper; only top half of the model shown), C05 ( middle) and D05 ( lower). |
| Open with DEXTER | |
In the case of models F, G, H, I and L, the transfer of longitudinal
momentum is also very efficient. The reason why these models, as well
as A05, B05 and B10, develop wide shear layers and transfer more than
50% of their initial momentum to the ambient could be turbulent
mixing triggered by the shock. In the case of models D10 and D20, the
processes of mixing and transfer of longitudinal momentum proceed at a
slower rate pointing to another mechanism. The plots of the time
evolution of the jet's transversal momentum (Fig. 6) for
the different models give us the answer. Jets disrupted by the shock
(as A05, B05, B10) have large relative values of transversal momentum
at saturation (>0.04) that decay very fast afterward (A05 is an
exception). The peak in transversal momentum coincides with the
shock formation and the fast lateral expansion of the jet at
![]() .
Contrarily, models D10 and D20 have a sustained value of
transversal momentum after saturation which could drive the process of
mixing and the transport of longitudinal momentum. In these models,
the originally high internal energy in the jet and the high jet
Lorentz factor (that allows for a steady conversion of jet kinetic
energy into internal) make possible the sustained values of
transversal momentum. Between these two kinds of behavior are hot,
slow
models C05, D05 that do not develop a shock having, then, thin
mixing layers, but transferring more than 50% of their longitudinal
momentum.
.
Contrarily, models D10 and D20 have a sustained value of
transversal momentum after saturation which could drive the process of
mixing and the transport of longitudinal momentum. In these models,
the originally high internal energy in the jet and the high jet
Lorentz factor (that allows for a steady conversion of jet kinetic
energy into internal) make possible the sustained values of
transversal momentum. Between these two kinds of behavior are hot,
slow
models C05, D05 that do not develop a shock having, then, thin
mixing layers, but transferring more than 50% of their longitudinal
momentum.
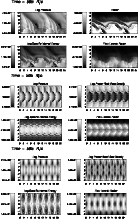 |
Figure 9: Same as Fig. 7 for models B10 ( upper; only top half of the model shown), C10 ( middle) and D10 ( lower; only top half of the model shown). |
| Open with DEXTER | |
Our previous analysis based in the width of the mixing layers and the fraction of longitudinal momentum transfered to the ambient can be used to classify our models:
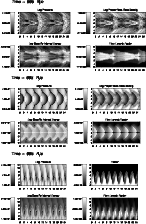 |
Figure 10: Same as Fig. 7 for models B20 ( upper), C20 ( middle) and D20 ( lower; only top half of the model shown). |
| Open with DEXTER | |
At the end of our simulations, the models continue with the processes of mixing, transfer of momentum and conversion ofkinetic to internal energy, however they seem to experience a kind of averaged quasisteady evolution which can be still associated with the evolution of a jet, i.e., a collimated flux of momentum. This jet is always wider, slower and colder than the original one and is surrounded by a broad shear layer. This section is devoted to the examination of the transition layers in distributions of gas density, jet mass fraction and internal energy as well as shearing layers in velocity, longitudinal momentum and Lorentz factor.
Let us start by analyzing the overall structure of the pressure
field for the different models at the end of our
simulations. Figure 11 shows the transversal,
averaged profiles of pressure accross the computational grid. Several
comments are in order. In the case of models A and B, the shock formed
at the end of the saturation phase is seen propagating (at
![]() in the case of model A, and at
in the case of model A, and at
![]() in the
case of models B) pushed by the overpressure of the post shock state.
In the case of models C and D, the wave associated with the peak in the
pressure oscillation amplitude seem to have left the grid (remember
that in our jet models, hotter jets have also hotter ambient
media). The most remarkable feature in the pressure profile is the
depression centered at
in the
case of models B) pushed by the overpressure of the post shock state.
In the case of models C and D, the wave associated with the peak in the
pressure oscillation amplitude seem to have left the grid (remember
that in our jet models, hotter jets have also hotter ambient
media). The most remarkable feature in the pressure profile is the
depression centered at
![]() in the case of models C10 and
C20 and at
in the case of models C10 and
C20 and at
![]() in the case of models D10, D20. These
pressure minima coincides with the presence of vortices (clearly seen
in models C20 and D20 in the corresponding panels of
Figs. 9 and 10). Also remarkable in
these plots is the almost total pressure equilibrium reached by models C05 and D05 and the overpressure of the jet in model D20.
in the case of models D10, D20. These
pressure minima coincides with the presence of vortices (clearly seen
in models C20 and D20 in the corresponding panels of
Figs. 9 and 10). Also remarkable in
these plots is the almost total pressure equilibrium reached by models C05 and D05 and the overpressure of the jet in model D20.
As we noted in the previous section the models evolve following four schemes. Jets belonging to the classes I and II disrupt leading to the dispersion of tracer contours for more than five initial jet radii. Model D20 of the II class is specific. It has not reached the tracer contour dispersion equal to five jet radii, but it clearly follows from Fig. 1 that this should happen around t=1100. The models belonging to the classes III and IV do not exhibit the dispersion of tracer contours for more than 5 jet radii and look different at the end of simulations.
Figure 12 displays, for models B05 and D05 representing classes I/II and III/IV respectively, the profiles of relevant physical quantities averaged along the jet at the end of the simulations. Let us note that different shear (in case of velocity related quantities) or transition layers (in case of material quantities) can be defined depending on the physical variable used.
 |
Figure 11: Longitudinal averaged profiles of gas pressure for all models. Different types of lines are used for models with different internal energies: Continuous line: model A; dotted line: model B; dashed line: model C; dashed-dotted line: model D. Line thickness increases with Lorentz factor (from 5, thinest line, to 20 thickest one). |
| Open with DEXTER | |
In case of model B05 all the material quantities (tracer, density
and internal energy) exhibit a wide broadening in the radial
direction. The distribution of tracer extends up to
![]() ,
which
means that jet material has been spread up to this radius, with a
simultaneous entrainment of the ambient material into the jet
interior. The latter effect is indicated by the lowering of the
maximum tracer value from 1 down to 0.4. The fine structure of the
tracer distribution displays random variations, which apparently
correspond to the turbulent flow pattern well seen in
Fig. 8 (upper set of panels). The curve of internal
energy is very similar to the one corresponding to tracer, however
variations are seen up to
,
which
means that jet material has been spread up to this radius, with a
simultaneous entrainment of the ambient material into the jet
interior. The latter effect is indicated by the lowering of the
maximum tracer value from 1 down to 0.4. The fine structure of the
tracer distribution displays random variations, which apparently
correspond to the turbulent flow pattern well seen in
Fig. 8 (upper set of panels). The curve of internal
energy is very similar to the one corresponding to tracer, however
variations are seen up to
![]() .
The profile of density is wider
than the profile of the tracer (the density is growing up to
.
The profile of density is wider
than the profile of the tracer (the density is growing up to
![]() ,
which can be explained by the heating of external medium, in the
jet neighborhood, by shocks associated with outgoing large amplitude
sound waves and by transversal momentum transmitted to the ambient
medium via sound waves. Finally, the profile of the specific
internal energy is consistent with the density profile and the fact of
the jet being in almost pressure equilibrium.
,
which can be explained by the heating of external medium, in the
jet neighborhood, by shocks associated with outgoing large amplitude
sound waves and by transversal momentum transmitted to the ambient
medium via sound waves. Finally, the profile of the specific
internal energy is consistent with the density profile and the fact of
the jet being in almost pressure equilibrium.
The dash-dot curve in Fig. 12 (top left panel)
represents the (internal) energy per unit volume held in jet matter.
Such a quantitiy, like the mean Lorentz factors in both inner jet and
shear layer are of special importance as they are directly related
to the emission properties of the model. Internal energy density in
jet particles is related to the fluid rest frame synchrotron
emissivity, whereas the fluid Lorentz factor governs the Doppler boosting
of the emitted radiation. As seen in the top right panel of
Fig. 12, the final mean profile of velocity is
similar in shape to the profile of internal energy, despite the fact
that it is smoother. Similarly to internal energy, the longitudinal
velocity variations extend up to
![]() .
This can be understood in
terms of large amplitude, nonlinear sound waves, which contribute to
the transport of internal and kinetic energies in the direction
perpendicular to the jet axis. The profiles of Lorentz factor and
longitudinal momentum are significantly narrower. Therefore in case
of models similar to B05 only the the most internal part, up to
.
This can be understood in
terms of large amplitude, nonlinear sound waves, which contribute to
the transport of internal and kinetic energies in the direction
perpendicular to the jet axis. The profiles of Lorentz factor and
longitudinal momentum are significantly narrower. Therefore in case
of models similar to B05 only the the most internal part, up to
![]() of the wide sheared jet, will be Doppler boosted, even
though the jet material quantities extend behind
of the wide sheared jet, will be Doppler boosted, even
though the jet material quantities extend behind
![]() .
.
A similar discussion can be performed for the model D05 representing
the other group of jets, which form a shear layer without experiencing
the phase of rapid disruption. As seen in the bottom panels of
Fig. 12, the jet of model D05 preserves sharp
boundaries between their interior and the ambient medium, although
both media are modified by the dynamical evolution at earlier
phases. The sharp boundary (transition layer) at
![]() is
apparent in the plots of all material quantities, i.e. tracer,
density, internal energy. The thickness of the transition layer for
all the quantities is comparable to one initial jet radius, 10 times
narrower than in case of B05. We note, however a smooth change of
ambient gas density in the range of
is
apparent in the plots of all material quantities, i.e. tracer,
density, internal energy. The thickness of the transition layer for
all the quantities is comparable to one initial jet radius, 10 times
narrower than in case of B05. We note, however a smooth change of
ambient gas density in the range of
![]() .
.
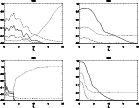 |
Figure 12:
Transversal averaged profiles of relevant physical quantities
at the end of simulations B05 and D05. Left column: tracer, f (full
line), rest mass density, |
| Open with DEXTER | |
Concerning the dynamical quantities, we note that there is no sharp
jump in the profiles of longitudinal velocity, Lorentz factor and
longitudinal momentum and the central core does not appear in profiles
of these quantities. Significant longitudinal velocities extend up to
![]() as in case of density, in contrast to tracer and
internal energy. As noted previously, the averaged pressure
distribution for model D05 is practically uniform in the whole
presented range of the transversal coordinate. Therefore as in case
B05 we can conclude that the variations of density in the ambient
medium are due to the heat deposited by nonlinear sound waves. On the
other hand the widths of the profiles of the Lorentz factor and
longitudinal momentum are comparable to those of jet mass fraction and
specific internal energy. Then the emission of the whole jet volume
will be Doppler boosted.
as in case of density, in contrast to tracer and
internal energy. As noted previously, the averaged pressure
distribution for model D05 is practically uniform in the whole
presented range of the transversal coordinate. Therefore as in case
B05 we can conclude that the variations of density in the ambient
medium are due to the heat deposited by nonlinear sound waves. On the
other hand the widths of the profiles of the Lorentz factor and
longitudinal momentum are comparable to those of jet mass fraction and
specific internal energy. Then the emission of the whole jet volume
will be Doppler boosted.
Models B05 and D05 were considered as representative cases of models
developing shear layers wider (group 1; classes I and II) and narrower
(group 2; classes III and IV), respectively, than
![]() .
Now the
question is up to which extent the characteristics of the shearing
flow of these two models are common to the models in the corresponding
groups. We note that given the large differences between the
initial parameters of models in classes I and II, on one hand, and III
and IV, on the other, we do not expect a perfect match among the
properties of the transversal structure in models within the same
group. For example, whereas models in class I develop wide shear
layers due to the action of a strong shock formed at the end of the
saturation phase, models in class II develop shear layers through a
continuous injection of transversal momentum and the generation of
large vortices at the jet ambient interface.
.
Now the
question is up to which extent the characteristics of the shearing
flow of these two models are common to the models in the corresponding
groups. We note that given the large differences between the
initial parameters of models in classes I and II, on one hand, and III
and IV, on the other, we do not expect a perfect match among the
properties of the transversal structure in models within the same
group. For example, whereas models in class I develop wide shear
layers due to the action of a strong shock formed at the end of the
saturation phase, models in class II develop shear layers through a
continuous injection of transversal momentum and the generation of
large vortices at the jet ambient interface.
We now investigate relations among the following averaged quantities
in the whole set of models at the final state: the dispersion of
tracer contours, the typical widths of profiles of density, internal
energy density in jet matter (re), velocity, Lorentz factor
(![]() )
and longitudinal momentum (rS) and the peak values of
Lorentz factor and the longitudinal momentum (
)
and longitudinal momentum (rS) and the peak values of
Lorentz factor and the longitudinal momentum (
![]() ). In all
cases the peak values were measured directly, whereas the typical
width of the profiles were taken as their width at the mean value
between the maximum and minimum ones. We find that for all models of
group 1,
). In all
cases the peak values were measured directly, whereas the typical
width of the profiles were taken as their width at the mean value
between the maximum and minimum ones. We find that for all models of
group 1,
![]() ,
,
![]() ,
,
![]() and
S/S0
< 0.2. In case of all models of group 2,
and
S/S0
< 0.2. In case of all models of group 2,
![]() ,
,
![]() ,
,
![]() and
and
![]() .
.
We have studied the non-linear evolution of the relativistic planar jet models considered in Paper I. The initial conditions considered cover three different values of the jet Lorentz factor (5, 10, 20) and a few different values of the jet specific internal energy (from 0.08c2 to 60.0c2). The models have been classified into four classes (I to IV) with regard to their evolution in the nonlinear phase, characterized by the process of mixing and momentum transfer. Cold, slow jets (class I) develop a strong shock in the jet/ambient interface at the end of the saturation phase leading to the development of wide, mixed, shear layers. Hot fast models (class II) develop wide shear layers formed by distinct vortices and transfer more than 50% of the longitudinal momentum to the ambient medium. In models within this class, the high Lorentz factor in the original jet and its high internal energy act as a source of transversal momentum that drives the process of mixing and momentum transfer. Between these classes we find hot, slow models (class III) that have intermediate properties. Finally we have found warm and fast models (class IV) as the most stable. Whether a jet is going to develop a strong shock and be suddenly disrupted seems to be encoded in the peak of the pressure oscillation amplitude at the end of the saturation phase and the related transversal Mach number.
The above picture is clarifying but is subject to the limitations of
our choice of initial parameters that was restricted to values with
![]() (see Paper I). This restriction together with
the initial pressure equilibrium lead to a constant jet-to-ambient
ratio of specific internal energies for all the models, i.e., hotter
jets are surrounded by hotter ambient media. In order to extend our
conclusions to a wider region in the initial parameter space, we have
performed a supplementary set of simulations (F-L) with the aim of
disentangling the effect of the ambient medium in the development of
the disruptive shock appearing after saturation. Thus,
hot, tenuous, slow/moderately fast
jets (F, G, H, I, L) behave like cold, dense ones in a cold
environment (A05, B05, B10). However, if these hot, tenuous jets are
faster (J, K), they behave as warm, fast models (e.g., C10, C20,
B20). The fact that the initial Lorentz factor is high seems to prevent
the transversal velocity from growing enough to generate the strong shock
which breaks the slower jets.
(see Paper I). This restriction together with
the initial pressure equilibrium lead to a constant jet-to-ambient
ratio of specific internal energies for all the models, i.e., hotter
jets are surrounded by hotter ambient media. In order to extend our
conclusions to a wider region in the initial parameter space, we have
performed a supplementary set of simulations (F-L) with the aim of
disentangling the effect of the ambient medium in the development of
the disruptive shock appearing after saturation. Thus,
hot, tenuous, slow/moderately fast
jets (F, G, H, I, L) behave like cold, dense ones in a cold
environment (A05, B05, B10). However, if these hot, tenuous jets are
faster (J, K), they behave as warm, fast models (e.g., C10, C20,
B20). The fact that the initial Lorentz factor is high seems to prevent
the transversal velocity from growing enough to generate the strong shock
which breaks the slower jets.
Models undergoing qualitatively different non-linear evolution are clearly grouped in well-separated regions in a jet Lorentz factor/jet-to-ambient enthalpy diagram (see Fig. 13). Models in the lower, left corner (low Lorentz factor and small enthalpy ratio) are those disrupted by a strong shock after saturation. Those models in the upper, left corner (small Lorentz factor and hot) represent a relatively stable region. Those in the upper right corner (large Lorentz factor and enthalpy ratio) are unstable although the process of mixing and momentum exchange proceeds on a longer time scale due to a steady conversion of kinetic to internal energy in the jet. Finally, those in the lower, right region (cold/warm, tenuous, fast) are stable in the nonlinear regime.
 |
Figure 13: Square root of the jet-to-ambient enthalpy ratio (see Paper I for definitions) versus jet Lorentz factor. Symbols represent different non-linear behaviors: crosses stand for shock disrupted jets (cold, slow jets, along with tenuous, hot, moderately fast or slow ones); diamonds for unstable, hot, fast jets; triangles for relatively stable hot, slow, and squares for stable, warm, fast, along with hot, tenuous, faster jets. |
| Open with DEXTER | |
Our results differ from those of Martí et al. (1997), Hardee et al. (1998) and Rosen et al. (1999) who found fast, hot jets as the more stable. The explanation given by Hardee et al. (1998) invoking the lack of appropriate perturbations to couple to the unstable modes could be partially true as fast, hot jets do not generate overpressured cocoons that let the jet run directly into the nonlinear regime. However, as pointed out in Paper I, the high stability of hot jets may have been caused by the lack of radial resolution, that leads to a damping in the perturbation growth rates. Finally, the simulations performed in the aforementioned papers only covered about one hundred time units, well inside the linear regime of the corresponding models for small perturbations. In this paper, the problem of the stability of relativistic jets is analyzed on the basis of long-term simulations that extend over the fully nonlinear evolution of KH instabilities.
At the end of our simulations, the models continue with the processes of mixing, transfer of momentum and conversion of kinetic to internal energy, however they seem to experience a kind of averaged quasisteady evolution which can be still associated with the evolution of a jet, i.e., a collimated flux of momentum. This jet is always wider, slower and colder than the original one and is surrounded by a distinct shear layer. Hence transversal jet structure naturally appears as a consequence of KH perturbation growth. The widths of these shear (in case of velocity related quantities) or transition layers (in case of material quantities) depend on the specific parameters of the original jet model as well as the physical variable considered. However, models in classes III and IV develop thin shear layers, whereas the shear layers of models in classes I and II are wider. The possible connection of these results to the origin of the FRI/FRII morphological dichotomy of jets in extended radiosources will be the subject of further research. Extensions of the present study to models with a superposition of perturbations, cylindrical symmetry and three dimensions are currently underway.
Acknowledgements
The authors want to thank H. Sol for clarifying discussions during earlier phases of development of this work. This work was supported in part by the Spanish Dirección General de Enseñanza Superior under grant AYA-2001-3490-C02 and by the Polish Committee for Scientific Research (KBN) under grant PB 404/P03/2001/20. M.H. acknowledges financial support from the visitor program of the Universidad de Valencia. M.P. has benefited from a predoctoral fellowship of the Universidad de Valencia (V Segles program).
In order to be aware of the limitations of the resolution used in
the results for the non-linear regime, we repeated model C05 (C16
here) with the same transversal resolution (400 cells/![]() )
and
changing the longitudinal resolution. First we double it (32
cells
)
and
changing the longitudinal resolution. First we double it (32
cells
![]() ,
C32) and then multiply it by four (64 cells
,
C32) and then multiply it by four (64 cells
![]() ,C64), and finally, in order to have similar resolutions in both
transversal and longitudinal directions, we performed this simulation
using
,C64), and finally, in order to have similar resolutions in both
transversal and longitudinal directions, we performed this simulation
using
![]() cells
cells
![]() (C128). Models C16, C32 and C64
were evolved up to a time larger than 600
(C128). Models C16, C32 and C64
were evolved up to a time larger than 600
![]() ,
whereas model C128
was stopped at
,
whereas model C128
was stopped at
![]() .
.
Table A.1 displays the data corresponding to
Table 2 for models C16, C32, C64, C128. Differences in
the duration of the phases are apparent but not significant. Regarding
the linear regime, perturbations in models C32 and C64 grow closer to
linear predictions (growth rate 0.093
![]() )
in both cases; to
be compared with the analytical value 0.114
)
in both cases; to
be compared with the analytical value 0.114
![]() )
rather
than C16 (0.085
)
rather
than C16 (0.085
![]() ). C128 has a slower growth rate (0.073
). C128 has a slower growth rate (0.073
![]() )
due to its smaller transversal resolution (see Appendix
of Paper I). Values of pressure perturbation at the peak range from 3
to 8, increasing generally from smaller to larger longitudinal resolution.
Moreover, transversal relativistic Mach numbers are also increasing
with resolution (from a value of about unity to two), so that we
observe a stronger, although still weak, shock in C64 and C128 than in C16
or C32. This is maybe due either to the instability giving
rise to the shock (see Sect. 3.1) being better captured
with increasing resolution or as the result of a smaller numerical
viscosity.
)
due to its smaller transversal resolution (see Appendix
of Paper I). Values of pressure perturbation at the peak range from 3
to 8, increasing generally from smaller to larger longitudinal resolution.
Moreover, transversal relativistic Mach numbers are also increasing
with resolution (from a value of about unity to two), so that we
observe a stronger, although still weak, shock in C64 and C128 than in C16
or C32. This is maybe due either to the instability giving
rise to the shock (see Sect. 3.1) being better captured
with increasing resolution or as the result of a smaller numerical
viscosity.
Figure A.1 shows the time evolution of the mean width of
the jet/ambient mixing layer and the total longitudinal momentum in
the jet for model C05 as a function of resolution. No noticeable
differences are found in the evolution of the different numerical
simulations within the linear phase (up to
![]() ). However, there is a clear tendency to develop wider mixing
layers and enhance momentum transfer in thosesimulations with higher
numerical resolutions as a result of the reduction of numerical
viscosity. In the case of model C128 the processes of jet/ambient
mixing and momentum exchange are further enhanced by the ratio of
longitudinal to transversal resolution close to unity which favors the
generation of vortices in the jet/ambient boundary. The enhancement of
mixing with numerical resolution and the generation of vortices in
model C128 is seen in the sequence of
Figs. A.2-A.3 displaying several jet
properties (pressure, specific internal energy, flow Lorentz factor
and tracer) at
). However, there is a clear tendency to develop wider mixing
layers and enhance momentum transfer in thosesimulations with higher
numerical resolutions as a result of the reduction of numerical
viscosity. In the case of model C128 the processes of jet/ambient
mixing and momentum exchange are further enhanced by the ratio of
longitudinal to transversal resolution close to unity which favors the
generation of vortices in the jet/ambient boundary. The enhancement of
mixing with numerical resolution and the generation of vortices in
model C128 is seen in the sequence of
Figs. A.2-A.3 displaying several jet
properties (pressure, specific internal energy, flow Lorentz factor
and tracer) at
![]() ,
the last computed time for model C128. Models C16 and C32 are very similar, whereas models C64 and C128
are totally mixed (see the maxima of the tracer values in the scales)
and colder (as a result of the enhanced mixing with the cold ambient
medium).
,
the last computed time for model C128. Models C16 and C32 are very similar, whereas models C64 and C128
are totally mixed (see the maxima of the tracer values in the scales)
and colder (as a result of the enhanced mixing with the cold ambient
medium).
Table A.1: Times for different phases in the evolution of simulations C16, C32, C64 and C128. See Table 2 for the meaning of the times at the table entries.
| |
Figure A.1: Same plots as 1 ( left) and 5 ( right) for models C16 (solid line), C32 (dotted line), C64 (dashed line) and C128 (dash-dotted line). |
 |
Figure A.2:
Snapshots at
|
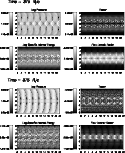 |
Figure A.3: Same as Fig. A.2 for models C64 ( upper) and C128 ( lower). |
Finally, Fig. A.4 shows mean transversal profiles of
relevant physical quantities at
![]() for models C16
and C128. The thin, hot core in model C16 disappears in model C128
due to the enhanced mixing. In model C32 mixing down to the axis
occurs after a long process. Models C64 and C128 develop weak shocks
after saturation and suffer sudden mixing, which goes on in time,
cooling down the remaining relativistic flow. Transition layers in
rest mass density, jet mass fraction and specific internal energy are
wider in model C128 due to the enhanced mixing. Longitudinal velocity
and momentum and Lorentz factor profiles are more similar in all the
cases although the relativistic core is thinner in model C128.
for models C16
and C128. The thin, hot core in model C16 disappears in model C128
due to the enhanced mixing. In model C32 mixing down to the axis
occurs after a long process. Models C64 and C128 develop weak shocks
after saturation and suffer sudden mixing, which goes on in time,
cooling down the remaining relativistic flow. Transition layers in
rest mass density, jet mass fraction and specific internal energy are
wider in model C128 due to the enhanced mixing. Longitudinal velocity
and momentum and Lorentz factor profiles are more similar in all the
cases although the relativistic core is thinner in model C128.