M. Perucho1 - M. Hanasz2 - J. M. Martí1 - H. Sol3
1 - Departamento de Astronomía y Astrofísica,
Universidad de Valencia, 46100 Burjassot, Spain
2 - Torun Centre for Astronomy, Nicholas Copernicus
University, 97-148 Piwnice k. Torunia, Poland
3 - LUTH,
Observatoire de Paris-Meudon, Pl. J. Jansen 5, Meudon
92195, France
Received 27 February 2004 / Accepted 11 July 2004
Abstract
The effects of relativistic dynamics and thermodynamics in
the development of Kelvin-Helmholtz instabilities in planar,
relativistic jets along the early phases (namely linear and saturation
phases) of evolution has been studied by a combination of linear
stability analysis and high-resolution numerical simulations for the
most unstable first reflection modes in the temporal approach. Three
different values of the jet Lorentz factor (5, 10 and 20) and a few
different values of specific internal energy of the jet matter (from
0.08 to 60.0 c2) have been considered. Figures
illustrating the evolution of the perturbations are also shown.
Our simulations reproduce the linear regime of evolution of the excited eigenmodes of the different models with a high accuracy. In all the cases the longitudinal velocity perturbation is the first quantity that departs from the linear growth when it reaches a value close to the speed of light in the jet reference frame. The saturation phase extends from the end of the linear phase up to the saturation of the transversal velocity perturbation (at approximately 0.5c in the jet reference frame). The saturation times for the different numerical models are explained from elementary considerations, i.e. from properties of linear modes provided by the linear stability analysis and from the limitation of the transversal perturbation velocity. The limitation of the components of the velocity perturbation at the end of the linear and saturation phases allows us to conclude that the relativistic nature of the flow appears to be responsible for the departure of the system from linear evolution.
The high accuracy of our simulations in describing the early stages of evolution of the KH instability (as derived from the agreement between the computed and expected linear growth rates and the consistency of the saturation times) establishes a solid basis to study the fully nonlinear regime, to be done elsewhere. The present paper also sets the theoretical and numerical background for these further studies.
Key words: galaxies: jets - hydrodynamics
Relativistic jets are found in many astrophysical objects like active galactic nuclei (see e.g. Zensus 1997), microquasars (Mirabel & Rodriguez 1999) and gamma-ray bursts (Sari et al. 1999). The basic physical property of jets is their huge flux of kinetic energy, taken away from compact unresolved or marginally resolved central regions. The presence of jets in such objects provides a unique opportunity to study the physics of these central regions through investigations of the jet flows. However, the extraction of information about the central object is not a simple task, because jets interact in complex ways with the surrounding interstellar and intergalactic medium. On one hand the dynamical interaction of the jet matter with the ambient medium leads to the formation of shocks, turbulence, acceleration of charged particles and subsequent emission of a broad-range electromagnetic radiation, which makes jets observable. On the other hand the complex nature of the interaction which is due to the presence of flow instabilities, especially the Kelvin-Helmholtz (KH) instability, makes it difficult to distinguish those properties which are directly related to the central object from those which are due to the interaction of jets with the ambient medium. As an example one can invoke the wavelike patterns in jets, which may result from the precession of the rotation axis of the accretion disk at the jet base, or from KH instability, which finds favorable conditions at the interface of jet and external medium (Trussoni et al. 1983). Very recently, the KH instability theory has been successfully used to interpret the structure of the pc-scale jet in the radio source 3C 273 (Lobanov & Zensus 2001).
At kiloparsec scales, the surprisingly stable propagation of relativistic jets in some sources (e.g., Cyg A) contrasts with the deceleration and decollimation observed in other sources (e.g., 3C 31). These two sources are representative examples of two kinds, which are classified into Fanaroff-Riley type I (FRI) and Fanaroff-Riley type II (FRII) radio sources (Fanaroff & Riley 1974). The morphological dichotomy of FRI and FRII sources may be related to the stability properties of relativistic jets with different kinetic powers.
This complex situation motivated us to study the interaction of relativistic jets with their ambient medium and more specifically the KH instability in detail, by applying a linear stability analysis along with numerical simulations.
The linear analysis of KH instability in relativistic jets started with the work of Turland & Scheuer (1976) and Blandford & Pringle (1976) who derived and solved a dispersion relation for a single plane boundary between the relativistic flow and the ambient medium. Next, Ferrari et al. (1978) and Hardee (1979) examined properties of KH instability in relativistic cylindrical jets by following the derivation of the dispersion relation in the nonrelativistic case, in the vortex sheet approximation, done by Gill (1965). They numerically solved the dispersion relation, found unstable KH modes and classified them into the fundamental (surface) and reflection (body) family of modes. The classification is related to the number of nodes, across the jet, of sound waves reflecting in between jet boundaries. An internal wave pattern is formed by the composition of oblique waves, for which the jet interior is a resonant cavity. The physical meaning of KH instability in supersonic jets has been discussed by Payne & Cohn (1985), who have shown that the presence of instability is associated with the overreflection of soundwaves (the modulus of reflection coefficient is larger than 1) on the sheared jet boundaries.
Subsequent studies include effects of magnetic field (Ferrari et al. 1981), the effects of the shear layer, replacing the vortex sheet in the nonrelativistic planar case (Ferrari et al. 1981; Ray 1982; Choudhury & Lovelace 1984), and conical and cylindrical jet geometry (Birkinshaw 1984; Hardee 1984, 1986, 1987). The effects of cylindrical a shear layer have been examined by Birkinshaw (1991) in the nonrelativistic case, attempted by Urpin (2002) in the relativistic case and the presence of multiple components (jet + sheath + ambient medium) was investigated by Hanasz & Sol (1996, 1998). Other authors have investigated current-driven modes in magnetized jets (Appl & Camenzind 1992; Appl 1996) in addition to KH modes.
An extension of the linear stability analysis in the relativistic case to the weakly nonlinear regime has been performed by Hanasz (1995) and led to the conclusion that Kelvin-Helmholtz instability saturates at finite amplitudes due to various nonlinear effects. An explanation of the nature of the mentioned nonlinearities has been proposed by Hanasz (1997). The most significant effect results from the relativistic character of the jet flow, namely from the fact that the velocity perturbation cannot exceed the speed of light.
A more recent approach is to perform a linear stability analysis in parallel with numerical simulations and to compare the results of both methods in the linear regime and then to follow the nonlinear evolution of the KH instability resulting from numerical simulations. Hardee & Norman (1988) and Norman & Hardee (1988) have made such a study for nonrelativistic jets in the spatial approach and Bodo et al. (1994) in the temporal approach. In the relativistic case this kind of approach was applied for the first time by Hardee et al. (1998) in the case of axisymmetric, cylindrical jets and then extended to the 3D case by Hardee et al. (2001).
Similarly to the linear stability analysis, the numerical simulations of jet evolution can be performed following both the spatial and the temporal approach, depending on the particular choice of initial and boundary conditions. In the temporal approach one considers a short slice of jet limited by periodic boundaries along the jet axis, and adds some specific perturbation, e.g. an eigenmode resulting from the linear stability analysis. Due to the periodic boundary conditions the growing perturbations can only be composed of modes having a wavelength equal to the length of the computational box and/or its integer fractions (Bodo et al. 1994, 1995, 1998). Whereas the spatial approach appears more appropriate to analyze the global dynamics and morphology of the whole jet, the temporal approach is suitable for the comparison between the numerical results and analytical studies of the jet stability because, due to the fact that only part of the jet is simulated, a high effective numerical resolution is achievable with limited computer resources.
Numerical simulations (Martí et al. 1997; Hardee et al. 1998; Rosen et al. 1999) demonstrate that jets with high Lorentz factors and high internal energy are influenced very weakly by the Kelvin-Helmholtz instability. Moreover, Hardee et al. (1998), Rosen et al. (1999) note that contrary to the cases with lower Lorentz factors and lower internal energies, the relativistically hot and high Lorentz factor jets do not develop modes of KH instability predicted by the linear theory. They interpret this fact as the result of a lack of appropriate perturbations generating the instability in the system. In the limit of high internal energies of the jet matter the Kelvin-Helmholtz instability is expected to develop with the highest growth rate.
In this paper we focus on the role of internal energy and the Lorentz factor for the stability of relativistic planar two-dimensional jets in the temporal approach. We chose this simple configuration in order to enhance our ability to understand the complex nonlinear evolution of the unstable KH modes in relativistic jets. For this purpose, we perform a linear analysis of the KH instability and construct perturbations analytically: the eigenmodes of the linear problem representing the most unstable first reflection mode for each set of jet parameters. These modes are then incorporated as initial states of numerical simulations. The choice of planar two-dimensional jets allows us to study symmetric and antisymmetric modes of KH instability which resemble, respectively, pinch and helical modes of cylindrical jets. Only the flutting modes of cylindrical jets, corresponding to azimuthal wavenumbers larger than 1, have no counterparts among the eigenmodes of planar two-dimensional jets. In the present paper we investigate only the symmetric modes.
![\begin{figure}
\par\includegraphics[angle=270,width=10.6cm,clip]{0349fi1.ps}\end{figure}](/articles/aa/full/2004/44/aa0349-04/Timg26.gif) |
Figure 1: The geometry of the flow considered in the linear stability analysis and the numerical simulations, including a description of the boundary conditions. |
| Open with DEXTER | |
Our aim is to investigate physical details of the process of transition of KH instability modes from the linear to the nonlinear regime. In the next step (Paper II) we shall investigate the relations of long-term nonlinear evolution of KH instability (including the mixing phase and the properties of the evolved flow at the end of our simulations) on the initial jet parameters.
The paper is organized as follows. In Sect. 2 we describe our method, i.e. perform the linear analysis of the KH instability for the relativistic planar case, then define perturbations and describe numerical algorithm and other details of numerical simulations. In Sect. 3 we present and discuss results of the both linear stability analysis and the numerical simulations. In Sect. 4 we summarize and conclude our paper.
Following the standard procedure (see e.g. Gill 1965; Ferrari et al. 1978; Hardee 1979) we derive the dispersion relation for the Kelvin-Helmholtz modes. We focus on the simplest geometrical configuration of two-dimensional planar relativistic jets and apply the temporal stability analysis.
The full set of equations describing the current problem consists of
the set of relativistic equations of hydrodynamics for a perfect fluid, (e.g.
Ferrari et al. 1978)
The assumed geometry of the jet considered in the forthcoming linear
stability analysis and the numerical simulations is sketched in
Fig. 1.
First of all the considered jet is 2D-planar and
symmetric with respect to the x=0 plane. The flow in the jet moves
in the positive z direction and its matter forms a contact
discontinuity (a vortex sheet) with the matter of external medium at
![]() and
and
![]() .
From now on all quantities
representing the jet will be assigned with the "j'' subscript and the
quantities representing the ambient medium will be assigned with
"a''.
.
From now on all quantities
representing the jet will be assigned with the "j'' subscript and the
quantities representing the ambient medium will be assigned with
"a''.
The following matching conditions are imposed on the interface
between the jet and the ambient medium
In addition, the Sommerfeld radiation condition (expressing the disappearance of perturbations at the infinity) will be applied for linear perturbations.
We assume that the initial state is an equilibrium
configuration. The initial equilibrium can be described by the
following set of independent parameters: the Lorentz factor
corresponding to the unperturbed longitudinal jet velocity, ![]() ,
,
![]() ,
the particle rest mass density
of the jet
,
the particle rest mass density
of the jet
![]() (the particle rest mass density of the ambient
medium is normalized to unity:
(the particle rest mass density of the ambient
medium is normalized to unity:
![]() )
and the specific
internal energy of the jet
)
and the specific
internal energy of the jet
![]() .
The ambient medium is
assumed to be at rest (
.
The ambient medium is
assumed to be at rest (
![]() ).
).
The other dependent parameters describing the equilibrium state are:
the internal jet Mach number
![]() corresponding
to the initial jet longitudinal velocity, the relativistic rest mass
density contrast
corresponding
to the initial jet longitudinal velocity, the relativistic rest mass
density contrast
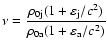 (or, equivalently, the enthalpy
contrast
(or, equivalently, the enthalpy
contrast
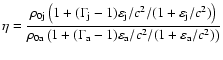 )
and the specific internal energy of
the ambient medium
)
and the specific internal energy of
the ambient medium
![]() ,
which is related
to the specific internal energy of the jet through the pressure
balance condition.
,
which is related
to the specific internal energy of the jet through the pressure
balance condition.
The first step towards the dispersion relation is to reduce the
Eqs. (1)-(5) to the dimensionless form
through the normalization of spatial coordinates to the jet radius
![]() ,
velocities to the sound speed of the jet material
,
velocities to the sound speed of the jet material
![]() ,
time to the dynamical time
,
time to the dynamical time
![]() and pressure to the
equilibrium pressure.
and pressure to the
equilibrium pressure.
The next step is to decompose each dependent quantity into the
equilibrium value and the linear perturbation. After the reduction of
equations to the dimensionless form and substitution of the perturbed
quantities in Eqs. (1)-(5), we obtain the
following set of dimensionless linearized equations. In the following
the dimensionless quantities will be assigned the same symbols as
the previous dimensional ones. The subscript "1'' stands for the
linear perturbation of the corresponding variable. For the jet medium
we get
The next step is to substitute perturbations of the form
with
![]() to describe
waves propagating in positive and negative x-directions in the beam.
Here we use
to describe
waves propagating in positive and negative x-directions in the beam.
Here we use
![]() and
and
![]() for longitudinal and
transverse wavenumbers. Perturbations in the external medium are of
the form
for longitudinal and
transverse wavenumbers. Perturbations in the external medium are of
the form
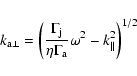 |
(18) |
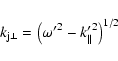 |
(19) |
The corresponding perturbation of the jet surface can be written as
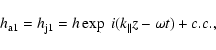 |
(20) |
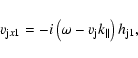 |
(21) |
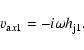 |
(22) |
The above dispersion relation is solved numerically with the aid of
the Newton-Raphson method (see, e.g., Press et al. 1992). In this way
we obtain the complex frequency as a function of the parallel
component of the wavenumber
![]() ,
since we choose the
temporal stability analysis for the present investigations.
,
since we choose the
temporal stability analysis for the present investigations.
Once the solutions of the dispersion relation ![]() are found,
the derivation of eigenstates of the system is straightforward. By
utilizing the set of relativistic Eqs. (6)-(9) one can relate perturbations of gas density and
velocity to the perturbation of pressure.
are found,
the derivation of eigenstates of the system is straightforward. By
utilizing the set of relativistic Eqs. (6)-(9) one can relate perturbations of gas density and
velocity to the perturbation of pressure.
First, we choose the amplitude of the pressure wave in the jet,
![]() ,
as a free constant and then relate the other constants to its
value. The corresponding "-'' amplitudes are computed by multiplying
these values by s in case of pressure and longitudinal velocity and
by -s in the case of transversal velocity.
,
as a free constant and then relate the other constants to its
value. The corresponding "-'' amplitudes are computed by multiplying
these values by s in case of pressure and longitudinal velocity and
by -s in the case of transversal velocity.
The amplitude of pressure wave in the ambient medium,
![]() ,
is
found from the pressure matching condition at x=1:
,
is
found from the pressure matching condition at x=1:
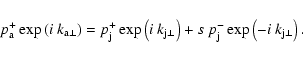 |
(24) |
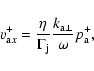 |
(25) |
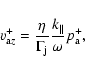 |
(27) |
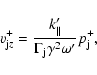 |
(28) |
Regarding specific internal energy and rest-mass density,
perturbations are calculated as follows:
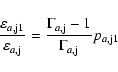 |
(29) |
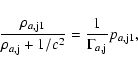 |
(30) |
In the forthcoming discussion of results of numerical simulations we
shall analyze the velocity components in the reference frame comoving
with the jet. The standard Lorentz transformation formulae for the
velocity components are
Now we proceed by performing numerical simulations of jet models
to study the growth of unstable modes through the
linear and non-linear phases. To this aim, we adopt as an equilibrium
initial state the one described in the former section. In order to
avoid the growth of random perturbations with wavelengths of the order
of the cell size, we replace the transverse discontinuous profiles of
equilibrium quantities by smooth profiles of the form
Table 1:
Equilibrium parameters of different simulated jet models
along with solutions of the dispersion relation (23),
corresponding to fastest growing first reflection mode, taken as input
parameters for numerical simulations. The meaning of the symbols is
as follows: ![]() :
jet flow Lorentz factor;
:
jet flow Lorentz factor;
![]() :
specific
internal energy;
:
specific
internal energy; ![]() :
sound speed; p: pressure;
:
sound speed; p: pressure; ![]() :
jet-to-ambient relativistic rest mass density contrast;
:
jet-to-ambient relativistic rest mass density contrast; ![]() :
jet-to-ambient enthalpy contrast;
:
jet-to-ambient enthalpy contrast; ![]() :
internal jet Mach number;
:
internal jet Mach number;
![]() :
longitudinal/transverse wavenumbers;
:
longitudinal/transverse wavenumbers;
![]() :
real/imaginary part of the wave frequency. Labels aand j refer to ambient medium and jet, respectively. The primes are
used to assign wavenumber and complex frequency in the reference frame
comoving with jet. The last column shows the linear growth rate of KH
instability in the jet reference frame expressed in dynamical time
units, i.e. in which time is scaled to
:
real/imaginary part of the wave frequency. Labels aand j refer to ambient medium and jet, respectively. The primes are
used to assign wavenumber and complex frequency in the reference frame
comoving with jet. The last column shows the linear growth rate of KH
instability in the jet reference frame expressed in dynamical time
units, i.e. in which time is scaled to
![]() .
All the
quantities in the table, except the last column, are expressed in
units of the ambient density,
.
All the
quantities in the table, except the last column, are expressed in
units of the ambient density,
![]() ,
the speed of light, c,
and the jet radius,
,
the speed of light, c,
and the jet radius, ![]() .
.
On the other hand the linear solutions derived in
Sect. 2.1.3 correspond to an idealized case with a
contact discontinuity at the jet interface. Finding of analogous
solutions for the corresponding sheared boundary problem is more
difficult from the numerical point of view (see Ray 1982; and
Choudhury & Lovelace 1984), therefore we decided to implement
corresponding smoothed eigenstates obtained for the vortex sheet limit
as approximate solutions for the case of sheared boundary. The
validity of this procedure is proven a posteriori by the
convergence of theoretical growth rates and the ones determined for
simulated KH modes. Since, in case of the vortex sheet approximation,
all first order dynamical variables (except pressure and the
transversal displacement of fluid element adjacent to the jet
boundary) are discontinuous, we apply the following smoothing of the
equilibrium quantities and linear perturbations at the thin layer
surrounding the jet boundary
Our first aim is to reproduce the linear evolution of unstable modes by means of hydrodynamical simulations. For this reason and in order to make the picture of evolution of the KH instability as clear and simple as possible, we perturb the equilibrium with the most unstable first reflection mode, which is smoothed at the jet interface according to formula (35). The length of the computational grid is in each simulation equal to the wavelength of the mentioned mode. Defining the initial state in such a way, we know precisely which growth rate to expect in numerical simulations. The difference between the expected and computed growth rates is a measure of the performance of the code in describing the linear regime and gives us confidence on the numerical results from the non-linear evolution.
The simulations have been performed using a high-resolution shock capturing code to solve the equations of relativistic hydrodynamics in Cartesian planar coordinates. The code is an upgrade of that used to study large scale (Martí et al. 1997) as well as compact relativistic jets (Gómez et al. 1997). The equations of relativistic hydrodynamics are written in conservation form and the time variation of the proper rest mass, momentum and total energy within numerical cells are calculated through the fluxes across the corresponding cell interfaces. Fluxes are calculated with an approximate Riemann solver that uses the complete characteristic information contained in the Riemann problems between adjacent cells (Donat & Marquina 1996). It is based on the spectral decomposition of the Jacobian matrices of the relativistic system of equations derived in Font et al. (1994) and uses analytical expressions for the left eigenvectors (Donat et al. 1998). The spatial accuracy of the algorithm is improved up to third order by means of a conservative monotonic parabolic reconstruction of the pressure, proper rest-mass density and the spatial components of the fluid four-velocity, as in GENESIS (see Aloy et al. 1999, and references therein). Integration in time is done simultaneously in both spatial directions using a total-variation-diminishing (TVD) Runge-Kutta scheme of high order (Shu & Osher 1988). See Martí et al. (1997) for the differential equations as well as their finite-difference form, and a description of exhaustive testing of the hydrodynamical code. Besides relativistic density, momentum and energy, the code also evolves a passive scalar representing the jet mass fraction. This allows us to distinguish between ambient and jet matter helping us to characterize processes like jet/ambient mixing or momentum exchange.
The parameters of the simulations presented in this paper are listed
in Table 1. Values of the parameters were chosen to be
close to those used in some simulations by Hardee et al. (1998) and
Rosen et al. (1999) and are chosen to span a wide range in
thermodynamical properties as well as beam flow Lorentz factors. In
all simulations, the density in the jet and ambient gases are
![]() ,
,
![]() respectively and the adiabatic exponent
respectively and the adiabatic exponent
![]() .
.
Since the internal rest mass density is fixed, there are two free
parameters characterizing the jet equilibrium: the Lorentz factor and
the jet specific internal energy displayed in Cols. 2 and 3 of
Table 1. Models whose names start with the same letter
have the same thermodynamical properties. Beam (and ambient) specific
internal energies grow from models A to D. Three different values of
the beam flow Lorentz factor have been considered for models B, C and
D. The other dependent parameters mentioned in
Sect. 2.1.1 are displayed in Cols. 4-10 of
Table 1. Note that given our choice of
![]() ,
the
ambient media associated to hotter models are also hotter. The next
three columns show the longitudinal wavenumber together with
oscillation frequency and the growth rate of the most unstable
reflection mode. The following three columns display the same
quantities in the jet reference frame. Next two columns show the
perpendicular wavenumbers of linear sound waves in jet and ambient
medium respectively. The last column shows the linear growth rate of
KH instability in the jet reference frame expressed in dynamical time
units, i.e. in which time is scaled to
,
the
ambient media associated to hotter models are also hotter. The next
three columns show the longitudinal wavenumber together with
oscillation frequency and the growth rate of the most unstable
reflection mode. The following three columns display the same
quantities in the jet reference frame. Next two columns show the
perpendicular wavenumbers of linear sound waves in jet and ambient
medium respectively. The last column shows the linear growth rate of
KH instability in the jet reference frame expressed in dynamical time
units, i.e. in which time is scaled to
![]() .
All other
quantities in the table, are expressed in units of the ambient
density,
.
All other
quantities in the table, are expressed in units of the ambient
density,
![]() ,
the speed of light, c, and the jet radius,
,
the speed of light, c, and the jet radius,
![]() .
.
As it is apparent in Table 1 growth rates tend to
increase with the specific internal energy of the beam and to decrease
with the beam flow Lorentz factor. Note that, in the jet reference
frame, models with the same thermodynamical properties tend to have
(within ![]() 10%) the same growth rates. Note also that in the
jet reference frame and in dynamical time units, all the models have
comparable (within a factor 1.5) linear growth rates.
10%) the same growth rates. Note also that in the
jet reference frame and in dynamical time units, all the models have
comparable (within a factor 1.5) linear growth rates.
The initial numerical setup consists of a steady two-dimensional
slab jet model (see Fig. 1). As stated above, a thin
shear layer between the ambient medium and the jet is used instead of
the vortex sheet. Due to symmetry properties, only half of the jet
(x>0) has to be computed. Reflecting boundary conditions are imposed
on the symmetry plane of the flow, whereas periodical conditions are
settled on both upstream and downstream boundaries. The numerical grid
covers a physical domain of one wavelength along the jet (3 to 20 ![]() ;
see Table 1) and 100
;
see Table 1) and 100 ![]() across (200
across (200 ![]() in
the case of models D). The size of the transversal grid is chosen to
prevent loses of mass, momentum and energy through the boundaries.
400 numerical zones per beam radii are used in the transverse
direction across the first 3
in
the case of models D). The size of the transversal grid is chosen to
prevent loses of mass, momentum and energy through the boundaries.
400 numerical zones per beam radii are used in the transverse
direction across the first 3 ![]() .
From this point up to the end of
the grid, 100 (200, in case of models D) extra numerical zones growing
geometrically have been added. The width growth factor between
contiguous zones is approximately 1.08 for models A, B and C and 1.04,
for models D. Along the jet, a resolution of 16 zones per beam radius
has been used. The agreement of the linear stability analysis with the
results of numerical simulations depends on the grid resolution (and
the width of the initial shear layer). The applied resolution of
.
From this point up to the end of
the grid, 100 (200, in case of models D) extra numerical zones growing
geometrically have been added. The width growth factor between
contiguous zones is approximately 1.08 for models A, B and C and 1.04,
for models D. Along the jet, a resolution of 16 zones per beam radius
has been used. The agreement of the linear stability analysis with the
results of numerical simulations depends on the grid resolution (and
the width of the initial shear layer). The applied resolution of
![]() grid zones per beam radius is chosen on the base of several
tests, which are presented in detail in Appendix A.
grid zones per beam radius is chosen on the base of several
tests, which are presented in detail in Appendix A.
The steady model is then perturbed according to the selected mode,
with an absolute value of the pressure perturbation amplitude inside
the beam of
![]() .
This means that those models with the
smallest pressure, like model A, have relative perturbations in
pressure three orders of magnitude larger than those with the highest
pressures, D. However this difference seems not to affect the linear
and postlinear evolution.
.
This means that those models with the
smallest pressure, like model A, have relative perturbations in
pressure three orders of magnitude larger than those with the highest
pressures, D. However this difference seems not to affect the linear
and postlinear evolution.
Table 2:
Times for the different phases in the evolution of the
perturbed jet models. In Cols. 2-4 we show:
![]() - end of
linear phase (the ratios of amplitudes of the different quantities are
not constant any longer),
- end of
linear phase (the ratios of amplitudes of the different quantities are
not constant any longer),
![]() - end of saturation phase (the
amplitude of the transverse speed perturbation reaches its maximum),
- end of saturation phase (the
amplitude of the transverse speed perturbation reaches its maximum),
![]() - the peak in the amplitude of the pressure
perturbation is reached. (see Fig. 2). Note that,
as a general trend,
- the peak in the amplitude of the pressure
perturbation is reached. (see Fig. 2). Note that,
as a general trend,
![]() .
In Col. 5 we show the saturation time in dynamical time units and
in the jet reference frame.
.
In Col. 5 we show the saturation time in dynamical time units and
in the jet reference frame.
![\begin{figure}
\par\includegraphics[width=4.5cm,clip]{0349fi21.ps}\hspace*{4.5cm...
...s}\hspace*{9mm}
\includegraphics[width=4.5cm,clip]{0349fi20.ps}\par\end{figure}](/articles/aa/full/2004/44/aa0349-04/Timg149.gif) |
Figure 2:
Evolution of the relative amplitudes of perturbations. Dotted
line: pressure perturbation (
|
| Open with DEXTER | |
Following the behaviour of simulated models we find that the evolution of the perturbations can be divided into a linear phase, a saturation phase and a mixing phase. This section is devoted to describing the properties of the linear and saturation phases in our models, focusing on the influence of the basic parameters. The remaining fully nonlinear evolution will be discussed in Paper II. Our description shares many points with that of Bodo et al. (1994) for the case of classical jets.
In order to illustrate the growth of perturbations and determine the duration of the linear and saturation phases in our simulations, we plot in Fig. 2 the amplitudes of the perturbations of the longitudinal and transversal velocities, inside the jet and in the jet reference frame, together with the pressure oscillation amplitude. We plot also the growth of the imposed eigenmodes resulting from the linear stability analysis. Both the velocity perturbations are transformed from the ambient rest frame to the unperturbed jet rest frame using the Lorentz transformation rules for velocity components, given by Eq. (31).
We define the characteristic times in the following way. During the
linear phase the ratios of the exponentially growing amplitudes of
pressure, longitudinal velocity and transversal velocity remain
constant by definition. We define the end of the linear phase
(
![]() )
as the moment at which one of quantities starts to
depart from the initial exponential growth. Within the set of our
models the first quantity to break the linear behaviour is the
longitudinal velocity perturbation.
)
as the moment at which one of quantities starts to
depart from the initial exponential growth. Within the set of our
models the first quantity to break the linear behaviour is the
longitudinal velocity perturbation.
Later on the transversal velocity saturates, i.e. stops growing at the
saturation time (
![]() ). We call the period between
). We call the period between
![]() and
and
![]() the saturation phase. We find also that the
pressure perturbation amplitude reaches a maximum. This moment is
denoted by
the saturation phase. We find also that the
pressure perturbation amplitude reaches a maximum. This moment is
denoted by
![]() .
In Paper II we will see that this peak
announces the entering of the fully nonlinear regime. The choice of
.
In Paper II we will see that this peak
announces the entering of the fully nonlinear regime. The choice of
![]() ,
,
![]() ,
,
![]() has been illustrated in
Fig. 2 (top panel).
has been illustrated in
Fig. 2 (top panel).
Table 2 collects times of the linear and saturation phases in the different models (Cols. 2-4). The last column shows the saturation time in dynamical units and in the jet reference frame. The change of reference frame eliminates the effects coming from the jet flow Lorentz factor that stretches out the rhythm of evolution in the ambient rest frame. Dynamical time units are adapted to the characteristic time of evolution of each model. Hence this change of units and reference frame allows us to compare the relevant scales of evolution of all the models directly.
In the linear phase the ratios of oscillation
amplitudes of different dynamical variables (density, pressure and
velocity components) are constant. We have used this property to
identify the end of the linear phase with the time
![]() at
which one of the variables deviates from linear growth in a
systematic way. Note that our definition is different from that of
Bodo et al. (1994) who associate the end of the linear phase with the
formation of the first shocks inside the jet.
at
which one of the variables deviates from linear growth in a
systematic way. Note that our definition is different from that of
Bodo et al. (1994) who associate the end of the linear phase with the
formation of the first shocks inside the jet.
| |
Figure 3: Pressure distribution at the end of linear phase for models B05 ( left panel) and D05 ( right panel). The continuous line corresponds to jet mass fraction equal to 0.5 and serves to distinguish jet and ambient media. |
| Open with DEXTER | |
We note that in our simulations, during the linear phase, the growth of perturbations of each dynamical variable follows the predictions of the linear stability analysis with relatively good accuracy. On average the growth rates measured for all our numerical experiments are about 20% smaller than corresponding growth rate resulting from the linear stability analysis. This small discrepancy may be partially a result of the application of the shearing layer in simulations and the vortex sheet approximation in the linear stability analysis, and also to a lack of transversal resolution in the numerical simulations (see Appendix A).
In all cases the amplitude of the longitudinal velocity oscillation is the first quantity to stop growing. The reason for the limitation of the velocity oscillations is obvious: the oscillations of velocity components (corresponding to sound waves propagating in the jet interior) cannot exceed the speed of light. This limitation (specific to relativistic dynamics) is easily noticeable in the jet reference frame, but it is obscured by the Lorentz factor (in the first and second power) in the reference frame of the ambient medium, as it follows from the formulae (32).
As seen in Fig. 2, model C20 evolves distinctly from the other models: at t = 270, the linear phase ends before the saturation of longitudinal speed. See the middle panels of Fig. 7 (especially the pressure panel) which could be responsible for the peculiar evolution of model C20. Note also that model C20 is the only one that has a theoretical perturbation growth rate smaller than the numerical one (probably associated with the excited short wavelength mode).
At the end of the linear phase, the values of quantities like density, pressure and flow Lorentz factor are still very close to the corresponding background values (the perturbation in pressure is between 10% and 50% of the background pressure in all the models). Figure 3 shows the distribution of pressure at the end of the linear phase for two representative models B05 and D05.
As it has been mentioned, the end of the linear phase coincides with
the limitation of the longitudinal oscillation velocity. At time
![]() the transversal velocity component is smaller than the
speed of light, by an order of magnitude approximately, so the
transversal velocity perturbation has still room to grow. We
defined
the transversal velocity component is smaller than the
speed of light, by an order of magnitude approximately, so the
transversal velocity perturbation has still room to grow. We
defined
![]() as the time corresponding to the
saturation of the transversal velocity and saturation phase as the
period between
as the time corresponding to the
saturation of the transversal velocity and saturation phase as the
period between
![]() and
and
![]() .
.
We find that the longitudinal velocity perturbation amplitude reaches almost the speed of light (more than 0.9 c) while the transversal perturbation amplitude stops its growth at the level of approximately 0.5c for all presented simulations. This can be explained in the following way. The eigenmodes are built of oblique sound waves overreflected at the jet/ambient medium interface. This means that the amplitude of the reflected wave is larger than the amplitude of the incident one. Sound waves are longitudinal waves, so the gas oscillation velocity can be split into the longitudinal and transversal components separately for the incident and reflected waves. Let us consider locally the incident wave and the reflected wave in the jet medium, in a fixed point close to the jet boundary. Then the longitudinal velocity components of the incident and reflected waves sum in phase, while the transversal ones sum in counterphase. This means that while the amplitude of the total longitudinal velocity oscillation component grows and approaches the speed of light, the oscillation amplitude of the total transversal component is a difference of the two velocities, each smaller than the speed of light. Therefore the oscillation amplitude of the total transversal component has to take values significantly smaller than the longitudinal one.
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{0349fi4.ps}
\par\par\end{figure}](/articles/aa/full/2004/44/aa0349-04/Timg151.gif) |
Figure 4: Snapshot around saturation of logarithmic maps of pressure, rest-mass density and specific internal energy and non-logarithmic Lorentz factor for model A05. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9.8cm,clip]{0349fi51.ps}\vspace*{12mm}...
...}\vspace*{12mm}
\par\includegraphics[width=10.1cm,clip]{0349fi53.ps}\end{figure}](/articles/aa/full/2004/44/aa0349-04/Timg152.gif) |
Figure 5: Same as Fig. 4 for models B05 ( upper), C05 ( middle) and D05 ( lower). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.8cm,clip]{0349fi61.ps}\vspace*{12mm...
...}
\par\hspace*{-4.8mm}\includegraphics[width=11cm,clip]{0349fi63.ps}\end{figure}](/articles/aa/full/2004/44/aa0349-04/Timg153.gif) |
Figure 6: Same as Fig. 4 for models B10 ( upper), C10 ( middle) and D10 ( lower). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12.6cm,clip]{0349fi71.ps}\vspace*{12mm...
...}
\par\hspace*{-4.8mm}\includegraphics[width=12cm,clip]{0349fi73.ps}\end{figure}](/articles/aa/full/2004/44/aa0349-04/Timg154.gif) |
Figure 7: Same as Fig. 4 for models B20 ( upper), C20 ( middle) and D20 ( lower). |
| Open with DEXTER | |
The duration of the saturation phase depends on the Lorentz factor and the specific internal energy with a tendency to increase with the former and to decrease with the latter (exception made of models C10 or D10 and C20). It ranges between a few tens of (absolute) time units to a few hundreds.
We note that the saturation times expressed in dynamical time units
and in the jet reference frame (see Table 2) are almost
equal for all models. This similarity can be explained by the
following argument. First, the amplitude of
pressure perturbations
![]() is the same for all
simulations. Second, the amplitudes of pressure and transversal
velocity perturbations are related by formula (26). The perturbation of perpendicular velocity is then
transformed to the jet reference frame following Eq. (32).
Following the results of numerical experiments, the transversal
velocity grows with the linear growth rate until the transversal
velocity perturbation reaches the upper limit, i.e.
is the same for all
simulations. Second, the amplitudes of pressure and transversal
velocity perturbations are related by formula (26). The perturbation of perpendicular velocity is then
transformed to the jet reference frame following Eq. (32).
Following the results of numerical experiments, the transversal
velocity grows with the linear growth rate until the transversal
velocity perturbation reaches the upper limit, i.e.
![]() .
If we express
.
If we express
![]() in dynamical time units then in the jet reference frame
in dynamical time units then in the jet reference frame
During the saturation phase, the jet inflates (Bodo et al. 1994
called this phase the expansion phase) and deforms due to transversal
oscillations. On the other hand, the saturation time
![]() coincides (within a few time units) with the appearance of an absolute
maximum in the pressure distribution (at
coincides (within a few time units) with the appearance of an absolute
maximum in the pressure distribution (at
![]() )
at the jet
boundary, and with the start of the mixing phase (to be studied in
Paper II). Figures 4-7 display snapshots
of several quantities close to the end of the saturation phase before
the distortion of the jet boundary.
)
at the jet
boundary, and with the start of the mixing phase (to be studied in
Paper II). Figures 4-7 display snapshots
of several quantities close to the end of the saturation phase before
the distortion of the jet boundary.
The structure of perturbations at the end of the saturation phase is quite similar in all models. The longitudinal wavelength of perturbations is given by the linear stability analysis and it is constant because of the fixed length of the computational domain. Along with the longitudinal wavelength, the opening angle of oblique waves, far from the jet symmetry plane, is given by the linear analysis. The opening angle of oblique waves is enlarged in the vicinity of the jet interface. Closer to the jet symmetry plane the perturbations are already in the nonlinear phase, which can be recognized by the apparent presence of oblique shock fronts in the jet itself and the ambient medium. These shocks form as a natural consequence of the nonlinear steepening of oblique sound waves as their amplitude becomes large. Practically all the four quantities displayed for a given model (i.e. pressure, rest-mass density, Lorentz factor and internal energy) show the same structure, so there is no need to discuss them separately. Therefore we treat the pressure distribution as a representative quantity. The following properties of the flow patterns can be noticed in Figs. 4-7:
This is the first of a series of papers devoted to the effects
of relativistic dynamics and thermodynamics in the development of KH
instabilities in planar relativistic jets, accross both linear and
fully nonlinear regimes. To this aim, we have performed a linear
stability analysis and high-resolution numerical simulations for the
most unstable first reflection modes in the temporal approach, for
three different values of the jet Lorentz factor ![]() (5, 10 and
20) and a few different values of specific internal energy of the jet
matter (from 0.08 to 60.0 c2). In this paper we concentrate in
the early stages of evolution of the KH instability, namely the linear
and saturation phases. The present paper is also intended to set the
theoretical and numerical background for the whole series of papers.
(5, 10 and
20) and a few different values of specific internal energy of the jet
matter (from 0.08 to 60.0 c2). In this paper we concentrate in
the early stages of evolution of the KH instability, namely the linear
and saturation phases. The present paper is also intended to set the
theoretical and numerical background for the whole series of papers.
Our simulations describe the linear regime of evolution of the excited eigenmodes of the different models with high accuracy. The growth rates of the perturbed modes in the vortex sheet approximation were determined with an average relative error of 20%.
In all the examined cases the longitudinal velocity perturbation is
the first quantity that departs from linear growth when it reaches
a value close to the speed of light in the jet reference frame. The
reason for this saturation, specific to relativistic dynamics, is not
so obvious in the reference frame of the external medium where it
saturates at a smaller value (
![]() ,
where
,
where ![]() is
the bulk flow Lorentz factor in the jet).
is
the bulk flow Lorentz factor in the jet).
The saturation phase extends from the end of the linear phase up to the saturation of the transversal velocity perturbation (at approximately 0.5c in the jet reference frame). The saturation times for the different numerical models have been explained from elementary considerations, i.e. from properties of linear modes provided by the linear stability analysis and from the limitation of the transversal perturbation velocity.
The limitation of the components of the velocity perturbation at the end of the linear and saturation phases allows us to conclude that the relativistic nature of the flow appears to be responsible for the departure of the system from linear evolution. This behaviour is consistent with the one deduced by Hanasz (1995, 1997) with the aid of analytical methods.
At the saturation time the perturbation structure is close to the structure of the initial perturbation (the one corresponding to the most unstable first reflection mode), except that the oblique sound waves forming the perturbation became steep due to their large amplitude. It is interesting to note that the oblique shocks are stronger (i.e., the pressure jumps are larger) in the colder cases.
Our simulations, performed for the most unstable first reflection
modes, confirm the general trends resulting from the linear stability
analysis: the faster (larger Lorentz factor) and colder jets have
smaller growth rates. As we mentioned in the Introduction, Hardee et
al. (1998) and Rosen et al. (1999) note an exception which occurs for
the hottest jets. These jets appear to be the most stable in their
simulations (see also the simulations in Martí et al. 1997). They
suggest that this behaviour is caused by the lack of appropriate
perturbations to couple to the unstable modes. This could be partially
true as fast, hot jets do not generate overpressured coocons that let
the jet run directly into the nonlinear regime. However, from the
point of view of our results, the high stability of hot jets may have
been caused by the lack of radial resolution that leads to a damping
in the perturbation growth rates. We note that the agreement between
the linear stability analysis and numerical simulations of KH
instability in the linear range has been achieved for a very high
radial resolution of 400 zones/![]() ,
which appears to be especially
relevant for hot jets. Finally, one should keep in mind that the
simulations performed in the aforementioned papers only covered
about one hundred time units, well inside the linear regime of the
corresponding models for small perturbations.
,
which appears to be especially
relevant for hot jets. Finally, one should keep in mind that the
simulations performed in the aforementioned papers only covered
about one hundred time units, well inside the linear regime of the
corresponding models for small perturbations.
The high accuracy of our simulations in describing the early stages of evolution of the KH instability (as derived from the agreement between the computed and expected linear growth rates and the consistency of the saturation times) establishes a solid basis to study the fully nonlinear regime, to be done in the second paper of this series. In this paper (Paper II) we will show that the similarities found in the evolution of all the models accross the linear and saturation phases is lost and very different nonlinear evolution is found depending on the initial jet parameters.
Acknowledgements
This work was supported in part by the Spanish Dirección General de Enseñanza Superior under grant AYA-2001-3490-C02 and by the Polish Committee for Scientific Research (KBN) under grant PB 404/P03/2001/20. M.H. acknowledges financial support from the visitor program of the Universidad de Valencia. M.P. has benefited from a predoctoral fellowship of the Universidad de Valencia (V Segles program). The authors want also to acknowledge financial support from the Spanish-French Picasso program and the Polish-French Joumelage program in the period 1997-98 when the research on relativistic jet stability was initiated.
Growth of the instability depends critically on the numerical viscosity of the algorithm. Hence our first aim was to look for suitable numerical resolutions by comparing numerical and analytical results for the linear regime. We performed a number of simulations based on model A05 changing longitudinal and radial resolution, and also the exponent m for the shear layer steepness (see Eqs. (33) and (34)). Figure A.1 shows results for several of those simulations.
A shear layer was included in order to avoid non-steadiness in initial
conditions given by discontinuous separation between the beam and the
external medium. Therefore, if for some transversal resolution we
introduced a shear layer which was too thin, we found a similar
non-steady behavior. However, in order to reproduce the linear regime,
we needed a steep enough shear layer, due to the fact that theory was
developed for a discontinuous separation between both media. We can
see in Fig. A.1 that m=10 models are considerably
damped with respect to the theoretical growth, independent of the
transversal resolution. Hence resolution perpendicular to the flow
appeared to be essential, requiring very high resolutions (400 zones/![]() )
and thin shear layers (m=40) with 40 to 45 zones, i.e.,
an equilibrium between steepness and number of cells. Lower
transversal resolutions and/or thicker shear layers led to
non-satisfactory results, with a slow or damped growth. A very low
longitudinal resolution results in damping of growth rate, too, as can
be seen from comparison of m=20 models, but rz=16 seems to give a
reasonable growth rate compared to theory. This (small) resolution of
16 zones/
)
and thin shear layers (m=40) with 40 to 45 zones, i.e.,
an equilibrium between steepness and number of cells. Lower
transversal resolutions and/or thicker shear layers led to
non-satisfactory results, with a slow or damped growth. A very low
longitudinal resolution results in damping of growth rate, too, as can
be seen from comparison of m=20 models, but rz=16 seems to give a
reasonable growth rate compared to theory. This (small) resolution of
16 zones/![]() along the jet was taken as a compromise between
accuracy and computational efficiency.
along the jet was taken as a compromise between
accuracy and computational efficiency.