A&A 427, 763-767 (2004)
DOI: 10.1051/0004-6361:20040300

Radiative rates for E1, E2, M1 and M2 transitions in Fe X[*]

K. M. Aggarwal - F. P. Keenan

Department of Pure and Applied Physics, The Queen's University of Belfast, Belfast BT7 1NN, Northern Ireland, UK

Received 19 February 2004/ Accepted 30 July 2004

Abstract
Energies of the 54 levels belonging to the (1s22s22p6) 3s23p5, 3s3p6, 3s23p43d and 3s3p53d configurations of Fe X have been calculated using the GRASP code of Dyall et al. (1989). Additionally, radiative rates, oscillator strengths, and line strengths are calculated for all electric dipole (E1), magnetic dipole (M1), electric quadrupole (E2), and magnetic quadrupole (M2) transitions among these levels. Comparisons are made with results available in the literature, and the accuracy of the data is assessed. Our energy levels are estimated to be accurate to better than 3%, whereas results for other parameters are probably accurate to better than 20%. Additionally, the agreement between measured and calculated lifetimes is better than 10%.

Key words: atomic data - atomic processes

1 Introduction

Iron is an abundant element, particularly in solar and fusion plasmas, and its emission lines are observed in almost all ionization stages. With a vast amount of observational data being available from recent space missions such as SOHO, Chandra and XMM Newton, many scientists are busy in calculating atomic data for its ions, due to a paucity of required experimental results. To this end we have also reported atomic data (namely, energy levels, radiative rates, collision strengths and excitation rate coefficients) for Fe XI (Aggarwal & Keenan 2003a,b), Fe XIII (Aggarwal & Keenan 2004), Fe XV (Aggarwal et al. 2003a), Fe XVII (Aggarwal et al. 2004), Fe XVIII (Jonauskas et al. 2004), Fe XXI (Aggarwal & Keenan 2001), and Fe XXIV (McKeown et al. 2004), and in this paper we present our results for energy levels and radiative rates for transitions in Fe X.

Emission lines of Cl-like Fe X in the extreme ultraviolet (EUV: 170-400 $\AA$) and ultraviolet (UV: 1000-2000 $\AA$) have been observed in the spectra of the solar atmosphere (Brosius et al. 1998) and late-type stars (Drake et al. 1995a,b). Several of the observed emission lines provide useful plasma diagnostics, as demonstrated by Foster et al. (1996). A famous visible transition of Fe X is the red line at $\sim$6375 $\AA$ belonging to the (3s23p5) 2P $^\circ_{3/2}$ - 2P $^\circ_{1/2}$ magnetic dipole (M1)transition. Hence, for diagnostics and modelling of plasmas theoretical results of various atomic parameters are of vital importance. Additionally, Fe X is one of the iron ions for which lifetimes of many levels have been measured in the laboratory, which provide a good check on the accuracy of theoretical data. Therefore, in this paper we report energies for 54 levels of the (1s22s22p6) 3s23p5, 3s3p6, 3s23p43d and 3s3p53d configurations, and radiative rates (A-values), oscillator strengths (f-values), and line strengths (S-values) for electric and magnetic dipole and quadrupole transitions among these levels.

Realising the importance of Fe X, a number of workers in the past have performed a variety of calculations to compute atomic parameters, particularly energy levels, radiative rates, oscillator strengths, and electron impact excitation collision strengths. The most notable among the available data are the calculations of Bhatia & Doschek (1995, henceforth BD) and Deb et al. (2002, henceforth DGM). BD have reported results for energy levels, radiative rates and collision strengths. However, the most recent and exhaustive results for energy levels and radiative rates for transitions in Fe X are of DGM, because they have included extensive configuration interaction (CI), apart from one-body relativistic operators, whereas BD have included CI among the basic 4 configurations only, because their focus is mainly on the calculations of collisional data. Therefore, the results of DGM should be the most accurate available to date. However, a close look at their Table 1 reveals that their energies for the highest 28 levels (27-54) are consistently lower than those of BD. The differences between the two sets of theoretical energies are generally within 5%, but the highest 8 levels of the 3s3p53d configuration differ up to 11% ($\le$0.9 Ryd). Therefore, in the absence of any other theoretical or experimental results, a fresh calculation with an independent approach may be useful in explaining these differences, and in assessing the accuracy of atomic data, so that results can be applied with confidence in plasma modelling. Additionally, DGM have reported radiative rates for only electric dipole (E1) transitions, whereas corresponding results for other types of transitions (namely, electric quadrupole E2, magnetic dipole M1 and magnetic quadrupole M2) are also required in the modelling of plasmas. Therefore, in this paper we report radiative rates for all types of transitions, and compare our calculated lifetimes with available measurements.

2 Energy levels

The 3s23p5, 3s3p6, 3s23p43d and 3s3p53d configurations of Fe X give rise to 54 fine-structure levels, listed in Table 1. To generate the wavefunctions, we have used the fully relativistic GRASP code of Dyall et al. (1989) with the option of extended average level (EAL), in which a weighted (proportional to 2j+1) trace of the Hamiltonian matrix is minimized. This produces a compromise set of orbitals describing closely lying states with moderate accuracy. Our calculations are in the jj coupling scheme, and Breit and QED corrections have been included.

A test calculation performed with only the above 4 configurations produced energy levels which closely agree (within 1%) with those of BD - see column GRASP4 in Table 1. Although Fe X is moderately heavy (Z = 26) and 9 times ionized, CI is still very important for an accurate determination of energy levels. Inclusion of additional CI with the 3s23p44$\ell$ and 3s3p54$\ell$ configurations did not make any significant improvement in energies. This is because their levels lie in the $\sim$9.5-17.0 Ryd energy range, which is above those of the 4 configurations under discussion. Similarly, inclusion of CI with the 3s3p44${\ell}^2$, 3p54${\ell}^2$, 3s23p45$\ell$ and 3s3p55$\ell$ configurations makes negligible effect on energy levels (<0.01 Ryd), and their orderings remain unchanged. This is again because of their higher energy ranges of $\sim$13.7 to 33.8 Ryd. Therefore, we may state with confidence that inclusion of configurations with $n \ge$ 4 does not make any appreciable effect on the energies or orderings of 54 levels of Fe X under discussion here. However, 615 levels of the 3p63d, 3s3p43d2, 3s23p33d2 and 3s23p23d3 configurations lie in an energy range $\sim$7.28-15 Ryd, and interact very closely with the 54 levels of the 3s23p5, 3s3p6, 3s23p43d and 3s3p53d configurations.

Therefore, we have performed a larger calculation with 669 levels of the above 8 configurations, and the energies obtained for the desired 54 levels are listed in Table 1 under column GRASP8. The effect of including CI with the additional 4 configurations, especially of 3s23p33d2, is quite pronounced, and this lowers the energies by $\sim$0.7 Ryd. Before we discuss our results further, we would like to mention that different combinations with other configurations, such as 3p53d2, 3s3p33d3 and 3s3p3d5 (and many other two, three and four electron excitation configurations listed in Table 1 of Glass 1983), have also been tried, but their effect on the desired 54 energy levels is insignificant, mainly because their energy range is quite high. Therefore, our conclusion is that for a reasonably accurate calculation of energy levels for Fe X, inclusion of CI among the 3s23p5, 3s3p6, 3s23p43d, 3s3p53d, 3p63d, 3s3p43d2, 3s23p33d2 and 3s23p23d3 configurations is necessary. Finally, inclusion of Breit and QED corrections has affected the orderings of two levels (4 and 5) in our GRASP8 calculations, but in Table 1 orderings of Coulomb energies have been retained because the subsequent results of radiative rates in Tables 2 and 3 follow these level indices.

Table 1: Target levels of Fe X and their threshold energies (in Ryd).

Also included in Table 1 are the experimentally compiled energies of NIST (http://www.physics.nist.gov/PhysRefData), and the theoretical results of BD and DGM. Experimental energies for all levels are not available, but the agreement for common levels is within 3%. Furthermore, the level orderings are (almost) the same in both theoretical and experimental results, which is highly satisfying. However, the energy levels of BD are clearly higher by up to 11%, and also differ in ordering in a few instances, such as levels 19, 21, 46 and 53. This is because of the exclusion of CI with additional configurations as stated earlier, and also confirmed by a good agreement between their results and our calculations (GRASP4) with the same 4 configurations. The agreement between our CI calculations (GRASP8) and those of DGM is within 3% for all levels, and the ordering is also the same for a majority of these. However, DGM suspected that the ordering of the 3s23p4(3P)3d 4F3/2 and 3s23p4(1D)3d 2P3/2 levels (i.e. 12 and 13) might be misprinted by NIST, because their ordering is reversed, whereas our calculations confirm the NIST ordering to be correct. Nevertheless, the 3s23p4(1D)3d 2P3/2 level is highly mixed, particularly with 3s23p4(3P)3d 4F3/2 and 3s23p4 (3P)3d 2P3/2 - see also the last column of Table 1 of DGM. Therefore, the positions of levels 12 and 13 are variable with different combinations of configurations and optimisation procedures for different orbitals. However, a major anomaly between our calculations and those of DGM is for the ordering of the 3s23p4(3P)3d 4P3/2 level (16), which is almost pure and does not have any considerable contribution from other levels, in both calculations. Although a corresponding experimental energy for this level is not available with which to compare, the DGM ordering for this level is in total contrast with our GRASP4 and GRASP8 calculations, and also that of BD. To conclude, we may state with confidence that the energy levels of NIST, DGM and our GRASP8 calculations listed in Table 1 are accurate to $\sim$3%, and also agree in general in the orderings. However, scope remains for further improvement in accuracy, which may be achieved by a larger relativistic calculation with about 5000 levels, as indicated by our test calculations.

3 Radiative rates

The absorption oscillator strength (fij) and radiative rate Aji (in s-1) for a transition $i \to j$ are related by the following expression:


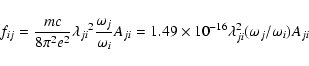\begin{displaymath}f_{ij} = \frac{mc}{8{\pi}^2{e^2}}{\lambda_{ji}}^2 \frac{{\ome... ...1.49 \times 10^{-16} \lambda^2_{ji} (\omega_j/\omega_i) A_{ji} \end{displaymath} (1)

where m and e are the electron mass and charge, respectively, c is the velocity of light, $\lambda_{ji}$ is the transition energy/wavelength in $\AA$, and $\omega_i$ and $\omega_j$ are the statistical weights of the lower i and upper j levels, respectively. Similarly, the oscillator strength fij (dimensionless) and the line strength S (in atomic unit, 1 au = $6.460\times10^{-36}$ cm2 esu2) are related by the following standard equations:

For the electric dipole (E1) transitions:

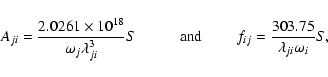\begin{displaymath}A_{ji} = \frac{2.0261\times{10^{18}}}{{{\omega}_j}\lambda^3_{... ...*{0.8 cm} f_{ij} = \frac{303.75}{\lambda_{ji}\omega_i} S, \\ \end{displaymath} (2)

for the magnetic dipole (M1) transitions:

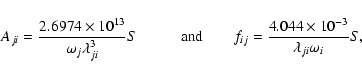\begin{displaymath}A_{ji} = \frac{2.6974\times{10^{13}}}{{{\omega}_j}\lambda^3_{... ...j} = \frac{4.044\times{10^{-3}}}{\lambda_{ji}\omega_i} S,~ \\ \end{displaymath} (3)

for the electric quadrupole (E2) transitions:

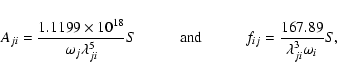\begin{displaymath}A_{ji} = \frac{1.1199\times{10^{18}}}{{{\omega}_j}\lambda^5_{... ...ce*{1.0 cm} f_{ij} = \frac{167.89}{\lambda^3_{ji}\omega_i} S, \end{displaymath} (4)

and for the magnetic quadrupole (M2) transitions:

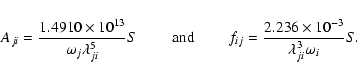\begin{displaymath}A_{ji} = \frac{1.4910\times{10^{13}}}{{{\omega}_j}\lambda^5_{... ...} = \frac{2.236\times{10^{-3}}}{\lambda^3_{ji}\omega_i} S. \\ \end{displaymath} (5)

In Table 2 we present transition energies ( $\Delta E_{ij}$ in $\AA$), radiative rates (Aji in s-1), oscillator strengths (fij, dimensionless), and line strengths (S in au), in length form only, for all 460 electric dipole (E1) transitions among the 54 levels of Fe X. The indices used to represent the lower and upper levels of a transition have already been defined in Table 1. Also, in calculating the above parameters we have used the Breit and QED corrected theoretical energies/wavelengths as listed in Table 1. Similar results for 590 electric quadrupole (E2), 437 magnetic dipole (M1), and 606 magnetic quadrupole (M2) transitions are listed in Table 3. Although E1 (allowed and intercombination) transitions are the most important for modelling applications, data for other transitions are also required, and that is why we have presented here a complete set of results for all types of transitions.

Before we discuss and compare our radiative rates, we would like to mention here that the effect of including additional CI with configurations such as: 3s3p44${\ell}^2$, 3p54${\ell}^2$, 3s23p45$\ell$ and 3s3p55$\ell$ has been assessed to be insignificant. For example, the above 18 configurations give rise to additional 993 levels, but radiative rates for E1 transitions among the 54 levels of Table 1 are affected by less than 10%, except for 5 transitions, namely 12-51, 14-54, 16-37, 17-43 and 22-34. All these 5 transitions have comparatively lower f-values of $\le$3.0$\times$10-4, and differences with our results listed in Table 2 remain within 23%. Therefore, we may state with confidence that additional inclusion of CI with n = 4 or 5 configurations is of no obvious advantage, either for the determination of energy levels or radiative rates.

The most complete and accurate set of A-values available in the literature for comparison purposes are those of DGM for the E1 transitions. For a majority of transitions, especially the stronger ones such as 1-30, 2-31 and 3-54, the agreement between the two calculations is better than 20%. However, for weaker transitions the differences are sometimes larger. This is because the weaker transitions are comparatively more sensitive to cancellation among mixing coefficients. However, weaker transitions generally do not play a dominant role in plasma diagnostics, and in general, both sets of radiative rates (ours and those of DGM) may be equally accurate for a majority of transitions, in spite of large differences for a few. Additionally, measurements of lifetimes for some levels of Fe X are available in the literature, which we compare below to further assess the accuracy of our results.

Table 4: Comparison of lifetimes for levels of Fe X.

4 Lifetimes

The lifetime $\tau$ of a level j is defined as follows:


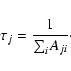\begin{displaymath}{\tau}_j = \frac{1}{{\sum_{i}^{}} A_{ji}}\cdot \end{displaymath} (6)

In Table 4 we compare our calculated lifetimes with the available measurements for common levels. Lifetimes of the 3s23p5 2P $^\circ_{1/2}$, 3s23p4(3P)3d 2F7/2 and 3s23p4(1D)3d 2F7/2 levels remain stable (within 10%) among different sets of calculations performed, and also agree to better than 10% with the measured values. The lifetime of the 3s3p6 2S1/2 level shows the largest variation (between 178 and 403 ps) among different test calculations, but our concluded value of 234 ps agrees within 10% with the measured result of Träbert (1996). Additionally, the calculated lifetimes of Biemont & Träbert (2000) and Deb et al. (2002) for this level are 240 ps and 233 ps, respectively. These are in excellent agreement with our results, indicating that the measurements may be slightly overestimated. Similarly, lifetime measurements for the 3s23p4(3P)3d 4F9/2 level by Träbert et al. (2003) appear to be overestimated, whereas the agreement between the present theoretical results and the earlier measurements of Moehs et al. (2000) is excellent. On the other hand, the measured lifetime of the 3s23p4(3P)3d 4F7/2 level by Moehs et al. is clearly overestimated, but it has a large error bar. If the lower limit of their measurement is taken into consideration then their results agree within 10% with our calculations, as well as with the later determination of Träbert et al. (2002). This leads us to suggest that the measured lifetime of the 3s23p4(1D)3d 2G9/2 level by Moehs et al. may also be overestimated, as theoretical results remain stable within 5%, from various test calculations. Additionally, Moehs et al. have measured a lifetime for this level on the basis of the identification of the 3s23p4(3P)3d 4F9/2 - 3s23p4(1D)3d 2G9/2 (8-20) transition, for which the dominant contribution comes from the above M1 transition (see Table 3), whose A-value is 62.17 s-1 corresponding to a lifetime of 16.08 ms. This agrees closely with their measurement of 17.8 ms. However, in our calculations of lifetimes, we have taken into account the contribution of other M1 transitions as well, and the significant ones among these are 5-20 (A = 4.470 s-1), 10-20 (A = 6.254 s-1), and 18-20 (A = 4.489 s-1), the net effect of which is to lower the lifetime by $\sim$20%. In fact, the same conclusion applies to the Moehs et al.'s measurements for the other two levels, namely 3s23p4(3P)3d 4F7/2 and 3s23p4(3P)3d 4F9/2, which are based on the identifications of the 3s23p4(3P)3d 4D7/2 - 3s23p4(3P)3d 4F7/2 (5-10) and 3s23p4(3P)3d 4D7/2 - 3s23p4(3P)3d 4F9/2 (5-8) transitions, whose A-values are 9.747 s-1 and 12.920 s-1, respectively, and lead to the lifetimes of 102.6 ms and 77.40 ms, respectively. For the 4F9/2 level, there is no other appreciable contribution from other transitions, but for the 4F7/2 level, significant contributions come from the 1-10 (A = 2.993 s-1 ), 4-10 (A = 0.620 s-1) and 8-10 (A = 4.280 s-1) transitions, which lower the lifetime from 102.60 ms to 56.47 ms. Therefore, based on this analysis and the possible uncertainty of 10% - 32% of Moehs et al., we may state in conclusion that theory and experiment agree well for transitions in Fe X, and hence confirm the accuracy of the presently reported radiative rates.

5 Conclusions

In this work, energy levels, radiative rates, oscillator strengths, and line strengths for transitions among 54 fine-structure levels of Fe X are computed using the fully relativistic GRASP code of Dyall et al. (1989), and results are reported for electric and magnetic dipole and quadrupole transitions. Energy levels agree in magnitude and orderings with the listings of NIST, and are assessed to be accurate to better than 3%. Additionally, CI is very important, apart from relativistic effects, for accurate determination of energy levels, particularly of the 3s3p53d configuration. Furthermore, our calculations confirm the accuracy of the results of DGM, but the corresponding available energy levels of BD are overestimated by up to 11%. However, the accuracy of other parameters (A, f and S) for a majority of strong transitions is $\sim$20%. Furthermore, theory and experiment are in excellent agreement (within 10%) for lifetimes, and hence confirm the accuracy of our calculated radiative rates.

Acknowledgements

This work has been financed by the Engineering and Physical Sciences and Particle Physics and Astronomy Research Councils of the United Kingdom. F.P.K. is grateful to A. W. E. Aldermaston for the award of a William Penny Fellowship.

References

 
Copyright ESO 2004