A&A 427, 319-334 (2004)
DOI: 10.1051/0004-6361:20041277

Two magnetic components in sunspot penumbrae

L. R. Bellot Rubio ¹ - H. Balthasar ² - M. Collados ³

1 - Kiepenheuer-Institut für Sonnenphysik, Schöneckstr. 6, 79104, Freiburg, Germany
2 - Astrophysikalisches Institut Potsdam, Telegrafenberg, 14473, Potsdam, Germany
3 - Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife, Spain

Received 12 May 2004 / Accepted 16 June 2004

Abstract
The magnetic and kinematic configuration of sunspot penumbrae is investigated by performing an inversion of the Stokes profiles of three infrared lines at 1565 nm. We use a two-component model atmosphere to describe, at least to first order, the unresolved structure of the penumbra. The observed Stokes profiles are successfully fitted, including those exhibiting abnormal shapes. The results of the inversion are consistent with the idea that the penumbra is formed by almost horizontal flux tubes embedded in a more vertical background magnetic field, as proposed by Solanki & Montavon (1993). The tubes possess weaker fields than the background except in the very outer penumbra, and carry most of the Evershed flow. We characterize the radial variation of the magnetic field vector and the velocity vector in these atmospheric components. In the middle penumbra and beyond, the magnetic field and the flow in the tubes are seen to return to the solar surface. Everywhere in the penumbra, there is a perfect alignment of the magnetic field vector and the velocity vector in the component describing the penumbral flux tubes. We find that the Evershed flow is supercritical in many places of the outer penumbra, and supersonic at some locations near the outer sunspot boundary. Based on these inversions, we suggest that the azimuthal fluctuations in the average magnetic field inclination and strength inferred from simple one-component models are caused by fluctuations in the filling factor (i.e., the fractional area of the resolution element occupied by flux tubes), not by changes in the intrinsic magnetic and kinematic properties of the background or the flux-tube atmospheres. Also, we confirm the jump of magnetic field azimuth proposed by Müller et al. (2002) to explain the observed net circular polarization of infrared lines.

Key words: polarization - Sun: sunspots - Sun: magnetic fields - Sun: photosphere - line: profiles

1 Introduction

The global structure of the penumbra is relatively well known from an observational point of view (see, e.g., Martínez Pillet 1997; del Toro Iniesta 2001; Solanki 2003). During the last decades, full spectropolarimetric measurements have been used to determine the organization of the magnetic field vector and the flow field in the penumbra. The underlying hypothesis in most of the analyses is that the observed Stokes profiles can be explained in terms of a single magnetic atmosphere filling the resolution element. Under this assumption, it has been found that the magnetic field strength decreases and the magnetic field inclination increases radially as the outer penumbral boundary is approached. Another important result is that the magnetic field vector and line-of-sight velocity undergo significant azimuthal fluctuations around the sunspot center (Beckers & Schröter 1969; Degenhardt & Wiehr 1991; Schmidt et al. 1992; Title et al. 1993; Lites et al. 1993; Stanchfield et al. 1997; Westendorp Plaza et al. 2001a,b; Bellot Rubio 2003; Mathew et al. 2003). These fluctuations occur on spatial scales much larger than the sizes of the penumbral fibrils.

The fine structure of the penumbra shows up prominently in high resolution images taken with large telescopes, adaptive optics, and speckle or phase diversity reconstruction techniques. The typical size of the bright and dark penumbral filaments is 150-250 km (Scharmer et al. 2002; Rouppe van der Voort et al. 2004; Sütterlin et al. 2004). This is much smaller than the spatial resolution of current spectropolarimetric measurements (700 km at best). Thus, the question arises as to how well the magnetic and kinematic properties inferred from one-component analyses describe the various (spatially unresolved) constituents of the penumbra. An answer to this question is important to decide on the reliability of the derived penumbral structure and to understand the origin of the observed azimuthal fluctuations.

Indications that the characterization of the penumbra in terms of one-component atmospheres may be inaccurate do exist. The most prominent example is perhaps the observation that the Evershed flow is more horizontal than the magnetic field vector by as much as 10$^{\circ}$ (Adam & Petford 1991; Title et al. 1993; Skumanich et al. 1994; Martínez Pillet 1997; Solanki 2003; Bellot Rubio 2003). This result contradicts the theoretical expectation that the magnetic field must be frozen in the photospheric plasma (e.g., Stix 2002). The explanation commonly put forward to resolve the problem is that the unresolved structure of the penumbra is not accounted for. The flow occurs preferentially in the more inclined fields and its inclination is compared with the inclination of the average magnetic field, which gets contributions from both highly inclined and more vertical structures. Therefore, the average magnetic field must appear more vertical than the velocity vector (Title et al. 1993; Martínez Pillet 1997), as observed. If this conjecture is correct, the lack of parallelism between the magnetic field and the flow would be an artifact induced by a too simplistic interpretation of the observations.

The shapes of the observed polarization profiles also suggest that the penumbra is formed by more than one magnetic component. A first indicator is the net circular polarization (NCP), defined as the integral of Stokes V over wavelength. The NCP of lines emerging from the penumbra is different from zero. Non-zero NCPs are produced by gradients or discontinuities of the atmospheric parameters along the line of sight (Auer & Heasley 1978; Sánchez Almeida & Lites 1992; Landolfi & Landi degl'Innocenti 1996; Schlichenmaier et al. 2002; Müller et al. 2002). Solanki & Montavon (1993) acknowledged this as a fundamental ingredient of sunspot penumbrae and incorporated the required discontinuities in their uncombed penumbral model. The uncombed model envisions the penumbra as a collection of small horizontal flux tubes embedded in a more vertical magnetic field, i.e., as a two-component structure. Another indicator is the observation that a significant fraction of penumbral Stokes V profiles of visible and infrared lines show anomalous shapes with three or even four lobes (Sánchez Almeida & Lites 1992; Westendorp Plaza et al. 2001a; del Toro Iniesta et al. 2001; Bellot Rubio et al. 2002; Schlichenmaier & Collados 2002; Bellot Rubio 2003). The abnormal shapes have been interpreted as the superposition of different signals produced by at least two magnetic components coexisting in the resolution element. The observed linear polarization profiles have more regular shapes, but they also provide indications of two different magnetic components (Collados 2002; Schlichenmaier & Collados 2002; Bellot Rubio 2003).

To improve our understanding of the penumbra, the obvious next step is to interpret the observations using a model capable of describing, at least to a first approximation, the unresolved structure of the penumbra, i.e., a model incorporating more than one magnetic component. In this paper, we present the first inversion of a complete spot in terms of a two-component model. On purpose, we adopt the simplest geometrical scenario possible and assume that the two magnetic atmospheres lie next to each other in the resolution element, without any vertical interlacing. In addition, the magnetic and kinematic parameters describing the two atmospheres are taken to be constant with height. This simple representation of the fine structure of the penumbra turns out to be sufficient to explain the polarization profiles of infrared lines. The two components of the model can be associated with penumbral flux tubes and the surrounding magnetic fields in which they are embedded. Our analysis resolves some conflicts generated by simple one-component interpretations of the observations. We find, for instance, a perfect alignment of the velocity vector and the magnetic field vector in the flux-tube component carrying the Evershed flow.

The paper is organized as follows. After describing the observations (Sect. 2), we present the geometrical model adopted and give details of the inversion (Sect. 3). Sections 4 and 5 are devoted to investigating the magnetic and kinematic configuration of the penumbra inferred from the two-component inversion. In Sect. 6 we discuss the azimuthal fluctuations of the atmospheric parameters indicated by one-component analyses, and the generation of the NCP of infrared lines. Finally, Sect. 7 summarizes our findings. Preliminary results of this work have been presented by Balthasar et al. (2003), Bellot Rubio (2003, 2004) and Bellot Rubio et al. (2003).

2 Observations and data reduction

On September 20, 1999 the main spot of NOAA Active Region 8704 was observed with the Tenerife Infrared Polarimeter (TIP; Martínez Pillet et al. 1999) attached to the Vacuum Tower Telescope of Teide Observatory (Tenerife, Spain). The spot was located at an heliocentric angle of 40$^{\circ}$. Large heliocentric angles are important to maximize the Doppler shifts induced by the almost horizontal Evershed flow, and also to separate the two magnetic components of the penumbra on the center side through the spectral signatures they leave on the linear polarization profiles. Maps of the spot were created by scanning the spectrograph slit (of length 35 arcsec and width 0.5 arcsec) across the solar disk in steps of 0.38 arcsec. The pixel size was 0.35 arcsec in the spatial direction and 2.9 pm in the spectral direction. The integration time for one slit position was 2 s, allowing us to reach a noise level of about 10^-3 in units of the continuum intensity. With this integration time, the total time needed to scan the spot was 6 min. The scanning was done with the help of a correlation tracker (Schmidt & Kentischer 1995; Ballesteros et al. 1996), which also served to reduce image motion due to turbulence in the Earth's atmosphere. The seeing conditions were fair, leading to an effective spatial resolution of about 1.1 arcsec. This value has been estimated from the average power spectrum of the quiet sun granulation.

TIP was used to record the four Stokes profiles of three neutral iron lines at 1565 nm (see Table 1). A detailed account of the properties of these lines is given by Cabrera Solana et al. (2005). The lines are very sensitive to magnetic fields not only because of the $\lambda^2$-dependence of the Zeeman splitting, but also because of their large Landé factors (the two stronger lines have $g_{\rm eff} = 3$ and $g_{\rm eff} = 1.45$, respectively). The observed lines probe very deep atmospheric layers due to the reduced opacity of H$^{\rm -}$ at these wavelengths (the minimum opacity occurs at 1642 nm). Also, the high excitation potentials of the lower atomic levels mean that the lines do not form in the cool layers above $\log \tau_5 \sim -2$, where $\tau_5$ represents continuum optical depth at 500 nm.

Figure 1: Continuum intensity ( left), total circular polarization ( middle), and total linear polarization ( right) maps of AR 8704 as observed with TIP on 1999 September 20 at 15:25 UT. The linear polarization L is defined as L2 = Q2 + U2. The arrow indicates the direction to disk center. It also represents the positive y-axis of the local reference frame. Contour levels for the inner and outer penumbral boundaries are 0.75 and 0.90 of the quiet sun continuum intensity. The continuum map shows an azimuthal path at a normalized radial distance of 0.7. The crosses mark the position of the Stokes profiles displayed in Fig. 3.

Open with DEXTER

Table 1: Atomic parameters of the observed lines. $\lambda _0$ is the laboratory central wavelength, $\chi _\ell$ the excitation potential of the lower level, and $\log gf$ the logarithm of the oscillator strength times the multiplicity of the level. The parameters $\alpha$ and $\sigma$ (in units of Bohr's radius, a₀) are used to calculate the broadening of the lines by collisions with neutral hydrogen atoms. The last column gives the effective Landé factor of the transition. Oscillator strengths are from Borrero et al. (2003a).

Dark subtraction, flatfielding, and merging of the two beams have been performed in the usual way. The resulting Stokes profiles have been corrected for instrumental polarization applying the statistical procedure explained by Schlichenmaier & Collados (2002) and Collados (2003). After correction, residual crosstalk from linear to circular polarization and vice versa is estimated to be $\sim$1%. The observed Stokes profiles have been normalized to the continuum intensity of the average quiet sun profile in the map, in order to have an absolute calibration of the intensity and polarization signals. This absolute calibration facilitates the recovery of temperatures and the determination of the amount of stray light contamination.

In the absence of telluric lines or other means to define an absolute velocity scale, we use the central wavelength of the average quiet sun intensity profile, corrected for convective blueshift, as the position of zero velocities. The convective blueshift of these lines is estimated to be 445 m s^-1 from the two-component model of the quiet sun of Borrero & Bellot Rubio (2002) and the results of Balthasar (1985). The absolute velocity calibration of the observations should be correct to within $\pm$100 m s^-1.

The red wing of the intensity profiles of Fe I 1564.8 nm is affected by a telluric blend. We have removed the blend by inverting the average quiet sun intensity profile of the line with the two-component model of Borrero & Bellot Rubio (2002). The difference between the observed average profile and the best-fit profile gives the shape of the blending line, allowing us to remove it from the individual spectra in the same way as done by Mathew et al. (2003).

Figure 1 shows the continuum intensity and polarization maps of AR 8704 as observed with TIP. The latter have been constructed by integrating the unsigned circular and linear polarization profiles of Fe I 1564.8 nm over wavelength (the linear polarization signal L is defined as L² = Q² + U²). With a spatial resolution of about 1 arcsec, the filamentary structure of the penumbra is still apparent in the continuum map. The total circular and linear polarization maps show large differences between the center-side and limb-side penumbra, due to projection effects. On those sides of the penumbra where the circular and linear signals are smaller, one can clearly distinguish radial structures with enhanced polarization. These structures were detected for the first time in maps taken with the Advanced Stokes Polarimeter (Elmore et al. 1992) and are sometimes referred to as spines and intra-spines (Lites et al. 1993). One-component analyses of the observed polarization profiles suggest that the spines and intra-spines are caused by azimuthal fluctuations in the inclination and strength of the magnetic field vector (see the discussion in Bellot Rubio 2003).

Figure 2: Spatial variation of the intensity ( left), circular polarization ( middle) and linear polarization ( right) profiles of the Fe I 1564.8 nm line in AR 8704 along the symmetry line connecting the disk center and the sunspot center. The horizontal and vertical axes represent the spectral and spatial directions, respectively. The center-side penumbra is at the top. The Stokes V and L profiles in each row have been normalized to their maximum absolute values for better visibility. Note that the maximum Doppler shifts occur near the spatial positions where Stokes V and Stokes L show discontinuities.

Open with DEXTER

Figure 2 demonstrates that at least two magnetic components must exist in sunspot penumbrae. Here we plot the spatial variation of the intensity, circular polarization, and linear polarization profiles emerging from AR 8704 along the symmetry line, i.e., the line connecting the disk center and the sunspot center. In the limb-side penumbra, Stokes V changes polarity at the position of the neutral line. This geometrical discontinuity divides the penumbra in two regions dominated by different magnetic signals. In the inner limb-side penumbra, the Stokes V profiles indicate strong magnetic fields and small flow velocities. Beyond the neutral line, the Stokes V signal suggests weaker field strengths and larger flow velocities. The transition between the two regimes is very abrupt. As first noticed by Collados (2002), the linear polarization profiles also show a "neutral line'' in the center-side penumbra. Again, this line separates two regions where the polarization signals are quite different. In agreement with the inferences from Stokes V, the linear polarization profiles indicate strong fields and small flow velocities in the inner center-side penumbra, and the opposite in the outer center-side penumbra. The very different Zeeman splittings and Doppler shifts observed immediately before and after the two discontinuities reveal that the penumbra is formed by at least two magnetic components with different field strengths, inclinations, and material flows. At locations where the geometry is favorable, the signals produced by these atmospheric components are clearly seen in the same resolution element as, for example, near the neutral lines. Conceivably, both components are present all over the penumbra, with different weights in different spatial locations so that one dominates in the outer penumbra and the other shows up more prominently in the inner penumbra. The two magnetic components indicated by the observations probably reflect the fine structure of the penumbra, and are compatible with existing theoretical models of the penumbra (Schlichenmaier et al. 1998; Thomas et al. 2002; Weiss et al. 2004). Earlier analyses of visible lines (Bernasconi et al. 1998; Lites et al. 2002) and infrared lines (Rüedi et al. 1999; del Toro Iniesta et al. 2001; Schlichenmaier & Collados 2002) have also revealed the existence of two magnetic components in sunspot penumbrae.

3 Model atmosphere and inversion

To account for the unresolved structure of the penumbra, at least to first order, we assume that each pixel contains two different magnetic atmospheres interlaced horizontally but not vertically. The atmospheric parameters describing the two components of the model are taken to be constant with height except for the temperature, which is allowed to vary with depth by means of two nodes (gas pressures and densities also change with height as specified by the condition of hydrostatic equilibrium). In particular, the magnetic field vector and the line-of-sight (LOS) velocity are constant in the two components. This choice is natural in the first application of such a complex model to real observations, but it entails a considerable simplification of the problem. For the present investigation, however, the assumption of height-independent parameters may be justified in view of the small range of optical depths to which our lines are sensitive: the line-forming region is not thicker than one or two decades in  $\log \tau_5$ (Mathew et al. 2003; Cabrera Solana et al. 2005), in sharp contrast to the case of visible lines. Our model is unable to produce any NCP because it does not incorporate discontinuities or gradients along the LOS. This, however, does not compromise the quality of the fits because the infrared lines studied here exhibit very little NCP (see Borrero et al. 2004, and Fig. 10a).

Throughout the paper, the two components of the model will be referred to as background and flux-tube atmospheres for simplicity. These magnetic components give rise to different Stokes profiles  $\vec{I}_{\rm b}$ and  $\vec{I}_{\rm t}$. Due to the lack of spatial resolution, the two signals are mixed according to a filling factor f which represents the fractional area of the pixel occupied by the flux-tube atmosphere. After accounting for scattered/stray light via a stray light factor $\alpha$, the Stokes profiles emerging from the resolution element, $\vec{I} = (I, Q, U, V)^{\rm T}$, are modeled as

$$% \vec{I} = (1-\alpha) \left[ (1-f) \vec{I}_{\rm b} + f \vec{I}_{\rm t} \right] + \alpha \vec{I}_{\rm stray}.$$ (1)

The stray light is assumed to be unpolarized, i.e., $\vec{I}_{\rm stray} = (I_{\rm stray}, 0, 0, 0)^{\rm T}$, where $I_{\rm stray}$represents the average intensity profile in the non-magnetic regions of the map.

The observed Stokes profiles have been inverted using the SIR code (Stokes Inversion based on Response functions; Ruiz Cobo & del Toro Iniesta 1992). SIR computes synthetic Stokes profiles by solving the radiative transfer equation for polarized light in the two-component model atmosphere under the assumptions of local thermodynamical equilibrium and hydrostatic equilibrium. A non-linear, least-squares Marquardt's algorithm (Press et al. 1986) is used to modify the parameters of an initial guess model until the synthetic profiles match the observed ones.

The inversion returns the temperature stratification, the three components of the magnetic field vector, and the LOS velocity of the two components of the model, together with a single value for the macroturbulent velocity. In addition, the stray light factor $\alpha$and the filling factor f of the flux-tube component are also determined. Thus, the total number of free parameters is 15. The availability of full Stokes profiles renders it possible to derive the three components of the magnetic field vector accurately. Also, the stray light contamination is determined accurately by forcing an agreement between the observed intensity profiles and the corresponding polarization signals.

Although we focus on the penumbra, the umbra of AR 8704 has been inverted as well. In the umbra, the Fe I 1565.2 nm line is blended with two molecular OH lines whose signals may be larger than that of the iron line itself (Mathew et al. 2003). Since the OH lines are not considered in the spectral synthesis, we have chosen not to fit the umbral Stokes I and V profiles of Fe I 1565.2 nm, in order to prevent the code from finding a wrong atmospheric model. That is, in the umbra we fit the four Stokes parameters of the Fe I lines at 1564.7 and 1564.8 nm, plus the Stokes Q and U profiles of Fe I 1565.2 nm. We keep the Q and U profiles of Fe I 1565.2 nm because the OH lines do not show up in linear polarization.

Similar two-component inversions have been carried out earlier by Bernasconi et al. (1998), Rüedi et al. (1999), Leka (2001), del Toro Iniesta et al. (2001), Lites et al. (2002), and Borrero et al. (2004). Most of these studies concentrate on a few spatial positions across the penumbra, without attempting the inversion of the full spot.

4 Results

The quality of the fits can be assessed from Fig. 3, where we display the observed and best-fit Stokes profiles emerging from two pixels in the center-side and limb-side penumbra (the latter near the neutral line). The center-side Stokes V profiles exhibit normal two-lobed shapes, but they possess extended red wings. The most remarkable feature in this example is the abnormal shape of Stokes Q, which seems to result from two very different signals. In the limb-side penumbra near the neutral line, the observed Stokes Vprofiles show abnormal shapes with three lobes. Interestingly, also the Stokes Q and U profiles display asymmetrical shapes.

As expected, the two-component model is able to provide a good fit to the observed Stokes profiles, with residuals only slightly larger than the noise (the examples shown in Fig. 3 represent the worst-case scenario, for more normal Stokes profiles are usually better reproduced). The rms difference between synthetic and observed profiles is of the order of 4 $\times$ 10^-3 in units of the continuum intensity. On average, the $\chi^2$-values of the fits are a factor of two lower than those resulting from a simpler one-component inversion of the same data (Bellot Rubio 2003). In fact, one-component inversions without gradients of the physical parameters cannot reproduce such abnormal profiles. Either two magnetic components or one-component inversions with gradients (e.g., Mathew et al. 2003; Bellot Rubio et al. 2002; Borrero et al. 2004) are required to explain the different polarities indicated by the observations.

Figure 3: Examples of observed (dots) and best-fit (solid lines) profiles emerging from the center-side ( left) and limb-side ( right) penumbra at the spatial locations marked in Fig. 1 with crosses. Note the abnormal Stokes Q profiles and the extended red wings of Stokes V on the center side. The example for the limb-side penumbra was observed near the neutral line. At this position, Stokes V shows three lobes and Stokes Q and U are clearly asymmetric.

Open with DEXTER

Figure 4: Magnetic and kinematic configuration of AR 8704 as derived from the two-component inversion of the observed Stokes profiles. From top to bottom: magnetic field strength, magnetic field inclination, magnetic field azimuth, and LOS velocity (positive values indicate redshifts) for the background ( left) and flux-tube ( right) atmospheres. All angles are expressed in the LRF. Azimuths are measured counterclockwise from the positive x-axis of the LRF. The umbra in the flux-tube component is displayed in black because the filling factor is nearly zero there.

Open with DEXTER

Figure 4 displays maps of the magnetic field vector and LOS velocity in AR 8704 as inferred from the two-component inversion for the background (left) and the flux-tube (right) atmospheres. The magnetic field inclination and azimuth are expressed in the local reference frame (LRF). The LRF is defined by the z-axis pointing away from the Sun along the local vertical and the y-axis pointing to disk center along the symmetry line. The transformation to the LRF has been done by computing the cartesian coordinates of the magnetic field vector in the LOS frame from the LOS inclinations and azimuths returned by the inversion code, and then applying a rotation of angle $\theta$ (the heliocentric angle) about the x-axis. The new cartesian coordinates in the LRF are converted back into zenith angles and azimuths using standard formulae. As revealed by Fig. 3, the spot is of negative polarity. In order to facilitate the interpretation of our results, the magnetic zenith angles $\gamma$ and azimuths $\psi$ are displayed throughout the paper as if the spot were of positive polarity, i.e., we have made the transformations $\gamma \rightarrow \pi - \gamma$ and $\psi \rightarrow \psi - \pi$. Zenith angles of 90$^{\circ}$ denote fields parallel to the solar surface. The 180$^{\circ}$ ambiguity of the LOS azimuth has been removed by demanding a smooth variation of the LRF magnetic field vector around the sunspot's center.

The maps of atmospheric parameters displayed in Fig. 4 are remarkably smooth in spite of the fact that they are based on the inversion of about 9100 individual pixels. We believe this testifies to the adequacy of the geometrical model adopted. A disturbance in the outer penumbra at coordinates (13,27) arcsec can be seen in some of the maps. The disturbance coincides with an anomalous penumbral region observed in high resolution images of the spot taken with the Dutch Open Telescope four hours earlier (Balthasar et al. 2001).

From Fig. 4 it is clear that the two magnetic components of the penumbra exhibit rather different properties. The first component, the background (left panels), is characterized by stronger and more vertical fields than the second (right panels). In both components, the field strength decreases and the magnetic zenith angle increases with radial distance, although at slightly different pace. As revealed by the magnetic azimuth maps, the magnetic field vector in the two components is essentially radial. We do not see the field azimuth variation across spine regions reported by Lites et al. (1993) and Skumanich et al. (1994) from one-component inversions of the Fe I lines at 630 nm. These variations were interpreted as a natural consequence of the strong spine fields forming a canopy over the surrounding, more horizontal flux tubes. Since the angular resolution of our observations is similar to that of Lites et al., we believe that the reason why such azimuth variations are not detected in the present analysis is that the infrared lines sample deeper layers coinciding more or less with those where the tubes reside. In addition, the line forming region is much narrower, its thickness being comparable to the diameter of the tubes. Under these conditions, the wrapping of the background field lines around the tubes may be less obvious in the infrared than in the visible (interestingly enough, the one-component inversions of AR 8704 presented by Bellot Rubio 2003 did not reveal significant azimuth variations near spine regions either). Figure 4 also shows that the LOS velocities in the background are negligible in the inner penumbra and small in the outer penumbra. By contrast, the LOS velocity in the flux tubes increases radially, reaching values as large as 6 km s^-1in the outer penumbra. The LOS velocity shows a marked azimuthal dependence, with redshifts in the limb-side and blueshifts in the center-side penumbra. This is the signature of the Evershed flow (see Thomas 1994, for a review).

An intriguing result of our inversions is the abrupt jump exhibited by the magnetic zenith angle of the background atmosphere in the middle penumbra, where the field suddenly becomes more horizontal when going from the umbra to the outer penumbral boundary. This jump is more pronounced on the limb side, but it can also be seen on the center side. We have no explanation for this behavior, although it is important to mention that it occurs beyond the neutral line (cf. Fig. 1). Apparently, a jump in the background magnetic zenith angle is required to provide a fit to the observed Stokes profiles: forcing the zenith angle of the background to be the same on either side of the discontinuity results in significantly poorer fits away from the umbra. We suspect that the jump is not real, but a consequence of our using a too simplistic model of the penumbra. It may well be that another atmospheric component is present in the middle penumbra and beyond. Since our model only contains two magnetic atmospheres, the third component could get mixed with the background atmosphere, which might result in a discontinuity in the radial variation of the zenith angle if the field is more inclined in the third component than in the background. This conjecture should be verified by increasing the complexity of the inversion, which will probably require more information in the form of simultaneous observations of visible and infrared lines. In any case, we would like to remark that the strange behavior of the background zenith angle in the middle penumbra affects the other atmospheric parameters very little, in particular those of the flux-tube component.

Figure 5 shows the spatial distribution of the filling factor, i.e., the fractional area of the resolution element covered by the flux-tube component. The map indicates that flux tubes are largely absent in the umbra. The visibility of the tubes increases rapidly in the inner penumbra, reaching a plateau in the middle penumbra. The behavior in the outer penumbra is less clear, with the limb side showing a pronounced decrease in filling factor and the center side featuring a smaller radial variation of this quantity. In the limb-side penumbra, the filling factor starts to decrease where the background magnetic zenith angle suddenly becomes more horizontal (see Fig. 4).

	Figure 5: Map of the fractional area of the resolution element occupied by the second magnetic component (the flux-tube atmosphere).
Open with DEXTER

   
5 The structure of the penumbra

The global behavior of the inferred magnetic field strengths (decreasing towards the outer edge of the spot), the magnetic zenith angles and the LOS velocities (both increasing radially) in the two components confirm earlier results based on simpler models (e.g., Beckers & Schröter 1969; Lites et al. 1993; Keppens & Martínez Pillet 1996; see also the review by Solanki 2003). Our inversions, however, provide separate information on these physical quantities for the two magnetic components of the penumbra.

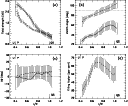Figure 6: Magnetic configuration of AR 8704 as inferred from the two-component inversions presented in this work. a) Azimuthally averaged magnetic field strength; b) magnetic zenith angle; c) relative magnetic azimuth; and d) filling factor for the background (solid lines) and flux-tube (dashed lines) atmospheres, as a function of normalized radial distance (R is the spot radius as seen in the continuum image). The inner and outer penumbral boundaries are indicated with small vertical bars on the x-axes. The relative azimuth $\Delta \psi$ is the azimuth difference between the observed magnetic field vector and a purely radial field (with zero azimuth along the positive x-axis of the LRF). Error bars represent the rms variation of the parameters along each azimuthal path. For clarity purposes, error bars in panel c are given only for the flux-tube component. The rms variations of the relative azimuth in the background are similar.

Open with DEXTER

To characterize the properties of the two magnetic components in a more quantitative way, we have constructed radial profiles by averaging the atmospheric parameters along azimuthal paths centered on the spot. Azimuthal paths are taken to be ellipses oriented in such a way that they mimic the spot shape locally, with semimajor axes covering all radial distances from the umbra/penumbra boundary to the outer penumbral boundary (normalized radial distances r/R from 0.4 to about 1.05, where R represents the radius of the spot in the continuum map). The azimuthal paths explicitly avoid the disturbance mentioned in the previous section. An example of azimuthal paths is shown in the continuum image of Fig. 1.

Figure 6 displays the radial variation of the azimuthally averaged field strength, zenith angle, and relative azimuth in the background and the flux-tube atmospheres, along with that of the filling factor. In the following, we describe the magnetic configuration of the penumbra based on these radial profiles.

5.1 Magnetic field configuration

As seen in Fig. 6a, the field strength in both the background and the flux-tube components decreases radially outwards. Interestingly, the magnetic field in the tubes is weaker (by some 500-800 G) than in the surroundings from the inner penumbra up to approximately 0.9 penumbral radii. At this position, the azimuthally averaged field strength in the tubes becomes slightly larger than in the background. Since the field strength difference is very small in the outer penumbra, we do not attach any particular relevance to this result. It is clear, however, that the radial variation of the field strength is slower in the tubes. Such a behavior, first noticed by Rüedi et al. (1999), has also been confirmed by Borrero et al. (2004). The latter authors suggest that this result may bear important consequences for the physical mechanism driving the Evershed flow. That the field strength in the tubes is weaker in the inner penumbra is not surprising if the tubes are hotter than the background, as suggested by the moving tube simulations of Schlichenmaier et al. (1998). The hotter plasma inside the tubes implies a larger gas pressure, hence the internal magnetic pressure (and correspondingly the field strength) must be smaller to maintain horizontal mechanical equilibrium. A larger field strength in the tubes compared with the surroundings near the outer penumbral boundary was first reported by Westendorp Plaza et al. (2001a). The enhanced field strength of the tubes in this part of the penumbra could be related to the cooling of the plasma as it flows along the tubes (Schlichenmaier et al. 1999). It could also result from the gradual shift of the background magnetic field towards higher layers required to explain the sunspot canopy (cf. Solanki et al. 1992). With the present data, however, we cannot confirm this idea because our inversion neglects possible gradients of the atmospheric parameters with height.

Figure 6b demonstrates that the inclination of the magnetic field vector in the background and the flux tubes increases with radial distance. However, the two components show quite different behaviors. The magnetic field in the background remains relatively vertical all the way from the inner to the outer penumbral boundary, with maximum inclinations of about 60$^{\circ}$. By contrast, the inclination of the magnetic field in the tubes changes from $\sim$70$^{\circ}$ near the umbra to some 100$^{\circ}$ at the outer penumbral edge. That is, the tubes are slightly inclined upwards in the inner penumbra, then become horizontal at about 0.8 penumbral radii, and finally dive below the solar surface at larger radial distances. In interpreting these results one must recall that single tubes cannot extend from the inner to the outer penumbra with the inclinations displayed in Fig. 6b, as they would quickly move outside the line forming region (cf. Schlichenmaier & Schmidt 2000). The behavior of the average inclination angle thus refers to the ensemble of tubes that are conceivably present at each radial distance. The individual tubes are crossed by any given azimuthal path at different positions from their inner footpoints, so they contribute to the average with different inclination angles (see Fig. 3 in Schmidt 2002, for a sketch).

It is important to mention that our results do not confirm the magnetic zenith angles inferred from simpler one-component models (e.g., Beckers & Schröter 1969; Lites & Skumanich 1990; Keppens & Martínez Pillet 1996; Stanchfield et al. 1997; see also Bellot Rubio 2003, for a one-component inversion of the spot studied here). In these analyses, the average inclination is found to increase from some 30$^{\circ}$ at the umbral boundary to about 75$^{\circ}$ at the outer sunspot edge. That is, the zenith angles determined from one-component analyses are too horizontal for the background atmosphere and too vertical for the flux-tube atmosphere. More importantly, these analyses do not reveal the existence of field lines going back to the solar surface in the middle penumbra and beyond, except perhaps at some isolated patches (Westendorp Plaza et al. 1997, 2001a; Mathew et al. 2003). By contrast, our two-component analysis indicates that negative polarity flux tubes are present almost everywhere in the outer penumbra. Similar two-component inversions of another spot by Borrero et al. (2004) also confirm that flux tubes return to the solar surface in the mid-penumbra and beyond. Magnetic fields pointing downwards in the penumbra are predicted by most theoretical models of the Evershed flow: the siphon flow model (Thomas & Montesinos 1993), the moving tube model (Schlichenmaier 2002) and the downward-pumping model of Thomas et al. (2002) and Weiss et al. (2004). Also, we want to stress that the magnetic field inclinations found in the background atmosphere coincide very well (at all radial distances) with those predicted by the current sheet sunspot models of Jahn (1989). This is quite remarkable, as the agreement is not satisfactory when the predicted inclinations are compared with the ones deduced by Beckers & Schröter (1969).

Figure 6c shows the relative azimuth  $\Delta \psi$, i.e., the LRF azimuth difference between the inferred magnetic field vectors and a purely radial field. This quantity gives an idea of the twist of the field lines in the flux tubes and the background. Almost everywhere in the penumbra, the relative azimuths are smaller than 5$^{\circ}$ in both atmospheric components, suggesting that the fields are essentially radial. Note, however, that the field lines may possess significant azimuthal components at some locations in the penumbra, as revealed by the rms fluctuations of the individual values. The small average relative azimuths detected in the flux tubes and the background are in excellent accord with the values reported earlier by Lites & Skumanich (1990), Westendorp Plaza et al. (2001a), and Mathew et al. (2003). We believe that at least part of the observed deviations from radial fields must be solar in origin, as they are larger than our uncertainty of about $\pm$$2^{\circ}$ in locating the origin of azimuths (defined by the orientation of the calibration optics in front of the polarimeter).

Figure 6d displays the radial variation of the azimuthally averaged filling factor. In the umbra, the flux-tube component is almost absent. Flux tubes show up in the inner penumbra, where the filling factor increases quickly, reaching a maximum of $\sim$65% at around 0.7 penumbral radii. Towards the outer sunspot boundary, the filling factor decreases slightly down to about 50%. Whether this reflects a smaller number of tubes or changing visibility conditions (e.g., a gradual shift of the tubes to layers below or above the line forming region) cannot be decided without a more realistic model including gradients of the atmospheric parameters. The extended height coverage required by such a model could be provided by simultaneous observations of infrared and visible lines.

5.2 Kinematic structure

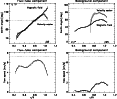Figure 7: Kinematic configuration of AR 8704 as deduced from the two-component inversions. Top panels: zenith angle of the velocity vector in the flux-tube ( left) and background ( right) atmospheres. For comparison purposes, the zenith angle of the magnetic field vector in each component is also depicted (thick lines). Bottom panels: magnitude of the velocity vector in each component. Error bars for the flow angles and flow speeds have been computed through error propagation of the uncertainties in the best-fit coefficients of Eq. (2). Error bars for the magnetic zenith angles represent the uncertainties in the azimuthal averages.

Open with DEXTER

The velocity vector cannot be inferred directly from the observations, because only the LOS component induces a Doppler shift in the Stokes profiles. To overcome this problem, clever geometrical methods have been developed in the past. Assuming that the flow is axially symmetric around the spot and that its magnitude v depends only on radial distance r, the projection of the velocity vector to the LOS would be given by

$$% v_{\rm LOS} (r, \varphi) = v_{r}(r) \sin \theta \cos \varphi - v_{z}(r) \cos \theta,$$ (2)

where v_r and v_z represent the radial and vertical components of the velocity vector in the LRF (positive outwards and upwards, respectively), $\theta$ is the heliocentric angle of the observations, and $\varphi$ is the position angle measured counterclockwise from the negative y-axis of the LRF. From the inversion we know $v_{\rm LOS} (r, \varphi)$ for the two atmospheric components, hence it is possible to determine v_r(r) and v_z(r) by least-squares fitting the observed variation of the LOS velocities around the sunspot center. The azimuthally averaged magnitude and inclination of the velocity vector at r are then given by v = (v_r²+v_z²)^1/2 and $\gamma_{v} = \arctan v_{r}/v_{z}$, respectively. This method, originally proposed by Kinman (1952), has been used in many studies (e.g., Maltby 1964; Schröter 1965; Title et al. 1993; Skumanich et al. 1994; Rimmele 1995; Martínez Pillet 1997; Schmidt & Schlichenmaier 2000; Schlichenmaier & Schmidt 2000; Bellot Rubio et al. 2003; Tritschler et al. 2004). The reliability of the inferred flow angles decreases when the azimuthal modulation caused by the first term on the right hand side of Eq. (2) is affected by noise. This happens when either v or v_r are small, i.e., when there is no flow or the flow is predominantly vertical. For the method to give reliable results, it is also necessary that the fluctuations in $v_{\rm LOS} (r, \varphi)$ caused by the fine structure of the penumbra be smaller than the sinusoidal variation of  $v_{\rm LOS}$. Since we account for this fine structure by considering two magnetic components in the resolution element, our LOS velocities should provide more realistic results than Doppler shifts deduced directly from, e.g., line bisectors, which cannot separate the effects of the different magnetic components of the penumbra.

Figure 7 displays the radial variation of the angle and the magnitude of the flow in the background and flux-tube atmospheres as deduced from two independent least-squares fits of the inferred LOS velocities to Eq. (2), one for each atmospheric component. Let us consider first the results for the flux-tube atmosphere (left panels). Because of the much larger flow speeds (up to 6.5 km s^-1), the magnetic component describing the penumbral tubes is responsible for the largest fraction of the total mass flux. The inclination of the flow in the tubes increases almost linearly from the inner to the outer penumbra. At a normalized radial distance of 0.8, the flow becomes horizontal, and further outwards it returns to the solar surface. There is a perfect alignment of the velocity and magnetic field in the flux tubes: the velocity vector and the magnetic field vector are parallel from the inner penumbra all the way to the outer penumbral boundary, with maximum differences of only $\pm$$2^{\circ}$, well within the error bars. This is a solid conclusion: a systematic error of 100 m s^-1 in the LOS velocities (due to uncertainties in the value of the convective blueshift) would change the flow angles by a mere $\pm$1.5$^{\circ}$. As pointed out by Bellot Rubio et al. (2003), this result solves the old problem of non-parallelism of the Evershed flow and the field lines, and shows that the origin of the problem is the inability of simpler one-component analyses to properly describe the fine structure of the penumbra. As can be seen in the upper left panel of Fig. 7, the only region where the Evershed flow would be more horizontal than the magnetic field is the very outer penumbra. A faster-than-expected decrease of the downward vertical velocity near the outer penumbral edge is responsible for the discrepancy. We believe that the downward penumbral velocities get more and more mixed with the upward granulation velocities as one moves to the outer parts of the spot, leading to the observed decrease in the magnitude of the vertical velocity. This idea is supported by the observation that, due to the irregular shape of the spot, the more external azimuthal paths encounter some quiet sun granulation intrusions. Thus, the angles derived near the outer penumbral boundary may not be representative of the true inclination of the flow.

Let us now turn our attention to the kinematic structure of the background component (right panels in Fig. 7). This atmosphere harbors very small motions in the inner penumbra, the flow speed never exceeding 0.4 km s^-1. Beyond r/R = 0.7, the flow speeds are larger, reaching maximum values of 2 km s^-1. Thus, the background is not at rest. Our non-zero background velocities are able to explain an important, but subtle, observational result. As spots cross the solar disk, the NCP of visible lines in the center-side penumbra near the symmetry line is observed to change sign at an heliocentric angle of $\theta \sim 16^{\circ}$ (Martínez Pillet 2000); that is, the NCP in the center-side penumbra is positive when $\theta < 16^{\circ}$ and negative when $\theta > 16^{\circ}$. Zero NCPs along the symmetry line occur when the LOS velocities in the background and the tubes are the same, i.e., when $v_{\rm back}~ \cos ~ (\gamma_{v,{\rm back}} \pm \theta) = v_{\rm tube} ~ \cos ~(\gamma_{v,{\rm tube}} \pm \theta)$, with the minus sign referring to the center side and the plus sign to the limb side. The flow speeds and inclinations displayed in Fig. 7 for the background and the flux tubes at r/R = 0.9 predict zero NCPs on the center side at $\theta = 14^{\circ}$. This is almost exactly what is observed. In addition, the non-zero background velocities prevent the NCP from changing sign in the limb-side penumbra where $\gamma_{v,{\rm tube}} < 90^{\circ}$, which also agrees with the observations (Martínez Pillet 2000). The similarity between predictions and observations is reassuring, because the heliocentric angle at which the NCP goes through zero depends sensitively on the exact geometry of the flow in the two atmospheric components.

In the outer penumbra, we find the velocity vector of the background to be more horizontal than the magnetic field by 10$^{\circ}$-20$^{\circ}$ (no calculations have been attempted in the inner penumbra because the small velocities make it impossible to derive accurate flow angles). The non-parallelism of the flow and the magnetic field in the background beyond r/R = 0.7 is reminiscent of the behavior deduced from one-component inversions. The analogy suggests that our background atmosphere is indeed a mixture of several magnetic components. That is, in the outer penumbra, the first component returned by the inversion probably represents a combination of the real (static) background and some penumbral tubes that continue upwards through the canopy, as sketched by del Toro Iniesta (2001). These tubes would be more horizontal than the background proper and more vertical than the regular tubes, carrying a small fraction of the Evershed flow to the upper layers.

The existence of such tubes could explain why the flow velocity in the background is significantly different from zero only in the outer penumbra, and why the flow seems to be more horizontal than the magnetic field. They could also explain the discontinuous behavior exhibited by the background magnetic zenith angle in the mid-penumbra (Fig. 4). Additional indications of tubes that do not return to the solar surface have been presented by Westendorp Plaza et al. (2001b) and Bellot Rubio (2004), so they deserve consideration in future analyses. Perhaps these tubes represent the inner footpoints of siphon flows ending in pores or strong magnetic flux concentrations outside the spot, as proposed by Meyer & Schmidt (1968), Thomas & Montesinos (1993), and others. We do not see the downstream footpoints of these structures because the transition from upflows to downflows occurs well above the line forming region. An alternative scenario is suggested by recent simulations of the dynamical evolution of flux tubes in the penumbra (Jahn 2003). The simulations seem to indicate that tubes originating at a depth of 5-6 Mm have the tendency to appear first in the mid-penumbra. It remains to be investigated whether or not the magnetic and kinematic properties of these flux tubes differ from those of the regular ones.

	Figure 8: Spatial positions (black pixels outside the umbra) where the flow speed in the flux-tube component is larger than the sound speed ( top) and the tube speed ( bottom). White pixels represent locations where the cosine of the LOS magnetic field inclination is smaller than 0.25. No calculations have been carried out in these pixels to avoid large extrapolations.
Open with DEXTER

The azimuthally averaged flow speed in the flux-tube component reaches values as large as 6.5 km s^-1 around 0.8-0.9 penumbral radii. This is only slightly smaller than the sound speed in the sunspot, so it is of interest to investigate if supersonic velocities exist in the penumbra. Having demonstrated that the Evershed flow is parallel to the field lines, we can determine the magnitude of the flow in each pixel using the individual LOS velocities and LOS magnetic field inclinations inferred for the flux-tube atmosphere. More specifically, the magnitude of the Evershed flow (corrected for the viewing angle) is computed as $v = v_{\rm LOS}/{\rm cos}~ \gamma_{\rm LOS}$. In addition, we can estimate for each pixel the local sound speed ($c_{\rm s}$) and the tube speed ( $c_{\rm t} = c_{\rm A} ~ c_{\rm s}/[c_{\rm A}^2+ c_{\rm s}^2]^{1/2}$, with $c_{\rm A}$ the Alfvén velocity) from the field strengths, temperatures and densities returned by the inversion code at $\log \tau_5 = -1$. In Fig. 8, overlying continuum images of AR 8704, pixels outside the umbra where the flow is supersonic (top) or supercritical (bottom) are displayed in black. To avoid large extrapolations, no calculations have been attempted where the cosine of the LOS magnetic field inclination is smaller than 0.25. White pixels represent the location of those points. As can be seen, the Evershed flow is supersonic in some places near the outer sunspot boundary, and supercritical in many pixels of the outer penumbra. Supersonic and supercritical velocities are found in 7% and 33% of the pixels, respectively. On average, the flow speeds in these pixels exceed the local sound and tube speeds by factors of 1.24 and 1.26. The maximum magnitude of the Evershed flow in the investigated penumbral area is 15.5 km s^-1. For comparison, the mean sound and tube speeds are 7.2 km s^-1 and 5.4 km s^-1, respectively. Thus, we confirm the flow speeds of 10-12 km s^-1 indicated by the moving tube simulations of Schlichenmaier (2002) and the large (sometimes supersonic) velocities observed by, among others, Bumba (1960), Wiehr (1995), del Toro Iniesta et al. (2001), and Penn et al. (2003). Our results also suggest that supercritical siphon flows may be necessary to explain the observations. Montesinos & Thomas (1997) have considered critical flows along arched magnetic flux tubes, finding that the velocity undergoes a smooth transition from subcritical to supercritical at the top of the arch. In the examples they present, however, supercritical velocities occur only beyond the outer penumbral edge, whereas we detect such velocities well within the penumbra.

6 Discussion

The structure of AR 8704 revealed by our two-component inversions is consistent with the notion of penumbral flux tubes embedded in a magnetic background atmosphere, as proposed by Solanki & Montavon (1993) and Martínez Pillet (2000). The simple inversions presented here provide a rough description of the properties of these distinct atmospheres. The magnetic field is more horizontal in the tubes than in the background. Indeed, the tubes return to the solar surface in the middle penumbra and beyond, whereas the background field lines continue upwards forming the sunspot canopy. The flux tubes carry most of the Evershed flow, which is found to be aligned with the magnetic field vector everywhere in the penumbra. By contrast, the background atmosphere is essentially at rest in the inner penumbra and harbors small flows in the outer penumbra (perhaps the signature of a different family of penumbral tubes that continue upwards without returning to the solar surface).

In general, our results confirm the signs of the radial variation of the magnetic field vector and the flow velocity deduced from one-component analyses. However, the details are significantly different. This is because we explicitly account for the unresolved structure of the penumbra, which allows us to characterize the various magnetic components contributing to the observed Stokes profiles. One-component inversions without gradients of the atmospheric parameters cannot separate these components, so they return the properties of the average magnetic field and flow velocity. Of course, such average quantities do not give much information about the individual magnetic atmospheres. At this point, we want to remark that one-component inversions with gradients of the physical parameters lead to essentially the same results as our two-component inversions. This has been demonstrated recently by Borrero et al. (2004), who analyzed the same set of infrared Stokes profiles emerging from the limb-side penumbra in terms of two different geometrical scenarios, namely, one-component atmospheres with gradients and two-component models without gradients. The main advantage of two-component models is that they are more intuitive and easier to interpret: the properties of the tubes and the background field are described by two independent atmospheres, whereas in one-component models the information on the tubes and the background is found at different optical depths.

In what follows, we use the two-component inversions to investigate two important aspects of sunspot penumbrae: the origin of the spine/intra-spine structure of the penumbra revealed by earlier analyses, and the generation of the net circular polarization exhibited by infrared lines.

6.1 Spine/intra-spine structure of the penumbra

If one accepts the hypothesis that the Stokes profiles emerging from the penumbra are produced by a single magnetic atmosphere, as it is implicitly assumed in one-component Milne-Eddington (ME) inversions, then the large azimuthal variations of the polarization signal of visible and infrared lines (cf. Fig. 1) can be explained as being due to azimuthal fluctuations in the inclination and strength of the average magnetic field vector. This has led to the concepts of fluted penumbra (Title et al. 1993) and spine/intra-spine organization of the magnetic field vector (Lites et al. 1993). Unless provision is made to account for the unresolved structure of the penumbra, there is no other way to understand the observations.

As can be seen in Fig. 4, our maps of magnetic field strength and zenith angle do not show significant azimuthal fluctuations in either of the two components. This is striking in view of the results mentioned above, and raises the following question: where do the rapid fluctuations indicated by one-component analyses come from? Figure 5 already provides an answer to this question: the filling factor derived from the two-component inversions do indeed show clear azimuthal fluctuations, especially in the inner and middle penumbra where the map is less noisy. Together with the lack of obvious fluctuations in Fig. 4, this suggests that the quantity that fluctuates azimuthally is the filling factor (i.e., the area of the resolution element covered by the flux-tube component), rather than the magnetic field inclination, the field strength or the LOS velocity of the two atmospheric components. In other words, the physical parameters of the background and the tubes do not seem to change much at a fixed radial distance, only the number of tubes does.

Figure 9: Left panels: field strength ( top) and field inclination ( bottom) resulting from one-component inversions of pixels along an azimuthal path crossing the inner penumbra at r/R = 0.6, versus the filling factors deduced from the two-component inversion of the same pixels. Right panels: field strengths ( top) and field inclinations ( bottom) in the background (open circles) and flux-tube (filled circles) atmospheres from the two-component inversion, as a function of the filling factor, along the same azimuthal path.

Open with DEXTER

Figure 9 lends support to our claim. In the left panels of that figure we plot the strengths and inclinations of the magnetic field vector resulting from a one-component, ME-like inversion of AR 8704 (see Bellot Rubio 2003) against the filling factors inferred from the present two-component inversions. The physical quantities have been extracted along an azimuthal path crossing the inner penumbra at a normalized radial distance of 0.6. The figure shows an excellent correlation between the fluctuations in field strength and field inclination indicated by the one-component inversions and the filling factor of the flux-tube atmosphere: the magnetic field appears weaker and more inclined in those pixels where the filling factor is larger, i.e., where there are more penumbral tubes. Note that the range of variation in field strength and zenith angle is 1400-2000 G and $40^{\circ}$- $65^{\circ}$, respectively, while the filling factor varies between 40% and 70%. For comparison, the right panels of Fig. 9 display the zenith angles and field strengths in the background and flux-tube atmospheres along the same azimuthal path. It is apparent that these quantities undergo much smaller fluctuations, i.e., they remain more or less constant along the chosen azimuthal path, in agreement with our idea. Other azimuthal paths crossing the inner and mid-penumbra also show the same tendencies, sometimes with larger scatter. We conclude that the fluctuations in the strength and inclination of the average magnetic field vector deduced from one-component analyses are actually caused by azimuthal variations in the number of tubes present in the resolution element (i.e., the filling factor), not by real changes in the physical conditions of the magnetic components of the penumbra.

It is tempting to think that the intra-spine regions observed in polarization maps at moderate spatial resolution are individual flux tubes (and, correspondingly, that spine regions represent a pure background). However, this association cannot be made because of the large horizontal sizes of intra-spines (about 1.5-2 arcsec according to the maps presented by, e.g., Lites et al. 2003 and Bellot Rubio 2003), much larger than the size of the penumbral filaments observed in high resolution images. In reality, spines and intra-spines should be considered as a collection of flux tubes interspersed with a background field. Hence, allowing for changing filling factors is essential if one wants to determine the magnetic properties of the basic building blocks of spines and intra-spines. To give an idea of the importance of this effect, consider the following argument. With tubes 200 km in diameter, there is plenty of room in the resolution element to accommodate up to 3-4 tubes horizontally if the angular resolution is 1 arcsec. Two adjacent pixels having, say, 3 and 1 identical tubes would show rather different polarization signals and hence magnetic properties if the profiles are interpreted in terms of one-component atmospheres, because the filling factor is changing by as much as 66% and this variation cannot be accounted for. Only in the special case in which the filling factor is 0 or 1 (i.e., when the pixel is filled with a pure background atmosphere or a pure flux-tube atmosphere, respectively) would the inferred magnetic field strengths and inclinations coincide with the real atmospheric parameters in the pixel.

Certainly, our two-component inversion reinforces the idea that the penumbra is fluted (as suggested by one-component analyses), because we observe the background and the flux-tube atmospheres to possess rather different magnetic properties. However, we caution that the field strengths and zenith angles of spine/intra-spine regions indicated by simple atmospheric models do not accurately represent the magnetic properties of the background and the flux tubes, because the influence of the filling factor is not considered. Acknowledging this limitation, Lites et al. (1993) warned that spines likely harbor even stronger and more vertical fields than inferred from their one-component inversions, due to the possibility that these structures are not resolved in the observations.

Figure 10: a) Observed NCP of Fe I 1564.8 nm. b) Difference between LOS magnetic field azimuths in the flux tube and the background ( $\Delta \psi _{\rm LOS} \equiv \psi ^{\rm tube}_{\rm LOS} - \psi ^{\rm back}_{\rm LOS}$). For better visibility, only the sign of the azimuth difference is displayed. LOS azimuths are measured counterclockwise from the positive x-axis of the LOS reference frame (corresponding to position angle $\varphi = 90^{\circ }$), which also coincides with the positive x-axis of the LRF. c) Azimuth differences  $\Delta \psi _{\rm LOS}$ along an azimuthal path crossing the inner penumbra at r/R = 0.6 (dots). The solid line represents the expected values for LRF magnetic field inclinations and relative azimuths in the background and flux-tube components taken from Fig. 6.

Open with DEXTER

Explaining why the number of tubes present in the resolution element changes azimuthally seems easier than explaining why the magnetic and kinematic configuration of the penumbra should undergo rapid azimuthal fluctuations. In the scenario set by the interchange convection model of Jahn & Schmidt (1994) and Schlichenmaier et al. (1998), one might speculate that the emergence of a flux tube at a given position angle makes it easier for other tubes to emerge at exactly the same location, simply because the background atmosphere is already perturbed. Examining the feasibility of this idea calls for detailed numerical simulations. Here we just mention that additional indications of azimuthal fluctuations in the filling factor have been gathered by Bellot Rubio (2004, his Fig. 7) from the analysis of two-dimensional filtergrams of another spot observed with adaptive optics.

6.2 Origin of the NCP of infrared lines

Schlichenmaier & Collados (2002) found that the NCP maps of spots observed in Fe I 1564.8 nm show the tendency to be antisymmetric about the line connecting disk center and sunspot center. As seen in Fig. 10a, this is the case for AR 8704 too. The figure also demonstrates that, even at an heliocentric angle of 40$^{\circ}$, the Fe I 1564.8 nm line exhibits very small NCPs in the penumbra (the mean absolute value is 2.3 mÅ).

Using the analytical results of Landolfi & Landi degl'Innocenti (1996), Schlichenmaier et al. (2002) and Müller et al. (2002) suggest that the antisymmetric distribution of the NCP of infrared lines is due to jumps in the magnetic field azimuth along the line of sight, together with discontinuities in the LOS velocity. The NCP created by discontinuities in the magnetic field strength and inclination is symmetric with respect to the line of symmetry. Thus, jumps in the magnetic field azimuth are the key ingredient to explain the observed NCP maps. Due to projection effects, two magnetic atmospheres in the resolution element having different LRF field inclinations will show different LOS magnetic azimuths even if their azimuths in the LRF are identical. Müller et al. (2002) have demonstrated that an uncombed atmosphere consisting of nearly horizontal flux tubes embedded in a more vertical background field produces the required azimuth jumps in a natural way. The LOS azimuth difference between the flux tubes and the background, $\Delta \psi _{\rm LOS} \equiv \psi ^{\rm tube}_{\rm LOS} - \psi ^{\rm back}_{\rm LOS}$, has to be positive to the right of the line of symmetry (position angles from 0$^{\circ}$ to 180$^{\circ}$) and negative to the left (position angles from 180$^{\circ}$ to 360$^{\circ}$) to explain the spatial distribution of the NCP of Fe I 1564.8 nm.

As mentioned earlier, our two-component model is unable to produce any NCP because it does not incorporate discontinuities along the line of sight. However, information on the magnetic field azimuths is extracted from the observed Stokes Q and U profiles. Therefore, it is of interest to check whether the LOS magnetic azimuths inferred from the inversion confirm the mechanism proposed by Müller et al. (2002) and Schlichenmaier et al. (2002). Figure 10b displays the sign of the LOS azimuth difference  $\Delta \psi _{\rm LOS}$ in AR 8704. We find that this quantity is predominantly positive to the right of the symmetry line and negative to the left, in excellent accord with the predictions of these authors. A similar result has been obtained by Borrero (2004).

Figure 10c shows the actual azimuth differences along an azimuthal path crossing the penumbra at r/R = 0.6. Azimuth jumps as large as 80$^{\circ}$ are observed, with a sharp transition from positive to negative values near the line of symmetry in the center-side penumbra ( $\varphi \sim 180^{\circ}$). The solid line in Fig. 10c indicates the LOS azimuth difference that would be produced by LRF magnetic field inclinations of 80$^{\circ}$ and  $40^{\circ}$ in the tubes and the background, together with LRF relative azimuths of  $3.5^{\circ}$ and  $-3^{\circ}$ in both atmospheric components, according to the formulae given by Müller et al. (2002). These inclination angles and relative azimuths have been taken from Fig. 6. As can be seen, the agreement between theoretical predictions and observations is quite satisfactory. We note that small relative azimuths are necessary to explain the non-zero azimuth jumps occurring on the limb side near the neutral line ( $\varphi \sim 0^{\circ}$). Non-zero relative azimuths also account for the shift of the whole $\Delta \psi _{\rm LOS}$curve toward positive values observed in Fig. 10c.

Thus, our results confirm the LOS azimuth jumps proposed by Müller et al. (2002) and Schlichenmaier et al. (2002) to explain the antisymmetric distribution of the NCP of infrared lines emerging from sunspots. We believe that this confirmation makes a strong case for the existence of two magnetic components in the penumbra.

7 Summary and outlook

We have characterized the magnetic and kinematic properties of a sunspot penumbra from an inversion of infrared Stokes profiles based on a two-component model atmosphere. Our model is meant to describe the different magnetic atmospheres coexisting in the resolution element. These atmospheres leave clear signatures in the observed polarization signals. We have chosen the simplest geometrical scenario possible for the first application of the model to a complete spot. In particular, we do not consider discontinuities along the line of sight or gradients of the atmospheric parameters with height. Thus, the model is unable to produce net circular polarization. Despite that, the observed Stokes profiles are reproduced very satisfactorily, including those near the neutral line.

In general, the results of the two-component inversions confirm the uncombed penumbral model of Solanki & Montavon (1993) and Martínez Pillet (2000). Our main findings can be summarized as follows:

1.

The penumbra can be explained in terms of magnetic flux tubes embedded in a background field. The radial variation of the properties of these atmospheres is rather smooth, as can be seen in Figs. 6 and 7.

2.

The magnetic field strength is weaker in the tubes than in the background except near the outer penumbral boundary. The variation of the field strength with radial distance is slower in the tubes than in the background, as found by Rüedi et al. (1999) and Borrero et al. (2004).

3.

The tubes are more horizontal than the background field. They are slightly inclined upwards in the inner penumbra, then become horizontal at about 0.8 penumbral radii, and finally return to the solar surface in the outer penumbra (with maximum zenith angles of $\sim$ $100^{\circ}$). The magnetic field of the background never returns to the solar surface. The inclination angles deduced for this atmospheric component are in excellent agreement with those predicted by sunspot models incorporating current sheets (Jahn 1989).

4.

The bulk of the Evershed flow is associated with the flux-tube component. We find a perfect alignment of the velocity vector and the magnetic field vector at all radial distances in the flux tubes. That is, the flow is also seen to return to the solar surface, which may potentially solve the problem of mass conservation of the Evershed flow (Solanki et al. 1994).

5.

The azimuthally averaged flow speed in the tubes reaches values as large as 6.5 km s^-1 at 0.8-0.9 penumbral radii. This is similar to the sound speed in the spot. By deprojecting the observed LOS velocities in the flux-tube component, we find that the flow is supercritical in many pixels of the outer penumbra and supersonic at some places near the outer sunspot edge. The maximum flow speed observed in AR 8704 is 15.5 km s^-1. This is consistent with the supersonic flows predicted by the moving tube model (Schlichenmaier 2002) and with the large velocities observed by del Toro Iniesta et al. (2001), and Penn et al. (2003).

6.

Material flows in the background component are negligible in the inner penumbra and small (<2 km s^-1) in the outer penumbra (normalized radial distances larger than about 0.7). In addition, the velocity vector is found to be more inclined than the magnetic field vector by some 10-20$^{\circ}$. This could be the signature of a new family of tubes that emerge in the mid-penumbra and never return to the solar surface, as suggested by Westendorp Plaza et al. (2001a,b). Due to the simplicity of our model, we cannot clearly separate these tubes from the real background, which is expected to be at rest.

7.

We see spines and intra-spines in circular and linear polarization (Fig. 1), but not in the maps of physical quantities (Fig. 4). The magnetic and kinematic properties of the flux tubes and the background at a given radial distance do not seem to vary much around the spot. The quantity that fluctuates azimuthally is the fraction of the resolution element occupied by the flux tubes. This suggests that the strong azimuthal fluctuations in the average field strength and field inclination indicated by one-component analyses are not real, but artifacts induced by the impossibility to separate the various magnetic components of the penumbra.

8.

Information on the field azimuths is successfully extracted from the observed linear polarization profiles. The difference between the LOS magnetic field azimuths in the flux-tube and the background atmosphere inferred from our two-component inversions is in excellent accord with that required to explain the antisymmetrical distribution of the NCP of Fe I 1564.8 nm with respect to the line of symmetry (Schlichenmaier et al. 2002; Müller et al. 2002). This result provides additional evidence for the existence of two magnetic components in sunspot penumbrae.

9.

The two-component model is able to reproduce the observed Stokes profiles of the infrared lines because their NCPs are very small (Borrero et al. 2004). What makes the infrared lines special is that they show clear signatures of two different magnetic atmospheres in the form of multi-lobed circular (linear) polarization profiles in the limb-side (center-side) penumbra. Our simple geometrical model incorporates the essential ingredients needed to interpret these signatures correctly. Two-component inversions without gradients of the atmospheric parameters may not be appropriate to analyze visible lines, because of the larger NCPs they exhibit. This is confirmed by the results of Lites et al. (2002), who found that a two-component model with gradients was necessary to explain the anomalous Stokes profiles of the Fe I lines at 630 nm observed in the penumbra of a complex $\delta$ spot.

We have shown that two-component inversions of infrared lines offer a consistent picture of the fine structure of the penumbra. They solve serious problems connected with one-component interpretations of the observations as, for example, the non-parallelism of the flow and the magnetic field in sunspot penumbrae. However, the simple two-component model used here is not well suited to characterize the vertical extent of the flux tubes, the height at which they are placed, or the discontinuities that occur along the line of sight. These aspects must be investigated by means of uncombed models that consider the vertical interlacing of the magnetic background and the flux tubes. Preliminary inversions based on uncombed models have been presented by Bellot Rubio (2003) and Borrero et al. (2003b). Interestingly enough, the results of these inversions seem to confirm the main tendencies described in this paper. The extended height coverage required by uncombed models can be provided by simultaneous polarimetric observations of visible and infrared lines. Such observations are now possible at the Vacuum Tower Telescope of Teide Observatory, where TIP and POLIS (POlarimetric Littrow Spectrograph; Schmidt et al. 2003) have been combined successfully. Further improvements in current inversion codes and new observations will hopefully allow us to isolate the basic building blocks of the penumbra.

Acknowledgements

We thank J.M. Borrero and R. Schlichenmaier for many useful comments and suggestions. We also thank the referee, Dr. B. Lites, for his constructive remarks. Financial support by the Deutsche Forschungsgemeinschaft under project SCHL 514/2-1 and by the Spanish Ministerio de Ciencia y Tecnología under project AYA2001-1649 is gratefully acknowledged. The cooperation of AIP and IAC is part of the European Solar Magnetism Network (TMR-ESMN) supported by the European Commission under contract HPRN-CT-2002-00313. The Vacuum Tower Telescope is operated by the Kiepenheuer-Institut für Sonnenphysik (Germany) at the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias. This research has made use of NASA's Astrophysical Data System.

References

• Adam, M. G., & Petford, A. D. 1991, Sol. Phys., 135, 319 [NASA ADS] (In the text)
• Auer, L. H., & Heasley, J. N. 1978, A&A, 64, 67 [NASA ADS] (In the text)
• Ballesteros, E., Collados, M., Bonet, J. A., et al. 1996, A&AS, 115, 353 [NASA ADS] (In the text)
• Balthasar, H. 1985, Sol. Phys., 99, 31 [NASA ADS] (In the text)
• Balthasar, H., Sütterlin, P., & Collados, M. 2001, AN, 322, 367 [NASA ADS] (In the text)
• Balthasar, H., Bellot Rubio, L. R., & Collados, M. 2003, AN, 324, 390 [NASA ADS] (In the text)
• Beckers, J. M., & Schröter, E. H. 1969, Sol. Phys., 10, 384 [NASA ADS] (In the text)
• Bellot Rubio, L. R. 2003, ASP Conf. Ser., 307, 301 [NASA ADS] (In the text)
• Bellot Rubio, L. R. 2004, Rev. Mod. Astron., 17, 21 [NASA ADS] (In the text)
• Bellot Rubio, L. R., Collados, M., Ruiz Cobo, B., & Rodríguez Hidalgo, I. 2002, Nuovo Cimento C, 25, 543 [NASA ADS] (In the text)
• Bellot Rubio, L. R., Balthasar, H., Collados, M., & Schlichenmaier, R. 2003, A&A, 403, L47 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Bernasconi, P. N., Keller, C. U., Solanki, S. K., & Stenflo, J. O. 1998, A&A, 329, 704 [NASA ADS] (In the text)
• Borrero, J. M. 2004, Ph.D. Thesis, Universitäts Göttingen (In the text)
• Borrero, J. M., & Bellot Rubio, L. R. 2002, A&A, 385, 1056 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Borrero, J. M., Bellot Rubio, L. R., Barklem, P. S., & del Toro Iniesta, J. C. 2003a, A&A, 404, 749 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Borrero, J. M., Lagg, A., Solanki, S. K., et al. 2003b, ASP Conf. Ser., 286, 235 [NASA ADS] (In the text)
• Borrero, J. M., Solanki, S. K., Bellot Rubio, L. R., Lagg, A., & Mathew, S. K. 2004, A&A, 422, 1093 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Bumba, V. 1960, Izv. Crim. Astrophys. Obs., 23, 253 [NASA ADS] (In the text)
• Cabrera Solana, D., Bellot Rubio, L. R., & del Toro Iniesta, J. C. 2005, A&A, in preparation (In the text)
• Collados, M. 2002, AN, 323, 254 [NASA ADS] (In the text)
• Collados, M. 2003, Proc. SPIE, 4843, 55 [NASA ADS] (In the text)
• Degenhardt, D., & Wiehr, E. 1991, A&A, 252, 821 [NASA ADS] (In the text)
• Elmore, D. F., Lites, B. W., Tomczyk, S., et al. 1992, Proc. SPIE, 1746, 22 [NASA ADS] (In the text)
• Jahn, K. 1989, A&A, 222, 264 [NASA ADS] (In the text)
• Jahn, K. 2003, in Turbulence, Waves, and Instabilities in the Solar Plasma, ed. E. Forgács-Dajka, K. Petrovay, & R. Erdélyi, Publications of the Astronomy Department of the Eötvös University, 13, 101 (In the text)
• Jahn, K., & Schmidt, H. U. 1994, A&A, 290, 295 [NASA ADS] (In the text)
• Keppens, R., & Martínez Pillet, V. 1996, A&A, 316, 229 [NASA ADS] (In the text)
• Kinman, T. D. 1952, MNRAS, 112, 425 [NASA ADS] (In the text)
• Landolfi, M., & Landi degl'Innocenti, E. 1996, Sol. Phys., 164, 191 [NASA ADS] (In the text)
• Leka, K. D. 2001, ASP Conf. Ser., 236, 571 [NASA ADS] (In the text)
• Lites, B. W., & Skumanich, A. 1990, ApJ, 348, 747 [NASA ADS] [CrossRef] (In the text)
• Lites, B. W., Elmore, D. F., Seagraves, P., & Skumanich, A. 1993, ApJ, 418, 928 [NASA ADS] [CrossRef] (In the text)
• Lites, B. W., Socas-Navarro, H., Skumanich, A., & Shimizu, T. 2002, ApJ, 575, 1131 [NASA ADS] [CrossRef] (In the text)
• Lites, B. W., Elmore, D. F., Streander, K. V., et al. 2003, ASP Conf. Ser., 307, 324 [NASA ADS] (In the text)
• Maltby, P. 1964, Astrophys. Norvegica, 8, 205 [NASA ADS] (In the text)
• Martínez Pillet, V. 1997, ASP Conf. Ser., 118, 212 [NASA ADS] (In the text)
• Martínez Pillet, V. 2000, A&A, 361, 734 [NASA ADS] (In the text)
• Martínez Pillet, V., Collados, M., Sánchez Almeida, J., et al. 1999, ASP Conf. Ser., 183, 264 [NASA ADS] (In the text)
• Mathew, S. K., Lagg, A., Solanki, S. K., et al. 2003, A&A, 410, 695 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Meyer, F., & Schmidt, H. U. 1968, Mitteilungen der Astronomischen Gesellschaft Hamburg, 25, 194 [NASA ADS] (In the text)
• Montesinos, B., & Thomas, J. H. 1997, Nature, 390, 485 [NASA ADS] [CrossRef] (In the text)
• Müller, D. A. N., Schlichenmaier, R., Steiner, O., & Stix, M. 2002, A&A, 393, 305 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Penn, M. J., Cao, W. D., Walton, S. R., Chapman, G. A., & Livingston, W. 2003, ApJ, 590, L119 [NASA ADS] [CrossRef] (In the text)
• Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1986, Numerical Recipes (Cambridge: Cambridge Univ. Press) (In the text)
• Rimmele, T. R. 1995, A&A, 298, 260 [NASA ADS] (In the text)
• Rouppe van der Voort, L. H. M., Löfdahl, M. G., Kiselman, D., & Scharmer, G. B. 2004, A&A, 414, 717 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Rüedi, I., Solanki, S. K., & Keller, C. U. 1999, A&A, 348, L37 [NASA ADS] (In the text)
• Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] (In the text)
• Sánchez Almeida, J., & Lites, B. W. 1992, ApJ, 398, 359 [NASA ADS] [CrossRef] (In the text)
• Sankarasubramanian, K., Elmore, D. F., Lites, B. W., et al. 2003, Proc. SPIE, 4843, 414 [NASA ADS]
• Scharmer, G. B., Gudiksen, B. V., Kiselman, D., Löfdahl, M. G., & Rouppe van der Voort, L. H. M. 2002, Nature, 420, 151 [NASA ADS] [CrossRef] (In the text)
• Schlichenmaier, R. 2002, AN, 323, 303 [NASA ADS] (In the text)
• Schlichenmaier, R., & Collados, M. 2002, A&A, 381, 668 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Schlichenmaier, R., & Schmidt, W. 2000, A&A, 358, 1122 [NASA ADS] (In the text)
• Schlichenmaier, R., Jahn, K., & Schmidt, H. U. 1998, A&A, 337, 897 [NASA ADS] (In the text)
• Schlichenmaier, R., Bruls, J. H. M. J., & Schüssler, M. 1999, A&A, 349, 961 [NASA ADS] (In the text)
• Schlichenmaier, R., Müller, D. A. N., Steiner, O., & Stix, M. 2002, A&A, 381, L77 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Schmidt, W. 2002, ESA-SP 505, 167 (In the text)
• Schmidt, W., & Kentischer, T. J. 1995, A&AS, 113, 363 [NASA ADS] (In the text)
• Schmidt, W., & Schlichenmaier, R. 2000, A&A, 364, 829 [NASA ADS] (In the text)
• Schmidt, W., Hofmann, A., Balthasar, H., Tarbell, T. D., & Frank, Z. A. 1992, A&A, 264, L27 [NASA ADS] (In the text)
• Schmidt, W., Beck, C., Kentischer, T. J., Elmore, D., & Lites, B. 2003, AN, 324, 300 [NASA ADS] (In the text)
• Schröter, E. H. 1965, Z. Astrophys., 62, 228 [NASA ADS] (In the text)
• Skumanich, A., Lites, B. W., & Martínez Pillet, V. 1994, in Solar Surface Magnetism, ed. R. J. Rutten, & C. J. Schrijver, NATO ASI Series C, 433 (Dordrecht: Kluwer), 99 (In the text)
• Solanki, S. K. 2003, ARA&A, 11, 153 [NASA ADS] (In the text)
• Solanki, S. K., & Montavon, C. A. P. 1993, A&A, 275, 283 [NASA ADS] (In the text)
• Solanki, S. K., Rüedi, I., & Livingston, W. 1992, A&A, 263, 339 [NASA ADS] (In the text)
• Solanki, S. K., Montavon, C., & Livingston, W. 1994, A&A, 283, 221 [NASA ADS] (In the text)
• Stanchfield, D. C. H., Thomas, J. H., & Lites, B. W. 1997, ApJ, 477, 485 [NASA ADS] [CrossRef] (In the text)
• Stix, M. 2002, The sun: an introduction (Berlin: Springer) (In the text)
• Sütterlin, P., Bellot Rubio, L. R., & Schlichenmaier, R. 2004, A&A, 424, 1049 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Title, A. M., Frank, Z. A., Shine, R. A., Tarbell, T. D., & Topka, K. P. 1993, ApJ, 403, 780 [NASA ADS] [CrossRef] (In the text)
• del Toro Iniesta, J. C. 2001, ASP Conf. Ser., 248, 35 [NASA ADS] (In the text)
• del Toro Iniesta, J. C., Bellot Rubio, L. R., & Collados, M. 2001, ApJ, 549, L139 [NASA ADS] [CrossRef] (In the text)
• Thomas, J. H. 1994, in Solar Surface Magnetism, ed. R. J. Rutten, & C. J. Schrijver, NATO ASI Series C, 433 (Dordrecht: Kluwer), 219 (In the text)
• Thomas, J. H., & Montesinos, B. 1993, ApJ, 407, 398 [NASA ADS] [CrossRef] (In the text)
• Thomas, J. H., Weiss, N. O., Tobias, S. M., & Brummell, N. H. 2002, Nature, 420, 390 [NASA ADS] [CrossRef] (In the text)
• Tritschler, A., Schlichenmaier, R., Bellot Rubio, L. R., & the KAOS Team 2004, A&A, 415, 717 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Westendorp Plaza, C., del Toro Iniesta, J. C., Ruiz Cobo, B., et al. 1997, Nature, 389, 47 [NASA ADS] [CrossRef] (In the text)
• Westendorp Plaza, C., del Toro Iniesta, J. C., Ruiz Cobo, B., et al. 2001a, ApJ, 547, 1130 [NASA ADS] [CrossRef] (In the text)
• Westendorp Plaza, C., del Toro Iniesta, J. C., Ruiz Cobo, B., & Martínez Pillet, V. 2001b, ApJ, 547, 1148 [NASA ADS] [CrossRef] (In the text)
• Weiss, N. O., Thomas, J. H., Brummell, N. H., & Tobias, S. M. 2004, ApJ, 600, 1073 [NASA ADS] [CrossRef] (In the text)
• Wiehr, E. 1995, A&A, 298, L17 [NASA ADS] (In the text)