A&A 427, 353-361 (2004)
DOI: 10.1051/0004-6361:20041260

Stability analysis of quiescent prominences using thermodynamic irreversible energy principles

A. Costa¹ - R. González^1,2 - A. C. Sicardi Schifino³

1 - Instituto de Astronomía y Física del Espacio, CONICET, 1428 Buenos Aires, Argentina
2 - Departamento de Física, FCEyN - UBA, Argentina
3 - Departamento de Física, Facultad de Ciencias, Facultad de Ingeniería, UR, Uruguay

Received 7 May 2004 / Accepted 15 July 2004

Abstract
Using methods of non-equilibrium thermodynamics that extend and generalize the MHD energy principle of Bernstein et al. (1958, Proc. Roy. Soc. A, 244, 17) we develop a formalism in order to analyze the stability properties of prominence models considered as dissipative states i.e. states far form thermodynamic equilibrium. As an example, the criterion is applied to the Kippenhahn-Schlüter model (hereafter K-S) considering the addition of dissipative terms in the coupled system of equations: the balance of energy equation and the equation of motion. We show from this application, that periods corresponding to typical oscillations of the chromosphere and photosphere (3 and 5 min respectively), that were reported as observations of the prominence structure, can be explained as internal modes of the prominence itself. This is an alternative explanation to the one that supposes that the source of these perturbations are the cold foot chromospheric and photospheric basis.

Key words: Sun: prominences - instabilities - waves

1 Introduction

1.1 Variational principles

Many stability criteria, based on energy principles, can be found in plasma physics literature, ranging from the classical criterion attributed to Bernstein et al. (1958) for ideal magnetohydrodynamics to more general and specific ones. Some astrophysical examples where variational principle are applied to spread a spectrum of different problems are: the modeling of pulsating stars (Costa et al. 2001; Ledoux & Walraven 1958), the calculations of stellar structures (Kennedy & Bludman 1997) or the characterization of the continuous Alfvén spectrum of line-tied coronal loops (Halberstadt & Goedbloed 1993). In relation to the subject of interest in this paper, many MHD prominence models - assuming both magnetohydrostatic and thermal equilibrium - have been proposed, e.g. Kippenhahn & Schluter (1957); Lerche & Low (1980); Oliver & Ballester (1996); Nagablushana (1998). However, stability is a crucial requirement for a model in order to give a realistic description of the problem. Thus, different stability analysis considering prominence models can be found in literature generally restricted to special type of perturbations and specific equilibrium models. A more general intent was performed by Zweibel (1982,1981) and also by Galindo Trejo (1989) who used the known Bernstein's MHD-variational principle in order to analyze the stability of different known two dimensional prominence models. They found that many of the situations described represented unstable equilibriums.

But, as was pointed out by Lerche & Low (1981) among all variational criteria there is an important and fundamental difference between them related to whether they assume adiabatical configurations or not. In the applications of Bernstein's criterion (Bernstein et al. 1958) the adiabaticity presupposes the irrelevancy of the energy balance equation and thus dissipation is impossible. A more realistic case, concerning stable configurations described by non-conservative equations with non-self-adjoint operators, was presented by Lerche & Low (1981). They proposed a Lagrangian principle in order to analyze quiescent prominences that can suffer thermal instabilities.

In this paper we provide a criterion in order to analyze the stability of prominences - considering dissipative terms - via the application of a general procedure derived recently by us (Sicardi et al. 2004; see also Sicardi et al. 1991,1989a,b, 1985). This procedure gives a general principle - based on firmly established thermodynamic laws - and can be understood as an extension of the Bernstein's MHD principle to situations far from thermodynamic equilibrium. It has then the advantage that many known results obtained by the simpler ideal MHD criterion (Bernstein et al. 1958) (e.g. Galindo Trejo 1989,1987) can be reexamined by a direct comparison with this analysis, and that, as it is obtained via a thermodynamic approach, it gives a maneuverable description of non-thermodynamic equilibrium situations.

1.2 Quiescent prominences

Quiescent prominences are known to be stable phenomena on the solar atmosphere. A great amount of observational analysis has been recently reviewed and it has become clear that an improvement of our understanding of filament's and prominence's structure and stability, together with knowledge about their link with the corona, can be acquire via the study of the - recently reported - variety of oscillations in the prominence structure.

The observational evidence of prominence seismology is reviewed in Oliver (1999): one can distinguish between the large amplitude oscillations due to a wavefront excited during a flare affecting the whole prominence, and small amplitude oscillations affecting only part of the prominence. Vial (1998) reviewed the typical periods observed in velocities which can be separated in three categories: short periods (less than 5 min), intermediate periods (between 6 and 20 min) and long periods (between 40 and 90 min) as seen recently by Régnier et al. (1999). Balthasar et al. (1999) had also established the existence of oscillations of very short period (30 s).

One of us (Blanco et al. 1999; Bocchialini et al. 2001) reported observational studies that exhibit correlation with the classification of oscillations cited above. We found that large energy content is localized in waves with periods between one and six minutes, which can be classified as intermediate and/or very short periods. These periods correspond to typical oscillations of the chromosphere and photosphere (3 and 5 min respectively) suggesting a possible source for these perturbations, which, outside from the prominence coronal observations, are known to be effectively stopped by the transition region (Gouttebroze et al. 2001).

Whether these range of oscillations represent intrinsic properties of the prominence (normal modes), or if they are a forced stable response to an external wavefront perturbation, is a fact that must be explained by theoretical prominence models that take into account thermal and mechanical stability considerations in order to guarantee that such models can exist. Thus, a crucial question of any theoretical model is one that inquires about the frequency stability range. Then, as the consideration of one or another model must be related to this analysis, we applied thermodynamic irreversible techniques in order to analyze both thermal and mechanical coupled stability. Our principle is applied to the known Kippenhahn-Schluter (hereafter K-S) model. It gives an example of the physical insight that the criterion can provide due to the advantages of the irreversible thermodynamic analysis. This is, - while more realistic cases require numerical treatment, a task that will be accomplish in next steps - this analytic example shows that the role of the different operators, that compose the equations describing the system, can be established in terms of their stability significance. Moreover, this results in the construction of a variational principle that associate stability with the sign of a quadratic form avoiding non-self-adjoint operators. In fact, obtaining a self-adjoint operator is a requirement for our principle to hold. Nevertheless, when this is accomplished the calculus result simplified due to an important mathematical property which greatly aids in the stability analysis. The self-adjoint character of an operator implies that the eigenvalues $\omega^{2}$ are purely real. Hence stability transitions always occur when $\omega^{2}$ crosses zero, rather than at some particular points of the real axis where the real part of the eigenvalue is different from zero, i.e. Re $( \omega) \neq 0$, leading to an efficient formulation for testing stability. Thus, the symmetry considerations of the self-adjoint operators, the fact that there is a diagonal form associated to this operators, and that the Rayleigh-Ritz theorem states the existence of a minimum eigenvalue, are important reasons to try to maintain self-adjointness in the consideration of stability.

2 The stability criterion

The thermodynamics of irreversible processes is described in terms of phenomenological relations between conjugate pairs of thermodynamic variables: the flows and the forces that cause them. It is a subject where a large amount of work has been done on both formal theory and applications. The first works, treating small deviations from the equilibrium state and including fluctuations in the neighborhood of this state, were performed by Onsager & Machlup (1953) and by Prigogine (1967). The criterion based on these first formulations was successfully applied to several linear non-equilibrium problems (Glansdorff et al. 1974; Nicolis & Prigogine 1979).

Linear thermodynamics studies the behavior of the system around the equilibrium state or around a non-equilibrium stationary one that is linearly close to it. They are states of detail balance between flows and forces and, as Onsager showed (1931), this is due to the microscopic reversible character of equilibrium. Thus, the empirical relations between flows and forces are linear and the resistance matrix ${\vec R}$ that relates them is symmetric and positive definite. It's symmetric character is guaranteed by the principle of microscopic reversibility and its positive definiteness by the proximity of the reference state to the thermodynamic equilibrium, where the entropy has a maximum.

But, there is no continuity between linear and nonlinear thermodynamical processes. When the system is beyond the immediate neighborhood of the stationary state the non-linearities become visible. Instabilities that cause dynamic transitions in open systems are responsible for the qualitative difference between linear and nonlinear thermodynamics. Therefore, dynamic cooperative phenomena can only arise in nonlinear thermodynamics. Thus, nonlinear thermodynamics is related to the stability properties of non-equilibrium stationary states, where the linear relation between flows and forces can become state dependent (i.e. ${\vec R}$ is not necessarily a symmetric positive definite matrix), and the problem of having a thermodynamic theory to provide a general criterion for the stability of the system - which is not evident through the integration of the variational equations- becomes a fundamental point. The theory was then extended to situations far from thermodynamic equilibrium (Glansdorff & Prigogine 1971; Keizer 1976; Graham 1978; Lavenda 1993,1987), where the relaxation of these processes to a steady state of non-equilibrium (nonlinear state) is described.

2.1 General thermodynamical concepts

As it is expressed by the second law of thermodynamics, in an isolated system the entropy S growth exponentially up to its maximum value

$$d_{t}S \geq 0.$$ (1)

In open systems where energy and matter with the neighbors can be exchange Eq. (1) is not longer true. The extended formulation was then proposed for all type of systems (Prigogine 1967)

$$dS = d_{\rm e}S + d_{\rm i}S, \ \ \ d_{\rm i}S\geq 0$$ (2)

where $d_{\rm e}S$ is the entropy exchange (of energy and matter) between system and neighbors and $d_{\rm i}S$ is the entropy produced, due to irreversible processes, in the system's interior.

If the system is isolated, then $d_{\rm e}S=0$ and Eq. (2) reduces to Eq. (1). Thus, even when $d_{\rm i}S$ is never negative the term $d_{\rm e}S$ has not a definite sign and a less than zero entropy state can be reached as a result of the evolution (i.e. final entropy less than its value at the thermodynamic equilibrium state). Moreover, the system can remain indefinitely in one of these states if it happens that dS=0, or equivalently, that $d_{\rm e}S=-d_{\rm i}S$ (note that $d_{\rm e}S$ must be $\leq$0). These states are known as stationary states and a coherent dynamic of the system could last if sufficient negative entropy flow is provided to it. Thus, the criterion that states the stability of this stationary state gives insight of the dynamic structures that can be found in nature.

The stability of the stationary state is determined by the thermodynamic properties of the system. In a linearized description of the system around the stationary state $q_1,q_2,\cdot \cdot \cdot ,q_n,$ (a nonlinear state) the first order of Eq. (2) is reduced to the balance of the forces of the system and its second order determines the stability. The physical meaning of this statement is immediate: in a thermodynamic system the time is a parameter as in the Newtonian dynamics, then the positive sign of the time reveals the direction of the evolution. The internal production of entropy associated to the dissipation of the system is a definite positive second order quantity that manifests the irreversibility of the processes. In other words, the spontaneous evolution of the system implies $d_{\rm i}S\geq 0$ and when a perturbation not satisfying this condition occurs the systems returns to the reference state. The criterion, by Onsager, that the principle of least dissipation of energy must govern the probability of a succession of non-equilibrium states towards a stationary one, results in the requirement that every perturbation that can arise must satisfy $\delta^{2}_{\rm i}S\leq 0$.

The mathematical expression of the stability condition can be formulated in the following form: the stationary solution for a physical system described by generalized coordinates $q_1,q_2,\cdot \cdot \cdot ,q_n,$ - the evolution of which is governed by a system of known differential equations - will be stable if a function $\theta$, called the "Lyapunov function'' - defined in a neighborhood of the stationary point ( q_1^o,q_2^o,...,q_n^o) in the configuration space of the system - can be found satisfying the following conditions

$$\theta (q_{_1},q_{_2},...,q_{_n})\geq 0,\qquad \theta (q_{_1^o},q_{_2^o},...,q_{_n^o})=0 \Leftrightarrow q_{i}=q_{i}^{0} ,$$ (3)

$$\frac{{\rm d}\theta }{{\rm d}t}=\sum \frac{\partial \theta }{\partial q_i}\dot q_i\leq 0 .$$ (4)

The existence of this function is a sufficient condition (Lefschetz 1977) for the stability of the stationary solution ( q_1^o,q_2^o,...,q_n^o). To obtain a Lyapunov function is equivalent to deriving an energy principle. Thus, if $\theta$ satisfies the relation Eq. (4) strictly, but not Eq. (3), the system is unstable.

Then, according to Lyapunov's theorem a sufficient condition for the stability of a steady state is that

$$\delta^{2}S>0, \ \ d_{t}\delta^{2}S \leq 0 .$$ (5)

If the reference state is the equilibrium or a near-equilibrium one is simple to show that last relations (Eq. (5)) are identically verified. In fact, as it is shown in what follows, this is an immediate consequence of the second law of the thermodynamics and of the principle of detail balance of the equilibrium, based on Onsager's microscopic reciprocal relations.

Taking into account that a system is completely described by a set of N extensive thermodynamic variables x_i=q_i-q_i⁰, and that the tendency of the system to seek equilibrium is measured by the thermodynamic forces $X=\frac{\partial}{\partial x}S(x)$ (where S(x) is the entropy of the non-equilibrium state) we find that, around the reference state, the excess entropy (the second order entropy variation $\delta^{2}S$) can be written as the quadratic form

$$\delta^{2}S=\frac{1}{2}\langle x,{\vec S}x \rangle$$ (6)

where ${\vec S}$ is the symmetric entropy matrix for near equilibrium states, determined by Gibbs relation. $\vert x\rangle$ is a vector that stands for the thermodynamic state variables x_iand $\langle,\rangle$ represent the inner product operation in the corresponding space vector. Then noting $\vert X\rangle$ as the corresponding forces

$$\vert X\rangle = \vert{\vec S}x\rangle$$ (7)

and taking the time derivative of Eq. (6) results

$$d_{t}\delta^{2}S= \langle\dot{x}, X\rangle$$ (8)

where $\vert\dot{x}\rangle$ are the flows.

The known phenomenological relations between flows and forces are expressed as

$$\vert X\rangle = - {\vec R} \cdot \dot{\vert x\rangle}.$$ (9)

Near equilibrium, matrix ${\vec R}$ is symmetric and positive definite due to the principle of detail balance, then:

$$d_{t}\delta^{2}S = - <\langle\dot{x}, {\vec R}\dot{x}\rangle\leq 0$$ (10)

and noting that the second law of the thermodynamics assures that

$$\delta^{2}S=\frac{1}{2}\langle x, {\vec S}x\rangle > 0$$ (11)

it results that for any near equilibrium state, $\delta^{2}S$ is a Lyapunov function that assures stability. The relations of Eq. (9), without attributing any definite symmetry property to the generalized resistance matrix and assuming state dependence, are the extension of the linear phenomenological relations to nonlinear processes. In next subsection we present the stability criterion for these cases.

2.2 The general criterion expression

The irreversible thermodynamic approach associates the Lyapunov function $\theta$ to the generalized potentials: the free energy excess or the entropy excess of the system (Eq. (5)) (both being second order quantities). It can be shown (Sicardi et al. 1991) that these relations admit a reformulation based on the principle of power balance due to Lavenda (1993). In a hand-waiving form this second order principle states that the dissipation that is not compensated by the work given to the system by the medium produces an augment of the entropy of the system. Lavenda extended the principle of power balance to the field of complex variables in order to decompose the fluctuations in normal modes. Thus, real vectors and matrices must be replaced by their complex equivalents, e.g. the property of symmetry is replaced by the hermitian one.

In the following we indicate the procedure to obtain an energy principle from the basic equations that describe the system of interest. A general mechanical and thermal description - the equation of motion coupled with the equation of energy balance - of an open system can be written as

$$\ddot{\vec{y}}= f_{1}(\vec{y},\dot{\vec{y}},\epsilon); \ {\rm and} \ \dot{\epsilon}=f_{2}(\vec{y},\epsilon)$$ (12)

where $\vec{y}$ (a general coordinate vector) and $\epsilon$ (the energy) are first order quantities linearized around a stationary state. Then Eq. (12) can be expressed in a more compact form as

$${\vec M} \vert\ddot{x}\rangle + ( {{\vec R}}^{\rm H}+ {{\vec R}}^{\rm A} )\vert \dot{x}\rangle + {{\vec S}}\vert x\rangle=0$$ (13)

where ${\vec R}$ - the generalized resistance matrix - has been separated into its hermitian and antihermitian parts. ${\vec M}$, ${\vec R}$, and ${\vec S}$ are linear operators (which eventually may include spatial derivatives) of a general vector space, and $\vert x\rangle$ is the resulting generalized vector. The hermitian part of matrix ${\vec R}$, ${\vec R}^{\rm H}$ is related to the internal dissipation of the system and is positive definite due to the principle of least energy dissipation. ${\vec R}^{\rm A}$ is associated to the non-working gyroscopic forces; e.g. Coriolis or magnetic forces. In most cases matrix ${\vec M}$, which is related to the inertia of the system, is hermitian and positive definite. Matrix ${\vec S}$ is generally hermitian, but, there are important physical examples where this is not the case. ${\vec S}^{\rm H}$ is related to conservative or potential forces, and ${\vec S}^{\rm A}$is associated to non-conservative forces called "circulatory forces'' which are not of our interest in this paper (an example of a Lyapuunov function considering these forces, where ${\vec S}^{\rm A}$ is not a vanishing matrix, is analyzed in (Costa et al. 2001).

The principle of power balance implies that a sufficient condition for the Lyapunov function to exist is that ${\vec M}$, and ${\vec S}$ are hermitian. Then, as we show in what follows, (Sicardi et al. 1991,2004; Costa et al. 2001) the general stability criterion has the form

$$\theta=\delta^{2}S=\frac{1}{2}\left( \left\langle \dot{x}, {\... ...t\rangle + \left\langle x, {\vec S} x\right\rangle\right) > 0.$$ (14)

Note that taking the temporal derivative of Eq. (14), the stability conditions (Eq. (5)) are also satisfied because

$$\begin{eqnarray*}\frac{{\rm d}\theta}{{\rm d}t}&= &\frac{1}{2}\left(\left\langle... ...eft\langle\dot{x}\vert{\vec R}^{\rm H}\dot{x}\right\rangle\leq 0 \end{eqnarray*}$$

due to the principle of least dissipation of energy.

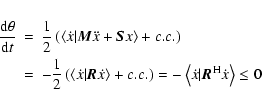
In summary, if ${\vec M}={\vec M}^{\rm H}$ and ${\vec S}={\vec S}^{\rm H}$, a sufficient condition for stability is that relation (14) holds. Then, Eq. (14): $\theta=\delta^{2}S> 0$ implies

$$\frac{{\rm d} \theta}{{\rm d}t}=d_{t}\delta^{2}S=- \langle \dot{x}, {\vec R}^{\rm H} \dot{x}\rangle \leq 0.$$ (15)

A few more words about energy principles can be added. Energy principles are less detailed but of easier application than normal modes methods. One of its powerful uses is to prove instability by a trial function (providing a sufficient condition for instability and a necessary condition for stability). In general, the great number of energy principles that can be found in literature are not necessarily derived from irreversible thermodynamic considerations as is the case of the principle used here. Thus, the equivalence between different criteria is not straightforward. In fact, the requirement of the self-adjoint character of ${\vec M}$ and ${\vec S}$ is on the basis of the stability criterion. Thus, the comparison between a criterion obtained independently from thermodynamic considerations with the criterion presented here is not always possible. In fact, whether the suitable variational principle obtained by Lerche & Low (1981) can be written in terms of the Lyapunov theorem is an open question; the equivalence between a particular principle and the principle presented here requires a specific probe. In Sicardi et al. (2004) we probe the equivalence between our energy principle and a principle - obtained independently of thermodynamic considerations - for a dissipative plasma in the fluid approximation (Tasso 1975). Also, in the Appendix, a similar task, for incompressible fluids is accomplished.

3 The magnetohydrodynamic equations

In order to board the stability analysis of the prominence problem the equations governing the dynamics of the system must be expressed in the form shown in last section. In the general case these equations can be written as a system of two coupled equations: the balance energy equation and the equation of motion (as shown in Eq. (12)). Thus, the perturbation analysis around a stationary state will imply considering a variable state vector of four independent components (i.e. the three component displacement and the temperature variation). In this section we deduce the stability principle (Eq. (14)) for the general prominence case. In the Appendix a simpler academic example to illustrate the procedure avoiding mathematical complications is presented. The fundamental magnetohydrodynamic equations to be considered are as follows. The mass conservation equation,

$$\frac{\partial \rho}{\partial t}+\nabla\cdot(\rho\vec{v})=0$$ (16)

where $\rho$ is the density of the plasma, $\vec{v}$ is the plasma velocity, and t the time. The perfect gas law or state equation,

$$p=\frac{k_{\rm B}}{m}\rho T$$ (17)

$k_{\rm B}$ is the Boltzmann constant, p the pressure, T the temperature and $m\equiv m_{\rm p}$ the proton mass (for a fully ionized H plasma $\rho\approx n{\rm e} m_{\rm p}$, ne being the number of electron particles, $n\equiv n{\rm e} + n{\rm p}= 2n$e, np the number of protons); the induction equation,

$$\frac{\partial \vec{B}}{\partial t}=\nabla\times(\vec{v}\times\vec{B})$$ (18)

$\vec{B}$ is the magnetic field vector. The magnetic diffusivity was discharged. The equation of motion for the problem results:

$$\rho\frac{D\vec{v}}{Dt}=-\nabla(p)+\frac{1}{4\pi}(\nabla\times\vec{B})\times\vec{B} -\rho\nabla\phi$$ (19)

where $g=-\nabla\phi$ is the gravity expression and $j=\frac{1}{4\pi}\nabla\times\vec{B}$ the current density. The energy balance equation takes the form:

$$\frac{\rho^{\gamma}}{(\gamma-1)}\frac{D}{D t}\left(\frac{p}{\rho^{\gamma}}\right)=-L$$ (20)

where $\gamma$ is the ratio of specific heats and L is the energy loss function:

$$L=-\nabla\cdot\vec{q}-L_{\rm r}+H$$ (21)

q is the heat flux due to particle conduction, $L_{\rm r}$ is the net radiation flux. The heat source was assumed to be proportional to the density i.e. $H = h \rho$. Last equation expresses the fact that the gain in particles energy (internal plus kinetic) is due to heat flow and radiation losses; ohmic dissipation $\frac{j^{2}}{\sigma}$ and all other heating sources were considered as vanishing terms implying that the optically thin assumption holds. Then $L_{\rm r}=n_{\rm e}n_{H}Q(T)$; the temperature variation ( $Q(T)=\chi T^{\alpha}$) was taken from Priest (1982). Also $q=-k \nabla T$ and, as conduction across the magnetic field has been discharged, then, for a total ionized plasma $q=-k_{0}T^{\frac{5}{2}}\nabla_{\parallel}T$. Finally Eq. (20) was written as

$$\frac{\rho^{\gamma}}{\gamma-1}\frac{D\left(\frac{p}{\rho^{\ga... ...frac{\rho^{2}}{m^{2}} \chi T^{\alpha}+\frac{\iota}{m^{2}}\rho.$$ (22)

3.1 Linearization procedure

The linearization procedure is performed by replacing $\rho=\rho_{0}+\rho_{1}$, T=T₀+T₁, B=B₀+B₁ and $\vec{v}=\vec{v_{0}}+\frac{\partial\vec{\xi}}{\partial t}$ in last equations, and assuming hydrostatic conditions for the equation of motion. Thus, $\vec{v_{0}}=0$ and $\vec{v_{1}}=\frac{\partial\vec{\xi}}{\partial t}$ where $\xi$ is the perturbation around the equilibrium of the equation of motion (the stationary state), also $\frac{\partial\rho_{0}}{\partial t}=0$ and $\frac{\partial B_{0}}{\partial t}=0$. Using the relation $\frac{\partial}{\partial t}\simeq {\rm i}\omega$ in Eqs. (16) and (18) the corresponding linearized equations (Eqs. (23)-(27)) result:

$$\rho_{1}+\nabla\cdot(\rho_{0}\vec{\xi})=0$$ (23)

$$p_{1}=\frac{k_{\rm B}}{m}(\rho_{0}T_{1}-T_{0}\nabla\cdot(\rho_{0}\vec{\xi}))$$ (24)

$$\vec{B_{1}}=-\nabla\times(\vec{B}_{0}\times\vec{\xi})$$ (25)

 

$$\rho_{0}\ddot{\vec{\xi}}=\frac{k_{\rm B}}{m}\nabla(T_{0}\nabla\cd... ... ) \times Q \right] + \bigtriangledown \phi \nabla \cdot ( \rho_{0} \vec{\xi })$$ (26)

 

$$\frac{k_{\rm B}}{m(\gamma-1)}\left[ \rho_{0} \dot{T_{1}}-(\gamma-1) \nabla \cdot ( \rho_{0} \dot{\vec{\xi}})T_{0}\right]-c \nabla$$

$$~~~~~~~~~\times\left[T_{0}^{\frac{5}{2}}\nabla_{\parallel}+\frac{... ..._{0})\right]T_{1} + \frac{\rho_{0}^{2}}{m^{2}}\chi \alpha T_{0}^{\alpha-1}T_{1}$$

$$~~~~~~~~~~~~~-\left(\frac{2\rho_{0}\chi T_{0}^{\alpha}}{m^{2}}-\frac{\iota}{m^{2}}\right)\nabla \cdot( \rho_{0}\vec{\xi})= 0$$ (27)

where $c=\frac{1.8\times 10^{-10}}{\ln\Lambda} \ {\rm W}~{\rm m}^{-1}~{\rm K}^{-1}$ and $Q=\vec{B}_{0}\times\vec{\xi}$. Then, Eqs. (23)-(25) were replaced in Eqs. (26) and (27) and the system of equations was rewritten as (Eqs. (28) and (29)):

$$\rho_{0}\ddot{\vec{\xi}}-F\xi+\frac{k_{\rm B}}{m}\nabla(\rho_{0}T_{1})=0$$ (28)

where F is the known Bernstein operator for the system:

$$\frac{k_{\rm B}}{m(\gamma-1)}\left[\rho_{0}\dot{T_{1}}-(\gamm... ...left(\rho_{0}\dot{\vec{\xi}}\right)\right]-AT_{1}+B\vec{\xi}=0$$ (29)

being $A=-[c\nabla \cdot (T_{0}^{\frac{5}{2}}\nabla _{\parallel }(\star)+\frac{5}{2}T_... ..._{\parallel }(T_{0}))-\frac{\rho _{0}^{2}}{m^{2}}\chi \alpha T_{0}^{\alpha -1}]$ and $B=\ \{\frac{k_{\rm B}}{m}\beta \nabla _{\bullet }(\rho _{0}\ ;\star )\}$; $\beta =\ \frac{-2(\rho _{0}\chi T_{0}^{\alpha }-\iota /2)}{k_{\rm B}m}$. The term $\ \nabla \cdot (\rho _{0}\dot{\xi})$ was discharged because it represents the total net flux of material through the magnetic tube. The two equations obtained are expressed in terms of the displacement and temperature perturbed variables $\vec{\xi}$ and T₁. $\star$represent the location for the perturbed variables when performing the matrix product. From them, we obtain the compact matrix equation:

$${\vec M}\vert \ddot{x}\rangle + {\vec R} \vert\dot{x}\rangle + {\vec S} \vert x\rangle = 0$$ (30)

with $x=\left \vert\begin{array}{c} \vec{\xi} \\ \ T_{1} \end{array} \right \vert, \ \$and

$${\vec M}= \left \vert\begin{array}{cc} -\beta \rho_{0}\ & 0 \... ...eta F \ \ & \ \ -B \\ B \ \ & \ \ A \end{array}\right \vert.$$ (31)

Note that in the space vector of the variables $\vert x\rangle$, ${\vec M}$ is positive definite, ${\vec S}$ is an hermitian operator (because $\vec{B}$ is an antihermitian one), and ${\vec R}$ is hermitian and positive definite. Taking the inner product of the space vector $\vert x\rangle$ with Eq. (30), the stability criterion, the extension of the Bernstein criterion to non-thermodynamic equilibrium states (Eq. (14)) can be written

 

$$\delta^{2} S = \frac{ 1}{ 2} \ \bigg [\int \-\dot{\vec{\xi^{*}}}\... ...1} +T_{1}^{*}B\vec{\xi} -\vec{\xi}^{*}B T_{1}\right) {\rm d}^{3}\bigg] x\geq 0.$$ (32)

For the non-dissipative cases last expression reduces to the well known Bernstein's MHD energy principle

$$\delta^{2} S = \frac{ 1}{ 2}\left [\int \-\dot{\vec{\xi^{*}}}... ...{ \vec{\xi^{*}} \beta F \vec{\xi}} {\rm d}^{3}\right] x\geq 0,$$ (33)

from where the eigenmodes and eigenfrequencies are calculated as

$$\omega^{2}=-\frac{\int \vec{\xi}^{*} \beta F\vec{\xi} {\rm d}^{3}x}{\int\vec{\xi}^{*}\beta \rho_{0}\vec{\xi} {\rm d}^{3}x }$$ (34)

and, the stability criterion is obtained by requiring the positivity of the potential energy of the perturbation (Galindo Trejo 1987)

$$\delta^{2} W_{\rm p(Bernstein)} = \frac{1}{2}\int \vec{\xi}^{*} \beta F\vec{\xi} {\rm d}^{3}x$$ (35)

subject to the normalization condition that the total kinetic energy is equal to one. Thus, the dissipative principle, the correction to Galindo Trejo's one, and the new frequencies are respectively:

$$\delta^{2} W_{\rm p} =\frac{1}{ 2}\int \Big( \vec{\xi}^{*} \b... ...{1}^{*}B\vec{\xi} -\vec{\xi}^{*}BT_{1}\Big)~{\rm d}^{3}x\geq 0$$ (36)

$$\omega^{2} =- \frac{\int \left( \vec{\xi}^{*} \beta F\vec{\xi... ...}^{3}x}{\int (\vec{\xi} \beta \rho_{0}\vec{\xi} ){\rm d}^{3}x}$$ (37)

with the same normalization condition.

4 Application to the Kippenhahn-Schlüter (K-S) model

The K-S model (Galindo Trejo 1989; Priest 1982), can be viewed as a current sheet concentrated in the region $-L_{x}/2\leq x\leq L_{x}/2$, $0\leq z\leq L_{z}$ exposed to the magnetic field

$$\vec{B}_{0}={B}_{z\infty}\ {\tanh x} % \ {e}_{z} \ + \ {B}_{x} \ {e}_{x}, % \ {B}_{x}\ =\rm const.$$ (38)

with $x=\tilde{x}/L$, L=2h₀/r, $% r=B_{z\infty }/B_{x}$, and the scale height $h_{0}=\frac{k_{\rm B}T_{0}}{mg}$. $\ T_{0}$ is the constant prominence temperature, $\tilde{x}$ is a dimensional variable. For the equilibrium the following density profile is assumed

$${\rho }_{0}=\frac{{B}_{x}\ }{ g}\frac{{ % {\rm d}B}_{z}}{{\rm d}x}\cdot$$ (39)

The fundamental constant parameters of the prominence were taken ranging in the following intervals:

 

$$T_{0} = \left(7 \times {10}^{3}\right)\ {\rm K}; \ B_{0} =\left(5... ...es {10}^{-4}\right)\ {\rm T}; \ h_{0}= \left( 211 \times {10}^{3}\right)\ \rm m$$

$${\rm average \ width}: \bar{X}=5 \times 10^{6}\ \rm m,$$

$${\rm average \ height}: \bar{Z}=(1.5{-}5) \times {10}^{7} \ \rm m,$$

$${g} = {274}; \ \frac{m}{{s}^{2}} \ ; r=0.25, {B}_{x} = 0.8944, \ {B}_{{% z\infty }} =0.2425,$$

$${L}_{x} = 2.96, \ \ {L}_{z}{ \ = \ 8.88{-}29.6,} \ \ \ 0.13\leq \ k \ \leq 0.52.$$ (40)

In order to guarantee equilibrium we required that for the isothermal static state the radiative loss globally balances with the heat source. Thus, $\iota$ satisfies

$$\int_{-{L}_{{x}}/2}^{{ L}_{{ x}}/2}{ {\rm d}x} \frac{\rho^{2}... ...iota}{m^{2}}\int_{-{L}_{{x}}/2}^{{ L}_{{ x}}/2}{ {\rm d}x}\rho$$

which as a dimensionless value results $\iota=0.158$. In spite of the fact that the heating function is required for the balance of the equilibrium state, the stability resulted vanishingly dependent of this $\iota$ value. An alternative to this heat function election is the one proposed by Low & Wu (1981). They introduced a heating term expressed as a function of the magnetic field, plasma density and pressure so the isothermal static state is self-consistent as an unperturbed equilibrium state in which the radiative loss is balanced at each point by the heat source. While the advantage of the solutions obtained by Lerche and Wu is that it allows a more general heat function it required a special choice of the $\alpha$($\alpha=1$) parameter in order to obtain analytic solutions of the problem. Our parameter choice was $\alpha=11.7, \ \chi=1.26\times 10^{-83}$. Note that, in any case, a more detailed study considering an extended range of parameters and non-isothermal situations require numerical analysis.

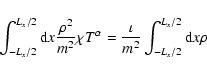
For the ideal MHD study, and in accordance with Anzer (1969), Galindo Trejo (1989) and Galindo Trejo & Schindler (1984), the model results stable due to Bernstein's MHD criterion. Also, Zweibel (1982), using this energy principle finds a sufficient condition for the stability of the K-S prominence model that represents an extension to more realistic situation i.e. without making an approximation of infinitesimal thickness of the prominence. Galindo Trejo (1989) postulates a displacement of the form

$$\xi (x,y,z)=\left[{\xi }_{x}{(x,z)e}_{x}\mathbf{\ }{+\xi }_{y... ... }{e}_{y}% {+\xi }_{z}{(x,z)\ e}_{z}\right]{\rm e}^{{\rm i}ky}$$ (41)

$${T}_{1}(x,y,z)=T_{1}{(x,z){\rm e}}^{{\rm i}ky}.$$ (42)

Then, he obtains that the most general displacement for the K-S model with a magnetic field B_y=0 and T₁=0 has the form (36) but with $\xi (x,z)=\zeta _{x}(x,z)e_{x}+i\eta _{y}(x,z)e_{y}+\zeta _{z}(x,z)\ e_{z}$.

The displacements must satisfy boundary conditions that for the case considered here assume the form $({T_{1}, \ \xi})_{\rm bound}=0$. Then, in function of the perturbations ((41) and (42)) the extended Bernstein principle that predicts stability acquires the form

 

$${\delta^{2}W_{\rm p}} = \frac{{ 1}}{{ 2}}% \int_{-{L}_{{x}}/2}^{{... ...x}}{\partial z} + B_{x}\frac{\partial \zeta_{ z}}{\partial z}\right)^{2}\right.$$

$$~+ \left(B_{z} \frac{\partial \eta_{y}}{\partial z}+B_{x}\frac{\p... ...x}\frac{\partial \zeta _{z}}{\partial x}\right)^{2}+k^{2}B_{z}^{2}\eta _{y}^{2}$$

$$~~~- \frac{\partial B_{z}}{\partial x}\left(B_{z}\zeta_{x}\frac{\... ...}{\partial x} - k B_{z}\eta_{y} \zeta_{x} + k B_{x} \eta_{ y} \zeta_{z} \right.$$

$$~~~ \left.- B_{x} \zeta_{z}\frac{\partial \zeta_{z}}{\partial z}\... ...t)^{2} + \alpha_{1} \left(\zeta_{x}\frac{\partial \rho_{0}}{ \partial x}\right)$$

$$~~~\times\left[ \frac{\partial \zeta_{x}}{\partial x} + \frac{\pa... ...rho_{0} % \zeta _{z}\right)}{\partial z} - k \rho_{0} \eta _{y} \right] \right]$$

$$~~~~~+ \alpha_{3} \left[ \frac{B_{x}^{2}}{B^{2}}\left( \frac{\partial T_{1}} {\partial x}\right)^2\right]+ \alpha_{4} \rho_{0}^{2} T_{1}^{2}$$

$$+ \alpha_{5} \left[ 2 \rho_{0} \zeta_{x} \frac{\partial}% {\parti... ...eft( \rho_{0} T_{1}\right) + 2 k \rho_0^2 {T}_{1} \eta_{y}\right]\bigg\} \geq 0$$ (43)

where,

$\alpha_{0}= 1; ~~~\alpha_{1} = 0.125; ~~~\alpha_{2} = 1 \;$

$$\alpha_{3} =7.77\times {10}^{-9};~~~ \alpha_{4} = 0.73125;~~~ \alpha_{5} = 0.125.$$ (44)

This inequality is also restricted by the normalization condition

$$\frac{1}{2}\int_{-L_{x}/2}^{L_{x}/2} {\rm d} x \int_{0}^{L_{z... ...}^{2} \left(\zeta_{x}^{2}+\eta_{y}^{2}+\zeta_{z}^{2}\right)=1.$$ (45)

5 Discussion and conclusions

As it is known quiescent prominences are stable structures with densities about hundreds times higher and temperatures about hundreds times lower than their surrounding corona. Thus, a crucial problem is to explain how is this thermal and mechanically possible. Different models in literature intended to attack the problem in a separated way: Chiuderi et al. (1979) analyzed the thermal equilibrium problem but discharged the mechanical one; between the models that investigated the mechanical equilibrium hypothesis is the early known Kippenhahn-Schluter model that neglects the important question about thermal equilibrium (Galindo Trejo 1989; Priest 1982). An attempt to combine the two aspects was made by Lerche & Low (1981) but their variational approach proceeded with non-self-adjoint quantities.

Here we proposed a self-adjoint stability criterion that takes into account the coupled thermal and mechanic balance conditions. This variational principle is a natural extension of the Bernstein's stability criterion for ideal MHD to more general states i.e. state far from thermodynamic equilibrium. The procedure to obtain the principle followed thermodynamic irreversible arguments and techniques.

As an example we applied the method to the known K-S model in its extension to dissipative situations, and in the scenario described by usual prominences parameters. The stability criterion can be rewritten in the form

 

$$\delta^{2}W_{\rm p}= \delta^{2} W_{\rm B} + \frac{{ 1}}{{ 2}} \in... ... T_{1}} {\partial x}\right)^2\right] + \alpha_{4} \rho_{0}^{2} T_{1}^{2}\right.$$

$$\left.+\alpha_{5} \left[ 2 \rho_{0} \zeta_{x} \frac{\partial} {\p... ...t( \rho_{0} T_{1}\right) + 2 k \rho_0^2 {T}_{1} \eta_{y}\right]\right\} \geq 0.$$ (46)

The mechanical stability for the most general displacement ( $\delta^{2} W_{\rm B}$; B indicates Bernstein criterion) in the MHD scenario was already been proved (Galindo Trejo 1989, Galindo Trejo & Schindler 1984) and thus, $\delta^{2} W_{\rm B}\geq 0$.

Moreover, considering both thermal and mechanical perturbations, is easy to note from last equation, that when the mechanical displacement vanishes ( $\zeta_x=\zeta_z=\eta _y=0$), it results $\delta^{2}W_{\rm p} \geq 0$ for any thermal perturbation T₁. Note that also, for any displacement of the form

$$\zeta_x= \zeta_z = 0,\; \eta _y \neq 0,$$ (47)

the principle acquires the form

 

$$\delta^{2} W_{\rm p} = \delta^{2} W_{\rm p}(\eta_y)+\frac{1}{2} \... ...ght) k^2 \eta _y^2 + \alpha_4 \rho_0^2 T_1^2 + 2 \alpha_5 k \rho_0^2 \eta_y T_1$$ (48)

with $\delta^{2} W_{\rm p}(\eta_y) \geq 0$. Thus, the quadratic form in ( $\eta _y , T_1)$: $( B_0^2 \rho_0 + P) k^2 \eta _y^2 + \alpha_4 \rho_0^2 T_1^2 + 2 \alpha_5 k \rho_0^2 \eta _y T_1 \geq 0$. This is, for the K-S model and for the particular displacement chosen here (considering dissipation), the associated quadratic form is positive definite because the "principal minors'' of the corresponding matrix are all positive definite. Then, the expression $\delta^{2} W_{\rm p} \geq 0,$ implies stable conditions for the range of parameters of the K-S model.

As an example, we applied the variational principle to the more general mode presented in this work (Eqs. (41) and (42)) to obtain the associated frequencies. In order to accomplish this task we followed the schematic procedure described by Galindo Trejo (1987) but we used a symbolic manipulation program to integrate the equations. $\delta^{2}W_{\rm p}$ and the perturbation were expanded in a two dimensional-Fourier basin that adjust to border conditions. Thus, a quadratic form for $\delta^{2}W_{\rm p}$ was obtained and was minimized with the Ritz variational procedure. Finally, a matrix discrete eigenvalue problem subject to a normalization constraint was obtained. The procedure is equivalent to solve Eq. (34) for Galindo Trejo's formulation and Eq. (37) for our modified principle.

Table 1: Periods and wavenumbers: comparison between the results of the K-S model considering dissipation with Galindo Trejo's calculus.

As the aim of our analysis was to find stable perturbation we were interested in the smallest eigenvalue that can be obtained by these procedure. Doing this, for the range of parameters and the displacement chosen, we obtained that stable modes with frequencies of about three and five minutes can be described as normal modes of the K-S model when dissipative terms are considered. The results are displayed in Table 1. The parameter range was chosen to be the same as in Galindo Trejo (1987). From the table it can be seen that the periods obtained range between 2 m and 6.55 m which is in agreement with reported observational data (e.g. in Blanco et al. 1999; Bocchialini et al. 2001). Moreover, comparing our results with Galindo Trejo's ones, it can be mentioned that the dissipative analysis exhibits deeper dependencies that in his results. We found a more markedly dependence of the period with the Lz dimension and also we found a more markedly dependence of the period with the wavenumber. The period augments with Lz increasing. Note that the Lz value more nearer to the 3 m period is Lz=8.88while the Lz value more nearer to the 5 m period is Lz=29.6. Also, k=0.13 represent the nearest wavenumber associated to the periods we are interested in (3 m and 5 m).

The example presented here is an illustrative one. It shows how the principle - the extension of Bernstein's principle to situations far from thermodynamic equilibrium - can be used in its application to the K-S model. It allowed us to obtain relevant information of the K-S prominence model when considered as a dissipative structure i.e., the periods associated to normal modes. Moreover, firm conclusions about type and structure of modes and the dependence between structures, wavenumber and periods must wait for a numerical analysis that explores different scales and prominence models. This point needs a complete eigenmode and eigenvalue analysis and will be accomplished in a next work.

Appendix: A simple illustrative example

In this Appendix we present the one-dimensional simple text-book example of the Rayleigh-Bénard convection in order to illustrate the procedure of the criterion. Bénard (1900) performed experimental studies to consider the stability of a nearly incompressible liquid and Rayleigh (1916) found the analytic condition for stability. Convection is the response of a system submitted to an unstable stratification of the density where the destabilizing force is the differential buoyancy suffered by a particle subject to a temperature fluctuation. Liquid incompressibility means that the density does not change on the application of pressure. However, it is necessary to take into account that the density decreases raising the temperature allowing the action of the differential buoyancy. With these considerations the liquid can become unstable to convection because the hotter lighter liquid at the bottom pushes to come on top of the colder liquid above. A simplified approach in terms of a temperature fluctuation $\theta$ coupled to the vertical motion v_z is sufficient to account for the main features of the instability mechanism. Moreover, since only the differential buoyancy between fluid particles at the same altitude is involved, a model including only the horizontal dependence is sufficient to describe the required condition. The balance of energy equation that describes the problem is (Manneville 1987):

$$\frac{\partial T}{\partial t}+\vec{v}\cdot \nabla T =\kappa \nabla^{2}T$$ (49)

where $\kappa=\frac{{\vec K}}{\rho c_{\rm p}}$ is the heat diffusivity; ${\vec K}$, the thermal conductivity, is assumed to be constant, $\rho$ is the density and $c_{\rm p}$ is the specific heat. If $T_{\rm b}$ and $T_{\rm t}$ are the temperatures at the bottom and the top of the liquid, then the equilibrium solution (i.e. the solution with $\frac{\partial}{\partial t}=0$ and $\vec{v}=0$) of the energy equation results:

$$T_{0}(z)=T_{b}-\beta z, \ {\rm where} \ \ \beta = \frac{T_{\rm b}-T_{\rm t}}{d}\cdot$$ (50)

We consider a temperature fluctuation in the horizontal direction $T=T_{0}(z)+\theta(x)$ (T₀(z) the equilibrium temperature) and the associated perturbation in the velocity v_z(x), (v₀=0). Thus, the temperature distribution generates a density distribution

$$\rho_{0}(z) = \rho( T_{0}(z))=\rho_{b}(1+\alpha \beta z)$$ (51)

where $\alpha$ is the coefficient of volume expansion with temperature. Then, the differential buoyancy reads

$$-g(\rho-\rho_{0})=g(\rho( T_{0}(z))-\rho(T_{0}+ \theta)=\rho_{b} \alpha g \theta.$$ (52)

Thus, the equation of motion, neglecting the vertical dependence of the fluctuation results:

$$\dot{v}_{z}-\nu \partial_{x}^{2}v_{z}-\alpha g \theta=0$$ (53)

where $\nu=\eta/\rho$ is the kinetic viscosity and $\eta$ is the dynamic viscosity. Note that an augment of $\dot{v}_{z}$corresponds an augment of $\theta$ meaning that to an upwards acceleration corresponds a positive temperature fluctuation.

Linearizing the energy equation, replacing the expression of T₀(z) and discarding second order terms we obtain:

$$\dot{\theta}-\kappa \partial_{x}^{2}\theta-\beta v_{z} =0.$$ (54)

Multiplying the first equation by $\beta$, and the second one by $\alpha g$, the compact matrix expression for the stability criterion is obtained:

 

$$x=\left \vert\begin{array}{c} v_{z} \\ \ T_{1} \end{array}\right \vert , \ \rm and$$

$${\vec M}= \left \vert\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array... ...\vert \begin{array}{cc} \beta & 0 \\ 0 & \alpha g \end{array}\right \vert\cdot$$ (55)

Taking into account that $\{ v_{z},\theta\}=\{V,\Theta\}\cos (k x)$ (Manneville 1987), then:

$$\delta^{2} S = \frac{ 1}{ 2}\left[\int_{D} {\rm d}x \left(\nu... ...heta + \alpha g \kappa k^2 \Theta^2 \right)\cos^2 (k x)\right]$$ (56)

where D is the one-dimension domain of integration. The integrand results a quadratic form in V and $\Theta$. Thus, due to the fact that the diagonal terms are positive ( $\nu \beta k^{2} > 0$ and $\alpha g \kappa k^{2} > 0$, also $\beta > 0$ meaning that the liquid is heated from bellow), the positive definiteness of $\delta^{2}S$ stands on the requirement that the determinant $\Delta=\alpha g \beta (\nu \kappa k^4 - \alpha g \beta)$ is positive. Then, in order to guarantee stability the condition that $\beta < \frac{\nu \kappa k^{4}}{\alpha g}$ is required; when $\beta > \frac{\nu \kappa k^{4}}{\alpha g}$ the system is unstable and when $\beta = \frac{\nu \kappa k^{4}}{\alpha g}$ the stability is marginal as is shown in Manneville (1987) using a normal modes analysis.

References

• Anzer, U. 1969, Sol. Phys., 8, 37 [NASA ADS] (In the text)
• Balthasar, H., Wiehr, E., Schleicher, H., & Wohl, H. 1993, A&A, 277, 635 [NASA ADS] (In the text)
• Blanco, S., Bochialini, K., Costa, A., Rovira, M., & Vial, J.-C. 1999, Sol. Phys., 186, 281 [NASA ADS] [CrossRef] (In the text)
• Bénard, H. 1900, Revue Gen. Sci. Pur. Appl., 11, 1261 [NASA ADS] (In the text)
• Bernstein, I. B., Frieman, E. A., Kruskal, M. D., & Kulsrud, R. M. 1958, Proc. Roy. Soc. A, 244, 17 [NASA ADS] [MathSciNet] (In the text)
• Bocchialini, K., Costa, A., Domenech, G., Rovira, M., & Vial, J.-C. 2001, Sol. Phys., 199, 1 [NASA ADS] [CrossRef], 133 (In the text)
• Chiuderi, C., & Van Hoven, G. 1979, ApJ, 232, L69 [NASA ADS] [CrossRef] (In the text)
• Costa, A., Ferro Fontán, C., González, R., & Sicardi Schifino, A. C. 2001, Physica A, 300, 468 [NASA ADS] (In the text)
• Galindo Trejo, J. 1987, Sol. Phys., 108, 2 [NASA ADS], 265
• Galindo Trejo, J. 1989, Rev. Mex. Astron. Astrofis., 17, 47 [NASA ADS] (In the text)
• Galindo Trejo, J., & Schindler, K. 1984, ApJ, 277, 422 [NASA ADS] [CrossRef] (In the text)
• Glansdorff, P., Nicolis, G., & Prigogine, I. 1974, Proc. Nat. Acad. Sci., 71, 197 [NASA ADS] [MathSciNet] (In the text)
• Glansdorff, P., & Prigogine, I. 1971, Structure Stability and Fluctuations (New York: Wiley Interscience) (In the text)
• Gouttebroze, P., Vial, J.-C., Bocchialini, K., Lemaire, P., & Leibacher, J. W. 1999, Sol. Phys., 184, 253 [NASA ADS] [CrossRef] (In the text)
• Graham, R. 1978, Lect. Notes Phys., 84, 83 [NASA ADS] [MathSciNet] (In the text)
• Halberstadt, G., & Goedbloed, J. P. 1993, A&A, 280, 647 [NASA ADS] (In the text)
• Keizer, J. 1976, J. Chem. Phys., 69, 2609 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
• Kennedy, D. C., & Bludman, S. A. 1997, ApJ, 484, 329 [NASA ADS] [CrossRef] (In the text)
• Kippenhahn, R., & Schluter, A. 1957, Z. Astrophys., 43, 36 [NASA ADS] (In the text)
• Lavenda, B. H. 1985, Nonequilibium Statistical Thermodynamics (Chicehster: Wiley-Interscience).
• Keizer, J. 1987, Statistical Thermodynamics of Nonequilibium Processes (New York: Springer-Verlag)
• Lavenda, B. H. 1993, Thermodynamics of Irreversible Processes (New York: Dover) (In the text)
• Ledoux, P., & Walraven, N., TH. 1958, Variable Stars, In Handbuch, Phys., 51, 353 (In the text)
• Lefschetz, S. 1977, Differential Equations: Geometric Theory (New York: Dover) (In the text)
• Lerche, I., & Low, B. C. 1980, Sol. Phys., 67, 229 [NASA ADS] (In the text)
• Lerche, I., & Low, B. C. 1981, Sol. Phys., 69, L327 [NASA ADS] (In the text)
• Low, B. C., & Wu, S. T. 1981, ApJ, 248, 335 [NASA ADS] [CrossRef] (In the text)
• Manneville, P. 1987, Dissipative Structures and weak Turbulence, (1.2 Chap. 3) (New York: Academic Press) (In the text)
• Nagablushana, B. S. 1998, A&A, 333, 1043 [NASA ADS] (In the text)
• Nicolis, G., & Prigogine, I. 1979, Proc. Acad. Sci., 76, 6060 [NASA ADS] [MathSciNet] (In the text)
• Oliver, R. 1999, The 9th European Meeting on Solar Physics ESA SSP-448, 425 (In the text)
• Oliver, R., & Ballester, J. L. 1996, ApJ, 456, 3930 [NASA ADS] (In the text)
• Onsager, L. 1931, Phys. Rev., 37, 405 [NASA ADS] [CrossRef] (In the text)
• Onsager, L., & Machlup, S. 1953, Phys. Rev., 91, 1505 [NASA ADS] [CrossRef] (In the text)
• Priest, E. 1982, Solar Magneto-hydrodynamcis (Boston: Publishing Company) (In the text)
• Prigogine, I. 1967, Thermodynamics of Irreversible Processes (New York: Wiley Interscience) (In the text)
• Rayleigh, L. 1916, Phil. Mag., 32, 529 [NASA ADS] (In the text)
• Régnier, S., Solomon, J., Vial, J.-C., Amari, D., & Mickey, T. 1999, The 9th European Meeting on Solar Physics, ESA SSP-448, 519 (In the text)
• Sicardi Schifino, A. C., Costa, A., & Ferro Fontán, C. 1991, J. Math. Phys., 32, 1350 [NASA ADS] [CrossRef] [MathSciNet] (In the text)
• Sicardi Schifino, A. C., & Ferro Fontán, C. 1985, Phys. Lett. A, 113, 263 [NASA ADS] [CrossRef] (In the text)
• Sicardi Schifino, A. C., & Ferro Fontán, C. 1989, Phys. Lett. A, 134, 371 [NASA ADS] [CrossRef]
• Sicardi Schifino, A. C., Ferro Fontán, C., González, R., & Costa, A. 2004, Physica A, 334, 201 [NASA ADS] (In the text)
• Sicardi Schifino, A. C., González, R., & Ferro Fontán, C. 1989, Phys. Lett. A, 137, 44 [NASA ADS] [CrossRef]
• Tasso, H. 1975, Plasma Phys., 17, 1131 [NASA ADS] [CrossRef] (In the text)
• Vial, J.-C. 1998, Solar Prominence Diagnostic, in IAU Coll., 167, ed. D. Webb, D. Rust, & B. Scmieder, ASPCS, 150, 175 (In the text)
• Zweibel, E. 1981, ApJ, 249, 731 [NASA ADS] [CrossRef]
• Zweibel, E. 1982, ApJ, 258, L53 [NASA ADS] [CrossRef] (In the text)