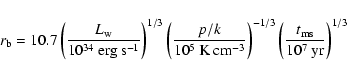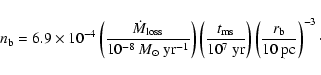A&A 427, 199-216 (2004)
DOI: 10.1051/0004-6361:20041154
XMM-Newton observations of the
supernova remnant RX J1713.7-3946 and its central source
G. Cassam-Chenaï1
- A. Decourchelle1 - J. Ballet1 - J.-L. Sauvageot1 - G. Dubner2 - E. Giacani2
1 - Service d'Astrophysique, CEA Saclay, 91191
Gif-sur-Yvette Cedex, France
2 -
Instituto de Astronomía y Física del Espacio,
CC 67, Suc. 28, 1428 Buenos Aires, Argentina
Received 23 April 2004 / Accepted 5 July 2004
Abstract
We present new results from the observations of the supernova remnant (SNR) RX J1713.7-3946 (also G347.3-0.5)
performed in five distinct pointings with the EPIC instrument on board the satellite XMM-Newton.
RX J1713.7-3946 is a shell-type SNR dominated by synchrotron radiation in the X-rays.
Its emission (emission measure and photon index) as well as the absorption along the line-of-sight has been characterized
over the entire SNR.
The X-ray mapping of the absorbing column density has revealed strong well-constrained variations
(
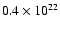 cm
cm
 cm-2)
and, particularly, a strong absorption in the southwest.
Moreover, there are several clues indicating that
the shock front of RX J1713.7-3946 is impacting the clouds responsible for the absorption as revealed for instance by
the positive correlation between X-ray absorption and X-ray brightness along the western rims.
The CO and HI observations show that the inferred cumulative absorbing column densities
are in excellent agreement with the X-ray findings in different parts of the remnant
on condition that the SNR lies at a distance of
cm-2)
and, particularly, a strong absorption in the southwest.
Moreover, there are several clues indicating that
the shock front of RX J1713.7-3946 is impacting the clouds responsible for the absorption as revealed for instance by
the positive correlation between X-ray absorption and X-ray brightness along the western rims.
The CO and HI observations show that the inferred cumulative absorbing column densities
are in excellent agreement with the X-ray findings in different parts of the remnant
on condition that the SNR lies at a distance of
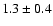 kpc, probably in the Sagittarius galactic arm,
instead of the commonly-accepted value of 6 kpc.
An excess in the CO emission is found in the southwest suggesting that the absorption is due to molecular clouds.
A search for OH masers in the southwestern region has been unsuccessful, possibly due to the low density of the clouds.
The X-ray mapping of the photon index has also revealed strong variations (
kpc, probably in the Sagittarius galactic arm,
instead of the commonly-accepted value of 6 kpc.
An excess in the CO emission is found in the southwest suggesting that the absorption is due to molecular clouds.
A search for OH masers in the southwestern region has been unsuccessful, possibly due to the low density of the clouds.
The X-ray mapping of the photon index has also revealed strong variations (
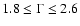 ).
The spectrum is steep in the faint central regions and flat at the
presumed shock locations, particularly in the southeast.
Nevertheless, the regions where the shock impacts molecular clouds have a steeper spectrum
than those where the shock propagates into a low density medium.
The search for the thermal emission in RX J1713.7-3946 has been unsuccessful leading
to a number density upper limit of
).
The spectrum is steep in the faint central regions and flat at the
presumed shock locations, particularly in the southeast.
Nevertheless, the regions where the shock impacts molecular clouds have a steeper spectrum
than those where the shock propagates into a low density medium.
The search for the thermal emission in RX J1713.7-3946 has been unsuccessful leading
to a number density upper limit of
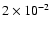 cm-3 in the ambient medium.
This low density corresponds to a reasonable kinetic energy of the explosion provided that the remnant is less than a few thousand years old.
A scenario based on a modified ambient medium due to the effect of a progenitor stellar wind is proposed and leads
to an estimate of RX J1713.7-3946's progenitor mass between 12 and
cm-3 in the ambient medium.
This low density corresponds to a reasonable kinetic energy of the explosion provided that the remnant is less than a few thousand years old.
A scenario based on a modified ambient medium due to the effect of a progenitor stellar wind is proposed and leads
to an estimate of RX J1713.7-3946's progenitor mass between 12 and
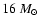 .
The X-ray bright central point source 1WGA J1713.4-3949 detected at the center of SNR RX J1713.7-3946
shows spectral properties very similar to those of the Compact Central Objects found in SNRs
and consistent in terms of absorption with that of the central diffuse X-ray emission arising from the SNR.
It is highly probable that the point source 1WGA J1713.4-3949
is the compact relic of RX J1713.7-3946's supernova progenitor.
.
The X-ray bright central point source 1WGA J1713.4-3949 detected at the center of SNR RX J1713.7-3946
shows spectral properties very similar to those of the Compact Central Objects found in SNRs
and consistent in terms of absorption with that of the central diffuse X-ray emission arising from the SNR.
It is highly probable that the point source 1WGA J1713.4-3949
is the compact relic of RX J1713.7-3946's supernova progenitor.
Key words: acceleration of particles - radiation mechanisms: non-thermal -
ISM: supernova remnants - ISM: individual objects: G347.3-0.5 (RX J1713.7-3946) -
X-rays: ISM - stars: individual: 1WGA J1713.4-3949
Supernova remnants (SNRs) are well known
to be sources of radio synchrotron emission from GeV relativistic electrons.
During the last 10 years, X-ray synchrotron
emission from TeV relativistic electrons has been discovered in several
shell-type SNRs among which are SN 1006 (Koyama et al. 1995),
RX J1713.7-3946 (Koyama et al. 1997; Slane et al. 1999)
and RX J0852.0-4622 (Slane et al. 2001).
This discovery bolstered the idea that collisionless
shocks in SNRs are very powerful and efficient electron accelerators,
possibly up to the "knee'' of the cosmic-ray (CR) spectrum up to 103 TeV.
It is reasonable to assume that protons are as well accelerated
by these shocks.
RX J1713.7-3946 is a shell-type SNR located in the Galactic
plane that was discovered with the ROSAT all-sky survey in the
constellation Scorpius (Pfeffermann & Aschenbach 1996).
It has a slightly elliptical shape with a maximum extent of
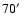 .
The observation of the northwestern shell of the SNR with the ASCA
satellite has shown the emission was exclusively non-thermal (Koyama et al. 1997).
.
The observation of the northwestern shell of the SNR with the ASCA
satellite has shown the emission was exclusively non-thermal (Koyama et al. 1997).
Further observations with ASCA of most of
the remnant did not reveal traces of the thermal emission, being likely
overwhelmed by the bright X-ray synchrotron emission (Slane et al. 1999,
hereafter SL99).
An upper limit on the mean density of the ambient medium has been
derived:
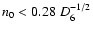 cm-3, where D6 is the
distance in units of 6 kpc.
Recently, this thermal component may have been detected
in the interior of the SNR over large fields-of-view using
ROSAT, ASCA and RXTE satellites
(Pannuti et al. 2003).
However, some possible local variations of absorbing
column density and photon index can compromise this interpretation.
cm-3, where D6 is the
distance in units of 6 kpc.
Recently, this thermal component may have been detected
in the interior of the SNR over large fields-of-view using
ROSAT, ASCA and RXTE satellites
(Pannuti et al. 2003).
However, some possible local variations of absorbing
column density and photon index can compromise this interpretation.
An intriguing X-ray point-source (1WGA J1713.4-3949) with no optical
and radio counterparts was also detected at the center of the remnant, being
possibly a neutron star or an extra-galactic object (SL99).
Recently, a combined Chandra and XMM-Newton spectral
analysis of this source has shown that its
X-ray properties
(two-component spectrum, luminosity, absence of pulsations) resemble
those of other compact central objects in SNRs and suggests
that 1WGA J1713.4-3949 is the
neutron star associated with RX J1713.7-3946 (Lazendic et al. 2003).
Neither the distance nor the age of RX J1713.7-3946 is well established.
From the X-ray measurements of the column density toward this source,
Koyama et al. (1997) derived
a distance of 1 kpc, while SL99 proposed a larger distance of 6 kpc
based on its probable association with three dense and massive molecular
clouds and the HII region G347.6+0.2 located northwest to it.
If the Sedov evolution is assumed with 6 kpc,
an age of a few 104 years results,
whereas an age of one order of magnitude below is compatible with 1 kpc.
Hence, this nearer distance could be in agreement
with the hypothesis proposed by Wang et al. (1997),
based on historical records, that RX J1713.7-3946 is the
remnant of the supernova (SN) that exploded in AD 393.
The following studies adopted the largest distance of 6 kpc, until
new XMM-Newton observations (Cassam-Chenaï et al. 2004b)
that re-opened the whole distance question together with
new high-resolution CO mm-wave observations (Fukui et al. 2003).
These new results suggest possible indications
of interaction between the SNR shock front and molecular gas located at 1 kpc
on the northwest and southwest sides of the SNR.
In the radio, the emission arises from faint filaments aligned with the
X-ray shell of RX J1713.7-3946, except for the brightest filament located
in the northwestern rim which is perpendicular to the shock and coincident
with part of the HII region G347.6+0.2 (SL99, Ellison et al. 2001;
Lazendic et al. 2004).
GeV  -ray emission was detected by the EGRET instrument
to the northeast of the SNR (Hartman et al. 1999).
This emission was interpreted as the decay of neutral pions attributed
to the interaction of CR nuclei (accelerated at the shock in RX J1713.7-3946)
with the massive and dense cloud assumed to be interacting with the remnant
(Butt et al. 2001).
By discussing the photon spectral index of the GeV source
(
-ray emission was detected by the EGRET instrument
to the northeast of the SNR (Hartman et al. 1999).
This emission was interpreted as the decay of neutral pions attributed
to the interaction of CR nuclei (accelerated at the shock in RX J1713.7-3946)
with the massive and dense cloud assumed to be interacting with the remnant
(Butt et al. 2001).
By discussing the photon spectral index of the GeV source
(
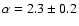 which is expected from the hadronic interactions of
CR source) and the non-detection in radio of the massive cloud.
Butt et al. (2001) ruled out the possibility that electrons are
responsible for the GeV luminosity.
which is expected from the hadronic interactions of
CR source) and the non-detection in radio of the massive cloud.
Butt et al. (2001) ruled out the possibility that electrons are
responsible for the GeV luminosity.
At TeV 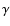 -rays, the CANGAROO imaging Cerenkov telescope
detected emission in the northwest of the SNR, which was interpreted as
Inverse Compton (IC) emission from accelerated electrons (Muraishi et al.
2000).
The low matter densities in the ambient medium is
unfavorable for the interpretation in terms of
-rays, the CANGAROO imaging Cerenkov telescope
detected emission in the northwest of the SNR, which was interpreted as
Inverse Compton (IC) emission from accelerated electrons (Muraishi et al.
2000).
The low matter densities in the ambient medium is
unfavorable for the interpretation in terms of 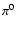 decay process.
A second CANGAROO observation of RX J1713.7-3946 leads to a TeV
decay process.
A second CANGAROO observation of RX J1713.7-3946 leads to a TeV
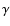 -ray spectrum (between 400 GeV and 8 TeV) whose photon spectral index
(
-ray spectrum (between 400 GeV and 8 TeV) whose photon spectral index
(
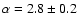 )
was shown to be consistent with the
)
was shown to be consistent with the 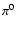 decay
process and no other mechanism (Enomoto et al. 2002).
However, such a spectrum would exceed the EGRET observed
emission by a factor three (Reimer & Pohl 2002; Butt et al. 2002).
decay
process and no other mechanism (Enomoto et al. 2002).
However, such a spectrum would exceed the EGRET observed
emission by a factor three (Reimer & Pohl 2002; Butt et al. 2002).
Several self-consistent models have been constructed using the broad-band
spectrum from radio to 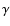 -ray wavelengths, essentially for the
northwest region of RX J1713.7-3946.
Using a non-linear diffusive shock acceleration model, Ellison et al.
(2001) were able to reproduce the broadband spectrum with synchrotron
emission from shock-accelerated electrons in X-rays and IC emission in
-ray wavelengths, essentially for the
northwest region of RX J1713.7-3946.
Using a non-linear diffusive shock acceleration model, Ellison et al.
(2001) were able to reproduce the broadband spectrum with synchrotron
emission from shock-accelerated electrons in X-rays and IC emission in
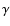 -rays.
In this model, more than
-rays.
In this model, more than 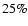 of the shock kinetic energy goes into
relativistic ions. Other attempts to reproduce the broadband spectrum were
undertaken (Uchiyama et al. 2003; Pannuti et al. 2003; Lazendic et al. 2004).
of the shock kinetic energy goes into
relativistic ions. Other attempts to reproduce the broadband spectrum were
undertaken (Uchiyama et al. 2003; Pannuti et al. 2003; Lazendic et al. 2004).
In this paper, we provide for the first time a detailed description of
the X-ray emission of RX J1713.7-3946 based on XMM-Newton observatory data.
Thanks to the large field-of-view provided by the EPIC imaging spectrometers,
we can cover the bulk of the SNR extent in a few pointings. The high
sensitivity of XMM-Newton allows us to carry out a spectral
analysis at medium-scale of the emission structures
and then to produce for the
first time a mapping of the spectral parameters of
RX J1713.7-3946.
In Sect. 2, we present our observations and the different data reduction methods that we have used.
In Sect. 3, we present the results obtained from the XMM-Newton data analysis.
Section 4 contains a discussion on
the potential association between the central point-like source 1WGA J1713.4-3949 and
SNR RX J1713.7-3946 (Sect. 4.1),
on the interaction between the remnant and clouds
as well as on the SNR distance (Sect. 4.2), on the SNR age and energetics
(Sect. 4.4) and finally on the overall picture that comes out from the results
(Sect. 4.5).
In Sect. 5, we summarize our results.
2 Data processing
Table 1:
Duration after flare rejection. The location of the different pointings is shown in Fig. 2.
SNR RX J1713.7-3946 was observed with the three EPIC instruments (namely the MOS1, MOS2 and pn cameras)
on board the XMM-Newton satellite in the course of the AO-1 program.
The observations were performed in five distinct pointings, each of around 10 ks duration.
Table 1 indicates the date of observation and the OBS_ID for each pointing.
The five pointings were chosen based on the ROSAT PSPC image (SL99) to allow a maximum coverage of the remnant
and the possibility to extract a local X-ray background.
The pointings correspond schematically to the center, northeast, northwest, southwest and southeast
(hereafter CE, NE, NW, SW, SE, respectively) parts of RX J1713.7-3946.
During the observation, the MOS and pn cameras were operated in
Full Frame and Extended Full Frame providing a temporal resolution of 2.6 s and 200 ms, respectively.
For all the pointings, the medium filter was used to avoid contamination
by visible sources contained in the field of view
and to limit the number of low energy photons (and hence pile-up) coming from the bright X-ray point source 1WGA J1713.4-3949.
The potential neutron star 1WGA J1713.4-3949 is located
roughly in the middle of the SNR at the position
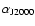 = 17h13m28.4s,
= 17h13m28.4s,
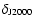 = -39
= -39 49
49
 54.5
54.5
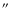 (Lazendic et al. 2003).
In the hope to detect thermal emission lines around 1 keV from 1WGA J1713.4-3949,
the RGS data were also processed in the central pointing.
(Lazendic et al. 2003).
In the hope to detect thermal emission lines around 1 keV from 1WGA J1713.4-3949,
the RGS data were also processed in the central pointing.
The Science Analysis System (SAS version 5.3) was used for data reduction.
First, we generated calibrated events files with the SAS tasks emchain and epchain.
To create light curves, spectra and images, we selected the single, double, triple and quadruple events
(pattern 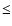 12) for the MOS cameras, and the singles and doubles (pattern
12) for the MOS cameras, and the singles and doubles (pattern 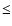 4) for the pn camera
(with FLAG = 0 for all cameras).
The data quality of the CE, SW, SE pointings is very good.
However, it is not the case for the NE and NW pointings which are contamined by soft protons flares.
The method used to clean the data from the flares
consists of applying a threshold on the light curves at high energy, i.e. where the
EPIC cameras are almost insensitive to X-ray photons.
We took a threshold of 18 counts per 100 s time interval in the 10-12 keV band for the MOS cameras (pattern
4) for the pn camera
(with FLAG = 0 for all cameras).
The data quality of the CE, SW, SE pointings is very good.
However, it is not the case for the NE and NW pointings which are contamined by soft protons flares.
The method used to clean the data from the flares
consists of applying a threshold on the light curves at high energy, i.e. where the
EPIC cameras are almost insensitive to X-ray photons.
We took a threshold of 18 counts per 100 s time interval in the 10-12 keV band for the MOS cameras (pattern 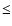 12)
and a threshold of 22 counts per 100 s time intervals in the 12-14 keV band for the pn camera (pattern = 0).
Table 1 indicates the remaining exposure time after flares cleaning for each EPIC camera.
12)
and a threshold of 22 counts per 100 s time intervals in the 12-14 keV band for the pn camera (pattern = 0).
Table 1 indicates the remaining exposure time after flares cleaning for each EPIC camera.
In this section, we describe the different methods that have been used to create the images, the hardness ratio maps,
the spectra and the mapping of the spectral parameters.
2.3.1 Images
All the mosaiced images of the X-ray emission presented here are background-subtracted,
exposure and vignetting corrected (Sect. 3.1).
The background used for the subtraction is only instrumental and
is estimated by using a reference observation (Read & Ponman 2003)
which was obtained with the same medium filter as in our observations.
No correction for the local astrophysical background is made because
we have no information on it in the center of the remnant and more further
it strongly varies around the remnant which renders difficult any extrapolation towards the interior.
To correct for the exposure and the vignetting, we divide the
mosaiced background-subtracted count image by its mosaiced exposure map
which includes the vignetting correction using the SAS task eexpmap.
Each time, the mosaiced count image is adaptively smoothed with the SAS task asmooth
and the resulting template is applied to smooth both the mosaiced background-subtracted count image
and its associated exposure map before the division.
We have not used the pn data for the intensity maps as it
introduces some problems of homogeneity
in the correction for vignetting and exposure
due to the lack of pn data in the NE pointing (see Table 1).
2.3.2 Hardness ratio maps
To create hardness ratio maps, we divide two background-subtracted images made in different energy bands that
are previously adaptively smoothed. For the smoothing, the template of the image with the lowest statistics is always
applied to that with higher statistics. When we compute the ratio of the two maps, the statistical fluctuations can be amplified.
To limit this effect, the MOS and pn data are used, but
in return, the NE is missing in the hardness ratio maps (Sect. 3.3).
2.3.3 Spectra
All spectral analyses use the weight method described in Arnaud et al. (2001) to correct for the vignetting.
For the background subtraction, we always use the double subtraction method described in Arnaud et al. (2002)
except for the mapping of the spectral parameters (see below, Sect. 2.3.4).
This method allows us to take into account the difference, at low energy, between the local astrophysical background
of our observations and the one found in the reference observation.
This is done for local spectral analyses which require a precise knowledge of the
spectrum at low energy (Sect. 3.3).
In our observations, there are two regions where the local astrophysical background can be
extracted with enough statistics: the SW and the SE.
Each time, we choose the nearest available local astrophysical background for each selected region.
The spectra are grouped so that each bin has a signal-to-noise ratio greater than 5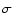 .
To fit the spectra, we use XSPEC (version 11.2, Arnaud 1996).
The chosen on-axis response files are
m*_medv9q20t5r6_all_15.rsp for MOS and
epn_ef20_sdY9_medium.rsp for pn.
.
To fit the spectra, we use XSPEC (version 11.2, Arnaud 1996).
The chosen on-axis response files are
m*_medv9q20t5r6_all_15.rsp for MOS and
epn_ef20_sdY9_medium.rsp for pn.
2.3.4 Mapping of the spectral parameters
The X-ray spectrum of SNR RX J1713.7-3946
can be well fitted by
a simple absorbed power-law model the spectral parameters of which
are the absorbing column
 and the photon index
and the photon index 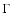 .
Here, we describe how we map the spatial variations of these two parameters (Fig. 4).
.
Here, we describe how we map the spatial variations of these two parameters (Fig. 4).
First, we build a spatial grid which takes into account
the statistics so that we have approximately the
same number of counts in each grid pixel.
The spatial grid is
constructed from a mosaiced count image (MOS+pn) between 0.8-10 keV
where all the point-like sources have been removed.
The mean number of total counts in a pixel is fixed to 9000 counts
from this image which corresponds approximately to 2500 and 4000 counts in most of the boxes of the MOS
and pn cameras, respectively.
For each pixel of the grid, we extract the X-ray spectra (MOS, pn)
and fit them with a simple absorbed power law.
A map of these parameters (
 ,
,
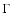 )
is constructed from the best-fit values in each grid pixel.
)
is constructed from the best-fit values in each grid pixel.
In this spectral analysis, we use a single background-subtracted method
(as described for the images, Sect. 2.3.1)
since it is not possible to have the true local astrophysical background
in each grid pixel.
Because of that, the spectral bins only above 0.8 keV are selected, i.e. where the
reference background
provided by Read & Ponman (2003) is almost one order of magnitude below the spectrum
of our observations.
We have checked that the absence of spectral bins below 0.8 keV did not
change significantly the value of the spectral parameters in the X-ray bright regions.
There is no significant difference between the single and the double background-subtraction methods
for the brightest regions.
Nevertheless, in the X-ray faint regions, the effect of the double substraction is to
increase
 and
and 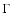 by a factor
by a factor 
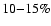 which is not
enough to alter our results and interpretation.
which is not
enough to alter our results and interpretation.
3 X-ray results
Unlike the X-ray spectra of typical shell-like SNRs which exhibit emission lines,
the spectrum of RX J1713.7-3946 is found to be featureless
as shown for example in Fig. 1.
This suggests a non-thermal origin and
has been interpreted as synchrotron X-ray emission
from TeV shock accelerated electrons (SL99).
RX J1713.7-3946 is a second example, after SN 1006, of a shell-like SNR for which non-thermal emission dominates the X-ray flux, but
more extreme in the sense that no thermal emission has been unambiguously detected yet.
Unlike SN 1006, a symmetrical limb-brightened type Ia remnant
located in a high-latitude environment,
RX J1713.7-3946 has a quite distorted morphology which may be
related to its complex surrounding environment in the Galactic plane and is likely to be the remnant
of a type II explosion as suggested by the presence of a central point source
detected at its center.
In Sect. 3.1, we describe in detail the unusual X-ray morphology of
RX J1713.7-3946,
and compare it to the radio continuum morphology.
In Sect. 3.2, we trace and accurately diagnose the spectral variations of the
synchrotron emission.
In Sect. 3.3, we search for the thermal emission and constraints on its properties.
Finally, in Sect. 3.4, we intent to give better spectral constraints on the nature of
the point-like source 1WGA J1713.4-3949 to
provide arguments in favor or against a potential association with
SNR RX J1713.7-3946.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{1154_fig1.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg59.gif) |
Figure 1:
EPIC pn spectra (double background subtraction)
of the SW and SE regions of SNR RX J1713.7-3946. The fit with a power-law model gives
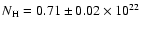 cm-2 and cm-2 and
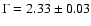 for the SW region and
for the SW region and
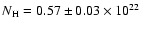 cm-2 and cm-2 and
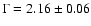 for the SE region at a 90% confidence level.
for the SE region at a 90% confidence level. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1154_fig2.eps}\hspace*{3mm}
\includegraphics[width=7.8cm,clip]{1154_fig3.eps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg60.gif) |
Figure 2:
Left panel: MOS mosaiced image of SNR RX J1713.7-3946
in the 0.8-2 keV energy band.
Right panel: same as left panel but in the 2-10 keV energy band.
The neutron star 1WGA J1713.4-3949 is located in the middle
of the CE pointing.
Both images were adaptively smoothed to a signal-to-noise ratio of 10.
The scaling is square root with the higher cut fixed to 30%
of the SNR maximum X-ray brightness.
The color bar numbers are in units of counts/s/pixel with a pixel
size of
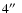 .
The bad resolution in the NE is due to a very short exposure time
(see Table 1).
Moreover, it is possible that the smoothing has removed a few
small-scale features in this NE pointing. .
The bad resolution in the NE is due to a very short exposure time
(see Table 1).
Moreover, it is possible that the smoothing has removed a few
small-scale features in this NE pointing. |
| Open with DEXTER |
3.1 X-ray morphology
The good spatial resolution and sensitivity of XMM-Newton combined with its large field-of-view
allow us for the first time to both have an overall view of RX J1713.7-3946 and resolve some X-ray emission features not seen before in the
ROSAT and ASCA images (SL99, Uchiyama et al. 2003).
Figure 2 shows the 5 pointings mosaiced image
of RX J1713.7-3946 in the 0.8-2 keV (left panel)
and 2-10 keV (right panel) energy bands.
However, the 5 pointings are not enough for a complete coverage of the SNR.
The general shape of this distorted remnant
resembles roughly an ellipse stretched out along the
NW-SE axis over 
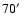 corresponding to
corresponding to  20 pc at 1 kpc or
20 pc at 1 kpc or  120 pc at
6 kpc.
An overall view of RX J1713.7-3946 obtained with ASCA
(Uchiyama et al. 2003) shows that the boundaries of
the SNR are irregular and suggests
that the remnant extends farther to the north.
120 pc at
6 kpc.
An overall view of RX J1713.7-3946 obtained with ASCA
(Uchiyama et al. 2003) shows that the boundaries of
the SNR are irregular and suggests
that the remnant extends farther to the north.
Except for the point-like sources,
the comparison between the low energy and high energy images (see Fig. 2)
does not show significant changes in the X-ray morphology at first sight,
at least for the brightest X-ray features.
From these images, the X-ray emission can be schematically classified in three distinct levels.
The lower intensity one is due to the diffuse X-ray emission of the local astrophysical background.
In both images, it can be found (in blue-black) on the outside of the NE, NW, SW and SE pointings.
It stands out that the local astrophysical background intensity varies around the remnant.
This fact is expected since RX J1713.7-3946 lies just below the Galactic Ridge
in an environment where the properties of the interstellar gas rapidly change
with Galactic latitude (which is the direction where the SNR is more stretched out).
The medium intensity level corresponds to the diffuse and faint X-ray emission arising from the SNR which clearly
dominates in the 0.8-2 keV energy band (in green and also in blue).
The higher intensity level is made of a more structured emission which appears in both
images but more clearly at high energy in the 2-10 keV band (in yellow and red).
Its surface brightness is about twice that of the diffuse emission associated with the SNR.
Both the NW and SW limbs are very bright in X-rays.
The X-ray emission in the western half is more structured than anywhere else in the SNR.
At large scales, a double-ring morphology stands out.
The internal ring is more or less circular whereas the external one looks broken into a few arcs.
At smaller scales, the Chandra image of the NW region shows
that the brightest X-ray features correspond to thin filaments of
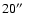 apparent width or hot spots embedded in a
diffuse plateau emission (Uchiyama et al. 2003; Lazendic et al. 2004).
This is confirmed by XMM-Newton in the NW and also in the SW.
apparent width or hot spots embedded in a
diffuse plateau emission (Uchiyama et al. 2003; Lazendic et al. 2004).
This is confirmed by XMM-Newton in the NW and also in the SW.
In spite of its bad quality, the NE observation shows that the inner circular thin shell seen in the west
seems to continue there (see Fig. 2, right panel).
Nevertheless, the diffuse X-ray emission from the NE pointing
seems to exhibit a concave border between the
remnant and the ambient medium (green emission in Fig. 2, left panel).
Such a shape is not naturally expected from an
explosion into a homogeneous low density interstellar medium.
That shape must be caused by some obstacles either interacting with
the SNR or obstructing the X-ray emission arising from it.
The X-ray emission from the SE is weak and diffuse but even
so we distinguish a possible border between the SNR and the ambient medium.
Finally, the central part of the SNR shows diffuse X-ray emission
rather weaker than in the NW and SW but similar to what is observed in the SE.
In addition, two point sources are observed.
The first one is 1 WGA J1714.4-3945 located at the position
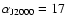 h14m30s,
h14m30s,
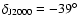 46
46
 00
00
 which disappears above 2 keV.
The second one located in the middle of the CE pointing is 1WGA J1713.4-3949,
a potential neutron star, which will be studied in detail in Sect. 3.4.
which disappears above 2 keV.
The second one located in the middle of the CE pointing is 1WGA J1713.4-3949,
a potential neutron star, which will be studied in detail in Sect. 3.4.
Figure 3 shows a high-resolution radio image
obtained at 1.4 GHz with ATCA (from Lazendic et al. 2004)
overlaid with the X-ray contours.
The radio morphology of RX J1713.7-3946 is
quite complex, with the brightest emission corresponding to the HII region
G347.6+0.2, to the NW corner. A well defined ring of emission, about 15
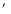 in size, is visible in the interior of the SNR. This radio feature
matches the inner X-ray bright ring, particularly towards the northern, northwestern and western
sides. Also, a very good correspondence is observed on the X-ray-bright outer rim to the SW.
The observed similar morphology in the radio and in the X-rays strongly suggests that
the synchrotron emission detected at the two spectral domains must originate in the same
electron population accelerated at the shocks.
in size, is visible in the interior of the SNR. This radio feature
matches the inner X-ray bright ring, particularly towards the northern, northwestern and western
sides. Also, a very good correspondence is observed on the X-ray-bright outer rim to the SW.
The observed similar morphology in the radio and in the X-rays strongly suggests that
the synchrotron emission detected at the two spectral domains must originate in the same
electron population accelerated at the shocks.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1154_fig4.eps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg64.gif) |
Figure 3:
1.4 GHz ATCA radio image (courtesy of J.S. Lazendic)
overlaid with the 2-10 keV contour of SNR RX J1713.7-3946.
The scaling is linear.
The contour values start at 10-5 MOS counts/s/pixel and are square root
spaced up to
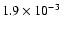 counts/s/pixel with a pixel size of counts/s/pixel with a pixel size of
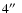 . . |
| Open with DEXTER |
3.2 Spatial and spectral characterization of the synchrotron emission
In this section, we present the maps of absorbing column density and photon index
(method described in Sect. 2.3.4).
Figure 4 (left panel) shows the mapping of absorbing column
density in the line-of-sight at medium scale.
The mean relative error on the absorbing column in each pixel
grid is 
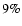 with a maximum value of
with a maximum value of 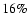 .
The variations of absorbing column density are strong
with
.
The variations of absorbing column density are strong
with
 varying from
varying from 
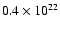 cm-2 to
cm-2 to

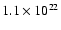 cm-2.
In the SE and CE pointings,
cm-2.
In the SE and CE pointings,
 is low with a value
is low with a value 
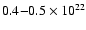 cm-2
whereas it is larger in the NW (
cm-2
whereas it is larger in the NW (
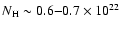 cm-2)
and even more in the SW (
cm-2)
and even more in the SW (
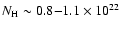 cm-2).
Figure 5 (top panel) illustrates the variations of
absorbing column from two spectra extracted in the SW region.
cm-2).
Figure 5 (top panel) illustrates the variations of
absorbing column from two spectra extracted in the SW region.
The comparison between the mapping of absorbing column
density and the X-ray brightness contours
(Fig. 4, left panel) suggests that there is
a positive correlation between them.
Figure 6 shows the X-ray brightness at 1 keV
versus
 in each grid pixel.
We see that the regions of large (small)
in each grid pixel.
We see that the regions of large (small)
 correspond to those of high (weak) X-ray brightness
confirming the significance of the observed correlation.
The fact that high absorbing column coincides with brighter
X-ray emission, as observed to the SW (and NW), is unexpected.
Indeed, a dense cloud located in front of an X-ray source
and not related to it must diminish the photon source flux in our direction (at low energy in particular).
That we observe a positive
correlation between the absorbing column density and the X-ray brightness
means that the increased ambient density somehow amplifies the X-ray brightness.
This strongly suggests that the remnant is interacting in the brightest regions
with part of the line-of-sight absorbing material.
correspond to those of high (weak) X-ray brightness
confirming the significance of the observed correlation.
The fact that high absorbing column coincides with brighter
X-ray emission, as observed to the SW (and NW), is unexpected.
Indeed, a dense cloud located in front of an X-ray source
and not related to it must diminish the photon source flux in our direction (at low energy in particular).
That we observe a positive
correlation between the absorbing column density and the X-ray brightness
means that the increased ambient density somehow amplifies the X-ray brightness.
This strongly suggests that the remnant is interacting in the brightest regions
with part of the line-of-sight absorbing material.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1154_fig5.eps}\hspace*{6mm...
...ps}\hspace*{6mm}
\includegraphics[width=7.9cm,clip]{1154_fig8.eps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg71.gif) |
Figure 4:
Left panel: absorbing column map
 (in units of 1022 cm-2)
overlaid with the contour of the 2-10 keV image of SNR RX J1713.7-3946.
The contour values start at 10-5 MOS counts/s/pixel and are square root
spaced up to
(in units of 1022 cm-2)
overlaid with the contour of the 2-10 keV image of SNR RX J1713.7-3946.
The contour values start at 10-5 MOS counts/s/pixel and are square root
spaced up to
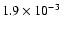 counts/s/pixel with a pixel size of counts/s/pixel with a pixel size of
 .
The big boxes of our adaptive grid found in the NE and NW pointings are due to the low exposure time there.
Right panel: photon index map overlaid with the same X-ray contours.
In both images, the scaling is linear. .
The big boxes of our adaptive grid found in the NE and NW pointings are due to the low exposure time there.
Right panel: photon index map overlaid with the same X-ray contours.
In both images, the scaling is linear. |
| Open with DEXTER |
Figure 4 (right panel) shows the mapping of the photon spectral index.
The mean relative error on the photon index value in each grid pixel is

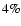 with a maximum value of
with a maximum value of 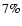 .
The variations of photon index are important
given that
.
The variations of photon index are important
given that 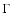 varies from
varies from  1.8 to
1.8 to  2.6.
The spectrum is steep in the faint central region whereas
it is a bit flatter in the NW and even more so in the SE.
The fact that the spectrum gets steeper as we move inwards
away from the shock front is expected in SNRs.
This effect is generally explained by the
adiabatic expansion of the remnant and the synchrotron
radiative losses (Reynolds 1998) as is also observed in SN 1006.
In the SW, the spectrum is generally steep, but some regions exhibit strong variations of spectral index
as is shown in Fig. 4 (right panel).
For illustration, Fig. 5 (bottom panel) shows the spectrum of
two regions in the SW, for which the index is very different.
2.6.
The spectrum is steep in the faint central region whereas
it is a bit flatter in the NW and even more so in the SE.
The fact that the spectrum gets steeper as we move inwards
away from the shock front is expected in SNRs.
This effect is generally explained by the
adiabatic expansion of the remnant and the synchrotron
radiative losses (Reynolds 1998) as is also observed in SN 1006.
In the SW, the spectrum is generally steep, but some regions exhibit strong variations of spectral index
as is shown in Fig. 4 (right panel).
For illustration, Fig. 5 (bottom panel) shows the spectrum of
two regions in the SW, for which the index is very different.
The synchrotron X-ray morphology, though quite complex,
can be related to the absorption along the line-of-sight (or equivalently brightness).
On the one hand, there is a weakly absorbed SE region which seems to extend far away from
the center of the SNR (taken as the point-like source 1WGA J1713.4-3949),
and on the other hand, a strongly absorbed western region which is closer
and where RX J1713.7-3946 is suspected to interact with the material that causes the absorption.
Such an asymmetry in the morphology and the absorption
must be the result of different ambient densities around the remnant.
To investigate how particle acceleration is modified in different environments,
we have selected two sets of points located at the presumed shock locations:
the one in the SW external rim coincident
with the radio emission (see Fig. 3) and in the SE.
These points are shown in Fig. 7 in the
absorbing column density-X-ray brightness plane (top panel) and
in the photon index-X-ray brightness plane (bottom panel).
It is obvious that two groups stand out.
The regions where the shock propagates in the SW have a steep spectrum
(
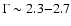 )
and those where the shock propagates
in the SE have a flat spectrum (
)
and those where the shock propagates
in the SE have a flat spectrum (
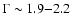 )
)![[*]](/icons/foot_motif.gif) .
This point is discussed further in Sect. 4.3.
.
This point is discussed further in Sect. 4.3.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{1154_fig9.ps}\vs...
...*{3mm}
\includegraphics[angle=-90,width=7.5cm,clip]{1154_fig10.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg76.gif) |
Figure 5:
Top panel: pn spectra of two SW regions of similar brightness (
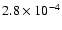 photons/cm2/s/keV/arcmin2)
and same photon index ( photons/cm2/s/keV/arcmin2)
and same photon index (
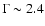 )
but with different absorbing column densities.
The absorbing column is )
but with different absorbing column densities.
The absorbing column is
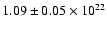 cm-2 for the top spectrum
(17h11m58.2s, -39 cm-2 for the top spectrum
(17h11m58.2s, -39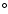 59 59
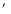 44.5 44.5
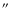 )
and )
and
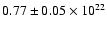 cm-2 for the other one
(17h11m52.5s, -39
cm-2 for the other one
(17h11m52.5s, -39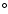 55 55
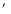 54.6. 54.6.
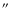 ).
Bottom panel: pn spectra of two SW regions of similar brightness ( ).
Bottom panel: pn spectra of two SW regions of similar brightness (
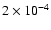 photons/cm2/s/keV/arcmin2)
and same absorbing column (
photons/cm2/s/keV/arcmin2)
and same absorbing column (
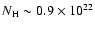 cm-2)
but with different photon index. cm-2)
but with different photon index.
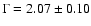 for the top spectrum
(17h12m26.7s, -39
for the top spectrum
(17h12m26.7s, -39 57 57
 34.4 34.4
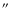 )
and )
and
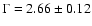 for the other one
(17h11m52.6s,
for the other one
(17h11m52.6s,
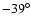 54 54
 49.0 49.0
 ). ). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1154_fig11.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg77.gif) |
Figure 6:
Correlation plot between the absorbing column
 (in units of 1022 cm-2) and the normalized
brightness at 1 keV.
Each point corresponds to the value found for a particular pixel of the mapping grid
(Sect. 2.3.4) and
the error bars are given at a 90% confidence level.
The symbols are defined as follow
(cf. Table 1):
(in units of 1022 cm-2) and the normalized
brightness at 1 keV.
Each point corresponds to the value found for a particular pixel of the mapping grid
(Sect. 2.3.4) and
the error bars are given at a 90% confidence level.
The symbols are defined as follow
(cf. Table 1):
 for NE, for NW,
for NE, for NW,  for SW,
for SW,  for SE,
for SE,  for CE.
The regions which are the more absorbed are the brightest.
They are mainly located in the SW.
The regions which have small
for CE.
The regions which are the more absorbed are the brightest.
They are mainly located in the SW.
The regions which have small
 are the less bright and are found in the CE
and SE.
are the less bright and are found in the CE
and SE. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1154_fig12.ps}\par\vspace*{3mm}
\includegraphics[width=8cm,clip]{1154_fig13.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg78.gif) |
Figure 7:
Top panel: correlation plots at the shock location
in the SW ( )
and SE ( )
and SE ( )
regions between
the absorbing column )
regions between
the absorbing column
 (in units of 1022 cm-2) and the normalized
brightness at 1 keV (in units of 10-4 photons/cm2/s/keV/arcmin2).
Each point corresponds to the value found for a
particular pixel of the mapping grid
(Sect. 2.3.4) and
the error bars are given at a
(in units of 1022 cm-2) and the normalized
brightness at 1 keV (in units of 10-4 photons/cm2/s/keV/arcmin2).
Each point corresponds to the value found for a
particular pixel of the mapping grid
(Sect. 2.3.4) and
the error bars are given at a 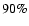 confidence level.
The points of the SW region are selected so that they are
above
confidence level.
The points of the SW region are selected so that they are
above
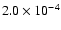 photons/cm2/s/keV/arcmin2.
Bottom panel:
correlation plots between the photon index photons/cm2/s/keV/arcmin2.
Bottom panel:
correlation plots between the photon index 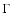 and
the normalized brightness at 1 keV for the same set of points as above.
The error bars are given at a
and
the normalized brightness at 1 keV for the same set of points as above.
The error bars are given at a 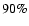 confidence level.
confidence level. |
| Open with DEXTER |
3.3 Thermal emission
Determining the thermal properties of the hot gas is crucial
to constrain the evolutionary state of the remnant.
That the thermal emission is not clearly detected in SNR RX J1713.7-3946
however sets strong limits on the temperature of the hot gas and, above all,
on its mean density.
On the one hand, the temperature determination is important
because it gives an idea of the shock velocity
(with a few assumptions on the heating of the electrons behind the shock).
On the other hand, the estimation of the mean ambient medium density is crucial to
provide an estimate of the swept-up mass (assuming that the distance to
the SNR is known) which then constrains the phase of evolution of the remnant.
To characterize the synchrotron emission (Sect. 3.2), the spectra of
SNR RX J1713.7-3946 were modelled by an absorbed phenomenological power-law
which provides, at the first order, an excellent representation of the data.
To search for the thermal emission, we add a second component, the thermal model,
which will not necessarily improve the spectral fit but will be essential
to constrain the properties of the thermal gas.
For this task, it is important to look at spectrally homogeneous areas
since the spectrum of a region with strong variations of
 and
and 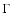 modelled with an uniformly absorbed single power-law could simulate artificially the need
for a thermal additional component instead of a second non-thermal component.
Eight particular regions (point-like sources removed) with no or few spectral variations were chosen based on the
low-energy and high-energy hardness ratio maps, and such that they
have enough statistics. They are shown in Fig. 8.
Although the hardness ratio maps do not give the value of
modelled with an uniformly absorbed single power-law could simulate artificially the need
for a thermal additional component instead of a second non-thermal component.
Eight particular regions (point-like sources removed) with no or few spectral variations were chosen based on the
low-energy and high-energy hardness ratio maps, and such that they
have enough statistics. They are shown in Fig. 8.
Although the hardness ratio maps do not give the value of 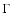 or
or
 ,
they permit us to retain more precise spatial information than
in the photon index or absorbing column map which
intrinsically depend on the shape and size of the pixels of the grid.
,
they permit us to retain more precise spatial information than
in the photon index or absorbing column map which
intrinsically depend on the shape and size of the pixels of the grid.
Like in previous studies where an attempt to investigate
the thermal emission properties was done (SL99, Pannuti et al. 2003),
we will first assume the plasma to be in an equilibrium ionization state.
This hypothesis will be discussed further.
In the following study, the elemental abundances are fixed to solar.
First, we investigate how our previous results (Sect. 3.2) might
be modified by the addition of a thermal component in the model.
Table 2 gives the best-fit parameters obtained for an absorbed power-law model
in each of the eight regions selected for this analysis, while Table 3
gives the results obtained with the addition of a thermal equilibrium ionization component.
It appears that the introduction of the thermal model
improves very slightly the fit
(
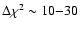 )
and does not change
qualitatively the results found for
the non-thermal emission as is shown in Fig. 9.
The derived parameters (
)
and does not change
qualitatively the results found for
the non-thermal emission as is shown in Fig. 9.
The derived parameters (
 ,
,
 )
are similarly changed for all the eight regions:
they always get slightly larger as we add the thermal component to the model.
)
are similarly changed for all the eight regions:
they always get slightly larger as we add the thermal component to the model.
The comparison between the fluxes of the thermal emission obtained in different regions of the SNR gives
an idea of the spatial distribution of the shocked medium density.
Table 3 gives the value of
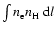 and the temperature found for the thermal emission (for the 8 regions).
The range of temperatures
and the temperature found for the thermal emission (for the 8 regions).
The range of temperatures
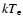 is always below 1 keV.
The values of the square density integrated along the line-of-sight are rather homogeneous
(
is always below 1 keV.
The values of the square density integrated along the line-of-sight are rather homogeneous
(
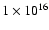 cm-5).
We note however that this quantity seems to increase from the
SNR shock front (regions 1 and 8) to the interior (regions 2 and 6) when we look at a temperature around 0.5-0.6 keV.
cm-5).
We note however that this quantity seems to increase from the
SNR shock front (regions 1 and 8) to the interior (regions 2 and 6) when we look at a temperature around 0.5-0.6 keV.
The postshock electronic number density
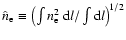 is determined by (assuming that
is determined by (assuming that
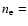
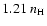 ):
):
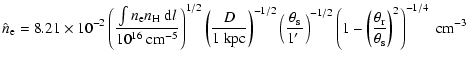 |
|
|
(1) |
where the angular distance between the center of the SNR
(taken as the position of the central point-like source 1WGA J1713.4-3949) and the
considered region is
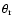 while that of the blast-wave is
while that of the blast-wave is
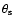 .
Table 4 shows that the average postshock electronic density is approximately
at the same level over the SNR (
.
Table 4 shows that the average postshock electronic density is approximately
at the same level over the SNR (
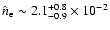 cm-3 for D = 1 kpc),
being a bit larger in the interior
(
cm-3 for D = 1 kpc),
being a bit larger in the interior
(
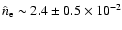 cm-3)
than close to the shock (
cm-3)
than close to the shock (
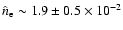 cm-3).
In a Sedov model, the average postshock density is similar to the mean number density in the
ambient medium in the inner regions of the SNR.
Then, the postshock densities lead to a mean hydrogen number density n0 of the ambient
preshock medium between 0.010 and 0.024
D1-1/2 cm-3.
cm-3).
In a Sedov model, the average postshock density is similar to the mean number density in the
ambient medium in the inner regions of the SNR.
Then, the postshock densities lead to a mean hydrogen number density n0 of the ambient
preshock medium between 0.010 and 0.024
D1-1/2 cm-3.
Nevertheless, because of the extremely low density in the ambient medium,
the assumption of equilibrium ionization state does not hold any more.
Indeed, since the ionization age must be lower than
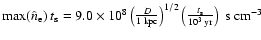 where
where 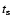 is the SNR age,
even a remnant of 105 years old would be insufficient to reach the ionization equilibrium.
Consequently, we have applied a non-equilibrium model instead of the equilibrium model
while keeping the power-law model.
This has been done by relating the ionization age
is the SNR age,
even a remnant of 105 years old would be insufficient to reach the ionization equilibrium.
Consequently, we have applied a non-equilibrium model instead of the equilibrium model
while keeping the power-law model.
This has been done by relating the ionization age 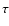 to the emission measure as described in Cassam-Chenaï et al. (2004a, Sect. 6.3).
It is found that this model does not improve the fit obtained with the power-law model alone.
In the power-law plus non-equilibrium model,
the power-law characteristics are the same as those obtained for a single
power-law model (Table 2).
The temperature of the thermal gas is found to be around 3 keV but is poorly constrained.
Moreover, an upper limit on the ionization age of
to the emission measure as described in Cassam-Chenaï et al. (2004a, Sect. 6.3).
It is found that this model does not improve the fit obtained with the power-law model alone.
In the power-law plus non-equilibrium model,
the power-law characteristics are the same as those obtained for a single
power-law model (Table 2).
The temperature of the thermal gas is found to be around 3 keV but is poorly constrained.
Moreover, an upper limit on the ionization age of
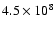 s cm-3 is obtained.
Assuming
s cm-3 is obtained.
Assuming
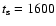 years (cf. Sect. 4.4), this leads to an upper limit of
years (cf. Sect. 4.4), this leads to an upper limit of
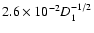 cm-3 for the average postshock electronic density and
cm-3 for the average postshock electronic density and
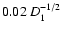 cm-3 for the mean hydrogen number density of the ambient
preshock medium (D1 is the distance in units of 1 kpc).
cm-3 for the mean hydrogen number density of the ambient
preshock medium (D1 is the distance in units of 1 kpc).
Whatever the thermal model (equilibrium or non-equilibrium) added to the
nonthermal model, we derive similar mean hydrogen number densities n0 of the ambient preshock medium.
In the following, we will adopt the upper limit
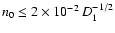 cm-3.
cm-3.
3.4 Central source 1WGA J1713.4-3949
The nature of the point-like source 1WGA J1713.4-3949 located at the center of SNR RX J1713.7-3946
is not clearly established: a neutron star or a background extra-galactic source seem to be
possible interpretations (SL99).
However, the neutron star hypothesis is the most attractive
because of the lack of radio emission and as optical counterpart,
and because the derived upper limit column density from the ASCA X-ray spectra
is comparable to the total absorption through the Galaxy in this direction (SL99).
Recently, Lazendic et al. (2003) have shown that no pulsation and
no long-term flux variability have been found using the ASCA, RXTE, Chandra and XMM-Newton data.
Besides, the radio pulsar PSR J1713-3945
(
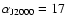 h14m23.3s,
h14m23.3s,
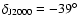 45
45
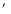 47.5
47.5
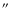 ,
P=392 ms, D=4.3 kpc) is not
associated with the X-ray point source 1WGA J1713.4-3949 nor with SNR RX J1713.7-3946.
,
P=392 ms, D=4.3 kpc) is not
associated with the X-ray point source 1WGA J1713.4-3949 nor with SNR RX J1713.7-3946.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1154_fig14.eps}\hspace*{4m...
...e*{4mm}
\includegraphics[width=8cm,height=1cm,clip]{1154_fig17.eps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg100.gif) |
Figure 8:
Left panel: spatial distribution of the hardness ratio
[0.7-0.9 keV]/[1.0-1.3 keV]
overlaid with the contour of the 2-10 keV image of SNR RX J1713.7-3946.
Right panel: spatial distribution of the hardness ratio [5-8 keV]/[1.6-2.0 keV] overlaid with the same X-ray contours.
In both images, the point-like sources have been removed. The scaling is linear.
Regions of extraction used for the search of the thermal emission are shown and labeled from 1
to 8. |
| Open with DEXTER |
Here, we intend to give better spectral constraints on the nature of this source 1WGA J1713.4-3949
thanks to the high sensitivity of XMM-Newton.
The spectral analysis of the source, as well as the knowledge of
the absorbing column density map of the remnant (Sect. 3.2),
must provide arguments in favor of or against a potential association with
the SNR RX J1713.7-3946.
We extracted the source counts from a
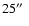 radius circle
and the background was taken in an annulus of radii
radius circle
and the background was taken in an annulus of radii
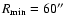 and
and
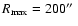 around the point source center.
The background subtracted source count rates obtained are
around the point source center.
The background subtracted source count rates obtained are
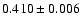 ,
,
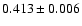 and
and
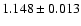 counts s-1 for MOS1, MOS2 and pn, respectively.
We extracted the spectrum of the central source in the 0.3-12.0 keV band.
As shown in Fig. 10, it does not extend higher than 6.5 keV.
No thermal spectral emission lines are found in the EPIC data, nor in the RGS data around 1 keV.
counts s-1 for MOS1, MOS2 and pn, respectively.
We extracted the spectrum of the central source in the 0.3-12.0 keV band.
As shown in Fig. 10, it does not extend higher than 6.5 keV.
No thermal spectral emission lines are found in the EPIC data, nor in the RGS data around 1 keV.
We first considered one component simple models, the results of which are summarized in Table 5.
Fitting the spectrum with a simple absorbed power law yields a large photon index
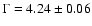 .
Such a value is much steeper than what is generally found in other young neutron stars which are well known
for their non-thermal emission from relativistic particles accelerated in the pulsar magnetosphere
(for instance, Willingale et al. 2001 give
.
Such a value is much steeper than what is generally found in other young neutron stars which are well known
for their non-thermal emission from relativistic particles accelerated in the pulsar magnetosphere
(for instance, Willingale et al. 2001 give
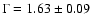 for the Crab pulsar).
Moreover, the fit overestimates the spectrum at high energy resulting in a bad
for the Crab pulsar).
Moreover, the fit overestimates the spectrum at high energy resulting in a bad
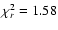 (for 475 d.o.f.).
The column density
(for 475 d.o.f.).
The column density
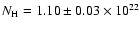 cm-2
inferred exceeds the values found in the SNR surrounding medium.
cm-2
inferred exceeds the values found in the SNR surrounding medium.
If the source is not an active pulsar but a neutron star, thermal radiation from the star surface can be observed.
A single blackbody model improves the fit (
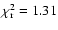 for 475 d.o.f.)
but does not reproduce the hard emission.
It yields a high temperature of
for 475 d.o.f.)
but does not reproduce the hard emission.
It yields a high temperature of
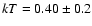 keV, a small radius
keV, a small radius
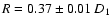 km of emitting area and a luminosity
of
km of emitting area and a luminosity
of
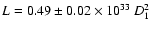
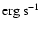 where D1 is the distance in units of 1 kpc.
The value of L is lower than predicted by standard cooling neutron star models
for which the typical luminosity is
where D1 is the distance in units of 1 kpc.
The value of L is lower than predicted by standard cooling neutron star models
for which the typical luminosity is 
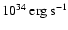 for a
neutron star of a few thousand years (e.g. Tsurata 1998).
Such a low luminosity could be explained by an accelerated cooling process.
However the small size of emitting area along with the high temperature means that the cooling
cannot take place from the entire neutron star surface.
Note that the temperature, radius and luminosity of the central point source 1WGA J1713.4-3949
are almost identical to what is found for the central point source in SNR RX J0852.0-4622 (also G266.2-1.2 or
"Vela Junior'') adopting a distance of 1 kpc (see Becker & Aschenbach 2002; Kargaltsev et al. 2002).
The column density
for a
neutron star of a few thousand years (e.g. Tsurata 1998).
Such a low luminosity could be explained by an accelerated cooling process.
However the small size of emitting area along with the high temperature means that the cooling
cannot take place from the entire neutron star surface.
Note that the temperature, radius and luminosity of the central point source 1WGA J1713.4-3949
are almost identical to what is found for the central point source in SNR RX J0852.0-4622 (also G266.2-1.2 or
"Vela Junior'') adopting a distance of 1 kpc (see Becker & Aschenbach 2002; Kargaltsev et al. 2002).
The column density
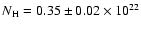 cm-2
is lower than the values found in the SNR.
We note that our range of temperatures is in the error bars given by SL99 whereas
both our column density and radius are lower (in SL99,
cm-2
is lower than the values found in the SNR.
We note that our range of temperatures is in the error bars given by SL99 whereas
both our column density and radius are lower (in SL99,
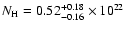 cm-2 and
cm-2 and
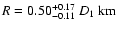 ).
The latter point should be related to the weak flux reduction.
Indeed, the unabsorbed flux in the
).
The latter point should be related to the weak flux reduction.
Indeed, the unabsorbed flux in the
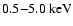 energy band
obtained with ASCA (
energy band
obtained with ASCA (
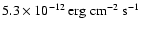 ,
SL99)
is larger than the one obtained with XMM-Newton
(
,
SL99)
is larger than the one obtained with XMM-Newton
(
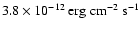 ).
).
A simple thermal bremsstrahlung yields an excellent fit (
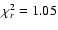 for 475 d.o.f.)
with a high temperature
for 475 d.o.f.)
with a high temperature
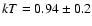 keV and an absorbing column density of
keV and an absorbing column density of
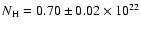 cm-2 compatible with the value derived
at the center of the SNR.
cm-2 compatible with the value derived
at the center of the SNR.
A more precise description of 1WGA J1713.4-3949 can be given by testing more
elaborate models with two spectral components.
Table 6 summarizes the results obtained.
To allow for different emission mechanisms, we first introduce a soft thermal component arising from
the neutron star surface with a blackbody model and a non-thermal component described by a power law due to
relativistic particles heating the polar caps of the neutron star.
The resulting fit is similar to that obtained with the thermal bremsstrahlung model.
The photon index
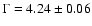 is steep in comparison to the spectral index found in young neutron stars.
Both the luminosity and the temperature are a bit lower
than what is expected for a cooling neutron star of a few thousand years (Tsurata 1998).
The column density
is steep in comparison to the spectral index found in young neutron stars.
Both the luminosity and the temperature are a bit lower
than what is expected for a cooling neutron star of a few thousand years (Tsurata 1998).
The column density
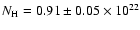 cm-2 inferred exceeds the values found in the SNR center.
cm-2 inferred exceeds the values found in the SNR center.
Table 2:
Best fit parameters for the power-law model using the MOS and pn data all at once.
The errors are in the range
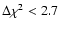 (90% confidence level) on one parameter.
The regions shown in Fig. 8.
Norm is given in units of photons/cm2/s/keV/arcmin2 at 1 keV.
(90% confidence level) on one parameter.
The regions shown in Fig. 8.
Norm is given in units of photons/cm2/s/keV/arcmin2 at 1 keV.
Table 3:
Best fit parameters for the power-law plus equilibrium model using the MOS and pn data all at once.
The errors are in the range
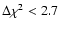 (90% confidence level) on one parameter.
The regions are shown in Fig. 8.
Norm is given in units of photons/cm2/s/keV/arcmin2 at 1 keV.
(90% confidence level) on one parameter.
The regions are shown in Fig. 8.
Norm is given in units of photons/cm2/s/keV/arcmin2 at 1 keV.
A two-component blackbody model allows us to represent the non-uniformity
of the surface temperature distribution of the neutron star.
The double blackbody is found to describe the data best (
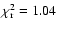 for 473 d.o.f.)
resulting in temperatures of
kT1 = 0.57+0.07-0.05 keV and
kT2 = 0.32+0.02-0.03 keV with
for 473 d.o.f.)
resulting in temperatures of
kT1 = 0.57+0.07-0.05 keV and
kT2 = 0.32+0.02-0.03 keV with
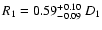 km and
km and
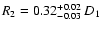 km for the radii of the emitting areas.
It suggests that the first thermal component is emitted from a small
fraction of the neutron star surface since the expected radius of a neutron star is
km for the radii of the emitting areas.
It suggests that the first thermal component is emitted from a small
fraction of the neutron star surface since the expected radius of a neutron star is 
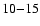 km.
The second thermal component emission can be due to the heating of polar
caps by relativistic particles which are accelerated in the magnetosphere or
to anisotropic heat conductivity in the neutron star crust (e.g. Becker & Aschenbach 2002).
The fit yields a column density
km.
The second thermal component emission can be due to the heating of polar
caps by relativistic particles which are accelerated in the magnetosphere or
to anisotropic heat conductivity in the neutron star crust (e.g. Becker & Aschenbach 2002).
The fit yields a column density
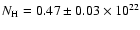 cm-2
that is compatible with the values found in the central part of the remnant.
cm-2
that is compatible with the values found in the central part of the remnant.
These results are globally compatible with those of Lazendic et al. (2003).
4 Discussion
4.1 On the nature of the central source
To say whether the neutron star is associated with SNR RX J1713.7-3946 or not,
we must compare the results of our spectral analysis with the values found for
other types of compact objects found in other SNRs.
On the other hand, the absorbing column value derived from the best-fit model must be consistent
with the absorbing column density found for the diffuse emission of the remnant in the central region.
The spectral properties (cf. Table 6)
of the central point source 1WGA J1713.4-3949 are
very similar to those of the Compact Central Objects (CCOs) in "Vela Junior'' (SNR G266.1-1.2 or
RX J0852-4622),
in Cas A and in Puppis A (Becker & Aschenbach 2002; Pavlov et al. 2002; Pavlov et al. 2004)![[*]](/icons/foot_motif.gif) .
.
In addition, the absorbing column
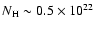 cm-2of the diffuse emission around central source 1WGA J1713.4-3949
(top panel of Fig. 4 and Table 7)
is consistent with the
cm-2of the diffuse emission around central source 1WGA J1713.4-3949
(top panel of Fig. 4 and Table 7)
is consistent with the
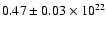 cm-2 found for the two-component blackbody model
(Table 6).
Note that this is also true considering the bremsstrahlung model
which leads to a still acceptable
cm-2 found for the two-component blackbody model
(Table 6).
Note that this is also true considering the bremsstrahlung model
which leads to a still acceptable
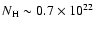 cm-2 (Table 5)
but is weakened adopting the blackbody+power-law model
which yields a too high (almost a factor 2) column density
cm-2 (Table 5)
but is weakened adopting the blackbody+power-law model
which yields a too high (almost a factor 2) column density
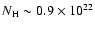 cm-2 (Table 6).
cm-2 (Table 6).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1154_fig18.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg136.gif) |
Figure 9:
For each of the 8 regions considered (see Fig. 8),
changes of the parameters (
 , ,
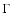 )
with the addition of a thermal component.
The star correspond to the power-law model (cf. Table 2).
The black triangle correspond to the power-law plus thermal equilibrium model
(cf.
Table 3).
The error bars are given at a )
with the addition of a thermal component.
The star correspond to the power-law model (cf. Table 2).
The black triangle correspond to the power-law plus thermal equilibrium model
(cf.
Table 3).
The error bars are given at a 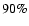 confidence level.
confidence level. |
| Open with DEXTER |
Table 4:
Values of postshock electronic number density for a few regions (see Fig. 8) using
Eq. (1) with
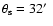 .
D1 is the distance in units of 1 kpc.
The selected regions are those for which the
thermal emission is detected for temperatures of
.
D1 is the distance in units of 1 kpc.
The selected regions are those for which the
thermal emission is detected for temperatures of  0.5-0.6 keV.
0.5-0.6 keV.
Thus, it is highly probable that the point source 1WGA J1713.4-3949
is the compact relic of the supernova progenitor
ranking RX J1713.7-3946 in the category of type II supernovae with strong particle acceleration.
4.2 Interaction with clouds and distance estimate
The mapping of the CO emission at
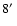 resolution
shown in SL99 has revealed the presence of three dense and massive clouds
probably belonging to the same molecular complex of a Galactic arm at 6 kpc.
An enhanced intensity ratio of the two lowest rotational transition of the
CO molecule was found in one of these clouds located north
of RX J1713.7-3946 suggesting that the SNR shock front is hitting this cloud.
Based on this interaction, it was concluded that the remnant
should be at a distance of 6 kpc.
resolution
shown in SL99 has revealed the presence of three dense and massive clouds
probably belonging to the same molecular complex of a Galactic arm at 6 kpc.
An enhanced intensity ratio of the two lowest rotational transition of the
CO molecule was found in one of these clouds located north
of RX J1713.7-3946 suggesting that the SNR shock front is hitting this cloud.
Based on this interaction, it was concluded that the remnant
should be at a distance of 6 kpc.
On the other hand, XMM-Newton has revealed a positive correlation between the absorbing column
density and the synchrotron X-ray brightness (see Fig. 6),
which strongly suggests that the brightest regions of the SNR interact with part of the
line-of-sight absorbing material (cf. Sect. 3.2).
In particular, this is the case of the bright southwestern region which exhibits the
strongest absorption in the line-of-sight.
At 6 kpc, however, the three dense and massive CO clouds are observed in the
north of the remnant; none is observed in the SW (SL99) where the highest absorption
and a clear interaction are found with XMM-Newton.
Independent information on the absorption in the line-of-sight of SNR RX J1713.7-3946
can be obtained from a map of integrated optical star light.
The optical star light is sensitive to the whole line-of-sight,
but it should reflect column density variations.
Figure 11 shows the red DSS optical image.
The absorption morphology in the optical is quite different from
the 6 kpc CO emission morphology presented in SL99 but similar to the X-ray absorption map.
The optical brightness appears to be high in the X-ray faint CE and
seems particularly weak in the X-ray bright SW region.
If we extract the optical brightness and
 for
each pixel of the mapping grid (Sect. 2.3.4),
we obtain a one dimensioned plot of these two quantities.
Figure 12 shows the very good inverse correlation obtained between our inferred column density
and the optical brightness towards RX J1713.7-3946.
This is consistent with the low and high absorptions found
in the
for
each pixel of the mapping grid (Sect. 2.3.4),
we obtain a one dimensioned plot of these two quantities.
Figure 12 shows the very good inverse correlation obtained between our inferred column density
and the optical brightness towards RX J1713.7-3946.
This is consistent with the low and high absorptions found
in the
 map
in the CE and SW, respectively (Fig. 4, left panel).
This last result provides additional support for
the reliability of the
map
in the CE and SW, respectively (Fig. 4, left panel).
This last result provides additional support for
the reliability of the
 distribution derived from the X-ray measurements.
distribution derived from the X-ray measurements.
The disagreement between the absorption morphology towards RX J1713.7-3946
and the molecular gas distribution at 6 kpc has an immediate consequence either
for the distance of the SNR or for the nature of the material interacting with the SNR.
If RX J1713.7-3946 is really located at 6 kpc, this implies that the remnant interacts with
an interstellar component of a different nature than molecular gas, such as HI gas for instance.
In the other alternative, if RX J1713.7-3946 is really impacting molecular clouds,
this implies that RX J1713.7-3946 is situated at a distance less or larger than 6 kpc.
Because there is no evidence that the absorption toward the SNR is strongest in the north,
contrary to what is observed in the CO map integrated up to 6 kpc (Bronfman et al. 1989, SL99),
it indicates that the remnant must be located at a distance less than 6 kpc.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{1154_fig19.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg139.gif) |
Figure 10:
EPIC spectra of the central source 1WGA J1713.4-3949 of the SNR RX J1713.7-3946 (MOS1 in black, MOS2 in red and pn in green).
Best-fit obtained with a double blackbody model. |
| Open with DEXTER |
An indirect estimate of the density of the absorbing material located in the SW can be obtained
from the local variations of column density in the interacting regions.
We assume that the angular size
 of the absorbing material is the same
along the line-of-sight and in projection on the sky.
If it is so, the density of the absorbing matter
of the absorbing material is the same
along the line-of-sight and in projection on the sky.
If it is so, the density of the absorbing matter
 is given by:
is given by:
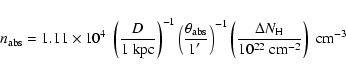 |
(2) |
where D is the SNR distance and
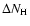 is
the variation of the absorbing column density between two regions separated by an
angular size
is
the variation of the absorbing column density between two regions separated by an
angular size
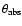 .
Typically in the SW (see left panel of Fig. 4),
.
Typically in the SW (see left panel of Fig. 4),
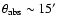 and
and
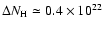 cm-2.
This gives
cm-2.
This gives
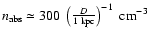 which corresponds to
which corresponds to
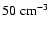 for a distance of the SNR of 6 kpc or
for a distance of the SNR of 6 kpc or
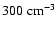 for 1 kpc,
a typical value for cold interstellar molecular clouds
(e.g. Tatematsu et al. 1990; Wilner et al. 1998).
for 1 kpc,
a typical value for cold interstellar molecular clouds
(e.g. Tatematsu et al. 1990; Wilner et al. 1998).
The pending question is then to determine the nature
and the distance of the matter interacting with RX J1713.7-3946.
Since the strongly absorbed regions are mainly found at the limit or around the SNR (particularly in the NW and SW)
and not inside, a possible scenario would be that the remnant
is within a wind-blown bubble created by the precursor star, and that the
SN shock is encountering the wall of such a bubble, as previously
suggested (SL99, Ellison et al. 2001).
However, the optical image shows that the thickness of
the regions of lowest optical brightness found at the edges of the remnant (Fig. 11)
is much higher than that expected from
a stellar wind shell. Then, the most plausible picture is
that of preexisting interstellar clouds, possibly pushed by the progenitor stellar wind, being struck by
the SNR shock front. This can be tested by CO and HI observations.
Table 5:
Best fit parameters for different one component spectral models for 1WGA J1713.4-3949 using the MOS and pn data all at once.
The errors are in the range
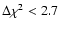 (90% confidence level) on one parameter. D1 is the distance in units of 1 kpc.
(90% confidence level) on one parameter. D1 is the distance in units of 1 kpc.
Table 6:
Best fit parameters for different two components spectral models for 1WGA J1713.4-3949 using the MOS and pn data all at once.
The errors are in the range
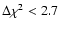 (90% confidence level) on one parameter. D1 is the distance in units of 1 kpc.
(90% confidence level) on one parameter. D1 is the distance in units of 1 kpc.
We have reanalyzed the behaviour of the absorbing material across the SNR
RX J1713.7-3946 based on data from the CfA CO survey (Dame et al. 2001)
and from the IAR High Sensitivity HI survey (Arnal et al. 2000). The
angular resolution of the CO J:1-0 data is 8
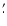 8, the grid
sampling of 7
8, the grid
sampling of 7
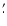 5 and the velocity resolution of 1.3 km s-1(note that although Dame et al.'s 2001 new
survey improves the sampling interval to half a beamwidth, the region
containing the SNR RX J1713.7-3946 in the fourth Galactic quadrant is
still based on the coarser sampling as published by Bronfman et al.
1989). For the HI data the angular resolution and the sampling are 30
5 and the velocity resolution of 1.3 km s-1(note that although Dame et al.'s 2001 new
survey improves the sampling interval to half a beamwidth, the region
containing the SNR RX J1713.7-3946 in the fourth Galactic quadrant is
still based on the coarser sampling as published by Bronfman et al.
1989). For the HI data the angular resolution and the sampling are 30
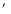 and the velocity resolution is 1.03 km s-1.
and the velocity resolution is 1.03 km s-1.
Figure 13 (top panel) displays the cumulative absorbing column density
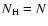 (HI)
(HI)
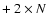 (H2) as a
function of the Local Standard of Rest (LSR) radial velocity, towards the NW (continuous
line), the SW (dotted line) and the center (dashed line).
The plotted curves to the NW and SW were obtained
from the average over
(H2) as a
function of the Local Standard of Rest (LSR) radial velocity, towards the NW (continuous
line), the SW (dotted line) and the center (dashed line).
The plotted curves to the NW and SW were obtained
from the average over 
 areas centered near
areas centered near
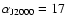 h11m45s,
h11m45s,
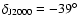 32
32
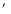 45
45
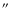 and
near
and
near
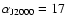 h11m50s,
h11m50s,
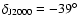 57
57
 00
00
 ,
respectively.
The third
,
respectively.
The third
 curve was calculated for a line-of-sight directed to
the bright central X-ray point-like source 1WGA J1713.4-3949. The
H2 column density was calculated from the carbon monoxide
distribution by adopting the molecular mass calibration ratio
curve was calculated for a line-of-sight directed to
the bright central X-ray point-like source 1WGA J1713.4-3949. The
H2 column density was calculated from the carbon monoxide
distribution by adopting the molecular mass calibration ratio
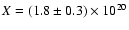 cm-2 (Dame et al. 2001).
The behaviour of Fig. 13 (top panel) is mainly
defined by the CO profile
because of the better angular resolution of these data as
compared with the HI survey used and its dominant contribution.
The galactic rotation curve for
cm-2 (Dame et al. 2001).
The behaviour of Fig. 13 (top panel) is mainly
defined by the CO profile
because of the better angular resolution of these data as
compared with the HI survey used and its dominant contribution.
The galactic rotation curve for
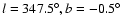 (from Fich
et al.'s 1989 circular galactic rotation model) is plotted in
Figure 13 (bottom panel) for comparison.
Table 7 gives the value of the cumulative absorbing column density
towards the NW, SW and center for several LSR radial velocities or
equivalently for several distances (only the closer distance is provided).
(from Fich
et al.'s 1989 circular galactic rotation model) is plotted in
Figure 13 (bottom panel) for comparison.
Table 7 gives the value of the cumulative absorbing column density
towards the NW, SW and center for several LSR radial velocities or
equivalently for several distances (only the closer distance is provided).
The line-of-sight towards
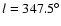 basically crosses three
galactic arms: Sagittarius, at an approximate distance of 1.4 kpc
(
basically crosses three
galactic arms: Sagittarius, at an approximate distance of 1.4 kpc
(
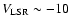 km s-1), Scutum-Crux at about 3.7 kpc
(
km s-1), Scutum-Crux at about 3.7 kpc
(
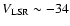 km s-1), and Norma at about 5.3 kpc
(
km s-1), and Norma at about 5.3 kpc
(
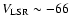 km s-1) (Georgelin & Georgelin 1976).
Figure 14 displays two average spectra obtained towards the NW (continuous line)
and towards the SW (dotted line), where, in addition to the local gas,
the three important galactic components are evident.
km s-1) (Georgelin & Georgelin 1976).
Figure 14 displays two average spectra obtained towards the NW (continuous line)
and towards the SW (dotted line), where, in addition to the local gas,
the three important galactic components are evident.
Table 7:
Values of the accumulative absorbing column density
towards the NW, SW and CE as obtained from CO and HI observations
for several LSR radial velocities or equivalently for several distances.
The values of
 which are in bold font are those compatible with the X-rays.
which are in bold font are those compatible with the X-rays.
From the X-ray absorption map (see Fig. 4, left panel), the
absorbing column density was found to be higher in the SW
(
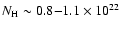 cm-2) than in the NW
(
cm-2) than in the NW
(
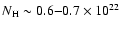 cm-2).
The
cm-2).
The
 curve obtained to the
SW from CO and HI observations, lies above the curve
obtained for the NW region only for velocities below
curve obtained to the
SW from CO and HI observations, lies above the curve
obtained for the NW region only for velocities below
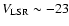 km s-1 as shown in Fig. 13 (top panel).
Although the limited angular
resolution of the available HI data "dilutes''
small spatial variations
and reduces the
km s-1 as shown in Fig. 13 (top panel).
Although the limited angular
resolution of the available HI data "dilutes''
small spatial variations
and reduces the
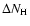 between the two regions,
this sets an upper limit on the SNR distance at
between the two regions,
this sets an upper limit on the SNR distance at  2.9 kpc using
the galactic rotation curve (Fig. 13, bottom panel).
2.9 kpc using
the galactic rotation curve (Fig. 13, bottom panel).
The absorbing column densities derived from the XMM-Newton data
are found to be
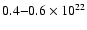 cm-2 towards
1WGA J1713.4-3949,
cm-2 towards
1WGA J1713.4-3949,
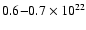 cm-2 towards the NW,
and
cm-2 towards the NW,
and
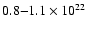 cm-2 towards the SW (Sect. 3.2).
These values match very well those found from the CO and HI observations
if the LSR radial velocity range is between
cm-2 towards the SW (Sect. 3.2).
These values match very well those found from the CO and HI observations
if the LSR radial velocity range is between  -6 and
-6 and  -11 km s-1 as
indicated on Table 7.
Then, it reduces the SNR distance range to
-11 km s-1 as
indicated on Table 7.
Then, it reduces the SNR distance range to  0.9-1.7 kpc.
0.9-1.7 kpc.
The only negative LSR velocities for which the CO emission
is clearly higher in the SW than in NW are found between 0 and -10 km s-1as revealed by the spectra displayed in Fig. 14.
Indeed,
the presence of a "shoulder'' of higher emission obtained to the SW (dotted line) can be noticed,
as compared to the NW spectra (solid line).
This constitutes an evidence for the presence of
molecular gas in the SW direction.
This feature is consistent with the
molecular cloud recently detected by Fukui et al. (2003) in the SW
(between -3 and -11 km s-1) on the basis of 2.6 mm
CO J:1-0 observations carried out with the NANTEN telescope.
The range of LSR velocities corresponding to the upper limit distance of 1.6 kpc,
using the circular galactic rotation model (Fich et al. 1989),
is compatible with the allowed distance range of  0.9-1.7 kpc.
0.9-1.7 kpc.
A search for the ground-state satellite line of the hydroxyl molecule at
1720.53 MHz was carried out towards two spots in G347.3-0.5 where
both X-rays and CO observations suggested strong shock/molecular cloud
interaction. The positive detection of OH (1720 MHz)
masers permits us to confirm the existence of such
interaction and to constrain the physical parameters of the
shock-excited gas on the basis of the very specific conditions required
to excite the 1720 MHz OH masers.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1154_fig20.eps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg170.gif) |
Figure 11:
Optical image between 2300 and 3000 Å (Second Generation Digitized Sky Survey in red color
at 450-600 THz)
overlaid with the contour of the 2-10 keV X-ray image of SNR RX J1713.7-3946.
The scaling is linear with the higher cut fixed at 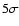 of the mean optical brightness value.
of the mean optical brightness value. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1154_fig21.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg171.gif) |
Figure 12:
Correlation plot between the absorbing column
 (in units of 1022 cm-2) and the normalized
optical brightness.
To obtain this plot, the optical image shown in Fig. 11
has been cut following the absorbing column map grid.
Each point corresponds to the value found for a particular pixel of the mapping grid
(Sect. 2.3.4) and
the error bars are given at a
(in units of 1022 cm-2) and the normalized
optical brightness.
To obtain this plot, the optical image shown in Fig. 11
has been cut following the absorbing column map grid.
Each point corresponds to the value found for a particular pixel of the mapping grid
(Sect. 2.3.4) and
the error bars are given at a 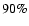 confidence level.
The symbols are defined as in Table 1.
confidence level.
The symbols are defined as in Table 1. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{1154_fig22.ps}\psfrag{NH}{$N_{{\rm H}}$ }\end{figure}](/articles/aa/full/2004/43/aa1154/Timg172.gif) |
Figure 13:
Top panel: the cumulative absorbing column density as
obtained from the atomic and molecular hydrogen, as a function of radial
velocity. The continuous line corresponds to the average NH estimated
towards the NW region, the dotted line corresponds to the SW region and
the dashed line to a line-of-sight directed to 1WGA J1713.4-3949.
Bottom panel: the rotation curve towards l=347.5, b=-0.5 as obtained from
Fich et al.'s (1989) circular galactic rotation model. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1154_fig23.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg173.gif) |
Figure 14:
Average CO spectra obtained towards the NW (continuous line)
and towards the SW (dotted line) from the CfA CO survey (Dame et al. 2001).
The SW emission is higher than the NW emission for LSR velocities between 0 and
-10 km s-1. |
| Open with DEXTER |
The observations were carried out with the Very Large Array
of NRAO![[*]](/icons/foot_motif.gif) in the
C-configuration for 2 h on March 11, 2004. Two 22
in the
C-configuration for 2 h on March 11, 2004. Two 22 fields
centered at (17h11m45s,
fields
centered at (17h11m45s,
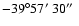 )
and
(17h11m45s,
)
and
(17h11m45s,
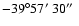 )
were observed.
A 256-channel spectrometer centered around -30 km s-1, with a channel
width of 3.05 kHz/channel (
)
were observed.
A 256-channel spectrometer centered around -30 km s-1, with a channel
width of 3.05 kHz/channel ( 0.5 km s-1 at 1720 MHz) and a
velocity range
0.5 km s-1 at 1720 MHz) and a
velocity range
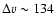 km s-1, was used. The data
were cleaned and calibrated using AIPS routine programs. The
synthesized beam was
km s-1, was used. The data
were cleaned and calibrated using AIPS routine programs. The
synthesized beam was
 and the noise level
of about 50
and the noise level
of about 50  Jy/beam per channel.
Jy/beam per channel.
The results of the search for OH (1720 MHz) masers were negative. This
fact is probably due either to the fact that the shocked molecular clouds
have a volume density smaller than that required to excite the masers, or
the shock front was not of a non-dissociative C-type (Wardle 1999).
The X-ray analysis of SNR RX J1713.7-3946 with XMM-Newton has revealed a strong absorption in the SW,
even stronger than in the NW.
The absorption derived from the optical star brightness is in agreement with the X-ray derived map.
This high absorption found in the SW was unexpected with regard to the morphology of the CO distribution at 6 kpc.
Moreover, the positive correlation between X-ray absorption and the X-ray brightness indicates that
the shock front of RX J1713.7-3946 is impacting the molecular clouds responsible for the absorption.
The CO and HI observations show that the inferred cumulative absorbing column densities
are in excellent agreement with the X-ray findings in different places of the remnant
provided that the SNR lies at a distance of
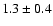 kpc, probably in the Sagittarius galactic arm.
Other indications of an interaction between the SNR blast-wave and molecular clouds
are provided by the existence of an excess of fast-moving HI gas (Koo et al. 2004)
and possibly, the existence of a broad CO profile in LSR velocity found in a
coincident bright X-ray feature in the SW at 1 kpc (Fukui et al. 2003).
Based on the absorption morphology and the probable association between the SNR and the molecular clouds,
the distance of SNR RX J1713.7-3946 is revised to
kpc, probably in the Sagittarius galactic arm.
Other indications of an interaction between the SNR blast-wave and molecular clouds
are provided by the existence of an excess of fast-moving HI gas (Koo et al. 2004)
and possibly, the existence of a broad CO profile in LSR velocity found in a
coincident bright X-ray feature in the SW at 1 kpc (Fukui et al. 2003).
Based on the absorption morphology and the probable association between the SNR and the molecular clouds,
the distance of SNR RX J1713.7-3946 is revised to
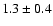 kpc instead of
the commonly accepted value of 6 kpc.
kpc instead of
the commonly accepted value of 6 kpc.
4.3 Particle acceleration
The asymmetry in the synchrotron X-ray emission morphology
is the result of the asymmetry in the ambient density around the remnant.
In the strongly absorbed bright SW rim, we have established that
the shock front of RX J1713.7-3946 is interacting with molecular clouds
as suggested by the positive correlation between X-ray absorption and X-ray brightness.
In the weakly absorbed faint SE region, the same correlation suggests that
the shock front of RX J1713.7-3946 is propagating into a tenuous ambient medium
which is consistent with the larger extent of the SNR there than in the SW.
In Sect. 3.2, we looked at the spatial modifications (in the SW and SE)
of particle acceleration at the shock in RX J1713.7-3946 through the photon spectral index changes.
The regions where the shock impacts the molecular clouds have a steeper spectrum
(
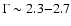 )
than those where the shock propagates
into a low density medium (
)
than those where the shock propagates
into a low density medium (
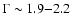 ).
).
Qualitatively, we can interpret such modifications in the synchrotron spectrum
by considering a modification of the acceleration in the interaction region with dense molecular clouds.
To investigate this, we used a simple model of nonlinear diffusive shock
acceleration (Berezhko & Ellison 1999; Ellison et al. 2000)
varying the upstream density n0, the shock speed
 and the magnetic field B0 for an injection (i.e.
fraction of gas particles which are accelerated) set to 10-3.
As the SNR blast-wave runs into a high density medium such as molecular clouds,
its velocity is expected to diminish according to the ram pressure conservation (
and the magnetic field B0 for an injection (i.e.
fraction of gas particles which are accelerated) set to 10-3.
As the SNR blast-wave runs into a high density medium such as molecular clouds,
its velocity is expected to diminish according to the ram pressure conservation (
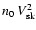 constant)
and the upstream magnetic field is expected to increase following the square root of the density (
constant)
and the upstream magnetic field is expected to increase following the square root of the density (
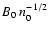 constant).
The result of the density increase is to lead to a steepening of the
synchrotron spectrum but no increase in brightness. Therefore, this cannot explain
the observed difference in X-ray brightness between the SE and the SW (for the same magnetic field orientation).
However, if the shock is preferentially tangential in the region of high density but normal in the region of lower density,
the X-ray brightness can be strongly enhanced due to the compression of the downstream magnetic field on condition that
the density contrast between the two regions is weak (not more than a factor 4).
Then, it is possible to explain stronger X-ray brightness and a steeper synchrotron spectrum in
the SW than in the SE
if the magnetic field is tangential in the SW but normal in the SE and if the acceleration process
occured before the shock entered the dense molecular clouds.
constant).
The result of the density increase is to lead to a steepening of the
synchrotron spectrum but no increase in brightness. Therefore, this cannot explain
the observed difference in X-ray brightness between the SE and the SW (for the same magnetic field orientation).
However, if the shock is preferentially tangential in the region of high density but normal in the region of lower density,
the X-ray brightness can be strongly enhanced due to the compression of the downstream magnetic field on condition that
the density contrast between the two regions is weak (not more than a factor 4).
Then, it is possible to explain stronger X-ray brightness and a steeper synchrotron spectrum in
the SW than in the SE
if the magnetic field is tangential in the SW but normal in the SE and if the acceleration process
occured before the shock entered the dense molecular clouds.
A modeling of these effects is beyond the scope of this paper.
Further smaller scale spectral studies with the Chandra satellite would help to
investigate the origin of the steepening of the spectrum in the SW.
4.4 SNR age and energetics
The study of the thermal emission with XMM-Newton has lead to an upper limit on the density
in the ambient medium of
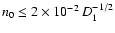 cm-3
where D1 is the distance in units of 1 kpc (cf. Sect. 3.3).
If the density derived from the emission measure is indeed representative of the
density in the ambient medium (which is not the case in the radiative phase),
an estimate of the swept-up mass is given by:
cm-3
where D1 is the distance in units of 1 kpc (cf. Sect. 3.3).
If the density derived from the emission measure is indeed representative of the
density in the ambient medium (which is not the case in the radiative phase),
an estimate of the swept-up mass is given by:
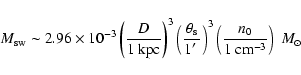 |
(3) |
where
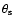 is the angular size of the blast-wave radius.
This leads to an upper limit on the swept-up mass of
is the angular size of the blast-wave radius.
This leads to an upper limit on the swept-up mass of
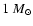 for a distance of 1 kpc and
for a distance of 1 kpc and
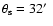 .
If RX J1713.7-3946 is the remnant of a type II explosion,
the initial mass of the progenitor is expected to be above
.
If RX J1713.7-3946 is the remnant of a type II explosion,
the initial mass of the progenitor is expected to be above
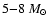 (Kennicutt 1984)
and then the mass of the ejected matter of a few solar masses.
This is well above the derived swept-up mass leading to the conclusion that
RX J1713.7-3946 must be in the free expansion phase.
(Kennicutt 1984)
and then the mass of the ejected matter of a few solar masses.
This is well above the derived swept-up mass leading to the conclusion that
RX J1713.7-3946 must be in the free expansion phase.
The hypothesis proposed by Wang et al. (1997),
based on historical records, that RX J1713.7-3946 is the
remnant of the supernova that exploded in AD 393 would imply an age of
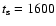 years.
Assuming self-similar solutions (Chevalier 1982), we can estimate the shock velocity
given by
years.
Assuming self-similar solutions (Chevalier 1982), we can estimate the shock velocity
given by
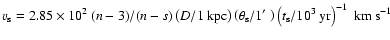 where n and s are the power-law indexes of the initial outer density profile in the ejecta and
of the initial ambient medium density profile, respectively.
where n and s are the power-law indexes of the initial outer density profile in the ejecta and
of the initial ambient medium density profile, respectively.
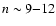 is typical of SN II,
s=0 corresponds to an homogeneous ambient medium, s=2 to an ambient medium modified by the progenitor wind.
For n=9,
is typical of SN II,
s=0 corresponds to an homogeneous ambient medium, s=2 to an ambient medium modified by the progenitor wind.
For n=9,
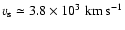 if s=0and
if s=0and
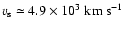 if s=2.
if s=2.
The determination of the kinetic energy of the explosion provides a strong argument for or against
the hypothesis that RX J1713.7-3946 is the remnant of the AD 393 stellar explosion.
In the framework of a spherical self-similar model (Chevalier 1982),
we can estimate the kinetic energy of the explosion as a function of the SNR age
for different progenitor masses and ambient medium densities.
The energy curves depend on three parameters among which n and s for a given progenitor mass (Decourchelle & Ballet 1994).
The power-law index n of the ejecta density profile was fixed to 9.
The power-law index s of the ambient density profile was fixed to 0 to simulate a flat ambient medium which seems
to be the situation in the SE.
The kinetic energy of the explosion is then determined by the relation:
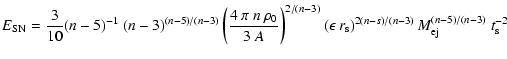 |
|
|
(4) |
where 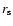 is the shock radius set to 10 pc,
is the shock radius set to 10 pc,
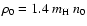 and
and 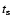 the SNR age.
The parameters A and
the SNR age.
The parameters A and 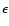 are determined by solving the self-similar hydrodynamical equations (Chevalier 1982).
are determined by solving the self-similar hydrodynamical equations (Chevalier 1982).
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1154_fig24.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg194.gif) |
Figure 15:
Kinetic energy of the explosion as a function of the SNR age for several solar masses of
the supernova ejecta (
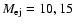 and
and
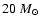 )
and different ambient medium densities
( )
and different ambient medium densities
(
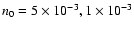 and
and
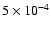 cm-3).
cm-3). |
| Open with DEXTER |
Energy curves are illustrated in Fig. 15
for supernova ejecta masses of
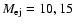 and
and
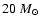 representative of type II supernova
and for different ambient medium densities between
representative of type II supernova
and for different ambient medium densities between
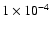 and
and
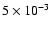 cm-3.
If we adopt the standard 1051 erg as the energy of the explosion,
it shows that an ambient medium density of 10-3 cm-3 is appropriate
for ejecta masses between
cm-3.
If we adopt the standard 1051 erg as the energy of the explosion,
it shows that an ambient medium density of 10-3 cm-3 is appropriate
for ejecta masses between
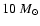 and
and
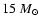 if we consider a remnant that is 1600 years old.
At this age, the higher density of the ambient medium (
if we consider a remnant that is 1600 years old.
At this age, the higher density of the ambient medium (
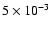 cm-3)
leads to a higher kinetic energy of the explosion, which is still possible, whereas
below 10-4 cm-3, the kinetic explosion energy begins to be too weak
cm-3)
leads to a higher kinetic energy of the explosion, which is still possible, whereas
below 10-4 cm-3, the kinetic explosion energy begins to be too weak
If we consider the effect of efficient cosmic-ray acceleration on the structure of the blast-wave
as described in Chevalier (1983), energy curves move slightly higher and
would only very slightly widen the range of allowed ambient medium densities.
Hence, these results based on an energy argumentation are consistent with the
picture of a young SNR expanding in a low density medium.
4.5 Evolutionary stage
Although the star formation process is complex, there is observational
evidence that massive stars are born in the densest parts of molecular clouds.
The presence of molecular clouds around the northern and southwestern parts of
RX J1713.7-3946 strongly suggests that its progenitor star is indeed born in such conditions.
Evolved SNRs interacting with molecular clouds are expected to be efficient electron accelerators
(Bykov et al. 1999) as observed in RX J1713.7-3946.
Nevertheless, these molecular clouds appear to be located at the periphery of the SNR at
 7 pc away from the center, assuming a distance of 1 kpc.
Massive stars are known to initiate and maintain powerful
stellar winds during their lives so that they can move the molecular clouds
from the vicinity of the progenitor star.
These winds may have homogeneized the immediate environment of the progenitor star,
explaining the extremely low mean density inside the SNR (McKee et al. 1984; Chevalier 1999).
7 pc away from the center, assuming a distance of 1 kpc.
Massive stars are known to initiate and maintain powerful
stellar winds during their lives so that they can move the molecular clouds
from the vicinity of the progenitor star.
These winds may have homogeneized the immediate environment of the progenitor star,
explaining the extremely low mean density inside the SNR (McKee et al. 1984; Chevalier 1999).
In the standard picture of a stellar wind interacting with the interstellar medium,
a four-zone structure (Castor et al. 1975; Weaver et al. 1977) settles very rapidly, consisting of
the innermost hypersonic stellar wind characterized by a density profile
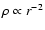 ,
a hot shocked stellar wind region,
a shell of shocked interstellar medium
and the ambient interstellar gas.
After a few thousand years,
the swept-up shocked interstellar gas collapses into a thin cold (
,
a hot shocked stellar wind region,
a shell of shocked interstellar medium
and the ambient interstellar gas.
After a few thousand years,
the swept-up shocked interstellar gas collapses into a thin cold (
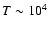 K)
shell strongly affected by radiative losses while
the low-density (<1 cm-3) shocked stellar wind region occupying most of the bubble volume
remains very hot (T > 106 K).
K)
shell strongly affected by radiative losses while
the low-density (<1 cm-3) shocked stellar wind region occupying most of the bubble volume
remains very hot (T > 106 K).
A possible interpretation of our observation of RX J1713.7-3946 is that the SN event occured in a wind-blown bubble.
In the SE, the shock front of the remnant is still propagating into the
low-density hot shocked wind (
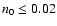 cm-3).
In the SW, the blast-wave of RX J1713.7-3946
has already progagated into the shocked stellar wind and is impacting the cold and dense
(
cm-3).
In the SW, the blast-wave of RX J1713.7-3946
has already progagated into the shocked stellar wind and is impacting the cold and dense
( 300 cm-3, see Eq. (2)) shell of shocked ambient material.
The remnant could be in the free expansion phase in the SE whereas in the radiative phase in the SW.
300 cm-3, see Eq. (2)) shell of shocked ambient material.
The remnant could be in the free expansion phase in the SE whereas in the radiative phase in the SW.
In this scenario, the size of the bubble provides an estimate of the strength of the wind and hence
of the progenitor mass.
From Fig. 2, the position of the bright X-ray rims in the NW and SW
(
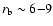 pc, taking into account the projection effects)
provides an estimate of the radius of the bubble
pc, taking into account the projection effects)
provides an estimate of the radius of the bubble
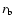 ,
assuming that the molecular clouds have been
removed from the vicinity of the star by the progenitor stellar wind.
,
assuming that the molecular clouds have been
removed from the vicinity of the star by the progenitor stellar wind.
Table 8:
Parameters for main sequence evolution for different progenitor masses 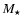 (from Chevalier 1999 and references therein).
(from Chevalier 1999 and references therein).
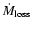 is the mass loss rate,
is the mass loss rate,
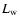 is the mechanical wind luminosity,
is the mechanical wind luminosity,
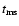 is the main-sequence age and
is the main-sequence age and
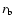 is the
maximum size of the wind bubble.
is the
maximum size of the wind bubble.
Then, an estimate of the mass of RX J1713.7-3946's progenitor star can be obtained by
directly comparing its wind-bubble size where the molecular clouds are located
with those estimated from observations of stars of different masses.
Table 8 shows two cases for which the bubble radii (5.3 and 10.0 pc)
are close to the 6-9 pc values estimated in the NW and SW for RX J1713.7-3946.
This implies that the mass of RX J1713.7-3946's progenitor must be between 12 and
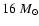 in the main sequence evolution phase, which corresponds to a B-star whose lifetime on the main sequence is about 107 years.
In Table 8, the mechanical wind luminosity
in the main sequence evolution phase, which corresponds to a B-star whose lifetime on the main sequence is about 107 years.
In Table 8, the mechanical wind luminosity
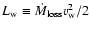 is computed assuming an appropriate wind velocity
is computed assuming an appropriate wind velocity
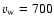 km s-1 as chosen in Chevalier (1999).
The maximum size of the wind bubble is given by (in pc):
km s-1 as chosen in Chevalier (1999).
The maximum size of the wind bubble is given by (in pc):
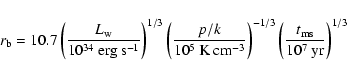 |
(5) |
assuming that the
surrounding interclump medium exerts a pressure
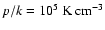 ,
typical of cloud (Chevalier 1999).
,
typical of cloud (Chevalier 1999).
From the characteristics of B-stars, we can estimate the mean density in the wind
before the supernova event
and compare it to the density derived from the thermal X-rays (see Sect. 3.3).
The mass lost during the lifetime of the progenitor diluted in the volume of the bubble gives
an estimate of the mean number density
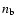 of the wind-bubble (in cm-3):
of the wind-bubble (in cm-3):
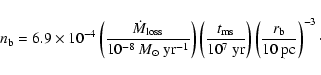 |
(6) |
For
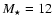 and
and
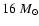 (cf. Table 8), we obtain a mean density of
(cf. Table 8), we obtain a mean density of
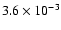 and
and
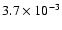 cm-3, respectively.
This is consistent with the
cm-3, respectively.
This is consistent with the 
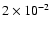 cm-3 upper limit found for the thermal emission in the X-rays.
Note that the mass lost in the red giant phase was not taken into account because
it produces a local excess in density only in the vicinity of the progenitor star.
cm-3 upper limit found for the thermal emission in the X-rays.
Note that the mass lost in the red giant phase was not taken into account because
it produces a local excess in density only in the vicinity of the progenitor star.
The proposed scenario in which the SNR blast wave expands into a low-density shocked wind medium
in the SE and strikes molecular clouds in the SW
appears to be a possible physical picture since
the density derived from the thermal X-ray emission measures can be found to be consistent
with the expected density in the pre-SN shocked stellar wind.
However, it is hard to understand why the shell of molecular clouds shocked by the SNR blast-wave
does not produce copious thermal X-ray emission since the X-ray brightness is proportional to the square of the density.
The regions of enhanced X-ray emission as observed in the SW are
those where there is a strong increase of the synchrotron X-ray emission
(correlated with an increased of absorbing column density),
but where there is no indication of any increase of the thermal X-ray emission.
However, if the SW rim of RX J1713.7-3946 is in the radiative phase, then we do not expect thermal X-ray
emission from the shocked interstellar clouds.
It would also explain why the thermal X-ray density does not follow the variations of the ambient density.
A high density of 300 cm-3 and a temperature of 105 K in the shocked interstellar clouds
yield a cooling time of  25 years.
25 years.
However, in SNRs where the shock is radiative, as observed in the Cygnus Loop,
bright optical filaments are generally observed (Levenson et al. 1996).
The optical emission is attributed to the cooling of the gas behind the shock front.
This cooling gas emits many optical lines including hydrogen Balmer lines with a temperature of  104 K.
If RX J1713.7-3946 is indeed in the radiative phase
where the blast wave has reached the cavity wall and is interacting with dense matter, such optical filaments
might be visible, although the absorption along the line-of-sight is much stronger in
RX J1713.7-3946 (
104 K.
If RX J1713.7-3946 is indeed in the radiative phase
where the blast wave has reached the cavity wall and is interacting with dense matter, such optical filaments
might be visible, although the absorption along the line-of-sight is much stronger in
RX J1713.7-3946 (
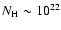 cm-2) than in
the Cygnus Loop SNR (
cm-2) than in
the Cygnus Loop SNR (
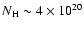 cm-2).
cm-2).
Finally, we could expect an enhancement of the thermal X-ray emission
in the shocked stellar wind just behind the shocked shell. Indeed,
a blast wave impacting on a dense cloud gives rise to both a reflected shock propagating back
and a transmitted shock propagating into the cloud (McKee & Cowie 1975).
The shocks that are reflected off molecular cloud surfaces
are expected to propagate back into the hot,
previously shocked gas, further heating and compressing it (e.g. Levenson et al. 1996).
Then, enhanced X-ray thermal emission is expected (Hester & Cox 1986).
However, the density in the shocked gas is still small so that its contribution might be negligeable.
5 Conclusion
XMM-Newton observations have yielded several new results on SNR RX J1713.7-3946.
The observation results and their astrophysical interpretation are summarized here:
- The X-ray bright central point source 1WGA J1713.4-3949 detected at the center of SNR RX J1713.7-3946
shows spectral properties very similar to those of the Compact Central Objects found in SNRs (e.g., Vela Junior) and which are
consistent with the absorbing column density of the central diffuse X-ray emission arising from the SNR.
It is highly probable that the point source 1WGA J1713.4-3949
is the compact relic of RX J1713.7-3946's supernova progenitor.
- The X-ray mapping of the absorbing column density has revealed strong variations
(
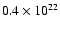 cm
cm
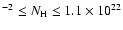 cm-2)
and, particularly, an unexpected strong absorption in the southwest.
The column density variations are well reflected by the extinction in the map of integrated optical star light.
The strong positive correlation between the X-ray absorption and the X-ray brightness along the western rims
suggests that the shock front of RX J1713.7-3946 is impacting molecular clouds there.
cm-2)
and, particularly, an unexpected strong absorption in the southwest.
The column density variations are well reflected by the extinction in the map of integrated optical star light.
The strong positive correlation between the X-ray absorption and the X-ray brightness along the western rims
suggests that the shock front of RX J1713.7-3946 is impacting molecular clouds there.
- CO and HI observations
show that the inferred cumulative absorbing column densities
are in excellent agreement with the X-ray measurements in different places of the remnant only
if the SNR is placed at a distance of
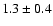 kpc, probably in the Sagittarius galactic arm,
and not at 6 kpc as previously claimed.
An excess in the CO emission found in the southwest at
kpc, probably in the Sagittarius galactic arm,
and not at 6 kpc as previously claimed.
An excess in the CO emission found in the southwest at  1 kpc strongly suggests
that molecular clouds produce the enhancement in absorption.
A search for OH masers in the southwestern region has been unsuccessful, possibly due to the low density of the clouds.
1 kpc strongly suggests
that molecular clouds produce the enhancement in absorption.
A search for OH masers in the southwestern region has been unsuccessful, possibly due to the low density of the clouds.
- The X-ray mapping of the photon index has revealed strong variations (
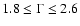 ).
The spectrum is steep in the faint central regions and flat at the
presumed shock locations, particularly in the southeast.
However, the regions where the shock strikes molecular clouds have a steeper spectrum
than those where the shock propagates into a low density medium.
).
The spectrum is steep in the faint central regions and flat at the
presumed shock locations, particularly in the southeast.
However, the regions where the shock strikes molecular clouds have a steeper spectrum
than those where the shock propagates into a low density medium.
- The search for thermal emission from RX J1713.7-3946 remains unsuccessful leading
to a number density upper limit of
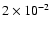 cm-3 in the ambient medium.
This low density in the ambient medium yields a reasonable kinetic energy of the
explosion provided that the remnant is less than a few thousand years old.
It can be reconciled with the high density in molecular clouds if the remnant is in the radiative phase
where the SNR shock encounters a dense ambient medium whereas it is in the free expansion phase elsewhere.
cm-3 in the ambient medium.
This low density in the ambient medium yields a reasonable kinetic energy of the
explosion provided that the remnant is less than a few thousand years old.
It can be reconciled with the high density in molecular clouds if the remnant is in the radiative phase
where the SNR shock encounters a dense ambient medium whereas it is in the free expansion phase elsewhere.
- RX J1713.7-3946's progenitor mass is estimated to lie between 12 and
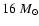 based on a scenario involving the effect of stellar wind of the progenitor star.
based on a scenario involving the effect of stellar wind of the progenitor star.
Acknowledgements
We acknowledge W. M. Goss for performing the OH VLA observations.
G.C.-C. is deeply indebted to Isabelle Grenier for many helpful discussions on HI and CO observations
and also on neutron stars.
The results presented here are based on observations obtained with XMM-Newton,
an ESA science mission with instruments and contributions
directly funded by ESA Member States and the USA (NASA).
Part of the project was supported by the CONICET (Argentina) - CNRS (France) cooperative
science program No. 10038.
- Arnal, E. M., Bajaja,
E., Larrarte, J. J., Morras, R., & Poppel, W. 2000, A&AS,
142, 35 [NASA ADS] (In the text)
- Arnaud, M.,
Neumann, D. M., Aghanim, N., et al. 2001, A&A, 365, L80 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Arnaud, M.,
Majerowicz, S., Lumb, D., et al. 2002, A&A, 390, 27 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Arnaud, K. A. 1996,
Astronomical Data Analysis Sofware and Systems V, ed. G. Jacoby,
& J. Barnes, ASP Conf. Ser., 101, 17
(In the text)
- Becker, W., &
Aschenbach, B. 2002, Proceedings of the 270, WE-Heraeus Seminar on
Neutrons Stars, Pulsars and Supernova Remnants
(In the text)
- Berezhko, E.
G., & Ellison, D. C. 1999, ApJ, 526, 385 [NASA ADS] [CrossRef] (In the text)
- Bronfman, L.,
Alvarez, H., Cohen, R. S., & Thaddeus, P. 1989, ApJS, 71,
481 [NASA ADS] [CrossRef] (In the text)
- Butt, Y. M., Torres, D.
F., Combi, J. A., Dame, T., & Romero, G. E. 2001, ApJ, 562,
L167 [NASA ADS] [CrossRef] (In the text)
- Butt, Y. M., Torres, D.
F., Romero, G. E., Dame, T. M., & Combi, J. A. 2002, Nature,
418, 499 [NASA ADS] (In the text)
- Bykov, A. M.,
Chevalier, R. A., Ellison, D. C., & Uvarov, Y. A. 2000, ApJ,
538, 203 [NASA ADS] [CrossRef]
-
Cassam-Chenaï, G., Decouchelle, A., Ballet, J., et al. 2004a,
A&A, 414, 545 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Cassam-Chenaï, G., Decouchelle, A., Ballet, J., & Dubner,
G. 2004b, Young Neutron Stars and Their Environments, IAU Symp.,
218, ed. F. Camilo, & B. M. Gaensler
- Castor, J., McCray,
R., & Weaver, R. 1975, ApJ, 200, L107 [NASA ADS] [CrossRef] (In the text)
- Chevalier, R.
A. 1982, ApJ, 258, 790 [NASA ADS] [CrossRef] (In the text)
- Chevalier, R.
A. 1983, ApJ, 272, 765 [NASA ADS] [CrossRef] (In the text)
- Chevalier, R.
A. 1999, ApJ, 511, 798 [NASA ADS] [CrossRef] (In the text)
- Crawford, F.,
Pivovaroff, M. J., Kaspi, V. M., & Manchester, R. N. 2002,
Neutrons Stars in Supernova Remnants, ASP Conf. Ser., 9999, ed. P.
O. Slane, & B. M. Gaensler
- Dame, T. M., Hatmann,
D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] (In the text)
-
Decourchelle, A., & Ballet, J. 1994, A&A, 287, 206 [NASA ADS] (In the text)
- Ellison, D. C.,
Berezhko, E. G., & Baring, M. G. 2000, ApJ, 540, 292 [NASA ADS] [CrossRef] (In the text)
- Ellison, D. C.,
Slane, P., & Gaensler, B. M. 2001, ApJ, 563, 191 [NASA ADS] [CrossRef] (In the text)
- Enomoto, R.,
Tanimori, T., Naito, T., et al. 2002, Nature, 416, 823 [NASA ADS] [CrossRef] (In the text)
- Fich, M., Blitz, L.,
& Stark, A. A. 1989, ApJ, 342, 272 [NASA ADS] [CrossRef] (In the text)
- Fukui, Y., Moriguchi,
Y., Tamura, K., et al. 2003, PASJ, 55, L61 [NASA ADS] (In the text)
- Georgelin, Y.
M., & Georgelin, Y. P. 1976, A&A, 49, 57 [NASA ADS] (In the text)
- Hartman, R. C.,
Bertsch, D. L., Bloom, S. D., et al. 1999, ApJS, 123, 79 [NASA ADS] [CrossRef] (In the text)
- Hester, J. J.,
& Cox, D. P. 1986, ApJ, 300, 675 [NASA ADS] [CrossRef] (In the text)
- Kargaltsev,
O., Pavlov, G. G., Sanwal, D., & Garmire, G. P. 2002, ApJ, 580,
1060 [NASA ADS] [CrossRef] (In the text)
- Koyama, K., Petre,
R., Gotthelf, E. V., et al. 1995, Nature, 378, 255 [NASA ADS] [CrossRef] (In the text)
- Koyama, K.,
Kinugasa, K., Matsuzaki, K., et al. 1997, PASJ, 49, L7 [NASA ADS] (In the text)
- Kennicutt, R.
C. 1984, ApJ, 277, 361 [NASA ADS] [CrossRef] (In the text)
- Koo, B.-C., Kang, J.,
& McClure-Griffiths, N. 2004, Young Neutron Stars and Their
Environments, IAU Symp., 218, ed. F. Camilo, & B. M.
Gaensler
(In the text)
- Lazendic, J.
S., Slane, P. O., Gaensler, B. M., et al. 2003, ApJ, 593, L27 [NASA ADS] [CrossRef] (In the text)
- Lazendic, J.
S., Slane, P. O., Gaensler, B. M., et al. 2004, ApJ, 602, 271 [NASA ADS] [CrossRef] (In the text)
- Levenson, N.
A., Graham, J. R., Hester, J. J., & Petre, R. 1996, ApJ, 468,
323 [NASA ADS] [CrossRef] (In the text)
- McKee, C. F., Van
Buren, D., & Lazareff, B. 1984, ApJ, 278, L115 [NASA ADS] [CrossRef]
- McKee, C. F., &
Cowie, L. L. 1975, ApJ, 195, 715 [NASA ADS] [CrossRef] (In the text)
- Muraishi, H.,
Tanimori, T., Yanagita, et al. 2000, A&A, 354, L57 [NASA ADS] (In the text)
- Pannuti, T. G.,
Allen, G. E., Houck, J. C., & Sturner, S. J. 2003, ApJ, 593,
377 [NASA ADS] [CrossRef] (In the text)
- Pavlov, G. G.,
Sanwal, D., Garmire, G. P., & Zavlin, V. E. 2002, Neutron Stars
in Supernova Remnants, ed. P. O. Slane, & B. M. Gaensler, ASP
Conf. Ser., 271, 247
(In the text)
- Pavlov, G. G.,
Sanwal, D., & Teter, M. A. 2004, Young Neutron Stars and Their
Environments, IAU Symp., 218, ed. F. Camilo, & B. M.
Gaensler
-
Pfeffermann, E., & Aschenbach, B. 1996, in Roentgenstrahlung
from the Universe, ed. H. H. Zimmermann, J. Trümper, & H.
Yorke (MPE Rep. 263; Garching: MPE), 267
(In the text)
- Read, A. M., &
Ponman, T. J. 2003, A&A, 409, 395 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Reimer, O., &
Pohl, M. 2002, A&A, 390, L43 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Reynolds, S. P.
1998, ApJ, 493, 375 [NASA ADS] [CrossRef] (In the text)
- Slane, P., Gaensler,
B. M., Dame, T. M., et al. 1999, ApJ, 525, 357 [NASA ADS] [CrossRef], SL99
(In the text)
- Slane, P., Hughes, J.
P., Edgar, R. J., et al. 2001, ApJ, 548, 814 [NASA ADS] [CrossRef] (In the text)
- Tatematsu,
K., Fukui, Y., Iwata, T., Seward, F. D., & Nakano, M. 1990,
ApJ, 351, 157 [NASA ADS] [CrossRef] (In the text)
- Tsurata, S. 1998,
Phys. Rep., 292, 1 [NASA ADS] [CrossRef] (In the text)
- Uchiyama, Y.,
Aharonian, F. A., & Takahashi, T. 2003, A&A, 400, 567 [EDP Sciences] [NASA ADS] [CrossRef] [MathSciNet] (In the text)
- Wang, Z.-R., Qu, Q.-Y.,
& Chen, Y. 1997, A&A, 318, L59 [NASA ADS] (In the text)
- Wardle, M. 1999,
ApJ, 525, L101 [NASA ADS] [CrossRef] (In the text)
- Weaver, R., McCray,
R., & Castor, J. 1977, ApJ, 218, 377 [NASA ADS] [CrossRef]
- Willingale,
R., Aschenbach, B., Griffits, R. G., et al. 2001, A&A, 365,
L212 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Wilner, D. J.,
Reynolds, S. P., & Moffett, D. A. 1998, AJ, 115, 247 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{1154_fig1.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg59.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1154_fig2.eps}\hspace*{3mm}
\includegraphics[width=7.8cm,clip]{1154_fig3.eps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg60.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{1154_fig4.eps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg64.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1154_fig5.eps}\hspace*{6mm...
...ps}\hspace*{6mm}
\includegraphics[width=7.9cm,clip]{1154_fig8.eps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg71.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{1154_fig9.ps}\vs...
...*{3mm}
\includegraphics[angle=-90,width=7.5cm,clip]{1154_fig10.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{1154_fig11.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg77.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1154_fig12.ps}\par\vspace*{3mm}
\includegraphics[width=8cm,clip]{1154_fig13.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg78.gif)
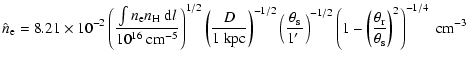
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1154_fig14.eps}\hspace*{4m...
...e*{4mm}
\includegraphics[width=8cm,height=1cm,clip]{1154_fig17.eps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg100.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1154_fig18.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg136.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.8cm,clip]{1154_fig19.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg139.gif)
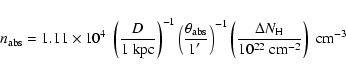
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1154_fig20.eps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg170.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1154_fig21.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg171.gif)
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{1154_fig22.ps}\psfrag{NH}{$N_{{\rm H}}$ }\end{figure}](/articles/aa/full/2004/43/aa1154/Timg172.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{1154_fig23.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg173.gif)
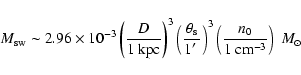
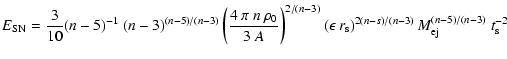
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{1154_fig24.ps}
\end{figure}](/articles/aa/full/2004/43/aa1154/Timg194.gif)