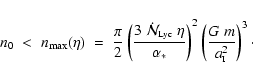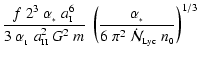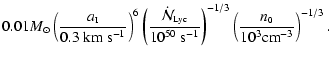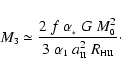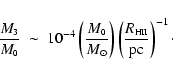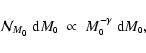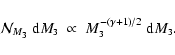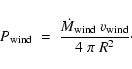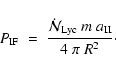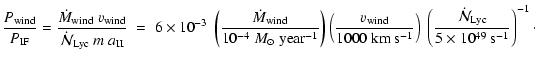A&A 427, 299-306 (2004)
DOI: 10.1051/0004-6361:20041131
The formation of free-floating brown dwarves
and planetary-mass objects
by photo-erosion of prestellar cores
A. P. Whitworth1 - H. Zinnecker2
1 - School of Physics & Astronomy, Cardiff University,
5 The Parade, Cardiff CF24 3YB, Wales, UK
2 -
Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam,
Brandenburg, Germany
Received 21 April 2004 / Accepted 22 July 2004
Abstract
We explore the possibility that, in the vicinity of an OB star, a prestellar
core which would otherwise have formed an intermediate or low-mass star may
form a free-floating brown dwarf or planetary-mass object, because the outer
layers of the core are eroded by the ionizing radiation from the OB star before
they can accrete onto the protostar at the centre of the core. The masses of
objects formed in this way are given approximately by 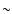
 ,
where
,
where 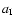 is the isothermal sound speed in the neutral gas of the core,
is the isothermal sound speed in the neutral gas of the core,
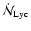 is the rate of emission of Lyman continuum photons
from the OB star (or stars), and
is the rate of emission of Lyman continuum photons
from the OB star (or stars), and 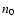 is the
number-density of protons in the HII region surrounding the core. We
conclude that the formation of low-mass objects by this
mechanism should be quite routine, because the mechanism operates over
a wide range of conditions (
is the
number-density of protons in the HII region surrounding the core. We
conclude that the formation of low-mass objects by this
mechanism should be quite routine, because the mechanism operates over
a wide range of conditions (
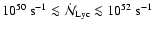 ,
,
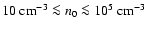 ,
,
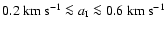 )
and is very effective. However, it is also a rather wasteful way of forming
low-mass objects, in the sense that it requires a relatively massive initial
core to form a single low-mass object. The effectiveness of photo-erosion
also implies that that any intermediate-mass protostars which have
formed in the vicinity of a group of OB stars must already have been well on
the way to formation before the OB stars switched on their ionizing radiation;
otherwise these protostars would have been stripped down to extremely low mass.
)
and is very effective. However, it is also a rather wasteful way of forming
low-mass objects, in the sense that it requires a relatively massive initial
core to form a single low-mass object. The effectiveness of photo-erosion
also implies that that any intermediate-mass protostars which have
formed in the vicinity of a group of OB stars must already have been well on
the way to formation before the OB stars switched on their ionizing radiation;
otherwise these protostars would have been stripped down to extremely low mass.
Key words: stars: formation - stars: low-mass, brown dwarfs - ISM: HII regions
The existence of brown dwarves was first proposed on theoretical grounds by
Kumar (1963a,b) and Hayashi & Nakano (1963),
but more than three decades passed before observations were able to establish
their existence unambiguously (Rebolo et al. 1995;
Nakajima et al. 1995; Oppenheimer et al. 1995). Now they are routinely
observed (e.g. McCaughrean et al. 1995; Luhman et al. 1998; Wilking et al. 1999; Luhman & Rieke 1999; Lucas & Roche 2000; Martín
et al. 2000; Luhman et al. 2000; Béjar et al. 2001;
Martín et al. 2001;
Wilking et al. 2002; McCaughrean et al. 2002). It appears that a
significant fraction of brown dwarves in clusters are not companions
to more massive stars, but rather they are free-floating.
Reipurth & Clarke (2001) have suggested that this is because brown dwarves
are ejected from nascent multiple systems before they can acquire sufficient
mass to become Main Sequence stars, and this suggestion is supported
by the numerical simulations of Bate et al. (2002), Delgado Donate et al. (2003) and Goodwin et al. (2004a,b). Here we explore an
alternative possibility, namely that in the central regions of clusters like the
Orion Nebula Cluster, isolated brown dwarves can form from pre-existing prestellar
cores which are eroded by the ambient ionizing radiation field. Similar
explanations for the formation of free-floating low-mass objects
have been proposed by Zapatero Osorio et al. (2000) and Kroupa (2002), but they
do not appear to have been explored in detail before now.
If a dense neutral core is immersed in an HII region, the ambient Lyman
continuum radiation drives an ionization front into the core. The ionization
front is normally preceded by a compression wave, and this may render the
core gravitationally unstable. At the same time, the flow of ionized gas off
the core reduces its mass and injects material and kinetic energy into
the surrounding HII region. This situation was analyzed by Dyson (1968; see
also Kahn 1969) who argued that it could explain the broadening and splitting
of emission lines from the Orion Nebula. Dyson also considered the circumstances
under which such a core might become gravitationally unstable.
Bertoldi (1989) and Bertoldi & McKee (1990) have developed semi-analytic
models for larger cometary globules created
by the interaction of ionizing radiation with a pre-existing cloud on the
edge of an HII region. They use these semi-analytic models to evaluate the
acceleration of the globule (due to the rocket effect; cf. Kahn 1954; Oort &
Spitzer 1955) and its gravitational stability. Their results agree broadly
with the numerical simulations of Sandford et al. (1982) and Lefloch &
Lazareff (1994). More recently Kessel-Deynet & Burkert (2002) have
modelled the radiation driven implosion of a pre-existing large cloud
having internal structure. They use Smoothed Particle Hydrodynamics to
handle the three-dimensional, self-gravitating gas dynamics, and find
that small-scale internal structure delays, and may even inhibit,
gravitational collapse.
However, in this paper we are concerned - like Dyson and Kahn - with
small-scale neutral cores immersed well within an HII region, in the vicinity
of the exciting stars, rather than large cometary globules at the edge of an
HII region. In particular, we wish to evaluate the competition
between erosion of material from the outer layers of such a core (due to
the ionization front which eats into the core), and the formation and growth
of a central protostar (triggered by the compression wave driven into the
core ahead of the ionization front).
In order to keep free parameters to a minimum in this exploratory
analysis, we make a number of simplifying assumptions. We
assume that there exists a prestellar core
in equilibrium, and that a nearby massive star (or group thereof) then
switches on its ionizing radiation instantaneously, and ionizes
the surroundings of the prestellar core, on a time-scale much shorter
than the sound-crossing time for the core (we justify this assumption
later). The resulting increase in external pressure triggers the collapse
of the core, from the outside in, and at the same time an ionization
front starts to eat into the core, thereby eroding it from the outside,
as it contracts. The final stellar mass is
therefore determined by a competition between the rate of accretion
onto the central protostar, and the rate of erosion at the boundary.
Erosion ceases to be effective when the ionization front has eaten
so far into the collapsing core that the newly ionized gas flowing
off the ionization front is - despite its outward kinetic energy -
still gravitational bound to the protostar.
The evolution consists of three phases, starting from the instant
t=0 when the surroundings of the prestellar core first become ionized.
At this juncture a compression wave is driven into the core setting
up a uniform, subsonic inward velocity field. When this wave impinges
on the centre at time
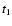 ,
the first phase terminates and
a central protostar is formed, which
then grows steadily by accretion. At the same time an expansion
wave is reflected and propagates outwards leaving an approximately
freefall velocity field in its wake. At time
,
the first phase terminates and
a central protostar is formed, which
then grows steadily by accretion. At the same time an expansion
wave is reflected and propagates outwards leaving an approximately
freefall velocity field in its wake. At time
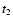 this outward
propagating expansion wave encounters the inward propagating
ionization front, and the second phase terminates. Thereafter the ionization
front is eroding material
which is falling ever faster inwards. Eventually, at time
this outward
propagating expansion wave encounters the inward propagating
ionization front, and the second phase terminates. Thereafter the ionization
front is eroding material
which is falling ever faster inwards. Eventually, at time
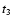 ,
the ionization front encounters material which is falling inwards so fast
that it cannot be unbound by the ionization front, and the third phase
terminates. The final stellar mass
is the mass interior to the ionization front at time
,
the ionization front encounters material which is falling inwards so fast
that it cannot be unbound by the ionization front, and the third phase
terminates. The final stellar mass
is the mass interior to the ionization front at time
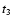 .
.
In Sect. 3 we derive an expression for the diffuse ionizing
radiation field in an HII region, and in Sect. 4 we formulate
the speed with which the ionization front eats into the core.
In Sect. 5, we describe the initial prestellar core and formulate
the time
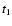 it takes for the compression wave to propagate to
its centre. In Sect. 6 we describe the modified density and
velocity field set up in the inner core by the outward propagating
expansion wave, and formulate the time
it takes for the compression wave to propagate to
its centre. In Sect. 6 we describe the modified density and
velocity field set up in the inner core by the outward propagating
expansion wave, and formulate the time
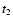 at which
the outward propagating expansion wave meets the inward propagating
ionization front. In Sect. 7 we formulate the time
at which
the outward propagating expansion wave meets the inward propagating
ionization front. In Sect. 7 we formulate the time
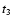 at which the ionization front has eaten so far into the modified density
field inside the expansion wave that it has encountered material
which is infalling too fast to be unbound by the act of ionization.
The material interior to the ionization front at time
at which the ionization front has eaten so far into the modified density
field inside the expansion wave that it has encountered material
which is infalling too fast to be unbound by the act of ionization.
The material interior to the ionization front at time
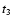 is
presumed to constitute the final star. We can therefore obtain an
expression for its mass.
is
presumed to constitute the final star. We can therefore obtain an
expression for its mass.
We shall assume that the HII region which engulfs the pre-existing
prestellar core is excited by a compact cluster of OB stars which
emits Lyman continuum (i.e. hydrogen ionizing) photons at a constant
rate
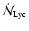 .
We shall also assume that most of the
surrounding space is occupied by a uniform gas in which the density
of hydrogen nuclei in all forms is
.
We shall also assume that most of the
surrounding space is occupied by a uniform gas in which the density
of hydrogen nuclei in all forms is
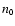 .
The radius of the
initial HII region is therefore
.
The radius of the
initial HII region is therefore
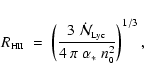 |
(1) |
where
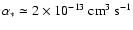 is the recombination coefficient into excited states only; in other
words, we are using the On-The-Spot Approximation.
is the recombination coefficient into excited states only; in other
words, we are using the On-The-Spot Approximation.
If we neglect the shadows cast by other prestellar cores and attenuation by
dust inside the HII region, the radial - or direct - number-flux of Lyman
continuum photons
 (i.e.
the number of ionizing photons crossing unit area in unit time) varies with
distance R from the OB cluster as
(i.e.
the number of ionizing photons crossing unit area in unit time) varies with
distance R from the OB cluster as
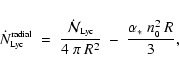 |
(2) |
where the first term on the righthand side represents geometric dilution and
the second term represents the absorptions which maintain ionization against
recombination. Hence the mean value of
 ,
averaged over the volume of the HII region, is
,
averaged over the volume of the HII region, is
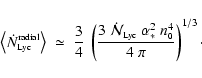 |
(3) |
The volume number-emissivity for the diffuse component of the Lyman continuum
radiation field (i.e. the number of ionizing photons emitted from unit volume
in unit time into unit solid angle, due to recombinations straight into the
ground state) is
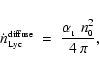 |
(4) |
where
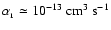 is
the recombination coefficient into the ground state only. The
mean diffuse flux is therefore of order
is
the recombination coefficient into the ground state only. The
mean diffuse flux is therefore of order
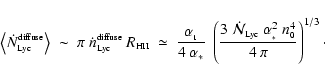 |
(5) |
Comparing Eqs. (3) and (5), we see that
the mean diffuse flux is smaller than the mean radial flux by a
factor 
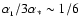 .
This is to some
extent compensated by the fact that a spherical core of
radius r presents a larger
effective cross-section to the diffuse flux (
.
This is to some
extent compensated by the fact that a spherical core of
radius r presents a larger
effective cross-section to the diffuse flux (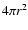 )
than
to the radial flux (
)
than
to the radial flux (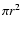 ), i.e. the net dose of Lyman
continuum radiation received by a spherical core divides roughly
in the ratio 60%
radial and 40% diffuse. In order to proceed with a spherically
symmetric analysis, we shall assume that the
flux of Lyman continuum radiation incident on a core is
constant, isotropic, and equal to
), i.e. the net dose of Lyman
continuum radiation received by a spherical core divides roughly
in the ratio 60%
radial and 40% diffuse. In order to proceed with a spherically
symmetric analysis, we shall assume that the
flux of Lyman continuum radiation incident on a core is
constant, isotropic, and equal to
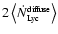 .
However, we should be mindful that this is a crude representation
of the Lyman continuum radiation field incident on a real core in
a real HII region. We will check retrospectively
that the cores we invoke are much smaller than the HII region in
which they are imersed (see Sect. 8).
.
However, we should be mindful that this is a crude representation
of the Lyman continuum radiation field incident on a real core in
a real HII region. We will check retrospectively
that the cores we invoke are much smaller than the HII region in
which they are imersed (see Sect. 8).
We denote the instantaneous radius of the neutral core by
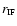 ,
and the density of hydrogen nuclei in all
forms in the neutral core by
,
and the density of hydrogen nuclei in all
forms in the neutral core by
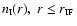 ,
where r is distance measured from the centre of the core. We
assume that the ionization front eats into the core at speed
,
where r is distance measured from the centre of the core. We
assume that the ionization front eats into the core at speed
![$\left[ -~\dot{r}_{\mbox{\tiny IF}} \right]~<~a_{\mbox{\tiny I}}~$](/articles/aa/full/2004/43/aa1131/img35.gif) ,
where
,
where
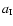 is the isothermal sound-speed in the neutral gas.
Consequently the ionization front is not preceded by a strong shock front,
just a weak compression wave. This is a reasonable assumption, except near
the beginning, when the ionization front advances very rapidly into the core.
We can only allow for this by performing numerical simulations. However, this
initial phase of rapid erosion does not last long, and will not greatly
affect the overall phenomenology of core erosion or the final protostellar
mass. It will simply shorten the time interval, t1, before the
protostar forms. Thus the expressions for the final protostellar mass which
we derive later (Eqs. (40) and (41)) should
be taken as indicative rather than precise.
is the isothermal sound-speed in the neutral gas.
Consequently the ionization front is not preceded by a strong shock front,
just a weak compression wave. This is a reasonable assumption, except near
the beginning, when the ionization front advances very rapidly into the core.
We can only allow for this by performing numerical simulations. However, this
initial phase of rapid erosion does not last long, and will not greatly
affect the overall phenomenology of core erosion or the final protostellar
mass. It will simply shorten the time interval, t1, before the
protostar forms. Thus the expressions for the final protostellar mass which
we derive later (Eqs. (40) and (41)) should
be taken as indicative rather than precise.
Conservation of mass across the ionization front
requires
![\begin{displaymath}
n_{\mbox{\tiny I}}(r_{\mbox{\tiny IF}})~
\left[ -\dot{r}_{\m...
...II}}(r_{\mbox{\tiny IF}})-
\dot{r}_{\mbox{\tiny IF}} \right] ,
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img37.gif) |
(6) |
where
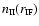 and
and
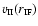 are - respectively - the density of hydrogen
nuclei in all forms and the radial speed of the ionized gas, just outside
the neutral core.
are - respectively - the density of hydrogen
nuclei in all forms and the radial speed of the ionized gas, just outside
the neutral core.
To proceed, we assume that the ionized gas flows away from the ionization
front at constant speed
![\begin{displaymath}
\left[ v_{\mbox{\tiny II}}(r) ~-~ \dot{r}_{\mbox{\tiny IF}} ...
...dot{r}_{\mbox{\tiny IF}}
\right] \;=\; a_{\mbox{\tiny II}} ,
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img40.gif) |
(7) |
where
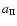 is the isothermal sound-speed in the ionized gas.
(In reality (Kahn 1969) the flow of ionized gas downstream from the ionization
front accelerates away from the core due to the pressure gradient, but
this only changes the result we derive below by a numerical factor of order
unity.) Hence the density in the ionized gas falls off approximately as r-2,
is the isothermal sound-speed in the ionized gas.
(In reality (Kahn 1969) the flow of ionized gas downstream from the ionization
front accelerates away from the core due to the pressure gradient, but
this only changes the result we derive below by a numerical factor of order
unity.) Hence the density in the ionized gas falls off approximately as r-2,
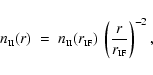 |
(8) |
until it approaches the background density
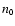 at radius
at radius
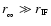 .
Also, substituting from Eq. (7) into
Eq. (6) gives
.
Also, substituting from Eq. (7) into
Eq. (6) gives
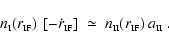 |
(9) |
Almost all the incident flux of Lyman continuum photons is used up
balancing recombinations in the outflowing ionized gas, so we can
put
In obtaining the final expression in Eq. (10), we have
assumed that
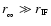 .
Again this is a
reasonable assumption except near the beginning.
.
Again this is a
reasonable assumption except near the beginning.
For the purpose of this exploratory calculation, we assume that
the pre-existing prestellar core is a singular isothermal sphere.
Generalizing the treatment to a non-singular (i.e. Bonnor-Ebert)
isothermal sphere should not change the result greatly, but would
necessitate a detailed numerical formulation of the problem; it
would tend to reduce the mass of the final protostar, and hence
assist in producing low-mass final objects.
In a singular isothermal sphere, the density of hydrogen nuclei
in all forms,
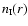 and the mass interior to radius r,
M(r), are given by
and the mass interior to radius r,
M(r), are given by
where
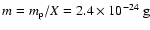 is the
mass associated with one hydrogen nucleus when account is taken
of other elements (in particular helium),
is the
mass associated with one hydrogen nucleus when account is taken
of other elements (in particular helium),
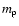 is the
mass of a proton, and X is the fractional abundance of hydrogen
by mass. If the boundary density is
is the
mass of a proton, and X is the fractional abundance of hydrogen
by mass. If the boundary density is
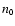 ,
the outer radius
and total mass are initially
,
the outer radius
and total mass are initially
When this core is first overrun by the HII region, at time t = 0,
the resulting increase in the external pressure drives a
compression wave into the core, thereby triggering its collapse.
We assume that the compression wave travels ahead of the ionization front.
It leaves in its wake a subsonic - and approximately uniform -
inward velocity field. The compression wave reaches the centre
at time
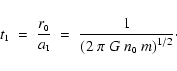 |
(17) |
i.e. after one sound-crossing time. We can now justify the assumption that
the time-scale on which the HII region overruns the core is much shorter
than a sound-crossing time. The time-scale for the establishment of the
Initial Strømgren Sphere is of order the recombination time-scale, viz.
so the condition becomes
 ,
or
,
or
This is easily satisfied since typically
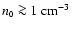 .
.
At
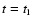 a central protostar forms and subsequently grows in
mass at a constant rate
a central protostar forms and subsequently grows in
mass at a constant rate
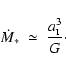 |
(18) |
We note that this result is true for the collapse of a singular isothermal
sphere irrespective of whether its collapse is triggered - as here - from outside-in by the inward propagation of a mild compression wave (see
Whitworth & Summers 1985), or - as in the Shu (1977) model - from
inside-out by a central perturbation.
At the same time that the compression wave converges on the centre,
an expansion wave is launched outwards at speed
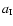 ,
relative to the gas. If we neglect the small
inward velocity already acquired by the gas due to the inward propagating
compression wave, the radius of the expansion wave is given by
,
relative to the gas. If we neglect the small
inward velocity already acquired by the gas due to the inward propagating
compression wave, the radius of the expansion wave is given by
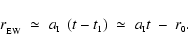 |
(19) |
We now introduce dimensionless variables
in terms of which the radius of the expansion wave is given by
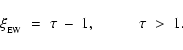 |
(22) |
Interior to the expansion wave, material flows inwards, to feed
the constant accretion rate onto the central protostar, and quickly
approaches a freefall-like profile. Therefore the density and velocity
can be approximated by
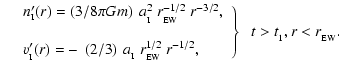 |
|
|
(23) |
There is a degree of freedom in specifying the coefficients of
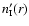 and
and
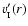 .
We have chosen
them so that (i) they are consistent with the constant accretion rate
(see Eq. (18)); and (ii) the mass of the central protostar
and the mass in the accretion flow interior to the expansion wave are
equal. Formally the velocity changes discontinuously across the expansion
wave, from zero outside to
.
We have chosen
them so that (i) they are consistent with the constant accretion rate
(see Eq. (18)); and (ii) the mass of the central protostar
and the mass in the accretion flow interior to the expansion wave are
equal. Formally the velocity changes discontinuously across the expansion
wave, from zero outside to
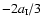 inside; in reality
the change will be much smaller since the inward propagating compression
wave during the first phase will have set up an inward velocity of comparable
magnitude (e.g. Whitworth & Summers 1985).
inside; in reality
the change will be much smaller since the inward propagating compression
wave during the first phase will have set up an inward velocity of comparable
magnitude (e.g. Whitworth & Summers 1985).
Substituting for
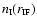 in Eq. (12)
from Eq. (13), we obtain
in Eq. (12)
from Eq. (13), we obtain
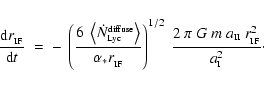 |
(24) |
If we now introduce a third dimensionless variable
Equation (24) reduces to
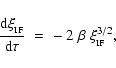 |
(26) |
with solution
![\begin{displaymath}
\xi_{_{\mbox{\tiny IF}}} \;=\; \left[ 1~+~\beta \tau \right]^{-2} .
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img81.gif) |
(27) |
To fix the constant of integration, we have used the initial
condition, viz.: at t=0,
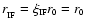 ;
and hence at
;
and hence at 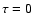 ,
,
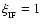 .
.
The ionization front meets the expansion wave at time
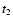 when
when
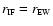 ,
or in terms of the
dimensionless variables, at
,
or in terms of the
dimensionless variables, at
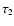 when
when
 .
Equating Eqs. (27) and (22), we obtain
.
Equating Eqs. (27) and (22), we obtain
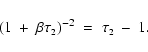 |
(28) |
With typical values
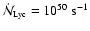 and
and
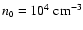 ,
we have
,
we have
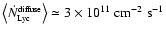 .
Putting
.
Putting
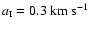 and
and
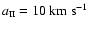 ,
we obtain
,
we obtain
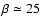 .
Hence,
if we put
.
Hence,
if we put
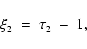 |
(29) |
it follows that
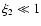 ,
and Eq. (28) becomes
,
and Eq. (28) becomes
![\begin{displaymath}
\left[ (1+\beta) ~+~ \beta \xi_{\mbox{\tiny 2}} \right]^2~
\xi_{\mbox{\tiny 2}} \;=\; 1 ,
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img97.gif) |
(30) |
with approximate solution
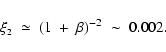 |
(31) |
This is the dimensionless radius of the inward propagating ionization front
when it meets the outward propagating expansion wave.
Once the inward propagating ionization front passes the outward
propagating expansion wave, the ionization front encounters
infalling gas with density and velocity given by Eq. (23).
Equation (9) therefore has to be adjusted to account for the
inward motion of the neutral gas:
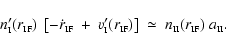 |
(32) |
Substituting for
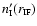 and
and
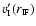 from Eq. (23) and for
from Eq. (23) and for
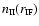 from Eq. (11), we obtain
from Eq. (11), we obtain
![\begin{displaymath}
\dot{\xi}_{\mbox{\tiny IF}} \;=\; -~\frac{2~(\tau - 1)^{1/2}...
...{\tiny IF}}^{-1/2} ~+~ 4~\beta~\xi_{\mbox{\tiny IF}} \right] .
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img102.gif) |
(33) |
The solution is
![\begin{displaymath}
(\tau - 1)^{3/2} \;=\; \xi_{\mbox{\tiny 2}}^{3/2} ~+~ \frac{...
...}}^{3/2}}
{1~+~ 4~\beta~\xi_{\mbox{\tiny IF}}^{3/2}} \right] ,
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img103.gif) |
(34) |
where we have fixed the constant of integration by requiring that
 at
at
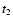 ;
or equivalently
;
or equivalently
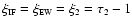 at
at
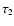 .
.
To follow the ionization front into the third phase, we pick ever smaller values
of
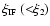 and calculate
and calculate 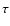 from
Eq. (34). The radial velocity of the ionization front is then given by
from
Eq. (34). The radial velocity of the ionization front is then given by
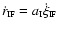 ,
where
,
where
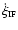 can be calculated from Eq. (33). The
specific kinetic energy of the newly ionized gas, relative to the central protostar
is therefore
can be calculated from Eq. (33). The
specific kinetic energy of the newly ionized gas, relative to the central protostar
is therefore
![\begin{displaymath}
\epsilon_{\mbox{\tiny KIN}} \;=\; \frac{1}{2}~\left[ \dot{r}...
...frac{a_{\mbox{\tiny II}}}{a_{\mbox{\tiny I}}}
\right]^2 \cdot
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img110.gif) |
(35) |
Taking into account the mass of the protostar,
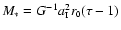 ,
plus the mass in the accretion flow interior to
the ionization front,
,
plus the mass in the accretion flow interior to
the ionization front,
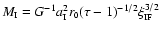 ,
the specific
binding energy of this material is
,
the specific
binding energy of this material is
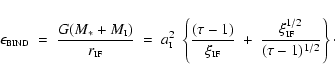 |
(36) |
We shall assume that ionization ceases to erode the core once the specific
kinetic energy,
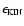 (Eq. (35)), is less
than the specific binding energy,
(Eq. (35)), is less
than the specific binding energy,
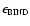 (Eq. (36)). The mass
(Eq. (36)). The mass
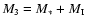 interior to the ionization front at this stage is the final mass of the protostar.
This occurs at time
interior to the ionization front at this stage is the final mass of the protostar.
This occurs at time
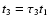 ,
where
,
where
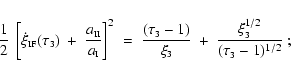 |
(37) |
and the final mass of the protostar is then given by
![\begin{displaymath}
\frac{M_{\mbox{\tiny 3}}}{M_{\mbox{\tiny0}}} \;=\; \frac{1}{...
...ox{\tiny 3}} - 1)^{-1/2}
\xi_{\mbox{\tiny 3}}^{3/2} \right] .
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img119.gif) |
(38) |
![\begin{figure}
\par\includegraphics[angle=-90,width=14cm,clip]{1131fig1.eps}
\end{figure}](/articles/aa/full/2004/43/aa1131/Timg127.gif) |
Figure 1:
For a)
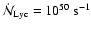 ;
b) ;
b)
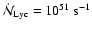 ;
and c) ;
and c)
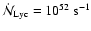 ,
the solid lines show the loci on the ,
the solid lines show the loci on the
![$(a_{\rm I},\log_{\rm 10}[n_0])$](/articles/aa/full/2004/43/aa1131/img123.gif) -plane
where free-floating objects of mass -plane
where free-floating objects of mass
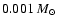 (one Jupiter mass),
(one Jupiter mass),
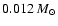 (the deuterium-burning limit) and
(the deuterium-burning limit) and
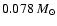 (the hydrogen-burning
limit) form due to photo-erosion of pre-existing cores. The dotted lines show the
predictions of the approximate Eq. (40). The dashed (dash-dot) line
is the locus below which the volume of the initial core is less than 0.001 (0.01) of
the volume of the whole HII region.
(the hydrogen-burning
limit) form due to photo-erosion of pre-existing cores. The dotted lines show the
predictions of the approximate Eq. (40). The dashed (dash-dot) line
is the locus below which the volume of the initial core is less than 0.001 (0.01) of
the volume of the whole HII region. |
| Open with DEXTER |
The procedure for obtaining the final protostellar mass
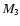 is therefore as follows. (i) Choose
is therefore as follows. (i) Choose
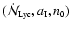 and calculate
and calculate 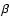 from Eq. (25). (ii) Solve
Eq. (30) for
from Eq. (25). (ii) Solve
Eq. (30) for
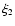 .
(iii) Solve
Eq. (34) for
.
(iii) Solve
Eq. (34) for
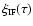 ,
(
,
(
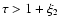 ). (iv) Identify
). (iv) Identify
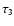 satisfying
Eq. (37). (v) Compute
satisfying
Eq. (37). (v) Compute
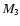 according to Eq. (38).
according to Eq. (38).
Figure 1 shows, for three representative values of
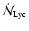 (i.e. (a)
(i.e. (a)
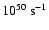 ;
(b)
;
(b)
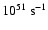 ;
and (c)
;
and (c)
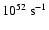 )
loci of contant
)
loci of contant
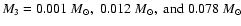 on the
on the
![$(a_{\rm I},{\rm\log}_{\rm 10}[n_0])$](/articles/aa/full/2004/43/aa1131/img139.gif) -plane. These values of
-plane. These values of
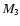 are chosen because they represent, respectively, one Jupiter
mass, the deuterium-burning limit, and the hydrogen-burning limit. Notionally objects
in the mass range
are chosen because they represent, respectively, one Jupiter
mass, the deuterium-burning limit, and the hydrogen-burning limit. Notionally objects
in the mass range
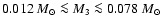 are
referred to as brown dwarves, whilst those in the mass range
are
referred to as brown dwarves, whilst those in the mass range
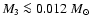 are referred to as planetary-mass objects. We see that for a
broad range of values of
are referred to as planetary-mass objects. We see that for a
broad range of values of
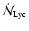 ,
,
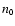 and
and
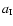 ,
there exists the possibility to form free-floating brown
dwarves and planetary-mass objects, provided suitable pre-existing cores are
available to be photo-eroded.
,
there exists the possibility to form free-floating brown
dwarves and planetary-mass objects, provided suitable pre-existing cores are
available to be photo-eroded.
In estimating the radiation field incident on a core, we have assumed that
the volume occupied by the core is much smaller than the volume of the HII region
around it (see Sect. 3). It is therefore necessary to check that this is the case.
If we require the ratio between the initial volume of a core and the volume of the
whole HII region to be less than some fraction 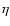 ,
then substituting from
Eqs. (1) and (15) we obtain the condition
,
then substituting from
Eqs. (1) and (15) we obtain the condition
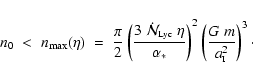 |
(39) |
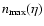 is plotted in Figure 1 for
is plotted in Figure 1 for
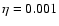 (dashed curve) and
(dashed curve) and
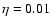 (dash-dot curve). Evidently this is a significant constraint for
(dash-dot curve). Evidently this is a significant constraint for
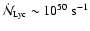 ,
but for higher
values of
,
but for higher
values of
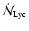 it is less important.
it is less important.
Since the protostar does not grow hugely during the Third Phase,
we can approximate the results by adopting the mass at the end of the
Second Phase. If in addition we assume
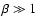 ,
so that from Eq. (31)
,
so that from Eq. (31)
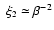 ,
we can write
,
we can write
Here
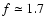 is a factor to account for the additional matter which accretes
onto the protostar after the ionization fron meets the expansion wave. We can
understand this factor as follows. In a collapsing singular isothermal sphere, the
infalling mass interior to the expansion wave is equal to the mass already in the
central protostar. Thus, in the problem considered here, when the ionization front
meets the expansion wave at
is a factor to account for the additional matter which accretes
onto the protostar after the ionization fron meets the expansion wave. We can
understand this factor as follows. In a collapsing singular isothermal sphere, the
infalling mass interior to the expansion wave is equal to the mass already in the
central protostar. Thus, in the problem considered here, when the ionization front
meets the expansion wave at
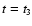 ,
the infalling mass interior to
the ionization front equals the mass already in the protostar. It follows that if
no further mass acretes onto the protostar, f = 1; and if all the infalling mass
interior to the ionization front at
,
the infalling mass interior to
the ionization front equals the mass already in the protostar. It follows that if
no further mass acretes onto the protostar, f = 1; and if all the infalling mass
interior to the ionization front at
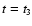 accretes onto the
protostar, then f = 2. The empirical value f = 1.7 suggests that most of the
infalling mass interior to the ionization front at
accretes onto the
protostar, then f = 2. The empirical value f = 1.7 suggests that most of the
infalling mass interior to the ionization front at
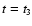 is
accreted onto the protostar.
is
accreted onto the protostar.
Equation (40) is plotted as a dotted line in Fig. 1. We see that
it is a very good approximation to the numerical results. Given the approximate
nature of the whole analysis, Eq. (40) can be viewed as our best
estimate of the final protostellar mass.
This exploratory analysis suggests that it is possible for a relatively
massive prestellar core which suddenly finds itself immersed in an HII
region to be stripped down to the mass of a brown dwarf, or even a planet,
by photo-erosion, before it can collapse to form a star. To improve on this
analysis, it is probably necessary to resort to numerical modelling. One
could then, in principle,
(i) use a more realistic configuration for the pre-existing prestellar
core; (ii) include the development of the HII region as it overruns the
core; (iii) treat properly the early phase when the ionization front
advances very rapidly into the outer layers of the core, and the
compression wave which is driven into the core; (iv) attempt to capture
effects due to departures from spherical symmetry, in particular the radiative
transfer aspects; (v) include self-gravity explicitly in the equations of
motion. We suspect that the photo-erosion mechanism may be somewhat more effective
than our analysis suggests, because firstly, with a prestellar core which is not
as centrally condensed as a singular isothermal sphere (e.g. Ward-Thompson et al. 1999; Bacmann et al. 2000), the protostar will
not form so quickly, giving the ionization front more time to erode;
and secondly, the ionization front will penetrate at higher speed into the
less dense central regions.
We can express the final protostellar mass
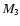 in terms of
the initial core mass
in terms of
the initial core mass
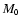 ,
by combining Eqs. (40), (16) and (1) to obtain
,
by combining Eqs. (40), (16) and (1) to obtain
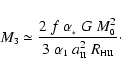 |
(41) |
There are two important deductions which we can make from this equation.
First, the ratio of the final protostellar mass to the initial core mass is
given by
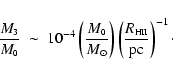 |
(42) |
The photo-erosion process is therefore very effective, in the sense that
it strips off most of the mass of the initial core. This makes it a rather
wasteful way of creating low-mass
protostars, in the sense that it requires a relatively massive initial core to
create a single final low-mass protostellar object. In addition, we infer
that any intermediate-mass protostars which have formed in the vicinity of a group
of OB stars must already have been well on the way to formation before the OB
stars switched on their ionizing radiation; otherwise these protostars would
have been stripped down to extremely low mass.
Second, if the number of cores in the mass interval
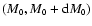 (i.e. the core mass function) has the form
(i.e. the core mass function) has the form
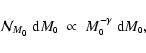 |
(43) |
then the initial mass function for brown dwarves and planetary-mass objects
formed by photo-erosion has the form
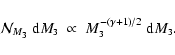 |
(44) |
Motte et al. (1998) find
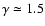 for
for
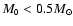 and
and
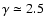 for
for
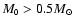 for the cores in
for the cores in
 Ophiuchus, and similar results are reported for the cores in Ophiuchus by
Johnstone et al. (2000), for the cores in Serpens by Testi & Sargent (1998), and
for the cores in the Orion B molecular cloud by Motte et al. (2001) and Johnstone
et al. (2001). Hence the exponent in the initial mass function for brown dwarves
and planetary-mass objetcs formed by photo-erosion should lie in the range -1.25 to -1.75, with the smaller value (-1.75) obtaining for
higher-mass cores. As the HII region expands
and engulfs additional cores,
Ophiuchus, and similar results are reported for the cores in Ophiuchus by
Johnstone et al. (2000), for the cores in Serpens by Testi & Sargent (1998), and
for the cores in the Orion B molecular cloud by Motte et al. (2001) and Johnstone
et al. (2001). Hence the exponent in the initial mass function for brown dwarves
and planetary-mass objetcs formed by photo-erosion should lie in the range -1.25 to -1.75, with the smaller value (-1.75) obtaining for
higher-mass cores. As the HII region expands
and engulfs additional cores,
 increases, and therefore for
fixed
increases, and therefore for
fixed
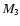 the progenitor cores have larger masses
the progenitor cores have larger masses
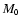 .
Consequently, as one moves away from the stars exciting the HII region, the density
of brown dwarves and planetary-mass objects formed by photo-erosion should decrease,
and their initial mass function should become slightly steeper.
.
Consequently, as one moves away from the stars exciting the HII region, the density
of brown dwarves and planetary-mass objects formed by photo-erosion should decrease,
and their initial mass function should become slightly steeper.
We have omitted from our analysis the possible effect of a stellar wind
impinging on a core (A. Burkert, private communication). A simple estimate
suggests that a stellar wind would need to be very powerful to have
a significant effect. Suppose that the central OB star blows a wind with
mass-loss rate
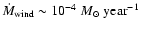 ,
and speed
,
and speed
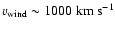 .
The resultant
ram pressure acting on a core at radius R is
.
The resultant
ram pressure acting on a core at radius R is
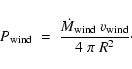 |
(45) |
We can compare this with the ram pressure of the ionized gas flowing off
the surface of a core which is exposed to the direct flux of ionizing radiation:
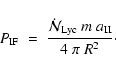 |
(46) |
Substituting typical values, we obtain
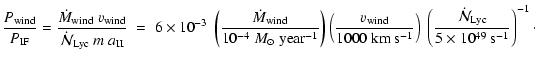 |
|
|
(47) |
This implies that the wind can have little effect. In reality, most of the
ionizing flux from the central star is spent maintaining ionization against
recombination in the flow of ionized gas from the core, rather than producing
new ionizations. Therefore Eq. (46) significantly overestimates
the ram pressure of the ionized gas flowing off the core, but probably not
by two orders of magnitude. The effect of a stellar wind will be
to modify the rate at which the ionized gas flowing off the core can disperse
(e.g. Richling & Yorke 1998; Hollenbach et al. 2000).
A bow shock will form on the side of the core facing into the wind (the
windward side), and the ionized gas flowing off this side of the core will
be swept back in the direction of the wind. This will have the effect of
increasing the density, and hence the recombination rate, in the ionized
gas flowing off the core, thereby reducing the rate of erosion somewhat.
On the leeward side of the core the effect of the wind will be minimal.
The analysis we have presented in this paper is based on several
assumptions and approximations, which, whilst reasonable, are
idealizations of what is likely to occur in nature. With this proviso,
we infer that, in the central regions of large clusters, free-floating
brown dwarves and planetary-mass objects may form when more massive
pre-existing cores are overrun by HII regions excited by newly-formed
massive stars. The sudden ionization of the surroundings of
a core drives a compression wave into the core, creating at its
centre a protostar which then grows by accretion. At the same time an
ionization front starts eating into the core, thereby removing its
outer layers. The final mass of the protostar is determined by a
competition between the rate at which it can accrete the infalling envelope, and
the rate at which the ionization front can erode the envelope. The simple
analysis presented here suggests that in large, dense clusters this will
result in the formation of free-floating brown dwarves and/or planetary-mass
objects. The process is both robust, in the sense that it operates
over a wide range of conditions, and also very effective, in the sense that
it strips off most of the mass of the initial core. This means that it is a
wasteful way of creating low-mass protostars, because a relatively massive
initial core is required to produce a single final brown dwarf or
planetary-mass object. It also means that any intermediate-mass protostars which
have formed in the vicinity of a group of OB stars must already have been
well on the way to formation before the OB stars switched on their ionizing
radiation; otherwise these protostars would have been stripped down to
extremely low mass.
Note added in proof. The idea that in the vicinity of OB stars final stellar masses may be determinated by photo-erosion (in the manner we have analysed here), and the idea that this is a mechanism for forming free-floating brown dwarves, are originally due to Hester (Hester et al. 1996; Hester 1997).
Acknowledgements
We thank the referee, Doug Johnstone, who drew our attention to a fundamental
error in the original version of this paper, and made several other important
suggestions which we have incorporated in the final version. We gratefully
acknowledge the support of a European Commission Research Training Network,
awarded under the Fifth Framework (Ref. HPRN-CT-2000-00155).
- Bacmann, A.,
André, P., Puget, J.-L., et al. 2000, A&A, 361, 555 [NASA ADS] (In the text)
- Bate, M. R., Bonnell,
I. A., & Bromm, V. 2002, MNRAS, 332, L65 [NASA ADS] [CrossRef] (In the text)
- Béjar, V. J. S.,
Martín, E. L., Zapatero Osorio, M. R., et al. 2001, ApJ, 556,
830 [NASA ADS] [CrossRef] (In the text)
- Bertoldi, F.
1989, ApJ, 346, 735 [NASA ADS] [CrossRef] (In the text)
- Bertoldi, F.,
& McKee, C. F. 1990, ApJ, 354, 529 [NASA ADS] [CrossRef] (In the text)
- Delgado-Donate, E.,
Clarke, C. J., & Bate, M. R. 2003, MNRAS, 342, 926 [NASA ADS] [CrossRef] (In the text)
- Dyson, J. E. 1968,
Ap&SS, 1, 388 [NASA ADS] (In the text)
- Goodwin, S. P.,
Whitworth, A. P., & Ward-Thompson, D. 2004a, A&A, 414,
633 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Goodwin, S. P.,
Whitworth, A. P., & Ward-Thompson, D. 2004b, A&A, 423,
169 [EDP Sciences] [NASA ADS] [CrossRef]
- Hayashi, C.,
& Nakano, T. 1963, Prog. Theor. Phys., 30, 460 [NASA ADS] (In the text)
- Hester J.
J. 1997, in Star Formation Near and Far, ed. S. S. Holt & L. G.
Mundy, AIP Conf. Proc., 393, 143
- Hester, J.
J., Scowen, P. A., Sankrit, R., et al. 1996, AJ, 111, 2349 [NASA ADS] [CrossRef]
- Hollenbach,
D. J., Yorke, H. W., & Johnstone, D. 2000, in Protostars and
Planets, IV (Tucson: University of Arizona Press), ed. V. Mannings,
A. P. Boss, & S. S. Russell, 401
(In the text)
- Johnstone,
D., Wilson, C. D., Moriarty-Schieven, G., et al. 2000, ApJ, 545,
327 [NASA ADS] [CrossRef] (In the text)
- Johnstone,
D., Fich, M., Mitchell, G. F., & Moriarty-Schieven, G. 2001,
ApJ, 559, 307 [NASA ADS] [CrossRef] (In the text)
- Kahn, F. D. 1954, Bull.
Astron. Inst. Netherlands, 12, 187 [NASA ADS] (In the text)
- Kahn, F. D. 1969,
Physica, 41, 172 [NASA ADS] [CrossRef] (In the text)
-
Kessel-Deynet, O., & Burkert, A. 2002, MNRAS, 338, 545 [NASA ADS] (In the text)
- Kroupa, P. 2002,
Science, 295, 82 [NASA ADS] [CrossRef] (In the text)
- Kumar, S. S. 1963a,
ApJ, 137, 1121 [NASA ADS] [CrossRef] (In the text)
- Kumar, S. S. 1963b,
ApJ, 137, 1126 [NASA ADS] [CrossRef]
- Lefloch, B.,
& Lazareff, B. 1994, A&A, 289, 559 [NASA ADS] (In the text)
- Lucas, P. W., &
Roche, P. F. 2000, MNRAS, 314, 858 [NASA ADS] [CrossRef] (In the text)
- Luhman, K. L.,
Rieke, G. H., Lada, C. J., & Lada, E. A. 1998, ApJ, 508,
347 [NASA ADS] [CrossRef] (In the text)
- Luhman, K. L.,
& Rieke, G. H. 1999, ApJ, 525, 440 [NASA ADS] [CrossRef] (In the text)
- Luhman, K. L.,
Rieke, G. H., Young, E. T., et al. 2000, ApJ, 540, 1016 [NASA ADS] [CrossRef] (In the text)
-
McCaughrean, M. J., Zinnecker, H., Rayner, J. T., & Stauffer,
J. 1995, in The bottom of the Main Sequence - and beyond, ESO
Astrophysics Symposium, ed. C. G. Tinney (Springer Verlag),
209
(In the text)
-
McCaughrean, M. J., Zinnecker, H., Andersen, M., Meeus, G., &
Lodieu, N. 2002, The Messenger, 109, 28 [NASA ADS] (In the text)
- Martín, E. L.,
Brandner, W., Bouvier, J., et al. 2000, ApJ, 543, 299 [NASA ADS] [CrossRef] (In the text)
- Martín, E. L.,
Zapatero Osorio, M. R., Barrado y Navascués, D., Béjar,
V. J. S., & Rebolo, R. 2001, ApJ, 558, L117 [NASA ADS] [CrossRef] (In the text)
- Motte, F.,
André, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] (In the text)
- Motte, F., André,
P., Ward-Thompson, D., & Bontemps, S. 2001, A&A, 372,
L41 [EDP Sciences] [NASA ADS]
- Nakajima, T.,
Oppenheimer, B. R., Kulkarni, S. R., et al. 1995, Nature, 378,
463 [NASA ADS] [CrossRef] (In the text)
- Oort, J. H., &
Spitzer, L. 1955, ApJ, 121, 6 [NASA ADS] [CrossRef] (In the text)
-
Oppenheimer, B. R., Kulkarni, S. R., Matthews, K., & Nakajima,
T. 1995, Science, 270, 1478 [NASA ADS] (In the text)
- Rebolo, R.,
Zapatero Osorio, M. R., & Martín, E. L. 1995, Nature, 377,
129 [NASA ADS] [CrossRef] (In the text)
- Reipurth, B.,
& Clarke, C. J. 2001, AJ, 122, 432 [NASA ADS] [CrossRef] (In the text)
- Richling, S.,
& Yorke, H. W. 1998, A&A, 340, 508 [NASA ADS] (In the text)
- Sandford, M. T.
II, Whitaker, R. W., & Klein, R. I. 1982, ApJ, 260, 183 [NASA ADS] [CrossRef] (In the text)
- Shu, F. H. 1977, ApJ,
214, 488 [NASA ADS] [CrossRef] (In the text)
- Testi, L., &
Sargent, A. I. 1998, ApJ, 508, L91 [NASA ADS] [CrossRef] (In the text)
-
Ward-Thompson, D., Motte, F., & André, P. 1999, MNRAS,
305, 143 [NASA ADS] [CrossRef] (In the text)
- Whitworth, A.
P., & Summers, D. 1985, MNRAS, 214, 1 [NASA ADS] (In the text)
- Wilking, B. A.,
Greene, T. P., & Meyer, M. R. 1999, AJ, 117, 469 [NASA ADS] [CrossRef] (In the text)
- Wilking, B. A.,
Mikhail, A., Carlson, G., Meyer, M. R., & Greene, T. P. 2002,
AJ, 127, 1131 [NASA ADS] (In the text)
-
Zapatero Osorio, M. R., Béjar, V. J. S., Martín, E. L.,
et al. 2000, Science, 290, 103 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2004
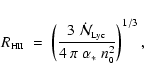
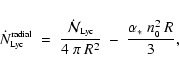
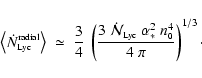
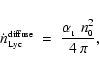
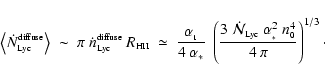
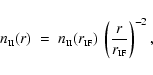
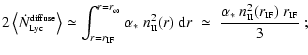
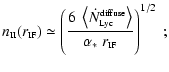
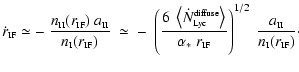
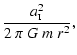
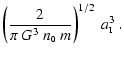
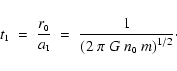
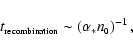
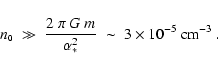
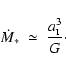
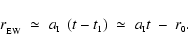
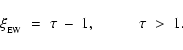
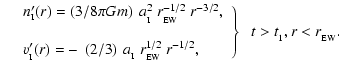
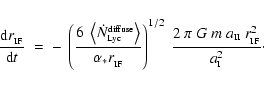
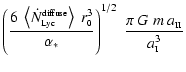
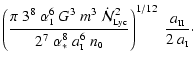
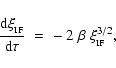
![\begin{displaymath}
\xi_{_{\mbox{\tiny IF}}} \;=\; \left[ 1~+~\beta \tau \right]^{-2} .
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img81.gif)
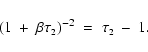
![\begin{displaymath}
\left[ (1+\beta) ~+~ \beta \xi_{\mbox{\tiny 2}} \right]^2~
\xi_{\mbox{\tiny 2}} \;=\; 1 ,
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img97.gif)
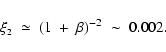
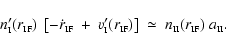
![\begin{displaymath}
\dot{\xi}_{\mbox{\tiny IF}} \;=\; -~\frac{2~(\tau - 1)^{1/2}...
...{\tiny IF}}^{-1/2} ~+~ 4~\beta~\xi_{\mbox{\tiny IF}} \right] .
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img102.gif)
![\begin{displaymath}
(\tau - 1)^{3/2} \;=\; \xi_{\mbox{\tiny 2}}^{3/2} ~+~ \frac{...
...}}^{3/2}}
{1~+~ 4~\beta~\xi_{\mbox{\tiny IF}}^{3/2}} \right] ,
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img103.gif)
![\begin{displaymath}
\epsilon_{\mbox{\tiny KIN}} \;=\; \frac{1}{2}~\left[ \dot{r}...
...frac{a_{\mbox{\tiny II}}}{a_{\mbox{\tiny I}}}
\right]^2 \cdot
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img110.gif)
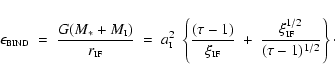
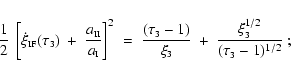
![\begin{displaymath}
\frac{M_{\mbox{\tiny 3}}}{M_{\mbox{\tiny0}}} \;=\; \frac{1}{...
...ox{\tiny 3}} - 1)^{-1/2}
\xi_{\mbox{\tiny 3}}^{3/2} \right] .
\end{displaymath}](/articles/aa/full/2004/43/aa1131/img119.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=14cm,clip]{1131fig1.eps}
\end{figure}](/articles/aa/full/2004/43/aa1131/Timg127.gif)