A&A 427, 179-192 (2004)
DOI: 10.1051/0004-6361:20035916
E. Habart1 - A. Natta1 - E. Krügel2
1 -
Osservatorio Astrofisico di Arcetri, INAF, Largo E. Fermi 5,
50125 Firenze, Italy
2 -
Max-Planck Instute fur Radioastronomie, Auf dem Hügel 69, Bonn, Germany
Received 19 December 2003 / Accepted 17 June 2004
Abstract
We investigate the presence and properties of PAHs on the surface of
circumstellar disks around Herbig Ae/Be stars by comparing the predictions of
disk models with observations. We present results of a radiation transfer code
for disks heated by the central star, in hydrostatic equilibrium in the vertical
direction (flared disks). The dust is a mixture of large grains in thermal
equilibrium, transiently heated small grains and PAHs. Special attention is
given to the influence of the stellar, disk and PAH properties on the strength
of the PAH emission lines and their spatial distribution. The models predict an
infrared SED showing PAH features at 3.3, 6.2, 7.7, and 11.3 ![]() m clearly visible
above the continuum, and with some of them very strong. The PAH emission,
spatially extended, comes mostly from the outer disk region (
m clearly visible
above the continuum, and with some of them very strong. The PAH emission,
spatially extended, comes mostly from the outer disk region (![]() AU)
while the continuum emission at similar wavelengths, mostly due to warm large
grains, is confined to the innermost disk regions (
AU)
while the continuum emission at similar wavelengths, mostly due to warm large
grains, is confined to the innermost disk regions (
![]() AU). We compare
the model results to infrared observations from ISO and ground-based telescopes
of some thirty Herbig Ae/Be stars. Most of the observed PAH features in objects
with spectral type later than B9 are well described by our disk models and we
discuss in some detail the PAH characteristics one can derive from the existing
data. Objects with strong radiation field (generally earlier than about B9) have the
3.3
AU). We compare
the model results to infrared observations from ISO and ground-based telescopes
of some thirty Herbig Ae/Be stars. Most of the observed PAH features in objects
with spectral type later than B9 are well described by our disk models and we
discuss in some detail the PAH characteristics one can derive from the existing
data. Objects with strong radiation field (generally earlier than about B9) have the
3.3 ![]() m feature (often the only one observed) much weaker than predicted, and we
discuss possible explanations (dissipation of the disk, photoevaporation or
modification of the PAH properties).
m feature (often the only one observed) much weaker than predicted, and we
discuss possible explanations (dissipation of the disk, photoevaporation or
modification of the PAH properties).
Key words: stars: circumstellar matter - stars: pre-main sequence - ISM: dust, extinction - radiative transfer - infrared: ISM - ISM: lines and bands
Features of PAHs (Polycyclic Aromatic Hydrocarbons) are detected in a number of pre-main-sequence stars of intermediate mass with circumstellar disks, with
characteristics that differ from those in the interstellar medium (see, e.g., Van Kerckhoven et al. 2002).
An origin of these features in the disk surface layers, which are directly exposed to the
ultraviolet (UV) stellar radiation, has been suggested by various authors (see, e.g., Meeus et al. 2001).
Recently, PAH emission has been resolved spatially in HD 100546,
HD 97048 (van Boekel et al. 2004) and WL 16 (Moore et al. 1998; Ressler & Barsony 2003), and shown to
have the size typical of circumstellar disk emission.
| Object | d | Sp. type |
|
Flared |
|
AIBs | Sil. | Cryst. | Ref. | ||
| [pc] | [K] | disk | [AU] | ||||||||
| AB Aur | 144 | B9/A0Ve | 9750 | 47 | 105 | 140 | - | (1) | |||
| HD 100 546 | 103 | B9Ve | 11 000 | 36 | 105 | 300(150b1) | (1) | ||||
| HD 142 527 | 200 | F7IIIe | 6250 | 31 |
|
(1) | |||||
| HD 179218 | 240 | B9e | 10 000 | 80 |
|
(<600b2) | (1) | ||||
| HD 100453 | 114 | A9Ve | 7500 | 9 |
|
- | - | (1) | |||
| HD 135344 | 84 | F4Ve | 6750 | 3 |
|
? | - | - | (1) | ||
| HD 139614 | 157 | A7Ve | 8000 | 12 | 104 | - | - | - | (1) | ||
| HD 169142 | 145 | A5Ve | 10 500 | 32 | 105 | 220 | - | - | (1) | ||
| HD 104237 | 116 | A4Ve | 10 500 | 40 | 105 | No | - | ? | (1) | ||
| HD 142666 | 116 | A8Ve | 8500 | 11 | 104 | No | (1) | ||||
| HD 144432 | 200 | A9Ve | 8000 | 32 |
|
No | - | ? | (1) | ||
| HD 150193 | 150 | A1Ve | 10 000 | 40 | 105 | No | - | (1) | |||
| HD 163296 | 122 | A3Ve | 10 500 | 30 | 105 | No | 360 | - | (1) | ||
| HD 97048 | 180 | B9-A0 | 10 000 | 31 | 105 | (300b1-900b2) | - | - | (2) | ||
| Elias 1 | 150 | A0-A6 | 8000 | 21 |
|
70 (<200b3) | ?d | (2) | |||
| Lk H |
800 | A0 | 9800 | 9 |
|
(<1200) | (3) | ||||
| HK Ori | 460 | A5 | 8300 | 12 | 104 | (70) | - | (3) | |||
| HD 245185 | 400 | A2 | 9100 | 17 |
|
(110) | (3) | ||||
| Lk H |
600 | A5 | 8300 | 6 |
|
(900) | - | (3) | |||
| BD+61 |
650 | B8 | 11 200 | 330 | 106 | (900) | - | (3) | |||
| T Ori | 460 | B9 | 10 700 | 83 |
|
(88) | - | - | (3) | ||
| V380 Ori | 460 | B9 | 10 700 | 85 |
|
(150) | - | (3) | |||
| HD 250550 | 700 | B7 | 12 300 | 240 | 106 | (410) | - | - | (3) | ||
| Lk H |
1000 | B7 | 12 300 | 210 | 106 | (1600) | - | (3) | |||
| VV Ser | 440 | B9 | 10 700 | 100 |
|
(410) | - | - | (3) | ||
| WW Vul | 700 | A3 | 8700 | 20 |
|
(88) | - | (3) | |||
| BD+46 |
1000 | A0 | 9800 | 508 | 106 | (190) | - | (3) | |||
| Lk H |
880 | A5 | 8300 | 30 |
|
(320) | - | (3) | |||
| WL 16 | 125 | B8-A7 | 9000 | 240 |
|
(450) | - | - | (4) |
|
a Far-ultraviolet (FUV, 6 b In parenthese we give estimate of the PAH emission extension. References: (b1) van Boekel et al. (2004); (b2) Siebenmorgen et al. (2000); (b3) Brooke et al. (1993). c Possible blend with the PAH 11.2(3) d Hanner et al. (1994). References: (1) Meeus et al. (2001) and references therein; (2) Van Kerckhoven et al. (2002) and references therein; (3) for astrophysical parameters Hillenbrand et al. (1992) (except for BD+46 |
| Object | 3.3 | 6.2 | "7.7'' | 8.6 | 11.2(3) | 12.7 | 16.4 | Ref. |
|
|
|
|
|
|
|
|
||
| AB Aur | <1a | 4.4(0.3) | 4.2(0.6) | 2(0.2) | 2(0.6) | - | - | (1) |
| HD 100546 | 2.5(0.5) | 14.3(0.4) | 19.2(0.8) | 4.6(0.5) | -b | - | - | (1) |
| HD 142527 | 1(0.6) | <1.5 | - | - | <0.5 | - | - | (1) |
| HD 179218 | 1.7(0.2) | 8.1(0.4) | 14.4(0.6) | 1.6(0.4) | - | - | - | (1) |
| HD 100453 | 1.3(0.2) | 2.6(0.5) | - | - | 1.2(0.3) | - | - | (1) |
| HD 135344 | <0.5 | <1.5 | ? | - | <1 | - | - | (2) |
| HD 139614 | <0.5 | <1.5 | - | - | <0.5 | - | - | (2) |
| HD 169142 | 1(0.2) | 2.8(0.3) | - | - | 2.3(0.5) | - | - | (1) |
| HD 104237 | <0.5 | <1.5 | - | - | - | - | - | (2) |
| HD 142666 | 0.3(0.2) | 2.6(0.3) | - | - | - | - | - | (1) |
| HD 144432 | <0.5 | <1.5 | - | - | - | - | - | (2) |
| HD 150193 | <0.08a | <1.5 | - | - | - | - | - | (2) |
| HD 163296 | <0.2a | <1.5 | - | - | - | - | - | (2) |
| HD 97048 | 1.3(0.3) | 6.9(0.8) | 11.8(1.3) | 2.4(0.6) | 3.4(0.4) | 1(0.2) | - | (2) |
| Elias 1 | 0.5c(0.1) | 6.1(0.6) | 9.4(0.1) | 2.3(0.1) | -d | - | - | (2) |
|
Lk H |
0.076(0.006) | (3) | ||||||
| HK Ori | 0.087(0.045) | (3) | ||||||
| HD 245185 | 0.035(0.018) | (3) | ||||||
| Lk H |
<0.15 | (3) | ||||||
| BD+61 |
<0.09 | (3) | ||||||
| T Ori | <0.15 | (3) | ||||||
| V380 Ori | <0.1 | (3) | ||||||
| HD 250550 | <0.12 | (3) | ||||||
| Lk H |
<0.03 | (3) | ||||||
| VV Ser | <0.05 | (3) | ||||||
| WW Vul | <0.09 | (3) | ||||||
| BD+46 |
<0.1 | (3) | ||||||
| Lk H |
<0.04 | (3) | ||||||
| WL 16 | 0.17(0.03) | 5(0.4) | (4) |
|
Integrated fluxes (after continuum substraction) and uncertainty (in between brackets) are in units of 10-14 W/m2.
For non-detections, we give for the 3.3, 6.2 and 11.3 a From Brooke et al. (1993). b In the spectrum of HD 100546 a 11.2(3) c Measured in ground-based spectrum (Geballe 1997). d Hanner et al. (1994) report the presence of an 11.2 References: (1) Van Kerckhoven et al. (2002); (2) Meeus et al. (2001); (3) Brooke et al. (1993); (4) From the spectrum of Tokunaga et al. (1991) and Hanner et al. (1992) for the 3.3 and 11.3 |
The presence of PAHs on disk surfaces is interesting for a number of reasons. First of all, as we will see in the following, PAHs are good tracers of the presence of very small particles mixed with the gas at large altitudes above the disk midplane, both near the star and in the very outer disk. Their emission can tell us if and where very small particles survive settling and coagulation processes that cause the majority of the original grain population to grow to very large sizes in the same objects (see, e.g., Natta & Testi 2003). A second point of interest is that the absence or presence of PAHs will have a significant impact on the physical properties of the gas and on the structure of the disk itself, since in photo-dissociation regions we believe that they contribute a large fraction of the gas heating (via the photoelectric effect, see, e.g., Habart et al. 2001; Weingartner & Draine 2001) and could dominate the H2 formation on dust surfaces (Habart et al. 2004).
The presence and properties of PAHs in circumstellar disks can be tested by comparing the observations with the predictions of disk models, which have been shown to reproduce well the global spectral energy distribution (SED) of the same stars (Dominik et al. 2003; Dullemond et al. 2001). We are interested in particular to check if the disk models can account for the observed intensity of the various features and their spatial distribution, when known. To the best of our knowledge, there are no such models available for disks around pre-main-sequence stars. These disks are optically thick to the stellar radiation and thus require a proper treatement of the radiation transfer. Recent models of the SED of HD 141569A (a young B9.5 star with a complex debris disk) by Li & Lunine (2003), which include PAHs, assume an optically thin disk, as appropriate for that particular object.
The paper is organized as follows. Section 2 provides a summary of the available observations of PAHs in intermediate-mass stars. The disk models and the radiation transfer scheme we use are described in Sects. 3.1 and 3.2. The dust on the disk surface is a mixture of large grains, which reach equilibrium with the stellar radiation field, very small grains, and PAHs, which are transiently heated by the UV stellar radiation. The details of the adopted dust model are given in Sect. 3.3. The results of the calculations are described in Sect. 4, which also explores the effect of varying the stellar, disk and PAHs properties. In Sect. 5 we compare the model results to the observations. Sect. 6 summarizes our main results.
From ground-based and airborne observations (Schutte et al. 1990; Brooke et al. 1993),
it is known that aromatic infrared emission bands (AIBs in the following)
attributed to PAHs exist in the spectra of some Herbig Ae/Be stars (hereafter HAeBe).
About 20% of the HAeBe stars surveyed to date have a firmly detected 3.3 ![]() m
feature (Brooke et al. 1993).
m
feature (Brooke et al. 1993).
In Table 1, we report for an ISO sample of HAeBe stars with
circumstellar disks (i) the astrophysical parameters of each star (distance,
spectral type, effective temperature, luminosity, and ![]() ,
i.e., FUV flux at 150 AU from the
star), (ii) the observational characteristics of the disk (evidence for a flared
disk and disk outer radius) and (iii) the dust spectral characteristics
(presence of AIBs, silicate bands and crystalline signatures). We also give, when available, estimates of the extension
of the PAH emission. The strengths of the PAH emission features at 3.3,
6.2, 7.7, 8.6, 11.2(3), 12.7 and 16.4
,
i.e., FUV flux at 150 AU from the
star), (ii) the observational characteristics of the disk (evidence for a flared
disk and disk outer radius) and (iii) the dust spectral characteristics
(presence of AIBs, silicate bands and crystalline signatures). We also give, when available, estimates of the extension
of the PAH emission. The strengths of the PAH emission features at 3.3,
6.2, 7.7, 8.6, 11.2(3), 12.7 and 16.4 ![]() m (where most commonly observed PAH
features occur) are given in Table 2. Most of these sources are
isolated HAeBe stars, with the exception of two objects, HD 97048 and
Elias 1, which are still embedded in a reflection nebula. These sources are
intermediate between embedded and isolated HAeBe stars. In Tables 1 and 2 we also report the characteristics of the
HAeBe stars observed at 3
m (where most commonly observed PAH
features occur) are given in Table 2. Most of these sources are
isolated HAeBe stars, with the exception of two objects, HD 97048 and
Elias 1, which are still embedded in a reflection nebula. These sources are
intermediate between embedded and isolated HAeBe stars. In Tables 1 and 2 we also report the characteristics of the
HAeBe stars observed at 3 ![]() m by Brooke et al. (1993) and of the young stellar
object WL 16 embedded in the
m by Brooke et al. (1993) and of the young stellar
object WL 16 embedded in the ![]() Ophiuchi cloud core (for a recent paper see Ressler & Barsony 2003).
Ophiuchi cloud core (for a recent paper see Ressler & Barsony 2003).
In the ISO sample of isolated HAeBe stars we can distinguish three different groups (Meeus et al. 2001): the first (group Ia) is made of stars with evidence of a flared disk and strong or moderately aromatic and silicate bands (with or without crystalline signatures); the second (group Ib) is also characterised by flared disks and the presence of AIBs, but the silicate bands are absent; finally, in the third group (group II) there is no evidence of a flared disk, there are weak or no AIBs, but the silicate emission features are strong (with various amounts of crystalline silicates). The presence of AIBs is not correlated with any of the stellar parameters. There is, on the other hand, an indication that PAH features are strong when disks are flared, since they are present in group I objects (both Ia and Ib) and only (and rather weakly) in one source of group II. This suggests that PAH emission originates in the outer regions of flared disks, where dust intercepts a large fraction of the UV emission coming from the star.
That in isolated HAeBe stars PAHs must be closely related to the star-disk
system is supported by the observations of HD 100546 and HD 179128 (both group
Ia) showing that the PAH emission occurs within ![]() 150 AU
(van Boekel et al. 2004; Grady et al. 2001) and
150 AU
(van Boekel et al. 2004; Grady et al. 2001) and ![]() 600 AU (Siebenmorgen et al. 2000) from the
star, respectively. Moreover, van Boekel et al. (2004) find that HD 104237 (group II) is
unresolved in their 10
600 AU (Siebenmorgen et al. 2000) from the
star, respectively. Moreover, van Boekel et al. (2004) find that HD 104237 (group II) is
unresolved in their 10 ![]() m spectroscopic observations using TIMMI2 at the ESO 3.6-m telescope with a spatial resolution of
m spectroscopic observations using TIMMI2 at the ESO 3.6-m telescope with a spatial resolution of ![]() 0.9
0.9
![]() .
This is consistent
with the idea that group II sources do not possess a flared outer disk. As far
as we know, no spatial information on the PAH emission is available for the
other isolated HAeBe stars but their isolated nature suggests that also in these
objects the PAH emission comes from the immediate circumstellar environment. On
the other hand, for the two intermediate sources, HD 97048 and Elias 1, the PAH
emission probably originates in a significant part from the illuminated
reflection nebula. HD 97048 observations show that the PAH emission extends
up to
.
This is consistent
with the idea that group II sources do not possess a flared outer disk. As far
as we know, no spatial information on the PAH emission is available for the
other isolated HAeBe stars but their isolated nature suggests that also in these
objects the PAH emission comes from the immediate circumstellar environment. On
the other hand, for the two intermediate sources, HD 97048 and Elias 1, the PAH
emission probably originates in a significant part from the illuminated
reflection nebula. HD 97048 observations show that the PAH emission extends
up to ![]() 1000 AU (Siebenmorgen et al. 2000). However, recent high spatial
resolution observations show that most of the emission of the 8.6, 11.3 and 12.7
1000 AU (Siebenmorgen et al. 2000). However, recent high spatial
resolution observations show that most of the emission of the 8.6, 11.3 and 12.7 ![]() m features comes in fact from a region of 200-300 AU, likely a disk
(van Boekel et al. 2004).
Additional evidence of the PAH emission disk origin in HAeBe stars comes from
recent (sub)arcsec-resolution mid-IR images of WL 16 by
Moore et al. (1998); Ressler & Barsony (2003), showing that the PAH emission has a size of
m features comes in fact from a region of 200-300 AU, likely a disk
(van Boekel et al. 2004).
Additional evidence of the PAH emission disk origin in HAeBe stars comes from
recent (sub)arcsec-resolution mid-IR images of WL 16 by
Moore et al. (1998); Ressler & Barsony (2003), showing that the PAH emission has a size of
![]() 450 AU. Finally, note that for the HAeBe stars observed from the ground
at 3
450 AU. Finally, note that for the HAeBe stars observed from the ground
at 3 ![]() m, Brooke et al. (1993) find that the aromatic features tend to be confined
to
m, Brooke et al. (1993) find that the aromatic features tend to be confined
to ![]() 1000 AU.
1000 AU.
It is also interesting that in HD 97048 and WL 16 the 10 ![]() m continuum
emission is spatially extended on scales comparable to those of the PAH emission
(Moore et al. 1998; van Boekel et al. 2004; Ressler & Barsony 2003). Together with the absence of
the spectral signature of silicate grains in both these sources (see references
in Table 1), this indicates that very small carbonaceous grains
are responsible for the continuum emission. Quite differently, the continuum
emission in HD 100546 arises from a much smaller (<30 AU) region than the
PAH emission (van Boekel et al. 2004). In this object, where silicate bands are present,
the continuum may be dominated by warm large silicates grains confined to the
innermost regions of the disk.
m continuum
emission is spatially extended on scales comparable to those of the PAH emission
(Moore et al. 1998; van Boekel et al. 2004; Ressler & Barsony 2003). Together with the absence of
the spectral signature of silicate grains in both these sources (see references
in Table 1), this indicates that very small carbonaceous grains
are responsible for the continuum emission. Quite differently, the continuum
emission in HD 100546 arises from a much smaller (<30 AU) region than the
PAH emission (van Boekel et al. 2004). In this object, where silicate bands are present,
the continuum may be dominated by warm large silicates grains confined to the
innermost regions of the disk.
Evidence of a disk origin of the PAH emission in HAeBe stars comes
also from the extensive study of the ISO spectra of a sample of embedded young
stellar objects, isolated HAeBe stars, evolved stars, reflection nebulae and HII
regions, which reveals the presence of variations in the profiles and peak
positions of the main bands from source to source
(Peeters et al. 2002; Hony et al. 2001; Van Kerckhoven et al. 2002). The largest variation is seen
in the 6-9 ![]() m region with systematic differences
between sources that have recently synthesized their PAHs in their ejecta
and sources that are illuminating general interstellar medium materials (Peeters et al. 2002).
The combined effect of PAH family and anharmonicity (dependence of the peak position on the temperature of the emitters) could be at the origin of these
variations. The 6.2 and 7.7
m region with systematic differences
between sources that have recently synthesized their PAHs in their ejecta
and sources that are illuminating general interstellar medium materials (Peeters et al. 2002).
The combined effect of PAH family and anharmonicity (dependence of the peak position on the temperature of the emitters) could be at the origin of these
variations. The 6.2 and 7.7 ![]() m features in isolated
HAeBe stars which resemble those in evolved stars are very different from those in sources with ISM material.
Moreover, large variations are observed in the ratio of the band strengths in
the 10-15
m features in isolated
HAeBe stars which resemble those in evolved stars are very different from those in sources with ISM material.
Moreover, large variations are observed in the ratio of the band strengths in
the 10-15 ![]() m region, especially in the 11.2/12.7
m region, especially in the 11.2/12.7 ![]() m ratio
(Hony et al. 2001). Together with the good correlation found between the 11.2 and
3.3
m ratio
(Hony et al. 2001). Together with the good correlation found between the 11.2 and
3.3 ![]() m band and between the 12.7 and 6.2
m band and between the 12.7 and 6.2 ![]() m band, Hony et al. (2001) suggest
that the spectra of HII regions where the 11.2 and 12.7
m band, Hony et al. (2001) suggest
that the spectra of HII regions where the 11.2 and 12.7 ![]() m are typically
equally strong are due to small or irregular (and preferentially ionized) PAHs.
On the other hand, the spectra of evolved stars with a small 12.7/11.2
m are typically
equally strong are due to small or irregular (and preferentially ionized) PAHs.
On the other hand, the spectra of evolved stars with a small 12.7/11.2 ![]() m
ratio may arise from large (
m
ratio may arise from large (![]() 100-150 C-atom) compact (and preferentially
neutral) PAHs. The 12.7
100-150 C-atom) compact (and preferentially
neutral) PAHs. The 12.7 ![]() m band cannot be seen in the low resolution spectra
of isolated HAeBe stars and the 12.7/11.2
m band cannot be seen in the low resolution spectra
of isolated HAeBe stars and the 12.7/11.2 ![]() m ratio is not known. But recent
ground-based observations (see reference in Van Kerckhoven et al. 2002)
confirm that, if present, the 12.7
m ratio is not known. But recent
ground-based observations (see reference in Van Kerckhoven et al. 2002)
confirm that, if present, the 12.7 ![]() m band must be very weak compared to the
11.2
m band must be very weak compared to the
11.2 ![]() m band. This indicates that the PAHs are larger and less ionized in
isolated HAeBe sources.
m band. This indicates that the PAHs are larger and less ionized in
isolated HAeBe sources.
In summary, there are indications that PAHs in HAeBe stars are somewhat different from those in the ISM, and more similar to PAHs in evolved stars. However, it is difficult to fully characterize the PAH properties in HAeBe stars from what is known at present, and in the following we will start our analysis from the assumption that PAHs in the ISM represent a good first approximation to the properties of PAHs in disks as well. We will then discuss possible differences, and come back to this point in our conclusions.
In this section, we describe the disk models and the radiation transfer used and give the details of the adopted dust model.
We consider disks heated by irradiation from the central star, in hydrostatic
equilibrium in the vertical direction, with gas and dust well mixed (flared
disks). We compute the disk structure using an improved version of the
Chiang & Goldreich (1997) two-layer models, described in Dullemond et al. (2001). For a
given star, the disk structure (i.e., pressure scale height ![]() and flaring
angle
and flaring
angle ![]() )
is completely defined once the inner and outer radii (
)
is completely defined once the inner and outer radii (
![]() and
and
![]() ), the surface density distribution
), the surface density distribution
![]() with R0a fiducial radius, and the dust model are specified.
with R0a fiducial radius, and the dust model are specified.
In these models, the stellar flux impinging with flaring
angle ![]() upon the disk
is absorbed in the upper layers of the disk, which will reradiate half of
the flux away from the disk and half down into its deeper layers.
Here, we compute the structure of the disk self-consistently using
an iterative scheme that gives the flaring angle
upon the disk
is absorbed in the upper layers of the disk, which will reradiate half of
the flux away from the disk and half down into its deeper layers.
Here, we compute the structure of the disk self-consistently using
an iterative scheme that gives the flaring angle ![]() and the midplane
temperature at each radius. The radiation transfer is solved in an effective,
simplified way, which, however, gives a disk structure very similar to that
obtained with a full, much more time consuming radiation transfer treatment
(Dullemond & Natta 2003).
and the midplane
temperature at each radius. The radiation transfer is solved in an effective,
simplified way, which, however, gives a disk structure very similar to that
obtained with a full, much more time consuming radiation transfer treatment
(Dullemond & Natta 2003).
The models are appropriate for disks that are optically thick to the stellar
radiation. This is generally the case for disks around pre-main-sequence stars,
up to very large radii (e.g., 5000 AU for a disk mass ![]()
![]() 0.2
0.2 ![]() ,
p=1).
,
p=1).
In spite of the success of the two-layer codes in predicting the disk structure and the overall SED, they tend to overestimate the disk emission in the near-infrared (Dullemond & Natta 2003). We have therefore decided to implement a full 1D radiation transfer scheme to compute more accurately the emission in the wavelength range where the PAH features occur. In practice, we first compute the disk structure using our two-layer code, with the adopted dust model (which includes transiently heated species), then, the disk structure fixed, we compute the emerging spectrum using the radiation transfer code. This procedure is not fully self-consistent, but we have checked that it does not introduce any significant inaccuracy in our results.
Dust scattering is incorporated. Scattering of stellar light may be relevant
because it can lead to a substantial reduction of the flux available for heating
the disk and because it allows stellar photons, after one scattering event, to
penetrate much deeper into the disk than one would expect given the smallness of
the flaring angle ![]() .
.
To calculate the emission of transiently heated small grains and of PAHs, we
compute the temperature distribution functions
![]() as in
Siebenmorgen et al. (1992) following the method outlined by Guhathakurta & Draine (1989).
as in
Siebenmorgen et al. (1992) following the method outlined by Guhathakurta & Draine (1989).
To determine the emission from the disk, we divide it into rings of radius rand small radial width ![]() .
At the center, at r=0, sits the star with
parameters
.
At the center, at r=0, sits the star with
parameters ![]() ,
,
![]() ,
,
![]() and
and
![]() .
For each ring we compute, as
described in the appendix, the radiative transfer perpendicular to the disk, in the
z-direction, and then add up the contributions from all rings.
.
For each ring we compute, as
described in the appendix, the radiative transfer perpendicular to the disk, in the
z-direction, and then add up the contributions from all rings.
The properties of dust in circumstellar disks differ significantly from those in
the ISM (see Sect. 2), and from star to star. It is difficult to
build a general, realistic dust model. However, this is not the purpose of this
study, where we only want to test the hypothesis that the observed PAH features
have their origin in the surface layers of circumstellar disks. Therefore, we
will start with a dust model that includes large grains (i.e., grains large
enough to be in thermal equilibrium with the local radiation field) with
properties that roughly account for the observed SEDs (including the silicate
emission at 10 ![]() m) of most pre-main-sequence stars.
To these, we will add very small particles and PAHs, with abundances and properties
typical of the ISM, which we will then vary.
m) of most pre-main-sequence stars.
To these, we will add very small particles and PAHs, with abundances and properties
typical of the ISM, which we will then vary.
a) Large grains. The large or big grains (BGs
in the following) consist of graphite and silicates with optical constants from
Draine (1985). These grains have an MRN size distribution (
![]() )
between a minimum and a maximum radius al=0.01
)
between a minimum and a maximum radius al=0.01 ![]() m and
au=0.74
m and
au=0.74 ![]() m for silicates and al=0.01
m for silicates and al=0.01 ![]() m and au=0.36
m and au=0.36 ![]() m for
graphite.
We assume that
all silicon and about 2/3 of the cosmic carbon
m for
graphite.
We assume that
all silicon and about 2/3 of the cosmic carbon![]() (
(
![]() )
are in these grains. This prescription gives a
good fit to the mid-IR SED (which originates from the disk surface) of many HAe
stars (Natta et al. 2001); we have found in our modeling that the details are not
very important for the purpose of this paper.
)
are in these grains. This prescription gives a
good fit to the mid-IR SED (which originates from the disk surface) of many HAe
stars (Natta et al. 2001); we have found in our modeling that the details are not
very important for the purpose of this paper.
b) Very small grains. To the BGs population of
grains, we add a tail of very small graphite particles (VSGs in the following)
with the same size distribution
![]() between al= 10 Å to
au= 100 Å. Optical constants are from Draine (1985). The fraction of
carbon in VSGs is 15% of that in BGs (
between al= 10 Å to
au= 100 Å. Optical constants are from Draine (1985). The fraction of
carbon in VSGs is 15% of that in BGs (
![]() ). VSGs
and BGs graphite grains probably form a continous population. The division
between BGs and VSGs is maintained mainly for computational purposes. Note that
there is no evidence in the ISM of very small silicates (Li & Draine 2001b).
). VSGs
and BGs graphite grains probably form a continous population. The division
between BGs and VSGs is maintained mainly for computational purposes. Note that
there is no evidence in the ISM of very small silicates (Li & Draine 2001b).
c) PAHs. Finally, we include in our dust model
a population of PAHs. In the ISM, PAHs are made up of a few tens up to a few
hundreds of carbon atoms; for reasons of simplicity, we start our models with one
PAH size,
![]() .
The hydrogen to carbon ratio is
.
The hydrogen to carbon ratio is
![]() (case of compact symmetric PAHs, see Omont 1986)
with
(case of compact symmetric PAHs, see Omont 1986)
with ![]() the hydrogenation fraction of the molecule.
We start our models assuming essentially fully
hydrogenated PAHs, i.e,
the hydrogenation fraction of the molecule.
We start our models assuming essentially fully
hydrogenated PAHs, i.e,
![]() .
The carbon locked up in PAHs has an abundance of
.
The carbon locked up in PAHs has an abundance of
![]() inferred from the 12
inferred from the 12 ![]() m emission per hydrogen atom in typical Galactic
cirrus (Boulanger & Perault 1988) and photo-dissociation regions (Habart et al. 2001)
and from comparison between observations of dust galactic emission and
extinction with detailed model calculations (Dwek et al. 1997; Li & Draine 2001a; Désert et al. 1990).
We take the absorption cross section as defined by Li & Draine (2001a) based both on
laboratory data and astrophysical spectra. They consider the bands at 3.3, 8.6,
11.3, 11.9 and 12.7
m emission per hydrogen atom in typical Galactic
cirrus (Boulanger & Perault 1988) and photo-dissociation regions (Habart et al. 2001)
and from comparison between observations of dust galactic emission and
extinction with detailed model calculations (Dwek et al. 1997; Li & Draine 2001a; Désert et al. 1990).
We take the absorption cross section as defined by Li & Draine (2001a) based both on
laboratory data and astrophysical spectra. They consider the bands at 3.3, 8.6,
11.3, 11.9 and 12.7 ![]() m from vibrational modes of the aromatic C-H bond; the
strong bands at 6.2 and 7.7
m from vibrational modes of the aromatic C-H bond; the
strong bands at 6.2 and 7.7 ![]() m due to vibrations of the aromatic C-C bonds;
and a few weak features probably caused by C-C bending modes at 16.4, 18.3, 21.2
and 23.1
m due to vibrations of the aromatic C-C bonds;
and a few weak features probably caused by C-C bending modes at 16.4, 18.3, 21.2
and 23.1 ![]() m. The band profiles have a Drude shape; the integrated cross
sections band profiles, positions and widths of the lines are found in their
Table 1
m. The band profiles have a Drude shape; the integrated cross
sections band profiles, positions and widths of the lines are found in their
Table 1![]() . The cross
section in the visible UV is determined from the laboratory absorption spectrum
of small species with a cut-off in the visible to near-IR whose wavelength
increases with
. The cross
section in the visible UV is determined from the laboratory absorption spectrum
of small species with a cut-off in the visible to near-IR whose wavelength
increases with ![]() ,
as defined by Désert et al. (1990).
,
as defined by Désert et al. (1990).
With respect to the charge, we start assuming that PAHs are mostly neutral.
Ideally, one can calculate the steady state charge distribution of PAHs from the
balance between electron capture rates and the photoelectron emission rates plus
the ion capture rates (see, e.g., Weingartner & Draine 2001). Since little is known
regarding the electron density ![]() and its distribution in the surface layers
of disks, precise determination of the PAH charge distribution in disks is not
possible. Instead, we can estimate the ratio between the photoionisation rate
of the grain to the electron-grain recombination rate,
and its distribution in the surface layers
of disks, precise determination of the PAH charge distribution in disks is not
possible. Instead, we can estimate the ratio between the photoionisation rate
of the grain to the electron-grain recombination rate, ![]() ,
which can be
approximated by
,
which can be
approximated by
![]() with
with
![]() a function giving the dependence of the
photo-electron ejection probability with the size (see Bakes & Tielens 1994). For a
disk heated by a typical HAe star, we have
a function giving the dependence of the
photo-electron ejection probability with the size (see Bakes & Tielens 1994). For a
disk heated by a typical HAe star, we have
![]() and
and
![]() cm-3 on the surface disk layer at 150 AU from the star (see next section).
Thus, assuming
cm-3 on the surface disk layer at 150 AU from the star (see next section).
Thus, assuming
![]() (as in typical photo-dissociation regions of the ISM)
and
(as in typical photo-dissociation regions of the ISM)
and
![]() K, we find
K, we find
![]() and
for a PAH with
and
for a PAH with
![]() we estimate
we estimate![]() that
that ![]() is less than 1.
This implies that PAHs must be neutral or negatively charged in the outer disk regions.
In the inner disk region and for stars with higher
is less than 1.
This implies that PAHs must be neutral or negatively charged in the outer disk regions.
In the inner disk region and for stars with higher ![]() ,
however,
,
however, ![]() becomes higher and PAHs will be in part positively charged. To keep the model
simple, we neglect that we probably have a mixture of neutral and charged PAHs
in disks and we assume that PAHs are neutral. The effect of charge is briefly
discussed in Sect. 4.2.1.
becomes higher and PAHs will be in part positively charged. To keep the model
simple, we neglect that we probably have a mixture of neutral and charged PAHs
in disks and we assume that PAHs are neutral. The effect of charge is briefly
discussed in Sect. 4.2.1.
Upon absorption of an energetic photon, small PAHs, with an insufficient number
of internal vibrational modes in which to distribute this photon energy, may
dissociate. In a strong FUV radiation field (
![]() ), destruction occurs
during multiphoton events where PAHs absorb an energy of more than 21 eV in a
time shorter than the cooling time (Guhathakurta & Draine 1989; Siebenmorgen 1993).
Recently, Li & Lunine (2003) estimated the photodestruction rate for the HD 141569A
disk
and suggest that PAHs with
), destruction occurs
during multiphoton events where PAHs absorb an energy of more than 21 eV in a
time shorter than the cooling time (Guhathakurta & Draine 1989; Siebenmorgen 1993).
Recently, Li & Lunine (2003) estimated the photodestruction rate for the HD 141569A
disk
and suggest that PAHs with
![]() will be photolytically unstable in
the inner R<100 AU region around the star (where
will be photolytically unstable in
the inner R<100 AU region around the star (where
![]() )
during the
life time of the disk.
For a PAH with
)
during the
life time of the disk.
For a PAH with
![]() ,
the maximum temperature reached just after the
deposit of an energy of 21 eV is about 2000 K (see, e.g., Omont 1986). In
our model, we assume that PAHs are destroyed when the probability that they are
at a temperature
,
the maximum temperature reached just after the
deposit of an energy of 21 eV is about 2000 K (see, e.g., Omont 1986). In
our model, we assume that PAHs are destroyed when the probability that they are
at a temperature
![]() exceeds a critical value
exceeds a critical value
![]() ,
i.e., when
,
i.e., when
![]() .
This procedure is numerically
simple and can probably correctly evaluate evaporation. However, we do not
derive
.
This procedure is numerically
simple and can probably correctly evaluate evaporation. However, we do not
derive
![]() from thermodynamical considerations. We used
from thermodynamical considerations. We used
![]() K
and
K
and
![]() and checked that for this choice, in the case of small
PAHs, the results are similar to the assumption that the grains are
photo-destructed if they absorb an energy of more than 21 eV in a time interval
shorter than the cooling time.
and checked that for this choice, in the case of small
PAHs, the results are similar to the assumption that the grains are
photo-destructed if they absorb an energy of more than 21 eV in a time interval
shorter than the cooling time.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0916.f1.ps}
\end{figure}](/articles/aa/full/2004/43/aa0916/Timg79.gif) |
Figure 1: Absorption coefficient (in cm2 per gram of gas) of large grains (BGs; dotted line), very small grains (VSGs; dashed line) and PAHs of 100 C atoms (solid line). See text for details. |
In summary, we adopt a dust model with BGs, VSGs and PAHs. The
silicate abundance in dust is
![]() ,
and the total carbon
abundance in dust is
,
and the total carbon
abundance in dust is
![]() .
Of this, 23% is in PAHs, 10% in
VSGs and 67% in large grains. Figure 1 shows the adopted
absorption coefficient for the various species. For a radiation field that has a
blackbody distribution at T=104 K, BGs will absorb 50% of the radiation, VSG 11% and PAHs 39%, respectively. The properties of BGs are somewhat different
from those of grains in the ISM, and have been chosen to approximately fit the
properties of dust on disk surfaces. VSGs and PAHs have properties derived from
the ISM. In the following, however, we will explore the effects on the predicted
spectra of some of our assumptions for the PAHs properties. Note, however, that
we will not try to reproduce the peculiarities of the features observed in some
isolated HAe stars, such as the shift of the peak positions, but we will limit
our discussion to the band strengths.
.
Of this, 23% is in PAHs, 10% in
VSGs and 67% in large grains. Figure 1 shows the adopted
absorption coefficient for the various species. For a radiation field that has a
blackbody distribution at T=104 K, BGs will absorb 50% of the radiation, VSG 11% and PAHs 39%, respectively. The properties of BGs are somewhat different
from those of grains in the ISM, and have been chosen to approximately fit the
properties of dust on disk surfaces. VSGs and PAHs have properties derived from
the ISM. In the following, however, we will explore the effects on the predicted
spectra of some of our assumptions for the PAHs properties. Note, however, that
we will not try to reproduce the peculiarities of the features observed in some
isolated HAe stars, such as the shift of the peak positions, but we will limit
our discussion to the band strengths.
In this section, we describe the results of the calculations and explore the effect of various stellar, disk and PAHs properties.
Firstly, we discuss the results for a model that we will use in the following as a template.
The disk is heated by a typical HAe star with effective temperature
![]() = 10 500 K, luminosity
= 10 500 K, luminosity ![]() = 32.0
= 32.0 ![]() and mass
and mass ![]() = 2.4
= 2.4 ![]() .
At a distance of 150 AU the FUV radiation field integrated between 912 and 2050 Å is
.
At a distance of 150 AU the FUV radiation field integrated between 912 and 2050 Å is ![]() times the average interstellar radiation field (
times the average interstellar radiation field (
![]() W m-2; Habing 1968).
W m-2; Habing 1968).
The disk mass is ![]() 0.1
0.1 ![]() .
Its inner radius is
.
Its inner radius is
![]() = 0.3 AU, close to
the BG evaporation radius, the outer radius is
= 0.3 AU, close to
the BG evaporation radius, the outer radius is ![]() = 300 AU. The surface density
profile is
= 300 AU. The surface density
profile is
![]() with
with
![]() g cm-2.
We assume that only half of the star is visible from any point on the disk
surface (
g cm-2.
We assume that only half of the star is visible from any point on the disk
surface (
![]() ). Figure 2 shows the run with radius of the
pressure (
). Figure 2 shows the run with radius of the
pressure (![]() )
and photospheric (
)
and photospheric (![]() )
scale height and of the flaring angle
)
scale height and of the flaring angle ![]() (bottom panel). In the top panel we show the temperature of silicates
and graphite grains of size a=0.01
(bottom panel). In the top panel we show the temperature of silicates
and graphite grains of size a=0.01 ![]() m at
m at ![]() .
The gas density at
.
The gas density at ![]() decreases from
decreases from
![]() cm-3 at
cm-3 at
![]() to
to
![]() cm-3 at
cm-3 at ![]() .
.
Each side of the disk intercepts and reprocesses about 10% of the stellar luminosity. The fractional contribution to the reprocessed radiation of BGs, VSGs and PAHs is, respectively, 60%, 13% and 27%. Note that the fraction emitted by PAHs is lower than the fraction of the stellar radiation they absorb (about 39%, see preceding section) because of their evaporation in the inner part of the disk. About 10% of the total absorbed flux is lost in PAH evaporation.
Figure 3 shows the calculated spectrum in the 2-40 ![]() m range of
a star/disk system seen face-on at a distance of 150 pc.
PAH features, which form in the optically thin disk surface, are clearly visible, and
some of them are very strong; in Table 3, we give the integrated
flux in the 3.3, 6.2, 7.7, 8.6, 11.3, 12.7 and 16.2
m range of
a star/disk system seen face-on at a distance of 150 pc.
PAH features, which form in the optically thin disk surface, are clearly visible, and
some of them are very strong; in Table 3, we give the integrated
flux in the 3.3, 6.2, 7.7, 8.6, 11.3, 12.7 and 16.2 ![]() m features after
continuum subtraction.
m features after
continuum subtraction.
The continuum is mostly due to the large grains which are very hot in the inner
regions (see Fig. 2). It is possible to see, for example, the broad
feature due to silicate emission peaking at about 10 ![]() m under the much
narrower PAH features. Some contribution to the continuum in the wavelength
range
m under the much
narrower PAH features. Some contribution to the continuum in the wavelength
range
![]()
![]() m is also due to the VSG, as shown by the SED of a model
which has all the parameters of the template model but no VSGs nor PAHs (dashed
line in Fig. 3).
m is also due to the VSG, as shown by the SED of a model
which has all the parameters of the template model but no VSGs nor PAHs (dashed
line in Fig. 3).
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{0916.f3.ps}
\par\end{figure}](/articles/aa/full/2004/43/aa0916/Timg88.gif) |
Figure 3:
Spectral energy distribution of a star/disk system
(template model) seen face-on at a
distance of 150 pc. The solid line shows the emission of the disk, the
dotted line that of the stellar photosphere.
The dashed line shows the SED of a model which has all the
parameters of the template model but no VSGs and no PAHs. The stellar
parameters are
|
| Model | 3.3 | 6.2 | 7.7 | 8.6 | 11.3 | 12.7 | 16.4 |
|
|
|
|
|
|
|
|
|
| Template | 2.8 | 5.4 | 10.2 | 1.3 | 2.5 | 0.6 | 2.6 |
| Ionized | 0.1 | 7.5 | 18.2 | 2.25 | 0.9 | 0.13 | 0.8 |
|
|
1.4 | 5.9 | 11 | 1 | 1.5 | 0.3 | 2.6 |
|
|
5.3 | 2.5 | 4.1 | 1.1 | 10.8 | 2.8 | 1 |
|
|
0.3 | 6.1 | 12 | 3 | 3.9 | 0.9 | 0.4 |
The PAH emission is much more extended than the adjacent continuum, as shown by
two figures, Figs. 4 and 5.
Figure 4 plots as function of the projected radius the
cumulative intensity of the feature and continuum at 3.3, 6.2 and 11.3 ![]() m.
The continuum reaches 50% of its intensity at a very small radius
(typically 2-5 AU) while the feature does so at larger radii (about 30 AU for
the 3.3
m.
The continuum reaches 50% of its intensity at a very small radius
(typically 2-5 AU) while the feature does so at larger radii (about 30 AU for
the 3.3 ![]() m feature and 80 AU for the 6.2 and 11.3
m feature and 80 AU for the 6.2 and 11.3 ![]() m features). This
behaviour basically reflects the different excitation mechanism of PAHs, i.e.,
single-photon excitation, and of the continuum at the same wavelength, which is
dominated by the emission of BGs, in thermal equilibrium with the radiation
field. Only very hot BGs, located in the innermost disk, emit at 3
m features). This
behaviour basically reflects the different excitation mechanism of PAHs, i.e.,
single-photon excitation, and of the continuum at the same wavelength, which is
dominated by the emission of BGs, in thermal equilibrium with the radiation
field. Only very hot BGs, located in the innermost disk, emit at 3 ![]() m whereas
PAHs also emit at the outer edge of the disk in the 3.3
m whereas
PAHs also emit at the outer edge of the disk in the 3.3 ![]() m feature.
m feature.
The ratio of short wavelength over long wavelength band strength decreases with
the intensity of the FUV radiation also for transiently heated particles.
Figure 4 shows that the contribution of the outer disk to the
3.3 ![]() m feature is small, while it is much larger for the features at 6.2 and
11.3
m feature is small, while it is much larger for the features at 6.2 and
11.3 ![]() m. We plot for comparison the run with radius of the cumulative fraction
of the FUV radiation intercepted by the disk surface. The similar behaviour with the
cumulative intensity of the less energetic PAH features reflects the fact that
the emission of PAHs roughly scales with the intensity of the FUV radiation
field (see Sect. 4.3.1 for more details).
m. We plot for comparison the run with radius of the cumulative fraction
of the FUV radiation intercepted by the disk surface. The similar behaviour with the
cumulative intensity of the less energetic PAH features reflects the fact that
the emission of PAHs roughly scales with the intensity of the FUV radiation
field (see Sect. 4.3.1 for more details).
Figure 5 shows the intensity profile obtained by convolving the
computed intensity with a two-dimensional gaussian of FWHM = 0.1
![]() .
As expected
from Fig. 4, the features at short wavelengths are strong in
the inner hot part of the disk, decreasing rapidly in the outer cold part,
whereas those at long wavelengths are weaker in the inner region (mostly because
the continuum is higher)
but more extended (the temperature required to excite them is lower).
In other words, the 3.3
.
As expected
from Fig. 4, the features at short wavelengths are strong in
the inner hot part of the disk, decreasing rapidly in the outer cold part,
whereas those at long wavelengths are weaker in the inner region (mostly because
the continuum is higher)
but more extended (the temperature required to excite them is lower).
In other words, the 3.3 ![]() m probes the inner (R<100 AU) region of the disk
while the other features probe its outer parts.
m probes the inner (R<100 AU) region of the disk
while the other features probe its outer parts.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0916.f5.ps}
\end{figure}](/articles/aa/full/2004/43/aa0916/Timg90.gif) |
Figure 5:
Surface brightness profiles convolved with a two-dimensional
gaussian of FWHM = 0.1
|
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0916.f6.ps}\vspace*{3mm}
\includegraphics[width=7.5cm,clip]{0916.f7.ps}
\end{figure}](/articles/aa/full/2004/43/aa0916/Timg91.gif) |
Figure 6:
The top panel shows the SEDs of models
containing positively ionized PAH (solid thick line) and
partially dehydrogenated PAHs with
|
In this section, we investigate the effect of the charge, hydrogenation parameter, size, photoevaporation and absorption cross section of PAHs on the predicted intensity of the features.
In Fig. 6, we show the spectra and the brightness distribution
for the same model shown in Figs. 3 and 5
but for PAH cations. The PAH
spectrum is a strong function of the PAH charge:
the strength of the C-C stretching modes between 6.2 and 8.6 ![]() m is much
stronger for ionized PAHs; the 7.7
m is much
stronger for ionized PAHs; the 7.7 ![]() m C-C feature to the 11.3
m C-C feature to the 11.3 ![]() m C-H feature ratio
is increased by a factor of
m C-H feature ratio
is increased by a factor of ![]() 5 (see Table 3).
Further, whereas neutral PAHs
show a strong 3.3
5 (see Table 3).
Further, whereas neutral PAHs
show a strong 3.3 ![]() m C-H features, the band almost vanishes when the PAHs
are positively ionized.
m C-H features, the band almost vanishes when the PAHs
are positively ionized.
The IR properties of PAH anions closely resemble those of PAH cations except for
the very strong 3.3 ![]() m enhancement in the anion (Szczepanski et al. 1995; Hudgins et al. 2000). However,
Bauschlicher & Bakes (2000) predict that PAH
anions have band strengths intermediate between those of neutrals (strong 3.3
m enhancement in the anion (Szczepanski et al. 1995; Hudgins et al. 2000). However,
Bauschlicher & Bakes (2000) predict that PAH
anions have band strengths intermediate between those of neutrals (strong 3.3
![]() m C-H stretching and 11.3, 11.9 and 12.7
m C-H stretching and 11.3, 11.9 and 12.7 ![]() m out-of-plane C-H bending modes)
and PAH cations (strong 6.2 and 7.7
m out-of-plane C-H bending modes)
and PAH cations (strong 6.2 and 7.7 ![]() m C-C stretching and 8.6
m C-C stretching and 8.6 ![]() m C-H
in-plane bending mode).
m C-H
in-plane bending mode).
Another effect which can significantly affect the PAH spectra
is dehydrogenation.
Strong dehydrogenation would make the C-H features disappear.
However, theoretical studies of dehydrogenation in the ISM
indicate that it is relevant only for the
smallest PAHs with
![]() (Allain et al. 1996; Tielens et al. 1987).
Upon absorption of an energetic photon, large PAHs
will not have C-H bond rupture since the absorbed energy will promptly
be redistributed among many vibrational modes.
Nevertheless, in the inner disk regions and for stars with high
UV fields dehydrogenation could become important even
for large PAHs. To estimate this effect, we run a model with PAHs
partially dehydrogenated, i.e., hydrogenation fraction
(Allain et al. 1996; Tielens et al. 1987).
Upon absorption of an energetic photon, large PAHs
will not have C-H bond rupture since the absorbed energy will promptly
be redistributed among many vibrational modes.
Nevertheless, in the inner disk regions and for stars with high
UV fields dehydrogenation could become important even
for large PAHs. To estimate this effect, we run a model with PAHs
partially dehydrogenated, i.e., hydrogenation fraction
![]() .
The results are shown in Fig. 6. The C-H features (3.3,
8.6, 11.3, 12.7
.
The results are shown in Fig. 6. The C-H features (3.3,
8.6, 11.3, 12.7 ![]() m) become lower (by a factor
m) become lower (by a factor ![]() 2, see Table 3), and the C-C features (6.2, 7.7
2, see Table 3), and the C-C features (6.2, 7.7 ![]() m) become slightly higher
(as expected from energy conservation).
m) become slightly higher
(as expected from energy conservation).
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{0916.f8.ps}\vspace*{3mm}
\includegraphics[width=6.5cm,clip]{0916.f9.ps}
\end{figure}](/articles/aa/full/2004/43/aa0916/Timg93.gif) |
Figure 7:
Same as Fig. 6 for model
containing neutral PAHs with
|
We now look at the influence of the PAH size.
In Fig. 7 we show a model for smaller PAHs with
![]() .
The relative strength of the PAH emission bands depends strongly
on the PAH size: small PAHs radiate strongly at 3.3
.
The relative strength of the PAH emission bands depends strongly
on the PAH size: small PAHs radiate strongly at 3.3 ![]() m, while
larger (colder) PAHs emit most of their power at longer wavelengths.
The 3.3/6.2
m, while
larger (colder) PAHs emit most of their power at longer wavelengths.
The 3.3/6.2 ![]() m ratio is
m ratio is ![]() 4 times higher for small PAHs than for large PAHs (see
Table 3).
In addition, since the H/C ratio decreases
with the size (see Sect. 3.3), the C-H features increase
for small PAHs.
4 times higher for small PAHs than for large PAHs (see
Table 3).
In addition, since the H/C ratio decreases
with the size (see Sect. 3.3), the C-H features increase
for small PAHs.
We note that decreasing the PAH size generally goes in the opposite
direction than increasing the fraction of ionized PAHs:
the emission in the 6-9 ![]() m range
decreases for smaller PAHs while for ionized PAHs it increases (see Sect. 4.2.1).
On the other hand, the emission at 3.3 and 11.3
m range
decreases for smaller PAHs while for ionized PAHs it increases (see Sect. 4.2.1).
On the other hand, the emission at 3.3 and 11.3 ![]() m goes up when
PAHs become
smaller, whereas it goes down when the fraction of ionized PAHs increases.
m goes up when
PAHs become
smaller, whereas it goes down when the fraction of ionized PAHs increases.
Therefore, we expect to find for small and ionized PAHs results similar to
those predicted by the template model with large and neutral PAHs. For illustration,
we show in Fig. 7 a model with small (
![]() )
and ionized
PAHs. In this case, we find in fact that the strength of the 6.2, 7.7 and
11.3
)
and ionized
PAHs. In this case, we find in fact that the strength of the 6.2, 7.7 and
11.3 ![]() m features are roughly similar to those predicted by the template model (see
Table 3).
However, size and ionization do not compensate each other fully and the 3.3
m features are roughly similar to those predicted by the template model (see
Table 3).
However, size and ionization do not compensate each other fully and the 3.3 ![]() m
band strength is considerably lower (by a factor of 10) than in the template
model.
But note that for small PAH anions, as mentioned in Sect. 4.2.1, the 3.3
m
band strength is considerably lower (by a factor of 10) than in the template
model.
But note that for small PAH anions, as mentioned in Sect. 4.2.1, the 3.3 ![]() m feature
strength will be higher.
m feature
strength will be higher.
Finally, we find that for small PAHs which are mostly destroyed in the inner
(hot) part of the disk - ![]() AU for
AU for
![]() - the brightness
profiles of the features are affected.
The emission is decreased in the inner part and a plateau appears reflecting the compensation
between the gradual coming out of PAHs and the decrease of the FUV flux.
In the next section, we discuss the photoeveporation effect.
- the brightness
profiles of the features are affected.
The emission is decreased in the inner part and a plateau appears reflecting the compensation
between the gradual coming out of PAHs and the decrease of the FUV flux.
In the next section, we discuss the photoeveporation effect.
With the formalism adopted here, we find that
large PAHs with
![]() will not be photo-evaporated
in most of the disk, except in the R>20 AU region,
while smaller PAHs with
will not be photo-evaporated
in most of the disk, except in the R>20 AU region,
while smaller PAHs with
![]() will be mostly photo-evaporated in the
will be mostly photo-evaporated in the ![]() AU region
(as mentioned above).
Larger PAHs are more stable since they can easily accommodate the absorbed photon energy.
But PAH evaporation, as discussed in Sect. 3.3, is a
complex process, and it is possible that our treatment of it
underestimates its effects.
For stronger photoevaporation, the strength of the most energetic features which come mostly from
the inner region will decrease and their brightness distribution will be affected;
the effect on the bands at longer
AU region
(as mentioned above).
Larger PAHs are more stable since they can easily accommodate the absorbed photon energy.
But PAH evaporation, as discussed in Sect. 3.3, is a
complex process, and it is possible that our treatment of it
underestimates its effects.
For stronger photoevaporation, the strength of the most energetic features which come mostly from
the inner region will decrease and their brightness distribution will be affected;
the effect on the bands at longer ![]() coming from
the outer region will on the contrary be negligible.
coming from
the outer region will on the contrary be negligible.
On the other hand, it is possible that continuous replenishment of PAHs via sublimation
of icy mantles (in which interstellar PAHs may have condensed during the dense
molecular cloud phase) or by accreting carbon atoms and/or ions from the gas
(see, e.g., Allain et al. 1996) could maintain PAHs throughout the disk.
For the template model without evaporation, the
strength of the 3.3 ![]() m feature will increase by a factor of
m feature will increase by a factor of ![]() 2
while the other features at longer wavelength will not.
2
while the other features at longer wavelength will not.
Finally, we discuss the influence of the absorption cross section.
First, the PAH spectra depend on the integrated cross sections of individual
features,
![]() ,
which, unfortunately, differ among various lab
measurements or between experimental and theoretical studies.
To get an idea of how these uncertainties affect the PAH spectra we
have computed models with enhancement factors of 2-3 in
,
which, unfortunately, differ among various lab
measurements or between experimental and theoretical studies.
To get an idea of how these uncertainties affect the PAH spectra we
have computed models with enhancement factors of 2-3 in
![]() .
In particular, we have taken for the 6.2, 7.7 and 8.6
.
In particular, we have taken for the 6.2, 7.7 and 8.6 ![]() m bands E6.2=3, E7.7=2 and
E8.6=2 as suggested by Li & Draine (2001a) in order to fit the 6.2/7.7, 7.7/11.3 and
8.6/7.7
m bands E6.2=3, E7.7=2 and
E8.6=2 as suggested by Li & Draine (2001a) in order to fit the 6.2/7.7, 7.7/11.3 and
8.6/7.7 ![]() m band strength ratios observed in ISM spectra.
Compared to the template model, the 6.2/7.7 and 7.7/11.3
m band strength ratios observed in ISM spectra.
Compared to the template model, the 6.2/7.7 and 7.7/11.3 ![]() m ratios
are higher by a factor
m ratios
are higher by a factor ![]() 2.
2.
Second, the intensities of the PAH bands depend on the absorption cross section in the
visible and UV which are rather uncertain. The cross section (
![]() )
defined in Sect. 3.3 has been derived for planar PAHs from
laboratory measurements of small species (
)
defined in Sect. 3.3 has been derived for planar PAHs from
laboratory measurements of small species (
![]() ,
Joblin et al. 1992) and, for
bigger species, from optical constants for graphite (Verstraete & Léger 1992). However, for astronomical PAHs with more complex 3-dimensional
structure very little is known. To estimate the effect of this uncertainty we
have computed a model with
,
Joblin et al. 1992) and, for
bigger species, from optical constants for graphite (Verstraete & Léger 1992). However, for astronomical PAHs with more complex 3-dimensional
structure very little is known. To estimate the effect of this uncertainty we
have computed a model with
![]() for small graphite spheres as in
Draine & Lee (1984). The power absorbed by
for small graphite spheres as in
Draine & Lee (1984). The power absorbed by
![]() is
is ![]() 2 times
lower than for
2 times
lower than for
![]() and, consequently, the intensity of the
features is reduced by
and, consequently, the intensity of the
features is reduced by ![]() 2.
2.
The SED of the template model depends not only on the dust model, and in particular on the PAH properties, but also on the star and disk properties. In this section, we investigate the influence of star/disk system parameters on the PAH emission features.
The range of values of the FUV radiation field is large even within the rather
limited range of spectral types we investigate in this paper, with ![]() (the
FUV field at a distance of 150 AU from the star) varying from 106 to a few times 102 (see Table 1).
(the
FUV field at a distance of 150 AU from the star) varying from 106 to a few times 102 (see Table 1). ![]() changes because both the luminosity
and the effective temperature of the stars change. We have therefore computed a
set of disk models for stars of different spectral types assuming that they are
on the main sequence, and plotted the results in Fig. 8 as
function of the corresponding value of
changes because both the luminosity
and the effective temperature of the stars change. We have therefore computed a
set of disk models for stars of different spectral types assuming that they are
on the main sequence, and plotted the results in Fig. 8 as
function of the corresponding value of ![]() .
The spectral types are also
displayed in the figure.
.
The spectral types are also
displayed in the figure.
As expected, the strength of the PAH features increases with ![]() .
The
dependence is not linear (see Fig. 8), because
the fraction of the stellar radiation absorbed by PAHs depends on its
wavelength dependence, i.e., on
.
The
dependence is not linear (see Fig. 8), because
the fraction of the stellar radiation absorbed by PAHs depends on its
wavelength dependence, i.e., on
![]() .
For example,
the power absorbed by PAHs, normalised by
.
For example,
the power absorbed by PAHs, normalised by ![]() ,
is two times higher for
,
is two times higher for
![]() K than for
K than for
![]() and ten times lower than for
and ten times lower than for
![]() K.
K.
Figure 8 shows the intensity of the 3.3, 6.2 and 11.3 ![]() m
features as function of
m
features as function of ![]() .
One sees that the 3.3
.
One sees that the 3.3 ![]() m one increases
faster than the others, since it is the most sensitive to the
PAH excitation temperature.
One can also note that the competing effect, i.e., the fact that PAH
evaporation is larger for higher
m one increases
faster than the others, since it is the most sensitive to the
PAH excitation temperature.
One can also note that the competing effect, i.e., the fact that PAH
evaporation is larger for higher ![]() ,
reducing the 3.3
,
reducing the 3.3 ![]() m feature
more than the others, does not compensate entirely the effect of higher
excitation temperatures.
However, one should keep in mind that for smaller PAHs
(
m feature
more than the others, does not compensate entirely the effect of higher
excitation temperatures.
However, one should keep in mind that for smaller PAHs
(
![]() ), the effect of evaporation could become much larger.
), the effect of evaporation could become much larger.
The dependence of the PAH emission on disk parameters is easily understood. The
quantity that most affects the resulting spectrum is the disk flaring angle,
which determines at each radius the fraction of FUV intercepted by the disk
surface. Lower values of the flaring can be caused by a variety of reasons, for
example if the dust settles toward the disk midplane. Also, if the disk mass is
fixed, a steeper dependence of the surface density profile than p=1 tends to
make the outer disk less flared, as the ratio of the photospheric to the
pressure scale height increases. In all cases, the value of the flaring angle
in the inner disk is practically fixed, since it is dominated by its geometrical
part (Chiang & Goldreich 1997; Dullemond et al. 2001). Therefore, less flared disks have lower
emission in all features, but a higher ratio of the 3.3 ![]() m intensity, which
forms mostly near the star, where the flaring is dominated by the geometrical
part, to that of the 6.2 and 11.3
m intensity, which
forms mostly near the star, where the flaring is dominated by the geometrical
part, to that of the 6.2 and 11.3 ![]() m ones, which have a much larger
contribution from the outer disk. In the extreme case of a geometrically flat
disk, the PAH feature strenghts decrease by 3 orders of magnitude but the ratio 3.3/11.3
m ones, which have a much larger
contribution from the outer disk. In the extreme case of a geometrically flat
disk, the PAH feature strenghts decrease by 3 orders of magnitude but the ratio 3.3/11.3 ![]() m
increases by a factor of 3 and only the 3.3
m
increases by a factor of 3 and only the 3.3 ![]() m band does not completly disappear.
The 3.3
m band does not completly disappear.
The 3.3 ![]() m band to continuum ratio decreases by a factor
of 4 and becomes equal to 1.1.
m band to continuum ratio decreases by a factor
of 4 and becomes equal to 1.1.
In a similar way, when the disk is larger, all features get stronger, but
the 3.3 ![]() m band less than the others. If
m band less than the others. If ![]() becomes very large, the disk turns
optically thin to the FUV radiation and the PAH emission does not increase further.
becomes very large, the disk turns
optically thin to the FUV radiation and the PAH emission does not increase further.
Another parameter to be considered is the disk inclination with
respect to the observer.
If the disk is inclined it will emit a lower continuum emission at long wavelengths;
for an inclination of
![]() deg (
deg (![]() for face-on disks)
the models predict a continuum
at
for face-on disks)
the models predict a continuum
at
![]()
![]() m about 20% lower than for face-on models,
while at shorter wavelengths there are practically no changes.
The continuum-substracted intensity of all the PAH features
we compute will not be affected at all.
m about 20% lower than for face-on models,
while at shorter wavelengths there are practically no changes.
The continuum-substracted intensity of all the PAH features
we compute will not be affected at all.
A major source of uncertainty in our results derives from the lack of knowledge
of the detailed structure of the inner disk. We have assumed in our
calculations that the disk is truncated at the dust sublimation radius, and that
each disk face is illuminated by 1/2 of the stellar surface. In fact, there is
good evidence that in most HAe stars the disk has a puffed-up rim at the dust
sublimation radius, due to the direct illumination of the stellar radiation
(Natta et al. 2001; Dullemond et al. 2001). The structure of this rim, and the effects of
the shade it projects further out on the disk are rather complex, depending on
the detailed 2D radiation transfer for a mixture of grains of different
properties. The correct treatment of the effects of this region on the PAH emission is well beyond the current capabilities of our models. However, we can
make some qualitative estimates in the following way. A puffed-up inner rim
will emit a strong continuum at short wavelengths. This affects mainly the
ratio of the 3.3 ![]() m band to the continuum; considering that models that
include the rim predict a 3.3
m band to the continuum; considering that models that
include the rim predict a 3.3 ![]() m continuum a factor of
m continuum a factor of ![]() 3 larger than
our models (see Natta et al. 2001), the 3.3
3 larger than
our models (see Natta et al. 2001), the 3.3 ![]() m peak to continuum ratio will
decrease by a factor of 2. However, the continuum-subtracted intensity of the
3.3
m peak to continuum ratio will
decrease by a factor of 2. However, the continuum-subtracted intensity of the
3.3 ![]() m feature will not be affected; also, the effect on the other features
at longer wavelength is negligible.
m feature will not be affected; also, the effect on the other features
at longer wavelength is negligible.
The geometrical effect of the rim on the
disk illumination can be much smaller than we have assumed by taking
![]() ,
to the limit of being entirely negligible. In this case, each
point on the disk will be illuminated by the entire stellar surface, and the
fraction of intercepted stellar radiation will increase by a factor of 2 with
respect to our template model. We have checked that this results, with a large
degree of accuracy, in a factor of 2 increase of all the strong PAH features.
The total IR excess will also be a factor of 2 larger, going from about 20%,
for a face-on disk, to about 40%. Most HAe stars have indeed an
IR excess
within this interval (Dullemond & Natta 2003; Meeus et al. 2001), and one expects that more
realistic models will be roughly intermediate between these two cases. However,
it should be noted that one can expect also some modest change in the ratio of
features at different wavelengths, as the rim shade will affect
different regions of the disk differently.
,
to the limit of being entirely negligible. In this case, each
point on the disk will be illuminated by the entire stellar surface, and the
fraction of intercepted stellar radiation will increase by a factor of 2 with
respect to our template model. We have checked that this results, with a large
degree of accuracy, in a factor of 2 increase of all the strong PAH features.
The total IR excess will also be a factor of 2 larger, going from about 20%,
for a face-on disk, to about 40%. Most HAe stars have indeed an
IR excess
within this interval (Dullemond & Natta 2003; Meeus et al. 2001), and one expects that more
realistic models will be roughly intermediate between these two cases. However,
it should be noted that one can expect also some modest change in the ratio of
features at different wavelengths, as the rim shade will affect
different regions of the disk differently.
A first test of our models can be made by comparing the predicted intensity of
the most commonly observed PAH features (i.e., at 3.3, 6.2 and 11.3 ![]() m) with the
observations. We do that in Fig. 9, which plots for each feature
the intensity normalized to the FUV flux of the star, as function of the value
of
m) with the
observations. We do that in Fig. 9, which plots for each feature
the intensity normalized to the FUV flux of the star, as function of the value
of ![]() (i.e., the FUV field at 150 AU from the star). Both quantities are
distance-independent. The solid lines show the prediction of models for
main-sequence stars of different spectral type (and
(i.e., the FUV field at 150 AU from the star). Both quantities are
distance-independent. The solid lines show the prediction of models for
main-sequence stars of different spectral type (and ![]() ), as described in
Sect. 4.3.1. The lower line refers to models where
), as described in
Sect. 4.3.1. The lower line refers to models where
![]() ,
the upper lines
to models with
,
the upper lines
to models with
![]() .
The thin lines show an uncertainty strip of
.
The thin lines show an uncertainty strip of ![]() a factor of 2 around these models. This, as we have discussed, is a
conservative estimate of the uncertainties due to deviations from the
assumptions of the template models, in the disk description (different surface
density profiles, flaring etc.) and in the assumed dust model.
a factor of 2 around these models. This, as we have discussed, is a
conservative estimate of the uncertainties due to deviations from the
assumptions of the template models, in the disk description (different surface
density profiles, flaring etc.) and in the assumed dust model.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0916.f11.ps}
\end{figure}](/articles/aa/full/2004/43/aa0916/Timg110.gif) |
Figure 9:
Comparison of model predictions and
observations. Upper Panel: Strength of the 3.3 |
In the following, in order to see if PAHs in disks are consistent with observations, we check for each star group described in Sect. 2 if the disk models can account for the observed PAH intensities.
Objects with flared disks, according to the classification of Meeus et al. (2001)
(group I) are marked as crosses in Fig. 9. This group dominates
among the detections, as expected from our models. They are in general well
accounted for by disk models with "standard" dust, as defined in
Sect. 3.3. This is true also for the two younger sources, i.e., HD 97048 and
Elias 1 (shown by triangles), especially if we correct for contamination in the
two longer wavelength bands by the associated reflection nebula (about
![]() 40% for HD 97048; van Boekel et al. 2004). We also show by asterisks the HAeBe stars
observed by Brooke et al. (1993) at 3.3
40% for HD 97048; van Boekel et al. 2004). We also show by asterisks the HAeBe stars
observed by Brooke et al. (1993) at 3.3 ![]() m. They cover a range of
m. They cover a range of ![]() from
about 104 to very high values (
from
about 104 to very high values (![]() 106), and we do not have detailed
information on their disk properties. However, the objects with
106), and we do not have detailed
information on their disk properties. However, the objects with
![]() are consistent with our disk predictions. No upper limit in objects
with
are consistent with our disk predictions. No upper limit in objects
with
![]() is significantly lower than the model predictions.
is significantly lower than the model predictions.
In 8 of these objects one has a measurement (or significant upper limit) of both
the 3.3 and the 6.2 ![]() m features. The ratio ranges from 0.1 to about 0.5,
somewhat lower than the value predicted by the model of
m features. The ratio ranges from 0.1 to about 0.5,
somewhat lower than the value predicted by the model of
![]() .
In four cases,
one can also measure the ratio of the 11.3 to the 6.2
.
In four cases,
one can also measure the ratio of the 11.3 to the 6.2 ![]() m feature. The values
are about 0.5 in 3 cases, and 0.8 (with an uncertainty of
m feature. The values
are about 0.5 in 3 cases, and 0.8 (with an uncertainty of ![]() 0.2) in the
fourth object, in good agreement with the template model predictions of
0.2) in the
fourth object, in good agreement with the template model predictions of
![]() .
It is likely, as we will discuss further in Sect. 5.3, that our models tend
to overestimate the intensity of the 3.3
.
It is likely, as we will discuss further in Sect. 5.3, that our models tend
to overestimate the intensity of the 3.3 ![]() m feature by a factor 2-3 in stars
with
m feature by a factor 2-3 in stars
with
![]() .
.
However, there are two groups of non-detections that are interesting. We discuss these in the following.
The first is the group of 5 diamonds, i.e., HAeBe stars with no evidence of a flared
disk (group II, Meeus et al. 2001). Of these, only in one case (HD 142666) PAHs
have been detected at 3.3 and 6.2 ![]() m; most of the non-detections are well
below the model predictions. This agrees quite well with our result that flat
disks should have very weak PAH features, even when PAHs are present with normal
properties on the disk surface.
m; most of the non-detections are well
below the model predictions. This agrees quite well with our result that flat
disks should have very weak PAH features, even when PAHs are present with normal
properties on the disk surface.
Other interesting objects are those with high values of
![]() ). Most of them (the exception being WL 16, which we discuss in more detail
in the following) are from Brooke et al. (1993), and only the 3.3
). Most of them (the exception being WL 16, which we discuss in more detail
in the following) are from Brooke et al. (1993), and only the 3.3 ![]() m feature has
been observed. All these objects with high
m feature has
been observed. All these objects with high ![]() have 3.3
have 3.3 ![]() m intensities
(or upper limits) well below the model predictions.
m intensities
(or upper limits) well below the model predictions.
The interpretation of this group of objects is not straightforward; it is quite
possible that their disks, if they ever existed, have been dissipated by the
strong radiation field of the star (Natta et al. 2000; Fuente et al. 2002), or that they
are flat (Hillenbrand et al. 1992).
There are, however, other possibilites. One is that the abundance of PAHs is
lower than we assumed. Photoevaporation, which increases rapidly with ![]() and for smaller PAHs, could easily reduce the PAH abundance well below our
assumed value. PAH evaporation, as discussed in Sect. 3.3, is a
complex process, and we may have underestimated its effects.
and for smaller PAHs, could easily reduce the PAH abundance well below our
assumed value. PAH evaporation, as discussed in Sect. 3.3, is a
complex process, and we may have underestimated its effects.
It is also possible that the PAHs are ionized and/or dehydrogenated in the inner
disk region, resulting in a much reduced 3.3 ![]() m band (see Sects. 4.2.2
and 4.2.1). Observations of the PAH emission from WL
16, shown by a square in Fig. 9
m band (see Sects. 4.2.2
and 4.2.1). Observations of the PAH emission from WL
16, shown by a square in Fig. 9![]() , favors this last
possibility. In fact, we find that while the models reproduce well the
11.3
, favors this last
possibility. In fact, we find that while the models reproduce well the
11.3 ![]() m feature strength, that of the 3.3
m feature strength, that of the 3.3 ![]() m feature is well below the
predictions. Moreover, Ressler & Barsony (2003) interpret the spatial variation of
the 7.7 (or 8.6)/11.3
m feature is well below the
predictions. Moreover, Ressler & Barsony (2003) interpret the spatial variation of
the 7.7 (or 8.6)/11.3 ![]() m flux ratio as due to a change of the PAH charge
state along the disk. In the inner region PAHs appear to be positively charged
while in the outer region they are neutral. Furthermore, the 12.7/11.3
m flux ratio as due to a change of the PAH charge
state along the disk. In the inner region PAHs appear to be positively charged
while in the outer region they are neutral. Furthermore, the 12.7/11.3 ![]() m
flux ratio, which increases in the outer part of the disk, could indicate the
presence of more hydrogenated PAHs in the outer part.
m
flux ratio, which increases in the outer part of the disk, could indicate the
presence of more hydrogenated PAHs in the outer part.
As we have just seen, our template model with relatively large (
![]() )
neutral PAHs fits very well the strength of the most commonly observed
features, with the possible exception of the 3.3
)
neutral PAHs fits very well the strength of the most commonly observed
features, with the possible exception of the 3.3 ![]() m one, which tends to be
much lower than predicted in stars with
m one, which tends to be
much lower than predicted in stars with
![]() .
.
In stars with lower ![]() (spectral type roughly later than B9), we can rule
out that PAHs are large and ionized, because they will produce
too low 3.3/6.2 and 11.3/6.2
(spectral type roughly later than B9), we can rule
out that PAHs are large and ionized, because they will produce
too low 3.3/6.2 and 11.3/6.2 ![]() m ratios (by a factor of
>10 and 4, respectively, see Sect. 4.2.1 and Table 3).
Similarly, large and strongly dehydrogenated PAHs are unlikely, since
they will also produce too low 3.3/6.2 and 11.3/6.2
m ratios (by a factor of
>10 and 4, respectively, see Sect. 4.2.1 and Table 3).
Similarly, large and strongly dehydrogenated PAHs are unlikely, since
they will also produce too low 3.3/6.2 and 11.3/6.2 ![]() m ratios
(see Sect. 4.2.2).
Further, we can rule
out that PAHs are much smaller than our assumed model (
m ratios
(see Sect. 4.2.2).
Further, we can rule
out that PAHs are much smaller than our assumed model (
![]() ),
because they will produce too high 3.3/6.2 and 11.3/6.2
),
because they will produce too high 3.3/6.2 and 11.3/6.2 ![]() m ratios
(by a factor of 4 and 10, respectively, see Sect. 4.2.3 and Table 3).
m ratios
(by a factor of 4 and 10, respectively, see Sect. 4.2.3 and Table 3).
On the other hand, we cannot exclude that PAHs are small and ionized. In
this case, we find that the strength of the 6.2 and 11.3 ![]() m features, as well
as their ratio will be roughly similar to the values predicted by the template model
with large and neutral PAHs (see Sect. 4.2.3). This is easily understood
considering that the effects of size and ionization compensate each
other. For small positively charged PAHs the compensation is nevertheless not
complete, and, the intensity of the 3.3
m features, as well
as their ratio will be roughly similar to the values predicted by the template model
with large and neutral PAHs (see Sect. 4.2.3). This is easily understood
considering that the effects of size and ionization compensate each
other. For small positively charged PAHs the compensation is nevertheless not
complete, and, the intensity of the 3.3 ![]() m feature will be lower than
in the template model by a factor
m feature will be lower than
in the template model by a factor ![]() 10 (see Table 3).
Therefore, this model, which underestimates the 3.3
10 (see Table 3).
Therefore, this model, which underestimates the 3.3 ![]() m feature strength by a
factor of 3 in stars with
m feature strength by a
factor of 3 in stars with
![]() but by a much
larger factor in stars with
but by a much
larger factor in stars with
![]() ,
seems unlikely. For small
negatively charged PAHs the 3.3
,
seems unlikely. For small
negatively charged PAHs the 3.3 ![]() m feature is expected to be stronger (see
Sect. 4.2.1) and could become comparable to the observations. However, it
is difficult to assess the reliability of this model, since the IR properties of
PAH anions are not well known.
m feature is expected to be stronger (see
Sect. 4.2.1) and could become comparable to the observations. However, it
is difficult to assess the reliability of this model, since the IR properties of
PAH anions are not well known.
To get some additional insight into the PAH properties, one can look at the
other weaker PAH features (i.e., 8.6, 12.7 or 16.4 ![]() m) even if they have been
only sporadically detected. This is probably due to the low S/N ratio of the spectra.
The models with large neutral PAHs and small
ionized PAHs predict similar strengths of the 8.6 and 12.7
m) even if they have been
only sporadically detected. This is probably due to the low S/N ratio of the spectra.
The models with large neutral PAHs and small
ionized PAHs predict similar strengths of the 8.6 and 12.7 ![]() m features, in
good agreement with observations (see Tables 2 and 3). On the other hand, large neutral PAHs will produce a 16.4
m features, in
good agreement with observations (see Tables 2 and 3). On the other hand, large neutral PAHs will produce a 16.4 ![]() m feature five
times stronger than small ionized PAHs. This favors the small ionized PAHs
model since this feature has not been detected in the ISO spectra of isolated
HAeBe stars (Van Kerckhoven et al. 2002). However, high S/N spectra in this
wavelength region are needed to determine the properties of the carrier of this
band.
m feature five
times stronger than small ionized PAHs. This favors the small ionized PAHs
model since this feature has not been detected in the ISO spectra of isolated
HAeBe stars (Van Kerckhoven et al. 2002). However, high S/N spectra in this
wavelength region are needed to determine the properties of the carrier of this
band.
The large and neutral PAH hypothesis is supported by the detailed studies of the PAH spectra in HAeBe stars based on both laboratory data and theoretical calculations (Peeters et al. 2002; Hony et al. 2001; Van Kerckhoven et al. 2002). Together with the comparison of the PAH profiles observed in evolved stars and ISM-like sources, they indicate that PAHs should be larger and less ionized in isolated HAeBe stars, in agreement with our template model.
It must be emphasized that there are several complications that we have
neglected in this study. The most obvious is that we have assumed that PAHs can
be characterized by a single size and charge state. This is unlikely to be the
case, and one can expect variations as a function of radius and depth in the
disk, as well as from object to object. For example, PAHs are likely to be more
positively ionized in the inner disk region and for stars with higher ![]() .
This could explain the gradual decrease of the 3.3
.
This could explain the gradual decrease of the 3.3 ![]() m feature strength with
m feature strength with ![]() seen in Fig. 9. In stars with
seen in Fig. 9. In stars with
![]() it is possible that we have an intermediate situation,
and in fact a model with a mixture of both large neutral and small ionized
PAHs will predict a 3.3
it is possible that we have an intermediate situation,
and in fact a model with a mixture of both large neutral and small ionized
PAHs will predict a 3.3 ![]() m feature strength lower than in the template model
by a factor of 2-3, close to the observed values.
m feature strength lower than in the template model
by a factor of 2-3, close to the observed values.
We conclude that in stars with
![]() PAHs may be preferentially
relatively large (
PAHs may be preferentially
relatively large (
![]() )
and neutral. But small and negatively
ionized PAHs can also reproduce the observations. For comparison,
Li & Lunine (2003), who have modelled the
emission features from the (debris) disk around HD 141596A (with
)
and neutral. But small and negatively
ionized PAHs can also reproduce the observations. For comparison,
Li & Lunine (2003), who have modelled the
emission features from the (debris) disk around HD 141596A (with
![]() )
conclude that PAHs must be mostly negatively charged. However, they show that
models consisting of a mixture of both neutral and charged PAHs are also capable
of reproducing the observations. For stars with
)
conclude that PAHs must be mostly negatively charged. However, they show that
models consisting of a mixture of both neutral and charged PAHs are also capable
of reproducing the observations. For stars with
![]() ,
the large
neutral PAH model tends to overestimate the intensity of the 3.3
,
the large
neutral PAH model tends to overestimate the intensity of the 3.3 ![]() m
feature. This could result from changes in the disk structure (e.g., disks may
have dissipated), or from changes in the characteristics of the PAHs, which can be
ionized, dehydrogenated or strongly photoevaporated in the inner disk regions.
m
feature. This could result from changes in the disk structure (e.g., disks may
have dissipated), or from changes in the characteristics of the PAHs, which can be
ionized, dehydrogenated or strongly photoevaporated in the inner disk regions.
From the integrated spectra, it is difficult to discriminate between the various effects due to ionization, dehydrogenation or evaporation. To provide better insight into evolution of PAH properties within the disk, high angular spatial spectroscopic observations in the bands are needed.
We have investigated the emission from PAHs on the surface of disks around HAeBe stars by comparing model predictions with observations. We have computed models of disks, heated by irradiation from the central source, that contain large grains, in thermal equilibrium with the radiation field, and transiently heated very small grains and PAHs. The disks are optically thick to the stellar radiation, in hydrostatic equilibrium in the vertical direction, with dust and gas well mixed (flared disks). We have used a 2-layer model to calculate the disk structure and implement a 1D radiative transfer code to compute the emerging spectrum. This scheme is reliable and efficient (see Sects. 3.1 and 3.2). Our main results can be summarized as follows.
Acknowledgements
We are grateful to F. Boulanger and L. Verstraete for fruitful discussions and relevant comments and suggestions.
The disk is divided into rings of radius r and small radial width ![]() .
At the center, at r=0, sits the star with parameters
.
At the center, at r=0, sits the star with parameters ![]() ,
,
![]() ,
,
![]() and
and
![]() .
For each ring we compute, as described below, the radiative
transfer perpendicular to the disk, in the z-direction, and then add up the
contributions from all rings.
.
For each ring we compute, as described below, the radiative
transfer perpendicular to the disk, in the z-direction, and then add up the
contributions from all rings.
Each ring is treated as a
plane-parallel slab. It displays mirror symmetry with respect to the mid-plane
at z=0. We solve the integral equations
There are two boundary conditions. One states that at the top of
the slab the incoming intensity I- =I0 is zero except towards the star where
it equals ![]() (
(
![]() ). The stellar hemisphere, which seen from a distance r subtends a solid angle
). The stellar hemisphere, which seen from a distance r subtends a solid angle
![]() ,
is replaced by a
luminous band of the same intensity
,
is replaced by a
luminous band of the same intensity ![]() (
(
![]() ). The band encircles the sky
at an elevation
). The band encircles the sky
at an elevation ![]() and has a width
and has a width
![]() ,
its solid
angle is also
,
its solid
angle is also ![]() .
The other boundary condition reads I+ =I- at z=0.
.
The other boundary condition reads I+ =I- at z=0.
One starts the calculation of the radiative transfer for a ring
with a guess for the vertical dust temperature profile T(z). This fixes the
source function ![]() once the dust properties have been specified. Then
one solves (1) and (2) for
once the dust properties have been specified. Then
one solves (1) and (2) for
![]() and
and
![]() and calculates from I+, I- the mean intensity of the
radiation field J(z). This makes it possible to compute a new temperature run T(z).
The procedure is iterated until T(z) converges.
and calculates from I+, I- the mean intensity of the
radiation field J(z). This makes it possible to compute a new temperature run T(z).
The procedure is iterated until T(z) converges.
Because in our examples the visual opacity of the disk in z-direction can be
very large (>105), we apply the following slight modification to what we
said above. We slice the disk into a completely opaque mid-layer sandwiched
between two thin top layers. The mid-layer, because of its high opticaldepth
and the lack of internal energy sources, is considered to be isothermal at
temperature
![]() ;
the value depends, of course, on r. We evaluate
the radiative transfer for the top layer according to the method described
before, and separately for the isothermal midlayer, but there it is trivial. A
boundary condition connects the two layers. In the calculation for the top
layer, we now position the zero point of the z-axis at the transition between
top and mid-layer. The intensity that enters the top layer from below in the
direction
;
the value depends, of course, on r. We evaluate
the radiative transfer for the top layer according to the method described
before, and separately for the isothermal midlayer, but there it is trivial. A
boundary condition connects the two layers. In the calculation for the top
layer, we now position the zero point of the z-axis at the transition between
top and mid-layer. The intensity that enters the top layer from below in the
direction
![]() is
is
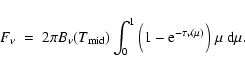 |
(A.4) |
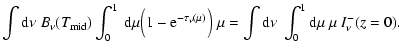 |
(A.5) |
We wish to make a few further points: a) the radiation that is absorbed in the top layer and then reemitted at
infrared wavelengths may leave the top layer, be again scattered or absorbed
there, or may enter the mid-layer. b) The net flux is always zero, but
the upward and downward integrated fluxes, F+ and F-, do depend on z, so
always
F+ +F- =0, but
![]() .
c) Good agreement in the
results of our radiative transfer code with another one is demonstrated on
the URL address
http://www.mpa-garching.mpg.de/dullemon/radtrans/benchmarks
.
c) Good agreement in the
results of our radiative transfer code with another one is demonstrated on
the URL address
http://www.mpa-garching.mpg.de/dullemon/radtrans/benchmarks