A&A 426, 1047-1063 (2004)
DOI: 10.1051/0004-6361:20035934
Emergence of magnetic flux from the convection zone
into the corona
V. Archontis 1 -
F. Moreno-Insertis
1,2 -
K. Galsgaard 3,4 -
A. Hood 3 -
E. O'Shea1
1 - Instituto de Astrofisica de Canarias (IAC), La Laguna
(Tenerife), Spain
2 -
Department of Astrophysics, Faculty of Physics,
Universidad de La Laguna, La Laguna (Tenerife), Spain
3 -
School of Mathematics and Statistics, University of St
Andrews, UK
4 -
Niels Bohr Institute for Astronomy, Physics and Geophysics,
Copenhagen, Denmark
Received 23 December 2003 / Accepted 21 April 2004
Abstract
Numerical experiments of the emergence of magnetic flux
from the uppermost layers of the solar interior to the
photosphere and its further eruption into the low
atmosphere and corona are carried out. We use idealized
models for the initial stratification and magnetic field
distribution below the photosphere similar to those used
for multidimensional flux emergence experiments in the
literature. The energy equation is adiabatic except for
the inclusion of ohmic and viscous dissipation terms,
which, however, become important only at interfaces and
reconnection sites. Three-dimensional experiments for the
eruption of magnetic flux both into an unmagnetized corona
and into a corona with a preexisting ambient horizontal
field are presented. The shocks preceding the rising
plasma present the classical structure of nonlinear Lamb
waves. The expansion of the matter when rising into the
atmosphere takes place preferentially in the horizontal
directions: a flattened (or oval) low plasma- ball
ensues, in which the field lines describe loops in the
corona with increasing inclination away from the vertical
as one goes toward the sides of the structure.
Magnetograms and velocity field distributions on
horizontal planes are presented simultaneously for the
solar interior and various levels in the atmosphere.
Since the background pressure and density drop over many
orders of magnitude with increasing height, the adiabatic
expansion of the rising plasma yields very low
temperatures. To avoid this, the entropy of the rising
fluid elements should be increased to the high values of
the original atmosphere via heating mechanisms not
included in the present numerical experiments.
ball
ensues, in which the field lines describe loops in the
corona with increasing inclination away from the vertical
as one goes toward the sides of the structure.
Magnetograms and velocity field distributions on
horizontal planes are presented simultaneously for the
solar interior and various levels in the atmosphere.
Since the background pressure and density drop over many
orders of magnitude with increasing height, the adiabatic
expansion of the rising plasma yields very low
temperatures. To avoid this, the entropy of the rising
fluid elements should be increased to the high values of
the original atmosphere via heating mechanisms not
included in the present numerical experiments.
The eruption of magnetic flux into a corona with a
preexisting magnetic field pointing in the horizontal
direction yields a clear case of essentially
three-dimensional reconnection when the upcoming and
ambient field systems come into contact. The coronal
ambient field is chosen at time t=0 perpendicular to the
direction of the tube axis and thus, given the twist of
the magnetic tube, almost anti-parallel to the field lines
at the upper boundary of the rising plasma ball. A thin,
dome-shaped current layer is formed at the interface
between the two flux systems, in which ohmic dissipation
and heating are taking place. The reconnection proceeds by
merging successive layers on both sides of the
reconnection site; however, this occurs not only at the
cusp of the interface, but, also, gradually along its
sides in the direction transverse to the ambient magnetic
field. The topology of the magnetic field in the
atmosphere is thereby modified: the reconnected field
lines typically are part of the flanks of the tube below
the photosphere but then join the ambient field system in
the corona and reach the boundaries of the domain as
horizontal field lines.
Key words: Sun: corona - Sun: magnetic fields - Sun: interior -
magnetohydrodynamics (MHD) - methods: numerical
- stars: activity
1 Introduction
The evolution of the solar corona is controlled by the local magnetic field.
However, the coronal magnetic field can be profoundly modified in response to
the emergence of magnetic flux from below the photosphere in active regions.
Large-scale emerging field is generated in the solar interior, probably in
the dynamo region around the bottom of the convection zone. The dynamo
effect may also produce field structures on smaller scales, especially closer
to the surface, leading to localized eruption processes as in, e.g., ephemeral
active regions.
In either case, the emergence of new magnetic fields can destabilize the
existing field structures and cause a variety of large-scale dynamic coronal
phenomena. Prominence eruptions, solar flares and Coronal Mass Ejections
(CMEs) are just a few.
Observations of large scale magnetic fields emerging into the corona have
been identified by the TRACE and SOHO satellites. The coronal fields are
normally outlined by plasma emitting in EUV or X-rays (e.g. TRACE and EIT). For the photosphere, direct measurements of the magnetic field, both by
satellite instruments (like MDI) as well as ground-based detectors, yield a
wealth of information. Vector magnetograms, in particular, permit the
reconstruction of all three components of the magnetic field. Shortly after
the appearance of flux at the photosphere, a system of bright coronal loops
appears in the EUV and X-ray detectors. These coronal loops seem to join the
opposite polarities of the active regions and probably delineate magnetic
field lines.
A necessary step for progress is to understand how the magnetic fields make
their way up through the convection zone and emerge through the photosphere
and chromosphere into the corona. In the deep convection zone, the
magnetic field is expected to become unstable to buoyant instabilities and,
thus, rise from the storage region to the photosphere throughout the solar
cycle. The emergence of individual thin magnetic tubes across the convection
zone has been the subject of active investigation during the past two
decades, both analytically and numerically, in most cases modelling the
magnetic tube as a 1D deformable continuum moving in the solar convection
zone (Moreno-Insertis 1986, 1997;
D'Silva & Choudhuri 1993; Caligari et al. 1995; Moreno-Insertis et al. 1994; Choudhuri 1987; Fan et al. 1994). However, once the field reaches levels close to the solar
surface, the magnetic tubes are no longer thin as regards the local
prevailing length scales, and a 1D approximation cannot be applied. Their
further rise across the photosphere and into the higher levels of the
atmosphere is still a largely unexplored research domain.
It is the aim of this paper to analyse and illustrate some of the fundamental
physical processes involved in the emergence of magnetic fields through a
series of 3D MHD simulations. In the past years, there has been much
interest in the literature in the eruption of magnetic flux through the
photosphere to the corona. Yet, given the complexity of this process and the
difficulty of discovering and explaining the basic phenomena taking place in
multidimensional numerical experiments, there are still large gaps in the
understanding of the physics involved. Numerical experimentation of this
kind stretches back to the late eighties. A first batch of models were
two-dimensional and dealt with the emergence of a horizontal flux sheet
through the development of a buoyant instability with
 (e.g., Shibata et al. 1989; 1992;
Nozawa et al. 1992, and references therein). In most cases, the initial
stratification consisted of two unmagnetized isothermal domains (simulating
photosphere and corona), with a convection zone underneath, which had
either an adiabatic or a superadiabatic temperature gradient. An interesting
feature presented in those papers was the appearance of self-similar behavior
in the nonlinear phase of the unstable evolution.
They also calculated eigenfunctions for the linear stability problem
associated with the particular initial condition they were using.
Shibata et al. (1992), while still 2D, included an ambient field in the
corona which was antiparallel to the field rising from the bottom of the
integration box. Another class of papers was also two-dimensional (or,
rather, 2.5 dimensional) but considered the rise of twisted magnetic
flux tubes with traslational symmetry of all variables along their axis
(Magara 2001; Krall et al. 1998), thereby extending to the atmosphere the 2.5D
magnetic tube rise calculations of Moreno-Insertis & Emonet (1996) and
Emonet & Moreno-Insertis (1998). Krall et al. (1998), in particular, included an
ambient field oriented vertically which could help lower the minimum
value of twist shown by Moreno-Insertis & Emonet (1996) to be necessary to maintain
the unity of the rising tube.
(e.g., Shibata et al. 1989; 1992;
Nozawa et al. 1992, and references therein). In most cases, the initial
stratification consisted of two unmagnetized isothermal domains (simulating
photosphere and corona), with a convection zone underneath, which had
either an adiabatic or a superadiabatic temperature gradient. An interesting
feature presented in those papers was the appearance of self-similar behavior
in the nonlinear phase of the unstable evolution.
They also calculated eigenfunctions for the linear stability problem
associated with the particular initial condition they were using.
Shibata et al. (1992), while still 2D, included an ambient field in the
corona which was antiparallel to the field rising from the bottom of the
integration box. Another class of papers was also two-dimensional (or,
rather, 2.5 dimensional) but considered the rise of twisted magnetic
flux tubes with traslational symmetry of all variables along their axis
(Magara 2001; Krall et al. 1998), thereby extending to the atmosphere the 2.5D
magnetic tube rise calculations of Moreno-Insertis & Emonet (1996) and
Emonet & Moreno-Insertis (1998). Krall et al. (1998), in particular, included an
ambient field oriented vertically which could help lower the minimum
value of twist shown by Moreno-Insertis & Emonet (1996) to be necessary to maintain
the unity of the rising tube.
Three-dimensional calculations of the emergence of magnetic flux through the
photosphere into the corona have been carried out by
Matsumoto & Shibata (1992), Matsumoto et al.
(1993, 1998),
Kusano et al. (1998), Fan (2001),
Magara & Longcope
(2001, 2003), and
Abbett & Fisher (2003). In spite of the low resolution of the early
simulation of Matsumoto et al. (1993), it yielded a number of important
features of the process of 3D emergence. These authors studied the
interchange (
 )
and quasi-interchange (
)
and quasi-interchange (
 with
with
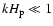 )
instabilities in a flux sheet and in a
magnetic tube in the photosphere, using as initial stratification two
isothermal domains in height (photosphere, corona) and not including any
convection zone below them. They obtained fast downflows within the flanks
of the rising loops, with shocks at their feet, marked horizontal expansion
in the higher atmospheric levels, and quasi self-similar expansion of the
magnetic loops. Matsumoto et al. (1998), Fan (2001) and
Magara & Longcope (2001,
2003) have all carried out simulations including, from
bottom to top, a convection zone, an isothermal photosphere and an isothermal
corona. They suggest similarities between their results and different
structures observed in the actual Sun, like sequences of S-shaped active
regions observed in X-rays (Matsumoto et al. 1998), photospheric observations
of the birth of active regions (Fan 2001) and X-ray sigmoids
(Magara & Longcope 2001).
Magara & Longcope (2003) study the force distribution along selected field
lines of the rising plasma, concluding the importance of the magnetic
pressure gradient to bring about the eruption. They also describe in detail
the injection of magnetic energy and helicity into the atmosphere following
the flux emergence process and discuss the relative contributions of
horizontal shear motions and vertical flux at the photosphere for both
quantities. Abbett & Fisher (2003), finally, carry out the time integration
separately for the convection zone and the atmosphere, with coupling between
them prescribed by using as input for the upper domain the distribution of
physical variables at a level close to the top of the convection zone.
)
instabilities in a flux sheet and in a
magnetic tube in the photosphere, using as initial stratification two
isothermal domains in height (photosphere, corona) and not including any
convection zone below them. They obtained fast downflows within the flanks
of the rising loops, with shocks at their feet, marked horizontal expansion
in the higher atmospheric levels, and quasi self-similar expansion of the
magnetic loops. Matsumoto et al. (1998), Fan (2001) and
Magara & Longcope (2001,
2003) have all carried out simulations including, from
bottom to top, a convection zone, an isothermal photosphere and an isothermal
corona. They suggest similarities between their results and different
structures observed in the actual Sun, like sequences of S-shaped active
regions observed in X-rays (Matsumoto et al. 1998), photospheric observations
of the birth of active regions (Fan 2001) and X-ray sigmoids
(Magara & Longcope 2001).
Magara & Longcope (2003) study the force distribution along selected field
lines of the rising plasma, concluding the importance of the magnetic
pressure gradient to bring about the eruption. They also describe in detail
the injection of magnetic energy and helicity into the atmosphere following
the flux emergence process and discuss the relative contributions of
horizontal shear motions and vertical flux at the photosphere for both
quantities. Abbett & Fisher (2003), finally, carry out the time integration
separately for the convection zone and the atmosphere, with coupling between
them prescribed by using as input for the upper domain the distribution of
physical variables at a level close to the top of the convection zone.
Against the background of the literature on this topic, our objective in the
present paper is twofold. Firstly, we carry out a numerical experiment with
initial conditions similar to those used in most of the 3D simulations
(initial magnetic tube below the surface, atmosphere consisting of two
isothermal stretches joined by a steep temperature gradient). Like those
simulations, we do not have radiative transfer or explicit coronal heating or
cooling in the calculation. Yet, we include ohmic and viscous dissipation. We
find and analyse various basic aspects of the emergence process which have
not been described, or only insufficiently, in the literature. Among them we
find: the propagation of shocks upward in the atmosphere preceding the
emerging region; the instability criterion for the buoyant instability
development when the magnetic tube reaches the photosphere; the low
temperatures and high densities of the plasma rising in the atmosphere if one
ignores all radiative or other thermal exchange processes in it; the large
predominance of horizontal over vertical expansion of the emerging plasma in
the transition region and corona, in an analogous manner to the shape of a
cake overflowing its mould as it bakes (Fig. 5); the large downflows
outside the erupting region which seem to fit the velocities observed
in transition region and corona; the behavior of magnetic and velocity fields
simultaneously at different heights from convection zone to corona, shown via
synchronous magnetograms and velocity vector distributions on
horizontal planes; etc.
Secondly, we perform a numerical experiment of a magnetic tube rising into an
atmosphere which is uniformly magnetized upward of some 1500 km above the
photosphere. The objective of this experiment is to have a first impression
of the interaction between the upcoming and existing flux systems. For the
configuration used here, with the ambient and upcoming magnetic fields
pointing in opposite directions, we find that the two systems reconnect
efficiently. This process occurs gradually as further plasma reaches coronal
heights. A drastic change of the overall topology of the field ensues: the
ambient coronal field lines starting from one side of the box get connected
to one of the flanks of the rising tube, those starting from the other side,
in turn, getting linked to the other flank of the tube. The rising plasma,
therefore, makes its way into the higher levels through reconnection
with the ambient field. As a result, in solar terms, the polarities of the
new active region get connected to external magnetic domains (a feature
repeatedly observed in satellite images of the eruption of an active region).
The layout of the paper is as follows: Sect. 2 presents the equations
and the numerical code used in the experiments. Section 3 is devoted
to a discussion of the initial condition used, both the background
stratification (3.1) and the initial field distribution in
the magnetic tube (3.2). The results of the experiment with a
field-free background atmosphere are presented in Sects. 4 through 6.
Section 7 describes the experiment with a pre-existing
ambient magnetic field in higher levels of the atmosphere and presents the
proof for ongoing reconnection, changes of connectivity and associated
phenomena. Section 8, finally contains a discussion and summary of
conclusions.
2 Equations and numerical approach
2.1 Equations
For the experiments described in this paper, the three-dimensional
time-dependent resistive MHD equations are solved numerically. For this
purpose the MHD equations are written in the form,
| |
|
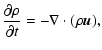 |
(1) |
| |
|
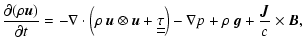 |
(2) |
| |
|
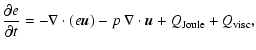 |
(3) |
| |
|
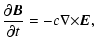 |
(4) |
| |
|
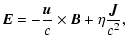 |
(5) |
| |
|
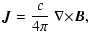 |
(6) |
| |
|
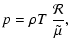 |
(7) |
with density 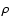 ,
velocity
,
velocity
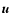 ,
acceleration of gravity
,
acceleration of gravity
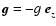 ,
thermal energy per unit volume e, average atomic mass per
particle
,
thermal energy per unit volume e, average atomic mass per
particle
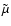 ,
magnetic field
,
magnetic field
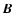 ,
electric field
,
electric field
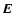 ,
magnetic
resistivity
,
magnetic
resistivity 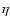 ,
electric current density
,
electric current density
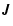 ,
viscous stress tensor
,
viscous stress tensor
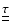 ,
gas pressure
,
gas pressure
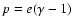 ,
viscous dissipation
,
viscous dissipation
 ,
Joule dissipation
,
Joule dissipation
 and speed of light c, respectively. The
expression
and speed of light c, respectively. The
expression
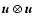 stands for the tensor (or dyadic) product of
stands for the tensor (or dyadic) product of
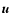 with itself. An ideal gas law (Eq. (7)) is assumed with
with itself. An ideal gas law (Eq. (7)) is assumed with
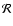 the gas constant and constant value for
the gas constant and constant value for
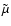 .
The ratio of
specific heats,
.
The ratio of
specific heats, 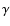 ,
is taken as 5/3.
,
is taken as 5/3.
2.2 Numerical approach
The equations are solved using a high order finite difference approach on
staggered grids. This way the conservation requirement of the MHD equations
are maintained to machine precision throughout the calculations. To calculate
the left hand side of the MHD equations above, variables have to be
communicated between the various staggered grids. For this a sixth-order
method is applied to derive the partial derivatives and a fifth-order method
is used for any interpolation required. The high order approach requires
special treatment of viscosity and magnetic resistivity to prevent
overshooting from the high order fitting at locations of steep gradients. For
this, viscosity and magnetic resistivity are both handled using a combined
second and fourth-order method with a discontinuous shock capturing mechanism
to provide the highest possible spatial resolution for the given numerical
resolution. This effectively gives a viscosity and resistivity treatment
that is locally dependent on the physical quantities and therefore give space
and time varing values of the respective Reynolds numbers. The density and
thermal energy change by many orders of magnitude from the lower boundary to
the upper boundary, with a substantial part of this change occurring over the
transition region. Interpolation in these variables is done using their
logarithmic counterparts. This limits the overshooting and at the same time
has a smoothing effect. The solution is advanced in time using a third-order
predictor-corrector method (a basic description of the code is available in
Nordlund & Galsgaard 1997, and at http://www.astro.ku.dk/~kg).
A challenge for this type of experiments is the requirement to resolve
various spatial regions, having a large domain and still being able to
compute the solution within a reasonable time. Low resolution tests have
shown which regions of the domain require high numerical resolution to
provide reliable solutions to the MHD equations. To increase resolution only
in these regions, stretched grids are applied in one or more directions. Two
regions, namely around the initial location of the flux tube and across the
transition region, are crucial. The region around the initial location of the
flux tube and across the transition region are crucial. If these regions are
not sufficiently resolved, spurious effects, such as unphysical changes in
the entropy, occur and the evolution of the emergence process is altered.
Below and above these regions less resolution is required as the length scale
of the flux tube is either of no importance for the emergence process or have
expanded significantly in size. The grid in the vertical direction is,
therefore, composed of a central region with an uniform grid covering the
initial tube location and the transition region. Outside this, the grid
spacing increases using a third order expansion. This has been used to
ensure the expansion function has a continuous second order derivative at the
transition points.
In all experiments in this paper a uniform grid in the horizontal direction
is used.
Simple boundary conditions are used: the grid is taken to be periodic in the
horizontal directions and closed in the height. The periodic condition has
the disadvantage that horizontal information propagates around the domain and
returns back after a crossing time and provides a perturbation of the
emergence process. The closed boundaries in height prevent information and
material from leaving/entering the numerical domain. This implies that the
upward propagating waves initiated by the emergence process are bounced back
at these boundaries and shortly afterwards interact with the emerging flux
tube. To limit the reflection from the closed boundaries, a damping zone has
been included at both ends of the domain. Here a fraction of the kinetic
energy in the zone is extracted per time unit, with the time scale depending
on the location along the damping zone. This works effectively for waves,
but has a more limited effect on large shocks.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0934f1.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg36.gif) |
Figure 1:
Distribution of gas pressure (solid), density (dashed),
temperature (dash-dotted), and magnetic pressure (solid curve labelled 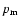 ). ). |
| Open with DEXTER |
3 Background stratification and magnetic tube at time t = 0
3.1 Background stratification
The initial stratification is a highly simplified model of the actual solar
case, including the upper layers of the solar interior, the low atmosphere,
transition region and corona. Following the tradition in flux emergence
calculations (e.g., Matsumoto et al. 1993; Fan 2001; Nozawa et al. 1992; Krall et al. 1998; Magara & Longcope 2003; Shibata et al. 1989), for the atmosphere we take two
isothermal ranges (which, for brevity, we call the low atmosphere and
the corona, respectively) at temperatures
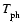 and
and
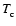 ,
with
,
with
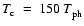 .
The transition between those layers is made via a region
with a steep temperature gradient that we call the transition region,
or TR for short. The bottom of the low atmosphere will be called
the photosphere and is placed at z=0. The values of pressure, density and
pressure scale-height at z=0, symbolized
.
The transition between those layers is made via a region
with a steep temperature gradient that we call the transition region,
or TR for short. The bottom of the low atmosphere will be called
the photosphere and is placed at z=0. The values of pressure, density and
pressure scale-height at z=0, symbolized
 and
and
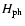 ,
will be
taken as physical units for the calculation in the rest of the paper. The
isothermal corona extends from
,
will be
taken as physical units for the calculation in the rest of the paper. The
isothermal corona extends from
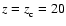 to the upper boundary. For
the transition region we choose a power-law temperature profile of the form
to the upper boundary. For
the transition region we choose a power-law temperature profile of the form
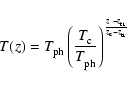 |
(8) |
extending between
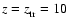 and the base of the corona,
and the base of the corona,
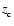 .
Underneath
the photosphere an isentropic domain with temperature growing linearly with
depth is chosen, simulating the average stratification of a convection zone
with an adiabatic temperature gradient. Hydrostatic equilibrium is assumed
everywhere (Fig. 1).
.
Underneath
the photosphere an isentropic domain with temperature growing linearly with
depth is chosen, simulating the average stratification of a convection zone
with an adiabatic temperature gradient. Hydrostatic equilibrium is assumed
everywhere (Fig. 1).
For the conversion to variables with dimensions, the following values for the
units can be used:
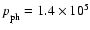 erg cm-3;
erg cm-3;
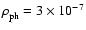 g cm-3;
g cm-3;
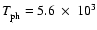 K;
K;
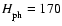 km. From these values, one
obtains a velocity unit,
km. From these values, one
obtains a velocity unit,
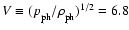 km s-1, a time unit
km s-1, a time unit
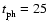 s and a magnetic field unit
s and a magnetic field unit
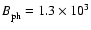 Gauss, chosen so that the Alfvén speed is unity for
Gauss, chosen so that the Alfvén speed is unity for
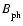 and
and
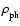 ,
and the plasma
,
and the plasma 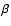 is 2 for a pressure
is 2 for a pressure
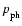 .
Surface gravity
is then
.
Surface gravity
is then
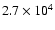 cm s-2, i.e., the solar value, and
cm s-2, i.e., the solar value, and
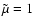 (in cg units), which is intermediate between the actual solar values in the
photosphere and the corona.
(in cg units), which is intermediate between the actual solar values in the
photosphere and the corona.
The grid for the calculation reported in this paper encompasses
the following dimensionless domain in x, y, z:
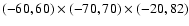 .
Resolution is critical in the vertical
direction, since the scale height is quite small in the low
atmosphere. The stretched grid provides a resolution of
.
Resolution is critical in the vertical
direction, since the scale height is quite small in the low
atmosphere. The stretched grid provides a resolution of
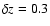 in all of the convection zone up to the base of the corona.
In x and y we use an unstretched grid. For these experiments
we typically used
in all of the convection zone up to the base of the corona.
In x and y we use an unstretched grid. For these experiments
we typically used
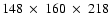 gridpoints.
gridpoints.
3.2 Initial condition for the magnetic tube
At time t=0 a magnetic flux tube is located at a height z=-12 (i.e., some
2000 km underneath the photosphere) with its axis along the y-direction
and centered in the x direction. At that depth, the pressure, density and
temperature are
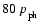 ,
density
,
density
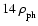 and temperature
and temperature
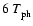 ,
respectively. A simple Gaussian profile is chosen for the longitudinal field
,
respectively. A simple Gaussian profile is chosen for the longitudinal field
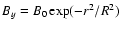 ,
with
,
with
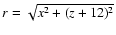 the radial
distance to the axis of the tube,
B0 = 11.8 and radius R= 2.5. The
total (
the radial
distance to the axis of the tube,
B0 = 11.8 and radius R= 2.5. The
total (
 )
dimensionless flux threading a cross section of the
tube is then
)
dimensionless flux threading a cross section of the
tube is then
 .
Using the units of Sect. 3.1, we
obtain
.
Using the units of Sect. 3.1, we
obtain
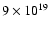 mx, as in a small active region (or a large ephemeral
active region).
mx, as in a small active region (or a large ephemeral
active region).
The ratio between the unperturbed stratified gas pressure and the magnetic
pressure at the position of the tube axis is
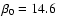 .
This is
substantially lower than the values expected on the basis of the calculations
of magnetic tubes rising across the convection zone (Caligari et al. 1995; Moreno-Insertis 2004). However, the timescale of the simulation in its initial
stages is proportional to
.
This is
substantially lower than the values expected on the basis of the calculations
of magnetic tubes rising across the convection zone (Caligari et al. 1995; Moreno-Insertis 2004). However, the timescale of the simulation in its initial
stages is proportional to
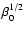 and this sets a severe upper limit
to the value we can choose to keep the duration of the simulation within
reasonable bounds. The value chosen here is a compromise in that at least it
yields central values of
and this sets a severe upper limit
to the value we can choose to keep the duration of the simulation within
reasonable bounds. The value chosen here is a compromise in that at least it
yields central values of 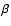 above unity while the tube is below the
photosphere. On the other hand, following Moreno-Insertis & Emonet (1996), the
field lines must be twisted around the central axis to a sufficient degree
for the rising tube to retain most of the initial magnetic flux and prevent
its being dragged to the wake. The precise criterion given by
Emonet & Moreno-Insertis (1998), valid for high-
above unity while the tube is below the
photosphere. On the other hand, following Moreno-Insertis & Emonet (1996), the
field lines must be twisted around the central axis to a sufficient degree
for the rising tube to retain most of the initial magnetic flux and prevent
its being dragged to the wake. The precise criterion given by
Emonet & Moreno-Insertis (1998), valid for high-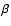 magnetic tubes with small
radius,
magnetic tubes with small
radius,
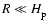 ,
(with
,
(with
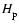 the local pressure scale-height) is
that the following condition be fulfilled:
the local pressure scale-height) is
that the following condition be fulfilled:
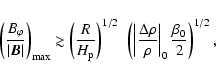 |
(9) |
where
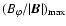 is to be calculated at the position of
the maximum of the transverse field,
is to be calculated at the position of
the maximum of the transverse field,
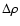 is the density
deficit in the tube compared with the original stratification and the right
hand side must be calculated at the centre of the tube. It is difficult to
fulfill this criterion for the conditions of the present paper, specially
since the ratio
is the density
deficit in the tube compared with the original stratification and the right
hand side must be calculated at the centre of the tube. It is difficult to
fulfill this criterion for the conditions of the present paper, specially
since the ratio
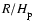 quickly grows along the rise. As in previous
flux emergence calculations (e.g., Fan 2001; Magara & Longcope 2001), we
choose helical field lines highly twisted around the central axis (albeit
with constant pitch):
quickly grows along the rise. As in previous
flux emergence calculations (e.g., Fan 2001; Magara & Longcope 2001), we
choose helical field lines highly twisted around the central axis (albeit
with constant pitch):
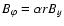 .
Our
.
Our 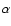 is 0.4.
This configuration yields marginal stability as regards criterion (9) for the initial magnetic tube. The field distribution above
is not force-free: there is no compelling argument for the vanishing of the
Lorentz force,
is 0.4.
This configuration yields marginal stability as regards criterion (9) for the initial magnetic tube. The field distribution above
is not force-free: there is no compelling argument for the vanishing of the
Lorentz force,
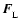 ,
since
,
since 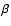 is well above unity. Yet, the Lorentz
force associated with the chosen field distribution is curl-free. Hence, a
gas pressure function can be chosen so that the sum of the isotropic gas
pressure tensor and the Maxwell stresses is continuous and equal to the gas
pressure tensor of the unperturbed stratification. This is a simple choice
for the gas pressure at time t=0 that also prevents the instantaneous
formation of a shock right from the outset.
is well above unity. Yet, the Lorentz
force associated with the chosen field distribution is curl-free. Hence, a
gas pressure function can be chosen so that the sum of the isotropic gas
pressure tensor and the Maxwell stresses is continuous and equal to the gas
pressure tensor of the unperturbed stratification. This is a simple choice
for the gas pressure at time t=0 that also prevents the instantaneous
formation of a shock right from the outset.
The choice of density (or, equivalently, entropy) distribution along the tube
can importantly influence the outcome of the simulation. Three canonical choices are available: equal density (as used by,
e.g., Caligari et al. 1995; Spruit & van Ballegooijen 1982; Moreno-Insertis 1986); equal entropy
(as used, e.g., by Moreno-Insertis & Emonet 1996; Dorch et al. 1999) or equal
temperature (as in the classical paper of Parker 1975 and in those of
D'Silva & Choudhuri 1993; and Fan et al. 1994). For flux tubes starting in the
deep convection zone, Caligari et al. (1998) have studied in detail the
physical basis and consequences of the equal-temperature and equal-density
initial conditions. In the present case, for the initial tube to yield a
rising 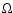 -loop, the central part (i.e., the region around y=0) must
be buoyant, or, at least, substantially more buoyant than the
feet. Alternatively, the central part could be imparted with an initial
upward velocity relative to the feet. Fan (2001) chose a non-uniform
distribution of entropy along the tube so that the flanks have equal density,
the centre equal temperature as the original unperturbed stratification. This
results in the central part being underdense by a relative factor
-loop, the central part (i.e., the region around y=0) must
be buoyant, or, at least, substantially more buoyant than the
feet. Alternatively, the central part could be imparted with an initial
upward velocity relative to the feet. Fan (2001) chose a non-uniform
distribution of entropy along the tube so that the flanks have equal density,
the centre equal temperature as the original unperturbed stratification. This
results in the central part being underdense by a relative factor 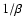 ,
which causes the rapid development of an
,
which causes the rapid development of an 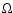 -loop shape and yields fast
emergence at the photosphere. Yet, this choice yields large entropy
differences between the centre and the flanks of the tube: in fact the
differences may be as large as those associated with the entropy loss through
radiation of plasma elements at the top of granules. Such large entropy
fluctuations are not expected in supergranules, or, even less, in the deep
convection zone (see, e.g., Spruit 1977). Hence, the origin of such
fluctuations is difficult to justify in flux tubes that erupt as active
regions (ephemeral or otherwise), given their length-scales and assumed
origin.
-loop shape and yields fast
emergence at the photosphere. Yet, this choice yields large entropy
differences between the centre and the flanks of the tube: in fact the
differences may be as large as those associated with the entropy loss through
radiation of plasma elements at the top of granules. Such large entropy
fluctuations are not expected in supergranules, or, even less, in the deep
convection zone (see, e.g., Spruit 1977). Hence, the origin of such
fluctuations is difficult to justify in flux tubes that erupt as active
regions (ephemeral or otherwise), given their length-scales and assumed
origin.
On the other hand, Matsumoto et al. (1993) and Magara & Longcope
(2001, 2003) choose an initial
tube which has the same density everywhere as the unperturbed stratified
atmosphere at the same height. To start the dynamical evolution, the latter
authors then pull the central region of the tube upward by artificially
adding vertical momentum during an interval (the first 3 min, using
their units) at the beginning of the simulation. The added vertical momentum
is given following a cosine distribution along the flux tube; the process is
stopped when the crest has been imparted a speed of 2.7 km s-1. An
isodensity initial condition is well justified at the bottom of the
convection zone (Caligari et al. 1998). Among other things, the corresponding
entropy distribution is uniform along the tube - which is more easily
compatible with the formation of the tube in a single environment. However,
at the shallow initial depth of the present kind of 3D simulations with 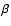 not far above one, the single value of entropy in the tube is below
any value that can be found in the whole convection zone. So, here, again it
is not immediate to justify this initial condition on physical grounds. The
initial conditions discussed in the foregoing
must then be seen mostly as convenient devices to yield a fast time evolution
of the tube.
not far above one, the single value of entropy in the tube is below
any value that can be found in the whole convection zone. So, here, again it
is not immediate to justify this initial condition on physical grounds. The
initial conditions discussed in the foregoing
must then be seen mostly as convenient devices to yield a fast time evolution
of the tube.
For simplicity, and to facilitate a better comparison with previous
literature, in the present paper we adopt one of the initial conditions just
explained. In the following sections we, therefore, use an initial density
distribution resembling the choice of Fan (2001), i.e.,
![$\rho(x,~y,~z) =
[p(x,y,z)/{p_{\rm st}}]\; {\rho_{\rm st}}(z)~\exp(-y^2/\lambda^2)$](/articles/aa/full/2004/42/aa0934/img82.gif) ,
with
,
with
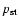 the
pressure of the unperturbed stratification and
the
pressure of the unperturbed stratification and
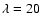 .
Experimenting
with other possible choices of initial condition is left for later work.
.
Experimenting
with other possible choices of initial condition is left for later work.
4 The emergence of magnetic field: Rise to the photosphere
4.1 Initial phase
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0934f2.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg85.gif) |
Figure 2:
The axial (By, solid lines) and transverse (Bx,
dotted lines) field components as a function of height along the vertical
axis at the centre of the box (x=y=0) at three different times during the
rise to the photosphere. The initial Gaussian profile (solid line at t=0)
decreases as the tube rises toward the surface, following the simple
expansion law
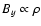 indicated by the dashed line. The
transverse component decreases more slowly than the axial field, so that the
field line pitch increases as the tube expands.
indicated by the dashed line. The
transverse component decreases more slowly than the axial field, so that the
field line pitch increases as the tube expands. |
| Open with DEXTER |
The rise through the adiabatically stratified convection zone is driven by
buoyancy, with the advance of the tube being countered basically by the drag
exerted by the surrounding medium: the Lorentz force associated with the
bending of the tube axis is too small at this phase to match the other forces
at play. A two-dimensional cut in the x-z plane (i.e., perpendicular to
the tube) through the crest of the tube shows similarities with the standard 2.5D cases calculated by Moreno-Insertis & Emonet (1996) and
Emonet & Moreno-Insertis (1998). There is only limited stretching of the tube in
the direction of the axis during most of the rise up to the photosphere.
Therefore, using the condition of magnetic flux conservation, we expect the
axial field strength to diminish following the law
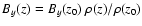 .
This law is indeed obeyed by the actual magnetic tube in
the present simulations (compare, in Fig. 2, the maximum of the
solid-line profiles with the dashed curve): the slight deviation, especially
in the final time shown, comes from the stretching of the tube in the axial
direction along the rise. On the other hand, the stronger buoyancy of the
tube centre makes it advance with respect to the periphery above it, so that
the azimuthal field component becomes enhanced at the front and weakened at
the rear in the initial stages. This is clearly visible in Fig. 2
by comparing the dotted lines at time t=0 and t=18.8. Toward the end of
the rise up to the photosphere, however, all components of the field decrease
due to the continued expansion of the tube. The decrease of the azimuthal
components, however, occurs at a slower rate than for the axial component, as
expected from flux conservation considerations. As a result, the field line
pitch increases as the tube rises. Concerning the flows around the tube, the
trailing wake does not reach the degree of development apparent in the cases
studied by Emonet & Moreno-Insertis (1998), possibly because of the higher
Reynolds number attainable in the 2.5D experiments. Full agreeement was found
in that the 3D experiments with a high level of twist (as those presented in
the current paper) retain the large majority of the initial magnetic flux as a
single tube rising in compact form, whereas test runs carried with a lower
twist yield the formation of a broad wake with two vortex rolls containing a
substantial fraction of the initial magnetic flux of the tube.
.
This law is indeed obeyed by the actual magnetic tube in
the present simulations (compare, in Fig. 2, the maximum of the
solid-line profiles with the dashed curve): the slight deviation, especially
in the final time shown, comes from the stretching of the tube in the axial
direction along the rise. On the other hand, the stronger buoyancy of the
tube centre makes it advance with respect to the periphery above it, so that
the azimuthal field component becomes enhanced at the front and weakened at
the rear in the initial stages. This is clearly visible in Fig. 2
by comparing the dotted lines at time t=0 and t=18.8. Toward the end of
the rise up to the photosphere, however, all components of the field decrease
due to the continued expansion of the tube. The decrease of the azimuthal
components, however, occurs at a slower rate than for the axial component, as
expected from flux conservation considerations. As a result, the field line
pitch increases as the tube rises. Concerning the flows around the tube, the
trailing wake does not reach the degree of development apparent in the cases
studied by Emonet & Moreno-Insertis (1998), possibly because of the higher
Reynolds number attainable in the 2.5D experiments. Full agreeement was found
in that the 3D experiments with a high level of twist (as those presented in
the current paper) retain the large majority of the initial magnetic flux as a
single tube rising in compact form, whereas test runs carried with a lower
twist yield the formation of a broad wake with two vortex rolls containing a
substantial fraction of the initial magnetic flux of the tube.
4.2 Initial upgoing shock
The start of the rise of the central section of the tube causes a
compression wave to be launched upward. The wave has small amplitude while in
the convection zone. The steep density gradient in the low atmosphere makes
it grow in amplitude and steepen to form a shock wave, reaching a large
amplitude upon rising several scale heights above the photosphere
(Fig. 3). In the low atmosphere, which has an isothermal
stratification between z=0 and z=10, the post-shock speed closely follows
an exponential law, as expected from the exponential decline of the
background density with height.
A clear deviation from the exponential behavior occurs in the transition
region (as seen in the figure for z>10). There, the unperturbed temperature
(hence the sound speed) steeply increases with height and this leads to a
slower increase, first, and, then, to a decrease of the post-shock speed.
When the shock finally enters the corona, the shock parameters change with
height very slowly. This is a consequence of the high coronal temperatures
which yield a background scaleheight of
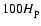 .
.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0934f3.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg88.gif) |
Figure 3:
The post-shock speed as a function of time follows an
exponential growth as the shock moves between the base of the photosphere
at z=0 and the lower level of the transition region (z=10). In the
transition region the growth is slower due to the steep temperature
rise. In the corona, finally, the large scaleheight leads to a very slow
variation of the shock strength with height. |
| Open with DEXTER |
The simulation shows further agreement with the theory of shock wave
propagation in atmospheres: in an isothermal stratification, an upgoing
compression pulse is followed by a wake in which the plasma oscillates
vertically with a frequency asymptotically approaching the acoustic cut-off
frequency,
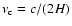 ,
(Kalkofen et al. 1994; Lamb 1932). The shock in
the present simulation develops that structure: in the low atmosphere a
vertical oscillation appears behind the upgoing shock. The first change of
sign of the oscillation occurs when the original shock is already propagating
at coronal heights. The upward-directed speed in every half-period of the
oscillation causes the upward launch of a new shock wave that ends up
propagating through the higher levels of the atmosphere. The evolution in the
low atmosphere (and even in the first several scale heights of the transition
region) is strongly reminiscent of the nonlinear results of
Kalkofen et al. (1994).
,
(Kalkofen et al. 1994; Lamb 1932). The shock in
the present simulation develops that structure: in the low atmosphere a
vertical oscillation appears behind the upgoing shock. The first change of
sign of the oscillation occurs when the original shock is already propagating
at coronal heights. The upward-directed speed in every half-period of the
oscillation causes the upward launch of a new shock wave that ends up
propagating through the higher levels of the atmosphere. The evolution in the
low atmosphere (and even in the first several scale heights of the transition
region) is strongly reminiscent of the nonlinear results of
Kalkofen et al. (1994).
4.3 Arrival at the photosphere
The main body of the rising tube acquires a rise speed of about 0.25 (some
1.7 km s-1) while still in the convection zone, so that it takes up
to time
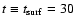 (12.5 min) for its crest to reach the
photosphere. By that time, the centre of the tube is still at a depth of
some 850 km (z=-5). The density contrast between initial depth and
photosphere (factor 14) causes a marked expansion of the tube. In fact,
vertical and horizontal expansion rates are different, since the former has
to do extra work against gravity: indeed, we see a large horizontal
expansion with only a moderate expansion in height (a result anticipated by
Spruit et al. 1987; and also visible in the figures of some of the 2.5D simulations cited in the introduction).
To quantify this effect, we consider a vertical cross section of the tube,
measure the full width at half maximum of the magnetic field both in
the vertical direction upward of the tube centre and horizontally from it and
calculate the ratio of those two quantities: the result at
(12.5 min) for its crest to reach the
photosphere. By that time, the centre of the tube is still at a depth of
some 850 km (z=-5). The density contrast between initial depth and
photosphere (factor 14) causes a marked expansion of the tube. In fact,
vertical and horizontal expansion rates are different, since the former has
to do extra work against gravity: indeed, we see a large horizontal
expansion with only a moderate expansion in height (a result anticipated by
Spruit et al. 1987; and also visible in the figures of some of the 2.5D simulations cited in the introduction).
To quantify this effect, we consider a vertical cross section of the tube,
measure the full width at half maximum of the magnetic field both in
the vertical direction upward of the tube centre and horizontally from it and
calculate the ratio of those two quantities: the result at
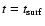 is 3. When the periphery of the tube reaches the surface (see, e.g., the solid
and dotted curves at t=35 in Fig. 2), the field lines are almost
at an angle of 90 deg to the initial direction of the axis, following the
pitch-angle increase described in Sect. 4.1 The plasma beta
of the mass elements reaching the photosphere is 4, not far from the actual
solar values: recent observational results obtained with Stokes polarimetry
by Martinez-Pillet (private communication) yield values of 600 G for the
rising magnetic field close to the photosphere, a figure which compares
favorably with the values obtained in the present simulation.
is 3. When the periphery of the tube reaches the surface (see, e.g., the solid
and dotted curves at t=35 in Fig. 2), the field lines are almost
at an angle of 90 deg to the initial direction of the axis, following the
pitch-angle increase described in Sect. 4.1 The plasma beta
of the mass elements reaching the photosphere is 4, not far from the actual
solar values: recent observational results obtained with Stokes polarimetry
by Martinez-Pillet (private communication) yield values of 600 G for the
rising magnetic field close to the photosphere, a figure which compares
favorably with the values obtained in the present simulation.
An isothermal stratification (as chosen for the low atmosphere,
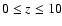 )
has logarithmic temperature gradient
)
has logarithmic temperature gradient
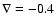 ,
and is,
therefore, stable against the convective instability. The further
upward motion of the tube thus involves lifting overdense plasma against
gravity. The tube cannot continue its rise unimpeded, and reduces its
velocity by about a factor 2. This, in turn, produces a relative pressure hill at the point of emergence: the upward moving plasma elements
at lower levels get deflected sideways (except those strictly on the vertical
midplane of the tube) and the area covered by magnetic plasma at the
photosphere increases with time. Thus, the tube enters an intermediate
phase, characterized by a slower rise of the magnetized plasma upward of the
photosphere and the enhanced expansion in the transverse direction.
,
and is,
therefore, stable against the convective instability. The further
upward motion of the tube thus involves lifting overdense plasma against
gravity. The tube cannot continue its rise unimpeded, and reduces its
velocity by about a factor 2. This, in turn, produces a relative pressure hill at the point of emergence: the upward moving plasma elements
at lower levels get deflected sideways (except those strictly on the vertical
midplane of the tube) and the area covered by magnetic plasma at the
photosphere increases with time. Thus, the tube enters an intermediate
phase, characterized by a slower rise of the magnetized plasma upward of the
photosphere and the enhanced expansion in the transverse direction.
The further evolution occurs on the basis of the buoyancy instability
experienced by the plasma above the photosphere. Buoyant instabilities, both
in magnetized and unmagnetized plasmas, have been thoroughly studied in the
literature (Newcomb 1961; Yu 1965; Acheson 1979; see
also the review by Hughes & Proctor 1988). The fundamental mechanism is
the fact that a magnetic intensity distribution which decreases with height,
by reducing the gas pressure gradient, promotes the top-heavy instability,
i.e., as when heavier fluid overlies lighter one. In the present case,
however, the strongly stabilizing effect of the subadiabatic stratification
above z=0 can effectively thwart the development of the instability: any
plasma packet rising adiabatically would soon become heavier than the
environment. The precise criterion for instability against perturbations
which bend the field lines reads (Newcomb 1961; Thomas & Nye 1975;
Acheson 1979)
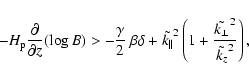 |
(10) |
with 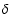 the superadiabatic excess,
the superadiabatic excess,
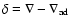 ,
, 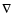 the logarithmic temperature gradient and
the logarithmic temperature gradient and
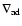 its adiabatic value, and
its adiabatic value, and
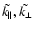 the
wavenumbers of the perturbation in the two horizontal directions parallel and
perpendicular, respectively, to the magnetic field in units of the local
scaleheight (Eq. (10) corresponds to the expression given by
Acheson 1979, rewritten with our variables). The left-hand side term
just describes the instability-promoting effect of the decrease of B with
height in the upper part of the tube (as apparent in Fig. 2). A
crucial term, containing the effect of the stratification, is the
the
wavenumbers of the perturbation in the two horizontal directions parallel and
perpendicular, respectively, to the magnetic field in units of the local
scaleheight (Eq. (10) corresponds to the expression given by
Acheson 1979, rewritten with our variables). The left-hand side term
just describes the instability-promoting effect of the decrease of B with
height in the upper part of the tube (as apparent in Fig. 2). A
crucial term, containing the effect of the stratification, is the
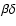 term on the right-hand side of the inequality. For an isothermal
stratification
term on the right-hand side of the inequality. For an isothermal
stratification
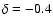 ,
which causes strong stabilization. However,
this term is multiplied by
,
which causes strong stabilization. However,
this term is multiplied by 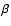 and, therefore, becomes small as the
magnetic pressure grows above the local gas pressure when the tube crosses
the photosphere. In the actual experiment, when the upper layers of the
rising tube reach the photosphere, the left-hand side term is well below the
stratification term on the right. As the topmost magnetic layers cross the
photosphere, their ratio quickly changes as the plasma
and, therefore, becomes small as the
magnetic pressure grows above the local gas pressure when the tube crosses
the photosphere. In the actual experiment, when the upper layers of the
rising tube reach the photosphere, the left-hand side term is well below the
stratification term on the right. As the topmost magnetic layers cross the
photosphere, their ratio quickly changes as the plasma 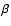 decreases. Finally, the ratio goes below 1: precisely at this time (
decreases. Finally, the ratio goes below 1: precisely at this time (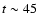 ,
i.e., some 10 min after arrival at the photosphere), the
subadiabatically stratified plasma above it can no longer check the further
rise of the tube and the buoyancy instability is launched, which takes the
magnetized plasma all the way up to the corona. By then the uppermost layers
of the tube are at z=6 and its centre has reached z=-2. We think this
also explains (at least partially) why the duration of the intermediate phase
is proportional to the intensity of the field reaching the photosphere, hence
also to the field strength of the tube at time t=0 (a fact already pointed
out by Magara 2001): the weaker the field that reaches the
photosphere, the longer it takes for the plasma
,
i.e., some 10 min after arrival at the photosphere), the
subadiabatically stratified plasma above it can no longer check the further
rise of the tube and the buoyancy instability is launched, which takes the
magnetized plasma all the way up to the corona. By then the uppermost layers
of the tube are at z=6 and its centre has reached z=-2. We think this
also explains (at least partially) why the duration of the intermediate phase
is proportional to the intensity of the field reaching the photosphere, hence
also to the field strength of the tube at time t=0 (a fact already pointed
out by Magara 2001): the weaker the field that reaches the
photosphere, the longer it takes for the plasma 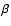 to go down
sufficiently so that the right-hand side of inequality (10)
becomes low enough. The instability described here is related with, but is
different from, the simple magnetic Rayleigh-Taylor instability of a heavy
fluid overlying a lighter, more strongly magnetized one, with a sharp
interface separating them. The gradients of field and entropy, in particular,
are absent from the simple RT-instability theory, but they are crucial to
determine threshold and growth rate. To our knowledge, criterion (10) has not been used in the previous literature cited in
the introduction.
to go down
sufficiently so that the right-hand side of inequality (10)
becomes low enough. The instability described here is related with, but is
different from, the simple magnetic Rayleigh-Taylor instability of a heavy
fluid overlying a lighter, more strongly magnetized one, with a sharp
interface separating them. The gradients of field and entropy, in particular,
are absent from the simple RT-instability theory, but they are crucial to
determine threshold and growth rate. To our knowledge, criterion (10) has not been used in the previous literature cited in
the introduction.
![\begin{figure}
\par\hspace*{2mm}\includegraphics[height=4.3cm,width=5.5cm,clip]{...
...ce*{4mm}
\includegraphics[height=4.4cm,width=5.3cm,clip]{0934f6.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg103.gif) |
Figure 4:
Anisotropic expansion of the rising plasma. The diagram on
the top shows the vertical velocity profile along the z axis going through
the centre of the box. A typical expansion profile between the photosphere
and the lower levels of the corona is apparent, with maximum velocity
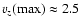 .
The diagrams in the center and on the bottom show the
distribution of horizontal speed in the plane z=20 along the x and yaxis, respectively. A clear expansion profile is found here as well, but the
velocities are much higher: .
The diagrams in the center and on the bottom show the
distribution of horizontal speed in the plane z=20 along the x and yaxis, respectively. A clear expansion profile is found here as well, but the
velocities are much higher:
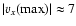 and
and
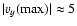 . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0934f7.ps}\par\includegraphi...
...8cm,clip]{0934f8.ps}\par\includegraphics[width=8cm,clip]{0934f9.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg106.gif) |
Figure 5:
3d ( upper panel) and 2d ( middle and bottom panels)
visualization of the magnetic field strength of the expanding tube at t=70.46. In the upper panel, the isosurface corresponds to
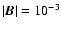 (maximum
(maximum 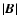 at this time is 2.4). The color map shows
the isointensity contours of the expanding tube in the midplane along the y-direction ( middle panel) and z-direction ( bottom panel). The dashed
lines are auxiliary lines for Fig. 6.
at this time is 2.4). The color map shows
the isointensity contours of the expanding tube in the midplane along the y-direction ( middle panel) and z-direction ( bottom panel). The dashed
lines are auxiliary lines for Fig. 6. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0934f10.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg107.gif) |
Figure 6:
Downflows in the periphery of the rising magnetic region as the tube enters
the corona (t=74). Shown is the distribution of vz with height along the
following lines: ( upper panel) vertical line situated within the x=0midplane of the box at y=46 (shown as a dashed line in Fig. 5,
central panel); ( lower panel) vertical line situated within the
y=0 midplane of the box the tube at x=40 (shown as a dashed line in
Fig. 5, bottom panel). The maximum downflow speeds in the
figure correspond to about 24 km s-1. |
| Open with DEXTER |
5 The expansion into the higher atmosphere
5.1 Runaway expansion of the magnetized plasma and downflows
in the periphery
For the parameters chosen in the simulation described here, the expansion
into the higher levels of the atmosphere (starting around t=60) occurs in a
runaway fashion. A clear sign of this is that the distribution of magnetic
pressure with height above the photosphere in the expanding magnetized
plasma volume is a few orders of magnitude larger than the gas pressure.
The vertical velocity of the rising plasma quickly
increases to
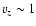 when the front of the expanding volume reaches
the bottom of the transition region (at z=10). By time t=70.4 the
velocity profile along the central vertical axis (x=0, y=0) within the
upgoing magnetic volume shows a monotonic increase of the vertical velocity
with height between
when the front of the expanding volume reaches
the bottom of the transition region (at z=10). By time t=70.4 the
velocity profile along the central vertical axis (x=0, y=0) within the
upgoing magnetic volume shows a monotonic increase of the vertical velocity
with height between
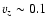 at z=2 and
at z=2 and
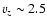 at z=27,
where the front of the tube is located (Fig. 4, upper panel).
at z=27,
where the front of the tube is located (Fig. 4, upper panel).
The runaway expansion also takes place in the horizontal directions, in fact
with higher speeds than in the vertical direction. For instance, at
t=70.5, the x-component of the velocity along the horizontal plane z=20(base of the corona) shows a quasi-monotonic expansion profile away from the
centre, reaching a speed of
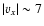 at
at
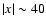 ,
which is where
the boundary of the magnetized region is located (see Fig. 4,
central panel). In a similar manner, the y-component of the velocity along
the same horizontal plane shows that the tube expands sideways with a maximum
velocity of
,
which is where
the boundary of the magnetized region is located (see Fig. 4,
central panel). In a similar manner, the y-component of the velocity along
the same horizontal plane shows that the tube expands sideways with a maximum
velocity of
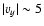 at
at
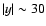 (Fig. 4, bottom
panel).
(Fig. 4, bottom
panel).
The resulting 3D image of the magnetic region can be visualized using
isointensity surfaces of the magnetic field (Fig. 5, upper panel) or
the corresponding isointensity contours within the vertical midplane along
the y-direction (Fig. 5, central panel) and along the
transverse (x) direction (bottom pannel). The
magnetized volume has the shape of a narrow region at the original level in
the convection zone around z=-10, suffering a first expansion up to the
photosphere and then a second (and much more marked) expansion in the
atmosphere, as a cake being baked which is contained in its mould in the
lower levels but overflowing it and expanding in all directions above it.
The plasma surrounding the rising magnetized ball also shows some dramatic
dynamics: it gets pushed sideways by the expanding plasma and reaches similar
horizontal velocities. Also, because of mass conservation, the fast rise and
expansion of the magnetic plasma causes strong downflows along its periphery
(see Fig. 6). Typical values for the downflow velocity can be
as high as
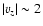 (i.e.,
(i.e., 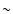 14 km s-1) at the height of
the transition region and
14 km s-1) at the height of
the transition region and
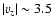 (
(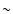 24 km s-1) above
the base of the corona. These values compare favorably with velocities
observed along the line of sight in developed active region loops at
chromospheric and coronal levels (Chae et al. 1998; Brekke et al. 1997).
24 km s-1) above
the base of the corona. These values compare favorably with velocities
observed along the line of sight in developed active region loops at
chromospheric and coronal levels (Chae et al. 1998; Brekke et al. 1997).
5.2 The magnetic field lines
Additionally to isosurfaces, actual field lines are necessary to illustrate
the structure and topology of the magnetic field. Previous authors
(Fan 2001; Magara & Longcope 2001, 2003)
have shown the shape of three individual field lines (the tube axis and two
more peripheral lines), pursuing them along time. In this section we would
like to show whole sets of field lines at a time when the eruption into the
corona is well advanced, to better visualize the global geometry of the
magnetic field and the linkage between different parts of the volume.
Figure 7 shows three sets of field lines (in blue,
green and red, respectively) all of them calculated at time t=72. Three
views are shown: front (uppermost panels), side (middle panels) and top view
(lower panels). To facilitate the visualization, an isosurface of the total
magnetic field strength at
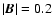 is added (maximum magnetic field
strength at that time is
is added (maximum magnetic field
strength at that time is
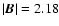 ,
located in the legs of the tube).
The first set of field lines (solid lines in blue color, left side)
is drawn starting from points close both to the tube axis and to the
y-boundary on the right side of the computational domain.
These lines
remain inside the volume limited by the isosurface in the flanks of the
tube. Only their windings in the central part traverse the isosurface (and
are thus visible in the figure). There, they reach moderate heights, at any
rate below the corona.
,
located in the legs of the tube).
The first set of field lines (solid lines in blue color, left side)
is drawn starting from points close both to the tube axis and to the
y-boundary on the right side of the computational domain.
These lines
remain inside the volume limited by the isosurface in the flanks of the
tube. Only their windings in the central part traverse the isosurface (and
are thus visible in the figure). There, they reach moderate heights, at any
rate below the corona.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{0934f11.ps}\includegraphic...
...7cm,clip]{0934f15.ps}\includegraphics[width=6.7cm,clip]{0934f16.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg119.gif) |
Figure 7:
Eight panels showing different views of the
fieldlines at time t=72, when the rising magnetic plasma has already
reached coronal heights. The panels on the left side of the figure show the
fieldlines closer to the
main axis of the tube (blue) and those who reach the top layer of the
transition region (green). The panels on the right side (in red color) show
more clearly the runaway expansion of the fieldlines into the corona. |
| Open with DEXTER |
The second set (green solid lines, left side)
consists of field lines starting right at
the isosurface close to the y-boundary. They remain by the isosurface in
the flanks but, upon reaching the central section, they describe large loops
linking the photosphere with the upper levels of the low atmosphere. The
sideways expansion in the axial direction experienced by the plasma along the
rise is clearly visible here (see the front view in the top-left panel). The
succesive windings as one goes from the vertical x-z midplane toward the
flanks are increasingly inclined, with each individual winding being
contained in a curved surface. These fieldines have an orientation more
perpendicular to the central axis of the tube than the innermost (blue)
fieldlines around the central part (see the top view shown in the bottom-left
panel). This shape is visible already in one of the field lines shown by the
authors cited above.
The third set (right side of Fig. 7, colored in red), consists
of field lines starting from points in the flanks of the tube slightly
outside the volume enclosed by the isosurface. This set of field lines
reaches the highest levels of the magnetized plasma, located well above the
original interface with the corona. Their shape illustrates, more clearly
than the second set, the strongly azimuthal nature of the field lines in the
central region and the effects of the predominance of the lateral expansion
of the upcoming plasma.
The isosurface shown in the figure, in turn, is particularly interesting
since it clearly shows (a) the flattened structure of the magnetic region at
the photosphere, following the processes discussed in Sect. 4.3,
and (b) an S-shaped structure along the y-direction (clearly discernible
in the top view panels). The S-shape is a consequence of the gradual
conversion of field line twist into writhe along the calculation. S-shapes
have also been found and discussed by previous authors (e.g., Fan 2001; Matsumoto et al. 1998; Magara 2001).
5.3 adiabatic cooling and resulting stratification
Further features associated with the runaway expansion are the adiabatic
cooling and the deviation of the stratification from the initial hydrostatic
profile. The present simulation has no radiative transfer or cooling built in
and so the moving plasma must behave adiabatically wherever the gradients are
not so large that the diffusion terms become important. On the other hand,
the initial stratification has two isothermal ranges, which have a steep
increase in entropy. Hence, the expanding plasma of the magnetic tube must
show marked differences in its pressure, density and thermal distributions
with height as compared with the pre-existing distributions at time t=0,
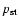 ,
,
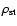 ,
,
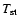 .
In fact, the profiles at time t=78.7 show (1)
much lower gas pressure and temperature than the original stratification,
with a maximum ratio of a few orders of magnitude; (2) dominating magnetic
pressure, well above the original gas pressure, and with the plasma
.
In fact, the profiles at time t=78.7 show (1)
much lower gas pressure and temperature than the original stratification,
with a maximum ratio of a few orders of magnitude; (2) dominating magnetic
pressure, well above the original gas pressure, and with the plasma 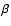 going down to
O(10-3) and (3)
going down to
O(10-3) and (3)
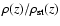 of order one in the
lower atmosphere but well above that value closer to the front of the
expanding tube, in fact, with a maximum of 100. It is remarkable that the
rising plasma ball can push up such dense matter, compared with the density
of the preexisting atmosphere. The reason is the high value of the magnetic
pressure gradient (as apparent in the left panel of
Fig. 8), which is well above the (gas) pressure gradient
in the background hydrostatic stratification.
of order one in the
lower atmosphere but well above that value closer to the front of the
expanding tube, in fact, with a maximum of 100. It is remarkable that the
rising plasma ball can push up such dense matter, compared with the density
of the preexisting atmosphere. The reason is the high value of the magnetic
pressure gradient (as apparent in the left panel of
Fig. 8), which is well above the (gas) pressure gradient
in the background hydrostatic stratification.
![\begin{figure}
\par\includegraphics[height=5.6cm,width=5.3cm,clip]{0934f17.ps}\h...
...e*{2mm}
\includegraphics[height=5.6cm,width=5.8cm,clip]{0934f19.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg123.gif) |
Figure 8:
Height distribution of pressure, density and temperature at
time t=0 (solid lines) and at time t=78.7 (dashed and dash-dotted
lines). Left panel: magnetic pressure (solid and dashed lines) and gas
pressure (solid and dash-dotted lines). Central panel: density. Right panel:
temperature. The emerging plasma is magnetically dominated, with the plasma
beta decreasing to order 10-3 in it, and has a higher density (factor 100) and lower temperature (factor 104) than the original coronal
values. |
| Open with DEXTER |
The thermal behavior of an actual active region in the Sun must deviate
from the above. In the low atmosphere, radiative transfer in the rising
plasma will be the main thermal agent causing its entropy to vary in time,
with the timescales for the radiative exchange in some spectral lines being
as short as seconds. In the higher levels of the atmosphere, coronal heating,
possibly ohmic heating associated with nanoflare reconnection or wave
dissipation, will increase the temperature of the magnetic plasma to coronal
levels. More complicated models will have to deal with these additional
aspects. The current results can be of interest in that they show how cool
the emerging plasma can get if the heating mechanisms are not in operation
(or are not fast enough).
6 Synthetic magnetograms and velocity fields at different levels
The lack of radiative transfer and explicit coronal heating processes in the
equations we are using limits the possibilities of carrying out comparisons
of our results with observations of the birth and rise into the corona of an
active region. However, it may be instructive to construct synthetic magnetograms and velocity vector fields of the active region produced
in the current simulation simultaneously at different heights in the box.
Figure 9 shows filled contours of the surface distribution of Bz on
horizontal cuts of the box situated at a depth of 850 km (z=-5), the
photosphere (z=0), the base of the transition region (z=10) and the base
of the corona (z=20). The corresponding distribution of the total velocity
is shown by arrows which are superimposed on the above magnetograms. For
clarity, in the two topmost panels only two cuts, corresponding to the
convection zone and the photosphere, are presented; the two lowermost panels,
in turn, show cuts for the photosphere, transition region and corona. For
the photosphere, magnetograms and velocity fields have been presented by
previous authors (Fan 2001; Magara & Longcope 2001,
2003); our results for that layer agree in broad terms
with theirs.
When the top part of the magnetic tube first reaches the photosphere (t
= 30.4, Fig. 9, top-left, upper slice), the vertical field
component, Bz, yields a simple bipolar structure constituting an
incipient active region. Its orientation at this very early stage of
evolution is perpendicular to the central axis of the tube (North-South,
or N-S, orientation in the following, for short). This is due to the
high level of twist of the field lines in the periphery of the tube (see
Fig. 2 and Sect. 5.2) together with the fact
that the flanks of the magnetic tube are not yet sufficiently inclined
for the axial field component to have a large enough projection on the
vertical direction. A magnetogram in the convection zone at the
same time (lower cut in the same panel), shows two N-S bipolar
structures, one at each flank of the magnetic tube, which, again are due
to the transverse field component and the small inclination of the tube
axis at that level. Also there, we see a strong upflow in the central
regions of the slice in the wake of the emerging active region, with a
weak downflow close to the footpoints. Strong upflow is also apparent in
the photosphere (upper slice) where the velocity distribution has a
divergence pattern with horizontal flows around the bipolar
region. These flows are directed away from the site of emergence, both
in the N-S and E-W directions.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0934f20.ps}\includegraphic...
...m,clip]{0934f22.ps}\includegraphics[width=7.5cm,clip]{0934f23.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg124.gif) |
Figure 9:
Synthetic magnetograms and velocity vector
distribution on two-dimensional cuts at different times and heights in
the convection zone and atmosphere. The panels in the top row show cuts
at z=-5 (convection zone, lower slice) and z=0 (photosphere, upper
slice) at time t=30.4 ( left panel) and t=42.4 ( right panel). The
panels at the bottom correspond to a later stage of the emergence
(t=57, left, and t=67, right) and show the photosphere (lowermost cut),
the transition region (z=10, central cut) and the corona (z=20, top
cut). The colour-scaled maps correspond to the vertical magnetic field, Bz; the arrows correspond to the velocity vector. |
| Open with DEXTER |
At a somewhat later time (t= 42.4, top-right panel), the emergence
process has progressed considerably: in the photosphere, upflow at the
centre and horizontal motions in the periphery are more marked than in
the panel on the left; the magnetized area in the photosphere is now
much larger, the feet of the tube in the convection zone have receded
toward the E-W boundaries. The inclination of the flanks is now larger,
which gives more weight to the positive (negative) Bz component on
the East (West) side of the magnetogram. As a result, we see in the
figure (upper panel) that the N-S bipolarity at the photosphere is
beginning to turn into an E-W alignment.
There is also a shear flow along the neutral (axis-aligned) line, with
the horizontal velocity component pointing toward the East on the north
side of the neutral line and toward the West on the south side.
As shown by Manchester (2001), this is a consequence of the Lorentz force,
which is no longer small in the photosphere, and the frozen-in condition for
magnetic field and plasma: the field line twist thus causes an extra pull to
the plasma in the direction parallel (antiparallel) to the tube axis on the
north (south) side.
At later stages of emergence (t=57 and t=67, shown in the two lower
panels of Fig. 9), the magnetogram in the photosphere (lowermost cut
in the panels) shows the magnetic distribution to have turned into a bipolar
structure roughly oriented in the E-W direction, as one expects from active
region observations: the polarity seen on each side corresponds to the sign
of the component of the field along the main axis of the tube; its flanks
have now a sufficient inclination for that polarity to be predominant. On one
side of the main polarity one sees a patch of weaker, opposite polarity
magnetic field. This is still due to the field line twist and is a remnant of
the situation described for the top panels in the figure; the opposite
polarity patches slowly fade away as the flanks of the tube become more
inclined. The panels include a cut at the base of the corona (z=20, topmost
cut in each panel) and a cut at the base of the transition region (z=10,
central cut). In all of them, the Bz-distribution shows N-S oriented
bipolarity. In the panel on the left, the magnetized region has just reached
the base of the corona; the velocity field there (slice at the top) shows an
upflow coinciding with the site of emergence. In the central cut of the left
panel and in both the TR and coronal cuts on the right, in contrast, the
velocity arrows indicate a strong horizontal expansion accompanied by a
weaker upflow component of the velocity. All of this is in agreement with the
magnetic field intensity isosurfaces (Fig. 5) and field line diagrams
(Fig. 7) described in Sect. 5.2, which show
the predominance of the expansion in the horizontal directions in terms of
velocity values and stretching rates as compared to the expansion in the
vertical direction.
7 Emergence of magnetic flux into an atmosphere with preexisting
horizontal magnetic field: Evidence of
reconnection
In the previous sections the dynamics of a magnetic tube rising into a
field-free atmosphere has been discussed. This section investigates the
implications of the presence of a simple background coronal magnetic
field prior to the emergence of the magnetized region from the convection
zone. The initial conditions of Sect. 3.1 are thus altered
by including a plane-parallel magnetic field above a certain height, as
follows.
The background magnetic field is taken to be uniform in the xy-plane as
well as at all heights above z=10. It shows a smooth decrease in strength to
zero in the lower part of the transition region. To maintain the hydrostatic
balance of the atmosphere, the gas pressure in those heights is decreased
accordingly. The background magnetic field is everywhere chosen to point in
the negative x-direction:
![${\vec{B}} = [B_x(z), 0, 0]$](/articles/aa/full/2004/42/aa0934/img125.gif) (S-N direction). The
sign and orientation of the coronal magnetic field is such that it optimizes
the magnetic reconnection with the magnetic flux system rising from the
convection zone: as shown in the previous sections the upper parts of the
upcoming magnetized region are predominantly oriented in the N-S direction.
A precursor to this experiment was done carried out by
(Shibata et al. 1992), although only in 2D. As explained in the following,
there are important differences between two- and three-dimensional
experiments.
(S-N direction). The
sign and orientation of the coronal magnetic field is such that it optimizes
the magnetic reconnection with the magnetic flux system rising from the
convection zone: as shown in the previous sections the upper parts of the
upcoming magnetized region are predominantly oriented in the N-S direction.
A precursor to this experiment was done carried out by
(Shibata et al. 1992), although only in 2D. As explained in the following,
there are important differences between two- and three-dimensional
experiments.
The evolution of the emerging flux tube, up to the time where the
flux of the rising tube comes into contact with the coronal
magnetic field, is nearly identical with the zero coronal magnetic
field case. The minor differences between the two cases are due to
the small change in the characteristic propagation speed in the
corona.
As the magnetized plasma rises through the transition region, the orientation
of the emerging magnetic field is nearly parallel to the x-direction as
described earlier. With the particular choice of 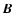 made for the
background corona and flux tube, when the two systems get in contact their
magnetic fields are antiparallel. For the flux tube to emerge into the
corona, it has to either push the ambient magnetic field away or reconnect
with it to open up a volume into which the emerging field can expand.
Figure 10 contains a series of panels
showing magnetic field lines traced from the boundaries in the
x-direction with two different orientations.
The starting points for the field line traces are chosen to
have a constant height in z and a uniform distribution along y. The
colours indicate starting points at three different heights, traced from
alternative locations near the x boundary. The time series shows how the
field lines maintain their clear horizontal direction despite the continual
buffeting by waves in the corona.
As the upper part of the rising flux tube reaches the lower part of the
coronal magnetic field, the coronal magnetic field is pushed upwards and a
current concentration is formed that has a dome-like structure (just as seen
in Fig. 12). The current magnitude increases with time and
magnetic reconnection eventually starts, firstly at the summit point of the
emerging flux and later on by spreading down along the sides (E-W direction)
of the emerging region in a direction aligned with the flux tube. This
creates two new distinct classes of field lines which connect parts of the
outer layers of the flux tube to the coronal magnetic field. One such class
contains field lines from the front/left x-boundary of the domain that
connect to the flux tube and reach the left/back y-boundary of the
image, represented by the light blue field lines. The other
class connects the field lines from the right/front y-boundary of
the flux tube to the back/right x-boundary of the box,
shown by the blue field lines.
Hence, we are witnessing full 3D reconnection. In 2D, the traditional
X-type reconnection
connects magnetic field from above and below the current sheet
region and produces newly connected field lines in the outflow
region that are formed from half of the field lines in each of the
inflow regions (Priest & Forbes 2000). Here the situation is similar for the
local region
in the neighbourhood of the reconnection site. The difference from
the 2D description increases with horizontal distance from the reconnection
site. This is because the field lines no longer stay in the 2D plane. It is the magnetic field component along the flux tube that
provides the preferred direction of connectivity for the field
lines on either side of the symmetry line along the emerging flux.
made for the
background corona and flux tube, when the two systems get in contact their
magnetic fields are antiparallel. For the flux tube to emerge into the
corona, it has to either push the ambient magnetic field away or reconnect
with it to open up a volume into which the emerging field can expand.
Figure 10 contains a series of panels
showing magnetic field lines traced from the boundaries in the
x-direction with two different orientations.
The starting points for the field line traces are chosen to
have a constant height in z and a uniform distribution along y. The
colours indicate starting points at three different heights, traced from
alternative locations near the x boundary. The time series shows how the
field lines maintain their clear horizontal direction despite the continual
buffeting by waves in the corona.
As the upper part of the rising flux tube reaches the lower part of the
coronal magnetic field, the coronal magnetic field is pushed upwards and a
current concentration is formed that has a dome-like structure (just as seen
in Fig. 12). The current magnitude increases with time and
magnetic reconnection eventually starts, firstly at the summit point of the
emerging flux and later on by spreading down along the sides (E-W direction)
of the emerging region in a direction aligned with the flux tube. This
creates two new distinct classes of field lines which connect parts of the
outer layers of the flux tube to the coronal magnetic field. One such class
contains field lines from the front/left x-boundary of the domain that
connect to the flux tube and reach the left/back y-boundary of the
image, represented by the light blue field lines. The other
class connects the field lines from the right/front y-boundary of
the flux tube to the back/right x-boundary of the box,
shown by the blue field lines.
Hence, we are witnessing full 3D reconnection. In 2D, the traditional
X-type reconnection
connects magnetic field from above and below the current sheet
region and produces newly connected field lines in the outflow
region that are formed from half of the field lines in each of the
inflow regions (Priest & Forbes 2000). Here the situation is similar for the
local region
in the neighbourhood of the reconnection site. The difference from
the 2D description increases with horizontal distance from the reconnection
site. This is because the field lines no longer stay in the 2D plane. It is the magnetic field component along the flux tube that
provides the preferred direction of connectivity for the field
lines on either side of the symmetry line along the emerging flux.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0934f24.eps}\hspace*{4mm}
...
...eps}\hspace*{4mm}
\includegraphics[width=7.7cm,clip]{0934f31.eps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg126.gif) |
Figure 10:
Magnetic field line traces and isosurfaces of strong
magnetic field in time show the changes in
the connectivity as the flux tube emerges into the coronal magnetic
field. The images represent the times 52.0, 66.7, 80.8, and 85.8
from the top down. Two different orientations of the domain are
shown from left to right. The box represents the full size of the domain.
From the right column the dark blue and green field lines are traced from
the right side boundary, the light blue are traced from the left side
boundary and the red field lines are traced from a line going through the
isosurface. |
| Open with DEXTER |
If magnetic reconnection only took place at the summit of the emerging field,
then only field lines from a region in the vicinity of this point would
undergo magnetic reconnection. For the tube to rise significantly into the
corona, it would have to push the rest of the coronal flux sideways,
resulting in a significant compression of the magnetic field in the
horizontal direction. This is not seen in the experiment. Instead, it is
found that the extension in the y-direction (E-W) of the flux connecting
from the x-boundaries to the flux rope is comparable to the area occupied
by the rising flux tube in the y=0 plane, leaving only a small compression
in the horizontal direction of the coronal magnetic field. This implies that
the magnetic field lines from the flux tube reconnect nearly as fast as they
are brought into contact with the coronal magnetic field and that
reconnection must take place over a large
part of the y-extent (E-W) of the rising loop at any height in z. From
Fig. 10 it is apparent that coronal field
lines from the same z-heights connect onto the same cylindrical radii of
the flux tube, despite the fact that they reconnect at different times. This
supports a picture whereby the outer layers of the flux tube are slowly
peeled off by the reconnection process in a similar manner to removing layers
of an onion. Therefore, the larger the z-height of a coronal layer that
connects to the tube, the smaller the radius of the flux tube that it
connects to. As a consequence, this requires the rising flux tube to have
a larger amount of flux than the coronal flux of the region that the
tube is rising into. If the flux in the rising tube is too small, then it
cannot rise into the corona and produce its own magnetic structure. It will
instead totally reconnect with the coronal magnetic field, so that the feet
of the magnetic tube will end up connected to different ambient sources. In
other words, the two polarities of the newly-emerged active regions would be
connected to different magnetic areas in the atmosphere instead of to each
other.
In 2D, magnetic reconnection can easily be recognized by the presence of a
quadrupolar vorticity structure aligned with the separator lines, e.g.,
(Sonnerup 1988). Figure 11 shows the xz-plane along the centre
of the tube, showing the y-component of the vorticity. The top and bottom
panels of the figure correspond to the cases without and with background
coronal magnetic field, respectively. Only in the case with background
magnetic field do we see a clear quadrupolar structure, namely the upper
x-structure in the figure, the lower one being due to a sudden increase of
emergence pushing its way up. The x-structured vorticity pattern can be
taken as a telltale signature of ongoing reconnection, even if we had no
magnetic field line traces to prove it.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0934f32.ps}\par\includegraphics[width=8cm,clip]{0934f33.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg127.gif) |
Figure 11:
The panels show the y-component
of the vorticity in the xz plane along the centre of the
tube. Dark blue and yellow represents opposite, positive-negative,
extrema of the vorticity. Top panel shows the case without a coronal
magnetic field, while the bottom panel shows the case with a coronal
magnetic field. The panels represent t=64.7 and t=70.0 respectively. |
| Open with DEXTER |
The reconnection of the magnetic field lines between the rising
flux tube and the overlying coronal field creates plasma heating
due to Joule dissipation. In Fig. 12, the impact of
Joule dissipation on the increase in thermal energy is illustrated
by means of isosurfaces of 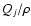 ,
with Qj the Joule heating rate.
The figure shows a prominent, narrow layer co-spatial with the vortex
structure seen in the previous figure. The Joule dissipation associated with
the magnetic reconnection between the rising flux tube and the coronal
magnetic field heats the plasma mostly in this region.
,
with Qj the Joule heating rate.
The figure shows a prominent, narrow layer co-spatial with the vortex
structure seen in the previous figure. The Joule dissipation associated with
the magnetic reconnection between the rising flux tube and the coronal
magnetic field heats the plasma mostly in this region.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0934f34.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg128.gif) |
Figure 12:
An isosurface of 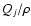 (red) and of constant magnetic
field strenght (green) are shown. The red isosurface
indicates the locations in space where the Joule dissipation
has a significant impact on the heating of the plasma. Notice
that the dome shaped structure outlining the region where the
coronal magnetic field interacts with the rising flux
tube (t=80.5). The box represents the full size of the domain.
(red) and of constant magnetic
field strenght (green) are shown. The red isosurface
indicates the locations in space where the Joule dissipation
has a significant impact on the heating of the plasma. Notice
that the dome shaped structure outlining the region where the
coronal magnetic field interacts with the rising flux
tube (t=80.5). The box represents the full size of the domain. |
| Open with DEXTER |
8 Discussion and conclusions
The problem of magnetic flux emergence from the solar convection zone through
the photospheric region and into the corona has been undertaken. The
numerical experiments presented consider a twisted magnetic flux tube lying
in an adiabatically stratified interior. The initial disturbance is created
by choosing a distribution of density along the tube axis so that the central
regions are buoyant and start to rise toward the photosphere. Two classes of
simulations have been undertaken.
Firstly, a series of simulations of a twisted flux tube emerging into a
field-free corona have been performed. To optimize the link with previous
attempts at this kind of experiment, we have used simplified initial
conditions as found in the literature (Matsumoto et al. 1993,
1998; Magara & Longcope 2001,
2003; Fan 2001), with, in particular, the
buoyancy distribution along the tube chosen as in the paper by
Fan. The aim of our simulations was to provide a physical
understanding of various physical processes not mentioned (or not explained)
in the previous literature. The initial stages of the rise show a clear
resemblance to the 2.5D tube rise calculations of
Moreno-Insertis & Emonet (1996). On the other hand, the initiation of the flux tube
rise, due to magnetic buoyancy, generates a compressive wave that rapidly
grows in amplitude and steepens to form a shock. We obtain excellent
agreement with the results of Kalkofen et al. (1994) and Lamb (1932),
which also serves as a further test of the numerical code, specially in view
of the strong stratification in the background density. The emergence occurs
in two distinct stages. The initial rise due to buoyancy slows down as the
flux tube reaches the isothermally stratified photosphere: if unmagnetized,
this very subadiabatic stratification would not allow the development of
buoyant instabilities, due to its steep increase in entropy with height. In
our case, though, the decrease of magnetic field intensity with height in the
upper part of the rising tube provides a source of instability that is related
(but different) to the Rayleigh-Taylor instability, as studied in detail in
the literature of the 1960's and 1970's cited in
Sect. 4.3. Instability ensues if the logarithmic magnetic pressure
gradient is steeper than the normalized entropy gradient
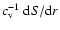 times the plasma
times the plasma 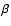 ,
with
,
with 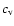 the specific heat at constant volume.
As the tube rises (even if slowly) in the photosphere, the plasma
the specific heat at constant volume.
As the tube rises (even if slowly) in the photosphere, the plasma 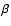 goes from well above 1 down to values below unity, and this allows the
buoyant instability to develop: a runaway expansion occurs, the magnetized
plasma rises and expands and it tries to fill the available coronal volume.
goes from well above 1 down to values below unity, and this allows the
buoyant instability to develop: a runaway expansion occurs, the magnetized
plasma rises and expands and it tries to fill the available coronal volume.
Pressure and density decrease steeply with height in the atmospheric regions
below the corona (see, e.g., Fig. 1) and it is there that the rising
plasma suffers the largest expansion. We note that the expansion takes place
preferentially in the horizontal directions, so that the rising ball
eventually adopts an oval, or flattened shape, with fast elongation in the
x and y directions (Fig. 5). This process is accompanied by
downflows in the surrounding plasma with speed comparable to those observed
in the solar transition region and corona. Also because of the sideways
expansion, the field line windings within the plasma ball
(Fig. 7, right column) are increasingly inclined toward the
flanks of the tube. This feature is akin to the fan-like shape seen
in satellite (e.g., TRACE) coronal loop images. Also apparent in that same
figure (top view panel), is that the horizontal projection of those field
lines is almost perpendicular to the direction of the initial tube axis. This
is a consequence of the high field line pitch in the tube at time t=0, and
its increase following the expansion, as expected from elementary MHD considerations. Thus, the mutual orientation of coronal magnetic field and
bipolar region in the surface cannot be easily matched with the corresponding
solar observations, at least during these initial phases of the eruption into
the atmosphere. A further consequence, discussed below, of the rapid
quasi-adiabatic expansion of the plasma in the atmosphere is that the
temperature falls dramatically, in fact to values well below those in the
initial stratification. Finally, the results of our simulations were used to
produce synthetic magnetograms and dopplergrams. The appearance of the
bipolar region on horizontal planes does depend on the height it is observed
at. This is also linked to the twist profile of the rising flux tube.
A second class of simulations involved the emergence of the flux tube into a
pre-existing horizontal coronal field. The orientation of the coronal field
was selected to optimize the possibility of magnetic reconnection with the
outermost flux tube field lines. When the upcoming and ambient coronal fields
come into contact, a thin, dome-shaped current sheet is formed and reconnection
is started, which changes the general topology of the magnetic field in the
box: the reconnected field lines start as horizontal field lines of the
coronal ambient field in the x-boundary, but end in the y-boundary as
twisted field lines of the magnetic tube. The reconnection process continues
by the pressing together of successive layers of upcoming plasma and
ambient field. In fact, as time goes on, the reconnection extends to field
lines situated sideways from the apex of the current sheet. The latter
constitutes a genuine 3D effect, not present in simple 2D models. The
reconnection process produces plasma heating due to Joule dissipation, but
the consequent rise in temperature is limited to just the region close to the
reconnection site.
Some of the features listed in the foregoing paragraphs need some further
discussion. The initial conditions for the magnetic field distribution used
in the current paper (as well as in basically all related literature) provide
for a fast emergence to the photosphere, which is a pre-condition for the
feasibility of this type of 3D numerical experiments. Choosing this kind of
initial condition, though, is not strictly in agreement with what we know
about the evolution of the magnetic field in the convection zone. From
general physical reasoning as well as through the results of the experiments
on the emergence of magnetic tubes across the convection zone, we expect the
rising tubes in the final few Megametres of their rise below the photosphere to
have (1) large rising speeds (say, up to order one tenth the local sound
speed); (2) a plasma beta clearly above unity; and (3) an entropy which
corresponds to that of their initial location, since the rise in the
convection zone should be faster than the local timescales for thermal
exchange and, hence, basically adiabatic. Condition (2), in particular,
means that there is no compelling argument to assume a force-free situation
for the initial tube. The choice of entropy distribution, on the other hand,
is not trivial, since it influences the buoyancy distribution and, hence, the
rise of the tube to the photosphere. In Sect. 3.2 we showed how the
standard choices in the literature of 3D flux emergence do not really fit
with either a deep origin of the magnetic flux at the bottom of the
convection zone nor a local assembling of the flux by, e.g., the
supergranules (to produce, say, small ephemeral active regions). So, the
initial condition chosen and its implications on the emergence process should
be subjected to detailed study in the future.
One of the major limitations of the 3D simulations of emergence into the
atmosphere so far is the lack of an adequate description of the entropy
sources in the energy equation (e.g., radiative transfer in photosphere
and chromosphere, or, from a different perspective, direct energy deposition
in chromosphere and corona via e.g. wave dissipation). This fact combined with
the large expansion of the plasma when rising above the photosphere without
explicit sources of chromospheric or coronal heating leads to low
temperatures in the magnetized volume in those levels, well below what can be
expected in the real Sun. Now, in the Sun the chromosphere is expected to
have a two-component structure, with cold and hot regions simultaneously
present, the latter being created by the dissipation of vertically running
waves generated mainly through the ongoing convection in the
(sub)photospheric levels and steepening to yield shocks (Carlsson & Stein 2002; Asensio Ramos et al. 2003; Wedemeyer et al. 2004; Ayres 1981). On the other hand, the
corona is expected to be heated through nanoflares or, perhaps, also wave
dissipation (see, e.g., Walsh 2002). Our code does not cope with all those
mechanisms, and including them at the present stage would unduly complicate
the simplicity of the current numerical experiments. Yet, even without extra
entropy sources, the experiments presented already show results which
resemble features observed in the Sun. As a simple alternative, one can use
an ad-hoc heating/cooling term directly proportional to the deviation from
the initial temperature profile (Newton's law), as used by
Abbett & Fisher (2003). Yet, even at the price of obtaining unrealistic
temperatures, in the present context it is better to carry out simulations
with as simple thermodynamics as possible, to spot the fundamental MHD
effects, leaving the inclusion of additional ingredients for future
papers. Nonetheless, in the present simulation there is ohmic and
viscous dissipation included via a hyperdiffusive ansatz, which are
important basically at interfaces and regions of sharp magnetic field
gradients. In fact, in the second set of simulations
(Sect. 7), we observe important heating in the thin
current sheet formed in the interface between upcoming plasma and ambient
coronal field. This heating being limited basically to a shell
(Fig. 12), can not heat the volume of rising magnetized plasma
below.
As a counterpart, numerical dissipation associated with the limitations on
spatial resolution can provide an unwanted source of entropy which can
importantly change the results of the experiments. A case in point has to do
with the buoyancy in the convection zone. The initial magnetic structure is
necessarily concentrated. Choosing too coarse a resolution for the volume
occupied by the initial tube leads to ohmic dissipation, which artificially
increases the entropy in the initial stages of the rise. This leads to an
increase of temperature, decrease of density and, from there, enhanced
buoyancy in the tube. Now, the dynamics of the initial phase is typically
driven by buoyancy with a density deficit of order the canonical Parker
value,
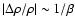 .
In a high-
.
In a high-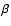 environment, one
has to take extra care that the density deficit is not unduly increased
through numerical dissipation. This puts a strict lower limit to the
resolution to be used in mapping the convection zone in the experiment. It
is perhaps of interest to note that one cannot assign a single value of the
viscous and magnetic Reynolds number as such for the whole experiment.
Values for
environment, one
has to take extra care that the density deficit is not unduly increased
through numerical dissipation. This puts a strict lower limit to the
resolution to be used in mapping the convection zone in the experiment. It
is perhaps of interest to note that one cannot assign a single value of the
viscous and magnetic Reynolds number as such for the whole experiment.
Values for 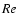 can be determined after the run, assuming that the Joule
dissipation is simply given by
can be determined after the run, assuming that the Joule
dissipation is simply given by 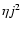 .
Doing this, one can obtain mean
values in the different regions varying between 100 and several thousand.
Similar difficulties apply when trying to define a global Lundquist number.
.
Doing this, one can obtain mean
values in the different regions varying between 100 and several thousand.
Similar difficulties apply when trying to define a global Lundquist number.
This paper represents a first attempt at a detailed description of the
process of eruption of magnetic field into the atmosphere. The parameters
chosen correspond to a small active region or a standard ephemeral active
region. To keep the physics simple (and, hence, to maximize the possibilities
of analyzing and understanding the results), we have used drastic
simplifications of the initial stratification and of the thermodynamics of
the plasma, not allowing for preexisting convection below the photosphere,
radiative transfer (which is important especially in the low atmosphere),
nor heat conduction or explicit radiative cooling (of importance in the
corona), in line with previous similar attempts in the literature. Future
work will have to incorporate gradually those additional features.
Acknowledgements
Computational time on the following massively parallel computers is
gratefully acknowledged: SRIF and PPARC funded Linux cluster in St. Andrews
(Scotland, UK); SGI Origin 2000 in CIEMAT (Madrid, Spain); MCYT and IAC
funded Linux Cluster in La Laguna (Tenerife, Spain); PPARC funded
Compaq MHD Cluster (St Andrews, UK); UK Astrophysical Fluids Facility
(UKAFF). This work has also benefited from financial support through the Platon European Research Training Network HPRN-CT-2000-00153 of the European
Commission and the CICYT project No. AYA2001-1649 of the Spanish Ministery of
Science and Technology (MCYT). KG was supported by PPARC in the form of an
Advanced Fellowship and by the Carlsberg Foundation in the form of a
fellowship.
- Abbett,
W. P., & Fisher, G. H. 2003, ApJ, 582, 475 [NASA ADS] [CrossRef] (In the text)
- Acheson, D. J.
1979, Sol. Phys., 62, 23 [NASA ADS] (In the text)
- Asensio
Ramos, A., Trujillo Bueno, J., Carlsson, M., & Cernicharo, J.
2003, ApJ, 588, 61L [NASA ADS] [CrossRef]
- Ayres, T. R. 1981,
ApJ, 244, 1064 [NASA ADS] [CrossRef]
- Brekke, P.,
Hassler, D. M., & Wilhelm, K. 1997, Sol. Phys., 175, 349 [NASA ADS] [CrossRef]
-
Caligari, P., Moreno-Insertis, F., & Schüssler, M. 1995,
ApJ, 441, 886 [NASA ADS] [CrossRef]
-
Caligari, P., Schüssler, M., & Moreno-Insertis, F. 1998,
ApJ, 502, 481 [NASA ADS] [CrossRef] (In the text)
-
Carlsson, M., & Stein, R. F. 1992, ApJ, 397, 59 [NASA ADS] [CrossRef]
-
Carlsson, M., & Stein, R. F. 2002, ApJ, 572, 626 [NASA ADS] [CrossRef]
-
Cattaneo, F., Chiueh, T., & Hughes, D. W. 1990, J. Fl. Mech.,
219, 1 [NASA ADS]
- Chae, J., Wang,
H., Qiu, J., Goode, P., & Wilhelm, K. 2000, ApJ, 533, 535 [NASA ADS] [CrossRef]
- Choudhuri, A.
R. 1987, ApJ, 316, 788 [NASA ADS] [CrossRef]
- Dorch, S. B.
F., Archontis, V., & Nordlund, A. 1999, A&A, 352, 79 [NASA ADS]
- D'Silva, S., &
Choudhuri, A. R. 1993, A&A, 272, 621 [NASA ADS]
-
Emonet, T., & Moreno-Insertis, F. 1998, ApJ, 492, 804 [NASA ADS] [CrossRef] (In the text)
- Fan, Y. 2001, ApJ, 554,
L111 [NASA ADS] [CrossRef] (In the text)
- Fan, Y.,
& Gibson, S. E. 2003, ApJ, 589, L105 [NASA ADS] [CrossRef]
- Fan, Y., Fisher,
G. H., & McClymont, A. N. 1994, ApJ, 436, 907 [NASA ADS] [CrossRef]
- Fan, Y., Zweibel,
E. G., Linton, M. G., & Fisher, G. H. 1998, ApJ, 505, L59 [NASA ADS] [CrossRef]
-
Hughes, D. W., & Proctor, M. R. E. 1988,
Ann. Rev. Fluid Mech, 20, 187 [NASA ADS] [CrossRef] (In the text)
-
Kalkofen, W., Rossi, P., Bodo, G., & Massaglia, S. 1994,
A&A, 284, 976 [NASA ADS]
- Krall, J.,
Chen, J., Santoro, R., et al. 1998, ApJ, 500, 992 [NASA ADS] [CrossRef]
- Kusano, K.,
Moriyama, K., & Miyoshi, T. 1998, Phys. Plasmas, 5, 2582 [NASA ADS] [CrossRef] (In the text)
- Lamb, H. 1932,
Hydrodynamics (New York: Dover)
- Magara, T. 2001,
ApJ, 549, 608 [NASA ADS] [CrossRef]
-
Magara, T., & Longcope, D. W. 2001, ApJ, 559, 55 [NASA ADS] [CrossRef] (In the text)
-
Magara, T., & Longcope, D. W. 2003, ApJ, 586, 630 [NASA ADS] [CrossRef] (In the text)
- Manchester,
W. 2001, ApJ, 547, 503 [NASA ADS] [CrossRef] (In the text)
-
Matsumoto, R., & Shibata, K. 1992, PASJ, 44, 167 [NASA ADS] (In the text)
-
Matsumoto, R., Tajima, T., Shibata, K., & Kaisig, M. 1993, ApJ,
414, 357 [NASA ADS] [CrossRef] (In the text)
-
Matsumoto, R., Tajima, T., Chou, W., Okubo, A., & Shibata, K.
1998, ApJ, 493, L43 [NASA ADS] [CrossRef] (In the text)
-
Moreno-Insertis, F. 1986, A&A, 166, 291 [NASA ADS] (In the text)
-
Moreno-Insertis, F. 1997, Mem. Soc. Astr. It., 68, 429 [NASA ADS] (In the text)
-
Moreno-Insertis, F. 2004, in preparation
-
Moreno-Insertis, F., & Emonet, T. 1996, ApJ, 472, L53 [NASA ADS] [CrossRef] (In the text)
- Moreno-Insertis, F., Caligari,
P., & Schüssler, M. 1994, Sol. Phys., 153, 449 [NASA ADS]
- Newcomb, W. A.
1961, Phys. Fl., 4, 391 [NASA ADS] (In the text)
- Nordlund, A., & Galsgaard, K.
1997, Tech. Rep., Astronomical Observatory, Copenhagen
University
(In the text)
- Nozawa, S.,
Shibata, K., Matsumoto, R., et al. 1992, ApJS, 78, 267 [NASA ADS] [CrossRef] (In the text)
- Parker, E. N. 1975,
ApJ, 198, 205 [NASA ADS] [CrossRef] (In the text)
- Priest,
E., & Forbes, T. 2000, Magnetic Reconnection MHD Theory
and Applications (Cambridge Univ. Press)
(In the text)
- Priest, E.,
Titov, V., Vekestein, G., & Rickard, G. 1994, J. Geophys. Res.,
99, A11 [NASA ADS] [CrossRef], 21
- Shibata,
K., Tajima, T., Matsumoto, R., et al. 1989, ApJ, 338, 471 [NASA ADS] [CrossRef] (In the text)
- Shibata,
K., Nozawa, S., & Matsumoto, R. 1992, PASJ, 44, 256 [NASA ADS] (In the text)
- Sonnerup, B. U.
Ö. 1988, Comp. Phys. Commun., 49, 142 [NASA ADS] (In the text)
- Spruit, H. C. 1977,
Ph.D. Thesis, Univ. Utrecht
(In the text)
- Spruit,
H. C., & van Ballegooijen, A. A. 1982, A&A, 106, 58 [NASA ADS]
- Spruit, H.
C., Title, A., & van Ballegooijen, A. A. 1987, Sol. Phys., 110,
115 [NASA ADS] (In the text)
- Thomas, J.
H., & Nye, A. H. 1975, Phys. Fl., 18, 490 [NASA ADS] (In the text)
- Walsh, R. W. 2002, in
From Solar Min to Max: Half a solar cycle with SOHO, ESA SP-508,
253
(In the text)
-
Wedemeyer, S., Freytag, B., Steffen, M., Ludwig, H.-G., &
Holweger, H. 2004, A&A, 414, 1121 [EDP Sciences] [NASA ADS] [CrossRef]
- Yu, C. P. 1965, Phys. Fl.,
8, 650 [NASA ADS] (In the text)
Copyright ESO 2004
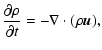
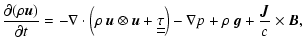
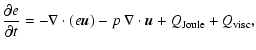
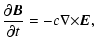
![\begin{figure}
\par\includegraphics[width=7cm,clip]{0934f1.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg36.gif)
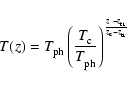
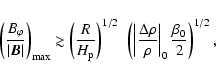
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0934f2.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg85.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{0934f3.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg88.gif)
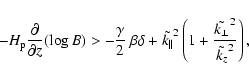
![\begin{figure}
\par\hspace*{2mm}\includegraphics[height=4.3cm,width=5.5cm,clip]{...
...ce*{4mm}
\includegraphics[height=4.4cm,width=5.3cm,clip]{0934f6.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg103.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0934f7.ps}\par\includegraphi...
...8cm,clip]{0934f8.ps}\par\includegraphics[width=8cm,clip]{0934f9.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg106.gif)
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{0934f10.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg107.gif)
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{0934f11.ps}\includegraphic...
...7cm,clip]{0934f15.ps}\includegraphics[width=6.7cm,clip]{0934f16.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg119.gif)
![\begin{figure}
\par\includegraphics[height=5.6cm,width=5.3cm,clip]{0934f17.ps}\h...
...e*{2mm}
\includegraphics[height=5.6cm,width=5.8cm,clip]{0934f19.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg123.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0934f20.ps}\includegraphic...
...m,clip]{0934f22.ps}\includegraphics[width=7.5cm,clip]{0934f23.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg124.gif)
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{0934f24.eps}\hspace*{4mm}
...
...eps}\hspace*{4mm}
\includegraphics[width=7.7cm,clip]{0934f31.eps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg126.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0934f32.ps}\par\includegraphics[width=8cm,clip]{0934f33.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg127.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0934f34.ps}
\end{figure}](/articles/aa/full/2004/42/aa0934/Timg128.gif)