A&A 426, L25-L28 (2004)
DOI: 10.1051/0004-6361:200400073
3-D numerical simulations of rotating jets
The case of the DG Tau microjet
A. H. Cerqueira
1 -
E. M. de Gouveia Dal Pino2
1 - LATO-DCET-UESC, Rodovia Ilhéus -
Itabuna, km 16, Ilhéus, Bahia, CEP
45662-260, Brazil
2 -
IAG-USP, Rua do Matão, 1226, Cidade
Universitária, São Paulo, São Paulo,
CEP 01060-970, Brazil
Received 29 April 2004 / Accepted 6 September 2004
Abstract
We here present results of three-dimensional Smoothed Particle hydro and
magnetohydrodynamics simulations of rotating jets, also including the
effects of radiative cooling, precession and velocity variability. Using
initial conditions and parameters which are particularly suitable for the
DG Tau microjet, we have been able to approximately reproduce its complex
knotty morphology and kinematics. We have also obtained radial velocity
maps which are in good agreement with the data obtained by Bacciotti et al.,
thus indicating that their interpretation that the DG Tau
microjet is rotating is correct. Finally, we have found that a magnetic
field of the order of 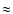 0.5 mG is sufficient to collimate the jet
against the lateral expansion that is caused by the centrifugal forces.
0.5 mG is sufficient to collimate the jet
against the lateral expansion that is caused by the centrifugal forces.
Key words: ISM: jets and outflows: Herbig-Haro objects - stars:
formation
The seek for the real nature of the accretion-ejection mechanism
underlying the formation of the jets is one of the major contributions of
the detailed analysis of Herbig-Haro (HH) jet data. The statement that
MHD models can be responsible for generating the jets associated with
Young Stellar Objects is still a matter of debate. The theoretical
discussion of the so-called magneto-centrifugal models for jet
launching (e.g., Blandford & Payne 1982; Königl 1982;
Spruit 1996), can be strongly constrained by the existence of
observational data.
Recent observations of microjets associated with T-Tauri stars, namely,
DG Tau, RW Aur, TH28 and LkH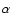 321 (Bacciotti et al. 2002;
Coffey et al. 2004), have revealed important trends in the
jet radial velocity field that are consistent with a rotation pattern
inside the jet beam. The presence of rotation could be understood in the
context of the magneto-centrifugal models as due to jet launching from
a Keplerian accretion disk along with the magnetic field lines which
are anchored into the disk-star system and provide the collimation of
the beam.
321 (Bacciotti et al. 2002;
Coffey et al. 2004), have revealed important trends in the
jet radial velocity field that are consistent with a rotation pattern
inside the jet beam. The presence of rotation could be understood in the
context of the magneto-centrifugal models as due to jet launching from
a Keplerian accretion disk along with the magnetic field lines which
are anchored into the disk-star system and provide the collimation of
the beam.
Motivated by these recent findings, we have carried out a set of
fully three-dimensional simulations of rotating jets, also taking into
account the presence of radiative cooling, jet precession, and velocity
variability (to allow the production of internal knots). All these are
necessary ingredients to address the kinematical complexity of the
microjets and we are here particularly interested in the DG Tau microjet
case, which is one of the best studied in the literature. We have also
investigated, in few models, the collimating effects of magnetic fields
upon rotating jets.
In order to examine the behaviour of the microjets and their early
evolution near the source under the effects of both rotation and
precession, we here employ modified versions of our three-dimensional
Smoothed Particle Hydrodynamics (3-D SPH) and Magnetohydrodynamics (3-D
SPMHD) codes which were previously designed to investigate the large scale
structure and evolution of protostellar jets either in the absence (see,
e.g., de Gouveia Dal Pino 2001) or in the presence of magnetic fields
(e.g, Cerqueira & de Gouveia Dal Pino 2001).
Our computational domain is a rectangular box that mimics the ambient
medium and has dimensions
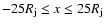 ,
and
,
and
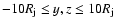 ,
where
,
where 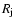 is the initial jet radius (which
is also the code distance unit). The Cartesian coordinate system has
its origin at the center of the box and the jet flow is continuously
injected into the bottom of the box [at the inlet which has coordinates
is the initial jet radius (which
is also the code distance unit). The Cartesian coordinate system has
its origin at the center of the box and the jet flow is continuously
injected into the bottom of the box [at the inlet which has coordinates
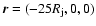 ]
with top-hat density and pressure profiles.
The jet and gas pressures are assumed to be in equilibrium at the inlet.
Inside the box, the SPH particles are initially regularly distributed
in a cubic lattice. An outflow boundary condition is assumed for the
boundaries of the box. The particles are smoothed out by a spherically
symmetric kernel function of width h, and the initial values of h were
chosen to be
]
with top-hat density and pressure profiles.
The jet and gas pressures are assumed to be in equilibrium at the inlet.
Inside the box, the SPH particles are initially regularly distributed
in a cubic lattice. An outflow boundary condition is assumed for the
boundaries of the box. The particles are smoothed out by a spherically
symmetric kernel function of width h, and the initial values of h were
chosen to be
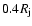 and
and
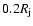 for the ambient and jet particles,
respectively. The adiabatic index of the ambient medium and the jet is
assumed to be
for the ambient and jet particles,
respectively. The adiabatic index of the ambient medium and the jet is
assumed to be
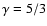 ,
and an ideal equation of state is used. The
radiative cooling, due to collisional excitation and recombination, is
implicitly calculated using a time-independent cooling function for a gas
of cosmic abundances cooling from
,
and an ideal equation of state is used. The
radiative cooling, due to collisional excitation and recombination, is
implicitly calculated using a time-independent cooling function for a gas
of cosmic abundances cooling from
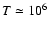 to
to
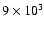 K.
K.
The adopted parameters for the simulations are appropriate to the
conditions generally found in protostellar jets and, in particular,
in the DG Tau microjet. We take a number density ratio between the
jet and the ambient medium
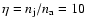 ;
;
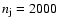 cm-3;
an average ambient Mach number
cm-3;
an average ambient Mach number
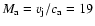 ,
where
,
where
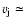 300 km s- 1 is the average jet velocity of DG Tau (e.g., Bacciotti
et al. 2002; Pyo et al. 2003), and
300 km s- 1 is the average jet velocity of DG Tau (e.g., Bacciotti
et al. 2002; Pyo et al. 2003), and
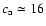 km s-1 is the
ambient sound speed for a gas with an average temperature of 104 K;
and
km s-1 is the
ambient sound speed for a gas with an average temperature of 104 K;
and
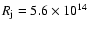 cm (see e.g., Dougados et al. 2000;
Bacciotti et al. 2002).
cm (see e.g., Dougados et al. 2000;
Bacciotti et al. 2002).
We have carried out several simulations considering both continuous
and pulsing jets (see below). In the latter cases, we have adopted a
sinusoidal profile to describe the ejection velocity time-variability
at the inlet:
![$v_{\rm o}(t)= v_{\rm j} [1 + A\cdot{\rm sin}({{2 \pi}\over
\tau_{\rm pul}} t)]$](/articles/aa/full/2004/41/aagd292/img21.gif) ,
where A is the velocity amplitude and
,
where A is the velocity amplitude and
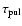 is
the period of the oscillation. The values for these parameters were
obtained from observations of the DG Tau microjet (see, e.g., Lavalley
et al. 1997; Raga et al. 2001) which suggest A=0.33, and
is
the period of the oscillation. The values for these parameters were
obtained from observations of the DG Tau microjet (see, e.g., Lavalley
et al. 1997; Raga et al. 2001) which suggest A=0.33, and
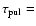 8 years =
8 years =
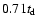 (where
(where
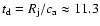 years corresponds to the transverse jet dynamical time). In the numerical
models where the jet precession has been also taken into account, we have
assumed an equal precession period (i.e.,
years corresponds to the transverse jet dynamical time). In the numerical
models where the jet precession has been also taken into account, we have
assumed an equal precession period (i.e.,
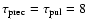 years) and a precession half-angle
years) and a precession half-angle
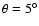 as indicated by the
DG Tau jet observations (Lavalley-Fouquet et al. 2000; Dougados et al.
2000).
as indicated by the
DG Tau jet observations (Lavalley-Fouquet et al. 2000; Dougados et al.
2000).
For the computation of the jet rotation around its main axis, we have
assumed that the flow conserves its angular momentum after its passage
through the Alfven surface (i.e.,
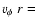 constant, where
constant, where
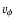 is the toroidal velocity in the normal direction to the jet
axis). This is consistent with magneto-centrifugal mechanisms for jet
launching (see, e.g., Spruit 1996) and is also suggested by
the observations of the DG Tau microjet (Bacciotti et al. 2002)
which imply
is the toroidal velocity in the normal direction to the jet
axis). This is consistent with magneto-centrifugal mechanisms for jet
launching (see, e.g., Spruit 1996) and is also suggested by
the observations of the DG Tau microjet (Bacciotti et al. 2002)
which imply
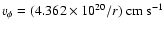 where r is the radial distance to the jet axis in cm. This gives
where r is the radial distance to the jet axis in cm. This gives
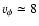 km s-1 at the jet surface (
km s-1 at the jet surface (
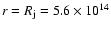 cm), and
cm), and
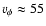 km s-1 near the jet axis
(at
km s-1 near the jet axis
(at
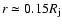 )
)
![[*]](/icons/foot_motif.gif) . It should be
emphasized that we are here mostly interested in carrying out simulations
of jet regions near the source but beyond the Alfven surface (e.g.,
Spruit 1996) where the flow has accelerated to velocities
larger than the Alfven speed and is believed to be already collimated,
and which are, at least in some cases, partially resolved by optical
observations (as for instance, DG Tau).
. It should be
emphasized that we are here mostly interested in carrying out simulations
of jet regions near the source but beyond the Alfven surface (e.g.,
Spruit 1996) where the flow has accelerated to velocities
larger than the Alfven speed and is believed to be already collimated,
and which are, at least in some cases, partially resolved by optical
observations (as for instance, DG Tau).
Table 1 summarizes the properties of the simulated models.
In model A,
we have run a precessing jet with constant velocity at injection and
no rotation. In model B, we have considered a pulsing precessing
jet also without rotation, and in model C we have run a jet which is
simultaneously pulsating, precessing, and rotating. All these three
models are purely hydrodynamical and share the same initial conditions
as described above. Their velocity distribution is compared in Fig. 1
after they have propagated over a time
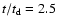 .
In model C, the jet is
precessing counter clockwise while rotating clockwise. The jet of model
A develops a V-shape structure at the head which is commonly detected
in precessing jets (e.g., Masciadri et al. 2002; Masciadri &
Raga 2003; Rosen & Smith 2004) and is due to the impact
of the parcels propagating in different directions in the wiggling flow
with the bow-shock front. In the jet of model B, the combined effects of
pulsation and precession produce internal working surfaces propagating
in different directions. In this case, a narrower bowshock structure
develops at the head that makes it to propagate slightly faster than the
jet of model A. The rotating jet of model C essentially bears the same
features of the previous models but develops an even larger head than
model A due to the centrifugal forces that tend to push the jet flow
outwards in the radial direction (see also Fig. 3 and discussion below).
.
In model C, the jet is
precessing counter clockwise while rotating clockwise. The jet of model
A develops a V-shape structure at the head which is commonly detected
in precessing jets (e.g., Masciadri et al. 2002; Masciadri &
Raga 2003; Rosen & Smith 2004) and is due to the impact
of the parcels propagating in different directions in the wiggling flow
with the bow-shock front. In the jet of model B, the combined effects of
pulsation and precession produce internal working surfaces propagating
in different directions. In this case, a narrower bowshock structure
develops at the head that makes it to propagate slightly faster than the
jet of model A. The rotating jet of model C essentially bears the same
features of the previous models but develops an even larger head than
model A due to the centrifugal forces that tend to push the jet flow
outwards in the radial direction (see also Fig. 3 and discussion below).
Table 1:
The jet models.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{Gd292_F1.eps}\end{figure}](/articles/aa/full/2004/41/aagd292/Timg36.gif) |
Figure 1:
Midplane velocity field distribution for
the jet models
A ( top), B ( middle) and C ( bottom), at
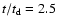 .
See the text
for details. .
See the text
for details. |
| Open with DEXTER |
Let us now concentrate on the early evolution of the rotating, pulsing,
precessing jet of Fig. 1c (model C) whose characteristics qualitatively
resemble those of the DG Tau microjet (Dougados et al. 2000;
Bacciotti et al. 2002). Figure 2a shows the jet of Fig. 1c
at an earlier time that corresponds to the inferred dynamical age of the
DG Tau microjet (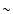 11.3 yr; see e.g., Dougados et al. 2000;
Lavalley et al. 1997; Pyo et al. 2003).
The density contour plot
presents nearly similar features to those observed in the DG Tau microjet:
an elongated, highly collimated beam near the jet base, a slight sideway
displacement of the beam that has been previously interpreted as an
evidence for precession of the jet axis, and a more prominent bow shock (at
11.3 yr; see e.g., Dougados et al. 2000;
Lavalley et al. 1997; Pyo et al. 2003).
The density contour plot
presents nearly similar features to those observed in the DG Tau microjet:
an elongated, highly collimated beam near the jet base, a slight sideway
displacement of the beam that has been previously interpreted as an
evidence for precession of the jet axis, and a more prominent bow shock (at
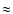
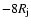 in Fig. 2a) which can be compared with the B1 knot of DG
Tau (Dougados et al. 2000; Lavalley-Fouquet et al. 2000).
in Fig. 2a) which can be compared with the B1 knot of DG
Tau (Dougados et al. 2000; Lavalley-Fouquet et al. 2000).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{Gd292_F2.eps}\end{figure}](/articles/aa/full/2004/41/aagd292/Timg39.gif) |
Figure 2:
a) Midplane density contour ( left panel)
and velocity
field ( rigth panel) distributions for the model C
(see Table 1),
at
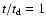 which approximately corresponds to
the dynamical age
of the DG Tau microjet; b) average radial
velocities across the jet for the
different positions along the beam that are
marked in Fig. 2a, above. We notice that the
jet axis is actually located at
which approximately corresponds to
the dynamical age
of the DG Tau microjet; b) average radial
velocities across the jet for the
different positions along the beam that are
marked in Fig. 2a, above. We notice that the
jet axis is actually located at
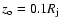 due
to the effects of the precession. The vertical bars
indicate the maximum and minimum values of
the radial velocities obtained for each radial
distance
(the distances are in units of the jet radius); c)
radial velocity differences between positions
across the jet which are symmetric with respect to
the jet center,
as a function of the radial distance. Crosses: our
results. Full line:
an approximate fitting to Bacciotti et al. (2002)
observations and Pesenti et al. (2004)
results (the distances are in units of
AU and the velocities in units of km s-1).
due
to the effects of the precession. The vertical bars
indicate the maximum and minimum values of
the radial velocities obtained for each radial
distance
(the distances are in units of the jet radius); c)
radial velocity differences between positions
across the jet which are symmetric with respect to
the jet center,
as a function of the radial distance. Crosses: our
results. Full line:
an approximate fitting to Bacciotti et al. (2002)
observations and Pesenti et al. (2004)
results (the distances are in units of
AU and the velocities in units of km s-1). |
| Open with DEXTER |
For a comparison with the radial velocities obtained from the HST
observations of DG Tau by Bacciotti et al. (2002), in
Fig. 2b we have built diagrams of the radial velocity across the
jet (taken at an angle of
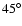 with respect to the jet axis,
in order to mimic the DG Tau inclination with respect to the line of
sight) in four different slices along the flow which are separated by
with respect to the jet axis,
in order to mimic the DG Tau inclination with respect to the line of
sight) in four different slices along the flow which are separated by
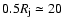 AU and are marked in Fig. 2a.
[These correspond to
the same slices examined in Fig. 1 of Bacciotti et al.:
AU and are marked in Fig. 2a.
[These correspond to
the same slices examined in Fig. 1 of Bacciotti et al.:
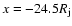 (Position I),
(Position I),
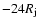 (Position II),
(Position II),
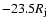 (Position III) and
(Position III) and
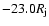 (Position IV).] Figure 2c depicts, for each diagram of
Fig. 2b, the radial velocity differences between positions which are
symmetric with respect to the central region of the jet, as a function
of the distance from the jet axis. We notice that the differences
in radial velocity are negative, therefore indicating that the net
velocity is oriented towards the -y direction. These negative shifts
in velocity are obviously a consequence of the fact that the jet of
model C is rotating clockwise. As expected, these shifts are null in
the jets that are only precessing, like those of
Figs. 1a and 1b. The
resulting radial velocity shifts in Fig. 2c,
(Position IV).] Figure 2c depicts, for each diagram of
Fig. 2b, the radial velocity differences between positions which are
symmetric with respect to the central region of the jet, as a function
of the distance from the jet axis. We notice that the differences
in radial velocity are negative, therefore indicating that the net
velocity is oriented towards the -y direction. These negative shifts
in velocity are obviously a consequence of the fact that the jet of
model C is rotating clockwise. As expected, these shifts are null in
the jets that are only precessing, like those of
Figs. 1a and 1b. The
resulting radial velocity shifts in Fig. 2c,
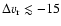 km s-1, are very similar to those obtained by Bacciotti et al.
which are approximately reproduced in the figure by the solid lines.
We note that these solid lines also reproduce the results recently
obtained by Pesenti et al.
(2004) assuming that the DG Tau
microjet is launched magnetocentrifugally by a warm accretion disk.
The consistency between the present results and their predictions is an
additional support for the magnetocentrifugal mechanism for jet launching.
km s-1, are very similar to those obtained by Bacciotti et al.
which are approximately reproduced in the figure by the solid lines.
We note that these solid lines also reproduce the results recently
obtained by Pesenti et al.
(2004) assuming that the DG Tau
microjet is launched magnetocentrifugally by a warm accretion disk.
The consistency between the present results and their predictions is an
additional support for the magnetocentrifugal mechanism for jet launching.
Finally, aiming to check the collimation effects of the magnetic
fields in rotating jets, we have performed simulations of continuous,
non-precessing flows under the presence of helical fields. Given the
present uncertainties related to the real orientation and strength of
the magnetic fields in protostellar jets we have assumed, as in previous
work (e.g., Cerqueira & de Gouveia Dal Pino 2001) a force-free helical
magnetic field which also extends to the ambient medium and whose radial
functional dependences for the toroidal and longitudinal components are
respectively given by:
![$\displaystyle B_{{\phi}}(r)=B_0 [f(r) d]^{1/2},$](/articles/aa/full/2004/41/aagd292/img47.gif) |
|
|
(1a) |
| Bx(r)=B0 [1 -f(r) (r+d)]1/2, |
|
|
(1b) |
where
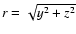 is the radial
distance from the
jet axis,
f(r) = 0.5 C r2/ (r+0.5 d)3,
and the constants C and d are
assumed to be 100
and
is the radial
distance from the
jet axis,
f(r) = 0.5 C r2/ (r+0.5 d)3,
and the constants C and d are
assumed to be 100
and
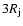 ,
respectively. In these equations,
B0 gives the maximum
strength of the magnetic field and corresponds to
the magnitude
of the longitudinal component at the jet axis and
the magnitude of the
toroidal component at
,
respectively. In these equations,
B0 gives the maximum
strength of the magnetic field and corresponds to
the magnitude
of the longitudinal component at the jet axis and
the magnitude of the
toroidal component at
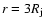 (see Cerqueira
& de Gouveia Dal Pino 2001).
(see Cerqueira
& de Gouveia Dal Pino 2001).
As an example, Fig. 3 compares the early evolution of one of these
MHD runs (model E of Table 1) with a purely hydrodynamical jet (model
D of Table 1). Both have the same initial conditions of the previous
models which are appropriate to DG Tau microjet. The MHD model has an
initial value of the ratio between the magnetic and the gas pressure
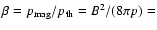 10 near the jet surface which
corresponds to a magnetic field intensity
10 near the jet surface which
corresponds to a magnetic field intensity 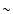 0.5 mG. The centrifugal
force upon the fluid in the radial directions causes the beam radius
of the hydrodynamical jet to increase as the central parts of the flow
tend to move laterally outwards. Though less obvious, we have previously
noticed the same unbalancing of radial forces and jet enlargement in the
rotating jet of Fig. 1c (model C), particularly in its head. When a
helical magnetic field (with surface
0.5 mG. The centrifugal
force upon the fluid in the radial directions causes the beam radius
of the hydrodynamical jet to increase as the central parts of the flow
tend to move laterally outwards. Though less obvious, we have previously
noticed the same unbalancing of radial forces and jet enlargement in the
rotating jet of Fig. 1c (model C), particularly in its head. When a
helical magnetic field (with surface
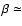 10) is introduced in
the system, we find that the tension force (or hoop stress) associated to
the toroidal component of the magnetic field is able to collimate the jet.
Smaller values of the surface
10) is introduced in
the system, we find that the tension force (or hoop stress) associated to
the toroidal component of the magnetic field is able to collimate the jet.
Smaller values of the surface 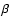 were found to be unable to prevent
the lateral expansion and similar results were also obtained for pulsing
jets under the same conditions (see discussion below).
were found to be unable to prevent
the lateral expansion and similar results were also obtained for pulsing
jets under the same conditions (see discussion below).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{Gd292_F3.eps}\end{figure}](/articles/aa/full/2004/41/aagd292/Timg54.gif) |
Figure 3:
Midplane velocity field distributions for
the purely
hydrodynamical model D ( left) and for the MHD
model E ( right) of Table 1,
at
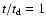 .
The distances are in units of .
The distances are in units of 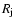 (
(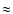 38 AU). 38 AU). |
| Open with DEXTER |
In the present work, we have explored the role of rotation on the
evolution of YSO microjets addressing, in particular, the DG Tau
microjet that has recently shown strong observational evidence for
rotation (Bacciotti et al. 2002). With the help of 3-D hydro
and magnetohydrodynamical simulations, we have investigated several
models that also included the effects of precession and pulsation
of the flow. Our main purpose here was to verify through fully 3-D
simulations whether the signature of rotation was really unique and
unmistakable in the jet flow when other effects, like precession and
pulsation, were also considered. The main conclusions of this study
can be summarized as follows:
- 1.
- The morphology and kinematics of the DG Tau microjet was best
reproduced in our simulations by model C (Figs. 1c and 2a), which
presents a jet with a sinusoidal velocity variability (with mean velocity
of 300 km s- 1, half-amplitude of 100 km s-1, and a period of
8 yr), a precession of the outflow axis (with half-angle of 5
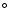 and 8 yr period), and a rotation around its axis with a velocity
and 8 yr period), and a rotation around its axis with a velocity
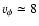 km s-1 at the jet surface, and
km s-1 at the jet surface, and 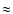 55 km s-1near the jet axis,. These latter conditions satisfy angular momentum
conservation and are consistent with magneto-centrifugal jet launching
models. As remarked before, these characteristics approximately match
those suggested by the observations reported in the literature. We note
also that previous numerical studies of the morphology and kinematics of
this object (e.g., Raga et al. 2001) have obtained similar
conclusions although they have not taken into account the effects of
rotation.
55 km s-1near the jet axis,. These latter conditions satisfy angular momentum
conservation and are consistent with magneto-centrifugal jet launching
models. As remarked before, these characteristics approximately match
those suggested by the observations reported in the literature. We note
also that previous numerical studies of the morphology and kinematics of
this object (e.g., Raga et al. 2001) have obtained similar
conclusions although they have not taken into account the effects of
rotation.
- 2.
- The simulated radial velocities for model C have revealed good
agreement with the data obtained by Bacciotti et al. (2002),
therefore suggesting that their interpretation that the DG Tau microjet
is rotating must be correct.
- 3.
- The inclusion in the models of a helical magnetic field permeating the
jet and the ambient medium, with a maximum value of
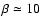 near the jet surface (corresponding to a toroidal magnetic field
near the jet surface (corresponding to a toroidal magnetic field 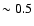 mG), has provided a collimation of the outflow which otherwise
would tend to expand laterally while propagating downstream (Fig. 3).
Though the MHD models here investigated were only simple cases involving
rotating continuous (or pulsing) jets without precession, the results
above suggest that the presence of magnetic fields of the order of
mG), has provided a collimation of the outflow which otherwise
would tend to expand laterally while propagating downstream (Fig. 3).
Though the MHD models here investigated were only simple cases involving
rotating continuous (or pulsing) jets without precession, the results
above suggest that the presence of magnetic fields of the order of
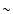 0.5 mG in the DG Tau microjet would be sufficient to collimate
the beam against the centrifugal forces. In fact, a simple estimate
of the magnetic tension forces that would be required to balance the
centrifugal forces at the DG Tau microjet surface gives a magnetic
field strength
0.5 mG in the DG Tau microjet would be sufficient to collimate
the beam against the centrifugal forces. In fact, a simple estimate
of the magnetic tension forces that would be required to balance the
centrifugal forces at the DG Tau microjet surface gives a magnetic
field strength
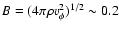 mG (where
mG (where
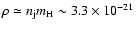 g cm-3 and
g cm-3 and
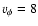 km s- 1), which is compatible with the required value above
from the simulations. We further notice that this would be the expected
strength of the magnetic field at radial distances
km s- 1), which is compatible with the required value above
from the simulations. We further notice that this would be the expected
strength of the magnetic field at radial distances 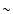 40 AU from the
source. Magnetic flux conservation would then imply strengths
40 AU from the
source. Magnetic flux conservation would then imply strengths
 100 G near the stellar surface which are compatible both with the values
expected for protostellar sources and also with magneto-centrifugal
mechanisms for jet production.
100 G near the stellar surface which are compatible both with the values
expected for protostellar sources and also with magneto-centrifugal
mechanisms for jet production.
Acknowledgements
We are indebted to Francesca Bacciotti and an anonymous referee for
their very helpful comments and suggestions. We also acknowledge
partial support of the Brazilian agencies FAPESB, FAPESP and CNPq,
the Milenium Institute, and the projects PROPP-UESC (00220.1300.327)
and PRODOC- UFBa (991042-88).
- Bacciotti, F., Ray, T.
P., Mundt, R., Eislöffel, J., & Solf, J. 2002, ApJ, 576,
222 [NASA ADS] [CrossRef] (In the text)
- Blandford, R. D.,
& Payne, D. G. 1982, MNRAS, 199, 1982 [NASA ADS] (In the text)
- Cerqueira, A. H., &
de Gouveia Dal Pino, E. M. 2001, ApJ, 560, 779 [NASA ADS] [CrossRef]
- Coffey, D.,
Bacciotti, F., Woitas, J., Ray, T. P., & Eislöffel, J.
2004, ApJ, 604, 758 [NASA ADS] [CrossRef] (In the text)
- de Gouveia Dal Pino, E. M.
2001, ApJ, 551, 347 [NASA ADS]
- Dougados, C., Cabrit, S.,
Lavalley, C., & Ménard, F. 2000, A&A, 357, L61 [NASA ADS] (In the text)
- Königl, A. 1982, ApJ,
261, 115 [NASA ADS] [CrossRef]
- Lavalley, C., Cabrit, S.,
Dougados, C., Ferruit, P., & Bacon, R. 1997, A&A, 327,
671 [NASA ADS] (In the text)
- Lavalley-Fouquet, C.,
Cabrit, S., & Dougados, C. 2000, A&A, 356, L41 [NASA ADS] (In the text)
- Masciadri, E., & Raga,
A. C. 2003, Rev. Mex. Astron. Astrofis., 15, 140 [NASA ADS] (In the text)
- Masciadri, E., de Gouveia
Dal Pino, E. M., Raga, A. C., & Noriega-Crespo, A. 2002, ApJ,
580, 950 [NASA ADS] [CrossRef] (In the text)
- Pesenti, N., Dougados,
C., Cabrit, S., et al. 2004, A&A, 416, L9 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Pyo, T.-S., Kobayashi, N.,
Hayashi, M., et al. 2003, ApJ, 590, 340 [NASA ADS] [CrossRef]
- Raga, A. C., Cabrit, S.,
Dougados, C., & Lavalley, C. 2001, A&A, 367, 959 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Reipurth, B., &
Bally, J. 2001, ARA&A, 39, 403 [NASA ADS]
- Rosen, A., &
Smith, M. D. 2004, MNRAS, 347, 1097 [NASA ADS] [CrossRef] (In the text)
- Spruit, H. C. 1996,
in Evolutionary processes in binary stars, NATO ASI Ser. C, 477,
249
(In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{Gd292_F1.eps}\end{figure}](/articles/aa/full/2004/41/aagd292/Timg36.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{Gd292_F2.eps}\end{figure}](/articles/aa/full/2004/41/aagd292/Timg39.gif)