A&A 426, 425-435 (2004)
DOI: 10.1051/0004-6361:20041301

A dust emission model of Lyman-break galaxies

T. T. Takeuchi1,[*] - T. T. Ishii2,[*]


1 - Laboratoire d'Astrophysique de Marseille, Traverse du Siphon, BP 8, 13376 Marseille Cedex 12, France
2 - Kwasan Observatory, Kyoto University, Yamashina-ku, Kyoto 607-8471, Japan

Received 16 May 2004 / Accepted 29 June 2004

Abstract
Lyman-break galaxies (LBGs) contain a non-negligible amount of dust. Takeuchi (2003a, MNRAS, 343, 839) (T03) constructed a model of the infrared spectral energy distribution (SED) for very young galaxies by taking into account the dust size distribution in the early stage of galaxy evolution, which can be different from that of present-day evolved galaxies. We applied the T03 model to LBGs and constructed their expected SED. In order to examine the grain size distribution of dust, we calculated the SEDs based on two distinct types of the distribution models: a single-sized distribution and a power-law distribution with a slope of ${\rm d}N/{\rm d}a \propto a^{-3.5}$. We found that the single-sized and power-law dust size distributions yield a very similar detectability of LBGs at submillimetres (submm). We also found that galaxies with a power-law dust distribution have much less flux in the mid-infrared (MIR) than the other type. By making use of this fact we will be able to explore the dust grain size distribution in high-redshift galaxies through (observer-frame) FIR observations in future observations. We then applied the model to a gravitationally lensed LBG MS 1512-cB58 (cB58), a unique probe of the dust emission from LBGs. Observations by SCUBA suggest that the galaxy has hot dust. Our model well reproduced the hot dust temperature under natural physical assumptions for the star formation rate (SFR), starburst age, and the radius of the star forming region in this galaxy. We also examined the detectability of LBGs at submm wavelengths in an eight-hour deep survey by ALMA. The LBG population with an age ${\ga} 10^8~{\rm yr}$ and a ${\rm SFR} \ga 10~M_\odot ~{\rm yr}^{-1}$ can be detected in such a survey. By integrating over their redshifted SEDs with the observed luminosity functions, we obtained the contribution of LBGs to the cosmic infrared background radiation (CIRB). Although they have a non-negligible amount of dust, their contribution was found to be small, especially in the ${\rm FIR} \sim 200~\mu$m. Thus, we need a strongly obscured population of galaxies which contains a large amount of star formation, at some epoch in the history of the universe.

Key words: ISM: dust, extinction - galaxies: evolution - galaxies: formation - galaxies: high redshift - infrared: galaxies

1 Introduction

Star formation and metal enrichment in the early stages of galaxies are of great importance for the understanding of the history of the universe. With the aid of a variety of new observational techniques and large facilities, studies of such young galaxies are being pushed to higher and higher redshifts. The surveys that have most efficiently secured large populations of galaxies at a redshift $z\sim 3$ are those that exploit the Lyman break to identify high-z candidates: Lyman-break galaxies (LBGs) (Steidel et al. 1999,2003).

Even in LBGs, there is clear evidence that they contain a non-negligible amount of dust (e.g., Shapley et al. 2001; Adelberger & Steidel 2000; Calzetti 2001; Sawicki & Yee 1998). Dust grains absorb stellar light and re-emit it in the far infrared (FIR), hence it is crucial to evaluate the intensity and spectrum of FIR emission from galaxies in order to understand their star formation properties (e.g., Hirashita et al. 2003; Buat et al. 2002, and references therein). Despite its importance, there still remains a large uncertainty in our understanding of the properties of dust emission from LBGs (for a review, see Calzetti 2001).

Ouchi et al. (1999) estimated the submm flux from LBGs and, for the first time, found empirically that the dust temperature should be high in order to explain their non-detection by SCUBA. Chapman et al. (2000) also pointed out that the SCUBA submm flux densities of LBGs were much lower than was expected from their UV spectral slope index. They found this hard to reconcile unless dust temperature T is higher than that of local starbursts ($T \ga 70~$K). For the analysis of the SCUBA flux of a highly lensed LBG, MS 1512-cB58 (hereafter cB58), Sawicki (2001) (S01) performed a thorough survey of the parameter space of dust temperature and emissivity index, and concluded that the dust temperature and/or emissivity index in cB58 is substantially higher than those found in local galaxies.

Another important issue to be addressed is the contribution of dust emission from LBGs to the cosmic infrared background (CIRB) (Gispert et al. 2000; Totani & Takeuchi 2002; Hauser & Dwek 2001; Takeuchi et al. 2001a). The star formation rate (SFR) density of LBGs is now believed to increase toward redshifts $z \ga 3$, if we "correct'' for dust extinction (Steidel et al. 1999). Then, the re-emission from dust in LBGs is an interesting target. Some recent observations suggest that their contribution to the total CIRB is not very large, at most $\sim $20% (Webb et al. 2003). If so, there must be other contributors to the CIRB that should undergo intense star formation comparable to or even larger than that in LBGs. Hence, the theoretical prediction of the dust emission plays an important role in the interpretation of the cosmic SFR and the CIRB.

To address these issues and to make a consistent picture of the dust emission from LBGs, we must consider properly their star formation history, chemical evolution and dust mass evolution, radiation processes with nonequilibrium temperature fluctuation, and dust composition. Recently, Hirashita et al. (2002) (H02) developed a model for the evolution of dust content in very young galaxies (age $t \la 10^9~ \mbox{yr}$). Type II supernovae (SNe II) are the dominant source for the production of dust grains in young star-forming galaxies (Dwek & Scalo 1980). H02 have modeled the evolution of FIR luminosity and dust temperature in such a young starburst on the basis of the SNe II grain formation model of Todini & Ferrara (2001) (TF01).

Takeuchi et al. (2003a) (T03) subsequently constructed a model of the infrared (IR) spectral energy distribution (SED) of galaxies starting from the H02 model. It has been believed that the size of dust grains formed in SNe II cannot be as large as $0.1 \mbox{--} 1~\mu$m (TF01), and the host galaxies are too young for grains to grow in interstellar space. The T03, for the first time, properly considered the dust size distribution peculiar to the very early stage of galaxy evolution, and constructed a model of the IR SED of very young galaxies. The T03 model successfully reproduced the peculiar SED of a local metal-deficient galaxy SBS 0335-052 ( $Z = 1/41~Z_\odot$), which we regard as an analogue of genuine young galaxies. However, in clear contrast, recently Nozawa et al. (2003) presented a new model of dust grain formation in SNe II, which produces larger grains ( ${\sim} 0.1 \mbox{--} 1\;\mu$m) than previously believed. Their dust has a broken power-law grain size distribution. Based on the known physical condition in LBGs, we discuss the possible geometrical configuration of dust, and show that we can test the dust size distribution at high redshift by an observation of the LBGs in the IR and submm. Such observations will be soon possible with, e.g., SPICA, Herschel, SMA and ALMA.

The layout of this paper is as follows: in Sect. 2 we briefly describe our model framework. We present our basic results for the SEDs of LBGs in Sect. 3. Related discussions are given in Sect. 4. First we focus on the gravitationally magnified LBG MS 1512-cB58, a unique probe of the internal physics of LBGs. Then we consider some cosmologically important problems. Section 5 is devoted to our summary and conclusions.

  
2 SED model for extremely young galaxies

2.1 SED construction

Since H02 treat the evolution of dust content in a galaxy younger than 108 yr, the only contributor to the total dust mass ( $M_{\rm dust}$) in a young (<108 yr) galaxy is the supply from SNe II. The SNe II rate is given by

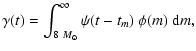$\displaystyle \gamma (t)=\int_{8~M_\odot}^{\infty} \psi (t-t_m)~ \phi (m)~ {\rm d}m ,$     (1)

where $\psi (t)$ is the SFR at age t (we define t=0 at the beginning of the star formation), $\phi (m)$ is the initial mass function (IMF), tm is the lifetime of a star whose mass is m, and it is assumed that only stars with $m>8~M_\odot$ produce SNe II. H02 assume a constant SFR, $\psi =\psi_0$, and a Salpeter IMF. Then the rate of increase of $M_{\rm dust}$ is written as $\dot{M}_{\rm dust}=m_{\rm dust}\gamma$ ( $m_{\rm dust}$ is the typical dust mass produced by one SN II). H02 adopted $m_{\rm dust}=0.4~M_\odot$.

In general we must take into account not only the production but also destruction of dust grains. However, the timescale of dust destruction is much longer than the timescale we consider in this work, hence the effect of the destruction appears to be negligible. A detailed evaluation can be found in H02 (their Eq. (2)).

Dust grains are roughly divided into silicate and carbonaceous grains. TF01 have shown the sizes of silicate and carbonaceous grains formed in SN II ejecta to be about 10 Å and 300 Å, respectively. Classical studies claimed that the dust grains originating from SNe II cannot be as large as those formed in the atmosphere of evolved AGB stars or grown in diffuse interstellar space (Kozasa & Hasegawa 1987; TF01). In this case, the discrete and small grain sizes cause the appearance of the IR SED of young galaxies to be drastically different from that of aged normal galaxies. On the other hand, recently Nozawa et al. (2003) proposed a drastically different picture of dust size distribution from SNe II. They showed that, in some conditions, dust grains can grow large even within the expansion timescale of SNe ejecta. Consequently, their size distribution of grains has a broken power-law shape. For comparison, we also consider this case by using the simple description of Galactic dust (Mathis et al. 1977) as

 
$\displaystyle \frac{{\rm d}N}{{\rm d}a} \propto a^{-3.5}$     (2)

for both grain species, i.e., for either grain species, silicate or carbon dust. Here we note that we do not include polycyclic aromatic hydrocarbons (PAHs) in our dust grain model, because they are rarely found in metal-poor systems and/or in intense radiation environments (e.g., Galliano et al. 2003; Madden 2000).

It is well accepted that very small grains are stochastically heated, that is, they cannot establish thermal equilibrium with the ambient radiation field (Draine & Li 2001; Draine & Anderson 1985): the heat capacity of a very small grain is too small to maintain its temperature until the next photon impinges. As a result, the temperature of a grain varies violently in time, and we can define a distribution of the instantaneous temperature of a grain, which will be introduced in Eq. (9). For the heat capacity of a grain, C(T), we apply the multidimensional Debye model according to Draine & Li (2001).

Then we calculated the temperature distribution of dust as a function of size a by Monte Carlo simulations, following Draine & Anderson (1985). The UV radiation field strength is determined by the history of OB star luminosity of H02 and the size of the star forming region $r_{\rm SF}$. For the geometry, we assume that the OB stars are concentrated in the centre of the system, and dust is assumed to be distributed as a shell. We regard the radius of the sphere, r as the size of the spherical star forming region, $r_{\rm SF}$. The flux is expressed by $J(t)=L_{\rm OB}(t)/(4\pi r_{\rm SF}^2)$, hence the UV energy density, u, is obtained by u=J(t)/c. The spectral UV energy density $u_\lambda$ is calculated from the assumed spectrum of the UV radiation field.


  \begin{figure} \par\includegraphics[angle=90,width=16.7cm,clip]{1301fig1.ps}\end{figure} Figure 1: The evolution of the SED for the single-sized dust size distribution. From left to right, the star formation rate (SFR) is 10, 30, and $100~M_\odot~\mbox{yr}^{-1}$. The dotted, dashed, dot-dashed, long-dashed, and solid lines give the age of major star formation in a galaxy as $1.0\times 10^7~$yr, $3.0\times 10^7~ $yr, $1.0\times 10^8~$yr, $3.0\times 10^8~$yr, $3.0\times 10^7~ $yr, and $1.0\times 10^9~$yr, respectively.
Open with DEXTER

The rate at which a grain absorbs a photon with energy $E \sim E+{\rm d}E$is expressed as[*]

 
$\displaystyle \frac{{\rm d}^2 p}{{\rm d}E{\rm d}t} = Q_{\rm abs} (a, \lambda)\pi a^2 u_\lambda \frac{\lambda^3}{h^2c} ,$     (3)

where $Q_{\rm abs}$ is the absorption efficiency of a dust grain. We used the values proposed by Draine & Lee (1984) for $Q_{\rm abs}$ of silicate and carbon grains. The heating is represented as follows:
 
$\displaystyle \frac{hc}{\lambda} = \frac{4\pi a^3}{3}\int_{T_0}^{T} C(T'){\rm d}T' ~ ,$     (4)

where T is the peak temperature achieved by a grain hit by a photon with energy $hc/\lambda$, and T0 is the grain temperature just before absorption. On the other hand, the grain cools through radiation as
 
$\displaystyle \frac{{\rm d} T}{{\rm d}t} = -\frac{3\pi}{aC(T)} \int_0^\infty Q_{\rm abs}(a,\lambda)~ B_\lambda(T) {\rm d}\lambda ,$     (5)

where $B_\lambda(T)$ is the blackbody function represented as a function of wavelength. From Eqs. (3)-(5), we obtain the sample path of a grain temperature as a function of time.

The total mass of each grain component is given by TF01. The mass ratio we adopt here is $M_{\rm sil}{:}M_{\rm C} = 0.56{:}0.44$(H02). With this value and with the material density of each species ( $\rho_{\rm sil}=3.50~\mbox{g}~\mbox{cm}^{-3}$ and $\rho_{\rm C}=2.26~\mbox{g}~\mbox{cm}^{-3}$: Draine & Lee 1984), we obtain the normalization of the dust size distribution ${\rm d}N_i/{\rm d}a_i'$,

 
$\displaystyle M_{\rm dust} f_i = \int \frac{4\pi {a_i'}^3 \rho_i}{3} \frac{{\rm d}N_i}{{\rm d}a_i'}{\rm d}a_i' ,$     (6)

where subscript i denotes the species of dust, "sil" or "C", and fi is the mass fraction of dust of species i. The total number of grains, Ni, is expressed as
 
$\displaystyle N_i = \int \frac{{\rm d}N_i}{{\rm d}a_i'}{\rm d}a_i' .$     (7)

For the TF01 dust distribution, ai is fixed for each dust component at a specific value ai, i.e., ${{\rm d}N_i}/{{\rm d}a_i'}=N_i\delta(a_i'-a_i)$. In this case, with Eqs. (7) and (6), the normalization reduces to
 
$\displaystyle N_i = \frac{3M_{\rm dust}f_i}{4\pi a_i^3\rho_i} \cdot$     (8)

We drop the prime in the following expressions.

The total IR emission spectrum from a galaxy is then calculated by superposing the continua from silicate and carbonaceous grains,

 
$\displaystyle L_{{\rm IR},\lambda}(t) = \sum_i \pi \int\int 4 \pi a_i^2 Q_{\rm ... ...\rm d}N_i}{{\rm d}a_i} \frac{{\rm d}P_i(u,a_i)}{{\rm d}T}~{\rm d}T {\rm d}a_i ,$     (9)

where ${\rm d}P_i(u,a_i)/{\rm d}T$ is the temperature probability density function, i.e., the fraction of time for which a grain of species i in a UV radiation field with energy density u stays in the temperature range $[T, T+{\rm d}T]$.

The starburst age is incorporated with Ni (i.e., ${\rm d}N_i/{\rm d}a_i$) and ${\rm d}P_i(u,a_i)/{\rm d}T$ through $M_{\rm dust}(t)$ and $u_\lambda (t)$. Here we put the constraint that the amount of absorbed light is equal to the FIR luminosity. Lastly, if the dust opacity is very large, then self-absorption occurs, and even MIR radiation from dust is absorbed by the dust itself. We treat the extinction as given by a shell model. We crudely approximate the dust opacity and extinction to the first order as

 
                               $\displaystyle \tau_{\rm dust}(\lambda)$ $\textstyle \simeq$ $\displaystyle \sum_i \pi a_i^2 Q_{{\rm abs},i} (\lambda)~ \frac{3 N_i}{4\pi \left[(r_{\rm SF}+\Delta r_{\rm SF})^3 - r_{\rm SF}^3\right]} \Delta r_{\rm SF}$  
  $\textstyle \simeq$ $\displaystyle \sum_i \pi a_i^2 Q_{{\rm abs},i} (\lambda)~ \frac{N_i}{4\pi r_{\rm SF}^2},$ (10)
$\displaystyle I(\lambda)$ = $\displaystyle I_0(\lambda) {\rm e}^{-\tau_{\rm dust}(\lambda)} .$ (11)

The absorbed light is re-emitted at longer wavelengths, mainly in the submm, and consequently, the SED is deformed by the self-absorption. The final SED is obtained via this absorption-re-emission process. For further technical details, see T03.

  
2.2 Input parameters for LBGs

Here we consider the input physical parameters in the model calculation for LBGs. We adopted the dust grain sizes $a_{\rm C}=200~\mbox{\AA}$ and $a_{\rm sil}=6~\mbox{\AA}$ for our canonical model. They are the same as those for SBS 0335-052 and I Zw 18 used in T03, because LBGs are thought to be young, and hence we expect similar dust properties for them.

The SFR of LBGs spreads over the range of $1 \mbox{--} 300~M_\odot ~\mbox{yr}^{-1}$ with a median value of ${\simeq} 20~M_\odot ~\mbox{yr}^{-1}$ (e.g., Erb et al. 2003). We assumed a constant SFR up to the age shorter than 109 yr, which may be a good approximation (e.g., Baker et al. 2004). Until young age of $t \simeq 10^9~$yr, neither SNe I nor RGB/AGB stars contribute to the dust production. Other dust growth mechanisms in the interstellar medium cannot work effectively, either (see, e.g., Whittet 1992). Thus, the basic framework of the T03 model is valid for LBGs.

The most important information for calculating the IR SED is the effective size of the star forming region, but it is the most uncertain quantity at the same time. It is still beyond the possibility of the present facilities to measure the size directly. The mean half-light radius of LBGs is estimated to be ${\sim} 1.6~h^{-1}~ \mbox{kpc}$ from HST observations (Erb et al. 2003), hence this may be a general value for LBG populations. The similarity between the restframe UV and optical morphologies suggests that the dust in LBGs may not preferentially obscure particular regions in these galaxies (Calzetti 2001; Dickinson 2000). Then we can safely use the galaxy radius $r_{\rm G}$ as the radius of a star-forming region, $r_{\rm SF}$, i.e., $r_{\rm SF} = 2~\mbox{kpc}$. We will revisit this issue with more physical considerations in Sect. 4.

  
3 Results


  \begin{figure} \par\includegraphics[angle=90,width=16.7cm,clip]{1301fig2.ps}\end{figure} Figure 2: The evolution of the SED for the power-law dust size distribution. In comparison with Fig. 1 we see a clear difference in the MIR.
Open with DEXTER

Based on the above-mentioned models and parameter values, we calculated the IR SEDs of LBGs with ${\rm SFR} = 10$, 30, and $100~M_\odot~\mbox{yr}^{-1}$ as representative cases. We traced the evolution of the SEDs from $t=10^7~\mbox{yr}$ to $10^9~\mbox{yr}$.

Figure 1 shows the evolution of the SED for the single-sized dust size distribution. The dust opacity is found to be not very large, and consequently, the silicate features appear in emission. Only in the case of ${\rm SFR}=100~M_\odot~\mbox{yr}^{-1}$, do these features represent significant absorption after $3 \times 10^8~\mbox{yr}$. Most of the LBGs have ${\rm SFR} < 100~M_\odot~ \mbox{yr}^{-1}$, hence basically we can expect the silicate emission band feature in their MIR spectra. Along the same lines, since the self-absorption is not significant for LBG spectra, we also expect a strong MIR continuum emission from LBGs if the single-sized dust distribution is valid.

For comparison, we next show the evolution of the SED for the power-law dust size distribution in Fig. 2. In this case, an obvious difference is that the MIR radiation is an order of magnitude weaker than for the single-sized dust results. This is because the power-law size distribution has a much smaller amount of small grains ( $a \la 100~$Å) than the single-sized distribution. The extinction properties are similar to those of the single-sized dust case, despite the drastic difference of the SEDs. Thus, if the geometrical configuration of dust is similar among LBGs, the MIR observation can be a strong tool for exploring the size distribution of dust grains.

  
4 Discussion

  
4.1 MS 1512-cB58

It is still difficult to compare the model prediction for young galaxies to observational data of LBGs. Among the LBGs, the typical L* LBG cB58 is a fortunate exception: it has been observed at various wavelengths (e.g., Baker et al. 2001; Ellingson et al. 1996; Teplitz et al. 2000; Nakanishi et al. 1997; Bechtold et al. 1997), because of strong magnification by gravitational lensing (factor $22\mbox{--}40$: Seitz et al. 1998). We adopt the commonly used value of 30 for the magnification. The half-light radius of cB58 is estimated to be $r_{\rm G} \simeq 1.4~h^{-1}~$kpc from a detailed image reconstruction (Seitz et al. 1998)[*].

From spectroscopic observations of nebular lines, the SFR of cB58 is estimated to be ${\simeq} 10 \mbox{--}20~h^{-2}~ M_\odot~ \mbox{yr}^{-1}$(Pettini et al. 2000). The age of major star formation in cB58 was estimated to be $t_{\rm SF} \simeq 35~\mbox{Myr}$ (Matteucci & Pipino 2002). An higher age estimate of $t_{\rm SF} = 140~$Myr is given by Baker et al. (2004), and we adopt both these values for our calculations. This is broadly consistent with other observational suggestions (e.g., Ellingson et al. 1996; Pettini et al. 2000), and significantly younger than the median value for general LBGs ( ${\sim} 350~$Myr: Shapley et al. 2001).

The optical extinction of cB58 is estimated to be $E(B-V) \simeq 0.27$ (Teplitz et al. 2000; Ellingson et al. 1996; Pettini et al. 2000). Emission from dust in cB58 is measured at two wavelengths: Sawicki (2001) observed this galaxy at $850~\mu$m by SCUBA on the JCMT, and no signal was detected above the $3\sigma$ level of 3.9 mJy. Another observation by SCUBA (van der Werf et al. 2001) detected an $850~\mu$m flux of $4.2\pm 0.9$ mJy. Baker et al. (2001) reported a detection at 1.2 mm by MAMBO (Max-Planck Millimeter Bolometer) array, and the flux was $1.06 \pm 0.35$ mJy ($4.4\sigma$).

The submm flux from the foreground cD galaxy (6'' away from cB58) may contaminate the observed data (Sawicki 2001). After careful examination of the new submm mapping data, it has been concluded that the contamination is $\sim $5% at $850~\mu$m and $\sim $22% at 1.2 mm, respectively (Baker et al. 2004), though there still remain some other uncertainties (e.g., Baker et al. 2004 discusses a possible contribution of emission lines or background sources. We may need an interferometric observation to solve this problem). In addition, the uncertainties in the lensing correction and in the UV based SFR estimation may also be as large as that of the contamination correction. We should keep these issues in mind in the following discussion.

  
4.1.1 IR SED

We use the commonly accepted value of $24~M_\odot~ \mbox{yr}^{-1}$ as the SFR (Baker et al. 2004) and assume the SFR to be constant in time. For the ages of the major star formation in cB58, as we mentioned above, we adopt 35 Myr and 140 Myr. Because of its young age, dust is predominantly produced by SNe II and the framework of the T03 model is again valid for cB58. The half-light radius of the reconstructed image of cB58 ( ${\simeq} 2~\mbox{kpc}$ Seitz et al. 1998) is very similar to that of general LBGs ( ${\sim} 1.6~ \mbox{kpc}$ Erb et al. 2003).


  \begin{figure} \par\includegraphics[angle=90,width=15.9cm,clip]{1301fig3.ps}\end{figure} Figure 3: Model spectral energy distribution (SED) of a lensed Lyman-break galaxy MS 1512-cB58 (cB58). The left panel shows the observed SED calculated based on the single-sized dust size distribution with silicate grain radius $a_{\rm sil}=6~\mbox{\AA}$ and carbon grain radius $a_{\rm C}=200~\mbox{\AA}$. The observed SED is magnified by a factor of 30. The right panel shows the SED for a power-law grain size distribution. Symbols represent the measured flux densities reported by Sawicki (2001) (upper limits), Baker et al. (2001) (open triangles) and van der Werf et al. (2001) (open squares). In both panels, dotted lines represent the SED at the age of $t_{\rm SF}=35~$Myr, and dashed lines at $t_{\rm SF} = 140~$Myr, respectively.
Open with DEXTER

We show the model SED of cB58 in Fig. 3. The left panel presents the SED for single-sized dust, and the right panel shows the SED for a power-law distribution (Eq. (2)), respectively. Symbols represent the measured flux densities reported by Sawicki (2001) (upper limits), Baker et al. (2001) (open triangles) and van der Werf et al. (2001) (open squares). There are two open symbols at each wavelength: the upper open symbols are the measured values, and the lower ones represent the flux densities corrected for possible contamination by the point source at the lens cluster center (Baker et al. 2004). It is still not clear whether the point source is the cD galaxy or not (Baker et al. 2004).

The apparent peak of the SED is located at a wavelength shorter than $100~\mu$m in the restframe of cB58. Actually, the dust temperature is higher than that of the local ($z\sim 0$) sample of normal galaxies observed by SCUBA, but comparable to the most intense dusty starburst galaxies (Dunne & Eales 2001). This is mainly because of the intense UV radiation field of cB58 and low dust opacity. The mean dust temperature of the power-law dust model is lower than that of the single-sized dust model, but the superposition makes the submm part of its final SED similar to that of hot dust emission. We find that both models predict slightly lower flux densities than observed. Considering the uncertainties mentioned above, we conclude that the model is roughly consistent with the observations within a factor of a few. Some authors claim that the submm flux density of cB58 is surprisingly low (e.g., Baker et al. 2004), but in our framework, they are naturally explained by our model, which predicts even smaller fluxes. The power-law model predicts a slightly larger flux at submm wavelengths, but it is difficult to distinguish the two models only by submm observations.

A prominent feature in the MIR is the silicate band at $9.7~\mu$m. For the single-sized dust model, the NIR-MIR part of the SED is dominated by the radiation from small silicate grains, and the FIR-submm part by larger carbonaceous grains. In contrast, the relatively low abundance of small grains in the power-law model makes the MIR radiation considerably weaker.

   
4.1.2 Extinction and size of the star-forming regions

Besides IR emission, dust extinction is a fundamental quantity for specifying the dust properties. We relate the extinction in magnitude ($A_\lambda$) with $\tau_{\rm dust} (\lambda)$ (Eq. (10)) by

\begin{displaymath}A_\lambda = 1.086 \tau_{\rm dust}(\lambda). \end{displaymath} (12)

When we adopt $r_{\rm SF} = 2~\mbox{kpc}$, the extinction in the K-band is $A_K =0.08~\mbox{mag}$. Again we adopt the extinction curve of Cardelli et al. (1989), we expect $A_{\rm V} =0.8~\mbox{mag}$ from our model. The measured color excess is E(B-V)=0.27, hence by adopting RV =3.1 as a representative value in a diffuse ISM (Krügel 2003), we have $A_{\rm V} = R_V E(B-V) \simeq 0.84~\mbox{mag}$, which is in perfect agreement with our model prediction. Vijh et al. (2003) performed a sophisticated analysis of the attenuation in LBGs using a radiative transfer model. They showed that the attenuation is in the range of $5.7\mbox{--}18.5$ at $1600~\mbox{\AA}$, and is well represented by the Calzetti law (Calzetti et al. 1994). Our extinction estimate is also consistent with their result. They also showed that the shell geometry is appropriate for the dust in LBGs, which is in accordance with our assumption. Thus, we see that the extinction in the visible stellar system of cB58 is consistent with its dust amount and spatial scale of $r_{\rm SF}\simeq 2~\mbox{kpc}$.

Can heavily hidden star formation exist in this galaxy? Actually, SBS 0335-052 hosts a completely extinguished starburst (Plante & Sauvage 2002; Hunt et al. 2001), and its SED is well understood from the T03 model. To consider this problem, we have calculated the SEDs with various smaller star-forming region sizes. This means that the bulk of the dust in cB58 could be confined in a small part of its volume. The SEDs are shown in Fig. 4. Dotted, dashed, and dot-dashed lines correspond to SEDs with $r_{\rm SF}=300~$pc, 120 pc, and 30 pc, respectively. Smaller sizes make the opacity in the region significantly larger, and the conversion from UV to FIR becomes much more efficient. Considering the observational upper limits, the smallest size allowed is $r_{\rm SF}=120~$pc, with a possible range of $50\mbox{--}200~\mbox{pc}$ if we take into account the uncertainties in the estimates of the SFR and lensing magnification.


  \begin{figure} \par\includegraphics[width=8.1cm,clip]{1301fig4.ps}\end{figure} Figure 4: Effect of the size of the star-forming regions on the model SED of cB58. The solid line is the canonical model (same as the solid line in the left panel of Fig. 3). Dotted, dashed, and dot-dashed lines indicate the SED calculated with a radius of the star-forming region, $r_{\rm SF}=300~\mbox{pc}$, 120 pc, and 30 pc, respectively. Note that the SED is presented here in the units of $\nu L_\nu~[L_\odot]$.
Open with DEXTER

It has been pointed out that the galactic wind can transport the dust to a larger radius (T03). Actually, precise spectroscopy by Pettini et al. (2003) clearly shows the outflowing motion of gas with a velocity of $v_{\rm wind} \simeq 255~\mbox{km~s}^{-1}$ in cB58. They consider the wind and extinction, and suggest that the superwind shell size is comparable to the galaxy size. Hence the wind crossing timescale is $t_{\rm cross} \sim 10^6~\mbox{yr}$. If dust is closely coupled with the gas motion, it is difficult to keep dust grains confined in a region much smaller than the galaxy size through its age of $t = 35\mbox{--}140~\mbox{Myr}$. Strong radiative pressure may also expand the dusty region, as suggested by Inoue (2002). Here we should comment on the effect of the patchiness of dust, which may be realistic for LBGs. In the FIR, since the opacity of dust is small ($\tau < 1$), the emission escapes from the galaxy without significant absorption. Then the flux is controlled simply by energy conservation, and the patchiness does not affect the result significantly (see, e.g., Witt et al. 2000; Gordon et al. 2000).

Together with its high SFR and SN rate, which are considered to provide a large amount of radiative and kinetic energy to the gas-dust system, we conclude that compact dusty star formation may not be plausible for cB58. Hence, the dust configuration of cB58 may be similar to the present model. This suggests that we can distinguish the effect of dust size distribution on the SED from that of the configuration and geometry of dust in the galaxy. Again, this conclusion can hardly be affected by the clumpiness of dust, for the same reason as mentioned above.

   
4.1.3 Follow-up observations of cB58

Our single-sized dust model provides an SED with bright continuum in the rest-wavelength NIR-MIR regime, hence we expect that cB58 will be detected in MIR-FIR observations ( $\lambda \sim 20\mbox{--}100~\mu$m). At present, Spitzer[*] MIPS and ASTRO-F[*] IRC will be suitable instruments for such observations. For example, both instruments have the same level of sensitivity around ${\sim} 20~\mu$m, and a flux of 0.06-0.08 mJy will be detected. For FIR, both can detect 0.8-1 mJy at $\lambda =60\mbox{--}70\;\mu$m. Therefore, the MIR continuum can be detected by the future MIR-FIR observations if the single-sized dust model is valid.

On the other hand, if the power-law distribution applies, the flux densities will be an order of magnitude smaller than those of our canonical model, because the number of the stochastically heated grains is reduced. As we mentioned, the uncertainty caused by the dust geometry is not very large for a LBG because the configuration becomes more or less shell-like in these galaxies just like a scale-up of SBS 0335-052. Therefore, the MIR observation will be a strong test for the size distribution.

We should note, however, that even with Spitzer, the confusion limit can be severe in the FIR (e.g., Ishii et al. 2002; Takeuchi & Ishii 2004; Dole et al. 2003). Larger space IR facilities such as the Herschel Space Observatory[*] or SPICA[*], and IR interferometry missions are expected to improve the confusion limit. At longer wavelengths, of course ALMA will be useful.

   
4.2 Observability of the dust emission from LBGs

Considering the non-negligible extinction in LBGs, the fraction of energy radiated in the IR should be significant (Calzetti 2001; Adelberger & Steidel 2000). Stimulated by this consideration, the relation between LBGs and dusty starbursts, another representative star-forming galaxy population at $z=2\mbox{--}5$, has caught the researchers' attention. In fact, however, most of the LBGs have not been detected by SCUBA observations (Webb et al. 2003; Chapman et al. 2000), except for a few extreme cases (e.g., Chapman et al. 2002). Calzetti et al. (2000) pointed out the possibility that the dust is hot in LBGs based on the observed SED of a low-metallicity galaxy Tol 1924-416. Hot dust in LBGs was also suggested by S01 from his observation of a lensed LBG cB58. Their suggestion is empirical, and we need some explanation for the hot dust, if it exists. As seen in the above, our model naturally predicts a high dust temperature. Here, we discuss how LBGs look in the IR/submm wavelengths. It is also useful to estimate the feasibility of observing LBGs by forthcoming submm facilities like ALMA.


  \begin{figure} \par\includegraphics[angle=90,width=16.85cm,clip]{1301fig5.ps}\end{figure} Figure 5: Prediction for the observed IR/submm SEDs of LBGs at z=2, 3, and 4. The star formation rate ( SFR) is $10~M_\odot ~{\rm yr}^{-1}$, and the dust grains are single-sized. The dotted, dashed, dot-dashed, long-dashed, and solid lines represent, as in Fig. 1, ages of major star formation in a galaxy of $1.0\times 10^7~$yr, $3.0\times 10^7~ $yr, $1.0\times 10^8~$yr, $3.0\times 10^8~$yr, $3.0\times 10^7~ $yr, and $1.0\times 10^9~$yr, respectively. The confusion limits of Herschel and detection limits of an ALMA 8-h survey are also shown by gray and black thick horizontal lines, respectively.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=16.85cm,clip]{1301fig6.ps}\end{figure} Figure 6: The same as Fig. 5, but for an SFR of $30~M_\odot ~{\rm yr}^{-1}$.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=16.85cm,clip]{1301fig7.ps}\end{figure} Figure 7: The same as Fig. 5, but for an SFR of $100~M_\odot ~{\rm yr}^{-1}$. The silicate feature finally appears in absorption.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=16.8cm,clip]{1301fig8.ps}\end{figure} Figure 8: Prediction for the observed IR/submm SEDs of LBGs at z=2, 3, and 4. The star formation rate (SFR) is $10~M_\odot ~{\rm yr}^{-1}$, and the dust grains are power-law.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=16.8cm,clip]{1301fig9.ps}\end{figure} Figure 9: The same as Fig. 8, but for an SFR of $30~M_\odot ~{\rm yr}^{-1}$.
Open with DEXTER


  \begin{figure} \par\includegraphics[angle=90,width=16.8cm,clip]{1301fig10.ps}\end{figure} Figure 10: The same as Fig. 8, but for an SFR of $100~M_\odot ~{\rm yr}^{-1}$.
Open with DEXTER

The observed flux density of a source at the observed frequency, $\nu_{\rm obs}$ is obtained by

 
$\displaystyle S_{\nu_{\rm obs}} = \frac{(1+z)L_{(1+z)\nu_{\rm obs}}}{4\pi d_{\rm L}(z)^2} = \frac{(1+z)L_{\nu_{\rm em}}}{4\pi d_{\rm L}(z)^2} ,$     (13)

where $d_{\rm L}(z)$ is the luminosity distance corresponding to a redshift z, and $\nu_{\rm obs}$ and $\nu_{\rm em}$ are observed and emitted frequency, respectively. We show the observed IR/submm SEDs of LBGs at z=2, 3, and 4 in Figs. 5-10. Figures 5-7 represent the SEDs for the single-sized dust size distribution, and Figs. 8-10 for the power-law distribution (Eq. (2)). The thick black short horizontal lines indicate the 3-$\sigma$ detection limits for an 8-h observation by ALMA. Here we assumed 64 antennas and three wavelength bands, 450, 850, and $1080~\mu$m. We also show the 3-$\sigma$ source confusion limit of Herschel in the 75, 160, 250, and 350$~\mu$m bands by thick gray horizontal lines. These limits are based on the "photometric criterion'' of Lagache et al. (2003). Ishii et al. (2002) report similar estimates for the confusion limits[*].

From Figs. 5-10, we recognize that the detectability of these galaxies in submm bands is not significantly dependent on the redshift. This is because of the "negative K-correction'', well-known in the field of submm astronomy. On the contrary, the galaxy age and SFR are more important for the detection of LBGs. If the age ${\ga} 10^8~{\rm yr}$ and ${\rm SFR} \ga 10~M_\odot~ {\rm yr}$, a LBG can be detected over a wide range of redshifts in the submm.

In general, the longer the wavelength is, the easier the detection becomes for millimetre (mm) observations. In the submm and mm wavelengths, the detectability is not very different for LBGs with single-sized dust and for those with power-law dust. It is a natural consequence that the radiation in these wavelengths is dominated by relatively large dust grains that can establish a thermal equilibrium with the radiation field.

The apparent peak of the dust emission lies at the relatively short wavelength of about $200\mbox{--}400~\mu$m at $z=2\mbox{--}4$. Thus, the accumulated background radiation spectrum from LBGs may have its peak in the FIR. The expected dust emission from LBGs is, however, too faint to be detected even by the Hershel deep survey, except for some rare exceptionally bright sources, e.g., lensed galaxies like MS 1512-cB58, or in the case of extremely high SFR (to reach the confusion limits, unrealistically long integration times might be required). Hence, at these wavelengths still more powerful instruments would be required.

At the shorter wavelengths (MIR-FIR), the size distribution affects the possibility of detection strongly, just as we have seen in the case of cB58 (Sect. 4.1). Surveys in the MIR by Spitzer and ASTRO-F will be desirable for detecting these objects. These observations are important for a direct comparison of the overall SEDs of LBGs with those of "local analogues'', such as SBS 0335-052 and I Zw 18. The existence of such local galaxies with hot dust has been reported in recent studies (see e.g., Takeuchi et al. 2003b; Calzetti et al. 2000). The similarity and difference between them provides us with a unique clue to the physics of galaxy formation.

4.3 Contribution of LBGs to the CIRB


  \begin{figure} \par\includegraphics[width=7.8cm,clip]{1301fig11.ps}\end{figure} Figure 11: The contribution of LBGs to the cosmic infrared background radiation (CIRB) (open symbols). Filled symbols and hatched area are the measured CIRB spectrum by COBE (Lagache et al. 1999; Fixsen et al. 1998; Hauser et al. 1998).
Open with DEXTER

The implication of hot dust also offers a potentially important cosmological insight into high-z galaxies: if dust in high-z objects is as cool as is usually assumed, we cannot expect a high comoving SFR density because in a realistic cosmology the cosmic IR background (CIRB) spectrum strongly constrains the high-z IR emission (Takeuchi et al. 2001a). However, very hot dust in such high-z objects reconciles the CIRB constraint with high SFR, and allows vigorous star formation hidden by dust in the early Universe (Totani & Takeuchi 2002).

Actually, non-detection of LBGs at the submm wavelengths (Webb et al. 2003; Chapman et al. 2000) suggests a hot dust temperature. Considering the non-negligible extinction in these galaxies, they radiate a significant fraction of their energy in the IR (Calzetti 2001; Adelberger & Steidel 2000). However, their contribution to the submm radiation cannot be very large because of the high dust temperature. In fact, the contribution to the extragalactic submm background radiation has been suggested to be at most ${\sim} 20$% (Webb et al. 2003).

Using our model SED and the luminosity function of LBGs (Shapley et al. 2001), we calculate the integrated IR light contribution from LBGs to the CIRB. In order to have a rough estimate, we correct the extinction to the observed luminosity function, and converted it to the distribution of the SFR by converting the UV luminosity to the SFR according to our model. Here we crudely assumed that all the LBGs have the same star forming region size $r_{\rm SF} = 2~\mbox{kpc}$. We also assumed that the number of LBGs rapidly decreases at $z \ga 4$[*]. By using the SFR distribution, we obtained the multiband FIR luminosity function of the LBGs. We finally integrated it over the FIR luminosity to get the CIRB intensity.

Our model predicts $0.4~\mbox{nW~m}^{-2}~\mbox{sr}^{-1}$ at $200~\mu$m, and $0.2~\mbox{nW~m}^{-2}~\mbox{sr}^{-1}$ at $850~\mu$m, respectively. A difference of the dust size distribution practically does not affect the CIRB spectrum at all. This result is shown in Fig. 11. The $850~\mu$m intensity is quite consistent with the LBG contribution at $850~\mu$m estimated by Webb et al. (2003). Since the CIRB intensity at $200~\mu$m is much smaller than the measured peak ( $\nu I_\nu =15~\mbox{nW~m}^{-2} ~\mbox{sr}^{-1}$ at $\lambda\simeq 140~\mu$m, Lagache et al. 1999), it strongly supports the existence of a heavily obscured dusty galaxy population. Therefore, LBGs are not the dominant population contributing to the CIRB.

The straightforward conversion of the UV radiation from galaxies into the IR by recent models cannot reproduce the strong peak (e.g., Balland et al. 2003). In addition, the large energy fraction radiated in the IR requires an effective energy release, which may related to starburst phenomena, even if the galaxies contributing to the IR radiation are in the nearby universe (Hauser & Dwek 2001; Takeuchi et al. 2001a; Franceschini et al. 2001). Therefore, hidden starbursts are necessary for explaining the strong evolution of submm source counts (e.g., Takeuchi et al. 2001b,a). At present, the redshifts of the starburst population contributing to the CIRB are almost unknown. If the dusty starburst is a low-z phenomenon, there must be a strongly obscured era at $z \sim 1$ (Takeuchi et al. 2001a). In this case it is interesting to discuss a possible relation between the activation of star formation and the peak of the merger rate in hierarchical structure formation scenarios (e.g., Lacey & Cole 1993; Kitayama & Suto 1996). On the other hand, if the obscured galaxies reside in a high-z Universe, it implies that the high-z cosmic SFR density may be higher than the dust-corrected value (Steidel et al. 1999) because it would be a sum of the contributions both from LBGs and hidden starbursts.

  
5 Summary and conclusion

Lyman-break galaxies (LBGs) contain a non-negligible amount of dust. Takeuchi et al. (2003a) (T03) constructed a model of the infrared spectral energy distribution (SED) for very young galaxies by taking into account the dust size distribution in the early stages of galaxy evolution, which can be different from that of present-day evolved galaxies.

In this work, we applied the T03 model to LBGs and constructed their expected SED. In order to examine the grain size distribution of dust, we calculated the SEDs based on two distinct types of distribution model: a single-sized distribution predicted by Todini & Ferrara (2001), and a power-law distribution with a slope of ${\rm d}N/{\rm d}a \propto a^{-3.5}$, which is often used to describe the Galactic dust (Mathis et al. 1977).

We found that the single-sized and power-law dust size distributions yield a very similar detectability of LBGs in the submm. We also found that the difference of the grain size distribution affects the SED drastically at mid-infrared (MIR) wavelengths. Galaxies with a power-law dust distribution have much less flux at MIR than the other type. Generally, strong outflow is observed in LBGs, and consequently the geometry of their dust configuration might be relatively simple. This reduces the uncertainty of complex radiative transfer, and we can safely explore the dust grain size distribution high-redshift galaxies by (observer-frame) FIR observations.

Then, we applied the model to a gravitationally lensed LBG MS 1512-cB58 (cB58), a unique probe of the dust emission from LBGs. Thanks to the large magnification factor, the dust emission has been detected in the submm by SCUBA observations. These observations suggest that this galaxy contains hot dust. Our model framework well reproduced the hot dust temperature under a natural assumption on the SFR, starburst age, and star-forming region radius for this galaxy.

We also examined the detectability of LBGs at submm wavelengths in an eight-hour deep survey by ALMA. The LBG population with age ${\ga} 10^8~{\rm yr}$ and ${\rm SFR} \ga 10~M_\odot ~{\rm yr}^{-1}$ can be detected in such a survey. The detectability of LBGs in the submm is not strongly affected by redshift, because of the well-known negative K-correction. Hence, the detected LBG sample will be undoubtedly an ideal sample to study the early evolution of metal and dust content in galaxies.

By integrating over their redshifted SEDs with the observed luminosity functions, we obtained the contribution of LBGs to the cosmic infrared background radiation (CIRB). Although they have a non-negligible amount of dust, their contribution was found to be small, especially in the ${\rm FIR} \sim 200~\mu$m. Thus, we need a strongly obscured population of galaxies which contains a large amount of star formation, at some epoch in the history of the universe.

Acknowledgements
First we deeply thank the anonymous referee whose careful comments improved the quality and clarity of this paper very much. This work has been motivated by a stimulating discussion with Marcin Sawicki at a conference on Mykonos. Akio K. Inoue is kindly thanked for his careful reading of the manuscript. We are greatly indebted to Hiroyuki Hirashita, Veronique Buat, Masato Onodera, Leslie K. Hunt, Andrea Ferrara, Atsunori Yonehara, Tracy M. Webb, Kouichiro Nakanishi, and Ichi Tanaka for their helpful comments and suggestions.

References

 
Copyright ESO 2004