A&A 426, 631-640 (2004)
DOI: 10.1051/0004-6361:20041031
The parallax, mass and age of the PSR J2145-0750
binary system
O. Löhmer 1 -
M. Kramer 2 -
T. Driebe 1 -
A. Jessner 1 -
D. Mitra 1 -
A. G. Lyne 2
1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69,
53121 Bonn, Germany
2 -
University of Manchester, Jodrell Bank Observatory,
Macclesfield, Cheshire SK11 9DL, UK
Received 6 April 2004 / Accepted 22 June 2004
Abstract
We present results of high-precision timing measurements of
the binary millisecond pulsar PSR J2145-0750. Combining
10 yrs of radio timing data obtained with the Effelsberg 100-m radio
telescope and the Lovell 76-m radio telescope we measure a
significant timing parallax of 2.0(6) mas placing the system at
500 pc distance to the solar system. The detected secular change of
the projected semi-major axis of the orbit
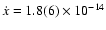 lt-s s-1, where
lt-s s-1, where
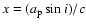 ,
is caused by
the proper motion of the system. With this measurement we can
constrain the orbital inclination angle to
,
is caused by
the proper motion of the system. With this measurement we can
constrain the orbital inclination angle to
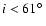 ,
with a
median likelihood value of
,
with a
median likelihood value of
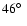 which is consistent with
results from polarimetric studies of the pulsar magnetosphere. This
constraint together with the non-detection of Shapiro delay rules
out certain combinations of the companion mass, m2, and the
inclination, i. For typical neutron star masses and using optical
observations of the carbon/oxygen-core white dwarf we derive a mass
range for the companion of
which is consistent with
results from polarimetric studies of the pulsar magnetosphere. This
constraint together with the non-detection of Shapiro delay rules
out certain combinations of the companion mass, m2, and the
inclination, i. For typical neutron star masses and using optical
observations of the carbon/oxygen-core white dwarf we derive a mass
range for the companion of
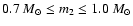 .
We apply evolutionary white dwarf cooling models to
revisit the cooling age of the companion. Our analysis reveals that
the companion has an effective temperature of
.
We apply evolutionary white dwarf cooling models to
revisit the cooling age of the companion. Our analysis reveals that
the companion has an effective temperature of
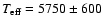 K and a cooling age of
K and a cooling age of
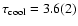 Gyr, which is roughly a factor of three lower than the
pulsar's characteristic age of 10.4 Gyr. The cooling age implies an
initial spin period of
P0=13.0(5) ms, which is very close to the
current period.
Gyr, which is roughly a factor of three lower than the
pulsar's characteristic age of 10.4 Gyr. The cooling age implies an
initial spin period of
P0=13.0(5) ms, which is very close to the
current period.
Key words: astrometry - stars: neutron - stars: white dwarfs -
stars: binaries: general - stars: pulsars: individual: PSR J2145-0750
1 Introduction
Millisecond pulsars (MSPs) have small spin periods (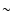 1.5-30 ms),
small spin-down rates (
1.5-30 ms),
small spin-down rates (
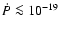 s s-1), and
are believed to be recycled by the accretion of mass from an evolving
companion star (e.g. Alpar et al. 1982). About
s s-1), and
are believed to be recycled by the accretion of mass from an evolving
companion star (e.g. Alpar et al. 1982). About
 80% of the MSP population in the Galactic plane are members of
binary systems. Most of those move in nearly circular orbits around
low-mass companions, forming the class of low-mass binary pulsars
(LMBPs). LMBPs have spin periods of
80% of the MSP population in the Galactic plane are members of
binary systems. Most of those move in nearly circular orbits around
low-mass companions, forming the class of low-mass binary pulsars
(LMBPs). LMBPs have spin periods of 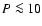 ms, small
eccentricities
ms, small
eccentricities
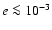 ,
and companions of mass
,
and companions of mass
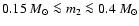 ,
presumably helium
(He)-core white dwarfs (WDs). The evolutionary history of LMBPs is
well understood. During the giant phase of the
,
presumably helium
(He)-core white dwarfs (WDs). The evolutionary history of LMBPs is
well understood. During the giant phase of the  1
1  companion star, mass overflows its Roche lobe and is accreted onto the
neutron star (NS). The stable mass accretion causes the pulsar to spin
up to millisecond periods and prevents a central helium ignition of
the giant, resulting in a binary system with a recycled millisecond
pulsar and a low-mass He-core WD (see review by Bhattacharya &
van den Heuvel 1991; Phinney & Kulkarni 1994).
companion star, mass overflows its Roche lobe and is accreted onto the
neutron star (NS). The stable mass accretion causes the pulsar to spin
up to millisecond periods and prevents a central helium ignition of
the giant, resulting in a binary system with a recycled millisecond
pulsar and a low-mass He-core WD (see review by Bhattacharya &
van den Heuvel 1991; Phinney & Kulkarni 1994).
In the last decade, pulsar surveys have revealed a new class of binary
pulsars, the intermediate-mass binary pulsars (IMBPs), with companion
masses above 0.45  .
Like in the LMBP case, the IMBPs have
almost circular orbits and WD companions, but show larger spin periods
.
Like in the LMBP case, the IMBPs have
almost circular orbits and WD companions, but show larger spin periods
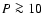 ms and slightly higher orbital eccentricities. As helium
ignition in the giant core starts above a core mass of 0.45
ms and slightly higher orbital eccentricities. As helium
ignition in the giant core starts above a core mass of 0.45 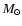 (Kippenhahn & Weigert 1990), the companions have to be
WDs with carbon/oxygen (CO) or oxygen/neon/magnesium (ONeMg)
cores. PSR J2145-0750 is most probably a member of the class of
IMBPs. Discovered by Bailes et al. (1994), the 16-ms
pulsar is in a nearly circular orbit, with an orbital period of 6.8 days. The system shows some of the peculiar properties of the IMBP
class: (1) The pulsar companion has a mass of m2>0.43
(Kippenhahn & Weigert 1990), the companions have to be
WDs with carbon/oxygen (CO) or oxygen/neon/magnesium (ONeMg)
cores. PSR J2145-0750 is most probably a member of the class of
IMBPs. Discovered by Bailes et al. (1994), the 16-ms
pulsar is in a nearly circular orbit, with an orbital period of 6.8 days. The system shows some of the peculiar properties of the IMBP
class: (1) The pulsar companion has a mass of m2>0.43 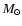 and
probably even larger than 0.51
and
probably even larger than 0.51 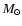 (50% C.L.), suggesting it to
be a CO-core WD. From optical observations of the PSR J2145-0750
system and using the dispersion measure (DM) distance of 500 pc,
Lundgren et al. (1996) concluded that the companion is
a WD. This is confirmed by our measurement of a timing parallax (see
Sect. 4.1) showing that the DM distance is the true
distance of the pulsar. (2) PSR J2145-0750 has a spin period of
16 ms, which is considerably longer than the average period of
(50% C.L.), suggesting it to
be a CO-core WD. From optical observations of the PSR J2145-0750
system and using the dispersion measure (DM) distance of 500 pc,
Lundgren et al. (1996) concluded that the companion is
a WD. This is confirmed by our measurement of a timing parallax (see
Sect. 4.1) showing that the DM distance is the true
distance of the pulsar. (2) PSR J2145-0750 has a spin period of
16 ms, which is considerably longer than the average period of
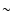 4 ms of LMBPs. (3) The surface magnetic field of the pulsar is
quite high:
4 ms of LMBPs. (3) The surface magnetic field of the pulsar is
quite high:
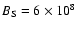 G. (4) Finally, the spin-down
age of the pulsar of
G. (4) Finally, the spin-down
age of the pulsar of 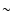 10 Gyr is very high and comparable to the
age of the Galaxy, raising interesting questions about its progenitor
and the initial spin period.
10 Gyr is very high and comparable to the
age of the Galaxy, raising interesting questions about its progenitor
and the initial spin period.
In contrast to LMBPs the evolution of IMBP progenitor systems is not
fully understood. Two models for the formation of heavy WDs in close
orbits have been proposed: (1) the system undergoes a Common Envelope (CE) evolution and spiral-in phase on the Red Giant Branch (RGB)
(Tauris 1996) or Asymptotic Giant Branch (AGB)
(van den Heuvel 1994), similar to the evolution of high-mass
binaries. (2) A massive companion progenitor loses much of its
envelope on the late main-sequence or early RGB through highly
super-Eddington mass transfer (Tauris et al. 2000; Taam et al. 2000).
For the particular case of PSR J2145-0750, van den Heuvel (1994)
proposed an evolutionary channel with a CE spiral-in phase on the AGB. In this scenario the progenitor system consisted of a
1-6 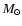 donor star, with an orbital period such that this star
overflows its Roche lobe on the AGB. During the CE phase, which is
similar to that of high-mass binary pulsar progenitors, the mass
accretion onto the pulsar is highly unstable. This results in an
incomplete recycling process of the pulsar and can explain the high
values for P and
donor star, with an orbital period such that this star
overflows its Roche lobe on the AGB. During the CE phase, which is
similar to that of high-mass binary pulsar progenitors, the mass
accretion onto the pulsar is highly unstable. This results in an
incomplete recycling process of the pulsar and can explain the high
values for P and 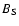 .
One possibility to test these
evolutionary channels is to measure the NS and companion masses. Here,
we report on new results from timing measurements of the PSR J2145-0750 binary system. They allow us to estimate the inclination
and companion mass of the binary. From the detection of a timing
parallax we derive an independent distance estimate of the pulsar.
.
One possibility to test these
evolutionary channels is to measure the NS and companion masses. Here,
we report on new results from timing measurements of the PSR J2145-0750 binary system. They allow us to estimate the inclination
and companion mass of the binary. From the detection of a timing
parallax we derive an independent distance estimate of the pulsar.
For a pulsar - white dwarf binary system one usually expects that the
cooling age of the WD matches the age of the pulsar. This is explained
by the fact that the cooling and spin-down clocks start ticking at
approximately the same time when the companion starts to contract to a
WD and the pulsar turns on at the end of the mass transfer phase. The
cooling age of the WD companion can be determined from its effective
temperature and its mass, using a WD cooling model. We use the
parallax distance along with optical observations to revisit the
cooling age of the WD companion, based on evolutionary WD cooling
models. We discuss the implications of our findings for the
evolutionary history of the binary.
2 Observations
We have made regular high-precision timing observations of
PSR J2145-0750 over a 10 yrs time span using both the 100-m
Effelsberg radio-telescope of the Max-Planck-Institut für
Radioastronomie in Bonn, Germany, and the 76-m Lovell radio-telescope
at Jodrell Bank, UK.
The Effelsberg observations have been carried out since April 1994 at
a centre frequency of 1410 MHz. Data have been acquired approximately
once per month, with a typical observing time of 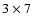 min. For
the observations we used a 1300-1700 MHz tunable HEMT receiver with
a system temperature of 30 K on the cold sky and an antenna gain of
1.5 K Jy-1. In order to monitor changes of the dispersion measure
(DM) we occasionally collected data at 860 MHz, using an uncooled HEMT
receiver with a system temperature of 65 K on the cold sky and a
gain of 1.5 K Jy-1. During the period April 1994-October
1996, the data were obtained using the Effelsberg Pulsar Observation
System (EPOS) (Seiradakis et al. 1995; Kramer et al. 1997, 1998). Here, the two
circular polarization signals were processed in a
min. For
the observations we used a 1300-1700 MHz tunable HEMT receiver with
a system temperature of 30 K on the cold sky and an antenna gain of
1.5 K Jy-1. In order to monitor changes of the dispersion measure
(DM) we occasionally collected data at 860 MHz, using an uncooled HEMT
receiver with a system temperature of 65 K on the cold sky and a
gain of 1.5 K Jy-1. During the period April 1994-October
1996, the data were obtained using the Effelsberg Pulsar Observation
System (EPOS) (Seiradakis et al. 1995; Kramer et al. 1997, 1998). Here, the two
circular polarization signals were processed in a
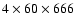 kHz filter bank combined with an incoherent hardware
de-disperser. The detected left- and right-hand circular signals in
each channel were de-dispersed on-line, added, and folded with the
topocentric pulse period to produce a total power pulse profile of
40 MHz bandwidth. Since October 1996 the observations were made with
the Effelsberg-Berkeley Pulsar Processor (EBPP), which corrects for
the dispersion smearing of the signal using a coherent de-dispersion
technique (Hankins & Rickett 1975). In the total power
mode the EBPP provides 32 channels for both polarizations with a
maximum total bandwidth of 112 MHz, depending on DM and observing
frequency (Backer et al. 1997). For PSR J2145-0750 a
total bandwidth of 90 MHz was available at 1410 MHz. The output
signals of each channel were fed into de-disperser boards for coherent
on-line de-dispersion and were synchronously folded at the pulse
period over 7-min integrations. To obtain a high signal-to-noise ratio
polarization profile of PSR J2145-0750 (see Sect. 5.3) we used
the EBPP in polarization mode where the four Stokes parameters are
available over 32 channels with a total bandwidth of 28 MHz.
kHz filter bank combined with an incoherent hardware
de-disperser. The detected left- and right-hand circular signals in
each channel were de-dispersed on-line, added, and folded with the
topocentric pulse period to produce a total power pulse profile of
40 MHz bandwidth. Since October 1996 the observations were made with
the Effelsberg-Berkeley Pulsar Processor (EBPP), which corrects for
the dispersion smearing of the signal using a coherent de-dispersion
technique (Hankins & Rickett 1975). In the total power
mode the EBPP provides 32 channels for both polarizations with a
maximum total bandwidth of 112 MHz, depending on DM and observing
frequency (Backer et al. 1997). For PSR J2145-0750 a
total bandwidth of 90 MHz was available at 1410 MHz. The output
signals of each channel were fed into de-disperser boards for coherent
on-line de-dispersion and were synchronously folded at the pulse
period over 7-min integrations. To obtain a high signal-to-noise ratio
polarization profile of PSR J2145-0750 (see Sect. 5.3) we used
the EBPP in polarization mode where the four Stokes parameters are
available over 32 channels with a total bandwidth of 28 MHz.
Lovell observations of PSR J2145-0750 were made from October 1992 to
January 1999 at centre frequencies of 606 and 1400 MHz. Both circular
polarization signals were detected and incoherently de-dispersed in a
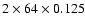 -MHz filter bank at 606 MHz and in a
-MHz filter bank at 606 MHz and in a
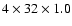 -MHz filter bank at 1400 MHz. The signals were added and
synchronously folded at the pulse period with a typical integration
time of 1-3 min. Details of the observing system can be found in
Gould & Lyne (1998).
-MHz filter bank at 1400 MHz. The signals were added and
synchronously folded at the pulse period with a typical integration
time of 1-3 min. Details of the observing system can be found in
Gould & Lyne (1998).
Both Effelsberg and Lovell data were time stamped with clock
information from a local hydrogen maser clock and later synchronized
to UTC(NIST) using the signals from the Global Positioning System (GPS). In order to calculate the pulse time-of-arrival (TOA) synthetic
templates of the pulse profile were constructed for each backend and
observing frequency, and fitted to the observed profiles with template
matching procedures (details can be found in Lange et al. 2001). TOA uncertainties were estimated using a method
described by Downs & Reichley (1983). Typical TOA errors
for EBPP observations are 2.8 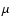 s at 860 MHz and
1.9
s at 860 MHz and
1.9 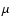 s at 1410 MHz, whereas for Lovell observations we found
5.2
s at 1410 MHz, whereas for Lovell observations we found
5.2 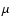 s at 606 MHz and 4.5
s at 606 MHz and 4.5 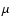 s at 1400 MHz.
s at 1400 MHz.
3 Timing analysis
The combined TOAs, weighted by their individual uncertainties, were
fitted to a spin-down model of the pulsar in a binary system with the
software package
TEMPO![[*]](/icons/foot_motif.gif) , using the DE200 planetary ephemerides (Standish 1990). PSR J2145-0750 lies close to the ecliptic plane, with an ecliptic latitude of only
, using the DE200 planetary ephemerides (Standish 1990). PSR J2145-0750 lies close to the ecliptic plane, with an ecliptic latitude of only
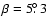 ,
resulting in less accurate position and proper
motion measurements if determined in the equatorial reference
frame. In order to minimize covariances between the astrometric
parameters we chose ecliptic coordinates for our timing model,
performing standard Monte-Carlo simulations to derive reliable values
for the proper motion
,
resulting in less accurate position and proper
motion measurements if determined in the equatorial reference
frame. In order to minimize covariances between the astrometric
parameters we chose ecliptic coordinates for our timing model,
performing standard Monte-Carlo simulations to derive reliable values
for the proper motion
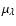 and
and 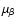 .
Since the pulsar
is moving in an almost circular orbit we applied the timing model for
binary systems with small eccentricities (ELL1) using the
Laplace-Lagrange parameters
.
Since the pulsar
is moving in an almost circular orbit we applied the timing model for
binary systems with small eccentricities (ELL1) using the
Laplace-Lagrange parameters
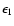 and
and
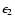 ,
as well as
the time of ascending node
,
as well as
the time of ascending node
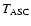 (Lange et al. 2001). The
three Keplerian parameters eccentricity e, epoch
(Lange et al. 2001). The
three Keplerian parameters eccentricity e, epoch 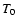 ,
and
longitude of periastron
,
and
longitude of periastron 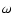 ,
are then calculated from the former
three parameters.
,
are then calculated from the former
three parameters.
In the fitting procedure the TOA segments obtained with EPOS, EBPP,
and Lovell data were fitted for a mutual offset accounting for
different templates and TOA reference points in the profiles. Using
the full TOA data set at all frequencies we then determined the DM
over the 10-yrs period. By excluding all TOAs with lines-of sight to
the pulsar lying closer than 30
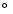 to the Sun we analysed the
influence of free electrons in the solar system on the DM, but found
no variations of the DM or other parameters larger than their
1
to the Sun we analysed the
influence of free electrons in the solar system on the DM, but found
no variations of the DM or other parameters larger than their
1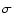 uncertainties. However, the multi-frequency timing fit
resulted in a detection of a secular DM variation of
uncertainties. However, the multi-frequency timing fit
resulted in a detection of a secular DM variation of
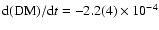 pc cm-3 yr-1. Variations of pulsar
DMs have been explained by a simple wedge model of electron density
fluctuations in the Galaxy, resulting in a square root dependence of
pc cm-3 yr-1. Variations of pulsar
DMs have been explained by a simple wedge model of electron density
fluctuations in the Galaxy, resulting in a square root dependence of
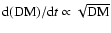 (Backer et al. 1993). Recently, Hobbs et al. (2004) showed that this
relation holds for a large group of pulsars, and derived a best-fit of
(Backer et al. 1993). Recently, Hobbs et al. (2004) showed that this
relation holds for a large group of pulsars, and derived a best-fit of
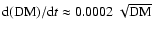 ,
with a scatter of one
order of magnitude. For PSR J2145-0750 our measurement of
,
with a scatter of one
order of magnitude. For PSR J2145-0750 our measurement of
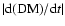 is consistent with the empirical relation. By holding the
values for DM and d
is consistent with the empirical relation. By holding the
values for DM and d
 fixed we then obtained the best-fit
timing model for the astrometric, rotational and binary parameters
using only the more accurate 1400 MHz TOAs from Effelsberg and Jodrell
Bank. We scaled the TOA errors by an appropriate factor to achieve a
uniform
fixed we then obtained the best-fit
timing model for the astrometric, rotational and binary parameters
using only the more accurate 1400 MHz TOAs from Effelsberg and Jodrell
Bank. We scaled the TOA errors by an appropriate factor to achieve a
uniform
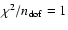 for each TOA segment.
for each TOA segment.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{1031fig1.eps}
\end{figure}](/articles/aa/full/2004/41/aa1031/Timg48.gif) |
Figure 1:
Post-fit timing residuals of the combined Effelsberg and Lovell 1400 MHz
timing data as a function of observing year.
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{1031fig2.eps}
\end{figure}](/articles/aa/full/2004/41/aa1031/Timg49.gif) |
Figure 2:
Distribution of the 1400 MHz post-fit timing residuals normalized by their
uncertainties.
|
| Open with DEXTER |
From the best-fit model we obtained post-fit timing residuals that are
displayed in Fig. 1. As seen from the figure, we obtained
a good coverage of the 10-yrs timing baseline. Note that the EPOS and
Lovell TOAs obtained from 1992-1999 have much higher uncertainties
than the EBPP data, which is due to the incoherent dispersion removal
technique. In order to test the statistical properties of our data
we generated a histogram of the deviations of the timing residuals
from the model as shown in Fig. 2. The post-fit residuals
are consistent with the expected Gaussian distribution. The timing
parameters of the best-fit model for PSR J2145-0750 are listed in
Table 1. Included in the table are upper limits as well
as derived parameters. The limits on the pulse frequency second
derivative, 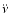 ,
and the orbital period derivative,
,
and the orbital period derivative,
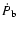 ,
were found by allowing the extra parameters to vary one at
a time in the global fit. Fitting for the derivatives of both the
Laplace-Lagrange parameters,
,
were found by allowing the extra parameters to vary one at
a time in the global fit. Fitting for the derivatives of both the
Laplace-Lagrange parameters,
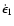 and
and
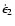 ,
led to the upper limits on the eccentricity derivative,
,
led to the upper limits on the eccentricity derivative, 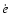 ,
and
the periastron rate of change,
,
and
the periastron rate of change,
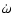 .
.
Table 1:
Timing model for PSR J2145-0750.
4 Astrometry and intrinsic pulsar parameters
4.1 Parallax, proper motion and transverse velocity
Pulsar distances are estimated from their DM using models for the
electron density distribution in the Galaxy (e.g. Taylor & Cordes
1993, updated model: Cordes & Lazio 2002,
hereafter NE2001). Independent distance measurements define an
absolute distance scale and hence are of fundamental importance to
calibrate models like NE2001. For pulsars, distances are derived from
trigonometric parallaxes using VLBI observations, or from pulsar
timing. In pulsar timing, the parallax is obtained by measuring the
time delay of the TOA caused by the curvature of the radio wave
fronts. However, the amplitude of the corresponding residual term,
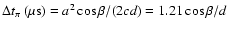 ,
is very small, allowing us to detect a timing
parallax only for a very few millisecond pulsars near the ecliptic
plane. Here, a is the Earth-Sun distance in kpc,
,
is very small, allowing us to detect a timing
parallax only for a very few millisecond pulsars near the ecliptic
plane. Here, a is the Earth-Sun distance in kpc, 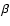 the
ecliptic latitude, and d the distance to the pulsar in kpc. Timing
parallaxes have been detected for pulsars such as PSR B1855+09 (Kaspi et al. 1991), PSR J1713+0747
(Camilo et al. 1994a), PSR J0437-4715
(Sandhu et al. 1997) and PSR J1744-1134
(Toscano et al. 1999). Nevertheless, due to an
ecliptic latitude of only
the
ecliptic latitude, and d the distance to the pulsar in kpc. Timing
parallaxes have been detected for pulsars such as PSR B1855+09 (Kaspi et al. 1991), PSR J1713+0747
(Camilo et al. 1994a), PSR J0437-4715
(Sandhu et al. 1997) and PSR J1744-1134
(Toscano et al. 1999). Nevertheless, due to an
ecliptic latitude of only
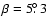 we were able to
detect for the first time a timing parallax for PSR J2145-0750 of
we were able to
detect for the first time a timing parallax for PSR J2145-0750 of
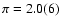 mas. This corresponds to a distance estimate of
mas. This corresponds to a distance estimate of
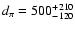 pc and agrees very well with the DM distances, i.e.
pc and agrees very well with the DM distances, i.e.
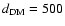 pc from the Taylor & Cordes (1993)
model and
pc from the Taylor & Cordes (1993)
model and
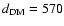 pc from the NE2001 model (with typical
uncertainties of
pc from the NE2001 model (with typical
uncertainties of  10%). Using the parallax distance we derive a
transverse velocity of
10%). Using the parallax distance we derive a
transverse velocity of
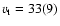 km s-1, which is in
excellent agreement with scintillation velocities of
km s-1, which is in
excellent agreement with scintillation velocities of 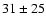 km s-1 obtained by Nicastro & Johnston (1995) and
Johnston et al. (1998).
km s-1 obtained by Nicastro & Johnston (1995) and
Johnston et al. (1998).
With a galactic position angle of 289
 the pulsar is moving
towards the Galactic plane. This is not in contradiction to the idea
that pulsars are born in the Galactic plane and then move to higher
latitudes, as the MSP population is very old (
the pulsar is moving
towards the Galactic plane. This is not in contradiction to the idea
that pulsars are born in the Galactic plane and then move to higher
latitudes, as the MSP population is very old (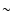 1 Gyr) and has
already reached a dynamic equilibrium in the Galactic gravitational
potential (e.g. Toscano et al. 1999). In this scenario PSR J2145-0750, with a characteristic age of 10 Gyr (see Sect. 4.3), would have already performed many oscillations in the
Galactic potential described by Kuijken & Gilmore (1989).
1 Gyr) and has
already reached a dynamic equilibrium in the Galactic gravitational
potential (e.g. Toscano et al. 1999). In this scenario PSR J2145-0750, with a characteristic age of 10 Gyr (see Sect. 4.3), would have already performed many oscillations in the
Galactic potential described by Kuijken & Gilmore (1989).
4.2 Doppler corrections
Accelerations in the Galactic gravitational potential introduce
contributions to the observed period derivative 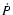 which cannot
be neglected for MSPs that have spin-down rates of about six orders of
magnitude lower than those of normal pulsars. Doppler effects arise
due to (a) the Galactic differential rotation, (b) the vertical
acceleration in the Galaxy (Damour & Taylor 1991), and
(c) the transverse velocity of the pulsar (Shklovskii
1970). Following these authors, the Doppler correction
to the period derivative can be written as
which cannot
be neglected for MSPs that have spin-down rates of about six orders of
magnitude lower than those of normal pulsars. Doppler effects arise
due to (a) the Galactic differential rotation, (b) the vertical
acceleration in the Galaxy (Damour & Taylor 1991), and
(c) the transverse velocity of the pulsar (Shklovskii
1970). Following these authors, the Doppler correction
to the period derivative can be written as
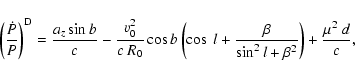 |
(1) |
where R0 and v0 denote the galactocentric radius and galactic
circular velocity of the Sun, respectively, l and b the galactic
longitude and latitude of the pulsar, and
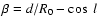 .
We
choose R0=8.0 kpc and v0= 220 km s-1 (Reid
1993). az is the vertical component of the galactic
acceleration and can be calculated from the Kuijken & Gilmore
(1989) model of the Galactic potential. For
PSR J2145-0750 we derive a kinematic correction of
.
We
choose R0=8.0 kpc and v0= 220 km s-1 (Reid
1993). az is the vertical component of the galactic
acceleration and can be calculated from the Kuijken & Gilmore
(1989) model of the Galactic potential. For
PSR J2145-0750 we derive a kinematic correction of
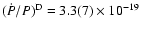 s-1, where the major contribution (73%) comes
from the Shklovskii term
s-1, where the major contribution (73%) comes
from the Shklovskii term
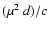 .
.
4.3 Characteristic age and magnetic field
Subtracting the kinematic contributions from the observed spin-down rate
of PSR J2145-0750 we obtain an intrinsic spin-down rate of
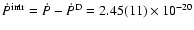 s s-1 which is 18% smaller than the observed value.
s s-1 which is 18% smaller than the observed value.
It is usually assumed that the evolution of the spin frequency
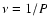 can be described by a power-law
can be described by a power-law
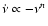 ,
where n is the so-called braking index. Then the pulsar age
can be calculated from
,
where n is the so-called braking index. Then the pulsar age
can be calculated from
![\begin{displaymath}
\tau = \frac{P}{(n-1)~\dot P}\:
\left[1-~\left(\frac{P_0}{P}\right)^{n-1}\right] ,
\end{displaymath}](/articles/aa/full/2004/41/aa1031/img96.gif) |
(2) |
where P0 is the initial period of the pulsar. Under the assumptions
that 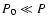 and that the spin-down is due to magnetic dipole
braking (n=3), the spin-down age is given by
and that the spin-down is due to magnetic dipole
braking (n=3), the spin-down age is given by
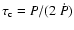 ,
the characteristic age of the pulsar.
Subtracting the Doppler contributions, for PSR J2145-0750 we thus
obtain
,
the characteristic age of the pulsar.
Subtracting the Doppler contributions, for PSR J2145-0750 we thus
obtain
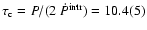 Gyr. As
the uncertainty of
Gyr. As
the uncertainty of
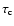 caused by the a priori unknown nand P0 can be considerable, an independent age estimate, as given
by the cooling age of the pulsar companion (see Sect. 6),
is highly desirable.
caused by the a priori unknown nand P0 can be considerable, an independent age estimate, as given
by the cooling age of the pulsar companion (see Sect. 6),
is highly desirable.
Assuming a pure dipolar magnetic field and using the intrinsic
spin-down rate we can estimate the surface magnetic field of the
pulsar to be
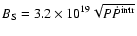 G = 6.35(14)
G = 6.35(14)
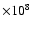 G. This magnetic field is more than
three orders of magnitude smaller than for normal pulsars, a clear
indication than PSR J2145-0750 has gone through a recycling phase.
G. This magnetic field is more than
three orders of magnitude smaller than for normal pulsars, a clear
indication than PSR J2145-0750 has gone through a recycling phase.
Any remaining non-gaussian noise in timing residuals is generally
explained by rotational instabilities intrinsic to the pulsar, or by
an incomplete timing model, such as unmodelled DM variations or the
existence of a planet in the system. For PSR J2145-0750 a fit for
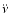 over the full timing baseline resulted in
over the full timing baseline resulted in
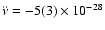 s-3. As this measurement is
hardly significant we conservatively quote
s-3. As this measurement is
hardly significant we conservatively quote 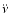 as an upper
limit in Table 1. At the same time, we do not detect
any DM variations that are not accounted for in the timing model. A
simultaneous fit of our multi-frequency data for third- and
fourth-order derivatives of DM as well as for
as an upper
limit in Table 1. At the same time, we do not detect
any DM variations that are not accounted for in the timing model. A
simultaneous fit of our multi-frequency data for third- and
fourth-order derivatives of DM as well as for 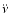 resulted in a
similar
resulted in a
similar 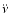 value, while d
value, while d
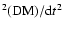 and d
and d
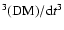 were not significant.
were not significant.
Arzoumanian et al. (1994) analysed the timing noise of
a number of slow and millisecond pulsars by quantifying the noisiness
with the noise parameter
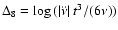 ,
where t=108 s. They quote a fit-by-eye to the data of the form
,
where t=108 s. They quote a fit-by-eye to the data of the form
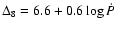 ,
with a large scatter of the data
points. Lommen (2002) revised this relation using new
MSP data and showed that at least seven MSPs have significantly lower
,
with a large scatter of the data
points. Lommen (2002) revised this relation using new
MSP data and showed that at least seven MSPs have significantly lower
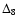 's than presented by Arzoumanian et al. (1994).
's than presented by Arzoumanian et al. (1994).
In order to estimate the timing noise of PSR J2145-0750 we divided
the total data set into three sub-intervals, each spanning 108 s
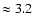 yr of TOAs. For each sub-interval we transformed
epoch, pulse frequency
yr of TOAs. For each sub-interval we transformed
epoch, pulse frequency 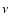 ,
and epoch of ascending node
,
and epoch of ascending node
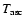 to an epoch near the centre of each sub-interval. We then fitted the
timing model of the pulsar, holding DM and d
to an epoch near the centre of each sub-interval. We then fitted the
timing model of the pulsar, holding DM and d
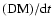 fixed and
allowing
fixed and
allowing 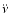 to vary. The resulting
to vary. The resulting 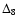 's for each
sub-interval are -4.0, -4.1, and -4.3, i.e. slightly larger than
the predicted value of
's for each
sub-interval are -4.0, -4.1, and -4.3, i.e. slightly larger than
the predicted value of
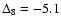 .
We thus conclude that PSR J2145-0750 is a possible candidate for intrinsic timing
noise. Future timing observations will resolve this assertion.
.
We thus conclude that PSR J2145-0750 is a possible candidate for intrinsic timing
noise. Future timing observations will resolve this assertion.
4.5 Secular changes in orbital parameters
For the first time we detected a secular variation of the projected
semi-major axis of PSR J2145-0750 of
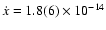 lt-s s-1. In order to test the robustness of this
measurement we divided the total set into five sub-intervals, each
spanning two years of TOAs. For every sub-interval the TOAs were
fitted to the timing model of the pulsar, with the variation of xheld fixed at zero. Hereby we transformed epoch, pulse frequency
lt-s s-1. In order to test the robustness of this
measurement we divided the total set into five sub-intervals, each
spanning two years of TOAs. For every sub-interval the TOAs were
fitted to the timing model of the pulsar, with the variation of xheld fixed at zero. Hereby we transformed epoch, pulse frequency  ,
and epoch of ascending node
,
and epoch of ascending node
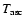 to an epoch near the centre
of each sub-interval. The fits resulted in an increase of x with
time, with a slope of
to an epoch near the centre
of each sub-interval. The fits resulted in an increase of x with
time, with a slope of
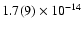 lt-s s-1, confirming
the value from the global fit.
lt-s s-1, confirming
the value from the global fit.
The timing data showed no evidence for secular changes in other
orbital parameters. In principle, the binary system could undergo both a
general relativistic (GR) advance of periastron and an orbital decay
due to the emission of gravitational radiation (Damour & Taylor
1991), i.e.
where the masses are in Solar units and
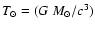 .
.
If we assume a pulsar mass of m1=1.4 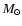 and a companion mass
of m2=0.51
and a companion mass
of m2=0.51 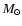 (using the mass function and a median
inclination
(using the mass function and a median
inclination
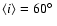 ), we expect
), we expect
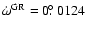 yr-1 and
yr-1 and
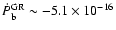 s s-1. However, as PSR J2145-0750 has a
very small eccentricity, all effects of secular variations in
s s-1. However, as PSR J2145-0750 has a
very small eccentricity, all effects of secular variations in 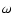 are fully absorbed by the redefinition of the binary period and are
therefore not observable in this system. The observed upper limit for
are fully absorbed by the redefinition of the binary period and are
therefore not observable in this system. The observed upper limit for
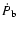 is four orders of magnitude higher which makes any
detection of the GR orbital decay highly unlikely.
is four orders of magnitude higher which makes any
detection of the GR orbital decay highly unlikely.
Moreover, the Shklovskii effect discussed in Sect. 4.2
also affects the observed value of
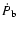 .
Using the
results from Sect. 4.2, we expect a contribution of
.
Using the
results from Sect. 4.2, we expect a contribution of
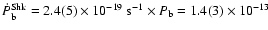 s s-1. This value is not only
of different sign as the expected GR contribution but also about three
orders of magnitude larger. Nevertheless, the Shklovskii term is
still consistent with the observations as it is yet a factor of 20 smaller than our derived upper limited.
s s-1. This value is not only
of different sign as the expected GR contribution but also about three
orders of magnitude larger. Nevertheless, the Shklovskii term is
still consistent with the observations as it is yet a factor of 20 smaller than our derived upper limited.
5.1 Secular change of x
The observed secular change of the projected semi-major axis
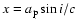 could, in principle, result from a variation of the major
axis of the pulsar orbit,
could, in principle, result from a variation of the major
axis of the pulsar orbit, 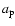 ,
of the orbital inclination, i, or a combination of both. The contributions to
,
of the orbital inclination, i, or a combination of both. The contributions to 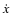 are
(Damour & Taylor 1992; Kopeikin 1996):
are
(Damour & Taylor 1992; Kopeikin 1996):
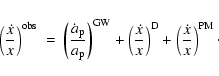 |
(5) |
The emission of gravitational waves (GW) leads to a shrinking of the
pulsar orbit given by
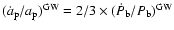 (e.g. Doroshenko et al. 2001). With Eq. (4) one expects
(e.g. Doroshenko et al. 2001). With Eq. (4) one expects
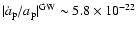 s-1which is seven orders of magnitude smaller than the observed
s-1which is seven orders of magnitude smaller than the observed
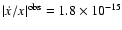 s-1. In general,
s-1. In general,
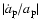 will be of the same order of magnitude as
will be of the same order of magnitude as
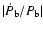 for typical astrophysical processes in a
binary. With the observed upper limit of
for typical astrophysical processes in a
binary. With the observed upper limit of
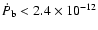 s-1 we derive
s-1 we derive
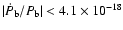 s-1, still three orders of magnitude smaller than
s-1, still three orders of magnitude smaller than
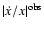 .
Therefore, the nonzero
.
Therefore, the nonzero 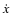 is most likely
not caused by orbital evolution.
is most likely
not caused by orbital evolution.
The Doppler correction affects the light-travel time across the orbit
in the same way as the pulse period, so that the term
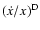 is identical to the one for the period derivative
(Eq. (1), see Damour & Taylor 1992). Its value is
therefore four orders of magnitude smaller than the observed value
is identical to the one for the period derivative
(Eq. (1), see Damour & Taylor 1992). Its value is
therefore four orders of magnitude smaller than the observed value
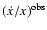 .
.
We conclude that the nonzero 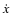 must arise from a change
in the observed inclination i of the orbit. The relative motion of
the binary and the observer causes a change of the orientation of the
line-of-sight to the binary which results in an apparent change of i. Kopeikin (1996) derived
must arise from a change
in the observed inclination i of the orbit. The relative motion of
the binary and the observer causes a change of the orientation of the
line-of-sight to the binary which results in an apparent change of i. Kopeikin (1996) derived
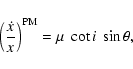 |
(6) |
where 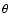 denotes the difference of the position angle of proper
motion and the position angle of ascending node. As
denotes the difference of the position angle of proper
motion and the position angle of ascending node. As 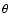 is a
priori unknown, we can only derive a firm upper limit for i using
is a
priori unknown, we can only derive a firm upper limit for i using
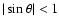 and the lower limit of allowed values for
and the lower limit of allowed values for 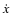 from Table 1, i.e.
from Table 1, i.e.
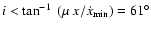 .
.
We performed Monte-Carlo simulations to derive the distribution of
inclination angles within this constraint, following a procedure
described by Nice et al. (2001). Assuming that the
orientation of the binary in space is arbitrary, 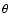 is a
uniformly distributed random variable and i is a random variable
distributed with uniform probability in
is a
uniformly distributed random variable and i is a random variable
distributed with uniform probability in 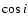 .
From these
distributions we select values of
.
From these
distributions we select values of 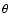 and i and retain only
those combinations which satisfy Eq. (6) within the
measurement errors. The resulting distribution for i is presented in
Fig. 3, showing a broad peak towards higher
inclinations. The median value and its asymmetric errors are
and i and retain only
those combinations which satisfy Eq. (6) within the
measurement errors. The resulting distribution for i is presented in
Fig. 3, showing a broad peak towards higher
inclinations. The median value and its asymmetric errors are
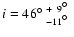 (68% C.L.).
(68% C.L.).
![\begin{figure}
\par\includegraphics[angle=-90,width=7.9cm,clip]{1031fig3.eps}
\end{figure}](/articles/aa/full/2004/41/aa1031/Timg142.gif) |
Figure 3:
Distribution of orbital inclinations i resulting from Monte-Carlo
simulations (see Sect. 5.1). The median of the distribution
is
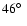 (solid line), and its lower
and upper 1 (solid line), and its lower
and upper 1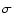 values are at values are at
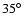 and
and
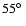 ,respectively (dashed lines). ,respectively (dashed lines). |
| Open with DEXTER |
5.2 Non-detection of Shapiro delay
The propagation of radio signals from pulsars in binary systems is
affected by a general-relativistic time delay of the signals in the
gravitational field of the companion star. For a pulsar in a circular
orbit this "Shapiro delay'' (Shapiro 1964) is given by
![\begin{displaymath}\Delta t = -2~ m_2\; T_{\odot}~ \ln[1-\sin i~ \sin(\Phi-\Phi_0)] ,
\end{displaymath}](/articles/aa/full/2004/41/aa1031/img143.gif) |
(7) |
where 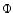 is the orbital phase in radians,
is the orbital phase in radians, 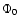 is the phase of
the ascending node, and
is the phase of
the ascending node, and
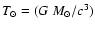 .
In practice,
Shapiro delay is conveniently expressed in terms of two observables,
the "range''
.
In practice,
Shapiro delay is conveniently expressed in terms of two observables,
the "range''
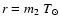 and the "shape''
and the "shape''
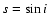 (Ryba & Taylor 1991), the post-Keplerian orbital
parameters which allow a determination of the companion mass, m2,
and the orbital inclination, i. However, for small inclination
angles the variation of
(Ryba & Taylor 1991), the post-Keplerian orbital
parameters which allow a determination of the companion mass, m2,
and the orbital inclination, i. However, for small inclination
angles the variation of 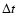 over the orbit is nearly sinusoidal
and cannot be separated from a small variation in x. For edge-on
orbits (
over the orbit is nearly sinusoidal
and cannot be separated from a small variation in x. For edge-on
orbits (
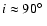 ),
), 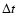 peaks at
peaks at
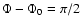 ,
where the pulsar is behind the companion. Here, the covariance with
the Keplerian parameters breaks, and a measurement of Shapiro delay
(and hence r and s) is possible. Because high inclination orbits
are relatively rare, Shapiro delay has been detected in only five
pulsar-white dwarf binaries, PSR B1855+09 (Ryba & Taylor 1991),
PSR J1713+0747 (Camilo et al. 1994a), PSR J0437-4715
(van Straten et al. 2001), PSR J1909-3744
(Jacoby et al. 2003), PSR J1640+2224
(Löhmer et al. 2004), and perhaps in PSR J0751+1807 (Nice et al. 2003).
,
where the pulsar is behind the companion. Here, the covariance with
the Keplerian parameters breaks, and a measurement of Shapiro delay
(and hence r and s) is possible. Because high inclination orbits
are relatively rare, Shapiro delay has been detected in only five
pulsar-white dwarf binaries, PSR B1855+09 (Ryba & Taylor 1991),
PSR J1713+0747 (Camilo et al. 1994a), PSR J0437-4715
(van Straten et al. 2001), PSR J1909-3744
(Jacoby et al. 2003), PSR J1640+2224
(Löhmer et al. 2004), and perhaps in PSR J0751+1807 (Nice et al. 2003).
We did not detect Shapiro delay in the timing data of PSR J2145-0750. However, we can use the non-detection to place limits
on allowed values for i and m2. Following a procedure described
by Nice et al. (2001), we tested a 2D grid of timing models, that
include the Shapiro parameters in the range of
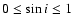 and
and
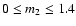
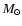 ,
allowing all other parameters to vary.
The resulting
,
allowing all other parameters to vary.
The resulting 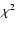 values are mostly very similar to a model
without Shapiro delay. However, for models with high inclination
angles and/or high companion masses we obtain significantly higher
values for
values are mostly very similar to a model
without Shapiro delay. However, for models with high inclination
angles and/or high companion masses we obtain significantly higher
values for 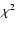 .
The failure of these models means that one would
have detected Shapiro delay had these been the true values of iand m2. In Fig. 4, the parameter space excluded
by models with
.
The failure of these models means that one would
have detected Shapiro delay had these been the true values of iand m2. In Fig. 4, the parameter space excluded
by models with
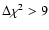 (i.e., 3
(i.e., 3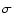 )
is shown.
)
is shown.
![\begin{figure}
\par\includegraphics[width=14cm,clip]{1031fig4.ps}
\end{figure}](/articles/aa/full/2004/41/aa1031/Timg157.gif) |
Figure 4:
Constraints on orbital inclination,
i, and WD mass, m2, from 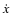 -measurement and limits on
Shapiro delay. Points inside the hatched rectangle are excluded by
measured -measurement and limits on
Shapiro delay. Points inside the hatched rectangle are excluded by
measured 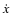 ,
points inside the curved hatched area are excluded
by the non-detection of Shapiro delay. From the mass function we
calculated the contours for constant neutron star masses, indicated by
the solid curves. The vertical lines denote the median value
( ,
points inside the curved hatched area are excluded
by the non-detection of Shapiro delay. From the mass function we
calculated the contours for constant neutron star masses, indicated by
the solid curves. The vertical lines denote the median value
(
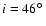 ,
solid) and its 1 ,
solid) and its 1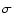 errors (at
errors (at
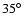 and
and
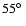 ,
dashed) for the distribution of inclination angles derived
from the observed ,
dashed) for the distribution of inclination angles derived
from the observed 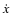 .
From these uncertainties we derive the
companion mass limits .
From these uncertainties we derive the
companion mass limits
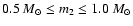 displayed by the horizontal dashed lines. Photometric studies of the
WD companion (see Sect. 6) result in a lower mass limit of displayed by the horizontal dashed lines. Photometric studies of the
WD companion (see Sect. 6) result in a lower mass limit of
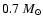 (horizontal dotted line).
(horizontal dotted line). |
| Open with DEXTER |
5.3 Polarimetry
During the recycling process of MSPs the neutron star is spun-up by
mass transfer from the companion star which is expected to cause an
alignment of pulsar spin and orbital angular momentum of the binary
system (Phinney & Kulkarni 1994). Assuming that this
holds for PSR J2145-0750 it is then possible to constrain the
orbital inclination from the known geometry of the pulsar
magnetosphere. We therefore observed PSR J2145-0750 at 1410 MHz
using the EBPP in polarization mode and derived a position angle that
is similar to the findings of Sallmen (1998) and Stairs
et al. (1999). The profile of PSR J2145-0750 shows at
least three components, with a bridge of emission between the two
strongest components. Unfortunately, the linear intensity at 1410 MHz
is very weak (but see also Xilouris et al. 1998;
Sallmen 1998), and the accompanying position-angle swing is extremely
complex, with multiple orthogonal mode changes (Stairs et al. 1999). Applying a rotating vector model (RVM) (Radhakrishnan &
Cooke 1969) to the observed position angle usually leads
to high uncertainties in the RVM fit. We fitted a RVM curve to the
position angle of the whole profile (including the precursor) and
found a best fit for a magnetic inclination of
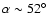 and an impact angle of
and an impact angle of
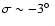 .
These values are
considerably different from those found by Sallmen (1998) which is
probably due to the inclusion of the precursor in our fit leading to a
longer baseline in pulse longitude. Even though the position angle is
poorly constrained leading to considerable errors in the RVM fits,
when we apply our best-fit values the angle between the pulsar
rotation axis and the line-of-sight results in
.
These values are
considerably different from those found by Sallmen (1998) which is
probably due to the inclusion of the precursor in our fit leading to a
longer baseline in pulse longitude. Even though the position angle is
poorly constrained leading to considerable errors in the RVM fits,
when we apply our best-fit values the angle between the pulsar
rotation axis and the line-of-sight results in
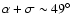 .
If one assumes that the pulsar rotation axis is aligned with
the orbital momentum, one derives
.
If one assumes that the pulsar rotation axis is aligned with
the orbital momentum, one derives
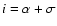 (or
(or
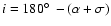 ), i.e.
), i.e.
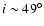 (or
(or
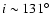 ).
).
One generally needs to be careful in interpreting the position angles
observed in recycled pulsars as being the reflection of the underlying
geometry. The position angle swings are typically much flatter and
often do not resemble the expected S-like swing (e.g. Xilouris et al. 1998; Stairs et al. 1999). Given this caveat, it is
interesting to note that the fitted inclination angle agrees very well
with the median value of
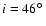 obtained from our
obtained from our 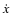 measurement. We conclude that the analysis of the pulsar
magnetosphere by polarimetry results in a consistent picture of the
orbital inclination, strongly supporting our earlier findings.
measurement. We conclude that the analysis of the pulsar
magnetosphere by polarimetry results in a consistent picture of the
orbital inclination, strongly supporting our earlier findings.
5.4 Companion mass
As demonstrated, the 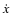 measurement and the limits on Shapiro
delay for PSR J2145-0750 can be used to put constraints on the
orbital inclination, i, and the companion mass, m2, as shown in
Fig. 4. From the observed
measurement and the limits on Shapiro
delay for PSR J2145-0750 can be used to put constraints on the
orbital inclination, i, and the companion mass, m2, as shown in
Fig. 4. From the observed 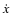 we derive an
upper limit on the inclination angle of
we derive an
upper limit on the inclination angle of
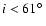 ,
so that all
points with
,
so that all
points with
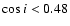 are excluded as indicated by the hatched
rectangle in the figure. The curved hatched area is the parameter
space excluded due to the non-detection of Shapiro delay in the
binary. From the mass function of PSR J2145-0750 we derive the
displayed contours for constant neutron star masses.
are excluded as indicated by the hatched
rectangle in the figure. The curved hatched area is the parameter
space excluded due to the non-detection of Shapiro delay in the
binary. From the mass function of PSR J2145-0750 we derive the
displayed contours for constant neutron star masses.
We cannot put any constraints on the companion mass from evolutionary
considerations of the binary as the PSR J2145-0750 system most
probably went through a phase of highly unstable mass accretion
(van den Heuvel 1994). Thus, a unique relation between the orbital period, 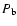 ,
and the secondary mass, m2, as found for LMBPs, is not
applicable for this system. However, from the distribution of allowed
inclination angles (see Sect. 5.1), and the contours for
constant pulsar masses we can estimate a range of allowed companion
masses. Using recent results of neutron star mass measurements
(Thorsett & Chakrabarty 1999; Stairs 2004,
and references therein) we apply a range of
,
and the secondary mass, m2, as found for LMBPs, is not
applicable for this system. However, from the distribution of allowed
inclination angles (see Sect. 5.1), and the contours for
constant pulsar masses we can estimate a range of allowed companion
masses. Using recent results of neutron star mass measurements
(Thorsett & Chakrabarty 1999; Stairs 2004,
and references therein) we apply a range of
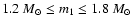 for the pulsar mass (for a discussion see
Sect. 7). As shown in Fig. 4, for
inclination angles within their 1
for the pulsar mass (for a discussion see
Sect. 7). As shown in Fig. 4, for
inclination angles within their 1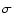 uncertainties we derive a
range of allowed companion masses of
uncertainties we derive a
range of allowed companion masses of
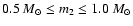 .
.
6 The nature and cooling age of the white dwarf companion
From the timing analysis we derive a range of companion masses of
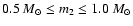 ,
and a global minimum of
,
and a global minimum of
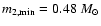 for an extremely low pulsar mass of
for an extremely low pulsar mass of
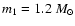 (see Sect. 7). The upper mass limit for
a helium (He)-core WD with solar metallicity is
(see Sect. 7). The upper mass limit for
a helium (He)-core WD with solar metallicity is
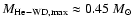 .
Hence we conclude that the companion is a
WD with carbon/oxygen (CO) core in the intermediate WD mass
range. This result is consistent with a CE evolution of the binary
system as proposed by van den Heuvel (1994). Using the derived mass
range of the WD companion and its photometrically determined effective
temperature it is possible to determine an age of the binary
system. This age is based on WD cooling models coming from stellar
evolution theory and can be compared with the characteristic pulsar
age.
.
Hence we conclude that the companion is a
WD with carbon/oxygen (CO) core in the intermediate WD mass
range. This result is consistent with a CE evolution of the binary
system as proposed by van den Heuvel (1994). Using the derived mass
range of the WD companion and its photometrically determined effective
temperature it is possible to determine an age of the binary
system. This age is based on WD cooling models coming from stellar
evolution theory and can be compared with the characteristic pulsar
age.
Optical observations of the WD companion with the HST from Lundgren et al. (1996) yielded
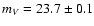 and
and
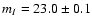 .
From these measurements the authors derived an
effective temperature of
.
From these measurements the authors derived an
effective temperature of
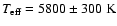 using the
color-temperature calibration from Bergeron et al. (1995) and the bolometric correction from Monet et al. (1992). With the same observational data from Lundgren
et al. (1996), Hansen & Phinney (1998) estimated
using the
color-temperature calibration from Bergeron et al. (1995) and the bolometric correction from Monet et al. (1992). With the same observational data from Lundgren
et al. (1996), Hansen & Phinney (1998) estimated
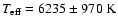 based on the V-I broad-band
colors of Bergeron et al. (1995). As conservative limits, we thus use
a range of effective temperatures for the companion between 5250 and
7200 K.
based on the V-I broad-band
colors of Bergeron et al. (1995). As conservative limits, we thus use
a range of effective temperatures for the companion between 5250 and
7200 K.
Figure 5 shows an age -
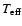 diagram with
evolutionary tracks of CO-core WD models from Blöcker
(1995) and Blöcker et al. (1997). The
horizontal lines indicate the observational range for
diagram with
evolutionary tracks of CO-core WD models from Blöcker
(1995) and Blöcker et al. (1997). The
horizontal lines indicate the observational range for
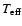 .
The curve at the very left of the diagram belongs to the
CO-core WD model with the lowest mass, followed by curves of
increasing core mass while going to the right. The WD models with
masses of 0.524 and 0.940
.
The curve at the very left of the diagram belongs to the
CO-core WD model with the lowest mass, followed by curves of
increasing core mass while going to the right. The WD models with
masses of 0.524 and 0.940 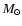 roughly bracket the mass range for
the companion derived from the timing analysis. As the vertical
dashed lines in Fig. 5 illustrate, a WD with
roughly bracket the mass range for
the companion derived from the timing analysis. As the vertical
dashed lines in Fig. 5 illustrate, a WD with
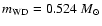 would have an age of
would have an age of
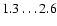 Gyr, whereas a
massive WD with
Gyr, whereas a
massive WD with
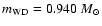 would have an age of
would have an age of
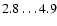 Gyr.
Gyr.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{1031fig5.eps}
\end{figure}](/articles/aa/full/2004/41/aa1031/Timg181.gif) |
Figure 5:
Age-temperature diagram with cooling
curves from evolutionary models of Blöcker (1995) and Blöcker
et al. (1997) for CO-core WDs (
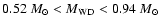 ). The labels give the WD masses in ). The labels give the WD masses in 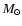 ,
and the
straight horizontal lines indicate the possible range of effective
temperatures for the WD companion of PSR J2145-0750 according to the
studies of Lundgren et al. (1996) and Hansen & Phinney (1998),
i.e. 5250 K ,
and the
straight horizontal lines indicate the possible range of effective
temperatures for the WD companion of PSR J2145-0750 according to the
studies of Lundgren et al. (1996) and Hansen & Phinney (1998),
i.e. 5250 K
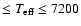 K. The thick dashed vertical
lines mark the intersections of these lines with the cooling curves
from the least and the most massive CO-core model ( K. The thick dashed vertical
lines mark the intersections of these lines with the cooling curves
from the least and the most massive CO-core model (
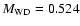 and
and
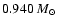 ,
respectively) to indicate the
corresponding age range. ,
respectively) to indicate the
corresponding age range.
|
| Open with DEXTER |
Using the photometric measurements of Lundgren et al. (1996) in the B, V, and I bands together with our
parallax distance for PSR J2145-0750, the mass, age, and
effective temperature of the WD companion can be further
constrained. With
d=500+210-120 pc and the apparent magnitudes
mB=23.9,
mV=23.7, and
mI=23.0 from Lundgren
et al. (1996) we find absolute magnitudes
MB=15.4+0.6-0.8,
MV=15.2+0.6-0.8, and
MI=14.5+0.6-0.8. Applying the bolometric corrections
BCI= 0.5 from Monet et al. (1992) and
BCV= -0.2 from
Bergeron et al. (1995), from both MV and
MI we obtain a bolometric brightness of
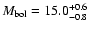 ,
which finally gives a WD luminosity of
,
which finally gives a WD luminosity of
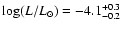 .
This value can be compared with
the luminosity predictions from the WD cooling models from Blöcker
(1995) and Blöcker et al. (1997) for
.
This value can be compared with
the luminosity predictions from the WD cooling models from Blöcker
(1995) and Blöcker et al. (1997) for
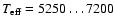 K. The model parameters are summarized
in Table 2.
K. The model parameters are summarized
in Table 2.
Table 2:
Cooling properties of the CO-core WD companion of PSR J2145-0750.
All values are taken from WD evolutionary models of
Blöcker (1995) and Blöcker et al. (1997).
As can be seen from Table 2, using
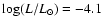 as an additional constraint a CO-core WD with
as an additional constraint a CO-core WD with
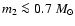 can be ruled out as companion for PSR
J2145-0750, since WDs with lower masses would be too
luminous. Here, a WD with
can be ruled out as companion for PSR
J2145-0750, since WDs with lower masses would be too
luminous. Here, a WD with
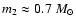 would just have
would just have
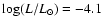 in accordance with the observations, and the
cooling age would be
in accordance with the observations, and the
cooling age would be
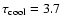 Gyr. On the other hand, a WD with
Gyr. On the other hand, a WD with
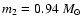 would be too faint at a temperature of
would be too faint at a temperature of
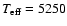 K. Using
K. Using
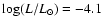 as constraint,
we obtain
as constraint,
we obtain
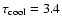 Gyr from the
Gyr from the
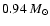 cooling
model, which in turn leads to a new upper limit for the effective
temperature of
cooling
model, which in turn leads to a new upper limit for the effective
temperature of
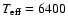 K (see Fig. 5).
Therefore, from the overall comparison of observational constraints
and WD models, we conclude that the PSR J2145-0750 companion has a
mass of
K (see Fig. 5).
Therefore, from the overall comparison of observational constraints
and WD models, we conclude that the PSR J2145-0750 companion has a
mass of
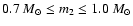 ,
an effective
temperature of
,
an effective
temperature of
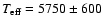 K, and a cooling age of
K, and a cooling age of
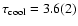 Gyr.
Gyr.
The WD mass range derived here is in accordance with the results from
our timing analysis (see Sect. 5.4), but provides a tighter
lower limit of
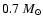 .
On the other hand, the results on the
WD properties are also in agreement with previous studies from
Lundgren et al. (1996) and Hansen & Phinney (1998). Taking the mass
range
.
On the other hand, the results on the
WD properties are also in agreement with previous studies from
Lundgren et al. (1996) and Hansen & Phinney (1998). Taking the mass
range
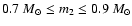 ,
we can also compare
our results with those obtained from the recent WD models of Richer et al. (2000). Using their models, we obtain
,
we can also compare
our results with those obtained from the recent WD models of Richer et al. (2000). Using their models, we obtain
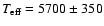 K and
K and
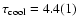 Gyr in line with our
results.
Gyr in line with our
results.
7 Discussion and conclusions
Our timing observations of the PSR J2145-0750 binary system
constrain the orbital inclination angle to be
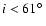 ,
with a
median value of
,
with a
median value of
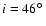 .
Polarimetric studies of the pulsar
magnetosphere lead to a consistent result but cannot provide stronger
constraints on the orbital inclination. From a statistical analysis of
allowed inclination angles we are able to derive proper mass limits
for the pulsar companion if we apply a realistic estimate for the
pulsar mass. Neutron stars are believed to have masses close to the
Chandrasekhar value of
.
Polarimetric studies of the pulsar
magnetosphere lead to a consistent result but cannot provide stronger
constraints on the orbital inclination. From a statistical analysis of
allowed inclination angles we are able to derive proper mass limits
for the pulsar companion if we apply a realistic estimate for the
pulsar mass. Neutron stars are believed to have masses close to the
Chandrasekhar value of 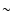 1.35
1.35 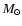 .
Thorsett & Chakrabarty
(1999) reviewed all neutron star mass measurements and found a
remarkably narrow distribution of
.
Thorsett & Chakrabarty
(1999) reviewed all neutron star mass measurements and found a
remarkably narrow distribution of
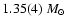 .
Recent
observations revealed neutron stars that have lower masses, e.g. PSR J0737-3039B with
.
Recent
observations revealed neutron stars that have lower masses, e.g. PSR J0737-3039B with
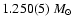 in the newly
detected double-pulsar system (Lyne et al. 2004), and
PSR J1141-6545 with
in the newly
detected double-pulsar system (Lyne et al. 2004), and
PSR J1141-6545 with
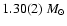 in a NS-WD system
(Bailes et al. 2003). New timing observations showed
that recycled pulsars in NS-WD binaries tend to have masses that are
significantly higher than the canonical value of
in a NS-WD system
(Bailes et al. 2003). New timing observations showed
that recycled pulsars in NS-WD binaries tend to have masses that are
significantly higher than the canonical value of
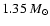 (Nice
2003), which is generally explained by a long phase of
extended mass transfer from the companion to the NS. This also holds
true for PSR J0621+1002 with a pulsar mass of
(Nice
2003), which is generally explained by a long phase of
extended mass transfer from the companion to the NS. This also holds
true for PSR J0621+1002 with a pulsar mass of
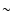 1.7
1.7 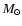 (Splaver et al. 2002), an IMBP
system with properties similar to PSR J2145-0750. The currently
known NS masses in recycled pulsar-WD systems lie in the range
(Splaver et al. 2002), an IMBP
system with properties similar to PSR J2145-0750. The currently
known NS masses in recycled pulsar-WD systems lie in the range
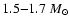 ,
with a median value of
,
with a median value of 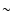 1.6
1.6 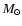 (ignoring PSR
J0751+1807 due to the large uncertainties in its mass measurements;
Stairs 2004, and references therein). Taking into account the
considerable uncertainties, we conservatively choose a range of
(ignoring PSR
J0751+1807 due to the large uncertainties in its mass measurements;
Stairs 2004, and references therein). Taking into account the
considerable uncertainties, we conservatively choose a range of
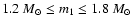 for the pulsar mass of PSR J2145-0750. As discussed in Sect. 5.4, this results in
allowed companion masses of
for the pulsar mass of PSR J2145-0750. As discussed in Sect. 5.4, this results in
allowed companion masses of
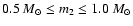 .
We hence conclude that the pulsar companion is a CO-core WD
in the intermediate WD mass range. For the median pulsar mass of
.
We hence conclude that the pulsar companion is a CO-core WD
in the intermediate WD mass range. For the median pulsar mass of
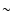 1.6
1.6 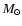 and the observed median inclination angle of
and the observed median inclination angle of
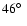 we obtain a median companion mass of
we obtain a median companion mass of 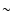 0.7
0.7 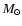 .
.
Using the measured parallax distance and the constraints coming from
photometrical observations of the WD companion of PSR J2145-0750,
the WD properties can be further constrained. Our analysis reveals
that the companion has a mass in the range
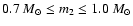 ,
a cooling age of
,
a cooling age of
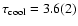 Gyr, and an
effective temperature of
Gyr, and an
effective temperature of
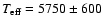 K, in good agreement
with results from previous studies (Lundgren et al. 1996; Hansen &
Phinney 1998; Richer et al. 2000). In particular, the WD model for a
companion mass of
K, in good agreement
with results from previous studies (Lundgren et al. 1996; Hansen &
Phinney 1998; Richer et al. 2000). In particular, the WD model for a
companion mass of
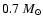 ,
the median value derived from the
timing analysis, exactly reproduces the measured WD luminosity for
,
the median value derived from the
timing analysis, exactly reproduces the measured WD luminosity for
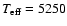 K.
K.
The WD cooling age is roughly a factor of 3 lower than the pulsar's
characteristic age of 10.4 Gyr, which is generally considered as a
rough upper limit of the system age (Camilo et al. 1994b). Under the assumption that the pulsar's magnetic
field does not decay, we can use the WD cooling age to estimate the
initial spin period P0 of PSR J2145-0750, by inverting
Eq. (2). The Doppler contributions are subtracted as we
apply the intrinsic spin-down rate
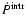 .
For the
derived system age of
.
For the
derived system age of
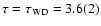 Gyr and typical
braking indices n=2...3 (Lyne 1996, and references
herein) we hence obtain an initial spin period of
P0=13.0(5) ms,
which is very close to the current period. Theories regarding the
spin-up of recycled pulsars to millisecond periods (Smarr & Blandford
1976; Ghosh 1995, and references therein)
predict that the initial period should be equal to the equilibrium
spin period of the neutron star in the X-ray binary phase, accreting
at the Eddington rate
Gyr and typical
braking indices n=2...3 (Lyne 1996, and references
herein) we hence obtain an initial spin period of
P0=13.0(5) ms,
which is very close to the current period. Theories regarding the
spin-up of recycled pulsars to millisecond periods (Smarr & Blandford
1976; Ghosh 1995, and references therein)
predict that the initial period should be equal to the equilibrium
spin period of the neutron star in the X-ray binary phase, accreting
at the Eddington rate
 .
For PSR J2145-0750 we find
.
For PSR J2145-0750 we find
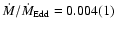 .
Hence the final accretion rate of
the pulsar was highly sub-Eddington, which has also been observed in
other IMBP systems (Lundgren et al. 1996). This is not surprising as
the unstable CE phase of the binary was too short to spin up the
pulsar to the equilibrium spin period. Instead, as proposed by
van den Heuvel (1994), the initial period may have resulted from sub-Eddington
accretion from the stellar wind of the giant star before reaching the
asymptotic giant branch phase.
.
Hence the final accretion rate of
the pulsar was highly sub-Eddington, which has also been observed in
other IMBP systems (Lundgren et al. 1996). This is not surprising as
the unstable CE phase of the binary was too short to spin up the
pulsar to the equilibrium spin period. Instead, as proposed by
van den Heuvel (1994), the initial period may have resulted from sub-Eddington
accretion from the stellar wind of the giant star before reaching the
asymptotic giant branch phase.
The prospects for measuring the pulsar mass of the PSR J2145-0750 system are quite low. As the pulsar companion is bright enough in the
optical, the system masses could in principle be determined by a
spectroscopic study (see van Kerkwijk et al. 1996). However, given the composition of the
companion, suitable lines might not be present. Similarly,
post-Keplerian effects beyond Shapiro delay will not be detectable in
the foreseeable future. As mentioned in Sect. 4.5,
relativistic effects such as orbital period decay or periastron
advance are fully absorbed by the redefinition of the binary period
and therefore not observable in this low-eccentricity binary. The
precision of the Shapiro delay measurement (or limit) cannot be
improved drastically with existing radio telescopes. It will need
telescopes like the Square-Kilometre-Array (SKA) to provide a large
sample of precision mass measurements.
Acknowledgements
We are very grateful to all staff at the Effelsberg and Jodrell Bank
observatories for their help with the observations. We thank Oleg
Doroshenko, Christoph Lange, and Norbert Wex for their assistance in
the Effelsberg timing project. We would also like to thank the referee
for useful suggestions that helped to improve the text. O.L. was
partially funded during this work by the European Commission, Marie
Curie Training Site programme, under contract No. HPMT-CT-2000-00069.
- Alpar, M. A., Cheng,
A. F., Ruderman, M. A., & Shaham, J. 1982, Nature, 300,
728 [NASA ADS] (In the text)
-
Arzoumanian, Z., Nice, D. J., Taylor, J. H., & Thorsett, S. E.
1994, ApJ, 422, 671 [NASA ADS] [CrossRef] (In the text)
- Backer, D. C.,
Dexter, M. R., Zepka, A., et al. 1997, PASP, 109, 61 [NASA ADS] [CrossRef] (In the text)
- Backer, D. C.,
Hama, S., & Hook, S. V. 1993, ApJ, 404, 636 [NASA ADS] [CrossRef] (In the text)
- Bailes, M.,
Harrison, P. A., Lorimer, D. R., et al. 1994, ApJ, 425, L41 [NASA ADS] [CrossRef] (In the text)
- Bailes, M., Ord, S.
M., Knight, H. S., & Hotan, A. W. 2003, ApJ, 595, L49 [NASA ADS] [CrossRef] (In the text)
- Bergeron, P.,
Saumon, D., & Wesemael, F. 1995, ApJ, 443, 764 [NASA ADS] [CrossRef] (In the text)
-
Bhattacharya, D., & van den Heuvel, E. P. J. 1991, Phys. Rep.,
203, 1 [NASA ADS]
- Blöcker, T.,
Herwig, F., Driebe, T., Bramkamp, H., & Schönberner, D.
1997, in White dwarfs, ed. J. Isern, M. Hernanz, & E.
Garcia-Berro, ASSL, 214, 57
(In the text)
- Blöcker, T.
1995, A&A, 299, 755 [NASA ADS] (In the text)
- Camilo, F., Foster,
R. S., & Wolszczan, A. 1994a, ApJ, 437, L39 [NASA ADS] [CrossRef] (In the text)
- Camilo, F.,
Thorsett, S. E., & Kulkarni, S. R. 1994b, ApJ, 421, L15 [NASA ADS] [CrossRef]
- Cordes, J. M.,
& Lazio, T. J. W. 2002, ApJ, submitted
[arXiv:astro-ph/0207156]
(In the text)
- Damour, T., &
Taylor, J. H. 1991, ApJ, 366, 501 [NASA ADS] [CrossRef] (In the text)
- Damour, T., &
Taylor, J. H. 1992, Phys. Rev. D, 45, 1840 [NASA ADS] [CrossRef] (In the text)
- Doroshenko,
O., Löhmer, O., Kramer, M., et al. 2001, A&A, 379,
579 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Downs, G. S., &
Reichley, P. E. 1983, ApJS, 53, 169 [NASA ADS] [CrossRef] (In the text)
- Ghosh, P. 1995,
JA&A, 16, 289 [NASA ADS] (In the text)
- Gould, D. M., &
Lyne, A. G. 1998, MNRAS, 301, 235 [NASA ADS] [CrossRef] (In the text)
- Hankins, T. H.,
& Rickett, B. J. 1975, in Methods in Computational Physics,
Radio Astronomy (New York: Academic Press), 14, 55
(In the text)
- Hansen, B. M. S.,
& Phinney, E. S. 1998, MNRAS, 294, 569 [NASA ADS] [CrossRef] (In the text)
- Hobbs, G., Faulkner,
A., Stairs, I. H., et al. 2004, MNRAS, 352, 1439 [NASA ADS] [CrossRef] (In the text)
- Jacoby, B. A.,
Bailes, M., van Kerkwijk, M. H., et al. 2003, ApJ, 599, L99 [NASA ADS] [CrossRef] (In the text)
- Johnston, S.,
Nicastro, L., & Koribalski, B. 1998, MNRAS, 297, 108 [NASA ADS] [CrossRef] (In the text)
- Kaspi, V. M., Taylor,
J. H., & Ryba, M. 1994, ApJ, 428, 713 [NASA ADS] [CrossRef]
- Kassim, N. E.,
& Weiler, K. W. 1990, Nature, 343, 146 [NASA ADS] [CrossRef]
- Kopeikin, S. M.
1996, ApJ, 467, L93 [NASA ADS] [CrossRef] (In the text)
- Kramer, M.,
Xilouris, K. M., Jessner, A., et al. 1997, A&A, 322, 846 [NASA ADS] (In the text)
- Kramer, M.,
Xilouris, K. M., Lorimer, D. R., et al. 1998, ApJ, 501, 270 [NASA ADS] [CrossRef] (In the text)
- Kuijken, K.,
& Gilmore, G. 1989, MNRAS, 239, 571 [NASA ADS] (In the text)
- Lange, C., Camilo,
F., Wex, N., et al. 2001, MNRAS, 326, 274 [NASA ADS] [CrossRef] (In the text)
- Löhmer, O.,
Lewandowski, W., Wolszczan, A., & Wielebinski, R. 2004, ApJ,
submitted
(In the text)
- Lommen, A. N. 2002,
in Neutron Stars, Pulsars, and Supernova Remnants, ed. W. Becker,
H. Lesch, & J. Trümper, 114
(In the text)
- Lundgren, S.
C., Foster, R. S., & Camilo, F. 1996, in Pulsars: Problems and
Progress, ed. S. Johnston, M. A. Walker, & M. Bailes (San
Francisco: ASP), IAU Coll., 160, 497
(In the text)
- Lyne, A. G. 1996, in
Pulsars: Problems and Progress, ed. S. Johnston, M. A. Walker,
& M. Bailes (San Francisco: ASP), IAU Coll., 160, 73
(In the text)
- Lyne, A. G., Burgay,
M., Kramer, M., et al. 2004, Science, 303, 1153 [NASA ADS] [CrossRef] (In the text)
- Monet, D. G., Dahn,
C. C., Vrba, F. J., et al. 1992, AJ, 103, 638 [NASA ADS] [CrossRef] (In the text)
- Nicastro, L.,
& Johnston, S. 1995, MNRAS, 273, 122 [NASA ADS] (In the text)
- Nice, D. J. 2003, in
Young Neutron Stars and Their Environments, ed. F. Camilo, & B.
M. Gaensler (San Francisco: ASP), IAU Symp., 218, 175
(In the text)
- Nice, D. J., Splaver,
E. M., & Stairs, I. H. 2001, ApJ, 549, 516 [NASA ADS] [CrossRef] (In the text)
- Nice, D. J., Splaver,
E. M., & Stairs, I. H. 2003, in Radio Pulsars, ed. M. Bailes,
D. J. Nice, & S. E. Thorsett, ASP Conf. Ser., 302, 75
- Phinney, E. S.,
& Kulkarni, S. R. 1994, ARA&A, 32, 591 [NASA ADS] (In the text)
-
Radhakrishnan, V., & Cooke, D. J. 1969, Astrophys. Lett., 3,
225 [NASA ADS] (In the text)
- Reid, M. J. 1993,
ARA&A, 31, 345 [NASA ADS] (In the text)
- Richer, H. B.,
Hansen, B., Limongi, M., et al. 2000, ApJ, 529, 318 [NASA ADS] [CrossRef] (In the text)
- Ryba, M. F., &
Taylor, J. H. 1991, ApJ, 371, 739 [NASA ADS] [CrossRef] (In the text)
- Sallmen, S. 1998,
Ph.D. Thesis, University of California at Berkeley
(In the text)
- Sandhu, J. S.,
Bailes, M., Manchester, R. N., et al. 1997, ApJ, 478, L95 [NASA ADS] [CrossRef] (In the text)
- Seiradakis,
J. H., Gil, J. A., Graham, D. A., et al. 1995, A&AS, 111,
205 [NASA ADS] (In the text)
- Shapiro, I. I.
1964, Phys. Rev. Lett., 13, 789 [NASA ADS] [CrossRef] (In the text)
- Shklovskii,
I. S. 1970, SvA, 13, 562 [NASA ADS] (In the text)
- Smarr, L. L., &
Blandford, R. 1976, ApJ, 207, 574 [NASA ADS] [CrossRef] (In the text)
- Splaver, E. M.,
Nice, D. J., Arzoumanian, Z., et al. 2002, ApJ, 581, 509 [NASA ADS] [CrossRef] (In the text)
- Stairs, I. H. 2004,
Science, in press
(In the text)
- Stairs, I. H.,
Thorsett, S. E., & Camilo, F. 1999, ApJS, 123, 627 [NASA ADS] [CrossRef] (In the text)
- Standish, E. M.
1990, A&A, 233, 252 [NASA ADS] (In the text)
- Taam, R. E., King, A.
R., & Ritter, H. 2000, ApJ, 541, 329 [NASA ADS] [CrossRef] (In the text)
- Tauris, T. M. 1996,
A&A, 315, 453 [NASA ADS] (In the text)
- Tauris, T. M., van
den Heuvel, E. P. J., & Savonije, G. J. 2000, ApJ, 530,
L93 [NASA ADS] [CrossRef] (In the text)
- Taylor, J. H.,
& Cordes, J. M. 1993, ApJ, 411, 674 [NASA ADS] [CrossRef] (In the text)
- Thorsett, S.
E., & Chakrabarty, D. 1999, ApJ, 512, 288 [NASA ADS] [CrossRef] (In the text)
- Toscano, M.,
Sandhu, J. S., Bailes, M., et al. 1999, MNRAS, 307, 925 [NASA ADS] [CrossRef] (In the text)
- van den
Heuvel, E. P. J. 1994, A&A, 291, L39 [NASA ADS] (In the text)
- van
Kerkwijk, M. H., Bergeron, P., & Kulkarni, S. R. 1996, ApJ,
467, L89 [NASA ADS] [CrossRef] (In the text)
- van
Straten, W., Bailes, M., Britton, M., et al. 2001, Nature, 412,
158 [NASA ADS] [CrossRef] (In the text)
- Xilouris, K.
M., Kramer, M., Jessner, A., et al. 1998, ApJ, 501, 286 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2004
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{1031fig1.eps}
\end{figure}](/articles/aa/full/2004/41/aa1031/Timg48.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{1031fig2.eps}
\end{figure}](/articles/aa/full/2004/41/aa1031/Timg49.gif)
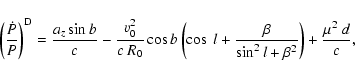
![\begin{displaymath}
\tau = \frac{P}{(n-1)~\dot P}\:
\left[1-~\left(\frac{P_0}{P}\right)^{n-1}\right] ,
\end{displaymath}](/articles/aa/full/2004/41/aa1031/img96.gif)
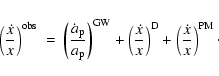
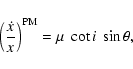
![\begin{figure}
\par\includegraphics[angle=-90,width=7.9cm,clip]{1031fig3.eps}
\end{figure}](/articles/aa/full/2004/41/aa1031/Timg142.gif)
![\begin{figure}
\par\includegraphics[width=14cm,clip]{1031fig4.ps}
\end{figure}](/articles/aa/full/2004/41/aa1031/Timg157.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{1031fig5.eps}
\end{figure}](/articles/aa/full/2004/41/aa1031/Timg181.gif)