A&A 426, 677-686 (2004)
DOI: 10.1051/0004-6361:20041029

The polarization of drifting subpulses

R. T. Edwards[*]

Astronomical Institute "Anton Pannekoek'', University of Amsterdam, Kruislaan 403, 1098 SJ Amsterdam, The Netherlands

Received 5 April 2004 / Accepted 12 July 2004

Abstract
Using new techniques based on the polarimetric fluctuation spectrum, the fluctuation behaviour of the polarization of individual pulses is examined in three pulsars that show drifting subpulses, allowing various aspects of the fluctuations to be quantified for the first time. Of the three pulsars studied, only PSR B0809+74 shows behaviour completely consistent with the superposition of orthogonal polarization modes (OPMs), and this only at 328 MHz and in superposition with an apparently randomly polarized component. The observed periodic pattern is decomposed into the sum of two orthogonally polarized, out-of-phase drift patterns, one of which shows a dramatic jump in subpulse phase near the leading edge of the pulse window, which probably relates to the phase jump earlier reported in total intensity at 1380 MHz. For PSR B0320+39 and PSR B0818-13, considerable periodic fluctuations away from OPM orientations are seen, a condition that also occurs in the trailing half of the pulse in PSR B0809+74 at 1380 MHz. In some cases the deviation is so strong that the periodic locus of the polarization vector in the Poincaré sphere is almost circular, in contrast to the strictly colinear states of superposed OPMs. Several possibilities are discussed for the physical origin of these patterns. The similarity between the subpulse patterns in one of the OPMs of PSR B0809+74 at 328 MHz to that of the total intensity signal at 1380 MHz supports a picture of superposed, out of phase drift patterns. To explain the full range of behaviour seen in the three pulsars, it must be possible to produce at least three arbitrarily polarized superposed patterns. While the data do not suggest a particular approach for the empirical decomposition of patterns into non-orthogonally polarized components, the specific, quantitative nature of the results should provide strong constraints for theoretically driven modelling.

Key words: plasmas - polarization - stars: pulsars : individual: PSR B0320+39, PSR B0809+74, PSR B0818-13 - waves

1 Introduction

In the analysis of the bewildering variety of shapes and polarizations of individual pulses, one tends to seek order, in the hope that an understanding of simple, repeatable phenomena might contribute to a more complete picture of the factors involved in pulsar emission. In this work two such phenomena are considered: the tendency of polarization states to cluster around two orthogonal orientations (orthogonal polarization modes; OPMs) and the periodic occurrence of subpulses that "drift'' across the pulse window (drifting subpulses). Both phenomena offer potential insight into the underlying physics, because they can be tied by simple models to the geometry of viewing emission that is beamed along dipolar magnetic field lines, if the polarization is oriented parallel or perpendicular to the magnetic field (Komesaroff 1970; Radhakrishnan & Cooke 1969; Manchester et al. 1975; Backer et al. 1976), and the drifting subpulses correspond to emitting entities that rotate as an ensemble about the magnetic axis (Wright 1981; Edwards & Stappers 2002; Ashworth 1988; Ruderman 1972).

That the polarization state is related to the subpulse modulation pattern has been known for some time. Due to insufficient instrumental time resolution, it was initially thought that a smooth transition of position angle occurred over the course of each subpulse (Taylor et al. 1971). It was later conclusively shown using data from four pulsars with drifting subpulses, that the changes are generally sharp jumps from one orthogonal state to another, with the point of transition being related to the subpulse position rather than the average profile (Manchester et al. 1975). Two of these pulsars (PSR B0031-07 and PSR B0809+74) show quasi-periodic drifting, with the consequence that, for any given pulse longitude, the OPM state alternates periodically at the period of the subpulse drifting. Using a high-resolution digital pulsar backend and modern visualisation technology, this picture was confirmed by Ramachandran et al. (2002) in observations of PSR B0809+74 at 328 MHz. A natural interpretation of this phenomenon in terms of the standard rotating spark "carousel'' model of drifting subpulses (Ruderman 1972) is that the observed beam is the incoherent superposition of two orthogonally polarized, azimuthally offset carousel beams (Rankin & Ramachandran 2003; Edwards et al. 2003), however to date a quantitative test of the model and determination of the required azimuthal offset have not been performed.

Much empirical model-building has been done on the basis of the interpretation of data in terms of the canonical geometric models of polarization (e.g., Rankin 1983; Mitra & Deshpande 1999; Rankin 1993; Lyne & Manchester 1988; Han & Manchester 2001) and drifting subpulses (e.g., Asgekar & Deshpande 2001; van Leeuwen et al. 2003; Deshpande & Rankin 1999; Gil & Sendyk 2003; Rankin et al. 2003; Deshpande & Rankin 2001). In practice, however, significant deviations from the models are frequently observed. In many pulsars, the distribution of polarization position angles in individual pulses is broadened beyond what is expected from the instrumental noise (e.g., Stinebring et al. 1984), and a distribution with bimodal peaks separated by an angle other than 90$^\circ $ is often observed (e.g., Backer & Rankin 1980). Related to this, mean polarization profiles are generally poorly fit by the simple geometric model (Everett & Weisberg 2001). Empirical models involving non-orthogonal modes (McKinnon 2003) and superposed randomly polarized radiation (RPR; McKinnon 2004) have been pursued as a first-order explanation for non-OPM behaviour, however in at least one known case (PSR B0329+54; Edwards & Stappers 2004), the distribution of polarization states on the Poincaré sphere shows a remarkably complicated form indicating a more complex origin, most likely in propagation effects. Likewise, in the case of drifting subpulses, deviations from the predictions of simple geometry appear to be the rule rather than the exception (Edwards & Stappers 2003b). It is important that these deviations are characterised and understood if physical information is to be garnered from observations of polarization and drifting subpulses.

In considering the deviations from model predictions in the shape of drift bands in PSR B0320+39, Edwards et al. (2003) arrived at the model of offset carousel beams mentioned earlier. They also noted that, while the beams should be roughly orthogonally polarized for PSR B0809+74, to explain the total intensity observations of PSR B0320+39 the beams must in this case be incompletely and/or non-orthogonally polarized. This is due to the fact that the two beams, offset by half the spacing of subbeams, must be of equal mean intensity near the centre of the pulse window in order to explain the complete lack of periodic subpulse modulation seen there through destructive interference. The superposition of equal amounts of completely, orthogonally polarized radiation is incompatible with the strong polarization present in this region of the mean pulse profile. Therefore, the true origin of polarized drifting subpulse patterns must in general be more complicated than, or at least different to, the model of offset OPMs considered by Rankin & Ramachandran (2003).

In this work we present an analysis of the polarization fluctuations associated with periodic subpulse modulation in PSR B0320+39, PSR B0818-13 and PSR B0809+74, with a view to quantifying not only the OPM behaviour and the associated phase offset between the modes, but also deviations from OPM. The observations and analysis techniques are described in Sect. 2. Section 3 presents the observational results, beginning with PSR B0809+74 as its behaviour proves easiest to understand. This is followed by the discussion (Sect. 4) and conclusions (Sect. 5).

   
2 Observations and analysis

2.1 Observations

 The observations used in this work were taken from the data archive accumulated since 1999 with the PuMa pulsar backend (Voûte et al. 2002) of the Westerbork Synthesis Radio Telescope. Of those pulsars known to show nearly coherent periodic drifting subpulses, observations were available of PSR B0320+39 (Izvekova et al. 1982), PSR B0818-13 (Ritchings 1976; Lyne & Ashworth 1983) and PSR B0809+74 (Sutton et al. 1970) in the 92 cm wavelength band, and for PSR B0809+74 also in the 20 cm band. At the start of each observing session, a linearly polarized point source was observed with the interferometric correlator, and the relative phases of both polarization channels of each of 14 telescopes determined. Given these phases, and the location of the source to be observed, the signals were added in each polarization of 1- $8 \times 10$ MHz-wide observing bands, and the resultant tied array signals processed by PuMa in its digital filterbank mode, producing the four Stokes parameters as a function of time and frequency. A full polarization calibration is not possible due to non-linear system components, however the quality of polarization measurements is sufficient if the grossest source of potential error, the relative phase of system gain in the X and Y polarizations, is determined and corrected (Edwards & Stappers 2004). In principle the phase difference is removed as a result of the telescope phase alignment performed at the start of each observing session, however for unknown reasons this often fails for observations in the 92 cm band, which can be noticed by the presence of Faraday modulation in the nominal Stokes V, and by comparison with previously published polarimetric pulse profiles. For this reason, observations in this band were calibrated for differential gain and phase in offline processing using the technique of Edwards & Stappers (2004). Samples were then combined across all frequency channels, including compensation for the effects of interstellar dispersion and Faraday rotation, and the resultant time series were divided into segments equal in length to the apparent pulse period, to form two dimensional arrays in pulse longitude and pulse number. It is important to note, particularly in the case of PSR B0809+74 where observations at two frequencies were used, that the alignment of "pulse longitude'' to the rotational phase of the pulsar includes an arbitrary offset.

   
2.2 Analysis

For the purposes of qualitative visualisation and comparison with earlier works, use is made use of plots of individual pulse sequences, mean drift bands (formed by folding the data modulo the subpulse modulation period), and histograms of the polarization orientation. However, these techniques do not extract all of the available information about polarization fluctuations, and to this end we define and use techniques that are a generalisation of the longitude-resolved fluctuation spectrum (LRFS; Backer 1970) to the four Stokes parameters. These techniques allow for a more sensitive and quantitative characterisation of the polarization fluctuations. Along with a general description of the form of fluctuations expected under orthogonal polarization modes (OPMs), polarimetric functions analogous to the LRFS were presented by Edwards & Stappers (2004) for the limited purpose of removing the effects of scintillation on aperiodic fluctuation statistics. The descriptions are repeated here with a particular view to application of these techniques to quasi-periodic polarization fluctuations.

The (complex) LRFS is obtained by taking the one-dimensional discrete Fourier transforms along vectors of constant pulse longitude:

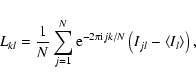\begin{displaymath}L_{kl} = \frac{1}{N}\sum_{j=1}^{N} {\rm e}^{-2\pi {\rm i}jk/N} \left(I_{jl} - \left<I_l\right>\right), \end{displaymath} (1)

where ${\rm i}=\sqrt{-1}$, N is the number of pulses, Ijlis the total intensity (Stokes I) in pulse longitude bin l of pulse number j, and angle brackets denote averaging over pulse number. The corresponding information for fluctuations in the abstract vector space of the Poincaré sphere, $\vec{p_{jl}}=\left(Q\;U\;V\right)^T$, is given by the "polarization LRFS'' (PLRFS):

 \begin{displaymath}\vec{P_{kl}} = \frac{1}{N}\sum_{j=1}^{N} {\rm e}^{-2\pi {\rm i}jk/N} \left(\vec{p_{jl}}-\left<\vec{p_l}\right>\right) . \end{displaymath} (2)

Any sequence of N integer values of k provides complete information on the fluctuation statistics, given the aliasing effected by the finite sample interval (one pulse period). It is most convenient to take k in the range (-N/2,N/2], in the knowledge that the part of the spectrum with $k\geq0$ corresponds to the spectrum of the analytic signal, while the fact that the input signal is real-valued gives the result that $\vec{P_{kl}} = \vec{P^*_{(-k)l}}$.

As with the complex LRFS, the PLRFS decomposes the signal in each longitude bin into a sum of sinusoids. Because subpulse modulations are not perfectly periodic, the fundamental response is not confined to a single coefficient of the spectrum, and some means to account for this is necessary for optimal sensitivity. The approach taken here is to take the LRFS and PLRFS of short (128-pulse) segments of data, over which the response is typically confined to one coefficient, and to add together, for each longitude bin, the appropriate coefficient from each of the spectra, after compensating them for an arbitrary, longitude-independent phase offset. The latter is determined iteratively using the algorithm given by Edwards et al. (2003). The results are longitude-dependent complex envelopes in total intensity and polarization. Because the phase and amplitudes can be different in each of the three components of $\vec{p}$, elements of the PLRFS or the complex polarization envelope in general describe ellipses in $\vec{p}$-space (see also, for example, Born & Wolf 1999, for a general treatment of complex 3-vectors as phased ellipses). The parameters of the ellipse may be obtained by observing that any complex vector $\vec{P}$ may be written in terms of the real orthogonal vectors describing the semi-major and semi-minor axes $\vec{A}$ and $\vec{B}$and the phase ($\phi$) at which $\vec{P}$ is measured

 \begin{displaymath}\vec{P} = \left(\vec{A} + {\rm i}\vec{B}\right){\rm e}^{{\rm i}\phi} . \end{displaymath} (3)

The phase may be determined (modulo $\pi$) from the argument of $\vec{P}^2 \equiv \vec{P}\cdot\vec{P}$:

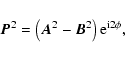\begin{displaymath}\vec{P}^2 = \left(\vec{A}^2 - \vec{B}^2\right){\rm e}^{{\rm i}2\phi}, \end{displaymath} (4)

and used to obtain $\pm\vec{A}$ and $\pm\vec{B}$ as the real and imaginary parts of $\vec{P}{\rm e}^{-{\rm i}\phi}$. Since orthogonal polarization states are anti-parallel in $\vec{p}$-space, fluctuations due to pure OPM behaviour should be strictly colinear, i.e. $\vert\vec{B}\vert=0$. In this case, the phases and amplitudes of modulations in the two modes can be determined as the arguments and moduli of m1 and m2, from the relations
                            L = m1 + m2 (5)
$\displaystyle \vec{P}$ = $\displaystyle \vec{A}{\rm e}^{{\rm i}\phi} = \vec{1}_A\left(m_1 - m_2\right),$ (6)

where $\vec{1}_A \equiv \vec{A}/\vert\vec{A}\vert$ is a unit vector parallel to the polarization orientation of mode 1 (i.e. the direction in which all fluctuations occur), L and $\vec{P}$ are elements of the LRFS and PLRFS or of the determined complex envelopes, and the longitude dependence is dropped for clarity. These relations describe the incoherent superposition of radiation in two orthogonally polarized modes, and can be trivially solved to give
  
                  m1 = $\displaystyle \left(L + \vec{P}\cdot\vec{1}_A\right)/2$ (7)
m2 = $\displaystyle \left(L - \vec{P}\cdot\vec{1}_A\right)/2.$ (8)

Note that the PLRFS is the analogue of the complex LRFS. In situations where phase information is irrelevant, or where the pulse sequence is to be divided into segments and the resulting spectra added (e.g. if the desired spectral resolution is much lower than the number of pulses available), LRF power spectra are generally used (e.g., Backer 1973; Edwards & Stappers 2003a). Unlike the LRFS, for the PLRFS the analogue of the power spectrum is not simply obtained by taking the element-wise squared magnitudes of the complex spectrum, for this would neglect possible correlation between the three components of $\vec{p}$. The complete autocorrelation statistics of $\vec{p}$ must also include covariance terms, a condition satisfied by the spectral density tensor

 \begin{displaymath}\vec{S_{kl}} = \vec{P_{kl}}\vec{P_{kl}}^\dag , \end{displaymath} (9)

where $^\dag $ denotes the Hermitian transpose. Unlike the PLRFS, the spectral density tensor contains no absolute phase information, and can thus be summed over multiple segments of data without the need to track phase from segment to segment (which in any case is only possible for nearly coherent signals). Viewed as a two-dimensional array of $3\times 3$ matrices, its elements are the coherence matrices of $\vec{p}$, for a given fluctuation frequency (k/N cycles per pulse period) in a given pulse longitude bin (l).

Summing the tensor over a range of k provides information on the fluctuation statistics of the data over the corresponding frequency range, with the limiting case that the sum over all k gives the real-valued covariance matrix of the data. In practice, small values of |k| from are excluded the sum to remove bias due to scintillation-induced fluctuations, and the mean spectral density tensor (estimated from off-pulse longitudes) is subtracted to remove measurement noise bias (Edwards & Stappers 2004). The covariance matrix can be subject to eigenvector decomposition to provide information on the principal directions of the fluctuations and the shape of the cloud formed in $\vec{p}$-space (McKinnon 2004; Edwards & Stappers 2004). These are specified in terms of an orthogonal basis composed of the three unit eigenvectors, in combination with the three eigenvalues that give the variance of $\vec{p}$ along the corresponding directions. The covariance of $\vec{p}$ between components in any pair of eigenvectors is zero, thus the decomposition effectively models the distribution of $\vec{p}$ as an ellipsoidal cloud, with the eigenvectors as its axes. In addition to the individual eigenvalues, use shall be made of the polarization entropy (Edwards & Stappers 2004), which combines the information from the three eigenvalues to give a measure of how isotropic the fluctuations are, on scale of 0 (all points colinear) to 1 (completely isotropic, spherical distribution). Since OPMs define antiparallel orientations in $\vec{p}$-space, the signature of pure OPM behaviour is perfect linear correlation, with only one significantly positive eigenvalue (with a corresponding vector aligned with the modal orientation) and an entropy of zero.

In principle one may also measure the covariance matrix summed over $k\geq0$, or a subset of positive k, to obtain the coherence matrix of the analytic signal, or a desired frequency interval of the analytic signal, corresponding for example to quasi-periodic modulations. The result could be decomposed using eigenanalysis into the incoherent sum of orthogonal elliptical fluctuations, or analysed using other techniques of three-dimensional polarimetry (e.g., Dennis 2004; Samson 1973; Carozzi et al. 2000). However, the pulsars covered in this work have sufficiently coherent fluctuations that the PLRFS and the real (scintillation-corrected) covariance matrix provide all of the required information on the periodic and non-periodic fluctuations observed.

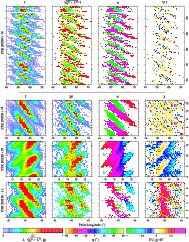  \begin{figure} \mbox{\hspace{2.6cm} $I$\space \hspace{3.2cm} $\sqrt{Q^2+U^2}/I$\... ...box{$^\circ$ }) \hspace{4.3cm} $V/I$ , $\chi/45\hbox{$^\circ$ }$ }\end{figure} Figure 1: Colour plots of polarimetric subpulse patterns, pulse number (ordinate) versus pulse longitude (abscissa). The top row shows a sequence of single pulses PSR B0809+74 at 328 MHz, after Ramachandran et al. (2002) but now correctly calibrated. The other rows show mean drift bands, produced by folding the Stokes parameters modulo subpulse modulation period, and plotted twice for continuity. From top to bottom: PSR B0809+74 at 328 MHz, PSR B0320+39 at 357 MHz and PSR B0818-13 at 328 MHz. In the folded plots, a parameterisation of the polarization that splits it into intensity ($\vert\vec{p}\vert$) and orientation (position angle, $\vert\psi \vert$ and ellipticity angle, $\chi=\frac{1}{2}\tan^{-1} V/(Q^2+U^2)^{1/2}$: see footnote to Sect. 3.1.1) are used to better assess consistency with OPMs. The colour scales used are shown at the bottom. Intensity parameters (left colour scale) are normalised by the peak value plotted in a given panel.
Open with DEXTER


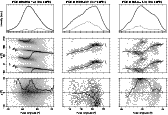  \begin{figure} \begin{tabular}{@{\extracolsep{-5mm}}ccc} \hspace{8mm} PSR B0809+... ...}} & \resizebox{5cm}{!}{\includegraphics{1029f2c.eps}}\end{tabular} \end{figure} Figure 2: Polarization histograms. The top panel shows the total intensity (solid) and polarized intensity (dotted) of the average pulse profile. The centre panel shows the longitude-dependent histogram of position angle (plotted twice for continuity) along with the position angle of the mean profile. The bottom panel shows the histogram of $\sin$$ 2\chi $ (where $\chi $ is the ellipticity angle), along with its counterpart from the mean profile. ($\sin$$ 2\chi $ is chosen over $\chi $ so that each bin samples an equal area of the Poincaré sphere; see Edwards & Stappers 2004.) For convenience the scale is drawn (non-linearly) in terms of $\chi $. Only samples with a polarized intensity greater than three times the RMS noise (estimated from the off-pulse) were included. The density scale is such that bins containing no samples are white, while other values are mapped linearly from medium grey to black.
Open with DEXTER


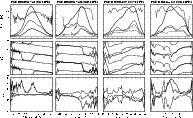  \begin{figure} \par\begin{tabular}{@{\extracolsep{-2mm}}cccc} \hspace{7mm}PSR B0... ...} & \resizebox{!}{10cm}{\includegraphics{1029f3d.eps}}\end{tabular} \end{figure} Figure 3: Results of eigenanalysis of the covariance matrices. The top panel shows the average intensity profile (thick solid line), the square roots of the eigenvalues (solid, dashed, dotted thin lines, in descending order of value), and the polarization entropy (thick dotted line). The middle panel shows the position angle of the mean polarization vector (thick line, plotted repeatedly at offsets of  $180\hbox {$^\circ $ }$ for continuity) and of the first eigenvector (thin line, plotted repeatedly at offsets of  $90\hbox {$^\circ $ }$ for continuity under the equivalence of antiparallel vectors as eigenvectors). The bottom panel shows the ellipticity angle of the mean polarization vector (thick line) along with the ellipticity angle of the first eigenvector, plotted twice with opposite signs.
Open with DEXTER

   
3 Results

3.1 PSR B0809+74

   
3.1.1 328 MHz
The observations of PSR B0809+74 presented here are the same ones used by Ramachandran et al. (2002), who found that, at 328 MHz, each subpulse experiences an abrupt transition between two elliptical OPMs. Unfortunately, it appears that this observation was affected by the the failure of the pre-observation phase calibration (Sect. 2.1). The resultant X-Y relative phase offset (which was measured as $-51\hbox{$^\circ$ }$) causes a rotation of $\vec{p}$about the Stokes Q axis, resulting in mixing of U and V. Although this effect is complicated by the attempted correction for Faraday rotation made before summing the frequency channels, the net effect was that some of the linear polarization masqueraded as circular polarization (and vice-versa). When correctly calibrated, the pattern is qualitatively similar to that presented by Ramachandran et al. (2002), except that periodic sign flips appear completely absent in Stokes V/I (Fig. 1), in agreement with the findings of Manchester et al. (1975). The second row of Fig. 1 shows the mean drift band, produced by folding a sequence of $\sim$300 pulses modulo the drift period, and plotting the result in terms of total and polarized intensity, and polarization orientation (position angle and ellipticity angle[*]). This sequence was selected as being unaffected by nulls and the associated modulation period variations (van Leeuwen et al. 2003; Cole 1970; Lyne & Ashworth 1983) which would smear out the drift band shape. Clearly seen is a reduction in the polarized intensity in the middle of the drift band, accompanied by sharp jumps in position angle. No analogous jump is seen in ellipticity angle, as would be expected for elliptical OPMs. The longitude-resolved histograms of position and ellipticity angles (Fig. 2) confirm this picture, and show that major random deviations from the nominal linear OPM orientations occur in both parameters.

The results of eigenanalysis of the covariance matrix (Fig. 3) provide quantitative support for the features noted above. The very small values of ellipticity angle for the dominant eigenmode concur with the lack of sign flips in Stokes V/I(Fig. 1), indicating that the OPMs are very nearly purely linearly polarized. Incidentally, we note that such a condition would be most unlikely under an arbitrary X-Y relative phase error (especially given the swing in position angle with pulse longitude), confirming the quality of the calibration. The position angle swing of the dominant eigenvector is nearly perfectly linear, being much more robust to slight deviations from orthogonality than the position angle of the average profile (see also Edwards & Stappers 2003b). The second and third eigenvalues are both significant and nearly equal in value at most pulse longitudes, indicating that the distribution in the Poincaré sphere is roughly that of a prolate spheroid. This is consistent with the superposition of an apparently randomly polarized component on top of the OPM radiation (McKinnon 2004).

To examine the relationship of OPMs with the drifting subpulse modulation in more detail, the longitude-dependent amplitude and phase of the quasi-periodic total intensity and polarimetric fluctuations were computed using the methods of Sect. 2.2. The result is shown in Fig. 4. The measured values of $\vert\vec{B}\vert$ (semi-minor axis) are small, showing that the periodic fluctuations in $\vec{p}$ are nearly confined to a line, consistent with an origin in OPMs. Working from this assumption, the observed periodicity was decomposed into the sum of two out-of-phase OPMs using Eqs. (7) and (8). The resultant longitude-dependent amplitude and phase envelopes for the two modes are also depicted in Fig. 4, along with their phase difference (for convenience). The amplitude peaks are offset in pulse longitude, and for most of the pulse window the phases are offset by $\sim$ $50\hbox{$^\circ$ }$. However, at pulse longitude $\sim$ $ 47\hbox{$^\circ$ }$ there is a sharp "jump'' of $\sim$ $ 120\hbox{$^\circ$ }$ in the phase envelope of one of the modes.

   
3.1.2 1380 MHz
Owing to the reduced depth of subpulse modulation of PSR B0809+74 at high frequencies (Nowakowski et al. 1982), it is difficult to obtain sensitive measurements of its subpulse properties at 1380 MHz. Although the best polarimetric observation available was of significantly lower quality than the total intensity observation used by Edwards & Stappers (2003b) (which apparently encountered extraordinarily strong amplification by the interstellar medium), some information on the subpulse behaviour can nevertheless be obtained. The position angle histogram is similar to the scatter plot of Ramachandran et al. (2002), while the ellipticity angle histogram is broad and featureless, so for brevity these are not displayed.

Turning to the results of eigenanalysis (Fig. 3), we see that the behaviour is very different on either side of pulse longitude $\sim$ $38\hbox{$^\circ$ }$. On the leading side, only one significant eigenvalue is measured, indicating very pure OPM-associated fluctuations. On the trailing side the fluctuations become almost isotropic, accompanied also by a $\sim$ $90\hbox {$^\circ $ }$ step in the polarization position angle of the mean profile.

Further insight is given by the decomposition of the periodic polarimetric fluctuations into their semi-major and semi-minor axes (Fig. 4). Firstly, it is seen that on the leading part of the profile, the periodic fluctuations are approximately linear (and of similar amplitude to those in Stokes I), while in the trailing part significant values of $\vert\vec{B}\vert$ are detected, indicating that the pattern cannot be produced by the superposition of two OPMs. The phase envelope of the semi-major axis ($\vec{A}$) closely follows that of the total intensity in the leading part of the profile, consistent (along with the equal amplitudes) with the presence of modulations in only one of the polarization modes. The step of $\sim$ $ 120\hbox{$^\circ$ }$ in the phase envelope of the total intensity (previously reported by Edwards & Stappers 2003b) is accompanied by a smoother, smaller transition of the opposite sense in the phase of the semi-major axis, although the meaning of this is not clear in the absence of a model for the origin of elliptical periodicities.

3.2 PSR B0320+39

The orientation histograms (Fig. 2) for PSR B0320+39 at 357 MHz show broad distributions in position angle and especially in ellipticity angle. This character is confirmed by the results of eigenanalysis (Fig. 3), which show that all three eigenvalues are generally significant, and all different in value. The position angle of the primary direction of fluctuation differs markedly from that of the average profile. The amplitude and phase envelopes of the periodic polarization fluctuations (Fig. 4) reveal, via the significant values for $\vert\vec{B}\vert$, that fluctuations in at least two directions in QUVspace contribute to the observed periodic patterns. In fact, this can be seen in the mean drift band (Fig. 1): around pulse longitudes 17-18$^\circ $ and 20-21$^\circ $ the periodicity in ellipticity angle is clearly smoothly varying, in contrast with the sign-reversing rectangular waveform expected under OPM. There is some evidence for similar behaviour in the position angle around longitude 18-20$^\circ $. Figure 4 shows that semi-major axis fluctuates roughly in phase with the total intensity, including the $\sim$ $180\hbox {$^\circ $ }$ step in phase (longitude $\sim$ $ 18.5\hbox{$^\circ$ }$), which more sensitive observations have shown is very sharp and accompanied by an almost complete lack of periodic modulations in total intensity (Edwards et al. 2003). In contrast to this, significant periodic polarization fluctuations (about an elliptical locus) are detected throughout this part of the pulse window.
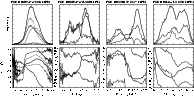  \begin{figure} \par\begin{tabular}{@{\extracolsep{-5mm}}cccc} \hspace{6mm} PSR B... ...}} & \resizebox{!}{8cm}{\includegraphics{1029f4d.eps}}\end{tabular} \end{figure} Figure 4: Amplitude ( top) and phase ( bottom) of subpulse modulations, in total intensity (thick solid line) and polarization (semi-major axis ($\vert\vec{A}\vert$): thick dashed, semi-minor axis ($\vert\vec{B}\vert$): thick dotted). The phase of the semi-minor axis is not plotted, since by definition it is offset from that of the semi-major axis by $\pm $ $90\hbox {$^\circ $ }$. In the left-most column only, the amplitude and phase of two OPMs (thin dotted and dashed lines) as inferred from the total intensity and semi-major axis values are plotted along with the phase difference (thin solid line). A constant slope was subtracted from all phases for clarity. The (dimensionless) slopes used were 25 for PSR B0809+74, -60 for PSR B0320+39, and 60 for PSR B0818-13.
Open with DEXTER

3.3 PSR B0818-13

The position angle histograms of PSR B0818-13 at 328 MHz (Fig. 2) reveal a chaotic jumble of preferred polarization directions as a function of pulse longitude. The distributions clearly differ strongly from the expectations of OPM. A clue to understanding the strange behaviour around longitude $39.5\hbox{$^\circ$ }$ is given in the distribution of ellipticity angles : most points scatter about the $V/\vert\vec{p}\vert=1$ pole of the Poincaré sphere. This is confirmed by Fig. 5, which shows the two-dimensional distribution on the Poincaré sphere in this longitude region. Although the position angle distribution is roughly bimodal, the true two-dimensional distribution is unimodal, with an extended shape that prefers some position angles over others. The results of eigenanalysis (Fig. 3) confirm the chaotic picture given by the histograms, which taken together show that there is no particular reason to consider OPMs to play a role in the polarization fluctuations. The periodic part of the fluctuations (Fig. 4) are just as complicated, with the pattern tracing an elliptical locus in $\vec{p}$-space, which is almost circular at longitude $\sim$ $39.5\hbox{$^\circ$ }$ (as indicated by the near equality of $\vert\vec{A}\vert$ and $\vert\vec{B}$). There is also evidence for this in the mean drift band (Fig. 1), in the form of continuous variations in the ellipticity angle, and roughly bimodal variations in the position angle.
  \begin{figure} \par\includegraphics[width=7.5cm,clip]{1029f5.eps} \end{figure} Figure 5: Distribution of polarization orientations in pulse longitudes 39-40$^\circ $ for PSR B0818-13 at 328 MHz. The projection is Lambert's azimuthal equal area, interrupted at the equator and centred on the poles of the Poincaré sphere ( $V/\vert\vec{p}\vert = \pm1$): see Edwards & Stappers (2004) for details. Meridians and parallels are marked at intervals of 30$^\circ $, with the upward vertical lines corresponding to a position angle of 0$^\circ $.
Open with DEXTER

   
4 Discussion

The observations presented here prove what was already suspected in the introduction: that periodic polarization modulations are more complicated than anything that can be produced by the out of phase superposition of two orthogonally polarized drift patterns (cf. Rankin & Ramachandran 2003). Of the three pulsars studied, only PSR B0809+74 fits this picture, and this only at 328 MHz. This is subject to the caveat that a significant component of randomly polarized radiation (RPR) appears to be present.

It seems pertinent to ask whether some other mechanism is responsible for the periodic polarization fluctuations seen in pulsars with drifting subpulses. Whatever the underlying mechanism for the production of drifting subpulses, it is somehow capable of modulating the total intensity of the emission produced in the magnetosphere. The local magnetospheric conditions also determine the path taken by plasma wave "rays'' in their propagation through the magnetosphere (e.g., Petrova 2000; Fussell & Luo 2004), the alterations imposed on their polarization through birefringent effects in the polarization limiting region (e.g., Lyubarskii & Petrova 1999; Cheng & Ruderman 1979), and, potentially, the degree of conversion to an orthogonal sense of polarization (Petrova 2001). It therefore seems plausible that these processes could also be modulated at the subpulse fluctuation period, giving rise to periodic changes in the polarization state. Only through careful modelling could the consistency of the observations with these effects be checked.

However, there is a striking feature of the 328 MHz observations that is particularly suggestive that the modulations do indeed arise due to the out of phase superposition of two or more periodic patterns. When the measured fluctuations were decomposed as the sum of out of phase OPM modulations, the longitude-dependent phase of one of the two modes was seen to execute a sudden jump of 120$^\circ $, accompanied by a reduction in the amplitude of fluctuations. A very similar feature is seen in the total intensity modulations at 1380 MHz (Edwards & Stappers 2003b), which, as shown in this study, occur in a single polarization mode (at least in the leading part of the pulse window). In our view, such a correspondence is highly unlikely to arise unless the decomposition performed at 328 MHz has a true physical basis. As already argued by Edwards & Stappers (2003b), the behaviour at 1380 MHz could be explained via superposed subpulse patterns with longitude-dependent phase offsets of an arbitrary amount (i.e. not just $180\hbox {$^\circ $ }$). If the same effect causes a phase jump in a single OPM (as observed at 328 MHz), which itself is apparently accompanied by an out-of-phase subpulse pattern in the complementary polarization mode, then there are at least three offset subpulse modulation components present in B0809+74.

A second important implication of the phase jump in one OPM of PSR B0809+74 at 328 MHz concerns the sampling of the polar cap effected in observations at low versus high frequencies. The apparent association of this feature with the phase jump in total intensity at 1380 MHz supports the frequency-dependent pulse profile alignment derived from time-stamped observations by Kuzmin et al. (1998), which differs from the (arbitrary, visual) alignment used by Edwards & Stappers (2003b). Under the updated alignment, the leading and trailing edges of the 1380 MHz mean profile occur significantly earlier than the corresponding features of 328 MHz pulse, arguing that observations at either frequency samples a region of magnetic azimuth not sampled by the other, and/or that symmetry-breaking effects such as abberation, retardation, refraction or asymmetric or patchy polar cap patterns play a role. This should be contrasted to the picture of low-frequency "absorption'' of emission solely on the leading edge of the profile, arrived at by Bartel et al. (1981). Their result derived from an unphysical frequency-dependent longitude scaling performed to explain a difference in drift rate that is actually due to the phase step (Edwards & Stappers 2003b).

The polarization fluctuations seen in PSR B0320+39 and PSR B0818-13 have a different character, in that the mean locus followed by the tip of $\vec{p}$ under the periodic modulation is elliptical, rather than linear as would be expected under the superposition of OPMs[*]. Therefore, if the picture of superposed, out of phase drift patterns is also to explain the modulation in these pulsars, the component patterns must be allowed to have polarization states that are not orthogonal (or aligned). That this should be the case is not surprising, for whatever effect is responsible for the offset in modulation phase could plausibly also affect their polarization, since both are believed to be tied to the differences in effective viewing geometry. Indeed, such considerations could potentially explain the slight non-orthogonality observed even at 328 MHz in PSR B0809+74.

Further insight into the phenomenon of superposed drift modes is likely to come only with a larger sample size. Two previous measurements are of relavance here. Deshpande & Rankin (2001) found that subbeam patterns in two OPM-segregated polar cap images of PSR B0943+10 were offset by roughly half the subbeam spacing. Similarly, Rankin & Ramachandran (2003) found that the phases of the fundamentals in the longitude-resolved fluctuation spectra of the two OPMs of PSR B1237+25 were offset by roughly 180$^\circ $. Unfortunately, the disjoint mode segregation algorithm used in both measurements is prone to produce anti-phase modulation even if the patterns arise from the nearly in-phase superposition of OPMs, since the modal patterns cannot overlap in the segregated signal. It is easily shown (Fig. 6) that in the pathological case of superposed sinusoidal modulations, the periodicity will be in complete anti-phase between the two inferred modes, regardless of the actual phase offset. For an accurate measurement, firstly it must ascertained whether the data are indeed quanitatively consistent with pure OPM, and secondly the mode separation method must take the superposition of radiation into account.

Unrelated to the phenomenon of drifting subpulses, the 1380 MHz results for PSR B0809+74 allow for some interesting constraints to be placed on the origin of randomly polarized radiation (RPR), in light of the fact that it only occurs in the trailing half of the pulse window (Fig. 3). That this should be accompanied by sudden, almost complete depolarization (Morris et al. 1981; Ramachandran et al. 2002) can be understood in one of two ways. One possibility is that the depolarization occurs due to the superposition of two OPMs of nearly equal intensity, with the RPR being associated with only one of the modes. The second possibility is that the RPR is not a superposed emission component, but rather arises due to a propagation effect, randomising the polarization of incoming radiation and causing depolarization of the average profile. It should be noted that this is different to the types of depolarising propagation effects usually encountered, where the electric field vector is altered on timescales comparable to the inverse of the observing frequency.

  \begin{figure} \par\includegraphics[width=5.2cm,clip]{1029f6.eps} \end{figure} Figure 6: Illustration of the results of three-way polarization mode segregation (Deshpande & Rankin 2001) on the superposition of sinusoidal OPMs. a) Simulated intensity of two OPMs (in a given longitude bin) as a function of time. b) Resultant signal in the component of $\vec{p}$corresponding to the modal orientations. c) Primary polarization mode intensity signal as inferred by three-way segregation (solid) and its fundamental Fourier component (dashed). d) As for (c) but for secondary mode. Note that the underlying OPMs are nearly in phase, while the fundamentals of the inferred signals are in pure anti-phase.
Open with DEXTER

The signature of RPR is significant polarization at an orientation that is consistent over some time scale longer than the averaging interval of the individual data samples, yet randomly varying on some longer time scale (in our case, the pulse period). In the case that the RPR is due to a propagation effect, this would imply a variable transfer function (Jones or Mueller matrix) with a decorrelation timescale that lies between the two timescales mentioned. McKinnon (2004) also mentions the viability of RPR as a depolarization mechanism, however he appears to assume that it must arise as superposed emission. Such a condition is not capable of reducing the polarized intensity, as is required for PSR B0809+74. Rather, just like unpolarized radiation, it can only reduce the fractional polarization, by increasing the total intensity without adding polarized intensity to the average profile. McKinnon (2004) considers the possibility of stochastic Faraday rotation in the pulsar magnetosphere as an origin of RPR, but rejects it because the magnetic field is unlikely to vary on short time scales, and in any case the effect cannot alter the Stokes V component of p. However, this is an inadequate basis on which to rule out an origin for RPR in propagation effects: birefringent effects in the magnetosphere can alter all of the Stokes parameters, as the propagation modes are believed to be linearly or elliptically polarized (rather than circularly, as is the case for Faraday rotation), and the fluctuations could be due to variations in plasma density and/or propagation path, rather than magnetic field (Petrova 2001, and references therein).

   
5 Summary and conclusions

We have presented a detailed study of the average periodic polarization fluctuations in three pulsars with drifting subpulses. The basic result of periodic switching between two OPMs in PSR B0809+74 (Ramachandran et al. 2002; Manchester et al. 1975) is confirmed at 328 MHz, albeit in superposition with an apparently randomly polarized component. The periodic pattern can be understood as the superposition of drift patterns in two orthogonal polarization modes that are offset by $\sim$ $50\hbox{$^\circ$ }$ in subpulse phase. The drift bands are roughly linear, however for one of the modes a sudden jump of  $ 120\hbox{$^\circ$ }$, accompanied by a reduction in the amplitude of modulations, is seen near the leading edge of the pulse profile. Very similar behaviour is seen in the total intensity modulations at 1380 MHz (Edwards & Stappers 2003b), which are probably composed of a single polarization mode. That such a correspondence is observed strongly supports the physical validity of the decomposition of the pattern as the superposition of out of phase drift patterns. Aligning the pulse profiles on the basis of the phase jump agrees with results derived from time-stamped observations (Kuzmin et al. 1998), implying either that different regions of magnetic azimuth are sampled at the two frequencies, with neither frequency presenting a complete image of the polar cap, or that other effects such as a non-dipolar magnetic field, refraction, aberration and/or retardation are important.

The results from PSR B0320+39 and PSR B0818-13 reveal that the behaviour deviates considerably from the predictions of OPM, tracing in general a quasi-elliptical path in the Poincaré sphere with each cycle of the subpulse modulation. In PSR B0818-13, the unimodal, asymmetric clustering of states around the $V/\vert\vec{p}\vert=1$pole of the Poincarè sphere leads to a deceptively complicated position angle histogram.

In order to explain the patterns seen in the three pulsars studied, considerable complications to the standard models are required, with in general no less than three offset, arbitrarily polarized drift patterns seen in superposition. For the non-orthogonal oscillations, no particular empirical basis for decomposition is suggested by the data, however it is hoped that the specific, quantitative nature of the results will prove highly constraining to theoretically-driven models.

Acknowledgements
I thank B. Stappers and W. van Straten for helpful comments on the text. The author is supported by a NOVA fellowship. The Westerbork Synthesis Radio Telescope is administered by ASTRON with support from the Netherlands Organisation for Scientific Research (NWO).

References

 
Copyright ESO 2004