A&A 426, 445-454 (2004)
DOI: 10.1051/0004-6361:20040336
The dynamical state of a thick cloudy torus around an AGN
T. Beckert1 - W. J. Duschl2,1
1 - Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69,
53121 Bonn, Germany
2 -
Institut für Theoretische Astrophysik der Universität Heidelberg,
Tiergartenstraße 15, 69121 Heidelberg, Germany
Received 25 February 2004 / Accepted 6 July 2004
Abstract
We present stationary models of obscuring dusty tori around active galactic nuclei.
Vertical and radial structure are discussed separately based on a dynamical approach
to a cloudy accretion flow. The vertical cloud distribution is described by a modified
isothermal disk for arbitrary thickness of the torus with a wide funnel along the
symmetry axis. The radial accretion flow is a consequence of cloud-cloud collisions.
Accretion in the combined gravitational potential of central black hole and stellar
cluster generates free energy, which is dissipated in collisions, and maintains the
thickness of the torus. We focus on the largest clouds at the tidal shear limit,
which will dominate the dynamics and the appearance of torus. Successful obscuration
as required by unified schemes of AGN is achieved for large mass accretion
rates above the Eddington limit of the central black hole. A complete quantitative
treatment for the putative torus in the prototypical Seyfert 2 nucleus of
NGC 1068
is given.
Key words: accretion, accretion disks - black hole physics - ISM: clouds - galaxies:
active - galaxies: nuclei - galaxies: individual: NGC 1068
Based on the pioneering work of Miller and Antonucci
(Antonucci & Miller 1985; Miller & Antonucci 1983), today the major difference
between Seyfert 1 and Seyfert 2 galaxies is attributed to
orientation effects, caused by an optically thick torus around
a super-massive black hole. According to the original
unification scheme all Seyfert 2 nuclei harbor a Seyfert 1 core.
A further distinction between true type 2 cores, where there is
no need for obscuration, and the obscured type 1s, which appear as
type 2s is required. These true type 2 Seyferts seem to be exclusively
low-luminosity systems and most samples are likely to be biased
against those objects. The observed ratio of Seyfert 2 to
Seyfert 1 galaxies of about 4 (Maiolino & Rieke 1995) would imply a
relative torus thickness of
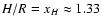 (R is the
distance from the black hole and H the thickness of the torus at
that location), if the distinction is solely due to the
orientation of the torus. Because Seyfert 1s are predominately
seen in face-on galaxies, the obscuration may partially
be due to dust in the galactic disk. If the orientation of the
torus is unrelated to the orientation of the galaxy, the torus
thickness
(R is the
distance from the black hole and H the thickness of the torus at
that location), if the distinction is solely due to the
orientation of the torus. Because Seyfert 1s are predominately
seen in face-on galaxies, the obscuration may partially
be due to dust in the galactic disk. If the orientation of the
torus is unrelated to the orientation of the galaxy, the torus
thickness
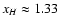 is to be seen as an upper limit. A
discussion of biases in different samples of Seyfert galaxies can
be found in Alonso-Herrero et al. (2003). It appears that effects of
the host galaxy and selection effects against low-luminosity
systems are difficult to account for quantitatively.
While the overall picture seems to be successful (see,
e.g., Schmitt et al. 2001), both, statistics over larger ensembles of
active galaxies, and spectral properties of individual objects
indicate that a simple, smooth torus is an oversimplification of
the actual situation (Tran 2001, and references therein).
This unification scheme is thought to apply to AGN in
general, and not only to Seyfert galaxies. Type 1 objects are
those in which a direct view towards the immediate vicinity of the
active nucleus is possible, while in type 2 objects, the direct
view is impeded by the obscuring torus and the light from the
nucleus proper can be seen only through reflection.
is to be seen as an upper limit. A
discussion of biases in different samples of Seyfert galaxies can
be found in Alonso-Herrero et al. (2003). It appears that effects of
the host galaxy and selection effects against low-luminosity
systems are difficult to account for quantitatively.
While the overall picture seems to be successful (see,
e.g., Schmitt et al. 2001), both, statistics over larger ensembles of
active galaxies, and spectral properties of individual objects
indicate that a simple, smooth torus is an oversimplification of
the actual situation (Tran 2001, and references therein).
This unification scheme is thought to apply to AGN in
general, and not only to Seyfert galaxies. Type 1 objects are
those in which a direct view towards the immediate vicinity of the
active nucleus is possible, while in type 2 objects, the direct
view is impeded by the obscuring torus and the light from the
nucleus proper can be seen only through reflection.
Since more than a decade, clumpy models for the circumnuclear
torus are under discussion
(Pier & Krolik 1992; Granato et al. 1997; Pier & Krolik 1993; Nenkova et al. 2002; Rowan-Robinson 1995). It has
been realized that a fit of the IR SED alone is not sufficient to
determine the various parameters of the different models
suggested. For the scenario of well separated clouds
Nenkova et al. (2002) derived the required properties of the torus
and the clouds embedded in it as far as they are constrained by
the SED.
In this paper we present a model for such a
non-selfgravitating cloudy torus around a black hole and
cospatial with a nuclear stellar cluster. We derive hydrodynamically
consistent physical properties of the individual clouds, as well
as the global structure of the torus. Finally, we compare the results
to observations of the prototypical Seyfert 2 galaxy NGC 1068 and
with the requirements derived by Nenkova et al. (2002).
The basic ideas of our model for a clumpy torus around an AGN are
described in Vollmer et al. (2004). The torus is thought to consist of a
large number of distinct, cold and dusty clouds. The dynamics of
the cloud distribution is governed by cloud-cloud collisions and
accompanied by accretion towards the AGN.
In these direct cloud-cloud collisions part of the kinetic
energy of the clouds is dissipated, thermalized, and radiated away.
These collisions also allow a redistribution of the angular
momentum of clouds and can lead to both an outward transport of
angular momentum and inward mass accretion in the combined
gravitational potential of black hole and central star cluster. In an
equilibrium state, where no mass is lost from or acquired
vertically by the torus, the radial mass accretion rate is
 |
(1) |
where
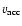 is the vertically averaged radial accretion velocity of clouds.
Here we neglect mass locked up in stars by star formation and the regain from
stellar winds. In Vollmer et al. (2004) we argued that clouds in a torus are quasi-stable
and created or destroyed in cloud collisions. Star formation and stellar feedback
appears to be unimportant, because the accretion time-scale is usually shorter
than the star formation time-scale and the momentum transfer from supernovae and stellar
winds is inefficient for quasi-stable clouds.
is the vertically averaged radial accretion velocity of clouds.
Here we neglect mass locked up in stars by star formation and the regain from
stellar winds. In Vollmer et al. (2004) we argued that clouds in a torus are quasi-stable
and created or destroyed in cloud collisions. Star formation and stellar feedback
appears to be unimportant, because the accretion time-scale is usually shorter
than the star formation time-scale and the momentum transfer from supernovae and stellar
winds is inefficient for quasi-stable clouds.
In an equilibrium state, local quantities like mass density
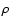 ,
sound speed in clouds
,
sound speed in clouds  ,
or velocity dispersion
,
or velocity dispersion 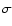 are meaningful quantities when averaged for a dynamical
time-scale
are meaningful quantities when averaged for a dynamical
time-scale
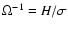 .
Substantial changes are
expected on a feeding time scale, when the mass supplied at an
outer boundary from the galactic disk varies. The outer
boundary is determined either by the transition to a multi-phase
ISM, where molecular clouds appear from and dissolve into
other phases of the ISM, or where other mechanisms than cloud
collisions like bar modes create a radial mass inflow.
.
Substantial changes are
expected on a feeding time scale, when the mass supplied at an
outer boundary from the galactic disk varies. The outer
boundary is determined either by the transition to a multi-phase
ISM, where molecular clouds appear from and dissolve into
other phases of the ISM, or where other mechanisms than cloud
collisions like bar modes create a radial mass inflow.
For the effective viscosity from cloud-cloud collisions we modify our model
of quasi-stable clouds developed in Vollmer et al. (2004) for a local description
of the torus. We follow Goldreich & Tremaine (1978) and use
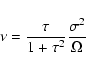 |
(2) |
for the viscosity. Here
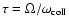 is the
dimensionless collision time. The viscosity reaches its maximum at
is the
dimensionless collision time. The viscosity reaches its maximum at
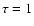 and its functional form is symmetric with respect to
and its functional form is symmetric with respect to
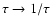 .
So Eq. (2) looks the same
when formulated in terms of the dimensionless collision frequency
.
So Eq. (2) looks the same
when formulated in terms of the dimensionless collision frequency
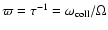 .
The absolute value of the
viscosity for a densely populated torus (
.
The absolute value of the
viscosity for a densely populated torus (
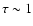 )
is
quantitatively relevant in our context. Vertical hydrostatic
equilibrium
)
is
quantitatively relevant in our context. Vertical hydrostatic
equilibrium
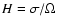 and the collision frequency
and the collision frequency
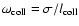 for a velocity dispersion
for a velocity dispersion
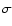 and mean free path
and mean free path
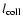 can be used to see that
can be used to see that
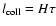 .
The frequency
.
The frequency 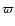 plays the role of
a vertical optical depth for intercepting a cloud.
plays the role of
a vertical optical depth for intercepting a cloud.
The torus resides in a well specified
gravitational potential, where we can make use of the Toomre parameter defined as
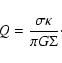 |
(3) |
Here the epicycle frequency 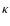 appears, which is relevant
in the transition region from the sphere of influence of the central point mass
to the region dominated by the star cluster. The stability criterion of
Toomre applies to thin disks and the geometrically thick torus is well in the stable
regime, so we use Q to relate velocity dispersion and surface density.
The assumption that clouds in the torus are mostly at the shear limit
(Vollmer et al. 2004)
appears, which is relevant
in the transition region from the sphere of influence of the central point mass
to the region dominated by the star cluster. The stability criterion of
Toomre applies to thin disks and the geometrically thick torus is well in the stable
regime, so we use Q to relate velocity dispersion and surface density.
The assumption that clouds in the torus are mostly at the shear limit
(Vollmer et al. 2004)
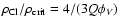 ,
with
,
with 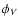 the volume filling factor of clouds, gives then an upper
limit for Q. This property makes Q valuable in our discussion.
the volume filling factor of clouds, gives then an upper
limit for Q. This property makes Q valuable in our discussion.
Cold, molecular and dusty clouds are the basic building blocks
of the torus model. In spite of the complexity of their internal physics,
we regard them as self-gravitating, spherical clouds, which are sufficiently
described by their radius
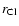 and internal sound speed
and internal sound speed  .
Photodisoziation fronts, non-isothermal structure, disturbed shapes
due to collisions or tidal forces are neglected in this approach.
The mean free path of these clouds is directly linked to their volume filling
factor
.
Photodisoziation fronts, non-isothermal structure, disturbed shapes
due to collisions or tidal forces are neglected in this approach.
The mean free path of these clouds is directly linked to their volume filling
factor 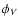 ,
which is determined by the average size of clouds.
We can assume that clouds are slightly self-gravitating,
which implies that the clouds free-fall time and the sound crossing time
are approximately equal. This leads to an expression
,
which is determined by the average size of clouds.
We can assume that clouds are slightly self-gravitating,
which implies that the clouds free-fall time and the sound crossing time
are approximately equal. This leads to an expression
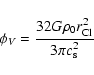 |
(4) |
in the torus midplane. The mean density in the midplane 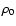 and the
surface density used in the definition of Q in
Eq. (3) are related by the vertical stratification of
the model. In a more general approach we assume a linear
dependence of surface density
and the
surface density used in the definition of Q in
Eq. (3) are related by the vertical stratification of
the model. In a more general approach we assume a linear
dependence of surface density 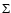 on
on 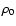 and H, so
that we write
and H, so
that we write
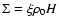 .
For the particular model
of Sect. 3.2 we discuss this relation in
Sect. 3.4 in more detail. With the value
.
For the particular model
of Sect. 3.2 we discuss this relation in
Sect. 3.4 in more detail. With the value
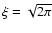 from Eq. (23) we find the mean free
path
from Eq. (23) we find the mean free
path
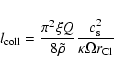 |
(5) |
where
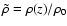 is the normalized vertical cloud distribution.
Using the optical depth in the midplane we get
is the normalized vertical cloud distribution.
Using the optical depth in the midplane we get
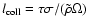 and the average cloud radius, which we assume to be
constant throughout the vertical structure, is
and the average cloud radius, which we assume to be
constant throughout the vertical structure, is
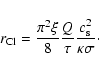 |
(6) |
Without referring to the accretion process and the viscosity we
have parameterized the mean free path of clouds and their radius.
It is the velocity dispersion, resulting from the angular
momentum transport, which connects the cloud properties to the
accretion process. Independently we can set a limit on Q and
determine the surface density parameter 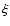 more precisely.
more precisely.
The appearance of the torus in radiative transfer calculations will be
dominated by the largest clouds, because they contribute most to the reduction of
the mean free path
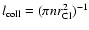 (n is the cloud number
density). But these large clouds are more likely to be disrupted by tidal forces
than smaller clouds and we follow the analysis of Vollmer et al. (2004) with the
modifications described above.
For a given sound speed
(n is the cloud number
density). But these large clouds are more likely to be disrupted by tidal forces
than smaller clouds and we follow the analysis of Vollmer et al. (2004) with the
modifications described above.
For a given sound speed  Eq. (6) can be used
to express the tidal disruption limit as a limit for Q instead of the cloud size
or the cloud density in the form
Eq. (6) can be used
to express the tidal disruption limit as a limit for Q instead of the cloud size
or the cloud density in the form
 |
(7) |
The shear limit in this form is independent of angular momentum or energy transport
through the torus.
3 The Vertical stratification of geometrically thick disks
The appearance of a thick disk or torus in radiative transfer calculations
does depend on their vertical structure. It must therefore be treated with
more care than in the case of thin disks.
The vertical structure of geometrically thin disks in the
potential of a point mass can be simplified by using the linear
term in an expansion of the potential in the vertical direction
around the midplane of the disk. Vertical velocity gradients
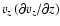 are always much smaller
than the pressure gradient supporting the vertical structure of
thin disks and the hydrostatic balance in the vertical direction
in cylindrical coordinates is given by
are always much smaller
than the pressure gradient supporting the vertical structure of
thin disks and the hydrostatic balance in the vertical direction
in cylindrical coordinates is given by
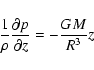 |
(8) |
where R is the radius from the central mass M in the disk plane
(radius in cylindrical coordinates).
Whenever a disk or torus becomes geometrically thick so that the disk
scale height
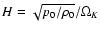 is not small compared to the
radius R anymore, the linear term in the expansion of the potential
gives a much too steep gradient
of that potential to be balanced by the pressure in the torus.
It is less obvious for a thick torus that vertical velocity gradients can be
neglected. Nonetheless we assume that the bulk velocity vz is
much smaller than the velocity dispersion
is not small compared to the
radius R anymore, the linear term in the expansion of the potential
gives a much too steep gradient
of that potential to be balanced by the pressure in the torus.
It is less obvious for a thick torus that vertical velocity gradients can be
neglected. Nonetheless we assume that the bulk velocity vz is
much smaller than the velocity dispersion 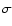 in the torus. The velocity
dispersion of an ensemble of cool clouds, which comprise the torus gives
rise to a dynamical pressure p.
in the torus. The velocity
dispersion of an ensemble of cool clouds, which comprise the torus gives
rise to a dynamical pressure p.
One may describe the ensemble of clouds by a polytropic
equation of state
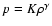 .
This includes the case of the dispersion
.
This includes the case of the dispersion 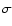 being independent (
being independent (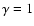 )
of the cloud density
)
of the cloud density
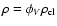 ,
where
,
where
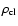 is the mean density of an
individual cloud and
is the mean density of an
individual cloud and 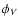 the volume filling factor of these clouds.
The vertical hydrostatic balance becomes an equation for the density
the volume filling factor of these clouds.
The vertical hydrostatic balance becomes an equation for the density
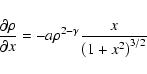 |
(9) |
with the parameter
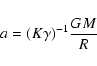 |
(10) |
and the rescaled vertical coordinate x = z/R. The
density distribution for vertical, hydrostatic equilibrium
(Eq. (9)) in the potential of a central point mass
has analytic solutions for
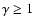 .
For
.
For
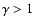 all
polytropic solutions have a finite height xH, where the density
reaches zero. We will only give the result for the isothermal case
and discuss a modified version for general potentials in
Sect. 3.2.
For a velocity dispersion independent of vertical position and
density the torus is equivalent to an isothermal disk. For the corresponding
polytropic index
all
polytropic solutions have a finite height xH, where the density
reaches zero. We will only give the result for the isothermal case
and discuss a modified version for general potentials in
Sect. 3.2.
For a velocity dispersion independent of vertical position and
density the torus is equivalent to an isothermal disk. For the corresponding
polytropic index 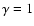 the hydrostatic balance is easily
solved by rewriting Eq. (9)
the hydrostatic balance is easily
solved by rewriting Eq. (9)
 |
(11) |
The integration of Eq. (11) gives
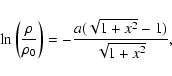 |
(12) |
where 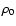 is the density in the torus midplane and the
density decreases exponentially. The parameter a is the
squared ratio of the Keplerian circular orbital velocity and the
velocity dispersion with
is the density in the torus midplane and the
density decreases exponentially. The parameter a is the
squared ratio of the Keplerian circular orbital velocity and the
velocity dispersion with
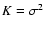 .
This special case
may be appropriate for a torus where cloud collisions are
not too frequent. In reality AGN produce outflows along the polar
axes, which are probably collimated by the torus. The interaction
of the torus with the outflow provides a finite pressure and a
vertical cut-off height, where gas at larger heights is
dynamically not part of the torus anymore but belongs to the
outflow.
.
This special case
may be appropriate for a torus where cloud collisions are
not too frequent. In reality AGN produce outflows along the polar
axes, which are probably collimated by the torus. The interaction
of the torus with the outflow provides a finite pressure and a
vertical cut-off height, where gas at larger heights is
dynamically not part of the torus anymore but belongs to the
outflow.
3.2 The modified isothermal torus
The inclusion of a cut-off height and the structure in a general
potential can be modeled with
a collisionless (lowered![[*]](/icons/foot_motif.gif) ) isothermal distribution of clouds in an external
potential. In analogy to the development of King models
exemplified by Binney & Tremaine (1987) we assume a distribution
function of clouds in phase space of the form
) isothermal distribution of clouds in an external
potential. In analogy to the development of King models
exemplified by Binney & Tremaine (1987) we assume a distribution
function of clouds in phase space of the form
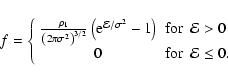 |
(13) |
This distribution is constructed like a Maxwell-Boltzmann
distribution with a specific energy
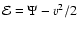 where v is the velocity of individual clouds and
where v is the velocity of individual clouds and
 |
(14) |
a potential constructed in such a way![[*]](/icons/foot_motif.gif) that f vanishes at vertical distances larger than a
presumed disk height H = xH R. We use r as the radius in spherical
coordinates and rH the cut-off radius corresponding to the cylindrical
radius R. The velocities allowed for
clouds lie in a range
that f vanishes at vertical distances larger than a
presumed disk height H = xH R. We use r as the radius in spherical
coordinates and rH the cut-off radius corresponding to the cylindrical
radius R. The velocities allowed for
clouds lie in a range
![$\vert v\vert \in [0, \sqrt{2\Psi}]$](/articles/aa/full/2004/41/aa0336-04/img75.gif) and the upper
limit changes with the potential
and the upper
limit changes with the potential 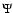 and gets successively
narrower when
and gets successively
narrower when
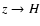 .
The local density due to
clouds is
.
The local density due to
clouds is
where erf(x) is the error-function (Abramowitz & Stegun 1972). For self-gravitating
spherical systems one derives a differential equation for these
King models, but in our case the potential is already specified by
Eq. (14), where the mass
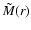 is provided by the
central black hole and a nuclear, stellar cluster. The density given by
Eq. (15) can be interpreted either as mass density
distribution or the number density of clouds. For a given external
potential the solution in Eq. (15) is a two parameter (
is provided by the
central black hole and a nuclear, stellar cluster. The density given by
Eq. (15) can be interpreted either as mass density
distribution or the number density of clouds. For a given external
potential the solution in Eq. (15) is a two parameter (
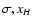 )
family of density distributions
)
family of density distributions
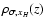 .
The square of the true one dimensional velocity
dispersion of this model is
.
The square of the true one dimensional velocity
dispersion of this model is
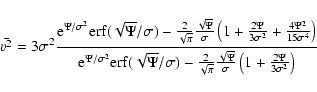 |
(16) |
and is not to be confused with the velocity 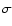 ,
which we nonetheless call velocity dispersion in this paper.
For a parameter pair
,
which we nonetheless call velocity dispersion in this paper.
For a parameter pair
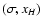 ,
the density
,
the density 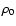 at the disk midplane
at the disk midplane
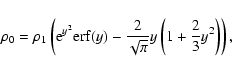 |
(17) |
depends on the parameter
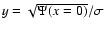 and can be
used to normalize the constant
and can be
used to normalize the constant 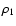 in the density
distribution of Eq. (15).
In the case of
a large torus thickness
xH = 1.33 and a moderate velocity
dispersion corresponding to y=5 in the potential of a
in the density
distribution of Eq. (15).
In the case of
a large torus thickness
xH = 1.33 and a moderate velocity
dispersion corresponding to y=5 in the potential of a
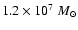 black
hole and an almost isothermal star cluster with
black
hole and an almost isothermal star cluster with
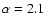 and a core
radius of
and a core
radius of
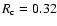 pc, which becomes dynamically important for
R>2 pc, we plot iso-density contours in Fig. 1.
The radial density profile is derived in Sect. 4.1
(Eq. (30)) with
pc, which becomes dynamically important for
R>2 pc, we plot iso-density contours in Fig. 1.
The radial density profile is derived in Sect. 4.1
(Eq. (30)) with
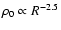 .
.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0336fig1.eps}
\end{figure}](/articles/aa/full/2004/41/aa0336-04/Timg93.gif) |
Figure 1:
Mass density contours in the meridional plane of the torus model.
Contour levels are stepping down a factor of 2 from the peak in density.
The model assumes
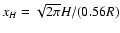 implied by the discussion
at the end of Sect. 3.4. The vertical collision depth is set to
implied by the discussion
at the end of Sect. 3.4. The vertical collision depth is set to
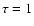 and the largest clouds are at the shear limit (Eq. (27)).
The potential described in Sect. 6
for NGC 1068 is used and the inner radius for dust sublimation is set to 1 pc.
For simplicity the sound speed in clouds is assumed to follow an r-1/4-law.
The radial distribution follows from Eq. (30) and the vertical
distribution is described in Sect. 3.2. The mass accretion rate
in the torus is taken to
and the largest clouds are at the shear limit (Eq. (27)).
The potential described in Sect. 6
for NGC 1068 is used and the inner radius for dust sublimation is set to 1 pc.
For simplicity the sound speed in clouds is assumed to follow an r-1/4-law.
The radial distribution follows from Eq. (30) and the vertical
distribution is described in Sect. 3.2. The mass accretion rate
in the torus is taken to
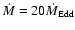 for
a
for
a
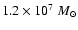 black hole and corresponds to the solid-lines
in Figs. 2 and 3.
black hole and corresponds to the solid-lines
in Figs. 2 and 3. |
| Open with DEXTER |
For a spherically symmetric star cluster we can use an 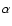 -model for
the density distribution which determines the gravitational potential
-model for
the density distribution which determines the gravitational potential 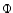 .
The model is described by a central density
.
The model is described by a central density
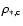 ,
a core radius
,
a core radius 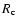 and a power-law slope
and a power-law slope 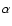 in the form
in the form
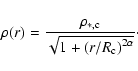 |
(18) |
The enclosed mass within a radius r is
 |
(19) |
where 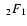 is a hypergeometric function, which has a series expansion
leading to a reasonable approximation for the enclosed mass outside the
core radius of
is a hypergeometric function, which has a series expansion
leading to a reasonable approximation for the enclosed mass outside the
core radius of
![\begin{displaymath}M(r) = \frac{4}{3} \pi \rho_{*,\rm c} R_{\rm c}^3
\left[ \fr...
...{\left(r/R_{\rm c}\right)^{3-\alpha}}{1-\alpha/3} \right]\cdot
\end{displaymath}](/articles/aa/full/2004/41/aa0336-04/img99.gif) |
(20) |
The mass density distribution from Eq. (18) can be used
to construct a gravitational potential by solving the Poisson equation.
The Potential 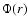 to be used for the relative potential
to be used for the relative potential
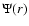 (Eq. (14)) which includes a central black hole
of mass
(Eq. (14)) which includes a central black hole
of mass
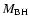 ,
reads
,
reads
For radii much larger than the core radius 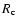 the series expansion
of the hypergeometric functions
the series expansion
of the hypergeometric functions 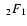 shows that the stellar contribution
to the potential varies as
shows that the stellar contribution
to the potential varies as
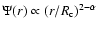 .
This is consistent because the gravitational force vanishes in an
isothermal cluster (
.
This is consistent because the gravitational force vanishes in an
isothermal cluster (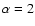 ).
).
3.4 The surface density
![\begin{figure}
\includegraphics[width=11cm,clip]{0336fig2.eps}
\end{figure}](/articles/aa/full/2004/41/aa0336-04/Timg112.gif) |
Figure 2:
The radial structure of the torus described in Sect. 4.1 with
the mass distribution from Sect. 6 for
NGC 1068 with 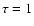 and Q at its local maximum (Eq. (27)).
Three different accretion rates are assumed
and Q at its local maximum (Eq. (27)).
Three different accretion rates are assumed 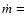 [30 (solid line),
10 (dashed), 3 (dash-dotted)], where
[30 (solid line),
10 (dashed), 3 (dash-dotted)], where 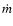 is the accretion
rate in units of the Eddington rate for the central black hole.
On the top left a) the velocity dispersion
is the accretion
rate in units of the Eddington rate for the central black hole.
On the top left a) the velocity dispersion 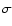 can be compared to the
Keplerian circular velocity (dashed-3
can be compared to the
Keplerian circular velocity (dashed-3  dotted). The top right b)
shows the volume filling fraction of dusty clouds dotted). The top right b)
shows the volume filling fraction of dusty clouds 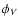 to be in the
range of
to be in the
range of 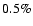 to
to 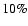 .
The star formation time-scale (Eq. (44))
is plotted
bottom left c) which smaller than the accretion time-scale .
The star formation time-scale (Eq. (44))
is plotted
bottom left c) which smaller than the accretion time-scale
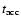 (Eq. (42))
displayed bottom right d) only in the innermost region. Plot d) also gives
the dissipation or collapse time (Eq. (45))
in the absence of heating (dotted) for
(Eq. (42))
displayed bottom right d) only in the innermost region. Plot d) also gives
the dissipation or collapse time (Eq. (45))
in the absence of heating (dotted) for
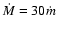 ,
which is the shortest
timescale considered. ,
which is the shortest
timescale considered. |
| Open with DEXTER |
The vertical structure discussed in Sect. 3.2 is a two-parameter
family of velocity dispersion 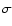 and cut-off height xH R.
For
and cut-off height xH R.
For
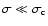 with
with
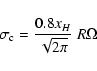 |
(22) |
the vertical density distribution is almost isothermal with a
typical scale height
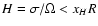 .
In that regime the surface density is well approximated by
.
In that regime the surface density is well approximated by
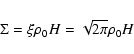 |
(23) |
where
 is the midplane density. In the regime of small
is the midplane density. In the regime of small 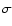 we find the expected relation between central density, scale height and surface density.
we find the expected relation between central density, scale height and surface density.
For
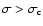 the surface density saturates at about
the surface density saturates at about
 |
(24) |
and is therefore independent of 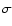 .
The density distribution is not
isothermal anymore and its variation vertically is weak until
it cuts off steeply when approaching xH R. The height of the torus bears
no relation to the scale height
.
The density distribution is not
isothermal anymore and its variation vertically is weak until
it cuts off steeply when approaching xH R. The height of the torus bears
no relation to the scale height
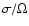 .
In the model discussed in the following we will use
.
In the model discussed in the following we will use
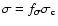 with
with
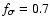 so that
Eq. (23) is valid and a fair approximation for the true surface
density, while the approximations Eqs. (23) and (24)
overestimate
so that
Eq. (23) is valid and a fair approximation for the true surface
density, while the approximations Eqs. (23) and (24)
overestimate 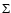 particularly for
particularly for
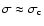 .
.
Like in ordinary accretion disks, the effective viscosity from
Eq. (2) allows mass to be accreted towards the black hole. The
angular momentum barrier is overcome by most of the clouds through
redistribution of angular momentum described by
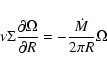 |
(25) |
in a stationary situation. Here 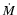 is the total mass accretion rate,
which we assume to be constant at all radii throughout the torus.
From Eqs. (25) and (2) we get the velocity
dispersion in terms of the accretion
rate in the form
is the total mass accretion rate,
which we assume to be constant at all radii throughout the torus.
From Eqs. (25) and (2) we get the velocity
dispersion in terms of the accretion
rate in the form
 |
(26) |
with the definition of the logarithmic derivative
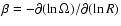 and the dimensionless growth time
and the dimensionless growth time
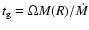 for
the enclosed total mass at radius R. The choice of
for
the enclosed total mass at radius R. The choice of 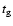 is
particularly useful for an isothermal stellar cluster (
is
particularly useful for an isothermal stellar cluster (
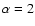 ),
where
),
where 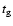 is constant.
is constant.
Inserting the velocity dispersion (Eq. (26)) from the
accretion process into the shear limit Eq. (7) gives
![\begin{displaymath}
Q \le \left[\frac{8 \tau^2 (1+\tau^2)}{ \pi^3 \xi^3 \beta t...
...\sqrt{\frac{2 \kappa}{\Omega}}\right]^{1/2}
= Q_{\rm limit} ,
\end{displaymath}](/articles/aa/full/2004/41/aa0336-04/img130.gif) |
(27) |
where
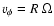 is the local rotation velocity of the torus.
It is worth noticing that the shear limit on Q has only a weak
radial dependence because
is the local rotation velocity of the torus.
It is worth noticing that the shear limit on Q has only a weak
radial dependence because
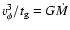 is
constant in a stationary state and the variation
is due to the variation of the sound
speed in clouds
is
constant in a stationary state and the variation
is due to the variation of the sound
speed in clouds
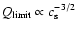 .
A weak additional
dependency on the potential is introduced through the ratio
.
A weak additional
dependency on the potential is introduced through the ratio
![$\sqrt[4]{2 \kappa/\Omega}$](/articles/aa/full/2004/41/aa0336-04/img134.gif) .
.
4.1 Radial structure
![\begin{figure}
\includegraphics[width=10.7cm,clip]{0336fig3.eps}
\end{figure}](/articles/aa/full/2004/41/aa0336-04/Timg135.gif) |
Figure 3:
For the same specific model assumed in Figs. 1
and 2
we plot the relative scale H/R at the top left a) for the three accretion
rates 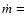 [30 (solid line), 10 (dashed), 3 (dash-dotted)] as a function
of radius. The cloud mass at top right b) is seen to be independent of
[30 (solid line), 10 (dashed), 3 (dash-dotted)] as a function
of radius. The cloud mass at top right b) is seen to be independent of 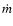 .
The coefficient of restitution .
The coefficient of restitution 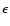 or elasticity in cloud collisions
required by our model (Eq. (37))
is shown bottom left c). The variation of the limiting value of
Toomre-Q is given bottom right d).
or elasticity in cloud collisions
required by our model (Eq. (37))
is shown bottom left c). The variation of the limiting value of
Toomre-Q is given bottom right d). |
| Open with DEXTER |
The density distribution in Fig. 1 and the radial variations of some
characteristic quantities plotted in Figs. 2 and 3 make use of the particular choice of the cut-off scale xH from Sect. 3.4 and the assumption of clouds living at the shear limit.
We now summarize the functional dependencies of this model and start with the
velocity dispersion
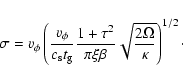 |
(28) |
For a thick torus the velocity dispersion must be a sizable fraction of
the Keplerian rotation velocity,
which implies that the factor
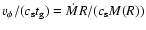 must be of
order unity. It follows directly that the mean free path for clouds
must be of
order unity. It follows directly that the mean free path for clouds
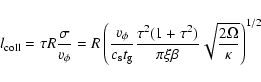 |
(29) |
is comparable to  for a thick torus. For the central density we find
for a thick torus. For the central density we find
![\begin{displaymath}
\rho_0 = \frac{M(R)}{2 R^3} \left[\frac{\xi \pi t_{\rm g} \...
...^3\right]^{1/2}~
\left(\frac{\kappa}{2 \Omega}\right)^{3/4} ,
\end{displaymath}](/articles/aa/full/2004/41/aa0336-04/img140.gif) |
(30) |
which shows that the cloud mass density in the torus is approximately
 times the stellar mass density divided by
times the stellar mass density divided by  .
The volume filling factor of clouds turns out to be
.
The volume filling factor of clouds turns out to be
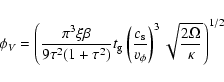 |
(31) |
and the mass of individual clouds is
 |
(32) |
The cloud mass
does not directly depend on the mass accretion rate, but
is a strong function of the sound speed within the clouds.
The surface density of this particular torus model is
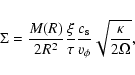 |
(33) |
which is also independent of  and proportional to the stellar surface
density times
and proportional to the stellar surface
density times
 .
.
The torus is energetically powered by accretion and
the corresponding radial accretion velocity is
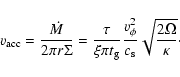 |
(34) |
The comparison with the velocity dispersion from Eq. (28) shows that both
velocities are of the same order for moderate to sparsely populated tori
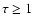 .
Only very dense cloud distributions
.
Only very dense cloud distributions
 with very short mean free
paths for clouds will
show the conventional behavior of accretion disks, where
with very short mean free
paths for clouds will
show the conventional behavior of accretion disks, where
 .
This approaches the hydrodynamic situation and the velocity dispersion is then
identified with the sound speed in the medium.
.
This approaches the hydrodynamic situation and the velocity dispersion is then
identified with the sound speed in the medium.
The large velocity dispersions and accretion velocities, which are a direct consequence of
the geometric thickness of the torus, hint at possible sub-Keplerian rotation of
the flow. For the discussion so far, Keplerian rotation was assumed, which is valid
if no other comparable terms besides the gravitational and the centrifugal force in
the radial momentum balance appears. While the advective term
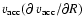 is weak in the region of a isothermal
stellar cluster, the pressure gradient
is weak in the region of a isothermal
stellar cluster, the pressure gradient
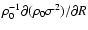 is not. This pressure term is
approximately
is not. This pressure term is
approximately
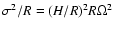 and supports the torus against
gravity. Sub-Keplerian rotation of the order
and supports the torus against
gravity. Sub-Keplerian rotation of the order
 |
(35) |
is to be expected, but the corrections are small as long as H/R < 0.7,
which is only violated for the torus model with
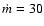 at large radii.
at large radii.
So far we have not made use of an energy equation, where we have to balance
the kinetic energy losses due to cloud collisions and an advective energy transport
with gains from mass accretion in the potential of black hole and stars.
The collisions
will be partly elastic and we use the coefficient of restitution 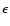 ,
which parameterizes the loss of tangential momentum in the collisions
(e.g. Goldreich & Tremaine 1978), to derive an
energy balance
,
which parameterizes the loss of tangential momentum in the collisions
(e.g. Goldreich & Tremaine 1978), to derive an
energy balance
 |
|
|
(36) |
The energy loss in collisions is calculated for an isotropic,
Maxwellian velocity distribution following Goldreich & Tremaine (1978).
The collision rate is quadratic in the number density of clouds
and we have corrected for this the vertically integrated
form of Eq. (36) by an additional factor 1/2 in the last term.
Neglecting variations of
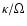 and
and 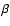 we can solve
this balance and find
with the assumption of an
we can solve
this balance and find
with the assumption of an
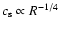 -law
-law
 |
(37) |
Depending on the uncertain physics of cloud-cloud collisions
we can only constrain
the coefficient of restitution to the interval
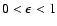 .
The resulting
.
The resulting 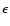 for our specific model for the mass distribution
in NGC 1068 (see Sect. 6) is shown in Fig. 3c.
for our specific model for the mass distribution
in NGC 1068 (see Sect. 6) is shown in Fig. 3c.
The range of
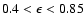 found in our models is in
reasonable agreement with the situation investigated by
Goldreich & Tremaine (1978) where they used an anisotropic velocity
distribution and neglected advective effects, which are important
at large mass accretion rates and provide an effective local
cooling process. The surprising result is that tori with
high accretion rates are geometrically thick in spite of
the smaller elasticity of collisions. This a due to the positive
entropy gradient in the distribution of clouds (left side of
Eq. (36)) so that an increased inward mass transport
allows collisions to transfer more specific entropy from the
random motion of clouds to internal heat.
found in our models is in
reasonable agreement with the situation investigated by
Goldreich & Tremaine (1978) where they used an anisotropic velocity
distribution and neglected advective effects, which are important
at large mass accretion rates and provide an effective local
cooling process. The surprising result is that tori with
high accretion rates are geometrically thick in spite of
the smaller elasticity of collisions. This a due to the positive
entropy gradient in the distribution of clouds (left side of
Eq. (36)) so that an increased inward mass transport
allows collisions to transfer more specific entropy from the
random motion of clouds to internal heat.
The large coefficient of restitution implied for cloud collisions
might be provided by magnetic fields in the clouds. An in depth
analysis of cloud collisions in the environment of an AGN is required
to test our model predictions on 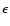 or to infer a
value of
or to infer a
value of 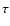 ,
the collision time, for a given radius and mass
accretion rate.
,
the collision time, for a given radius and mass
accretion rate.
4.2 Scaling laws
The near- to mid-infrared radiation from the torus will be dominated by emission from
the innermost region, where the influence of the black hole is strongest. Optically
thin mid- to far-infrared emission will come from areas where the mass of the stellar
cluster is dominant and where most of the mass of the torus is located.
Outside the core radius of the cluster, where the stellar mass density decreases
as
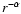 (
(
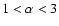 ),
we can give simple scalings with radius and sound speed. All the uncertain physics is
hidden in the sound speed, which depends on the heating by collisions, direct and
indirect heating by hard AGN radiation, radiative cooling, and pressure balance
with the inter-cloud medium. From the Eqs. (28)-(34)
we summarize the scaling laws:
),
we can give simple scalings with radius and sound speed. All the uncertain physics is
hidden in the sound speed, which depends on the heating by collisions, direct and
indirect heating by hard AGN radiation, radiative cooling, and pressure balance
with the inter-cloud medium. From the Eqs. (28)-(34)
we summarize the scaling laws:
 |
(38) |
It is important to note that the mean free path for clouds grows not as fast as
would be guessed from the central density alone. The steep mass density
gradient is partly compensated by an increased cloud radius
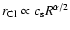 .
The required coefficient of
restitution in
cloud collisions in our model (Eq. (37)) depends on the ratio
.
The required coefficient of
restitution in
cloud collisions in our model (Eq. (37)) depends on the ratio
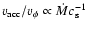 and
and 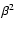 .
In our scenario
the changes at small radii arise from the transition in the potential
at the sphere of influence of the black hole, while at large radii changes
are due to the assumed dependence on R of the sound speed in clouds
.
In our scenario
the changes at small radii arise from the transition in the potential
at the sphere of influence of the black hole, while at large radii changes
are due to the assumed dependence on R of the sound speed in clouds
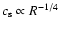 as can be seen in Fig. 3c.
as can be seen in Fig. 3c.
The size of clouds (Eq. (6)) and their mass (Eq. (32)
and Fig. 3b) is independent of the mass accretion rate
and show a trend of decreasing size and mass when approaching the black hole.
This is consistent with clouds being disrupted in collisions, so that an increasing
number of smaller and smaller clouds are transported through the torus.
To estimate the life time and possible variability of the torus we collect
the main time-scales connected to the overall structure. Fluctuations due to
the small number of clouds responsible for processes like the opacity along
a particular line of sight, e.g. to the central black hole, can occur on much shorter
time intervals.
In our scenario viscosity generates accretion towards the center on the viscous
time-scale
 |
(42) |
where the scaling with radius on right in the proportionality is for a stellar
cluster as in Sect. 4.2.
The mass consumed in star formation is locked in stars until part of it is regained
from stellar winds and supernovae.
We parameterize the star formation rate following Vollmer & Beckert (2003)
 |
(43) |
and derive a consumption time-scale for torus mass by
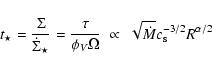 |
(44) |
with the same assumption for the scaling law on the right as
in Eq. (42).
Another relevant time-scale is the dissipative lifetime of the torus in the
absence of reheating.
We estimate it as the ratio of randomized kinetic energy of
clumps
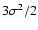 to the energy loss rate in collisions
to the energy loss rate in collisions
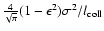 and get
and get
 |
(45) |
which is much longer than the orbital time only for sparsely populated tori with
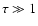 .
.
In Figs. 2c and 2b we compare the accretion with the star formation
time-scale and the collapse time for the case of NGC 1068 for different mass accretion
rates.
The typical star formation time-scale 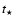 at a radius of 10 pc
is a few times 106 years.
Apart from the innermost region the accretion time is smaller than the star formation
time in models with high mass accretion rates considered here.
If our parameterization of star formation is correct the accretion process
is faster
than the time needed for effective star formation and this justifies our assumption
that star formation and subsequent supernovae are unimportant for the dynamics
of the torus. The short collapse or dissipative lifetime in these inner regions probably
requires a more accurate energy balance than presented here.
at a radius of 10 pc
is a few times 106 years.
Apart from the innermost region the accretion time is smaller than the star formation
time in models with high mass accretion rates considered here.
If our parameterization of star formation is correct the accretion process
is faster
than the time needed for effective star formation and this justifies our assumption
that star formation and subsequent supernovae are unimportant for the dynamics
of the torus. The short collapse or dissipative lifetime in these inner regions probably
requires a more accurate energy balance than presented here.
5 Obscuration by the torus
The well constrained model of a torus developed in the preceding sections
determines the orientation dependent obscuration required for a successful
unification of Seyfert and quasar nuclei of types 1 and 2.
We consider two possible definitions of an obscuration angle, measured
from the torus midplane, for our cloud distribution.
Our first definition of an obscuration angle iN is the inclination for which
we have on average
N(iN) = 1 or any other number of clouds along a line of sight to
the central AGN. For a given inner and outer radius of the torus the number of clouds
as a function of angle i measured from the midplane is
 |
(46) |
The mean free path is found from
Eq. (29) in the midplane and the reduced density from the vertical
structure discussed in Sect. 3.2. For the actual calculation
we use 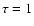 and the model of the gravitational potential of
NGC 1068 (see Sect. 6) as a representative example.
The sound speed is assumed to follow a
and the model of the gravitational potential of
NGC 1068 (see Sect. 6) as a representative example.
The sound speed is assumed to follow a
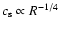 -law with
-law with  approximately 3 km s-1 at the sublimation radius
(inner boundary) of R=1 pc.
The free parameter is thus
approximately 3 km s-1 at the sublimation radius
(inner boundary) of R=1 pc.
The free parameter is thus 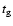 or equivalently the mass accretion rate in the torus,
which we specify in terms of the Eddington rate for the assumed
or equivalently the mass accretion rate in the torus,
which we specify in terms of the Eddington rate for the assumed
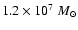 black hole of NGC 1068.
Equation (46) can be inverted numerically to find the obscuration angle iN and
the results are plotted in Fig. 4 for finding N between 1 and 6 clouds along
the line of sight to the center.
black hole of NGC 1068.
Equation (46) can be inverted numerically to find the obscuration angle iN and
the results are plotted in Fig. 4 for finding N between 1 and 6 clouds along
the line of sight to the center.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0336fig4.eps}
\end{figure}](/articles/aa/full/2004/41/aa0336-04/Timg186.gif) |
Figure 4:
The obscuration angle iN and
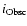 as function of
mass accretion rate derived from the model adapted for NGC 1068
with vertical density structure given by Eq. (15).
The outer radius of the torus is set to
as function of
mass accretion rate derived from the model adapted for NGC 1068
with vertical density structure given by Eq. (15).
The outer radius of the torus is set to
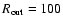 pc.
The dashed lines show the angle iN for having on average
N=[1,2,3,4,5,6] clouds along the line of sight. Due to the
vertical stratification of the torus the probability of seeing more
clouds increases for smaller angles and the dashed lines are
ordered accordingly. The solid lines show the obscuration angle pc.
The dashed lines show the angle iN for having on average
N=[1,2,3,4,5,6] clouds along the line of sight. Due to the
vertical stratification of the torus the probability of seeing more
clouds increases for smaller angles and the dashed lines are
ordered accordingly. The solid lines show the obscuration angle
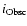 for finding an average hydrogen column density
of
for finding an average hydrogen column density
of
![$N_{\rm H} = [10^{22}, 10^{23}, 10^{24}, 2\times 10^{24}, 4\times 10^{24}, 6\times 10^{24}]$](/articles/aa/full/2004/41/aa0336-04/img18.gif) per cm2. Again the stratification leads to an increased column for smaller
angles and the identification of lines with column density is obvious. per cm2. Again the stratification leads to an increased column for smaller
angles and the identification of lines with column density is obvious.
|
| Open with DEXTER |
The second criterion for an obscuration angle is by the mean hydrogen
column density in clouds along a line of sight
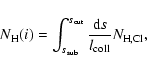 |
(47) |
which is the equivalent to Eq. (46) including the column density.
The column for an individual cloud is
 |
(48) |
Here the mean column scales as
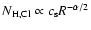 and
is independent of the mass accretion rate.
The resulting
and
is independent of the mass accretion rate.
The resulting
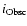 of the inversion for various column densities of
of the inversion for various column densities of
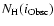 is also shown in Fig. 4. If an obscuration
angle iN=1 above 40
is also shown in Fig. 4. If an obscuration
angle iN=1 above 40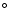 is required for the average Seyfert nucleus, this implies
an accretion rate 10 times larger than the Eddington rate for the corresponding
black hole.
These average Seyfert nuclei seen as type 2's at an inclination
is required for the average Seyfert nucleus, this implies
an accretion rate 10 times larger than the Eddington rate for the corresponding
black hole.
These average Seyfert nuclei seen as type 2's at an inclination
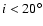 will
have hydrogen columns
will
have hydrogen columns
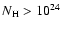 cm-2 in the clouds alone. But the number
of clouds along the line of sight to the center is only between 6 and 10,
so that substantial fluctuations are expected.
cm-2 in the clouds alone. But the number
of clouds along the line of sight to the center is only between 6 and 10,
so that substantial fluctuations are expected.
A key parameter for the success of the clumpy radiative transfer
of Nenkova et al. (2002) is the mean number of clouds along a line
of sight to the center in the torus midplane. For the specific
case of the NGC 1068 torus we find from Eq. (46)
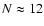 at
at
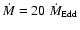 and from
Eq. (29) one sees that N(i=0) is a moderate function
the mass accretion rate:
and from
Eq. (29) one sees that N(i=0) is a moderate function
the mass accretion rate:
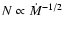 .
The range
preferred by Nenkova et al. (2002) of 5 to 10 clouds corresponds to
.
The range
preferred by Nenkova et al. (2002) of 5 to 10 clouds corresponds to
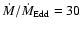 to 120.
Due to the reduced scale
height in the inner, black hole influenced, region of the torus
the integral in Eq. (46) is dominated by contributions
from small radii.
to 120.
Due to the reduced scale
height in the inner, black hole influenced, region of the torus
the integral in Eq. (46) is dominated by contributions
from small radii.
An estimate for the mass lost in an outflow from the inner region of a torus
is given by Krolik & Kriss (2001) and shows that the ratio
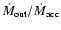 can reach
can reach 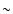 100.
This estimate refers to an ionization parameter
100.
This estimate refers to an ionization parameter 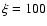 ,
a wind
velocity of 500 km s-1, and a covering fraction of wind material around
the nucleus of
,
a wind
velocity of 500 km s-1, and a covering fraction of wind material around
the nucleus of 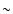 1/6. An ionizing radiation efficiency of 5% for the accretion
flow into the black hole is assumed to relate accretion rate to the
ionizing luminosity. It follows that substantially more mass can be transported
through the torus and lost in an outflow than is actually swallowed by the black hole.
1/6. An ionizing radiation efficiency of 5% for the accretion
flow into the black hole is assumed to relate accretion rate to the
ionizing luminosity. It follows that substantially more mass can be transported
through the torus and lost in an outflow than is actually swallowed by the black hole.
We apply our model to the proposed torus around the AGN of the extensively
studied Seyfert 2 Galaxy NGC 1068.
The
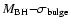 -relation predicts a black hole mass
of about
-relation predicts a black hole mass
of about
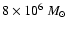 ,
where we used the slope and normalization by
Tremaine et al. (2002). Some of the observed H2O-maser spots
(Greenhill & Gwinn 1997) around the radio core component S1 (Gallimore et al. 2001),
which corresponds to component 2 in earlier MERLIN maps (Muxlow et al. 1996)
trace a rotating disk or ring. The maser velocities appear inconsistent with
Keplerian rotation around a central point mass and the rotation velocity falls off
with radius as
,
where we used the slope and normalization by
Tremaine et al. (2002). Some of the observed H2O-maser spots
(Greenhill & Gwinn 1997) around the radio core component S1 (Gallimore et al. 2001),
which corresponds to component 2 in earlier MERLIN maps (Muxlow et al. 1996)
trace a rotating disk or ring. The maser velocities appear inconsistent with
Keplerian rotation around a central point mass and the rotation velocity falls off
with radius as 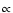 r-0.35 (Kumar 1999). Neglecting non-gravitational
forces, the enclosed mass at 0.65 pc from the
center is
r-0.35 (Kumar 1999). Neglecting non-gravitational
forces, the enclosed mass at 0.65 pc from the
center is
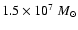 .
The rotation profile can be due to a massive disk
(Huré 2002), but we follow Kumar (1999) and find a reasonable
model with a black hole mass of
.
The rotation profile can be due to a massive disk
(Huré 2002), but we follow Kumar (1999) and find a reasonable
model with a black hole mass of
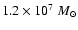 and a strongly concentrated stellar cluster with
and a strongly concentrated stellar cluster with
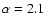 ,
a core radius of 0.32 pc and a core density
of
,
a core radius of 0.32 pc and a core density
of
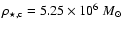 pc-3. Core radius and density are
comparable
to the stellar cluster centered on Sgr A* (Schödel et al. 2003), the radio source at
the dynamical center of our Galaxy. The stellar core mass used for NGC 1068 is only
1.4 times larger in spite of the four times larger black hole mass.
The dusty torus beyond 2 pc is dynamically dominated by
the potential of the stellar cluster in our assumed mass distribution.
pc-3. Core radius and density are
comparable
to the stellar cluster centered on Sgr A* (Schödel et al. 2003), the radio source at
the dynamical center of our Galaxy. The stellar core mass used for NGC 1068 is only
1.4 times larger in spite of the four times larger black hole mass.
The dusty torus beyond 2 pc is dynamically dominated by
the potential of the stellar cluster in our assumed mass distribution.
The currently estimated AGN-luminosity of NGC 1068 is
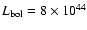 erg/s
(Pier et al. 1994), which corresponds to mass accretion at about one third of
the Eddington rate (10% radiation efficiency) for our mass estimate.
In addition to the radiated luminosity, the AGN also drives a jet and
an outflow.
From the estimate of the mass outflow rate at the end of
Sect. 5 an accretion rate through the torus of
erg/s
(Pier et al. 1994), which corresponds to mass accretion at about one third of
the Eddington rate (10% radiation efficiency) for our mass estimate.
In addition to the radiated luminosity, the AGN also drives a jet and
an outflow.
From the estimate of the mass outflow rate at the end of
Sect. 5 an accretion rate through the torus of 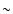 30 times
the Eddington accretion rate of the black hole seems possible. This is also the rate
required to raise the torus obscuration angle to
30 times
the Eddington accretion rate of the black hole seems possible. This is also the rate
required to raise the torus obscuration angle to
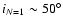 and is thus
consistent with the aspect angle dependent unification of type 1 and type 2 AGN.
While Crenshaw & Kraemer (2000) derive velocities in the NLR of NGC 1068 of more than
1000 km/s far from the nucleus, Ogle et al. (2003) find smaller velocities
and is thus
consistent with the aspect angle dependent unification of type 1 and type 2 AGN.
While Crenshaw & Kraemer (2000) derive velocities in the NLR of NGC 1068 of more than
1000 km/s far from the nucleus, Ogle et al. (2003) find smaller velocities
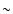 400 km s-1and covering factors of 6% in the electron scattering region,
but small ionization parameters
400 km s-1and covering factors of 6% in the electron scattering region,
but small ionization parameters
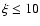 in X-ray NLR clouds.
Both observations support high mass outflow rates and therefore high accretion
rates in the torus.
in X-ray NLR clouds.
Both observations support high mass outflow rates and therefore high accretion
rates in the torus.
From H and K-band observations of CO and Si features Thatte et al. (1997) derive a
surface brightness profile of stellar light from late type stars
corrected for dilution by hot dust from within 2'' of the nucleus. The surface
brightness profile is consistent with a power-law
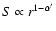 with
with
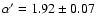 between 0.3'' and 4'' in radius.
The central cluster extends therefore out
to 250 pc and the dusty torus lives in the gravitational potential of this cluster.
between 0.3'' and 4'' in radius.
The central cluster extends therefore out
to 250 pc and the dusty torus lives in the gravitational potential of this cluster.
Form velocity dispersion measurements Dressler (1984) of
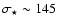 km s-1 one derives an upper limit of
km s-1 one derives an upper limit of
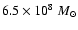 within 1'' while the extension of the central
cluster in our model with
within 1'' while the extension of the central
cluster in our model with
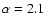 contributes
contributes
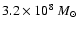 .
.
If the stellar light distribution traces mass we expect an enclosed mass
profile
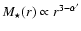 and the circular
velocity curve
and the circular
velocity curve
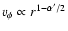 rises outwards. Under the the
assumption that the slope of the central cluster equals the inferred slope at larger
radii
rises outwards. Under the the
assumption that the slope of the central cluster equals the inferred slope at larger
radii
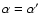 the circular velocity rises to 205 km s-1 at 1''.
the circular velocity rises to 205 km s-1 at 1''.
The rotation curve at even larger radii from Garcia-Lorenzo et al. (1997) is
consistent with this upper limit for inclinations less than
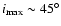 .
When the inner torus and the outer stellar disk are in the same plane,
an inclination of
.
When the inner torus and the outer stellar disk are in the same plane,
an inclination of
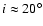 is more likely and the rotation velocity
is about 150 km s-1 in the torus region with an enclosed mass of
is more likely and the rotation velocity
is about 150 km s-1 in the torus region with an enclosed mass of
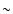
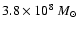 (
(
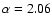 )
within 1''. The stellar mass
distribution used in our model for the central cluster leaves therefore room for
additional mass traced at larger radii and is close to isothermal.
)
within 1''. The stellar mass
distribution used in our model for the central cluster leaves therefore room for
additional mass traced at larger radii and is close to isothermal.
We developed a dynamical model for the radial and vertical
structure of a clumpy torus around an AGN based on the ideas
described in Vollmer et al. (2004).
The vertical stratification of
arbitrarily thick rotating cloud distributions in the potential of
galactic nuclei is derived under the assumption of hydrostatic
equilibrium. For modified isothermal distributions we present
cloud number densities depending on the vertical scale height Hand a cut-off height xH. Such a configuration with cut-off
can be produced by a massive outflow from the central regions of AGNs.
The derived vertical structure is combined with an accretion
scenario for a geometrically and optically thick torus surrounding
the AGN. We show that large mass accretion rates in the torus will
produce obscuring cloud distributions with scale heights H > 0.5
R. The mean number of clouds along particular lines of sight to
the center are calculated and it is found that for angles >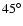 w.r.t. the torus midplane a line of sight to the AGN may
intercept, on average, one cloud.
w.r.t. the torus midplane a line of sight to the AGN may
intercept, on average, one cloud.
The thickness of the cloud distribution is supported by
randomizing the ordered rotation velocities in the torus.
Cloud collisions will destroy clouds and produce new ones
leading to more smaller clouds at small radii.
We describe the appearance of the resulting distribution by considering
only the largest clouds present. The size of clouds is limited by
tidal shear, where larger clouds are not sufficiently kept
together by self-gravity. These large clouds determine the mean
free path between clouds and the optical depth for photons. An
optically thick torus at optical and NIR wavelength requires
massive clouds (>
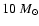 in our model) and a mean free path
not much larger than H, so that the collision time for clouds is
about the dynamical time of the torus
in our model) and a mean free path
not much larger than H, so that the collision time for clouds is
about the dynamical time of the torus
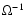 .
The thickness
of the torus implies a coefficient of restitution
.
The thickness
of the torus implies a coefficient of restitution 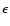 between 0.4 and 0.85 depending on
the mass accretion rate, which itself is a result of the
cloud collisions.
between 0.4 and 0.85 depending on
the mass accretion rate, which itself is a result of the
cloud collisions.
We use the prototypical Seyfert 2 nucleus of NGC 1068 as a
testbed for our model. The torus in the combined potential of a
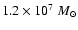 black hole and a nuclear stellar cluster will
have the typical thickness of tori expected from the unified
scheme of AGN for mass accretion rates above ten times the Eddington
accretion rate of the black hole. Taking NGC 1068 as
representative of partly obscured bright AGN, one can conclude
that all obscured AGN must generate outflows to get rid of a large
fraction of the mass transported through the torus.
black hole and a nuclear stellar cluster will
have the typical thickness of tori expected from the unified
scheme of AGN for mass accretion rates above ten times the Eddington
accretion rate of the black hole. Taking NGC 1068 as
representative of partly obscured bright AGN, one can conclude
that all obscured AGN must generate outflows to get rid of a large
fraction of the mass transported through the torus.
The dynamical considerations for a cloudy torus are
consistent with the model assumed by Nenkova et al. (2002) as the
basis of their radiative transfer treatment for mass accretion rates
of 30 times the Eddington rate for the black hole.
The huge mass accretion rates through the torus are
necessarily accompanied by massive outflows driven by
photoevaporation at the inner rim of the torus. Only a small
fraction of the mass eventually reaches the black hole
but is sufficient to generate the ionizing luminosity.
Detailed radiative
transfer calculations using the derived cloud distribution
presented here will produce simulated images and SEDs, which will
allow observational tests of our model.
Acknowledgements
We wish to thank Bernd Vollmer, Werner Tscharnuter and Gerd Weigelt for stimulating
discussions. Part of this work was support by the DFG through
grant SFB439 (W.J.D.).
-
Abramowitz, M., & Stegun, I. A. 1972, Handbook of
Mathematical Functions (New York: Dover)
(In the text)
-
Alonso-Herrero, A., Quillen, A. C., Rieke, G. H., Ivanov,
V. D., & Efstathiou, A. 2003, AJ, 126, 81 [NASA ADS] [CrossRef] (In the text)
-
Antonucci, R. R. J., & Miller, J. S. 1985, ApJ,
297, 621 [NASA ADS] [CrossRef]
- Binney, J., & Tremaine, S.
1987, Galactic dynamics (Princeton, NJ: Princeton University
Press), 747
(In the text)
- Crenshaw,
D. M., & Kraemer, S. B. 2000, ApJ, 532, L101 [NASA ADS] [CrossRef] (In the text)
- Dressler,
A. 1984, ApJ, 286, 97 [NASA ADS] [CrossRef] (In the text)
-
Gallimore, J. F., Henkel, C., Baum, S. A., et al.
2001, ApJ, 556, 694 [NASA ADS] [CrossRef] (In the text)
-
Garcia-Lorenzo, B., Mediavilla, E., Arribas, S., & del Burgo,
C. 1997, Ap&SS, 248, 43 [NASA ADS] (In the text)
-
Goldreich, P., & Tremaine, S. D. 1978, Icarus, 34,
227 [NASA ADS] [CrossRef] (In the text)
- Granato,
G. L., Danese, L., & Franceschini, A. 1997, ApJ, 486,
147 [NASA ADS] [CrossRef]
-
Greenhill, L. J., & Gwinn, C. R. 1997, Ap&SS,
248, 261 [NASA ADS] (In the text)
- Huré, J.-M.
2002, A&A, 395, L21 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Krolik,
J. H., & Kriss, G. A. 2001, ApJ, 561, 684 [NASA ADS] [CrossRef] (In the text)
- Kumar, P. 1999,
ApJ, 519, 599 [NASA ADS] [CrossRef] (In the text)
- Maiolino,
R., & Rieke, G. H. 1995, ApJ, 454, 95 [NASA ADS] [CrossRef] (In the text)
- Miller,
J. S., & Antonucci, R. R. J. 1983, ApJ, 271,
L7 [NASA ADS] [CrossRef]
- Muxlow,
T. W. B., Pedlar, A., Holloway, A. J., Gallimore,
J. F., & Antonucci, R. R. J. 1996, MNRAS, 278,
854 [NASA ADS] (In the text)
- Nenkova, M.,
Ivezic, Z., & Elitzur, M. 2002, ApJ, 570, L9 [NASA ADS] [CrossRef]
- Ogle, P. M.,
Brookings, T., Canizares, C. R., Lee, J. C., &
Marshall, H. L. 2003, A&A, 402, 849 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Pier, E. A.,
& Krolik, J. H. 1992, ApJ, 401, 99 [NASA ADS] [CrossRef]
- Pier, E. A.,
& Krolik, J. H. 1993, ApJ, 418, 673 [NASA ADS] [CrossRef]
- Pier, E. A.,
Antonucci, R., Hurt, T., Kriss, G., & Krolik, J. 1994, ApJ,
428, 124 [NASA ADS] [CrossRef] (In the text)
- Rowan-Robinson, M.
1995, MNRAS, 272, 737 [NASA ADS]
-
Schödel, R., Ott, T., Genzel, R., et al. 2003, ApJ, 596,
1015 [NASA ADS] [CrossRef] (In the text)
- Schmitt,
H. R., Antonucci, R. R. J., Ulvestad, J. S.,
et al. 2001, ApJ, 555, 663 [NASA ADS] [CrossRef] (In the text)
- Thatte, N.,
Quirrenbach, A., Genzel, R., Maiolino, R., & Tecza, M. 1997,
ApJ, 490, 238 [NASA ADS] [CrossRef] (In the text)
- Tran, H. D.
2001, ApJ, 554, L19 [NASA ADS] [CrossRef] (In the text)
- Tremaine,
S., Gebhardt, K., Bender, R., et al. 2002, ApJ, 574, 740 [NASA ADS] [CrossRef] (In the text)
- Vollmer, B.,
& Beckert, T. 2003, A&A, 404, 21 [EDP Sciences] [NASA ADS] (In the text)
- Vollmer, B., Beckert,
T., & Duschl, W. J. 2004, A&A, 413, 949 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2004


![]() ,
sound speed in clouds
,
sound speed in clouds ![]() ,
or velocity dispersion
,
or velocity dispersion ![]() are meaningful quantities when averaged for a dynamical
time-scale
are meaningful quantities when averaged for a dynamical
time-scale
![]() .
Substantial changes are
expected on a feeding time scale, when the mass supplied at an
outer boundary from the galactic disk varies. The outer
boundary is determined either by the transition to a multi-phase
ISM, where molecular clouds appear from and dissolve into
other phases of the ISM, or where other mechanisms than cloud
collisions like bar modes create a radial mass inflow.
.
Substantial changes are
expected on a feeding time scale, when the mass supplied at an
outer boundary from the galactic disk varies. The outer
boundary is determined either by the transition to a multi-phase
ISM, where molecular clouds appear from and dissolve into
other phases of the ISM, or where other mechanisms than cloud
collisions like bar modes create a radial mass inflow.
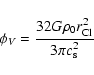
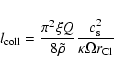
![]() are always much smaller
than the pressure gradient supporting the vertical structure of
thin disks and the hydrostatic balance in the vertical direction
in cylindrical coordinates is given by
are always much smaller
than the pressure gradient supporting the vertical structure of
thin disks and the hydrostatic balance in the vertical direction
in cylindrical coordinates is given by
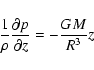
![]() is not small compared to the
radius R anymore, the linear term in the expansion of the potential
gives a much too steep gradient
of that potential to be balanced by the pressure in the torus.
It is less obvious for a thick torus that vertical velocity gradients can be
neglected. Nonetheless we assume that the bulk velocity vz is
much smaller than the velocity dispersion
is not small compared to the
radius R anymore, the linear term in the expansion of the potential
gives a much too steep gradient
of that potential to be balanced by the pressure in the torus.
It is less obvious for a thick torus that vertical velocity gradients can be
neglected. Nonetheless we assume that the bulk velocity vz is
much smaller than the velocity dispersion ![]() in the torus. The velocity
dispersion of an ensemble of cool clouds, which comprise the torus gives
rise to a dynamical pressure p.
in the torus. The velocity
dispersion of an ensemble of cool clouds, which comprise the torus gives
rise to a dynamical pressure p.
![]() .
This includes the case of the dispersion
.
This includes the case of the dispersion ![]() being independent (
being independent (![]() )
of the cloud density
)
of the cloud density
![]() ,
where
,
where
![]() is the mean density of an
individual cloud and
is the mean density of an
individual cloud and ![]() the volume filling factor of these clouds.
The vertical hydrostatic balance becomes an equation for the density
the volume filling factor of these clouds.
The vertical hydrostatic balance becomes an equation for the density
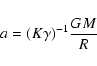
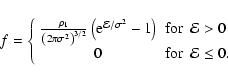
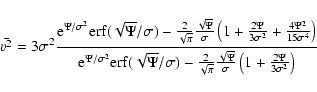
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0336fig1.eps}
\end{figure}](/articles/aa/full/2004/41/aa0336-04/Timg93.gif)
![\begin{displaymath}M(r) = \frac{4}{3} \pi \rho_{*,\rm c} R_{\rm c}^3
\left[ \fr...
...{\left(r/R_{\rm c}\right)^{3-\alpha}}{1-\alpha/3} \right]\cdot
\end{displaymath}](/articles/aa/full/2004/41/aa0336-04/img99.gif)
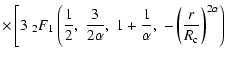
![$\displaystyle - \left.
2\;_2F_1\left(\frac{1}{2},\;\frac{3}{2 \alpha},\;1+\frac...
...2 \alpha},
\;-\left(\frac{r}{R_{\rm c}}\right)^{2 \alpha} \right)
\right] \cdot$](/articles/aa/full/2004/41/aa0336-04/img106.gif)
![\begin{figure}
\includegraphics[width=11cm,clip]{0336fig2.eps}
\end{figure}](/articles/aa/full/2004/41/aa0336-04/Timg112.gif)
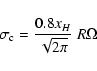
![]() the surface density saturates at about
the surface density saturates at about
![\begin{figure}
\includegraphics[width=10.7cm,clip]{0336fig3.eps}
\end{figure}](/articles/aa/full/2004/41/aa0336-04/Timg135.gif)
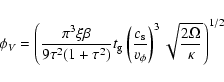
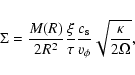
![]() is weak in the region of a isothermal
stellar cluster, the pressure gradient
is weak in the region of a isothermal
stellar cluster, the pressure gradient
![]() is not. This pressure term is
approximately
is not. This pressure term is
approximately
![]() and supports the torus against
gravity. Sub-Keplerian rotation of the order
and supports the torus against
gravity. Sub-Keplerian rotation of the order

![]() ,
which parameterizes the loss of tangential momentum in the collisions
(e.g. Goldreich & Tremaine 1978), to derive an
energy balance
,
which parameterizes the loss of tangential momentum in the collisions
(e.g. Goldreich & Tremaine 1978), to derive an
energy balance
![]() found in our models is in
reasonable agreement with the situation investigated by
Goldreich & Tremaine (1978) where they used an anisotropic velocity
distribution and neglected advective effects, which are important
at large mass accretion rates and provide an effective local
cooling process. The surprising result is that tori with
high accretion rates are geometrically thick in spite of
the smaller elasticity of collisions. This a due to the positive
entropy gradient in the distribution of clouds (left side of
Eq. (36)) so that an increased inward mass transport
allows collisions to transfer more specific entropy from the
random motion of clouds to internal heat.
found in our models is in
reasonable agreement with the situation investigated by
Goldreich & Tremaine (1978) where they used an anisotropic velocity
distribution and neglected advective effects, which are important
at large mass accretion rates and provide an effective local
cooling process. The surprising result is that tori with
high accretion rates are geometrically thick in spite of
the smaller elasticity of collisions. This a due to the positive
entropy gradient in the distribution of clouds (left side of
Eq. (36)) so that an increased inward mass transport
allows collisions to transfer more specific entropy from the
random motion of clouds to internal heat.
![]() or to infer a
value of
or to infer a
value of ![]() ,
the collision time, for a given radius and mass
accretion rate.
,
the collision time, for a given radius and mass
accretion rate.


![]() at a radius of 10 pc
is a few times 106 years.
Apart from the innermost region the accretion time is smaller than the star formation
time in models with high mass accretion rates considered here.
If our parameterization of star formation is correct the accretion process
is faster
than the time needed for effective star formation and this justifies our assumption
that star formation and subsequent supernovae are unimportant for the dynamics
of the torus. The short collapse or dissipative lifetime in these inner regions probably
requires a more accurate energy balance than presented here.
at a radius of 10 pc
is a few times 106 years.
Apart from the innermost region the accretion time is smaller than the star formation
time in models with high mass accretion rates considered here.
If our parameterization of star formation is correct the accretion process
is faster
than the time needed for effective star formation and this justifies our assumption
that star formation and subsequent supernovae are unimportant for the dynamics
of the torus. The short collapse or dissipative lifetime in these inner regions probably
requires a more accurate energy balance than presented here.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{0336fig4.eps}
\end{figure}](/articles/aa/full/2004/41/aa0336-04/Timg186.gif)

![]() at
at
![]() and from
Eq. (29) one sees that N(i=0) is a moderate function
the mass accretion rate:
and from
Eq. (29) one sees that N(i=0) is a moderate function
the mass accretion rate:
![]() .
The range
preferred by Nenkova et al. (2002) of 5 to 10 clouds corresponds to
.
The range
preferred by Nenkova et al. (2002) of 5 to 10 clouds corresponds to
![]() to 120.
Due to the reduced scale
height in the inner, black hole influenced, region of the torus
the integral in Eq. (46) is dominated by contributions
from small radii.
to 120.
Due to the reduced scale
height in the inner, black hole influenced, region of the torus
the integral in Eq. (46) is dominated by contributions
from small radii.
![]() can reach
can reach ![]() 100.
This estimate refers to an ionization parameter
100.
This estimate refers to an ionization parameter ![]() ,
a wind
velocity of 500 km s-1, and a covering fraction of wind material around
the nucleus of
,
a wind
velocity of 500 km s-1, and a covering fraction of wind material around
the nucleus of ![]() 1/6. An ionizing radiation efficiency of 5% for the accretion
flow into the black hole is assumed to relate accretion rate to the
ionizing luminosity. It follows that substantially more mass can be transported
through the torus and lost in an outflow than is actually swallowed by the black hole.
1/6. An ionizing radiation efficiency of 5% for the accretion
flow into the black hole is assumed to relate accretion rate to the
ionizing luminosity. It follows that substantially more mass can be transported
through the torus and lost in an outflow than is actually swallowed by the black hole.
![]() erg/s
(Pier et al. 1994), which corresponds to mass accretion at about one third of
the Eddington rate (10% radiation efficiency) for our mass estimate.
In addition to the radiated luminosity, the AGN also drives a jet and
an outflow.
From the estimate of the mass outflow rate at the end of
Sect. 5 an accretion rate through the torus of
erg/s
(Pier et al. 1994), which corresponds to mass accretion at about one third of
the Eddington rate (10% radiation efficiency) for our mass estimate.
In addition to the radiated luminosity, the AGN also drives a jet and
an outflow.
From the estimate of the mass outflow rate at the end of
Sect. 5 an accretion rate through the torus of ![]() 30 times
the Eddington accretion rate of the black hole seems possible. This is also the rate
required to raise the torus obscuration angle to
30 times
the Eddington accretion rate of the black hole seems possible. This is also the rate
required to raise the torus obscuration angle to
![]() and is thus
consistent with the aspect angle dependent unification of type 1 and type 2 AGN.
While Crenshaw & Kraemer (2000) derive velocities in the NLR of NGC 1068 of more than
1000 km/s far from the nucleus, Ogle et al. (2003) find smaller velocities
and is thus
consistent with the aspect angle dependent unification of type 1 and type 2 AGN.
While Crenshaw & Kraemer (2000) derive velocities in the NLR of NGC 1068 of more than
1000 km/s far from the nucleus, Ogle et al. (2003) find smaller velocities
![]() 400 km s-1and covering factors of 6% in the electron scattering region,
but small ionization parameters
400 km s-1and covering factors of 6% in the electron scattering region,
but small ionization parameters
![]() in X-ray NLR clouds.
Both observations support high mass outflow rates and therefore high accretion
rates in the torus.
in X-ray NLR clouds.
Both observations support high mass outflow rates and therefore high accretion
rates in the torus.
![]() km s-1 one derives an upper limit of
km s-1 one derives an upper limit of
![]() within 1'' while the extension of the central
cluster in our model with
within 1'' while the extension of the central
cluster in our model with
![]() contributes
contributes
![]() .
.
![]() and the circular
velocity curve
and the circular
velocity curve
![]() rises outwards. Under the the
assumption that the slope of the central cluster equals the inferred slope at larger
radii
rises outwards. Under the the
assumption that the slope of the central cluster equals the inferred slope at larger
radii
![]() the circular velocity rises to 205 km s-1 at 1''.
the circular velocity rises to 205 km s-1 at 1''.
![]() .
When the inner torus and the outer stellar disk are in the same plane,
an inclination of
.
When the inner torus and the outer stellar disk are in the same plane,
an inclination of
![]() is more likely and the rotation velocity
is about 150 km s-1 in the torus region with an enclosed mass of
is more likely and the rotation velocity
is about 150 km s-1 in the torus region with an enclosed mass of
![]()
![]() (
(
![]() )
within 1''. The stellar mass
distribution used in our model for the central cluster leaves therefore room for
additional mass traced at larger radii and is close to isothermal.
)
within 1''. The stellar mass
distribution used in our model for the central cluster leaves therefore room for
additional mass traced at larger radii and is close to isothermal.
![]() w.r.t. the torus midplane a line of sight to the AGN may
intercept, on average, one cloud.
w.r.t. the torus midplane a line of sight to the AGN may
intercept, on average, one cloud.
![]() in our model) and a mean free path
not much larger than H, so that the collision time for clouds is
about the dynamical time of the torus
in our model) and a mean free path
not much larger than H, so that the collision time for clouds is
about the dynamical time of the torus
![]() .
The thickness
of the torus implies a coefficient of restitution
.
The thickness
of the torus implies a coefficient of restitution ![]() between 0.4 and 0.85 depending on
the mass accretion rate, which itself is a result of the
cloud collisions.
between 0.4 and 0.85 depending on
the mass accretion rate, which itself is a result of the
cloud collisions.
![]() black hole and a nuclear stellar cluster will
have the typical thickness of tori expected from the unified
scheme of AGN for mass accretion rates above ten times the Eddington
accretion rate of the black hole. Taking NGC 1068 as
representative of partly obscured bright AGN, one can conclude
that all obscured AGN must generate outflows to get rid of a large
fraction of the mass transported through the torus.
black hole and a nuclear stellar cluster will
have the typical thickness of tori expected from the unified
scheme of AGN for mass accretion rates above ten times the Eddington
accretion rate of the black hole. Taking NGC 1068 as
representative of partly obscured bright AGN, one can conclude
that all obscured AGN must generate outflows to get rid of a large
fraction of the mass transported through the torus.