L. Jamet1 - E. Pérez2 - M. Cerviño2 - G. Stasinska1 - R. M. González Delgado2 - J. M. Vílchez2
1 - LUTH, Observatoire de Meudon, 5 place Jules Janssen, 92195 Meudon
Cedex, France
2 - Instituto de Astrofísica de Andalucía (CSIC),
Apartado 3004, 18080 Granada, Spain
Received 24 January 2004 / Accepted 21 June 2004
Abstract
We present the results of a double analysis of the ionizing cluster
in NGC 588, a giant H II region (GHR) in the outskirts of the
nearby galaxy M 33. For this purpose, we obtained ground based
long-slit spectroscopy and combined it with archival ground based and space
borne imaging and spectroscopy, in the wavelength range 1100-9800 Å. A first
modeling of the cluster was performed using integrated properties, such as the
spectral energy distribution (SED), broad band colors, nebular emission
H![]() equivalent width, the main ultraviolet resonance lines, and the
presence of Wolf-Rayet star features. By applying standard assumptions about
the initial mass function (IMF), we were unable to fit satisfactorily these
observational data. This contradictory result led us to carry out a second
modeling, based on a resolved photometric analysis of individual stars in
Hubble Space Telescope (HST) images, by means of finding the best fit isochrone
in color-magnitude diagrams (CMD), and assigning a theoretical SED to each
individual star. The overall SED of the cluster, obtained by integrating the
individual stellar SEDs, is found to fit better the observed SED than the best
solution found through the integrated first analysis, but at a significantly
later stage of evolution of the cluster of 4.2 Myr, as obtained from the best
fit to the CMD. A comparative analysis of both methods traces the different
results to the effects of statistical fluctuations in the upper end of the IMF,
which are significant in NGC 588, with a
computed cluster mass of 5600
equivalent width, the main ultraviolet resonance lines, and the
presence of Wolf-Rayet star features. By applying standard assumptions about
the initial mass function (IMF), we were unable to fit satisfactorily these
observational data. This contradictory result led us to carry out a second
modeling, based on a resolved photometric analysis of individual stars in
Hubble Space Telescope (HST) images, by means of finding the best fit isochrone
in color-magnitude diagrams (CMD), and assigning a theoretical SED to each
individual star. The overall SED of the cluster, obtained by integrating the
individual stellar SEDs, is found to fit better the observed SED than the best
solution found through the integrated first analysis, but at a significantly
later stage of evolution of the cluster of 4.2 Myr, as obtained from the best
fit to the CMD. A comparative analysis of both methods traces the different
results to the effects of statistical fluctuations in the upper end of the IMF,
which are significant in NGC 588, with a
computed cluster mass of 5600 ![]() ,
as predicted by Cerviño et al. (2002,
A&A, 381, 51).
We discuss the results in terms of
the strong influence of the few most massive stars, six in the case of
NGC 588, that dominate the overall SED and, in particular, the
ionizing far ultraviolet range beyond the Lyman limit.
,
as predicted by Cerviño et al. (2002,
A&A, 381, 51).
We discuss the results in terms of
the strong influence of the few most massive stars, six in the case of
NGC 588, that dominate the overall SED and, in particular, the
ionizing far ultraviolet range beyond the Lyman limit.
Key words: stars: evolution - stars: luminosity function, mass function - stars: Hertzsprung-Russell (HR) and C-M diagrams - stars: Wolf-Rayet - ISM: individual objects: NGC 588 - galaxies: individual: M 33
Despite their small number in comparison with Sun-like stars, massive stars are
most influential in their host galaxies. They are responsible for the release
in the interstellar medium of most of the mechanical energy, metals such as
oxygen, neon, sulfur, etc. and possibly carbon, and hard radiation. However,
their formation is still poorly understood. It is generally admitted that
massive stars form mainly in instantaneous starbursts, with a power-law initial
mass function (IMF) with universal slope (e.g., Massey 2003), although
Scalo (1998) estimates that this slope may comprise a natural scatter of a few
tenths between different clusters. Most massive stars are observed and studied
in very massive clusters embedded in giant H II regions (GHRs), in which
the ionized gas provides information on the intensity of the (unobservable)
stellar Lyman continuum, via the equivalent width of the nebular H![]() line.
Inversely, modeling accurately a GHR from its emission spectrum requires a good
knowledge of the ionizing spectrum of its source, which is one of the elements
that control the temperature and ionization state of the gas. This ionizing
spectrum is unobservable, and can only be derived from a model of the stellar
source.
line.
Inversely, modeling accurately a GHR from its emission spectrum requires a good
knowledge of the ionizing spectrum of its source, which is one of the elements
that control the temperature and ionization state of the gas. This ionizing
spectrum is unobservable, and can only be derived from a model of the stellar
source.
The stellar content of a GHR can be determined in two ways: either by observing
the individual stars, or making assumptions regarding the distribution of their
initial masses. The first solution can be used to study the cluster itself via
color-magnitude diagrams (CMDs, e.g. Malamuth et al. 1996) or to synthesize an
ionizing spectrum to be input to photoionization models (Relaño et al. 2002). However,
such a procedure requires quite high resolution and sensitivity for
extragalactic objects, which can in general be reached only with the HST. In the
vast majority of other cases, only integrated properties of the cluster can be
used, and an IMF, generally a continuous power law, must be supposed.
Nevertheless, Cerviño et al. (2002) showed that if the total initial mass of a cluster
is less than ![]() 104
104 ![]() ,
statistical fluctuations around the mean IMF can strongly affect the main diagnostics of the cluster, like the H
,
statistical fluctuations around the mean IMF can strongly affect the main diagnostics of the cluster, like the H![]() equivalent width
equivalent width
![]() ,
as well as the determined ionizing spectrum
(see also Cerviño et al. 2003). The effects of these fluctuations need to be tested
with observational data.
,
as well as the determined ionizing spectrum
(see also Cerviño et al. 2003). The effects of these fluctuations need to be tested
with observational data.
In this article, we show that the cluster embedded in NGC 588 nicely illustrates the issue of IMF statistical sampling. Section 2 describes all the data sets used, spectroscopic and photometric, ground based and space borne, either obtained by us or retrieved from different archives. Further data processing is detailed in Sect. 3. Section 4 describes a first modeling of the star cluster, using a "classical'' approach, aimed at fitting its integrated spectral properties with a model assuming an analytical IMF. In Sect. 5 we introduce the importance of modeling the effects of statistical fluctuations. In Sect. 6, we measure the fluxes of the individual stars detected in HST images, and use the photometric results to analyze the stellar content of the cluster, by assigning a model SED to each individual star. The results from the two methods of modeling are significantly discrepant, and in Sect. 7 we explore how this discrepancy can be attributed to the role of the few most massive stars, whose number is heavily affected by statistical fluctuations in the case of the low mass cluster ionizing NGC 588.
We have performed ground based optical spectroscopic observations of NGC 588 and have retrieved the available archival spectroscopic and imaging data sets from the Hubble Space Telescope (HST), the International Ultraviolet Explorer (IUE), and the Isaac Newton Group (ING). Table 1 contains a summary of the different data sets used in this study.
Optical spectra were obtained in 1998 August 27/28 with the 3.5 m telescope at
the Centro Astronómico Hispano Alemán (CAHA, Calar Alto, Almería). The
observations were made with the dual beam TWIN spectrograph, using the blue and
red arms simultaneously, with the beam-splitter at 5500 Å, and SITe-CCDs of
![]() 15
15 ![]() pixels. Four exposures of 1800 s each were taken with
the blue arm in the range 3595-5225 Å, while two 1800 s exposures in the
range 5505-7695 Å and two 1800 s in the range 7605-9805 Å were taken
in the red arm (hereafter, the B, R1 and R2 ranges, respectively). The gratings T7 in the blue and T4 in the red give dispersions of 0.81 and 1.08 Å/pixel in
second and first spectral order, respectively. A slit, oriented at
pixels. Four exposures of 1800 s each were taken with
the blue arm in the range 3595-5225 Å, while two 1800 s exposures in the
range 5505-7695 Å and two 1800 s in the range 7605-9805 Å were taken
in the red arm (hereafter, the B, R1 and R2 ranges, respectively). The gratings T7 in the blue and T4 in the red give dispersions of 0.81 and 1.08 Å/pixel in
second and first spectral order, respectively. A slit, oriented at
![]() (Fig. 1), of size
(Fig. 1), of size
![]() provided a spectral resolution, similar in
both arms, of
provided a spectral resolution, similar in
both arms, of
![]() Å, as measured in the background sky emission
lines.
Å, as measured in the background sky emission
lines.
These spectra were reduced, following the standard procedure, by means of the
IRAF![]() package noao.twodspec.longslit. Photometric calibration
was achieved by means of three standard stars, BD+28 4211,
G191-B2B and GD71, observed during the same night and setup,
but through a wide slit. We estimated the resulting photometric accuracy to be 3% in color, except for the
package noao.twodspec.longslit. Photometric calibration
was achieved by means of three standard stars, BD+28 4211,
G191-B2B and GD71, observed during the same night and setup,
but through a wide slit. We estimated the resulting photometric accuracy to be 3% in color, except for the
![]() Å range (residuals are
Å range (residuals are ![]() 5% intrinsic to this range,
5% intrinsic to this range, ![]() 15% with respect to the global spectrum),
where the sensitivity curve drops, and for the
15% with respect to the global spectrum),
where the sensitivity curve drops, and for the
![]() Å range
(accuracy
Å range
(accuracy ![]() %), which is strongly affected by telluric absorption
bands. The absolute photometric level was determined with
%), which is strongly affected by telluric absorption
bands. The absolute photometric level was determined with ![]() 10% accuracy.
The reduction included the subtraction of the background measured in the slit
aside the nebula, and consequently, the light of the underlying stellar
population of M 33 was removed from our spectra.
10% accuracy.
The reduction included the subtraction of the background measured in the slit
aside the nebula, and consequently, the light of the underlying stellar
population of M 33 was removed from our spectra.
We retrieved two spectra from the final archive IUE Newly Extracted Spectra
(INES![]() : González-Riestra et al. 2000; Rodríguez-Pascual et al. 1999; Cassatella et al. 2000). The SWP and LWR spectra
cover a total range of 1150-3350 Å, and were obtained in the
low-resolution mode (
: González-Riestra et al. 2000; Rodríguez-Pascual et al. 1999; Cassatella et al. 2000). The SWP and LWR spectra
cover a total range of 1150-3350 Å, and were obtained in the
low-resolution mode (![]() 5 Å) through the large aperture (
5 Å) through the large aperture (
![]() ;
cf. Fig. 1).
;
cf. Fig. 1).
The two IUE spectra were retrieved from the archive in two formats: the integrated, fully calibrated spectra, and the two-dimensional frames, linearized in wavelength and position. The slit position and mean angular resolution were known with an accuracy of a few arcseconds, a scale comparable to that of the densest spatial structures of the cluster, and we re-determined them more accurately following the procedure detailed in Sect. 3.2. Furthermore, due to significant uncertainties in the photometry of the LWR spectrum, we limited our use of IUE data to the SWP spectrum.
We downloaded a set of images of NGC 588 from the Isaac Newton Group
of telescopes archive. These images were taken with the 1 m Jacobus Kapteyn
Telescope (JKT) at the Observatorio del Roque de los Muchachos (La Palma),
through the filters H![]() +[N II], H
+[N II], H![]() ,
and a continuum narrow
band filter close to H
,
and a continuum narrow
band filter close to H![]() .
.
Line emission only images were obtained by subtracting a version of the
continuum image scaled with stars common to the three filter images. Then, we
divided the H![]() +[N II] image by the H
+[N II] image by the H![]() one, thus establishing
an extinction map of the nebula (the intensity of the [N II]
one, thus establishing
an extinction map of the nebula (the intensity of the [N II] ![]() 6548+6583 doublet being small compared to H
6548+6583 doublet being small compared to H![]() ,
according to our
spectra). We observed no significant gradient of extinction across the object.
We also registered the images with respect to the HST images, in order to
locate the slits of the different spectrographs over the nebula
(Fig. 2).
,
according to our
spectra). We observed no significant gradient of extinction across the object.
We also registered the images with respect to the HST images, in order to
locate the slits of the different spectrographs over the nebula
(Fig. 2).
We retrieved five pairs of WFPC2 images from the HST archive, taken through the filters F547M, F439W, F336W, F170W and F469N. The images were calibrated with the on-the-fly calibration system. Each pair of exposures within a filter was combined with crrej in order to perform cosmic ray rejection.
The images were corrected for filter contamination, as recommended by
McMaster & Whitmore (2002). These corrections consisted of increasing the measured fluxes by 0.044 mag for filter F170W, 0.006, for F336W and 0.002, for F439W. We
also accounted for charge-transfer efficiency loss (Whitmore et al. 1999). This was
necessary because of the low background levels in our images (![]() 0.3 to 0.5 DN). In the case of individual stellar photometry (Sect. 6.1), we
applied directly the formulae of Whitmore et al. (1999) to correct the number of counts
in each star. In the case of integrated fluxes (Sect. 4), we used
an average correction for each filter based on the rough locus of the cluster
on the images (
0.3 to 0.5 DN). In the case of individual stellar photometry (Sect. 6.1), we
applied directly the formulae of Whitmore et al. (1999) to correct the number of counts
in each star. In the case of integrated fluxes (Sect. 4), we used
an average correction for each filter based on the rough locus of the cluster
on the images (![]() and
and ![]() )
and on the approximate counts found
in the stars that dominate the total cluster flux. These corrections are of 0.037, 0.035, 0.036 and 0.044 mag for filters F547M, F439W, F336W and
F170W, respectively. We neglected the effects of geometric distortions, because
the cluster is close to the center of the images, and the photometric effects
of these distortions are small compared to other errors.
)
and on the approximate counts found
in the stars that dominate the total cluster flux. These corrections are of 0.037, 0.035, 0.036 and 0.044 mag for filters F547M, F439W, F336W and
F170W, respectively. We neglected the effects of geometric distortions, because
the cluster is close to the center of the images, and the photometric effects
of these distortions are small compared to other errors.
We computed the barycentric wavelengths of the filters. For this, we multiplied the spectral response of each filter by a few SEDs characteristic of young OB associations, and calculated the corresponding barycentric wavelengths. For F547M, F439W, F336W, F170W and F469N, we respectively found 5470, 4300, 3330, 1740 and 4690 Å. These wavelengths were then used to compute the values of the extinction laws to be applied.
The HST archive contains three STIS spectra through NGC 588, covering
the two wavelength ranges 1447-3305 Å (with the grating G230L) and 1075-1775 Å (with the grating G140L), the two spectra covering the latter
range having a resolution of ![]() 1.5 Å. We retrieved these spectra with
on-the-fly calibration. The spectra pass only through the brightest star of NGC 588 (Fig. 1), and we used them to identify its spectral
class (Sect. 6.2 below).
1.5 Å. We retrieved these spectra with
on-the-fly calibration. The spectra pass only through the brightest star of NGC 588 (Fig. 1), and we used them to identify its spectral
class (Sect. 6.2 below).
Once the spectra were reduced, we performed a self-consistent procedure to
deredden the nebular lines, based on the Balmer lines H![]() through H
through H![]() .
First, the emission line fluxes were corrected for foreground
Galactic extinction, which amounts to
EB-V=0.045 (Burstein & Heiles 1984), the
Galactic law being here the ensemble of the Seaton (1979) ultraviolet law and of
the optical law of Nandy et al. (1975) (as shown in Seaton's paper). Then a reddening
law was fitted to the thus corrected Balmer decrement, taking into account the
photometric and measurement errors of these emission lines
.
First, the emission line fluxes were corrected for foreground
Galactic extinction, which amounts to
EB-V=0.045 (Burstein & Heiles 1984), the
Galactic law being here the ensemble of the Seaton (1979) ultraviolet law and of
the optical law of Nandy et al. (1975) (as shown in Seaton's paper). Then a reddening
law was fitted to the thus corrected Balmer decrement, taking into account the
photometric and measurement errors of these emission lines![]() . This process was performed for each spatial
increment along the slit independently, thus obtaining the reddening along the
slit. The residuals from the actual line ratios to the fitted law were then
plotted along the slit, giving statistical fluctuations around a mean offset
value (due to a small residual photometric calibration) except at those
locations where the underlying stellar population has a significant
contribution of Balmer lines in absorption. The equivalent width of the lines
at these locations was thus computed and the correction applied to the
intensity of the emission lines, then computing the corrected value of
reddening. Assuming the LMC extinction law (Howarth 1983), a priori adequate due
to the metallicity of the object (Vílchez et al. 1988), we derived an EB-V curve
along the slit, and found it to be almost constant, with a value of
. This process was performed for each spatial
increment along the slit independently, thus obtaining the reddening along the
slit. The residuals from the actual line ratios to the fitted law were then
plotted along the slit, giving statistical fluctuations around a mean offset
value (due to a small residual photometric calibration) except at those
locations where the underlying stellar population has a significant
contribution of Balmer lines in absorption. The equivalent width of the lines
at these locations was thus computed and the correction applied to the
intensity of the emission lines, then computing the corrected value of
reddening. Assuming the LMC extinction law (Howarth 1983), a priori adequate due
to the metallicity of the object (Vílchez et al. 1988), we derived an EB-V curve
along the slit, and found it to be almost constant, with a value of
![]() around the stellar cluster. This result is virtually independent
of the selected extinction law, since different laws predict nearly the same
relative extinctions within the H
around the stellar cluster. This result is virtually independent
of the selected extinction law, since different laws predict nearly the same
relative extinctions within the H![]() -H
-H![]() wavelength range.
wavelength range.
We have registered precisely the position of the CAHA slit with respect to the
HST images. This is achieved by convolving the HST images with the atmospheric
point spread function (PSF) at the time of the ground based observations, and
comparing the spatial flux distributions. In order to compute the atmospheric PSF we modeled the spatial flux distribution of a point source in the 2D spectral frames in the following way. We assumed the atmospheric PSF to be a
Moffat (1969) function![]() ,
,
![]() .
We selected a standard star observed just before
NGC 588, and examined its profile along the slit around 4400 Å.
This profile was clearly asymmetrical, indicating image distortion inside the
spectrograph. We found that the observed star profile is very well reproduced
by a model of the form
.
We selected a standard star observed just before
NGC 588, and examined its profile along the slit around 4400 Å.
This profile was clearly asymmetrical, indicating image distortion inside the
spectrograph. We found that the observed star profile is very well reproduced
by a model of the form
![]() ,
where x is the
spatial increment variable, ci the spatial location of the peak of each
component and ai its weight, and M(x) is the Moffat PSF integrated across
the slit width. Thus, we assumed that the signal of the observed object was
convolved by a Moffat function determined by turbulence, truncated by the slit,
and split into three components within the spectrograph, before hitting the
detector. The same analysis near 6600 Å and 8700 Å led to similar
models. Once the PSF model was established, we proceeded as follows.
,
where x is the
spatial increment variable, ci the spatial location of the peak of each
component and ai its weight, and M(x) is the Moffat PSF integrated across
the slit width. Thus, we assumed that the signal of the observed object was
convolved by a Moffat function determined by turbulence, truncated by the slit,
and split into three components within the spectrograph, before hitting the
detector. The same analysis near 6600 Å and 8700 Å led to similar
models. Once the PSF model was established, we proceeded as follows.
The blue 2D spectral frame was multiplied by the response of the HST filter F439W and the result integrated along the wavelength axis; in this way we
obtained from the spectral frames the spatial flux distribution of NGC 588 through the HST filter F439W. Then, we applied our image degradation model
to the HST image for different values of the Moffat parameters Rc and ![]() (that tend to vary with time), placed a synthetic slit on the blurred
image, and extracted the profile integrated across the slit. Rc,
(that tend to vary with time), placed a synthetic slit on the blurred
image, and extracted the profile integrated across the slit. Rc, ![]() and
the central position of the slit were fit by maximizing the correlation between
the profiles extracted from the spectrum and from the image. We found
and
the central position of the slit were fit by maximizing the correlation between
the profiles extracted from the spectrum and from the image. We found
![]() and
and
![]() ,
corresponding to a seeing of
,
corresponding to a seeing of
![]() arcsec. The PSF and the slit position were used to calculate the
aperture throughputs used in Sects. 4 and 6.
arcsec. The PSF and the slit position were used to calculate the
aperture throughputs used in Sects. 4 and 6.
We also used the two-dimensional frames and the F170W HST/WFPC2 image to
determine accurately the slit position and angular resolution of the IUE data,
assuming a Gaussian PSF and using the same technique as for the optical
spectra. The resulting correlation is very good for a FWHM of 6.4
![]() ,
with however a strong photometric mismatch between the data: the IUE flux
integrated within the F170W band was found to be higher than the HST one by a
factor 1.41. This mismatch between IUE and HST absolute calibrations has been
found also for NGC 604 (González Delgado & Pérez 2000). HST absolute photometry is
accurate to a few %, so we decided not to correct the HST image, but to divide
the IUE spectra by the factor 1.41.
,
with however a strong photometric mismatch between the data: the IUE flux
integrated within the F170W band was found to be higher than the HST one by a
factor 1.41. This mismatch between IUE and HST absolute calibrations has been
found also for NGC 604 (González Delgado & Pérez 2000). HST absolute photometry is
accurate to a few %, so we decided not to correct the HST image, but to divide
the IUE spectra by the factor 1.41.
To analyze the spectral properties of the cluster itself, we removed the
nebular continuum from our spectra. For this, we calculated it according to
Osterbrock (1974), including the HI free-free, free-bound and two-photon components as
well as the HeI free-free and free-bound emissions, assuming a gas temperature
of 11 000 K (Vílchez et al. 1988); we reddened the computed nebular continuum to match
the observations, normalized it with the nebular H![]() emission line
intensity in the spatial zone of the optical slit selected to study the cluster
(knowing the H
emission line
intensity in the spatial zone of the optical slit selected to study the cluster
(knowing the H![]() equivalent width with respect to the nebular continuum),
and removed it.
equivalent width with respect to the nebular continuum),
and removed it.
Once the optical and UV slit positions and angular PSFs were determined (see
Sect. 3.2), we calculated the aperture throughputs of the slits for
the whole cluster, i.e. the fraction of light transmitted by these slits. For
this, we computed the sky background of each image by averaging, at a given
position, the pixels contained in a rectangular box and close enough to the
median value of this box. The resulting map of the sky and of the nebula was
removed from the original in order to keep only the stellar signal. The
remaining stellar images were then convolved by the optical or UV PSFs, and in
each band, we compared the total flux of the cluster to the one entering the
slit. In optical, the aperture throughputs were found to be independent of the
band (F170W, F336W, F439W or F547M), and we retained a mean value of 0.169 for
a slit width of 1.2'', valid in the whole optical range. This throughput was
proportional to the chosen slit width, known to ![]() 20% accuracy. The
uncertainty on the PSF led to an uncertainty of 10% on the throughput. For the
IUE spectra, we found a throughput of 0.83 in the F170W filter. This means that
we had to divide the CAHA spectra by 0.169, and the IUE spectra, by 0.83, in
order to obtain the integrated spectrum of the whole cluster. We also
calculated the aperture throughputs for nebular emission: 0.062 for the optical
spectra, and 0.44 for IUE data.
20% accuracy. The
uncertainty on the PSF led to an uncertainty of 10% on the throughput. For the
IUE spectra, we found a throughput of 0.83 in the F170W filter. This means that
we had to divide the CAHA spectra by 0.169, and the IUE spectra, by 0.83, in
order to obtain the integrated spectrum of the whole cluster. We also
calculated the aperture throughputs for nebular emission: 0.062 for the optical
spectra, and 0.44 for IUE data.
The cluster was first modeled in the classical way, i.e. as a stellar
population whose IMF is rigorously a continuous power law
![]() ,
,
![]() .
Assuming instantaneous star
formation, we used Starburst99 (Leitherer et al. 1999), with
.
Assuming instantaneous star
formation, we used Starburst99 (Leitherer et al. 1999), with
![]() ,
making use of standard mass-loss evolutionary tracks at metallicities Z=0.004(Charbonnel et al. 1993) and Z=0.008 (Schaerer et al. 1993), close to the metallicity of the gas
(Vílchez et al. 1988) (the solar value is here Z=0.02). We selected the atmosphere
models of Lejeune et al. (1997), Hillier & Miller (1998) and Pauldrach et al. (2001), the latter two ones
having been compiled by Smith et al. (2002). The age
,
making use of standard mass-loss evolutionary tracks at metallicities Z=0.004(Charbonnel et al. 1993) and Z=0.008 (Schaerer et al. 1993), close to the metallicity of the gas
(Vílchez et al. 1988) (the solar value is here Z=0.02). We selected the atmosphere
models of Lejeune et al. (1997), Hillier & Miller (1998) and Pauldrach et al. (2001), the latter two ones
having been compiled by Smith et al. (2002). The age ![]() of the cluster, its
metallicity Z, and the IMF slope
of the cluster, its
metallicity Z, and the IMF slope ![]() and upper limit
and upper limit
![]() were
constrained with observables available for the cluster as a whole. These are:
i) the UV and optical colors, integrated over the entire cluster; ii) the
H
were
constrained with observables available for the cluster as a whole. These are:
i) the UV and optical colors, integrated over the entire cluster; ii) the
H![]() equivalent width
equivalent width
![]() measured over the whole object
(nebula and cluster); iii) the profiles of the UV stellar lines present in the
IUE spectrum; iv) the presence or absence of the main Wolf-Rayet (WR) emission
lines in the optical SED.
measured over the whole object
(nebula and cluster); iii) the profiles of the UV stellar lines present in the
IUE spectrum; iv) the presence or absence of the main Wolf-Rayet (WR) emission
lines in the optical SED.
The SED colors were used to determine the amount and the law of extinction of
the stellar flux. Indeed, the color excess EB-V derived from the Balmer
lines of a nebula has been found not to apply systematically to its ionizing
source (e.g., Mas-Hesse & Kunth 1999). Furthermore, whereas different extinction laws
generally do not differ significantly from each other in the optical range and
cannot be discriminated by the use of the nebular Balmer lines, they strongly
vary in the UV counterpart. Fortunately, the intrinsic UV and optical colors of
an OB association little depend on the age and IMF of the latter, and can be
used to characterize the extinction, provided that one knows approximately the
main characteristics of this association. Mas-Hesse & Kunth (1999) found an age of 2.8 Myr
for a very flat IMF (![]() )
with an upper mass cutoff of 120
)
with an upper mass cutoff of 120 ![]() ,
for the cluster of NGC 588. We computed SEDs for a range of ages, IMF
slopes and upper mass cutoffs around these values, and calculated the
corresponding fluxes in the four bands F547M, F439W, F336W and F170W. Then, the
colors of the cluster were measured on the HST images cleared of their diffuse
background. Table 2 shows the measured colors and some model
outputs. The differences of color between the observations and the models were
attributed to interstellar reddening. We tested three extinction laws: Galactic
(Nandy et al. 1975; Seaton 1979), LMC (Howarth 1983) and SMC (Prévot et al. 1984; Bouchet et al. 1985), whose values at
the barycentric wavelengths of the bands are summarized in Table 2.
For any set of model colors, the best fit was obtained with the SMC law and
,
for the cluster of NGC 588. We computed SEDs for a range of ages, IMF
slopes and upper mass cutoffs around these values, and calculated the
corresponding fluxes in the four bands F547M, F439W, F336W and F170W. Then, the
colors of the cluster were measured on the HST images cleared of their diffuse
background. Table 2 shows the measured colors and some model
outputs. The differences of color between the observations and the models were
attributed to interstellar reddening. We tested three extinction laws: Galactic
(Nandy et al. 1975; Seaton 1979), LMC (Howarth 1983) and SMC (Prévot et al. 1984; Bouchet et al. 1985), whose values at
the barycentric wavelengths of the bands are summarized in Table 2.
For any set of model colors, the best fit was obtained with the SMC law and
![]() (the error bar includes the uncertainties in the
observational data and the spread in the theoretical colors). This value is
compatible with the amount of extinction derived from the nebular Balmer lines,
meaning that there is no indication of differential extinction between the
stellar and the nebular fluxes. Since the nebular value,
(the error bar includes the uncertainties in the
observational data and the spread in the theoretical colors). This value is
compatible with the amount of extinction derived from the nebular Balmer lines,
meaning that there is no indication of differential extinction between the
stellar and the nebular fluxes. Since the nebular value,
![]() ,
was determined more accurately, we have also adopted it for the cluster in the
following. Considering these results and the 800 kpc distance of M 33
(Lee et al. 2002), we derived the cluster luminosity in the F439W band:
,
was determined more accurately, we have also adopted it for the cluster in the
following. Considering these results and the 800 kpc distance of M 33
(Lee et al. 2002), we derived the cluster luminosity in the F439W band:
![]() erg s-1 Å-1.
erg s-1 Å-1.
This quantity is often used in modeling of massive stellar populations, as a
way to characterize the ratio of the ionizing photon rate to the optical
continuum. It is mainly sensitive to the global distribution of effective
temperatures of the stars, although it also depends on the fraction of the
ionizing flux absorbed by the nebular gas. Since this fraction is a priori
unknown, we decided only to require the model to predict
![]() greater than or equal to the observed value.
greater than or equal to the observed value.
The value of
![]() used here is the ratio of the total nebular
H
used here is the ratio of the total nebular
H![]() flux to the stellar H
flux to the stellar H![]() continuum integrated over the cluster.
The integrated values of these two quantities were obtained by dividing the
values measured in the blue CAHA spectrum (cleared of the nebular continuum;
see Sect. 3.3) by the aperture throughputs of the optical slit for
the nebular gas and for the stellar continuum (Sect. 3.4). This
estimate of
continuum integrated over the cluster.
The integrated values of these two quantities were obtained by dividing the
values measured in the blue CAHA spectrum (cleared of the nebular continuum;
see Sect. 3.3) by the aperture throughputs of the optical slit for
the nebular gas and for the stellar continuum (Sect. 3.4). This
estimate of
![]() is affected by the error in the
nebular-to-stellar ratio of the two aperture throughputs, evaluated to
is affected by the error in the
nebular-to-stellar ratio of the two aperture throughputs, evaluated to ![]() 10%. We found
10%. We found
![]() Å.
Å.
The UV lines that form in the atmospheres of massive stars were studied by
Sekiguchi & Anderson (1987a). They showed the correlation existing between the shapes and
intensities of the Si IV ![]() 1400 and C IV
1400 and C IV ![]() 1550 lines
and the spectral type and luminosity class of early-type stars. The use of
these two lines and, in some cases, the He II
1550 lines
and the spectral type and luminosity class of early-type stars. The use of
these two lines and, in some cases, the He II ![]() 1640 line, can be a
good complement to
1640 line, can be a
good complement to
![]() ,
for the determination of the evolutionary
status and IMF of the cluster, due to their sensitivity to the luminosity class
of the stars (e.g., Mas-Hesse & Kunth 1991; Sekiguchi & Anderson 1987b; Robert et al. 1993; Mas-Hesse & Kunth 1999).
,
for the determination of the evolutionary
status and IMF of the cluster, due to their sensitivity to the luminosity class
of the stars (e.g., Mas-Hesse & Kunth 1991; Sekiguchi & Anderson 1987b; Robert et al. 1993; Mas-Hesse & Kunth 1999).
The IUE short-wavelength spectrum of NGC 588 has low resolution and signal-to-noise ratio, and was not used directly in the fit of the population parameters. Instead, it served to discuss and possibly reject some models determined with the other observables, by visual comparison between model and observed spectra. Furthermore, we assumed this spectrum to be representative of the whole cluster, since the IUE slit covers nearly all the flux of the cluster (see Sect. 3.4).
The optical spectra clearly show the broad He II
![]() emission
line produced by one or more WR stars. No corresponding C IV
emission
line produced by one or more WR stars. No corresponding C IV
![]() feature was found, showing that the detected WR stars are of WN type. The
presence of such stars in the cluster fixes its age to 3.2-4.4 Myr if Z=0.004,
and 2.8-4.5 Myr if Z=0.008, according to Starburst99. These age ranges are
valid for
feature was found, showing that the detected WR stars are of WN type. The
presence of such stars in the cluster fixes its age to 3.2-4.4 Myr if Z=0.004,
and 2.8-4.5 Myr if Z=0.008, according to Starburst99. These age ranges are
valid for
![]()
![]() ,
and are narrower for lower mass cutoffs.
,
and are narrower for lower mass cutoffs.
Since the optical slit covers only a fraction of the cluster, our optical spectra do not necessarily include the signatures of all the kinds of stars present in the cluster. Consequently, we were unable to estimate the total number of WN stars in the entire cluster. Therefore, to constrain the models, we only used the fact that this number is of at least 1. Likewise, we ignored the non-detection of WC star in the optical spectrum, and did not process the number of WC stars predicted by the models.
Table 3:
Results of the canonical analytical modeling of the cluster, for the
two metallicities Z=0.004 and Z=0.008. Single values correspond to the best
fits. Parenthesized ranges correspond to theapproximate 3![]() ranges.
ranges.
We performed a chi-square-like fit of ![]() ,
, ![]() and Z over
and Z over
![]() and the number of WN stars
and the number of WN stars
![]() ,
using the
outputs of the Starburst99 code.
,
using the
outputs of the Starburst99 code.
![]() ,
the total mass
,
the total mass
![]() and the number
and the number
![]() of O stars were multiplied
by the coefficient needed to reproduce the luminosity of the cluster in filter F439W. The chi-square formula we used is the following:
of O stars were multiplied
by the coefficient needed to reproduce the luminosity of the cluster in filter F439W. The chi-square formula we used is the following:
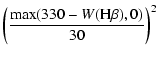 |
(1) |
The results of the fit are summarized in Table 3. The model
associated to the minimum ![]() is described by
is described by ![]() Myr,
Myr,
![]()
![]() and Z=0.008. However, this model, with a reduced
and Z=0.008. However, this model, with a reduced ![]() as high as 7, shows significant discrepancies with the observations: both
as high as 7, shows significant discrepancies with the observations: both
![]() and
and
![]() are well below the observed
value. We can also note that due to the small value of
are well below the observed
value. We can also note that due to the small value of
![]() ,
the model He II
,
the model He II ![]() 4686 WR bump is negligible (see Fig. 3). The bad fit of
4686 WR bump is negligible (see Fig. 3). The bad fit of
![]() when
when
![]() is high enough can be attributed to the presence of blue supergiants (BSGs),
defined here as having effective temperatures
is high enough can be attributed to the presence of blue supergiants (BSGs),
defined here as having effective temperatures
![]() K,
in the model cluster such that each of them, being alone in the nebula, would
cause
K,
in the model cluster such that each of them, being alone in the nebula, would
cause
![]() Å: according to the best-fit model,
their number is
Å: according to the best-fit model,
their number is
![]() .
In a
general way, such stars were predicted at any age with high enough values of
.
In a
general way, such stars were predicted at any age with high enough values of
![]() ,
resulting in the absence of a good compromise between
,
resulting in the absence of a good compromise between
![]() and
and
![]() ;
this is illustrated by Figs. 4 and 5.
;
this is illustrated by Figs. 4 and 5.
![\begin{figure}
\par\includegraphics[angle=90,width=8.2cm,clip]{0136fg03.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg68.gif) |
Figure 3: Observed SED vs. SED constructed with the best-fit parameters. The observed SED is here supposed to be representative of the whole cluster, even though the slits (in particular the optical one) only sample a portion of the cluster. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0136fg04.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg70.gif) |
Figure 4:
Evolution of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0136fg05.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg71.gif) |
Figure 5: Same as Fig. 4 for Z=0.008. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=4cm,clip]{0136fg06.eps}\hspac...
...pace*{2mm}
\includegraphics[angle=90,width=4cm,clip]{0136fg09.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg72.gif) |
Figure 6: Observed vs. synthetic UV spectra for different IMF slopes. The synthetic spectra were convolved by a 5 Å FWHM Gaussian curve to match IUE's resolution. |
| Open with DEXTER | |
So far, we were unable to determine the IMF slope more accurately than
constraining it to the range 1.5-3. Now, we show how we can discard IMFs
flatter than
![]() .
Figure 6 shows the observed and
model UV spectra in the case of the IMF slopes
.
Figure 6 shows the observed and
model UV spectra in the case of the IMF slopes ![]() ,
1.7, 2.35 and 3, and for the best-fit metallicity (Z=0.008), age (2.8 Myr) and upper mass limit (120
,
1.7, 2.35 and 3, and for the best-fit metallicity (Z=0.008), age (2.8 Myr) and upper mass limit (120 ![]() ). The synthetic UV spectra were created with the LMC/SMC library of Starburst99 (Leitherer et al. 2001). The depths of the Si IV
). The synthetic UV spectra were created with the LMC/SMC library of Starburst99 (Leitherer et al. 2001). The depths of the Si IV ![]() 1400 and C
IV
1400 and C
IV ![]() 1550 lines were found to decrease with increasing IMF slope, due
to the conservation of their equivalent widths and increase of their spectral
widths. This result is in agreement with Robert et al. (1993). Due to excessive depths
of the lines, the cases
1550 lines were found to decrease with increasing IMF slope, due
to the conservation of their equivalent widths and increase of their spectral
widths. This result is in agreement with Robert et al. (1993). Due to excessive depths
of the lines, the cases ![]() and 1.7 were rejected, while we considered
the fits reasonably good for the other, steeper IMF slopes.
and 1.7 were rejected, while we considered
the fits reasonably good for the other, steeper IMF slopes.
In the previous section, we obtained a model attempting to reproduce as well as
possible
![]() ,
the numbers of WN stars and the UV stellar lines in
the framework of a classical cluster analysis, that only takes into account the
accuracy of the observational data. According to this model, the mass of the
cluster is
,
the numbers of WN stars and the UV stellar lines in
the framework of a classical cluster analysis, that only takes into account the
accuracy of the observational data. According to this model, the mass of the
cluster is ![]() 3000
3000 ![]() .
Meanwhile, assuming a metallicity Z=0.004and using the same evolutionary tracks, Mas-Hesse & Kunth (1999) obtained a cluster age
.
Meanwhile, assuming a metallicity Z=0.004and using the same evolutionary tracks, Mas-Hesse & Kunth (1999) obtained a cluster age
![]() ,
an IMF slope
,
an IMF slope ![]() and a total mass of 534
and a total mass of 534 ![]() ,
by the
analysis of, mainly, the IUE-SWP and IUE-LWR spectra, but in absence of
knowledge about the WR content of the cluster.
,
by the
analysis of, mainly, the IUE-SWP and IUE-LWR spectra, but in absence of
knowledge about the WR content of the cluster.
In both works, the results have been obtained under the following
assumptions: correct stellar evolutionary tracks, instantaneous burst
hypothesis and the implicit existence of a zero age main sequence (but
see Tenorio-Tagle et al. 2003) and a number of stars in the cluster large enough to perfectly
sample the IMF. However the estimated masses in both cases are about two orders
of magnitude below the 105 ![]() mass for which, according to
Cerviño & Mas-Hesse (1994), the whole IMF would be well filled. Hence, it is expected that
sampling effects in the IMF will strongly affect any classical integrated
analysis of this cluster.
mass for which, according to
Cerviño & Mas-Hesse (1994), the whole IMF would be well filled. Hence, it is expected that
sampling effects in the IMF will strongly affect any classical integrated
analysis of this cluster.
Furthermore, the F439W luminosity of the cluster, with a value of -10.08 mag.
is lower than the luminosity of the brightest star in the isochrone of the
fitted model, -11.42 mag., that Cerviño & Luridiana (2004) showed to be the lowest luminosity
limit under which a cluster cannot be modeled with classical population
synthesis. Even worse, this limit is brighter than the entire cluster by as
much as 1.4 mag. This implies that the results of classical synthesis
models regarding magnitudes and colors can be strongly biased (Cerviño & Valls-Gabaud 2003).
Unfortunately, the actual theoretical status of statistical modeling of stellar
clusters is not ready yet to solve such a situation. The only realistic
assessments that can be robustly obtained are: (i) due to the presence of at
least one WN star, the age range is between 2.8 and 4.5 Myr (assuming there is
no issue in isochrone computations and that WR star formation is not due to the
evolution of binary systems); and (ii) the amount of gas transformed into stars
at the onset of the burst does not exceed about 104 ![]() (for a
Salpeter IMF and
(for a
Salpeter IMF and
![]()
![]() ), for which the luminosity of the
cluster would reach the lowest luminosity limit.
), for which the luminosity of the
cluster would reach the lowest luminosity limit.
This implies that the discussion about ages, IMF and discrepancies between the models and the observations in the analysis made with standard synthesis models hardly makes sense in our case.
One of our main objectives is to infer a plausible shape of the ionizing continuum, which implies the use of a technique different from the standard modeling as we show in the next section.
Due to the small number of stars influencing the observables and the ionizing flux of the NGC 588 cluster, and because of the unsatisfactory results of the analysis detailed in Sect. 4, we decided to study not only the cluster as a whole, but also its individual stars. We achieved photometry of these stars, used isochrone curves to parameterize the cluster, attributed a model to each star, and synthesized spectra to be compared to the observations.
We performed photometric measurements of the stars on the five HST images,
using the noao.digiphot.daophot package of IRAF. In each band, we ran
daofind and phot to detect candidate stars and measure their
intensities in 6 pixel radius apertures. The brightest isolated stars served to
compute analytical PSFs for all the bands. We then ran allstar to
reject the artifacts of the daofind routine and measure more
accurately the intensities of the remaining objects. We selected again bright
and isolated stars to carefully calculate the aperture corrections for the
bands with the mkapfile routine of the noao.digiphot.photcal
package, and derive the stellar intensities integrated over the full PSF extents. The intensities were corrected for charge-transfer inefficiency and filter contamination (see Sect. 2.4), and converted into apparent
magnitudes with the DN-to-flux keyword PHOTFLAM of the image headers. The
apparent magnitudes were converted into absolute (but reddened) magnitudes with
the distance modulus 24.52 (Lee et al. 2002). The densest part of the cluster was
not resolved by daofind, but from visual inspection, we found it to
contain five clearly distinct stars. Using the Levenberg-Marquardt's
least-square method, and already knowing the PSF mathematical models, we fitted
the positions and fluxes of these five stars in each of the images; we detected
no other star in the residuals of the fits, and retained our five-star
detection. The final photometric lists were composed of 536 stars in band F547M, 698 in F439W, 353 in F336W, 574 in F170W and 179 in F469N. 173 of them
were common to bands F547M and F439W, 56, to F547M, F439W, F336W and F170W, and 20 to all bands. Table 4 lists the 56 stars common to F547M,
F439W, F336W and F170W. In terms of absolute magnitudes, the 3![]() detection limits were estimated to be approximately 0.8, -0.1, -0.8,
-3.8 and -2.8 in filters F547M, F439W, F336W, F170W and F469N,
respectively.
detection limits were estimated to be approximately 0.8, -0.1, -0.8,
-3.8 and -2.8 in filters F547M, F439W, F336W, F170W and F469N,
respectively.
The star observed with STIS is star #1 from Table 4. From the stars with available M469, star #2 is the only one exhibiting a clear He II excess, and was identified as the only or main WN star responsible for the He II bump in the optical spectrum.
![\begin{figure}
\par\includegraphics[angle=90,width=4cm,clip]{0136fg10.eps}\hspac...
...space*{2mm}
\includegraphics[angle=90,width=4cm,clip]{0136fg13.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg75.gif) |
Figure 7: STIS vs. LMC/SMC spectra: B0II, B0I, WNL and WCL, respectively. The 1600-1700 Å region was unavailable for the B0I star. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{0136fg14.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg76.gif) |
Figure 8:
Optical spectra near the WR He II |
| Open with DEXTER | |
To identify the nature of the star observed with STIS, we first compared its
spectrum with the ones of the LMC/SMC library of Leitherer et al. (2001), paying attention
to the Si IV ![]() 1400, C IV
1400, C IV ![]() 1550 and, when available,
He II
1550 and, when available,
He II ![]() 1640 lines. The four acceptable matches
(Fig. 7) indicated the star to be of class B0II, B0I, late WN
(WNL) or late WC (WCL). We found a significant He II
1640 lines. The four acceptable matches
(Fig. 7) indicated the star to be of class B0II, B0I, late WN
(WNL) or late WC (WCL). We found a significant He II ![]() 4686 bump in
the CAHA slit zone situated within the PSF extent of this quite isolated star
(see Fig. 8 for this star and for star #2 of
Table 4). The intensity of this bump being compatible with the
(quite inaccurate) value derived from the photometric measurements, we deduced
that the star is a WR. In absence of any optical carbon feature, in contrast
with the well-defined He II
4686 bump in
the CAHA slit zone situated within the PSF extent of this quite isolated star
(see Fig. 8 for this star and for star #2 of
Table 4). The intensity of this bump being compatible with the
(quite inaccurate) value derived from the photometric measurements, we deduced
that the star is a WR. In absence of any optical carbon feature, in contrast
with the well-defined He II ![]() 4686 bump, we concluded that it is a
WNL star.
4686 bump, we concluded that it is a
WNL star.
Considering the presence of such a star in the cluster, we inferred the age range of the latter for both metallicities Z=0.004 and Z=0.008: 3.2-3.7 and 2.8-4.5 Myr, respectively.
We constructed isochrone curves calling the same evolutionary tracks and model
atmospheres as in Sect. 4. The effective temperatures and
bolometric luminosities of these isochrones were computed with the original
Starburst99 code. The corresponding magnitudes, however, were derived from them
by means of an interpolation method different from the one of Starburst99. The
latter mainly consists in nearest-neighbor selection of the spectra in the
![]() plane,
plane,
![]() being the effective
temperature, and g, the surface gravity. This induces step-like
discontinuities in plots such as color-magnitude diagrams. This is why we
exploited an alternative interpolation method, explicated in the Appendix, that
consists, at each wavelength, of applying a bilinear interpolation of the
logarithm of the flux in the
being the effective
temperature, and g, the surface gravity. This induces step-like
discontinuities in plots such as color-magnitude diagrams. This is why we
exploited an alternative interpolation method, explicated in the Appendix, that
consists, at each wavelength, of applying a bilinear interpolation of the
logarithm of the flux in the
![]() plane, y being a variable that
depends both on the effective temperature and on the wavelength.
plane, y being a variable that
depends both on the effective temperature and on the wavelength.
Depending on the stellar parameters, various kinds of model atmospheres, listed in Sect. 4, were exploited. This implies an artificial jump in the isochrone diagrams at the locus of transition from Lejeune et al. (1997) models to the one of Smith et al. (2002). Fortunately, this transition occurs in a zone where it is smaller than the error bars, and consequently it has a negligible impact.
We first investigated the extinction law, since a priori it may be different
from the one inferred from the canonical study of the cluster (cf.
Sect. 4.1). We considered several isochrones in the age range of the
cluster, and for each of them and each of the three tested extinction laws
(Galactic, LMC and SMC), we proceeded as follows. We first estimated the color
excess of each star in Table 4 by shifting the measured points
towards the isochrone curve in the
(M439,M336-M547) diagram
according to the tested law, assuming stars #1 and #2 to be WN stars, and all
the other ones to be on the main sequence. Then, we dereddened each star in the
(M439,M170-M547) diagram, and compared the resulting points with the
theoretical isochrone. Independently of the reference isochrone (i.e., in
practice, the age), the SMC law was favored, as the systematic discrepancy
between the isochrone and the locus of the stars, in particular the brightest
ones, was small for the SMC law and significantly larger for the other two
laws. Numerically, the discrepancy between the observational points in the
(M439,M170-M547) diagram dereddened with the use of the
(M439,M336-M547) one and the theoretical isochrone is characterized
by a reduced ![]() ranging in the approximate intervals 2.3-3.3 for the
Galactic law, 1.8-2.0 for the LMC one and 0.6-0.8 for the SMC one, obtained
with 56 stars. The fact that this
ranging in the approximate intervals 2.3-3.3 for the
Galactic law, 1.8-2.0 for the LMC one and 0.6-0.8 for the SMC one, obtained
with 56 stars. The fact that this ![]() is close to 1 with the SMC law made
us confident in the latter, and is also an indication that none of the 56 considered stars is significantly affected by blending with an unresolved
companion. The procedure of selection of an extinction law is illustrated in
Fig. 9 for an age of 3.5 Myr, and in Fig. 10
for 4.5 Myr.
is close to 1 with the SMC law made
us confident in the latter, and is also an indication that none of the 56 considered stars is significantly affected by blending with an unresolved
companion. The procedure of selection of an extinction law is illustrated in
Fig. 9 for an age of 3.5 Myr, and in Fig. 10
for 4.5 Myr.
Once the extinction law chosen, we re-considered the individual color excess
EB-V of the stars. For the stars used in the selection of the extinction
law, we started from the values already estimated in the
(M439,M336-M547) diagram. For the stars that, once dereddened, were
found to be brighter than
M439=-6, we conserved the values of EB-Vfound in this diagram and the corresponding uncertainties, the latter including
the (small) scatters of values found with the different possible isochrones.
However, for the stars dimmer than
M439=-6, we used the constancy of the
isochrones in the
(M439,M170-M547) diagram to estimate EB-Vwith better accuracy. Indeed, the uncertainty in EB-V determined in one of
the
(M439,MX-M547) diagrams (X=170 or X=336) is roughly the ratio
![]() ,
where
,
where
![]() is the
uncertainty in the
MX-M547 color, and in our case, this ratio in
EB-V is smaller for X=170 than for X=336. With a few exceptions, we
found all the color excess to be compatible with the nebular value,
EB-V=0.11, and when this was the case and the dereddened F439W magnitude
was dimmer than -6, we set them to this value. An important departure from
EB-V=0.11 is the case of star #2:
is the
uncertainty in the
MX-M547 color, and in our case, this ratio in
EB-V is smaller for X=170 than for X=336. With a few exceptions, we
found all the color excess to be compatible with the nebular value,
EB-V=0.11, and when this was the case and the dereddened F439W magnitude
was dimmer than -6, we set them to this value. An important departure from
EB-V=0.11 is the case of star #2:
![]() .
All stars with
unavailable F170W and F336W magnitudes were dereddened with
EB-V=0.11,
compatible with the
(M439,M439-M547) theoretical curve.
Figure 11 testifies to the correctness of setting almost all the 173
stellar color excesses to the nebular one.
.
All stars with
unavailable F170W and F336W magnitudes were dereddened with
EB-V=0.11,
compatible with the
(M439,M439-M547) theoretical curve.
Figure 11 testifies to the correctness of setting almost all the 173
stellar color excesses to the nebular one.
In all what follows, the color-magnitude diagrams (CMDs) refer to the dereddened stellar magnitudes.
![\begin{figure}
\par\includegraphics[angle=90,width=7.5cm,clip]{0136fg23.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg83.gif) |
Figure 11:
Histogram of the dispersion of the stellar color excesses EB-Varound the nebular one 0.11. The abscissa axis variable is the discrepancy term
|
| Open with DEXTER | |
The age and metallicity of the cluster were constrained by simultaneously fitting the isochrone to the dereddened observational points in the (M439,M170-M547) diagram, and by comparing synthetic spectra and derived properties to the observations. For a given isochrone, each star was identified to the nearest point of the isochrone in terms of chi-square (i.e., accounting for the error bars) in the (M439,M170-M547) diagram or, when the F170W magnitude was unavailable, in the (M439,M439-M547)diagram, thus attributing the most appropriate model spectrum to the considered star. If the cluster spectrum was synthesized to simulate what is seen through a slit (CAHA or IUE), the spectrum selected for a given star was multiplied by its corresponding aperture throughput (known from its position with respect to the slit and from the angular PSF or seeing of the considered data) and a function representing its possible differential extinction (with respect to the reference value EB-V=0.11) along the processed wavelength range, and added to the total cluster spectrum to compute. If the total cluster spectrum was to be synthesized, then the individual stellar spectra were summed without being previously modified.
We computed the isochrone curves for the different ages multiple of 0.1 Myr belonging to the ranges constrained by the presence of a WNL star. Here, we show the curves obtained for the ages 3.2 and 3.7 Myr in the case Z=0.004(Fig. 12), and 3.0, 3.5, 4.0 and 4.5 Myr for Z=0.008(Fig. 13). At both metallicities, the isochrone high-luminosity main-sequence branch was found to move, with increasing age, from regions of low values of the M170-M547 color towards the somewhat "red'' observational points.
The synthesized spectra were exploited as follows. For a given tested
isochrone, the spectrum simulated for the optical slit was used to
extract the model ratio
![]() related to the
Balmer jump, which is a diagnostic of the effective temperature of a cluster
dominated by hot stars. Indeed, in the spectrum of a hot star, the intensity of
the Balmer jump decreases with increasing effective temperature, and usually
serves to determine the subtypes of B stars, whereas it is negligible in the
spectra of O stars. The observed value, whose uncertainty is dominated by the
local fluctuating residues in photometric calibration, is
related to the
Balmer jump, which is a diagnostic of the effective temperature of a cluster
dominated by hot stars. Indeed, in the spectrum of a hot star, the intensity of
the Balmer jump decreases with increasing effective temperature, and usually
serves to determine the subtypes of B stars, whereas it is negligible in the
spectra of O stars. The observed value, whose uncertainty is dominated by the
local fluctuating residues in photometric calibration, is
![]() .
The constructed UV spectrum was visually compared to the IUE observed one.
Finally, we derived the predicted
.
The constructed UV spectrum was visually compared to the IUE observed one.
Finally, we derived the predicted
![]() from the total cluster
spectrum, assuming again that the nebula absorbs all the ionizing photons, and
thus requesting the predicted
from the total cluster
spectrum, assuming again that the nebula absorbs all the ionizing photons, and
thus requesting the predicted
![]() to be greater than or equal to
the observed one.
to be greater than or equal to
the observed one.
Mathematically, we used the following ![]() estimator to constrain the age
and the metallicity of the cluster:
estimator to constrain the age
and the metallicity of the cluster:
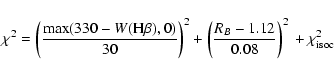 |
The SED of the best-fit model is shown in Fig. 16. We
considered it to satisfactorily reproduce the observations, except for the
strength of the optical WR bumps. However, the model atmospheres used for WR
stars here are not intended to compute reliably these bumps, and we did not pay
attention to their strength. Instead, we estimated them from Table 1 of
Schaerer & Vacca (1998), knowing that star #2 was finally classified as a WNL from its
hydrogen surface abundance. The results, satisfying but somewhat inaccurate
(due in particular to the scatter of the model bump intensities), are
summarized in Table 6. The synthetic UV spectrum, superimposed to
the observed one in Fig. 17, was found to satisfactorily
reproduce the C IV ![]() 1550 line. It also contains an undetected
Si IV
1550 line. It also contains an undetected
Si IV ![]() 1400 feature. However, the UV line spectrum is dominated by
a small number of massive stars, that are not necessarily well represented by
the spectra LMC/SMC library, in particular the WNL ones. In consequence, we did
not consider the Si IV
1400 feature. However, the UV line spectrum is dominated by
a small number of massive stars, that are not necessarily well represented by
the spectra LMC/SMC library, in particular the WNL ones. In consequence, we did
not consider the Si IV ![]() 1400 discrepancy as a critical one.
1400 discrepancy as a critical one.
Table 5: Numerical results of the star-by-star analysis of the cluster. The parenthesized age ranges indicate the 90% confidence limits.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{0136fg30.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg90.gif) |
Figure 14: Final adopted (M439,M170-M547) diagram. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{0136fg31.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg91.gif) |
Figure 15: Final adopted HR diagram for all the detected stars. The circles show the selected individual stellar model. The dashed part of the diagram is the WR branch. The two dotted curves represent the HR diagram at 3.0 Myr (upper curve) and 5.5 Myr (lower curve). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.2cm,clip]{0136fg32.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg92.gif) |
Figure 16:
Optical and UV SEDs synthesized for Z=0.008 and |
| Open with DEXTER | |
Table 6: WR line strengths, observed/predicted in the dereddened CAHA spectrum.
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{0136fg33.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg93.gif) |
Figure 17:
UV spectrum synthesized for Z=0.008 and |
| Open with DEXTER | |
From the initial mass associated with each star, we computed the mean power-law
IMF of the cluster. More specifically, we constructed a histogram of the
logarithm of the initial masses, from
![]() to
to
![]() (m=6.3to m=58
(m=6.3to m=58 ![]() ), with a bin of 0.03 (equivalent to a factor of 1.07
between two successive bins), and fit it with an exponential law, assuming
Poissonian noise in each bin, knowing that a power-law IMF d
), with a bin of 0.03 (equivalent to a factor of 1.07
between two successive bins), and fit it with an exponential law, assuming
Poissonian noise in each bin, knowing that a power-law IMF d
![]() can be translated into the law d
can be translated into the law d
![]() .
The lower limit of the initial mass range was chosen
in order to ensure that the stars of the cluster belonging to a given bin were
all detected, and the upper limit corresponds to the highest possible initial
mass at the age and metallicity of the cluster. The result is shown in
Fig. 18. We found an IMF slope
.
The lower limit of the initial mass range was chosen
in order to ensure that the stars of the cluster belonging to a given bin were
all detected, and the upper limit corresponds to the highest possible initial
mass at the age and metallicity of the cluster. The result is shown in
Fig. 18. We found an IMF slope
![]() ,
and
retained the compatible Salpeter slope, resulting in an inferred IMF
d
,
and
retained the compatible Salpeter slope, resulting in an inferred IMF
d
![]() .
The corresponding total initial mass
integrated in the range
.
The corresponding total initial mass
integrated in the range
![]() is
is
![]() .
.
![\begin{figure}
\par\includegraphics[angle=90,width=7.8cm,clip]{0136fg34.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg103.gif) |
Figure 18:
IMF histogram and fit. Full line: best fit. Dashed line: fit for the
Salpeter slope. The error bars are equivalent to 1 |
| Open with DEXTER | |
From the mean IMF computed in Sect. 6.4, we derived the mean expected numbers of several kinds of massive stars susceptible to change significantly the spectral properties of the cluster. Here we present these results and discuss them.
According to our stellar models, at 4.2 Myr and for Z=0.008, BSGs (as defined
in Sect. 4.5) are stars with initial masses ranging from 44 to 55 ![]() .
The number expectancy, derived from the integration, between these
two limits, of the mean power-law IMF computed in Sect. 6.4, is
.
The number expectancy, derived from the integration, between these
two limits, of the mean power-law IMF computed in Sect. 6.4, is
![]() .
The associated Poisson probability to observe no
BSG, as is our case, is
.
The associated Poisson probability to observe no
BSG, as is our case, is
![]() %. We added an
artificial continuous population composed by this kind of stars, weighted by
the Salpeter IMF slope, to the actual stellar content of the cluster.
Independently of the optical absolute luminosity - which would be
automatically fit in a classical modeling of the cluster - the most striking
change in the computed spectral properties is, as expected, the large drop of
%. We added an
artificial continuous population composed by this kind of stars, weighted by
the Salpeter IMF slope, to the actual stellar content of the cluster.
Independently of the optical absolute luminosity - which would be
automatically fit in a classical modeling of the cluster - the most striking
change in the computed spectral properties is, as expected, the large drop of
![]() :
in presence of the BSG population, the latter quantity would
be only 133 Å, instead of 342 Å.
:
in presence of the BSG population, the latter quantity would
be only 133 Å, instead of 342 Å.
We computed the expected number of the different WR stars (WNL, WNE, WCL, WCE,
WO), derived from the mean IMF of Sect. 6.4; we found
![]() ,
,
![]() ,
,
![]() ,
,
![]() and
and
![]() ,
according to
the star classification of Starburst99. The resulting Poisson likelihood of the
observed WR content of the cluster is 0.7%, a small value that is however much
more satisfactory than the 0.04% likelihood derived from the analytical model.
Furthermore, we simulated a spectrum obtained by replacing the two WR stars of
the cluster with an analytical, complete population of 0.51 WN star following
the Salpeter IMF. This population was expected to produce less luminous but
possibly harder or softer radiation than the two actually detected WR, as the
WR branch of the HR diagram (Fig. 15) spans a significant range of
effective temperatures. We found that whereas
,
according to
the star classification of Starburst99. The resulting Poisson likelihood of the
observed WR content of the cluster is 0.7%, a small value that is however much
more satisfactory than the 0.04% likelihood derived from the analytical model.
Furthermore, we simulated a spectrum obtained by replacing the two WR stars of
the cluster with an analytical, complete population of 0.51 WN star following
the Salpeter IMF. This population was expected to produce less luminous but
possibly harder or softer radiation than the two actually detected WR, as the
WR branch of the HR diagram (Fig. 15) spans a significant range of
effective temperatures. We found that whereas
![]() is smaller with
the modified stellar population, the latter produces harder radiation than the
"true'' one in the Lyman continuum range, especially below the threshold of
ionization of He+, as summarized in Table 7.
is smaller with
the modified stellar population, the latter produces harder radiation than the
"true'' one in the Lyman continuum range, especially below the threshold of
ionization of He+, as summarized in Table 7.
Table 7: Some spectral properties derived from the observed stellar content (2nd column) and from the one with BSG, WR and whole population replaced with the one predicted by the fitted power-law IMF (3rd, 4th and 5th columns, respectively). Q(X) designates the photon rate able to ionize the ion "X'' population of a nebula. aThe 5th and 6th columns correspond to analytical models, whose total mass here reproduce the observed F439W luminosity. bBest-fit model of the canonical analysis.
In Sects. 7.1.1 and 7.1.2, we saw the significance of fluctuations in the population of some characteristic kinds of massive stars upon the spectral properties of a cluster as moderately massive as the one of NGC 588. This issue can be generalized to all sorts of very massive stars, that can radiate intensely in the optical and/or ionizing spectral range and whose numbers are subject to the largest relative statistical fluctuations.
![\begin{figure}
\par\includegraphics[angle=90,width=8.4cm,clip]{0136fg35.eps}\par...
...pace*{2mm}\includegraphics[angle=90,width=8.2cm,clip]{0136fg36.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg116.gif) |
Figure 19: Top: SEDs of the whole cluster (full line), of the 6 brightest stars (dashed line) and of the remaining 167 stars (dotted line). Bottom: ratio of the brightest 6 stars SED (full line) and of the remaining 167 star SED (dotted line) to the total SED. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{0136fg37.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg118.gif) |
Figure 20:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=8.6cm,clip]{0136fg38.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg119.gif) |
Figure 21:
Star-by-star constructed SED (full lines), and SEDs of the analytical
populations, for Z=0.008 and
|
| Open with DEXTER | |
In Fig. 19 are plotted the SEDs of the whole cluster, of the 6 brightest stars (in filter F439W) and of the remaining 167 stars, as well as
the fractional contribution of the 6 brightest stars to the total SED. It is
evident that these 6 stars are very influential on the total spectrum, whether
at observable wavelengths (where they are responsible for about half the total
flux) or in the high-energy range, where they generate approximately two thirds
of the hydrogen-ionizing photons, even though they constitute only about 1/30 of the whole set of detected stars. These 6 stars, which also are the most
massive ones, are specifically the stars situated in the temperature-luminosity
zone that varies significantly within the first few millions of years of the
cluster, as one can see in Fig. 15. Figure 20 shows the
![]() diagram of the detected stars. The most striking
feature is the quasi-vacuousness of the curve in the region of the 6 dominating
stars, in particular the BSG branch that drops towards negligible Lyman
continuum at high band F439W luminosities. If the IMF of the cluster were
complete, as assumed in a classical model of stellar population, then the main
spectral diagnostic,
diagram of the detected stars. The most striking
feature is the quasi-vacuousness of the curve in the region of the 6 dominating
stars, in particular the BSG branch that drops towards negligible Lyman
continuum at high band F439W luminosities. If the IMF of the cluster were
complete, as assumed in a classical model of stellar population, then the main
spectral diagnostic,
![]() ,
would be significantly lower than what
we observe at the age and metallicity we derived from the star-by-star
approach. This is illustrated in Fig. 21, where the SED found with
the classical approach is also shown. In this figure, we can appraise the
significance of the drop of the Lyman-to-optical continuum ratio, as well as
the increase of the magnitude of the Balmer jump and the decrease of the global
slope of the SED at observable wavelengths, when passing from the star-by-star
SED to the one of the analytical model.
,
would be significantly lower than what
we observe at the age and metallicity we derived from the star-by-star
approach. This is illustrated in Fig. 21, where the SED found with
the classical approach is also shown. In this figure, we can appraise the
significance of the drop of the Lyman-to-optical continuum ratio, as well as
the increase of the magnitude of the Balmer jump and the decrease of the global
slope of the SED at observable wavelengths, when passing from the star-by-star
SED to the one of the analytical model.
In Sects. 7.1 and 7.2, we saw the significant
consequences of the deviation of the actual (discrete and statistically
fluctuating) IMF of NGC 588 from the mean and continuously sampled
analytical one. In this cluster of ![]() 6000
6000 ![]() (integrated in the
interval of individual initial stellar masses 1-58
(integrated in the
interval of individual initial stellar masses 1-58 ![]() ), the stars
massive enough to rule its spectral properties, whether observable (
), the stars
massive enough to rule its spectral properties, whether observable (
![]() ,
Balmer jump, etc.) or not (e.g., hardness of the Lyman continuum),
are only 6, which can easily explain the encountered issues.
,
Balmer jump, etc.) or not (e.g., hardness of the Lyman continuum),
are only 6, which can easily explain the encountered issues.
![\begin{figure}
\par\includegraphics[angle=90,width=8.6cm,clip]{0136fg39.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg122.gif) |
Figure 22:
Histogram of
|
| Open with DEXTER | |
In order to estimate quantitatively the uncertainties related to the
fluctuations of massive stellar populations of same age, metallicity and IMF as
the ones of NGC 588, we performed a simple Monte-Carlo simulation
where the mean IMF of Sect. 6.4 was divided into 0.01 ![]() wide
mass bins, in which 1977 stars (1977 being the number of stars integrated in
the mean IMF) were randomly distributed, according to the probability of each
bin to be filled with a given star, this probability being given by the mean
analytical IMF. We performed 106 such Monte-Carlo realizations. This model
assumes the stars of the cluster to have random masses, uncorrelated to each
other (a simplification that may be corrected when the actual properties of
star formation in clusters are better known), and following a likelihood
function given by the mean IMF. For each random distribution, we calculated the
resulting
wide
mass bins, in which 1977 stars (1977 being the number of stars integrated in
the mean IMF) were randomly distributed, according to the probability of each
bin to be filled with a given star, this probability being given by the mean
analytical IMF. We performed 106 such Monte-Carlo realizations. This model
assumes the stars of the cluster to have random masses, uncorrelated to each
other (a simplification that may be corrected when the actual properties of
star formation in clusters are better known), and following a likelihood
function given by the mean IMF. For each random distribution, we calculated the
resulting
![]() ;
we found
;
we found
![]() to follow a
roughly Gaussian distribution with standard deviation 0.24 dex (as also
obtained analytically by Cerviño et al. 2002). The histogram of
to follow a
roughly Gaussian distribution with standard deviation 0.24 dex (as also
obtained analytically by Cerviño et al. 2002). The histogram of
![]() is
shown in Fig. 22. According to the simulation, the
maximum-likelihood value of
is
shown in Fig. 22. According to the simulation, the
maximum-likelihood value of
![]() is 68 Å, and the 90% likelihood interval for this quantity is as wide as 40-244 Å. The observed
value
is 68 Å, and the 90% likelihood interval for this quantity is as wide as 40-244 Å. The observed
value
![]() Å is marginal, the likelihood of realizing
a value greater than or equal to this one being
Å is marginal, the likelihood of realizing
a value greater than or equal to this one being ![]() 1%. This likelihood
is of same order of magnitude as the 0.4% one to observe, as we do, no BSG and 2 WNL stars, given the mean IMF of the cluster.
1%. This likelihood
is of same order of magnitude as the 0.4% one to observe, as we do, no BSG and 2 WNL stars, given the mean IMF of the cluster.
Using the same kind of simulations, we established that, for the same IMF slope
and cutoffs, the fluctuation of
![]() would still be
would still be ![]() 20%
for a cluster as massive as
20%
for a cluster as massive as
![]()
![]() .
.
In this work we have gathered the widest range of data available for the stellar cluster ionizing the giant H II region NGC 588, both imaging and spectroscopy, covering a wide wavelength range from the ultraviolet to the far red.
In the first part (Sects. 2 and 4), we showed the
importance of endeavoring to obtain and process as numerous and accurate
observable data as possible, in order to constrain models of the most common
form of OB associations within the limits of the relevance of these models,
rather than within the measurement errors and uncertainties. We discussed the
problems encountered when fitting overall integrated nebular and stellar
parameters, by means of a standard evolutionary population synthesis approach.
In particular, by assuming an analytical IMF, the best fit model predicts the
presence of BSGs simultaneous to the required (since observed) existence of WNs, and consequently predicts too a low value of
![]() .
This
failure can be imputed mainly to two physical issues: the still important
uncertainties in our knowledge of the evolution of massive stars (as
reviewed by Massey 2003), and the effects associated with IMF sampling (as
studied by Cerviño et al. 2002). We explored the latter in Sect. 5 through
7. In Sect. 6, we achieved quite a robust model of
the cluster, and obtained good results. However, in this approach, we inferred
a cluster age 50% higher than with the analytical approach, and a mass twice
as large. In Sect. 7, we estimated the effects of departure of
the observed set of stars from the one derived from the full sampling of the
mean cluster IMF. In particular, we established that a diagnostic such as
.
This
failure can be imputed mainly to two physical issues: the still important
uncertainties in our knowledge of the evolution of massive stars (as
reviewed by Massey 2003), and the effects associated with IMF sampling (as
studied by Cerviño et al. 2002). We explored the latter in Sect. 5 through
7. In Sect. 6, we achieved quite a robust model of
the cluster, and obtained good results. However, in this approach, we inferred
a cluster age 50% higher than with the analytical approach, and a mass twice
as large. In Sect. 7, we estimated the effects of departure of
the observed set of stars from the one derived from the full sampling of the
mean cluster IMF. In particular, we established that a diagnostic such as
![]() is very sensitive to the BSG content of the cluster, and that
the hardness of the ionizing radiation, an unobservable spectral property that
plays an important role in photoionization models of nebulae, depends
significantly on the WR content. More generally, we assessed that the radiation
field of NGC 588 is one among a large variety of possible SEDs for
such a cluster, and that this is easily explained by the following statements:
the most massive stars dominate the flux of the cluster both in the
observable and Lyman-continuum wavelength ranges, show a wide variety of
spectral properties, and are subject to strong population fluctuations.
is very sensitive to the BSG content of the cluster, and that
the hardness of the ionizing radiation, an unobservable spectral property that
plays an important role in photoionization models of nebulae, depends
significantly on the WR content. More generally, we assessed that the radiation
field of NGC 588 is one among a large variety of possible SEDs for
such a cluster, and that this is easily explained by the following statements:
the most massive stars dominate the flux of the cluster both in the
observable and Lyman-continuum wavelength ranges, show a wide variety of
spectral properties, and are subject to strong population fluctuations.
We suggest three practical considerations that will help to better understand and characterize the evolutionary stage of massive ionizing star clusters: (i) A "best fit model'' statement may not be very meaningful per se, and should not make us complacent that it implies the best solution. (ii) When possible, use color-magnitude diagrams to obtain the integrated properties of the ionizing cluster, as opposed to assuming a perfectly sampled mass function. (iii) Assess the importance of the few most massive stars on the overall SED of the cluster, both at ionizing and at non-ionizing wavelengths; this can be easily done by applying the lowest luminosity limit criteria established by Cerviño et al. (2003) and Cerviño & Luridiana (2004). If possible, use Monte-Carlo population models, provided they are relevant, and pending a more mature development of this approach to population synthesis.
We also established that the initial mass distribution of the stars detected in NGC 588 is compatible with a Salpeter IMF, if it is treated as a stochastic process.
Finally, in this work, we used the very common hypothesis of instantaneous starburst. However, recent works, like the one of Tenorio-Tagle et al. (2003), show that star formation in massive clusters spans time ranges such that the instantaneous formation hypothesis may not be valid for them. This statement does not call into question the significance of the disturbances caused by fluctuations in the high mass end of the IMF, but it is an additional uncertainty that is worth accounting for in further models of massive star clusters.
Acknowledgements
This work could not have been done without the contemporary direct access to a variety of publicly available astronomical archives. It is based on observations taken with the 3.5 m telescope at the Centro Astronómico Hispano-Alemán (CAHA, Calar Alto, Almería), on observations taken with the NASA/ESA Hubble Space Telescope, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555, on INES data from the IUE satellite, and on data from the ING Archive taken with the JKT operated on the island of La Palma by Isaac Newton Group of Telescopes in the Spanish Observatorio del Roque de Los Muchachos of the Instituto de Astrofísica de Canarias.
Funding was provided by French CNRS Programme National GALAXIES, by Spanish grants AYA-2001-3939-C03-01, AYA-2001-2089, and AYA2001-2147-C02-01, by Mexican grant CONACYT 36132-E, and by French-Spanish bi-lateral program PICASSO/Acción Integrada HF2000-0143.
We also thank Daniel Schaerer for his help on the WR bumps. We are also grateful to Miguel Mas-Hesse and the referee of the present article for careful reading and very useful comments and suggestions.
Table 1: Journal of Observations.
Table 2:
Observed and model colors with filter F547M as the zero point. The
observed colors are here corrected for foreground Galactic extinction. The
three models (a), (b) and (c) shown here stand for
![]()
![]() ,
Z=0.004, and respectively,
,
Z=0.004, and respectively, ![]() ,
1 and 2.35 and
,
1 and 2.35 and ![]() ,
3 and 4 Myr. We
also show the three tested extinction laws in the form
,
3 and 4 Myr. We
also show the three tested extinction laws in the form
![]() .
The color differences
.
The color differences
![]() between the observations and a given model were to be well fit by a function of
the form
between the observations and a given model were to be well fit by a function of
the form
![]() for the tested extinction law to be accepted.
for the tested extinction law to be accepted.
Table 4: Positions, reddened absolute magnitudes, EB-V coefficients, and initial masses of the brightest stars of NGC 588. The extinction is discussed in Sect. 6.3.2, and the initial masses, in Sect. 6.4. aValues eventually set to 0.11.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0136fg01.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg138.gif) |
Figure 1: HST image of NGC 588 in filter F439W and the spectral slits. The peculiar stars (WNL, WN) are discussed in Sect. 6. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0136fg02.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg139.gif) |
Figure 2:
H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.1cm,clip]{0136fg15.eps}\hspace*{2mm}...
...17.eps}\hspace*{3mm}
\includegraphics[width=4cm,clip]{0136fg18.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg140.gif) |
Figure 9: Illustration of the dereddening procedure. The isochrone shown here was established for an age of 3.5 Myr and for Z=0.008. Panel a): observed (M439,M336-M547) diagram. Other panels: (M439,M170-M547) diagram dereddened with the (M439,M336-M547) one and the Galactic b), LMC c) and SMC d) laws. The dotted lines are the WR branches of the isochrone curves. The two WR stars are signalized by open circles. The arrows indicate the shift that the observational points undergo by if dereddened for EB-V=0.1. In the diagrams of panels b), c) and d), the error bars account for uncertainties of EB-V. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.1cm,clip]{0136fg19.eps}\hspace*{2mm}...
....eps}\hspace*{3.2mm}
\includegraphics[width=4cm,clip]{0136fg22.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg141.gif) |
Figure 10: Same as Fig. 9 for the isochrone of 4.5 Myr. |
| Open with DEXTER | |
| |
Figure 12: Observed vs. isochrone (M439,M170-M547) diagram for Z=0.004. The two WR stars are marked with open circles. The WR branches of the isochrones are shown as dashed lines. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=4.2cm,clip]{0136fg26.eps}\hspace*{2mm}...
....eps}\hspace*{2mm}
\includegraphics[width=4.2cm,clip]{0136fg29.eps}
\end{figure}](/articles/aa/full/2004/41/aa0136-04/Timg143.gif) |
Figure 13: Same as Fig. 12 for Z=0.008. |
| Open with DEXTER | |
At given age and metallicity, the isochrone data available from our programs
consist in an array of physical parameters of model stars, each line containing
the following parameters for the current star: the initial mass M, the
effective temperature
![]() ,
the bolometric luminosity
,
the bolometric luminosity
![]() ,
and the surface abundances, in particular the hydrogen one X. From these
parameters, we wanted to derive absolute magnitudes, to be compared to the
observations, from atmosphere models. In our case, four kinds of models were
available: Lejeune et al. (1997), Pauldrach et al. (2001), Hillier & Miller (1998) and black body. For each of
the first three kinds of models, whose selection for given physical parameters
was operated the same way as Starburst99 does, stellar fluxes are tabulated for
a fix array of wavelengths and for various effective temperatures; in the case
of Lejeune and Pauldrach models, the surface gravity g is also present. When
one of these grids is selected, Starburst99 performs nearest research
interpolation along the
,
and the surface abundances, in particular the hydrogen one X. From these
parameters, we wanted to derive absolute magnitudes, to be compared to the
observations, from atmosphere models. In our case, four kinds of models were
available: Lejeune et al. (1997), Pauldrach et al. (2001), Hillier & Miller (1998) and black body. For each of
the first three kinds of models, whose selection for given physical parameters
was operated the same way as Starburst99 does, stellar fluxes are tabulated for
a fix array of wavelengths and for various effective temperatures; in the case
of Lejeune and Pauldrach models, the surface gravity g is also present. When
one of these grids is selected, Starburst99 performs nearest research
interpolation along the
![]() axis (for Hillier grids) or in the
axis (for Hillier grids) or in the
![]() plane (for Lejeune and Pauldrach grids) to select a
flux array, and normalizes the latter for its total to be equal to
plane (for Lejeune and Pauldrach grids) to select a
flux array, and normalizes the latter for its total to be equal to
![]() .
This non-continuous interpolation method can be exploited to compute the
total spectrum of a model cluster, as the interpolation errors will tend to
cancel each other. However, the resulting isochrone curve in a
magnitude-magnitude of color-magnitude diagram will be irregular, with jumps
resulting from the sudden transition from an array of the exploited grid to
another. Here we suggest another form of interpolation to obtain more
accurately determined model magnitudes.
.
This non-continuous interpolation method can be exploited to compute the
total spectrum of a model cluster, as the interpolation errors will tend to
cancel each other. However, the resulting isochrone curve in a
magnitude-magnitude of color-magnitude diagram will be irregular, with jumps
resulting from the sudden transition from an array of the exploited grid to
another. Here we suggest another form of interpolation to obtain more
accurately determined model magnitudes.
Let us first consider the case of the black-body emission law: the wavelength-and-temperature-dependent flux is
 |
(A.1) |
| |
= |  |
(A.2) |
| = | 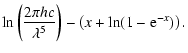 |
(A.3) |